Variations in Athlete Heat-Loss Potential Between Hot-Dry and Warm-Humid Environments at Equivalent Wet-Bulb Globe Temperature Thresholds

Abstract

Context

Many organizations associated with sports medicine recommend using wet-bulb globe temperature (WBGT)-based activity-modification guidelines that are uniform across the country. However, no consideration has been given to whether the WBGT thresholds are appropriate for different weather conditions, such as warm-humid (WH) relative to hot-dry (HD), based on known differences in physiological responses to these environments.

Objective

To identify if personnel in regions with drier conditions and greater evaporative cooling potential should consider using WBGT-based activity-modification thresholds that differ from those in more humid weather.

Design

Observational study.

Setting

Weather stations across the contiguous United States.

Main Outcome Measure(s)

A 15-year hourly WBGT dataset from 217 weather stations across the contiguous United States was used to identify particular combinations of globe temperature, wet-bulb temperature, and air temperature that produce WBGTs of 27.9°C, 30.1°C, and 32.3°C. A total of 71 302 observations were clustered into HD and WH environmental conditions. From these clusters, maximum heat-loss potential and heat-flux values were modeled at equivalent WBGT thresholds with various activity levels, clothing, and equipment configurations.

Results

We identified strong geographic patterns, with HD conditions predominant in the western half and WH conditions predominant in the eastern half of the country. Heat loss was systematically greater in HD than in WH conditions, indicating an overall less stressful environment, even at equivalent WBGT values. At a WBGT of 32.3°C, this difference was 11 W·m⁻² at an activity velocity of 0.3 m·s⁻¹, which doubled for an activity velocity of 0.7 m·s⁻¹. The HD and WH difference increased with the WBGT value, demonstrating that evaporative cooling differences between HD and WH conditions were even greater at a higher, rather than lower, WBGT.

Conclusions

Potential heat loss was consistently greater in HD than in WH environments despite equal WBGTs. These findings support the need for further clinical studies to determine the appropriate WBGT thresholds based on environmental and physiological limits to maximize safety while avoiding unnecessary limitations.

Key Points

• The environmental conditions affecting human heat stress depend on air temperature, humidity, wind speed, and radiation.

• Equivalent wet-bulb globe temperature (WBGT) values occurred across different environmental conditions (warm-humid versus hot-dry), which resulted in different abilities to cool the body during times of heat stress.

• Hot-dry environmental conditions offered a 13% to 17% greater ability to cool than warm-humid conditions at an equivalent WBGT value of 32.3°C and activity velocity of 0.3 to 0.7 m·s⁻¹.

• Heat-loss differences by environmental context increased as the severity of WBGT increased, as wind speed and player movement increased, and as the amount of clothing worn decreased.

Weather-based activity modification is a pillar of modern heat-safety policies.¹ A variety of measures are available for assessing heat stress; however, the wet-bulb globe temperature (WBGT) has been widely adopted for use in athletics, the military, and industry.^2–4 The WBGT, first developed by Yaglou and Minard,⁵ integrates the influences of air temperature (T_a), humidity, radiant heating, and wind speed to give a “first approximation of the heat stress on a person.”⁶ The WBGT is computed as a weighted average of the dry-bulb T_a, natural wet-bulb temperature (T_w), and globe temperature (T_g) as follows:

The particular thresholds for activity modification are set by different governing bodies (eg, Racinais et al⁷). A critical WBGT threshold for event cancellation that is common among many heat guidelines is 32.3°C (90.1°F). For the current study, we considered activity-modification thresholds for athletes recommended by the American College of Sports Medicine (ACSM)² and the National Athletic Trainers' Association (NATA).⁸ These thresholds are based on those developed by the US military⁹ using studies of exertional heat illness (EHI) incidence among military personnel¹⁰ and slightly adapted for specific sports and activities, clothing, and acclimatization status.

Using standardized thresholds and the related activity or clothing assumptions allows us to best compare study results. The ACSM² and NATA⁸ have recommended 1 set of activity- and clothing-based guidelines depending on the WBGT and acclimatization status but have not considered whether adjustments to this threshold are appropriate based on the environmental context or climate regime. Researchers^11–14 have suggested, however, that different meteorologic configurations of temperature and humidity at the same WBGT have different effects on human heat balance. Specifically, Budd¹² reported that the WBGT could underestimate heat stress in high-humidity and low-wind conditions but overestimate it in very dry conditions with free evaporation, although the WBGT was equivalent for both situations. Such findings are similar to those of Ramanathan and Belding¹³ in 1973 at a fixed WBGT value. These routine differences between humid- and dry-heat conditions may occur because the initial testing environment and evaluations to create the current thresholds and WBGT equation occurred in very humid (Virginia, South Carolina)^4,5 as opposed to hot and dry environments. Therefore, WBGT-based activity-modification thresholds may need to be regionally adapted to account for different environmental conditions. For instance, the T_w is lower in the western United States and higher in the east, indicating that the critical need to cool via perspiration would function with different efficiencies depending on the region.¹⁵ Appropriate thresholds are important for safety and to avoid the opportunity costs of lost work, training, or competition if the local weather permits safe participation.¹¹

We used a large multiyear dataset of modeled hourly WBGT values from across the contiguous United States¹⁶ in conjunction with a human heat-loss model¹⁷ to study physiological responses to equivalent WBGT levels in regions that present distinct environmental contexts based on T_a, relative humidity, and radiation. The purpose of our study was to assess whether personnel in regions of the country with drier conditions and greater evaporative cooling potential should consider using different WBGT thresholds than those in regions with more humid environments. We hypothesized that, for an equivalent WBGT, individuals would experience less heat strain in hot-dry (HD) than in warm-humid (WH) environments. We sought to answer the following questions: How does maximum potential heat loss differ in an HD versus a WH environment under equivalent WBGT values? What are the main avenues of heat exchange (ie, convective, radiative, or evaporative) in each environmental type during stressful environmental conditions, as defined by a constant WBGT value? As we investigated these questions within the environmental contexts, we also considered different clothing configurations and activity velocities.

METHODS

Study Scenario

We considered the human energy balance and the influence of clothing type and movement of an individual (or activity velocity) in HD and WH environments. We examined 3 WBGT thresholds (27.9°C, 30.1°C, and 32.3°C²) for which activity modifications are recommended by the ACSM for fit, acclimatized athletes and emphasize the findings at the 32.3°C threshold throughout the main results herein, as 32.3°C is the level at which the ACSM recommends practice activities be cancelled for an “acclimatized person in non-continuous activity in T-shirt, shorts, sneakers.”² Therefore, our main modeling scenario was an American football lineman in shorts and T-shirt with an activity velocity of 0.3 m·s⁻¹. We further modeled different clothing and equipment configurations and activity velocities for football and modeled a scenario in soccer. All further results are presented in Supplemental Tables 1–11 and Supplemental Figures 1 and 2. Football players were the focus because they are highly susceptible to EHIs and linemen, in particular, have the highest incidence of fatal exertional heat-stroke events.^18,19 Our study did not involve human participants and, therefore, did not require institutional review board approval.

We used a 15-year (1991–2005) dataset of modeled hourly outdoor sun-exposed WBGTs for 217 weather stations located across the contiguous United States.¹⁶ Observed wind speeds were adjusted from 10-m to 2-m heights using a mathematical logarithmic wind-profiling function that accounts for surface friction to better represent conditions on a practice field.²⁰ Modeled WBGT components took the place of observations, as they are not routinely measured together and no observational WBGT dataset has high spatial and temporal resolutions. The model of Liljegren et al²¹ uses thermodynamic principles of heat exchange to compute the T_g and T_w from T_a, humidity, wind speed, and solar radiation. The T_g and T_w are combined with the T_a to calculate the WBGT (Equation 1). Additional details, equations, and code for the model can be found in Liljegren et al.²¹ This model is considered either the best or among the best models for computing outdoor, nonshaded WBGT.²² It has been well tested against other models and in a variety of climates across the United States, which was of particular interest to us. Specifically, the model has been shown to accurately estimate measurements to within 1°C in both dry (Yuma, AZ; Deseret, UT; Pueblo, CO; Umatilla, OR) and humid (Anniston, AL; Griffin, GA; Pine Bluff, AR; Blue Grass, KY) climates.^21,23 Meteorologic input data for the model of Liljegren et al²¹ were acquired from the National Solar Radiation Database.²⁴

In total, there were 5505 WBGT values of 32.3°C, 24 273 values of 30.1°C, and 41 524 values of 27.9°C. Various combinations of T_w, T_a, and T_g may have led to these particular WBGT values. A 2-step clustering approach was used to identify groups in this database with common combinations of the 3 variables that composed the final WBGT values (ie, T_w, T_a, and T_g) via SPSS Statistics TwoStep cluster analysis (version 26; IBM Corp, Armonk, NY). For example, dry areas were expected to produce higher T_g values and lower T_w values than more humid regions of the country. We used this 2-step clustering approach because it is well suited for large datasets. Two-step clustering describes a hybrid technique of identifying groupings via running preclustering and then a hierarchical method. Several cluster sizes (ie, 2, 3, and 4 clusters) were tested for cluster quality using the silhouette coefficient, which ranges from −1 to +1.²⁵ A high positive coefficient (close to 1) indicates that a value is well matched to its own cluster and poorly matched to other clusters. We found that 2 clusters had the highest silhouette coefficients for all 3 WBGT thresholds, with silhouette values of 0.7 for 32.3°C and 0.6 for both 30.1°C and 27.9°C. Therefore, for the analysis, we used 2 clusters, which are denoted in a comparative sense as HD and WH (Figure 1) based on relative differences in humidity and temperature. Differences in T_w, T_a, and T_g between the 2 clusters and geographic patterns were investigated. Student t tests were calculated to determine differences in weather variables and energy balance components within the 2 clusters (HD versus WH) at a given WBGT threshold, using a P value of <.01. All statistical tests and clustering were conducted using SPSS.

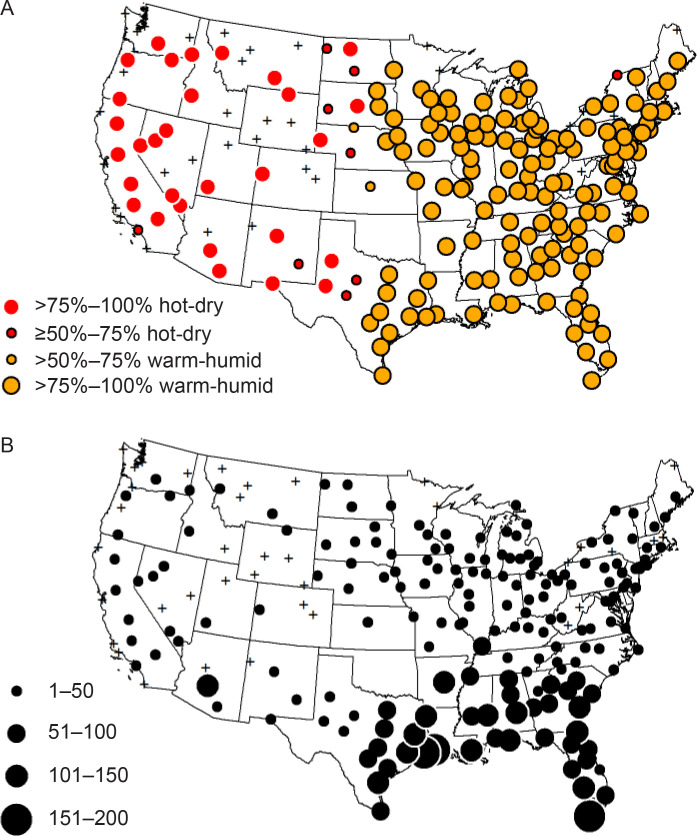
Figure 1.

A, Percentage of 32.3°C wet-bulb globe temperatures (WBGTs) classified as hot-dry or warm-humid. B, The count of 32.3°C WBGT values during the years 1991–2005. Approximately 90% of the 32.3°C WBGT thresholds reached were in the warm and humid areas of the country, focused heavily in the southeast. Crosses indicate locations with no 32.3°C WBGTs.

Human Heat-Loss Modeling

We calculated the maximum heat-loss potential (H_total) for all instances of the 3 WBGT thresholds (eg, heat-loss potential was calculated for 41 524 instances in which the WBGT was 27.9°C). To model H_total, we applied a human heat-balance approach based on the work of Parsons²⁶ and applied by Deren et al.¹⁷ The final output of the model provides a value of H_total by assuming that skin wettedness is 1.0 (maximal sweat rate). We further assumed that mean skin temperature was equal to 35.4°C based on empirical results in football players as reported by Deren et al.¹⁷

We used 3 clothing and equipment configurations (shorts and T-shirt [shorts], shells, and full gear [full]) and 2 activity velocities (0.7 and 0.3 m·s⁻¹). The activity velocities were chosen based on the average self-generated speed by nonlinemen during wind sprints (approximately 0.7 m·s⁻¹) and the average speed of linemen during individual drills (approximately 0.3 m·s⁻¹).¹⁷ Although we focused the results on the effect of a 32.3°C WBGT in an acclimatized lineman (activity velocity = 0.3 m·s⁻¹) in the shorts configuration, specific findings for different clothing and equipment configurations, activity velocities, and lower thresholds are provided in Supplemental Tables 1–8. Finally, H_total at the 3 WBGT thresholds was also tested for soccer players, with the modeling specifics and results presented in Supplemental Tables 9–11.

Sensible Heat Loss

Sensible heat loss is determined as the flux (in W·m⁻²) of combined convective and radiative heat loss at the skin:

where C is convective heat loss, R is radiative exchange, 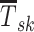is mean skin temperature, t_o represents the mean operative temperature (in °C; equation presented in this subsection), R_cl is the clothing resistance (in m²·K·W⁻¹), f_cl is the clothing area factor, and h is the combined heat-transfer coefficient. The clothing resistance and clothing area factor values were previously determined by McCullough and Kenney²⁷ using thermal manikins and 3 equipment configurations (shorts, shells, and full gear). The clothing resistance values applied in our study were 0.05425 m²·K·W⁻¹ for shorts, 0.09765 m²·K·W⁻¹ for shells, and 0.15190 m²·K·W⁻¹ for full, and the clothing area factor values were 1.1085 for shorts, 1.1953 for shells, and 1.3038 for full (Table 1). The combined heat-transfer coefficient value was calculated as the sum of the convective and radiative heat-transfer coefficients (h_c and h_r, respectively), where the convective heat-transfer coefficient (in W·m⁻¹·K⁻¹) was calculated for activity velocities (v_a) > 0.2 m·s⁻¹ as follows:

and the radiative heat-transfer coefficient (in W·m⁻²·K⁻¹) was calculated as

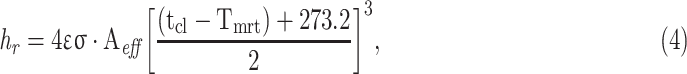where 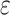is the emissivity of the clothed body surface (approximately 0.95); 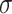is the Stefan-Boltzmann constant (5.6710⁻⁸ W·m⁻²·K⁻⁴); A_eff is the effective radiative area, assumed to be 0.73 for standing position²⁶; t_cl is the mean temperature of the clothed body; and T_mrt is the mean radiant temperature. The t_cl was determined iteratively using a radiative heat-transfer coefficient and an initial mean temperature of the clothed body of 0.0, for which a final mean temperature of the clothed body was obtained (from Equation 4) until the change in the mean temperature of the clothed body between 2 sequential values was <0.01, as in the work of Parsons.²⁶

Table 1.

Variables Used to Estimate Resistance to Heat and Vapor Exchanges Due to Clothing Worn by Football Players^27,28,a

Clothing and Equipment Configuration	Clothing Resistance, m2·K·W−1	Evaporative Heat-Transfer Resistance of Clothing, m2·kPa·W−1	Clothing Area Factor, Unitless
Shorts	0.05425	0.0220	1.1085
Shells	0.09765	0.0170	1.1953
Full	0.15190	0.0090	1.3038

^aFootball players were tested at 2 activity velocities (0.7 m·s⁻¹ and 0.3 m·s⁻¹).

The mean radiant temperature, which is the sum of all short- and longwave radiation fluxes to which the human body is exposed, was calculated based on a standard black globe as follows²⁹:

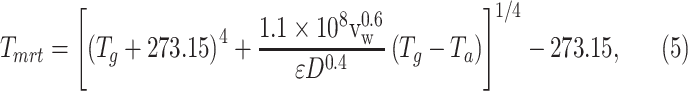where T_g is determined via the model of Liljegren et al,²¹ v_w is wind velocity, and D is the diameter of a standard black globe (0.15 m).

From these variables, the mean operative temperature was calculated as

Evaporative Heat Losses

The maximum evaporative capacity of the ambient environment (E_max), assuming skin wettedness (ω) is 1.0 (hence, the skin evaporation is equal to E_max), was calculated as follows:

where P_sk,s is the water vapor pressure at skin temperature (in kPa), which is assumed to be fully saturated at skin temperature; P_a is water vapor pressure in air (in kPa); R_e,cl is the evaporative heat-transfer resistance of the 3 clothing ensembles, as previously measured by van Marken Lichtenbelt et al²⁸ (see Table 1 for values); and h_e is the evaporative heat-transfer coefficient (in W·m⁻²·kPa⁻¹) calculated as follows:

Finally, H_total was computed by summing the sensible and evaporative heat losses:

Given this equation, any positive value is considered a loss of heat and any negative value is considered a gain of heat. In our study, E_max was always a heat loss (positive value in Equation 9), whereas (C + R) may be negative (a gain of sensible heat) or positive (a loss of sensible heat). In general, as the H_total increases, the stress of the environment decreases. The H_total will be highest when the E_max flux is high (ie, under conditions with a higher gradient between water vapor pressure at skin temperature and water vapor pressure in air and low clothing resistance) and the gradient between skin temperature and mean operative temperature is large.

The (C + R) component of H_total, as determined in Equation 9, can also be broken down to determine the contributions from each C and R³⁰:

Excess Heat and Core Temperature Estimations for Football Scenarios

To provide an example of the effect of heat-loss potential on core body temperature in different environmental contexts, we applied energy-balance principles and average metabolic expenditures to produce excessive heat in W·m⁻²:

where B is the energy balance, M_act is the metabolic intensity of the individual (in W·m⁻²), and f is a correction for the heat loss consumed through breathing, which was calculated as

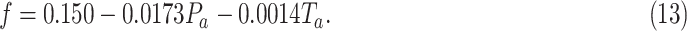For the purposes of our study, we calculated the core temperature rise over 5 minutes based on an average individual metabolic intensity of 465 W·m⁻² (8 metabolic equivalents) and body surface area of 2.5 m² based on empirical data.¹⁷

RESULTS

Wet-Bulb Globe Temperature Component Clustering

We examined the hourly dataset of 217 weather stations (amounting to 71 302 WBGT values) to identify combinations of T_g, T_w, and T_a that would produce WBGTs of 27.9°C, 30.1°C, and 32.3°C. For all 3 cases, we observed 1 cluster of data that could be characterized as HD and 1 that could be characterized as WH. The meteorologic characteristics of these clusters for a WBGT of 32.3°C are shown in Table 2, and the geographic variability is shown in Figure 1. Across all thresholds, the WH cluster was characterized by lower radiant heating and incoming solar radiation and lower T_a but greater atmospheric moisture than the HD cluster. At the 32.3°C threshold, for instance, a typical T_a value in the HD cluster was 37.1°C, compared with 32.7°C in the WH cluster; respective values for vapor pressure were 1.67 kPa and 2.8 kPa and for solar radiation were 832 W·m⁻² and 765 W·m⁻². These differences resulted in the HD cluster having average T_g values almost 7°C higher, whereas the T_w values were about 3°C cooler than in the WH cluster. Wind speeds also differed slightly, with a 0.5 m·s⁻¹ greater 2-m wind speed in WH conditions. The magnitude of differences among the 3 WBGT temperature components decreased for 27.9°C and 30.1°C, but the overall patterns were similar between clusters.

Table 2.

Comparison of Globe Temperature, Air Temperature, Natural Wet-Bulb Temperature, 2-m Wind Speed, Incoming Solar Radiation, Relative Humidity, and Vapor Pressure Between Hot-Dry (HD) and Warm-Humid (WH) Clusters at an Equivalent 32.3°C Wet-Bulb Globe Temperature

Measure	Cluster, Mean ± SD		Difference Between Clusters (HD-WH), Mean
	Hot-Dry	Warm-Humid
Globe temperature, °C	55.0 ± 2.7	48.1 ± 2.3	6.9
Air temperature, °C	37.1 ± 3.7	32.7 ± 2.4	4.4
Natural wet-bulb temperature, °C	25.1 ± 0.9	27.7 ± 0.7	−2.6
2-m wind speed, m·s−1	1.4 ± 1.1	1.9 ± 1.1	−0.5
Incoming solar radiation, W·m−2	832 ± 124.7	765 ± 140.4	67.3
Relative humidity, %	27.0 ± 8.3	57.1 ± 9.9	−30.0
Vapor pressure, kPa	1.67 ± 0.40	2.80 ± 0.34	−1.13

Furthermore, at all 3 thresholds, the Student t test indicated differences among each of the cluster components (ie, T_g, T_w, and T_a; P < .01). Importantly, the WH cluster was responsible for most of the WBGT thresholds reached in the United States (Figure 1B). Specifically, of the 5505 instances when a 32.3°C WBGT occurred in the United States, 90% of these were in the WH cluster. Additionally, WH conditions occurred in 67% of 30.1°C WBGTs and 63% of 27.9°C WBGTs.

We observed strong geographic patterns in the WBGT clusters. The HD conditions were focused in the western half of the country, whereas WH conditions predominated in the eastern half. The pattern was strongest for 32.3°C: the configuration of weather conditions mostly clustered within the HD cluster in the south (75%–100% of the time) and the WH cluster in the east (75%–100% of the time; Figure 1A). At the 2 lower WBGT thresholds, this geographic pattern was still evident, but the percentage of HD conditions increased somewhat for many stations in the eastern half of the country. In Atlanta, Georgia, for instance, WH conditions occurred in 63% of cases at 27.9°C, 56% at 30.1°C, and 92% at 32.3°C WBGT.

Human Heat-Loss Potential at an Equivalent WBGT of 32.3°C

Here, we focus the results on the WH versus HD environmental differences at a WBGT of 32.3°C for an acclimatized player moving at an activity velocity of 0.3 m·s⁻¹ wearing a T-shirt, shorts, and sneakers,² reviewing H_total and each energy balance flux of interest. Full results for the WBGT thresholds of 27.1°C and 30.1°C, as well as for soccer, clothing differences, and activity velocity changes, are presented briefly here and provided fully in Supplemental Tables 1–11.

Under the real-world meteorologic conditions tested, evaporative heat loss, convective heat loss, and radiative heat gain generally displayed similar results as the WBGT components of T_w, T_a, T_g, respectively, between the HD and WH environmental types (Figure 2). For example, at a WBGT of 32.3°C, greater evaporative heat loss occurred in HD locations due to lower vapor pressure, the highest convective heat loss was present in WH locations due to lower T_a, and the highest radiative heat gain was present in HD conditions due to high T_g and T_a.

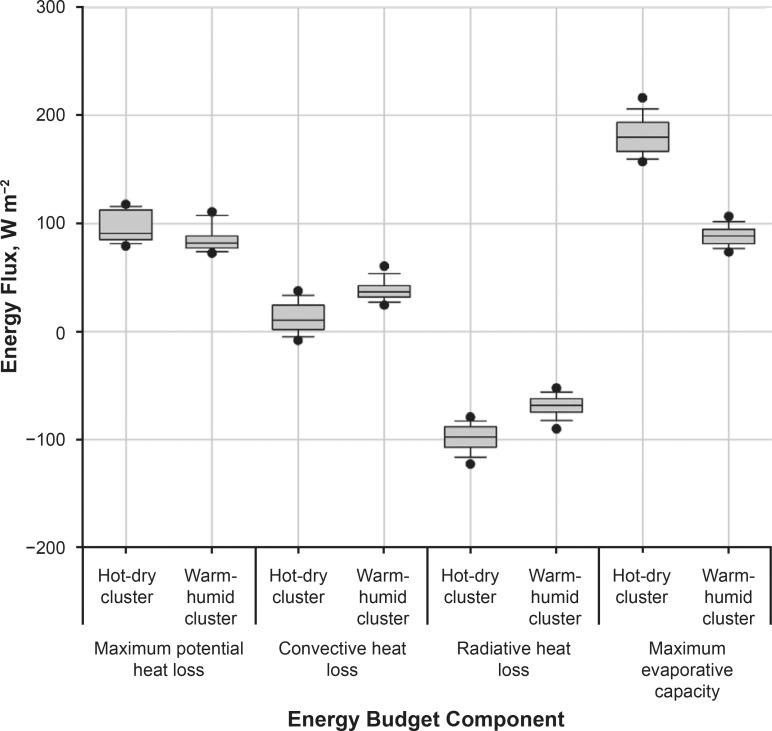
Figure 2.

Comparison of energy budget components between hot-dry and warm-humid clusters for a football player in T-shirt and shorts at 0.3 m·s⁻¹ movement speed. Each box represents the upper and lower quartiles, the line within each box is the median, the whiskers are the 90th and 10th percentiles, and the dots outside the whiskers represent the 95th and 5th percentiles.

When balanced to provide an H_total (Equation 9), the ability to lose heat from the body to the environment was greater in HD conditions than in WH conditions, whereby the change in H_total was 11.1 W·m⁻²; however, this value more than doubled to 22.8 W·m⁻² if we increased the activity velocity from 0.3 to 0.7 m·s⁻¹, which was primarily due to the effect of air movement increasing the vapor pressure gradient to increase E_max. Importantly, these differences in heat-loss potential were present although the WBGT was equivalent. Moreover, under the combined average T_a and relative humidity (RH) values at an equivalent WBGT of 32.3°C, players in the WH environment (mean T_a = 32.7°C, RH = 57.1%) would experience uncompensable heat stress while wearing full gear or shells, whereas in average HD conditions (mean T_a = 37.1°C, RH = 27%), heat stress would be uncompensable only when players wore full gear.¹⁴

The E_max presented the highest magnitude of energy exchange (via heat loss) to the environment compared with convective and radiative heat losses, which was partly due to assuming the maximum sweat rate in all conditions (skin wettedness = 1.0). The E_max was on average 3.0- to 5.5-fold higher than convective heat loss (approximately 5.5-fold under HD conditions and 3.3-fold in WH conditions) across all clothing ensembles. The cooling from evaporative heat loss was merely 1.6-fold that of radiative heat gain, a magnitude that was equal across HD and WH conditions.

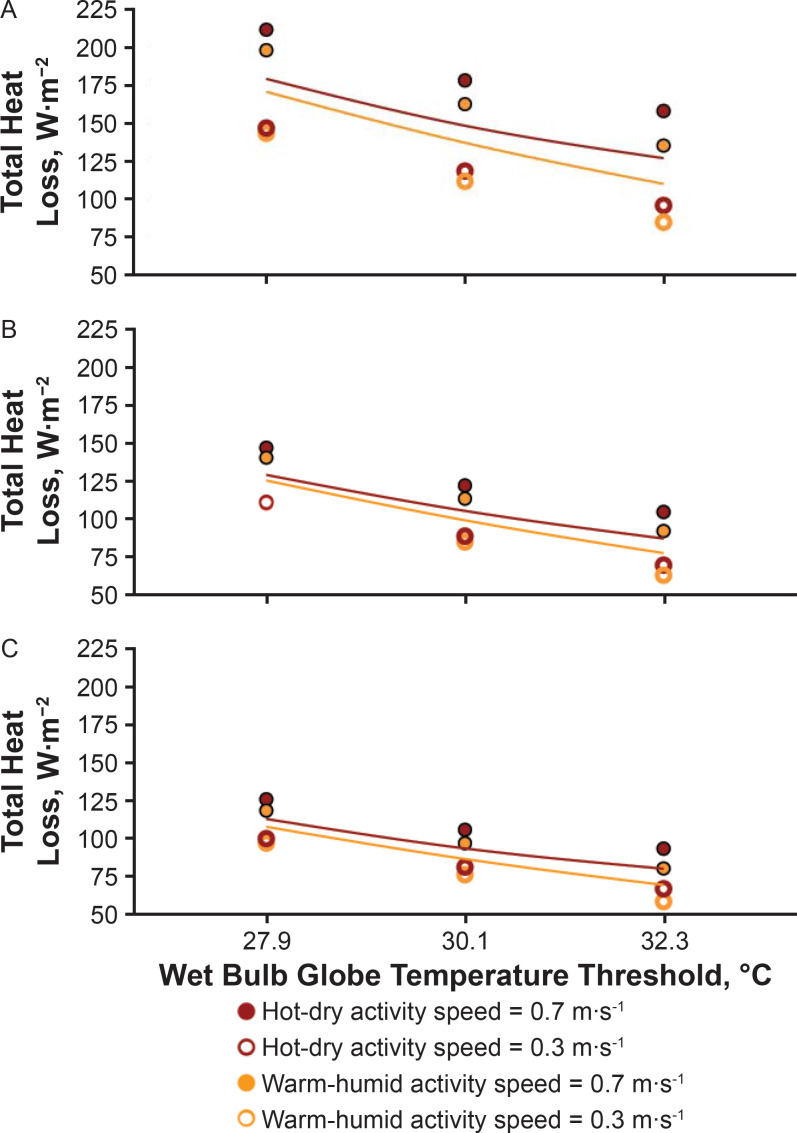
On average, E_max was higher during HD conditions at an activity velocity of 0.3 m·s⁻¹, resulting in 50.1 W·m⁻² excess energy compared with WH conditions (in shorts). These differences were less when clothing was added (38.2 W·m⁻² for shells, 33.7 W·m⁻² for full). Furthermore, the differences were considerably higher if we increased the activity velocity to 0.7 m·s⁻¹ (65.9, 46.0, and 39.1 W·m⁻² for shorts, shell, and full clothing, respectively), indicating greater evaporative cooling ability at higher activity velocities. Moreover, the differences in total heat loss between the WH and HD conditions were also greatest at 32.3°C (Figure 3).

Figure 3.

Total heat-loss potential in hot-dry and warm-humid conditions for each wet-bulb globe temperature threshold value (27.9°C, 30.1°C, and 32.3°C) and each football clothing and equipment configuration worn at practices. A, T-shirt and shorts. B, Shells. C, Full gear. Dots indicate average at activity velocities of 0.7 m·s⁻¹ and 0.3 m·s⁻¹; solid lines show the overall average for both velocities for a given environmental type.

Conversely, the convective heat loss was always higher in WH conditions, averaging 10.3 W·m⁻² more than in HD conditions (shorts; activity velocity = 0.3 m·s⁻¹) because of lower T_a and slightly higher wind speeds. The ability to lose heat through convection was diminished as the T_a increased, and this convective loss switched to a gain (shown as negative values in Figures 2 and 3) in 19.7% of HD simulations at 32.3°C WBGT, which occurred when T_a rose above the mean temperature of the clothed body (Equation 10). Finally, radiative heat gain was 28.6 W·m⁻² higher (24.9 W·m⁻² for all clothing ensembles) in HD environments because of a higher overall incoming solar radiation load. Solar radiation increased the mean radiant temperature, which increased radiative heat transfer.

Because the wind speeds over the 15-year period were slightly higher on average in the WH than in the HD condition, the mean radiant temperature experienced by a player was also slightly higher in the WH condition, relatively speaking (based on Equation 5), which slightly diminished the differences between the HD and WH conditions. However, the effect of higher wind speed in WH conditions on evaporative and convective heat losses greatly overrode the radiative exchange differences in the HD and WH conditions and, assuming equivalent wind speed and activity velocity in the HD and WH conditions, caused an even greater difference in H_total than reported in the real-world environments (27 versus 11 W·m⁻²). This difference was primarily owing to changes in E_max and convection. We provide the full methods and results of this example in Supplemental Figure 2.

Summary of Total Heat Loss by Activity Velocity, WBGT Threshold, and Clothing

The general patterns in the difference between H_total in WH versus HD conditions were as follows (see Figure 3):

• As the WBGT threshold increased from 27.9°C to 32.3°C, the difference in the heat-loss potential between HD and WH conditions increased, demonstrating that at higher WBGT levels, the ability to cool through evaporation in HD conditions was comparatively even more effective than at a lower WBGT.

• A greater amount of clothing limited the ability to cool because of the added clothing resistance or proportion of the body covered (or both), which was a more important factor in humid environments, which have the added evaporative restriction because of a low vapor pressure deficit between skin and air. Our data also showed that the evaporative difference between the HD and WH environments at the same clothing level increased as the WBGT value rose from 27.9°C to 32.3°C (Supplemental Tables 1–8), indicating how well the dry environments supported heat loss as conditions became more stressful.

• The activity velocity and wind speed had important effects in helping to cool the body, with H_total values always higher at the higher activity velocity of 0.7 m·s⁻¹. This cooling effect from wind flow caused a greater difference in H_total between the HD and WH conditions as the WBGT increased. However, additional clothing lowered the overall cooling effect from wind or movement and, thus, the difference in HD versus WH conditions.

DISCUSSION

Meteorologic conditions that yielded the same WBGT levels resulted in different H_total values depending on whether it was an HD or WH environment. Therefore, although a seemingly equivalent “heat-stress” situation was present, the ability of the body to lose heat was greater under HD than WH conditions, as summarized in Figure 3. Our modeling results for athletes were consistent with both laboratory and field studies in which researchers^12,13 have indicated that WBGT underestimates heat stress in high-humidity, low wind-speed conditions, which limit evaporative cooling, yet that higher WBGTs might be tolerated in dry environments that allow free evaporation. For instance, a field study¹² of firefighters suppressing brush fires reinforced the importance of evaporative cooling and demonstrated that individuals can tolerate WBGTs up to 9°C above recommended limits in conditions with unrestricted evaporation and with appropriate behavioral responses.

Furthermore, Ramanathan and Belding¹³ investigated the physiological responses of individuals in a heat chamber subjected to the same WBGT but using different combinations of humidity, air speed, and radiant heating. For example, at a fixed WBGT of 31.94°C (89.5°F), greater physiological strain was observed in individuals exposed to no radiant heating, high humidity, and a low level of air movement than those exposed to radiant heating, low humidity, and a high level of air movement. Our results support the conclusions of Ramanathan and Belding¹³ that the ability of WBGT to predict heat strain degraded at higher WBGT levels, such as those encountered by athletes and in industry. Such routine differences between HD and WH environments may be present because the initial environmental contexts and evaluations used to set the current thresholds and WBGT equation occurred in WH environments (Virginia, South Carolina)^4,5 as opposed to HD environments.

Recognizing that different physiological responses may occur for a given combination of weather variables that create equivalent WBGT values, researchers have recommended establishing WBGT thresholds based on RH at 50%, 75%, and 100% levels³¹ or 2 sets of WBGT limit levels––1 for humid conditions and 1 for dry.¹³ Ramanathan and Belding¹³ further proposed including wind speed because of its importance in evaporative heat loss, as we demonstrated in Supplemental Figure 1. To our knowledge, such distinctions in WBGT thresholds have not been tested in environmental physiology studies.

For the athletic community, a uniform set of WBGT-based activity modifications, such as those proposed by the ACSM,² is still the standard recommendation, although the differences in compensable heat stress vary with clothing level based on the combination of RH and T_a as shown here and by others.^2,14 The efficacy of WBGT-based activity modifications in mitigating EHIs in athletes has been well supported in humid regions of the United States, such as Georgia,³² where the evaporative capacity of the environment is the limiting factor to heat loss, but in arid environments, the limits have been physiologically based. In general, field research is lacking on the effectiveness and appropriate thresholds of WBGT for proper activity and environmental modifications (eg, use of fans) in more arid environments, specifically as they relate to heat strain. Adequate air movement via fans or the player's activity velocity aids in heat loss under most environmental conditions. Morris et al³³ showed that only under extremely hot and dry conditions (ie, T_a > 45°C and RH < 10%) were fans detrimental. At the highest WBGT threshold of 32.3°C, the T_a and RH values averaged only 37.1°C ± 3.7°C and 27.0% ± 8.3%, respectively, and thus, fans on the playing field can aid heat loss.

Research focused on heat injury and physiological responses (eg, core temperature and sweat response) will help refine the WBGT guidelines, which may have important implications for heat-health protection. For example, our core temperature simulations illustrated the potential differences in the rise in core temperature between HD and WH environments (Table 3), indicating the greatest risk to individuals in the WH cluster at low activity velocities wearing full gear. Overall, the WH conditions caused a faster increase in core temperature than the HD conditions, reflecting more oppressive conditions for equivalent WBGT, clothing configurations, and activity velocities. Our results are generalizable to a wide population, but it is well known that core temperature and thermoregulatory responses demonstrate a high degree of individual variability because of various physiological and biophysical factors.³⁴ Even so, our findings highlight the importance of conducting further clinical and field studies of appropriate activity-modification thresholds for athletes in arid environments.

Table 3.

Potential Core Temperature Rise per 5 min^a

Activity Velocity	Clothing and Equipment Configuration	Cluster, °C (Mean ± SD)
		Hot-Dry	Warm-Humid
0.3 m·s−1	Shorts	0.23 ± 0.02	0.25 ± 0.02
	Shells	0.28 ± 0.02	0.29 ± 0.02
	Full	0.28 ± 0.03	0.30 ± 0.01
0.7 m·s−1	Shorts	0.13 ± 0.04	0.16 ± 0.03
	Shells	0.22 ± 0.03	0.24 ± 0.02
	Full	0.24 ± 0.02	0.26 ± 0.02

^aAssuming 2.5-m² body surface area, maximum potential heat loss assumed for heat loss, 8 metabolic equivalents, activity velocities of 0.3 or 0.7 m·s⁻¹, and fully warmed up with a skin wettedness of 1.0, at a 32.3°C wet-bulb globe temperature.

LIMITATIONS

We assumed that players were sweating at maximal rates that resulted in skin wettedness of 1.0, in essence causing a higher evaporative heat loss at the skin. This value was assumed for all WBGT thresholds and clothing ensembles but may not always be the case. However, the value of 1.0 is recommended for fully acclimatized adults and has often been used by others.^17,26 Hence, in the early stages of the season (first 2 weeks), when players may not be fully acclimatized, our results may overestimate the potential heat loss. According to Parsons,²⁶ skin wettedness of unacclimated individuals for heat strain models is 0.85, which would lower the evaporative heat loss in both dry and humid conditions because sweating would be less. Furthermore, one would not observe skin wettedness of 1.0 at the start of exercise, also lowering H_total in both situations.

In our study, we first assumed that self-generated wind (ie, activity velocity) for Equation 3 would control for the cooling effect of winds on evaporative and convective cooling. Greater variabilities in relative wind velocities are expected based on the actual movements of the players and wind mixing. These winds will also differ depending on the venue of choice and local wind and temperature conditions. Understanding local environmental measurements and their effects on players is important for an accurate estimate of heat stress, so reports from distant airport weather stations are not always appropriate.³⁵

CONCLUSIONS

Equivalent values of WBGT resulted in different abilities to cool the body (higher H_total values) during times of heat stress, with HD environmental conditions offering a 13% to 17% greater ability to cool than WH conditions at an equivalent WBGT value of 32.3°C and activity velocity of 0.3 to 0.7 m·s⁻¹. This finding was based on 15 years of modeled WBGT data from the contiguous United States. Moreover, these heat-loss differences by environmental type increased as the severity of the WBGT increased, as the wind speed or player movement increased, and as the amount of clothing worn decreased.

A satisfactory index of heat stress should evoke the same physiological response for all combinations of its constituent variables.⁹ Although the WBGT has proven to be a convenient and comprehensive index of heat stress, it does not necessarily represent heat strain, which refers to individual physiological responses when exposed to heat stress.⁷ We and other researchers demonstrated that the WBGT does not evoke the same response in all situations. Anecdotally, some athletic trainers in HD climates, such as Arizona, do not use the WBGT because national guidelines may rely on activity-modification thresholds that appear too low and would severely limit outdoor activities. This anecdote may pose a barrier to adopting a WBGT-based activity-modification policy. In humid environments, the evaporative capacity of the environment is the limiting factor to heat loss; however, in arid environments, the limits to heat loss are physiologically based, and using WBGT in these dry environments deserves greater attention in field-based clinical research.

To improve measures for preventing EHIs using WBGT thresholds, the inherent limitations need to be addressed through clinical studies and empirical real-world EHI data collection of the potential overestimation of heat stress in HD environments and underestimation in WH environments, particularly the nonlinearity of the heat effects. Such studies could aid in more appropriate implementation of preventive countermeasures, with thresholds that first address the environmental type (humid versus dry) in addition to sporting event, clothing, and time of year, among other personal factors.