Abstract
In this paper we address the possibility to perform imaging of two samples within the same acquisition time using coupled ceramic resonators and one transmit/receive channel. We theoretically and experimentally compare the operation of our ceramic dual‐resonator probe with a wire‐wound solenoid probe, which is the standard probe used in ultrahigh‐field magnetic resonance microscopy. We show that due to the low‐loss ceramics used to fabricate the resonators, and a favorable distribution of the electric field within the conducting sample, a dual probe, which contains two samples, achieves an SNR enhancement by a factor close to the square root of 2 compared with a solenoid optimized for one sample.
Keywords: dielectric resonators, electromagnetic coupling, magnetic resonance microscopy, signal‐to‐noise ratio, solenoid
The possibility of simultaneous imaging of two samples is theoretically and experimentally studied using coupled resonators. Our ceramic probe is compared with a compact solenoid probe, the standard probe in ultrahigh‐field magnetic resonance microscopy. Due to low‐loss ceramics and a beneficial distribution of the electric field in a conducting sample, a dual probe containing two samples achieves an SNR enhancement by a factor close to the square root of 2 compared with a solenoid optimized for one sample.
Abbreviations used
- DR
dielectric resonator
- FOV
field of view
- HEM
hybrid electric and magnetic
- MRM
magnetic resonance microscopy
- RF
radiofrequency
- SAM
semi‐analytical model
- SNR
signal‐to‐noise ratio
- TE
transverse electric
- TM
transverse magnetic
1. INTRODUCTION
Magnetic resonance microscopy (MRM) consists of imaging small samples with a spatial resolution better than 100 μm. 1 MRM is used to study a wide variety of samples, including biological tissues, porous media and plants. The resolution, which is typically of the order of tens of micrometers, depends on the sample size and structure, imaging hardware specifications, and the time available to perform the acquisition. 2 To achieve very high resolution, very high static magnetic field strengths, B0, of up to 22 T, are typically used. 1 , 3 High resolution images of 3‐4 isotropic micrometers, have been obtained using very small RF detectors, but these required very long acquisition times (tens of hours). 4 , 5 These long acquisition times are a great challenge for high‐throughput studies and put MRM at a clear disadvantage when compared with other imaging or spectroscopic techniques. The most straightforward way to improve the throughput is to image multiple samples during the same acquisition time slot. This can be done by increasing the coil size to accommodate multiple samples, 6 however, this solution has the disadvantage that it significantly decreases the sensitivity, and therefore the achievable spatial resolution.
An alternative is to employ probes comprising multiple small detectors, each of them containing its own sample. With proper alignment in the field of view (FOV), this enables simultaneous imaging of multiple samples without an increase in the acquisition time when compared with that of imaging one single sample. Several multiple‐coil probe prototypes, based on solenoids, have been proposed in the literature. While they all allow the acquisition of images from several samples during the same slot, they differ in their structure and the image quality they provide. Multiple‐coil probes can be cast into two main categories:
Those for which each coil element has its own tuning and matching circuit and receiver channel, and hence have the same signal‐to‐noise ratio (SNR) as a single coil, at the cost of a more complicated construction which requires minimizing intercoil coupling. 7 , 8
Those that involve inductively coupled elements and a single transmit/receive channel,9 then the acquired signal comes from one sample but the noise from all the elements.
As explained by Wang et al, 9 this second category leads to a reduction of the SNR compared with a single element probe. The SNR of a combination of N identical coupled resonators used as a probe for N samples has a maximum value of , with SNRopt,N = 1 being the optimal value of the SNR of a single RF coil. The term is denoted ξ and defined as a SNR degradation coefficient in the following. Despite this SNR penalty, these multiple probes are, from a practical point of view, advantageous when compared with those in the first category as they are much easier to build and cheaper since they do not require multiple receiver systems, which is an expensive option for performing multiple sample MRM. Additionally, they are of a great interest at ultrahigh fields, where the SNR is sufficiently high without signal averaging and the main challenge is to reduce the acquisition time necessary for full k‐space coverage. In this article, we investigate the possibility of improving the performance of two coupled resonators by reducing their losses (intrinsic contributions and feeding network).
All the multiple‐coil probes described in the literature are based on solenoids, as the solenoidal coil is the reference volume coil for MRM. 10 In the past, an alternative microscopy probe design was proposed, based on the resonance of ceramic disks or rings. 11 , 12 , 13 Dielectric resonators support a variety of eigenmodes, for which the frequency distribution depends on the resonator geometry and the electromagnetic properties of the constitutive material. Such modes are divided into three categories: transverse electric (TE), transverse magnetic (TM), and hybrid electric and magnetic (HEM). The first TE mode (TE01δ) of high permittivity cylindrical resonators exhibits a magnetic field (H) that is axial and has a maximum in the center, along the axis of symmetry. 14 In ring resonators, 12 , 13 the sample is placed in the hole, where the magnetic field, used as the excitation and reception field B 1 in MR acquisitions, is strong and accompanied by a low electric field (E) that reaches its maximum values in the dielectric ring itself. Due to this feature, the noise contribution from a conductive sample is minimized. In comparison with a solenoid coil, a dielectric disk or ring resonator creates no quasi‐static axial electric field, therefore having a much higher Q‐factor when loaded with a conductive sample. The probe intrinsic noise contribution is driven by the loss factor of the dielectric material used to build the ring. An example from a recent study13 demonstrates that such a probe enhances the SNR by a factor of more than 3 for a biological tissue‐mimicking sample material, and by more than 5 for much lower permittivity samples, as compared with the optimal solenoid. In practice, an experimental demonstration of this work showed an enhancement factor of 2.2. This was made possible by using a unique ceramic material specially designed to have low dielectric losses and high permittivity, which enables the confinement of the electric field in the ceramics and minimizes its conservative component within the hole in which the sample is located, and therefore ensures a low E/H ratio in the sample. 15
To perform imaging of two samples within the same acquisition time slot using only one receive channel, the work presented in this paper exploits the electromagnetic coupling of two dielectric resonators (DRs). More precisely, the interaction of the above‐mentioned TE01δ modes of two identical resonators gives rise to two coupled modes, the symmetric (++) and the antisymmetric (+−) modes, as represented in Figure 1. These modes are the solutions of the eigenvalue problem derived from the energy‐coupled mode theory. 16 , 17 As can be seen in the figure, the coupled modes have different properties. The symmetric mode is similar to the constructive addition of two magnetic dipoles, resulting in an equivalent longer magnetic dipole and therefore lower resonance frequency than that of a single resonator, f 0. The antisymmetric mode appears as two opposite magnetic dipoles facing each other, with destructive interference of the electromagnetic field in between, and a higher resonance frequency than the single resonator. This hybridization scheme is inverse to that found previously for metallic metamaterials. 18 The frequency shift of the coupled modes depends on the coupling strength, which is strongly correlated to the spatial distance between the resonators.
FIGURE 1.
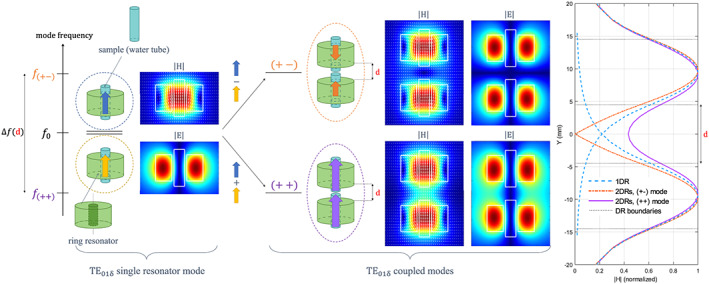
Hybridization scheme and mode field profiles of the first transverse electric (TE) mode of two coupled dielectric resonators. The electromagnetic coupling of the individual TE01δ modes of the single DRs, initially at the same frequency f0 gives rise to two coupled modes whose frequencies are shifted lower and higher than f0.The lower‐frequency, symmetric mode is denoted (++) and is equivalent to a magnetic dipole longer than the initial TE01δmode with zero coupling. The higher‐frequency, antisymmetric mode, denoted (+‐), corresponds to two magnetic dipoles aligned in opposite directions such that the electromagnetic (EM) field maps represent the H‐ and E‐fields of the single resonator TE01δ mode and of the coupled modes. The maps were obtained with the Eigenmode Solver of CST Studio, normalized w.r.t. the maximum in each case and plotted on a linear scale from 0 to 1. The graph on the right represents the H‐field magnitude profiles along the resonator axis for the (++) (purple line) and (+‐) (orange dotted line) modes. For comparison, the H‐field amplitude of the original TE01δ mode has been displayed for each single resonator (blue dashed line)
The topic of coupling ceramic resonators in the context of MRM has already been addressed by Neuberger et al 11 with a different purpose than ours, which is imaging more than one sample. In their study, the sample was placed between two ceramic disks, where the first TE modes of the disks interfered constructively in the symmetric mode. The authors showed how the interdisk gap influences the (++) mode frequency, which was used for pretuning the probe to a certain frequency. Fine tuning at the Larmor frequency was achieved by sliding copper strips close to the resonators from outside the magnet bore. However, coupled dielectric resonators have never been used in MRM for multiple sample imaging, and reduction of their intrinsic losses by improving ceramics properties has not been explored. An advantage of using new ceramic materials with lower losses is the decrease in the noise generated by each resonator, leading to a globally improved SNR.
In this paper, we propose a new type of volume multiple‐coil probe for MRM built from two coupled ceramic rings, each of them including one sample. The (++) coupled mode frequency is set at the Larmor frequency of a 17.2 T scanner (730 MHz) by adjusting the relative positions of the two identical rings. Such rings were previously designed for MRM at 17.2 T and they demonstrated, when used individually, greater than 2‐fold SNR enhancement compared with the optimal solenoid. 13 With the dual‐ring probe, it is therefore expected to degrade the single ring SNR by a factor ξ close to , and to overcome the optimal solenoid SNR by a factor close to . The principle of this probe is detailed in section 2, while the methods used for its characterization are presented in section 3. The results are provided in section 4 and discussed in section 5.
2. THEORY
The dual dielectric ring probe is based on the coupling between the individual modes of the ring resonators. The electromagnetic coupling of metallic or dielectric resonant structures and its effect on the resonator's induced field have been the topic of various studies in both the optical 19 and microwave 20 frequency ranges. In this paper we consider the interaction between the first TE modes of two dielectric resonators operating in the radiofrequency domain. The TE01δ mode of a high‐permittivity ring resonator has previously been exploited for RF excitation and reception in microscopy applications. 11 , 12 , 13
Generally speaking, the resonant modes resulting from the coupling of electromagnetic resonators can be seen as a linear combination of the uncoupled modes, provided that the resonators have dimensions smaller than the resonant wavelength. 21 In coupled mode theory, the coupled modes are then written as the weighted sum of the uncoupled modes. 22 In Equation 1, and are the electric and magnetic fields of the γ‐indexed coupled mode, and are the electric and magnetic fields of the n‐th resonator, and and their respective coefficients in the modal expansion.
| (1) |
The energy‐coupled mode theory exploits the principle of energy conservation and the equality of time‐averaged stored magnetic and electric energies at resonance. For nonmagnetic materials, it leads to the eigenvalue problem , expressed in terms of the electric field coefficients vector , the angular frequency at the resonance , the electrical polarization operator and the free space operator . 21
In this work, two dielectric resonators are used as an extended probe for two samples; their electromagnetic coupling can be modeled as follows:
There is no coupling with higher‐order modes: only the two TE01δ modes interact. Indeed, the aspect ratio and the high permittivity of the considered resonators are such that there is no overlap in the frequency domain between the two first adjacent modes. This is correct in the vicinity of the resonant frequency of each resonator. In practice, the closest higher mode is the HEM11δmode whose frequency is 215 MHz higher than the frequency of the TE01δ mode. As a result, in Equation 1, n varies from 1 to 2, the eigenvector contains two elements, and the operators and are 2 × 2 matrices.
Any difference between rings that may arise due to fabrication is neglected: the dielectric rings are strictly identical, with the same material properties (relative permittivity ɛ r = 530, loss tangent tanδ = 8 · 10−4) and identical dimensions (height L = 10 mm, outer radius r d = 9 mm, inner radius r h = 2.8 mm). Thus, both DRs support the same TE01δ mode at frequency f 0 = 741 MHz and pulsation denoted ω 0. In practice, there is some variation of the material properties and the resonators’ dimensions, but the higher order modes can be neglected as long as the frequency deviation they imply is less than the frequency splitting due to coupling. Consequently, the coupling eigenvalue problem reduces to with , and defined as follows through their (i,k) component: , and . In these definitions, ɛ i is the permittivity of resonator i equal to ɛ 0 ɛ r, ɛ 0 is the permittivity of vacuum and ɛ the permittivity distribution of the coupled resonators system, that is, ɛ 0 ɛ r within resonators 1 and 2 and ɛ 0 elsewhere.
The general definition of the coupling coefficient involves contributions from the reaction integrals between electric fields, and the reaction integrals between magnetic fields. 16 However, it has been shown that in the case of identical dielectric resonators, due to the identity (μ 0 being the vacuum permeability), the coupling eigenvalue problem reduces to the contribution of the reaction integrals between electric fields 21 , 22 (Equation 2):
| (2) |
| (3) |
The coupling coefficient κ is defined in Equation 3, with V 1 the volume occupied by resonator 1. From this definition, the coupling interaction is described here with the spatial overlap of the individual DR E‐field distributions. 17 Note that κ is defined with respect to the permittivity of resonator 1 for the following reason: since the electric field induced by resonator 1 at resonator 2 is identical to that induced by resonator 2 at resonator 1, this definition can be written unequivocally as a function of the resonator 1 or resonator 2 permittivity distribution. The coupled modes frequencies depend on the strength of coupling arising between the individual modes. More precisely, the coupled modes resonant frequencies are respectively lower and higher than the single TE01δ mode frequency, f 0. These shifts are computed from the coupling coefficient κ. The coupled modes frequencies are then given by the formula in Equation 4, which is deduced by solving the coupling eigenvalue problem. 17
The individual eigenmode electromagnetic fields are denoted { , } and { , "/> } for resonators 1 and 2, respectively. Each coupled mode is written as a linear combination of the two individual eigenmodes. In particular, since the two resonators are identical and therefore synchronous (their eigenmodes have the same resonant frequencies), the coupled modes are expressed by Equation 5, where
| (4) |
denotes the E‐ or H‐field distribution, and the subscript the DR index or the coupled mode type.
| (5) |
| (6) |
As shown in Figure 1, the lowest frequency‐coupled mode, which was chosen in this study, is obtained by summing the individual modes. In this case, the axial components of the magnetic field of the two resonators add constructively along the common axis of the two resonators. As a result, the magnetic field between the rings is nonzero. By contrast, the highest frequency‐coupled mode field distribution has a reduced active region along the axis in each ring due to the destructive interference occurring between the individual modes. This mode could also be used for dual‐sample imaging applications but with a reduced FOV since the axial magnetic field is significantly reduced in the middle of the coupled resonators. These properties are shown in the field profiles in Figure 1.
The TE01δ mode of a single ring ceramic resonator has already been exploited in MRM. 13 This mode is easily excited using a simple copper loop, placed outside the resonator and perpendicular to its axis. This design limits the metallic parts of the probe and therefore its intrinsic losses. To be precise, besides the sample, only the ceramic ring contributes to losses, and this contribution is low, due to the low dissipation factor tan δ of the material itself. Another advantage of using ceramic rings to provide the excitation field B1 is that the ratio E/H in the sample is reduced compared with a solenoid. 13 , 15 It follows that, for a given sample diameter, the electric field being minimum in the FOV region, a change in sample permittivity has a limited impact on the mode frequency and on the field distribution.15
All these advantages of the single ring resonators hold for the dual ceramic probe used in this study. From a practical point of view, the coupled mode field distribution is easily excited with a single loop placed strictly in the middle of the two resonators. In this configuration, the symmetry of the setup (coaxial alignment of the two resonators and location of the loop in the plane of mirror symmetry) enables selective excitation of the (++) mode without exciting the (+−) mode. 23 The latter is a trapped mode, which could be excited by breaking the structural symmetry of the system. 18 , 24
3. METHODS
3.1. Semi‐analytical method
The TE01δ mode frequency of a single ring resonator containing a sample is computed using an approximation method15 that estimates the mode frequency of the corresponding disk (same outer dimensions and permittivity ɛ r as the ring). The resonator modes frequencies are affected in proportion to the permittivity difference between the sample and the ring materials, multiplied by the squared electric field, multiplied by the sample volume: . As the first TE mode generates a low electric field in the center of the resonator, considering the disk instead of the ring and its sample is a reasonable approximation. Quantitatively speaking, for the relative permittivity (ɛ r~500) and the inner to outer radii ratio of the ring (r h/r d~0.3) considered here, the frequency shift between the disk and the ring is less than 2%. 15
The field distribution of a single TE01δ mode is estimated with a variant of a previously developed method15 with improved accuracy for the estimation of the field outside the resonator (while the initial approach presented better accuracy for the field inside the resonator). This modified method, termed SAM* in the following analysis, refers to a volume integral equation method which considers the electric field inside the probe as an equivalent volume source current distribution 25 also known as contrast sources "/> (Δɛ: the permittivity difference with respect to the surrounding media; "/>: the field inside the resonator). The field outside the probe is estimated through computation of the magnetic vector potential , as expressed in Equation 6, with the free space Green function and V s the probe volume. 25 The electric field is deduced from the vector potential using Equation 7. In the case of the TE01δ mode, Equation 7 reduces to its second term only ( "/> due to the mode symmetry. In practice, the computational complexity was simplified by considering disk resonators instead of ring ones. In that case, the electric field inside the probe is described by a cosine for the axial variations, and a single Bessel function for the radial dependence.15 It is then possible to analytically derive an intermediate formulation of Equation 6, and therefore to reduce the final computation time.
| (7) |
| (8) |
For the electric field maps of the coupled modes in Figure 2, the individual E‐field distributions were estimated with the SAM* method for each resonator, and then combined as described in Equation 5 for each interdisk gap. The individual field maps were also used to compute the coupling coefficient in Equation 3 and to estimate the coupled mode frequencies depicted in the same figure.
FIGURE 2.
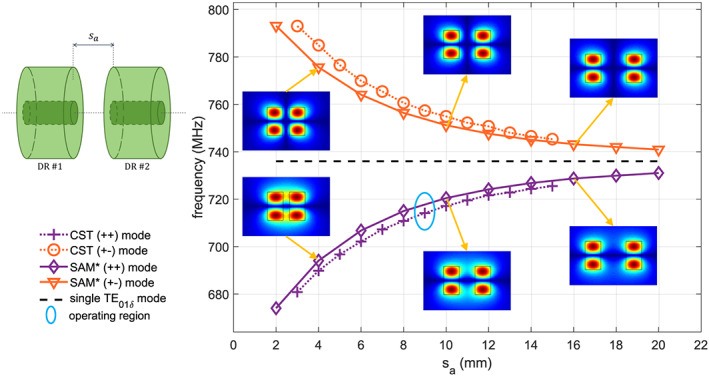
Coupled modes frequencies. Left: relative position of the two resonators. Right: coupled modes frequencies versus distance sa between resonators. The results from numerical simulations (CST) with a frequency domain solver and a semi‐analytical model (SAM*) are compared (see Section 3). In the first case, each resonator consists of a dielectric ring containing a sample tube, and the coupled modes are excited with a copper loop (see Section 3.2). In the second case, the resonator consists of a dielectric disk with the same permittivity as the ring. Insets represent the E‐field modulus of the coupled modes, computed with the semi‐analytical model, for different values of the axial shift. The operating region of the experimental probe is indicated with a blue circle
This method was compared with numerical simulation results as presented below.
3.2. Numerical simulations
First, the Eigenmode solver of the commercial software CST Microwave Studio was used to compute the electromagnetic field maps in Figure 1 and to confirm both the coupling theory and the SAM* method. In these simulations, the two ring resonators were placed facing each other, each one containing a sample of the same height as the rings, and with a varying axial shift 𝑠 a. This solver enabled the estimation of the TE01δ coupled modes frequencies and field distributions.
Second, the setup of the experiments was studied with numerical simulations using the Frequency Domain Solver of the same software (Figure 3). In these simulations, the ceramic probe was represented by two dielectric rings separated from each other by varying the axial shift s a between their opposing faces, from 7 to 14 mm. Each ring had a height L of 10 mm, an outer radius r d of 9 mm and an inner radius r h of 2.8 mm. The ring dielectric material had a relative permittivity ɛ r of 536 and a dielectric loss tangent tanδ of 8 · 10−4.
FIGURE 3.
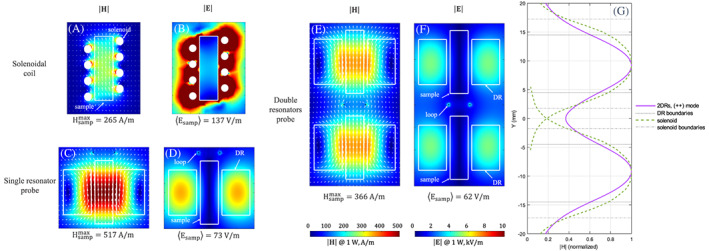
Electromagnetic field (modulus) maps from numerical simulations (CST Studio) for 1 Watt of input power (impedance matched case). Left, top: (a) H‐field and (b) E‐field of the solenoid; left, bottom: (c) H‐field and (d) E‐field of the single dielectric ring resonator probe. Right: (e) H‐field and (f) E‐field of the dual dielectric ring resonators probe. In each case, the probe contains one (or two) saline water sample(s) of diameter 4 mm, height 14 mm, conductivity 1.59 S/m and relative permittivity 81. The maximum value of magnetic field reached in the sample and the mean value of the electric field in this region are given for comparison. White arrows represent the magnetic field lines. The graph on the right (g) represents the H‐field magnitude profiles, extracted from the magnetic field maps, along the resonator axis and in its centre, for comparison of the (++) coupled mode with the solenoid coil. To this end, the solenoid field profile is represented twice, at the location of each of the coupled DRs
The sample was represented by a cylinder filled with saline water (relative permittivity ɛ r,s = 81 and electrical conductivity σ s = 1.59 S/m) of height 14 mm and radius 2 mm, placed within the hole of the dielectric ring. A circular copper loop (outer radius 2.6 mm) was placed between the two rings, at an equal distance from each of them.
The loop excited the resonator symmetric coupled mode, with its impedance matched to 50 Ω at the resonance frequency of the (++) mode. This probe was placed in a metallic (assumed to be a Perfect Electric Conductor in the models) hollow cylinder of diameter 91 mm and length 600 mm, mimicking the MRI system bore, with its axis orthogonal to the probe axis.
3.3. Experiments
The dual ceramic probe consisted of two identical ceramic resonators13 as presented in Figures 2 and 4. The ceramic resonators were built from a BaTiO3/SrTiO3 = 50/50 compound containing 20 and 5 wt% total additions of MgO and Mg2TiO4, respectively, over 100% of the initial mixture (Tsin = 1400°C). 26 , 27 , 28 The probe was mounted on a 3D‐printed holder built with polylactic acid, which was designed such that the distance between the resonators notches, s a on Figure 2, was 9 mm, with the possibility to slide the resonators by a few mm and therefore adjust the effective axial shift s a between 7 and 11 mm. The feeding loop (8 mm diameter circular copper loop) was placed on the loop holder, which could be mechanically moved from outside the MRI bore, to adjust the loop shift 𝑠 l within a range of 0 to 6 mm, for real‐time matching at the Larmor frequency.
FIGURE 4.
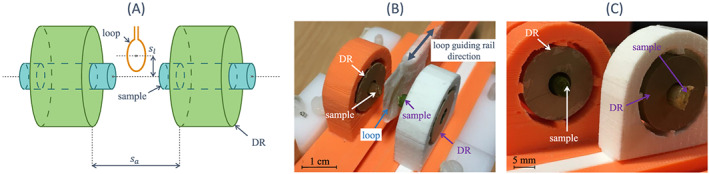
Experimental dual ceramic probe. (a): schematic. (b): view of the probe with the two DRs, and their respective samples, the feeding loop and the direction of displacement. The loop holder can be slid on the rail from the outside of the MR device bore. (c): view of the two DRs with their samples
All MRI experiments were performed on a horizontal bore animal scanner operating at 730 MHz (17.2 T, Bruker BioSpin, Ettlingen, Germany) equipped with a triaxial gradient system with a maximum strength of 1 T/m. During the acquisitions, the temperature of the ceramic resonators was kept constant using a circulating water pad (Grant TC120, Grant Instruments, Shepreth, UK). The thermostat temperature was carefully monitored so that the probe resonance corresponded to the proton Larmor frequency of 730 MHz. The design and performance of the specially constructed optimal solenoidal coil used as a reference have been presented previously.13
For experimental SNR estimation, we acquired images of a liquid phantom (water containing 1 g L−1 CuSO4 and 3.6 g L−1 NaCl) using a gradient echo sequence with the following parameters: TR/TE: 1000/6 ms, flip angle: 30°, FOV: 10 mm × 10 mm, slice thickness: 0.5 mm, matrix size: 128 × 128, in plane resolution: 0.078 mm × 0.078 mm, acquisition time: 2 minutes 8 seconds. The image orientation was chosen such that the slice‐encoded direction was along the long axes of the resonators. Both resonators were imaged simultaneously, so that a total of 40 slices were acquired for a scanning time corresponding to 20 slices. The SNR was computed in slices positioned in the center of each resonator. On these slices, a small box placed within the sample was used to estimate the mean signal, and the root‐mean‐square of the noise was estimated from a box placed outside the sample, as shown in Figure 5.
FIGURE 5.
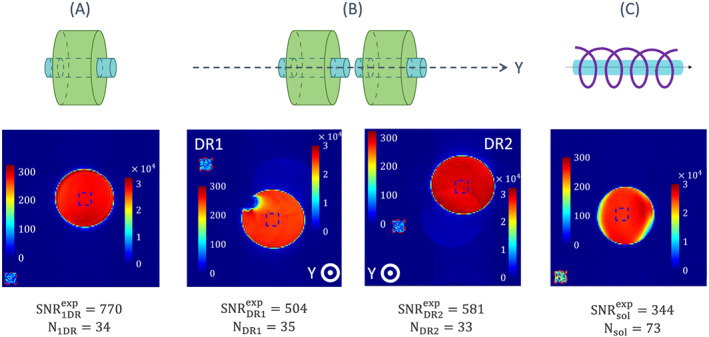
Experimental SNR investigation. SNR maps of (a) a single ceramic probe, (b) a dual ceramic probe and (c) the optimal solenoid. The signal and noise boxes are represented in blue and red dashed contours, respectively, with their own color scale. The signal value is computed from the mean value of the pixels in the signal box, within the sample, and the noise from the standard deviation of the noise box located outside the sample, as shown on each slice. The numerical values of the noise level and the SNR are given below each figure. The sample is a saline water tube of relative permittivity 81 and electrical conductivity 1.59 S/m in this range of frequencies. In the left map of (b), the low signal region within the tube is an air bubble
Images of plant petioles (stalk between the stem and the leaf) were acquired using a 2D FLASH acquisition: TR/TE: 550/6.1 ms, flip angle: 30°, number of averages: four, FOV: 8 mm × 8 mm, slice thickness: 0.5 mm, matrix size: 320 × 320, in plane resolution: 25 μm × 25 μm, acquisition time: 12 minutes. The SNR was computed in these acquisitions as the ratio of the local pixel value divided by the noise level, estimated as previously by the root‐mean‐square of the pixel values contained in a box placed outside the sample.
4. RESULTS
From the theoretical point of view, the electromagnetic coupling of the resonators’ single TE modes allows adjustment of the (++) coupled mode frequency from 670 to 735 MHz (Figure 2). The difference between the SAM* method and the numerical simulations can be explained by the influence of coupling on the feeding loop in the CST model, which was not considered in the theoretical approach. This relative error is always below 2%, which validates the coupling theory statements used to develop the SAM* technique: the electromagnetic coupling between these resonators can be well described through the E‐field distributions overlap and it is minimally affected by the sample.
From Figure 3, the magnetic fields induced by all probes are similar to each other in terms of spatial distribution, while there is clearly a lower electric field induced in the sample(s) with the ceramic probes than with the solenoid, as reflected by the mean value of the electric field. The magnetic field, given for 1 W accepted power in the transmit mode, is proportional to the SNR of each probe . As a result, and as presented in Table 1, the single ceramic probe provides an SNR almost two times higher than that of the solenoid. The double ceramic resonator had an SNR value lower than the single ceramic one, and the degradation factor was approximately equal to , which confirms the general theory presented in the Introduction and still enables an SNR 1.38‐fold higher than for the single optimal solenoid.
TABLE 1.
SNR comparison of the single ceramic probe, the solenoid probe and the dual ceramic probe, in numerical simulations and experiments.
|
|
|
|
||||
|---|---|---|---|---|---|---|
| Numerical simulations | 1.95 ≈ 2 |
|
1.38 | |||
| Experimental results | 2.2 | 1.53 (DR1) 1.32 (DR2) | 1.47 (DR1) 1.70 (DR2) |
The images used to compute the experimental SNR in saline water are shown in Figure 5 for the single dielectric resonator , for the dual ring probe , and for the optimal solenoid , while the values are reported in Table 1. The single DR provides an SNR more than two times higher than the optimal solenoid, as reported previously. 13 In the samples contained in the dual ring probe, the SNR is different from one sample to the other, most likely due to differences in the two resonators, and lower than that of the single DR probe. Overall, the dual ring probe still provides an SNR at least 1.47‐fold higher than the optimal solenoid probe.
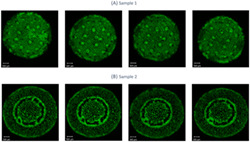
Figure 6 illustrates an example of a practical application of the dual ceramic probe: the simultaneous imaging of two different plant petioles. Images of one of the samples held by the dual ceramic probe are compared with images of the same sample acquired with the solenoid probe, qualitatively with selected slices from both acquisitions, and quantitatively with the SNR histogram profiles. The image acquired with the solenoid coil has lower SNR values than the image acquired with the dual ceramic probe. The highest SNR value reached with the dual ceramic probe in this sample is 148, that is, 1.21‐fold higher than the one with the solenoid coil.
FIGURE 6.
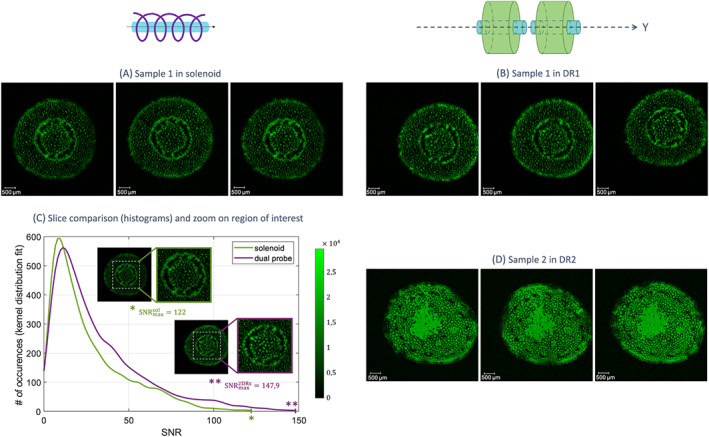
MR acquisitions of plant petioles with the dual ring probe and with the solenoid coil. Images were selected from the same acquisition for the two samples imaged with the dual probe. Two petioles from two different plants were used as samples 1 and 2. Sample 1 was imaged with (a) the solenoid coil and (b) the dual probe (in DR1) using identical acquisition parameters. In selected slices of these acquisitions (based on the similarity of the imaged part of the petiole), the histogram profiles (fitted by a kernel distribution) of the pixel values were plotted for each probe, divided by their respective noise level (c). This provides the distribution of SNR values pixel by pixel in the selected slices. The highest SNR value reached with the proposed dual ceramic probe is 1.21 times higher than that of the solenoid coil. (d) Sample 2 was imaged with the dual probe (in DR2) during the same acquisition time slot as sample 1. In (a), (b) and (d), the selected images are represented with a linear scale from 0 to 1 since they are normalized with respect with their respective maximum values. In (c), the compared slices are represented with the same, indicated linear scale
5. DISCUSSION
The coupling theory presented in section 2 to explain the principle of the dual ceramic probe was validated with numerical simulations. Since the coupled modes frequencies were computed with SAM* assuming dielectric disk resonators (no sample), and fitted the numerical simulations, this confirmed the robustness of the ceramic probe towards the sample electromagnetic properties.
In the case of the homogeneous sample consisting of saline water, numerical simulations predicted a degradation coefficient of the single ceramic probe SNR close to for the dual ceramic probe, that is, containing N = 2 elements, very close to the optimal value. In addition, experiments demonstrated that despite being different for the two resonators comprising the dual ceramic probe, this degradation coefficient was close to the theoretical predictions in both cases: versus and (from the SNR values given in Table 1). This difference could come from the ceramic rings not being exactly identical, or not exactly at the same distance from the feeding loop. Also, as tuning at the Larmor frequency was performed by thermostating the ceramics with a heating pad, the temperature of the resonators, made of temperature‐sensitive ceramics, may have been different in the two resonators.
Acquisitions on plant petioles enabled the comparison of the image quality obtained with the solenoid coil and the dual ceramic probe in realistic samples. Regarding the compared slices in Figure 6C, the maximum SNR ratio is / . This is consistent with previous results, especially since this comparison is affected by the slight difference in the positions of the selected slices (the slices are not exactly the same), and since this sample has different properties from saline water.
6. CONCLUSION
The dual ceramic probe studied in this work was made with two high permittivity dielectric resonators that were previously used as single probes for microscopy acquisitions at 17.2 T. Such resonators have demonstrated the possibility to overcome the optimal solenoid SNR by a factor of more than two, from both theoretical and experimental points of view. In this paper, the possibility was demonstrated to improve the optimal solenoid SNR by a factor close to , depending on the sample properties and with an experimental setup at low complexity and cost, while being able to image two samples during the same acquisition time slot and just one receive channel. In the framework of ultrahigh‐field MRI, this is of interest to reduce the acquisition time.
ACKNOWLEDGEMENTS
This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 736937. Numerical simulations were supported by the Russian Foundation for Basic Research (grant no. 18‐3220115). Stanislav B. Glybovski was supported by the President of the Russian Federation (MK‐3620.2019.8) and acknowledges the support from the Metchnikoff Programme by the Embassy of France in the Russian Federation. Andrew G. Webb was partially supported by a H2020 ERC Advanced Grant (NOMA‐MRI 670629).
Moussu MAC, Glybovski SB, Abdeddaim R, et al. Imaging of two samples with a single transmit/receive channel using coupled ceramic resonators for MR microscopy at 17.2 T. NMR in Biomedicine. 2020;33:e4397 10.1002/nbm.4397
REFERENCES
- 1. Ciobanu L. Microscopic magnetic resonance imaging: A practical perspective. Singapore: Pan Stanford Publishing; 2017. [Google Scholar]
- 2. Glover P, Mansfield P. Limits to magnetic resonance microscopy. Rep Prog Phys. 2002;65(10):1489‐1511. [Google Scholar]
- 3. Schadewijk VR, Krug JR, Shen D, et al. Magnetic resonance microscopy at cellular resolution and localised spectroscopy of Medicago truncatula at 22.3 Tesla. Sci Rep. 2020;10(1):1‐11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Weiger M, Schmidig D, Denoth S, et al. NMR microscopy with isotropic resolution of 3.0 𝜇m using dedicated hardware and optimized methods. Concepts Magn Reson Part B: Magn Reson Eng: Educat J. 2008;33(2):84‐93. [Google Scholar]
- 5. Ciobanu L, Seeber D, Pennington C. 3D MR microscopy with resolution 3.7 𝜇m by 3.3 𝜇m by 3.3 𝜇m. J Magn Reson. 2002;158(1–2):178‐182. [DOI] [PubMed] [Google Scholar]
- 6. Gutman DA, Keifer OP Jr, Magnuson ME, et al. A DTI tractography analysis of infralimbic and prelimbic connectivity in the mouse using high‐throughput MRI. Neuroimage. 2012;63(2):800‐811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Ciobanu L, Jayawickrama DA, Zhang X, Webb AG, Sweedler JV. Measuring reaction kinetics by using multiple microcoil NMR spectroscopy. Angewandte Chemie International Edition. 2003;42(38):4669‐4672. [DOI] [PubMed] [Google Scholar]
- 8. Purea A, Neuberger T, Webb AG. Simultaneous NMR microimaging of multiple single‐cell samples. Concepts Magn Reson Part B: Magn Reson Eng: Educat J. 2004;22(1):7‐14. [Google Scholar]
- 9. Wang T, Ciobanu L, Zhang X, Webb A. Inductively coupled RF coil design for simultaneous microimaging of multiple samples. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering: An Educational Journal. 2008;33(4):236‐243. [Google Scholar]
- 10. Minard KR, Wind RA. Solenoidal microcoil design. Part I: Optimizing RF homogeneity and coil dimensions. Concepts Magn Reson. 2001;13(2):128‐142. [Google Scholar]
- 11. Neuberger T, Tyagi V, Semouchkina E, et al. Design of a ceramic dielectric resonator for NMR microimaging at 14.1 tesla. Concepts Magn Reson Part B: Magn Reson Eng. 2008;33B(2):109‐114. [Google Scholar]
- 12. Haines K, Neuberger T, Lanagan M, Semouchkina E, Webb A. High Q calcium titanate cylindrical dielectric resonators for magnetic resonance microimaging. J Magn Reson. 2009;200(2):349‐353. [DOI] [PubMed] [Google Scholar]
- 13. Moussu MA, Ciobanu L, Kurdjumov S, et al. Systematic analysis of the improvements in magnetic resonance microscopy with ferroelectric composite ceramics. Adv Mater. 2019;31(30):1900912 10.1002/adma.201900912 [DOI] [PubMed] [Google Scholar]
- 14. Kajfez D, Guillon P. Dielectric resonators. Atlanta: Noble Publishing Corporation; 1998. [Google Scholar]
- 15. Moussu MAC, Abdeddaim R, Dubois M, et al. A semi‐analytical model of high permittivity dielectric ring resonators for magnetic resonance imaging. IEEE Trans Anten Propag. 2020;68(8):6317‐6329. [Google Scholar]
- 16. Awai I, Zhang Y. Coupling coefficient of resonators—An intuitive way of its understanding. Electron Commun Japan (Part II: Electronics). 2007;90(9):11‐18. [Google Scholar]
- 17. Elnaggar SY, Tervo RJ, Mattar SM. General expressions and physical origin of the coupling coefficient of arbitrary tuned coupled electromagnetic resonators. Journal of Applied Physics. 2015;118(19):194901 10.1063/1.4935634 [DOI] [Google Scholar]
- 18. Abdeddaim R, Ourir A, de Rosny J. Realizing a negative index metamaterial by controlling hybridization of trapped modes. Physical Review B. 2011;83(3):033101. [Google Scholar]
- 19. Mivelle M, Grosjean T, Burr GW, Fischer UC, Garcia‐Parajo MF. Strong modification of magnetic dipole emission through diabolo nanoantennas. ACS Photon. 2015;2(8):1071‐1076. [Google Scholar]
- 20. Boudarham G, Abdeddaim R, Bonod N. Enhancing the magnetic field intensity with a dielectric gap antenna. Appl Phys Lett. 2014;104(2):021117. [Google Scholar]
- 21. Elnaggar SA, Mattar S, Petersen B, Colpitts B. Coupled‐mode Theory for RF and Microwave Resonators. PhD thesis. University of New Brunswick, 2013.
- 22. Awai I, Zhang Y. New expression of coupling coefficient between resonators based on overlap integral of EM field. IECIE Trans Electron. 2005;E88‐C(12):2295‐2301. [Google Scholar]
- 23. Jouvaud C, Abdeddaim R, Larrat B, De Rosny J. Volume coil based on hybridized resonators for magnetic resonance imaging. Applied Physics Letter. 2016;108(2):023503. [Google Scholar]
- 24. Fedotov V, Rose M, Prosvirnin S, Papasimakis N, Zheludev N. Sharp trapped‐mode resonances in planar metamaterials with a broken structural symmetry. Physical Review Letter. 2007;99(14):147401. [DOI] [PubMed] [Google Scholar]
- 25. Capolino F. Theory and phenomena of metamaterials. Boca Raton: CRC press; 2009. [Google Scholar]
- 26. Nenasheva E, Kartenko N, Gaidamaka I, et al. Low loss microwave ferroelectric ceramics for high power tunable devices. J Eur Ceram Soc. 2010;30(2):395‐400. [Google Scholar]
- 27. Nenasheva EA, Kanareĭkin AD, Dedyk AI, Pavlova YV. Electrically controlled BST‐Mg ceramic components for applications in accelerator technology. Phys Solid State. 2009;51(8):1557‐1560. [Google Scholar]
- 28. Nenasheva EA, Kartenko NF, Gaidamaka IM, Redozubov SS, Kozyrev AB, Kanareykin AD. Low permittivity ferroelectric composite ceramics for tunable applications. Ferroelectrics. 2017;506(1):174‐183. [Google Scholar]


