A Simple Low-Cost Wearable Sensor for Long-Term Ambulatory Monitoring of Knee Joint Kinematics

Abstract

Objective:

Accurate monitoring of joint kinematics in individuals with neuromuscular and musculoskeletal disorders within ambulatory settings could provide important information about changes in disease status and the effectiveness of rehabilitation programs and/or pharmacological treatments. This paper introduces a reliable, power efficient, and low-cost wearable system designed for the long-term monitoring of joint kinematics in ambulatory settings.

Methods:

Seventeen healthy subjects wore a retractable string sensor, fixed to two anchor points on the opposing segments of the knee joint, while walking at three different self-selected speeds. Joint angles were estimated from calibrated sensor values and their derivatives in a leave-one-subject-out cross validation manner using a random forest algorithm.

Results:

The proposed system estimated knee flexion/extension angles with a root mean square error (RMSE) of 5.0° ± 1.0° across the study subjects upon removal of a single outlier subject. The outlier was likely a result of sensor miscalibration.

Conclusion:

The proposed wearable device can accurately estimate knee flexion/extension angles during locomotion at various walking speeds.

Significance:

We believe that our novel wearable technology has great potential to enable joint kinematic monitoring in ambulatory settings and thus provide clinicians with an opportunity to closely monitor joint recovery, develop optimal, personalized rehabilitation programs, and ultimately maximize therapeutic outcomes.

I. Introduction

Accurate monitoring of joint angles in the ambulatory setting could provide important information regarding the progress of rehabilitation in patients with neuromuscular and musculoskeletal disorders, such as stroke [1], Parkinson’s disease [2], osteoarthritis (OA) [3], anterior cruciate ligament injury [4], and rotator cuff injury [5]. Traditionally, kinematic analysis has been performed within laboratory settings using optoelectronic motion capture systems—the gold standard for human kinematic analysis—which utilize an array of infrared cameras to capture the positions of reflective markers placed on predefined anatomical landmarks to create a three-dimensional (3D) skeletal model. These systems are useful in clinical and research environments, but the availability of well-equipped gait laboratories in clinical settings is often lacking, and is limited by cost and technical expertise. Most importantly, assessments restricted to laboratory settings provide a narrow snapshot of function and do not capture natural free-living gait patterns, thus representing a severely under-sampled view of patients’ conditions [6]. Frequent, longitudinal monitoring of kinematic parameters in ambulatory settings could provide an objective assessment of physical function and disease progression, allowing the development of personalized treatments and rehabilitation programs to cope with dynamically changing functional performance levels [7].

Much effort has been made to develop wearable sensors that can facilitate real-time, continuous joint health and movement monitoring in free-living conditions [8], including approaches that leverage near-infrared spectroscopy [9], [10], bio-acoustics [11], [12], electrical bioimpedience [12], [13], and kinematic modeling. In particular, a wide range of sensing methodologies have been studied to enable kinematic modeling, such as inertial measurement units (IMUs) [14], [15], radio frequency [16], ultrasonic sensors [17], rigid electrogoniometers [18], [19], conductive ink-based flex sensors [20], fiber-optic sensors [21], [22], e-textile sensors [23], [24], inductive sensors [25], [26], liquid metal sensors [27], and string sensors [28]. However, few wearable systems support a comprehensive solution that is 1) power efficient, 2) cost effective, 3) safe, 4) easy-to-use, 5) flexible enough to comply with highly dynamic, heterogeneous human body shapes, and 6) accurate enough to support the 5° estimation accuracy suggested by the American Medical Association for movement analysis in a clinical context [29], which are important characteristics for long-term field study deployment [28].

This paper introduces a reliable, power efficient, and low-cost wearable sensor designed for long-term monitoring of joint kinematics in the ambulatory setting. In particular, this sensor was developed to monitor the knee joint angles of patients with knee OA. The proposed sensing platform uses a retractable string sensor that is both bendable and stretchable. This soft sensor measures changes in the string length between two anchor points positioned at opposing segments of the joint during movements, which is analogous to the measurement of skin stretch over the joint, and uses data-driven modeling to estimate the joint angle. As a proof of concept, we focus on estimating the knee flexion/extension angle during level ground walking at different speeds. We show that our wearable system can be used to estimate knee angles with acceptable accuracy throughout the gait cycle and at varying walking speeds.

II. Related Work

Existing wearable sensors for joint kinematic monitoring can be categorized into two broad approaches. One approach computes the relative positions of sensors placed at the two extremities of the joint (i.e., proximal and distal body segments) and indirectly estimates angles via biomechanical modeling. Another approach connects the two extremities and directly measures changes in the angle using rigid or soft materials.

Inertial Measurement Units (IMUs), which include an accelerometer, gyroscope, and/or magnetometer, are the most common form factor of wearable sensors that indirectly estimate joint angles [14], [15]. Kinematic parameters are obtained from IMUs by attaching units to the two opposing segments of a joint and measuring the orientation difference between the units. The measured difference is then processed to estimate the corresponding joint angle via biomechanical modeling. However, IMU-based approaches require either significant computational capability for signal processing (e.g., Kalman filtering), and/or continuous calibration by employing additional sensing units or modeling to diminish the effects of orientation drift [27], [30]. An alternative indirect approach leverages radio frequency or ultrasound signals to estimate joint angular displacement [16], [17]. A signal transmitter and receiver are positioned on the opposite ends of a joint and the receiver computes the distance between the two units based on the received signal characteristics, estimating the joint angle via biomechanical modeling. However, the continuous transmission of a wireless signal between transmitter and receiver leads to large power consumption and the transmitted signals are susceptible to electromagnetic or acoustic interference.

A number of studies have directly estimated joint angles by employing a rotational potentiometer positioned at the hinge of the joint and connecting the opposing segments using a rigid component [18], [19]. Although this approach is relatively inexpensive and power efficient, rigid components often fail to accommodate the variability in body shapes and sizes observed in sedentary patient populations making the system uncomfortable and inaccurate. To overcome this limitation, some studies used more flexible materials to cope with dynamic body profiles, such as flex sensors [20], fiber-optic sensors [21], [22], e-textile sensors [23], [24], and inductive sensors [25], [26]. Flex and fiber-optic sensors are bendable but not necessarily stretchable. Therefore, these sensors suffer from similar limitations in body-compliance as rigid electrogoniometers. On the other hand, e-textile and inductive sensors are both bendable and stretchable. However, despite the ability to bend and stretch in different geometric dimensions, they produce a 1D sensing output (i.e., resistance for e-textiles and inductance for inductive sensors). Therefore, the estimation accuracy of joint kinematics in a specific body plane (e.g., knee flexion/extension angle in the sagittal plane) may be reduced since the deformation of the sensing materials in other planes (e.g., the coronal and transverse planes) during movement can be reflected on the measurement and act as noise. This issue may be more pronounced in clinical populations (e.g., knee OA) where the disease contributes to malalignment of the limb. A unique approach towards estimating joint angles is the use of liquid metal sensors [27], which provide a flexible interface and accurate estimation. However, these sensors could require sophisticated fabrication processes and could lead to health hazards due to the potential toxicity of liquid metals. Our research group previously introduced a flexible wearable sensor that leveraged a retractable string sensor to estimate knee flexion/extension angles [28]. However, this preliminary work employed a proof-of-concept system where the sensor data were collected via a non-wearable device (i.e., a laptop computer) and analyzed using a rather simple biomechanical model to estimate the joint angle (i.e., a 3^rd order polynomial fitting between the sensor readings and joint angles) that does not effectively capture different mechanical behaviors of the sensor during knee flexion vs. extension movements (see Section III for details). Furthermore, the study employed only nine subjects to validate the concept of a string-based flexible wearable sensor for human kinematic analysis.

III. Methods

A. Proposed Sensor System

Fig. 1a illustrates our wearable sensing device. The key component of the proposed system is a retractable string sensor that provides a highly flexible (i.e., both bendable and stretchable) form factor to comply with heterogeneous and dynamic body morphology. The retractable sensor consists of a nylon string, a reel, a clock spring that provides torque to retract the reel, and a potentiometer that measures the number of rotations of the reel. The reel and sensor enclosures were 3D-printed as shown in Fig. 1b. The sensing unit (i.e., the reel and potentiometer) was designed to be placed on the shank near the ankle either by 1) using a series of Velcro straps as shown in Fig. 1a or 2) directly attaching the device to the skin using adhesives. The end of the string was extended over the knee joint and affixed to the thigh, and the string was run through guidance tubes in order to secure its position and trajectory during joint movements. This specific placement configuration (i.e., the sensing unit on the shank and the tip of the string on the thigh) was chosen to minimize the chances of migration of the sensor position from muscle movements during human locomotion. The wearable device, excluding the Velcro straps, weighed only 98 g, which minimally disturbed the gait performance.

Fig. 1.

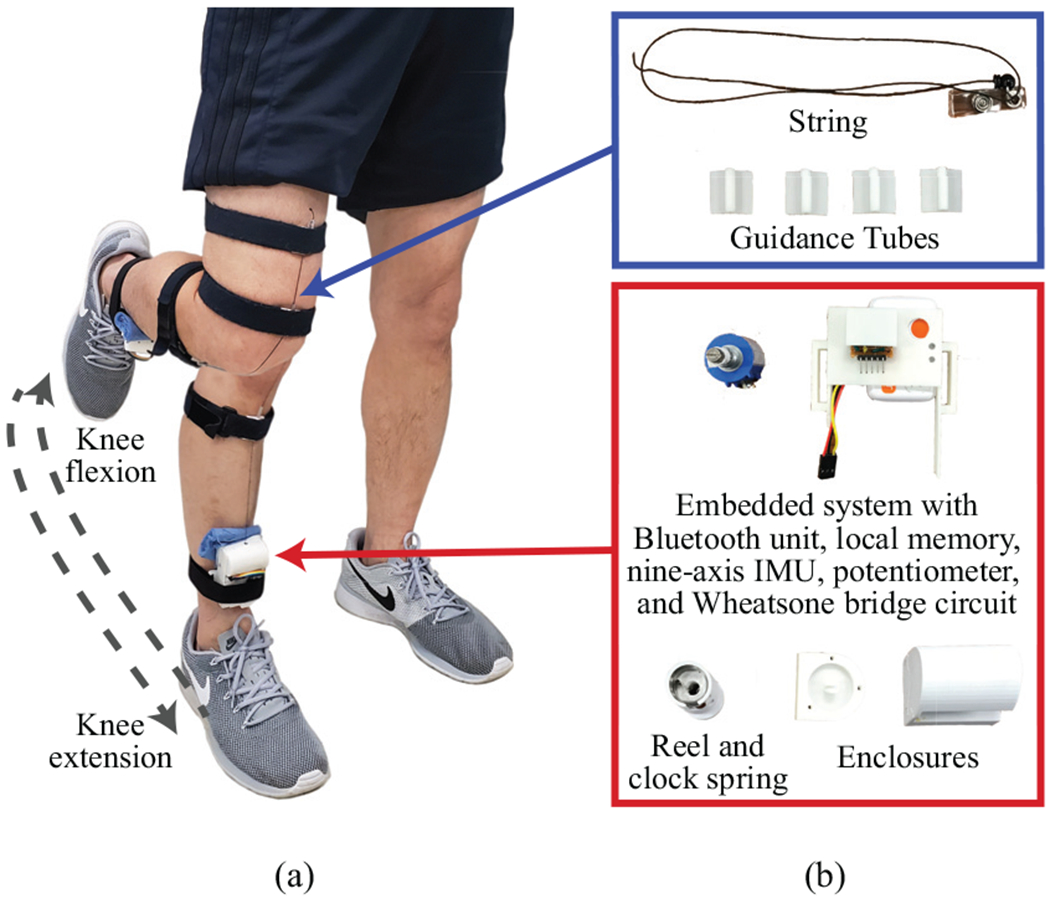
(a) The final design of the proposed system at knee extension and flexion positions. (b) Individual components of the proposed system.

Fig. 2.

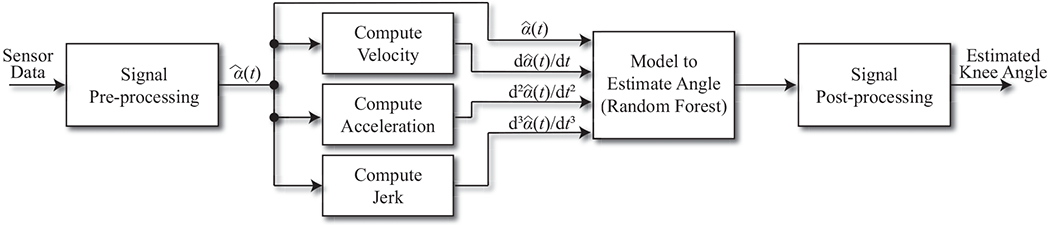
The processing pipeline for estimating knee angles given potentiometer readings transmitted by the sensor. Calibration consists of recording readings at 0° and 90° knee flexion. The calibrated readings and their first three derivatives are the only inputs to the Random Forest model.

The clock spring generated a constant torque to retract the string. Thus, during knee extension the clock spring retracted the string by rotating the reel. Conversely, during knee flexion the string was pulled out of the enclosure by the human-generated torque. The magnitude of the clock spring’s torque was not perceivable by subjects during walking and hence did not restrict the performance of leg movements. The potentiometer that measured the rotation of the reel—thereby measuring the extension and retraction of the string during knee flexion and extension, respectively—operated in a high resistance range (~ 0.1 MΩ) at 3.3 V and thus, the power draw of the sensing component was negligible. The retractable sensing unit was integrated with an off-the-shelf product (Shimmer Sensing, Dublin, Ireland) that contained an ultra-low power microcontroller, a nine-axis IMU, a wireless (Bluetooth) transceiver, local data storage, and a battery. Though the off-the-shelf sensor contained an IMU, it was not used for this experiment. A Wheatstone bridge circuit adjusted the operational voltage range (0–3.3 V) to the resistance range of the potentiometer to maximize the resolution of the sensor readings detected by the microcontroller. Analog input data collected from the potentiometer (more precisely, the Wheatstone bridge circuit) were sampled at 50 Hz and digitized using an embedded analog-to-digital converter.

B. Data Collection

A total of 17 subjects (21.9±3.7 years, mean ± standard deviation; 9 females and 8 males) were recruited at the University of Massachusetts Amherst. The recruitment criteria stipulated that subjects had to be healthy and between 18 and 50 years old. Subjects who had any musculoskeletal, neurological, orthopedic or similar disorders that could alter gait patterns while walking were excluded from the experiment. Research staff equipped subjects with our wearable device on their right legs using four Velcro straps, as shown in Fig. 1a. The two outer straps acted as anchor points and the two inner straps helped to guide the string over the midline of the patella. Although research staff visually confirmed that string ran straight down the midline of the knee, the device placement was not strictly controlled. Rigid clusters of reflective markers were placed on the ankle, knee, and hip to track segment motion during gait using an optoelectronic motion capture system (Qualisys AB, Göteborg, Sweden). Three-dimensional knee angles were calculated using a Cardan XYZ rotation sequence in the Visual3D software package and the flexion/extension angle was used as ground truth. Wearable sensor readings at knee flexion angles of 0° (i.e., full extension) and 90° were measured with a goniometer for the purpose of sensor calibration during data preprocessing (see Section III-C for details). Subjects walked at self-selected preferred, slow, and fast speeds and performed twenty repetitions of each speed. The experimental procedures were approved by the Internal Review Board of the University of Massachusetts Amherst (#2017-4405) and subjects provided written informed consent.

C. Data Analysis

Fig. 2 illustrates the data analytic pipeline used to process the sensor readings and estimate knee flexion/extension angles. Raw voltage data from the sensor were first digitally low-pass filtered at 5 Hz to remove any noise generated by non-human elements (e.g., sensor measurement noise) using a second order Butterworth filter. The cutoff frequency was chosen based on previous studies suggesting that typical walking and running step frequencies are less than 5 Hz [31]. Particularly, walking occurs at step frequencies of less than 2.5 Hz [31]. Then, calibrated sensor readings, $\widehat{\alpha }\left(t\right)$, were obtained from the filtered sensor readings, α(t), by

$$\widehat{\alpha }\left(t\right)=\frac{\alpha \left(t\right)-C_0}{C_{90}-C_0},$$ (1)

where t represents the time index and C₀ and C₉₀ are sensor readings at 0° and 90° flexion obtained during the calibration process, respectively. By subtracting the string length at 0° from α(t) and normalizing to the length difference between 0° and 90°, $\widehat{\alpha }\left(t\right)$ calculates the normalized changes in the string length during knee flexion and extension with respect to each subject’s string length difference between 0° and 90° flexion angles. The unit of $\widehat{\alpha }\left(t\right)$ is percentage. Because the value of C₉₀ – C₀ does not change over time, the calibration process that measures this parameter needs to be performed only once. On the other hand, whenever the sensor is re-positioned (e.g., during the donning/doffing of the sensor), the value of α(t) – C₀ may change because the value of C₀ can be different at the new position. Fortunately, C₀ can be easily updated by asking the user to fully extend their leg (e.g., stand up straight).

Knee joint movement requires a complex anatomical model because the knee is not a hinge joint and the axis of rotation changes during flexion and extension [32]. In other words, a linear transformation from $\widehat{\alpha }$ to the knee flexion/extension angle would not be feasible. We therefore employed a non-parametric machine learning algorithm—a Random Forest with 100 trees—to flexibly define the relationship between calibrated sensor readings and ground truth knee angles. The number of trees was chosen based on a prior study indicating that most performance gains occur when training the first 100 trees [33]. The input features to the model were the calibrated sensor readings and their first three derivatives (i.e., $\widehat{\alpha }$, $d\widehat{\alpha }/dt$, $d^2\widehat{\alpha }/d{t}^2$, and $d^3\widehat{\alpha }/d{t}^3$), which provide sufficient information about the non-linear sensor-to-angle relationships (see Section IV for more details). Furthermore, we observed different sensor-to-angle relationships during knee flexion and extension, because different torques drove string extension and retraction—i.e., human-generated torque pulled the string against the force of the clock spring during knee flexion, and the clock spring retracted the string during knee extension. To compensate for this behavior, we trained separate Random Forest models for flexion and extension. The appropriate model was selected based on the derivative of the calibrated sensor readings; negative derivatives indicated knee extension (driven by the clock spring) and non-negative derivatives indicated knee flexion (driven by human-generated torque).

The estimated time-series produced by the Random Forest models had high frequency noise (i.e., estimation errors) because the models estimated each angle independently without considering the temporal relationships of the sensor readings. Though machine learning algorithms that model temporal sequences may have better captured the specific dynamics of walking, we instead chose to only model the cross-sectional sensor-to-angle relationship to minimize the likelihood of overfitting the machine learning models to healthy walking patterns and maximize the opportunity to translate our methods and findings to other activities of daily living. Because we did not explicitly model the temporal relationships of the sensor readings, we instead attenuated the high frequency noise by smoothing the estimated knee angles using a second order Butterworth filter with a low-pass cutoff frequency of 5 Hz, which preserves walking and running frequencies [31].

The proposed system’s accuracy was evaluated using the Leave-One-Subject-Out Cross Validation (LOSOCV) technique. LOSOCV trains a model for each subject, in which the subject is left out as the testing set and the model is trained on the remaining subjects’ data. LOSOCV provides a fair evaluation of the estimation accuracy by applying the trained model to a previously unseen subject. For our data, the training set within each iteration of LOSOCV contained between 135,756 and 140,872 observations from sixteen subjects and the respective testing set contained between 5,649 and 10,765 observations from a single subject. The overall and averaged subject-level Root Mean Square Errors (RMSE) and Mean Absolute Errors (MAE) between the estimated and actual knee angles were used as evaluation metrics.

We also evaluated our model’s performance in terms of RMSE and MAE at four kinematic parameters that capture important features of knee motion throughout the gait cycle (e.g., related to the severity and progression of knee OA [34], [35]). The parameters were: 1) the flexion angle at the heel strike, 2) the peak flexion angle during the stance phase, 3) the flexion angle at the toe-off, and 4) the peak flexion angle during the swing phase. To identify these parameters, we manually segmented walking trials into complete gait cycles and applied dynamic time warping [36] to align the ground truth and estimated gait cycles. The time locations of the parameters within a gait cycle were manually annotated based on the warped time-series. A one-way ANOVA test was used to determine if differences between these parameters at different speeds were significant.

IV. Results

Table I summarizes the the RMSE and MAE between the estimated knee angles based on the proposed wearable system and the ground truth knee angles measured by the optoelectronic system that were computed over the study subjects (termed as subject-level RMSE and MAE hereafter) for all walking speeds. The subject-level RMSE and MAE were 5.0° ± 1.0° and 3.9° ± 0.8° respectively, which supports the recommended 5° accuracy for movement analysis in a clinical context [29]. The RMSE and MAE were consistent across all three walking speeds as determined by one-way ANOVA (p = 0.79 for the RMSE and p = 0.70 for the MAE). Fig. 4 illustrates the estimation performance for every data sample collected by the wearable device from all subjects. The black diagonal represents the perfect estimations. Each point is colored according to densities determined by a 2D histogram, which shows that most estimated angles are clustered tightly around the perfect prediction line despite some degree of variability. The overall estimations demonstrate a strong agreement to the ground-truth with R² = 0.94.

TABLE 1:

Subject-level root mean square errors (RMSE) and mean absolute errors (MAE) for each walking speed. One-way ANOVA tests indicated no difference between speeds.

	RMSE (°)	MAE (°)
All Speeds	5.0 ± 1.0	3.9 ± 0.8
Slow Speed	5.0 ± 1.2	4.1 ± 0.9
Preferred Speed	4.8 ± 1.3	3.8 ± 1.0
Fast Speed	4.7 ± 1.0	3.8 ± 0.8

Fig. 4.

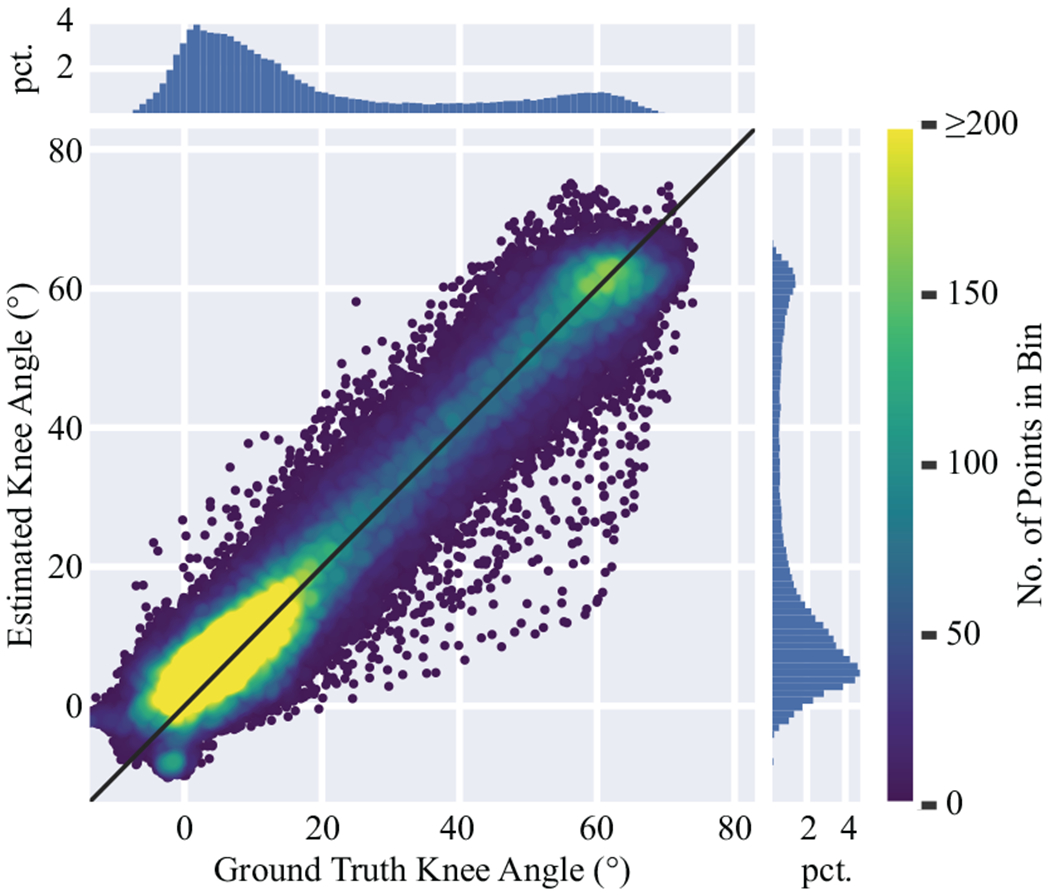
Overall knee angle estimation performance, excluding the outlier subject, illustrated by a scatter plot of ground truth vs. estimated knee angles. The diagonal (y = x) line represents perfect estimations. Color corresponds to point density, determined by the number of points in each bin of a 2D histogram. The color scale stops at 200 points per bin to better show the density differences for larger angles. The marginal histograms show the percentage (pet.) of data in each marginal bin.

It is important to note that there was an outlier subject whose estimation performance deviated from the other subjects. Fig. 3 shows the distribution of the knee angle estimation performance in terms of subject-level RMSE and MAE, where the outlier subject is annotated with text. The outlier subject had z-scores of 3.6 and 3.8 standard deviations for the RMSE and MAE, respectively. The estimation performance reported in the previous paragraph was obtained after removing this outlier. The subject-level RMSE and MAE before removing the outlier were 5.5° ± 2.2° and 4.5° ± 2.2°, respectively. Upon further investigation, the outlier subject’s estimated knee angles were consistently under-predicted, though the shapes of the estimated trajectories closely resembled the ground truth. Manually adding a constant bias to each of the outlier’s walking trials resulted in a subject RMSE of 4.2° and MAE of 3.5°, which is consistent with the unaltered results for other subjects shown in Fig. 3. Therefore, we believe that the outlier is likely the result of an incorrectly measured C₀ in the nominator of (1) and is not reflective of our model’s estimation performance. We thus excluded the outlier subject from additional results.

Fig. 3.

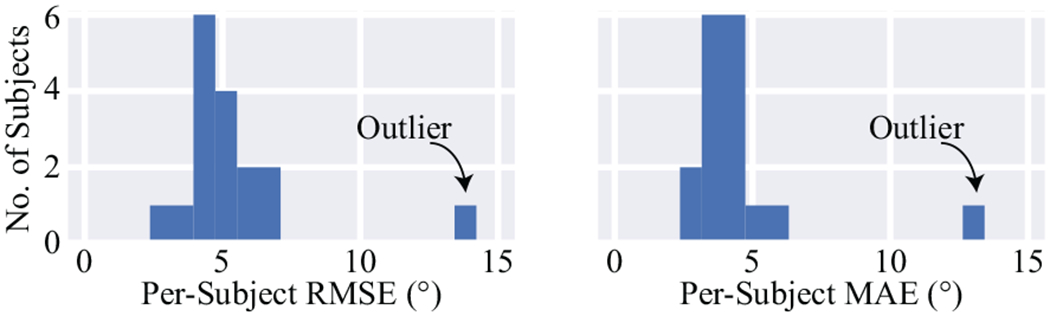
The root mean square error (RMSE) and mean absolute error (MAE) of the estimated knee angles for each subject. One subject is a clear outlier.

Fig. 5 shows the time-warped ground truth and estimated knee angles throughout the gait cycle. The black line and shading represent the mean and standard deviation of all gait cycles, respectively. The estimated knee angles clearly resemble the ground truth angles. The actual timing of the gait parameters was also consistent—when comparing the non-time-warped ground truth and estimated time-series—with MAEs of 0.03 s, 0.03 s, and 0.01 s for the peak flexion during stance, the flexion/extension at toe-off, and the peak flexion during swing with respect to the heel strike. Table II lists the values of the ground truth and estimated knee angles and the RMSE between the ground truth and estimations for the four important kinematic gait parameters considered in this work. Overall, the RMSE was 6.9° for the knee flexion/extension angle at the heel strike, 4.7° for the peak flexion angle during the stance phase, 4.8° for the knee flexion/extension angle at the toe-off, and 5.5° the peak flexion angle during the swing phase. We also report values for each speed separately. Oneway ANOVA tests indicated no differences in the absolute errors of different speeds for the knee flexion/extension angle at the heel strike (p = 0.09) and the toe-off (p = 0.11), but did indicate differences in the absolute errors of different speeds at the peak flexion angle during the stance (p < 0.01) and swing (p < 0.05) phases. These speed-related differences may manifest at the peak angles because the tension of the string increases as it extends from the clock spring, possibly resulting in slightly different extension and retraction mechanics at different speeds.

Fig. 5.

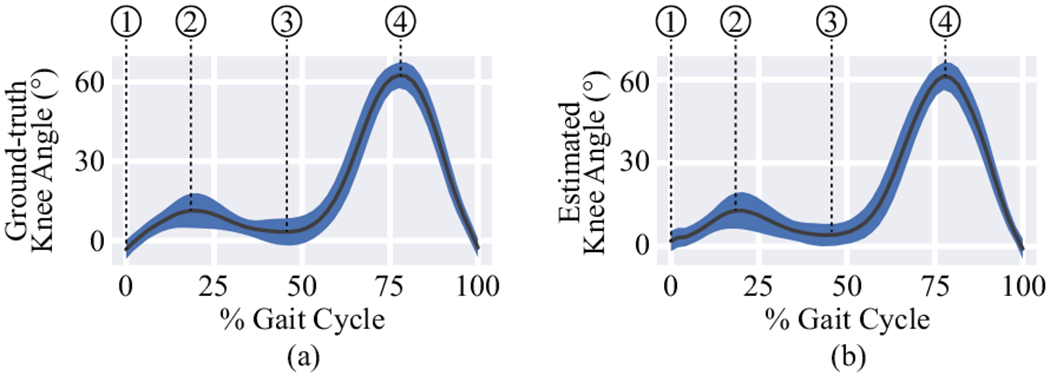
Comparison of a) ground truth gait cycles and b) gait cycles estimated from sensor readings. The solid line is the mean knee angle and the shaded area represents one standard deviation. Four important kinematic parameters during gait are annotated in the figures: 1) the knee flexion/extension angle at the heel strike, 2) the peak flexion angle during the stance phase, 3) the knee flexion/extension angle at the toe-off, and 4) the peak flexion angle during the swing phase.

TABLE 2:

Ground truth (GT) and estimated knee angles, and the root mean square error (RMSE) between knee angles, at four important phases of the gait cycle. Each walking speed is shown separately. The outlier subject is not included. One-way ANOVA tests were applied to determine if absolute errors differed between speeds.

	All Speeds (°)			Slow Speed (°)			Preferred Speed (°)			Fast Speed (°)			p-value (ANOVA)
	GT	Est.	RMSE	GT	Est.	RMSE	GT	Est.	RMSE	GT	Est.	RMSE
Flexion at Heel Strike	−3.3±3.6	1.9±3.7	6.9	−4.1±3.1	2.2±3.9	7.5	−4.0 ± 3.4	1.4±3.6	7.1	−1.6±3.8	2.1±3.4	5.8	0.09
Peak Flexion during Stance	11.3±6.5	12.8±6.4	4.7	8.5±5.7	10.5±6.4	4.9	11.4±4.9	12.9±4.6	4.0	15.2±7.1	15.9±7.0	5.2	< 0.01
Flexion at Toe-Off	3.3±5.1	4.1±4.0	4.8	2.7±4.1	4.2±4.0	4.2	3.3±5.0	3.1±2.1	5.0	4.1±6.2	5.0±5.3	5.3	0.11
Peak Flexion during Swing	62.5±4.9	61.3±5.0	5.5	61.0±4.3	61.5±4.7	5.4	63.0±4.5	61.3±4.8	5.2	64.1±5.4	61.0±5.4	5.9	< 0.05

We investigated the importance of including the derivatives as features by training an alternate model with only the calibrated sensor readings as an input. The subject-level RMSE and MAE of this alternate model—excluding the outlier for fair comparison—were 7.6° ± 1.8° and 5.9° ± 1.3° respectively, which were significantly higher than the aforementioned model that leverages the derivatives as detennined by an unpaired t-test (p < 0.01). These results confirm that using the derivatives improves estimation performance. To better analyze these sensor inputs, Fig. 6 visualizes the calibrated sensor readings and their derivatives (i.e., the inputs to the Random Forest model) vs. the ground truth knee angles measured by the optoelectronic system. For clarity of the demonstration, only a subset of a single subject’s data is shown. The difference between the flexion (orange) and extension (blue) points in all plots highlights the different mechanical responses of the clock spring during extension and retraction of the string, respectively. Fig. 6a also shows the non-linear relationship between the ground truth angles and the calibrated readings for both flexion and extension. Furthermore, considering Fig. 6b–d in combination with Fig. 6a demonstrates that, in addition to better capturing the differences in flexion and extension, the derivatives help to capture the stance and swing phases of the gait cycle. In particular, the derivatives may help to differentiate between the stance and swing phases when $\widehat{\alpha }\left(t\right)$ is low (whereas a high value of $\widehat{\alpha }\left(t\right)$ during gait implies the swing phase). For example, Fig. 6b shows that large values of $d|\widehat{\alpha }\left(t\right)|/dt$ likely indicate the stance phase for smaller flexion angles. Hence, the calibrated sensor readings and their derivatives could together help the Random Forest model capture different sensor-to-angle relationships during flexion vs. extension and stance vs. swing phases. We also experimented with adding additional derivatives as inputs to the model. However, the performance gains were marginal, indicating that the first three derivatives are sufficient to capture the dynamics of the sensor-to-angle relationship.

Fig. 6.

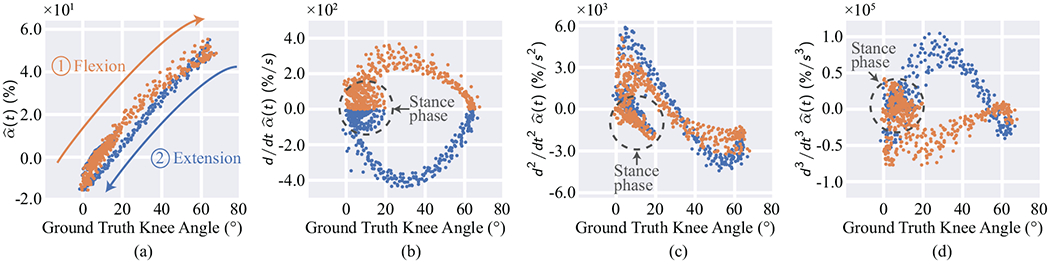
Ground truth knee angles vs. calibrated sensor values and their derivatives for two walking trials of each speed for a single subject. Flexion and extension are represented as orange and blue points, respectively. All plots demonstrate differences between flexion and extension. (a) also demonstrates the nonlinear relationship between sensor readings and ground truth angles. (b)-(d), when considered in combination with (a), show that the derivatives help to differentiate between the stance and swing phases of the gait cycle, particularly for small angles. For example, (b) shows that larger magnitudes of the first derivative indicate the stance phase for small knee angles. Dotted circles in (b)-(d) indicate the stance phase.

V. Discussion

Our results show that the proposed flexible (i.e., bendable and stretchable) sensing device can accurately measure knee flexion/extension angles at a variety of walking speeds with an RMSE of 5.0° ± 1.0° and an MAE of 3.9° ± 0.8°, which specifically support the recommended 5° accuracy for clinical applications [29]. The proposed system—in comparison to existing wearable solutions—offers an attractive means to enable the long-term monitoring of key biomechanical parameters in remote settings based on its 1) simple string-based wearable form-factor that leverages low-cost sensing components (i.e., a potentiometer and clock spring), 2) ability to support a diverse range of body types as opposed to semi-rigid or rigid alternatives, 3) wearability and accessibility, as users can easily instrument and operate the sensor without precise positioning and/or calibration, and 4) reliability against potential alteration in sensing performance over a long-term period (e.g., sensing drifts over time).

There are a number of factors that we believe contribute to the observed estimation error rate of the proposed sensor (i.e., RMSE of 5.0° ± 1.0° and MAE of 3.9° ± 0.8°). For example, Table II shows that angles measured during heel strike have relatively high errors than the other kinematic parameters. The larger errors at the heel-strike occur because the sensor was not designed to capture hyperextension of the knee joint causing a momentarily slack string, which is more likely to occur during the heel-strike than the other gait phases. We believe optimizing the string’s tension may reduce these errors. Table II also reports significant differences in the peak flexion angle during both the stance and swing phases with larger errors for the fast speed, which were likely attributed to the sparser data points across a wider range of knee angles and the larger differences in tension at relatively high angular velocities of the knee. We believe that further optimization of the string’s tension and collection of additional training data will reduce errors, especially those introduced by uncertainties in the machine learning pipeline.

The differences between sensor readings and their derivatives that occur during flexion and extension, as shown in Fig. 6, warrant further discussion because other wearable sensors that rely on non-human forces (e.g., the elasticity of any soft wearable sensors [20]–[24], [27]) may also have similar considerations. For the proposed system, these differences arise because the string extends when pulled by humangenerated torque against the torque of the clock spring and retracts solely through the torque applied by the clock spring. If the clock spring’s torque is too low, retraction of the string will be sluggish and the disparity between extension and flexion will widen. Conversely, high tension could alter gait kinematics or cause discomfort as a result of stiffness or by tugging on the skin. As emphasized previously, future work needs to identify the optimal tension between the two opposite ends of the joint that maximizes measurement performance while minimizing the chance of sensor drift, discomfort, or altered gait.

We envision a clinical scenario in which the proposed system would be used first in rehabilitation facilities as part of routine therapy sessions to teach patients how to use the system. The system could also be used to monitor therapy dosage and range of motion over the course of the in-patient intervention. Patients would then be given the system and encouraged to wear it during the performance of activities of daily living in their home and community settings. Continuous, unobtrusive monitoring of kinematic parameters (e.g., range of motion or peak knee flexion/extension angle during the stance phase) can provide important information on changes in disease status and effectiveness of rehabilitation and/or pharmacological treatments for individuals with joint disorders [37]. Therefore the ambulatory use of this system would provide clinicians with an opportunity to closely monitor the joint recovery process and develop optimal, personalized rehabilitation programs to maximize individuals’ quality of life, which is the ultimate goal of rehabilitation [38]. Recent studies have shown that tele-rehabilitation in various conditions can be effective in improving joint function and pain, reduce healthcare cost, improve access to care, and delay the need for surgical intervention [39]. The proposed system can also be utilized to monitor the performance (e.g., quantity and quality) of tele-rehabilitation exercises, which requires near real-time feedback regarding the performed movements to maximize therapeutic outcomes [40].

This study has a number of limitations worth discussing. First, our prior work [28] reported slightly better performance despite the algorithm used in [28] producing inferior performance when applied to this data set. We believe this discrepancy may be a result of our prior work using a more tightly controlled data collection procedure and a smaller number of subjects who shared similar anthropometic characteristics. In contrast, this work used a larger subject population (16 when excluding the outlier) with heterogeneous characteristics. Second, the performance of our system could potentially be affected by improperly performed calibration, as evidenced by the outlier subject. C₉₀ – C₀ in the denominator of (1), which is a constant value that do not change over time, can initially be measured in a clinical setting using a goniometer or other reference measurement. It is important to note that our previous work based on the preliminary prototype version of our system found that the values of C₉₀ – C₀ showed no significant difference when subjects measured based on visual inspection vs. when a trained professional measured them using a goniometer [28], which supports that the user can easily re-calibrate the value when needed (e.g., due to growth in pediatric patients). The value of C₀ of the nominator, on the other hand, needs to be updated when the sensor is re-positioned on the body. It remains as important future work to verify the updated value of C₀ by monitoring the value of α(t) during the use of the device and possibly correcting erroneous values (e.g., C₀ should be close to the minimal value of α(t) during use). Third, investigation of the proposed system’s reliability for its use in real-world settings remains as important future work. For example, changes in the ambient temperature can affect the resistance of the rotational potentiometer, although they should have a marginal impact on the reported findings (i.e., the resistance would change by a factor of 0.15 % between 0 °C and 30 °C). Future works could leverage 1) additional sensing modalities to account for potential environmental factors (e.g., a temperature sensor) and their empirically defined relationships to the performance of the potentiometer, or 2) other methods of measuring the rotation of the reel that are less susceptible to such environmental factors (e.g., digital encoders are less affected by ambient temperature). Fourth, further work is also needed to investigate the impacts of various factors including different sensor-to-body attachment mechanisms, patient self-administration of the device, and non-walking activities, such as stair climbing. Because our study did not strictly control the positioning of the device, we believe patients can be trained to visually position the wearable device and that remaining placement errors are already reflected in our reported results. Furthermore, the proposed system should be adaptable to other activities because we did not explicitly incorporate any a priori knowledge of walking in our data-driven model. Finally, the proposed system is designed to only measure the flexion/extension angle, with the guidance tubes ensuring that the measurements are not impacted by movement in other planes. We believe a crossshaped arrangement of strings routed over the patella may be able to estimate movement in multiple planes, but leave the validation of this concept to important future work.

VI. Conclusion

We presented an accurate, cost-effective, power-efficient, flexible, and easy-to-operate wearable sensor system designed to enable long-term monitoring of joint kinematics in ambulatory environments. The proposed system employs a string to measure changes in distance between two anchor points positioned at the opposing segments of the joint, which is analytically converted to estimated joint angles. This approach enables the system to cope with dynamic, heterogeneous body profiles of different individuals. Compared to the benchmark optoelectronic system, the proposed system achieved an RMSE of 5.0° ± 1.0° and MAE of 3.9° ± 0.8° based on a data-driven algorithm once an outlier—which was likely the result of incorrect calibration—was removed. We believe that with further development the proposed system can be deployed in clinical and ambulatory environments to monitor important kinematic variables and to better inform clinicians of disease progression and the effectiveness of prescribed therapies.