Abstract
Vibrational spectroscopy is an essential tool in chemical analyses, biological assays, and studies of functional materials. Over the past decade, various coherent nonlinear vibrational spectroscopic techniques have been developed and enabled researchers to study time-correlations of the fluctuating frequencies that are directly related to solute-solvent dynamics, dynamical changes in molecular conformations and local electrostatic environments, chemical and biochemical reactions, protein structural dynamics and functions, characteristic processes of functional materials, and so on. In order to gain incisive and quantitative information on the local electrostatic environment, molecular conformation, protein structure and inter-protein contacts, ligand binding kinetics, and electric and optical properties of functional materials, a variety of vibrational probes have been developed and site-specifically incorporated into molecular, biological, and material systems for time-resolved vibrational spectroscopic investigation. However, still, an all-encompassing theory that describes the vibrational solvatochromism, electrochromism, and dynamic fluctuation of vibrational frequencies has not been completely established mainly due to the intrinsic complexity of intermolecular interactions in condensed phases. In particular, the amount of data obtained from the linear and nonlinear vibrational spectroscopic experiments has been rapidly increasing, but the lack of a quantitative method to interpret these measurements has been one major obstacle in broadening the applications of these methods. Among various theoretical models, one of the most successful approaches is a semiempirical model generally referred to as the vibrational spectroscopic map that is based on a rigorous theory of intermolecular interactions. Recently, genetic algorithm, neural network, and machine learning approaches have been applied to the development of vibrational solvatochromism theory. In this review, we provide comprehensive descriptions of the theoretical foundation and various examples showing its extraordinary successes in the interpretations of experimental observations. In addition, a brief introduction to a newly created repository website (http://frequencymap.org) for vibrational spectroscopic maps is presented. We anticipate that a combination of the vibrational frequency map approach and state-of-the-art multidimensional vibrational spectroscopy will be one of the most fruitful ways to study the structure and dynamics of chemical, biological, and functional molecular systems in the future.
Graphical Abstract
1. Introduction
The vibrational spectra of a polyatomic molecule, which depend strongly on its chemical structure and interactions with the surrounding environment and dynamical transformations between multiple conformations, can be accurately measured with linear absorption and inelastic light scattering spectroscopy in both the gas and condensed phases.1,2 As such, Fourier-transform IR absorption and Raman scattering spectroscopy have become essential tools in chemical analyses, biological assays, and studies of functional materials. Over the past decade, we have witnessed revolutionary developments in coherent nonlinear vibrational spectroscopy such as multidimensional electronic, IR, THz, IR-Raman, IR-vis, vis-IR, and THz-Raman techniques.3–37 From the coherent multidimensional spectroscopy measurements, researchers have extracted the solvation-induced frequency shifts and the time-correlations of the fluctuating frequencies and provided crucial insights into the spontaneously fluctuating motions of solvent molecules, dynamical changes in molecular conformations and local electrostatic environments, chemical and biochemical reactions, protein structural dynamics and functions, characteristic processes of functional materials, and so on.
To quantitatively analyze and interpret the spectroscopic observations, researchers have site-specifically introduced vibrational probes into molecular, biological, and material systems using a variety of organic and biochemical techniques.38–51 Such vibrational probes could be invasive when they are added to a solvated molecular system via their hydrogen-bonding interactions with surrounding solvent molecules or biomolecular residues. However, they are still significantly smaller than fluorophores, which makes them attractive probes for studying local environments. These IR-probe-labeled molecules, proteins, nucleic acids, functional materials, and chemically reactive systems have been subject to linear and nonlinear vibrational spectroscopic investigations to gain incisive and quantitative information on the local electric field, molecular conformation, protein contacts, energy transfer, ligand binding kinetics, and function-defining features of materials. This rapidly expanding library of experimental results has been reviewed recently by a few groups of researchers.38–42 However, the data generated through these experiments have inevitably required an interpretive method with atom-level chemical accuracy. Despite prolonged efforts in this area, an all-encompassing theory that describes the vibrational solvatochromism, electrochromism, and dynamic fluctuation of vibrational frequencies and how they reflect the chemistry and biology of the molecules has not been established. This is not only because the intermolecular interactions in the condensed phases are intrinsically complex,52–65 but also because the vibrational frequency shifts induced by the varying intermolecular interactions are very small quantities, e.g., fractions of thermal energy, and are difficult to model even with high-level quantum chemistry calculation methods.
To describe vibrational solvatochromic effects on molecular spectra quantitatively, a community of researchers have worked assiduously to find systematic and theoretically sound approaches by considering electric potential and field expansion of intermolecular interaction, distributed multipole analysis, effective fragment potential, and/or hybrid quantum chemistry-molecular mechanics simulation methods. They have designed a series of ab initio, semiempirical, or empirical models for specific IR probes of interest and referred to them as vibrational spectroscopic maps, which we will abbreviate jointly as the VSMs in this review. Using a rigorous theory of intermolecular interactions, extensive ab initio calculation results, and sometimes experimentally measured spectroscopic data, a variety of VSMs have been developed and successfully used to interpret the linear and nonlinear vibrational spectroscopic signals of complex systems at the molecular level.38,40,66–69 An example of such a vibrational frequency map is schematically depicted in Figure 1. The vibrational frequency of a localized vibrational mode is mapped onto a set of points, called the distributed sites, which are located within the IR chromophore and sense the spatial distribution of local electrostatic potential and electric field around it much like an antenna. Therefore, the VSMs correctly capture the sensitivity of the IR chromophores to their electrostatic environment and can be readily applied to study spontaneous fluctuation-induced chemical and physical processes in the condensed phases with unprecedented time and spatial resolution, in conjunction with the coherent nonlinear vibrational spectroscopy experiments.
Figure 1.
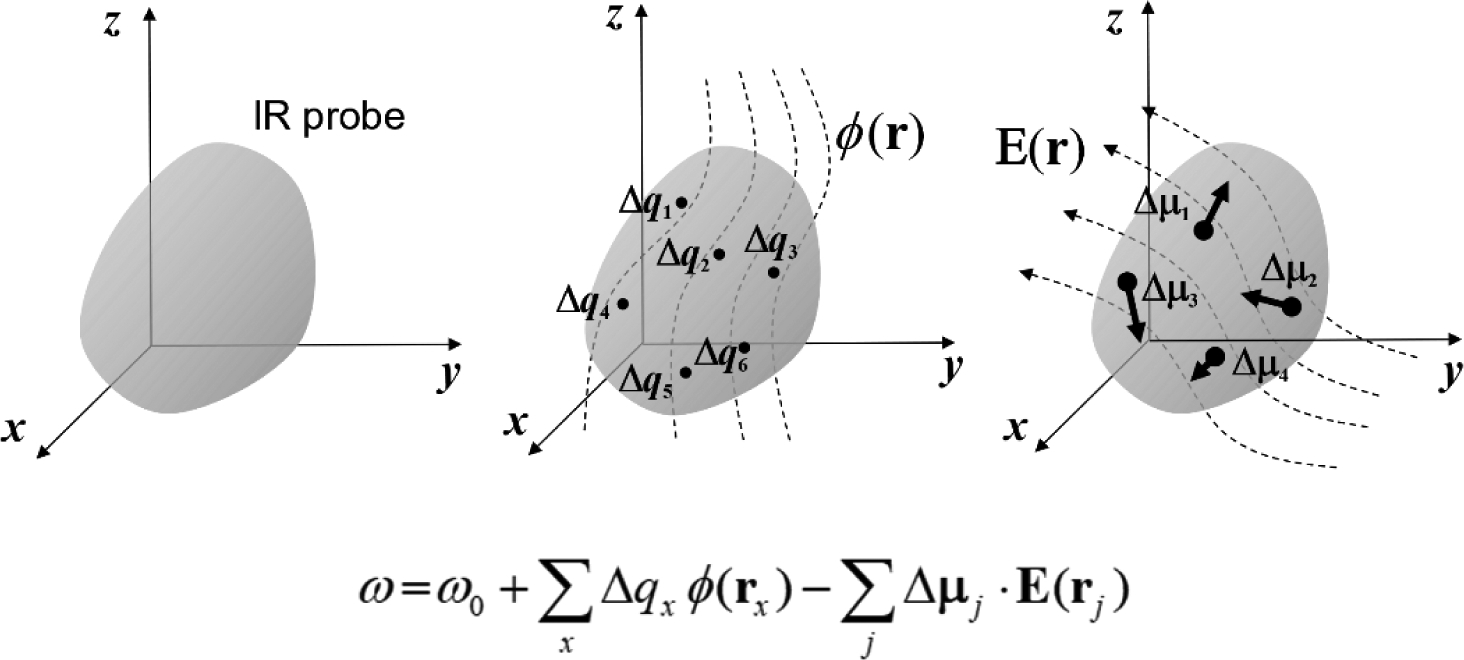
Vibrational frequency mapping with solvent electric potential and field. The vibrational frequency ω of a normal mode of an IR probe is mapped onto a set of points, called distributed sites, that interact with the electrostatic potential ϕ and electric field E exerted by the molecular environment. Note that the map parameters Δqx, which are vibrational solvatochromic charges, are scalar quantities whereas Δμx, which are vibrational solvatochromic dipoles, are Cartesian vectors. The vibrational reference frequency, ω0, which could also be a part of the map, corresponds to that of the IR probe in the absence of solvent electrostatic potential and electric field.
To demonstrate the working principles of linear and nonlinear vibrational spectroscopy techniques, we first note that molecular spectroscopy involves an interaction of the oscillating charged particles in a molecule with an external electromagnetic field whose frequency is close to one of the vibrational or electronic oscillations. Upon resonance between the molecular vibrations and the electromagnetic waves, the quantum transition amplitude becomes very large, which results in a high transition probability between two vibrational eigenstates of the molecule. IR absorption spectroscopy measures the distribution of these transition probabilities by detecting the attenuation of the incident IR beam, and Raman spectroscopy probes the inelastic light scattering cross-section of the molecule of interest.
As one of the recent additions to the inventory of molecular spectroscopic techniques, coherent multidimensional vibrational spectroscopy4,5,70 can be considered as a vibrational analog of multidimensional NMR spectroscopy.71,72 In general, such an experiment involves multiple ultrashort pulses with controlled delay times. More specifically, a series of coherent laser pulses with specific relative phases are used to interrogate the molecular system and to probe the correlation between distinctive vibrational transitions at different times. These pulses induce multiple transitions in the molecule, create nonlinear polarization in the system, and generate the electric field that carries the quantitative information about the multi-point time correlations of these vibrational transitions. Thus, the detected signal is intrinsically multidimensional in the time domain, and its Fourier transforms with respect to the judiciously chosen delay times give the time-resolved multidimensional spectra. For example, coherent two-dimensional (2D) vibrational spectroscopy employs three femtosecond laser pulses in the IR frequency range to induce the third-order polarization in molecular systems, which produces the third-order electric field oscillating with a frequency determined by the molecular vibrational frequency. As demonstrated in Figure 2, the generated signal electric field can be measured and presented in two frequency dimensions that are conjugate to the time intervals between the first and second pulses, τ, and between the third pulse and the detection, t. One can then plot a series of 2D IR spectra with respect to the waiting time, Tw, which is defined as the time interval between the second and the third pulses, to track the time evolution of the vibrational excitations.
Figure 2.
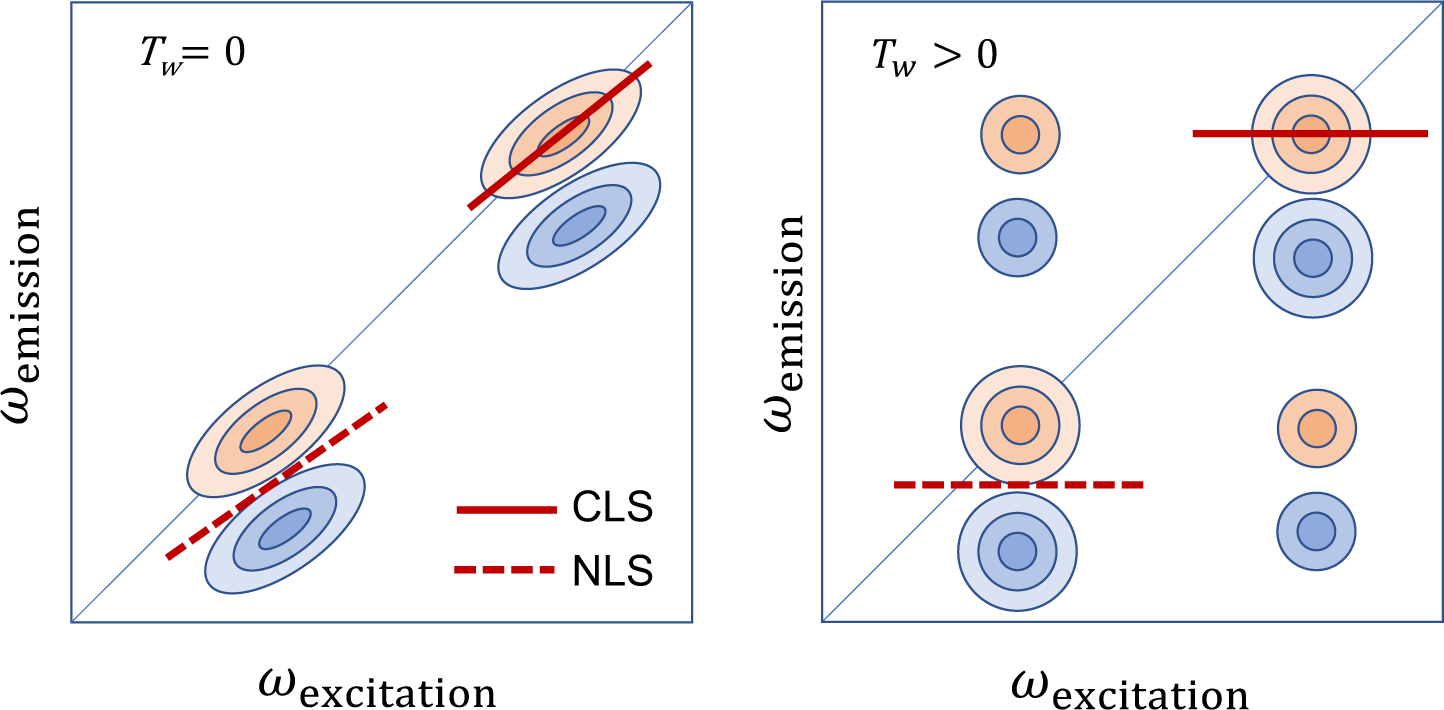
Schematic diagram of the 2D IR spectra of two oscillators. The x and y axes represent the excitation (pump) and emission (probe) frequencies, respectively. Here, it should be mentioned that sometimes 2D spectra are plotted with the two axes swapped. Two diagonal peaks with positive (red) amplitudes originate from the ground-state bleach and stimulated emission, whereas those with negative (blue) amplitudes are from the excited-state absorption. The center line slope (CLS) and nodal line slope (NLS) are related to the frequency-frequency correlation function and the inhomogeneity of the transition frequencies.73 If the two oscillators are coupled with each other via wave function overlap, one can find cross-peaks at zero waiting time. If the two oscillators exchange energy or undergo chemical exchange, the cross-peaks in the off-diagonal region of the 2D IR spectrum appear as the waiting time, Tw, increases.
Clearly, 2D vibrational spectroscopy is an ultrafast measurement technique. In a 2D spectrum, the changes of the diagonal and off-diagonal peaks provide unique information on the molecular vibrations, which cannot be extracted from the conventional one-dimensional vibrational spectroscopy. To name a few, these include the homogeneous and inhomogeneous line-broadenings, the anharmonic frequency shift of a given normal mode, the solute-solvent interaction induced spectral diffusion, and mode-mode vibrational coupling constants. As a result, 2D IR and other multidimensional spectroscopy techniques have been used as powerful tools for studying (i) the structure and dynamics of peptides,74–82 proteins,25,44,83–92 protein-ligand complexes,93 DNA,94–97 RNA,98 and lipid bilayers,99,100 (ii) the energy transfer dynamics between coupled oscillators in condensed phases,23,101–103 (iii) the hydrogen-bonding (H-bonding) structure and dynamics of liquid water and its isotopologues,104,105 (iv) the configurational and H-bonding dynamics of biomolecules,106,107 (v) the molecular exciton dynamics in photovoltaic materials,108 etc.
The amount of data obtained from the linear and nonlinear vibrational spectroscopic experiments has been rapidly increased, but the lack of a quantitative method to interpret various vibrational spectroscopic observations has often been one major obstacle in broadening the applications of these methods. Motivated by experimental needs, there has been rapid development of vibrational frequency maps of localized modes of molecules in the condensed phases, vibrational coupling maps for interacting vibrational modes, and vibrational transition dipole/polarizability maps for determining the corresponding IR/Raman transition amplitudes over the past decades. To collect all those vibrational spectroscopy maps reported and to make them available to everyone who is interested in utilizing such maps or developing a new map for different vibrational probes, a repository internet site (http://frequencymap.org/) has been created. We thus anticipate that the marriage of vibrational frequency map approach with state-of-the-art multidimensional vibrational spectroscopy will be one of the most fruitful ways to study the structure and dynamics of chemical, biological, and functional molecular systems in the future.
2. A Brief Theoretical Account of Vibrational Spectroscopy
2.1. Radiation-matter interaction and time-dependent perturbation theory
In molecular spectroscopy,3 the system of interest interacts with the incident electric field. In the electric dipole approximation, the interaction Hamiltonian can be written as
| (1) |
where is the electric dipole operator and E(r,t) is the electric field. In the case of inelastic scattering spectroscopy utilizing spontaneous Raman, stimulated Raman, or coherent anti-Stokes Raman scattering processes of polyatomic molecules induced by electronically non-resonant electric fields, the effective field-matter interaction Hamiltonian is approximately given by , where is the electric polarizability operator.4 In the semiclassical approximation where the external electromagnetic field is treated classical mechanically, whereas the molecular system is quantum mechanically, the total Hamiltonian of the composite system is assumed to be the sum of the material Hamiltonian in the absence of radiation and the interaction Hamiltonian, Hint(t). More specifically, the total Hamiltonian is given by
| (2) |
where HS is the molecular Hamiltonian of the system, HBath the bath Hamiltonian, HRad that of the radiation, and HS-B represents the solute-bath interaction energy. Hereafter, the radiation Hamiltonian is ignored, and the zeroth-order Hamiltonian H0 is assumed to be the sum of the solute, bath, and solute-bath interaction energies.
The system evolves in time according to the quantum Liouville equation for the density operator ρ(t) of the system as follows
| (3) |
Quantitative information about physical observables of the system, denoted as A(t), can be obtained through the expectation value where Tr denotes the trace of a matrix and is the corresponding quantum operator associated with observable A. A diagonal element ρaa of the density matrix in a basis set {|a >} represents the probability that the system is in state a, or the population of the system in state a. The off-diagonal element ρab of the density matrix, which is related to coherence or super-position state evolution of two states a and b, gives rise to the temporal oscillation of the aforementioned probability with a frequency determined by the energy difference of the two states.
Treating Hint(t) as the perturbation to the reference molecular Hamiltonian H0, Eq. (3) can be formally solved by applying the time-dependent perturbation theory. The solution is, in general, expressed as a power series expansion of ρ(t) in interaction Hamiltonian,3,4 i.e., ρ(r,t) = ρ(0)(r,t) + ρ(1) (r,t)+⋯, where the zeroth-order term is just the equilibrium density operator for the unperturbed system ρ(0)(t) = ρeq in the absence of external radiation. The nth-order correction term denoted as ρ(n)(t) contains Hint(t) in the nth power in a time-ordered Dyson integral accounting for all possible field-matter interactions.
From the perturbation expansion form of the system density operator ρ(t), one can calculate the material polarization induced by field-matter interactions and the nth-order polarization P(n)(r,t), which is given by , is
| (4) |
where the nth-order molecular response function is defined as
| (5) |
with the Heaviside step functions θ(t) due to the causality principle. Here, is the dipole operator in the interaction picture, and the angular bracket denotes the trace of a matrix. The linear response corresponds to the case of n=1 in Eqs. (4) and (5). The second- and third-order polarizations that are related to the surface vibrational spectroscopy and four-wave-mixing-type time-resolved vibrational spectroscopy, respectively, are determined by the corresponding the second- and third-order response functions. Note that R(n) is a real function because P(n)(r,t) and E(r,t) in Eq. (4) are both real quantities, even though individual terms comprising R(n) are complex in general and represent different quantum transition pathways.
2.2. Linear response vibrational spectroscopy
The IR absorption (Raman scattering) spectroscopy can be fully described by considering the expectation value of the time-evolved electric dipole (polarizability) operator.3,4 Using the cumulant expansion technique,3 one can obtain an approximate expression for the linear response function, which is given by
| (6) |
where and represents the average transition frequency determined by the energy difference between the ground (|g>) and excited (|e>) states. Here, γ is the relaxation constant introduced in an ad hoc manner to take into account both the finite lifetime of the excited state and the rotational relaxation time of chromophores in solutions. In Eq. (6), the line-broadening function that mainly determines the frequency-dependent lineshape of the absorption spectrum is
| (7) |
where the autocorrelation function of fluctuating chromophore-solvent interaction energy can be related to the fluctuating vibrational frequency-frequency correlation function (FFCF) as
| (8) |
In the above equation, the angle bracket on the right-hand side of Eq. (8) represents the classical mechanical average over the phase space spanned by the bath degrees of freedom. From Eqs. (7), we now have the line-broadening function g(t) related to the FFCF as
| (9) |
Note that the instantaneous vibrational frequency of a given mode of the jth solute molecule at time t can be decomposed into three terms as
| (10) |
where ω0 is the vibrational frequency of the IR probe mode when the solute molecule is in the gas phase, Δω is the average frequency shift due to the vibrational solvatochromism, and δωj (t) is the fluctuating part of the vibrational frequency of the jth molecule. The average vibrational frequency is given by the sum of ω0 and Δω, i.e., . From the decomposed expression (Eq. (10)) for the instantaneous vibrational frequency of the jth molecule, it becomes clear that the theoretical description of the solvation-induced vibrational frequency shift, Δω, in terms of chromophore-solvent interactions is immensely important to understand the changes in the peak position of the IR absorption spectrum due to varying solvent properties such as polarity, hydrophobicity, proticity, and so on. From the peak frequency of the IR absorption spectrum, one can accurately measure the solvatochromic vibrational frequency shift Δω within the Condon approximation.
In addition, the width of each IR spectrum is related to the standard deviation of δωj (t), i.e., < δω2 >1/2, when the line-broadening is dictated by pure dephasing process. However, in general, the width of the IR absorption spectrum is determined not just by < δω2 >1/2 but also by the width of the inhomogeneous distribution of transition frequency and the rates of vibrational energy and rotational relaxation processes. If there is no static inhomogeneity in vibrational frequencies and if the vibrational lifetime-broadening and rotational relaxation-induced dephasing are negligibly small, the whole line broadening is determined by the pure dephasing, which makes the linear response function decay as described by exp(−g(t)) in Eq. (6). Kubo’s exponential model for C(t) has long been used to describe the lineshape of the linear vibrational spectrum.3,4 Let us assume that the FFCF is an exponentially decaying function as
| (11) |
where the decay constant Γ corresponds to the loss rate of correlation between vibrational frequencies at two different times. With this exponential FFCF, the correlation time is given by
| (12) |
Inserting Eq. (11) into (9), one can find
| (13) |
If the correlation time tc is much shorter than the inverse of < δω2 >1/2, that is the case when the vibrational frequency loses its memory almost instantaneously. This is the Markovian limit and the line-broadening function g(t) becomes a linear function of time as
| (14) |
and the linear response function decays exponentially with respect to t. Within this Markovian approximation to the FFCF, the absorption spectrum in the frequency domain becomes a Lorentzian function.
If the correlation time tc is much longer than the inverse of < δω2 >1/2, the line-broadening function in Eq. (13) can be approximated as a quadratic function of time, i.e.,
| (15) |
Then, the lineshape of the absorption spectrum becomes a Gaussian function with a width determined by < δω2 >1/2. If the line-broadening function g(t) is assumed to be a sum of exponential and Gaussian functions in the time domain, the corresponding absorption lineshape in the frequency domain becomes the well-known Voigt profile.
The linear response function that determines the lineshape of the absorption and emission spectra of optical and vibrational chromophores can be approximately described in terms of the instantaneous fluctuations of the vibrational transition frequencies and dipole moments. Therefore, if an accurate VSM is available for a given set of vibrational modes of molecules in condensed phases, the center frequencies of the absorption and emission spectra and their linewidths can be reproduced and even predicted by using MD simulations combined with the VSM theory. Nevertheless, it should be emphasized that even though the lineshape analysis of linear spectra provides invaluable information about chromophore-solvent interaction strength, it is impossible to extract direct information about the time correlation function of the chromophore-solvent dynamics from the corresponding 1D spectrum. Furthermore, if inhomogeneous-broadening effects are not negligible, one cannot extract quantitative information about < δω2 >1/2 from the 1D spectrum because the full-width-at-half-maximum of the spectrum is determined by both the standard deviation of fluctuating frequency and the width of the inhomogeneous frequency distribution. In this respect, time-resolved vibrational spectroscopy has found its use for studying such locally heterogeneous environments around IR probes and for measuring time scales of vibrational energy relaxation, rotational dynamics, transitions from one conformer to another, chemical exchange dynamics among non-covalently bonded chemical species, energy or particle transfer processes from one state to another, and transient dynamics between different solvation configurations. All these transient processes involve changes in vibrational frequencies of solute molecules because any molecular structural changes affect the multidimensional potential energy surface of the molecule, which then induce changes in vibrational frequencies.
2.3. Time-resolved vibrational spectroscopy
In general, most nonlinear vibrational spectroscopic measurements are conducted in two steps. The first is the preparation step, where molecular systems under investigation are excited by incident radiations. The second is the detection step, where the signal generated through nonlinear field-matter interactions is measured and presented. In time-resolved IR pump-probe (PP), the first two electric field-matter interactions occur with the pump pulse. The time-delayed probe pulse interacts with the molecules in the sample, which generates the third-order macroscopic polarization in the sample. The macroscopic material polarization is usually a linear sum of all the third-order dipole moments of chromophores dissolved in solutions when their couplings are weak. The generated IR PP signal field interferes with the same incident probe field, and the interference term is selectively measured.
For 2D IR spectroscopy, the system is usually irradiated with three coherent laser pulses. The generated 2D IR signal field is heterodyne-detected, and the 2D IR spectrum is presented in two frequency dimensions representing two distinct vibrational coherence oscillations separated by a waiting (population) time Tw.4,5,70 The 2D IR is four-wave-mixing spectroscopy because the signal field arises from three preceding field-matter interactions that are each linear in the applied electromagnetic field. In each of the four field-matter interaction events, a quantum transition takes place between vibrational states of the system. Depending on the configuration of the optical laser pulses such as the frequency, direction of propagation (wavevector), and polarization, as well as on the detection methods, different quantum transition pathways can be differently generated and selectively measured.4
Time-resolved IR spectroscopy, e.g., IR PP and 2D IR, involves quantum transitions up to the second vibrational excited state denoted as |f>. Therefore, a three-level system with eigenstates | g > , |e>, and |f> is a useful model for developing a theory of nonlinear response function that is directly relevant to time-resolved four-wave-mixing spectroscopy in general. As well-known, the third-order vibrational response function vanishes for a perfect bosonic oscillator; the model system should represent an anharmonic oscillator where the fundamental transition frequency ωeg differs from ωfe.
The evaluation of a realistic response function critically depends on the accurate description of the system-bath interactions or generally intermolecular interactions that are responsible for chemical dynamics and spectroscopic phenomena such as dephasing, relaxation, reorientation, spectral diffusion, and population and coherence transfers. Methods to incorporate the effect of the environment as well as the multimode vibrational coupling have been discussed in various review articles and books.3–5,7,70 Here, we briefly outline the theory of nonlinear vibrational response function and its interplay with vibrational solvatochromism and vibrational frequency-frequency correlation function. We focus on a simple three-level chromophore interacting with the environment, where the corresponding Hamiltonian is given by
| (16) |
where is the energy of state m(m = g, e, f) in the absence of bath, Vm(q) is the chromophore-bath interaction energy of the state m that depends on the bath degrees of freedom q, HB(q) is the energy of the bath, and the basis states |m> are chosen as eigenstates of an isolated chromophore. Note that the off-diagonal elements of the chromophore-bath interaction such as Jmn|m><n| that approximately describe state-to-state vibrational energy transfer processes are assumed negligible for the sake of simplicity. Thus, the chromophore-bath interaction described by Eq. (16) modulates the energy gap between two different eigenstates of the target oscillator.
The third-order signal electric field that is under detection in nonlinear spectroscopy is obtained by solving Maxwell’s equation taking the nonlinear polarization P(3)(r,t) as the radiation source. Often, the following assumptions are made: (i) the signal field is only weakly absorbed by the medium, (ii) the envelopes of polarization and signal fields vary slowly in time compared to the optical period, (iii) the signal field envelope spatially varies slowly compared to its wavelength, (iv) the frequency dispersion of the medium refractive index is weak. The approximate solution for the signal electric field envelope is given by
| (17) |
Here n(ω) is the refractive index of the medium and is the polarization component propagating with wave vector ks and frequency ωs that are one of the combinations ±k1 ±k2 ±k3 and ±ω1 ±ω2 ±ω3, respectively. Note that Eq. (17) gives the approximate signal field arising from a single Fourier component of the third-order polarization expanded as3,4
| (18) |
By changing the location of the detector appropriately, individual components of the polarization with different ks can be selectively measured. Note that the assumption (ii) known as slowly-varying-envelope approximation becomes invalid for far-IR and THz spectroscopy because typical pulse duration time is quantitatively similar to the period of such low-frequency far-IR and THz radiation. In that case, one should solve the corresponding Maxwell’s wave equation rather numerically, which is not of major difficulty. In the present work, we shall focus on IR probes whose oscillation frequencies are in mid-IR and near-IR domains (>1000 cm−1), so the slowly-varying-envelope approximation is still valid.
The general third-order response function in Eq. (5) has three nested commutators, so it can be expanded and rewritten as the sum of eight terms3,109
| (19) |
where the components Ri(t3,t2,t1) are given by
| (20) |
Here, μab is the transition dipole between states a and b, is the energy gap averaged over bath degrees of freedom, and is the line shape function which can be approximated by exponential functions containing difference potential energies Uab(q)=Ua(q)–Ub(q).4 Alternatively, one can invoke the second-order cumulant expansion approximation, which becomes exact when the fluctuation of the energy gap obeys the Gaussian statistics, to obtain
| (21) |
where the auxiliary functions are given by
| (22) |
and g(t) defined by Eq.(9). The other contributions to R3 and R4, which involve coherence evolution of |f><g| during t2, are not included in Eq. (21) and the energy fluctuation between states g and f is usually assumed to be twice that between g and e, i.e., δωfg(t) ≅ 2δωeg(t).4
The six response functions in Eq. (21) can be classified, based on their physical interpretation, as ground state bleach (GB) and stimulated emission (SE) that involve transitions between g and e, and excited-state absorption involving transitions between e and f. They can also be classified into rephasing and non-rephasing terms, depending on whether the optical coherence during the times t1 and t3 evolves in the same or opposite direction. If chromophores have a broad distribution of heterogeneous environments, which makes the vibrational transition frequency broadly distributed, the molecular nonlinear response function should be calculated by averaging over the inhomogeneous distribution of vibrational frequencies, i.e.,
| (23) |
where is the variable representing the frequency shift due to heterogeneously distributed local solute-solvent interaction environments, solute conformations, phases, or microscopic states. For instance, the first nonlinear response function after average over the normalized distribution is given by
| (24) |
where is the inverse Fourier transformation of . As t1 and t3 increase, due to the inhomogeneous distribution of vibrational frequencies, the response function additionally decays and it does not produce any echo signal. In contrast with , the averaged nonlinear response function of over becomes
| (25) |
Since peaks at t = 0, with respect to t3 reaches its maximum at t3 = t1, which is the signature of echo generation due to inhomogeneity-induced rephasing process. Therefore, R2 and R3 are rephasing terms that are responsible for the generation of the photon echo (PE) signal from chromophores having a broad inhomogeneous frequency distribution, and R1 and R4 are referred to as non-rephasing terms.
When the vibrational modes are spectators in chemical reactions the Gaussian approximation109,110 making the foundation of the line-broadening function breaks down. The response function formulation presented above is still valid, but they need to be evaluated explicitly including the resulting non-Gaussian fluctuations.111–120 In these cases, the numerical integration of the Schrödinger equation (NISE)121 and the nonlinear exciton propagation (NEP) algorithms122 should be of use.110
2.4. Two-dimensional lineshape analysis and spectral diffusion
The average vibrational frequency shift of IR-active modes, which is induced by solute-solvent interactions, can be accurately measured by analyzing the FTIR spectra of IR probes. However, to obtain information on the time scale of vibrational frequency fluctuation, it is necessary to use nonlinear vibrational spectroscopic techniques as they are capable of measuring the frequency-frequency correlation function. Photon echo spectroscopy has been used as one of the most popular techniques for studying ultrafast solvent dynamics, through measuring photon echo peak shift (PEPS) in the time domain.4,123 More recently, 2D vibrational, electronic, and electronic-vibrational spectroscopy experiments have been extensively performed to extract solvent dynamics and frequency-frequency correlation function from the analyses of nodal line slope, center line slope, and ellipticity of two-dimensional peaks on the diagonal and off-diagonal regions of the 2D spectra (Figure 2).4,5,7,70,73
Using the FFCF formulation to describe the solute-solvent interaction-induced fluctuation of vibrational frequency, one can, in principle, calculate the nonlinear response functions in Eq. (21). However, the more useful information can be extracted by analyzing the 2D lineshape changes in time. To establish the relationship between the analytical expressions for the nonlinear response functions and the waiting time-dependent 2D lineshape, one can use a short-time approximation to the line-broadening function.4,5,7,73 Assuming that the pulse envelope function can be approximated as a Dirac delta function and carrying out the two-dimensional Fourier transformations of the PE signal field, it was shown that the complex 2D photon echo spectrum of an anharmonic oscillator system, which can be approximated as a three-level system, is given by
| (26) |
where SE, GB, and EA represent the stimulated emission, ground-state bleaching, and excited-state absorption (EA) terms, respectively, and they are
| (27) |
Here, the vectorial dipole moment associated with the transition from the ground state g to the first excited state e is denoted as μeg and the unit vector of the polarization of the jth pulsed electric field is as ej. In Eq. (27), is the normalized FFCF defined as
| (28) |
The auxiliary functions in Eq. (27) are defined as, with β = 1/kBT,
| (29) |
In Eq. (27), F(x) is the Dawson integral defined as . In Eq. (29), λ is the solvent reorganization energy, and it is related to the variance of fluctuating vibrational frequency as . Typical vibrational lifetime and rotational relaxation time of small molecules are on the order of a few picoseconds, and the vibrational absorption linewidth is mainly determined by the standard deviation of fluctuating vibrational frequency, which is . If the linewidth is 30 cm−1, the solvent reorganization energy λ is about 2 cm−1 at room temperature. Therefore, unlike UV-vis spectroscopy involving electronic transitions of optical chromophores in condensed phases, the Stokes shift or the vibrational excitation-induced solvent reorganization energy is negligibly small compared to the absorption linewidth and anharmonic frequency shift . Therefore, in the interpretation of 2D IR spectral evolution, the Stokes shift or solvation dynamics of the vibrationally excited state is not taken into consideration.
To obtain the above approximately 2D Gaussian lineshape function expression for the real part of the 2D photon echo spectrum, we assumed that the coupled bath mode frequencies are smaller than kBT at room temperature. These approximate descriptions are not valid at low temperatures. From Eqs. (26)–(29), one can predict the time-dependent changes in center and nodal line slopes of 2D peak, the frequency difference between SE+GB peak and EA peak along the ωt axis, ellipticity of each diagonal peak, and both the diagonal and antidiagonal linewidths of diagonal peak in terms of the waiting time-dependent FFCF, C(T) (see Figure 2). More specifically, the nodal and center line slopes, NLS and CLS, with respect to waiting time T are approximately given by73
| (30) |
The full-width-at-half-maximum (FWHM) of the diagonal peak along the diagonal line, which is denoted as Δωdiag (T), and that along the antidiagonal line, denoted as Δωanti–diag(T), are also determined by the FFCF as
| (31) |
From Eq. (31), the ratio of diagonal width to anti-diagonal width becomes a function of waiting time as, at T > 0,4,73
| (32) |
Equation (32) clearly shows that the 2D peak-shape at a short waiting time is diagonally elongated, but the degree of such diagonal elongation decreases in waiting time and approaches zero. Therefore, after a long waiting time T >> tc, the 2D peak-shape becomes round with the same diagonal and antidiagonal widths. Again, from the waiting time-dependence of diagonal elongation, it is possible to extract direct information on the normalized FFCF.
In this section, we specifically discussed how 2D vibrational spectroscopy can be used to study ultrafast solute-solvent interaction dynamics through analyzing 2D peak-shape evolution in waiting time. For certain vibrational modes, e.g., OH and OD stretch modes of HDO in water or heavy water, the FFCF extracted from the 2D IR data was directly compared with that predicted using vibrational solvatochromism theory and molecular dynamics simulation methods. However, still, such quantitative comparisons between theory and experiment for many IR probes incorporated into complicated biological molecules or functional materials are very challenging and have rarely been reported. Only when the numerically calculated FFCF and average solvatochromic frequency shift of a given IR oscillator with quantum chemistry calculation, MD simulation, or any combination of electronic structure calculation and molecular simulation are in quantitative agreement with experimental results, one can conclude that the computational methods used are quantitatively reliable and spectroscopically valid.
2.5. Numerical integration of the vibrational Schrödinger equation
A variety of applications of ab initio MD simulation methods to the studies of chemical and biological reactions and processes have been reported. However, still, it is prohibitively expensive to use such methods to accurately calculate the fluctuating vibrational frequencies and transition dipole moments of molecules in condensed phases. In contrast, the combination of VSMs, i.e., vibrational frequency, transition dipole, vibrational coupling constant, and anharmonicity maps, and classical MD simulations provides an efficient means to calculate various linear and nonlinear IR spectra when using Eqs. (6), (20) and (21). In a more general case, when multiple vibrational modes are non-negligibly coupled and non-adiabatic effects on the vibrational eigenstates need to be considered, the required computational step is to develop a method to numerically solve the corresponding time-dependent vibrational Schrödinger equations. This approach, widely referred to as Numerical Integration of the Schrödinger Equation (NISE) theory,124 assumes that a given vibrational mode can be approximated as a weakly anharmonic oscillator so that only the lowest three vibrational levels are enough for modeling 2D vibrational spectroscopy. When the oscillators are close to one another through space or chemical bonds, their vibrations are correlated. Such vibrational coupling effects can also be quantitatively described by using various VSMs. Here, the vibrational frequencies, transition dipole moments, and even anharmonic frequency shifts fluctuate in time due to the solute-solvent interactions. These intermolecular interaction-induced fluctuations are all taken into account by considering their time-dependent modulation of the parameters of the quantum oscillator.
In general, for coupled multi-oscillator systems interacting with external electric fields, the corresponding time-dependent Hamiltonian can be written as
| (33) |
Here, and an are the creation and annihilation operators of the nth harmonic oscillator considered quantum mechanically. The individual local vibrations are characterized by their frequency ωn(t), transition dipole μn(t), transition polarizability αn(t), and anharmonicity Δn(t). Any pair of local vibrations are mixed by their mutual couplings Jnm(t). In this approach, the time dependence of these parameters strictly arises from the coupling of each individual oscillator with bath degrees of freedom. The last two terms in Eq. (33) account for the interaction of the oscillating dipoles and molecular polarizabilities with the applied electric field(s) E(t), respectively, depending on the specific experimental configuration.
Determining the fluctuating frequencies, transition moments, and coupling constants in the above time-dependent Hamiltonian depends on the system under consideration.110 Once there exist quantitatively reliable models for these parameters, time-evolution operator approaches can be used to calculate the response functions. The critical step is to divide the propagation time into sufficiently short time intervals so that the Hamiltonian during these intervals is approximately independent of time. The solution for the time-dependent Schrödinger equation for each short time interval can then be easily obtained. Successive applications of the finite-difference time-evolution operators for neighboring time-intervals enable the time-dependent vibrational wavefunction of the coupled multi-oscillator systems to be calculated. Open source implementations of NISE and closely related variations122 are available.125,126
The success of this NISE approach120,127–130 relies on the accuracy of the computed parameters needed to construct the time-dependent Schrödinger equation. The vibrational frequency and transition dipole moment of a given oscillator depend on the local environment and are determined by the intermolecular interaction potential and the anharmonicity of the multidimensional intramolecular vibrational potential. For instance, an early attempt to calculate the solute-solvent interaction-induced shift of vibrational frequency assumes that the solute-solvent interaction is dictated by electrostatic interactions. The vibrational frequency shift of an oscillator was considered to be dependent on the solvent electric potential, electric field, or sometimes the electric field gradient on specific sites of the solute molecule. These vibrational frequency mappings have allowed the frequency trajectories of the coupled oscillators to be obtained from equilibrium MD trajectories. However, recently, it has been shown that the vibrational solvatochromic frequency shift is determined by not just electrostatic interactions but also dispersive interaction, short-range Pauli repulsion, polarization, and even multipole-multipole interactions.40
The anharmonicity of a given molecular vibration also depends on its interaction with the solvent molecules. For multi-oscillator systems, the vibrational coupling constant between any pair of local modes should be accurately calculated to describe the delocalized nature of the vibrational modes. One of the most popular models is the transition-dipole coupling model, which assumes that the two oscillators interact with each other through electric dipole-dipole interactions. So far, this form of semiempirical mapping has been found to be exceptionally useful, achieving a spectroscopic accuracy within a few wavenumbers, something which cannot be easily achieved using current classical or even ab initio MD simulation methods.
The quantum-classical methods discussed here have a number of crucial advantages.110 One of the commonly used methods, which incorporates second-order cumulant approximation or other methods that require an assumption that the coupled bath degrees of freedom are harmonic oscillators obeying Gaussian statistics, cannot account for intermolecular interaction-induced effects properly. On the other hand, quantum-classical methods take them correctly. Nevertheless, hybrid quantum-classical methods still have definite limitations. The time-dependent Hamiltonian for NISE does not allow for the relaxations between the different excitation manifolds.110 Furthermore, while these quantum-classical methods are able to account for the effect that the bath exerts on the system, the feedback of the system to the bath when in an excited state is unable to be considered. Consequently, the method cannot reproduce the correct thermalization in quantum systems, which results in artifacts at low temperatures. Another inherent difficulty of NISE is that quantum mechanical oscillators need to be well defined and localized. If the nature of an oscillator changes over time (e.g., H-bond vibrations and delocalized intermolecular modes), it is not possible to treat them quantum mechanically.
As mentioned in this section, despite the prolonged efforts to develop approximate theory and computational methods, clear limitations in the accurate calculation of the coherent multidimensional spectra of molecules in condensed phases still exist. Although a simple approach for modeling absorption lineshape such as Kubo model has been widely used in many cases, it is also true that more advanced methods for accurately computing both linear and nonlinear vibrational spectra are available. However, it must be emphasized that they all require an accurate mapping of the vibrational frequency to local environments around the mode of interest, which is the reason why the development of vibrational maps has been one of the most important research subjects in the field.
3. Vibrational Solvatochromism
3.1. Intermolecular interaction potential and its solute-solvent separability
The frequencies associated with transitions between vibrational quantum states of polyatomic molecules under IR absorption or Raman scattering processes depend on their structure, i.e., atomic configuration. In solutions, the surrounding microscopic environment inevitably exerts external forces on the normal modes, which affect their force constants, vibrational transition dipole moment and polarizability, and the couplings between modes leading to vibrational energy relaxations. Consequently, the vibrational frequencies of molecules in solutions differ from those in the gas phase, which has been referred to as vibrational solvatochromism. Here, the intermolecular interaction potential52 essentially determines a variety of the vibrational solvatochromism phenomena such as vibrational frequency shifts and transition moment changes.38–40 Since the development of VSMs requires separability in terms of the well-defined independent constituents, the intermolecular interaction potential needs to be described in terms of solute (IR probe) and solvent (environment) parts of the whole system separately.
One of the most frequently used approaches to describe the intermolecular interaction potential approximately is to treat the solute’s molecular surroundings by continuum solvent models.131 In the simplest and oldest variant of this approach,132–135 the solute molecule is represented by its total charge, dipole moment, and higher multipole moments (quadrupole, octupole and so on), and placed at the center of a dielectric cavity that is surrounded by a dielectric continuum that is entirely characterized by dielectric constant, ε. The solute’s multipole moments approximately reflect its charge distribution ρ(r), whereas the cavity approximately represents the shape and dimension of the solute molecule as well as defines the boundary between solute and its environment. In the special case that the cavity can be modeled as a sphere of a vacuum of radius a0 and the solute molecule is neutral in charge, the leading contribution to the interaction potential is given by the dipole-dipole term, i.e.,
| (34) |
where μ0 is the solute’s permanent dipole moment and the so-called Onsager reaction field is
| (35) |
with μ(ε, a0) being the total solute’s (permanent and induced) dipole moment and , the so-called Onsager factor. Eq. (34) together with Eq. (35) describes the Onsager dipole model of solvation. Although the essential element of the solvent effect on the solvation energy is qualitatively captured by this model for moderately polar solute molecules dissolved in aprotic polar solvents, it cannot encompass a variety of specific effects originating from detailed structures and charge distributions of complicated solute molecules in condensed phases. For instance, the model is inaccurate not only when the dominant interaction is from H-bonds but also when the solute molecule has a solvent-accessible surface that is notably different from a sphere. In modern versions of continuum models of solvation, such as the polarizable continuum model136,137 (PCM) or the conductor-like screening model138 (COSMO) for example, electrostatic and non-electrostatic effects have been taken into account significantly in details, which allow improved and quantitative modeling of static solvation effects in isotropic solutions. However, it is not straightforward to separate the solute and solvent contributions to the PCM or COSMO interaction potentials, making it challenging to be used for developing VSMs.
However, to describe far more complicated heterogeneous environments around solute molecules and to study real-time molecular dynamics, it is necessary to simulate solute-solvent interactions at the atomistic level by considering all the molecular surroundings explicitly. To achieve this, one should parameterize the total energy of the system with an efficient and sufficiently accurate functional form that involves atomic and possibly also non-atomic sites of solute and surrounding solvent molecules. According to the molecular mechanics (MM) approximation (known as force field approximation), the total potential energy function is decomposed into a ‘bonded’ part associated with the changes in the bond lengths, bond angles, and dihedral angles, and the ‘non-bonded’ part that involves through-space interactions such as long-range electrostatic and short-range van der Waals interactions. In this way, the solute-solvent interaction potential can be partitioned into parameters associated with particular fragments, or residues, fitting into a requirement to build a VSM.
Unfortunately, even though these MM approaches were found to be usually quite sufficient for the description of the intermolecular forces and molecular dynamics of complex molecular systems in their electronic ground states, commonly used force field parameters are not accurate enough to reproduce the vibrational properties such as vibrational frequencies and transition moments.139 Therefore, they cannot be used to simulate vibrational spectra of the IR probes that are either useful normal modes or small chemical groups site-specifically incorporated into biomolecules or functional materials in condensed phases. This lack of spectroscopic accuracy of force fields for spectroscopic applications stimulated extensive research to develop significantly sophisticated and accurate models that connect solute-solvent interaction potentials to vibrational spectroscopic properties.
Contrary to most of the semiempirical force field methods, quantum chemistry calculation approach provides a quantitative description of the intermolecular potential in terms of the physically sound and intuitive solute-solvent contributions such as electrostatics, dispersive, and repulsive interactions.52,64,65,131,140–142 One of the most rigorous, accurate, and sophisticated approach is the symmetry adapted perturbation theory (SAPT), which partitions the intermolecular interaction operator into electron correlation perturbation and intermolecular interaction energy perturbation by using the double exchange-perturbation theory.141 Among many contributions to the SAPT interaction energy, the most important components is the pseudo-classical Coulombic interaction energy between the unperturbed solute and solvent charge densities, the associated exchange-repulsion energy, the induction and exchange-induction interaction energies, and the intermolecular dispersion energy. As the order of electron correlation increases, more contributions to the interaction potential are to be included, but their physical meanings become less intuitive, and they just reflect the technicality of the wavefunction model based on the series expansion of Slater determinants. For the sake of practical applications in condensed phase systems, one might require a computationally more efficient model of the intermolecular interaction potential which can be made entirely separable between solute and solvent. Here, we consider an approximation to SAPT in which the intramolecular electron correlation corrections are ignored, and the electron exchange effects are included only in the first order with respect to the interaction Hamiltonian. The Coulombic interaction energy is given by
| (36) |
where |0A ⊗ 0B〉 is the Hartree product of the unperturbed solute and solvent wavefunctions. The exchange-repulsion interaction energy can be obtained from
| (37) |
where |0A0B〉 is the wavefunction of the solute-solvent complex and is the standard antisymmetrization operator that exchanges the labels of electron pairs in between |0A〉 and |0B〉. For a typical molecular complex in the equilibrium geometry, EEx-Rep is substantial and cannot be neglected. Induction and dispersion interaction energies are, up to the second-order in the intermolecular interaction, given as
| (38) |
| (39) |
where and the summations count all the electronically excited states.
To evaluate expressions in Eqs. (36)–(39) and to achieve solute-solvent separability, can be approximated by the multipole expansion of the electrostatic potential operator and its spatial derivatives52
| (40) |
where A and B are interacting molecules, , and are the distributed charge, dipole, and quadrupole operators associated with the ath site on A, and T(ab;n) are the nth-rank interaction tensors. The first few interaction tensors in Eq. (60) are given by143
| (41) |
| (42) |
| (43) |
| (44) |
with rab = ra – rb. Under this approximation, the interaction potential operator adopts the following familiar form
| (45) |
Replacing the operators in Eq. (45) with the corresponding expectation values leads to the approximate expression for the electrostatic interaction energy. Eq. (45) can also be used to approximate the induction and dispersion interaction energies. For instance, for a single closed-shell molecule in a uniform external electric field, Eq. (38) can be written as
| (46) |
where the ground-state polarizability tensor is defined as
| (47) |
Equations (36)–(39) serve as the theoretical basis for the effective fragment potential (EFP2) method64 that is one of the most efficient non-empirical methods used in a variety of molecular dynamics simulations. The EFP2 potential, which is an ab initio force field with parameters derived from first-principles rather than fitting to some benchmark data, can be written as
| (48) |
In the above equation, the Coulomb, exchange-repulsion, induction, dispersion, and charge-transfer contributions are functions of the effective fragment parameters that consist of the atomic numbers and coordinates, distributed multipole moments up to octupoles, distributed dipole-dipole static and frequency-dependent polarizabilities, Gaussian basis set used to expand the wavefunction along with the associated atomic orbital-molecular orbital (AO-MO) coefficients, and the Fock matrix in AO basis. EFP2 interaction potential is quite similar to the SAPT interaction potential but is formulated within the Hartree-Fock (HF) or the density functional theory (DFT) methods only, in which the many-electron wavefunction can be approximated by a single Slater determinant. Moreover, EFP2 model is an effective one-electron potential, hence only the evaluation of computationally inexpensive one-electron integrals is necessary to calculate the entire interaction potential, unlike SAPT and full quantum mechanical methods that require calculations of electron repulsion integrals as well. The charge-transfer contribution, UCT, which is a part of induction energy in the SAPT model, is separately calculated in the EFP2 model,144 though it is rarely evaluated due to its relatively high computational cost.
In summary, the intermolecular interaction potential is a very complicated function of the atomic coordinates and, in general, quantum mechanical description of the solute-solvent complex is necessary to accurately describe molecular vibrations induced by detailed structural distortions due to the solute-solvent interactions. Using the multipole expansion of the intermolecular interaction potential operator , one can describe the intermolecular interaction in terms of the solute- and solvent dependent parts separately, which in turn enabled us to develop various ab initio and semiempirical VSMs. We next discuss the fundamentals of VSMs that are based on quantitative relationships between vibrational observables and intermolecular interaction potentials.
3.2. Theoretical foundations of vibrational spectroscopic mapping
The vibrational frequency shift of the jth normal mode can be defined as a difference between the actual vibrational frequency of the mode in solution and that in a reference state, typically in the gas phase, i.e.,
| (49) |
The frequency ωj depends on the electronic structure of the IR probe and its molecular surroundings. The general theory describing the vibrational solvatochromism of a spatially localized normal mode based on the intermolecular interaction potential was developed by Buckingham62,145,146, and later generalized to any arbitrary normal mode by Cho.147,148 The vibrational frequency spectrum of the solute in the presence of molecular environment is determined by the effective Hamiltonian,
| (50) |
where Pi are the vibrational momentum operators and the vibrational potential energy function is defined up to a constant offset by
| (51) |
Here, Mi and ωi are the gas-phase reduced mass and the vibrational frequency of the ith normal mode Qi, respectively. gijk is the cubic anharmonic constant, whereas U denotes the solute-solvent interaction potential, a function of solute’s molecular structure Q. U can be expanded in a Taylor series around the equilibrium geometry of solute in the gas phase,
| (52) |
The resulting vibrational potential energy function in Eq. (52) with U(Q) in Eq. (52) can be directly compared with the potential energy re-expressed in the normal coordinates in the solute-solvent cluster ,
| (53) |
for which it must hold that
| (54) |
because the system is at the lowest energy. From the above condition, it follows that the new normal coordinates are approximately given by
| (55) |
Applying this linear transformation to Eq. (53), one can immediately identify the effective vibrational force constant (or Hessian) matrix148 as
| (56) |
Note that the effective force constants in the Hessian matrix explicitly depend on not U but its first and second derivatives evaluated for the gas-phase geometry, Q0. Solvation-induced vibrational frequencies and the resulting new set of normal modes of the solute molecule in solutions can be directly obtained by diagonalizing the Hessian matrix with elements kjk.
In the limiting case that the vibrational couplings of the normal mode of interest with other vibrational degrees of freedom are relatively weak, it is possible to approximately express the vibrational frequency shift and the change of the vibrational transition dipole as functions of the derivatives of the intermolecular interaction potential. Under such a weak-coupling approximation (WCA) that has been found to be valid for spatially localized vibrational modes, the vibrational solvatochromic frequency shift from the gas-phase frequency is given by,62,148
| (57) |
where the electric anharmonicity (EA) and mechanical anharmonicity (MA) operators, and , respectively, defined as148
| (58) |
| (59) |
A few quantum chemistry calculation studies were performed to test the validity of the theoretical expressions given in Eq. (57) for modes that are highly localized on two atoms in small molecules149–153 as well as for multiple normal modes in polyatomic molecules.143,154–156 It was found that the WCA and the resulting theory for vibrational solvatochromism are quantitatively reliable for a variety of localized modes such as C-H stretch,153 amide I mode,143,154 and −C≡N155 and −N≡C156 stretches. In fact, these small IR-active vibrations have served as important IR probes and widely used to study the structure and dynamics of biomolecules and materials in combination with the linear and nonlinear vibrational spectroscopic methods. Despite the success of the WCA-based vibrational solvatochromism theories, there exist cases that one might need to go beyond the WCA limit. For example, when normal modes become coupled and delocalized, and when the solute-solvent interactions induce mode mixings, the WCA cannot be acceptable. In the simplest case, i.e., where normal modes are coupled in a pairwise manner, the vibrational frequency shift becomes
| (60) |
where the mode coupling contribution to the frequency shift is
| (61) |
In practice, one might need to evaluate the general expression given in Eq. (60) and find eigenvalues of the effective Hessian matrix. Nevertheless, as long as U is computable accurately and solute-solvent separably, the vibrational frequency shifts of most of the normal modes can be expressed as an ab initio VSM, treating the normal modes of the solute molecule in the gas phase as the basis modes.
From Eq. (57), it becomes clear that the vibrational solvatochromism of IR probes relies on accurate and efficient modeling of U and its derivatives with respect to the normal coordinates, where the intermolecular interaction potential U at various intermolecular separation regimes is described in terms of well-known and intuitive physical approximations.157 In the limiting case of relatively large intermolecular separation, molecular wavefunctions sense only the electrostatic potential created by the other surrounding molecules. In this case, the interaction energy equals the pseudo-classical Coulombic energy between unperturbed charge densities of the solute and solvent molecules. As the two molecules get close to each other, the electrostatic potential becomes strong enough to induce relevant changes in the wavefunctions due to the self-polarization of their charge densities. This induction process always leads to a stabilization of the system. Also, quantum effects cause electrons to correlate their movements, which exert instantaneous attractive forces known as dispersion interactions. Once the distance becomes very small enough to create a non-negligible overlap between wavefunctions, the Pauli exclusion principle causes the electrons to pull away from the overlap region, which is the underlying physics behind repulsive forces. At the same time, the indistinguishability of electrons reduces this repulsion to some extent, which is a quantum exchange effect. Furthermore, the smaller the distance is, and the larger the overlap is, the more severe electronic structure rearrangement takes place, which eventually leads to a change in a net electric charge of interacting molecules. This intermolecular charge transfer is an attractive interaction and further stabilizes the system energetically. As the intermolecular distance becomes smaller, the nature of the interactions becomes more complicated, requiring higher-level theoretical descriptions. This, in turn, indicates that vibrational solvatochromism and properties of solute or IR probe molecules in solutions do result from highly complicated intermolecular interaction potential as well as intramolecular anharmonicities and couplings. However, due to the linearity of the WCA expression with respect to U – note that there is no second-order (in the intermolecular interaction potential) term in Eq. (57), it is, in principle, legitimate to partition the vibrational solvatochromic frequency shift into separate contributions originating from distinct physical approximations, such as electrostatic, exchange-repulsion, induction, dispersion, and charge-transfer. Sometimes, even simpler approaches utilizing a less formal but more chemically intuitive set of intermolecular interaction potential descriptors such as solute and solvent polarity, acidity/basicity, H-bonding strength and so on were found to be useful to interpret experimentally measured spectroscopic observables such as vibrational frequency, oscillator strength, linewidth, and vibrational dynamics. Therefore, as long as the degree of separability between unperturbed solute and perturbing environment is acceptable, the mapping of vibrational observables, e.g., frequencies, transition dipole moments, and polarizabilities, onto a universal set of parameters becomes possible and can be justified theoretically. In the following sections, we introduce those approaches that are based on the solute-solvent separable forms of vibrational frequency maps, which served as groundworks and bases for further development of the more robust empirical vibrational frequency maps later.
3.3. Vibrational solvatochromism: Bulk phenomenological descriptions
Due to an unduly complex nature of the solute-solvent intermolecular potential and associated computational cost of employing full quantum mechanical calculation method for systems in condensed phases, a few decades of extensive theoretical and experimental studies have been performed to develop approximate, efficient, but highly accurate methods useful for quantitatively describing the vibrational solvatochromism of important IR probes in terms of a relatively small set of adjustable parameters. Such approaches, though often derived from first principles, used a variety of fitting procedures to link general descriptors of solute/solvent properties like polarity, Lewis/Brønsted acidity/basicity, and H-bond donating/accepting ability with the vibrational frequency, IR absorption coefficient, and Raman scattering cross-section of a given mode in a wide range of solvents.
It was nearly eight decades ago when Bauer and Magat noticed that the vibrational frequencies of solute tend to undergo redshifts with increasing dielectric constant of the solvent.158 According to the Kirkwood-Bauer-Magat (KBM) limiting law based on the Kirkwood-Onsager continuum model of solvation,134,159 vibrational frequency is a linear function of the Onsager factor. It is well known that the KBM law works well only for aprotic solvents and breaks down when solvent’s permanent dipole moment is not vanishingly small.155 Later, Ben-Amotz et al.160 used the theory of Buckingham62,145,146 to study the relationship between the vibrational frequency shift of acetonitrile C≡N stretch mode and the applied pressure, and found the dependence of the vibrational frequency with the bulk solvent density. Later, Fawcett et al.161,162 expressed the solute’s vibrational frequency in terms of the Gutmann solvent acceptor and donor numbers163, the solute and solvent dielectric constant and the refractive index, as well as four adjustable parameters. One of the most important findings in the Ben-Amotz et al.’s and Fawcett et al.’s studies is that the dispersion plays an important role in the vibrational barochromism of acetonitrile C≡N stretch mode at low densities and the repulsive interaction causes a strong blueshift at high densities. In addition, Fawcett et al.’s model accurately predicted the peak maxima of the C≡N stretch mode of acetonitrile in a wide range of solvents. In 1998, Reimers and Hall164 investigated in great detail the solvation of acetonitrile based on the Ben-Amotz et al.’s and Fawcett et al.’s models at ambient conditions. They considered thirty-three different solvents that range from nonpolar and non-protic CCl4, strongly polar aprotic DMSO, to acidic trifluoroacetic acid (TFA). They noticed that the electrostatic nonspecific interactions cause much smaller redshifts than the dispersion interactions do. Note that the latter cannot be correlated with solvent electrostatic potential or electric field at all. What is also interesting in their work is that they reported specific (short-range) frequency blueshifts that are caused by solvent molecules with H-bonding capability. The stronger the H-bond between MeCN and a solvent molecule forms, the larger the blueshift is. However, since it was not possible to separately calculate various short-range interaction contributions to the frequency blueshift, the detailed mechanism was not entirely clear.
It is of great interest to elucidate the effect of H-bonding interaction on the vibrational frequency because many useful IR probes act as a sensitive reporter providing information on the local H-bonding environment. Boxer and coworkers165,166 proposed that the vibrational spectroscopy of IR probes can be combined with the nuclear magnetic resonance (NMR) spectroscopy to separate the frequency shifts induced by the H-bonding interaction and the other interactions. Recently, Zhang et al. proposed an empirical method based on the Kamlet-Taft (KT) solvent parameters, which enables one to separately estimate the solvent polarity and H-bonding effects on the vibrational solvatochromism.167,168 They suggested that vibrational frequency shift can be mapped to KT parameters as
| (62) |
where the coefficients A and B are fitting parameters. Note that the solvent KT parameters were originally determined from the solvatochromic shift of absorption maximum of electronic chromophores in solution. Based on the analyses of different spectroscopic observables, three types of KT parameters are defined and parameterized: the H-bond accepting169 βKT, the H-bond donating170 αKT, and the polarity171 . Zhang et al. showed that their method is applicable to quite complicated solute molecules like 5-cyanotryptophan dissolved in a broad range of solvents, including strongly polar and protic solvent like trifluoroethanol (TFE). They showed that this empirical model is especially useful for studying IR probes that can donate and accept H-bonds via various functional groups.
3.4. Onsager reaction field theory: Dipolar solute and continuum solvent model
At the turn of the 20th century, Hush and Reimers172,173 and Andrews and Boxer174,175 studied vibrational electrochromism to quantitatively relate experimentally measured vibrational properties with an applied external electric field. This vibrational Stark effect (VSE) spectroscopy that measures field-dependent spectra for isotropic samples was thoroughly described by Liptay.176 To provide a quantitative interpretation of VSEs on vibrational frequency shift and the changes in absorbance and lineshape, which has been referred to as vibrational electrochromism, it was necessary to develop a theoretical framework by treating the interaction between molecular dipole and polarizability and applied spatially uniform electric field.148,172–174 As a result, the vibrational frequency shift of a jth normal mode was shown to be related to the electric field as follows
| (63) |
where Δμj is the vibrational Stark dipole moment and Δαj is the vibrational Stark polarizability that accounts for the quadratic effect with respect to the electric field, E. From VSE spectroscopic investigations, it was shown that this quadratic term can often be ignored because the applied electric field strength is weak. Consequently, only the first-order term in Eq. (63), which is based on the approximation that the applied electric field interacts with molecular dipoles, is important in quantitatively describing the VSE on vibrational frequency shift, i.e.,
| (64) |
where is the vibrational Stark tuning rate and Ej is the electric field component. The vibrational Stark tuning rates of a variety of IR probes were reported.177,178 Also, they were calculated using quantum chemistry calculation methods and found to be in quantitative agreement with experimental data.174,175,179 Typically, the vibrational Stark tuning rates are in a range of 0.4‒1.0 cm−1/(MV/cm). To make use of the vibrational Stark theory for quantitatively describing the vibrational frequency shift of IR probe molecule in solutions, one needs to take into consideration the fact that the effective local electric field around it differs from the applied external field. Thus, an empirical scaling factor, so-called the local field correction factor, f, was introduced to modify the VSE theory as
| (65) |
In typical solvents, the local field correction factor f is estimated to be approximately 2.180–182 In practice, the factor f has been treated as an adjustable parameter to fit the VSE model to experimental results. Due to the simplicity of vibrational Stark effect theory for vibrational frequency shift induced by molecule-field interaction, it has been extensively used to quantitatively describe vibrational solvatochromism of IR probes in solutions. However, because the local electric field around molecules in solutions is not spatially uniform, the vibrational Stark effect theory in Eq. (65) is not quantitatively reliable even in the case that the vibrational solvatochromism is determined by the Coulomb interaction between solute and solvent molecules.180,181
A good example of this effect is the dependence of nitrile solvatochromism by hydrogen-bonding angle. Using a density functional theory, Cho and cowokers183 calculated the nitrile stretching frequency in acetonitrile and methyl thiocyanate in water clusters as a function of the angle (θ) between the hydrogen being donated to the nitrogen lone pair and the nitrile, shown in Figure 3. At large values of θ > 120°, the H-bond is accepted by the nitrile lone pairs, which sit in an antibonding orbital. This has the effect of strengthening the nitrile bond and increasing the nitrile stretching frequency. At smaller values of θ, 90–120°, the H-bond is accepted by electrons in a π bonding orbital of the nitrile triple bond. This has the effect of weakening the nitrile bond and decreasing the nitrile stretching frequency. Webb and coworkers184 investigated this effect experimentally by engineering the noncanonical amino acid p-cyanophenylalanine into a variant of green fluorescent protein (GFP) at a variety of both solvent-accessible and solvent-excluded locations within the protein structure. Measured nitrile absorption energies from these vibrational probes could not be straightforwardly explained through the Stark effect in Eq. (65). However, MD simulations of the nitrile-containing variants revealed that the nitriles experienced a range of hydrogen bonding geometries, either to solvent or to the protein itself, based on their positions within the protein structure. As in Cho’s theoretical work, the value of θ was strongly correlated to nitrile stretching frequency (Figure 3), providing the first experimental demonstration of this prediction. This result serves as a warning for interpreting vibrational spectra purely in terms of electrostatic effects without other information, such as MD simulations or temperature-based experiments. It also demonstrates that in heterogeneous and complex environments, every local interaction is important in determining the vibrational spectra of many interesting probes (including the nitrile), and justifies the approach of using empirical frequency maps for calculating and interpreting spectra.
Figure 3.
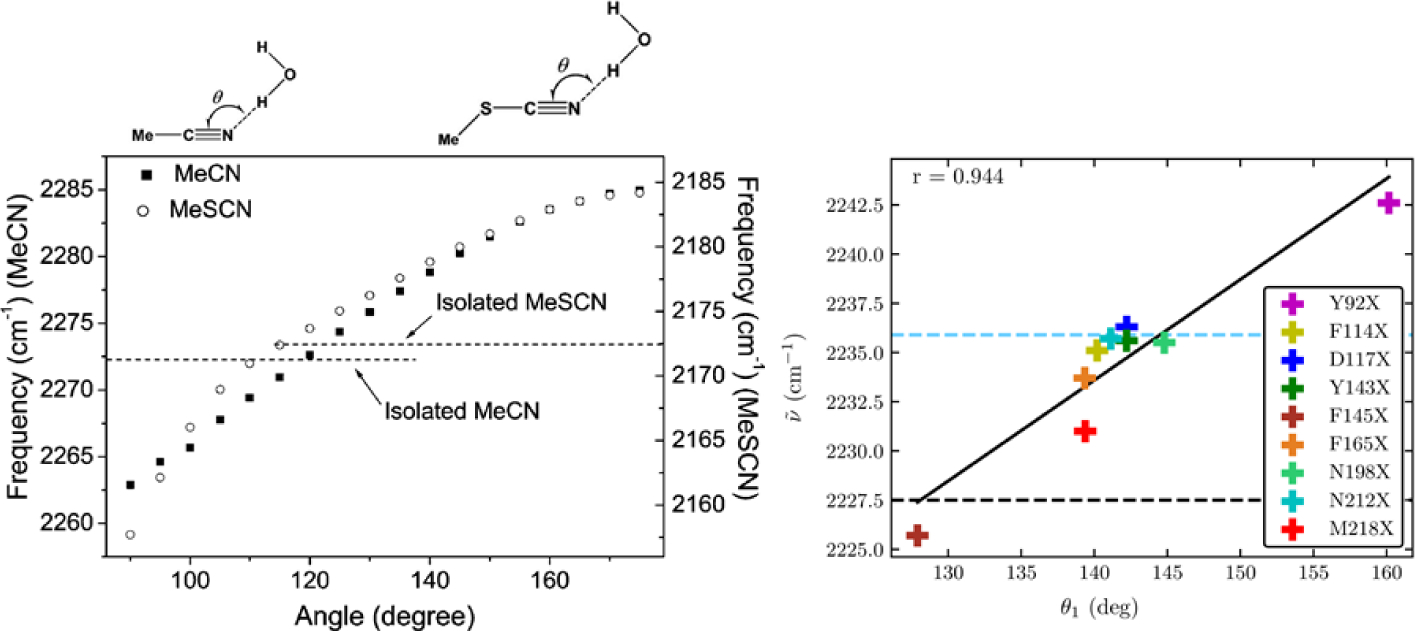
Left: Nitrile stretching mode frequencies of acetonitrile (MeCN, closed squares) and methyl thiocyanate (MeSCN, open circles) plotted with respect to the hydrogen-bond angle, θ, between the nitrile’s N atom and the hydrogen atom of the H-bonded water molecule. Reproduced from Figure 2 of Ref.183 Copyright 2008 AIP Puplishing. Right: Experimentally measured mean nitrile vibrational frequency plotted with respect to the average value of θ from MD simulations of nine variants of GFP containing p-cyanophenylalanine (given in the figure key). Reproduced from Figure 8(B) of Ref.184 Copyright 2018 The American Chemical Society.
Instead of considering the dipole-electric field interaction only, using the more general intermolecular interaction of the solute molecule with dielectric continuum solvent, one can obtain the more general relationship between the vibrational frequency and intermolecular interaction potential. Invoking the WCA in Eq. (57), the first-principles formula for the vibrational frequency shift was obtained and it is given by the sum of the three contributions: (i) the Coulombic term associated with the permanent dipole moment, (ii) the induction term associated with the induced dipole moment, and (iii) the electric field-correction term,185 i.e.,
| (66) |
In Eq. (66), a0 is the Onsager cavity radius, EOns is the Onsager reaction field given in Eq. (35), and
| (67) |
| (68) |
| (69) |
The effective gas-phase and solvation-induced vibrational solvatochromic dipole moments are
| (70) |
| (71) |
whereas the vibrational solvatochromic polarizability tensor is
| (72) |
Here, μ0 and α0 are the permanent dipole moment and the polarizability of the solute molecule, respectively. It should be noted that the electric field-correction term in Eq. (69), Δωj(EOns), arises from the change of the electric field along the normal coordinate.
Now, taking into consideration the linear terms with respect to the Onsager reaction field in Eq. (35), the frequency shift in Eq. (66) simplifies as
| (73) |
This expression can be directly compared to the empirical relationship in Eq. (89), which suggests that the local field correction could be associated with the induced solvatochromic dipole effect as well as the electric-field correction term.
Since Eq. (66) shows that the vibrational frequency shift is proportional to the solute’s dipole moment, the dipole-approximated VSE theory has been frequently used in combination with the Onsager’s solvation model. That is to say, the Onsager reaction field generated by the vibrational Stark dipole moment interacts with that dipole, which results in a simplified expression for the vibrational frequency shift given as
| (74) |
where V is the molecular volume.178 In Eq. (74), the solvent’s refractive index n is included in the reaction field to take into account the effect of solvent polarizability. This approximate theory in Eq. (74) was found to be useful to describe the vibrational solvatochromism of C=O stretching modes in ketones and amides. However, because of the approximate natures of the solute-solvent interaction potential and dielectric continuum solvent model considered, it does not provide quantitative descriptions of vibrational solvatochromism of other IR probes. Despite the limited validity, the VSE theory of vibrational solvatochromism is still often used by researchers, especially when the more refined theoretical model is challenging to implement or not available.186,187
3.5. Electrostatic effect: Distributed multipole analysis
To overcome the limitations of dipole interaction-based theory for vibrational solvatochromism, one should consider local electric potential created by surrounding solvent molecules more realistically. Indeed, the solvent electric field experienced by a given solute molecule in solution is highly non-uniform in space. Assuming that the solute-solvent intermolecular interaction potential can be fully described by the distributed charges, dipoles, and high-order multipoles interacting with solvent electric potential and its linear and nonlinear gradients, it was shown that the vibrational solvatochromic frequency shift is given as148
| (75) |
where the vibrational solvatochromic monopole (charge; lx;j), dipole (μx;j), quadrupole (Θx;j), and octupole (Ωx;j) moments are defined as
| (76) |
| (77) |
| (78) |
| (79) |
These charges and multipoles are distributed over a generalized set of centers placed on the solute molecule (typically atomic centers). They interact with the solvent electric potential ϕx (evaluated at the xth distributed site), electric field (Ex = −∇ϕx), the gradient of electric field gradient, and so on, thus sensing the electric field created by surrounding solvent molecules. These vibrational solvatochromic charges and multipoles, i.e., qx, μx, Θx, and Ωx, can be calculated using the cumulative atomic multipole moment (CAMM) calculation method developed by Sokalski and Poirier or any other distributed multipole expansion method.185 Eq.(72) is essentially a very general form of the electrochromic VSM.
In the limiting case that only one interaction site, e.g., the center of mass, of a solute molecule is considered, the vibrational solvatochromic charge is zero due to the charge conservation condition and the distributed multipole expansion form of the vibrational solvatochromic frequency shift in Eq. (75) becomes highly simplified as188
| (80) |
where the first term is nothing but the well-known VSE theory. From the quantum chemistry calculations for a few IR probes, such as C≡N stretches in CN–, MeCN, MeSCN, p-tolunitrile and 4-cyanopyridine, asymmetric azido stretch in MeN3, and C–F stretches in fluorobenzene and 3-fluoropyridine, it was found that the terms up to vibrational solvatochromic quadrupoles should be included to adequately describe the vibrational frequency shift.
3.6. Electrostatic and non-electrostatic interactions: Effective fragment potential approach
As opposed to many studies concentrating on electrostatic interaction-induced vibrational solvatochromism,38 there are just a few reports considering non-electrostatic interaction contributions to the frequency shift due to solvation. Rey and Hynes189 decomposed the atomic forces obtained from classical molecular dynamics (CMD) simulations. They found that the van der Waals interaction induces a strong blueshift of the C≡N stretch mode in cyanide anion in solution. A similar conclusion was drawn by Morales and Thompson, who investigated MeCN/water system by using classical MD simulation methods.190 There also exist other works showing the non-negligible exchange-repulsion-induced effect on vibrational frequency shifts.191–196 By correlating various interaction potential components with frequency shifts, the repulsive potential was found to be responsible for vibrational frequency blueshifts. Zierkiewicz et al. studied a series of both blue- and red-shifting complexes.193 They attributed the blueshift of vibrational frequency to a ‘repulsion wall’ caused by the Pauli exclusion principle. Furthermore, the dispersion interaction term also plays a role in causing vibrational frequency shifts. Rodziewicz et al. combined Buckingham’s theory for a diatomic molecule with SAPT and studied vibrations involving C–H or C–X stretches, where X denotes a halogen atom.194 They found that the exchange-repulsion effects cause a vibrational frequency blueshift, though the underlying mechanism of these frequency shifts is very complicated. Choi et al. studied the effects of charge transfer on the vibrational frequency of ionic IR probes such as CN− or N3− anions dissolved in water.197 Although a considerable charge transfer between solute and water molecules was found, the net charge transferred appeared to be in no correlation with the vibrational frequency shifts. That led them to suggest that the charge transfer phenomenon can be neglected when considering the intermolecular interaction-induced frequency shifts for the studied systems. However, recently, charge transfer was found to be important in a certain case by Brinzer et al.,198 where they studied CO2 asymmetric stretching (ν3) mode as an IR probe for sensing the local molecular environments in ionic liquids. Moreover, it was demonstrated recently that the solvation-induced vibrational frequency shifts of pyrimidine vibrations are correlated with charge transfer between pyrimidine and various polar solvents, including water, methanol, and hexylamine.199 To examine both electrostatic and non-electrostatic interaction-induced frequency shifts theoretically, the WCA based theory combined with the hybrid variational-perturbational interaction energy decomposition scheme (SolEDS) was applied to the vibrational solvatochromism of amide I mode and C≡N stretch modes of MeSCN in various solvents. This approach revealed that exchange-repulsion blueshifts and non-Coulombic redshifts due to dispersion and induction interactions are equally important.143,154–156
In order to accurately predict and simulate the non-electrostatic interaction effects on the vibrational solvatochromism of IR probes, high-level quantum mechanical description of the solute-solvent interaction potential is needed. To systematically study and predict the electrostatic and non-electrostatic effects on the vibrational frequency shifts in condensed phases directly by utilizing MD simulations of various IR probes, the optimized quantum mechanics/molecular mechanics (OQM/MM) method was introduced by the Skinner group69 and later further developed by the Corcelli group42,200,201. In their method, the semi-empirical Hamiltonian of an IR-active fragment and its bath-coupling parameters are re-parameterized from the original set of parameters, e.g., PM3 minimal basis model of Hamiltonian202. The vibrational solvatochromism is described at a hybrid level of PM3 and classical force fields with an electrostatic embedding scheme, making this approach very efficient when combined with MD simulations. It was shown that OQM/MM is easily transferable to other solute and solvent systems and capable of accurately simulating the IR spectra of complicated systems, including proteins in water. Recently, the OQM/MM method was shown to be of limited use for describing the frequency shifts of SCN probe incorporated in calmodulin. This limitation is likely to originate from the electrostatic embedding approximation that has been a common choice in QM/MM treatment of the interactions between QM and MM parts of the system.203 In general, the quantum embedding of an IR probe’s Hamiltonian into QM/MM can be a relatively expensive and difficult task, especially if the exchange-repulsion and dispersion interactions are to be explicitly included in the system-bath interaction. To circumvent this problem, one can combine the WCA theory with a quantum mechanical model for intermolecular interaction potential, U.
Inserting the expression for the intermolecular interaction potential given in Eq. (48) into the WCA expression for the vibrational frequency shift in Eq. (57), one can obtain the vibrational solvatochromism theory based on the effective fragment potential theory,40,143,154,155 which was referred to as SolEFP. Unlike the OQM/MM model, the SolEFP model is a VSM because it is derived from the solute-solvent-separable EFP2 intermolecular potential. The resultant expression for the vibrational frequency shift of a jth normal mode is given as a sum of the Coulombic, exchange-repulsion, induction, and dispersion contributions, i.e.,
| (81) |
The Coulombic term can be factorized into two components as
| (82) |
where is the distributed multipole contribution to the vibrational frequency shift (see Eq. (75)).185 The second term, , represents the contribution originating from the vibrational coordinate-dependence of electric potential created by surrounding solvent molecules. Usually, this secondary effect is small. Nevertheless, in practice, to estimate , only the monopole terms in the multipole expansion series are taken into consideration due to a convergence issue. Then, is given as143
| (83) |
where is the vibrational eigenvector element associated with the xth solute’s atom in the ith normal mode and the relative position vector of the yth solvent atom is defined as rxy = rx – ry.
The exchange-repulsion term in the SolEFP originates from the exchange-repulsion interaction potential obtained by Gordon and coworkers,204,205 where they assumed a single electron pair exchange between the unperturbed Hartree-Fock wave functions and the spherical Gaussian overlap. Under such an approximation, it was shown that
| (84) |
when neglecting the electronic anharmonicity contribution to . The vibrational force associated with the exchange-repulsion potential is given as
| (85) |
here Sab and Tab are the one-electron overlap and kinetic integrals between the ath and bth localized molecular orbitals (LMOs), respectively, is the Fock matrix element of molecule X, and Zx is the atomic number of the xth atom. The relative distance rαβ = |rα – rβ|. Here, the indices a, b, c, and d refer to LMOs located at their charge centroids of charge ra, whereas indices x and y do to atoms in molecules A (solute) and B (solvent), respectively. Because the exchange-repulsion is approximately pairwise-additive,206–210 one can use Eq. (85) to calculate the corresponding frequency shift of an IR probe molecule even in complicated environments. Also, it is relatively easy to evaluate from MD simulations because the calculation requires only one-electron integrals. Although there are many derivatives to be calculated in Eq. (85), they are just the first derivatives of one-electron integrals with respect to interatomic distances, which can be computed analytically. In addition, the first derivatives of the LMO centroids and Fock matrix elements can be calculated numerically and treated as SolEFP parameters, much like the way to determine EFP2 parameters.
The vibrational frequency shift due to the induction interaction is given as143
| (86) |
where the induced vibrational solvatochromic dipole and the permanent vibrational solvatochromic polarizability of the entire system are, respectively,
| (87) |
| (88) |
The generalized electric field Φ and the inverse polarizability tensor D are
| (89) |
| (90) |
where αa(0) is the distributed anisotropic polarizability tensor evaluated at zero frequency. αa(0) can be calculated by using the coupled-perturbed Hartree-Fock theory and it is essentially the response of the LMOs against electric field perturbation. The derivatives of Φ and D with respect to the normal coordinates are calculated with pre-computed numerically and used as the SolEFP parameters.
The dispersion contribution to the vibrational frequency shift is given by154
| (91) |
where α(a)(iΞ) is the imaginary frequency-dependent anisotropic polarizability tensor associated with the ath LMO of solute molecule. The derivatives of the product of dipole-dipole interaction tensors can be easily evaluated analytically and are the numerically calculated SolEFP parameters.
Since the EFP2 model describes inherently rigid molecular fragments, SolEFP was first applied to N-methylacetamide (NMA) and MeSCN dissolved in solvents of varying polarity as well as in water. Recently, SolEFP was further developed to make it of use for vibrational frequency shift calculations of IR probes in proteins. This extended version of SolEFP is denoted as Bio-SolEFP. In the Bio-SolEFP method,155,203 the vibrational frequency shift of an IR probe is given by
| (92) |
where accounts for the Coulombic frequency shift due to the closest peptide groups for which the superimposition of EFP2 fragments is impossible due to close contact with the IR probe’s SolEFP fragment, ΔωThrough bond–effect is the constant offset due to the attachment of the IR probe to protein, and ΔωSolEFP is the remaining contribution modeled by SolEFP. It was shown that Bio-SolEFP applied to the molecular configurations sampled from classical MD trajectories of the SCN-labeled calmodulin in water can successfully reproduce the C≡N stretch IR spectra of SCN groups that have different solvent environments.203 In fact, the SolEFP/MM method is of comparable cost as OQM/MM method. However, still due to a number of approximations used in SolEFP/MM method, e.g., neglecting the electric anharmonicity terms in the non-electrostatic interaction-induced frequency shift and the charge-transfer and penetration effects, SolEFP was found to suffer from systematic errors that lead to a slight overestimation of the frequency blueshift. Furthermore, the evaluation of the second derivatives of the exchange-repulsion and induction interaction potentials with respect to the normal coordinates is computationally expensive. Nonetheless, in the case of the amide I and the nitrile stretch modes, from ab initio calculations of such electric anharmonicity-induced frequency shifts originating from non-Coulombic interaction for a few model solute-solvent clusters, we found that they cancel out with each other to a great extent. This is indirect evidence supporting the assumption that the mechanical anharmonicity-induced frequency shifts originating from the non-Coulombic intermolecular potentials are dominant. Still, it would be desirable to further develop the SolEFP theory by including those neglected terms more accurately in the near future. The SolEFP VSM and Bio-SolEFP are available in the Solvshift quantum chemistry program at https://globulion.github.io/slv. Multiple IR probes as well as solvent and protein fragments are parameterized at the HF/6–311++G** level of theory in a fragment library, which is interfaced via the MDAnalysis211,212 library with popularly used MD trajectory file formats such as those used by GROMACS,213 AMBER214 and NAMD215 molecular dynamics software. This makes the Solvshift code easy to use even for complex heterogeneous systems such as IR probes in bulk solvents and even proteins. The automatic generation of custom fragment parameters is also possible.
4. Semiempirical Approaches: Vibrational Spectroscopic Maps
Several rigorous theories for vibrational solvatochromism and electrochromism based on physical approximations have been presented and discussed before, as reviewed in Sec. 3. However, those highly sophisticated models require extensive quantum chemistry calculations at high levels with a large basis set. It is not practical to use fully ab initio simulation methods, not only because the molecular systems of interest are complicated and heterogeneous solutions containing biomolecules, ions, and polymers, but also because they have complex molecular dynamics such as conformational transitions, protein-protein interactions, protein-ligand dynamics, and ultrafast solvation and chemical reaction dynamics. Note that the current ab initio MD simulation methods do not provide vibrational frequencies that can be directly compared with experimentally measured frequency shifts on the order of a few wavenumbers. Consequently, vibrational solvatochromism theory that utilizes pre-calculated parameters from high-level quantum chemistry calculations of solute molecule in the gas phase is exceptionally useful and has been shown to be capable of predicting vibrational frequencies using the configurations and structures of solute and solvent molecules from MD trajectories.
However, there is a complication that cannot be easily overcome, even with semiempirical vibrational frequency maps. A solute molecule samples an ensemble of structures in solutions that are different from the geometries optimized in the gas phase using quantum chemistry calculation methods. Thus, it is not straightforward to match ab initio calculated molecular structures to those from MD trajectories. This difficulty in superposing gas-phase structures onto those in solutions, which will be referred to as geometrical superposition error (GSE), is a complicated problem and sometimes can lead to frequency shifts that are far from the experimental results. The GSE becomes especially critical when a short-range repulsive interaction between solute and solvent molecules via H-bonding interactions plays the dominant role in vibrational solvatochromism, e.g., CN stretch frequency shift of nitrile-derivatized compounds in protic solvents. Furthermore, the gas-phase calculations often cannot accurately reproduce the anharmonic potential energy surface of the solute molecule in solution and lead to inaccurate prediction of vibrational solvatochromic parameters. The anharmonicities of the multidimensional potential energy surfaces of an ensemble of solute molecules in solution are also strongly affected by the detailed intermolecular interactions between the solute and solvent molecules. Hereafter, this difficulty will be referred to as potential anharmonicity solvatochromism problem. To overcome these major difficulties in accurately calculating vibrational solvatochromism parameters, one of the simplest ways is to use multivariate least-square fitting analyses with a sufficiently large set of training database. In the present section, we shall discuss the general theoretical background and present real applications to a variety of IR probes used over the past two decades.
4.1. General consideration and motivation: Linear combination of basis functions based on physical approximations
Quantum mechanics makes it feasible to quantitatively describe chemical bonds and to understand molecular structures in terms of wavefunctions of constituent particles like electrons and nuclei. However, there are only a handful of examples of which Schrödinger equations are mathematically solvable. Even the Schrödinger equation for the simplest molecule, H2, cannot be solved analytically. However, due to the dramatic advance in computational chemistry calculation and numerical analysis methods, it becomes possible to calculate the energies of small molecules accurately. Up until now, the most successful way to obtain molecular orbitals is to write them as linear combinations of atomic orbitals (LCAO-MO). For the sake of computational convenience and efficiency, we assume the atomic orbitals of constituent atoms in a given molecule are Gaussian functions:
| (93) |
Here is the jth molecular orbital, is the kth atomic orbital, N is the number of atomic orbitals, and ajk are the expansion coefficients. This set of mathematical functions used to construct both the atomic orbitals and the molecular orbitals is known as the basis set. It should be noted that the Gaussian functions in each basis set do not have to have long exponential tails like the H-atomic orbitals. However, if they are well-behaved quantum mechanically and useful for computational purposes, the lack of long radial tails of basis functions is not a serious problem. Bearing this aspect in mind, let us consider the vibrational frequency map functions developed and used over the past decade.
One of the early attempts is to expand the solvation-induced vibrational frequency shift in terms of the solvent electric potentials at distributed atomic sites on the target solute molecule.38,147 The solvent electric potentials at the solute sites are calculable by considering atomic partial charges of surrounding solvent molecules. When the solvent molecules have atomic configurations determined by Q, the instantaneous frequency shift of the solute molecule, Δωj(Q), of the jth vibrational mode can be written as a linear combination of solvent electric potential,
| (94) |
where ωj(Q) is the vibrational frequency of the jth normal mode in solution, ωj0 is the vibrational frequency of the same jth mode in the gas phase, N is the number of distributed sites on the molecule, ϕk(Q) is the solvent electric potential at the kth site of the solute molecule, and bjk are the expansion coefficients. Comparing Eq. (94) for vibrational frequency shifts with Eq. (93) for LCAO-MO, one can find the analogy between the two approaches. It should be mentioned that the wavefunction in Eq. (93) enters the expectation value of quantum mechanical observables as in Eq. (94) quadratically. One of the critical differences between the two, aside from the observable itself and the functional forms of the basis functions, lies in the way of determining the corresponding expansion coefficients. The expansion coefficients ajk for an LCAO-MO are determined by applying the variation principle to the calculation of the ground state energy. On the other hand, the expansion coefficients bjk for a vibrational frequency shift Δωj(Q) are determined by carrying out a multivariate least-square fitting analysis for a training database obtained from ab initio calculations of the vibrational frequency shifts of the jth mode for many clusters containing a solute and multiple solvent molecules. The number of clusters should be sufficiently larger than the number of expansion coefficients or that of distributed sites on the solute molecule.
The electric potential model in Eq. (94) was derived rigorously from the quantum mechanical perturbation theory with treating the associated solute-solvent interaction energy as a perturbation to the potential energy function of vibrational degrees of freedom of a given solute molecule.147 The solute-solvent intermolecular interactions are assumed to be dictated by the Coulomb interactions of atomic partial charges of the solvent molecules with the distributed charges of the solute. Although the formal expression for the expansion coefficients bjk was presented elsewhere147 in terms of transition charges, potential anharmonic coefficients of solute molecule in the gas phase, vibrational frequencies, reduced masses, and so on, they were treated as fitting parameters for multivariate least square analyses of a set of ab initio calculated solute-solvent clusters. Thus, even though the solvent electric potential model in Eq. (94) is based on rigorous physical approximations, the key parameters bjk were obtained in an empirical manner by fitting to the quantum chemistry calculation results for many clusters.
Another popular model for theoretically describing such vibrational solvatochromic frequency shifts assumes that the frequency shift can be expanded in terms of solvent electric fields at distributed sites on the target solute molecule,
| (95) |
where Ek(Q) is the solvent electric field, or negative gradient of solvent electric potential, at the kth site on the solute molecule, μjk is the vectorial expansion coefficients connecting Ek(Q) to Δωj(Q), and and are the mth Cartesian components of μjk and Ek(Q) vectors, respectively. From these two models in Eqs. (94) and (95), the vibrational frequency shift is expanded as a linear combination of the basis functions, which are either solvent electric potentials or electric fields at solute’s distributed sites. The solvent electric field model in Eq. (95) assumes that the solute-solvent intermolecular interaction can be described by the sum of Coulomb interactions between distributed solute electric dipoles and solvent electric fields. Again, the expansion coefficients, , are determined by performing a multivariate least-square fitting analysis for a set of ab initio calculated vibrational frequencies for a set of solute-solvent clusters with Eq. (95).
These two representative models assume that the solute-solvent interaction can be fully described by the Coulomb interactions between solute charges (dipoles) with solvent electric potential (field). The expansion coefficients, either bjk in Eq. (94) or in Eq. (95), are obtained from a training database from a series of quantum chemistry vibrational analyses of a large number of solute-solvent clusters. Once the set of parameters is determined, one can use the corresponding Eq. (94) or (95) to predict the frequency shift Δωj(Q) of the oscillator in any solutions or condensed phases by calculating the solvent electric potential or field using instantaneous solvent configurations and the corresponding partial charges described by MD force fields.
Considering a more sophisticated intermolecular interaction model, one can expand the set of basis functions. For instance, short-range Pauli repulsive interactions between the solute and solvent molecules cause blueshifts of the nitrile stretch frequency when the nitrile forms a strong H-bond with water or other protic solvent molecules. This leads to the development of more general approaches based on physical approximations to the solute-solvent intermolecular interaction energy. Thus, one can make a generalization of vibrational frequency as
| (96) |
where χk(Q) constitute the basis set of functions that can be based on physical approximations or that can adopt any arbitrary mathematical forms as long as they are well-behaved functions without singularity or divergence. Here, cjk are the expansion coefficients. The most critical assumption for all the semiempirical vibrational frequency maps, which include vibrational frequency shift, vibrational transition dipole and polarizability, and vibrational coupling maps, is that the best set of parameters {cjk} are obtained by carrying out multivariate least-square fitting analysis for a training database from quantum chemistry calculation results for various clusters.
In this section, we shall compare theorerically developed VSMs for a variety of IR probe modes with experimental results or high-level ab initio calculations. Unfortunately, it is difficult to establish a simple set of criteria used to assess the validity of VSM in a quantitative manner, because the magnitudes of solvatochromic vibrational frequency shifts are in a wide range from just a few wavenumbers to hundreds of wavenumbers. However, there is an interesting paper reported by the Ge group,216,217 where they compared different VSMs for amide I vibration and used them to make interpretations of their 2DIR spectroscopic results (Sec. 4.3). It would be interesting to carry out benchmarking studies of various IR probes other than the most extensively studied amide I vibration in the future.
4.2. General parameterization method
Essentially all the VSMs proposed to date, both semiempirical and ab initio, can be recast in the following form,
| (97) |
where Y is the vibrational spectroscopic observable of interest, and are the associated vibrational solvatochromic parameters such as charges, multipoles and so on, and is the conjugate field created by the surrounding solvent molecules. Here, should be evaluated at the xth interaction site of the solute, that could be an atomic site, an LMO centroid, or any other point within the IR probe’s charge density distribution. The superscript “T” denotes the type of intermolecular interaction, e.g., Coulombic, induction, etc., of rank R. For example, the rank-zero field is a scalar, and the rank-one field is a vector. The Greek subscript indices in Eq. (97) represent the Cartesian coordinates. For example, when R=0 could represent a vibrational Stark tuning rate. The vibrational solvatochromic quadrupole is with R=2. In the second term in the curly bracket of Eq. (97), vibrational solvatochromic parameter could be vibrational solvatochromic polarizability when R=R’=1. In an extreme case, the conjugate field can adopt a very complex tensor form as in, for example, the SolEFP model, in which not only electrostatic but also wavefunction overlap and dispersion effects are mapped in a way that formally fits the functional form of Eq.(94). On the other hand, it is also the way the VSM is parameterized, and conjugate fields are defined, which allows the explicit function in the form of Eq.(94) to be designed in a relatively simpler form, allowing computationally more robust VSMs to be developed in terms of semiempirical mapping procedures.
In Sec. 4.1, we have already reviewed two popular semiempirical vibrational parameterization schemes. They are broadly referred to as the electrostatic fitting methods (ESF), which correlate benchmark ab initio or density functional theory (DFT)-calculated vibrational properties with electric potentials or electric fields on/around the IR probe in condensed phases.66,67,111,183,188,197,218–241 The expansion sites are called the “interaction centers or interaction sites”, and they are chosen in a way to effectively represent the local electric potential or field created by surrounding solvent molecules. The non-electrostatic interaction-induced effects on the vibrational spectroscopic observables can also be taken into account similarly. There are a few examples of vibrational frequency maps connecting H-bond distances240 or van der Waals forces241 with the vibrational frequency of the IR probe.
Most previous works focused on just one type of parameters, e.g. scalar vibrational solvatochromic charges111,183,188,197,218–220,222–224,232,234,236,238,242 and vectorial vibrational solvatochromic dipoles66,67. However, there are also maps utilizing multiple types of parameters, as well. Torii and coworkers237,239 considered both scalar charges and vectorial dipoles as vibrational solvatochromic parameters, whereas Jansen and Knoester231 and Mukamel and coworkers227,228 considered vectorial dipoles and tensorial quadrupoles as vibrational solvatochromic parameters. In order to account for the non-electrostatic effects in the VSMs and intramolecular mode couplings, the van der Waals effects should be parameterized by combining MD simulations with experimentally measured protein spectra as reference data.240,241 Such an approach is specifically designed for very large systems like proteins in water. In the following subsections, various vibrational spectroscopic maps developed so far are reviewed.
4.3. Amide I vibration: Frequency and coupling maps
In the protein backbone, repeating units of peptide bonds link amino acids together and their vibrations create a series of normal modes in the 1200 – 1800 cm−1 region that are characteristic of the protein structures. From higher to lower frequencies, these normal modes are called the amide I, II and III modes.233 The amide I mode is the most extensively studied vibration in protein spectroscopy, and we will use Sections 4.3 and 4.4 to summarize the theoretical methods to model its vibrational features and demonstrate how it can be combined with isotope labeling to reveal site-specific information. We will then discuss the amide II and III bands in Section 4.5.
The amide I band, which appears in the 1600 – 1800 cm−1 spectral region, arises mainly from the peptide bond C=O stretch with minor contributions from the amide C-N stretch and Cα-C-N deformation. It shows distinctive features for different secondary structures in polypeptide chains and thus has been widely used in linear and nonlinear vibrational spectroscopies to detect the structures and dynamics of polypeptides and proteins.25,111,139,242–254 These spectroscopy experiments in the amide I region are particularly useful for systems that are not easily studied using standard techniques of protein structural analysis such as NMR and X-ray scattering, including membrane proteins, intrinsically disordered peptides, and systems undergoing triggered folding or unfolding. For example, 2D IR spectroscopy has been applied to monitor the conformational dynamics in the folding and unfolding of proteins, revealing the gating mechanism and water dynamics of transmembrane proton channels, and uncovering the structures and aggregation pathways of amyloid proteins.75,83,106,107,255,256 The intrinsic ultrafast time scale of the amide I vibration (~20 fs) makes amide I spectroscopy much less susceptible to the motional narrowing difficulties encountered in NMR spectroscopy.
To quantitatively relate the amide I spectral features with the structures and dynamics of proteins, researchers often use a mixed quantum mechanical/classical mechanical approach that treats all the amide I vibrations in a protein quantum mechanically and the low-frequency degrees of freedom (such as those along main-chain dihedral angles) classically.124,127,257 If a protein contains N amide I modes, the single-quantum vibrational Hamiltonian is a N × N matrix, in which the diagonal terms are the site frequencies of each chromophore and the off-diagonal terms are the couplings between them. In principle, one can obtain the vibrational Hamiltonian from quantum chemical (such as DFT) calculations. However, it is impractical to perform high-level quantum chemical calculations on large proteins in the condensed phases,258 particularly if we want to follow the time course of structures along the dynamics of the proteins. Alternatively, researchers have designed a variety of frequency and coupling maps for the amide I vibrations so that one can efficiently compute the elements of the vibrational Hamiltonian based on the time series of structures obtained from MD simulations.259
Among other factors, electrostatic interactions play a major role in determining the shifts in vibrational frequencies and the coupling between peptide chromophores in the amide I vibrational chromophores. In particular, inhomogeneous and fluctuating electrostatic environment around the vibrational chromophores alters their site frequencies and broadens the absorption bands. TheVSMs developed so far for the amide I mode relate the site frequencies to the electrostatic potentials and/or electric fields (and electric field gradients in some cases) on the atomic sites (and some other points, such as bond centers, if needed) in the peptide group.67,217,219–221,225,228,231,233,235,237,238,260–263 They often take the form of Eq. (94) or (95) and are based on N-methylacetamide (NMA) as a model compound to mimic the most typical peptide groups, i.e., the secondary amide groups, of the protein backbone. The parameters in the frequency maps are determined by referring to the results of quantum chemical calculations, or in a few cases, directly to the experimental spectral features.233,240,260,261,264 For example, Cho and coworkers developed the first amide I frequency map by considering a series of NMA-D2O complexes and carrying out ab initio quantum chemical calculations to obtain their amide I frequencies. They then used Eq. (94) and obtained the linear combination coefficients from multivariate least-squares fitting analysis to the quantum chemical results.220 Taking a similar approach, Skinner and coworkers examined deuterated NMA/water clusters and provided the first electric field-based amide I frequency map.67 While most of the frequency maps developed so far employ the electrostatic potentials or the electric fields on the atomic sites to represent the electrostatic environment,260 it has also been shown237,238 that both the electrostatic potentials and the electric fields on those sites can be essential in describing the inhomogeneity of the electrostatic environment. To account for the electrostatic effects in various solvent environments, Jansen and Knoester embedded deuterated NMA in 75 charge environments and developed a frequency map that incorporates the electric field and its gradient on the C, O, N and D atoms of the chromophore and demonstrated its transferability in common organic solvents231 and need to include multipole and polarizability in solvents like chloroform.265 Skinner and coworkers have also adopted an empirical approach by optimizing the coefficients against experimental spectra of deuterated NMA in D2O, DMSO, and chloroform and designed a frequency map that is transferrable to different electrostatic environments.261 A similar approach has been adopted by the Tokmakoff group, who have developed an extensive set of experimental standards (including 28 model dipeptides and 5 isotope-edited protein constructs) that can be used to test and refine vibrational frequency maps.45,260,264 These frequency maps have been extensively tested and applied to predict the linear and 2D IR spectra of polypeptides and proteins.217,259,266
In most cases, one can apply an amide I frequency map to all peptide bonds, regardless of its composition of amino acids. A notable exception is the peptide bond involving the N atom of a proline residue, i.e., the peptide bond of the form Xxx-Pro, where Xxx represents any amino acid. Typically, the amide I mode of this tertiary amide group is shifted strongly (~35 cm−1) to the red in comparison to that of a secondary amide. Thus, it must be treated separately either by adding an overall shift to the standard map or through a separate parameterization.235,260,267 In the latter case, N,N-dimethylacetamide has been chosen as the model compound for the map parametrization. Due to the large redshift, peptides containing the Xxx-Pro amide bonds show an amide I absorption peak well separated from the main band in the IR spectru, which provides a unique and excellent probe for investigating local structural and dynamical changes in proline-rich proteins such as collagen and elastin. In addition to modeling the backbone amide I chromophores, vibrational frequency maps have also been developed for the side chains of asparagine and glutamine, which contain primary amide groups.261
Although electrostatic interactions strongly shift the site frequencies of the amide I mode in the condensed phases, it has been shown that special treatment is needed to account for the nearest neighbor (NN) effects on the frequencies. Accordingly, DFT-based maps for NN-induced frequency shifts230,268,269 have been developed. The site frequency of an amide I vibration is given by
| (98) |
where ωelst is the frequency derived from an electrostatic frequency map, and ΔωN and ΔωC are the frequency shifts affected by the nearest neighbors of the vibrational chromophore on the N- and C-terminus sides of the chromophore, respectively. ΔωN and ΔωC depend on the ϕ and ψ dihedral angles in the protein backbone as used in the Ramachandran plot. The method of deriving those DFT-based maps will be discussed later, together with the NN vibrational coupling maps.
The electrostatic interactions also play an important role in determining the vibrational couplings between the amide I vibrations of peptide groups. The simplest model in describing these couplings is the transition dipole coupling (TDC) model.139,270–274 Here, each amide I chromophore is treated as a transition dipole moment and their couplings Fij are given by
| (99) |
In this equation, and are the transition dipoles of the ith and jth vibrational chromophores in the unit of D Å−1 amu−1/2. rij is the distance between the two vibrational chromophores and is the unit vector that connects them. The dielectric constant ϵ is usually taken to be 1. The conversion factor A is 0.1 if Fij is represented in units of mdyn Å−1 amu−1. It is possible to convert it to the coupling in units of cm−1 by assuming the “central frequency” of 1650 cm−1 and multiplying further by 848619/1650 (i.e., using A = 0.1×848619 / 1650).139,273 Parameters in the TDC model include the location, orientation, and magnitude of the transition dipoles, and are determined by fitting to experimental peak splitting or ab initio quantum chemical calculation results.270,271 To go beyond the dipole approximation, researchers have also developed models such as the transition charge coupling (TCC) method230,272 and the transition density derivative distribution method.275
Despite the success of the TDC model in predicting long-range interactions between the amide I chromophores, it is not sufficient to describe the couplings between adjacent or nearest neighbor peptide groups.271,272 To overcome this situation, NN coupling maps have been developed for the amide I mode based on quantum chemical calculations.230,268,269,271,272,276 In deriving those maps, ab initio MO or DFT calculations were carried out for peptide dimers with the ϕ and ψ dihedral angles of the main chain being varied for all possible ranges of values at appropriate intervals. The calculated force constant matrix was then size-contracted to the vibrational subspace of the amide I mode by using, for example, the Hessian Matrix Reconstruction (HMR) method277 to obtain the site frequencies (for the maps of NN-induced frequency shifts) and the coupling constants for each particular set of ϕ and ψ. The maps were made by collecting those site frequencies and coupling constants, represented by the diagonal and off-diagonal terms of the size-contracted matrix, as functions of ϕ and ψ. In using those maps, one can estimate the site frequencies and coupling constants for any set of ϕ and ψ by interpolation. In contrast, the TDC model is sufficiently accurate when modeling the couplings between the amide I modes of the peptide groups that are not nearest neighbors.
Vibrational frequency maps that further include non-electrostatic perturbations have been presented as well for the amide I local mode frequencies.240,241,278 For example, in the vibrational frequency map developed by Malolepsza et al.,241 the corresponding vibrational frequency shift is computed using two independent sets of distributed vectorial parameters: the first describes the usual vibrational response of the amide I mode to the solvent electric field (Ei) and the second is associated with van der Waals force exerted to each atom in a given peptide, i.e.,
| (100) |
where i runs over atoms in the peptide CONH group. It was shown that the map, initially optimized for NMA in three different solvents, is accurate enough to model the amide I IR spectra of a few different proteins that include ubiquitin, ribonuclease, myoglobin, and concanavalin. In other works,240,278 the vibrational solvatochromism maps for amide I vibrations of proteins were developed by considering their backbone structures and H-bonding environment only. More specifically, the vibrational frequency shift of the amide I mode of a given peptide in a protein is assumed to be240,278
| (101) |
The backbone structure of the peptide group is determined by the two Ramachandran angles so that the frequency shift depends on its backbone structure, which is described by the term Δω(ϕ,ψ) in Eq. (101) (see also Eq. (98)). The vibrational frequency shift due to its H-bonding interaction with surrounding solvent molecules is described by the term which is mainly determined by the extent of water exposure, i.e., solvent accessible surface area, of the CONH unit. The effect of interpeptide H-bonds on the vibrational frequency shift, , is assumed to be proportional to the Kabsch-Sander bonding energy,279 which is determined by the H-bond length and angle between the amide CO group (H-bond acceptor) and the amide NH group (H-bond donor) in the same protein. To determine these parameters, they used forty-four experimentally measured IR absorption spectra of protein systems in water.240
All these frequency maps are typically validated against experimental data for NMA in different solvents.226,228,235,241,260,261,264,280 Validation of the coupling maps proves more challenging, because it is difficult to thoroughly sample the flexible structures of small peptides in simulations and it is challenging to extract useful information from the broad and congested IR absorption bands of large proteins with well-defined structures. 2D IR spectra are more sensitive to couplings, although they are time-consuming to calculate for full proteins.281 Despite these computational challenges, Jansen and coworkers have calculated the 2D IR spectra of a selection of proteins and compared the theoretical spectra using different mappings266,282 with the experimental ones.283 Among the methods tested, they have concluded154 that the electrostatic frequency map of Skinner261 combined with the OPLS/AA force field,284 the TDC map of Torii and Tasumi271 and the NN maps of Jansen230 have the best performance. Spectral simulations of liquid NMA285 and its mixtures with water286 provided a further benchmark suggesting that the long-range TCC model possibly overestimates the coupling constants.
One thing that is counter-intuitive in the electrostatic frequency map of Skinner261 is that the electrostatic situation of O atom of the peptide group, which acts as an H-bond acceptor and vibrates with large amplitude in the amide I mode, is not involved in calculating the frequency shift of the amide I mode. It was shown that this is because of the mutual cancellation between the effects of electrostatic potential and the electric field on the frequency shift, and is related to a general property of H-bond accepting stretching modes.237,238
Other localized coordinate approaches have also been recently developed for use in ab initio anharmonic vibrational frequency calculations, where the anharmonicity is calculated explicitly.287–296 In a similar way, site-specific frequencies, NN coupling terms, and non-nearest neighbor coupling terms can be determined directly from harmonic vibrational calculations on molecules of (in principle) any size, using the technique put forward by Hanson-Heine et al.297 In this technique a subset of the normal coordinate eigenvectors from a harmonic frequency calculation are rotated by applying a unitary transformation that maximizes one of the objective functions proposed by Jacob and Reiher,298 where the transformation either maximizes the sum of the squares of the atomic contributions to the normal modes,
| (102) |
where μ and i are normal modes and nuclei, respectively, and M is the total number of nuclei, or the transformation maximizes the distance between the centers of the modes,
| (103) |
where Ri is the position vector of each nucleus in the molecular coordinate system. If an appropriately localized subset of normal coordinates is chosen, such as the amide I manifold, then site-specific frequencies and coupling terms can be derived from the diagonal and off-diagonal elements of the mass-weighted Hessian matrix in the newly transformed coordinates.
This approach has been successfully applied to vibrational exciton calculations of 2D IR spectra for the amide I band of a range of dipeptides and the hexapeptide Z-Aib-L-Leu-(Aib)2-Gly-Aib-OtBu. However, the approach is not specific to the amide I mode and can, in principle, be applied to any system for which the localized modes have an appropriate form. Semiempirical maps of site-specific frequencies and NN couplings across different ϕ and ψ angles can be obtained by considering small model systems. The newly created local coordinates are also not localized on to a subset of atoms chosen a priori, leading to amide I modes that contained significant motion of the nitrogen atom for the species originally tested, which is consistent with the true nature of the amide I mode. However, care should be taken when selecting the subset of coordinates to be transformed, so that the automatically generated coordinates remain correct.
To test the validity of the frequency and vibrational coupling map of amide I mode, one should consider peptides with relatively rigid structures to avoid the need for statistical averaging of multiple backbone conformations in MD simulations. One particularly good system for such a test, as demonstrated by the Ge group, is a peptide with Cα-alkylated amino acid residues, such as Aib (Cα,α-dimethylglycine) and (αMe)Val (Cα-methyl valine). Because of the steric hindrance caused by the alkyl side chains, these unnatural residues restrict the available dihedral angles in the Ramachandran plot and hence can dictate a peptide to fold into a well-defined conformation. Ge and coworkers measured polarization-dependent 2D IR rephasing and non-rephasing spectra of a capped octapeptide Z-[L-(αMe)Val]8-OtBu (Z, benzyloxycarbonyl; OtBu: tert-butoxy) in deuterated chloroform (CDCl3), and used the amide I spectral signatures to judge spectra calculated based on MD trajectories and six different combinations of electrostatic frequency maps and NN coupling maps.216 The main differences in the frequency maps are the parameterized sites in a peptide unit, whether the amide I frequency fluctuation is estimated from electric potentials or electric fields and field-gradients on the sites, whether the partial charges are taken from an MD force field or from the frequency map parametrization, whether nearest-neighbor frequency shift (NNFS) map is used, and the gas-phase frequency origin (Figure 4a). The chromophore definition in each model is chosen to ensure charge neutrality within the chromophore.
Figure 4.
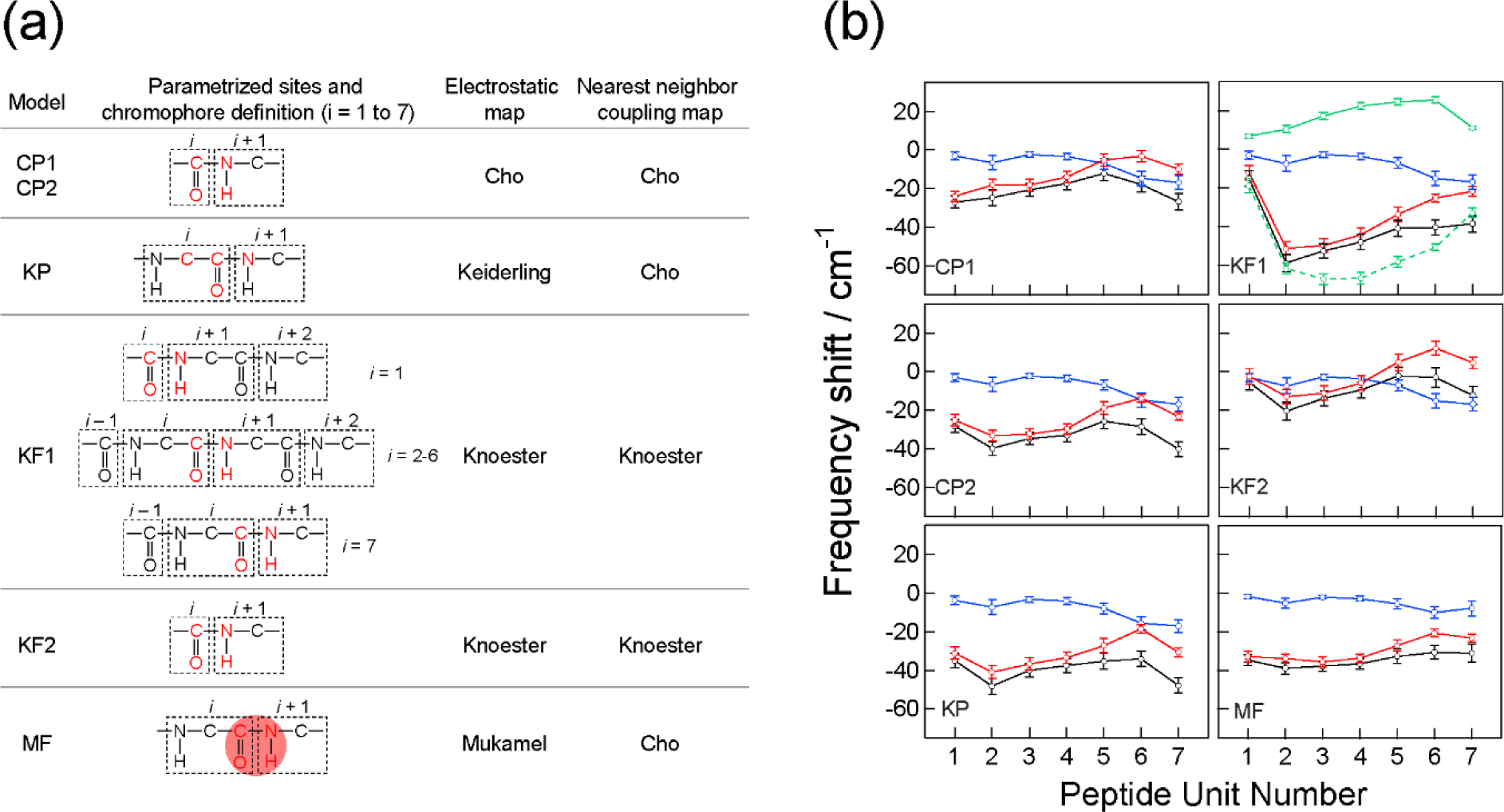
(a) Summary of the models used for spectral calculations. Parametrized sites are shown in red. The red shading in the MF model schematically indicates the transition charge region for sampling. Cho-Potential model 1 (CP1) utilized parametrized partial charges whereas other models utilize partial charges defined in MD simulations. Knoester-Field model 1 (KF1) utilized NNFS maps. (b) The amide-I local mode frequency shifts calculated with the six models for the restrained trajectory. Blue circles: solvent contributions ; red circles: peptide backbone and side-chain contributions ; black circles: total shifts . The vertical bars indicate the range enclosed by ± one standard deviation (σi). Green symbols with solid and dash lines in KF1 are the NNFS and electrostatic contributions in , respectively. Reproduced from Table 1 and Figure 8 of Ref.216 Copyright 2009 The American Chemical Society.
On the basis of the number of peaks, relative peak positions and intensities in the computed linear and 2D IR spectra, especially the cross-peak patterns obtained from the double-crossed polarizations, it was determined that the potential-based model (CP2: Cho-Potential 2) developed by Cho and coworkers262 and the field-based model (MF) in the computation package SPECTRON created by Mukamel and coworkers228,273 performed the best and similarly reproduced the measured spectra (Figure 5) when using an MD trajectory with the peptide dihedral angles restrained near the crystal structure values. Structural ensembles sampled from unrestrained MD simulations are too broad. Comparing the different models, the solvent contributions to the total frequency shifts are very similar in the magnitude and the variations across the peptide backbone, whereas the peptide contributions exhibit more differences (Figure 4b). The widths of calculated spectra are dominated by the relative spread of the frequency shifts. All models require a redshift of simulated spectra by 10–40 cm−1. This is most likely because the frequency maps were computed for N-methylacetamide solvated with water molecules whereas the experimental spectra were acquired for the octapeptide in CDCl3. A model that takes into account strong dispersion forces may be more suitable for a better agreement between experiment and calculation.265 This study demonstrates that 2D IR can provide a large set of spectral constraints that are useful for further refining classical force fields and testing theoretical models. In particular, the double-crossed polarization nonrephasing spectrum exhibits the highest sensitivity to structural ensembles and models.
Figure 5.
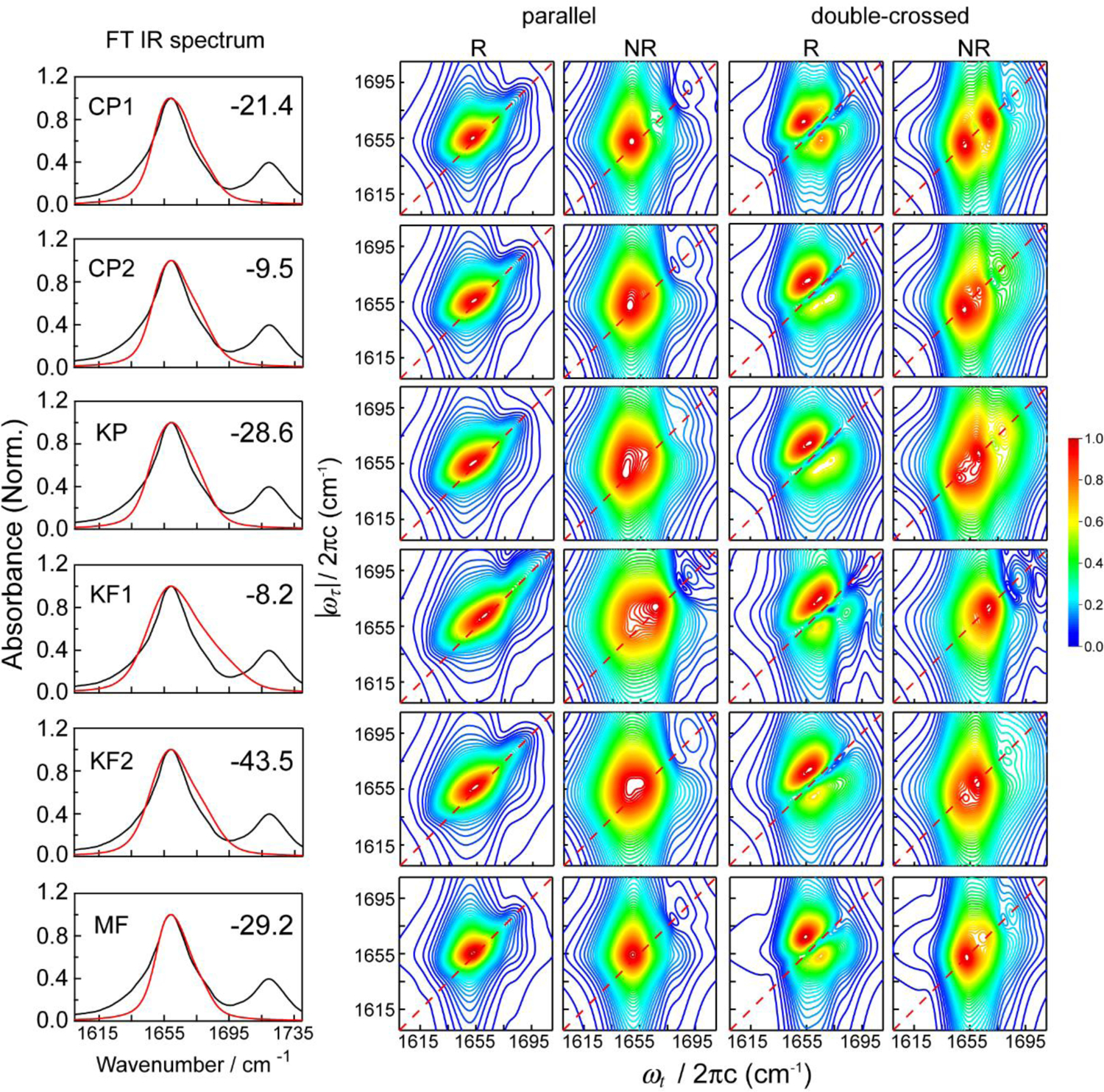
The linear and 2D IR spectra calculated with the CP1, CP2, KP, KF1, KF2, and MF models for the restrained trajectory. The number in the upper right corner of the FT IR spectrum panel indicates the frequency shift (in cm−1) applied to the calculated spectra. Red and black lines in the linear spectra correspond to the simulated and experimental data, respectively. Reproduced from Figure 7 of Ref.216. Copyright 2009 The American Chemical Society.
4.4. Amide I vibration: Isotope-labeled proteins
While the amide I band provides critical information on the structural arrangements and conformational dynamics of proteins in the condensed phase, the relatively short vibrational lifetime of the amide I mode (around 1 ps in aqueous systems), together with a relatively narrow frequency range (typically 1600 – 1700 cm−1) and a large number of amide bonds in typical polypeptides and proteins, often leads to considerable congestion in the measured spectra. This issue obscures the information content of label-free amide I spectra and makes it difficult to disentangle the vibrational patterns of each chromophore.
Combining vibrational spectroscopy in the amide I region and the isotope labeling technique provides an effective way to reveal site-specific information in complex protein systems. For example, replacing 12C with 13C or 16O with 18O in a C=O group reduces its stretch frequency by about 40 cm−1,299,300 thus shifting its vibrational absorption out of the main amide I band. The frequency changes due to the presence of a C or O isotope can be estimated by treating the C=O stretch as a harmonic oscillator whose angular frequency is . Here k and μ are the force constant and reduced mass of the harmonic oscillator, where mC and mO are the masses of the C and O atoms, respectively. As isotope labeling introduces a minor perturbation to the molecular vibration, one can assume that the force constant of the C=O group remains the same. Replacing 12C with 13C thus changes the frequency of the chromophore by
| (104) |
After its first development in 1991,299 the 13C labeling technique has enabled researchers to probe the secondary structures of polypeptides and amyloid fibrils with residue-specific resolution using linear and 2D IR spectroscopy.43,255,299–303 In addition, Chen and coworkers have demonstrated that the 13C-isotope labels can be combined with the vibrational sum-frequency generation (SFG) spectroscopy in the amide I region to detect the structures and orientations of surface-bound peptides at the single residue level.304 Despite these advances, the 13C-isotope editing method has two main drawbacks. First, the isotopically labeled vibrational modes are often not well resolved in the vibrational spectra and appear as shoulders on the broad amide I band. Second, the natural abundance of 13C is 1.1%, and thus proteins containing 90 or more amino acids would possibly exhibit IR signals from non-labeled 13C=O groups and complicate the spectra.277,304,305
To overcome these issues, researchers have designed the 13C=18O isotope label, which redshifts the absorption frequency of a C=O group by about 65 cm−1 and spectroscopically isolates the vibrational mode from the rest of the protein. For example, Arkin and coworkers have utilized isotope-edited IR spectroscopy to measure the conformations and orientations of membrane proteins at a variety of residue positions.300,305,306 By incorporating the 13C=18O label on 11 amino acids, one at a time, along the transmembrane helical bundle of the CD3ζ peptide, Zanni and coworkers have measured the homogeneous and inhomogeneous line widths of the 2D IR spectra and revealed the structural distributions and dynamics of the protein.86 Furthermore, they have conducted a series of 2D IR experiments with isotope labeling to elucidate the pathway and inhibition of the amyloid formation of the human amyloid polypeptide (hIAPP), which is closely related to type 2 diabetes.307–310 As demonstrated in Figure 6, Buchanan et al. have placed a series of 13C=18O labels in the β-sheet and loop region of hIAPP and measured their 2D IR spectra in both the lag phase and equilibrium phase of the aggregation.307 The 13C=18O signal of V17 in Figures 6C and 6D shows that the residue changes from a disordered region to a β-sheet structure upon fibril formation. In contrast, Figures 6D and 6F suggest that residue F23 undergoes the opposite conformational change. By detecting the 2D IR spectra of all the isotope labels, as highlighted in Figures 6A and 6B, they could monitor the structural evolution of hIAPP in the aggregation process with residue-specific resolution and identify the structural features of the oligomeric intermediate in the lag phase.307
Figure 6.
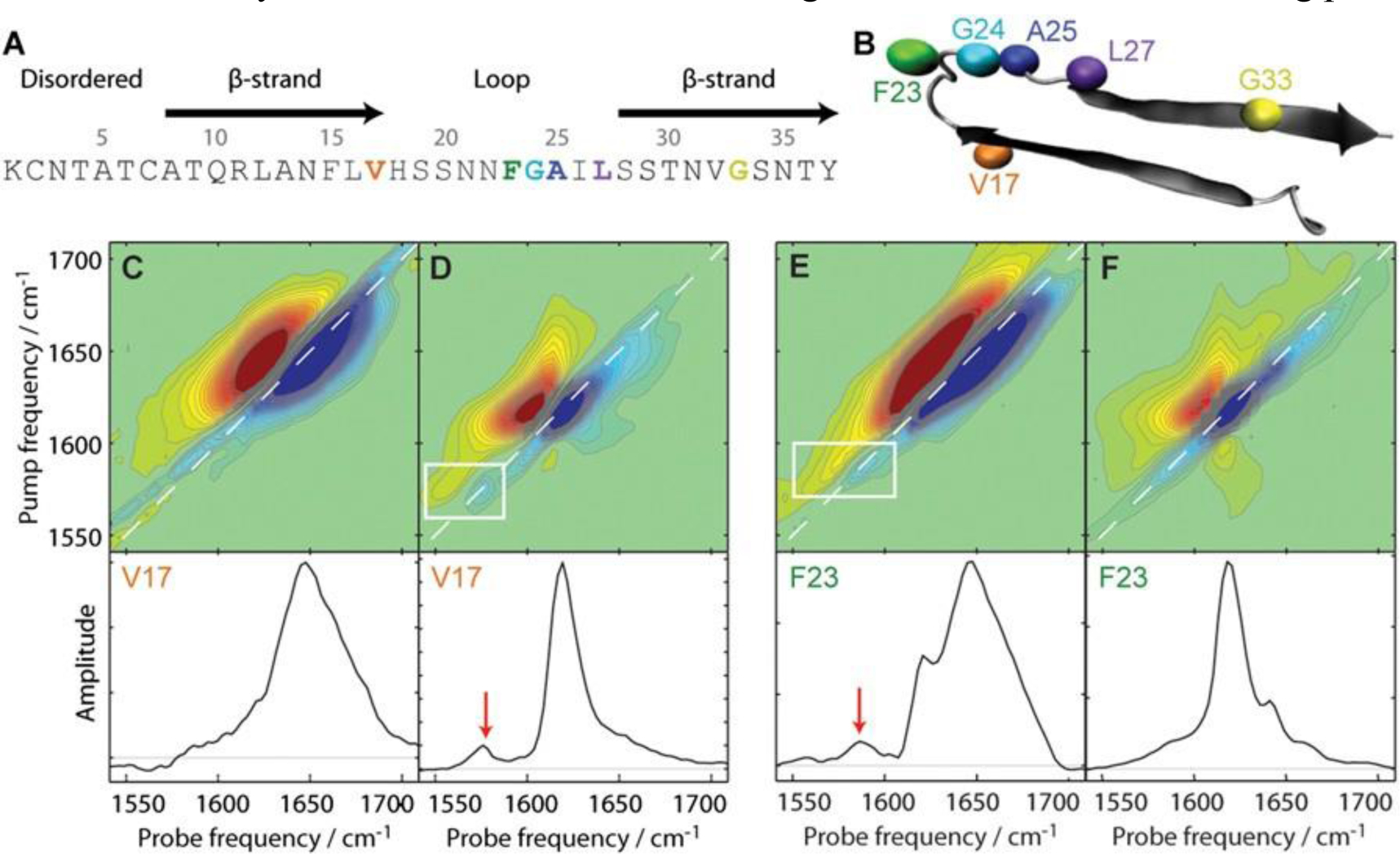
Structure and 2D IR spectra of isotope-labeled hIAPP from reference307. The sequence (A) and structural model (B) of hIAPP with the 13C=18O isotope labels highlighted. 2D IR spectra and the diagonal intensity slices of the lag-phase and equilibrium phase V17 (C sand D) and F23 (E and F) labeled proteins. The boxes and arrows indicate the 13C=18O labeled modes. Reproduced from Figure 1 of Ref.307 Copyright 2013 the National Academy of Sciences of the United States of America.
By combining isotope-edited vibrational spectroscopy and theoretical spectroscopy modeling, researchers have successfully probed the vibrational Hamiltonian in the amide I region and revealed the conformations and dynamics of peptides and proteins with residue-specific resolution. Combining the theoretical vibrational spectroscopic maps and the 2D IR spectroscopy experiments with the 18O or 13C=18O isotope labels, researchers have determined the site frequencies of individual amino acids, which constitute the diagonal elements of the vibrational Hamiltonian matrix. They have further used the sensitivity of these site frequencies to the interactions between amino acids and their nearby biological and solvent molecules to elucidate the site-specific structural fluctuations of peptides in a heterogeneous environment, the location and orientation of an antimicrobial peptide in lipid bilayers, and the conformational transformations of a β-hairpin peptide in the melting process.44,100,233,259,311,312
In addition, one can utilize multiple isotope-labeled IR probes in the 2D IR measurements to characterize the interactions between the amide chromophores. For example, Hochstrasser and coworkers incorporated 13C and 13C=18O labels on alanine residues that are separated by 1, 2 or 3 amino acids and determined the magnitude and sign of the coupling constants in an α-helical peptide.91,301 Zanni and coworkers performed 2D IR measurements on a macrocycle that adopts a parallel β-sheet conformation and labeled several pairs of residues with 13C=18O, as demonstrated in Figure 7.313 They then calculated the 2D IR spectra using a vibrational frequency map261 and a variety of coupling schemes, including the through-bond nearest-neighbor couplings method230 and the through-space TDC and TCC models.230,271,272,314 As shown in Figure 7B, the theoretical approaches can predict the 2D IR line widths that are in quantitative agreement with experiments.313 More recently, Tokmakoff and coworkers combined IR spectroscopy and 13C and 13C=18O isotope labeling to systematically evaluate the performance of the vibrational frequency maps and the vibrational coupling models in the amide I region, providing a benchmark for the theoretical developments in the field.45 In addition to probing the couplings between amide I modes, Ge and coworkers utilized a combination of 13C=18O and 15N labels to reveal the interactions between the amide I and II modes.77 With quantum chemistry calculations and the TCC model, they determined the coupling constants and their dependence on the three-dimensional peptide structure. All of these examples demonstrate that a close collaboration between theoretical and experimental spectroscopy methods, in conjunction with the isotope labeling technique, provides a powerful way to reveal the vibrational Hamiltonian and detect the structure and dynamics of peptides and proteins.
Figure 7.
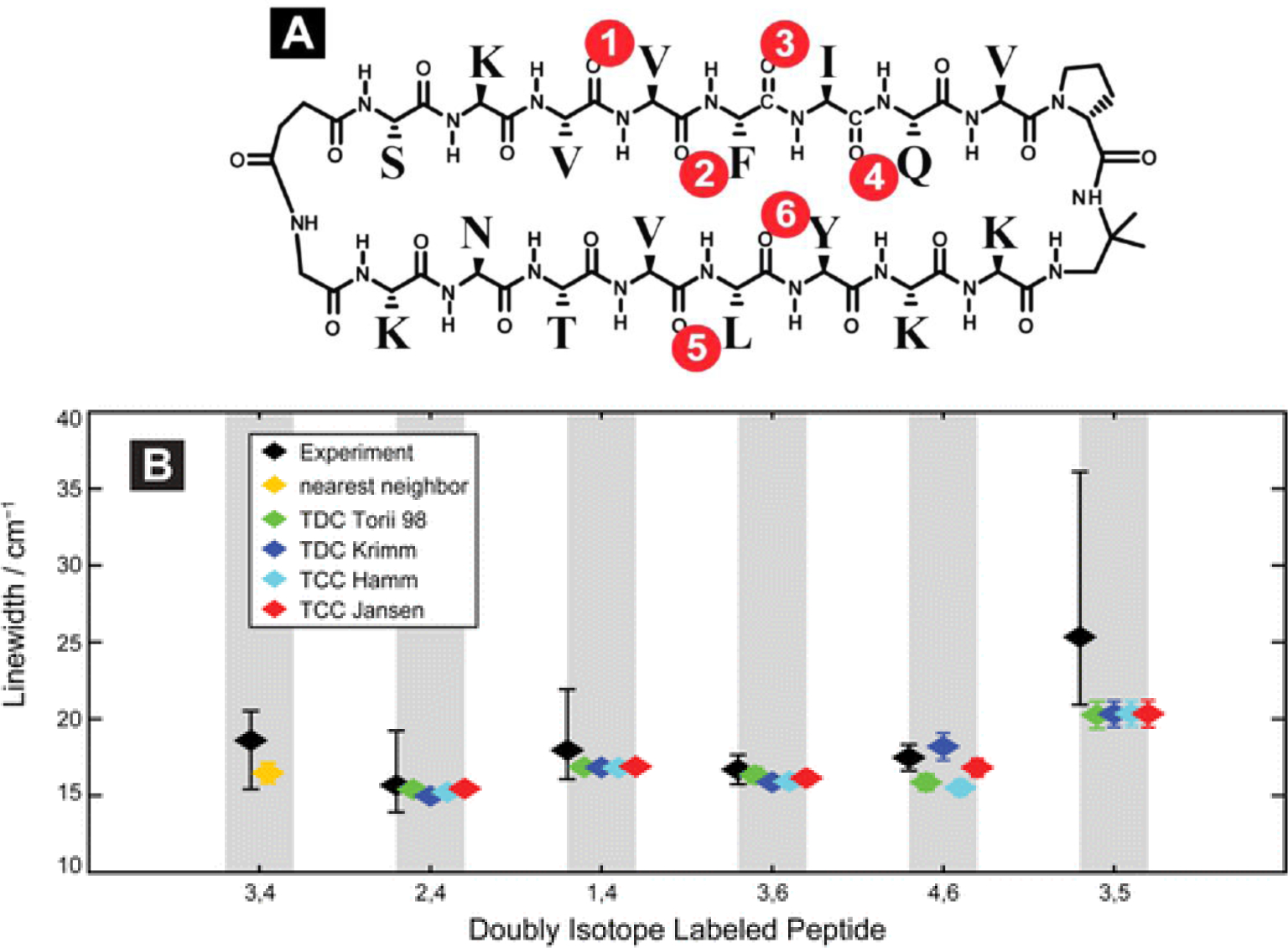
(A) Sequence of the macrocycle with the isotope labeled positions highlighted. (B) Comparison of experimental and theoretical 2D IR line widths. The theoretical spectra are calculated using various coupling schemes. Reproduced from Figure 1A and Figure 6 of Ref.313 Copyright 2012 American Chemical Society.
It is still challenging to use the amide I maps to predict the amide I spectra that are in quantitative agreement with experiments.45,261,266,282 A major issue is the accuracy of the models used, such as the quantum chemistry methods chosen for the map developments and the sampling of conformational distribution using MD simulations. Therefore, it is desirable to have reliable experimental standards so that researchers can develop or evaluate a vibrational frequency map directly and systematically. While isotope labeling isolates a C=O from the other amide I vibrations and offers a unique opportunity to examine the frequency map predictions, preparing isotope-edited protein standards often falls into a dilemma between synthetic difficulty and reliability of the underlying protein conformation.45 For example, isotope-labeled short peptides can be obtained using a standard peptide synthesis approach, but these peptides are usually conformationally disordered. It has been shown that even the well-studied tripeptide Ala‒Ala‒Ala exhbits conformational heterogeneity, and the current protein force fields cannot correctly predict the conformational distribution.74,315 On the other hand, larger proteins usually have well-folded conformations, but synthesis with site-specific isotope-labeling is almost prohibitive.
To develop experimental standards, the Tokmakoff group used isotope-enriched protein expression to produce residue-specific isotope-edited NuG2b protein, which has strong structural stability to mitigate the issue of conformational disorder for short peptides.45 From the direct evaluation of vibrational frequency maps against experiments, they found that the empirical one-site field map parameterized against the dipeptide set failed to qualitatively describe some of the isotope-labeled spectra, although the map had a good performance for the dipeptide set. They also showed that representative sampling of the N‒H electrostatics were required to obtain qualitative agreement since hydrogen bonding interactions around the N‒H group can affect the amide I frequency.220 In addition, the predicted peak frequencies of the labeled C=O chromophore depend strongly on the force field employed in the spectroscopic simulations,260,267 which creates issues of the transferability of the frequency maps across different force fields and their ability to predict the amide I spectra quantitatively. The Tokmakoff group later developed an empirically optimized four-site potential map against the IR spectra of the isotope-edited NuG2b proteins, which related the amide I frequency to the electrostatic potential evaluated at the C, O, N, and D atoms.264 The map quantitatively described the isotope-labeled spectral features (Figure 8) and achieved ~2 cm−1 frequency error against the dipeptide spectra. From these examples, new experimental data are imperative to evaluate and refine the existing frequency maps so that they can be applied to crucial biological problems such as determining conformational ensemble and interconversion dynamics of intrinsically disordered peptides and proteins.74,266,267,282
Figure 8.
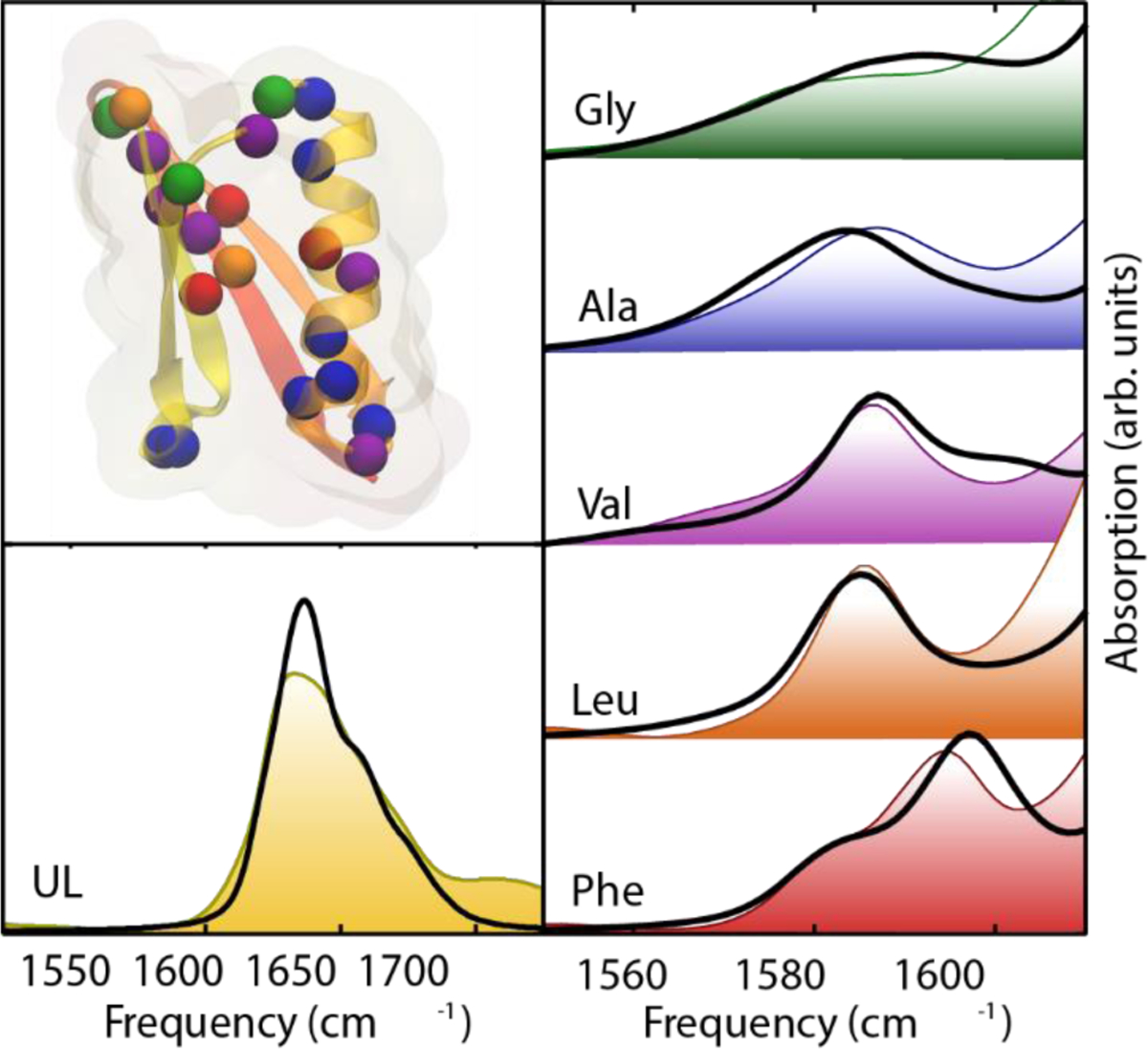
(Taken from Figure 8 of Ref259) Comparison of the frequencies, line widths, and intensities of experimental spectra with simulated spectra starting from MD simulations of the crystal structure of the protein G mutant NuG2b.45 Copyright 2016 Annual Reviews.
4.5. Amide II and III vibrations
The amide II and III modes are the out-of-phase and in-phase combinations of N-H in-plane bend and C-N stretch of the peptide bonds, respectively. In addition to the amide I band, the peak positions and lineshapes of these modes are highly sensitive to the secondary structure of polypeptides and proteins. Given the high computational cost for performing ab initio vibrational analyses of proteins in the condensed phase, researchers have developed the vibrational coupled oscillator model and the fragmentation approach so that one only needs to consider the vibrational properties of a single unit, e.g., amide I, II, and III local mode frequencies, and the vibrational couplings between adjacent amide local modes. One of such methods is HMR, which requires quantum chemistry calculation of a chosen spectroscopic unit and fragmentation analysis of a polypeptide.
In the HMR method, one first divides a polypeptide consisting of N amino acids into N fragments. For example, it is natural to consider a dipeptide as a two-fragment system with peptides 1 and 2, as shown in Figure 9. Then, the full Hessian matrix of the dipeptide is rearranged such that the sub-matrix 1, , corresponds to the Hessian matrix associated with the atoms of peptide 1 and similarly the sub-matrix, , to those associated with the atoms constituting peptide 2. For these two sub-Hessian matrices, one can find eigenvector matrices and that diagonalize them, respectively. From the eigenvectors of the vibrational modes localized in peptides 1 and 2, one can identify the amide I, II, and III local modes and obtain their frequencies. In addition, the off-diagonal matrix elements correspond to the vibrational coupling force constants. For instance, considering the amide I, II, and III vibrations of a given dipeptide, one can obtain the reconstructed Hessian matrix by using the following similarity transformation method:
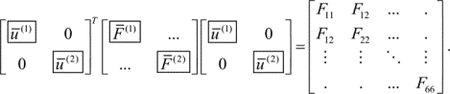 |
(105) |
Here, the diagonal elements F11 – F33 (F44 – F66) are the force constants of the amide I, II, and III local modes of peptide 1 (2). Once the reconstructed Hessian matrix in the basis set of local modes is determined, its diagonalization provides both the delocalized normal mode frequencies and corresponding eigenvectors. After obtaining the transition dipole moment or polarizability of a given peptide unit from high-level ab initio calculations, one can write the transition dipole moments or polarizabilities of the normal modes as linear combinations of those local modes, where the weighting coefficients are the associated eigenvector elements.
Figure 9.
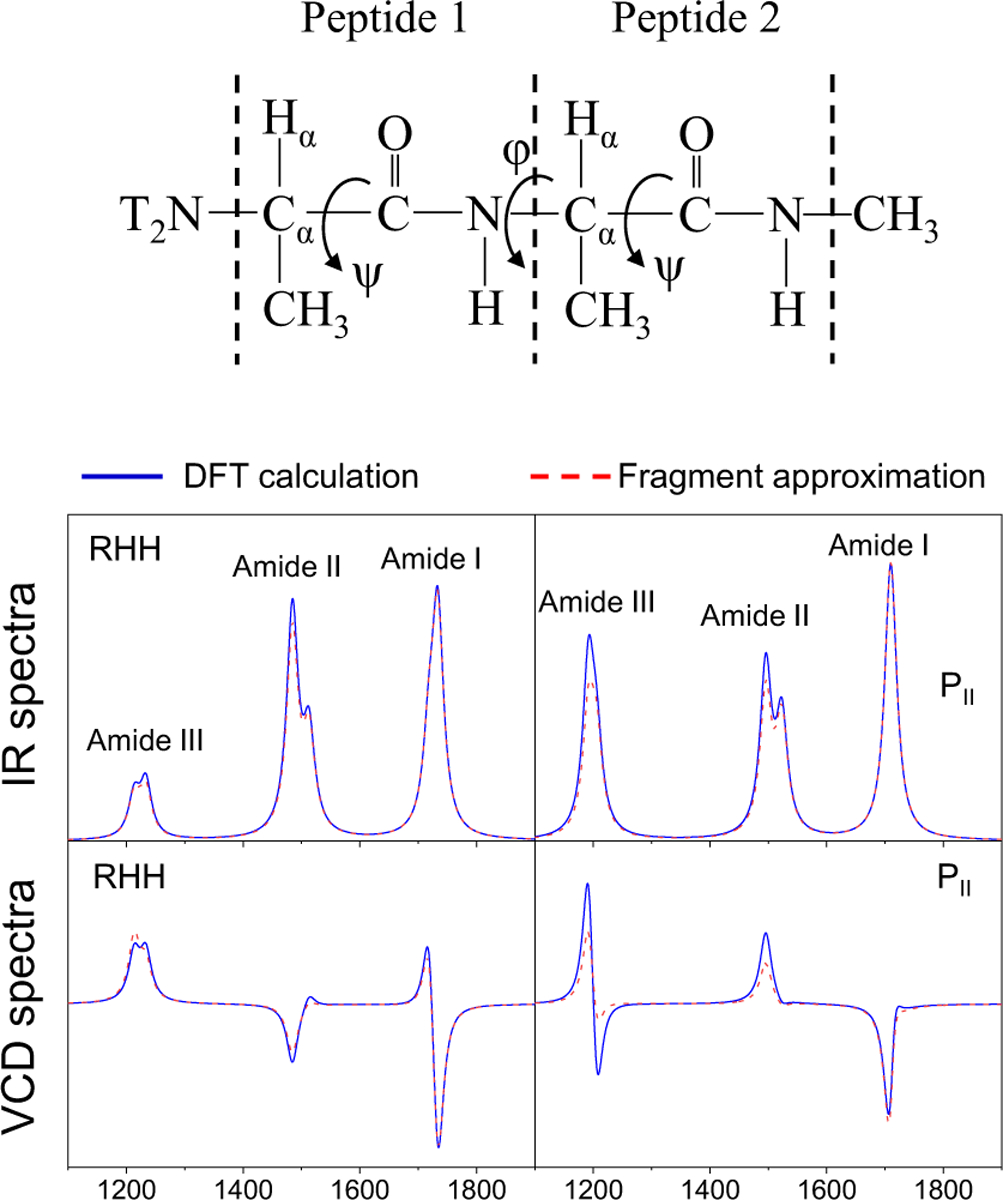
Molecular structures of alanine dipeptide in the upper panel. IR and VCD spectra of amide I, II, and III modes are displayed for its RHH and PII conformations in the bottom panel. The blue solid and red dashed lines correspond to the simulated spectra obtained from DFT calculation and the fragment approximation, respectively. Reproduced from Figures 1, 3, and 4 of Ref.316. Copyright 2009 Elsevier.
For example, Cho and coworkers used the HMR method to calculate the IR and vibrational circular dichroism (VCD) spectra of a model dipeptide and compared them to the spectra obtained from DFT calculations.316 For the right-handed helix (RHH: ϕ = −57° and ψ = −47°) and polyproline II (PII: ϕ = −78° and ψ = 149°) conformations of the dipeptide, the IR and VCD spectra agreed quantitatively between the two methods, as shown in Figure 9. The VCD spectra of the amide modes are critically dependent on the backbone conformation, and thus the spectral features of the amide I, II, and III modes are considerably different for the RHH and PII configurations (Figure 9). Specifically, the amide II mode of the helical structure RHH displays a negative peak in the VCD spectrum, while the extended structure PII exhibits a positive peak pattern. These are consistent with the experimental results of the polypeptide with helical or extended β-sheet secondary structures. The good agreement between the HMR method and DFT calculations demonstrates that the fragment approximation method can be used to numerically simulate the vibrational spectra of large polymer systems consisting of repeating monomer units such as proteins, nucleic acids, and sugars.
While most simulations of amide I modes are performed assuming these modes are independent of other vibrations, 2D IR spectra of amide groups in solutions exhibit cross peaks between the amide I and II modes even at short waiting times.85,317 This observation indicates that these modes are coupled to each other. In this representation, these basis states interact through harmonic coupling terms and all of the Hamiltonian elements fluctuate in aqueous solutions. Frequency maps that describe the fluctuations of the amide I and amide II energies and the amide I – amide II harmonic couplings were developed.318 The dependencies of these quantities as well as the coupling between neighboring peptide units on dihedral angles were also parameterized by using the HMR method.319 Simulations that employ these maps can be used to investigate vibrational relaxation and the origin of the short lifetime of the amide I vibration.318
The amide II mode has been used to study the structural stability of biological macromolecules, hydrogen-deuterium exchange kinetics, and molecular conformation by linear IR and vibrational circular dichroism spectroscopy. In the past decade, 2D IR experiments have been performed on the amide II modes of NMA,78,320 small peptides78,321–323 and proteins85,324,325, and thereby theoretical efforts have been made to compute the diagonal peaks of the amide II modes and their cross-peaks with the amide I modes.319,326
Several groups have mapped out the NN couplings of not only amide I/amide I but also amide I/amide II and amide II/amide II based on quantum mechanical calculation for N-acetyl-glycine N’-methylamide (AcGlyNHMe)78,319,327 Hayashi and Mukamel obtained couplings of the amide modes between neighboring peptide units using the anharmonic vibrational Hamiltonian from the DFT calculation at the BPW91/6–31G(d,p) level.327 They reported the NN amide II/II and II/I coupling maps, but not the amide I/II coupling map. It is expected that the amide I/II and amide II/I coupling maps are different because of the asymmetric arrangement of the amide I and amide II modes in the two peptide units. Ge and coworkers carried out DFT calculations at the B3LYP/6–31+G(d) level for a complete mapping of the amide I/I, I/II, II/I and II/II coupling strengths, and the reported amide I/II and II/I maps showed distinct dihedral angle dependence of coupling strength (Figure 10).78 Choi and Cho developed a computational procedure of generalized HMR and estimated the NN amide couplings, including amide II modes, for six pairs of dihedral angles for representative protein secondary structures.316 Knoester and coworkers performed a HMR calculation based on writing the eigenmodes of a dipeptide, which they obtained from DFT calculations with the ADF TZ2P basis set and the RPBE exchange-correlation functional, as a linear superposition of the eigenmodes in two NMA-d7 molecules.319 Whilel the amide I/II, II/I, II/II coupling maps created from different protocols have qualitatively similar patterns, their ϕ-ψ dependences have quantitative differences and more work in this field is required to produce a universal coupling scheme.
Figure 10.
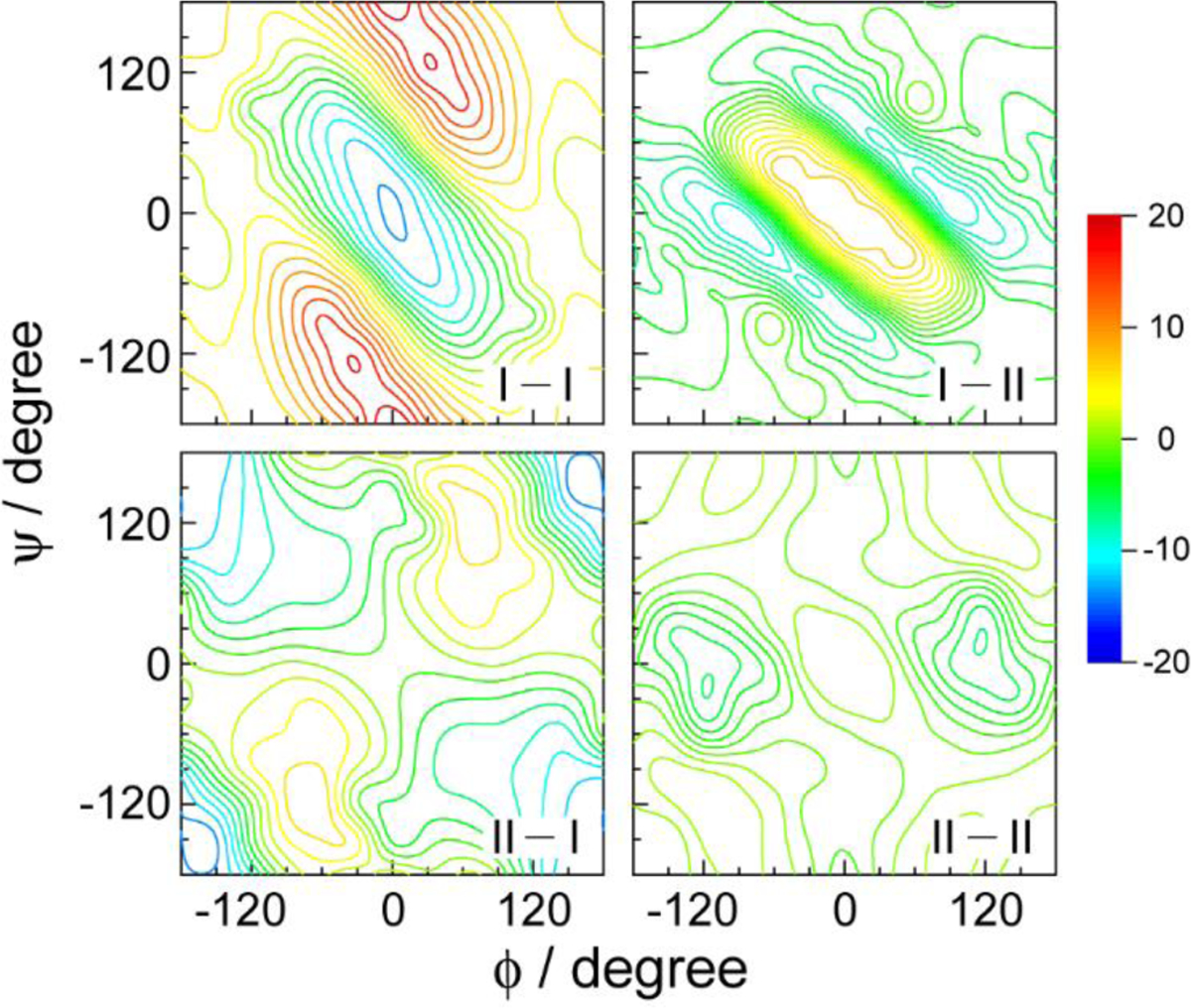
Nearest-neighbor amide I/I, I/II, II/I, and II/II coupling maps calculated for AcGlyNHMe at the B3LYP/6–31+G(d) level with fixed dihedral angles. All four maps are plotted in a single color scale and the unit of couplings is cm−1. Reproduced from Figure 8 of Ref.78. Copyright 2009 The American Chemical Society.
The NN couplings between proline and other amino acids are likely to be different from those modeled by AcGlyNHMe, because the unique five-membered ring of the proline residue imposes spatial constraints on the peptide structure. Sul et al. performed DFT calculations and normal-mode analyses on the trans conformer of a model dipeptide, N-acetyl-L-prolinamide (AcProNH2), in vacuo at the B3LYP/6–31+G(d,p) level, and calculated the NN amide I/I and I/II coupling maps by extending the HMR method, carbonyl population analysis,328 to include the amide II mode.329
In addition to the NN couplings, the bilinear amide I/II coupling in the same peptide unit is also important for calculating the amide I and II spectra of oligo- and longer peptides. This coupling strength is about 27–39 cm−1 as obtained experimentally from the 2D IR spectra of NMA,320 NMA-d7,78,317 and AcProNH2.330 As its magnitude is much larger than the other inter-unit amide couplings, it is useful to know how this amide I/II intrapeptide-unit coupling depends on the dihedral angles of a polypeptide and the surrounding environment. From DFT calculations at the B3LYP/6–31+G(d) level, Ge and coworkers found the coupling constant to be ±33 cm−1 for AcGlyNHMe.78 They further found the couplings to be ±23.8 cm−1 for the trans-C7 conformer and ±30.6 cm−1 for the cis conformer of AcProNH2 in chloroform based on DFT calculations at the B3LYP/6–311++G(d,p) level and a self-consistent reaction field polarizable continuum model.329 In addition to calculating the coupling constants for two specific conformations,329 they also mapped out the coupling constant as well as the angle between the amide I and II transition dipoles for the trans AcProNH2 at 105 different dihedral angles in vacuo at the B3LYP/6–31+G(d,p) level. While it is often assumed that this angle is independent of the peptide conformations, their study demonstrated the variations of this angle and provided an additional constraint to narrow down the allowed conformational space for the structural determinations of polypeptides. Besides these studies on dipeptides, Knoester and coworkers also parameterized the electrostatic effects on the intra-site coupling between the amide I and II modes of NMA-d7 and their transition dipole moments.319
To establish a relationship between the amide II local mode frequency and the electrostatic properties around the peptide unit, several groups carried out theoretical studies on NMA and parameterized frequency maps for the amide II mode based on electric potential217,229 or electric field and gradient.228,318,319 To evaluate the amide I and II maps, Maekawa and Ge carried out MD simulations of a 310-helical hexapeptide Z-Aib-L-Leu-(Aib)2-Gly-OtBu and compared the calculated spectra with the experimental linear and 2D IR spectra.217 As shown in Figures 11 and 12, different models predict vastly different amide II spectral signatures, while the amide I band profiles show less variations. Interestingly even though the amide II mode is more delocalized than the amide I mode, the simulation results show that it does not necessarily require a multi-site model that is more spatially spread to correlate its frequency with the electrostatic properties: A simple model involving four atom sites on a peptide unit performs quite well. Also, DFT calculations with a larger basis set do not necessarily improve the agreement between the simulated and experimental peaks of the amide II modes. Moreover, it has been shown that a simple semiempirical model works equally well as the best performing four-site potential model. This semi-empirical model considers the intramolecular C=O⋯H–N H-bonding as the only contribution from the peptide to the amide I and II frequency shifts. The frequency shifts were parameterized based on the H-bond energies calculated at the C=O and N–H sites.78 Similar comparative studies are required to test further the validity of the amide II frequency and coupling maps.
Figure 11.
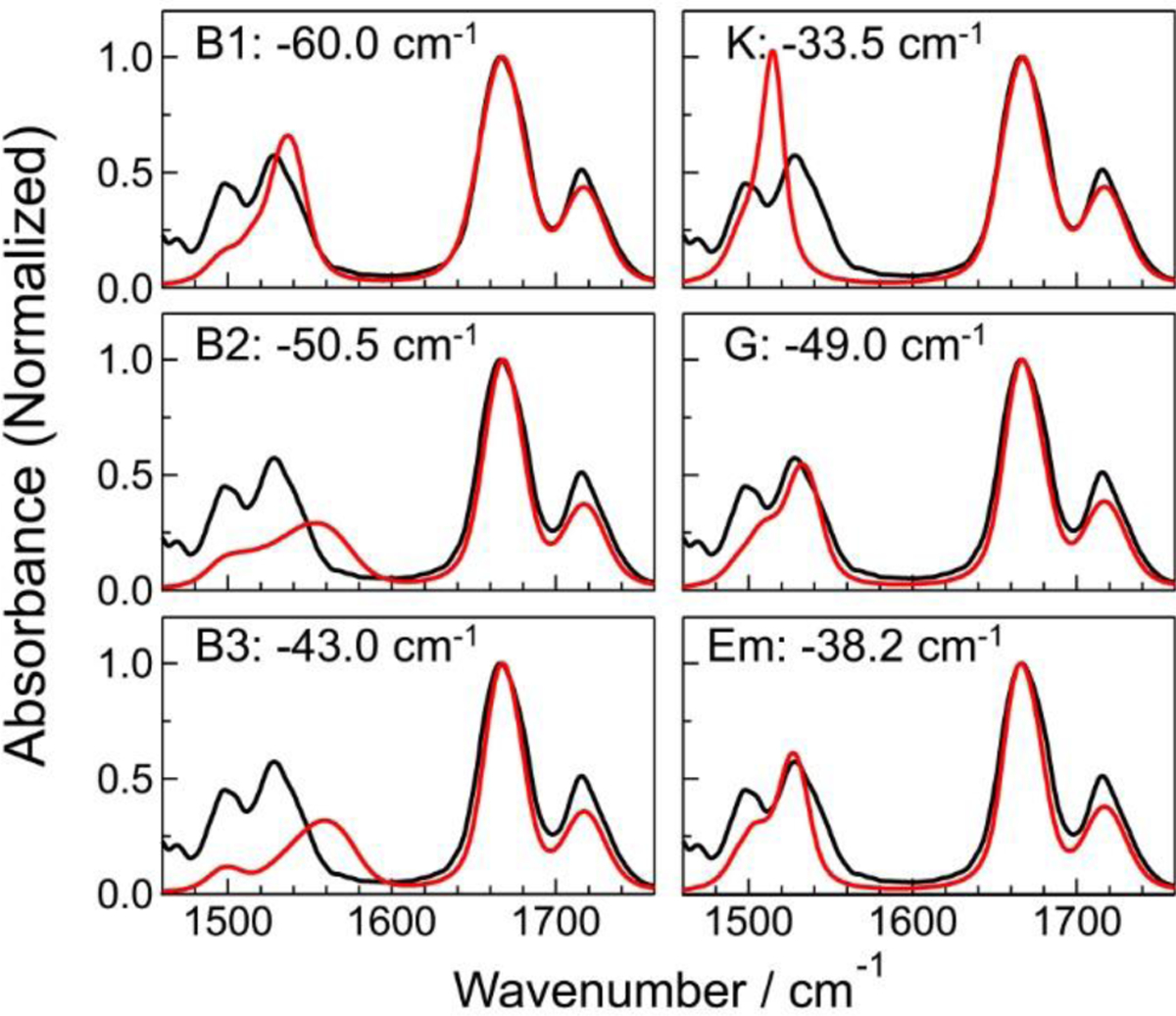
Experimental (black) and simulated (red) linear IR spectra of a 310-helical hexapeptide Z-Aib-L-Leu-(Aib)2-Gly-OtBu in CDCl3 in the amide I and II regions.217 B1, B2, and B3 are six-site potential models,229 K is a four-site field/gradient model,318 G is a four-site potential model,217 and Em is a semiempirical model.78 The local amide I frequency was shifted from the gas phase value by the value reported in each panel. Reproduced from Figure 8 of Ref.217. Copyright 2010 The American Chemical Society.
Figure 12.
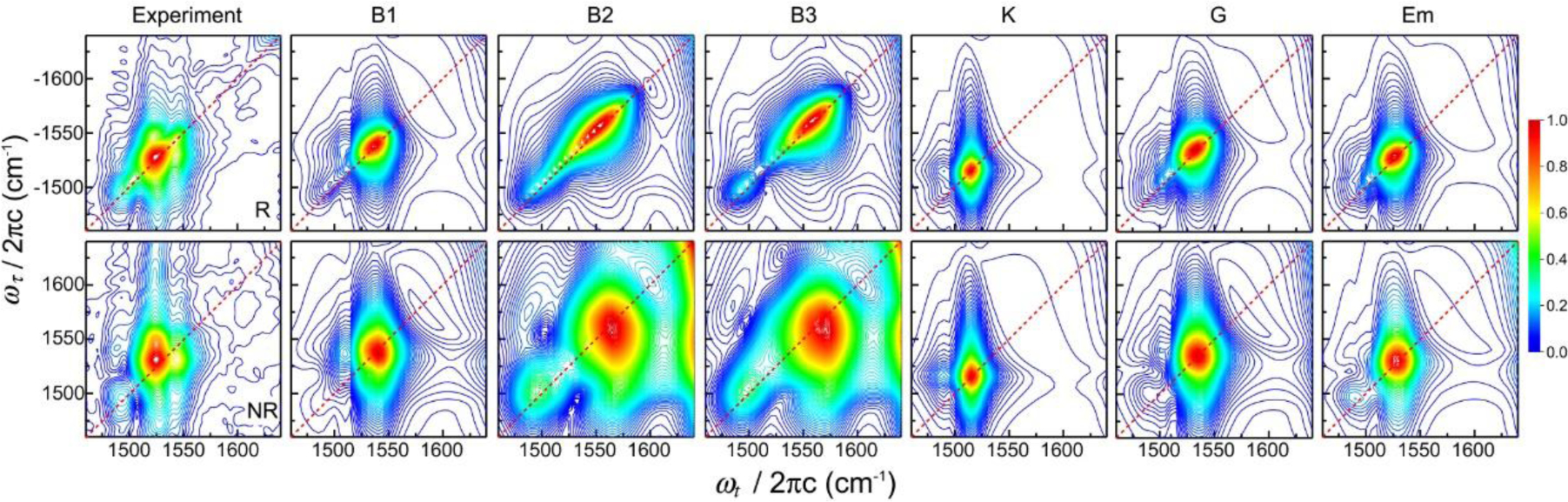
Experimental and simulated absolute 2D IR rephasing (top) and nonrephasing (bottom) spectra of a 310-helical hexapeptide Z-Aib-L-Leu-(Aib)2-Gly-OtBu in the amide II frequency region. Each spectrum is normalized by the peak intensity of the diagonal amide II band.217 Reproduced from Figure 10 of Ref.217. Copyright 2010 The American Chemical Society.
The application of VSMs of amide modes is not limited to polypeptides and proteins composed of α-amino acids. Recently, Wang and coworkers theoretically determined the coefficients to calculate the amide I frequency of N-ethylpropionamide (NEPA), a model compound of β-amino acid, based on electrostatic potentials on the N, H, C and O atoms of the peptide unit,331 and the calculated linear spectra of NEPA in three different solvents were in reasonable agreement with the experimental results. They also computed the coupling strengths of the amide I and II modes for five helical β-peptide conformers,332,333 and showed that the coupling strengths for shorter inter-amide distances could not be described well by the TDC model. It thus will be useful to obtain NN coupling maps as a function of dihedral angles for the β-dipeptides, and including an additional pair of ϕ and ψ around the β-carbon in the parameterization.
Researchers have also reported other empirical relationships between the amide I and II local mode frequencies and H-bond energy76,78,278:
| (106) |
where and are the frequency shifts of the amide I and II modes due to the presence of H-bond at the C=O (N–H) group, respectively. The frequency shifts were found to be in good correlation with the electrostatic energy of the intramolecularly hydrogen-bonded C=O⋯H–N groups, denoted as EKS.279 By matching the model frequency shift to the results obtained from quantum mechanical calculations of NMA-water clusters,334 the correlation coefficients in the above equations were obtained.78,278 In addition to the intramolecular H-bonding effects, if the C=O or N–H group is exposed to solvent, it is necessary to consider an additional decrease (increase) of the amide I (II) mode frequency due to the effect of solvation (δωsolvent). The latter was empirically included as a constant shift of and by the Ge group. Such semiempirical models have been successfully applied to calculate the 2D IR spectra in the amide I region for 310-and α-helical peptides,278 their chain length dependence,76 as well as the amide II spectra and their cross-peaks with the amide I modes.78,217
4.6. Nitrile stretch
The nitrile stretching mode at around 2260 cm−1 has the advantage of not overlapping the frequency regions of the water bending and stretching modes and is known as an important compact IR probe that can be inserted into peptides and proteins to sensitively measure the local electrostatic environment of the peptide and protein active sites. Specifically, as the nitrile group forms an H-bond with the surrounding water, the stretch mode frequency of the molecule undergoes a significant blue shift of ~10 cm−1, and the spectral bandwidth increases. Due to the sensitivity of the nitrile stretch mode as a reporter sensing the local electric field, this IR probe has been critically used to explore the solvation dynamics as well as the protein active-site structures. 2D IR vibrational spectroscopic measurements of the CN stretch mode of cyanophenylalanine in the villin headpiece (HP35) protein revealed that the solvent-exposed nitrile group exhibited a blue shifting behavior compared to other CN groups in the hydrophobic environments. Furthermore, Chung et al.84 showed through 2D IR vibrational spectroscopic experiments on the HP35 protein that the spectral diffusion of unfolded peptides is much faster than that of folded peptides and is very similar to that of PheCN, meaning that the solvent molecules make significant contributions to frequency fluctuation and dephasing process the dynamics probed by the CN stretch. Vibrational Stark Effect Spectroscopy has been extensively applied to nitrile-incorporated chemical systems and measures the local electric field around the IR probe using a vibrational Stark tuning rate (see Eq. (64)) of a nitrile of about 0.4 to 1.1 cm−1/(MV/cm). However, the linear Stark theory considering only the electric field parallel to the CN bond fails to predict the vibrational frequency shift of the nitrile in a strong H-bonding system such as aqueous solutions, whereas using six electric field vectors located at two atoms of the CN bond leads to a reasonable calculation of the frequency shift in the CH3CN-water solution. Boxer’s group, who recently performed IR and NMR spectroscopic measurements, showed that H-bonding interactions with IR probes should be considered differently compared to nonspecific electrostatic interactions.182 The Thielges group has introduced PheCN at multiple sites in several proteins for linear and 2D IR spectroscopy, but report limited success in applying a linear Stark model.46,87,88 In addition, Gai and coworkers showed that the vibrational frequency of the nitrile stretch mode of 5-cyanotryptophan could be determined by the linear relationship of the Kamlet-Taft solvent parameters, including solvent polarity and H-bonding accepting or donating capability, while the individual parameters do not correlate with the nitrile stretching mode frequency. Bredenbeck and coworkers335 have shown that the solvatochromic properties of cyanotryptophan depend on the position of the nitrile on the ring, with 4-cyanotryptophan being more sensitive to solvent polarity then 5-cyanotryptophane. Due to their short CN stretch vibrational lifetime of 1.5 ps or less, however, cyanotryptophans are mainly attractive because they can serve as a combined label for linear IR spectroscopy and fluorescence spectroscopy and not so much for 2D IR spectroscopy. To take into account the effect of an H-bond between OH group and nitrile N atom to the vibrational solvatochromism in an ad hoc manner, Biava et al. modified the vibrational Stark effect theory considering two different CN groups, i.e., non-H-bonded and H-bonded nitriles.336 They are then treated differently so that the net vibrational frequency shift of the CN stretch mode is expressed as a function of the fraction of the H-bonded species, XHB , i.e.,
| (107) |
where ω0,non is the unperturbed vibrational frequency, Δμnon the vibrational Stark tuning rate, XHB is the mole fraction of the H-bonded nitrile, and Ef,s is the average solvent electric field on the CN group, kHB is the vibrational Stark tuning rate for H-bonded species, ω0,HB is the zero-field vibrational frequency of H-bonded species, and ECN–H is the effective average solvent electric field for H-bonded species. Since this phenomenological model involves calculations of the ensemble-averaged solvent electric field from molecular dynamics simulations, they can only be used to estimate the average vibrational frequency shift, Δω, not fluctuating instantaneous vibrational frequency, δω(t) (see Eq.(10) in Section 2.2) that is necessary to simulate linear and nonlinear vibrational spectra of molecular systems in condensed phases.
The above results and failures in developing a rigorous and systematic theory for vibrational solvatochromism of CN stretching vibration in solutions suggest that the vibrational solvatochromic frequency shifts of the nitrile stretching mode result from various contributions from quadrupole and higher-order multipole terms and non-Coulomb interactions in addition to the dipolar term. By employing the Bio-SolEFP method for the vibrational frequency shift of the IR probe, Błasiak et al. demonstrated that the nitrile stretching frequency shift due to H-bonding interaction with surrounding water molecules is determined not only by the contribution of Coulomb interactions but also by the dispersion interactions and the exchange-repulsion contributions.40,155 Despite the success of the Bio-SolEFP method and the modified linear Stark theory to calculate the vibrational frequency of the nitrile stretching mode in aqueous solution, a semiempirical approach using vibrational frequency maps is still useful in consideration of reasonable computational cost and high accuracy in simulating the linear and nonlinear vibrational spectra of nitrile-inserted chemical systems.
To estimate the solvation-induced vibrational frequency shift of various IR probes such as nitrile and thiocyanate quantitatively, and azido moieties, the multivariate linear relationship between the IR frequency shift and electrostatic potentials around the IR probe has been established. That is, the solvatochromic vibrational mode frequency shift of the IR probe is assumed to be described by electrochromic relationships involving electric field or electrostatic potential evaluated at various points within the IR probe. For instance, the simplest map of this kind is the dipolar map that can be recast in the following form,183,337
| (108) |
where EX denotes the electric field at the X atom of CN, and C and N are the vectorial parameters. Another frequency map is the so-called antenna model for the vibrational solvatochromism, where the frequency shift in wavenumber is described as a sum of products of vibrational solvatochromic charge and solvent electric potential at the interaction site of the solute molecule, i.e.,
| (109) |
Here, and la are the Coulomb electrostatic potential created from water molecules at the ath site of the IR probe group and the vibrational solvatochromic charge at the site, respectively. The C≡N group has two different H-bonding interactions with neighboring water molecules, one is the H-bonding interaction between the lone pair orbital of the nitrogen atom and a hydrogen atom of a water molecule (σ-H-bonding), and the other is the H-bonding interaction between the CN π-orbitals and a hydrogen atom of a water molecule (π-H-bonding). In a previous study to describe the vibrational frequency shift of the nitrile stretch mode, a solvatochromic dipole vector model was employed, but the use of only the dipole interaction term is inappropriate for describing these complicated two interactions including the σ-H-bonding causing the blue-shifting behavior of the CN stretch mode and the π-H-bonding inducing the red-shift of the frequency.
A crucial step in evaluating the solvatochromic frequency shift arising from these two competing interactions is to introduce a set of distributed interaction sites around the IR probe and determine the solvatochromic charges using quantum chemical calculations. In the case of MeCN in Figure 13, a total of 20 sites are considered describing the lone pair of the N atom and the CN π bonding orbitals where the number of independent coefficients is 5 because of the charge neutrality condition, that is, .
Figure 13.
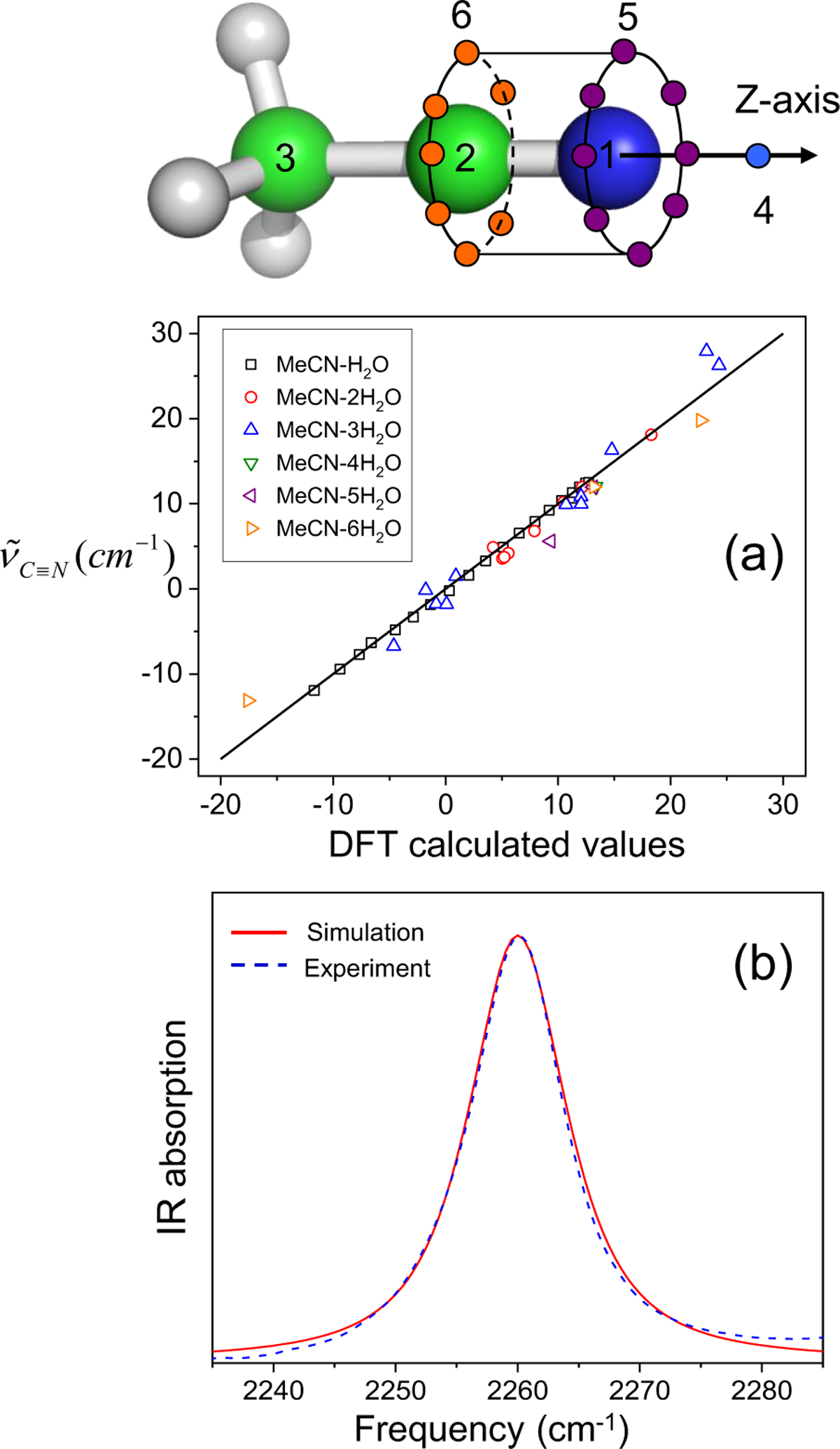
Solvatochromic charge model with distributed interaction sites for MeCN in the upper panel. The calculated nitrile stretching mode frequency shift using Eq. (109) is directly compared to the DFT calculation results in (a). The numerically simulated IR spectrum of the CN stretch mode (solid red line) is plotted with the experimentally measured result (blue dashed line) in (b). The figure of the interaction sites and (a) is reproduced from Figure 5(a) Ref.183 and (b) is reproduced from Figure 10(a) of Ref.218. Copyright 2008 AIP Puplishing.
The solvatochromic charges la were determined by a multivariate least-squares fitting procedure by performing DFT calculations on numerous CH3CN-water complexes and the vibrational frequency shifts obtained from Eq. (109) were found to be in good agreement with the results of DFT calculations in Figure 13(a). By performing MD simulations for an aqueous MeCN solution, the time-varying frequency shift of the CN stretch mode was evaluated from the MD trajectory using Eq. (109). The average CN frequency shift is 9.0 cm−1, indicating a blue-shift, which is consistent with the experimental result of 7.9 cm−1 compared to the gas phase frequency and mainly resulted from the σ-H-bonding interaction between CN and water. The numerically simulated IR spectrum using the Fourier transform procedure was found to be consistent with the experimentally measured band shape (Figure 13(b)). Thus, the hybrid method using the frequency map and MD simulations is confirmed to be useful for obtaining information on the structures and dynamics near the IR probe in proteins.
Another approach to incorporating the two competing interactions is to take both the electrostatic potentials and the electric fields on the atomic sites in the electrostatic frequency map.239,338 It has been shown that the frequency blue-shift of the nitrile CN stretch due to σ-H-bonding arises from the spatially inhomogeneous nature of the electrostatic environment generated by the H-bond donating group (such as the OH group in water).338 The vector component, representing the vibrational response to the electric field on the nitrile N atom, is responsible for the blue-shift due to the σ-H-bonding (with a large electric field on the N atom along the CN bond direction), which is counteracted by the scalar component, representing the vibrational response to the electrostatic potential, which is effective in both the σ- and π-H-bonding and lowers the frequency (Note that the electric field on the N atom along the CN bond direction is smaller in π-H-bonding). The difference between the cases of the uniform electric field (employed in the vibrational Stark effect experiment) and the H-bonding environment is the uniform/non-uniform nature of the local electric field, which causes a change in the relative weights of the vibrational response parameters on the nitrile N and C atoms in calculating the frequency shifts.
4.7. Thiocyanato stretch
The vibrational properties of thiocyanato stretch mode are quite similar to that of the nitrile mode in that the SCN frequency shift and band shape depend on the extent of exposure to surrounding water molecules. Quantum chemistry calculations on various CH3SCN-water complexes were performed to determine the solvatochromic charge parameters la of MeSCN in Eq. (109). A total of 21 sites were considered for MeSCN (Figure 14), where the number of independent coefficients to be determined is just six. The vibrational frequency shifts calculated with Eq. (109) with pre-determined solvatochromic charges, la, are found to be in excellent agreement with the DFT calculation results (Figure 14(a)). The average frequency shift of thiocyanato stretch mode calculated with Eq. (109) and MD trajectory is 1.9 cm−1 for MeSCN, and it is close to the experimental result of 5.5 cm−1. The main contribution results from the linear H-bond between the N atom of SCN and the H atom of water. The numerically simulated IR spectrum was shown to be in good agreement with the experimentally measured spectrum (see Figure 14(b)).
Figure 14.
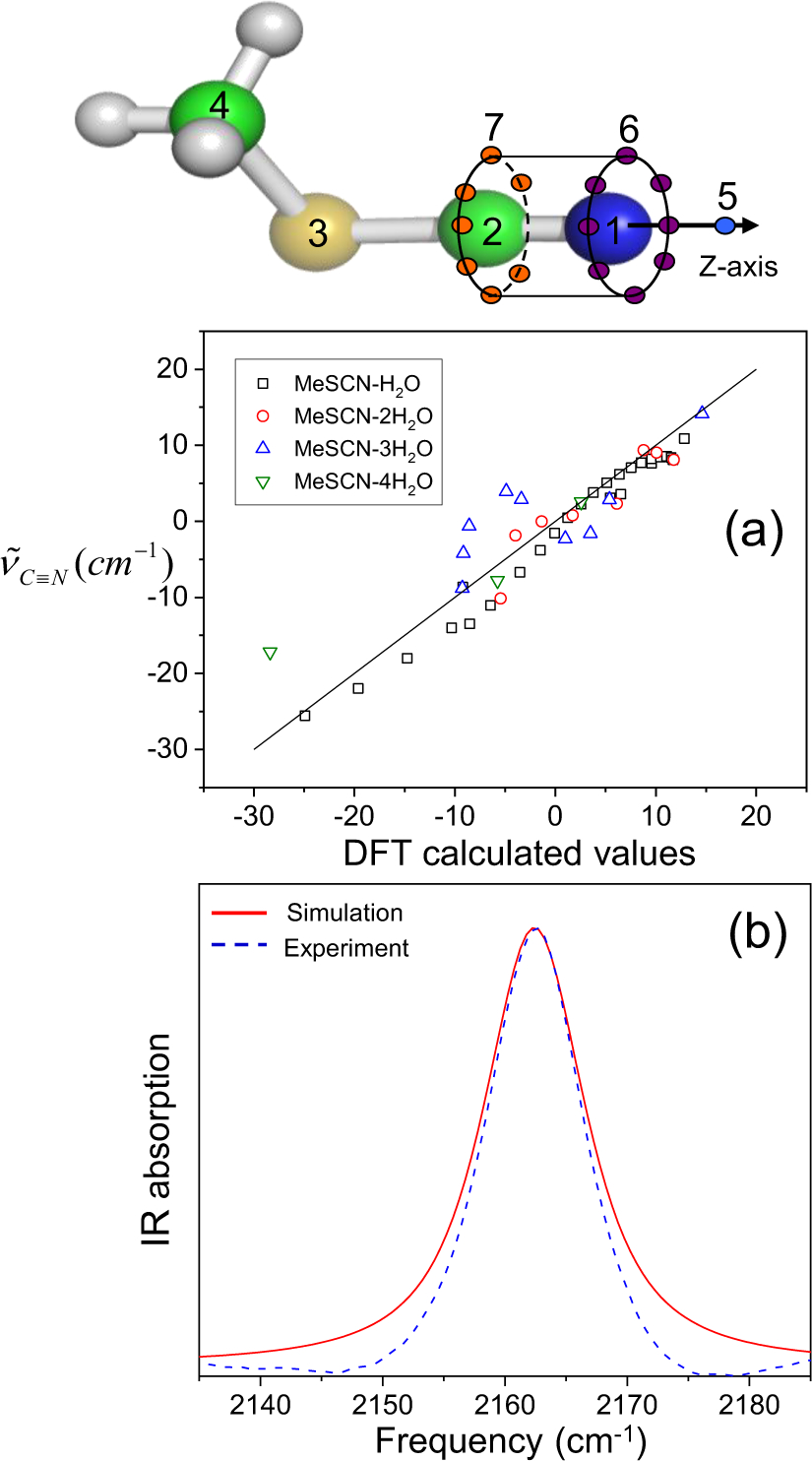
Solvatochromic charge model with distributed interaction sites for MeSCN in the upper panel. The y-axis in (a) corresponds to the thiocyanato stretch mode frequency obtained with Eq. (109) and the x-axis to the DFT calculated results. The numerically simulated IR spectrum of the SCN stretch mode (red solid line) is plotted with the experimentally measured result (blue dashed line) in (b). The figure of the interaction sites and (a) is reproduced from Figure 5(b) of Ref.183 and (b) is reproduced from Figure 10(b) of Ref.218. Copyright 2008 AIP Puplishing.
Maienschein-Cline and Londergan investigated the IR absorption spectra of methyl thiocyanate in various solvent environments and showed that SCN stretch mode could be used as an excellent reporter for specific H-bonding and local dynamics around the IR probe by observing the temperature dependence of the peak position and shape of the SCN stretch mode.339 A later solvatochromic study showed that the peak position depends on not only the H-bonding but also solvent polarity.48,340 While H-bonding causes a blue-shift, increasing polarity leads to a red-shift. Consequently, the two effects can compensate each other. For example, the SCN band in the nonpolar and aprotic perchloroethylene has almost the same wavenumber as in the polar and protic water. Methyl thiocyanate lifetimes of up to 150 ps have been observed, rendering the SCN stretch a very interesting label for probing protein dynamics by 2D IR despite its low transition dipole moment. Furthermore, cyanylation of cysteine in the target protein enables the site-specific insertion of the label without synthesizing the entire protein. Various processes in proteins have been studied by observing the change of the vibrational frequency in the SCN stretch mode, such as inhibitor binding to an enzyme in the case of ketosteroid isomerase,341 or conformational changes during the photocycle of the photoreceptor PYP.342 Londergan and his coworkers employed cyanylated cysteine incorporated to a peptide of calmodulin (CaM)-binding domain to examine the binding affinity of CaM to the target protein of skeletal muscle myosin light chain kinase and showed the use of SCN probe allows monitoring of site-specific changes in the CaM-peptide complex without any perturbation.47 Recently, Bredenbeck and his coworkers performed time-resolved 2D IR spectroscopic measurements of the SCN stretch mode of cyanylated cysteine in the bovine hemoglobin protein and demonstrated that the isotope-labeled S13C15N incorporated into protein could be critically used as a reporter for probing local structural dynamics around the IR probe.48 More recently, it was shown that the vibrational lifetime of the SCN label, incorporated into the photoreceptor protein PYP, is a very reliable probe for bulk solvent exposure. As the lifetime notably differs between H2O and D2O buffer for a solvent-exposed label, comparison of the lifetimes in H2O and D2O measurements allows determination of the solvent accessibility of the SCN label in proteins.343 Schmidt-Engler et al. showed that the long vibrational lifetime of the -SCN label in proteins allows for tracking spectral diffusion up to 120 ps in 2D IR spectra and applied the label to look at ion- and ligand-binding in calmodulin.89
In addition to various experimental measurements on SCN stretch mode, there have been theoretical attempts to establish a relationship between electric field nearby IR probe and the vibrational frequency shift based on the linear vibrational Stark theory. To overcome the inability of the vibrational Stark effect to predict the SCN stretch mode frequency in an H-bonding system, Bagchi and his coworkers showed the correlation of the local electrostatic field around the IR probe with the SCN frequency in various solvents, taking into account specific H-bonding interactions and nonspecific electrostatic interactions differently.344 Furthermore, using QM/MM MD simulation with reparametrized PM3 potential, Layfield and Hammes-Schiffer successfully described the vibrational line shape of the SCN group inserted to protein active site.345 However, this semiempirical approach has difficulties in transferring force field parameters to various chemical systems, Błasiak et al. recently developed an effective fragment potential approach taking into account the contribution of dispersion and exchange repulsion to SCN stretch mode frequency calculation, as well as electrostatic contribution. The combination of QM/MM MD and the SolEFP approach was shown to successfully reproduce the vibrational spectrum of the SCN group incorporated into the target peptide of the CaM-peptide complex while QM/MM calculation without the SolEFP method fails in predicting the experimental result.203 Although the semi-experimental approach using a vibration frequency map is based on electrostatic interaction between the IR probe and the adjacent environment without considering dispersion and exchange repulsion, multivariate least-squares fitting analysis of Eq. (94) on the DFT results works well when simulating the vibration spectrum of the SCN stretch mode in various chemical systems.
The solvatochromic charge model with distributed interaction sites have also been applied to SCN− anion346 and 2-nitro-5-thiocyanate benzoic acid (NTBA) in water49 by Tominaga and co-workers. The SCN frequency shifts are described by using 28 and 35 interaction sites for SCN− and NTBA, respectively. The solvatochromic charge model can reproduce experimental blue shifts of the SCN frequencies of SCN− and NTBA in water. It was found that the calculated FFCFs of SCN− and NTBA in water are fitted by a double exponential function and that the slow component with the time scale of ~1 ps arises from the H-bond network rearrangements around the solute molecules. By examining the spatially-resolved SCN frequency fluctuation, Okuda et al., showed that the SCN frequency fluctuation of SCN− is mainly determined by water molecules in the first hydration shell, i.e., within ~3.5 Å from the SCN− molecule, whereas that of NTBA is affected by water molecules in more extended region, i.e., within ~7 Å from the NTBA molecule.
4.8. Selenothiocyanato stretch
CN stretch mode in SeCN group is a valuable IR probe because it has a significantly longer vibrational lifetime as compared to the CN stretch modes in SCN or CN groups.347 Yet, it is similarly sensitive to the environment as all other nitrile-containing groups. The electrochromic map developed by Yamada, Thompson, and Fayer for SeCN− anion was used to study the dynamics of the H-bonding network in water.348 In their map, they addressed not only the vibrational frequency corresponding to the fundamental transition but also the first vibrational excited state absorption frequency, transition dipole moment derivative of the fundamental transition as well as the anharmonicity constants. In their map, the magnitude of the solvent electric field along the SeCN− molecular axis evaluated on the carbon atom, EC, is assumed to be the sole perturbation inducing changes in the vibrational properties, i.e.,
| (110) |
where x is one of the vibrational spectroscopic quantities, and Ax and Bx are the fit parameters. Considering various SeCN−-(D2O)n clusters sampled from MD trajectories and carrying out DFT calculations at B3LYP/aug-cc-pVDZ level, they constructed a set of data for obtaining the optimized parameters. To better describe the long-range intermolecular interaction effect on the vibrational solvatochromism of SeCN− while preserving computational efficiency, the first nine nearest water molecules relative to the anion’s center of mass are treated quantum mechanically at the DFT level, whereas the other water molecules beyond the cutoff distance of 10 Å from the center of mass of SeCN− are represented by the corresponding atomic point charges. The linear relationships between the electric field and spectroscopic properties are used to calculate the 1D and 2D IR spectra for the sake of comparisons with their experimental results. Furthermore, their model was found to be useful for explaining the anisotropy decay of the IR PP signal and the time-dependent decay of the CLS of SeCN− in D2O. They argue that SeCN− is an excellent IR probe to study the H-bond reorganization dynamics even though it is not a neutral molecule, and its size is large as compared to the OD stretch of HOD that has been used routinely in various studies of water H-bonding network structure and dynamics.
4.9. Azido stretch
The azido-incorporated amino acids have been applied to study different conformational states of the rhodopsin and to investigate the structural change in the protein folding-unfolding process through monitoring the peak position and lineshape of azido stretch mode. Genetically incorporating p-azido-phenylalanine into CaM protein, Creon et al. showed that azido stretch mode is a sensitive IR probe for investigating the electrostatic environment around the azido group in the CaM-CaM binding domain complex.349 Performing 2D IR spectroscopic measurements on azido stretch mode with the incorporation of azido group into the specific residue of protein, Fayer and his coworkers demonstrated that the N3 IR probe is of critical use for probing protein dynamics in MbCO active site by analyzing FFCF extracted from 2D IR measurements.350 Interpretation of the dynamic line shape of aromatic azides, such as p-azido-phenylalanine can be complicated by Fermi resonance.351–353 However, the azido stretch mode has an increased sensitivity advantage over other IR probes such as the −CN and −SCN groups due to its large transition dipole moment, which makes it the probe of choice for vibrational energy transfer experiments in proteins.354 To describe the vibrational absorption spectrum of the azido stretch mode, the semiempirical approach was successfully used in terms of the electrostatic potential at distributed sites, while the vibrational Stark theory does not work correctly due to the significant contribution of quadrupole term to the solvatochromic frequency shift. The distributed interaction site model for azido stretch mode is shown in Figure 15, where 29 sites serve as an antenna sensing the local electrostatic potential around the IR probe.232 The azido stretch mode frequency is predicted with Eq. (94), where the bjk coefficients are determined by using multivariate least square fitting method and quantum mechanical calculations for various methyl azide-water complexes.
Figure 15.
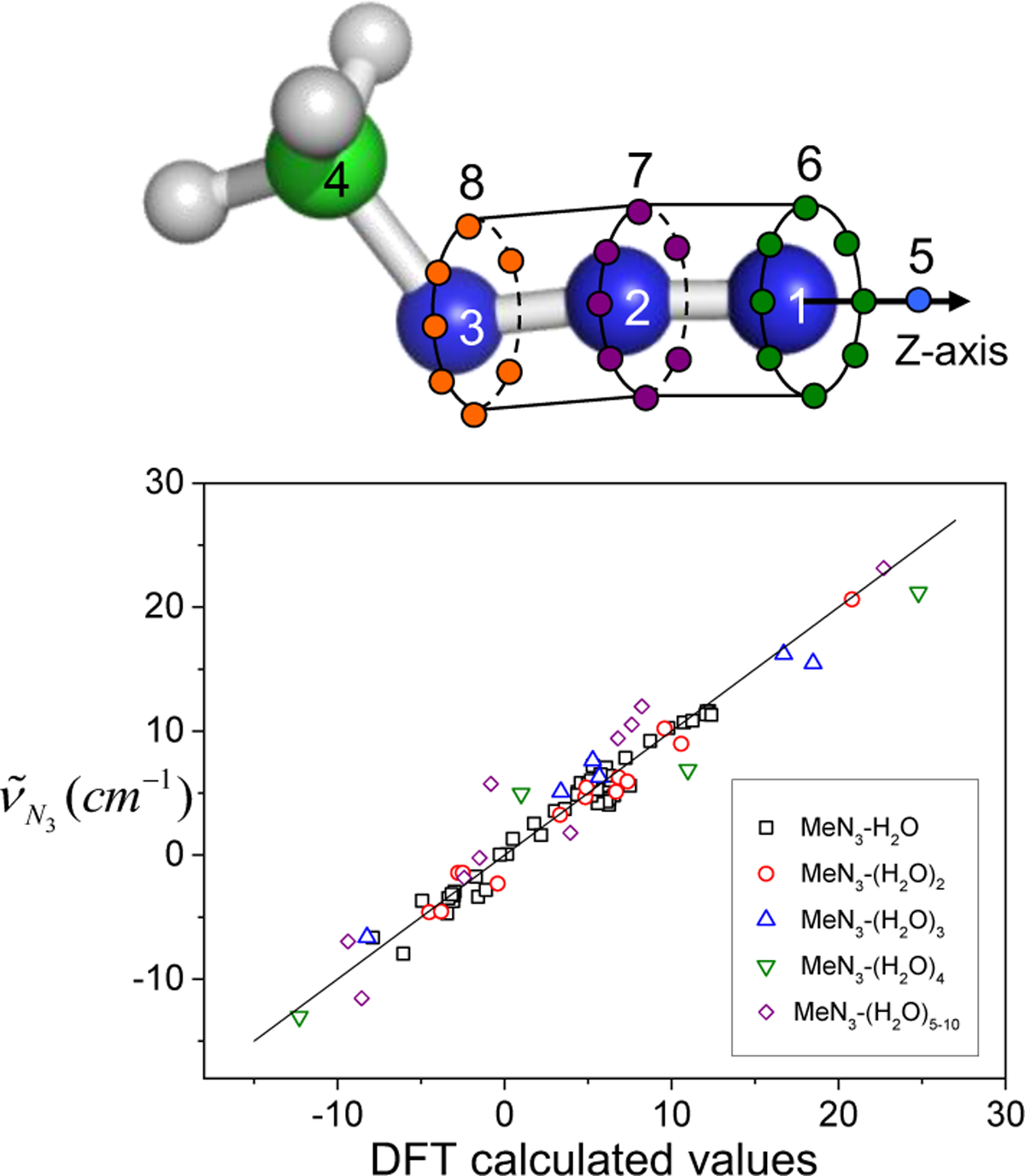
Solvatochromic charge model with distributed interaction sites for MeN3 in the upper panel. The y-axis in the bottom panel represents the azido stretch mode frequency obtained with Eq. (109) and the x-axis to the DFT calculated results. Reproduced from Figures 4(b) and 5 of Ref.232. Copyright 2008 AIP Puplishing.
The semiempirical approach of describing the frequency shift of the azido stretch mode was used to examine the electrostatic environment of the azidohomoalanine-incorporated NTL9 protein that is the N-terminal domain of the ribosome protein. Taskent-Sezgin et al.355 measured the IR spectra of two mutants of NTL9, Met1Aha, and NTL9-Ile4Aha. The showed that the azido IR probes in the two mutants are exposed to different local electrostatic environments, that is, hydrophobic pocket (Figure 16(a)) and solvent water (Figure 16(b)). Quantitative analyses of the IR spectra for these two mutants were made by performing QM/MM MD simulations of aqueous NTL9 mutant solutions and estimating the fluctuating frequency shift of the azido stretch mode with Eq. (94).236 For the azido frequency shift of Met1Aha, the contribution from the peptide backbone is 12.5 cm−1, and this strong blue shift results from the electrostatic interaction of carbonyl oxygen atom of Met1 with middle N-atom of azido group (see the inset of Figure 16(c)). Surrounding water molecules cause a red-shift of −6.9 cm−1, indicating that the presence of hydrophobic pocket in Met1Aha prevents water molecules from making linear H-bonds with the azido group. Since the azido group of Ile4Aha in Figure 16(b) is fully exposed to the solvent, water molecules can form a linear H-bonding interaction with the terminal N-atom of N3 and causes a large blue shift of 8.4 cm−1 whereas the contribution of neighboring peptides is relatively small, exhibiting a blue-shift of 1.3 cm−1. Although the total frequency shift difference of about 4 cm−1 in the N3 mode between Met1Aha and Ile4Aha is smaller than that of the experimentally measured value of 11 cm−1, the blue-shifting pattern is reproduced by considering two contributions from water and neighboring peptide backbone atoms. The calculated spectral lineshapes of the azido stretch mode for both mutants were found to be consistent with the experimental results (Figures 16(c) and 16(d)). In short, the combination of QM/MM MD with vibrational frequency maps is successful in reproducing the IR spectrum of azido-homoalanine and in extracting the critical information on the native protein structure and the solvent effect on the IR probe.
Figure 16.
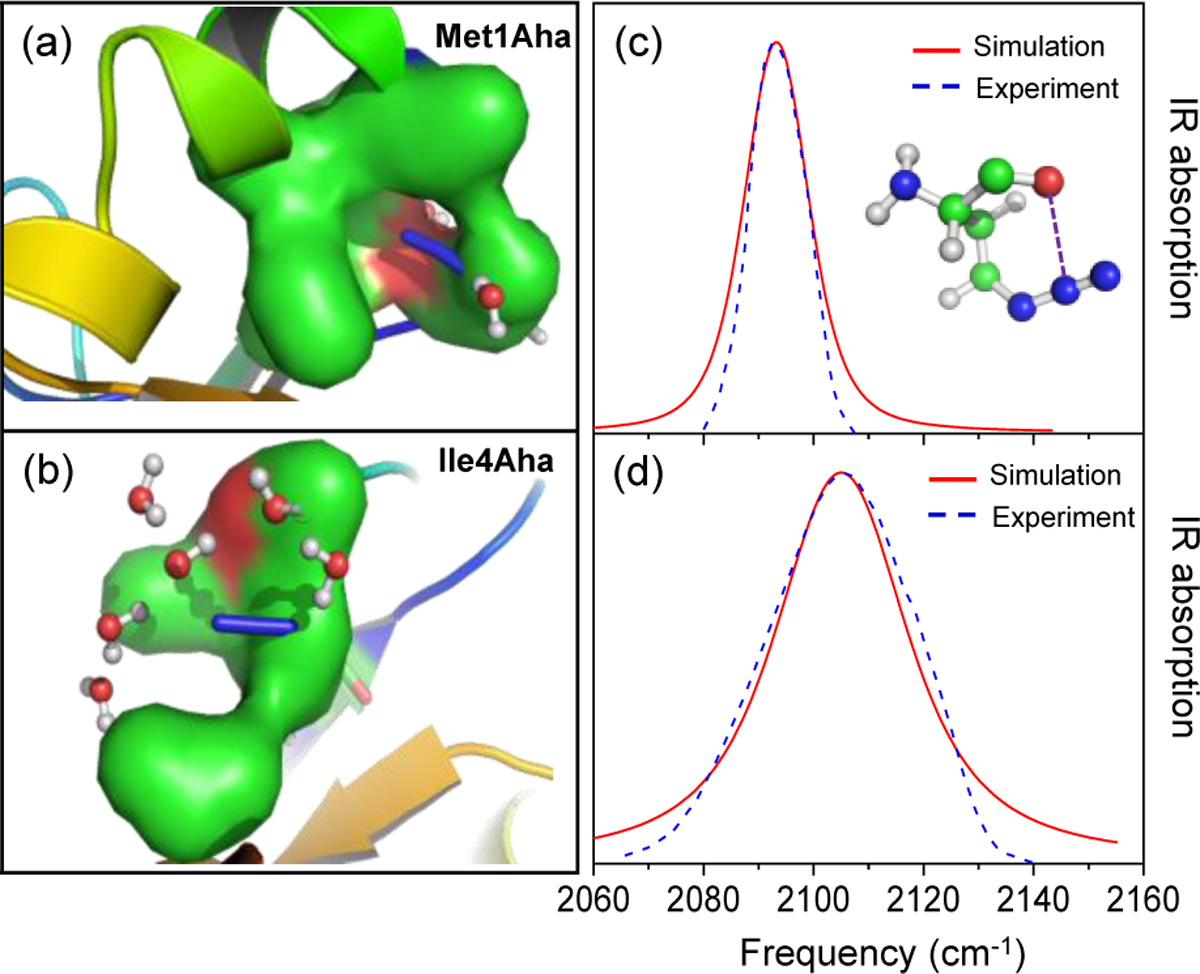
(a) Azido group in the hydrophobic pocket of Met1Aha NTL9 mutant (b) fully hydrated azido group of Ile4Aha NTL9 mutant. The numerically calculated IR spectra of the azido stretch mode (solid red line) of Met1Aha in (c) and Ile4Aha in (d) are displayed with the experimental results (blue dashed line). Reproduced from Figures 1 and 4 of Ref.236. Copyright 2011 The American Chemical Society.
More recently, Zanobini et al.50 employed the frequency map developed by Choi et al. to estimate vibrational frequency shifts caused by changes in the electrostatic environment of the azidohomoalanine (Aha) incorporated in the vicinity of the binding groove of the PDZ2 domain in the study of protein-ligand interactions of the K38Aha mutant of apo-PDZ2.
4.10. Carbonmonoxy stretch
When CO is bound to a heme group in proteins, the CO stretch transition dipole moment is enhanced; the vibrational Stark tuning rate of the CO stretch mode for CO bound to a heme group was estimated to be 2.4/f cm−1/(MV/cm−1) with the local field correction factor f. In contrast, the free CO in an organic solvent solution has a smaller value of ~0.7 / f cm−1/(MV/cm1).356 Thus, the CO stretch mode of proteins containing heme groups such as myoglobin and hemoglobin can be used as an excellent IR probe to study the electrostatic environment in the protein active sites. When CO binds to the heme of myoglobin, the CO stretch mode shows two distinct peaks in the vibrational absorption spectrum, which were assigned to the vibrational sub-state of A1 at ~1944 cm−1 and to A3 at ~1932 cm−1. Recently, the Fayer group performed linear and 2D IR spectroscopic measurements of the wild-type and double mutant, T67R/S92D, myoglobins, where such site-specific mutations significantly enhance the catalytic activity of peroxidase compared to wild-type myoglobin. They found that the chemical exchange rates between the conformational states of A1 and A3 are substantially different from each other. Upon visible light illumination, CO is cleaved from the heme iron and populates the so-called docking state in the vicinity of the heme within a few picoseconds, producing the so-called B-states in the IR spectrum.357 Using triggered 2D-IR exchange spectroscopy, Bredenbeck et al.93 established the relationships between the bound states A1 and A3 and the different B states at the docking site, which have been the target of detailed theoretical investigations as well.
Along with numerous experimental works of vibrational spectroscopic measurements to explore the active site structures and dynamics of CO-bound heme proteins, theoretical attempts have been made to simulate the CO stretch spectra of MbCO and to directly compare them with the experimental data, both, for the heme-bound CO in the A-states and the CO at the docking site (B-states). To describe the vibrational spectrum of the CO stretch mode in the CO bound heme associated with the B1 and B2 states corresponding to the two orientations of CO at the docking site, that is, CO pointing either with its O or C atom towards its former binding site of the Fe atom, respectively, Anselmi et al. carried out MD simulations of CO-bound Mb and numerically simulated the CO stretch IR spectrum of the CO ligand within the distal heme pocket using the perturbed matrix method to describe the vibrationally excited states of a given molecule. In direct comparison with the experimental vibrational spectra of the CO stretch mode of the complex of heme and CO, the simulated CO stretch IR spectrum exhibits two distinct peaks that are assigned to the vibrational spectroscopic states of B1 and B2,358 confirming the assignment proposed by Lim et al.357 Recently, to describe the vibrational frequency shift of the CO stretch mode caused by swapping the CO orientation in the docking site, Wang et al. successfully described the CO stretch IR spectrum associated with the B1 and B2 states with a match between the theoretical result of 13.1 cm−1 and the experimentally measured value of 11.5 cm−1.359 On the other hand, to estimate the vibrational frequency shift of the CO stretch mode in the A-states, where CO is bound to the iron atom, in consideration of the H-bonding interaction between the oxygen atom of CO and the hydrogen atom of the neighboring His 64 residue, the semiempirical approach of Eq. (94) was used with the treatment of electrostatic potential generated from water solvents and neighboring peptides.360 The distributed solvatochromic charge model was used to estimate the CO stretch frequency shift of MbCO, reflecting the change in the electrostatic potential on the CO ligand. Note that the IR probe is not an isolated CO but is the CO-heme complex, where the CO ligand forms a strong d-π* back bonding interaction with the iron atom. Since the heme pocket contains not only water but also various residues such as arginine and histidine, DFT calculations were performed on various heme-CO complexes to determine the solvatochromic charge parameters la in Eq. (94). As can be seen in Figure 17, the VSM model for predicting the CO stretch frequency shift is suitable for reproducing the DFT calculation results. Using the MD simulation and the multivariate equation with Eq. (94), the numerically simulated IR spectra of the two mutants are shown to be consistent with those of the experiments (Figure 18). The relative decrease in the A3 peak intensity in the double mutant could be attributed to the rotational restriction of the imidazole ring and an increase in the H-bonding interaction of the CO ligand with the Nε-H of imidazole.
Figure 17.
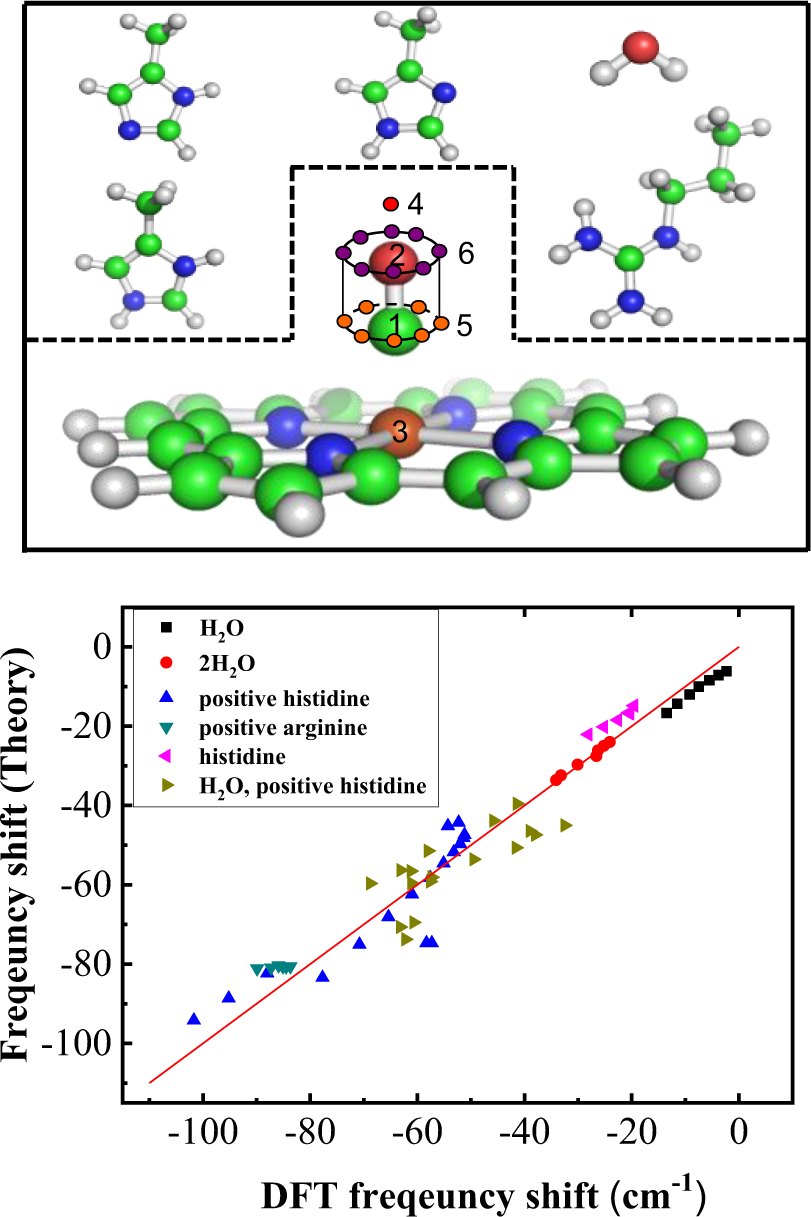
The heme-CO complex, a distributed solvatochromic charge model of the top panel, is shown along with model compounds such as neutral histidine, positively charged histidine protonated at the atom of Nε or Nδ, positively charged arginine and water molecules. In the bottom panel, the frequency shift of the CO stretch mode theoretically obtained from the Eq. (109) is compared with the DFT calculation result. Reproduced from Figures 1 and 2 of Ref.360. Copyright 2013 The American Chemical Society.
Figure 18.
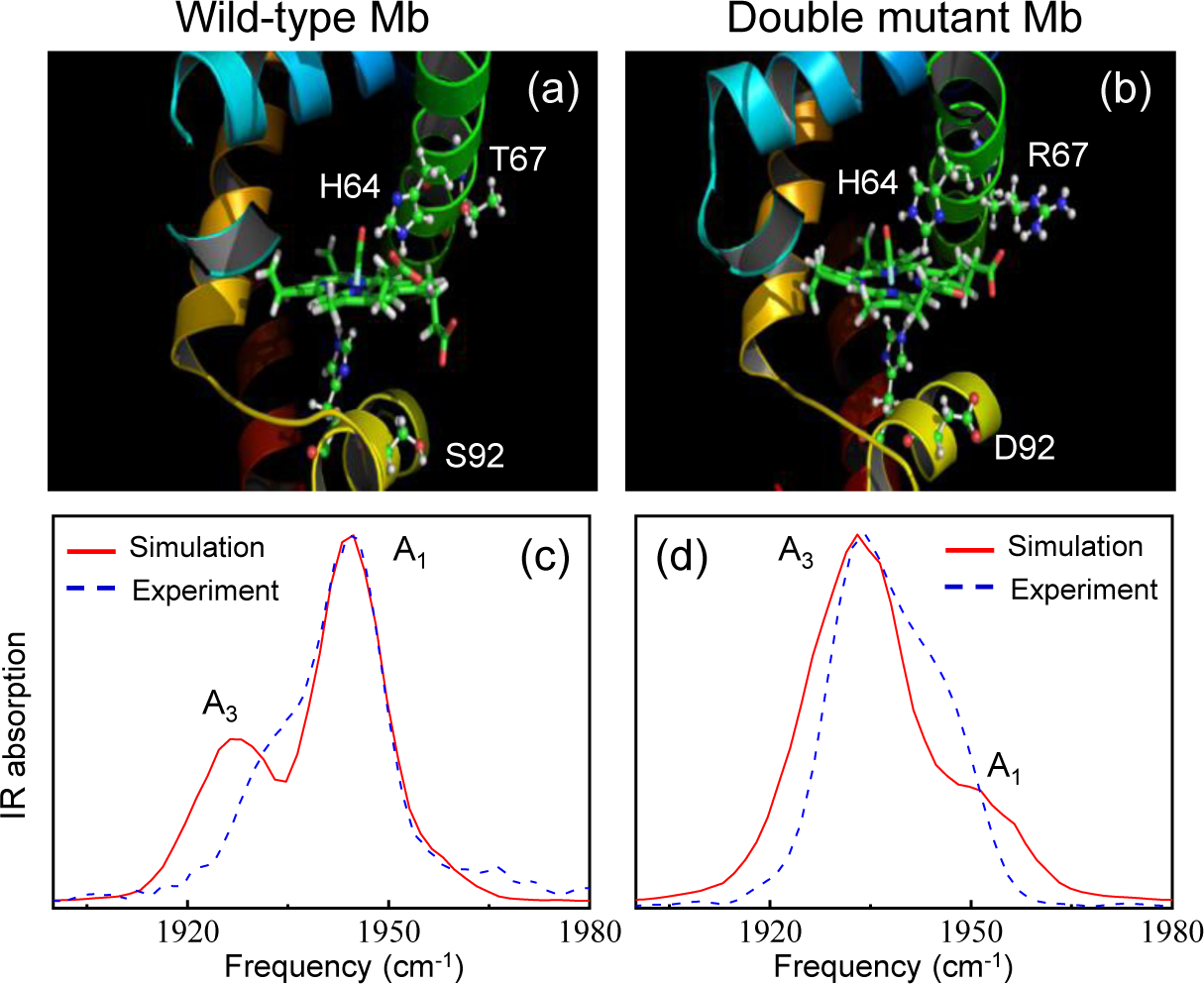
(a) Protein structures obtained from MD simulation of native MbCO in (a) and the double mutant MbCO in (b). The double mutant has two substituted residues of Arg67 (R67) and Asp92 (D92) instead of Thr67 (T67) and Ser92 (S92) in the wild type. The numerically calculated IR spectra of the CO stretch mode (solid red line) of native MbCO in (c) and the double mutant in (d) are displayed with the experimental results (blue dashed line). Reproduced from Figures 4 and 9 of Ref.360. Copyright 2013 The American Chemical Society.
By calculating the nonlinear response functions directly, Choi et al. obtain numerically simulated 2D IR spectra of the double mutant T67R/S92D, which appear to be significantly different from that of the wild-type MbCO.
In addition to CO, nitric oxide (NO) and the cyanide anion (CN−) also work as ligands to the heme and are sensitive to the electrostatic environment around them.179,361 Electrostatic frequency maps that encompass both the dipolar solvation cases and the hydrogen-bonding cases (with rather uniform and significantly non-uniform electric field environment, respectively) have been developed for the heme (FeII)…CO, heme (FeII)…CN−, and heme (FeIII)…CN− complexes, which have been shown to demonstrate rather linear dependence of the stretching frequency to the electric field.238,362
4.11. Ester carbonyl stretch
Ester carbonyls are intrinsic probes of biological membranes and are also common features in industrial biofuels and surfactants. In lipid membranes, ester carbonyls are positioned precisely at the ~1 nm interface between hydrophobic and hydrophilic regions, making them ideal reporters of interfacial hydration, heterogeneity, and water penetration into the lipid bilayer.363,364 The spectral properties of ester carbonyls are similar to the amide I vibrations in amino acids; however, vibrational maps of these modes have only been developed recently.
Ester carbonyls are especially useful reporters of hydrogen-bonding in protic solvents such as aqueous solutions. The ester C=O frequency exhibits an approximate red-shift of 15 cm−1 per hydrogen bond, similar to amides.365 Gai and coworkers measured the center frequencies of methyl acetate and methyl propionate in different solvents and found a simple Stark shift with a tuning rate of 1.3 cm−1/(MV/cm).51 Building on this work, Baiz and coworkers developed an electric-field map that semi-quantitatively reproduces the absorption lineshapes of ethyl acetate in eight different solvents spanning a wide polarity range.366 This electrostatic map consists of six electric field parameters computed at the positions of the three atoms that compose the ester group, O-C=O.
The parameters were directly optimized against the experiment by minimizing the differences between calculated and measured absorption spectra in eight common solvents. Combining the Baiz frequency map and MD simulations, Yu and Shi have simulated the IR absorption spectra of [6,6]-phenyl-C61-butyric acid methyl ester, an organic semiconducting material widely used in photovoltaic devices, in a set of organic solvents and revealed how its solvatochromic shifts arise from specific interactions between the ester carbonyl group and the solvent molecules.367 More recently, Wang and coworkers have applied this combined approach to study the structure, dynamics, and IR spectra of omega-3 fatty acids that are widely used in dietary supplements. These calculations elucidate the packing and dynamical fluctuations of these polyunsaturated fatty acids in the liquid phase and uncover how the conformations and intermolecular interactions of these molecules result in distinct IR spectral features of their ethyl esters and triglycerides.368
Despite the success of the Baiz frequency map, one outstanding challenge is that its parameterization against the experiment relies on the MD simulations sampling the correct H-bond ensemble populations; as such, force fields are usually modified to produce accurate H-bond populations prior to parameterizing the maps. Alternatively, when peaks are well-separated, individual H-bond populations can be treated independently in the simulation and experiment. Figure 19 shows the performance of the map in which the average frequencies of individual H-bond populations in protic solvents are plotted.
Figure 19.
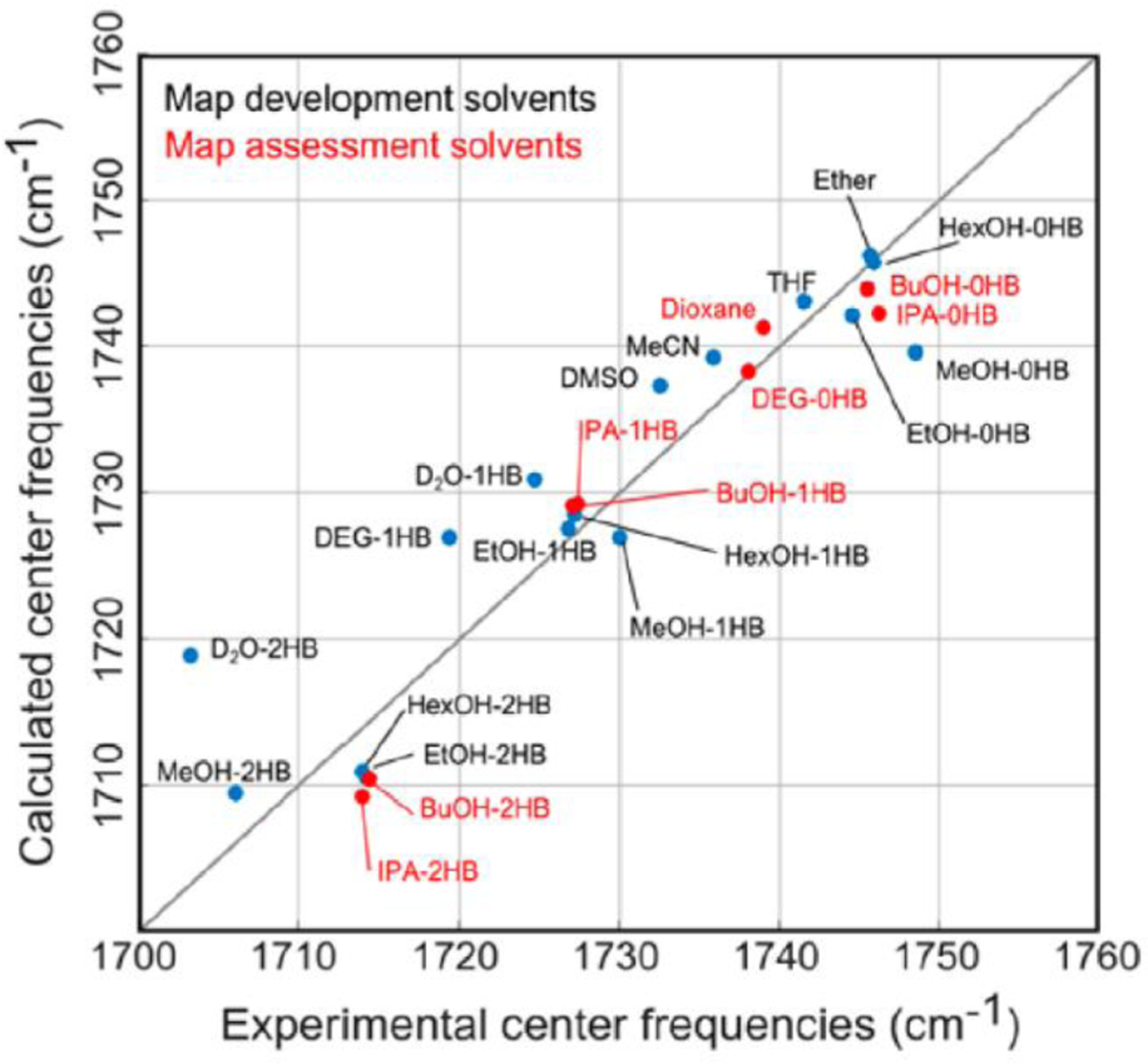
Comparison between computed and experimental CO center frequencies and line widths in all solvents. Solvents used to parametrize the map are indicated in blue, and solvents used to evaluate the map performance are shown in red. The solvents are labeled Ether = diethyl ether, THF = tetrahydrofuran, MeCN = acetonitrile, HexOH = hexanol, EtOH = ethanol, MeOH = methanol, BuOH = butanol, IPA = isopropanol, and DEG = diethylene glycol. Reproduced from Figure 7 of Ref.366. Copyright 2016 The American Chemical Society.
To overcome this problem, Zhuang and coworkers have parameterized an ab initio map for methyl acetate.369 This map contains 20 parameters, which include electrostatic potential, electric fields and gradients at the C, and terminal and bridging O sites. Together these models have become useful in mapping the frequency-frequency correlation functions of carbonyls in interfacial environments, producing frequency fluctuation correlation functions that are a near-quantitative agreement with experiments.370
Using 2D IR spectroscopy, Chutonov and coworkers recently observed H-bond-dependent Fermi resonances induced by intermolecular interactions.371 These effects are most prevalent in small molecules, such as methyl acetate, but are lifted in larger molecules. Thus, future parameterizations must account for potential Fermi resonances to more accurately predict the H-bond populations of ester carbonyls in protic solvents.
4.12. Carbonate carbonyl stretch
Carbonyl stretch mode in amide, ester, and ketone compounds has a very large transition dipole moment, and its frequency appears to be highly sensitive to local H-bonding interaction with H-bond donating solvent molecules in solutions or neighboring peptide residues in proteins. Therefore, modeling the C=O stretch frequency maps has been an important research subject in the field. Recently, the C=O stretch mode of carbonate attracted a great deal of attention because a variety of carbonate molecules have been used in the electrolytes of lithium-ion batteries (LIB) that are commercially available and used extensively in portable electronic devices, electric cars, and mobile vehicles. However, still, the relationship between microscopic solvent dynamics and macroscopic ion conductivity in carbonate electrolytes with a high concentration of lithium-ion has not been elucidated yet.
Improving the performance of LIB requires understanding the lithium-ion mobility mechanism in mixed carbonate solutions.372 Linear and cyclic carbonates are usually used as a mixture for the electrolyte in LIB, and they are assumed to have different roles. More specifically, cyclic carbonates such as propylene carbonate (PC) and ethylene carbonate (EC) have larger dipole moments and more polar than linear carbonates. Therefore, those cyclic carbonates have been used as the principal solvent dissolving and solvating lithium ions, and they tend to hinder any formation of ion pairs between lithium cation and counter anions. In contrast, the linear carbonates like diethyl carbonate (DEC) and dimethyl carbonate (DMC) act as a medium facilitating the transport of ion-solvent complexes, e.g., lithium-ion solvated by mainly cyclic carbonates. This hypothesis about the different roles of the cyclic and linear carbonates has been considered to be reasonable because of the differences in their polarities and viscosities. However, recent linear and 2D IR experiments of the carbonyl stretch mode of carbonates in LiPF6/carbonate solutions revealed interesting structure and dynamics of lithium ion-solvent complexation in linear and cyclic carbonate solvents.101,373–377 To extract quantitative information about the solvation structure and chemical exchange dynamics from the experimental results, it is necessary to numerically simulate the steady-state and time-resolved IR spectra using the vibrational frequency map of the carbonate CO stretching mode and carrying out numerical calculation of the vibrational Schrödinger equation.110 Liang et al.375 employed the electric field vectors located at the carbonate group to estimate the time-varying frequency and transition dipole moment, which were then used to simulate the carbonyl stretch IR spectra and the time-resolved 2D IR spectra of various lithium salt/carbonate solutions. They showed that the increasing cross-peak in the 2D IR spectra mainly originates from the chemical exchange process between free carbonate and lithium-ion bound carbonate molecules in the LiPF6/carbonate solutions. Also, by examining the waiting-time dependent 2D IR spectra, the solvation dynamics associated with the formation and dissociation process of the lithium-ion-carbonate378 complexes were found to be faster in cyclic carbonate solvent compared to the linear carbonate solvent.375 This is an excellent example showing that the marriage of vibrational frequency maps of critical IR probe modes and the state-of-the-art 2D IR spectroscopic techniques is capable of providing unique piece of information about the detailed ultrafast solvent dynamics as well as the specific roles of different carbonate molecules in LIB electrolytes containing a mixture of both cyclic and linear carbonate solvents.
4.13. Water OH and OD stretch modes: Frequency map, non-Condon effect, and anharmonicity
Spectroscopic maps have been considered essential tools for understanding the IR absorption and 2D IR spectroscopy of liquid water. The first IR photon echo experiments on the OH stretch vibration of HOD in D2O were reported by Stenger et al.379–381 and Yeremenko et al.382 Tokmakoff and coworkers reported the measurement of the spectral diffusion dynamics of the OH stretch of dilute HOD in D2O.104 Soon thereafter, Fayer and coworkers reported the same for dilute HOD in H2O.383,384 The experimental and theoretical advantage of studying HOD in D2O is to isolate the OH stretch vibrational frequency of the HOD solute from the myriad of OD stretches in surrounding D2O solvent. Studies of HOD in H2O isolate the OH stretch of HOD. In their study of HOD in D2O, Fecko et al. assumed that the shift of the OH stretch vibrational frequency of HOD from its value in the gas-phase could be modeled as a linear Stark effect, where the electric field along the OH bond of HOD was computed from a classical MD simulation, and the Stark tuning rate was calculated with first-order perturbation theory.104 Similar perturbative approaches were utilized previously by Hynes and coworkers385 and by Lawrence and Skinner.386 However, the formula employed by Fecko et al. to compute the OH stretch vibrational frequencies of HOD was, in essence, a spectroscopic map that assumed a causal relationship between the value of the electric field from the solvent and the vibrational frequency. Calculations of the normalized frequency correlation function of the OH stretch of HOD in D2O were in good agreement with experiment with a long-time decay (600 fs) that was about a factor of two faster than in the experiment. Later, the discrepancy between the calculated long-time frequency fluctuation dynamics with the experiment was found to be typical of nonpolarizable water models.387,388
In 2004, Corcelli, Lawrence, and Skinner developed the first empirical DFT-based spectroscopic map for the OH and OD vibrations of dilute HOD in water.66 Their approach was to harvest 100 statistically independent clusters from an MD simulation containing HOD with 4 – 9 water molecules. The OH or OD stretch vibrational frequency of interest was calculated by first computing the one-dimensional potential energy curve moving only the H or D atom along its OH or OD bond. The potential energy curve was then fit to a Morse oscillator whose fully-anharmonic vibrational frequencies are known analytically. The 100 vibrational frequencies were fit to a linear function of the electric field due to the solvent projected along the OH or OD bond. The spectroscopic map developed by Skinner and coworkers did not assume a causal relationship between the electric field and vibrational frequency. Instead, the map exploited the electric field as a descriptor of the solvent environment that correlates with the vibrational frequency of the OH or OD stretch of interest.
In later studies by Skinner and coworkers, the approach for developing spectroscopic maps for the OH and OD vibrations of HOD was refined. Vibrational frequencies were computed from the one-dimensional potential energy curves with the more efficient and accurate Colbert-Miller discrete variable representation (DVR)389 method. Collecting more snapshots from the MD simulations for DFT analysis showed that the vibrational frequencies were better correlated to a quadratic function of the electric field.390 Alternate strategies for constructing OH and OD frequency maps were developed by other groups. For example, Mukamel and coworkers developed a map using electronic structure calculations of HOD in uniform and spatially varying electric fields.130,227,391 The resulting map required the electric field and its gradients from an MD simulation at the atomic sites of the HOD molecule. OH and OD frequency maps have been applied to water in a variety of contexts, for example, aqueous electrolyte solutions,392 as a solute in ionic liquids,393 air-water interfaces,394–400 gas-phase water clusters,401,402 near lipid bilayers,403–407 in reverse micelles,408,409 and ice.378,410–412 The transferability of the maps is noteworthy. Figure 20 shows that the same spectroscopic map can be used to describe the OH vibrational frequency and anharmonicity for HOD isolated in the gas-phase, embedded in a water hexamer at 80 K, in liquid water, in ice Ih at 100 K, and at the vacuum/water interface.413 In 2019, Skinner and coworkers utilized a machine learning approach, whereby a neural network is trained on DFT-computed vibrational frequencies, to study the vibrational spectroscopy of HOD in water.414
Figure 20.
Reproduced with permission from Figure 2 of Ref.413. (a) DFT calculations of the OH stretch vibrational frequency, ω10, of HOD in various environments, including (black) a gas-phase monomer, (red) a water hexamer at 80 K, (blue) liquid water, (green) ice Ih at 100 K, and (orange) the water/vacuum interface. The dashed line is a spectroscopic map in terms of the electric field, E, along the OH bond evaluated at the site of the H atom. (b) Calculated anharmonicity, Δ, of the OH vibration. Copyright 2013 The American Chemical Society.
In 2005, Skinner and coworkers reported on the importance of non-Condon effects in describing the vibrational spectroscopy of HOD in water.68,415 Non-Condon effects refer to the dependence of the transition dipole moment of vibration on its solvation environment. These studies found that the transition dipole moment of the OH or OD vibration of HOD in water can vary by a factor of five across its IR absorption band.415 High frequency OH vibrations were found to have small transition dipole moments, whereas lower frequency vibrations have large transition dipole moments. Remarkably, the magnitude of the transition dipole moment is linearly related to the electric field along the OH bond.390,415 Because the IR absorption depends on the transition dipole moment squared, the non-Condon effects have profound implications for the calculation of the IR absorption line shape. In contrast, the transition polarizability, which is relevant for Raman spectroscopy, does not display significant non-Condon effects. Corcelli and Skinner showed that the differences in non-Condon effects are directly related to the differences in the IR and Raman spectra of HOD in water.415 Schmidt, et al. showed that the non-Condon effects play a significant role in the calculation and interpretation of 2D IR spectra, which depend on the fourth power of the transition dipole moment.68
The spectroscopic maps for the OH and OD vibrations of HOD in water are a starting point for understanding the vibrational spectroscopy of liquid water. The complication of moving from HOD to pure water is that the nearly resonant OH vibrations can couple.416–418 Auer and Skinner developed maps for both the intra- and intermolecular coupling of OH vibrations in water. These maps facilitated the theoretical study of the vibrational spectroscopy of water.419 They also formed a basis to study the SFG spectroscopy of the vacuum/water interface of liquid water.395–398,400 Several groups have developed causal spectroscopic maps for OH vibrational frequencies, transition moments, and couplings in liquid water. Utilizing the work of Hush and Reimers on describing the vibrational Stark effect,172 in 2006, Torii investigated the vibrational spectroscopy of water, including the role of coupling but without incorporating non-Condon effects, although the paper did acknowledge that such effects might be relevant.420 In 2013, Choi and Cho utilized an HMR approach to describe the frequencies, transition dipole moments, and coupling constants of OH vibrations in water in terms of the local environment and electrostatics.421
Isotopically diluted OH or OD stretch modes are vastly used as perfect sensors of the local environment to study the dynamics of the H-bond network in aqueous systems including liquid water, ice, and heterogeneous systems such as hydrated lipid multi-bilayers.413 Due to the fact that the OH (OD) stretch mode is highly anharmonic, the vibrational frequency maps need to parameterize the changes of anharmonicity due to the molecular surroundings. The first group of vibrational maps, developed by Skinner group, are effectively electrochromic and choose only a single collective variable – electric field evaluated at the location of the water hydrogen atom along the direction of the OH (OD) bond.378,400,404,410,411,419,422 For each configuration of water molecules, the electric field is computed from the point charges utilized in the molecular dynamics forcefield. The quadratic form of the fitting functional is usually chosen according to
| (111) |
where x can be the absorption frequency ωnm, dipole moment derivative with respect to the OH (OD) normal coordinate μ′, position matrix elements or momentum matrix elements . It was reported that the higher-order polynomial functionals do not improve the performance of the vibrational maps for OH/OD stretch mode. In most of the applications, only the fundamental and first excited state absorption transitions are considered. To fit the parameters Ax, Bx, and Cx, one can follow the standard procedure based on collecting anharmonic analysis results from small molecular clusters at the DFT level and performing the least-squares multivariate analysis. Another approach was used based on adjusting to the correct distribution of DFT frequencies, p(ω), given the distribution of electric fields p(E) in the liquid-state simulation, i.e.,410
| (112) |
referred sometimes as the ‘cumulative vibrational mapping. For this, standard water forcefields such as SPC/E390,419 and TIP4P378,410 were used to run MD simulations and generate the ensemble of configurations and distributions of the electric field. Intramolecular coupling matrix elements were also parameterized according to the functional form,378,411
| (113) |
where the j and k indices refer to the coupled vibrational chromophores, and a, b and c are adjustable parameters.
Another class of vibrational solvatochromism maps was developed by Tokmakoff and coworkers423 that is applicable for OH/OD stretches with much larger anharmonicity such as excess proton in hydronium cations. They initially maintained the electrochromic form of the map for the dipole moment derivatives (with the quadratic functional of the electric field) but used the solvation coordinate as a conjugate perturbation to describe the vibrational transition frequencies, i.e.,
| (114) |
where ΔE is defined as the difference in potential energy at appropriately selected two reference points along the OH bond. They also found that correlating the dipole derivatives with the transition frequencies
| (115) |
results in better agreement with the benchmark DFT data, as compared to the electrochromic maps. In order to translate the DFT solvation energy onto the molecular mechanics level, the auxiliary mapping was established as
| (116) |
where ΔEEVB is the solvation energy from the multi-state empirical valence bond (MS-EVB) simulation,105 computed as the difference between the EVB potential energy of solvated hydronium ion with OH bond length set to be 1.0 Å (equilibrium bond length in bulk water) and that with OH bond length set to be 1.4 Å (position of the second minimum of the double-well potential of D2O⋯H⋯OD2 complex). The benchmark data for parameterizing the maps were obtained from the database of the MS-EVB water clusters analyzed by using the B3LYP/6–311++G** method and concomitant anharmonic analysis yielding the reference transition frequencies and dipole moment derivatives up until the 4th vibrational excited state. The simulated excess proton spectral response of OH stretch in bulk D2O qualitatively captures the experimental features for isotopically dilute excess protons. The model was also used to decompose IR spectra into contributions from different aqueous proton configurations.
4.14. Strongly correlated OH stretch modes: Local mode or collective mode
Understanding the vibrational dynamics in bulk424,425 and confined water426–428 is a challenging task. The OH-stretch vibrations within a water molecule are strongly coupled, leading to symmetric and asymmetric stretch modes in the gas phase. The hydrogen bond distance in water is so short that the coupling between OH-stretch vibrations on different water molecules can be expected to be comparable to the intra-molecular coupling in size. A good way of disentangling these effects is the study of isolated water molecules in hydrophilic solvents as acetonitrile.120,429 Two-dimensional infrared experiments of this system reveal strong but imperfect coupling of the intermolecular OH-stretches, which make the low-frequency eigenstate a mixture between symmetric state and a state of the strongest H-bonded OH-stretch vibration.120 The eigenstates, thus, rapidly scramble within the individual water molecule. As intermolecular couplings are included, the vibrational dynamics further speed-up one broad spectral feature is formed, which contains states with continuously changing identity across the line.69,430 Water confined in reverse micelles exhibit contributions from bulk-like water and surface water where the latter behaves more like the isolated water in acetonitrile.408,409
As water is frozen forming ice, the OH-stretch peaks get sharper, and distinct peaks arise due to different vibrational symmetries imposed by the oxygen ordering in the Ih phase of ice.431 This behavior is well described with the mappings developed for bulk water.378,390,412,419 The distinct peaks appearing in the hydrogen order ice II phase are also well described,128 while more complex high-density ices still pose a challenge.
The behavior of water near heterogeneous liquid interfaces is complex and different from water in bulk and at less-complex air-water interfaces. To capture the sole effects of local structures and dynamics on the water spectra for such complex interfaces, Skinner and coworkers focused on investigating local mode vibrations of water using computational spectroscopy.400,406,407 They considered a series of lipid- and surfactant-water interfaces with different local interfacial curvatures and chemical structures. For example, their computed vibrational sum-frequency generation (VSFG) spectra of water at flat cationic or anionic lipid or surfactant interfaces showed the existence of water molecules that have OH chromophores pointing away from the interface (indicated by negative peaks) or pointing towards the interface (indicated by positive peaks) while forming hydrogen bonds with the lipid or surfactant headgroups. Interestingly, the coexistence of these two types of interfacial water molecules is observed near interfaces between water and mixtures of cationic and anionic lipids, as revealed by the presence of both negative and positive VSFG peaks. In the case of zwitterionic lipid interfaces, OH orientation is toward the interface on the average, resulting in positive VSFG peaks.
The two-dimensional variants of VSFG, namely 2DSFG, enable characterization of the dynamics of interfacial water at the flat interfaces. 2DSFG could distinguish the dynamics of interfacial water as a function of the lipid charge and headgroup-water chemistry. It was shown that the orientational relaxation of interfacial water is much slower compared to the bulk water due to conformational constraints imposed by strong headgroup-water H-bonding and electrostatics. Computation of H-bonding and rotational correlation functions revealed that the separation of interfacial water from the bulk water in terms of water dynamics is possible, which occurs about 7 Å away from the interface. Note that Tahara and coworkers performed a series of VSFG and 2DSFG experiments on different lipid/surfactant-water interfaces; their findings were in good agreement with this computational work.99,432–435
In addition to studying flat interfaces, investigating the structure and dynamics of water near concave and convex surfaces is necessary to complete the picture about the effects of membrane surface geometry on the behavior of interfacial water molecules. Skinner and coworkers investigated H-bonding dynamics of interfacial water within a normal (Type I) lyotropic gyroid phase formed by a gemini dicarboxylate surfactant self-assembly using a combination of 2D IR spectroscopy and MD simulations.436 This phase has convex surfactant headgroup-water interfaces. It was found that the dynamics of water near the convex surfaces is slower than bulk water dynamics. However, the dynamics of water near convex surfaces are faster than those of water confined in a reverse spherical micelle of sulfonate surfactants that form the concave surfactant headgroup-water interface, given that the water pool in the reverse micelle and the water pore in the gyroid phase have roughly the same diameters. This difference in confined water dynamics likely arises from the significantly reduced curvature-induced frustration at the convex interfaces of the normal gyroid, as compared to the concave interfaces of a reverse spherical micelle.436
4.15. C-D stretch: Non-perturbative IR probe
Like the nitrile and azido vibrations, carbon-deuterium vibrations have been explored for the characterization of specific sites in proteins. The substitution of hydrogen for deuterium shifts the vibrational frequencies to the transparent frequency window of the protein IR spectrum, enabling single absorptions to be discerned apart from the spectral congestion arising from the multitude of native protein vibrations. The advantage of C-D bonds is that they do not introduce unnatural moieties into the protein and thus are virtually non-perturbative. In addition to reporting on their surrounding environment, C-D vibrations enable probing the structure of the protein itself. While less utilized than the nitrile or azido probes, a few research groups have been applying C-D bonds for the study of proteins and peptides. C-D probes have provided insight into protein folding, molecular recognition, and catalysis.437–443 However, their widespread adoption likely has been hindered by their weak absorptions due to the small transition dipole strengths. High (mM) protein concentrations are typically required, and discerning the absorption bands requires careful matching of reference and sample transmission spectra to achieve flat background absorbance. Nonetheless, some delicate protein regions, such as surrounding redox centers, are likely to be perturbed by the introduction of the other non-native transparent window probes. For such regions, C-D bonds may be the only probes that can be introduced while preserving native function.
As their applications, efforts at the theoretical description of C-D probes are less developed compared to nitriles and azido groups. However, DFT calculations of vibrational frequencies have been reported for many C-D labeled amino acids, including glycine, alanine, proline, methionine, lysine, and histidine.441,444–448 For backbone Cα-D bonds and the γ-methylene CD2 of proline, the calculated frequencies show dependence on amino acid conformation and therefore have been proposed as a way to measure local protein or peptide structure. Many experimental studies have taken advantage of the sensitivity to learn about protein or peptide conformational ensembles.441,443,448–451 An extensive QM/MM study reported by Corcelli and coworkers has aimed to account for the absorption lineshape of Cα-D backbone deuterated d1-alanine in aqueous solution; the power spectrum of the fluctuating electric dipole moment was determined from PM3 calculations of snapshots along a classical MD simulation.452
In addition to investigating backbone structure, C-D probes have been introduced at side chains of amino acids to take advantage of their sensitivity to their local protein environment. In many cases, C-D probes have been employed simply as qualitative reporters that a specific residue of a protein contributes to a functional process, such as folding or recognition.450,453,454 The influence of the local reaction field on C-D vibrations has been more quantitatively considered for methyl-d3-methionine by DFT calculations of the amino acid in the presence of a varying external field.439 However, in addition to the local field, H-bonding by water molecules to the adjacent sulfur was found to impact the C-D frequency substantially. When installed as a ligand to the copper center of plastocyanin, the C-D vibrations of methyl-d3-methionine were found by DFT calculations to be primarily sensitive to interaction of the sulfur orbitals and charged metal. Specific water H-bonding likewise affects the vibrational frequencies of Cα-D bonds of alanine peptides.455 Thus, a theoretical description of C-D bonds, like the other transparent window probes, must account for multiple contributions, including local potential and specific local interactions with the environment. Future extension of the Bio-SolEFP approach for C-D probes should assist in more rigorously understanding their spectroscopy to fully exploit them for investigating the complex environments of proteins in the future.
4.16. S=O stretch
The sulfinyl (S=O) group is common in a wide range of compounds such as dimethyl sulfoxide (DMSO), one of the most routinely used solvents in many areas of chemistry. In biology, DMSO is commonly used as a cryopreservation agent. The S=O group interacts strongly with water and prevents toxic ice-crystal growth in cells and tissues.456 The large dipole moment and the polarizability of the S=O group are responsible for DMSO’s amphiphilic behavior, which produces abnormal bulk properties in aqueous mixtures.457
The S=O stretch is characterized by a strong solvatochromic shift, from 1071 cm−1 in non-polar solvents to approximately 1016 cm−1 in water.458 Hydrogen-bonding environments can be directly quantified from the IR absorption lineshapes. In water, a single H-bond induces a red-shift of the S=O stretch frequency by approximately 20 cm−1. The S=O stretch oscillator strength is dependent on its substituents; for the case of DMSO in water, the transition dipole moment is 0.14 D, approximately half that of the C=O stretch.458,459 Together, the strong solvatochromism and relatively large oscillator strength make the S=O stretch an attractive IR probe for nonlinear spectroscopy. However, ultrafast measurements on the S=O stretch remain scarce due to the experimental challenges of operating in the fingerprint region.460
Torii and Noge used density functional theory (DFT) calculations to quantify the dependence of the S=O stretch frequency on some structural parameters, i.e., the S=O bond length, the O⋯H hydrogen-bond distance, and the S=O⋯H angle.239 Strong dependence of the S=O stretch frequency on the S=O⋯H angle was obtained with larger red-shifts being correlated with larger bent angles along rather isotopically around the S=O bond axis. These frequency shifts were parameterized using a combination of electric fields at the S and O atoms projected along the S=O bond axis, together with the electrostatic potentials at the S, O, and C atoms. Building on the work by Torii, recently, Baiz and coworkers have parameterized a fully empirical S=O stretch frequency map using the IR absorption spectra of DMSO in water as a reference. The parameterization is able to semi-quantitatively reproduce the S=O lineshape over a wide range of concentrations of the DMSO/water mixtures and has also been benchmarked against experimental 2D IR spectra (Figure 21).461
Figure 21.
Experimental and computed IR absorption spectra of the S=O stretching mode at different concentrations in binary DMSO/water mixtures. Computed spectra were obtained using the map of Oh and Baiz. Vertical bars represent the average experimental frequencies of the four DMSO species present in solution: singly hydrogen-bonded (1HB), doubly-hydrogen bonded (2HB), Aggregate (Agg), and non-hydrogen bonded (Free) from low to high frequency respectively. Adapted from Figure 1 of Ref.461 Copyright 2019 AIP Puplishing.
4.17. Phosphate modes
Phosphate groups are ubiquitous in biological molecules, including DNA, RNA, ADP, ATP, etc. Phosphate group vibrations involving the PO2− moiety consist of a symmetric stretch vibration at about 1100 cm−1 and an antisymmetric stretch around 1250 cm−1. Phosphate vibrations have been extensively applied as a probe to understand enzymatic hydrolysis of ATP and GTP using time-resolved IR spectroscopy.462–464 Phosphate vibrations have also revealed insights about DNA hydration.465 The antisymmetric PO2− stretch exhibits a red frequency shift with an increased relative humidity of DNA from about 0% to 92%, which is intimately related to the local hydration environment around PO2−.466,467 The symmetric stretch, however, exhibits only a slight blue shift with increasing hydration.467 Because of the sensitivity to local hydration environment, 2D IR spectroscopy has been used to study the spectral diffusion dynamics of phosphate vibrations, showing a fast component (~0.3 ps) of local structural fluctuations around the phosphate group, and a slow component (>10 ps) accounting for the persistence of water-phosphate hydrogen bond.468
Levinson et al. utilized vibrational Stark spectroscopy on phospholipids to investigate the electric field dependence of the phosphate stretch vibrations.467 Their experiments demonstrated that the frequency shifts of the symmetric stretch and the asymmetric stretch could be described as a linear Stark effect, with the Stark tuning rates of 0.54 ± 0.02 and 1.35 ± 0.02 cm−1/(MV/cm), respectively.467 DFT calculations on dimethyl phosphate as a model system shows that the Stark tuning rates result from the component of the electric field along the C2 axis of the PO2− group, while the electric field dependence along O‒O axis is quadratic and results in only modest frequency shifts. The DFT-based calculation thus established a spectroscopic map for phosphate group vibrations.
Corcelli and co-workers applied this spectroscopic map of the asymmetric phosphate stretch to the DNA hydration environment, showing that the frequency shift is not a monotonic red-shift with increasing water solvation and distance from the phosphate group.469 The closest four water molecules around the phosphate group induce a red frequency shift of −34.6 cm−1 to the asymmetric phosphate stretch due to direct H-bond to the oxygen atoms of the PO2− group. In contrast, the fifth and sixth water molecules induce a blue-shift of 9.0 cm−1, which comes from interacting with the oxygen atoms covalently linked to the PO2−. Frequency time correlation functions showed a qualitative agreement with the experimental 2D IR result.468 This phosphate spectroscopic map shows an almost quantitative agreement to the experimental frequency shift as a function of relative humidity, assuming that there is a residual water molecule per phosphate group at 0 % relative humidity, which is also suggested experimentally.465,470
In recent papers by Elsaesser and coworkers,381,471,472 the interaction of phosphate groups with alkali and alkaline earth ions in water has been studied by using the linear and femtosecond 2D IR spectroscopy. The 2D IR spectra of the prototypical system dimethyl phosphate in water with an excess concentration of Mg2+ display two distinct and uncoupled vibrational bands due to phosphate groups with and without an Mg2+ ion in close contact, and the band of the contact ion pairs exhibits a frequency blue-shift. Fingerhut et al. calculated the fluctuating electric force exerted on the (PO2)− moiety by the ab initio based effective fragment potential approach to establish a linear relation for the solvent field-induced solvatochromic shift.472
4.18. Nucleic acid base modes
The vibrational modes of DNA bases that absorb in the frequency range of 1400–1800 cm−1 are strongly IR-active and highly sensitive to DNA structures such as the base pairing and helical geometries in the A, B, and Z forms. These vibrational marker bands are mainly composed of the in-plane carbonyl stretch mode and the NH2 or N-H bending modes of the bases, and have been used to extract critical information on the H-bonding interactions between base pairs, as well as the melting processes and structural transitions of DNA. For example, Polyanichko et al. investigated the effect of the transition metal ion Mn2+ on the DNA structure by analyzing the IR absorption and vibrational CD spectra of the marker bands and showed that the observed B- to C-form conformational transition arisen due to the interaction of Mn2+ with the bases of DNA.473 Furthermore, Krummel et al. carried out 2D IR spectroscopic measurement to investigate the carbonyl stretch modes of the guanine and cytosine bases in dG5dC5 and d(GC)8 double helices in D2O. Combining 2D IR measurements and numerical simulations, they showed that the base pairs that are held together by H-bonds are strongly coupled.474
In conjunction with the experimental spectroscopy measurements, theoretical spectral simulations based upon normal mode analysis have provided crucial insights into DNA structural properties and the vibrational properties of delocalized excitons in the bases. Note that it is impractical to perform ab initio vibrational analysis of the nucleic acids because they have large system sizes and complicated interactions with the solvent water molecules. As a natural extension of the HMR method, which has been successfully applied to polypeptides,277,475 the extended HMR method was developed to analyze the vibrational mode characteristics of base pairs and to simulate the vibrational spectra of various DNA oligomers.476–479 It was found that the vibrational coupling constants are strongly dependent on H-bonding interactions between nucleobases. The IR spectra of a few different DNA model systems in D2O were simulated and compared with the experimentally measured spectra. These calculations reveal that the hydration effects, which lead to solvatochromic frequency shifts of the basis modes, are important for quantitative descriptions of the IR absorption spectra of DNA molecules.476,477
The 2D IR spectra of dGn:dCn and dAn:dTn double helices were simulated by using the basis mode frequencies and vibrational coupling constants. The vibrational anharmonicities of the basis modes were estimated with DFT calculation method, and the conformational inhomogeneity and solvation dynamics were examined by analyzing classical MD trajectories.478,479 The simulation results for the 2D IR spectra of double-helical DNAs showed a weak correlation between the IR spectra and the number of base pairs, which is consistent with the previous experimental observations. From quantum chemistry calculations of A-, B-, and Z-form DNAs, the vibrational coupling constants were shown to be strongly dependent on the DNA conformation. In particular, the coupling constants between base modes in the Z-DNA are fairly small, causing localization of vibrational modes. In contrast, those in A-DNA are large, leading to delocalized vibrational modes.
Among the base vibrational modes, the carbonyl stretch modes are particularly sensitive to the H-bonding patterns and base stacking configurations in nucleic acids.94–97,474,480–483 For example, pioneering 2D IR experiments focusing on the C=O vibrations have revealed the inter- and intrastrand couplings in model A- and B-form DNA and elucidated the dissociation pathway of DNA duplexes.94,96,97,474
To facilitate the interpretation of the vibrational spectroscopy experiments, Jiang and Wang have recently developed two vibrational frequency maps to describe the C=O stretch mode in nucleobases and a C=C frequency map to account for the interactions between the C=O and C=C vibrations in pyrimidine bases.484 These frequency maps are developed using nucleoside 5’-monophosphates (NMPs) as model systems and take the form of
| (117) |
In the C=O frequency map, i indexes C, O, and N atoms, and m represents the x, y and z directions as defined in Figure 22a. For the C=C frequency map, i indexes the C5 and C6 atoms in pyrimidine bases and the coordinate system is shown in Figure 22b. Eim is the electric field on atom i in direction m, which is exerted by all the solvent molecules and counterions around the solute molecules. The intercept ω0 and the coefficients cim are determined by minimizing the differences in vibrational frequencies as predicted from the maps and DFT calculations on 1200 NMP-water clusters.484
Figure 22.
Coordinate systems of the (a) C=O and (b) C=C vibrational frequency maps. The atoms used to define the axes are shown in red.484 Reproduced from Figure 4 of Ref.484. Copyright 2019 The American Chemical Society.
The C=O and C=C frequency maps provide an efficient way to calculate the vibrational frequencies of nucleobases directly from MD simulations. Jiang and Wang have shown that one can combine the frequency maps with a mixed quantum/classical treatment of the line shape theory and capture the IR spectra of NMP in aqueous solutions.484 They have further demonstrated that the frequency maps are applicable to nucleobase derivatives and are transferrable in different solvents. For example, Figure 23a shows that the calculations correctly predict a two-peak feature in the IR spectrum of deoxycytidine 5’-monophosphate in D2O, which comes from the coupled vibrations of the C=O and C=C group in the cytosine base. In contrast, the predicted IR spectrum of inosine 5’-monophosphate, a nucleobase derivative, contains a single peak at 1663 cm−1. As shown in Figure 23b, the theoretical and experimental485 IR line shapes agree well with each other, and their peak positions differ by only 7 cm−1.484 The C=O and C=C frequency maps can thus be readily applied to model the linear and 2D IR spectra of nucleic acids in the carbonyl stretch region and elucidate the molecular origin of the experimental spectra.
Figure 23.
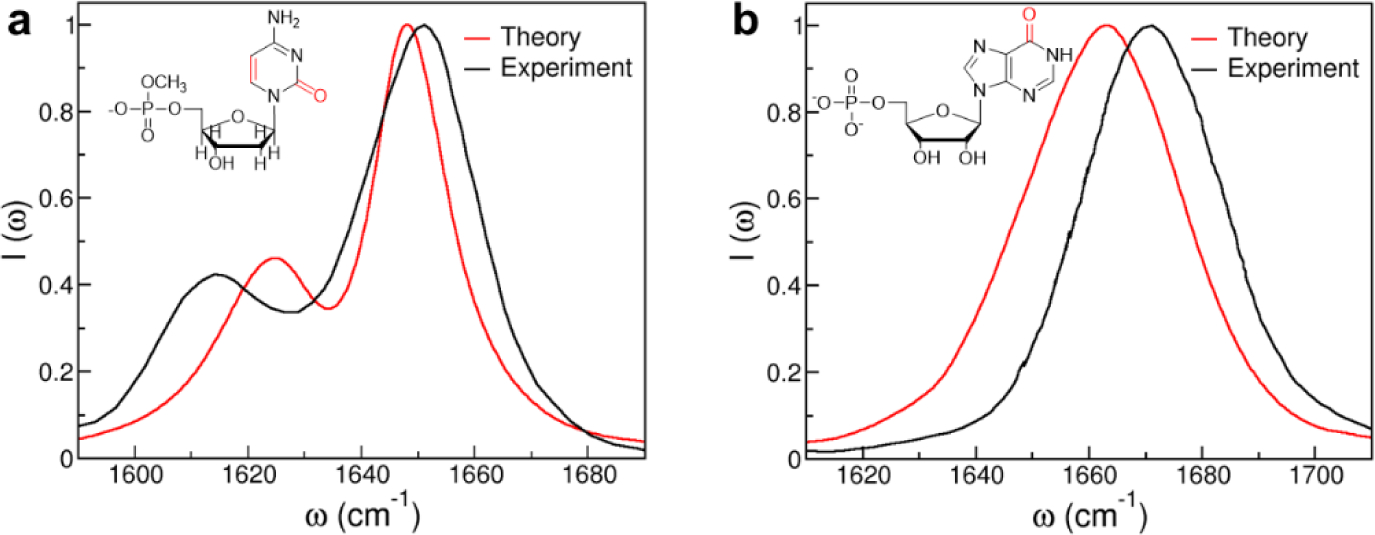
Theoretical and experimental6,11 IR spectra of (a) deoxycytidine 5’-monophosphate and (b) inosine 5’-monophosphate in D2O. The chemical structures of the molecules are shown in the insets with their chromophores highlighted in red.484 Reproduced from Figure 7 and Figure 9 of Ref.484. Copyright 2019 The American Chemical Society.
4.19. Other vibrational frequency maps
The alcohol OH-stretch mode was treated quite successfully486,487, assuming that the frequency and dipole fluctuations are similar to those found in water and that the water map390 is a good approximation apart from an overall frequency shift. A mapping was developed for the OD-stretch of methanol in carbon tetrachloride488,489 using the electric field on deuterium, DFT frequencies, and a polarizable MD approach.
4.19.1. Alcohols
Semiempirical maps for the OH and OD stretching vibrations in alcohols were developed primarily in the electrochromic formulation with the electric field as a conjugate vibrational perturbation. In the map proposed by Mosele and Thompson,490 the relevant spectroscopic quantities are expressed in terms of the electric field exerted on the OH (or OD) group hydrogen atom by the surrounding neat liquid. Due to the substantial anharmonicity of the OH (OD) stretch vibration, anharmonic constants as well as the vibrationally excited state absorption frequency were parameterized with the functional form identical to the one in Eq. (109). Benchmark data were obtained by using the discrete variable representation (DVR) method for one-dimensional vibrational potential energy curves along OH (OD) stretch normal coordinate, obtained at the B3LYP/6–311++G** level of DFT approximation. It was found, by examining methanol, ethanol, n-propanol, and n-butanol, that the derived map is transferable and quite independent of the alkyl groups. IR Absorption spectra and reorientation time calculated for the isotopically diluted deuterated alcohols agreed well with experiment (FTIR and NMR data, respectively), in contrast to the 2D-IR photo echo spectra, in which the time scales of the spectral diffusion were overestimated.
4.19.2. Water bending mode
In addition to the water OH or OD stretch modes, the other water vibrational mode whose frequency is also sensitive to local H-bonding environment is the HOH bending vibration.491–504 Vibrational spectroscopy of the water bending mode has also been performed to establish the relationship between the lineshape of water bend and the H-bonding network structure of water in solution.492–501 Ni and Skinner, using a hybrid quantum/classical MD simulation method, calculated the theoretical IR and sum-frequency generation spectra of the HOH bend in liquid water as well as at the water liquid/vapor interface. They carried out classical MD simulation and took into consideration the three-body interactions to describe the air-water interface. Ni and Skinner developed the maps for water bend transition frequency, dipole, polarizability, and intermolecular coupling. The good agreement between their calculated IR and SFG spectra and the experimental measurements indicate the validity of their vibrational spectroscopic maps.
4.19.3. Mapping of strongly coupled vibrations
As has been discussed in detail above, vibrational frequency mapping approaches work best for localized modes that have relatively weak coupling to both the environments and to other local modes. In addition to water (both H2O and D2O), there are useful vibrational transitions where the spectroscopic modes are delocalized over many atoms, such as phosphate (—OPO2O—) and carboxylate (—COO−) organic species, as well as numerous organometallic complexes containing transition metal carbonyls, cyanides, and nitrosyls. Mapping approaches for these systems are much less advanced and need developments. A key step in that direction has been the detailed decomposition of the delocalized anharmonic modes into local modes, which are more physically amenable to electrostatic mapping procedures. Baiz et al.,505 computed anharmonic vibrational modes of two transition metal complexes, rhodium(acetylacetonato)dicarbonyl (RDC) and dimanganese decacarbonyl (DMDC). These anharmonic modes were recast in a basis of local modes described as Morse oscillators, with only bilinear coupling among these local modes. The advantage of this method is that the vibrational anharmonicity for the coupled states is obtained automatically. Explicitly including the effects of H-bonding by treating clusters containing methanol, it was possible to deduce that the H-bonding effects are additive, though their impact is delocalized within the coupled modes. These kinds of considerations will be important not only for solvation probes but also for using MD simulations to help interpret reactive motions that induce spectral diffusion,506,507 as well as to establish links between environmental factors and intramolecular vibrational energy redistribution,507,508 and coherence transfer dynamics.509–511 The extension of frequency mapping to strongly coupled vibrations will enable a more broad adoption of these methods to widely used chemical probes such as methyl groups and aromatic rings.
5. Repository, Perspective, and a few Concluding Remarks
5.1. Vibrational frequency map repository
Because of the rapidly growing number of vibrational frequency maps reported in the literature, it is desirable and useful to collect all those maps and make them available to everyone interested in utilizing them for their researches. Therefore, we have created a repository internet site, http://frequencymap.org/, for voluntary deposition of vibrational frequency map files by the developers themselves and for downloading of those files by the users. In addition to free deposition and downloading of vibrational frequency map files, this site can be considered as an internet forum for discussing and updating recent developments and news in this research field. Any map file that is to be uploaded should contain information on the vibrational mode, such as CO stretch or HOH bending, in addition to the parameters constituting the map. Users have free access to those deposited files.
5.2. Format of the deposited map file
Various research groups developing vibrational frequency maps tend to use their style of data files. To make the repository site useful among the researchers in this field, however, it is necessary to have a common standard format for all the deposited files. In addition to vibrational frequencies, some maps have also been developed for other vibrational properties, such as vibrational transition dipoles and polarizabilities, or coupling between two neighboring local vibrations. Therefore, each map file should essentially contain the following three elements: (i) the identity of the molecule, the vibrational mode, and its property, e.g., frequency shift, for which the map is developed, (ii) the structural information on the molecule concerned and the interaction sites (the number of those sites and their locations) at which perturbations should be calculated, and (iii) the parameter values for mapping those perturbations to the properties. Each map file is a plain text file with the extension ‘.vbm’ denoting a ‘vibration map’. It consists of sections whose titles start with the ‘%’ character. The details of the format defined for each of the three elements of the vbm file are explained in Supporting Information.
5.3. New approaches based on genetic algorithm, neural network, and machine learning
In recent publications in the field of chemistry, we observe an increasing number of reports employing machine learning approaches in calculating energy and other physicochemical properties of molecular systems. The total number of possible small organic molecules that populate ‘chemical space’ has been estimated to exceed 1060.512 To find or design molecules or materials having desired quantum mechanical properties, machine learning approaches have been actively employed to avoid computationally demanding methods of electronic structure calculations. Recently, Faber et al513 assessed performances of various machine learning methods such as Bayesian ridge regression, elastic net regularization,514 kernel ridge regression,515 graph convolution,516 and gated graph neural networks517 in modeling electronic ground-state properties of organic molecules such as free energies and enthalpies of atomization, HOMO/LUMO gap, dipole moment, static polarizability, zero-point vibrational energy, heat capacity, and highest fundamental vibrational frequency. Their work shows numerical evidence that, even though there is no single machine learning model that works superbly for all the considered cases, the best machine learning model for each considered property reaches the accuracy of density functional theory at the B3LYP level.
Another active area in which machine learning methodology has been receiving considerable attention is the computational study using MD simulation methods. Classical MD uses MM force fields to calculate the energies and forces for a large number of atomic configurations, but the results of the MD simulations depend greatly on the accuracy of the molecular potentials and their parameters. Employing electronic structure calculations in ab initio MD simulation can remove the force field dependence of the simulation results, but considerably reduce the size and time of the simulation. Machine learning models of potential energy surface of molecular or solid-state systems can achieve the accuracy of the electronic structure method with the efficiency of the classical force fields MD. The conventional force fields in MD simulations have limitations in treating reactive events of breaking and forming of chemical bonds due to the fixed functional forms employed in the MM force fields. Even for the cases of simulating nonreactive dynamics, the classical force fields having the potential energy functions constructed under various physical approximations have difficulties in treating the polarization and charge transfer effects. Machine learning methods make it possible to construct potential energy surfaces that are not restricted by any functional form based on physical approximations and can describe polarization, charge transfer, and reactive processes with accuracy approaching that of electronic structure calculations.
Highly reliable potential energy surfaces are also an essential prerequisite for obtaining accurate values of vibrational frequency shifts. Methods using vibrational frequency map to calculate the frequency shifts assume a specific functional form to relate the geometrical configurations of the solute-solvent system to the vibrational frequency shifts. The parameters in functions of fixed form are obtained by fitting to electronic structure calculations or experimental spectra. Although the information of the multidimensional potential energy surfaces can be incorporated in the process of constructing the frequency maps by the fitting procedure, these maps are limited by the assumptions on the dominating factors among various types of interatomic interactions. Machine learning approaches can provide the possibility of constructing mappings from geometry to vibrational frequency shifts incorporating the information of the potential energy surfaces without the limit of preassigned functional dependencies.
In this regard, it is pertinent, as the first step toward machine learning schemes for vibrational frequency shifts, to try to develop a model of vibrational frequency shifts, which is not constrained by any preliminary set of assumptions about the physical nature of the factors inducing the frequency shifts. Recently, Kwac and Cho showed that a differential evolution algorithm approach, which is one of the genetic algorithms for global optimization, is useful for describing vibrational solvatochromism.518 In their model, the solvation-induced vibrational frequency shifts are expressed as a polynomial function expanded by the inverse power of interatomic distances.
| (118) |
where A and B denote the interaction sites of the solute and solvent molecules, respectively. M is the order of the polynomial, W is the number of solvent molecules for each configuration of the solute-solvent clusters. We obtain the coefficients using the frequency shifts calculated by quantum chemistry methods for a set of clusters of a solute molecule surrounded by solvent molecules, where the set of clusters can be considered as a training data set. The crucial step in this model is to represent the frequency shift Δω by a sum of the contribution Δωn which is due to the 1/rn interaction term only so that
| (119) |
| (120) |
where 0 ≤ cn ≤ 1 and . Then for a given set of values {c1, … , cM} , we solve the following M equations for Δωn by singular value decomposition
| (121) |
We use thus obtained coefficients to calculate the root mean square error (RMSE) defined as
| (122) |
where S is the number of configurations. Δωpredict(k) is the frequency shift calculated by Eq. (118) for the kth configuration. ΔωQM(k) is the frequency shift calculated by quantum chemistry calculation methods. The whole process from the selection of {c1, … , cM} to the calculation of dRMSE in Eq. (122) can be regarded as a function H whose input is {c1, … , cM} and the output is dRMSE such that
| (123) |
This procedure is schematically shown in Figure 24.
Figure 24.
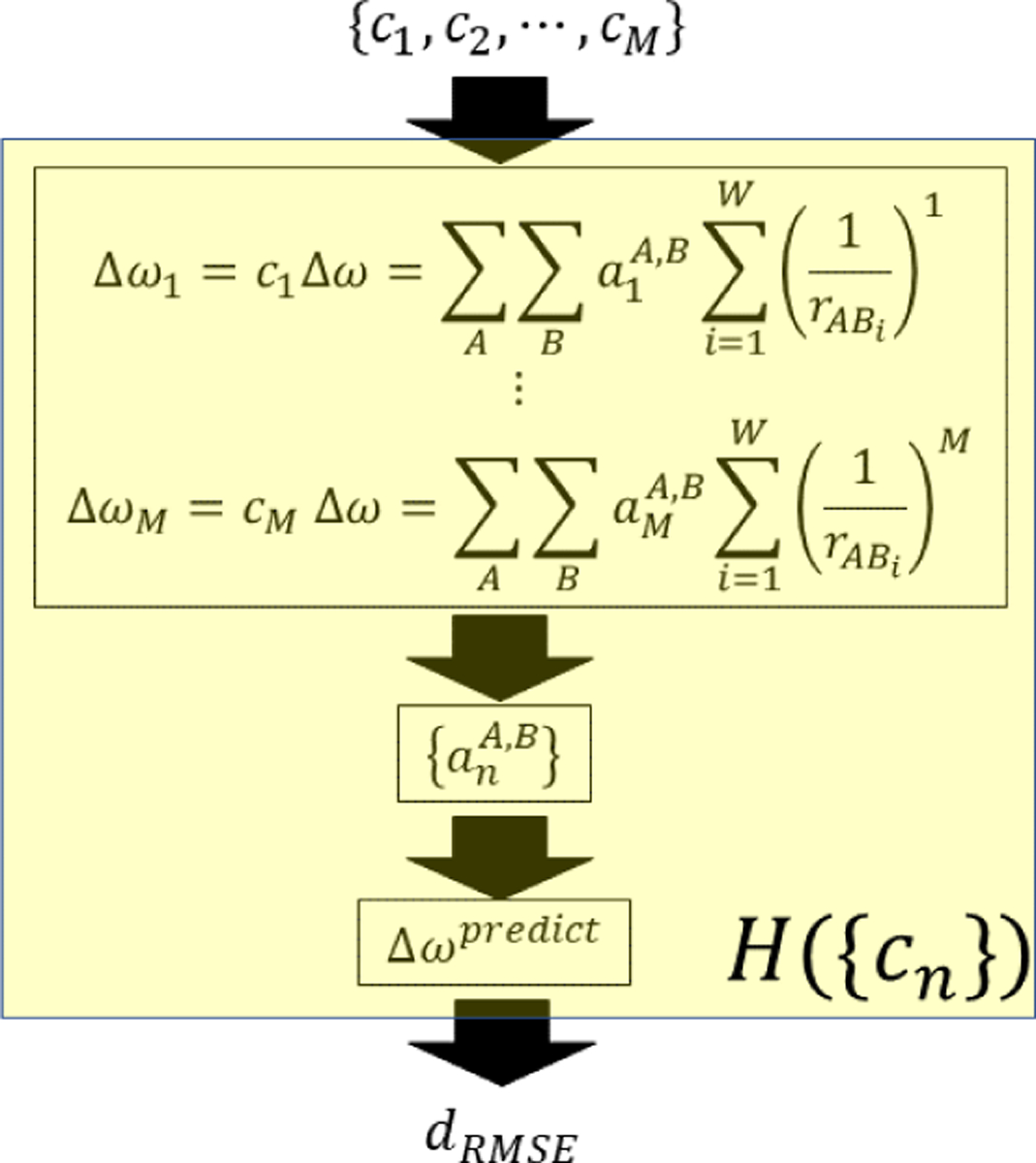
Schematic diagram of the procedure from the relative contributions cn to the RMSE value, dRMSE.
We employ a differential evolution algorithm (DEA)519,520 to optimize the function H with respect to {c1, … , cM}, thereby we obtain the coefficients that minimize the value of dRMSE. Differential evolution algorithm is one of the genetic algorithms that have been developed to solve optimization problems by employing an evolutionary mechanism in biology. In the differential evolution approach, one generation evolves into the next generation by mutation, crossover, and survival of the fittest. This evolutionary mechanism tries to find the optimum partitioning of the contributing terms in the model to reproduce as closely as possible the vibrational frequency shifts of the configurations in the training set that plays a role much like an environment inducing evolutionary development in biology. This differential evolution algorithm has been applied to the vibrational frequency shifts of the amide I and II modes of NMA in water and the CN stretch mode of MeCN in water using a 14-order polynomial (M = 14) and considering about five hundred configurations of the solute-solvent system as a training set. The results of optimization with the differential evolution algorithm are such that only a few selected orders of terms dominate the contribution to the frequency shifts, and the remaining terms are virtually zero. The dominating orders of the terms in the polynomial are different depending on the vibration mode of interest. The dominating orders of the terms are also susceptible to the size of the configurations used in the training set, as shown in Figure 25 where ‘1W’, ‘2–5W’, ‘6–35W’, and ‘50W’ denote the configurations having one water, 2–5 water molecules, 6–35 water molecules and 50 water molecules, respectively. The fifth panel in Figure 25 shows the relative contributions {cn} when all the four types of configurations are used in the training set. Since the genetic algorithm employed in this work is not based on any physical assumption, we could not interpret each nominating terms as originating from a specific type of physical interaction. However, regardless of the sensitive change according to the type of the training set, a general trend is observed that only two to four selected orders are the dominating ones, and these dominating orders are distributed so that usually one order occurs in each of low range, middle range, and high range orders in all cases of vibration mode considered in this work.
Figure 25.
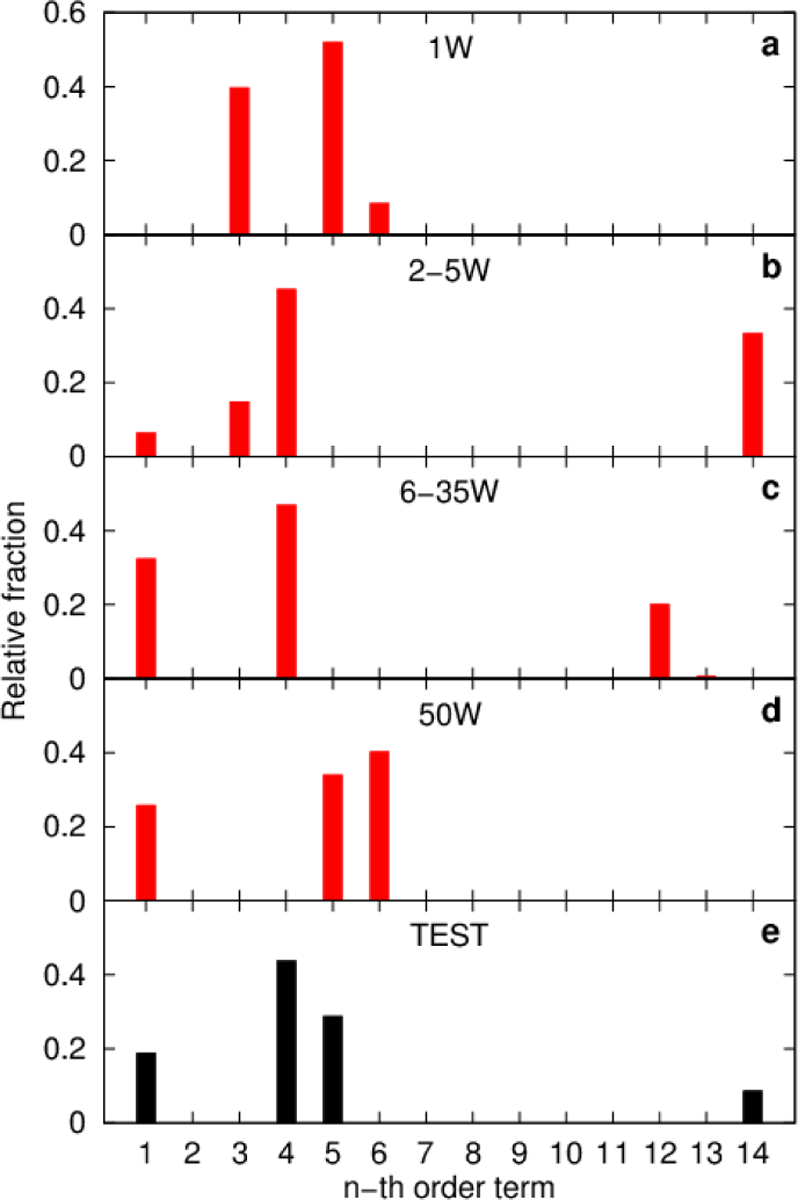
(a-d) Magnitude of relative contributions ci when we use as a training set (a) 1W, (b) 2–5W, (c) 6–35W, and (d) 50W set. (e) Relative contributions ci for the training set of the study in Ref.518 Reproduced from Figure 10 of Ref.518. Copyright 2019 AIP Puplishing.
The observation that only a few orders of the terms in the polynomial model dominate the contribution to the frequency shift while the other terms with different orders are nearly zero can be understood from the viewpoint of the complexity of the model. Having a larger number of parameters in a model is equivalent to having a more complex model. The complexity resulting from the differential evolution algorithm corresponds to the four dominating orders terms in the polynomial in the case of the amide I mode of NMA in water, which is very similar in complexity to the result obtained by a rigorous first-principles theory.154 In the previous studies on the vibrational frequency shifts based on various physical assumptions, the complexity of the model was prefixed by assuming that specific types of interactions such as electrostatic, dispersion, or repulsion are the origins of the vibrational frequency shift. In the paper by Kwac and Cho who applied the DEA to the development of vibrational solvatochromism theory, both the complexity of the model and the parameters therein are optimized simultaneously, and this is one of the most significant differences from the previous studies that are strictly based on various prefixed physical approximations. We anticipate that this work can be a first step toward further developing different genetic algorithms and machine learning schemes for applying to vibrational spectroscopic studies.
In a recent paper by Kananenka et al.,414 an attempt to go beyond the spectroscopic maps in modeling spectroscopic properties of a vibrational mode was made by adapting machine learning methodologies called the Gaussian process regression521 and Δ -machine learning.522 In their approach, a property P[{Q}] of a vibrational mode, such as the vibrational frequency or transition dipole, dependent of the local chemical environment Q, is provided by
| (124) |
where Pb[{Q}] is the baseline estimate of P[{Q}] provided the already established vibrational frequency maps, and is a correction modeled using an ML method. Specifically, in their work, OH-stretch frequencies and transition dipoles of water were considered by describing the local chemical environment Q using the atom-centered symmetry functions.523,524 They prepared a data set consisting of 40000 configurations of water molecules and corresponding OH stretch frequencies and transition dipoles obtained by DFT calculations on the grids of varied OH bond lengths. The production of this large-sized data set was possible because they reduced the number of necessary grid points for DFT calculation by interpolating the potential energy surface using the method of Gaussian process regression. The correction term in Eq. (124) is estimated by training the feed-forward artificial neural network (ANN) with one hidden layer containing 100 nodes. The results are summarized in Figure 26. The resulting root mean square errors in transition frequency of the OH-stretch local mode is improved from 63.4 cm−1 of the spectroscopic maps to about 35 cm−1 by employing the Δ -machine learning approach. The RMSE of 0.0730 a.u. of the dipole derivative of the OH-stretch mode by the spectroscopic maps is reduced to as low as 0.0283 a.u. by the Δ -machine learning approach. We anticipate that the genetic algorithm and machine learning approaches will be useful for developing novel computational methods to calculate various vibrational spectroscopic properties.
Figure 26.
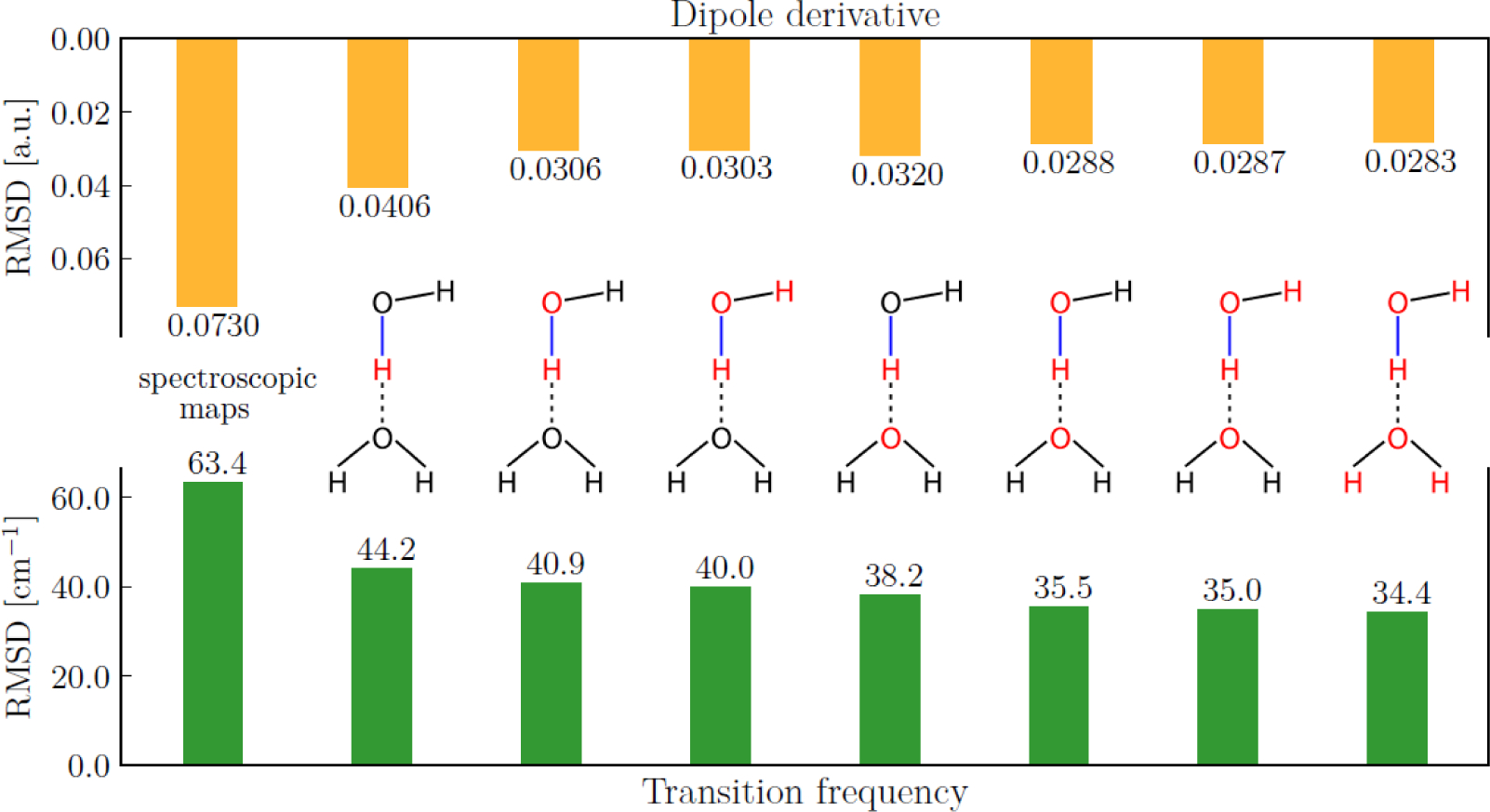
RMSE in transition frequency and dipole derivative of the OH-stretch (blue line) local mode depending on which atoms’ local chemical environment is used as an input to ANN (marked in red). The leftmost set of bars corresponds to RMSEs of the spectroscopic maps developed in Ref413, all others correspond to the Δ -ML approach of ref. (Adapted from Figure 2 of Ref.414) Copyright 2019 The American Chemical Society.
In a recently published paper by Kwac and Cho,525 the authors tried to directly apply machine learning approaches in describing vibrational solvatochromism without employing any established vibrational frequency maps. In that work, the authors employed the feed-forward and the convolutional neural networks to describe the frequency shifts of the amide I mode vibration of NMA in water and assessed the performance of neural network models by comparing the results with those of the differential evolution algorithm approach using the same data sets. The data sets contain snapshots of molecular dynamics simulation trajectories where a single NMA molecule is surrounded by more than a thousand of water molecules. The corresponding frequency of the amide I mode of NMA for each configuration is calculated by a QM/MM method treating a selected number of nearest water molecules to the NMA molecule with QM method and the remaining water molecules by classical force fields.
In applying ML methods to describe vibrational solvatochromism, it is important to employ a suitable set of descriptors that properly represent the configuration of the solute and solvent molecules and simultaneously satisfy translation, rotation, and permutation symmetry. In that work, the authors tried two different representations of configurations of NMA in water: one is the atom centered symmetry functions (ACSF),523,524 which have been successfully employed in previous ML molecular dynamics simulations, and the other is the terms of a polynomial function of the inverse of interatomic distances already used in the DEA approach.
The ACSFs consist of two-body radial and three-body angular symmetry functions whose distance dependence is described by a Gaussian function. In that work, two sets of ACSFs, denoted as ACSF-I and ACSF-II, which have different parametrization so that the position and width of the Gaussian functions, the behavior of decay to zero, the angular resolution and the position of the extrema are different between the two sets. When feed-forward neural networks having one or two hidden layers are employed to describe the amide I mode vibrational frequency shifts of NMA in water using the carbonyl C atom of NMA and the O atom of water as the interaction sites, any noticeable difference in the performance is not observed between the ACSF-I and ACSF-II symmetry functions. In both cases, the obtained test RMSE value is about 18 cm−1. In contrast, a significant improvement is observed by considering more of the interaction sites on the NMA and water molecules. If we consider 6 sites (two methyl carbon and the C, O, N, H atom of the amide bond) on NMA with the oxygen and hydrogen sites of water, the test RMSE values are 11.8 and 11.1 cm−1 for ACSF-I and ACSF-II, respectively.
Next, the authors in that paper considered the terms of the polynomial function as descriptors to be input to the feed-forward neural network. By considering the six sites on NMA, two sites, O and H atoms, on water, and up to 14-order terms of the polynomial functions, each of which has a form of
| (125) |
where A represents one of the six sites of NMA and Bi does O or H atom of ith water molecule, is the distance between A and Bi, and n is an integer between 1 and 14, the authors obtained the optimized parameters of the feed forward neural network to give the test RMSE of 8.91 cm−1, which is an improved result compared to the atom centered symmetry functions, ACSF-I and ACSF-II, employed in that work. In addition to the feed forward neural network, the authors in that paper also tried the convolutional neural network (CNN),526 which has been successfully applied to image processing. They prepared the input of the CNN as a form of matrix or third-rank tensor with the third dimension to be unity using the terms of the polynomial function, as shown in Figure 27(a). Figure 27(b) shows the process of the training of the neural networks using a plot of the training and the validation RMSE as a function of the elapse of epochs where one epoch corresponds to one cycle of processing all the data in the training set to update the parameters of the network. The optimized parameters at the epoch of the minimum validation RMSE give the test RMSE of 8.56 cm−1, which is an improved result compared to the differential evolution algorithm result. Thus it is shown that the neural network models for vibrational solvatochromism can work better than the DEA method for the case of the amide I mode of NMA in water.
Figure 27.
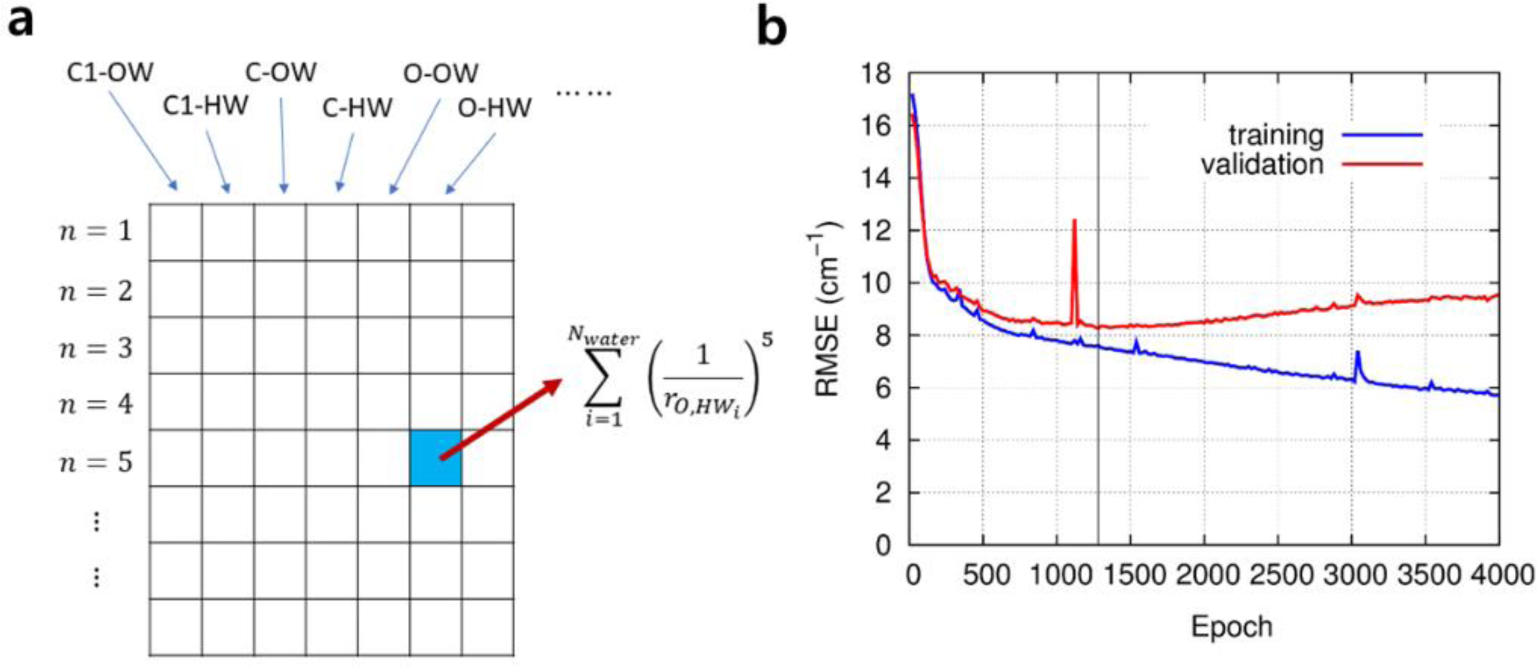
The plot of the training and the validation RMSE values as a function of elapsed epochs in the training of the feed forward neural network model with the unscaled terms of the polynomial function. Adapted from Figures 7 and 8(a) of Ref.525 Copyright 2020 AIP Puplishing.
5.4. Perspective
In solutions, the spectator molecule in question is often solvated by a relatively small number of polar solvent molecules that create varying electrostatic potential.188,221,233 The perturbing fields can also be applied in many directions.227–231,235 It is also possible to account for molecular anharmonicity when the model gas-phase Hamiltonian with a polynomial expansion of anharmonic potential is used and perturbed by external electric fields.231 Subsequent multivariate least-square analyses of these model systems are then performed to obtain the vibrational solvatochromic parameters (or maps) for a given IR probe molecule, from which the benchmark results could be reproduced. There are a few reports showing that the vibrational map parameters associated with the electrostatic potential or electric field can achieve a high degree of transferability between solvent or even solute molecules, without the need of additional re-parameterization.111,226,231,236 However, it is not clear to what extent the universality is preserved, especially when the change of environment is drastic. For example, put a probe in a completely non-polar solvent such as CCl4 that has no net molecular dipole moment. Since CCl4 molecules are rather unlikely to exert strong electrostatic fields around the IR probe one might expect very small frequency shifts. But the examples of MeCN and MeSCN probes dissolved in this solvent show very pronounced frequency redshifts that are roughly – 10 cm−1 relative to that in the gas phase, which is, in magnitude, comparable to frequency shifts in water. This is just one example showing the limitation of current approaches based on physical approximations. Although electrostatic maps have proven to be a powerful and efficient way to simulate IR spectra of various IR probes in solutions and highly heterogeneous environments like proteins or nucleic acids, still it is necessary to refine theoretical models that are capable of describing vibrational spectroscopic properties and dynamics of complex molecules accurately.
Artificial intelligence (AI) and machine learning (ML) approaches527,528 can be employed in developing more accurate models of vibrational solvatochromism with similar advantages as the differential evolution algorithm since those ML methods are free from any preliminary physical assumptions. Another advantage of the ML approach is the flexibility in that we model the molecular interactions in a non-analytical form so that the functional form of the model is also optimized. One challenging question is how to control or optimize the complexity of models as in the differential evolution algorithm to avoid the pitfall of overfitting in ML approach to model vibrational solvatochromism. Another challenge is about how to reduce the size of the training data set since the necessary number of sample configurations in ML approaches can be significantly larger than that in the previous studies of frequency maps obtained using physical approximations. One of the other possibilities employing ML is not directly modeling the vibrational frequency shifts, but modeling the closely related quantities such as molecular dipole or polarizability using ML approach and calculate the vibrational spectrum from these quantities.529 Finally, there is an issue about how and what kind of physical insights we can extract from such ML models of vibrational solvatochromism, even though the procedures of the ML approach are driven solely by data in training sets without any physical assumptions.
5.5. Summary and a few concluding remarks
In the present article, we have reviewed both the theoretical and experimental works on vibrational solvatochromism, vibrational spectroscopy, and their relations with intermolecular interactions. Over the past two decades, technological developments in coherent nonlinear vibrational spectroscopy such as multidimensional electronic, IR, THz, IR-Raman, IR-vis, vis-IR, and THz-Raman measurement methods have enabled to extract solvation-induced frequency shifts and time-correlation of fluctuating frequencies of IR probes that are site-specifically incorporated into a variety of chemical, biological, and material systems. Due to the increased number of IR probes and time-resolved vibrational spectroscopic data sets, interpretive methods with atom-level chemical accuracy have been needed and developed. Some of them are based on physical approximations, but more recent works show that using a genetic algorithm, vibrational solvatochromism can be described without relying on physical approximations.
One of the most successful approaches to quantitatively describing vibrational solvatochromic effects on molecular spectra is to use a vibrational frequency map for a specific IR probe of interest, which is a semiempirical model using a set of ab initio calculations results or spectroscopic data. Recently, a website (http://frequencymap.org) has been created as a repository site for vibrational frequency maps that have been successfully used to quantitatively describe vibrational frequency shifts and fluctuations of various peptide modes, small IR probe oscillators incorporated into proteins and functional materials, and so on. Although the theoretical development of various vibrational frequency map approaches is mainly motivated by experimental needs, rapid developments of vibrational frequency maps of localized modes of molecules in condensed phases, vibrational coupling maps for interacting vibrational modes, and vibrational transition dipole/polarizability maps for determining the corresponding IR/Raman transition amplitudes developed over the past decades have been found to be amazing. There is no doubt that judicious use of vibrational frequency map approaches with state-of-the-art coherent multidimensional vibrational spectroscopy will be one of the most useful methods for studying structure and dynamics of chemical, biological, and functional molecular systems in the future.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported by IBS-R023-D1 (MC). BB wishes to thank the European Union’s Horizon 2020 under the Marie Skłodowska-Curie Grant Agreement No. 665778, as well as the National Science Centre, Poland (grant no. 2016/23/P/ST4/01720). CRB acknowledges generous support from the National Science Foundation (CHE-1847199, BIO-1815354), the National Institutes of Health (R35GM133359), and the Welch Foundation (F-1891). MWDHH and JDH thank the University of Nottingham, Green Chemicals Beacon for funding toward this research. MCT acknowledges support from Department of Energy (DE-SC0018983), National Science Foundation (1552996), and National Institutes of Health (GM114500). AGD would like to thank Prof Andrei Tokmakoff for discussing amide modes when he was a PhD student. LW acknowledges the support from the National Institutes of Health through Award R01GM130697. SAC acknowledges support from National Science Foundation (CHE-1565471)
6. Glossary of Acronyms
- 1D
one-dimensional
- 2D
two-dimensional
- 2D IR
two-dimensional infrared
- 2D SFG
two-dimensional sum-frequency generation
- AcGlyNHMe
N-acetyl-glycine N’-methylamide
- AcProNH2
N-acetyl-L-prolinamide
- AI
artificial intelligence
- ANN
artificial neural network
- AO-MO
atomic orbital-molecular orbital
- BP
Buckingham potential
- CaM
calmodulin
- CAMM
cumulative atomic multipole moment
- CDCl3
deuterated chloroform
- CLS
center line slope
- CMD
classical molecular dynamics
- COSMO
conductor-like screening model
- CP1
Cho-Potential model 1
- CP2
Cho-Potential model 2
- DCBS
dimer-centered basis set
- DEA
differential evolution algorithm
- DEC
diethyl carbonate
- DFT
density functional theory
- DMC
dimethyl carbonate
- DMDC
dimanganese decacarbonyl
- DMSO
dimethyl sulfoxide
- DNA
deoxyribonucleic acid
- EA
excited state absorption
- EC
ethylene carbonate
- EFP
effective fragment potential
- ESF
electrostatic fitting
- FFCF
frequency-frequency correlation function
- FWHM
full width at half maximum
- GB
ground state bleaching
- GFP
green fluorescent protein
- GSE
geometrical superposition error
- H-bond
hydrogen-bond
- HF
Hartree-Fock
- hIAPP
human amyloid polypeptide
- HMR
Hessian matrix reconstruction
- HP35
villin headpiece protein
- IR-Raman
infrared-Raman
- IR-vis
infrared-visible
- IR
infrared
- KBM
Kirkwood-Bauer-Magat
- KF1
Knoester-Field model 1
- KF2
Knoester-Field model 2
- KT
Kamlet-Taft
- LCAO-MO
linear combinations of atomic orbitals
- LIB
lithium ion battery
- LJ
Lennard-Jones
- LMO
localized molecular orbital
- MCBS
monomer-centered basis set
- MD
molecular dynamics
- MeCN
acetonitrile
- MeSCN
methyl thiocyanate
- ML
machine learning
- MM
molecular mechanics
- MS-EVB
multi-state empirical valence bond
- NEP
non-linear exciton propagation
- NEPA
N-ethylpropionamide
- NISE
numerical integration of the Schrödinger equation
- NLS
nodal line slope
- NMA
N-methylacetamide
- NMA-d7
deuterated N-methylacetamide
- NMP
nucleoside 5’-monophosphate
- NMR
nuclear magnetic resonance
- NN
nearest neighbor
- NNFS
nearest neighbor frequency shift
- NTBA
2-nitro-5-thiocyanate benzoic acid
- OQM/MM
optimized quantum mechanics/molecular mechanics
- PC
propylene carbonate
- PCM
polarizable continuum model
- PE
photon echo
- PEPS
photon echo peak shift
- PheCN
cyanophenylalanine
- PII
polyproline II
- PM3
Parametric Method 3
- PP
pump-probe
- QM
quantum mechanics
- RDC
rhodium(acetylacetonato)dicarbonyl
- RHH
right-handed helix
- RMSE
root mean squared error
- RNA
ribonucleic acid
- SAPT
symmetry adapted perturbation theory
- SE
stimulated emission
- SFG
sum-frequency-generation
- SolEDS
hybrid variational-perturbational interaction energy decomposition scheme
- SolEFP
vibrational solvatochromism theory based on the effective fragment potential theory
- TCC
transition charge coupling
- TDC
transition dipole coupling
- TFA
trifluoroacetic acid
- TFE
trifluoroethanol
- THz-Raman
terahertz-Raman
- THz
terahertz
- Tw
waiting time
- VCD
vibrational circular dichroism
- vdW
van der Waals
- vis-IR
visible-infrared
- VSE
vibrational Stark effect
- VSFG
vibrational sum-frequency generation
- VSM
vibrational solvatochromic maps
- WCA
weak-coupling approximation
Biographies
Carlos R. Baiz is a faculty member at the University of Texas at Austin. His lab studies the biophysics of complex systems such as heterogeneous lipid membranes and membrane proteins using ultrafast two-dimensional infrared spectroscopy and molecular dynamics simulations. His group also develops vibrational models, including frequency maps to connect experiments with simulations. He has a Ph.D. in Chemistry from the University of Michigan where he worked in the lab of Prof. Kevin Kubarych and postdoctoral training at MIT and University of Chicago with Prof. Andrei Tokmakoff.
Bartosz Błasiak was born in Oleśnica, Poland in 1988. In 2012, he received his M.S. in chemistry from Wroclaw University of Technology in Wrocław, Poland. He did his PhD studies at Korea University, Seoul, Korea, which he graduated in August 2016. In 2017, he was a post-doctoral fellow in Institute for Biophysics at Goethe University Frankfurt. Currently, he is an assistant professor in the Department of Physical and Quantum Chemistry at Wroclaw University of Science and Technology, Poland. He is interested in developing quantum chemistry and theoretical methods for the description of extended molecular aggregates and molecular spectroscopy.
Jens Bredenbeck obtained his Diploma in chemistry in 2000 with Reinhard Schinke (MPI for Flow Research, Göttingen) and his Dr. sc. nat. in 2005 with Peter Hamm (Max Born Institute of Nonlinear Optics, Berlin, and University of Zurich). After postdoctoral research with Mischa Bonn (AMOLF, Amsterdam) he received the Sofja-Kovalevskaja Award of the Humboldt-Foundation and established his group at Goethe University, Frankfurt, in 2007. Since 2010 he is a full professor of Experimental Biophysics and Chemical Physics at the Institute of Biophysics of Goethe University. His research explores molecular structure and dynamics over a wide range of time scales and the development of nonlinear vibrational spectroscopies and spectroscopic probes.
Minhaeng Cho is the director of the IBS Center for Molecular Spectroscopy and Dynamics, established in Dec. 2014 and Professor of Chemistry at Korea University, Seoul, Korea, since 1996. He grew up in Seoul, where he attended the public schools. He received his B.S. and M.S. from Seoul National University in 1987 and 1989, respectively, before studying in the U.S. A. where he received his Ph.D. in 1993 from the University of Chicago. He returned to Korea in 1996 as an Assistant Professor at the Korea University after a two-year post-doctoral research experience at MIT, Cambridge, USA. He became a full Professor at the Korea University in 2003 before his directorship with IBS in 2014. IBS Center for Molecular Spectroscopy and Dynamics (CMSD), located in the Seoul campus of Korea University, emphasizes developments of novel time- and space-resolved spectroscopy techniques and their applications to chemically reactive and biologically important systems. He is a member of the Korean Academy of Science and Technology (KAST) and received numerous awards given by the American Chemical Society, National Science Foundation in Korea, KAST, Kyung-Am Science Foundation, and National Academy of Science in Korea.
Jun-Ho Choi has been on the faculty of Gwangju Institute of Science and Technology since 2018. He received a B.S., M.S., and Ph.D. in chemistry from Seoul National University in 1990, 1992 and 1996 and worked as a research professor at the IBS Center for Molecular Spectroscopy and Dynamics from 2014 to 2018. His research interests are computational spectroscopy and computer-aided molecular design.
Steven A. Corcelli is a theoretical chemist whose research focuses on the structure, dynamics, and spectroscopy of molecular and biomolecular solutes in solution. He graduated from Brown University in 1997 (Sc.B. in Chemistry). In 2002, he was awarded a Ph.D. from Yale University where he trained with Dr. John Tully. From 2002 – 2005, he was a postdoctoral scholar with Dr. Jim Skinner at the University of Wisconsin-Madison. Dr. Corcelli began his independent academic career in 2005 at the University of Notre Dame, where he has been the grateful recipient of several awards, including the Camille and Henry Dreyfus New Faculty Award, an NSF CAREER Award, a Sloan Research Fellowship, and twice the Rev. Edmund P. Joyce, C.S.C. Award for Excellence in Undergraduate Teaching.
Arend G. Dijkstra received his Ph.D. from the University of Groningen in the Netherlands, where he worked on nonlinear vibrational spectroscopy of peptides supervised by Profs Jasper Knoester and Thomas la Cour Jansen. He then performed postdoctoral work with Profs Yoshitaka Tanimura in Kyoto, Jianshu Cao at MIT and R. J. Dwayne Miller in Hamburg, before starting his group as a University Academic Fellow at the University of Leeds. His work has focused on the theoretical description of light-induced ultrafast processes in large molecules and materials.
Chi-Jui Feng received a B.Sc. in chemistry from National Taiwan University in 2013, working on structure-based modeling of excitation energy transfer dynamics in pigment-protein complexes, under the supervision of Prof. Yuan-Chung Cheng. He is a Ph.D. candidate from University of Chicago under the supervision of Prof. Andrei Tokmakoff, working on dynamics of coupled folding and binding processes in protein recognition using two-dimensional infrared spectroscopy and amide I computational spectroscopy.
Sean Garrett-Roe received his B.S in Chemistry from Princeton University (1999) and his Ph.D. from the University of California, Berkeley (2005). From 2006 to 2011, he was a postdoctoral scientist at the University of Zurich with Prof. Peter Hamm. Sean joined the chemistry department of the University of Pittsburgh as an assistant professor in 2011 and was promoted to associate professor with tenure in 2018. At Pitt, his research has focused on ultrafast vibrational spectroscopy (2D-IR) of ionic liquids. He has published over 40 peer reviewed journal papers. He was awarded the Chancellor’s Distinguished Teaching Award (2017).
Nien-Hui Ge is a Professor of Chemistry at the University of California at Irvine. She received her B.S. and M.S. from National Taiwan University, working on NMR spectroscopy of quadrupolar nuclei. She received her Ph.D. from the University of California at Berkeley in the group of Prof. Charles Harris in 1998, focusing on two-photoemission spectroscopy of metaldielectric interfaces. During her post-doctoral research in the Robin Hochstrasser group at the University of Pennsylvania, she was involved with the development of coherent two-dimensional infrared spectroscopy. She joined UC Irvine in 2002 and received National Science Foundation CAREER award in 2005. Her current research focuses on the study of chemical, biological, and material processes using a combination of ultrafast spectroscopy and microscopy (2D IR, SFG, s-SNOM) and plasmonics.
Magnus Hanson-Heine is a research fellow working in quantum chemistry at the University of Nottingham, where he received his Ph.D. in 2010. His research interests include method development for modeling molecular spectroscopy and vibrational dynamics, modeling molecular excited state behavior using DFT, and work simulating catalytic reaction pathways.
Jonathan Hirst is a Professor of Computational Chemistry at the University of Nottingham, where he has been since 1999. He received a BA from the University of Oxford in 1990 and was awarded a Ph.D. in 1993 from the University of London, based on his research conducted at the Imperial Cancer Research Fund. He moved to the USA in 1993, first to Carnegie Mellon University and then, with a Human Frontiers Science Programme Fellowship, to The Scripps Research Institute, La Jolla, becoming Assistant Professor in 1996. In 1999, he returned to the UK, to the University of Nottingham, becoming full Professor in 2004. He served as Head of the School of Chemistry from 2013 to 2017. His ongoing research includes applications of computational chemistry to the study of the structure, dynamics and spectroscopy of biological molecules and the development and application of computer-aided molecular design.
Thomas L.C. Jansen is working in the Zernike Institute for Advanced Materials at the University of Groningen, Groningen, the Netherlands since 2005. He grew up in Denmark and received his B.S. and M.S. in Chemistry from the University of Copenhagen in 1996 and 1998, respectively. He then moved to The Netherlands, where he received his Ph.D. degree cum laude from the University of Groningen in 2002. He then moved to University of Rochester, New York, United States, to work with Professor Shaul Mukamel. In 2003, he moved with the Mukamel group to the University of California at Irvine, Irvine, California. In 2005, he returned to the University of Groningen on a Dutch VENI grant and in 2008 he received a VIDI grant to continue his research then focused on the theory of infrared spectroscopy of proteins. His current research extends to the study of electronic spectroscopy and transport properties of biological and artificial systems with an emphasis on real-time dynamics and method development.
Kevin J. Kubarych is Professor of Chemistry and of Biophysics at the University of Michigan. Kevin has spent his scientific career developing and using multidimensional spectroscopy, starting with graduate research using 2D fifth-order Raman spectroscopy at the University of Toronto working with R. J. Dwayne Miller. After graduating in 2003, Kevin was a Human Frontier Science Program postdoctoral fellow at the CNRS Laboratoire d’Optique et Biosciences at Ecole Polytechnique where he worked with Manuel Joffre to develop upconversion IR detection and pulse-shaping based nonlinear spectroscopy. Since 2005, Kevin’s independent research group at the University of Michigan has used 2D-IR spectroscopy to study chemical dynamics in a variety of contexts, ranging from photocatalysis to interfacial protein hydration. He was a recipient of an NSF CAREER award and the Camille Dreyfus Teacher-Scholar award.
Kijeong Kwac received his B.S in chemistry education in 1992 and his M.S. and Ph. D. in chemistry from Seoul National University in 1994 and 2001, respectively. He worked as a postdoctoral researcher at universities in South Korea and the United States. He is a research professor at the IBS Center for Molecular Spectroscopy and Dynamics since 2018.
Casey H. Londergan is Chair and Associate Professor of Chemistry at Haverford College. He received his B.S. in Chemistry in 1997 from Williams College and his M.S. and Ph.D. in Chemistry in 2000 and 2003, respectively, from University of California, San Diego in the group of Clifford Kubiak. He was a NRSA Kirschstein postdoctoral fellow at the University of Pennsylvania in the group of Robin Hochstrasser. He received Henry Dreyfus Teacher-Scholar award, Cottrell College Science award, and NSF-CAREER Early Career Development award. He is a member of ACS, Sigma Xi, Biophysical Society, and Protein Society.
Hiroaki Maekawa was born in Osaka, Japan, and graduated from Kobe university with B.Sc. (1999) and M. Sc. (2001) degrees. He received his Ph.D. in 2004 from the same university under the supervision of Prof. Keisuke Tominaga. He is currently working as an associate specialist of Prof. Nien-Hui Ge’s group at the University of California, Irvine. His research interests include mid-infrared nonlinear spectroscopy, microscopy, and nanoscopy.
Mike Reppert received his BSc from Kansas State University in 2009. After a year as a Fulbright scholar at the Polish Academy of Sciences, he studied amide I two-dimensional spectroscopy under Andrei Tokmakoff at the Massachusetts Institute of Technology, completing his PhD in 2016. As a Banting postdoctoral fellow in the Chemical Physics Theory Group at the University of Toronto, he then worked with Paul Brumer to probe the similarities and distinctions between quantum and classical dynamics in ultrafast spectroscopy. He is currently an Assistant Professor of Chemistry at Purdue University, where his group develops new experimental and computational approaches to describing the optical and infrared properties of proteins and pigment/protein complexes.
Santanu Roy is a postdoctoral research associate in the Chemical Separations Group, Chemical Sciences Division, Oak Ridge National Laboratory (ORNL). He received his Ph.D. in Natural Sciences from the Center for Theoretical Physics, Zernike Institute for Advanced Materials, University of Groningen, The Netherlands in 2012. He was a postdoctoral research associate in the Department of Chemistry, University of Wisconsin at Madison (2012–2014) and at Pacific Northwest National Laboratory (2014–2017) before joining ORNL. His research expertise includes ab initio and force field-based molecular dynamics (MD) simulations, development of reaction rate theory, and modeling and simulation of different molecular spectroscopic measurements including two-dimensional infrared/sum-frequency generation, X-ray scattering/absorption, and neutron scattering for condensed phase systems. His experience and interests lie in a wide variety of research problems, including protein folding/misfolding, structures of elastic biopolymers, clean water and water in energy, mechanisms of ion-pairing, solvation, and chemical separation, molecular self-assembly, recovery of rare-earth minerals, and chemistry of molten salts.
Shinji Saito received his Ph.D. from The Graduate University for Advanced Studies in 1995. He worked at Nagoya University as Research Associate and Associate Professor for about 12 years. Since 2005, he has been Professor at Institute for Molecular Science. He has worked on dynamical and thermodynamic aspects in condensed phases theoretically and computationally. More specifically, he has been interested in spatiotemporally heterogeneous dynamics in (supercooled) water and reaction dynamics and functions in biomolecules.
James L. Skinner is the Crown Family Professor and Deputy Dean for Faculty Affairs at the Pritzker School of Molecular Engineering at the University of Chicago. He received his Ph.D. in Chemical Physics from Harvard in 1979, and started his academic career as an Assistant Professor at Columbia University in 1981. In 1990 he moved to the University of Wisconsin as the Joseph O. Hirschfelder Professor of Chemistry, and in 2017 he moved to his current position at the University of Chicago. He served for a decade as Associate and then Deputy Editor of the Journal of Chemical Physics, and was President of the Telluride Science Research Center in 2018. He was elected to the National Academy of Sciences in 2012 and has served on the Scientific Advisory Board of the Welch Foundation since 2015.
Gerhard Stock studied Physics at the Technical University of Munich (TUM) and got his doctorate 1990 with Professor Wolfgang Domcke. He spent 1991/1992 at the University of California, Berkeley with Professor William H. Miller as a postdoctoral fellow of the Deutsche Forschungsgemeinschaft (DFG). Back at the TUM, he worked as a DFG Habilitation fellow and obtained his Habilitation in 1996. From 1997 to 2000 he was a Heisenberg Professor at the Department of Physics at the University of Freiburg, before he moved to the Goethe University in Frankfurt am Main, where he held a full professorship in Theoretical Chemistry. Since 2009, he holds a Chair of Theoretical Physics (successor of John Briggs) at the University of Freiburg. His ‘Biomolecular Dynamics group’ aims to develop new theoretical and computational methods to model the dynamics and spectroscopy of complex molecular systems.
John E. Straub is Professor of Chemistry at Boston University. He received his B.S. in Chemistry in 1982 from the University of Maryland at College Park, where he worked with Millard Alexander on quantum scattering theory, and his Ph.D. in Chemical Physics in 1987 from Columbia University, where he worked with Bruce Berne on chemical research rate theory and simulation. He was a NIH Postdoctoral Fellow at Harvard University, where he worked with Martin Karplus on theory and simulation of protein dynamics, before joining the faculty of Boston University in 1990. His research explores the dynamics and thermodynamics of proteins, membrane, and complex molecular assemblies, as well as algorithmic development for optimization, enhanced sampling, and long-time dynamics. He has served as President of the Telluride Science Research Center (TSRC), Phi Beta Kappa National Visiting Scholar, and is an Associate Editor of The Journal of Chemical Physics.
Megan C. Thielges received her Ph.D. in biophysics at The Scripps Research Institute (La Jolla, CA) in 2009 and completed postdoctoral studies in multidimensional IR spectroscopy at Stanford University. In 2012, she joined the faculty at Indiana University and became an associate professor in 2018. Her primary research interests center around elucidating the conformations and dynamics of proteins and understanding how they are involved in function. In support of these goals, her research program aims to advance experimental methods of site-specific linear and multidimensional infrared spectroscopy for characterizing protein dynamics with high spatial and temporal detail.
Andrei Tokmakoff earned his B.S. in Chemistry from California State University in 1988. He went on to earn an M.S. and Ph.D., both in Chemistry and from Stanford University, in 1991 and 1995. He became an Alexander von Humboldt Research Fellow at Technical University Munich from 1995–96. Then, he was a National Science Foundation Postdoctoral Research Fellow at the University of Chicago, University of California Berkeley, and the Lawrence Berkeley National Laboratory. In 1998, he became a professor at MIT, eventually becoming Robert T. Haslam and Bradley Dewey Professor of Chemistry in 2012. He now serves as Henry G. Dale Distinguished Service Professor at the University of Chicago. He has received many awards, including the Coblentz Award, the National Fresenius Award, the Earle K. Plyler Prize for Molecular Spectroscopy & Dynamics, and the 2014 Ellis R. Lippincott Award from OSA.
Keisuke Tominaga received a B.Sc. (Kyoto University, 1985), M.Sc. (Kyoto University, 1987), and D.Sc. (Kyoto University, 1990). He was a postdoctoral fellow at the University of Minnesota (1990), a research associate at the Institute for Molecular Science (1992), an associate professor at Kobe University (1998), and a professor at the Molecular Photoscience Research Center, Kobe University (2001). His research focuses on time-resolved spectroscopy of condensed phases.
Hajime Torii is a professor at the Department of Applied Chemistry and Biochemical Engineering, Faculty of Engineering, and Department of Optoelectronics and Nanostructure Science, Graduate School of Science and Technology, Shizuoka University. He received his Ph.D. from the University of Tokyo in 1992. After working as a research associate at the University of Tokyo, he moved to Shizuoka University in 2001 as an associate professor (PI), and was promoted to a professor in 2008. He had been the chair of the Japanese Molecular Liquids Group (JMLG) from 2010 to 2019. His present research interests focus on theories and computations on intermolecular interactions, structures, dynamics, and spectroscopic properties (including IR, THz, 2D-IR, and Raman) of liquids and biomolecules.
Lu Wang is an assistant professor in the Department of Chemistry and Chemical Biology at Rutgers University. She received her Ph.D. degree in Physical Chemistry from the University of Wisconsin-Madison under the supervision of Professor Jim Skinner. She then worked as a postdoctoral fellow with Professor Tom Markland at Stanford University before starting her independent career in 2016. Her research uses theoretical and computational tools to elucidate the structure and dynamics of condensed phase systems, with a particular emphasis on the vibrational spectroscopy and quantum effects of biological macromolecules.
Lauren J. Webb is an associate professor of chemistry at The University of Texas at Austin. She obtained her A.B. in chemistry (music minor) from Bowdoin College in 2000. She entered graduate school at the California Institute of Technology and earned her Ph.D. in chemistry in 2005. From 2005 to 2008 she was a postdoctoral fellow in the laboratory of Dr. Steven Boxer in the Department of Chemistry at Stanford University. Her research focused on quantifying electrostatic fields in proteins using vibrational Stark effect spectroscopy. Dr. Webb moved to UT-Austin in 2008, where she has developed a research program based on her training in both surface and biological chemistry. Her research interests are centered on understanding and manipulating the mechanisms of interaction, organization, and self- assembly of biological macromolecules in both natural and artificial environments.
Martin T. Zanni is the Meloche-Bascom Professor of Chemistry at the University of Wisconsin-Madison. He is one of the early pioneers of 2D IR spectroscopy and has made many technological innovations that has broadened the capabilities and scope for a wide range of multidimensional spectroscopies and microscopies. He utilizes these new techniques to study topics in biophysics, chemical physics, photovoltaics, and surfaces. He has received many accolades for his research and was recently elected to the American Academy of Arts and Sciences. He founded PhaseTech Spectroscopy Inc., which is the first company to commercialize ultrafast 2D spectroscopy.
Footnotes
The authors declare no competing financial interest.
SUPPORTING INFORMATION
Detailed format of the deposited map file.
References
- (1).Herzberg G Molecular Spectra and Molecular Structure I: Spectra of Diatomic Molecules; Van Nostrand, 1950. [Google Scholar]
- (2).Herzberg G Molecular Spectra and Molecular Structure II: Infrared and Raman of Polyatomic Molecules; Van Nostrand, 1956. [Google Scholar]
- (3).Mukamel S Principles of Nonlinear Optical Spectroscopy; Oxford University Press: Oxford, 1995. [Google Scholar]
- (4).Cho M Two-Dimensional Optical Spectroscopy; CRC Press: Boca Raton, 2009. [Google Scholar]
- (5).Hamm P; Zanni MT Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press: New York, 2011. [Google Scholar]
- (6).Mukamel S Multidimensional Femtosecond Correlation Spectroscopies of Electronic and Vibrational Excitations. Annu. Rev. Phys. Chem 2000, 51, 691–729. [DOI] [PubMed] [Google Scholar]
- (7).Cho M Coherent Two-Dimensional Optical Spectroscopy. Chem. Rev 2008, 108, 1331–1418. [DOI] [PubMed] [Google Scholar]
- (8).Jonas DM Vibrational and Nonadiabatic Coherence in 2D Electronic Spectroscopy, the Jahn–Teller Effect, and Energy Transfer. Annu. Rev. Phys. Chem 2016, 69, 327–352. [DOI] [PubMed] [Google Scholar]
- (9).Nihonyanagi S; Mondal JA; Yamaguchi S; Tahara T Structure and Dynamics of Interfacial Water Studied by Heterodyne-Detected Vibrational Sum-Frequency Generation. Annu. Rev. Phys. Chem 2013, 64, 579–603. [DOI] [PubMed] [Google Scholar]
- (10).Tanimura Y; Mukamel S Two-Dimensional Femtosecond Vibrational Spectroscopy of Liquids. J. Chem. Phys 1993, 99, 9496–9511. [Google Scholar]
- (11).Cho M; Fleming GR Fifth-Order Three-Pulse Scattering Spectroscopy: Can We Separate Homogeneous and Inhomogeneous Contributions to Optical Spectra? J. Phys. Chem 1994, 98, 3478–3485. [Google Scholar]
- (12).Park K; Cho M Time- and Frequency-Resolved Coherent Two-Dimensional IR Spectroscopy: Its Complementary Relationship with the Coherent Two-Dimensional Raman Scattering Spectroscopy. J. Chem. Phys 1998, 109, 10559–10569. [Google Scholar]
- (13).Hybl JD; Albrecht AW; Gallagher Faeder SM; Jonas DM Two-Dimensional Electronic Spectroscopy. Chem. Phys. Lett 1998, 297, 307–313. [Google Scholar]
- (14).Zhao W; Wright JC Spectral Simplification in Vibrational Spectroscopy Using Doubly Vibrationally Enhanced Infrared Four Wave Mixing. J. Am. Chem. Soc 1999, 121, 10994–10998. [Google Scholar]
- (15).Savolainen J; Ahmed S; Hamm P Two-Dimensional Raman-Terahertz Spectroscopy of Water. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 20402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Elsaesser T; Reimann K; Woerner M Focus: Phase-Resolved Nonlinear Terahertz Spectroscopy—from Charge Dynamics in Solids to Molecular Excitations in Liquids. J. Chem. Phys 2015, 142, 212301. [DOI] [PubMed] [Google Scholar]
- (17).Shalit A; Ahmed S; Savolainen J; Hamm P Terahertz Echoes Reveal the Inhomogeneity of Aqueous Salt Solutions. Nature Chemistry 2016, 9, 273. [DOI] [PubMed] [Google Scholar]
- (18).Courtney TL; Fox ZW; Slenkamp KM; Khalil M Two-Dimensional Vibrational-Electronic Spectroscopy. J. Chem. Phys 2015, 143, 154201. [DOI] [PubMed] [Google Scholar]
- (19).Courtney TL; Fox ZW; Estergreen L; Khalil M Measuring Coherently Coupled Intramolecular Vibrational and Charge-Transfer Dynamics with Two-Dimensional Vibrational–Electronic Spectroscopy. J. Phys. Chem. Lett 2015, 6, 1286–1292. [DOI] [PubMed] [Google Scholar]
- (20).Lewis NHC; Dong H; Oliver TAA; Fleming GR Measuring Correlated Electronic and Vibrational Spectral Dynamics Using Line Shapes in Two-Dimensional Electronic-Vibrational Spectroscopy. J. Chem. Phys 2015, 142, 174202. [DOI] [PubMed] [Google Scholar]
- (21).Oliver TAA; Lewis NHC; Fleming GR Correlating the Motion of Electrons and Nuclei with Two-Dimensional Electronic–Vibrational Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2014, 111, 10061–10066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Cyran JD; Backus EHG; Nagata Y; Bonn M Structure from Dynamics: Vibrational Dynamics of Interfacial Water as a Probe of Aqueous Heterogeneity. J. Phys. Chem. B 2018, 122, 3667–3679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Zhang Z; Piatkowski L; Bakker HJ; Bonn M Ultrafast Vibrational Energy Transfer at the Water/Air Interface Revealed by Two-Dimensional Surface Vibrational Spectroscopy. Nature Chemistry 2011, 3, 888–893. [DOI] [PubMed] [Google Scholar]
- (24).Matsuzaki K; Kusaka R; Nihonyanagi S; Yamaguchi S; Nagata T; Tahara T Partially Hydrated Electrons at the Air/Water Interface Observed by UV-Excited Time-Resolved Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy. J. Am. Chem. Soc 2016, 138, 7551–7557. [DOI] [PubMed] [Google Scholar]
- (25).Hamm P; Lim M; Hochstrasser RM Structure of the Amide I Band of Peptides Measured by Femtosecond Nonlinear-Infrared Spectroscopy. J. Phys. Chem. B 1998, 102, 6123–6138. [Google Scholar]
- (26).Cho M In Advances in Multi-Photon Processes and Spectroscopy; Lin SH; Villaeys AA; Fujimura Y, Eds.; World Scientific: Singapore, 1999; Vol. 12. [Google Scholar]
- (27).Hahn S; Park K; Cho M Two-Dimensional Vibrational Spectroscopy. I. Theoretical Calculation of the Nonlinear Raman Response Function of Chcl3. J. Chem. Phys 1999, 111, 4121–4130. [Google Scholar]
- (28).Park K; Cho M; Hahn S; Kim D Two-Dimensional Vibrational Spectroscopy. II. Ab Initio Calculation of the Coherent 2D Infrared Response Function of Chcl3 and Comparison with the 2D Raman Response Function. J. Chem. Phys 1999, 111, 4131–4139. [Google Scholar]
- (29).Cho M Two-Dimensional Vibrational Spectroscopy. III. Theoretical Description of the Coherent Two-Dimensional IR-Raman Spectroscopy for the Investigation of the Coupling between Both IR- and Raman-Active Vibrational Modes. J. Chem. Phys 1999, 111, 4140–4147. [Google Scholar]
- (30).Hahn S; Kwak K; Cho M Two-Dimensional Vibrational Spectroscopy. IV. Relationship between through-Space Vibrational Coupling and Intermolecular Distance. J. Chem. Phys 2000, 112, 4553–4556. [Google Scholar]
- (31).Cho M Two-Dimensional Vibrational Spectroscopy. V. Novel 2-Dimensional Surface Vibrational Spectroscopies of Adsorbed Molecules on Surfaces or at Interfaces. J. Chem. Phys 2000, 112, 9978–9985. [Google Scholar]
- (32).Park K; Cho M Two-Dimensional Vibrational Spectroscopy. Vi. Higher-Order Contributions to the Two-Dimensional Vibrational Response Functions. J. Chem. Phys 2000, 112, 10496–10509. [Google Scholar]
- (33).Cho M Two-Dimensional Vibrational Spectroscopy. Vii. Investigation of the Vibronic and Vibrational Couplings by Using Novel Triply Resonant Two-Dimensional Vibrational Spectroscopies. J. Chem. Phys 2000, 113, 7746–7755. [Google Scholar]
- (34).Bonn M; Hess C; Miners JH; Heinz TF; Bakker HJ; Cho M Novel Surface Vibrational Spectroscopy: Infrared-Infrared-Visible Sum-Frequency Generation. Phys. Rev. Lett 2001, 86, 1566–1569. [DOI] [PubMed] [Google Scholar]
- (35).Cho M Two-Dimensional Vibrational Spectroscopy. Viii. Infrared Optical Kerr Effect and Two-Color Infrared Pump–Probe Measurements. J. Chem. Phys 2001, 114, 9982–9992. [Google Scholar]
- (36).Cho M Ultrafast Vibrational Spectroscopy in Condensed Phases. PhysChemComm 2002, 5, 40–58. [Google Scholar]
- (37).van Wilderen LJGW; Bredenbeck J From Ultrafast Structure Determination to Steering Reactions: Mixed IR/Non-IR Multidimensional Vibrational Spectroscopies. Angew. Chem. Int. Ed 2015, 54, 11624–11640. [DOI] [PubMed] [Google Scholar]
- (38).Kim H; Cho M Infrared Probes for Studying the Structure and Dynamics of Biomolecules. Chem. Rev 2013, 113, 5817–5847. [DOI] [PubMed] [Google Scholar]
- (39).Ma J; Pazos IM; Zhang W; Culik RM; Gai F Site-Specific Infrared Probes of Proteins. Annu. Rev. Phys. Chem 2015, 66, 357–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Błasiak B; Londergan CH; Webb LJ; Cho M Vibrational Probes: From Small Molecule Solvatochromism Theory and Experiments to Applications in Complex Systems. Acc. Chem. Res 2017, 50, 968–976. [DOI] [PubMed] [Google Scholar]
- (41).Adhikary R; Zimmermann J; Romesberg FE Transparent Window Vibrational Probes for the Characterization of Proteins with High Structural and Temporal Resolution. Chem. Rev 2017, 117, 1927–1969. [DOI] [PubMed] [Google Scholar]
- (42).Lindquist BA; Furse KE; Corcelli SA Nitrile Groups as Vibrational Probes of Biomolecular Structure and Dynamics: An Overview. Phys. Chem. Chem. Phys 2009, 11, 8119–8132. [DOI] [PubMed] [Google Scholar]
- (43).Moran SD; Woys AM; Buchanan LE; Bixby E; Decatur SM; Zanni MT Two-Dimensional IR Spectroscopy and Segmental 13C Labeling Reveals the Domain Structure of Human γD-Crystallin Amyloid Fibrils. Proc. Natl. Acad. Sci. U.S.A 2012, 109, 3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Baiz, Carlos R; Tokmakoff, A. Structural Disorder of Folded Proteins: Isotope-Edited 2D IR Spectroscopy and Markov State Modeling. Biophys. J 2015, 108, 1747–1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Reppert M; Roy AR; Tokmakoff A Isotope-Enriched Protein Standards for Computational Amide I Spectroscopy. J. Chem. Phys 2015, 142, 125104. [DOI] [PubMed] [Google Scholar]
- (46).Basom EJ; Maj M; Cho M; Thielges MC Site-Specific Characterization of Cytochrome P450cam Conformations by Infrared Spectroscopy. Anal. Chem 2016, 88, 6598–6606. [DOI] [PubMed] [Google Scholar]
- (47).Dalton SR; Vienneau AR; Burstein SR; Xu RJ; Linse S; Londergan CH Cyanylated Cysteine Reports Site-Specific Changes at Protein–Protein-Binding Interfaces without Perturbation. Biochemistry 2018, 57, 3702–3712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).van Wilderen LJGW; Kern-Michler D; Müller-Werkmeister HM; Bredenbeck J Vibrational Dynamics and Solvatochromism of the Label SCN in Various Solvents and Hemoglobin by Time Dependent IR and 2D-IR Spectroscopy. Phys. Chem. Chem. Phys 2014, 16, 19643–19653. [DOI] [PubMed] [Google Scholar]
- (49).Okuda M; Higashi M; Ohta K; Saito S; Tominaga K Theoretical Investigation on Vibrational Frequency Fluctuations of SCN-Derivatized Vibrational Probe Molecule in Water. Chem. Phys 2018, 512, 82–87. [Google Scholar]
- (50).Zanobini C; Bozovic O; Jankovic B; Koziol KL; Johnson PJM; Hamm P; Gulzar A; Wolf S; Stock G Azidohomoalanine: A Minimally Invasive, Versatile, and Sensitive Infrared Label in Proteins to Study Ligand Binding. J. Phys. Chem. B 2018, 122, 10118–10125. [DOI] [PubMed] [Google Scholar]
- (51).Pazos IM; Ghosh A; Tucker MJ; Gai F Ester Carbonyl Vibration as a Sensitive Probe of Protein Local Electric Field. Angew. Chem. Int. Ed 2014, 53, 6080–6084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Stone AJ The Theory of Intermolecular Forces; Clarendon Press, Oxford, 1996. [Google Scholar]
- (53).Buckingham AD Molecular Quadrupole Moments. Quarterly Reviews, Chemical Society 1959, 13, 183–214. [Google Scholar]
- (54).Ritchie JP; Copenhaver AS Comparison of Potential-Derived Charge and Atomic Multipole Models in Calculating Electrostatic Potentials and Energies of Some Nucleic Acid Bases and Pairs. J. Comput. Chem 1995, 16, 777–789. [Google Scholar]
- (55).Buckingham AD; Fowler PW Do Electrostatic Interactions Predict Structures of van der Waals Molecules? J. Chem. Phys 1983, 79, 6426–6428. [Google Scholar]
- (56).Koch U; Popelier PLA; Stone AJ Conformational Dependence of Atomic Multipole Moments. Chem. Phys. Lett 1995, 238, 253–260. [Google Scholar]
- (57).Price SL; Stone AJ The Electrostatic Interactions in van der Waals Complexes Involving Aromatic Molecules. J. Chem. Phys 1987, 86, 2859–2868. [Google Scholar]
- (58).Koch U; Stone AJ Conformational Dependence of the Molecular Charge Distribution and Its Influence on Intermolecular Interactions. J. Chem. Soc., Faraday Trans 1996, 92, 1701–1708. [Google Scholar]
- (59).Price SL; Stone AJ Electrostatic Models for Polypeptides: Can We Assume Transferability? J. Chem. Soc., Faraday Trans 1992, 88, 1755–1763. [Google Scholar]
- (60).Longuet-Higgins HC; Coulson CA The Electronic States of Composite Systems. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1956, 235, 537–543. [Google Scholar]
- (61).Longuet-Higgins HC Spiers Memorial Lecture. Intermolecular Forces. Discuss. Faraday Soc 1965, 40, 7–18. [Google Scholar]
- (62).Buckingham AD Solvent Effects in Vibrational Spectroscopy. Trans. Faraday Society 1960, 56, 753–760. [Google Scholar]
- (63).Gordon MS; Slipchenko L; Li H; Jensen JH In Annual Reports in Computational Chemistry; Spellmeyer DC; Wheeler R, Eds.; Elsevier, 2007; Vol. 3. [Google Scholar]
- (64).Gordon MS; Smith QA; Xu P; Slipchenko LV Accurate First Principles Model Potentials for Intermolecular Interactions. Annu. Rev. Phys. Chem 2013, 64, 553–578. [DOI] [PubMed] [Google Scholar]
- (65).Gordon MS; Fedorov DG; Pruitt SR; Slipchenko LV Fragmentation Methods: A Route to Accurate Calculations on Large Systems. Chem. Rev 2012, 112, 632–672. [DOI] [PubMed] [Google Scholar]
- (66).Corcelli SA; Lawrence CP; Skinner JL Combined Electronic Structure/Molecular Dynamics Approach for Ultrafast Infrared Spectroscopy of Dilute HOD in Liquid H2O and D2O. J. Chem. Phys 2004, 120, 8107–8117. [DOI] [PubMed] [Google Scholar]
- (67).Schmidt JR; Corcelli SA; Skinner JL Ultrafast Vibrational Spectroscopy of Water and Aqueous N-Methylacetamide: Comparison of Different Electronic Structure/Molecular Dynamics Approaches. J. Chem. Phys 2004, 121, 8887–8896. [DOI] [PubMed] [Google Scholar]
- (68).Schmidt JR; Corcelli SA; Skinner JL Pronounced Non-Condon Effects in the Ultrafast Infrared Spectroscopy of Water. J. Chem. Phys 2005, 123, 044513. [DOI] [PubMed] [Google Scholar]
- (69).Li S; Schmidt JR; Corcelli SA; Lawrence CP; Skinner JL Approaches for the Calculation of Vibrational Frequencies in Liquids: Comparison to Benchmarks for Azide/Water Clusters. J. Chem. Phys 2006, 124, 204110. [DOI] [PubMed] [Google Scholar]
- (70).Cho M Coherent Multidimensional Spectroscopy; Springer Nature, 2019. [Google Scholar]
- (71).Ernst RR; Bodenhausen G; Wokaun A Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clarendon Press: New York, 1987. [Google Scholar]
- (72).Wüthrich K NMR of Proteins and Nucleic Acids; Wiley, 1991. [Google Scholar]
- (73).Kwac K; Cho M Two-Color Pump-Probe Spectroscopies of Two- and Three-Level Systems: 2-Dimensional Line Shapes and Solvation Dynamics. J. Phys. Chem. A 2003, 107, 5903–5912. [Google Scholar]
- (74).Feng C-J; Dhayalan B; Tokmakoff A Refinement of Peptide Conformational Ensembles by 2D IR Spectroscopy: Application to Ala-Ala-Ala. Biophys. J 2018, 114, 2820–2832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Jones KC; Peng CS; Tokmakoff A Folding of a Heterogeneous β-Hairpin Peptide from Temperature-Jump 2D IR Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 2828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Maekawa H; Formaggio F; Toniolo C; Ge N-H Onset of 310-Helical Secondary Structure in Aib Oligopeptides Probed by Coherent 2D IR Spectroscopy. J. Am. Chem. Soc 2008, 130, 6556–6566. [DOI] [PubMed] [Google Scholar]
- (77).Maekawa H; Ballano G; Formaggio F; Toniolo C; Ge N-H 13C=18O/15N Isotope Dependence of the Amide-I/II 2D IR Cross Peaks for the Fully Extended Peptides. J. Phys. Chem. C 2014, 118, 29448–29457. [Google Scholar]
- (78).Maekawa H; Poli MD; Moretto A; Toniolo C; Ge N-H Toward Detecting the Formation of a Single Helical Turn by 2D IR Cross Peaks between the Amide-I and -II Modes. J. Phys. Chem. B 2009, 113, 11775–11786. [DOI] [PubMed] [Google Scholar]
- (79).Hamm P; Lim M; DeGrado WF; Hochstrasser RM Pump/Probe Self Heterodyned 2D Spectroscopy of Vibrational Transitions of a Small Globular Peptide. J. Chem. Phys 2000, 112, 1907–1916. [Google Scholar]
- (80).Wang J; Zhuang W; Mukamel S; Hochstrasser R Two-Dimensional Infrared Spectroscopy as a Probe of the Solvent Electrostatic Field for a Twelve Residue Peptide. J. Phys. Chem. B 2008, 112, 5930–5937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Selig O; Cunha AV; van Eldijk MB; van Hest JCM; Jansen TLC; Bakker HJ; Rezus YLA Temperature-Induced Collapse of Elastin-Like Peptides Studied by 2DIR Spectroscopy. J. Phys. Chem. B 2018, 122, 8243–8254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (82).Huerta-Viga A; Domingos SR; Amirjalayer S; Woutersen S A Salt-Bridge Structure in Solution Revealed by 2D-IR Spectroscopy. Phys. Chem. Chem. Phys 2014, 16, 15784–15786. [DOI] [PubMed] [Google Scholar]
- (83).Chung HS; Ganim Z; Jones KC; Tokmakoff A Transient 2D IR Spectroscopy of Ubiquitin Unfolding Dynamics. Proc. Natl. Acad. Sci. U.S.A 2007, 104, 14237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Chung JK; Thielges MC; Fayer MD Dynamics of the Folded and Unfolded Villin Headpiece (Hp35) Measured with Ultrafast 2D IR Vibrational Echo Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2011, 108, 3578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).DeFlores LP; Ganim Z; Nicodemus RA; Tokmakoff A Amide I′−II′ 2D IR Spectroscopy Provides Enhanced Protein Secondary Structural Sensitivity. J. Am. Chem. Soc 2009, 131, 3385–3391. [DOI] [PubMed] [Google Scholar]
- (86).Mukherjee P; Kass I; Arkin IT; Zanni MT Picosecond Dynamics of a Membrane Protein Revealed by 2D IR. Proc. Natl. Acad. Sci. U.S.A 2006, 103, 3528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (87).Ramos S; Horness RE; Collins JA; Haak D; Thielges MC Site-Specific 2D IR Spectroscopy: A General Approach for the Characterization of Protein Dynamics with High Spatial and Temporal Resolution. Phys. Chem. Chem. Phys 2019, 21, 780–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Ramos S; Le Sueur AL; Horness RE; Specker JT; Collins JA; Thibodeau KE; Thielges MC Heterogeneous and Highly Dynamic Interface in Plastocyanin–Cytochrome F Complex Revealed by Site-Specific 2D-IR Spectroscopy. J. Phys. Chem. B 2019, 123, 2114–2122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (89).Schmidt-Engler JM; Zangl R; Guldan P; Morgner N; Bredenbeck J Exploring the 2D-IR Repertoire of the −SCN Label to Study Site-Resolved Dynamics and Solvation in the Calcium Sensor Protein Calmodulin. Phys. Chem. Chem. Phys 2020, 22, 5463–5475. [DOI] [PubMed] [Google Scholar]
- (90).Woutersen S; Hamm P Time-Resolved Two-Dimensional Vibrational Spectroscopy of a Short A-Helix in Water. J. Chem. Phys 2001, 115, 7737–7743. [Google Scholar]
- (91).Fang C; Wang J; Kim YS; Charnley AK; Barber-Armstrong W; Smith AB; Decatur SM; Hochstrasser RM Two-Dimensional Infrared Spectroscopy of Isotopomers of an Alanine Rich α-Helix. J. Phys. Chem. B 2004, 108, 10415–10427. [Google Scholar]
- (92).King JT; Arthur EJ; Brooks CL; Kubarych KJ Site-Specific Hydration Dynamics of Globular Proteins and the Role of Constrained Water in Solvent Exchange with Amphiphilic Cosolvents. J. Phys. Chem. B 2012, 116, 5604–5611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (93).Bredenbeck J; Helbing J; Nienhaus K; Nienhaus GU; Hamm P Protein Ligand Migration Mapped by Nonequilibrium 2D-IR Exchange Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2007, 104, 14243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (94).Krummel AT; Mukherjee P; Zanni MT Inter and Intrastrand Vibrational Coupling in DNA Studied with Heterodyned 2D-IR Spectroscopy. J. Phys. Chem. B 2003, 107, 9165–9169. [Google Scholar]
- (95).Ramakers LAI; Hithell G; May JJ; Greetham GM; Donaldson PM; Towrie M; Parker AW; Burley GA; Hunt NT 2D-IR Spectroscopy Shows That Optimized DNA Minor Groove Binding of Hoechst33258 Follows an Induced Fit Model. J. Phys. Chem. B 2017, 121, 1295–1303. [DOI] [PubMed] [Google Scholar]
- (96).Sanstead PJ; Stevenson P; Tokmakoff A Sequence-Dependent Mechanism of DNA Oligonucleotide Dehybridization Resolved through Infrared Spectroscopy. J. Am. Chem. Soc 2016, 138, 11792–11801. [DOI] [PubMed] [Google Scholar]
- (97).Sanstead PJ; Tokmakoff A Direct Observation of Activated Kinetics and Downhill Dynamics in DNA Dehybridization. J. Phys. Chem. B 2018, 122, 3088–3100. [DOI] [PubMed] [Google Scholar]
- (98).Bruening EM; Schauss J; Siebert T; Fingerhut BP; Elsaesser T Vibrational Dynamics and Couplings of the Hydrated Rna Backbone: A Two-Dimensional Infrared Study. J. Phys. Chem. Lett 2018, 9, 583–587. [DOI] [PubMed] [Google Scholar]
- (99).Singh PC; Inoue K; Nihonyanagi S; Yamaguchi S; Tahara T Femtosecond Hydrogen Bond Dynamics of Bulk-Like and Bound Water at Positively and Negatively Charged Lipid Interfaces Revealed by 2D Hd-Vsfg Spectroscopy. Angew. Chem. Int. Ed. Engl 2016, 55, 10621–10625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (100).Woys AM; Lin Y-S; Reddy AS; Xiong W; de Pablo JJ; Skinner JL; Zanni MT 2D IR Line Shapes Probe Ovispirin Peptide Conformation and Depth in Lipid Bilayers. J. Am. Chem. Soc 2010, 132, 2832–2838. [DOI] [PubMed] [Google Scholar]
- (101).Fulfer KD; Kuroda DG A Comparison of the Solvation Structure and Dynamics of the Lithium Ion in Linear Organic Carbonates with Different Alkyl Chain Lengths. Phys. Chem. Chem. Phys 2017, 19, 25140–25150. [DOI] [PubMed] [Google Scholar]
- (102).Kurochkin DV; Naraharisetty SRG; Rubtsov IV A Relaxation-Assisted 2D IR Spectroscopy Method. Proc. Natl. Acad. Sci. U.S.A 2007, 104, 14209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (103).Lin Z; Rubtsov IV Constant-Speed Vibrational Signaling Along Polyethyleneglycol Chain up to 60-Ç Distance. Proc. Natl. Acad. Sci. U.S.A 2012, 109, 1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (104).Fecko CJ; Eaves JD; Loparo JJ; Tokmakoff A; Geissler PL Ultrafast Hydrogen-Bond Dynamics in the Infrared Spectroscopy of Water. Science 2003, 301, 1698–1702. [DOI] [PubMed] [Google Scholar]
- (105).Roberts ST; Petersen PB; Ramasesha K; Tokmakoff A; Ufimtsev IS; Martinez TJ Observation of a Zundel-Like Transition State During Proton Transfer in Aqueous Hydroxide Solutions. Proc. Natl. Acad. Sci. U.S.A 2009, 106, 15154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (106).Ghosh A; Qiu J; DeGrado WF; Hochstrasser RM Tidal Surge in the M2 Proton Channel, Sensed by 2D IR Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2011, 108, 6115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (107).Manor J; Mukherjee P; Lin Y-S; Leonov H; Skinner JL; Zanni MT; Arkin IT Gating Mechanism of the Influenza a M2 Channel Revealed by 1D and 2D IR Spectroscopies. Structure 2009, 17, 247–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (108).Pensack RD; Banyas KM; Barbour LW; Hegadorn M; Asbury JB Ultrafast Vibrational Spectroscopy of Charge-Carrier Dynamics in Organic Photovoltaic Materials. Phys. Chem. Chem. Phys 2009, 11, 2575–2591. [DOI] [PubMed] [Google Scholar]
- (109).Mukamel S Nonimpact Unified Theory of Four-Wave Mixing and Two-Photon Processes. Phys. Rev. A 1983, 28, 3480–3492. [Google Scholar]
- (110).Jansen TLC; Saito S; Jeon J; Cho M Theory of Coherent Two-Dimensional Vibrational Spectroscopy. J. Chem. Phys 2019, 150, 100901. [DOI] [PubMed] [Google Scholar]
- (111).Kwac K; Lee H; Cho M Non-Gaussian Statistics of Amide I Mode Frequency Fluctuation of N-Methylacetamide in Methanol Solution: Linear and Nonlinear Vibrational Spectra. J. Chem. Phys 2004, 120, 1477–1490. [DOI] [PubMed] [Google Scholar]
- (112).Roy S; Pshenichnikov MS; Jansen TLC Analysis of 2D Cs Spectra for Systems with Non-Gaussian Dynamics. J. Phys. Chem. B 2011, 115, 5431–5440. [DOI] [PubMed] [Google Scholar]
- (113).Dinpajooh M; Matyushov DV Non-Gaussian Lineshapes and Dynamics of Time-Resolved Linear and Nonlinear (Correlation) Spectra. J. Phys. Chem. B 2014, 118, 7925–7936. [DOI] [PubMed] [Google Scholar]
- (114).Woutersen S; Mu Y; Stock G; Hamm P Hydrogen-Bond Lifetime Measured by Time-Resolved 2D-IR Spectroscopy: N-Methylacetamide in Methanol. Chem. Phys 2001, 266, 137–147. [Google Scholar]
- (115).Kim YS; Hochstrasser RM Chemical Exchange 2D IR of Hydrogen-Bond Making and Breaking. Proc. Natl. Acad. Sci. U.S.A 2005, 102, 11185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (116).Šanda F; Mukamel S Stochastic Simulation of Chemical Exchange in Two Dimensional Infrared Spectroscopy. J. Chem. Phys 2006, 125, 014507. [DOI] [PubMed] [Google Scholar]
- (117).Kwak K; Zheng J; Cang H; Fayer MD Ultrafast Two-Dimensional Infrared Vibrational Echo Chemical Exchange Experiments and Theory. J. Phys. Chem. B 2006, 110, 19998–20013. [DOI] [PubMed] [Google Scholar]
- (118).Jansen TLC; Knoester J Calculation of Two-Dimensional Infrared Spectra of Ultrafast Chemical Exchange with Numerical Langevin Simulations. J. Chem. Phys 2007, 127, 234502. [DOI] [PubMed] [Google Scholar]
- (119).Farag MH; Hoenders BJ; Knoester J; Jansen TLC Spectral Line Shapes in Linear Absorption and Two-Dimensional Spectroscopy with Skewed Frequency Distributions. J. Chem. Phys 2017, 146, 234201. [DOI] [PubMed] [Google Scholar]
- (120).Jansen TLC; Cringus D; Pshenichnikov MS Dissimilar Dynamics of Coupled Water Vibrations. J. Phys. Chem. A 2009, 113, 6260–6265. [DOI] [PubMed] [Google Scholar]
- (121).Liang C; Jansen TLC An Efficient N3-Scaling Propagation Scheme for Simulating Two-Dimensional Infrared and Visible Spectra. J. Chem. Theory Comput 2012, 8, 1706–1713. [DOI] [PubMed] [Google Scholar]
- (122).Falvo C; Palmieri B; Mukamel S Coherent Infrared Multidimensional Spectra of the OH Stretching Band in Liquid Water Simulated by Direct Nonlinear Exciton Propagation. J. Chem. Phys 2009, 130, 184501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (123).Fleming GR; Cho M Chromophore-Solvent Dynamics. Annu. Rev. Phys. Chem 1996, 47, 109–134. [Google Scholar]
- (124).Jansen TLC; Knoester J Nonadiabatic Effects in the Two-Dimensional Infrared Spectra of Peptides: Application to Alanine Dipeptide. J. Phys. Chem. B 2006, 110, 22910–22916. [DOI] [PubMed] [Google Scholar]
- (125). https://mukamel.ps.uci.edu/software.html.
- (126). https://github.com/GHlacour/NISE_2015.
- (127).Torii H Time-Domain Calculations of the Polarized Raman and Two-Dimensional Infrared Spectra of Liquid N,N-Dimethylformamide. Chem. Phys. Lett 2005, 414, 417–422. [Google Scholar]
- (128).Tran H; Cunha AV; Shephard JJ; Shalit A; Hamm P; Jansen TLC; Salzmann CG 2D IR Spectroscopy of High-Pressure Phases of Ice. J. Chem. Phys 2017, 147, 144501. [DOI] [PubMed] [Google Scholar]
- (129).Kobus M; Gorbunov RD; Nguyen PH; Stock G Nonadiabatic Vibrational Dynamics and Spectroscopy of Peptides: A Quantum-Classical Description. Chem. Phys 2008, 347, 208–217. [Google Scholar]
- (130).Paarmann A; Hayashi T; Mukamel S; Miller RJD Probing Intermolecular Couplings in Liquid Water with Two-Dimensional Infrared Photon Echo Spectroscopy. J. Chem. Phys 2008, 128, 191103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (131).Tomasi J; Mennucci B; Cammi R Quantum Mechanical Continuum Solvation Models. Chem. Rev 2005, 105, 2999–3094. [DOI] [PubMed] [Google Scholar]
- (132).Kirkwood JG On the Theory of Strong Electrolyte Solutions. J. Chem. Phys 1934, 2, 767–781. [Google Scholar]
- (133).Kirkwood JG The Dielectric Polarization of Polar Liquids. J. Chem. Phys 1939, 7, 911–919. [Google Scholar]
- (134).Onsager L Electric Moments of Molecules in Liquid. J. Am. Chem. Soc 1936, 58, 1486–1493. [Google Scholar]
- (135).Rivail J-L; Rinaldi D A Quantum Chemical Approach to Dielectric Solvent Effects in Molecular Liquids. Chem. Phys 1976, 18, 233–242. [Google Scholar]
- (136).Cammi R; Tomasi J Remarks on the Use of the Apparent Surface Charges (ASC) Methods in Solvation Problems: Iterative Versus Matrix-Inversion Procedures and the Renormalization of the Apparent Charges. J. Comput. Chem 1995, 16, 1449–1458. [Google Scholar]
- (137).Miertuš S; Scrocco E; Tomasi J Electrostatic Interaction of a Solute with a Continuum. A Direct Utilizaion of Ab Initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys 1981, 55, 117–129. [Google Scholar]
- (138).Klamt A; Schüürmann G Cosmo: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc. Perkin Trans 2 1993, 799–805. [Google Scholar]
- (139).Krimm S; Bandekar J In Adv. Protein Chem; Anfinsen CB; Edsall JT; Richards FM, Eds.; Academic Press, 1986; Vol. 38. [Google Scholar]
- (140).Hobza P; Zahradnik R Intermolecular Interactions between Medium-Sized Systems. Nonempirical and Empirical Calculations of Interaction Energies. Successes and Failures. Chem. Rev 1988, 88, 871–897. [Google Scholar]
- (141).Jeziorski B; Moszynski R; Szalewicz K Perturbation-Theory Approach to Intermolecular Potential-Energy Surfaces of van der Waals Complexes. Chem. Rev 1994, 94, 1887–1930. [Google Scholar]
- (142).Kitaura K; Morokuma K A New Energy Decomposition Scheme for Molecular Interactions within the Hartree-Fock Approximation. Int. J. Quantum Chem 1976, 10, 325–340. [Google Scholar]
- (143).Błasiak B; Cho M Vibrational Solvatochromism. II. A First-Principle Theory of Solvation-Induced Vibrational Frequency Shift Based on Effective Fragment Potential Method. J. Chem. Phys 2014, 140, 164107. [DOI] [PubMed] [Google Scholar]
- (144).Li H; Gordon MS; Jensen JH Charge Transfer Interaction in the Effective Fragment Potential Method. J. Chem. Phys 2006, 124, 214108. [DOI] [PubMed] [Google Scholar]
- (145).Buckingham AD Solvent Effects in Infra-Red Spectroscopy. Proc. R. Soc. London, Ser. A 1958, 248, 169–182. [Google Scholar]
- (146).Buckingham AD; Sutherland GBBM; Pople JA; Pullin ADE; Thompson HW A Theory of Frequency, Intensity and Band-Width Changes Due to Solvents in Infra-Red Spectroscopy. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1960, 255, 32–39. [Google Scholar]
- (147).Cho M Correlation between Electronic and Molecular Structure Distortions and Vibrational Properties. I. Adiabatic Approximations. J. Chem. Phys 2003, 118, 3480–3490. [Google Scholar]
- (148).Cho M Vibrational Solvatochromism and Electrochromism: Coarse-Grained Models and Their Relationships. J. Chem. Phys 2009, 130, 094505. [DOI] [PubMed] [Google Scholar]
- (149).McDowell SAC; Buckingham AD A Theory of Vibrational Frequency Shifts Revisited: Application to Dimers of LiH with the Inert Gases He, Ne, Ar and Kr. Mol. Phys 2005, 103, 257–262. [Google Scholar]
- (150).McDowell SAC; Buckingham AD On the Correlation between Bond-Length Change and Vibrational Frequency Shift in Hydrogen-Bonded Complexes: A Computational Study of Y⋯HCl Dimers (Y = N2, CO, BF). J. Am. Chem. Soc 2005, 127, 15515–15520. [DOI] [PubMed] [Google Scholar]
- (151).McDowell SAC; Buckingham AD Comparison of Some Vibrational Features of FArH⋯ Rg and FH⋯ Rg Complexes (Rg=He, Ne, Ar, Kr). Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2005, 61, 1603–1609. [DOI] [PubMed] [Google Scholar]
- (152).Buckingham AD; Del Bene JE; McDowell SA C. The Hydrogen Bond. Chem. Phys. Lett 2008, 463, 1–10. [Google Scholar]
- (153).Herrebout WA; Delanoye SN; van der Veken BJ Blue-Shifting or Red-Shifting Hydrogen Bonding? Predictions for Haloform Complexes with Dimethyl Ether on the Basis of Perturbation Theory. J. Phys. Chem. A 2004, 108, 6059–6064. [Google Scholar]
- (154).Błasiak B; Cho M Vibrational Solvatochromism. III. Rigorous Treatment of the Dispersion Interaction Contribution. J. Chem. Phys 2015, 143, 164111. [DOI] [PubMed] [Google Scholar]
- (155).Błasiak B; Ritchie AW; Webb LJ; Cho M Vibrational Solvatochromism of Nitrile Infrared Probes: Beyond the Vibrational Stark Dipole Approach. Phys. Chem. Chem. Phys 2016, 18, 18094–18111. [DOI] [PubMed] [Google Scholar]
- (156).Maj M; Ahn C; Błasiak B; Kwak K; Han H; Cho M Isonitrile as an Ultrasensitive Infrared Reporter of Hydrogen-Bonding Structure and Dynamics. J. Phys. Chem. B 2016, 120, 10167–10180. [DOI] [PubMed] [Google Scholar]
- (157).Mandado M; Hermida-Ramón JM Electron Density Based Partitioning Scheme of Interaction Energies. J. Chem. Theory Comput 2011, 7, 633–641. [DOI] [PubMed] [Google Scholar]
- (158).Bauer E; Magat M Sur La Déformation Des Molécules En Phase Condensée Et La « Liaison Hydrogène ». J. Phys. Radium 1938, 9, 319–330. [Google Scholar]
- (159).Kirkwood JG Theory of Solutions of Molecules Containing Widely Separated Charges with Special Application to Zwitterions. J. Chem. Phys 1934, 2, 351–361. [Google Scholar]
- (160).Ben-Amotz D; Lee MR; Cho SY; List DJ Solvent and Pressure-Induced Perturbations of the Vibrational Potential Surface of Acetonitrile. J. Chem. Phys 1992, 96, 8781–8792. [Google Scholar]
- (161).Fawcett WR; Liu G; Kessler TE Solvent-Induced Frequency Shifts in the Infrared Spectrum of Acetonitrile in Organic Solvents. J. Phys. Chem 1993, 97, 9293–9298. [Google Scholar]
- (162).Fawcett WR; Kloss AA Solvent-Induced Frequency Shifts in the Infrared Spectrum of Dimethyl Sulfoxide in Organic Solvents. J. Phys. Chem 1996, 100, 2019–2024. [Google Scholar]
- (163).Gutmann V; Resch G; Linert W Structural Variability in Solutions. Coord. Chem. Rev 1982, 43, 133–164. [Google Scholar]
- (164).Reimers JR; Hall LE The Solvation of Acetonitrile. J. Am. Chem. Soc 1999, 121, 3730–3744. [Google Scholar]
- (165).Fafarman AT; Sigala PA; Herschlag D; Boxer SG Decomposition of Vibrational Shifts of Nitriles into Electrostatic and Hydrogen-Bonding Effects. J. Am. Chem. Soc 2010, 132, 12811–12813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (166).Bagchi S; Fried SD; Boxer SG A Solvatochromic Model Calibrates Nitriles’ Vibrational Frequencies to Electrostatic Fields. J. Am. Chem. Soc 2012, 134, 10373–10376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (167).Zhang W; Markiewicz BN; Doerksen RS; Smith IIIAB; Gai F C≡n Stretching Vibration of 5-Cyanotryptophan as an Infrared Probe of Protein Local Environment: What Determines Its Frequency? Phys. Chem. Chem. Phys 2016, 18, 7027–7034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (168).Rodgers JM; Abaskharon RM; Ding B; Chen J; Zhang W; Gai F Fermi Resonance as a Means to Determine the Hydrogen-Bonding Status of Two Infrared Probes. Phys. Chem. Chem. Phys 2017, 19, 16144–16150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (169).Kamlet MJ; Taft RW The Solvatochromic Comparison Method. I. The β-Scale of Solvent Hydrogen-Bond Acceptor (HBA) Basicities. J. Am. Chem. Soc 1976, 98, 377–383. [Google Scholar]
- (170).Taft RW; Kamlet MJ The Solvatochromic Comparison Method. 2. The α-Scale of Solvent Hydrogen-Bond Donor (HBD) Acidities. J. Am. Chem. Soc 1976, 98, 2886–2894. [Google Scholar]
- (171).Kamlet MJ; Abboud JL; Taft RW The Solvatochromic Comparison Method. 6. The π* Scale of Solvent Polarities. J. Am. Chem. Soc 1977, 99, 6027–6038. [Google Scholar]
- (172).Hush NS; Reimers JR Vibrational Stark Spectroscopy. 1. Basic Theory and Application to the CO Stretch. J. Phys. Chem 1995, 99, 15798–15805. [Google Scholar]
- (173).Reimers JR; Zeng J; Hush NS Vibrational Stark Spectroscopy. 2. Application to the CN Stretch in Hcn and Acetonitrile. J. Phys. Chem 1996, 100, 1498–1504. [Google Scholar]
- (174).Andrews SS; Boxer SG Vibrational Stark Effects of Nitriles II. Physical Origins of Stark Effects from Experiment and Perturbation Models. J. Phys. Chem. A 2002, 106, 469–477. [Google Scholar]
- (175).Andrews SS; Boxer SG Vibrational Stark Effects of Nitriles I. Methods and Experimental Results. J. Phys. Chem. A 2000, 104, 11853–11863. [Google Scholar]
- (176).Liptay W Electrochromism and Solvatochromism. Angewandte Chemie International Edition in English 1969, 8, 177–188. [Google Scholar]
- (177).Suydam IT; Boxer SG Vibrational Stark Effects Calibrate the Sensitivity of Vibrational Probes for Electric Fields in Proteins. Biochemistry 2003, 42, 12050–12055. [DOI] [PubMed] [Google Scholar]
- (178).Levinson NM; Fried SD; Boxer SG Solvent-Induced Infrared Frequency Shifts in Aromatic Nitriles Are Quantitatively Described by the Vibrational Stark Effect. J. Phys. Chem. B 2012, 116, 10470–10476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (179).Dalosto SD; Vanderkooi JM; Sharp KA Vibrational Stark Effects on Carbonyl, Nitrile, and Nitrosyl Compounds Including Heme Ligands, CO, CN, and NO, Studied with Density Functional Theory. J. Phys. Chem. B 2004, 108, 6450–6457. [DOI] [PubMed] [Google Scholar]
- (180).Bublitz GU; Boxer SG Stark Spectroscopy: Applications in Chemistry, Biology, and Materials Science. Annu. Rev. Phys. Chem 1997, 48, 213–242. [DOI] [PubMed] [Google Scholar]
- (181).Wortmann R; Bishop DM Effective Polarizabilities and Local Field Corrections for Nonlinear Optical Experiments in Condensed Media. J. Chem. Phys 1998, 108, 1001–1007. [Google Scholar]
- (182).Fried SD; Boxer SG Measuring Electric Fields and Noncovalent Interactions Using the Vibrational Stark Effect. Acc. Chem. Res 2015, 48, 998–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (183).Choi J-H; Oh K-I; Lee H; Lee C; Cho M Nitrile and Thiocyanate IR Probes: Quantum Chemistry Calculation Studies and Multivariate Least-Square Fitting Analysis. J. Chem. Phys 2008, 128, 134506. [DOI] [PubMed] [Google Scholar]
- (184).First JT; Slocum JD; Webb LJ Quantifying the Effects of Hydrogen Bonding on Nitrile Frequencies in GFP: Beyond Solvent Exposure. J. Phys. Chem. B 2018, 122, 6733–6743. [DOI] [PubMed] [Google Scholar]
- (185).Błasiak B; Lee H; Cho M Vibrational Solvatochromism: Towards Systematic Approach to Modeling Solvation Phenomena. J. Chem. Phys 2013, 139, 044111. [DOI] [PubMed] [Google Scholar]
- (186).Schkolnik G; Utesch T; Salewski J; Tenger K; Millo D; Kranich A; Zebger I; Schulz C; Zimányi L; Rákhely G et al. Mapping Local Electric Fields in Proteins at Biomimetic Interfaces. Chem. Commun 2012, 48, 70–72. [DOI] [PubMed] [Google Scholar]
- (187).Oklejas V; Sjostrom C; Harris JM Surface-Enhanced Raman Scattering Based Vibrational Stark Effect as a Spatial Probe of Interfacial Electric Fields in the Diffuse Double Layer. J. Phys. Chem. B 2003, 107, 7788–7794. [Google Scholar]
- (188).Lee H; Choi J-H; Cho M Vibrational Solvatochromism and Electrochromism. II. Multipole Analysis. J. Chem. Phys 2012, 137, 114307. [DOI] [PubMed] [Google Scholar]
- (189).Rey R; Hynes JT Vibrational Phase and Energy Relaxation of CN− in Water. J. Chem. Phys 1998, 108, 142–153. [Google Scholar]
- (190).Morales CM; Thompson WH Molecular-Level Mechanisms of Vibrational Frequency Shifts in a Polar Liquid. J. Phys. Chem. B 2011, 115, 7597–7605. [DOI] [PubMed] [Google Scholar]
- (191).Li X; Liu L; Schlegel HB On the Physical Origin of Blue-Shifted Hydrogen Bonds. J. Am. Chem. Soc 2002, 124, 9639–9647. [DOI] [PubMed] [Google Scholar]
- (192).Delanoye SN; Herrebout WA; van der Veken BJ Blue Shifting Hydrogen Bonding in the Complexes of Chlorofluoro Haloforms with Acetone-d6 and Oxirane-d4. J. Am. Chem. Soc 2002, 124, 11854–11855. [DOI] [PubMed] [Google Scholar]
- (193).Zierkiewicz W; Jurečka P; Hobza P On Differences between Hydrogen Bonding and Improper Blue-Shifting Hydrogen Bonding. ChemPhysChem 2005, 6, 609–617. [DOI] [PubMed] [Google Scholar]
- (194).Rodziewicz P; Rutkowski KS; Melikova SM; Koll A Ab Initio Studies of Electron Acceptor–Donor Interactions with Blue- and Red-Shifted Hydrogen Bonds. ChemPhysChem 2005, 6, 1282–1292. [DOI] [PubMed] [Google Scholar]
- (195).Zhou P-P; Qiu W-Y Red-Shifted Hydrogen Bonds and Blue-Shifted van der Waals Contact in the Standard Watson-Crick Adenine-Thymine Base Pair. J. Phys. Chem. A 2009, 113, 10306–10320. [DOI] [PubMed] [Google Scholar]
- (196).Mo Y; Wang C; Guan L; Braïda B; Hiberty PC; Wu W On the Nature of Blueshifting Hydrogen Bonds. Chem. Eur. J 2014, 20, 8444–8452. [DOI] [PubMed] [Google Scholar]
- (197).Lee H; Choi J-H; Cho M Vibrational Solvatochromism and Electrochromism of Cyanide, Thiocyanate, and Azide Anions in Water. Phys. Chem. Chem. Phys 2010, 12, 12658–12669. [DOI] [PubMed] [Google Scholar]
- (198).Brinzer T; Berquist EJ; Ren Z; Dutta S; Johnson CA; Krisher CS; Lambrecht DS; Garrett-Roe S Ultrafast Vibrational Spectroscopy (2D-IR) of CO2 in Ionic Liquids: Carbon Capture from Carbon Dioxide’s Point of View. J. Chem. Phys 2015, 142, 212425. [DOI] [PubMed] [Google Scholar]
- (199).Wright AM; Howard AA; Howard JC; Tschumper GS; Hammer NI Charge Transfer and Blue Shifting of Vibrational Frequencies in a Hydrogen Bond Acceptor. J. Phys. Chem. A 2013, 117, 5435–5446. [DOI] [PubMed] [Google Scholar]
- (200).Lindquist BA; Corcelli SA Nitrile Groups as Vibrational Probes: Calculations of the C≡N Infrared Absorption Line Shape of Acetonitrile in Water and Tetrahydrofuran. J. Phys. Chem. B 2008, 112, 6301–6303. [DOI] [PubMed] [Google Scholar]
- (201).Lindquist BA; Haws RT; Corcelli SA Optimized Quantum Mechanics/Molecular Mechanics Strategies for Nitrile Vibrational Probes: Acetonitrile and para-Tolunitrile in Water and Tetrahydrofuran. J. Phys. Chem. B 2008, 112, 13991–14001. [DOI] [PubMed] [Google Scholar]
- (202).Stewart JJP Optimization of Parameters for Semiempirical Methods II. Applications. J. Comput. Chem 1989, 10, 221–264. [Google Scholar]
- (203).Xu RJ; Błasiak B; Cho M; Layfield JP; Londergan CH A Direct, Quantitative Connection between Molecular Dynamics Simulations and Vibrational Probe Line Shapes. J. Phys. Chem. Lett 2018, 9, 2560–2567. [DOI] [PubMed] [Google Scholar]
- (204).Jensen JH; Gordon MS An Approximate Formula for the Intermolecular Pauli Repulsion between Closed Shell Molecules. II. Application to the Effective Fragment Potential Method. J. Chem. Phys 1998, 108, 4772–4782. [Google Scholar]
- (205).Jensen JH; Gordon MS An Approximate Formula for the Intermolecular Pauli Repulsion between Closed Shell Molecules. Mol. Phys 1996, 89, 1313–1325. [Google Scholar]
- (206).Chen Y; Li H Intermolecular Interaction in Water Hexamer. J. Phys. Chem. A 2010, 114, 11719–11724. [DOI] [PubMed] [Google Scholar]
- (207).Chen W; Gordon MS Energy Decomposition Analyses for Many-Body Interaction and Applications to Water Complexes. J. Phys. Chem 1996, 100, 14316–14328. [Google Scholar]
- (208).Antony J; Brüske B; Grimme S Cooperativity in Noncovalent Interactions of Biologically Relevant Molecules. Phys. Chem. Chem. Phys 2009, 11, 8440–8447. [DOI] [PubMed] [Google Scholar]
- (209).Gora RW; Sokalski WA; Leszczynski J; Pett VB The Nature of Interactions in the Ionic Crystal of 3-Pentenenitrile, 2-Nitro-5-oxo, Ion(−1), Sodium. J. Phys. Chem. B 2005, 109, 2027–2033. [DOI] [PubMed] [Google Scholar]
- (210).Chaudret R; Gresh N; Parisel O; Piquemal J-P Many-Body Exchange-Repulsion in Polarizable Molecular Mechanics. I. Orbital-Based Approximations and Applications to Hydrated Metal Cation Complexes. J. Comput. Chem 2011, 32, 2949–2957. [DOI] [PubMed] [Google Scholar]
- (211).Michaud-Agrawal N; Denning EJ; Woolf TB; Beckstein O Mdanalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations. J. Comput. Chem 2011, 32, 2319–2327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (212).Gowers RJ; Linke M; Barnoud J; Reddy T. y. J. E.; Melo MN; Seyler SL; Domanski J; Dotson DL; Buchoux S; Kenney IM et al. In Proceedings of the 15th Python in Science Conference; Benthall S; Rostrup S, Eds., 2016.
- (213).Abraham MJ; Murtola T; Schulz R; Páll S; Smith JC; Hess B; Lindahl E Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar]
- (214).Case DA; Ben-Shalom IY; Brozell SR; Cerutti DS; Cheatham, I. TE; Cruzeiro VWD; Darden TA; Duke RE; Ghoreishi D; Gilson MK et al. Amber 2018; University of California: San Francisco, 2018. [Google Scholar]
- (215).Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kalé L; Schulten K Scalable Molecular Dynamics with Namd. J. Comput. Chem 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (216).Sengupta N; Maekawa H; Zhuang W; Toniolo C; Mukamel S; Tobias DJ; Ge N-H Sensitivity of 2D IR Spectra to Peptide Helicity: A Concerted Experimental and Simulation Study of an Octapeptide. J. Phys. Chem. B 2009, 113, 12037–12049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (217).Maekawa H; Ge N-H Comparative Study of Electrostatic Models for the Amide-I and -II Modes: Linear and Two-Dimensional Infrared Spectra. J. Phys. Chem. B 2010, 114, 1434–1446. [DOI] [PubMed] [Google Scholar]
- (218).Oh K-I; Choi J-H; Lee J-H; Han J-B; Lee H; Cho M Nitrile and Thiocyanate IR Probes: Molecular Dynamics Simulation Studies. J. Chem. Phys 2008, 128, 154504. [DOI] [PubMed] [Google Scholar]
- (219).Kwac K; Cho M Molecular Dynamics Simulation Study of N-Methylacetamide in Water. I. Amide I Mode Frequency Fluctuation. J. Chem. Phys 2003, 119, 2247–2255. [Google Scholar]
- (220).Ham S; Kim J-H; Lee H; Cho M Correlation between Electronic and Molecular Structure Distortions and Vibrational Properties. II. Amide I Modes of NMA–nD2O Complexes. J. Chem. Phys 2003, 118, 3491–3498. [Google Scholar]
- (221).Bouř P; Keiderling TA Empirical Modeling of the Peptide Amide I Band IR Intensity in Water Solution. J. Chem. Phys 2003, 119, 11253–11262. [Google Scholar]
- (222).Hahn S; Lee H; Cho M Theoretical Calculations of Infrared Absorption, Vibrational Circular Dichroism, and Two-Dimensional Vibrational Spectra of Acetylproline in Liquids Water and Chloroform. J. Chem. Phys 2004, 121, 1849–1865. [DOI] [PubMed] [Google Scholar]
- (223).Choi J-H; Hahn S; Cho M Amide I IR, VCD, and 2d IR Spectra of Isotope-Labeled α-Helix in Liquid Water: Numerical Simulation Studies. Int. J. Quantum Chem 2005, 104, 616–634. [Google Scholar]
- (224).Kwac K; Cho M Hydrogen Bonding Dynamics and Two-Dimensional Vibrational Spectroscopy: N-Methylacetamide in Liquid Methanol. J. Raman Spectrosc 2005, 36, 326–336. [Google Scholar]
- (225).Watson TM; Hirst JD Theoretical Studies of the Amide I Vibrational Frequencies of [Leu]-Enkephalin. Mol. Phys 2005, 103, 1531–1546. [Google Scholar]
- (226).DeCamp MF; DeFlores L; McCracken JM; Tokmakoff A; Kwac K; Cho M Amide I Vibrational Dynamics of N-Methylacetamide in Polar Solvents: The Role of Electrostatic Interactions. J. Phys. Chem. B 2005, 109, 11016–11026. [DOI] [PubMed] [Google Scholar]
- (227).Hayashi T; Jansen TLC; Zhuang W; Mukamel S Collective Solvent Coordinates for the Infrared Spectrum of HOD in D2O Based on an ab initio Electrostatic Map. J. Phys. Chem. A 2005, 109, 64–82. [DOI] [PubMed] [Google Scholar]
- (228).Hayashi T; Zhuang W; Mukamel S Electrostatic DFT Map for the Complete Vibrational Amide Band of NMA. J. Phys. Chem. A 2005, 109, 9747–9759. [DOI] [PubMed] [Google Scholar]
- (229).Bouř P; Michalík D; Kapitán J Empirical Solvent Correction for Multiple Amide Group Vibrational Modes. J. Chem. Phys 2005, 122, 144501. [DOI] [PubMed] [Google Scholar]
- (230).Jansen TLC; Dijkstra AG; Watson TM; Hirst JD; Knoester J Modeling the Amide I Bands of Small Peptides. J. Chem. Phys 2006, 125, 044312. [DOI] [PubMed] [Google Scholar]
- (231).Jansen TLC; Knoester J A Transferable Electrostatic Map for Solvation Effects on Amide I Vibrations and Its Application to Linear and Two-Dimensional Spectroscopy. J. Chem. Phys 2006, 124, 044502. [DOI] [PubMed] [Google Scholar]
- (232).Choi J-H; Oh K-I; Cho M Azido-Derivatized Compounds as IR Probes of Local Electrostatic Environment: Theoretical Studies. J. Chem. Phys 2008, 129, 174512. [DOI] [PubMed] [Google Scholar]
- (233).Lin YS; Shorb JM; Mukherjee P; Zanni MT; Skinner JL Empirical Amide I Vibrational Frequency Map: Application to 2D-IR Line Shapes for Isotope-Edited Membrane Peptide Bundles. J. Phys. Chem. B 2009, 113, 592–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (234).Choi J-H; Cho M Vibrational Solvatochromism and Electrochromism of Infrared Probe Molecules Containing C≡O, C≡N, C=O, or C-F Vibrational Chromophore. J. Chem. Phys 2011, 134, 154513. [DOI] [PubMed] [Google Scholar]
- (235).Roy S; Lessing J; Meisl G; Ganim Z; Tokmakoff A; Knoester J; Jansen TLC Solvent and Conformation Dependence of Amide I Vibrations in Peptides and Proteins Containing Proline. J. Chem. Phys 2011, 135, 234507. [DOI] [PubMed] [Google Scholar]
- (236).Choi J-H; Raleigh D; Cho M Azido Homoalanine Is a Useful Infrared Probe for Monitoring Local Electrostatistics and Side-Chain Solvation in Proteins. J. Phys. Chem. Lett 2011, 2, 2158–2162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (237).Torii H Amide I Vibrational Properties Affected by Hydrogen Bonding Out-of-Plane of the Peptide Group. J. Phys. Chem. Lett 2015, 6, 727–733. [DOI] [PubMed] [Google Scholar]
- (238).Torii H Strategy for Modeling the Electrostatic Responses of the Spectroscopic Properties of Proteins. J. Phys. Chem. B 2018, 122, 154–164. [DOI] [PubMed] [Google Scholar]
- (239).Torii H; Noge S Roles of the Scalar and Vector Components of the Solvation Effects on the Vibrational Properties of Hydrogen- or Halogen-Bond Accepting Stretching Modes. Phys. Chem. Chem. Phys 2016, 18, 10081–10096. [DOI] [PubMed] [Google Scholar]
- (240).Karjalainen E-L; Ersmark T; Barth A Optimization of Model Parameters for Describing the Amide I Spectrum of a Large Set of Proteins. J. Phys. Chem. B 2012, 116, 4831–4842. [DOI] [PubMed] [Google Scholar]
- (241).Małolepsza E; Straub JE Empirical Maps for the Calculation of Amide I Vibrational Spectra of Proteins from Classical Molecular Dynamics Simulations. J. Phys. Chem. B 2014, 118, 7848–7855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (242).Miyazawa T; Blout ER The Infrared Spectra of Polypeptides in Various Conformations: Amide I and II Bands. J. Am. Chem. Soc 1961, 83, 712–719. [Google Scholar]
- (243).Ganim Z; Chung HS; Smith AW; DeFlores LP; Jones KC; Tokmakoff A Amide I Two-Dimensional Infrared Spectroscopy of Proteins. Acc. Chem. Res 2008, 41, 432–441. [DOI] [PubMed] [Google Scholar]
- (244).Ghosh A; Ostrander JS; Zanni MT Watching Proteins Wiggle: Mapping Structures with Two-Dimensional Infrared Spectroscopy. Chem. Rev 2017, 117, 10726–10759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (245).Byler DM; Susi H Examination of the Secondary Structure of Proteins by Deconvolved FTIR Spectra. Biopolymers 1986, 25, 469–487. [DOI] [PubMed] [Google Scholar]
- (246).Miyazawa T Perturbation Treatment of the Characteristic Vibrations of Polypeptide Chains in Various Configurations. J. Chem. Phys 1960, 32, 1647–1652. [Google Scholar]
- (247).Mantsch HH; Casal HL; Jones RN In Spectroscopy of Biological Systems; Clark RJH; Hester RE, Eds.; Wiley: New York, 1986; Vol. 13. [Google Scholar]
- (248).Surewicz WK; Mantsch HH; Chapman D Determination of Protein Secondary Structure by Fourier Transform Infrared Spectroscopy: A Critical Assessment. Biochemistry 1993, 32, 389–394. [DOI] [PubMed] [Google Scholar]
- (249).Torii H; Tasumi M In Infrared Spectroscopy of Biomolecules; Mantsch HH; Chapman D, Eds.; Wiley-Liss: New York, 1996. [Google Scholar]
- (250).Barth A Infrared Spectroscopy of Proteins. Biochim. Biophys. Acta, Bioenerg 2007, 1767, 1073–1101. [DOI] [PubMed] [Google Scholar]
- (251).Schweitzer-Stenner R Visible and UV-Resonance Raman Spectroscopy of Model Peptides. J. Raman Spectrosc 2001, 32, 711–732. [Google Scholar]
- (252).Brauner JW; Flach CR; Mendelsohn R A Quantitative Reconstruction of the Amide I Contour in the IR Spectra of Globular Proteins: From Structure to Spectrum. J. Am. Chem. Soc 2005, 127, 100–109. [DOI] [PubMed] [Google Scholar]
- (253).Chen XG; Schweitzer-Stenner R; Krimm S; Mirkin NG; Asher SA N-Methylacetamide and Its Hydrogen-Bonded Water Molecules Are Vibrationally Coupled. J. Am. Chem. Soc 1994, 116, 11141–11142. [Google Scholar]
- (254).Hamm P; Lim M; DeGrado WF; Hochstrasser RM The Two-Dimensional IR Nonlinear Spectroscopy of a Cyclic Penta-Peptide in Relation to Its Three-Dimensional Structure. Proc. Natl. Acad. Sci. U.S.A 1999, 96, 2036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (255).Buchanan LE; Carr JK; Fluitt AM; Hoganson AJ; Moran SD; de Pablo JJ; Skinner JL; Zanni MT Structural Motif of Polyglutamine Amyloid Fibrils Discerned with Mixed-Isotope Infrared Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2014, 111, 5796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (256).Serrano AL; Lomont JP; Tu L-H; Raleigh DP; Zanni MT A Free Energy Barrier Caused by the Refolding of an Oligomeric Intermediate Controls the Lag Time of Amyloid Formation by hIAPP. J. Am. Chem. Soc 2017, 139, 16748–16758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (257).Torii H Effects of Intermolecular Vibrational Coupling and Liquid Dynamics on the Polarized Raman and Two-Dimensional Infrared Spectral Profiles of Liquid N,N-Dimethylformamide Analyzed with a Time-Domain Computational Method. J. Phys. Chem. A 2006, 110, 4822–4832. [DOI] [PubMed] [Google Scholar]
- (258).Torii H Electrostatic Origin of the Cooperative Effect on the CO Bond Lengths and the Amide I Vibrational Frequencies of the N-Methylacetamide Oligomers. J. Mol. Struct 2005, 735–736, 21–26. [Google Scholar]
- (259).Reppert M; Tokmakoff A Computational Amide I 2D IR Spectroscopy as a Probe of Protein Structure and Dynamics. Annu. Rev. Phys. Chem 2016, 67, 359–386. [DOI] [PubMed] [Google Scholar]
- (260).Reppert M; Tokmakoff A Electrostatic Frequency Shifts in Amide I Vibrational Spectra: Direct Parameterization Against Experiment. J. Chem. Phys 2013, 138, 134116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (261).Wang L; Middleton CT; Zanni MT; Skinner JL Development and Validation of Transferable Amide I Vibrational Frequency Maps for Peptides. J. Phys. Chem. B 2011, 115, 3713–3724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (262).Ham S; Cho M Amide I Modes in the N-Methylacetamide Dimer and Glycine Dipeptide Analog: Diagonal Force Constants. J. Chem. Phys 2003, 118, 6915–6922. [Google Scholar]
- (263).Andrushchenko V; Matějka P; Anderson DT; Kaminský J; Horníček J; Paulson LO; Bouř P Solvent Dependence of the N-Methylacetamide Structure and Force Field. J. Phys. Chem. A 2009, 113, 9727–9736. [DOI] [PubMed] [Google Scholar]
- (264).Reppert M; Tokmakoff A Communication: Quantitative Multi-Site Frequency Maps for Amide I Vibrational Spectroscopy. J. Chem. Phys 2015, 143, 061102. [DOI] [PubMed] [Google Scholar]
- (265).Jansen TLC Linear Absorption and Two-Dimensional Infrared Spectra of N-Methylacetamide in Chloroform Revisited: Polarizability and Multipole Effects. J. Phys. Chem. B 2014, 118, 8162–8169. [DOI] [PubMed] [Google Scholar]
- (266).Bondarenko AS; Jansen TLC Application of Two-Dimensional Infrared Spectroscopy to Benchmark Models for the Amide I Band of Proteins. J. Chem. Phys 2015, 142, 212437. [DOI] [PubMed] [Google Scholar]
- (267).Reppert M; Roy AR; Tempkin JOB; Dinner AR; Tokmakoff A Refining Disordered Peptide Ensembles with Computational Amide I Spectroscopy: Application to Elastin-Like Peptides. J. Phys. Chem. B 2016, 120, 11395–11404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (268).Jansen TLC; Dijkstra AG; Watson TM; Hirst JD; Knoester J Erratum: “Modeling the Amide I Bands of Small Peptides” [J. Chem. Phys. 125, 044312 (2006)]. J. Chem. Phys 2012, 136, 209901. [DOI] [PubMed] [Google Scholar]
- (269).Gorbunov RD; Kosov DS; Stock G Ab Initio-Based Exciton Model of Amide I Vibrations in Peptides: Definition, Conformational Dependence, and Transferability. J. Chem. Phys 2005, 122, 224904. [DOI] [PubMed] [Google Scholar]
- (270).Moore WH; Krimm S Transition Dipole Coupling in Amide I Modes of β Polypeptides. Proc. Natl. Acad. Sci. U.S.A 1975, 72, 4933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (271).Torii H; Tasumi M Ab Initio Molecular Orbital Study of the Amide I Vibrational Interactions between the Peptide Groups in Di- and Tripeptides and Considerations on the Conformation of the Extended Helix. J. Raman Spectrosc 1998, 29, 81–86. [Google Scholar]
- (272).Hamm P; Woutersen S Coupling of the Amide I Modes of the Glycine Dipeptide. Bull. Chem. Soc. Jpn 2002, 75, 985–988. [Google Scholar]
- (273).Zhuang W; Abramavicius D; Hayashi T; Mukamel S Simulation Protocols for Coherent Femtosecond Vibrational Spectra of Peptides. J. Phys. Chem. B 2006, 110, 3362–3374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (274).Torii H; Tasumi M Model Calculations on the Amide-I Infrared Bands of Globular Proteins. J. Chem. Phys 1992, 96, 3379–3387. [Google Scholar]
- (275).Moran A; Mukamel S The Origin of Vibrational Mode Couplings in Various Secondary Structural Motifs of Polypeptides. Proc. Natl. Acad. Sci. U.S.A 2004, 101, 506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (276).Gorbunov RD; Stock G Ab Initio Based Building Block Model of Amide I Vibrations in Peptides. Chem. Phys. Lett 2007, 437, 272–276. [DOI] [PubMed] [Google Scholar]
- (277).Ham S; Cha S; Choi J-H; Cho M Amide I Modes of Tripeptides: Hessian Matrix Reconstruction and Isotope Effects. J. Chem. Phys 2003, 119, 1451–1461. [Google Scholar]
- (278).Maekawa H; Toniolo C; Broxterman QB; Ge N-H Two-Dimensional Infrared Spectral Signatures of 310- and α-Helical Peptides. J. Phys. Chem. B 2007, 111, 3222–3235. [DOI] [PubMed] [Google Scholar]
- (279).Kabsch W; Sander C Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers 1983, 22, 2577–2637. [DOI] [PubMed] [Google Scholar]
- (280).Cai K; Han C; Wang J Molecular Mechanics Force Field-Based Map for Peptide Amide-I Mode in Solution and Its Application to Alanine Di- and Tripeptides. Phys. Chem. Chem. Phys 2009, 11, 9149–9159. [DOI] [PubMed] [Google Scholar]
- (281).Choi J-H; Lee H; Lee K-K; Hahn S; Cho M Computational Spectroscopy of Ubiquitin: Comparison between Theory and Experiments. J. Chem. Phys 2007, 126, 045102. [DOI] [PubMed] [Google Scholar]
- (282).Cunha AV; Bondarenko AS; Jansen TL C. Assessing Spectral Simulation Protocols for the Amide I Band of Proteins. J. Chem. Theory Comput 2016, 12, 3982–3992. [DOI] [PubMed] [Google Scholar]
- (283).Baiz CR; Peng CS; Reppert ME; Jones KC; Tokmakoff A Coherent Two-Dimensional Infrared Spectroscopy: Quantitative Analysis of Protein Secondary Structure in Solution. Analyst 2012, 137, 1793–1799. [DOI] [PubMed] [Google Scholar]
- (284).Jorgensen WL; Tirado-Rives J Potential Energy Functions for Atomic-Level Simulations of Water and Organic and Biomolecular Systems. Proc. Natl. Acad. Sci. U.S.A 2005, 102, 6665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (285).Cunha AV; Salamatova E; Bloem R; Roeters SJ; Woutersen S; Pshenichnikov MS; Jansen TLC Interplay between Hydrogen Bonding and Vibrational Coupling in Liquid N-Methylacetamide. J. Phys. Chem. Lett 2017, 8, 2438–2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (286).Salamatova E; Cunha AV; Bloem R; Roeters SJ; Woutersen S; Jansen TLC; Pshenichnikov MS Hydrophobic Collapse in N-Methylacetamide–Water Mixtures. J. Phys. Chem. A 2018, 122, 2468–2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (287).Cheng X; Steele RP Efficient Anharmonic Vibrational Spectroscopy for Large Molecules Using Local-Mode Coordinates. J. Chem. Phys 2014, 141, 104105. [DOI] [PubMed] [Google Scholar]
- (288).Panek PT; Jacob CR Efficient Calculation of Anharmonic Vibrational Spectra of Large Molecules with Localized Modes. ChemPhysChem 2014, 15, 3365–3377. [DOI] [PubMed] [Google Scholar]
- (289).Hanson-Heine MWD Examining the Impact of Harmonic Correlation on Vibrational Frequencies Calculated in Localized Coordinates. J. Chem. Phys 2015, 143, 164104. [DOI] [PubMed] [Google Scholar]
- (290).Molina A; Smereka P; Zimmerman PM Exploring the Relationship between Vibrational Mode Locality and Coupling Using Constrained Optimization. J. Chem. Phys 2016, 144, 124111. [DOI] [PubMed] [Google Scholar]
- (291).Zimmerman PM; Smereka P Optimizing Vibrational Coordinates to Modulate Intermode Coupling. J. Chem. Theory Comput 2016, 12, 1883–1891. [DOI] [PubMed] [Google Scholar]
- (292).Hanson-Heine MWD Intermediate Vibrational Coordinate Localization with Harmonic Coupling Constraints. J. Chem. Phys 2016, 144, 204116. [DOI] [PubMed] [Google Scholar]
- (293).Panek PT; Jacob CR Anharmonic Theoretical Vibrational Spectroscopy of Polypeptides. J. Phys. Chem. Lett 2016, 7, 3084–3090. [DOI] [PubMed] [Google Scholar]
- (294).Panek PT; Jacob CR On the Benefits of Localized Modes in Anharmonic Vibrational Calculations for Small Molecules. J. Chem. Phys 2016, 144, 164111. [DOI] [PubMed] [Google Scholar]
- (295).Hanson-Heine MWD Reduced Basis Set Dependence in Anharmonic Frequency Calculations Involving Localized Coordinates. J. Chem. Theory Comput 2018, 14, 1277–1285. [DOI] [PubMed] [Google Scholar]
- (296).Panek PT; Hoeske AA; Jacob CR On the Choice of Coordinates in Anharmonic Theoretical Vibrational Spectroscopy: Harmonic vs. Anharmonic Coupling in Vibrational Configuration Interaction. J. Chem. Phys 2019, 150, 054107. [DOI] [PubMed] [Google Scholar]
- (297).Hanson-Heine MWD; Husseini FS; Hirst JD; Besley NA Simulation of Two-Dimensional Infrared Spectroscopy of Peptides Using Localized Normal Modes. J. Chem. Theory Comput 2016, 12, 1905–1918. [DOI] [PubMed] [Google Scholar]
- (298).Jacob CR; Reiher M Localizing Normal Modes in Large Molecules. J. Chem. Phys 2009, 130, 084106. [DOI] [PubMed] [Google Scholar]
- (299).Tadesse L; Nazarbaghi R; Walters L Isotopically Enhanced Infrared Spectroscopy: A Novel Method for Examining Secondary Structure at Specific Sites in Conformationally Heterogeneous Peptides. J. Am. Chem. Soc 1991, 113, 7036–7037. [Google Scholar]
- (300).Arkin IT Isotope-Edited IR Spectroscopy for the Study of Membrane Proteins. Curr. Opin. Chem. Biol 2006, 10, 394–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (301).Fang C; Wang J; Charnley AK; Barber-Armstrong W; Smith III AB; Decatur SM; Hochstrasser RM Two-Dimensional Infrared Measurements of the Coupling between Amide Modes of an α-Helix. Chem. Phys. Lett 2003, 382, 586–592. [Google Scholar]
- (302).Moran SD; Decatur SM; Zanni MT Structural and Sequence Analysis of the Human γD-Crystallin Amyloid Fibril Core Using 2D IR Spectroscopy, Segmental 13C Labeling, and Mass Spectrometry. J. Am. Chem. Soc 2012, 134, 18410–18416. [DOI] [PubMed] [Google Scholar]
- (303).Huang R; Kubelka J; Barber-Armstrong W; Silva RAGD; Decatur SM; Keiderling TA Nature of Vibrational Coupling in Helical Peptides: An Isotopic Labeling Study. J. Am. Chem. Soc 2004, 126, 2346–2354. [DOI] [PubMed] [Google Scholar]
- (304).Ding B; Laaser JE; Liu Y; Wang P; Zanni MT; Chen Z Site-Specific Orientation of an α-Helical Peptide Ovispirin-1 from Isotope-Labeled SFG Spectroscopy. J. Phys. Chem. B 2013, 117, 14625–14634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (305).Manor J; Arkin IT Gaining Insight into Membrane Protein Structure Using Isotope-Edited FTIR. Biochimica et Biophysica Acta (BBA) - Biomembranes 2013, 1828, 2256–2264. [DOI] [PubMed] [Google Scholar]
- (306).Manor J; Arbely E; Beerlink A; Akkawi M; Arkin IT Use of Isotope-Edited FTIR to Derive a Backbone Structure of a Transmembrane Protein. J. Phys. Chem. Lett 2014, 5, 2573–2579. [DOI] [PubMed] [Google Scholar]
- (307).Buchanan LE; Dunkelberger EB; Tran HQ; Cheng P-N; Chiu C-C; Cao P; Raleigh DP; de Pablo JJ; Nowick JS; Zanni MT Mechanism of IAPP Amyloid Fibril Formation Involves an Intermediate with a Transient β-Sheet. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 19285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (308).Shim S-H; Gupta R; Ling YL; Strasfeld DB; Raleigh DP; Zanni MT Two-Dimensional IR Spectroscopy and Isotope Labeling Defines the Pathway of Amyloid Formation with Residue-Specific Resolution. Proc. Natl. Acad. Sci. U.S.A 2009, 106, 6614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (309).Middleton CT; Marek P; Cao P; Chiu C.-c.; Singh S; Woys AM; de Pablo JJ; Raleigh DP; Zanni MT Two-Dimensional Infrared Spectroscopy Reveals the Complex Behaviour of an Amyloid Fibril Inhibitor. Nature Chemistry 2012, 4, 355–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (310).Dunkelberger EB; Buchanan LE; Marek P; Cao P; Raleigh DP; Zanni MT Deamidation Accelerates Amyloid Formation and Alters Amylin Fiber Structure. J. Am. Chem. Soc 2012, 134, 12658–12667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (311).Smith AW; Lessing J; Ganim Z; Peng CS; Tokmakoff A; Roy S; Jansen TLC; Knoester J Melting of a β-Hairpin Peptide Using Isotope-Edited 2D IR Spectroscopy and Simulations. J. Phys. Chem. B 2010, 114, 10913–10924. [DOI] [PubMed] [Google Scholar]
- (312).Wang L; Middleton CT; Singh S; Reddy AS; Woys AM; Strasfeld DB; Marek P; Raleigh DP; de Pablo JJ; Zanni MT et al. 2DIR Spectroscopy of Human Amylin Fibrils Reflects Stable β-Sheet Structure. J. Am. Chem. Soc 2011, 133, 16062–16071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (313).Woys AM; Almeida AM; Wang L; Chiu C-C; McGovern M; de Pablo JJ; Skinner JL; Gellman SH; Zanni MT Parallel β-Sheet Vibrational Couplings Revealed by 2D IR Spectroscopy of an Isotopically Labeled Macrocycle: Quantitative Benchmark for the Interpretation of Amyloid and Protein Infrared Spectra. J. Am. Chem. Soc 2012, 134, 19118–19128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (314).Moore WH; Krimm S Vibrational Analysis of Peptides, Polypeptides, and Proteins. I. Polyglycine I. Biopolymers 1976, 15, 2439–2464. [DOI] [PubMed] [Google Scholar]
- (315).Woutersen S; Pfister R; Hamm P; Mu Y; Kosov DS; Stock G Peptide Conformational Heterogeneity Revealed from Nonlinear Vibrational Spectroscopy and Molecular-Dynamics Simulations. J. Chem. Phys 2002, 117, 6833–6840. [Google Scholar]
- (316).Choi J-H; Cho M Calculations of Intermode Coupling Constants and Simulations of Amide I, II, and III Vibrational Spectra of Dipeptides. Chem. Phys 2009, 361, 168–175. [Google Scholar]
- (317).DeFlores LP; Ganim Z; Ackley SF; Chung HS; Tokmakoff A The Anharmonic Vibrational Potential and Relaxation Pathways of the Amide I and II Modes of N-Methylacetamide. J. Phys. Chem. B 2006, 110, 18973–18980. [DOI] [PubMed] [Google Scholar]
- (318).Bloem R; Dijkstra AG; Jansen TLC; Knoester J Simulation of Vibrational Energy Transfer in Two-Dimensional Infrared Spectroscopy of Amide I and Amide II Modes in Solution. J. Chem. Phys 2008, 129, 055101. [DOI] [PubMed] [Google Scholar]
- (319).Dijkstra AG; Jansen TLC; Knoester J Modeling the Vibrational Dynamics and Nonlinear Infrared Spectra of Coupled Amide I and II Modes in Peptides. J. Phys. Chem. B 2011, 115, 5392–5401. [DOI] [PubMed] [Google Scholar]
- (320).Rubtsov IV; Wang J; Hochstrasser RM Dual-Frequency 2D-IR Spectroscopy Heterodyned Photon Echo of the Peptide Bond. Proc. Natl. Acad. Sci. U.S.A 2003, 100, 5601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (321).Maekawa H; Ballano G; Toniolo C; Ge N-H Linear and Two-Dimensional Infrared Spectroscopic Study of the Amide I and II Modes in Fully Extended Peptide Chains. J. Phys. Chem. B 2011, 115, 5168–5182. [DOI] [PubMed] [Google Scholar]
- (322).Maekawa H; De Poli M; Toniolo C; Ge N-H Couplings between Peptide Linkages across a 310-Helical Hydrogen Bond Revealed by Two-Dimensional Infrared Spectroscopy. J. Am. Chem. Soc 2009, 131, 2042–2043. [DOI] [PubMed] [Google Scholar]
- (323).Dunkelberger EB; Woys AM; Zanni MT 2D IR Cross Peaks Reveal Hydrogen–Deuterium Exchange with Single Residue Specificity. J. Phys. Chem. B 2013, 117, 15297–15305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (324).DeFlores LP; Tokmakoff A Water Penetration into Protein Secondary Structure Revealed by Hydrogen-Deuterium Exchange Two-Dimensional Infrared Spectroscopy. J. Am. Chem. Soc 2006, 128, 16520–16521. [DOI] [PubMed] [Google Scholar]
- (325).Giubertoni G; Meister K; DeVries AL; Bakker HJ Determination of the Solution Structure of Antifreeze Glycoproteins Using Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. Lett 2019, 10, 352–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (326).Hayashi T; Mukamel S Two-Dimensional Vibrational Lineshapes of Amide III, II, I and a Bands in a Helical Peptide. J. Mol. Liq 2008, 141, 149–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (327).Hayashi T; Mukamel S Vibrational-Exciton Couplings for the Amide I, II, III, and a Modes of Peptides. J. Phys. Chem. B 2007, 111, 11032–11046. [DOI] [PubMed] [Google Scholar]
- (328).Harms GS; Pauls SW; Hedstrom JF; Johnson CK Tyrosyl Fluorescence Decays and Rotational Dynamics in Tyrosine Monomers and in Dipeptides. Journal of Fluorescence 1997, 7, 273–282. [Google Scholar]
- (329).Sul S; Feng Y; Le U; Tobias DJ; Ge N-H Interactions of Tyrosine in Leu-Enkephalin at a Membrane-Water Interface: An Ultrafast Two-Dimensional Infrared Study Combined with Density Functional Calculations and Molecular Dynamics Simulations. J. Phys. Chem. B 2010, 114, 1180–1190. [DOI] [PubMed] [Google Scholar]
- (330).Rubtsov IV; Hochstrasser RM Vibrational Dynamics, Mode Coupling, and Structural Constraints for Acetylproline-NH2. J. Phys. Chem. B 2002, 106, 9165–9171. [Google Scholar]
- (331).Cai K; Du F; Zheng X; Liu J; Zheng R; Zhao J; Wang J General Applicable Frequency Map for the Amide-I Mode in β-Peptides. J. Phys. Chem. B 2016, 120, 1069–1079. [DOI] [PubMed] [Google Scholar]
- (332).Zhao J; Wang J Understanding the Amide-II Vibrations in β-Peptides. J. Phys. Chem. B 2015, 119, 14831–14839. [DOI] [PubMed] [Google Scholar]
- (333).Zhao J; Wang J Dissecting Amide-I Vibration in β-Peptide Helices. J. Phys. Chem. B 2015, 119, 3387–3397. [DOI] [PubMed] [Google Scholar]
- (334).Kim J-H; Cho M Interplay of the Intramolecular Water Vibrations and Hydrogen Bond in N-Methylacetamide-Water Complexes: Ab Initio Calculation Studies Bull. Korean Chem. Soc 2003, 24, 1061. [Google Scholar]
- (335).van Wilderen LJGW; Brunst H; Gustmann H; Wachtveitl J; Broos J; Bredenbeck J Cyano-Tryptophans as Dual Infrared and Fluorescence Spectroscopic Labels to Assess Structural Dynamics in Proteins. Phys. Chem. Chem. Phys 2018, 20, 19906–19915. [DOI] [PubMed] [Google Scholar]
- (336).Biava H; Schreiber T; Katz S; Völler J-S; Stolarski M; Schulz C; Michael N; Budisa N; Kozuch J; Utesch T et al. Long-Range Modulations of Electric Fields in Proteins. J. Phys. Chem. B 2018, 122, 8330–8342. [DOI] [PubMed] [Google Scholar]
- (337).Devereux CJ; Fulfer KD; Zhang X; Kuroda DG Vibrational Spectroscopy Modeling of a Drug in Molecular Solvents and Enzymes. Chem. Phys 2017, 495, 1–9. [Google Scholar]
- (338).Torii H Unified Electrostatic Understanding on the Solvation-Induced Changes in the CN Stretching Frequency and the NMR Chemical Shifts of a Nitrile. J. Phys. Chem. A 2016, 120, 7137–7144. [DOI] [PubMed] [Google Scholar]
- (339).Maienschein-Cline MG; Londergan CH The CN Stretching Band of Aliphatic Thiocyanate Is Sensitive to Solvent Dynamics and Specific Solvation. J. Phys. Chem. A 2007, 111, 10020–10025. [DOI] [PubMed] [Google Scholar]
- (340).van Wilderen LJGW; Kern-Michler D; Müller-Werkmeister HM; Bredenbeck J Correction: Vibrational Dynamics and Solvatochromism of the Label SCN in Various Solvents and Hemoglobin by Time Dependent IR and 2D-IR Spectroscopy. Phys. Chem. Chem. Phys 2017, 19, 9676–9678. [DOI] [PubMed] [Google Scholar]
- (341).Sigala PA; Fafarman AT; Bogard PE; Boxer SG; Herschlag D Do Ligand Binding and Solvent Exclusion Alter the Electrostatic Character within the Oxyanion Hole of an Enzymatic Active Site? J. Am. Chem. Soc 2007, 129, 12104–12105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (342).Blankenburg L; Schroeder L; Habenstein F; Błasiak B; Kottke T; Bredenbeck J Following Local Light-Induced Structure Changes and Dynamics of the Photoreceptor PYP with the Thiocyanate IR Label. Phys. Chem. Chem. Phys 2019, 21, 6622–6634. [DOI] [PubMed] [Google Scholar]
- (343).Schmidt-Engler JM; Blankenburg L; Błasiak B; Wilderen L. J. G. W. v.; Cho M; Bredenbeck, J. Anal. Chem 2019, in press. [DOI] [PubMed] [Google Scholar]
- (344).Deb P; Haldar T; Kashid SM; Banerjee S; Chakrabarty S; Bagchi S Correlating Nitrile IR Frequencies to Local Electrostatics Quantifies Noncovalent Interactions of Peptides and Proteins. J. Phys. Chem. B 2016, 120, 4034–4046. [DOI] [PubMed] [Google Scholar]
- (345).Layfield JP; Hammes-Schiffer S Calculation of Vibrational Shifts of Nitrile Probes in the Active Site of Ketosteroid Isomerase Upon Ligand Binding. J. Am. Chem. Soc 2013, 135, 717–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (346).Okuda M; Higashi M; Ohta K; Saito S; Tominaga K Vibrational Frequency Fluctuations of Ionic Vibrational Probe in Water: Theoretical Study with Molecular Dynamics Simulation. Chem. Phys. Lett 2017, 683, 547–552. [Google Scholar]
- (347).Park K-H; Jeon J; Park Y; Lee S; Kwon H-J; Joo C; Park S; Han H; Cho M Infrared Probes Based on Nitrile-Derivatized Prolines: Thermal Insulation Effect and Enhanced Dynamic Range. J. Phys. Chem. Lett 2013, 4, 2105–2110. [Google Scholar]
- (348).Yamada SA; Thompson WH; Fayer MD Water-Anion Hydrogen Bonding Dynamics: Ultrafast IR Experiments and Simulations. J. Chem. Phys 2017, 146, 234501. [DOI] [PubMed] [Google Scholar]
- (349).Creon A; Josts I; Niebling S; Huse N; Tidow H Conformation-Specific Detection of Calmodulin Binding Using the Unnatural Amino Acid P-Azido-Phenylalanine (AzF) as an IR-Sensor. Struct. Dyn 2018, 5, 064701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (350).Thielges MC; Axup JY; Wong D; Lee HS; Chung JK; Schultz PG; Fayer MD Two-Dimensional IR Spectroscopy of Protein Dynamics Using Two Vibrational Labels: A Site-Specific Genetically Encoded Unnatural Amino Acid and an Active Site Ligand. J. Phys. Chem. B 2011, 115, 11294–11304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (351).Zhang J; Wang L; Zhang J; Zhu J; Pan X; Cui Z; Wang J; Fang W; Li Y Identifying and Modulating Accidental Fermi Resonance: 2D IR and DFT Study of 4-Azido-L-Phenylalanine. J. Phys. Chem. B 2018, 122, 8122–8133. [DOI] [PubMed] [Google Scholar]
- (352).Müller-Werkmeister HM; Li Y-L; Lerch E-BW; Bigourd D; Bredenbeck J Ultrafast Hopping from Band to Band: Assigning Infrared Spectra Based on Vibrational Energy Transfer. Angew. Chem. Int. Ed 2013, 52, 6214–6217. [DOI] [PubMed] [Google Scholar]
- (353).Lešetický L; Barth R; Nêmec I; Štícha M; Tišlerová I Synthesis and Spectra of N-15 Labelled Phenylazides. Czech. J. Phys 2003, 53, A777–A782. [Google Scholar]
- (354).Baumann T; Hauf M; Schildhauer F; Eberl KB; Durkin PM; Deniz E; Löffler JG; Acevedo-Rocha CG; Jaric J; Martins BM et al. Site-Resolved Observation of Vibrational Energy Transfer Using a Genetically Encoded Ultrafast Heater. Angew. Chem. Int. Ed 2019, 58, 2899–2903. [DOI] [PubMed] [Google Scholar]
- (355).Taskent-Sezgin H; Chung J; Banerjee PS; Nagarajan S; Dyer RB; Carrico I; Raleigh DP Azidohomoalanine: A Conformationally Sensitive IR Probe of Protein Folding, Protein Structure, and Electrostatics. Angew. Chem. Int. Ed 2010, 49, 7473–7475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (356).Park ES; Boxer SG Origins of the Sensitivity of Molecular Vibrations to Electric Fields: Carbonyl and Nitrosyl Stretches in Model Compounds and Proteins. J. Phys. Chem. B 2002, 106, 5800–5806. [Google Scholar]
- (357).Lim M; Jackson TA; Anfinrud PA Ultrafast Rotation and Trapping of Carbon Monoxide Dissociated from Myoglobin. Nature Structural Biology 1997, 4, 209–214. [DOI] [PubMed] [Google Scholar]
- (358).Anselmi M; Aschi M; Di Nola A; Amadei A Theoretical Characterization of Carbon Monoxide Vibrational Spectrum in Sperm Whale Myoglobin Distal Pocket. Biophys. J 2007, 92, 3442–3447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (359).Wang X. w.; Zhang JZH; He X Ab Initio Quantum Mechanics/Molecular Mechanics Molecular Dynamics Simulation of CO in the Heme Distal Pocket of Myoglobin. Chin. J. Chem. Phys 2017, 30, 705–716. [Google Scholar]
- (360).Choi J-H; Kwak K-W; Cho M Computational Infrared and Two-Dimensional Infrared Photon Echo Spectroscopy of Both Wild-Type and Double Mutant Myoglobin-CO Proteins. J. Phys. Chem. B 2013, 117, 15462–15478. [DOI] [PubMed] [Google Scholar]
- (361).Park ES; Andrews SS; Hu RB; Boxer SG Vibrational Stark Spectroscopy in Proteins: A Probe and Calibration for Electrostatic Fields. J. Phys. Chem. B 1999, 103, 9813–9817. [Google Scholar]
- (362).Torii H Theoretical Analysis and Modeling of the Electrostatic Responses of the Vibrational and NMR Spectroscopic Properties of the Cyanide Anion. J. Mol. Liq 2019, 284, 773–779. [Google Scholar]
- (363).Dluhy R; Cameron DG; Mantsch HH; Mendelsohn R Fourier Transform Infrared Spectroscopic Studies of the Effect of Calcium Ions on Phosphatidylserine. Biochemistry 1983, 22, 6318–6325. [Google Scholar]
- (364).Valentine ML; Cardenas AE; Elber R; Baiz CR Physiological Calcium Concentrations Slow Dynamics at the Lipid-Water Interface. Biophys. J 2018, 115, 1541–1551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (365).Guerin AC; Riley K; Rupnik K; Kuroda DG Determining the Energetics of the Hydrogen Bond through FTIR: A Hands-on Physical Chemistry Lab Experiment. J. Chem. Educ 2016, 93, 1124–1129. [Google Scholar]
- (366).Edington SC; Flanagan JC; Baiz CR An Empirical IR Frequency Map for Ester C═O Stretching Vibrations. J. Phys. Chem. A 2016, 120, 3888–3896. [DOI] [PubMed] [Google Scholar]
- (367).Yu Y; Shi L Vibrational Solvatochromism of the Ester Carbonyl Vibration of PCBM in Organic Solutions. J. Chem. Phys 2019, 151, 064501. [Google Scholar]
- (368).Meng W; Jiang Y; Rothschild D; Lipke M; Hall G; Wang L Modeling the structure and infrared spectra of omega-3 fatty acid esters. J. Chem. Phys 2020, 153, 035101. [DOI] [PubMed] [Google Scholar]
- (369).Fang B; Wang T; Chen X; Jin T; Zhang R; Zhuang W Modeling Vibrational Spectra of Ester Carbonyl Stretch in Water and Dmso Based on Molecular Dynamics Simulation. J. Phys. Chem. B 2015, 119, 12390–12396. [DOI] [PubMed] [Google Scholar]
- (370).Baryiames CP; Teel M; Baiz CR Interfacial H-Bond Dynamics in Reverse Micelles: The Role of Surfactant Heterogeneity. Langmuir 2019, 35, 11463–11470. [DOI] [PubMed] [Google Scholar]
- (371).Ghosh A; Cohn B; Prasad AK; Chuntonov L Quantifying Conformations of Ester Vibrational Probes with Hydrogen-Bond-Induced Fermi Resonances. J. Chem. Phys 2018, 149, 184501. [DOI] [PubMed] [Google Scholar]
- (372).Xu K Electrolytes and Interphases in Li-Ion Batteries and Beyond. Chem. Rev 2014, 114, 11503–11618. [DOI] [PubMed] [Google Scholar]
- (373).Lee K-K; Park K; Lee H; Noh Y; Kossowska D; Kwak K; Cho M Ultrafast Fluxional Exchange Dynamics in Electrolyte Solvation Sheath of Lithium Ion Battery. Nature Communications 2017, 8, 14658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (374).Lim J; Lee K-K; Liang C; Park K-H; Kim M; Kwak K; Cho M Two-Dimensional Infrared Spectroscopy and Molecular Dynamics Simulation Studies of Nonaqueous Lithium Ion Battery Electrolytes. J. Phys. Chem. B 2019, 123, 6651–6663. [DOI] [PubMed] [Google Scholar]
- (375).Liang C; Kwak K; Cho M Revealing the Solvation Structure and Dynamics of Carbonate Electrolytes in Lithium-Ion Batteries by Two-Dimensional Infrared Spectrum Modeling. J. Phys. Chem. Lett 2017, 8, 5779–5784. [DOI] [PubMed] [Google Scholar]
- (376).Fulfer KD; Kuroda DG Solvation Structure and Dynamics of the Lithium Ion in Organic Carbonate-Based Electrolytes: A Time-Dependent Infrared Spectroscopy Study. J. Phys. Chem. C 2016, 120, 24011–24022. [Google Scholar]
- (377).Fulfer KD; Kuroda DG Ion Speciation of Lithium Hexafluorophosphate in Dimethyl Carbonate Solutions: An Infrared Spectroscopy Study. Phys. Chem. Chem. Phys 2018, 20, 22710–22718. [DOI] [PubMed] [Google Scholar]
- (378).Li F; Skinner JL Infrared and Raman Line Shapes for Ice Ih. II. H2O and D2O. J. Chem. Phys 2010, 133, 244504. [DOI] [PubMed] [Google Scholar]
- (379).Stenger J; Madsen D; Hamm P; Nibbering ETJ; Elsaesser T A Photon Echo Peak Shift Study of Liquid Water. J. Phys. Chem. A 2002, 106, 2341–2350. [Google Scholar]
- (380).Stenger J; Madsen D; Hamm P; Nibbering ETJ; Elsaesser T Ultrafast Vibrational Dephasing of Liquid Water. Phys. Rev. Lett 2001, 87, 027401. [Google Scholar]
- (381).Schauss J; Kundu A; Fingerhut BP; Elsaesser T Contact Ion Pairs of Phosphate Groups in Water: Two-Dimensional Infrared Spectroscopy of Dimethyl Phosphate and Ab Initio Simulations. J. Phys. Chem. Lett 2019, 10, 6281–6286. [DOI] [PubMed] [Google Scholar]
- (382).Yeremenko S; Pshenichnikov MS; Wiersma DA Hydrogen-Bond Dynamics in Water Explored by Heterodyne-Detected Photon Echo. Chem. Phys. Lett 2003, 369, 107–113. [Google Scholar]
- (383).Asbury JB; Steinel T; Stromberg C; Corcelli SA; Lawrence CP; Skinner JL; Fayer MD Water Dynamics: Vibrational Echo Correlation Spectroscopy and Comparison to Molecular Dynamics Simulations. J. Phys. Chem. A 2004, 108, 1107–1119. [Google Scholar]
- (384).Asbury JB; Steinel T; Kwak K; Corcelli SA; Lawrence CP; Skinner JL; Fayer MD Dynamics of Water Probed with Vibrational Echo Correlation Spectroscopy. J. Chem. Phys 2004, 121, 12431–12446. [DOI] [PubMed] [Google Scholar]
- (385).Rey R; Moller KB; Hynes JT Hydrogen Bond Dynamics in Water and Ultrafast Infrared Spectroscopy. J. Phys. Chem. A 2002, 106, 11993–11996. [Google Scholar]
- (386).Lawrence CP; Skinner JL Vibrational Spectroscopy of HOD in Liquid D2O. III. Spectral Diffusion, and Hydrogen-Bonding and Rotational Dynamics. J. Chem. Phys 2003, 118, 264–272. [Google Scholar]
- (387).Schmidt JR; Roberts ST; Loparo JJ; Tokmakoff A; Fayer MD; Skinner JL Are Water Simulation Models Consistent with Steady-State and Ultrafast Vibrational Spectroscopy Experiments? Chem. Phys 2007, 341, 143–157. [Google Scholar]
- (388).Corcelli SA; Lawrence CP; Asbury JB; Steinel T; Fayer MD; Skinner JL Spectral Diffusion in a Fluctuating Charge Model of Water. J. Chem. Phys 2004, 121, 8897–8900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (389).Colbert DT; Miller WH A Novel Discrete Variable Representation for Quantum-Mechanical Reactive Scattering Via the S-Matrix Kohn Method. J. Chem. Phys 1992, 96, 1982–1991. [Google Scholar]
- (390).Auer B; Kumar R; Schmidt JR; Skinner JL Hydrogen Bonding and Raman, IR, and 2D-IR Spectroscopy of Dilute HOD in Liquid D2O. Proc. Natl. Acad. Sci. U.S.A 2007, 104, 14215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (391).Paarmann A; Hayashi T; Mukamel S; Miller RJD Nonlinear Response of Vibrational Excitons: Simulating the Two-Dimensional Infrared Spectrum of Liquid Water. J. Chem. Phys 2009, 130, 204110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (392).Lin YS; Auer BM; Skinner JL Water Structure, Dynamics, and Vibrational Spectroscopy in Sodium Bromide Solutions. J. Chem. Phys 2009, 131, 144511. [DOI] [PubMed] [Google Scholar]
- (393).Terranova ZL; Corcelli SA Molecular Dynamics Investigation of the Vibrational Spectroscopy of Isolated Water in an Ionic Liquid. J. Phys. Chem. B 2014, 118, 8264–8272. [DOI] [PubMed] [Google Scholar]
- (394).Stiopkin IV; Weeraman C; Pieniazek PA; Shalhout FY; Skinner JL; Benderskii AV Hydrogen Bonding at the Water Surface Revealed by Isotopic Dilution Spectroscopy. Nature 2011, 474, 192–195. [DOI] [PubMed] [Google Scholar]
- (395).Pieniazek PA; Tainter CJ; Skinner JL Interpretation of the Water Surface Vibrational Sum-Frequency Spectrum. J. Chem. Phys 2011, 135, 044701. [DOI] [PubMed] [Google Scholar]
- (396).Ni Y; Skinner JL Communication: Vibrational Sum-Frequency Spectrum of the Air-Water Interface, Revisited. J. Chem. Phys 2016, 145, 031103. [DOI] [PubMed] [Google Scholar]
- (397).Auer BM; Skinner JL Water: Hydrogen Bonding and Vibrational Spectroscopy, in the Bulk Liquid and at the Liquid/Vapor Interface. Chem. Phys. Lett 2009, 470, 13–20. [Google Scholar]
- (398).Auer BM; Skinner JL Vibrational Sum-Frequency Spectroscopy of the Water Liquid/Vapor Interface. J. Phys. Chem. B 2009, 113, 4125–4130. [DOI] [PubMed] [Google Scholar]
- (399).Auer BM; Skinner JL Vibrational Sum-Frequency Spectroscopy of the Liquid/Vapor Interface for Dilute HOD in D2O. J. Chem. Phys 2008, 129, 214705. [DOI] [PubMed] [Google Scholar]
- (400).Ni Y; Gruenbaum SM; Skinner JL Slow Hydrogen-Bond Switching Dynamics at the Water Surface Revealed by Theoretical Two-Dimensional Sum-Frequency Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2013, 110, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (401).Tainter CJ; Ni Y; Shi L; Skinner JL Hydrogen Bonding and OH-Stretch Spectroscopy in Water: Hexamer (Cage), Liquid Surface, Liquid, and Ice. J. Phys. Chem. Lett 2013, 4, 12–17. [DOI] [PubMed] [Google Scholar]
- (402).Tainter CJ; Skinner JL The Water Hexamer: Three-Body Interactions, Structures, Energetics, and OH-Stretch Spectroscopy at Finite Temperature. J. Chem. Phys 2012, 137, 104304. [DOI] [PubMed] [Google Scholar]
- (403).Gruenbaum SM; Pieniazek PA; Skinner JL Vibrational Spectroscopy of Water in Hydrated Lipid Multi-Bilayers. II. Two-Dimensional Infrared and Peak Shift Observables within Different Theoretical Approximations. J. Chem. Phys 2011, 135, 164506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (404).Gruenbaum SM; Skinner JL Vibrational Spectroscopy of Water in Hydrated Lipid Multi-Bilayers. I. Infrared Spectra and Ultrafast Pump-Probe Observables. J. Chem. Phys 2011, 135, 075101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (405).Gruenbaum SM; Skinner JL Vibrational Spectroscopy of Water in Hydrated Lipid Multi-Bilayers. III. Water Clustering and Vibrational Energy Transfer. J. Chem. Phys 2013, 139, 175103. [DOI] [PubMed] [Google Scholar]
- (406).Roy S; Gruenbaum SM; Skinner JL Theoretical Vibrational Sum-Frequency Generation Spectroscopy of Water near Lipid and Surfactant Monolayer Interfaces. II. Two-Dimensional Spectra. J. Chem. Phys 2014, 141, 22d505. [DOI] [PubMed] [Google Scholar]
- (407).Roy S; Gruenbaum SM; Skinner JL Theoretical Vibrational Sum-Frequency Generation Spectroscopy of Water near Lipid and Surfactant Monolayer Interfaces. J. Chem. Phys 2014, 141, 18c502. [DOI] [PubMed] [Google Scholar]
- (408).Bakulin AA; Cringus D; Pieniazek PA; Skinner JL; Jansen TLC; Pshenichnikov MS Dynamics of Water Confined in Reversed Micelles: Multidimensional Vibrational Spectroscopy Study. J. Phys. Chem. B 2013, 117, 15545–15558. [DOI] [PubMed] [Google Scholar]
- (409).Pieniazek PA; Lin Y-S; Chowdhary J; Ladanyi BM; Skinner JL Vibrational Spectroscopy and Dynamics of Water Confined inside Reverse Micelles. J. Phys. Chem. B 2009, 113, 15017–15028. [DOI] [PubMed] [Google Scholar]
- (410).Li F; Skinner JL Infrared and Raman Line Shapes for Ice Ih. I. Dilute HOD in H2O and D2O. J. Chem. Phys 2010, 132, 204505. [DOI] [PubMed] [Google Scholar]
- (411).Shi L; Gruenbaum SM; Skinner JL Interpretation of IR and Raman Line Shapes for H2O and D2O Ice Ih. J. Phys. Chem. B 2012, 116, 13821–13830. [DOI] [PubMed] [Google Scholar]
- (412).Shi L; Skinner JL; Jansen TLC Two-Dimensional Infrared Spectroscopy of Neat Ice Ih. Phys. Chem. Chem. Phys 2016, 18, 3772–3779. [DOI] [PubMed] [Google Scholar]
- (413).Gruenbaum SM; Tainter CJ; Shi L; Ni Y; Skinner JL Robustness of Frequency, Transition Dipole, and Coupling Maps for Water Vibrational Spectroscopy. J. Chem. Theory Comput 2013, 9, 3109–3117. [DOI] [PubMed] [Google Scholar]
- (414).Kananenka AA; Yao K; Corcelli SA; Skinner JL Machine Learning for Vibrational Spectroscopic Maps. J. Chem. Theory Comput 2019, 15, 6850–6858. [DOI] [PubMed] [Google Scholar]
- (415).Corcelli SA; Skinner JL Infrared and Raman Line Shapes of Dilute HOD in Liquid H2O and D2O from 10 to 90 °C. J. Phys. Chem. A 2005, 109, 6154–6165. [DOI] [PubMed] [Google Scholar]
- (416).Auer BM; Skinner JL Dynamical Effects in Line Shapes for Coupled Chromophores: Time-Averaging Approximation. J. Chem. Phys 2007, 127, 104105. [DOI] [PubMed] [Google Scholar]
- (417).Yang M; Skinner JL Signatures of Coherent Vibrational Energy Transfer in IR and Raman Line Shapes for Liquid Water. Phys. Chem. Chem. Phys 2010, 12, 982–991. [DOI] [PubMed] [Google Scholar]
- (418).Yang M; Skinner JL Time-Averaging Approximation in the Interaction Picture: Absorption Line Shapes for Coupled Chromophores with Application to Liquid Water. J. Chem. Phys 2011, 135, 154114. [DOI] [PubMed] [Google Scholar]
- (419).Auer BM; Skinner JL IR and Raman Spectra of Liquid Water: Theory and Interpretation. J. Chem. Phys 2008, 128, 224511. [DOI] [PubMed] [Google Scholar]
- (420).Torii H Time-Domain Calculations of the Polarized Raman Spectra, the Transient Infrared Absorption Anisotropy, and the Extent of Delocalization of the OH Stretching Mode of Liquid Water. J. Phys. Chem. A 2006, 110, 9469–9477. [DOI] [PubMed] [Google Scholar]
- (421).Choi J-H; Cho M Computational IR Spectroscopy of Water: OH Stretch Frequencies, Transition Dipoles, and Intermolecular Vibrational Coupling Constants. J. Chem. Phys 2013, 138, 174108. [DOI] [PubMed] [Google Scholar]
- (422).Li F; Skinner JL Erratum: “Infrared and Raman Line Shapes for Ice Ih. II. H2O and D2O” [J. Chem. Phys. 133, 244504 (2010)]. J. Chem. Phys 2011, 134, 099901. [DOI] [PubMed] [Google Scholar]
- (423).Biswas R; Carpenter W; Voth GA; Tokmakoff A Molecular Modeling and Assignment of IR Spectra of the Hydrated Excess Proton in Isotopically Dilute Water. J. Chem. Phys 2016, 145, 154504. [DOI] [PubMed] [Google Scholar]
- (424).Cowan ML; Bruner BD; Huse N; Dwyer JR; Chugh B; Nibbering ETJ; Elsaesser T; Miller RJD Ultrafast Memory Loss and Energy Redistribution in the Hydrogen Bond Network of Liquid H2O. Nature 2005, 434, 199–202. [DOI] [PubMed] [Google Scholar]
- (425).Lindner J; Vöhringer P; Pshenichnikov MS; Cringus D; Wiersma DA; Mostovoy M Vibrational Relaxation of Pure Liquid Water. Chem. Phys. Lett 2006, 421, 329–333. [Google Scholar]
- (426).Tan H-S; Piletic IR; Fayer MD Orientational Dynamics of Water Confined on a Nanometer Length Scale in Reverse Micelles. J. Chem. Phys 2005, 122, 174501. [DOI] [PubMed] [Google Scholar]
- (427).Piletic IR; Moilanen DE; Spry DB; Levinger NE; Fayer MD Testing the Core/Shell Model of Nanoconfined Water in Reverse Micelles Using Linear and Nonlinear IR Spectroscopy. J. Phys. Chem. A 2006, 110, 4985–4999. [DOI] [PubMed] [Google Scholar]
- (428).Bakulin AA; Pshenichnikov MS Reduced Coupling of Water Molecules near the Surface of Reverse Micelles. Phys. Chem. Chem. Phys 2011, 13, 19355–19361. [DOI] [PubMed] [Google Scholar]
- (429).Cringus D; Jansen TLC; Pshenichnikov MS; Wiersma DA Ultrafast Anisotropy Dynamics of Water Molecules Dissolved in Acetonitrile. J. Chem. Phys 2007, 127, 084507. [DOI] [PubMed] [Google Scholar]
- (430).Jansen TLC; Auer BM; Yang M; Skinner JL Two-Dimensional Infrared Spectroscopy and Ultrafast Anisotropy Decay of Water. J. Chem. Phys 2010, 132, 224503. [DOI] [PubMed] [Google Scholar]
- (431).Perakis F; Hamm P Two-Dimensional Infrared Spectroscopy of Neat Ice Ih. Phys. Chem. Chem. Phys 2012, 14, 6250–6256. [DOI] [PubMed] [Google Scholar]
- (432).Adhikari A; Re S; Nishima W; Ahmed M; Nihonyanagi S; Klauda JB; Sugita Y; Tahara T Water Orientation at Ceramide/Water Interfaces Studied by Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy and Molecular Dynamics Simulation. J. Phys. Chem. C 2016, 120, 23692–23697. [Google Scholar]
- (433).Inoue K; Nihonyanagi S; Singh PC; Yamaguchi S; Tahara T 2D Heterodyne-Detected Sum Frequency Generation Study on the Ultrafast Vibrational Dynamics of H2O and HOD Water at Charged Interfaces. J. Chem. Phys 2015, 142, 212431. [DOI] [PubMed] [Google Scholar]
- (434).Singh PC; Nihonyanagi S; Yamaguchi S; Tahara T Interfacial Water in the Vicinity of a Positively Charged Interface Studied by Steady-State and Time-Resolved Heterodyne-Detected Vibrational Sum Frequency Generation. J. Chem. Phys 2014, 141, 18C527. [DOI] [PubMed] [Google Scholar]
- (435).Singh PC; Nihonyanagi S; Yamaguchi S; Tahara T Ultrafast Vibrational Dynamics of Water at a Charged Interface Revealed by Two-Dimensional Heterodyne-Detected Vibrational Sum Frequency Generation. J. Chem. Phys 2012, 137, 094706. [DOI] [PubMed] [Google Scholar]
- (436).Roy S; Skoff D; Perroni DV; Mondal J; Yethiraj A; Mahanthappa MK; Zanni MT; Skinner JL Water Dynamics in Gyroid Phases of Self-Assembled Gemini Surfactants. J. Am. Chem. Soc 2016, 138, 2472–2475. [DOI] [PubMed] [Google Scholar]
- (437).Chin JK; Jimenez R; Romesberg FE Direct Observation of Protein Vibrations by Selective Incorporation of Spectroscopically Observable Carbon-Deuterium Bonds in Cytochrome C. J. Am. Chem. Soc 2001, 123, 2426–2427. [DOI] [PubMed] [Google Scholar]
- (438).Sagle LB; Zimmermann J; Dawson PE; Romesberg FE Direct and High Resolution Characterization of Cytochrome C Equilibrium Folding. J. Am. Chem. Soc 2006, 128, 14232–14233. [DOI] [PubMed] [Google Scholar]
- (439).Thielges MC; Case DA; Romesberg FE Carbon-Deuterium Bonds as Probes of Dihydrofolate Reductase. J. Am. Chem. Soc 2008, 130, 6597–6603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (440).Groff D; Thielges MC; Cellitti S; Schultz PG; Romesberg FE Efforts toward the Direct Experimental Characterization of Enzyme Microenvironments: Tyrosine100 in Dihydrofolate Reductase. Angew. Chem. Int. Ed 2009, 48, 3478–3481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (441).Adhikary R; Zimmermann J; Liu J; Forrest RP; Janicki TD; Dawson PE; Corcelli SA; Romesberg FE Evidence of an Unusual N–H⋯N Hydrogen Bond in Proteins. J. Am. Chem. Soc 2014, 136, 13474–13477. [DOI] [PubMed] [Google Scholar]
- (442).Le Sueur AL; Schaugaard RN; Baik M-H; Thielges MC Methionine Ligand Interaction in a Blue Copper Protein Characterized by Site-Selective Infrared Spectroscopy. J. Am. Chem. Soc 2016, 138, 7187–7193. [DOI] [PubMed] [Google Scholar]
- (443).Bukowski GS; Horness RE; Thielges MC Involvement of Local, Rapid Conformational Dynamics in Binding of Flexible Recognition Motifs. J. Phys. Chem. B 2019, 123, 8387–8396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (444).Mirkin NG; Krimm S A New Vibrational Spectroscopic Tool for the Determination of Peptide Conformation: The Isotope-Edited CαHα Stretch Mode. J. Phys. Chem. A 2004, 108, 10923–10924. [Google Scholar]
- (445).Mirkin NG; Krimm S Conformation Dependence of the CαDα Stretch Mode in Peptides. 1. Isolated Alanine Peptide Structures. J. Phys. Chem. A 2007, 111, 5300–5303. [DOI] [PubMed] [Google Scholar]
- (446).Bykov SV; Myshakina NS; Asher SA Dependence of Glycine CH2 Stretching Frequencies on Conformation, Ionization State, and Hydrogen Bonding. J. Phys. Chem. B 2008, 112, 5803–5812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (447).Miller CS; Ploetz EA; Cremeens ME; Corcelli SA Carbon-Deuterium Vibrational Probes of Peptide Conformation: Alanine Dipeptide and Glycine Dipeptide. J. Chem. Phys 2009, 130, 125103. [DOI] [PubMed] [Google Scholar]
- (448).Bukowski GS; Thielges MC Residue-Specific Conformational Heterogeneity of Proline-Rich Sequences Uncovered Via Infrared Spectroscopy. Anal. Chem 2018, 90, 14355–14362. [DOI] [PubMed] [Google Scholar]
- (449).Cremeens ME; Zimmermann J; Yu W; Dawson PE; Romesberg FE Direct Observation of Structural Heterogeneity in a β-Sheet. J. Am. Chem. Soc 2009, 131, 5726–5727. [DOI] [PubMed] [Google Scholar]
- (450).Horness RE; Basom EJ; Mayer JP; Thielges MC Resolution of Site-Specific Conformational Heterogeneity in Proline-Rich Molecular Recognition by Src Homology 3 Domains. J. Am. Chem. Soc 2016, 138, 1130–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (451).Adhikary R; Zimmermann J; Liu J; Dawson PE; Romesberg FE Experimental Characterization of Electrostatic and Conformational Heterogeneity in an SH3 Domain. J. Phys. Chem. B 2013, 117, 13082–13089. [DOI] [PubMed] [Google Scholar]
- (452).Kinnaman CS; Cremeens ME; Romesberg FE; Corcelli SA Infrared Line Shape of an A-Carbon Deuterium-Labeled Amino Acid. J. Am. Chem. Soc 2006, 128, 13334–13335. [DOI] [PubMed] [Google Scholar]
- (453).Sagle LB; Zimmermann J; Dawson PE; Romesberg FE A High-Resolution Probe of Protein Folding. J. Am. Chem. Soc 2004, 126, 3384–3385. [DOI] [PubMed] [Google Scholar]
- (454).Sagle LB; Zimmermann J; Matsuda S; Dawson PE; Romesberg FE Redox-Coupled Dynamics and Folding in Cytochrome C. J. Am. Chem. Soc 2006, 128, 7909–7915. [DOI] [PubMed] [Google Scholar]
- (455).Mirkin NG; Krimm S Conformation Dependence of the CαDα Stretch Mode in Peptides. II. Explicitly Hydrated Alanine Peptide Structures. Biopolymers 2009, 91, 791–800. [DOI] [PubMed] [Google Scholar]
- (456).Karow AM Jr Cryoprotectants—a New Class of Drugs. J. Pharm. Pharmacol 1969, 21, 209–223. [DOI] [PubMed] [Google Scholar]
- (457).Rasmussen DH; Mackenzie AP Phase Diagram for the System Water–Dimethylsulphoxide. Nature 1968, 220, 1315–1317. [DOI] [PubMed] [Google Scholar]
- (458).Oh K-I; Rajesh K; Stanton JF; Baiz CR Quantifying Hydrogen-Bond Populations in Dimethyl Sulfoxide/Water Mixtures. Angew. Chem. Int. Ed 2017, 56, 11375–11379. [DOI] [PubMed] [Google Scholar]
- (459).Cutress NC; Grindley TB; Katritzky AR; Shome M; Topsom RD Infrared Intensities as a Quantitative Measure of Intramolecular Interactions. Part XXIX. Methyl Phenyl Sulphones and Sulphoxides. J. Chem. Soc. Perkin Trans 2 1974, 268–273. [Google Scholar]
- (460).Keating CS; McClure BA; Rack JJ; Rubtsov IV Sulfoxide Stretching Mode as a Structural Reporter Via Dual-Frequency Two-Dimensional Infrared Spectroscopy. J. Chem. Phys 2010, 133, 144513. [DOI] [PubMed] [Google Scholar]
- (461).Baiz CR; Oh K-I Empirical Vibrational Frequency Map for the S=O Stretch. J. Chem. Phys 2019, 151, 234107. [DOI] [PubMed] [Google Scholar]
- (462).Du X; Frei H; Kim S-H The Mechanism of GTP Hydrolysis by Ras Probed by Fourier Transform Infrared Spectroscopy. J. Biol. Chem 2000, 275, 8492–8500. [DOI] [PubMed] [Google Scholar]
- (463).Allin C; Ahmadian MR; Wittinghofer A; Gerwert K Monitoring the Gap Catalyzed H-Ras GTPase Reaction at Atomic Resolution in Real Time. Proc. Natl. Acad. Sci. U.S.A 2001, 98, 7754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (464).Liu M; Krasteva M; Barth A Interactions of Phosphate Groups of ATP and Aspartyl Phosphate with the Sarcoplasmic Reticulum Ca2+-ATPase: An FTIR Study. Biophys. J 2005, 89, 4352–4363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (465).Dwyer JR; Szyc Ł; Nibbering ETJ; Elsaesser T Ultrafast Vibrational Dynamics of Adenine-Thymine Base Pairs in DNA Oligomers. J. Phys. Chem. B 2008, 112, 11194–11197. [DOI] [PubMed] [Google Scholar]
- (466).Szyc Ł; Yang M; Nibbering ETJ; Elsaesser T Ultrafast Vibrational Dynamics and Local Interactions of Hydrated DNA. Angew. Chem. Int. Ed 2010, 49, 3598–3610. [DOI] [PubMed] [Google Scholar]
- (467).Levinson NM; Bolte EE; Miller CS; Corcelli SA; Boxer SG Phosphate Vibrations Probe Local Electric Fields and Hydration in Biomolecules. J. Am. Chem. Soc 2011, 133, 13236–13239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (468).Siebert T; Guchhait B; Liu Y; Costard R; Elsaesser T Anharmonic Backbone Vibrations in Ultrafast Processes at the DNA–Water Interface. J. Phys. Chem. B 2015, 119, 9670–9677. [DOI] [PubMed] [Google Scholar]
- (469).Floisand DJ; Corcelli SA Computational Study of Phosphate Vibrations as Reporters of DNA Hydration. J. Phys. Chem. Lett 2015, 6, 4012–4017. [DOI] [PubMed] [Google Scholar]
- (470).Falk M; Hartman KA; Lord RC Hydration of Deoxyribonucleic Acid. I. A Gravimetric Study. J. Am. Chem. Soc 1962, 84, 3843–3846. [Google Scholar]
- (471).Schauss J; Dahms F; Fingerhut BP; Elsaesser T Phosphate–Magnesium Ion Interactions in Water Probed by Ultrafast Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. Lett 2019, 10, 238–243. [DOI] [PubMed] [Google Scholar]
- (472).Fingerhut BP; Costard R; Elsaesser T Predominance of Short Range Coulomb Forces in Phosphate-Water Interactions—a Theoretical Analysis. J. Chem. Phys 2016, 145, 115101. [Google Scholar]
- (473).Polyanichko AM; Andrushchenko VV; Chikhirzhina EV; Vorob’ev VI; Wieser H The Effect of Manganese(II) on DNA Structure: Electronic and Vibrational Circular Dichroism Studies. Nucleic Acids Res 2004, 32, 989–996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (474).Krummel AT; Zanni MT DNA Vibrational Coupling Revealed with Two-Dimensional Infrared Spectroscopy: Insight into Why Vibrational Spectroscopy Is Sensitive to DNA Structure. J. Phys. Chem. B 2006, 110, 13991–14000. [DOI] [PubMed] [Google Scholar]
- (475).Choi J-H; Ham S; Cho M Local Amide I Mode Frequencies and Coupling Constants in Polypeptides. J. Phys. Chem. B 2003, 107, 9132–9138. [Google Scholar]
- (476).Lee C; Park K-H; Cho M Vibrational Dynamics of DNA. I. Vibrational Basis Modes and Couplings. J. Chem. Phys 2006, 125, 114508. [DOI] [PubMed] [Google Scholar]
- (477).Lee C; Cho M Vibrational Dynamics of DNA. II. Deuterium Exchange Effects and Simulated IR Absorption Spectra. J. Chem. Phys 2006, 125, 114509. [DOI] [PubMed] [Google Scholar]
- (478).Lee C; Park K-H; Kim J-A; Hahn S; Cho M Vibrational Dynamics of DNA. III. Molecular Dynamics Simulations of DNA in Water and Theoretical Calculations of the Two-Dimensional Vibrational Spectra. J. Chem. Phys 2006, 125, 114510. [DOI] [PubMed] [Google Scholar]
- (479).Lee C; Cho M Vibrational Dynamics of DNA: IV. Vibrational Spectroscopic Characteristics of A-, B-, and Z-Form DNA’s. J. Chem. Phys 2007, 126, 145102. [DOI] [PubMed] [Google Scholar]
- (480).Taillandier E; Liquier J In Methods Enzymol; Academic Press, 1992; Vol. 211. [DOI] [PubMed] [Google Scholar]
- (481).Banyay M; Sarkar M; Gräslund A A Library of IR Bands of Nucleic Acids in Solution. Biophys. Chem 2003, 104, 477–488. [DOI] [PubMed] [Google Scholar]
- (482).Elsaesser T Two-Dimensional Infrared Spectroscopy of Intermolecular Hydrogen Bonds in the Condensed Phase. Acc. Chem. Res 2009, 42, 1220–1228. [DOI] [PubMed] [Google Scholar]
- (483).Peng CS; Jones KC; Tokmakoff A Anharmonic Vibrational Modes of Nucleic Acid Bases Revealed by 2D IR Spectroscopy. J. Am. Chem. Soc 2011, 133, 15650–15660. [DOI] [PubMed] [Google Scholar]
- (484).Jiang Y; Wang L Development of Vibrational Frequency Maps for Nucleobases. J. Phys. Chem. B 2019, 123, 5791–5804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (485).Tajmir-Riahi HA; Theophanides T An FT-IR Study of cis- and trans-Dichlorodiammineplatinum(II) Bound to Inosine-5′-Monophosphate. Can. J. Chem 1984, 62, 1429–1440. [Google Scholar]
- (486).van der Vegte CP; Knop S; Vöhringer P; Knoester J; Jansen TLC OH-Stretching in Synthetic Hydrogen-Bonded Chains. J. Phys. Chem. B 2014, 118, 6256–6264. [DOI] [PubMed] [Google Scholar]
- (487).Shinokita K; Cunha AV; Jansen TLC; Pshenichnikov MS Hydrogen Bond Dynamics in Bulk Alcohols. J. Chem. Phys 2015, 142, 212450. [DOI] [PubMed] [Google Scholar]
- (488).Kwac K; Geva E Mixed Quantum-Classical Molecular Dynamics Study of the Hydroxyl Stretch in Methanol/Carbon-Tetrachloride Mixtures II: Excited State Hydrogen Bonding Structure and Dynamics, Infrared Emission Spectrum, and Excited State Lifetime. J. Phys. Chem. B 2012, 116, 2856–2866. [DOI] [PubMed] [Google Scholar]
- (489).Kwac K; Geva E A Mixed Quantum-Classical Molecular Dynamics Study of the Hydroxyl Stretch in Methanol/Carbon Tetrachloride Mixtures: Equilibrium Hydrogen-Bond Structure and Dynamics at the Ground State and the Infrared Absorption Spectrum. J. Phys. Chem. B 2011, 115, 9184–9194. [DOI] [PubMed] [Google Scholar]
- (490).Mesele OO; Thompson WHA “Universal” Spectroscopic Map for the OH Stretching Mode in Alcohols. J. Phys. Chem. A 2017, 121, 5823–5833. [DOI] [PubMed] [Google Scholar]
- (491).Ni Y; Skinner JL IR and SFG Vibrational Spectroscopy of the Water Bend in the Bulk Liquid and at the Liquid-Vapor Interface, Respectively. J. Chem. Phys 2015, 143, 014502. [DOI] [PubMed] [Google Scholar]
- (492).Falk M The Frequency of the H · O · H Bending Fundamental in Solids and Liquids. Spectrochimica Acta Part A: Molecular Spectroscopy 1984, 40, 43–48. [Google Scholar]
- (493).Pavlović M; Baranović G; Lovreković D Raman Study of the Bending Band of Water. Spectrochimica Acta Part A: Molecular Spectroscopy 1991, 47, 897–906. [Google Scholar]
- (494).Devlin JP; Sadlej J; Buch V Infrared Spectra of Large H2O Clusters: New Understanding of the Elusive Bending Mode of Ice. J. Phys. Chem. A 2001, 105, 974–983. [Google Scholar]
- (495).Vinaykin M; Benderskii AV Vibrational Sum-Frequency Spectrum of the Water Bend at the Air/Water Interface. J. Phys. Chem. Lett 2012, 3, 3348–3352. [Google Scholar]
- (496).Ashihara S; Fujioka S; Shibuya K Temperature Dependence of Vibrational Relaxation of the OH Bending Excitation in Liquid H2O. Chem. Phys. Lett 2011, 502, 57–62. [Google Scholar]
- (497).Ashihara S; Huse N; Espagne A; Nibbering ETJ; Elsaesser T Vibrational Couplings and Ultrafast Relaxation of the O–H Bending Mode in Liquid H2O. Chem. Phys. Lett 2006, 424, 66–70. [Google Scholar]
- (498).Bodis P; Larsen OFA; Woutersen S Vibrational Relaxation of the Bending Mode of HDO in Liquid D2O. J. Phys. Chem. A 2005, 109, 5303–5306. [DOI] [PubMed] [Google Scholar]
- (499).Huse N; Ashihara S; Nibbering ETJ; Elsaesser T Ultrafast Vibrational Relaxation of O–H Bending and Librational Excitations in Liquid H2O. Chem. Phys. Lett 2005, 404, 389–393. [Google Scholar]
- (500).Larsen OFA; Woutersen S Vibrational Relaxation of the H2O Bending Mode in Liquid Water. J. Chem. Phys 2004, 121, 12143–12145. [DOI] [PubMed] [Google Scholar]
- (501).Nagata Y; Hsieh C-S; Hasegawa T; Voll J; Backus EHG; Bonn M Water Bending Mode at the Water–Vapor Interface Probed by Sum-Frequency Generation Spectroscopy: A Combined Molecular Dynamics Simulation and Experimental Study. J. Phys. Chem. Lett 2013, 4, 1872–1877. [DOI] [PubMed] [Google Scholar]
- (502).Jeon J; Lim JH; Kim S; Kim H; Cho M Simultaneous Spectral and Temporal Analyses of Kinetic Energies in Nonequilibrium Systems: Theory and Application to Vibrational Relaxation of O–D Stretch Mode of HOD in Water. J. Phys. Chem. A 2015, 119, 5356–5367. [DOI] [PubMed] [Google Scholar]
- (503).Jeon J; Hsieh C-S; Nagata Y; Bonn M; Cho M Hydrogen Bonding and Vibrational Energy Relaxation of Interfacial Water: A Full DFT Molecular Dynamics Simulation. J. Chem. Phys 2017, 147, 044707. [DOI] [PubMed] [Google Scholar]
- (504).Liang C; Jeon J; Cho M Ab Initio Modeling of the Vibrational Sum-Frequency Generation Spectrum of Interfacial Water. J. Phys. Chem. Lett 2019, 10, 1153–1158. [DOI] [PubMed] [Google Scholar]
- (505).Baiz CR; Kubarych KJ; Geva E; Sibert EL Local-Mode Approach to Modeling Multidimensional Infrared Spectra of Metal Carbonyls. J. Phys. Chem. A 2011, 115, 5354–5363. [DOI] [PubMed] [Google Scholar]
- (506).Nilsen IA; Osborne DG; White AM; Anna JM; Kubarych KJ Monitoring Equilibrium Reaction Dynamics of a Nearly Barrierless Molecular Rotor Using Ultrafast Vibrational Echoes. J. Chem. Phys 2014, 141, 134313. [DOI] [PubMed] [Google Scholar]
- (507).Eckert PA; Kubarych KJ Dynamic Flexibility of Hydrogenase Active Site Models Studied with 2D-IR Spectroscopy. J. Phys. Chem. A 2017, 121, 608–615. [DOI] [PubMed] [Google Scholar]
- (508).King JT; Anna JM; Kubarych KJ Solvent-Hindered Intramolecular Vibrational Redistribution. Phys. Chem. Chem. Phys 2011, 13, 5579–5583. [DOI] [PubMed] [Google Scholar]
- (509).Nee MJ; Baiz CR; Anna JM; McCanne R; Kubarych KJ Multilevel Vibrational Coherence Transfer and Wavepacket Dynamics Probed with Multidimensional IR Spectroscopy. J. Chem. Phys 2008, 129, 084503. [DOI] [PubMed] [Google Scholar]
- (510).Baiz CR; Kubarych KJ; Geva E Molecular Theory and Simulation of Coherence Transfer in Metal Carbonyls and Its Signature on Multidimensional Infrared Spectra. J. Phys. Chem. B 2011, 115, 5322–5339. [DOI] [PubMed] [Google Scholar]
- (511).Eckert PA; Kubarych KJ Vibrational Coherence Transfer Illuminates Dark Modes in Models of the Fefe Hydrogenase Active Site. J. Chem. Phys 2019, 151, 054307. [Google Scholar]
- (512).Kirkpatrick P; Ellis C Chemical Space. Nature 2004, 432, 823–823. [Google Scholar]
- (513).Faber FA; Hutchison L; Huang B; Gilmer J; Schoenholz SS; Dahl GE; Vinyals O; Kearnes S; Riley PF; von Lilienfeld OA Prediction Errors of Molecular Machine Learning Models Lower Than Hybrid DFT Error. J. Chem. Theory Comput 2017, 13, 5255–5264. [DOI] [PubMed] [Google Scholar]
- (514).Zou H; Hastie T Regularization and Variable Selection Via the Elastic Net. J. Royal Stat. Soc. B 2005, 67, 301–320. [Google Scholar]
- (515).Muller K; Mika S; Ratsch G; Tsuda K; Scholkopf B An Introduction to Kernel-Based Learning Algorithms. IEEE Trans. Neural Netw 2001, 12, 181–201. [DOI] [PubMed] [Google Scholar]
- (516).Kearnes S; McCloskey K; Berndl M; Pande V; Riley P Molecular Graph Convolutions: Moving Beyond Fingerprints. J. Comput. Aided Mol. Des 2016, 30, 595–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (517).Li Y; Tarlow D; Brockschmidt M; Zemel R; arXiv:1511.05493, 2015.
- (518).Kwac K; Cho M Differential Evolution Algorithm Approach for Describing Vibrational Solvatochromism. J. Chem. Phys 2019, 151, 134112. [DOI] [PubMed] [Google Scholar]
- (519).Storn R; Price K Differential Evolution – a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Global Optim 1997, 11, 341–359. [Google Scholar]
- (520).Price KV; Storn RM; Lampinen JA Differential Evolution: A Practical Approach to Global Optimization; Springer: New York, 2005. [Google Scholar]
- (521).Rasmussen CE; Williams CKI Gaussian Processes for Machine Learning; The MIT Press: Cambridgs, MA, USA, 2006. [Google Scholar]
- (522).Ramakrishnan R; Dral PO; Rupp M; von Lilienfeld OA Big Data Meets Quantum Chemistry Approximations: The Δ-Machine Learning Approach. J. Chem. Theory Comput 2015, 11, 2087–2096. [DOI] [PubMed] [Google Scholar]
- (523).Behler J; Parrinello M Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett 2007, 98, 146401. [DOI] [PubMed] [Google Scholar]
- (524).Behler J Atom-Centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials. J. Chem. Phys 2011, 134, 074106. [DOI] [PubMed] [Google Scholar]
- (525).Kwac K; Cho M Machine Learning Approach for Describing Vibrational Solvatochromism. J. Chem. Phys 2020, 152, 174101. [DOI] [PubMed] [Google Scholar]
- (526).Krizhevsky A; Sutskever I; Hinton GE In Advances in Neural Information Processing Systems 25, 2012. [Google Scholar]
- (527).Mitchell T Machine Learning; McGraw Hill, 1997. [Google Scholar]
- (528).Murphy KP Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, 2012. [Google Scholar]
- (529).Gastegger M; Behler J; Marquetand P Machine Learning Molecular Dynamics for the Simulation of Infrared Spectra. Chem. Sci 2017, 8, 6924–6935. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


