Adaptability and stability analyses of plants using random regression models

Michel Henriques de Souza; José Domingos Pereira Júnior; Skarlet De Marco Steckling; Jussara Mencalha; Fabíola dos Santos Dias; João Romero do Amaral Santos de Carvalho Rocha; Pedro Crescêncio Souza Carneiro; José Eustáquio de Souza Carneiro

doi:10.1371/journal.pone.0233200

. 2020 Dec 2;15(12):e0233200. doi: 10.1371/journal.pone.0233200

Adaptability and stability analyses of plants using random regression models

Michel Henriques de Souza ^1,^*, José Domingos Pereira Júnior ¹, Skarlet De Marco Steckling ², Jussara Mencalha ¹, Fabíola dos Santos Dias ¹, João Romero do Amaral Santos de Carvalho Rocha ², Pedro Crescêncio Souza Carneiro ², José Eustáquio de Souza Carneiro ¹

Editor: Paulo Eduardo Teodoro³

PMCID: PMC7710123 PMID: 33264283

Abstract

The evaluation of cultivars using multi-environment trials (MET) is an important step in plant breeding programs. One of the objectives of these evaluations is to understand the genotype by environment interaction (GEI). A method of determining the effect of GEI on the performance of cultivars is based on studies of adaptability and stability. Initial studies were based on linear regression; however, these methodologies have limitations, mainly in trials with genetic or statistical unbalanced, heterogeneity of residual variances, and genetic covariance. An alternative would be the use of random regression models (RRM), in which the behavior of the genotypes is characterized as a reaction norm using longitudinal data or repeated measurements and information regarding a covariance function. The objective of this work was the application of RRM in the study of the behavior of common bean cultivars using a MET, based on Legendre polynomials and genotype-ideotype distances. We used a set of 13 trials, which were classified as unfavorable or favorable environments. The results revealed that RRM enables the prediction of the genotypic values of cultivars in environments where they were not evaluated with high accuracy values, thereby circumventing the unbalanced of the experiments. From these values, it was possible to measure the genotypic adaptability according to ideotypes, according to their reaction norms. In addition, the stability of the cultivars can be interpreted as variation in the behavior of the ideotype. The use of ideotypes based on real data allowed a better comparison of the performance of cultivars across environments. The use of RRM in plant breeding is a good alternative to understand the behavior of cultivars in a MET, especially when we want to quantify the adaptability and stability of genotypes.

Introduction

In the final stages of a breeding program, the most promising lines are evaluated in trials conducted in different environments, composed of different years, places, and seasons. This set of trials, known as multi-environment trials (MET), can provide useful information about the performance of genotypes in environments where we want to recommend a cultivar [1]. In Brazil, these tests are called Value for Cultivation and Use (Valor de Cultivo e Uso–VCU), and their results are the basis for the recommendation of a new cultivar [2]. In addition, the data from a MET also allows determination of the effect of the genotype by environment interaction (GEI) on the performance of genotypes and make predictions regarding the breeding values of the genotypes in other environments [3]. The evaluation of superior materials across several locations is an essential practice to ensure that the next cultivars have known performance [4].

A method to determine the behavior of genotypes, as well as the effect of the GEI acting on them, is through studies of adaptability and stability. The adaptability is defined as the ability of a genotype to respond advantageously to its environment, while its stability is related to the predictability of its behavior [5, 6]. It is possible to identify genotypes that have wide or specific adaptability to favorable or unfavorable environments. Finlay and Wilkinson [5] defined favorable and unfavorable environments as those that result in the average performance of the genotype being above or below the average of all the trials, respectively.

In recent decades, several methods to evaluate the adaptability and stability have been proposed, based on different statistical principles, such as those methodologies that are based on linear regression models [5–8]. Some of the previous methods to determine the adaptability and stability also included the ideotype concept [9, 10], and resulted in an improved understanding of the relative behavior of the genotypes from a smaller number of parameters. In a review, Eeuwijk et al. [11] show that there are other methodologies to assess the behavior of genotypes that are of note, such as AMMI (Additive Main effects and Multiplicative Interaction) [12] and GGE biplot (Genotype main effects and Genotype x Environment interaction effects) [13].

However, the adaptability and stability analyses still have limitations, especially when used with trials with genetic or statistical unbalanced, heterogeneity of residual variances, and genetic covariance. Another relevant factor is that traditional methodologies for the analyses of adaptability and stability, the behavior of the genotypes is predicted by a linear model adjusted according to an environmental gradient [5, 14], that is, composed of a set of straight lines (one for each genotype in the environments) modeling the G x E interaction in a single dimension [15]. Thus, the predictability of the behavior is compromised if the behavior of the genotypes in the face of environmental variations differs from that predicted by the linear model. Consequently, recommendations based on these methodologies can be biased. An alternative would be the use of Random Regression Models (RRM), as they allow for improved modeling of the behavior of the genotypes. RRM were first proposed by Kirkpatrick et al. [16], and later extended by Schaeffer and Dekkers [17] and Meyer and Hill [18].

The RRM is used mainly in animal breeding, where the phenotypic behavior of animals is characterized by longitudinal data or repeated measurements and information regarding a covariance function [19–22]. The first methods used were based on parametric functions that adjusted regression equations for fixed and random effects [23, 24]. However, these functions have convergence difficulty, mainly in the evaluation of bovine lactation curves, resulting in the search for new functions, with emphasis on orthogonal polynomials. The covariates based on orthogonal polynomials reduce problems with rounding and provide relatively small correlations between the estimated regression coefficients [21]. Among the orthogonal polynomials, Legendre's polynomials, which describe the structures of variation and covariance between genetic and environmental components, are distinct [16, 25] and present computational advantages such as reduced correlations between the estimated coefficients and better convergence properties [26].

In plant science, the application of RRM is recent, as in the works of Sun et al. [27], Ly et al. [28], Momen et al. [29] and Baba et al. [30], where it is used to model the behavior of individuals along a MET, especially when these trials are on a continuous and gradual scale, in order to capture and predict the variation in the behavior of the genotypes due to environmental changes, even in places where the genotypes have not been evaluated. Thus, these models can be used to select genotypes with responses to environmental variations, maintaining the high ability to predict unmeasured values [27–30]. When considering phenotypic variations in time, as in the case of lactation curves in cattle, the term random regression is common; however, in the case of spatial variation from phenotypic records, as in a MET, the term reaction norm seems to be more acceptable. This term, first described in the field of ecology to describe the natural adaptation of individuals [31], refers to an individual's phenotypic plasticity in response to environmental variation, i.e., a specific relationship between genotype, phenotype, and environmental gradient. The distinction between the terms is subtle, although it is also related to the nature of the variation in the measures [32, 33].

According to Streit et al. [34], one way to treat genotype variation in environments is to consider the multitrait approach, analyzing the information for each environment as a distinct variable. The use of reaction norm models are appropriate to evaluate gradual and continuous variations in the environments, with few parameters and without the need to group individuals in the environments [34]. Thus, knowledge of the reaction norms modeled using Legendre's polynomials can better quantify the adaptability and stability of a set of genotypes evaluated in different environments, aiming for greater accuracy in cultivar recommendations. Therefore, the objective of this investigation was the application of the random regression models in the study of genotypes behavior along a MET, based on Legendre polynomials and genotype-ideotype distances.

Material and methods

Genetic material

We evaluated 105 common bean cultivars (Phaseolus vulgaris L.), 56 of which were Carioca grains and 49 were Black grains. These cultivars have been recommended in Brazil by breeding programs since 1959. The cultivars used, as well as the institutions of origin and year of recommendation, are listed in S1 and S2 Tables (supporting information).

Trials

The trials were conducted in different environments (seasons, years, and places), during the dry and winter seasons, between 2013 and 2018, at the Experimental Stations in Coimbra county–Minas Gerais (Unidade de Ensino, Pesquisa e Extensão—UEPE Coimbra: latitude 20°49ʹ44″ S, longitude 42°45ʹ56″ W and altitude of 713 meters) and Viçosa–Minas Gerais (Aeroporto, latitude 20°44ʹ38″ S, longitude 42°50'40” W and altitude of 654 meters; Horta Nova: latitude 20°45ʹ47″ S, longitude 42°49ʹ25″ W and altitude of 664 meters; Vale da Agronomia: latitude 20°46ʹ04″ S, longitude 42°52ʹ11″ W and altitude of 662 meters), totaling 13 trials. Over the years in which the trials were carried out, the cultivars that were recently launched by the breeding programs were included, thus causing a genetic unbalanced (variation in the number of cultivars in the trials). The 13 trials and their characteristics are listed in S3 Table (supporting information).

The trials were designed in randomized blocks with three replications. The plots consisted of four lines of two meters (m), spaced 0.5 m apart. The treatments used were in accordance with the recommendations for common bean cultures [30]. The evaluated characteristic was grain yield, and they were harvested from the two central lines of each plot. The data were corrected to 13% moisture and converted to kg ha^-1.

Statistical analyses

We use RRM to evaluate the behavior of the genotypes as a function that describes this behavior over the gradual and continuous changes in the trials. The genotype’s behavior is quantified as their reaction norm. For this, initially, the 13 trials in which the genotypes were evaluated were classified in an environmental gradient, according to the index proposed by Finlay and Wilkinson [5]. According to these authors, the genotype's ability to respond to continuous environmental improvements is a description of its adaptability. The environmental index was determined as follows:

I_{j} = ({\bar{Y}}_{j} - \bar{Y})

(1)

where ${\bar{Y}}_{j}$ is the average of the genotypes j-th trial (j = 1, 2,…, na, where na is the total number of trials) and $\bar{Y}$ is the general mean. Negative and positive index values indicate unfavorable and favorable trials, respectively. The values of the environmental index were later standardized to the range of orthogonal functions (−1 to 1) to avoid problems of collinearity among the data [35], according to the equation adapted by Schaeffer [36]:

I_{j s} = - 1 + 2 (\frac{I_{j} - I_{1}}{I_{13} - I_{1}})

(2)

where I_js is the standardized environmental index, I_j is the value obtained in Eq 1 for each trial, and I₁ and I₁₃ are the index values (Eq 1) obtained for the trials of lowest and highest averages, respectively.

To adjust the behavior of the genotypes along the environmental gradient, it is necessary to test different models of reaction norms. The number of models to be tested depends on the number of trials used (determines the maximum order of the polynomial), the number of effects included in the model via the Legendre polynomials, and the residual covariance structures. Thus, we fitted 14 reaction norm models, where seven were considered with homogeneous residual variance (H) and the other seven with heterogeneous diagonal residual variance (D). The models were fitted with Legendre's polynomials, considering the various polynomial orders, based on the general model, was as follows:

y_{i j k} = A_{j} + R / A_{j k} + \sum_{m = 0}^{M - 1} α_{i m} Ф_{i j m} + e_{i j k}

(3)

where: y_ijk is the observation of the i-th genotype (i = 1, 2,…, ng, where ng is the total number of genotypes), in the j-th trial (j = 1, 2,…, na, where na is the total number of trials), in the k-th block (k = 1, 2, 3); A_j is the effect of the trial; R/A_jk is the fixed effect of the blocks within each trial; α_im is the reaction norm coefficient for the Legendre polynomial of order m for the genotypic effects of the genotypes; Ф_ijm is Legendre's m-th polynomial for the j-th trial, standardized from -1 to +1 for the i-th genotype; M is the order of polynomials of the Legendre polynomial for genotypic effects; and e_ijk is the residual random effect associated with y_ijk.

In a matrix, the model above is described as: y = Xb+Zg+e, where: y is the vector of phenotypic data; b is the vector of the fixed effects of the combination of blocks × trials added to the general average; g is the vector of genetic effects (assumed to be random); and e is the residual vector (random). X and Z represent the incidence matrix for these effects, respectively. It is assumed that: g ~ N (0, Kg ⊗ I_ng), and e ~ N (0, ∑ ⊗ I_np), where I_ng and I_np are identity matrices of the order ng (ng is the total number of genotypes) and np (np is the number of genotypes x the number of blocks), respectively. The symbol ⊗ denotes the Kronecker product. Kg is the matrix of covariance coefficients for genotypic effect. ∑ represents the matrix of residual variances.

After obtaining several models, we choose the one best fit (with lowest mean square error and greater parsimony). For that, some criteria were used, namely: Akaike Information Criterion (AIC) [37], Bayesian Information Criterion (BIC) [38], and Penalizing Adaptively the Likelihood (PAL) [39]. These criteria are described as follows:

A I C = - 2 l n L + 2 p

(4)

B I C = - 2 l n L + p l n [n - r (x)]

(5)

P A L = - 2 l n L + n l n (ñ) \frac{l n (r_{n} + 1)}{l n (ρ_{n} + 1)}

(6)

where;

r_{n} = 2 l n L_{n - 1} - 2 l n L_{1}

ρ_{n} = 2 l n L_{ñ} - 2 l n L_{n - 1}

and lnL is the logarithm of the likelihood function; p is the number of estimated parameters; n is the number of observations; r(x) is the rank of the fixed effects matrix; and ñ is the highest number of parameters for the models.

From the chosen model, we utilized the Likelihood Ratio Test (LRT) [40] to test the genetic effects. The LRT is used which is as follows:

L R T = ‐ 2 * (L o g L_{m o d . r} - L o g L_{m o d . c})

(7)

where: LogL_mod.r is the logarithm value of the maximum likelihood function obtained for the reduced model (without the genotypic effect), and LogL_mod.c is the logarithm value of the maximum likelihood function obtained for the complete model.

We use the equation proposed by Kirkpatrick et al. [16] to predict the genotypic values ( ${\hat{g}}_{i j}$ ) for the all genotypes in the trials. The equation is described as:

{\hat{g}}_{i j} = \sum_{m = 0}^{M - 1} {\hat{α}}_{i m} Ф_{i j m}

(8)

where: ${\hat{α}}_{i m}$ is the reaction norm coefficient of order m for the genetic effects of the i-th genotype.

Another point that we find relevant is to provide an estimate of the prediction accuracy of the genotypic values, in order to know the reliability of the results. For that, the prediction accuracy was estimated according to the following equation, adapted from Gilmour et al. [41], and according to Kirkpatrick et al. [16].

{r_{\hat{g} g}}_{i j} = \sqrt{1 - \frac{{Ф_{i j m} P E V}_{i j} Ф_{i j m}^{'}}{Ф_{i j m} {\hat{K}}_{g} Ф_{i j m}^{'}}}

(9)

where: ${r_{\hat{g} g}}_{i j}$ is the correlation between the predicted and real genotype values for genotype i in trial j, that is, the estimated accuracy; PEV_ij is the Predicted Error Variance, obtained from the diagonal elements of the matrix of the estimated coefficients for genotype i in trial j; and ${\hat{K}}_{g}$ is the covariance matrix of the coefficients, estimated for the genotypic effect.

Finally, after choosing the appropriate reaction norm model and predicting the genotype values, we quantify the individual reaction norm for each genotype aiming to know their adaptability and stability. For that, we used the genotype-ideotype distance (converted into probability), according to three ideotypes: i) genotypes of general adaptability (genotypes of maximum performance in both unfavorable and favorable environments); ii) genotypes of maximum adaptability to unfavorable environments (genotypes of maximum performance in unfavorable environments, regardless of their performance in favorable environments); and iii) genotypes of maximum adaptability to favorable environments (genotypes of maximum performance in favorable environments, regardless of their performance in unfavorable environments). Each ideotype was based on the phenotypic values of each environment. From the genotypic values, thus, we obtained the value of the genotype-ideotype distance (converted into probability), according to the estimator adapted from Rocha et al. [42], as described:

P_{i k} = \frac{\frac{1}{G I D_{i k}}}{\sum_{i = 1}^{n g} \frac{1}{G I D_{i k}}}

(10)

where P_ik are the probabilities referring to genotype i with regard to ideotype k (k = 1, 2, 3; where 1 = genotypes of general adaptability; 2 = genotypes of maximum adaptability to unfavorable environments; and 3 = genotypes of maximum adaptability to favorable environments); and ng is the total number of genotypes. GID_ik is the standardized average Euclidean distance for genotype i in ideotype k, as given by:

G I D_{i k} = \sqrt{\frac{\sum_{j} [{\hat{g}}_{i j} - i d e ({\hat{g}}_{i j})]^{2}}{n j}}

(11)

where, if k = 1, j = 1,…, na; if k = 2, j = 1,…, nd; if k = 3, j = 1,…, nf; na is the highest assumed value for j; nd and nf represent the number of unfavorable and favorable environments, respectively; $ide {(\hat{g}}_{i j})$ is the ideotype drawn from the standardized genotypic values.

It is important to emphasize that the estimators used above also considered the stability of the genotypes' behavior in relation to the ideotype, where the stability can be highlighted as variation regarding the behavior of the ideotype.

We evaluated the performance only in those genotypes that present an accuracy value of at least 80% in the trials, since the accuracy is indicative of the precision in the prediction of genotypic values. Thus, the average accuracy of the trials considered in the cultivar recommendation will also show values equal to or greater than 80%. The standard value is based on that of Resende and Duarte [43], who claimed to have at least 80% accuracy values in cultivar comparison trials.

After obtaining the values of probability of the cultivars, we selected the top ten cultivars (highest probability value) to plot their curves with their respective reaction norms, to view the results. The genotypic value of each cultivar was added, plus the environment average, and the general average, as well as two checks, Pérola (Carioca bean) and Ouro Negro (Black bean), for comparison purposes. These two cultivars were selected as check, as they are used as references for the productivity and quality of grain in consumer markets for the Carioca and Black beans, respectively [44]. The accuracy values (S4 Table) and the values of the genotype-ideotype distance (recommendation probability values—S5 Table) are available in the supporting information.

Software used

The joint analyses was carried out using ASREML software [45]. The study of the adaptability and stability of cultivars was carried out using R [46] according to the ASReml-R and R Stats packages. The code for the analyses is available in the S1 Code (supporting information).

Results

The environmental index values, according to Finlay and Wilkinson [5], are shown in Table 1. Positive index values indicate favorable environments, while negative values indicate unfavorable ones [7]. Trials 12, 9, 4, 10, 8, and 6 were classified as unfavorable environments, while trials 5, 2, 3, 7, 1, 11, and 13 were favorable. In addition, we added a column with the standardized environmental index value.

Table 1. Trials evaluated with their environmental index.

Trial	Description	Environmental index	Standardized environmental index
12	Dry/2017/Aeroporto	-1028.89	-1.00
9	Dry/2016/UEPE Coimbra	-868.67	-0.89
4	Winter/2013/Vale da Agronomia	-607.25	-0.71
10	Winter/2016/UEPE Coimbra	-500.76	-0.64
8	Dry/2016/Aeroporto	-466.43	-0.61
6	Winter/2015/UEPE Coimbra	-167.35	-0.41
5	Dry/2015/UEPE Coimbra	31.02	-0.27
2	Dry/2013/Vale da Agronomia	106.80	-0.22
3	Winter/2013/Coimbra	127.71	-0.20
7	Dry/2016/UEPE Coimbra	259.39	-0.11
1	Dry/2013/Coimbra	486.60	0.05
11	Winter/2016/Horta Nova	758.98	0.23
13	Winter/2017/UEPE Coimbra	1868.83	1.00

Open in a new tab

We found that the different criteria (AIC, BIC, and PAL) pointed to different models as having a better fit. The AIC criterion identified model Leg.6.D, which has a diagonal structure for the residuals and an order six for the Legendre polynomials, as having the best fit (Table 2). The BIC and PAL criteria however, identified the Leg.5.D model as having the best fit. The AIC and BIC criteria prioritize, respectively, efficiency and consistency in their choices of model [47, 48]. Corrales et al. [48], using simulated data, reported that when the true model was among the candidate models, the PAL and BIC criteria selected the same model. Furthermore, when the PAL and AIC criteria were used, the model selection was not always the same. When the real model was unknown, the AIC was more precise in choosing the best model, compared to the BIC. According to Vrieze [49], for very complex models (which include a high number of parameters) the BIC criterion was preferred over the AIC. Corrales et al. [48] stated that the PAL criterion simultaneously considers the consistency and efficiency of a model and should, therefore, be preferred over the AIC and BIC criteria when choosing models. The model ultimately chosen was Leg.5.D.

Table 2. Different fitted models using the Legendre polynomials (Leg).

Model¹	Order	P²	AIC	BIC	PAL	LRT
Leg.0.H	0	2	11306.5	11318.9	11302.5	377.7^*
Leg.1.H	1	4	11287.6	11312.4	11279.6	400.6^*
Leg.2.H	2	7	11255.3	11298.8	11256.8	438.8^*
Leg.3.H	3	11	11218.1	11286.4	11229.1	484.1^*
Leg.4.H	4	16	11191.4	11290.9	11217.4	520.7^*
Leg.5.H	5	22	11149.6	11286.3	11197.3	574.5^*
Leg.6.H	6	29	11134.4	11314.6	11243.4	603.7^*
Leg.0.D	0	14	11006.7	11093.7	10978.7	507.6^*
Leg.1.D	1	16	10983.4	11082.8	10951.4	534.9^*
Leg.2.D	2	19	10928.4	11046.5	10930.0	595.9^*
Leg.3.D	3	23	10865.1	11008.1	10885.4	667.2^*
Leg.4.D	4	28	10739.6	10913.6	10778.8	802.7^*
Leg.5.D	5	34	10648.1	10859.4	10729.9	906.2^*
Leg.6.D	6	41	10645.4	10900.2	10880.5	922.9^*

Open in a new tab

¹These models can assume homogeneous (H) or diagonal (D) residual variance structure. ²Number of parameters

*Significant with the LRT test.

Based on the chosen model (Leg.5.D), the random effects of the cultivars were modeled as linear functions using the Legendre polynomials, with order five and heterogeneous residual variance (diagonal). This resulted in 34 estimated parameters, 13 of which were associated with residuals, that is, one for each trial, and 21 related to the model's genotypic components. It is of note that the genetic effect was significant with the LRT test for all fitted models, indicating high variability between the cultivars evaluated (Table 2).

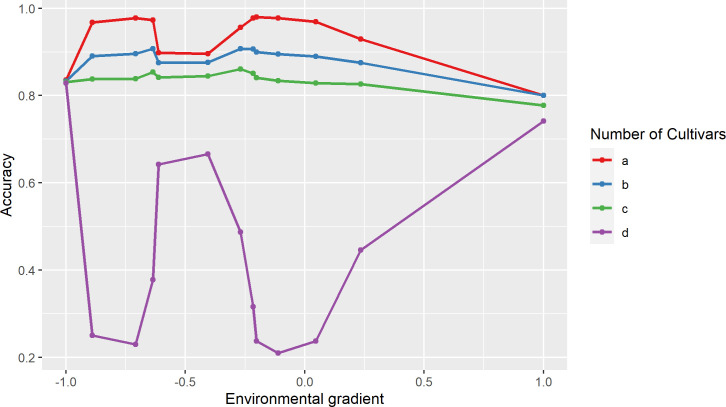
The average accuracy for the prediction of the genotypic values for each cultivar, based on the Leg.5.D model, are shown in Fig 1. We found that the average accuracy of predictions was greater when more trials were used to evaluate the cultivars. The accuracy observed for the cultivars that were present in the 13 environments was the highest, while the accuracy estimates for the cultivars evaluated in only two environments were the lowest. The accuracy values of each cultivar in each environment are available in S4 Table (supporting information).

Using the RRM, the adaptability and stability of 100 of the 105 cultivars was quantified as a reaction norm. These 100 cultivars were evaluated in at least nine of the 13 trials, with the accuracy in predicting their genotypic values, equal to or greater than 80%, including for those trials in which the cultivars were not evaluated (S4 Table).

According to Eq 10, the cultivars were recommended by comparing them with the three proposed ideotypes (three scenarios): cultivars of general adaptability, cultivars of maximum adaptability to unfavorable environments, and cultivars of maximum adaptability to favorable environments. The probability values of each cultivar in each scenario are presented in S5 Table.

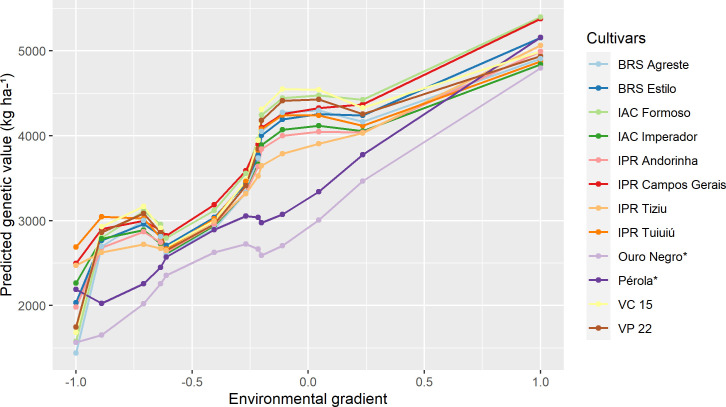
Fig 2 shows the reaction norm curves of the ten common bean cultivars with the highest potential (highest probability value), considering the general adaptability scenario (ideotype—maximum performance genotypes in both unfavorable and favorable environments), as well as the cultivars used as checks (Pérola and Ouro Negro). The probability of each cultivar was calculated according to Eq 10, in relation to the ideotype for the scenario of general adaptability. Among the ten selected cultivars, six had the Carioca grain type (BRS Estilo, IAC Formoso, IAC Imperador, IPR Andorinha, IPR Campos Gerais and VC 15), and four had the Black grain type (BRS Agreste, IPR Tiziu, IPR Tuiuiú and VP 22). The IPR Campos Gerais cultivar surpassed the Pérola cultivar in all trials, while the VP 22 cultivar surpassed the Ouro Negro cultivar in all trials.

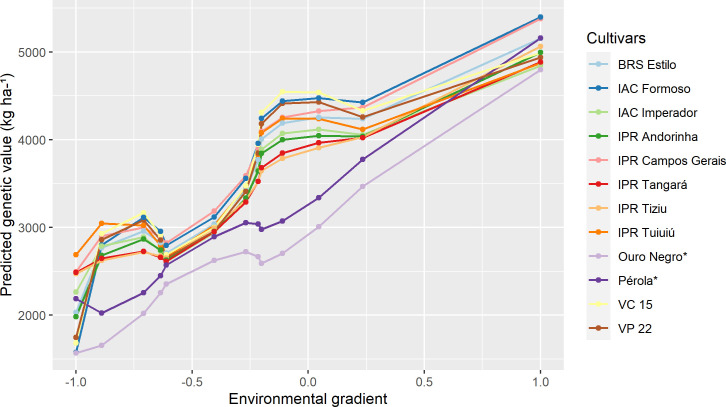
The reaction norm curves of the ten common bean cultivars with the greatest potential (highest probability value), considering the scenario of maximum adaptability to unfavorable environments (ideotype—maximum performance genotypes in unfavorable environments, regardless of their performance in favorable environments), as well as the cultivars used as checks, are presented in Fig 3. Of the ten selected cultivars, seven had Carioca grain (BRS Estilo, IAC Formoso, IAC Imperador, IPR Andorinha, IPR Campos Gerais, IPR Tangará and VC 15) and three had Black grain (IPR Tiziu, IPR Tuiuiú and VP 22). The cultivar IPR Campos Gerais surpassed the cultivar Pérola in all trials, and the IPR Tuiuiú, IPR Tiziu, and VP 22 cultivars exceeded the Ouro Negro cultivar.

Fig 3 — The trials are ordered according to the standardized environmental index (Table 1). *Cultivars used as checks.

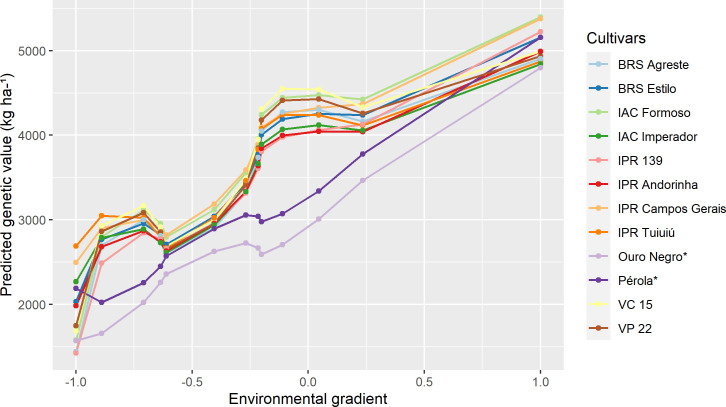
In Fig 4, the reaction norm curves for the ten cultivars with the highest potential (highest probability value), considering the scenario of maximum adaptability to favorable environments (ideotype—maximum performance genotypes in favorable environments, regardless of their performance in unfavorable environments), as well as the cultivars used as checks, are shown. Of the ten selected cultivars, seven had Carioca grain (BRS Estilo, IAC Formoso, IAC Imperador, IPR Andorinha, IPR Campos Gerais, IPR 139 and VC 15) and three had Black grain (IPR Agreste, IPR Tuiuiú and VP 22). The IPR Campos Gerais cultivar surpassed the Pérola cultivar, in all trials, and the IPR Agreste, IPR Tuiuiú, and VP 22 Black common bean cultivars exceeded the Ouro Negro cultivar, in all trials.

Discussion

Rating the variations of a set of trials, according to an environmental gradient, is essential when using methods based on linear regression that aim to quantify the adaptability of a cultivar. Finlay and Wilkinson [5] proposed using the average performances of the cultivars in each trial as a gradient, and estimating an environmental index using the differences between the average of the cultivars evaluated in each trial and the general average of the cultivars in all trials. Additionally, the fit of the regression model for each cultivar was made according to its performance, relative to the environmental index, in order to increase the values. The lack of an environmental gradient complicates the interpretation of the behavior of the genotypes in the face of the environmental variations [5]. Thus, the ordering of environments along a gradient rather than a set of arbitrarily defined groups of the data is necessary in reaction norm models, because these models describe the phenotype of an individual expressed as a function of the gradual and continuous change in environments [50, 51].

When classifying the trials with the environmental index (in favorable or unfavorable environments), it was observed that the seasons, places, and years in which the trials were conducted did not determine the classification, as the trials from the same place and year could have very different results (trials 7 and 9), while those from different seasons, places, and years could be very similar (for example, environments 1 and 11). It should be noted that trial 9 was planted 44 days after trial 7, which may be one of the justifications for the different environmental index values. These results could be caused by edaphoclimatic variations, as well as variations in the incidence of pests and diseases in the environments in which the cultivars were evaluated, resulting in GEI. Several authors have also previously [52–55] reported the influence of these factors on the environmental classification, resulting in significant GEI. For Ramalho et al. [56], the most significant contributions to the GEI in the common bean culture were due to the combinations of cultivar × season and cultivar × years.

The development of methods to model GEI is coupled with the availability of more genotypic and environmental information, in line with the advances in data collection and analyses. The first analyses were based on analyses of variance [57, 58], with a single parameter to interpret the adaptability and stability. The advances with the development of new methodologies however, are based on regression analyses, with interpretations based on more parameters, such as the average, the regression coefficient, the regression deviation, and new definitions of adaptability and stability [5, 8, 14].

Currently, the effects of genotypes and environmental conditions can be modeled by phenotypic values in regression with genetic markers and in environmental covariates, via mixed models [59]. However, these models consider that the genotype behavior is linear, which may not equate to the genotypes actual behavior. Thus, RRM in conjunction with Legendre polynomials are used to establish the order of the polynomials of the regression parameters later, according to the behavior of the genotypes in a MET. Additionally, the mixed model approach also allows for the genotypic values of individuals to be predicted, as adaptability and stability are genotypic, and not phenotypic.

According to Ni et al. [60], reaction norm models allow for the adjustment of an individual’s genetic effects with their exposure to the environmental effects, so that the genotypes are adjusted as a nonlinear function of a continuous environmental gradient. The adjustment of reaction norm models, as a function of the environmental gradient, considering Legendre polynomials, captures more adequately the behavior of the genotypes in a MET. These fact is an advantage of the reaction norms in relation to the traditional methods of analyses of adaptability and stability.

The inclusion of kinship information between the individuals evaluated, whether via pedigree or genomics, could contribute to the use of RRM, which is based on the estimation of the variance components using the method of Restricted Maximum Likelihood associated with the Best Linear Unbiased Predictor (REML/BLUP) [61]. This information can be incorporated into the incidence matrix of the genetic values in the matrix model, allowing more accurate estimates, and consequently, increasing the prediction accuracy. Several studies are available that show that the inclusion of kinship information provides better adjusted models and lower values of residual variance estimates [27, 62–65].

In addition, the availability of environmental information, such as temperature, soil moisture, and rainfall data, can help in estimating the environmental values used in the reaction norms. Ly et al. [28] showed in their work that much of the variation caused by the GEI is owing to the changes caused by environmental covariates. One of the most standard ways of adding spatial variations to a statistical model is through structures of spatial variance and covariance, as proposed by Cullis and Gleeson [66] and later refined by Gilmour et al. [67]. Furthermore, several studies have incorporated the effects of environmental covariates in their statistical models, through the inclusion of random effects in the incidence matrices [27, 28, 68, 69].

Jarquín et al. [59] state that it is possible to simultaneously model the effects of environmental covariates and the genomic data obtained. However, this approach would lead to very demanding analyses with a high number of parameters. Thus, these authors proposed models of random effects where the effects of markers and environmental covariates are modeled together, through covariance structures, which can significantly improve the prediction accuracy.

To quantify the adaptability and stability using reaction norms, the prediction accuracy represents the reliability in the evaluation of the behavior of the evaluated genotypes in different environments. In this work, most of the accuracy estimates obtained for each cultivar in each environment were greater than 80%, which also resulted in an average accuracy of the 13 trials that was higher than this value. In the VCU trials, Resende and Duarte [43] recommended that the accuracy should be at least 80%. Other previous investigations have also highlight the importance of prediction accuracies, using the reaction norm models in plant breeding experiments [59, 70, 71].

Another advantage of using reaction norm is the prediction of genotypic values for the cultivars for environments in which they were not evaluated, when the MET presents genetic imbalance. When using trials with unbalanced data, or just a sample of the cultivars, the prediction accuracy estimates tend to be lower, and the model may not be efficient in evaluating the performance of the cultivars [72, 73]. Viana et al. [74] working with unbalanced data, showed that the lack of data resulted in relevant effects on the estimation of genetic variances, the accuracy of prediction and the ranking of predicted genetic values, which can affect the efficiency of selection.

For Smith et al. [1], using accurate information for the behavior of the cultivars, allowed breeders to choose the best varieties, according to the needs of farmers, in order to maximize profitability and food security. One of the difficulties in assessing the behavior of a group of cultivars over MET was due to the fact that new genotypes were included in the trials over the years, in addition to the loss of information due to problems that occurred over the trials, resulting in genetic and statistical unbalanced.

As noted, only 12 cultivars of superior performance were found in Figs 2–4, with eight Carioca bean cultivars and four Black bean cultivars, instead of 30 cultivars (10 per figure). This was because there were some cultivars that were widely adaptable and highly stable that were selected for more than one scenario, such as the IPR Campos Gerais and IPR Tuiuiú.

Cultivars with high phenotypic averages for high yield were identified, but they were not included in Figs 2–4, as those selected by the reaction norm models. This can be explained by the fact that the methodology when calculating the probability of each cultivar that was based on the cultivar-ideotype distance penalizes cultivars that showed great variation in their productivity during the trials, even if they presented high general averages. Thus, the reaction norm models can also quantify the stability of cultivars, defined as the variation regarding the behavior of the ideotype across environments. Eeuwijk et al. and Van Oijen and Höglind [11, 75] also reported this property of reaction norms. It is also worth mentioning that the use of the ideotype that was established from the data itself, had the advantage of comparing the genotypes with a real situation observed for that MET, since the ideotype is defined as the maximum value predicted in each trial.

The reaction norms, based on RRM, can also model the heterogeneity of the genetic variations and correlations between the environments, in addition to the spatial trends in the trials [16]. Furthermore, these models allow for more accurate estimations of the genotypes in the trials, as well as better estimations of the genetic parameters, such as heritability, variances, covariances, and genetic correlations, while they become more difficult in models with only fixed effects [11].

The maintenance of productivity in different environments is explained by the response to the environmental stimulus, being caused by the differential expression of the genes present in each individual. In this way, the adaptability and stability indicated in the reaction norm curves of the cultivars, provides information regarding their capacity to express phenotypes that may better adjust to the environmental conditions [76]. In this sense, one way to improve the adaptability of cultivars to the different environments in which they will be cultivated, is to pyramid the genes of maximum expression in both the unfavorable and favorable environments. The superior cultivars in each studied scenario were developed in different breeding programs from four institutions (EMBRAPA, UFV, IAC, and IAPAR). This is indicative of the effort and success of these breeding programs, as well as the genetic diversity between them, since the breeding programs are independent, with their own parental lines. Several studies have reported the decrease of genetic diversity in crops with genetic breeding, including common beans [77–80]. The hybridization between cultivars developed by different programs and adapted to different locations may result in the maintenance of genetic diversity and the possibility of gains with the selection. Thus, these cultivars evaluated in this work also have the potential to be used in common bean breeding programs.

Finally, we can summarize that the use of reaction norm models associated with the Legendre polynomials, allows to adjust the behavior of the genotypes along a MET (as a function of a gradient). The methodology has the capacity to predict the genotypic values of individuals, even in places without phenotypic data, heterogeneity of genetic variations, correlations between environments, and spatial trends in the trials. Then, from the genotypic values and using an ideotype, it is possible to estimate the adaptability and stability of individuals.

Conclusion

The random regression models to evaluate the adaptability and stability of cultivars appears to be an alternative in the evaluation of multi-environment trials, because it allows you to deal with unbalanced data, as well an improved evaluation of cultivar behavior.

The cultivars IPR Campos Gerais, IAC Formoso and VC 15 were the most adapted to the scenario of general adaptability, while the cultivars IPR Campos Gerais, IPR Tuiuiú and BRS Estilo performed better in unfavorable environments and the cultivars IAC Formoso, IPR Campos Gerais and VC 15 were better in places with favorable conditions.

Supporting information

S1 Table. Carioca bean cultivars, institutions of origin and year of recommendation.

(DOCX)

Click here for additional data file.^{(15.7KB, docx)}

S2 Table. Black bean cultivars, institutions of origin and year of recommendation.

(DOCX)

Click here for additional data file.^{(15.5KB, docx)}

S3 Table. Description of the trials.

(DOCX)

Click here for additional data file.^{(12.1KB, docx)}

S4 Table. Accuracy of 105 cultivars in each trial.

(DOCX)

Click here for additional data file.^{(41.3KB, docx)}

S5 Table. Recommendation probability values for each cultivar in each scenario.

(DOCX)

Click here for additional data file.^{(21.6KB, docx)}

S1 Code. Script for analyses.

(DOCX)

Click here for additional data file.^{(23.5KB, docx)}

S1 DOI. Dataset availability.

(DOCX)

Click here for additional data file.^{(11KB, docx)}

Acknowledgments

We would like to thank the students of the Programa Feijão for their contribution with the help of data collection for this work. We would like to thank Editage (www.editage.com) for English language editing.

Data Availability

The dataset are available in the Figshare online repository, at the link: https://doi.org/10.6084/m9.figshare.12668390.v1.

Funding Statement

This work was financed with support resources received by professors Pedro Crescêncio Carneiro and José Eustáquio de Souza Carneiro, these resources being transferred to the Programa Feijão. In addition, the other authors of this work are graduate students who receive resources from three financial support agencies: CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico), FAPEMIG (Fundação de Apoio à Pesquisa do Estado de Minas Gerais) and CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior). There are still research projects funded by these same agencies that assist in conducting experiments in the Feijão Program. Authors: M.H. Souza: scholarship CNPq J. D. P. Júnior: scholarship FAPEMIG S.D.M. Steckling: scholarship CNPq J. Mencalha: scholarship CNPq F.S. Dias: scholarship CNPq J.R.A.S.C. Rocha: scholarship CNPq P.C. Carneiro: research grant CNPq J.E.S. Carneiro: research grant CNPq.

References

1.Smith AB, Ganesalingam A, Kuchel H, Cullis BR. Factor analytic mixed models for the provision of grower information from national crop variety testing programs. Theor Appl Genet. 2015;128: 55–72. 10.1007/s00122-014-2412-x [DOI] [PMC free article] [PubMed] [Google Scholar]
2.MAPA. Formulários para Registro de Cultivares—Ministério da Agricultura, Pecuária e Abastecimento. 2019 [cited 10 Jan 2019]. Available: http://www.agricultura.gov.br/assuntos/insumos-agropecuarios/insumos-agricolas/sementes-e-mudas/registro-nacional-de-cultivares-2013-rnc-1/formularios-para-registro-de-cultivares
3.Burgueño J, Crossa J, Cotes JM, Vicente FS, Das B. Prediction assessment of linear mixed models for multienvironment trials. Crop Sci. 2011;51: 944–954. 10.2135/cropsci2010.07.0403 [DOI] [Google Scholar]
4.Yau SK. Regression and AMMI Analyses of Genotype × Environment Interactions: An Empirical Comparison. Agron J. 1995;87: 121–126. 10.2134/agronj1995.00021962008700010021x [DOI] [Google Scholar]
5.Finlay K, Wilkinson G. The analysis of adaptation in a plant-breeding programme. Aust J Agric Res. 1963;14: 742 10.1071/AR9630742 [DOI] [Google Scholar]
6.Eberhart SA, Russell WA. Stability Parameters for Comparing Varieties1. Crop Sci. 1966;6: 36 10.2135/cropsci1966.0011183x000600010011x [DOI] [Google Scholar]
7.Verma MM, Chahal GS, Murty BR. Limitations of conventional regression analysis a proposed modification. Theor Appl Genet. 1978;53: 89–91. 10.1007/BF00274335 [DOI] [PubMed] [Google Scholar]
8.Cruz CD, Torres RD, Vencovsky R. An alternative approach to the stability analysis proposed by Silva and Barreto. Rev Bras Genética. 1989;12: 567–580. [Google Scholar]
9.Nascimento M, Ferreira A, Mota Campana AC, Salgado CC, Cruz CD. Multiple Centroid Methodology to analyze genotype adaptability. Crop Breed Appl Biotechnol. 2009;9: 8–16. 10.12702/1984-7033.v09n01a02 [DOI] [Google Scholar]
10.Oliveira RL de, Von Pinho RG, Ferreira DF, Pires LPM, Melo WMC. Selection index in the study of adaptability and stability in maize. Sci World J. 2014;2014: 1–6. 10.1155/2014/360570 [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Van Eeuwijk FA, Bustos-korts DV, Malosetti M. What Should Students in Plant Breeding Know About the Statistical Aspects of Genotype x Environment Interactions? Crop Sci. 2016;56: 2119–2140. 10.2135/cropsci2015.06.0375 [DOI] [Google Scholar]
12.Gauch HG. Statistical analysis of regional yield trials: AMMI analysis of factorial designs. 1st ed. Gauch HGJ, editor. Ithaca, NY: Elsevier; 1992. [Google Scholar]
13.Yan W, Hunt LA. Interpretation of genotype X environment interaction for winter wheat yield in Ontario. Crop Sci. 2001;41: 19–25. [Google Scholar]
14.Eberhart SA, Russell WA. Stability Parameters for Comparing Varieties. Crop Sci. 1966;6: 36–40. 10.2135/cropsci1966.0011183x000600010011x [DOI] [Google Scholar]
15.Vargas M, Crossa J, Van Eeuwijk FA, Sayre KD, Reynolds MP. Statistics: Interpreting treatment × environment interaction in agronomy trials. Agron J. 2001;93: 949–960. 10.2134/agronj2001.934949x [DOI] [Google Scholar]
16.Kirkpatrick M, Lofsvold D, Bulmer M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics. 1990;124: 979–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Schaeffer LR, Dekkers JCM. Random regressions in animal models for test-day production in dairy cattle. Guelph, Ontario, Canada; 1994. [Google Scholar]
18.Meyer K, Hill WG. Estimation of genetic and phenotypic covariance functions for longitudinal or “repeated” records by restricted maximum likelihood. Livest Prod Sci. 1997;47: 185–200. 10.1016/S0301-6226(96)01414-5 [DOI] [Google Scholar]
19.Meyer K. Estimating covariance functions for longitudinal data using a random regression model. Genet Sel Evol. 1998;30: 221–240. 10.1186/1297-9686-30-3-221 [DOI] [Google Scholar]
20.Jamrozik J, Schaeffer LR, Dekkers JCM. Genetic Evaluation of Dairy Cattle Using Test Day Yields and Random Regression Model. J Dairy Sci. 1997;80: 1217–1226. 10.3168/jds.S0022-0302(97)76050-8 [DOI] [PubMed] [Google Scholar]
21.Schaeffer LR. Application of random regression models in animal breeding. Livest Prod Sci. 2004;86: 35–45. 10.1016/S0301-6226(03)00151-9 [DOI] [Google Scholar]
22.Jamrozik J, Bohmanova J, Schaeffer LR. Relationships between milk yield and somatic cell score in Canadian Holsteins from simultaneous and recursive random regression models. J Dairy Sci. 2010;93: 1216–1233. 10.3168/jds.2009-2585 [DOI] [PubMed] [Google Scholar]
23.Ali TE, Schaeffer LR. Accounting for covariances among test day milk yields ind dairy cows. Can J Anim Sci. 1987;67: 637–644. 10.4141/cjas87-067 [DOI] [Google Scholar]
24.Wilmink JBM. Adjustment of lactation yield for age at calving in relation to level of production. Livest Prod Sci. 1987;16: 321–334. 10.1016/0301-6226(87)90002-9 [DOI] [Google Scholar]
25.Kirkpatrick M, Heckman N. A quantitative genetic model for growth, shape, reaction norms, and other infinite-dimensional characters. J Math Biol. 1989;27: 429–450. 10.1007/BF00290638 [DOI] [PubMed] [Google Scholar]
26.Bohmanova J, Miglior F, Jamrozik J, Misztal I, Sullivan PG. Comparison of random regression models with legendre polynomials and linear splines for production traits and somatic cell score of Canadian Holstein cows. J Dairy Sci. 2008;91: 3627–3638. 10.3168/jds.2007-0945 [DOI] [PubMed] [Google Scholar]
27.Sun J, Rutkoski JE, Poland JA, Crossa J, Jannink J-L, Sorrells ME. Multitrait, Random Regression, or Simple Repeatability Model in High-Throughput Phenotyping Data Improve Genomic Prediction for Wheat Grain Yield. Plant Genome. 2017;10: 1–15. 10.3835/plantgenome2016.11.0111 [DOI] [PubMed] [Google Scholar]
28.Ly D, Huet S, Gauffreteau A, Rincent R, Touzy G, Mini A, et al. Whole-genome prediction of reaction norms to environmental stress in bread wheat (Triticum aestivum L.) by genomic random regression. F Crop Res. 2018;216: 32–41. 10.1016/j.fcr.2017.08.020 [DOI] [Google Scholar]
29.Momen M, Campbell MT, Walia H, Morota G. Predicting longitudinal traits derived from high-throughput phenomics in contrasting environments using genomic Legendre polynomials and B-splines. G3 Genes, Genomes, Genet. 2019;9: 3369–3380. 10.1534/g3.119.400346 [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Baba T, Momen M, Campbell MT, Walia H, Morota G. Multi-trait random regression models increase genomic prediction accuracy for a temporal physiological trait derived from high-throughput phenotyping. Ortiz R, editor. PLoS One. 2020;15: e0228118 10.1371/journal.pone.0228118 [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Woltereck R. Weitere experimentelle Untersuchungen über Artveränderung, speziel über das Wesen quantitativer Artunterschiede bei Daphnien. Verhandlungen der Dtsch. 1909;19: 110–173. [Google Scholar]
32.Martin JGA, Nussey DH, Wilson AJ, Réale D. Measuring individual differences in reaction norms in field and experimental studies: A power analysis of random regression models. Methods Ecol Evol. 2011;2: 362–374. 10.1111/j.2041-210X.2010.00084.x [DOI] [Google Scholar]
33.Van de Pol M. Quantifying individual variation in reaction norms: How study design affects the accuracy, precision and power of random regression models. Methods Ecol Evol. 2012;3: 268–280. 10.1111/j.2041-210X.2011.00160.x [DOI] [Google Scholar]
34.Streit M, Reinhardt F, Thaller G, Bennewitz J. Reaction norms and genotype-by-environment interaction in the German Holstein dairy cattle. J Anim Breed Genet. 2012;129: 380–389. 10.1111/j.1439-0388.2012.00999.x [DOI] [PubMed] [Google Scholar]
35.Liu X. Linear Mixed-Effects Models. In: Liu X, editor. Methods and Applications of Longitudinal Data Analysis 1st ed. Academic Press; 2015. pp. 61–94. [Google Scholar]
36.Schaeffer LR. Animal Models. Self-Published; 2019. [Google Scholar]
37.Akaike H. A new look at the statistical identification model. A new look Stat Identif Model. 1974;19: 716. [Google Scholar]
38.Wolfinger R. Covariance structure selection in general mixed models. Commun Stat—Simul Comput. 1993;22: 1079–1106. 10.1080/03610919308813143 [DOI] [Google Scholar]
39.Stoica P, Babu P. Model order estimation via penalizing adaptively the likelihood (PAL). Signal Processing. 2013;93: 2865–2871. 10.1016/J.SIGPRO.2013.03.014 [DOI] [Google Scholar]
40.Rao CR. Linear statistical inference and its application. New York: John Wiley and Sons; 1965. Available: https://academic.oup.com/jlms/article-abstract/s1-42/1/382/844079 [Google Scholar]
41.Gilmour AR, Gogel BJ, Cullis BR, Thompson R. ASReml User Guide Release 3.0. VSN International Ltd, Hemel Hempsted, HP1 1ES, UK; 2009. Available on: www.vsni.co.uk
42.Rocha JR do AS de C, Marçal T de S, Salvador FV, Silva AC da, Machado JC, Carneiro PCS. Genetic insights into elephantgrass persistence for bioenergy purpose. Feltus FA, editor. PLoS One. 2018;13: e0203818 10.1371/journal.pone.0203818 [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Resende MDV de, Duarte JB. Precisão e controle de qualidade em experimentos de avaliação de cultivares. Pesqui Agropecuária Trop. 2007;37: 182–194. [Google Scholar]
44.Melo CLP de, Carneiro, José Eustáquio de Souza Carneiro PCS, Cruz CD, Barros, Everaldo Gonçalves de Moreira MA. Linhagens de feijão do cruzamento “Ouro Negro” x “Pérola” com características agronômicas favoráveis. Pesqui Agropecuária Bras. 2006;41: 1593–1598. [Google Scholar]
45.Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R. ASReml User Guide Release 4.1 Structural Specification, VSN International Ltd, Hemel Hempstead, HP1 1ES, UK; 2015. Available: www.vsni.co.uk
46.Computing RF for S. R Development Core Team. Austria, Vienna; 2015.
47.Yang Y. Can the strengths of AIC and BIC be shared? A conflict between model indentification and regression estimation. Biometrika. 2005;92: 937–950. 10.1093/biomet/92.4.937 [DOI] [Google Scholar]
48.Corrales JD, Munilla S, Cantet RJC. Polynomial order selection in random regression models via penalizing adaptively the likelihood. J Anim Breed Genet. 2015;132: 281–288. 10.1111/jbg.12130 [DOI] [PubMed] [Google Scholar]
49.Vrieze SI. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol Methods. 2012;17: 228–243. 10.1037/a0027127 [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Kolmodin R, Strandberg E, Madsen P, Jensen J, Jorjani H. Genotype by environment interaction in Nordic dairy cattle studied using reaction norms. Acta Agric Scand—Sect A Anim Sci. 2002;52: 11–24. 10.1080/09064700252806380 [DOI] [Google Scholar]
51.Calus MPL, Veerkamp RF. Estimation of environmental sensitivity of genetic merit for milk production traits using a random regression model. J Dairy Sci. 2003;86: 3756–3764. 10.3168/jds.S0022-0302(03)73982-4 [DOI] [PubMed] [Google Scholar]
52.Pereira HS, Melo LC, Del Peloso MJ, de Faria LC, Wendland A. Complex interaction between genotypes and growing seasons of carioca common bean in Goiás/Distrito Federal. Crop Breed Appl Biotechnol. 2011;11: 207–215. 10.1590/S1984-70332011000300002 [DOI] [Google Scholar]
53.Torga PP, Melo PGS, Pereira HS, de Faria LC, Del Peloso MJ, Melo LC. Interaction of common beans cultivars of the black group with years, locations and sowing seasons. Euphytica. 2013;189: 239–248. 10.1007/s10681-012-0793-y [DOI] [Google Scholar]
54.Tusiime G. Genotype x Environment interactions for higher Iron and Zinc in selected bean varieties. Ambit J Agric. 2015;1: 16–39. [Google Scholar]
55.Correa AM, Gonçalves MC, Teodoro PE. Pattern analysis of multi-environment trials in common bean genotypes. Biosci J. 2016;32: 328–336. 10.14393/BJ-v32n2a2016-29572 [DOI] [Google Scholar]
56.Ramalho MAP, Abreu A de FB, Santos PSJ dos. Interações genótipos x épocas de semeadura, anos e locais na avaliação de cultivares de feijão nas regiões Sul e Alto Paranaíba em Minas Gerais. Cienc agrotec. 1998;22: 175–181. [Google Scholar]
57.Wricke G. Zur Berechnung der Ökovalenz bei Sommerweizen und Hafer. Pflanzenzuchtung. 1965;52: 127–138. [Google Scholar]
58.Plaisted RL, Peterson LC. A technique for evaluating the ability of selections to yield consistently in different locations or seasons. Am Potato J. 1959;36: 381–385. 10.1007/BF02852735 [DOI] [Google Scholar]
59.Jarquín D, Crossa J, Lacaze X, Du Cheyron P, Daucourt J, Lorgeou J, et al. A reaction norm model for genomic selection using high-dimensional genomic and environmental data. Theor Appl Genet. 2014;127: 595–607. 10.1007/s00122-013-2243-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
60.Ni G, Van der Werf J, Zhou X, Hyppönen E, Wray NR, Lee SH. Genotype–covariate correlation and interaction disentangled by a whole-genome multivariate reaction norm model. Nat Commun. 2019;10 10.1038/s41467-019-10128-w [DOI] [PMC free article] [PubMed] [Google Scholar]
61.Resende MDV. Software Selegen-REML/BLUP: A useful tool for plant breeding. Crop Breed Appl Biotechnol. 2016;16: 330–339. 10.1590/1984-70332016v16n4a49 [DOI] [Google Scholar]
62.Cellon C, Amadeu RR, Olmstead JW, Mattia MR, Ferrao LFV, Munoz PR. Estimation of genetic parameters and prediction of breeding values in an autotetraploid blueberry breeding population with extensive pedigree data. Euphytica. 2018;214 10.1007/s10681-018-2165-8 [DOI] [Google Scholar]
63.Piepho HP, Möhring J, Melchinger AE, Büchse A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica. 2008;161: 209–228. 10.1007/s10681-007-9449-8 [DOI] [Google Scholar]
64.Oakey H, Verbyla A, Pitchford W, Cullis B, Kuchel H. Joint modeling of additive and non-additive genetic line effects in single field trials. Theor Appl Genet. 2006;113: 809–819. 10.1007/s00122-006-0333-z [DOI] [PubMed] [Google Scholar]
65.Howard JT, Jiao S, Tiezzi F, Huang Y, Gray KA, Maltecca C. Genome-wide association study on legendre random regression coefficients for the growth and feed intake trajectory on Duroc Boars. BMC Genet. 2015;16: 1–11. 10.1186/s12863-014-0153-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
66.Cullis BR, Gleeson AC. Spatial Analysis of Field Experiments-An Extension to Two Dimensions. Biometrics. 1991;47: 1449 10.2307/2532398 [DOI] [Google Scholar]
67.Gilmour AR, Cullis BR, Verbyla AP. Accounting for Natural and Extraneous Variation in the Analysis of Field Experiments. J Agric Biol Environ Stat. 1997;2: 269–293. 10.2307/1400446 [DOI] [Google Scholar]
68.Campbell M, Momen M, Walia H, Morota G. Leveraging Breeding Values Obtained from Random Regression Models for Genetic Inference of Longitudinal Traits. Plant Genome. 2019;12: 180075 10.3835/plantgenome2018.10.0075 [DOI] [PubMed] [Google Scholar]
69.Sarmento JLR, Torres RA, Sousa WH, Lôbo RNB, Albuquerque LG, Lopes PS, et al. Random regression models for the estimation of genetic and environmental covariance functions for growth traits in Santa Ines sheep. Genet Mol Res. 2016;15: 1–13 10.4238/gmr.15025749 [DOI] [PubMed] [Google Scholar]
70.Burgueño J, de los Campos G, Weigel K, Crossa J. Genomic Prediction of Breeding Values when Modeling Genotype × Environment Interaction using Pedigree and Dense Molecular Markers. Crop Sci. 2012;52: 707 10.2135/cropsci2011.06.0299 [DOI] [Google Scholar]
71.Pérez-Rodríguez P, Crossa J, Bondalapati K, De Meyer G, Pita F, Campos G de los. A pedigree-based reaction norm model for prediction of cotton yield in multienvironment trials. Crop Sci. 2015;55: 1143 10.2135/cropsci2014.08.0577 [DOI] [Google Scholar]
72.Lian L, Jacobson A, Zhong S, Bernardo R. Genomewide prediction accuracy within 969 maize biparental populations. Crop Sci. 2014;54: 1514–1522. 10.2135/cropsci2013.12.0856 [DOI] [Google Scholar]
73.Lorenzana RE, Bernardo R. Accuracy of genotypic value predictions for marker-based selection in biparental plant populations. Theor Appl Genet. 2009;120: 151–161. 10.1007/s00122-009-1166-3 [DOI] [PubMed] [Google Scholar]
74.Viana JMS, de Lima RO, Faria VR, Mundim GB, de Resende MDV, Silva FF. Relevance of pedigree, historical data, dominance, and data unbalance for selection efficiency. Agron J. 2012;104: 722–728. 10.2134/agronj2011.0358 [DOI] [Google Scholar]
75.Van Oijen M, Höglind M. Toward a Bayesian procedure for using process-based models in plant breeding, with application to ideotype design. Euphytica. 2016;207: 627–643. 10.1007/s10681-015-1562-5 [DOI] [Google Scholar]
76.Xue B, Leibler S. Benefits of phenotypic plasticity for population growth in varying environments. Proc Natl Acad Sci USA. 2018;115: 12745–12750. 10.1073/pnas.1813447115 [DOI] [PMC free article] [PubMed] [Google Scholar]
77.Sicard D, Nanni L, Porfiri O, Bulfon D, Papa R. Genetic diversity of Phaseolus vulgaris L. and P. coccineus L. landraces in central Italy. Plant Breed. 2005;124: 464–472. 10.1111/j.1439-0523.2005.01137.x [DOI] [Google Scholar]
78.Cowling WA. Genetic diversity in Australian canola and implications for crop breeding for changing future environments. F Crop Res. 2007;104: 103–111. 10.1016/j.fcr.2006.12.014 [DOI] [Google Scholar]
79.Rauf S, da Silva J, Khan A, Naveed A. Consequences of Plant Breeding on Genetic Diversity. Int J Plant Breed. 2010;4: 1–21. [Google Scholar]
80.Tester M, Langridge P. Breeding technologies to increase crop production in a changing world. Science. American Association for the Advancement of Science; 2010. pp. 818–822. 10.1126/science.1183700 [DOI] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0233200.r001

Decision Letter 0

Roberto Fritsche-Neto

8 Jun 2020

PONE-D-20-12530

New genotypic adaptability and stability analyses using Legendre polynomials and genotype-ideotype distances

PLOS ONE

Dear Dr. de Souza,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Please submit your revised manuscript by Jul 23 2020 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

We look forward to receiving your revised manuscript.

Kind regards,

Roberto Fritsche-Neto, Ph.D.

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. We note that you have stated that you will provide repository information for your data at acceptance. Should your manuscript be accepted for publication, we will hold it until you provide the relevant accession numbers or DOIs necessary to access your data. If you wish to make changes to your Data Availability statement, please describe these changes in your cover letter and we will update your Data Availability statement to reflect the information you provide.

3. We note that you have included the phrase “data not shown” in your manuscript. Unfortunately, this does not meet our data sharing requirements. PLOS does not permit references to inaccessible data. We require that authors provide all relevant data within the paper, Supporting Information files, or in an acceptable, public repository. Please add a citation to support this phrase or upload the data that corresponds with these findings to a stable repository (such as Figshare or Dryad) and provide and URLs, DOIs, or accession numbers that may be used to access these data. Or, if the data are not a core part of the research being presented in your study, we ask that you remove the phrase that refers to these data.

4. Please amend your manuscript to include your abstract after the title page.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Partly

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: No

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: No

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: Overview

The proposed methodology could be an alternative to traditional models in the study of MET. It uses the phenotypic values of the genotypes across trials to create an environmental gradient and fits a reaction norm model using Legendre polynomials to predict the genotype performance. Although, using only the means of genotypes and general mean to create the environmental gradient may not be best alternative due disregard edaphoclimatic conditions.

The use of ideotypes to study the adaptability and stability seems to be a good alternative. It is possible to obtain four classes of ideotypes and from this select the desired genotypes.

A few considerations must be pointed:

The author may hypothesize why using Environmental gradient applying Finlay and Wilkinson is advantageous than environment traits to obtain the Environmental gradient;

The authors did not compare the proposed methodology to established methodologies. This could enhance the discussion;

Is it possible to use covariance matrix for the genotypic effect? It was used in the Phaseolus vulgaris L application?

A detailed description follows below:

Introduction:

Introduction underline the importance of genotype x environment studies. Although, it lacks reference that reinforce the proposed methodology and its theoretical background.

Line 35-36: Check the reference

Line 47-54: Need reference for theses affirmations

Line 66: imbalances or unbalanced? check in the text

Methods description (step by step):

Well written and understandable.

Application of the method with Phaseolus vulgaris L.

Results

Line 240: humidity to moisture

Line 267: witnesses to check

Discussion

Usually, in animals and plants, Legendre polynomials and other random regression are used to model the growth of the individual. In the presented methodology, it was not clear the “biological” meaning of modeling reaction norm using only environmental gradient with only the same priori information. see DOI 10.1007/s00122-013-2243-1. How the model deal with genotype x environment interaction? Is it feasible to extrapolate the presented methodology to unobserved environments? Since the Mixed model approach is used.

Line 424-425: How the presented methodology could incorporate the genomic matrix and environmental data in order to increase predictive ability?

Line 429-430: Which studies are these? What are the connections between the presented methodology and them?

Line 431-437: “The fact that an individuals' behavior is not predetermined, is an advantage of the proposed methodology in relation to the traditional methods of analysis of adaptability and stability.” I do not understand this affirmation. The model doesn’t use the environmental gradient defined a prioi from observed genotypes?

Line 446-454: Advantage over which other methodology? The presented work did not compare with the most common methodologies applied.

Line 452-454: It was not clear if it was used a cross-validation scenario to obtain these predictive accuracies. If it wasn’t, interpretation regarding predictive accuracy must be pondered.

Line 460-461: Comparison among mixed models and others approach must be careful since the present work did not evaluate any other approach.

Line 482-524: These paragraphs focus mainly on bean recommendation. Although very important, these do not seem to be the main focus of the study.

Reference

Many references are in Portuguese or are from books. These type of refences should be avoided in order to ensure access to the readers.

Reviewer #2: The authors applied random regression models (RRM) to investigate the reaction norms in common bean cultivars. This is a timely topic because understanding the genotype by environment is increasingly becoming important given the recent climate change. Although the topic discussed here is fascinating, there are a number of subjects that the authors may want to expand.

The authors argued as if they developed RRM to investigate phenotypic plasticity or reaction norm. For instance, this is reflected in the title, "We propose a new methodology" in the Abstract, and "Thus, the objectives of this investigation were to propose a new methodology for ..." However, this is incorrect as the use of RRM for phenotypic plasticity analysis has been an active research area in animal breeding and ecology for more than decades. You are applying the previously developed methodology to study phenotypic plasticity in plants by treating multi-environment trials as environmental gradients. This manuscript would be much more appealing to plant breeders if written in the context of those works by others.

My second reservation pertains to the Introduction section that lacks a good structure. First, start by framing why adaptability/stability analysis is an important research area in the context of multi-environment trials (MET) and genotype by environment (GEI). Note that MET and GEI were never mentioned in the Introduction in the current version. The term MET first appears in the Methods section and GEI is only referred to in the Discussion section. Second, briefly review rich literature on how and why RRM has been widely used to study plasticity or GEI in animal breeding and ecology. Lastly, clearly state the objective of this paper, which is the application of RRM to investigate reaction norms in plant breeding. Also, just saying linear mixed models coupled with Legendre polynomials is not sufficient. Explicitly mention that the model you are using is RRM. I suggest entirely rewriting the Introduction.

The third major concern is the lack of methodological clarity and smoothness. The current Methods section is written like a step by step software manual with a disconnection between them. Not quite sure how Ij defined in step 1 is relevant to the subsequent steps. Steps in L131 and L144 can be combined with others because they are well-known statistics. I believe the methodology part can be significantly improved.

The utility of RRM is limited in this study because the authors did not use any genetic data (pedigree or genomics). Consider adding one or two paragraphs, regarding the impact of genetics on adaptability and stability analyses in the Discussion section.

Below are my specific comments.

Data availability statement. It is a bit strange to say that the data will be available upon acceptance of this manuscript. The data should be made available for reviewers and editors through the reviewing process if you intend to make them open.

L47: It was not clear to me what you are referring to by current technologies and lower level technologies.

L123: How is the vector of phenotypes constructed? Is it ordered by genotypes or trials? This will determine how you specify the variance-covariance terms for g and e. There is an inconsistency in your notation because Kg is on the left side of the Kronecker product, while Sigma_e is on the right side of the Kronecker product.

L155, L163, L168: It is misleading to say "at the original scale". You are just predicting breeding values from estimated random regression coefficients.

L157: What BLUPs are you referring to? I do not see any connection between this and the preceding subsections.

L173: Clarify how PEV was computed from a random regression model.

Equation 9: A reference is needed.

L204: I did not understand this paragraph. What does it mean by "through the invariance in multi environment trials (MET)."?

Genetic material (L216) and Trials (L223) should be placed before the Methods description (L83) according to the flow.

L218: How population structure of Carioca grains and Black grains were accounted for. I believe this will impact the interpretation of results.

L322: It is not evident in Figure 1, which ones are environmental gradients six and eight.

L324: This is essential information. I suggest you show a table or a figure related to variance components.

Figure 1: Clarify why the x-axis is ranging from -1 to 1. This does not agree with Table 1.

L340: You previously mentioned in L264 that the cultivars of minimal adaptability will not be considered for recommendations. Why do the cultivars of minimal adaptability appear here again?

L406: Introduce the concept of genotype by environment interactions first in the Introduction section rather than in the Discussion.

L426: This paragraph should be placed in the Introduction section.

L446: You did not propose the method (reaction norm analysis using RRM), but you applied.

Minor comments.

L117: Consider replacing order of adjustment with order of polynomials

L122, L293, L308: residue -> residual or residuals

L200: Why na appears twice for k = 1 and k = 4?

L281: table 1 -> Table 1.

L293: Consider replacing grade six with order six. Also, see L306.

Table 2: The column LOG L is redundant if all models converged.

L313: There is no need to redefine DEG, AIC, BIC, PAL, LRT, H, and D again.

L322: figure 1 -> Figure 1

L401-402: Be consistent with the use of trials vs. environments

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2020 Dec 2;15(12):e0233200. doi: 10.1371/journal.pone.0233200.r002

Author response to Decision Letter 0

17 Jul 2020

The authors of this paper would like to thank the reviewers' comments and suggestions. His excellent tips contributed greatly to the improvement of this work, leading to greater understanding and ease of interpretation. We carefully analyze each comment and seek to meet the requests of both reviewers. In the file named "response to reviewers", there is a detailed description of each suggestion and the change made to the article, in order to simultaneously serve the reviewers.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(25.9KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0233200.r003

Decision Letter 1

Roberto Fritsche-Neto

27 Aug 2020

PONE-D-20-12530R1

Adaptability and stability analyses of plants using random regression models

PLOS ONE

Dear Dr. de Souza,

Please submit your revised manuscript by Oct 11 2020 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Roberto Fritsche-Neto, Ph.D.

Academic Editor

PLOS ONE

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: I would like to thank the authors for having accepted my suggestions and or clarified my doubts. The application of random regressions models and ideotypes proved to be suitable in the studies of genotype by environment interaction (GEI) in beans. Although the authors did not use any genomic/pedigree data or environmental information, the methodologies used provide opportunities for further research regarding the use of environmental and genomics data using Random Regression models in multi environmental trials studies.

A detailed description with minor review follows below:

L.48: Replace “imbalance” to “unbalanced”

L.155: Replace “Genetic imbalance” to “Genetic Unbalanced”

L. 293: Replace "Witnesses" to "check"

L. 294: Replace "as witnesses to check" "as check"

L.248: Equation 9. Reference needed

L.381: Replace "Witnesses" to "check"

L. 657: Remove

Reviewer #2: The authors have addressed most of my comments adequately. Below are my additional comments to improve the readability and strengthen the manuscript.

L103: This is incorrect. Henderson proposed BLUP, linear mixed model, and mixed model equations, but not RRM. The initial form of RRM was first proposed by Kirkpatrick et al. 1990 [1] and later extended by Schaeffer and Dekkers 1994 [2] and Meyer and Hill 1997 [3].

[1] Kirkpatrick et al. 1990 Analysis of the inheritance, selection and evolution of growth trajectories. Genetics 124: 979–993.

[2] Schaeffer LR, Dekkers JCM. Random regressions in animal models for test-day production in dairy cattle. Proc 5th World Congress on Genetics Applied to Livestock Production; 1994; Guelph, 18:443-446.

[3] Meyer K, Hill WG. Estimation of genetic and phenotypic covariance functions for longitudinal or repeated records by restricted maximum likelihood. Livest Prod Sci. 1997; 47:185–200.

It is important to note that the current work is not the first time to apply RRM to univariate or multivariate plant breeding data. The authors failed to refer to the earlier work of Sun et al. 2017 [4], Ly et al. 2018 [5], Momen et al. 2019 [6], and Baba et al. 2020 [7] in the Introduction section. Put them after animal breeding literature you referred and mention their contribution/relevance with respect to the current work.

[4] Sun et al. Multitrait, random regression, or simple repeatability model in high-throughput phenotyping data improve genomic prediction for wheat grain yield. Plant Genome. 2017; 10. pmid:28724067

[5] Ly et al. Whole-genome prediction of reaction norms to environmental stress in bread wheat (Triticum aestivum 736 L.) by genomic random regression. F Crop Res. 2018;216.

[6] Momen et al. Predicting longitudinal traits derived from high-throughput phenomics in contrasting environments using genomic Legendre polynomials and B-splines. G3: Genes, Genomes, Genetics. 2019. 9:3369-3380.

[7] Baba et al. Multi-trait random regression models increase genomic prediction accuracy for a temporal physiological trait derived from high-throughput phenotyping. PLoS ONE 2020. 15(2): e0228118.

In sum, the introduction section should be framed in the context of earlier work by others.

L185: I believe you meant the lowest and highest averages rather than lower and higher averages.

L191-194: What do you mean by "adjusted"? Perhaps "adjusted" is not the best term to use here.

L196, Equation 3: Why don't you include fixed random regression coefficients designed to capture the mean trajectory of environmental gradients? Almost all of the previous RRM literature include this term to account for the mean trend.

L248: Provide a reference for equation 9.

L264: Remove "thus"

L293, L375: What witnesses are? I am not familiar with this term. I believe you meant checks?

Table 2: Clarify what H or D means (first column) in the table caption.

L765: Smith et al. 2015 has been cited twice. Ref 1 and Ref 73.

Ref 20. Wrong journal title. Should be Journal of Dairy Science.

Ref 38: It says "Available: file:///C:/Users/Sandrinho/Downloads/artículo_redalyc_253021631009.pdf". Note that this is the author's locale file on a computer. Readers will not have access to it.

Lastly, I agree with reviewer 2 that references are used to support or defend your claims you made in your research. Note that PLOS ONE has a wide range of readers from around the world. I could not assess many references such as 9, 38-39, 42, 48-52, 61, 72, 76 because they are not written in English. Consider replacing them, if possible, with more suitable references that everyone can read, understand, and discuss.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

PLoS One. 2020 Dec 2;15(12):e0233200. doi: 10.1371/journal.pone.0233200.r004

Author response to Decision Letter 1

1 Oct 2020

Response to Reviewers

Dear reviewers,

The authors of this paper would like to thank the reviewers' comments and suggestions. We believe that this tips contributed greatly to the improvement of this work, leading to greater understanding and ease of interpretation. We carefully analyze each comment and seek to meet the requests of both reviewers. Below is a detailed description of each suggestion and the change made to the article, in order to simultaneously serve the reviewers.

Reviewer #1)

• L.48: Replace “imbalance” to “unbalanced”

• L.155: Replace “Genetic imbalance” to “Genetic Unbalanced”

• L. 293: Replace "Witnesses" to "check"

• L. 294: Replace "as witnesses to check" "as check"

• L.248: Equation 9. Reference needed

• L.381: Replace "Witnesses" to "check"

• L. 657: Remove

Authors reply: We would like to thank you the reviewer for the suggestions. We think they made this work better. We have been made the changes in the text.

Reviewer #2:

• L103: This is incorrect. Henderson proposed BLUP, linear mixed model, and mixed model equations, but not RRM. The initial form of RRM was first proposed by Kirkpatrick et al. 1990 [1] and later extended by Schaeffer and Dekkers 1994 [2] and Meyer and Hill 1997 [3].

[1] Kirkpatrick et al. 1990 Analysis of the inheritance, selection and evolution of growth trajectories. Genetics 124: 979–993.

[3] Meyer K, Hill WG. Estimation of genetic and phenotypic covariance functions for longitudinal or repeated records by restricted maximum likelihood. Livest Prod Sci. 1997; 47:185–200.

Authors reply: We apologize for the mistake. In this way, we understood the suggestions pointed out by the reviewer and made changes to the text, as suggested. We would like to thank you for the suggestions.

• It is important to note that the current work is not the first time to apply RRM to univariate or multivariate plant breeding data. The authors failed to refer to the earlier work of Sun et al. 2017 [4], Ly et al. 2018 [5], Momen et al. 2019 [6], and Baba et al. 2020 [7] in the Introduction section. Put them after animal breeding literature you referred and mention their contribution/relevance with respect to the current work.

[4] Sun et al. Multitrait, random regression, or simple repeatability model in high-throughput phenotyping data improve genomic prediction for wheat grain yield. Plant Genome. 2017; 10. pmid:28724067

[5] Ly et al. Whole-genome prediction of reaction norms to environmental stress in bread wheat (Triticum aestivum 736 L.) by genomic random regression. F Crop Res. 2018;216.

[7] Baba et al. Multi-trait random regression models increase genomic prediction accuracy for a temporal physiological trait derived from high-throughput phenotyping. PLoS ONE 2020. 15(2): e0228118.

In sum, the introduction section should be framed in the context of earlier work by others.

Authors reply: Again, we made a mistake in not mentioning some works that used RRM previously. Then, we read these articles recommended by the reviewer and made the corrections in the text. Thank you for the suggestion.

• L185: I believe you meant the lowest and highest averages rather than lower and higher averages.

Authors reply: Yes, we wanted to mean the lowest and highest averages. Thank you for the suggestion. We changed these words in the text.

• L191-194: What do you mean by "adjusted"? Perhaps "adjusted" is not the best term to use here.

Authors reply: It is true; the term adjusted was not the best in this sentence. We changed the word in the text to ‘fitted’.

• L196, Equation 3: Why don't you include fixed random regression coefficients designed to capture the mean trajectory of environmental gradients? Almost all of the previous RRM literature include this term to account for the mean trend.

• Thank for you doubt, reviewer. The reason why we did not use the coefficients for the fixed part of the model was that, specifically in this work, we were not interested in estimating a mean for a not existing environment throughout the MET. However, as the reviewer said that this is common in the literature, we also affirm that this could have been done, without problems for the model. It was just our option to choose this model, with the fixed part without the drawing of a trajectory.

• L248: Provide a reference for equation 9.

Authors reply: We added the reference in the text for this equation.

• L264: Remove "thus"

Authors reply: the word “thus” was removed from the text.

• L293, L375: What witnesses are? I am not familiar with this term. I believe you meant checks?

• Authors reply: we accepted this suggestion and changed the word in the text to ‘checks’.

• Table 2: Clarify what H or D means (first column) in the table caption.

Authors reply: We put the D and H means in the table 2 caption.

• L765: Smith et al. 2015 has been cited twice. Ref 1 and Ref 73.

Authors reply: We fixed those citations in the text.

• Ref 20. Wrong journal title. Should be Journal of Dairy Science.

Authors reply: We fixed this reference in the text.

• Ref 38: It says "Available: file:///C:/Users/Sandrinho/Downloads/artículo_redalyc_253021631009.pdf". Note that this is the author's locale file on a computer. Readers will not have access to it.

• Authors reply: We fixed this reference in the text.

• Lastly, I agree with reviewer 2 that references are used to support or defend your claims you made in your research. Note that PLOS ONE has a wide range of readers from around the world. I could not assess many references such as 9, 38-39, 42, 48-52, 61, 72, 76 because they are not written in English. Consider replacing them, if possible, with more suitable references that everyone can read, understand, and discuss.

• Authors reply: thank you for the comment. We tried to change these references written in Portuguese and we did this for most of them. We just could not find works corresponding to references 38, 39 and 52, since they are very specific references to VCU trials and common beans trials in Brazil, with no similar articles in international journals.

These references are in the following order in the text:

[41] Resende MDV de, Duarte JB. Precisão e controle de qualidade em experimentos de avaliação de cultivares. Pesqui Agropecuária Trop. 2007;37: 182–194.

[42] Melo CLP de, Carneiro, José Eustáquio de Souza Carneiro PCS, Cruz CD, Barros, Everaldo Gonçalves de Moreira MA. Linhagens de feijão do cruzamento “Ouro Negro” x “Pérola” com características agronômicas favoráveis. Pesqui Agropecuária Bras. 2006;41: 1593–1598.

[54] Ramalho MAP, Abreu A de FB, Santos PSJ dos. Interações genótipos x épocas de semeadura, anos e locais na avaliação de cultivares de feijão nas regiões Sul e Alto Paranaíba em Minas Gerais. Ciência e Agrotecnologia. 1998;22: 175–181.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(21.4KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0233200.r005

Decision Letter 2

Paulo Eduardo Teodoro

20 Oct 2020

PONE-D-20-12530R2

Adaptability and stability analyses of plants using random regression models

PLOS ONE

Dear Dr. de Souza,

Please submit your revised manuscript by Dec 04 2020 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Paulo Eduardo Teodoro, Dr.

Academic Editor

PLOS ONE

Additional Editor Comments (if provided):

Dear authors, your manuscript was returned to the initial reviewers. One accepted and another requested Minor Revision. I am also requesting some corrections. Answer the comments point-to-point so that I can make the Final Decision in the next round.

- Throughout the text use "common bean" instead of just "bean";

- quote all R packages used for the analyzes;

- In the Discussion, insert a final paragraph about what advances the proposed method has in relation to the dozens of methods in the literature;

- Add in the conclusions the best genotypes identified by RR models.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

Reviewer #1: (No Response)

Reviewer #2: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: (No Response)

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: (No Response)

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: (No Response)

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: (No Response)

**********

6. Review Comments to the Author

Reviewer #1: The authors addressed most of my comments. Follows some additional suggestions to improve the manuscript:

Please, check if the term "imbalances" is correct

I did not understand equation 9 and I did not find a direct connection between the citation. Considering that part of your conclusions is based on it, I recommend that you explain it better or reference it.

Reviewer #2: (No Response)

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

PLoS One. 2020 Dec 2;15(12):e0233200. doi: 10.1371/journal.pone.0233200.r006

Author response to Decision Letter 2

13 Nov 2020

Dear editor and reviewers,

Editor:

- Throughout the text use "common bean" instead of just "bean";

Authors reply: Thank you for the suggestion. We made the changes in the text.

- quote all R packages used for the analyzes;

Authors reply: Thank you for the suggestion. We added the packages on the article and on the supporting information.

- In the Discussion, insert a final paragraph about what advances the proposed method has in relation to the dozens of methods in the literature;

Authors reply: Thanks for the suggestion. We added a paragraph at the end of the Discussion showing the advantages of the proposed method. In addition, over the Introduction and Discussion sections, we show a more detailed description of the method's advantages over those already available in the literature.

- Add in the conclusions the best genotypes identified by RR models.

Authors reply: Thank you for the suggestion. We did that.

Reviewer #1:

Please, check if the term "imbalances" is correct

Authors reply: Thank you for the suggestion. We check that in the text and made some changes aiming a better understanding.

Authors reply: Dear reviewer, thanks for the suggestion. We try to understand your doubts about the accuracy equation. We used the equation adapted from Gilmour et al. (1990), using the PEV (Predictor Error Variance) and Kg (covariance coefficients for genotypic effect) matrices. However, using Legendre orthogonal polynomials, we made an adaptation in the equation, pre and post multiplying the PEV and Kg by the Фijm matrix (Legendre's m-th polynomial for the j-th trial and the i-th genotype), in order to transform the values obtained from the Legendre scale to the original scale, as proposed by Kirkpatrick et al. 1990. In addiction, we add the two references cited below in the article.

[1] Gilmour, A.R., Gogel, B.J., Cullis, B.R., and Thompson, R. ASReml User Guide Release 3.0 VSN International Ltd, Hemel Hempstead, HP1 1ES, UK; 2009. www.vsni.co.uk

[2] Kirkpatrick M, Lofsvold D, Bulmer M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics. 1990;124: 979–993.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(16.6KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0233200.r007

Decision Letter 3

Paulo Eduardo Teodoro

16 Nov 2020

Adaptability and stability analyses of plants using random regression models

PONE-D-20-12530R3

Dear Dr. de Souza,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Paulo Eduardo Teodoro, Dr.

Academic Editor

PLOS ONE

PLoS One. doi: 10.1371/journal.pone.0233200.r008

Acceptance letter

Paulo Eduardo Teodoro

19 Nov 2020

PONE-D-20-12530R3

Adaptability and stability analyses of plants using random regression models

Dear Dr. de Souza:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Professor Paulo Eduardo Teodoro

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Table. Carioca bean cultivars, institutions of origin and year of recommendation.

(DOCX)

Click here for additional data file.^{(15.7KB, docx)}

S2 Table. Black bean cultivars, institutions of origin and year of recommendation.

(DOCX)

Click here for additional data file.^{(15.5KB, docx)}

S3 Table. Description of the trials.

(DOCX)

Click here for additional data file.^{(12.1KB, docx)}

S4 Table. Accuracy of 105 cultivars in each trial.

(DOCX)

Click here for additional data file.^{(41.3KB, docx)}

S5 Table. Recommendation probability values for each cultivar in each scenario.

(DOCX)

Click here for additional data file.^{(21.6KB, docx)}

S1 Code. Script for analyses.

(DOCX)

Click here for additional data file.^{(23.5KB, docx)}

S1 DOI. Dataset availability.

(DOCX)

Click here for additional data file.^{(11KB, docx)}

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(25.9KB, docx)}

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(21.4KB, docx)}

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(16.6KB, docx)}

Data Availability Statement

The dataset are available in the Figshare online repository, at the link: https://doi.org/10.6084/m9.figshare.12668390.v1.

[pone.0233200.ref001] 1.Smith AB, Ganesalingam A, Kuchel H, Cullis BR. Factor analytic mixed models for the provision of grower information from national crop variety testing programs. Theor Appl Genet. 2015;128: 55–72. 10.1007/s00122-014-2412-x [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref002] 2.MAPA. Formulários para Registro de Cultivares—Ministério da Agricultura, Pecuária e Abastecimento. 2019 [cited 10 Jan 2019]. Available: http://www.agricultura.gov.br/assuntos/insumos-agropecuarios/insumos-agricolas/sementes-e-mudas/registro-nacional-de-cultivares-2013-rnc-1/formularios-para-registro-de-cultivares

[pone.0233200.ref003] 3.Burgueño J, Crossa J, Cotes JM, Vicente FS, Das B. Prediction assessment of linear mixed models for multienvironment trials. Crop Sci. 2011;51: 944–954. 10.2135/cropsci2010.07.0403 [DOI] [Google Scholar]

[pone.0233200.ref004] 4.Yau SK. Regression and AMMI Analyses of Genotype × Environment Interactions: An Empirical Comparison. Agron J. 1995;87: 121–126. 10.2134/agronj1995.00021962008700010021x [DOI] [Google Scholar]

[pone.0233200.ref005] 5.Finlay K, Wilkinson G. The analysis of adaptation in a plant-breeding programme. Aust J Agric Res. 1963;14: 742 10.1071/AR9630742 [DOI] [Google Scholar]

[pone.0233200.ref006] 6.Eberhart SA, Russell WA. Stability Parameters for Comparing Varieties1. Crop Sci. 1966;6: 36 10.2135/cropsci1966.0011183x000600010011x [DOI] [Google Scholar]

[pone.0233200.ref007] 7.Verma MM, Chahal GS, Murty BR. Limitations of conventional regression analysis a proposed modification. Theor Appl Genet. 1978;53: 89–91. 10.1007/BF00274335 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref008] 8.Cruz CD, Torres RD, Vencovsky R. An alternative approach to the stability analysis proposed by Silva and Barreto. Rev Bras Genética. 1989;12: 567–580. [Google Scholar]

[pone.0233200.ref009] 9.Nascimento M, Ferreira A, Mota Campana AC, Salgado CC, Cruz CD. Multiple Centroid Methodology to analyze genotype adaptability. Crop Breed Appl Biotechnol. 2009;9: 8–16. 10.12702/1984-7033.v09n01a02 [DOI] [Google Scholar]

[pone.0233200.ref010] 10.Oliveira RL de, Von Pinho RG, Ferreira DF, Pires LPM, Melo WMC. Selection index in the study of adaptability and stability in maize. Sci World J. 2014;2014: 1–6. 10.1155/2014/360570 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref011] 11.Van Eeuwijk FA, Bustos-korts DV, Malosetti M. What Should Students in Plant Breeding Know About the Statistical Aspects of Genotype x Environment Interactions? Crop Sci. 2016;56: 2119–2140. 10.2135/cropsci2015.06.0375 [DOI] [Google Scholar]

[pone.0233200.ref012] 12.Gauch HG. Statistical analysis of regional yield trials: AMMI analysis of factorial designs. 1st ed. Gauch HGJ, editor. Ithaca, NY: Elsevier; 1992. [Google Scholar]

[pone.0233200.ref013] 13.Yan W, Hunt LA. Interpretation of genotype X environment interaction for winter wheat yield in Ontario. Crop Sci. 2001;41: 19–25. [Google Scholar]

[pone.0233200.ref014] 14.Eberhart SA, Russell WA. Stability Parameters for Comparing Varieties. Crop Sci. 1966;6: 36–40. 10.2135/cropsci1966.0011183x000600010011x [DOI] [Google Scholar]

[pone.0233200.ref015] 15.Vargas M, Crossa J, Van Eeuwijk FA, Sayre KD, Reynolds MP. Statistics: Interpreting treatment × environment interaction in agronomy trials. Agron J. 2001;93: 949–960. 10.2134/agronj2001.934949x [DOI] [Google Scholar]

[pone.0233200.ref016] 16.Kirkpatrick M, Lofsvold D, Bulmer M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics. 1990;124: 979–993. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref017] 17.Schaeffer LR, Dekkers JCM. Random regressions in animal models for test-day production in dairy cattle. Guelph, Ontario, Canada; 1994. [Google Scholar]

[pone.0233200.ref018] 18.Meyer K, Hill WG. Estimation of genetic and phenotypic covariance functions for longitudinal or “repeated” records by restricted maximum likelihood. Livest Prod Sci. 1997;47: 185–200. 10.1016/S0301-6226(96)01414-5 [DOI] [Google Scholar]

[pone.0233200.ref019] 19.Meyer K. Estimating covariance functions for longitudinal data using a random regression model. Genet Sel Evol. 1998;30: 221–240. 10.1186/1297-9686-30-3-221 [DOI] [Google Scholar]

[pone.0233200.ref020] 20.Jamrozik J, Schaeffer LR, Dekkers JCM. Genetic Evaluation of Dairy Cattle Using Test Day Yields and Random Regression Model. J Dairy Sci. 1997;80: 1217–1226. 10.3168/jds.S0022-0302(97)76050-8 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref021] 21.Schaeffer LR. Application of random regression models in animal breeding. Livest Prod Sci. 2004;86: 35–45. 10.1016/S0301-6226(03)00151-9 [DOI] [Google Scholar]

[pone.0233200.ref022] 22.Jamrozik J, Bohmanova J, Schaeffer LR. Relationships between milk yield and somatic cell score in Canadian Holsteins from simultaneous and recursive random regression models. J Dairy Sci. 2010;93: 1216–1233. 10.3168/jds.2009-2585 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref023] 23.Ali TE, Schaeffer LR. Accounting for covariances among test day milk yields ind dairy cows. Can J Anim Sci. 1987;67: 637–644. 10.4141/cjas87-067 [DOI] [Google Scholar]

[pone.0233200.ref024] 24.Wilmink JBM. Adjustment of lactation yield for age at calving in relation to level of production. Livest Prod Sci. 1987;16: 321–334. 10.1016/0301-6226(87)90002-9 [DOI] [Google Scholar]

[pone.0233200.ref025] 25.Kirkpatrick M, Heckman N. A quantitative genetic model for growth, shape, reaction norms, and other infinite-dimensional characters. J Math Biol. 1989;27: 429–450. 10.1007/BF00290638 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref026] 26.Bohmanova J, Miglior F, Jamrozik J, Misztal I, Sullivan PG. Comparison of random regression models with legendre polynomials and linear splines for production traits and somatic cell score of Canadian Holstein cows. J Dairy Sci. 2008;91: 3627–3638. 10.3168/jds.2007-0945 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref027] 27.Sun J, Rutkoski JE, Poland JA, Crossa J, Jannink J-L, Sorrells ME. Multitrait, Random Regression, or Simple Repeatability Model in High-Throughput Phenotyping Data Improve Genomic Prediction for Wheat Grain Yield. Plant Genome. 2017;10: 1–15. 10.3835/plantgenome2016.11.0111 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref028] 28.Ly D, Huet S, Gauffreteau A, Rincent R, Touzy G, Mini A, et al. Whole-genome prediction of reaction norms to environmental stress in bread wheat (Triticum aestivum L.) by genomic random regression. F Crop Res. 2018;216: 32–41. 10.1016/j.fcr.2017.08.020 [DOI] [Google Scholar]

[pone.0233200.ref029] 29.Momen M, Campbell MT, Walia H, Morota G. Predicting longitudinal traits derived from high-throughput phenomics in contrasting environments using genomic Legendre polynomials and B-splines. G3 Genes, Genomes, Genet. 2019;9: 3369–3380. 10.1534/g3.119.400346 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref030] 30.Baba T, Momen M, Campbell MT, Walia H, Morota G. Multi-trait random regression models increase genomic prediction accuracy for a temporal physiological trait derived from high-throughput phenotyping. Ortiz R, editor. PLoS One. 2020;15: e0228118 10.1371/journal.pone.0228118 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref031] 31.Woltereck R. Weitere experimentelle Untersuchungen über Artveränderung, speziel über das Wesen quantitativer Artunterschiede bei Daphnien. Verhandlungen der Dtsch. 1909;19: 110–173. [Google Scholar]

[pone.0233200.ref032] 32.Martin JGA, Nussey DH, Wilson AJ, Réale D. Measuring individual differences in reaction norms in field and experimental studies: A power analysis of random regression models. Methods Ecol Evol. 2011;2: 362–374. 10.1111/j.2041-210X.2010.00084.x [DOI] [Google Scholar]

[pone.0233200.ref033] 33.Van de Pol M. Quantifying individual variation in reaction norms: How study design affects the accuracy, precision and power of random regression models. Methods Ecol Evol. 2012;3: 268–280. 10.1111/j.2041-210X.2011.00160.x [DOI] [Google Scholar]

[pone.0233200.ref034] 34.Streit M, Reinhardt F, Thaller G, Bennewitz J. Reaction norms and genotype-by-environment interaction in the German Holstein dairy cattle. J Anim Breed Genet. 2012;129: 380–389. 10.1111/j.1439-0388.2012.00999.x [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref035] 35.Liu X. Linear Mixed-Effects Models. In: Liu X, editor. Methods and Applications of Longitudinal Data Analysis 1st ed. Academic Press; 2015. pp. 61–94. [Google Scholar]

[pone.0233200.ref036] 36.Schaeffer LR. Animal Models. Self-Published; 2019. [Google Scholar]

[pone.0233200.ref037] 37.Akaike H. A new look at the statistical identification model. A new look Stat Identif Model. 1974;19: 716. [Google Scholar]

[pone.0233200.ref038] 38.Wolfinger R. Covariance structure selection in general mixed models. Commun Stat—Simul Comput. 1993;22: 1079–1106. 10.1080/03610919308813143 [DOI] [Google Scholar]

[pone.0233200.ref039] 39.Stoica P, Babu P. Model order estimation via penalizing adaptively the likelihood (PAL). Signal Processing. 2013;93: 2865–2871. 10.1016/J.SIGPRO.2013.03.014 [DOI] [Google Scholar]

[pone.0233200.ref040] 40.Rao CR. Linear statistical inference and its application. New York: John Wiley and Sons; 1965. Available: https://academic.oup.com/jlms/article-abstract/s1-42/1/382/844079 [Google Scholar]

[pone.0233200.ref041] 41.Gilmour AR, Gogel BJ, Cullis BR, Thompson R. ASReml User Guide Release 3.0. VSN International Ltd, Hemel Hempsted, HP1 1ES, UK; 2009. Available on: www.vsni.co.uk

[pone.0233200.ref042] 42.Rocha JR do AS de C, Marçal T de S, Salvador FV, Silva AC da, Machado JC, Carneiro PCS. Genetic insights into elephantgrass persistence for bioenergy purpose. Feltus FA, editor. PLoS One. 2018;13: e0203818 10.1371/journal.pone.0203818 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref043] 43.Resende MDV de, Duarte JB. Precisão e controle de qualidade em experimentos de avaliação de cultivares. Pesqui Agropecuária Trop. 2007;37: 182–194. [Google Scholar]

[pone.0233200.ref044] 44.Melo CLP de, Carneiro, José Eustáquio de Souza Carneiro PCS, Cruz CD, Barros, Everaldo Gonçalves de Moreira MA. Linhagens de feijão do cruzamento “Ouro Negro” x “Pérola” com características agronômicas favoráveis. Pesqui Agropecuária Bras. 2006;41: 1593–1598. [Google Scholar]

[pone.0233200.ref045] 45.Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R. ASReml User Guide Release 4.1 Structural Specification, VSN International Ltd, Hemel Hempstead, HP1 1ES, UK; 2015. Available: www.vsni.co.uk

[pone.0233200.ref046] 46.Computing RF for S. R Development Core Team. Austria, Vienna; 2015.

[pone.0233200.ref047] 47.Yang Y. Can the strengths of AIC and BIC be shared? A conflict between model indentification and regression estimation. Biometrika. 2005;92: 937–950. 10.1093/biomet/92.4.937 [DOI] [Google Scholar]

[pone.0233200.ref048] 48.Corrales JD, Munilla S, Cantet RJC. Polynomial order selection in random regression models via penalizing adaptively the likelihood. J Anim Breed Genet. 2015;132: 281–288. 10.1111/jbg.12130 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref049] 49.Vrieze SI. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol Methods. 2012;17: 228–243. 10.1037/a0027127 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref050] 50.Kolmodin R, Strandberg E, Madsen P, Jensen J, Jorjani H. Genotype by environment interaction in Nordic dairy cattle studied using reaction norms. Acta Agric Scand—Sect A Anim Sci. 2002;52: 11–24. 10.1080/09064700252806380 [DOI] [Google Scholar]

[pone.0233200.ref051] 51.Calus MPL, Veerkamp RF. Estimation of environmental sensitivity of genetic merit for milk production traits using a random regression model. J Dairy Sci. 2003;86: 3756–3764. 10.3168/jds.S0022-0302(03)73982-4 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref052] 52.Pereira HS, Melo LC, Del Peloso MJ, de Faria LC, Wendland A. Complex interaction between genotypes and growing seasons of carioca common bean in Goiás/Distrito Federal. Crop Breed Appl Biotechnol. 2011;11: 207–215. 10.1590/S1984-70332011000300002 [DOI] [Google Scholar]

[pone.0233200.ref053] 53.Torga PP, Melo PGS, Pereira HS, de Faria LC, Del Peloso MJ, Melo LC. Interaction of common beans cultivars of the black group with years, locations and sowing seasons. Euphytica. 2013;189: 239–248. 10.1007/s10681-012-0793-y [DOI] [Google Scholar]

[pone.0233200.ref054] 54.Tusiime G. Genotype x Environment interactions for higher Iron and Zinc in selected bean varieties. Ambit J Agric. 2015;1: 16–39. [Google Scholar]

[pone.0233200.ref055] 55.Correa AM, Gonçalves MC, Teodoro PE. Pattern analysis of multi-environment trials in common bean genotypes. Biosci J. 2016;32: 328–336. 10.14393/BJ-v32n2a2016-29572 [DOI] [Google Scholar]

[pone.0233200.ref056] 56.Ramalho MAP, Abreu A de FB, Santos PSJ dos. Interações genótipos x épocas de semeadura, anos e locais na avaliação de cultivares de feijão nas regiões Sul e Alto Paranaíba em Minas Gerais. Cienc agrotec. 1998;22: 175–181. [Google Scholar]

[pone.0233200.ref057] 57.Wricke G. Zur Berechnung der Ökovalenz bei Sommerweizen und Hafer. Pflanzenzuchtung. 1965;52: 127–138. [Google Scholar]

[pone.0233200.ref058] 58.Plaisted RL, Peterson LC. A technique for evaluating the ability of selections to yield consistently in different locations or seasons. Am Potato J. 1959;36: 381–385. 10.1007/BF02852735 [DOI] [Google Scholar]

[pone.0233200.ref059] 59.Jarquín D, Crossa J, Lacaze X, Du Cheyron P, Daucourt J, Lorgeou J, et al. A reaction norm model for genomic selection using high-dimensional genomic and environmental data. Theor Appl Genet. 2014;127: 595–607. 10.1007/s00122-013-2243-1 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref060] 60.Ni G, Van der Werf J, Zhou X, Hyppönen E, Wray NR, Lee SH. Genotype–covariate correlation and interaction disentangled by a whole-genome multivariate reaction norm model. Nat Commun. 2019;10 10.1038/s41467-019-10128-w [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref061] 61.Resende MDV. Software Selegen-REML/BLUP: A useful tool for plant breeding. Crop Breed Appl Biotechnol. 2016;16: 330–339. 10.1590/1984-70332016v16n4a49 [DOI] [Google Scholar]

[pone.0233200.ref062] 62.Cellon C, Amadeu RR, Olmstead JW, Mattia MR, Ferrao LFV, Munoz PR. Estimation of genetic parameters and prediction of breeding values in an autotetraploid blueberry breeding population with extensive pedigree data. Euphytica. 2018;214 10.1007/s10681-018-2165-8 [DOI] [Google Scholar]

[pone.0233200.ref063] 63.Piepho HP, Möhring J, Melchinger AE, Büchse A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica. 2008;161: 209–228. 10.1007/s10681-007-9449-8 [DOI] [Google Scholar]

[pone.0233200.ref064] 64.Oakey H, Verbyla A, Pitchford W, Cullis B, Kuchel H. Joint modeling of additive and non-additive genetic line effects in single field trials. Theor Appl Genet. 2006;113: 809–819. 10.1007/s00122-006-0333-z [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref065] 65.Howard JT, Jiao S, Tiezzi F, Huang Y, Gray KA, Maltecca C. Genome-wide association study on legendre random regression coefficients for the growth and feed intake trajectory on Duroc Boars. BMC Genet. 2015;16: 1–11. 10.1186/s12863-014-0153-0 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref066] 66.Cullis BR, Gleeson AC. Spatial Analysis of Field Experiments-An Extension to Two Dimensions. Biometrics. 1991;47: 1449 10.2307/2532398 [DOI] [Google Scholar]

[pone.0233200.ref067] 67.Gilmour AR, Cullis BR, Verbyla AP. Accounting for Natural and Extraneous Variation in the Analysis of Field Experiments. J Agric Biol Environ Stat. 1997;2: 269–293. 10.2307/1400446 [DOI] [Google Scholar]

[pone.0233200.ref068] 68.Campbell M, Momen M, Walia H, Morota G. Leveraging Breeding Values Obtained from Random Regression Models for Genetic Inference of Longitudinal Traits. Plant Genome. 2019;12: 180075 10.3835/plantgenome2018.10.0075 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref069] 69.Sarmento JLR, Torres RA, Sousa WH, Lôbo RNB, Albuquerque LG, Lopes PS, et al. Random regression models for the estimation of genetic and environmental covariance functions for growth traits in Santa Ines sheep. Genet Mol Res. 2016;15: 1–13 10.4238/gmr.15025749 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref070] 70.Burgueño J, de los Campos G, Weigel K, Crossa J. Genomic Prediction of Breeding Values when Modeling Genotype × Environment Interaction using Pedigree and Dense Molecular Markers. Crop Sci. 2012;52: 707 10.2135/cropsci2011.06.0299 [DOI] [Google Scholar]

[pone.0233200.ref071] 71.Pérez-Rodríguez P, Crossa J, Bondalapati K, De Meyer G, Pita F, Campos G de los. A pedigree-based reaction norm model for prediction of cotton yield in multienvironment trials. Crop Sci. 2015;55: 1143 10.2135/cropsci2014.08.0577 [DOI] [Google Scholar]

[pone.0233200.ref072] 72.Lian L, Jacobson A, Zhong S, Bernardo R. Genomewide prediction accuracy within 969 maize biparental populations. Crop Sci. 2014;54: 1514–1522. 10.2135/cropsci2013.12.0856 [DOI] [Google Scholar]

[pone.0233200.ref073] 73.Lorenzana RE, Bernardo R. Accuracy of genotypic value predictions for marker-based selection in biparental plant populations. Theor Appl Genet. 2009;120: 151–161. 10.1007/s00122-009-1166-3 [DOI] [PubMed] [Google Scholar]

[pone.0233200.ref074] 74.Viana JMS, de Lima RO, Faria VR, Mundim GB, de Resende MDV, Silva FF. Relevance of pedigree, historical data, dominance, and data unbalance for selection efficiency. Agron J. 2012;104: 722–728. 10.2134/agronj2011.0358 [DOI] [Google Scholar]

[pone.0233200.ref075] 75.Van Oijen M, Höglind M. Toward a Bayesian procedure for using process-based models in plant breeding, with application to ideotype design. Euphytica. 2016;207: 627–643. 10.1007/s10681-015-1562-5 [DOI] [Google Scholar]

[pone.0233200.ref076] 76.Xue B, Leibler S. Benefits of phenotypic plasticity for population growth in varying environments. Proc Natl Acad Sci USA. 2018;115: 12745–12750. 10.1073/pnas.1813447115 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0233200.ref077] 77.Sicard D, Nanni L, Porfiri O, Bulfon D, Papa R. Genetic diversity of Phaseolus vulgaris L. and P. coccineus L. landraces in central Italy. Plant Breed. 2005;124: 464–472. 10.1111/j.1439-0523.2005.01137.x [DOI] [Google Scholar]

[pone.0233200.ref078] 78.Cowling WA. Genetic diversity in Australian canola and implications for crop breeding for changing future environments. F Crop Res. 2007;104: 103–111. 10.1016/j.fcr.2006.12.014 [DOI] [Google Scholar]

[pone.0233200.ref079] 79.Rauf S, da Silva J, Khan A, Naveed A. Consequences of Plant Breeding on Genetic Diversity. Int J Plant Breed. 2010;4: 1–21. [Google Scholar]

[pone.0233200.ref080] 80.Tester M, Langridge P. Breeding technologies to increase crop production in a changing world. Science. American Association for the Advancement of Science; 2010. pp. 818–822. 10.1126/science.1183700 [DOI] [PubMed] [Google Scholar]

PERMALINK

Adaptability and stability analyses of plants using random regression models

Michel Henriques de Souza

José Domingos Pereira Júnior

Skarlet De Marco Steckling

Jussara Mencalha

Fabíola dos Santos Dias

João Romero do Amaral Santos de Carvalho Rocha

Pedro Crescêncio Souza Carneiro

José Eustáquio de Souza Carneiro

Roles

Abstract

Introduction

Material and methods

Genetic material

Trials

Statistical analyses

Software used

Results

Table 1. Trials evaluated with their environmental index.

Table 2. Different fitted models using the Legendre polynomials (Leg).

Fig 1. Average accuracy of the prediction in each trial for the genotypic values of the cultivars.

Fig 2. Cultivars of Carioca and Black common bean of general adaptability according to the ideotype.

Fig 3. Cultivars of Carioca and Black common bean of maximum adaptability for unfavorable environments according to the ideotype.

Fig 4. Cultivars of Carioca and Black common bean of maximum adaptability for favorable environments according to the ideotype.

Discussion

Conclusion

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Roberto Fritsche-Neto

Roles

Author response to Decision Letter 0

Decision Letter 1

Roberto Fritsche-Neto

Roles

Author response to Decision Letter 1

Decision Letter 2

Paulo Eduardo Teodoro

Roles

Author response to Decision Letter 2

Decision Letter 3

Paulo Eduardo Teodoro

Roles

Acceptance letter

Paulo Eduardo Teodoro

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases