On the heterozygosity of an admixed population

Abstract

In this study, we consider admixed populations through their expected heterozygosity, a measure of genetic diversity. A population is termed admixed if its members possess recent ancestry from two or more separate sources. As a result of the fusion of source populations with different genetic variants, admixed populations can exhibit high levels of genetic diversity, reflecting contributions of their multiple ancestral groups. For a model of an admixed population derived from K source populations, we obtain a relationship between its heterozygosity and its proportions of admixture from the various source populations. We show that the heterozygosity of the admixed population is at least as great as that of the least heterozygous source population, and that it potentially exceeds the heterozygosities of all of the source populations. The admixture proportions that maximize the heterozygosity possible for an admixed population formed from a specified set of source populations are also obtained under specific conditions. We examine the special case of K = 2 source populations in detail, characterizing the maximal admixture in terms of the heterozygosities of the two source populations and the value of F_ST between them. In this case, the heterozygosity of the admixed population exceeds the maximal heterozygosity of the source groups if the divergence between them, measured by F_ST, is large enough, namely above a certain bound that is a function of the heterozygosities of the source groups. We present applications to simulated data as well as to data from human admixture scenarios, providing results useful for interpreting the properties of genetic variability in admixed populations.

1. Introduction

Admixed populations are populations that possess ancestry from multiple source groups. They result from the fusion of populations that have long been separated, in processes such as long-distance migration and hybrid-zone formation at population boundaries.

Several features of ancestry and allele frequencies are characteristic of admixed populations (Chakraborty, 1986; Long, 1991; Verdu & Rosenberg, 2011; Gravel, 2012). In an admixed population, the values of allele frequencies are typically intermediate between those of the various sources. Unlike in a mixture that pools individuals taken from separate populations, in an admixed population, alleles from different sources cooccur within individuals. The contributions from the source populations are each large enough that most members of an admixed population have ancestry in more than one source group.

In admixed populations, the history of mating among populations is recent enough that time has not yet eroded differences among admixed individuals in their relative proportions of ancestry. This feature of high levels of variability in admixture proportions has been central to studies of admixed populations. Investigations of such phenomena as the timing and contributions of the source populations (Verdu & Rosenberg, 2011; Gravel, 2012), the effect of admixture levels on assortative mating patterns (Risch et al., 2009; Zou et al., 2015), and the genetic basis of traits in admixed populations (Buerkle & Lexer, 2008; Zhu et al., 2008) all make use of variation in levels of admixture levels across admixed individuals.

A second aspect of variability in admixed populations is potentially of interest: the variability of alleles as captured by genetic diversity measures. The effect of admixture in contributing to increased genetic diversity, however, is not simple. For example, in a study of the genetics of populations founded by relatively small groups, Mooney et al. (2018) examined genetic diversity in admixed and non-admixed populations, some of which were regarded as founder populations. Mooney et al. (2018) observed that genetic diversity was relatively high in multiple admixed populations of Latin America. This pattern was observed even for populations that, on the basis of small population size and past history of isolation, might have been expected to have relatively low levels of genetic diversity.

Here, to deepen understanding of the relationship between admixture and genetic variability, we focus in admixed populations on levels of genetic diversity computed from allele frequencies, rather than on variability among individuals in admixture proportions. For a model of an admixed population with K source groups, we derive a relationship between genetic diversity, as measured by heterozygosity, and proportions of admixture drawn from the various source populations. The model is the same model we have previously used to examine the genetic differentiation between admixed populations and their source groups, as measured by F_ST (Boca & Rosenberg, 2011). We show that for all values of the admixture contributions from the source populations, the heterozygosity of the admixed population is greater than or equal to the smallest of the source population heterozygosities. We further examine the maximal values of the heterozygosity of the admixed population over the space of possible admixture proportions. We consider in more detail special cases with K = 2 and K = 3 source populations, providing explicit results for K = 2 in terms of relatively few parameters. Finally, we use simulations and example analyses from human population data to illustrate the mathematical results.

2. Notation and model

We consider a model with K ⩾ 2 source populations and an admixed population arising from these sources. A single polymorphic locus is considered, with J ⩾ 2 alleles, such that each of the J alleles appears in at least one of the K source populations.

In Sections 2.1, 2.2, and 2.3, respectively, we define the expected heterozygosity and the fixation index, and we provide a result about relationships between fixation indices and heterozygosities. In Section 2.4, we introduce the admixture model. Notation is summarized in Table 1.

Table 1:

Notation

Type of quantity	Symbol	Description
Indices	j = 1,..., J	Index over alleles
	k = 1,..., K	Index over source populations
Allele frequencies	pkj	Frequency of allelic type j in population k
	$\frac{p_k}{P}$	J × 1 vector of allele frequencies for population k J × K matrix of allele frequencies in the source populations
	${\overline{p}}_j$	Frequency of allelic type j in the admixed population
Admixture fractions	γk	Admixture fraction for population k
	γ	K × 1 vector of admixture fractions
Heterozygosities	Hk	Heterozygosity for population k; probability that two alleles drawn from population k differ in type
	Hadm	Heterozygosity for the admixed population
	Ckℓ	Probability that an allele drawn from population k and an allele drawn from population ℓ differ in type
Fixation index	Fkℓ	Fixation index FST between populations k and ℓ

2.1. Expected heterozygosity

The expected heterozygosity is a measure of genetic diversity, giving the probability that two alleles randomly drawn from a population differ in type.

Definition 1. The expected heterozygosity in a population for a given locus with J distinct alleles is defined as $H=1-{\sum }_{j=1}^J{p}_j^2$, where p_j is the frequency of allelic type j.

We denote by p_kj the frequency of allelic type j, 1 ⩽ j ⩽ J, in source population k, 1 ⩽ k ⩽ K, with 0 ⩽ p_kj ⩽ 1. We denote by H_k the expected heterozygosity of source population k at a locus. We have 0 ⩽ H_k < 1, with H_k = 0 if and only if source population k has only a single allelic type of nonzero frequency. For fixed J, the maximal value of H_k is $1-\frac{1}{J}$, attained when all J alleles have the same frequency, namely $\frac{1}{J}$ (Reddy & Rosenberg, 2012, Lemma 4). We refer to expected heterozygosity simply as heterozygosity.

2.2. Fixation index

The fixation index F_ST is a measure of genetic divergence among a set of subpopulations. In its general form, it is computed from H_S, the mean of the heterozygosities of the subpopulations, and H_T, the heterozygosity of a population formed by pooling the subpopulations into a single “total” population.

Definition 2. The fixation index, F_ST is defined as F_ST = (H_T − H_S)/H_T, where H_T is the heterozygosity of the total population and H_S is the mean heterozygosity across subpopulations.

The fixation index can be regarded as a measure of genetic divergence between two populations, with F_kℓ denoting the value of F_ST between source populations k and ℓ. For its calculation, the two subpopulations have the same contribution to the overall population, so that they are weighted equally in producing the total population. We assume that when pooled together, the two subpopulations produce a polymorphic population. In other words, for each (k, ℓ), we disallow the case in which there is some allelic type 1 ⩽ j ⩽ J for which p_kj = p_ℓj = 1. Our assumption that pooling any two populations produces a polymorphic population avoids a denominator of 0 in the formula for F_kℓ.

For this pairwise scenario, H_S = (H_k + H_ℓ)/2, $H_T=1-{\sum }_{j=1}^J{\left[\left(p_{kj}+p_{\ell j}\right)/2\right]}^2$, and

$$F_{k\ell }=\frac{\left[1-{\sum }_{j=1}^J{\left(\frac{p_{kj}+p_{\ell j}}{2}\right)}^2\right]-\frac{H_k+H_{\ell }}{2}}{1-{\sum }_{j=1}^J{\left(\frac{p_{kj}+p_{\ell j}}{2}\right)}^2}.$$ (1)

We can observe by the Cauchy-Schwarz inequality that 0 ⩽ F_kℓ ⩽ 1, with F_kℓ = 0 requiring p_kj = p_ℓj for all j. F_kℓ = 1 requires H_S = H_k = H_ℓ = 0.

2.3. The fixation index in relation to the heterozygosities

We will need a result on the relationship between the fixation index for source populations k and ℓ, F_kℓ, and the heterozygosities of those source populations, H_k and H_ℓ. We first introduce a quantity, C_kℓ, the probability that, when randomly drawing one allele from population k and one allele from population ℓ, the two alleles differ in type. For population k, let $\underset{\_}{p_k}$ denote a J × 1 column vector of its allele frequencies. C_kℓ can then be written as 1 minus the dot product of the allele frequency vectors of populations k and ℓ:

$$C_{k\ell }=1-{\underset{\_}{p_k}}^{\prime }\cdot \underset{\_}{p_{\ell }}=1-\sum _{j=1}^J{p}_{kj}{p}_{\ell j}.$$ (2)

This quantity is a generalization of heterozygosity to two populations, as H_k = C_kk. Because we exclude the case in which populations k and ℓ are fixed for the same allelic type, C_kℓ strictly exceeds 0, so that 0 < C_kℓ ⩽ 1. The upper bound of 1 is achieved if populations k and ℓ share no allelic types in common.

We can rewrite eq. 1 as

$$F_{k\ell }=\frac{2C_{k\ell }-H_k-H_{\ell }}{2C_{k\ell }+H_k+H_{\ell }}.$$ (3)

If F_kℓ < 1, then we can solve for C_kℓ:

$$C_{k\ell }=\left(\frac{H_k+H_{\ell }}{2}\right)\left(\frac{1+F_{k\ell }}{1-F_{k\ell }}\right).$$ (4)

Recall that F_kℓ = 1 implies H_k = H_ℓ = 0, so that populations k and ℓ each have only a single allelic type with nonzero frequency. We have excluded the case in which the two populations are fixed for the same allelic type; hence, they must be fixed for different allelic types, and C_kℓ = 1 in eq. 2.

We have previously shown by the Cauchy-Schwarz inequality that $1-\sqrt{\left(1-H_k\right)\left(1-H_{\ell }\right)}⩽C_{k\ell }⩽1$ (Mehta et al., 2019, eq. 7). Equality in the lower bound requires p_kj = p_ℓj for all j, and hence H_k = H_ℓ. Rewriting this inequality with eq. 4, we obtain the allowable space of F_kℓ given H_k, H_ℓ ∈ [0, 1):

$$F_{k\ell }\in \left[\frac{2-H_k-H_{\ell }-2\sqrt{\left(1-H_k\right)\left(1-H_{\ell }\right)}}{2+H_k+H_{\ell }-2\sqrt{\left(1-H_k\right)\left(1-H_{\ell }\right)}},\frac{2-H_k-H_{\ell }}{2+H_k+H_{\ell }}\right].$$ (5)

The lower limit is achieved if and only if the two populations k and ℓ are identical, with H_k = H_ℓ and p_kj = p_ℓj for all j. The upper limit is achieved if and only if populations k and ℓ share no allelic types in common. This result adds to the understanding of constraints on F_ST placed by genetic diversity (Nagylaki, 1998; Hedrick, 1999; Long & Kittles, 2003; Rosenberg et al., 2003; Hedrick, 2005; Boca & Rosenberg, 2011; Maruki et al., 2012; Jakobsson et al., 2013; Edge & Rosenberg, 2014; Alcala & Rosenberg, 2017, 2019; Mehta et al., 2019). We use the allowable region to constrain our examples to permissible values of (H_k, H_ℓ, F_ST).

Appendix A of Mehta et al. (2019) shows that given H_k and H_ℓ in [0, 1), if the number of distinct alleles J is not fixed, then we can choose allele frequency vectors $\underset{\_}{p_k}$ and $\underset{\_}{p_{\ell }}$ such that each C_kℓ value in $[1-\sqrt{\left(1-H_k\right)\left(1-H_{\ell }\right)},1]$ is achievable. The lower bound is achievable only if H_k = H_ℓ. Hence, each value in the interval in eq. 5 for F_ST is also achievable by some pair $\underset{\_}{p_k}$ and $\underset{\_}{p_{\ell }}$, the lower bound only if H_k = H_ℓ.

2.4. Admixture model

We use an admixture model that describes current patterns of variation in an admixed population, rather than mechanistic dynamics. This model follows a commonly used approach, treating allele frequencies in the admixed population as linear combinations of those of the source populations (e.g. Pritchard et al., 2000; Boca & Rosenberg, 2011).

In our K-source-population model, K ⩾ 2, we follow Section 2.2 in assuming that no two populations are fixed for the same allelic type. We now make a stronger assumption that no two populations are identical, so that for each (k, ℓ), some j exists for which p_kj ≠ p_ℓj. Further, it is convenient to assume that no source population can have its vector of allele frequencies written as the linear combination of vectors of allele frequencies of other source populations; otherwise, an admixed population would not have a unique representation as a linear combination of sources. We thus assume that not only are no two source populations identical, no source can be described as an admixture of two or more of the other sources.

Note that the assumption that no population is a linear combination of the others also excludes linear combinations with one or more negative coefficients. Because the maximal number of vectors of length J that can be linearly independent is J, the linear independence assumption implies J ⩾ K. A succinct way of describing the assumption is that if we define the J×K matrix of allele frequencies in the source populations,

$$P=\left(\begin{array}{cccc}{p}_{11}& p_{21}& \dots & p_{K1}\\ p_{12}& p_{22}& \dots & p_{K2}\\ \dots & \dots & \dots & \dots \\ p_{1J}& p_{2J}& \dots & p_{KJ}\end{array}\right)=\left(\underset{\_}{p_1},\underset{\_}{p_2},\dots ,\underset{\_}{p_K}\right),$$ (6)

then we assume that P has rank K.

For the admixed population generated from the K source populations, we denote by γ_k the admixture fraction for source population k; for each k with 1 ⩽ k ⩽ K, fraction γ_k of the ancestry of the admixed population, 0 ⩽ γ_k ⩽ 1, derives from source k. We denote by γ the K×1 column vector of admixture fractions. This vector lies in the simplex Δ^K−1, the set of all vectors of K nonnegative entries with ${\sum }_{k=1}^K{\gamma }_k=1$.

The frequency of allele j in the admixed population is denoted ${\overline{p}}_j$. By the linear combination assumption,

$${\overline{p}}_j=\sum _{k=1}^K{\gamma }_k{p}_{kj}.$$ (7)

In the special case that ${\gamma }_k=\frac{1}{K}$ for each K, the admixed population is equivalent to the “pooled population” used in defining the fixation index F_ST among the K populations.

3. General case: K source populations

Our goal is to study the heterozygosity of the admixed population. Using Definition 1 with eq. 7, we compute the heterozygosity for the admixed population, which we denote by H_adm:

$$H_{\text{adm}}=1-\sum _{j=1}^J{\overline{p}}_j^2=1-\sum _{j=1}^J{\left(\sum _{k=1}^K{\gamma }_k{p}_{kj}\right)}^2.$$ (8)

The heterozygosity of the admixed population can be written in terms of the heterozygosities of the source populations and the dot products of the allele frequencies. Using eq. 4 in eq. 8, we have:

$$H_{\text{adm}}=\sum _{k=1}^K{\gamma }_k^2{H}_k+2\sum _{k=1}^{K-1}\sum _{\ell =k+1}^K{\gamma }_k{\gamma }_{\ell }{C}_{k\ell }$$ (9)

$$=\sum _{k=1}^K{\gamma }_k^2{H}_k+\sum _{k=1}^{K-1}\sum _{\ell =k+1}^K{\gamma }_k{\gamma }_{\ell }\left(H_k+H_{\ell }\right)\left(\frac{1+F_{k\ell }}{1-F_{k\ell }}\right).$$ (10)

The last simplification can be made only for F_kℓ ≠ 1; if F_kℓ = 1, then eq. 9 is used, or, as noted after eq. 4, (H_k + H_ℓ)(1 + F_kℓ)/(1 − F_kℓ) is understood to equal 2.

With the formula for H_adm established, we now explore how H_adm varies in relation to the admixture fractions γ. Given the allele frequencies P, we determine the range of H_adm over the space of possible values of γ. We write H_m for the smallest heterozygosity among the source populations, $H_m={\min }_{k\in \{1,2,\dots ,K\}}{H}_k$, and H_M for the largest heterozygosity among the source populations, $H_M={\max }_{k\in \{1,2,\dots ,K\}}{H}_k$.

3.1. Minimum of H_adm in terms of the ancestry proportions

For the minimum of H_adm over vectors (γ₁, γ₂, …, γ_K), we can immediately observe from the form of eq. 10 that for a fixed set of source population allele frequencies P, H_adm is minimized as a function of the admixture fractions when the admixed population consists of only one of the source populations.

Proposition 3. The minimum of H_adm as a function of the ancestry proportions γ is $H_m={\min }_{k\in \{1,2,\dots ,K\}}{H}_k$, the smallest heterozygosity among the source populations, and it is obtained when the admixed population consists solely of that source population.

Proof. To obtain this result, we use eq. 10 and the fact that H_k ⩾ H_m for all k:

$$\begin{gathered} H_{\text{adm}}=\sum _{k=1}^K{\gamma }_k^2{H}_k+\sum _{k=1}^{K-1}\sum _{\ell =k+1}^K{\gamma }_k{\gamma }_{\ell }\left(H_k+H_{\ell }\right)\left(\frac{1+F_{k\ell }}{1-F_{k\ell }}\right) \\ ⩾\sum _{k=1}^K{\gamma }_k^2{H}_m+\sum _{k=1}^{K-1}\sum _{\ell =k+1}^{K}2{\gamma }_k{\gamma }_{\ell }{H}_m \\ ={\left(\sum _{k=1}^K{\gamma }_k\right)}^2{H}_m=H_m. \end{gathered}$$

Because equality is achieved when γ_m = 1 and γ_k = 0 for all k ≠ m, we have shown that the minimal value of H_adm as a function of the ancestry proportions is H_m. □

The result finds that nonzero admixture inflates heterozygosity at least above the level seen in the least heterozygous source. It applies whether or not H₁, H₂, …, H_K are mutually distinct. If two or more of H₁, H₂, …, H_K are tied for the minimal heterozygosity H_m, then the minimum of H_adm is achieved at each vector associated with complete ancestry from one of the minimally heterozygous populations.

A consequence of Proposition 3 is that if all K populations have the same heterozygosity H_m—for example, in cases where the different alleles have distinct frequencies and each population has an allele frequency vector that is a permutation of the vectors for the other populations—then H_adm > H_m for all ancestry vectors γ with two or more nonzero entries. In particular, note that F_kℓ > 0 for each (k, ℓ), k ≠ ℓ, by the assumption that each pair of source populations has distinct allele frequencies. Hence, (H_k +H_ℓ)(1+ F_kℓ)/(1 − F_kℓ) > 2H_m for each (k, ℓ), k ≠ ℓ. Because at least one product γ_kγ_ℓ is positive, the inequality ${\gamma }_k{\gamma }_{\ell }\left(H_k+H_{\ell }\right)\left(1+F_{k\ell }\right)/\left(1-F_{k\ell }\right)⩾2{\gamma }_k{\gamma }_{\ell }{H}_m$ is strict for at least one (k, ℓ), so that $H_{\text{adm}}>{({\sum }_{k=1}^K{\gamma }_k)}^2{H}_m=H_m$. This same reasoning shows that if two or more populations are tied with heterozygosity H_m, then H_adm > H_m for each γ with two or more nonzero entries.

We note that the result $H_{\text{adm}}⩾{\min }_{k\in \{1,2,\dots ,K\}}{H}_k$ for all γ ∈ Δ^K−1 in Proposition 3 can be quickly obtained from the classic Wahlund principle, by which the heterozygosity of a population formed by mixing populations 1, 2, …, K, with proportion γ_k of the mixed population taken from population k, 0 ⩽ γ_k ⩽ 1, is greater than or equal to the mean of the K population heterozygosities (e.g. Rosenberg & Calabrese, 2004, Theorem 2). The heterozygosity of the population mixture in the setting of the Wahlund principle is the same as the heterozygosity of the admixed population in our scenario. Thus, in our notation, setting ${\gamma }_k=\frac{1}{K}$ for all k, the Wahlund principle gives $H_{\text{adm}}⩾\frac{1}{K}{\sum }_{k=1}^K{H}_k$. Because the mean $\frac{1}{K}{\sum }_{k=1}^K{H}_k$ is greater than or equal to the minimum ${\min }_{k\in \{1,2,\dots ,K\}}{H}_k$, it immediately follows that $H_{\text{adm}}⩾{\min }_{k\in \{1,2,\dots ,K\}}{H}_k$.

3.2. Maximum of H_adm in terms of the ancestry proportions

To obtain the maximum of H_adm over the space of values of γ, we write eq. 9 as a quadratic form:

$$H_{\text{adm}}(\underset{\_}{\gamma })={\underset{\_}{\gamma }}^{\prime }A\underset{\_}{\gamma }.$$

Here, γ′ represents the transpose of the column vector γ and A is the K × K symmetric matrix with the H_k on the diagonal and the C_kℓ off the diagonal:

$$A=\left(\begin{array}{cccc}{H}_1& C_{12}& \dots & C_{1K}\\ C_{12}& H_2& \dots & C_{2K}\\ \dots & \dots & \dots & \dots \\ C_{1K}& C_{2K}& \dots & H_K\end{array}\right)={\underset{\_}{11}}^{\prime }-\left(\begin{array}{cccc}\sum _{j=1}^J{p}_{1j}^2& \sum _{j=1}^J{p}_{1j}{p}_{2j}& \dots & \sum _{j=1}^J{p}_{1j}{p}_{Kj}\\ \sum _{j=1}^J{p}_{1j}{p}_{2j}& \sum _{j=1}^J{p}_{2j}^2& \dots & \sum _{j=1}^J{p}_{2j}{p}_{Kj}\\ \dots & \dots & \dots & \dots \\ \sum _{j=1}^J{p}_{1j}{p}_{Kj}& \sum _{j=1}^J{p}_{2j}{p}_{Kj}& \dots & \sum _{j=1}^J{p}_{Kj}^2\end{array}\right)={\underset{\_}{11}}^{\prime }-P^{\prime }P,$$ (11)

where P is the J × K allele frequency matrix (eq. 6) and 1 is a K × 1 vector of ones.

Maximizing H_adm in terms of γ is equivalent to finding ${\max }_{\underset{\_}{\gamma }\in {\mathrm{\Delta }}^{K-1}}{\underset{\_}{\gamma }}^{\prime }A\underset{\_}{\gamma }$ subject to 1′γ = 1. We denote by γ_{arg max} the location of the maximal value of H_adm. We first observe that γ_{arg max} is sometimes interior to the simplex, and that it sometimes lies at a vertex. In other words, for a fixed set of sources, a population nontrivially admixed among the sources can sometimes have a higher heterozygosity than all of the sources, but sometimes, no population admixed among the sources has higher heterozygosity than all the sources.

Proposition 4. Consider the case of K source populations, K ⩾ 2.

(i) There exists some collection of source population allele frequencies P and some collection of admixture proportions γ for which the heterozygosity of the admixed population exceeds the heterozygosity H_M of the most heterozygous source population.

(ii) There exists some collection of source population allele frequencies P for which no collection of admixture proportions γ produces an admixed population with heterozygosity greater than the heterozygosity H_M of the most heterozygous source population.

Proof. (i) Consider K populations, each with different allele frequencies, but identical heterozygosity: $\underset{\_}{p_k}\ne \underset{\_}{p_{\ell }}$ for k ≠ ℓ but H_k = H for k = 1, 2, …, K. Suppose that a locus has K + 1 distinct alleles, and that the allele frequencies are $\underset{\_}{p_1}=\left(\frac{1}{2},\frac{1}{2},0,0,\dots ,0\right)$, $\underset{\_}{p_2}=\left(\frac{1}{2},0,\frac{1}{2},0,\dots ,0\right),\dots ,\underset{\_}{p_K}=\left(\frac{1}{2},0,0,\dots ,0,\frac{1}{2}\right)$. By eq. 9, $H_{\text{adm}}=\frac{3}{4}-\frac{1}{4}{\sum }_{k=1}^K{\gamma }_k^2$, which is minimized if and only if ${\sum }_{k=1}^K{\gamma }_k^2=1$ or $\underset{\_}{\gamma }=\underset{\_}{e_k}$ for some k. The minimal value of H_adm is thus $\frac{1}{2}$, all other values of the admixture proportions resulting in $H_{\text{adm}}>H=\frac{1}{2}$.

(ii) Consider K populations and a locus with K distinct alleles. Suppose that the number of distinct alleles at the locus is k for population k, with $\underset{\_}{p_k}=\left(\frac{1}{k},\dots ,\frac{1}{k}\right)$. Hence, $H_k=1-\frac{1}{k}$ and, in particular, H₁ < … < H_K. We show that H_adm ⩽ H_K irrespective of γ.

By eq. 9,

$$H_{\text{adm}}=1-{\left({\gamma }_1+\frac{{\gamma }_2}{2}+\dots +\frac{{\gamma }_K}{K}\right)}^2-\dots -{\left(\frac{{\gamma }_K}{K}\right)}^2.$$

By the Cauchy-Schwarz inequality:

$$\left[{\left({\gamma }_1+\frac{{\gamma }_2}{2}+\dots +\frac{{\gamma }_K}{K}\right)}^2+\dots +{\left(\frac{{\gamma }_K}{K}\right)}^2\right]K⩾{\left({\gamma }_1+\frac{{\gamma }_2}{2}2+\dots +\frac{{\gamma }_K}{K}K\right)}^2={\left(\sum _{k=1}^K{\gamma }_k\right)}^2=1.$$

Thus, $H_{\text{adm}}⩽1-\frac{1}{K}=H_K$. □

The proof is constructive, exhibiting example source groups for which specific features are obtained. In part (i), each source has an allele that is not present in the other sources, and a nontrivially admixed population—which possesses all of these private alleles—is necessarily more heterozygous than each source. For part (ii), we have a sequence of increasingly heterozygous source populations, each with one additional allele, and no population admixed among them is more heterozygous than the most heterozygous source. Other constructive examples are possible, with, for example, low heterozygosities but distinct alleles across populations generating additional examples along the lines of Proposition 4i.

Note that it is trivial to see that in general, ${\max }_{\underset{\_}{\gamma }\in {\mathrm{\Delta }}^{K-1}}{H}_{\text{adm}}(\underset{\_}{\gamma })⩾\max \left\{H_1,\dots ,H_K\right\}$: the K source populations simply correspond to the K vertices of the simplex. This result that the maximal H_adm is at least is great as the heterozygosity of the most heterozygous source population immediately implies ${\max }_{\underset{\_}{\gamma }\in {\mathrm{\Delta }}^{K-1}}{H}_{\text{adm}}(\underset{\_}{\gamma })⩾\frac{1}{K}{\sum }_{k=1}^K{H}_k$.

Having established that the maximum can be at a vertex or an interior point of the simplex—a trivial admixed population consisting only of a single source population, or a population admixed among all the sources—we now provide a general theorem. The theorem gives the location of the maximum when it lies in the interior of Δ^K−1, rather than on the boundary, assuming a condition applies on the allele frequencies. The proof is in Appendix 1, making use of a general constrained quadratic optimization procedure.

Theorem 5. Suppose that 1′(P′P)⁻¹1 ≠ 1. Suppose also that $\frac{A^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}\in {\mathrm{\Delta }}^{K-1}$. Then the maximum of H_adm as a function of the ancestry proportions γ ∈ Δ^K−1 is attained at γ_{arg max} = γ*, where:

$${\underset{\_}{\gamma }}^{*}=\frac{A^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}=\frac{{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}}.$$

The maximum is equal to:

$$H_{\text{adm}}\left({\underset{\_}{\gamma }}^{*}\right)=\frac{1}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}=1-\frac{1}{{\underset{\_}{1}}^{\prime }{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}}.$$

If $\frac{A^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}\notin {\mathrm{\Delta }}^{K-1}$, then γ_{arg max} lies on the boundary of the set {γ : 1′γ = 1 and γ ∈ Δ^K−1}.

The “boundary” of a set R is the set of points in R for which a neighborhood around them always contains both points in R and points in the complement of R. For simplex Δ^K−1, the boundary includes all points for which at least one of the K coordinates is 0, with the vertices occurring at locations where all of the coordinates except one are 0.

The following corollary, also proven in Appendix 1, further describes the possible locations of the maximal H_adm. Note that if the maximum is not at γ∗, then it lies at a point that has some elements equal to 0, the nonzero subvector having a similar form to γ∗, but in a lower number of dimensions. Thus, the maximum can occur in a scenario in which the admixture involves only a strict subset of the source populations.

Consider a nonempty subset $\mathcal{S}\subset \{1,2,\dots ,K\}$. Define by $A_{\mathcal{S}}$ the $|\mathcal{S}|\times |\mathcal{S}|$ matrix that has diagonal terms H_k for each $k\in \mathcal{S}$ and off-diagonal terms C_kℓ for each distinct $k,\ell \in \mathcal{S}$. Additionally, denote by $P_{\mathcal{S}}$ the matrix consisting of the columns of P corresponding to the subset $\mathcal{S}$. $P_{\mathcal{S}}$ contains the allele frequencies for the source populations in $\mathcal{S}$.

Corollary 6. Suppose that ${\underset{\_}{1}}^{\prime }{\left(P_{\mathcal{S}}^{\prime }{P}_{\mathcal{S}}\right)}^{-1}\underset{\_}{1}\ne 1$ for all nonempty $\mathcal{S}\subset \{1,2,\dots ,K\}$. Then the maximum of H_adm as a function of the ancestry proportions γ ∈ Δ^K−1 is attained at a point that has nonzero elements for some nonempty subset of the source populations ${\mathcal{S}}^{*}\subset \{1,2,\dots ,K\}$. The nonzero subvector of ancestry proportions at the location of the maximum is equal to $\underset{\_}{{\gamma }_{{\mathcal{S}}^{*}}}=\frac{A_{{\mathcal{S}}^{*}}^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}_{{\mathcal{S}}^{*}}^{-1}\underset{\_}{1}}$.

In particular, note that γ_{arg max} = γ* corresponds to ${\mathcal{S}}^{*}=\{1,2,\dots ,K\}$: all source populations contribute nonzero admixture fractions. The K vertices of the simplex Δ^K−1 correspond to the cases of ${\mathcal{S}}^{*}=\left\{k\right\}$, at which only one source population contributes. $\mathcal{S}$ has 2^K − 1 nonempty subsets, each representing a distinct collection of source populations.

4. K = 2 source populations

With general results established for the case of arbitrary K, we now focus on the simplest case, with K = 2 source populations contributing to the admixed population.

We continue to exclude the scenario in which the allele frequencies for the two source populations are identical, so that we assume $\underset{\_}{p_1}\ne \underset{\_}{p_2}$. Noting that γ₂ = 1 − γ₁, we can consider H_adm in terms of a single admixture coefficient γ₁, the admixture fraction of the first population, with γ₁ ∈ [0, 1]. Using eqs. 9 and 10 with this substitution, we obtain:

$$H_{\text{adm}}={\gamma }_1^2{H}_1+{\left(1-{\gamma }_1\right)}^2{H}_2+2{\gamma }_1\left(1-{\gamma }_1\right)C_{12}$$ (12)

$$={\gamma }_1^2{H}_1+{\left(1-{\gamma }_1\right)}^2{H}_2+{\gamma }_1\left(1-{\gamma }_1\right)\left(H_1+H_2\right)\frac{1+F_{12}}{1-F_{12}}$$ (13)

$$={\gamma }_1^2\left(H_1+H_2-2C_{12}\right)-2{\gamma }_1\left(H_2-C_{12}\right)+H_2.$$ (14)

In particular, we note from eq. 13 that H_adm is increasing as a function of F₁₂.

From eq. 14, we can see that H_adm is concave down in γ₁. We have $d^2{H}_{\text{adm}}/d{\gamma }_1^2=2\left(H_1+H_2-2C_{12}\right)$. By Definition 1 and eq. 2, $2\left(H_1+H_2-2C_{12}\right)=-2{\sum }_{j=1}^J{\left(p_{1j}-p_{2j}\right)}^2$. Because $\underset{\_}{p_1}\ne \underset{\_}{p_2},p_{1j}\ne p_{2j}$ for at least one choice of j, and hence $d^2{H}_{\text{adm}}/d{\gamma }_1^2<0$. By symmetry, H_adm is also concave down in γ₂.

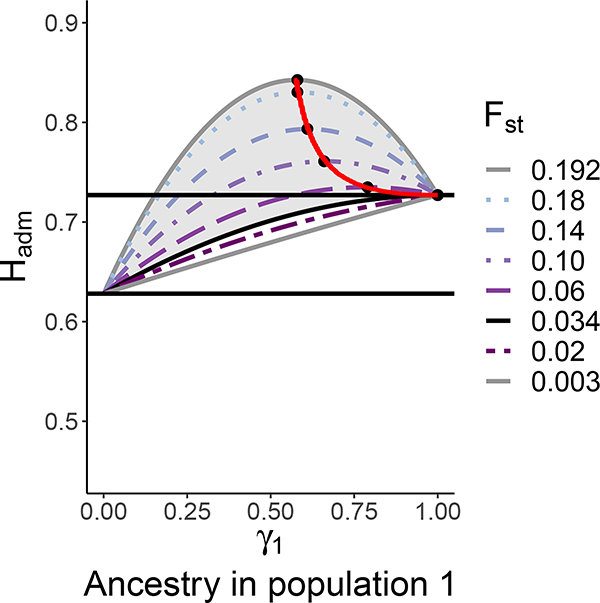
To illustrate eq. 13, for H₁ and H₂ fixed, Figure 1 plots the concave-down H_adm as a function of γ₁ for a variety of values of F₁₂. We observe that for each value of F₁₂ considered, the minimum of H_adm occurs at (γ₁, γ₂) = (0, 1), reflecting the result of Proposition 3 that the minimum occurs when the admixed population consists solely of the less heterozygous source population. In accord with the fact that in eq. 13, H_adm increases for fixed H₁, H₂, and γ₁ with increasing F₁₂, the value at the maximum increases with increasing F₁₂. The location of the maximum lies at a value of ${\gamma }_1⩾\frac{1}{2}$, decreasing with increasing F₁₂. This location has a pattern where for larger values of F₁₂, it lies interior to the unit interval, and for smaller values of F₁₂, it occurs when the admixed population consists solely of the more heterozygous source population. We now consider this pattern in more detail.

Figure 1:

H_adm versus γ₁ for fixed values of H₁ and H₂. We choose H₁ = 0.727 and H₂ = 0.628; the horizontal lines represent H_adm = H₁ and H_adm = H₂. Eq. 13 is plotted for multiple values of F₁₂, considering the allowable range of F₁₂ values in [0.003,0.192] as specified by eq. 5. The red curve, which plots (γ₁, H_adm) in terms of H₁, H₂, and F₁₂ in the form of eqs. 24 and 25, indicates the maxima of H_adm as F₁₂ varies, with black dots specifying the maxima for the specific plotted values of F₁₂. The shaded region corresponds to the region where ${\gamma }_1^{*}\in (0,1)$, as specified by Corollary 10; the value F₁₂ ≈ 0.034 gives the boundary of this region. The values chosen for H₁ and H₂ are, respectively, the mean heterozygosities across 8 European and 29 Native American populations, based on population-wise estimates in Table S20 of Pemberton et al. (2013). The value of γ₁ can be viewed as the fraction of European ancestry in an admixed population and 1 − γ₁ can be considered the fraction of Native American ancestry.

4.1. Minimum and maximum of H_adm in terms of the ancestry proportions

Applying the results from Section 3.1 on the minimum and maximum of H_adm as a function of γ, by Proposition 3, H_adm has minimum min{H₁, H₂}. The maximum can occur in one of three locations.

Proposition 7. Consider two source populations with distinct allele frequencies, p₁ ≠ p₂. As a function of γ₁, H_adm is maximized at ${\gamma }_1={\gamma }_1^{*}$, where ${\gamma }_1^{*}$ takes one of three forms.

(i) If H₁ < C₁₂ and H₂ < C₁₂, then ${\gamma }_1^{*}\in (0,1)$ satisfies

$${\gamma }_1^{*}=\frac{C_{12}-H_2}{2\left(C_{12}-H_S\right)}=\frac{1}{2}+\frac{H_1-H_2}{8\left(H_T-H_S\right)},$$ (15)

and H_adm has maximum equal to

$$H_{\text{adm}}\left({\gamma }_1^{*}\right)=\frac{C_{12}^2-H_1{H}_2}{2\left(C_{12}-H_S\right)}=H_T+\frac{{\left(H_1-H_2\right)}^2}{16\left(H_T-H_S\right)}.$$ (16)

(ii) If H₁ < C₁₂ and H₂ ⩾ C₁₂, then ${\gamma }_1^{*}=0$ and H_adm has maximum H₂.

(iii) If H₁ ⩾ C₁₂ and H₂ < C₁₂, then ${\gamma }_1^{*}=1$ and H_adm has maximum H₁.

An elementary proof appears in Appendix 2. The locations specified in Proposition 7 accord with Theorem 5 and Corollary 6. For K = 2, the result of Theorem 5 gives ${\underset{\_}{\gamma }}^{*}=\frac{A^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}=\left(\frac{C_{12}-H_2}{2\left(C_{12}-H_S\right)},\frac{C_{12}-H_1}{2\left(C_{12}-H_S\right)}\right)$, where

$$A=\left(\begin{array}{ll}{H}_1\hfill & C_{12}\hfill \\ C_{12}\hfill & H_2\hfill \end{array}\right).$$

The locations in Corollary 6 are ${\gamma }_1^{*}=\frac{A_1^{-1}}{A_1^{-1}}=1$ and ${\gamma }_2^{*}=0$, and ${\gamma }_1^{*}=0$ and ${\gamma }_2^{*}=\frac{A_2^{-1}}{A_2^{-1}}=1$.

We now give two corollaries of Proposition 7, providing more features of the maximal H_adm for specific cases. Proofs appear in Appendix 2. In accord with the observation in Figure 1 that the maximal H_adm lies at a value of ${\gamma }_1⩾\frac{1}{2}$ in an example with H₁ ⩾ H₂, Corollary 8 demonstrates ${\gamma }_1^{*}⩾\frac{1}{2}$ if and only if H₁ ⩾ H₂.

Corollary 8. Consider two source populations with distinct allele frequencies, $\underset{\_}{p_1}\ne \underset{\_}{p_2}$. As a function of γ₁, H_adm is maximized at ${\gamma }_1^{*}⩾\frac{1}{2}$ if and only if H₁ ⩾ H₂.

A second corollary is that the maximal H_adm is always at least as great as H_T.

Corollary 9. Consider two source populations with distinct allele frequencies, $\underset{\_}{p_1}\ne \underset{\_}{p_2}$. Then $H_{\text{adm}}\left({\gamma }_1^{*}\right)⩾H_T$, with equality occurring if H₁ = H₂.

We can also succinctly describe the region where ${\gamma }_1^{*}$ lies interior to (0, 1).

Corollary 10. Consider two source populations with distinct allele frequencies, $\underset{\_}{p_1}\ne \underset{\_}{p_2}$. ${\gamma }_1^{*}$ lies in (0, 1) if and only if the following inequality holds:

$$F_{12}>\frac{\left|H_1-H_2\right|}{2\left(H_1+H_2\right)+\left|H_1-H_2\right|}.$$ (17)

This corollary is proven in Appendix 2. Note that if H₁ + H₂ is fixed, then the right-hand side of eq. 17 increases with |H₁ −H₂|, from a minimum of 0 when H₁ = H₂ to a maximum of $\frac{1}{3}$ as |H₁ −H₂| approaches H₁+H₂. Thus, in accord with the observation in Section 3.1 that H_adm > H for all nontrivial admixtures of equal-heterozygosity source populations, the maximal H_adm exceeds max{H₁, H₂} over a broader range of F₁₂ values if |H₁−H₂| is small rather than large. Moreover, if $F_{12}>\frac{1}{3}$, then eq. 17 necessarily holds. Hence, irrespective of H₁ and H₂, if the source populations are distant enough that $F_{12}>\frac{1}{3}$, then the maximal heterozygosity exceeds the heterozygosities of the source populations.

4.2. Special case of J = 2 alleles

For K = 2 sources, when the locus has only J = 2 allelic types, further simplifications are possible, as results can be stated in terms of frequencies of one specific allele. We substitute p₁₂ = 1 − p₁₁ and p₂₂ = 1 − p₂₁.

Proposition 11. Consider two source populations with distinct allele frequencies, $\underset{\_}{p_1}\ne \underset{\_}{p_2}$. For a biallelic locus, H_adm is maximized at ${\gamma }_1={\gamma }_1^{*}$, where ${\gamma }_1^{*}$ takes one of three forms.

(i) If $p_{11}>\frac{1}{2}>p_{21}$ or $p_{21}>\frac{1}{2}>p_{11}$, then ${\gamma }_1^{*}\in (0,1)$ satisfies

$${\gamma }_1^{*}=\frac{1-2p_{21}}{2\left(p_{11}-p_{21}\right)},$$ (18)

and H_adm has maximum equal to

$$H_{\text{adm}}\left({\gamma }_1^{*}\right)=\frac{1}{2}.$$ (19)

(ii) If $\frac{1}{2}⩾p_{21}>p_{11}$ or $p_{11}>p_{21}⩾\frac{1}{2}$, then ${\gamma }_1^{*}=0$ and H_adm has maximum H₂.

(iii) If $\frac{1}{2}⩾p_{11}>p_{21}$ or $p_{21}>p_{11}⩾\frac{1}{2}$, then ${\gamma }_1^{*}=1$ and H_adm has maximum H₁.

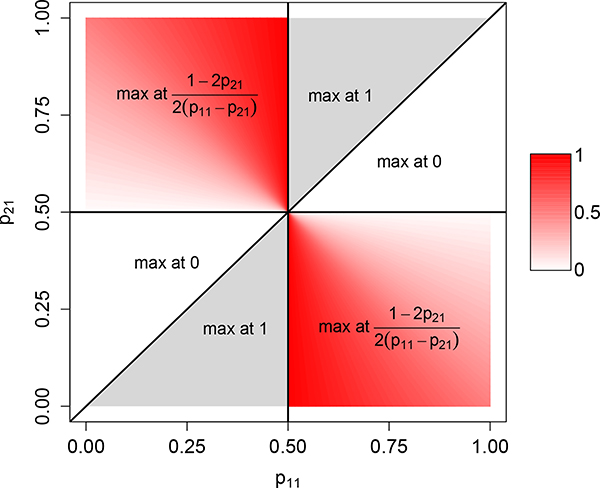
The result is proven in Appendix 2. The unit square representing possible values of the location of the maximum appears in Figure 2. It has six nonoverlapping regions: in Proposition 11, each of the three cases generates two disjoint subsets of [0,1]². A smooth gradient exists for regions in case (i). However, an abrupt transition occurs at the line p₂₁ = p₁₁ between case-(ii) regions where ${\gamma }_1^{*}=0$ and case-(iii) regions where ${\gamma }_1^{*}=1$. Note that the p₂₁ = p₁₁ line, where the two populations have equal allele frequencies, is disallowed.

Figure 2:

The admixture coefficient γ₁ that maximizes H_adm in the case of K = 2 source populations and J = 2 allelic types. The plot shows the unit square for (p₁₁, p₂₁). In the red regions, the maximizing value of γ₁ lies in (0,1), whereas in the white and gray regions, it lies on one or the other boundary. The figure depicts the result of Proposition 11.

5. Simulations

We illustrate properties of H_adm by simulating population sets for different values of K and J. Given a value of K, we generated allele frequency vectors for the K source populations from independent and identically distributed symmetric multivariate J-dimensional Dirichlet distributions with a common concentration parameter α = 1. This distribution corresponds to a uniform distribution on the simplex Δ^J−1. A number of mathematical results can be obtained in this Dirichlet setting; these appear in Appendix 3.

First, for K = 2 and K = 3, we assessed the probability that the maximal H_adm over possible admixture vectors γ occurs interior to the simplex Δ^K−1, rather than on its boundary. This computation gives the probability that the heterozygosity-maximizing admixture vector contains nonzero contributions from all K source populations. We considered 2 ⩽ J ⩽ 30 for K = 2 and 3 ⩽ J ⩽ 30 for K = 3, recalling the condition J ⩾ K for the K allele frequency vectors to be linearly independent.

For each (K, J), we ran 10,000 simulation replicates. In each replicate, to determine the location of the maximum, we applied Theorem 5 and Corollary 6 to identify the locations specified for each choice $\mathcal{S}$ of the nonempty subset of the K populations with nonzero allele frequencies. Among these 2^K−1 locations, excluding those outside the simplex Δ^K−1, we identified the point with the largest H_adm. Note that in each replicate, we observed that the ${\underset{\_}{1}}^{\prime }{\left(P_{\mathcal{S}}^{\prime }{P}_{\mathcal{S}}\right)}^{-1}\underset{\_}{1}\ne 1$ condition of Corollary 6 was satisfied for each $\mathcal{S}$.

Figure 3 finds that, for both K = 2 and K = 3, the maximum of H_adm is increasingly likely to be in the interior of the simplex as the number of distinct alleles, J, increases. For K = 3, we also observe that the probability that H_adm is maximized on an edge, corresponding to nonzero contributions from two of three sources, exceeds the probability that it is maximized at a vertex, with only one contributing source.

Figure 3:

Location of the maximum of H_adm in simulation replicates. (A) K = 2. (B) K = 3. The location γ_{arg max} can be in the interior of the simplex Δ^K−1, corresponding to nontrivial admixture of all source groups, or on the boundary of the simplex. For K = 3, it can be on an edge, corresponding to admixture of two of three source populations, and for both K = 2 and K = 3, it can be at a vertex, corresponding to membership in only one source population. For each (K, J), points plotted are based on 10,000 simulations with independently and identically distributed Dirichlet-(1, 1, …, 1) distributions for the allele frequency vectors $\underset{\_}{p_k}$ in the K populations.

Next, we assessed the probability $\mathbb{P}\left[H_{\text{adm}}>\max \left\{H_1,\dots ,H_K\right\}\right]$ in a scenario in which both the allele frequency vectors p_k and the admixture fractions γ were chosen from independent Dirichlet distributions. We simulated the p_k as before, additionally simulating γ from a K-dimensional symmetric Dirichlet-(1, 1, …, 1) distribution. For each (K, J) with K = 2, 3, 4, 5 and J = 2, 3, …, 30, we simulated 50,000 replicate populations. Note that here, unlike in Section 2.4, we impose no restrictions on linear combinations of allele frequency vectors from the source populations, so that it is not necessarily true that J ⩾ K.

The fraction of replicates with $\mathbb{P}\left[H_{\text{adm}}>\max \left\{H_1,\dots ,H_K\right\}\right]$ appears in Figure 4. We see that this fraction increases with K: for an admixture involving more populations, the probability is larger that the admixed population exceeds all source populations in heterozygosity. This probability also increases with J.

Figure 4:

The fraction of simulation replicates for which H_adm > max{H₁, …, H_K}, for various values of K and J. For each (K, J), points plotted are based on 50,000 simulation replicates with independently and identically distributed Dirichlet-(1, 1, …, 1) distribitions for the allele frequency vectors $\underset{\_}{p_k}$ in the K populations, and a Dirichlet-(1, 1, …, 1) distribution for the admixture coefficient vector γ.

For (K, J) = (2, 2), Proposition 17 in Appendix 3 obtains the probability analytically, $\mathbb{P}[H_{\text{adm}}>\max \left\{H_1,H_2\right\}]=1-\log 2\approx 0.307$. Following this result, the K = 2 curve in Figure 4 begins near (2, 0.307).

Figure 5 provides further detail on H_adm in the K = 2 case by graphing H_adm versus γ₁ for 10 simulation replicates chosen at random for each of three values of J. The figure illustrates that H_adm is a concave-down quadratic polynomial in γ₁, as in eq. 14. Averaging across replicates, by examining the figure panels from left to right, we can also observe that $\mathbb{E}\left[H_{\text{adm}}\right]$ increases as a function of J, as in Corollary 16 of Appendix 3. For J = 2, as in Proposition 11, the possible values of H_adm at the maximum are H₁, H₂, and $\frac{1}{2}$.

Figure 5:

H_adm versus γ₁ for 10 simulation replicates for K = 2 source populations, for each of three values of the number of allelic types J. For each replicate, allele frequency vectors $\underset{\_}{p_k}$ in the two populations are simulated according to Dirichlet-(1, 1, …, 1) distributions, and H_adm is plotted as a function of γ₁ according to eq. 8. The maximum of H_adm is indicated by a black circle in each replicate. The red dashed lines represent the expected values of H_adm according to Corollary 16 in Appendix 3.

6. Application to data

Next, we illustrate the mathematical results using data from human populations. As multiallelic loci satisfy J ⩾ K with both K = 2 and K = 3, we focus on a multiallelic data example. First, we begin with a simpler biallelic data set whose set of individuals overlaps with the multiallelic data set, illustrating our maximal heterozygosity results in the case of K = 2 source populations. For both data sets, we treat allele frequencies, heterozygosities, and F_ST values computed from the data as parametric values rather than estimates.

6.1. Biallelic loci: K = 2 source populations

We consider the single-nucleotide polymorphism (SNP) data of Li et al. (2008), as employed by Pemberton et al. (2012) in phased form with no missing data. In this data set, which contains 640,034 autosomal SNPs, we consider Europeans and Native Americans as putative source populations for an admixed population, considering the 156 Europeans and 63 Native Americans in the data. We drop from consideration the 32,989 SNPs with identical allele frequencies in the two populations; 32,888 of these are monomorphic.

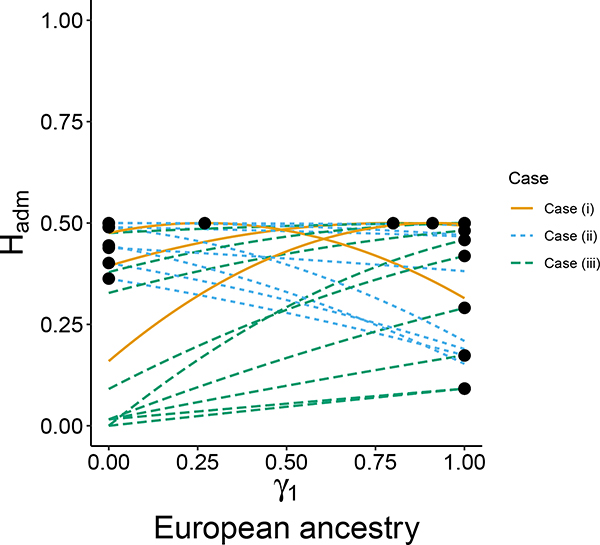
We select 20 loci at random from the data set for illustration. Treating γ₁ as the fraction of European ancestry in an admixed population and 1 − γ₁ as the fraction of Native American ancestry, for each locus, the plot for H_adm versus γ₁ appears in Figure 6. Following Proposition 3, the minimum of H_adm lies either at γ₁ = 0 or at γ₁ = 1 for all loci. For 3 of the 20 loci, the maximum lies in the interior of the unit interval (case (i) of Proposition 11); 8 loci have the maximum at γ₁ = 0, representing membership in the less heterozygous Native American population (case (ii)); and 9 loci have the maximum at γ₁ = 1, representing membership in the more heterozygous European population (case (iii)). Following Proposition 11i, at each locus for which the maximum lies in the interior, the maximum is equal to $\frac{1}{2}$.

Figure 6:

H_adm versus γ₁ for 20 random biallelic loci from Pemberton et al. (2012). The two source populations providing the allele frequencies are the European and Native American populations, with γ₁ corresponding to membership in the European population. H_adm is plotted according to eq. 8. Circles indicate the location of the maximum along each curve. Different colors and line types correspond to the three cases in Proposition 11 for the location of the maximal H_adm.

Examining all 607,045 loci, 19% have the maximum in the interior, 27% at γ₁=0, and 54% at γ₁ = 1. That more loci have the maximum at γ₁ = 1 than γ₁ = 0 is expected from the fact that European populations generally have greater heterozygosity than Native American populations (e.g. Pemberton et al., 2013).

6.2. Multiallelic loci: K = 2 source populations

For our multiallelic data set, we follow Boca & Rosenberg (2011) in considering data from Wang et al. (2008) on 678 microsatellite loci typed in 160 Europeans, 463 Native Americans, 123 Africans, and 249 individuals from admixed Mestizo populations. To represent Mestizo populations under our model, we use Europeans and Native Americans as source populations in the K = 2 case, also including Africans for K = 3.

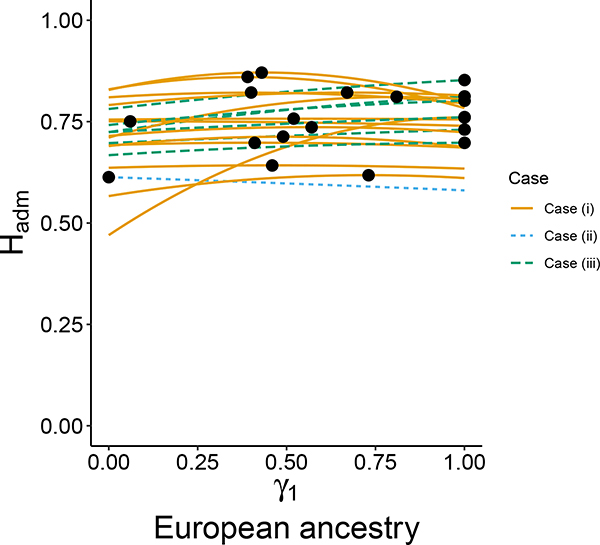
As we did in the biallelic data set, we select 20 loci at random from Wang et al. (2008), choosing the same loci as in Boca & Rosenberg (2011). Again treating γ₁ as the fraction of European ancestry and 1 − γ₁ as the fraction of Native American ancestry in an admixed population, for each locus, the plot for H_adm versus γ₁ appears in Figure 7. Comparing Figures 7 and 6, we see that the maximum of H_adm lies in the interior of the unit interval for γ₁ more often for the multiallelic than for the biallelic loci. Indeed, examining all 678 loci, 53% have the maximum in the interior—a greater number than for the SNPs. The fraction with the maximum at γ₁ = 1 is 39%, and 8% have the maximum at γ₁ = 0.

Figure 7:

H_adm versus γ₁ for 20 random multiallelic loci from Wang et al. (2008). The two source populations providing the allele frequencies are the European and Native American populations, with γ₁ corresponding to membership in the European population. H_adm is plotted according to eq. 8. Circles indicate the location of the maximum along each curve. Different colors and line types correspond to the three cases in Proposition 7 for the location of the maximal H_adm.

The Dirichlet model in Corollary 16 in Appendix 3 and Figures 3 and 5 predicts a dependence of the location of the maximum on the number of distinct alleles of a locus, with the probability that the maximum lies in the interior increasing with the number of distinct alleles. The multiallelic data produce a trend in the same direction as this prediction. The mean numbers of distinct alleles are 9.36, 10.40, and 10.75, for the loci with ${\gamma }_1^{*}$ at 0, 1, and in (0, 1), respectively (one-way ANOVA, P = 0.008, F test, 2 df). The mean number of distinct alleles for the loci with the maximum on either boundary is 10.24, smaller than the mean of 10.74 for those with the mean in the interior (P = 0.03, two-tailed t test).

6.3. Comparison of predicted H_adm to observed H_adm

We next compare predicted and observed H_adm values for the 678 loci for the admixed Mestizo population. In this approach, we used estimated locus-wise values of γ₁ in the Mestizo population together with locus-wise heterozygosities in the European and Native American populations to “predict” locus-wise Mestizo heterozygosities. The prediction is compared to the observed heterozygosity value to examine if our formulas for the heterozygosity of an admixed population are reflected in actual heterozygosities in an admixed group.

This computation follows a similar computation of Boca & Rosenberg (2011). The estimated admixture fractions, computed for the same data, are taken from Schroeder et al. (2009), who obtained them by a maximum likelihood approach (Millar, 1987) that does not take into account source population heterozygosities. Using these estimates, locus-wise heterozygosity estimates in the source populations, and locus-wise F_ST values calculated from allele frequencies in the source populations, we predicted H_adm with eq. 13.

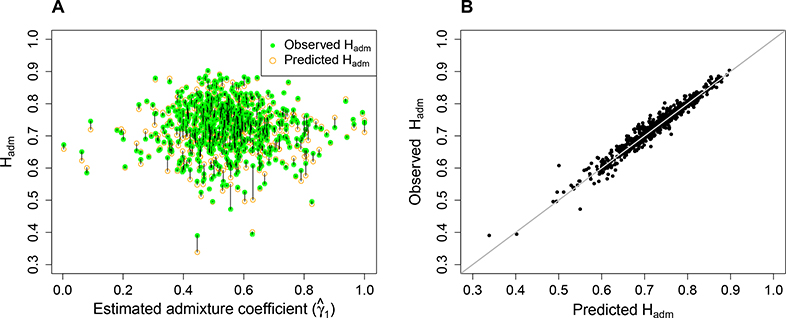
The predicted and observed H_adm values for individual loci are compared in Figure 8. In general, the observation closely matches the prediction (Figure 8A), with the correlation between the observed and predicted H_adm values equaling 0.978 (Figure 8B). For 56% of the 678 loci, the prediction provides an underestimate of the observed value.

Figure 8:

Predicted and observed H_adm. (A) The predicted and observed H_adm values for an admixed Mestizo population are plotted against the locus-wise estimated European admixture fraction ${\widehat{\gamma }}_1$ in the Mestizo population, estimated by maximum likelihood. The prediction is based on eq. 8, using European and Native American allele frequencies estimated from Wang et al. (2008) as $\underset{\_}{p_1}$ and $\underset{\_}{p_2}$, respectively, together with the maximum likelihood estimate of γ₁. The observation is based on H_adm computed from Definition 1, inserting estimated allele frequencies from Wang et al. (2008) for the Mestizo population. (B) The observed H_adm value is plotted against the predicted H_adm value. The identity line is shown in gray. In both panels, each point represents one of the 678 loci used. The correlation coefficient between the predicted and observed H_adm values is 0.978.

6.4. K = 3 source populations

We now consider the European, Native American, and African populations as the source populations, using γ₁ for the proportion of European ancestry, γ₂ for Native American ancestry, and γ₃ for African ancestry. We select 3 loci for illustration, choosing the same ones as in a similar analysis of Boca & Rosenberg (2011).

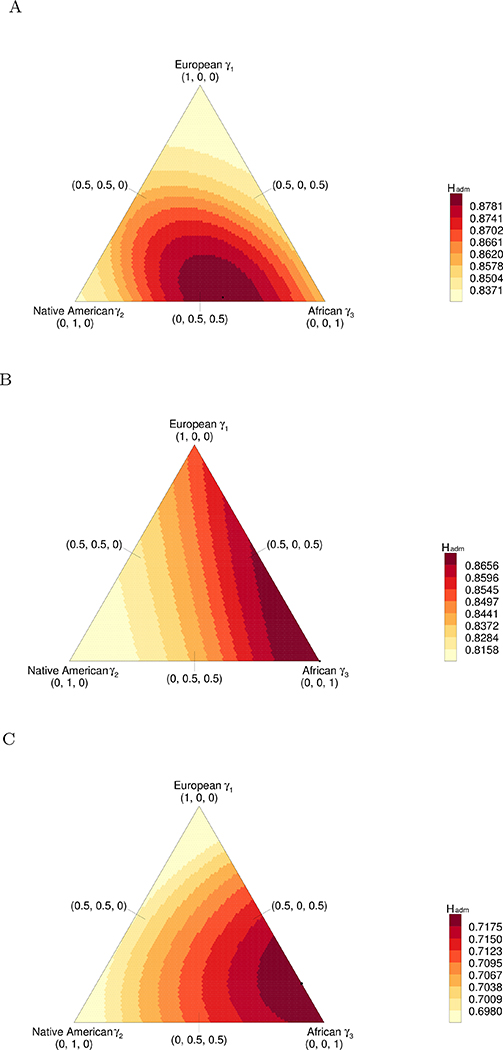
Plots for H_adm over the unit simplex for (γ₁, γ₂, γ₃) appear in Figure 9. Each plot depicts H_adm as a function of (γ₁, γ₂, γ₃) for a specific locus. The three panels show the possible locations of the maximal value of H_adm: in the first panel, the maximum lies in the interior of the simplex; in the second panel, at a vertex, and in the third panel, on an edge.

Figure 9:

H_adm versus (γ₁, γ₂, γ₃) for three loci. The loci are from Wang et al. (2008) and have 14, 14, and 8 distinct alleles, respectively. The value of H_adm is computed from eq. 8. Black circles indicate the maximum H_adm. (A) Locus D2S1399: the maximum lies in the interior of the region. (B) Locus GATA101G01: the maximum lies at the (0, 0, 1) vertex. (C) Locus GATA146D07: the maximum lies on the γ₂ = 0 edge.

Considering all 678 loci, 15% have the maximum in the interior of the region, with γ₁ > 0, γ₂ > 0, and γ₃ > 0. The fractions with the maximum on an edge are 20% for a maximum on the edge with γ₁ = 0, 26% on the γ₂ = 0 edge, and 5% on the γ₃ = 0 edge. The fractions with the maximum at a vertex are 27% for the vertex (0, 0, 1), 2% for (0, 1, 0), and 5% for (1, 0, 0). The observations that (0, 0, 1) is the vertex with the largest number of maxima and (1, 0, 1) is the edge with the most maxima accord with the fact that African populations have generally higher heterozygosity than European populations, which in turn have higher heterozygosity than Native American populations (e.g. Pemberton et al., 2013).

7. Discussion

We have considered the heterozygosity H_adm of an admixed population in terms of the admixture fractions of the source populations, and their heterozygosities and F_ST values at a locus. We have derived formulas describing H_adm in relation to these quantities (eqs. 8–10). In particular, we showed that H_adm is minimized over the set of possible admixture coefficient vectors when the admixed population consists of only one of the source populations (Proposition 3): an admixed population is at least as heterozygous as the least heterozygous source population. The maximal H_adm is more complicated, as its heterozygosity can either exceed or equal that of the most heterozygous source population (Proposition 4).

In studying the possible locations of the maximal H_adm for a fixed set of source populations, we found that the maximum can lie either in the interior of the region describing the allowable values of the admixture fractions—in which case all source populations contribute to the admixed population—or on the boundary, where one or more source populations does not contribute to the admixed population (Propositions 4–6, Figures 1–3). Simulations under a Dirichlet model for allele frequencies suggest that the maximal value of H_adm lies with increasing frequency in the interior of the allowable region as K and J increase (Figure 4).

For K = 2 source populations, we obtained further results, in particular showing that H_adm is a concave-down quadratic polynomial in the admixture coefficient γ₁ (eqs. 12–14). We obtained an analytical expression for the maximal heterozygosity of an admixture of a specific pair of source populations in terms of H₁, H₂, and the F_ST value between the two populations (Proposition 7). For fixed values of H₁, H₂, and the admixture fraction γ₁, H_adm is increasing as a function of F_ST (eq. 13, Figure 1). If H₁ > H₂, then the admixture fraction in source population 1 that maximizes H_adm is greater than $\frac{1}{2}$ (Proposition 7), meaning that at the maximal heterozygosity of the admixed population, the contribution of the more heterozygous source population exceeds that of the less heterozygous one. Interestingly, for the K = 2 case with J = 2 allelic types, if the location of the maximal value lies in (0, 1), then heterozygosity at the maximum is always $\frac{1}{2}$ (Proposition 11 and Figure 5): irrespective of the allele frequencies of the source populations, a linear combination (γ₁, γ₂) always exists so that the admixed population has frequencies of $\frac{1}{2}$ for both alleles.

For K = 2 source populations, a key result is that the maximal value of H_adm exceeds the larger of the two source population heterozygosities if and only if F_ST exceeds a bound defined by those heterozygosities (Corollary 10). Thus, with all other quantities equal, combining source populations that are more rather than less divergent is more likely to lead to an admixed population with heterozygosity exceeding those of the source populations. To obtain this result, it was important to utilize bounds on F_ST that constrain its values within a possibly narrow region of the unit interval, particularly for high-heterozygosity loci.

In multiallelic human data, we observed that for heterozygosities and F_ST values for putative sources of Mestizo populations, the maximal H_adm was more likely to be in the interior of the unit simplex or on an edge rather than at a vertex (Figures 7 and 9). This result indicates that the heterozygosities and F_ST values of these populations lie in a parameter range for which admixed populations are frequently more heterozygous than all their source populations. Examining heterozygosities of 267 worldwide populations in Table S20 of Pemberton et al. (2013), the 13 Mestizo populations all have heterozygosities exceeding all 29 Native American populations, and 4 have heterozygosities exceeding all 8 European populations. Interestingly, the 10 most heterozygous populations among the 267 include all five admixed populations involving a source population from the high-heterozygosity region of Africa: a Cape Mixed Ancestry group from South Africa, and four African-American populations. Thus, our mathematical results predicting that admixed populations often exceed all their source populations in heterozygosity are reflected in admixed human groups.

For K = 2, our model successfully predicted the heterozygosities in an admixed population from the source population heterozygosities, F_ST between the source populations, and the estimated admixture coefficient ${\widehat{\gamma }}_1$ (Figure 8). Because H_adm is not necessarily monotonic in γ₁, however, the reverse problem of using H_adm to estimate γ₁ is problematic—unlike for the monotonically varying F_ST between an admixed population and one of the source populations (Boca & Rosenberg, 2011, Theorem 3). Given H_adm, source population heterozygosities H₁ and H₂, and F_ST between the source populations, two solutions to eq. 13 might exist for γ₁—so that although H_adm can be predicted from γ₁, it is inadvisable to proceed in the reverse direction to estimate γ₁ from the heterozygosity of an admixed population.

We note that we have assumed J ⩾ K: the number of alleles is greater than or equal to the number of populations. While the results are suited to biallelic markers for K = 2, they apply primarily to multiallelic markers. Thus, in addition to the microsatellite loci we have used, we can use them with haplotype loci, for which each distinct haplotype over a length of genome is regarded as a separate allele (Mehta et al., 2019), and haplotype clusters, for which haplotypes are grouped into a fixed number of clusters and each individual is assigned a haplotype cluster membership at each site in the genome (San Lucas et al., 2012).

Our approach has followed the study of F_ST and admixture from Boca & Rosenberg (2011), and it shares similar limitations. The model assumes source population allele frequencies are known rather than estimated, and it considers population-level rather than individual-level admixture. It relies on patterns of variation from a single time point and does not incorporate mechanistic admixture processes or a bottleneck at the founding of the admixed population; strong genetic drift since the onset of admixture might interfere with the linear combination assumption for allele frequencies in the admixed population. Despite these limitations, the observed H_adm values and those predicted under our model are correlated in the Mestizo example (Figure 8B), indicating that the model captures key features relevant to the relationship between admixture and heterozygosity. Thus, the empirical results suggest that assessing this relationship in the mathematical formulations we have presented can be useful for understanding the genetics of admixed populations.

Appendix 1. Proofs for arbitrary K: Theorem 5 and Corollary 6

For the proof of Theorem 5, we first show (i) that P′P and A are both invertible under the conditions stated in the theorem, and that:

$$\frac{1}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}=1-\frac{1}{{\underset{\_}{1}}^{\prime }{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}}.$$

We then (ii) use constrained optimization via Lagrange multipliers to obtain the maximum of γ′Aγ subject to 1′γ = 1. This step consists of the first-derivative test to find a stationary point, coupled with the second-derivative test, in Lemma 12, to show that the stationary point defines a local maximum. Finally, we (iii) show that this means that the overall maximum is either at the local maximum γ∗ as described in the statement of the theorem or on the boundary of the set {γ : 1′γ = 1 and γ ∈ Δ^K−1}.

Proof of Theorem 5 (i) Because P is a J × K matrix with column rank K, K × K matrix P′P is positive definite. As a positive definite matrix, P′P is invertible and (P′P)⁻¹ is also positive definite (Graybill, 1976, pp. 21–22).

To show that A = 11′ − P′P is invertible, we use the Sherman-Morrison formula for the inverse of a rank-one update of an invertible matrix (Horn & Johnson, 2012, pp. 18–19). This formula states that for an invertible square n × n matrix X and n × 1 column vectors y and z, X + yz′ is invertible if and only if 1 + z′X⁻¹y ≠ 0, with:

$${\left(X+\underset{\_}{y{z}^{\prime }}\right)}^{-1}=X^{-1}-\frac{X^{-1}\underset{\_}{y{z}^{\prime }}{X}^{-1}}{1+\underset{\_}{z^{\prime }}{X}^{-1}\underset{\_}{y}}.$$

Because we assumed 1′(P′P)⁻¹1 ≠ 1, the Sherman-Morrison formula applies with −(P′P) in the role of X, and K × 1 column vectors 1 in the role of y and z. A has inverse:

$$A^{-1}=\frac{{\left(P^{\prime }P\right)}^{-1}{\underset{\_}{11}}^{\prime }{\left(P^{\prime }P\right)}^{-1}}{{\underset{\_}{1}}^{\prime }{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}-1}-{\left(P^{\prime }P\right)}^{-1}.$$ (20)

Left-multiplying by 1′ and right-multiplying by 1, we obtain

$$\frac{1}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}=1-\frac{1}{{\underset{\_}{1}}^{\prime }{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}}.$$

Because (P′P)⁻¹ is positive definite, 1′(P′P)⁻¹1 > 0 by definition, and because 1′(P′P)⁻¹1 ≠ 1 by assumption, we conclude that $\frac{1}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}$ is always defined.

(ii) To maximize γ′Aγ subject to 1′γ = 1, we use Lagrange multipliers. Let f(γ) = γ′Aγ, and let g(γ) = 1′γ. The Lagrange function is defined as:

$$\mathrm{\Lambda }(\underset{\_}{\gamma },\lambda )=f(\underset{\_}{\gamma })+\lambda [g(\underset{\_}{\gamma })-1].$$

Denoting by 0 is a column vector of length K, we solve a system of equations for γ and λ,

$$\left(\frac{\delta \mathrm{\Lambda }(\underset{\_}{\gamma },\lambda )}{\delta \underset{\_}{\gamma }},\frac{\delta \mathrm{\Lambda }(\underset{\_}{\gamma },\lambda )}{\delta \lambda }\right)=(\underset{\_}{0},0).$$ (21)

Eq. 21 includes K equations $\delta \mathrm{\Lambda }(\underset{\_}{\gamma },\lambda )/\delta {\gamma }_k=0$ for 1 ⩽ k ⩽ K.

A is symmetric, so we have

$$\begin{gathered} \frac{\delta f(\underset{\_}{\gamma })}{\delta \underset{\_}{\gamma }}=\frac{\delta \left({\underset{\_}{\gamma }}^{\prime }A\underset{\_}{\gamma }\right)}{\delta \underset{\_}{\gamma }}=\left(A+A^{\prime }\right)\underset{\_}{\gamma }=2A\underset{\_}{\gamma } \\ \frac{\delta g(\underset{\_}{\gamma })}{\delta \underset{\_}{\gamma }}=\underset{\_}{1}. \end{gathered}$$

For the derivatives of the Lagrange function, we have:

$$\left(\frac{\delta \mathrm{\Lambda }(\underset{\_}{\gamma },\lambda )}{\delta \underset{\_}{\gamma }},\frac{\delta \mathrm{\Lambda }(\underset{\_}{\gamma },\lambda )}{\delta \lambda }\right)=\left(2A\underset{\_}{\gamma }+\lambda \underset{\_}{1},{\underset{\_}{1}}^{\prime }\underset{\_}{\gamma }-1\right).$$

Setting the derivatives with respect to γ to 0 leads to:

$$(\underset{\_}{\gamma },\lambda )=\left(-\frac{\lambda }{2}{A}^{-1}\underset{\_}{1},-\frac{2}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}\right).$$

Hence, the solution for γ is:

$${\underset{\_}{\gamma }}^{*}=\frac{A^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}.$$

Because γ′Aγ is a differentiable function of γ, its maximum on Δ^K−1 can occur either on the boundary or at a critical point. The following lemma shows that the critical point ${\underset{\_}{\gamma }}^{*}=\frac{A^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}$ is a local maximum.

Lemma 12. The critical point ${\underset{\_}{\gamma }}^{*}=\frac{A^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}$ is a local maximum of H_adm seen as a function of γ on Δ^K−1, under the conditions stated in Theorem 5.

Proof. To show that γ∗ is a local maximum, we use the second-derivative test for constrained optimization (e.g. Magnus & Neudecker, 2007, p. 155). This test considers the bordered Hessian matrix, representing the matrix of second derivatives of the Lagrange function Λ with respect to λ and the components of γ:

$$F=\left(\begin{array}{cc}\frac{{\delta }^2\mathrm{\Lambda }}{\delta {\lambda }^2}& {\left(\frac{{\delta }^2\mathrm{\Lambda }}{\delta \underset{\_}{\gamma }\delta \lambda }\right)}^{\prime }\\ \frac{{\delta }^2\mathrm{\Lambda }}{\delta \underset{\_}{\gamma }\delta \lambda }& \frac{{\delta }^2\mathrm{\Lambda }}{\delta {\underset{\_}{\gamma }}^2}\end{array}\right)=\left(\begin{array}{cc}0& {\left(\frac{\delta g}{\delta \underset{\_}{\gamma }}\right)}^{\prime }\\ \frac{\delta g}{\delta \underset{\_}{\gamma }}& \frac{{\delta }^2\mathrm{\Lambda }}{\delta {\underset{\_}{\gamma }}^2}\end{array}\right)=\left(\begin{array}{cc}0& {\underset{\_}{1}}^{\prime }\\ \underset{\_}{1}& 2A\end{array}\right).$$

We must consider the principal minors—determinants of matrices in the upper-left corner—of F. We denote the upper-left corner matrix of size r × r of F by F_r, for r = 2, 3, …, K. The principal minors are the det(F_r). Using the definition of A from eq. 11, we obtain

$$F_r=\left(\begin{array}{ccccc}0& 1& 1& \dots & 1\\ 1& 2H_1& 2C_{12}& \dots & 2C_{1r}\\ 1& 2C_{12}& 2H_2& \dots & 2C_{2r}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& 2C_{1r}& 2C_{2r}& \dots & 2H_r\end{array}\right)$$

A sufficient condition for the critical point to be a local maximum is for (−1)^r det(F_r) > 0 for each r (Magnus & Neudecker, 2007, p. 155). We now show that this condition is satisfied.

Using the fact that multiplying a row or column of a matrix by a scalar multiplies the determinant by that scalar, we multiply rows 2 through r + 1 by −1 and get

$$\det \left(F_r\right)=\det \left(\begin{array}{ccccc}0& 1& 1& \dots & 1\\ 1& 2H_1& 2C_{12}& \dots & 2C_{1r}\\ 1& 2C_{12}& 2H_2& \dots & 2C_{2r}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& 2C_{1r}& 2C_{2r}& \dots & 2H_r\end{array}\right)={(-1)}^r\text{det}\left(\begin{array}{ccccc}0& 1& 1& \dots & 1\\ -1& -2H_1& -2C_{12}& \dots & -2C_{1r}\\ -1& -2C_{12}& -2H_2& \dots & -2C_{2r}\\ ⋮& ⋮& ⋮& ⋮& \dots \\ -1& -2C_{1r}& -2C_{2r}& \dots & -2H_r\end{array}\right).$$

Using the fact that adding a multiple of a row or column to another row does not change the determinant, we add −2 times the first column to each of the remaining columns. We also multiply the first column by −1. We then have

$${(-1)}^r\det \left(F_r\right)={(-1)}^{2r+1}\det \left(\begin{array}{cc}0& \underset{\_}{1_r\prime }\\ {\underset{\_}{1}}_r& 2M_r\end{array}\right)=-\det \left(\begin{array}{cc}0& \underset{\_}{1_r\prime }\\ \underset{\_}{1_r}& 2M_r\end{array}\right),$$ (22)

where M_r is the r × r matrix consisting of the upper-left corner of matrix P′P, and $\underset{\_}{1_r}$ is the column vector of length r consisting of 1s.

We now apply a result for the determinant of partitioned matrices (Graybill, 1976, pp. 19–20). If W is invertible, then

$$\det \left(\begin{array}{cc}X& Y\\ Z& W\end{array}\right)=\det (W)\det \left(X-Y{W}^{-1}Z\right).$$

Applying this result to eq. 22, we obtain

$$\begin{gathered} {(-1)}^r\det \left(F_r\right)=-\det \left(2M_r\right)\det \left(-\underset{\_}{1_r\prime }{\left(2M_r\right)}^{-1}\underset{\_}{1_r}\right) \\ =-\left[2^r\det \left(M_r\right)\right]\left[\left(-\frac{1}{2}\right)\underset{\_}{1_r\prime }{M}_r^{-1}\underset{\_}{1_r}\right] \\ =2^{r-1}\det \left(M_r\right)\left(\underset{\_}{1_r\prime }{M}_r^{-1}{\underset{\_}{1}}_r\right). \end{gathered}$$

Because P′P is positive definite, M_r is also positive definite. To demonstrate this result, note that because x′P′Px > 0 for each nonzero column vector x, x′P′Px > 0 for each nonzero x with x_k = 0 for k > r. Because M_r is positive definite, det(M_r) > 0 and $M_r^{-1}$ is also positive definite, leading to $\underset{\_}{1_r\prime }{M}_r^{-1}{\underset{\_}{1}}_r>0$. We conclude

$${(-1)}^r\det \left(F_r\right)>0,$$

so that the critical point is the location of a local maximum. □

Concluding the proof of Theorem 5. Returning to part (iii) of the proof, following Lemma 12, if ${\underset{\_}{\gamma }}^{*}=\frac{A^{-1}1}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}$ is interior to the simplex Δ^K−1, then H_adm is maximal at γ = γ∗, with maximum $H(\underset{\_}{\gamma })=\frac{1}{{\underset{\_}{1}}^{\prime }{A}^{-1}\underset{\_}{1}}$. This value is the reciprocal of the sum of the elements of A⁻¹. If γ∗ is not interior to Δ^K−1, then the maximum lies on the boundary of Δ^K−1.

Finally, we note that ${\gamma }^{*}=\frac{{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}}{{\underset{\_}{1}}^{\prime }{\left(P^{\prime }P\right)}^{-1}\underset{\_}{1}}$ by using eq. 20. □

Proof of Corollary 6. In Theorem 5, the maximum of H_adm occurs either in the interior of the simplex Δ^K−1 or on its boundary, {γ : 1′γ = 1 and γ ∈ Δ^K−1}.

The boundary of the simplex is the union of K faces, which are themselves (K − 2)-simplices. If the maximum lies on the boundary of Δ^K−1, then without loss of generality, we can permute the labels of the source populations so that γ_K = 0.

We drop column K from matrix P and apply Theorem 5 with this new J ×(K −1) matrix, P_{{1,…,K−1}}, which has rank K − 1. By assumption, ${\underset{\_}{1}}^{\prime }{\left(P_{\{1,\dots ,K-1\}}^{\prime }{P}_{\{1,\dots ,K-1\}}\right)}^{-1}\underset{\_}{1}\ne 1$.

We then apply Theorem 5 to P_{{1,…,K−1}}. The maximum of H_adm occurs either at the point ${\gamma }_{\mathcal{S}}$, where $\mathcal{S}=\{1,2,\dots ,K-1\}$, or on the boundary of the set {γ : 1′γ = 1 and γ ∈ Δ^K−2}.

We repeat this method of descent, decrementing the dimension (and permuting population labels without loss of generality) until we reach the case of only two source populations. A final application of Theorem 5 then finds that H_adm is maximized either interior to the 1-simplex—the line connecting vertices (1, 0) and (0, 1)—or at one of these vertices. □

Appendix 2. Proofs for K = 2: Propositions 7–11

Proof of Proposition 7. We maximize the quadratic polynomial in eqs. 12–14 over γ ∈ [0, 1]. The maximum occurs at the unique critical point or on the boundary of the interval.

Setting the derivative of eq. 14 with respect to γ₁ to 0, we find that the critical point is

$$\left({\gamma }_1^{*},H_{\text{adm}}\right)=\left(\frac{C_{12}-H_2}{2\left(C_{12}-H_S\right)},\frac{C_{12}^2-H_1{H}_2}{2\left(C_{12}-H_S\right)}\right).$$ (23)

Because the leading coefficient of eq. 14 is negative for $\underset{\_}{p_1}\ne \underset{\_}{p_2}$, the critical point is a maximum. Hence, if (C₁₂ − H₂)/[2(C₁₂ − H_S)] ∈ (0, 1), then the maximum of H_adm on the interval [0, 1] lies at γ₁ = (C₁₂ − H₂)/[2(C₁₂ − H_S)]. Otherwise, the maximum lies either at γ₁ = 0, in which case it equals H₂, or at γ₁ = 1, in which case it equals H₁.

The conditions describing the location of the maximum can be written in terms of H₁, H₂, and C₁₂. Because the denominator of ${\gamma }_1^{*}$ in eq. 23 is always positive for $\underset{\_}{p_1}\ne \underset{\_}{p_2}$ (Section 4), ${\gamma }_1^{*}\in (0,1)$ becomes equivalent to C₁₂ > H₁ and C₁₂ > H₂, the former inequality arising from the condition ${\gamma }_1^{*}<1$ and the latter from the condition ${\gamma }_1^{*}>0$.

If the requirement C₁₂ > H₁ and C₁₂ > H₂ for ${\gamma }_1^{*}\in (0,1)$ fails, then the maximum occurs on the boundary of the unit interval. We have H_adm(0) = H₂ and H_adm(1) = H₁. Thus, the maximum lies at γ₁ = 0 if H₂ > H₁ and at γ₁ = 1 if H₁ > H₂.

If C₁₂ > H₁ and C₁₂ > H₂ do not both hold, then one of them must hold, as we showed in Section 4 that 2C₁₂ > H₁ + H₂. Combining the fact that either C₁₂ > H₁ or C₁₂ > H₂ holds with the observation that H₂ > H₁ leads to a maximum at γ₁ = 0 and H₁ > H₂ leads to a maximum at γ₁ = 1, we complete the characterization of the three cases.

Note that the three cases in the statement of the proposition capture all possible values of (H₁, H₂, C₁₂). By the Cauchy-Schwarz inequality, (1 − C₁₂)² ⩽ (1 − H₁)(1 − H₂), with equality requiring $\underset{\_}{p_1}=\underset{\_}{p_2}$. Hence, with $\underset{\_}{p_1}\ne \underset{\_}{p_2}$ assumed, either 1 − C₁₂ < 1 − H₁ and 1 − C₁₂ ⩾ 1 − H₂ (case (ii)), 1 − C₁₂ < 1 − H₂ and 1 − C₁₂ ⩾ 1 − H₁ (case (iii)), or both 1 − C₁₂ < 1 − H₁ and 1 − C₁₂ < 1 − H₂ (case (i)).

Alternative expressions in terms of H₁, H₂, and F₁₂ can be derived by noting that $H_S=\frac{1}{2}\left(H_1+H_2\right)$, $H_1{H}_2=H_S^2-{\left[\left(H_1-H_2\right)/2\right]}^2$ and C₁₂ = H_S(1 + F₁₂)/(1 − F₁₂), the latter simply restating eq. 4 (recalling C₁₂ = 1 for F₁₂ = 1). Thus, we have

$${\gamma }_1^{*}=\frac{C_{12}-H_2}{2\left(C_{12}-H_S\right)}=\frac{1}{2}+\frac{H_1-H_2}{4\frac{F_{12}}{1-F_{12}}\left(H_1+H_2\right)}$$ (24)

$$H_{\text{adm}}\left({\gamma }^{*}\right)=\frac{C_{12}^2-H_1{H}_2}{2\left(C_{12}-H_S\right)}=\frac{H_1+H_2}{2\left(1-F_{12}\right)}+\frac{{\left(H_1-H_2\right)}^2}{8\frac{F_{12}}{1-F_{12}}\left(H_1+H_2\right)}.$$ (25)

Another formulation uses the heterozygosity of a population formed by equal admixture of populations 1 and 2, or H_T. Because F₁₂ = 1−H_S/H_T by eq. 1, F₁₂/(1−F₁₂) = (H_T −H_S)/H_S. Using this relationship in eqs. 24 and 25,

$${\gamma }_1^{*}=\frac{1}{2}+\frac{H_1-H_2}{8\left(H_T-H_S\right)}$$

$$H_{\text{adm}}\left({\gamma }^{*}\right)=H_T+\frac{{\left(H_1-H_2\right)}^2}{16\left(H_T-H_S\right)}.$$

□

Proof of Corollary 8. Suppose H₁ ⩾ H₂. If case (i) from Proposition 7 applies, then because H_T > H_S, ${\gamma }_1^{*}⩾\frac{1}{2}$. Case (ii) cannot apply because H₁ < C₁₂, H₂ ⩾ C₁₂, and H₁ ⩾ H₂ cannot hold simultaneously. In case (iii), ${\gamma }_1^{*}=1⩾\frac{1}{2}$. For the reverse direction, if H₁ < H₂ and case (i) or case (ii) applies, then ${\gamma }_1^{*}<\frac{1}{2}$. Case (iii) cannot apply because H₁ ⩾ C₁₂, H₂ < C₁₂, and H₁ < H₂ cannot hold simultaneously. □

Proof of Corollary 9. First, we see that $H_{\text{adm}}\left({\gamma }_1^{*}\right)⩾H_T$ in case (i) of Proposition 7. In case (ii), H₂ > H_T = (H₁ + H₂ + 2C₁₂)/4 because H₂ > H₁ and H₂ ⩾ C₁₂. In case (iii), H₁ > H_T because H₁ > H₂ and H₁ ⩾ C₁₂. Note that if H₁ = H₂, then case (i) applies, producing $H_{\text{adm}}\left({\gamma }_1^{*}\right)=H_T$. □

Proof of Corollary 10. We restate the condition 0 < (C₁₂ − H₂)/[2(C₁₂ − H_S)] < 1 as

$$0<\frac{1}{2}+\frac{\left(\frac{H_1-H_2}{2}\right)}{2\frac{F_{12}}{1-F_{12}}\left(H_1+H_2\right)}<1.$$

Subtracting $\frac{1}{2}$ from both sides and multiplying by 2, an equivalent condition is

$$-1<\frac{\left(H_1-H_2\right)}{2\frac{F_{12}}{1-F_{12}}\left(H_1+H_2\right)}<1,$$

or, equivalently, $\left|H_1-H_2\right|/\left[2\frac{F_{12}}{1-F_{12}}\left(H_1+H_2\right)\right]<1$. We rearrange this last expression to obtain the desired result. □

Proof of Proposition 11. We apply Proposition 7 with J = 2. Substituting p₁₂ = 1 − p₁₁ and p₂₂ = 1 − p₂₁ in eqs. 15 and 16, we obtain C₁₂ −H₂ = (p₁₁ −p₂₁)(1−2p₂₁), C₁₂ −H₁ = (p₂₁ −p₁₁)(1−2p₁₁), C₁₂ −H_S = (p₁₁ − p₂₁)², and $C_{12}^2-H_1{H}_2={\left(p_{11}-p_{21}\right)}^2$. Thus, because p₁₁ = p₂₁ is not permitted, the quantities in eqs. 15 and 16 reduce to those of eqs. 18 and 19, respectively.

To complete the application of Proposition 7 to K = 2, note that case (i) of Proposition 7 occurs when (p₁₁ − p₂₁)(1 − 2p₂₁) > 0 and (p₂₁ − p₁₁)(1 − 2p₁₁) > 0. The first of this pair of inequalities requires both p₁₁ − p₂₁ > 0 and 1 − 2p₂₁ > 0, so that p₁₁ > p₂₁ and $\frac{1}{2}>p_{21}$, or both p₁₁ − p₂₁ < 0 and 1 − 2p₂₁ < 0, so that p₁₁ < p₂₁ and $\frac{1}{2}<p_{21}$. The second inequality requires both p₂₁ − p₁₁ > 0 and 1 − 2p₁₁ > 0, so that p₂₁ > p₁₁ and $\frac{1}{2}>p_{11}$, or both p₂₁ − p₁₁ < 0 and 1 − 2p₁₁ < 0, so that p₂₁ < p₁₁ and $\frac{1}{2}<p_{11}$. Thus, the conditions of case (i) of Proposition 7 obtain if and only if $p_{11}>\frac{1}{2}>p_{21}$ or $p_{21}>\frac{1}{2}>p_{11}$.

Similarly, using the expressions for H₁, H₂, and C₁₂ when K = 2, the conditions of case (ii) of Proposition 7 are equivalent to $\frac{1}{2}⩾p_{21}>p_{11}$ or $p_{11}>p_{21}⩾\frac{1}{2}$. The conditions of case (iii) are equivalent to $\frac{1}{2}⩾p_{11}>p_{21}$ or $p_{21}>p_{11}⩾\frac{1}{2}$. □

Appendix 3: Dirichlet model for allele frequencies

We first provide results concerning H_adm in the case that the K source populations have independently and identically distributed (IID) allele frequency vectors. Next, we specify these IID vectors to be Dirichlet distributions.

IID allele frequency vectors

We begin by examining the expected values of H_k and H_adm.

Proposition 13. Suppose the allele frequency vectors $\underset{\_}{p_k}$ are independently and identically distributed for 1 ⩽ k ⩽ K. Then $\mathbb{E}\left[H_{\text{adm}}\right]=\mathbb{E}\left[H_1\right]+\left(1-{\sum }_{k=1}^K{\gamma }_k^2\right)\left({\sum }_{j=1}^J\mathrm{Var}\left[p_{1j}\right]\right)$.

Proof. We use eq. 8:

$$\mathbb{E}\left[H_{\text{adm}}\right]=1-\sum _{k=1}^K{\gamma }_k^2\left(\sum _{j=1}^J\mathbb{E}\left[p_{kj}^2\right]\right)-2\sum _{k=1}^{K-1}\sum _{l=k+1}^K{\gamma }_k{\gamma }_{\ell }\left(\sum _{j=1}^J\mathbb{E}\left[p_{kj}{p}_{lj}\right]\right).$$

Using the IID assumption and simplifying by noting that $1={({\sum }_{k=1}^K{\gamma }_k)}^2=({\sum }_{k=1}^K{\gamma }_k^2)+(2{\sum }_{k=1}^{K-1}{\sum }_{\ell =k+1}^K{\gamma }_k{\gamma }_{\ell })$, we have

$$\begin{gathered} \mathbb{E}\left[H_{\text{adm}}\right]=1-\left(\sum _{k=1}^K{\gamma }_k^2\right)\left(\sum _{j=1}^J\mathbb{E}\left[p_{1j}^2\right]\right)-2\sum _{k=1}^{K-1}\sum _{\ell =k+1}^K{\gamma }_k{\gamma }_{\ell }\left[\sum _{j=1}^J{\left(\mathbb{E}\left[p_{1j}\right]\right)}^2\right] \\ =1-\sum _{j=1}^J\mathbb{E}\left[p_{1j}^2\right]+\sum _{j=1}^J\mathbb{E}\left[p_{1j}^2\right]\left(1-\sum _{k=1}^K{\gamma }_k^2\right)-\sum _{j=1}^J{\left(\mathbb{E}\left[p_{1j}\right]\right)}^2\left(1-\sum _{k=1}^K{\gamma }_k^2\right), \end{gathered}$$

from which the result follows. □

An immediate corollary of Proposition 13 is that H_adm has expectation greater than or equal to the expectation of the heterozygosity of each of the source populations.

Corollary 14. Suppose the allele frequency vectors $\underset{\_}{p_k}$ are independently and identically distributed for 1 ⩽ k ⩽ K. Then $\mathbb{E}\left[H_{\text{adm}}\right]⩾\mathbb{E}\left[H_k\right]$.

A second corollary results from the Cauchy-Schwarz inequality, by which ${\sum }_{k=1}^K{\gamma }_k^2⩾\frac{1}{K}$, with equality if and only if $\left({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_K\right)=\left(\frac{1}{K},\frac{1}{K},\dots ,\frac{1}{K}\right)$.

Corollary 15. Suppose the allele frequency vectors $\underset{\_}{p_k}$ are independently and identically distributed for 1 ⩽ k ⩽ K. Considering all admixture vectors $\underset{\_}{\gamma }\in {\mathrm{\Delta }}^{K-1},\mathbb{E}\left[H_{\text{adm}}\right]$ is maximized at $\underset{\_}{\gamma }=\left(\frac{1}{K},\frac{1}{K},\dots ,\frac{1}{K}\right)$, and has maximal value $\mathbb{E}\left[H_1\right]+\left(1-\frac{1}{K}\right){\sum }_{j=1}^J\mathrm{Var}\left[p_{1j}\right]$.

IID allele frequency vectors from a symmetric Dirichlet distribution

We now further assume that the independently and identically distributed allele frequency vectors follow a symmetric multivariate Dirichlet distribution. This distribution is frequently used for allele frequency distributions (Balding & Nichols, 1995; Pritchard et al., 2000; Huelsenbeck & Andolfatto, 2007), and it is a natural probability distribution to assume for allelic types with the same marginal distributions.

The J-dimensional Dirichlet-(α₁, α₂, …, α_J) distribution is defined over the open unit (J − 1)-simplex Δ^J−1 and has concentration parameters α_j > 0. The means and variances for the individual allele frequencies are (Lange, 1997; Kotz et al., 2000, chapter 49):

$$\begin{gathered} \mathbb{E}\left[p_{kj}\right]=\frac{{\alpha }_j}{J\overline{\alpha }} \\ \mathrm{Var}\left[p_{kj}\right]=\frac{{\alpha }_j\left(J\overline{\alpha }-{\alpha }_j\right)}{J^2{\overline{\alpha }}^2(J\overline{\alpha }+1)}, \end{gathered}$$

where $\overline{\alpha }=\frac{1}{J}{\sum }_{j=1}^J{\alpha }_j$.

The symmetric Dirichlet distribution assumes ${\alpha }_1={\alpha }_2=\dots ={\alpha }_J=\overline{\alpha }$, leading to:

$$\begin{gathered} \mathbb{E}\left[p_{kj}\right]=\frac{1}{J} \\ \mathrm{Var}\left[p_{kj}\right]=\frac{J-1}{J^2(J\overline{\alpha }+1)}. \end{gathered}$$

Making these substitutions in Proposition 13, we obtain the expectation of H_adm under the assumption that the allele frequency vectors follow independent Dirichlet distributions.

Corollary 16. Suppose the allele frequency vectors $\underset{\_}{p_k}$ are independently and identically distributed for 1 ⩽ k ⩽ K, all with symmetric multivariate Dirichlet distributions with concentration parameter $\overline{\alpha }$. Then

$$\begin{gathered} \mathbb{E}\left[H_k\right]=\left(1-\frac{1}{J}\right)\left(1-\frac{1}{J\overline{\alpha }+1}\right), \\ \mathbb{E}\left[H_{\text{adm}}\right]=\left(1-\frac{1}{J}\right)\left(1-\frac{1}{J\overline{\alpha }+1}\sum _{k=1}^K{\gamma }_k^2\right). \end{gathered}$$

This corollary implies that both $\mathbb{E}\left[H_k\right]$ and $\mathbb{E}\left[H_{\text{adm}}\right]$ are increasing functions of J and $\overline{\alpha }$.

The next proposition considers the special case of K = 2 and J = 2, further specifying a uniform distribution for γ₁.

Proposition 17. Consider K = 2 and J = 2. Suppose that the values of p₁₁ and p₂₁ are independently chosen from a uniform-[0,1] distribution. Suppose also that γ₁ is also chosen from a uniform-[0, 1] distribution. Then $\mathbb{P}\left[H_{\text{adm}}\left({\gamma }_1\right)>\max \left\{H_1,H_2\right\}\right]=1-\log 2\approx 0.307$.

Proof. Using Proposition 11, we identify the regions of the unit square for (p₁₁, p₂₁) in which ${\max }_{{\gamma }_1\in (0,1)}{H}_{\text{adm}}\left({\gamma }_1\right)>\max \left\{H_1,H_2\right\}$. These regions are $\left\{\left(p_{11},p_{21}\right)\mid \frac{1}{2}<p_{11}<1,0<p_{21}<\frac{1}{2}\right\}$ and $\left\{\left(p_{11},p_{21}\right)\mid 0<p_{11}<\frac{1}{2},\frac{1}{2}<p_{21}<1\right\}$.

Within those regions, we must determine the portion of the unit interval for γ₁ in which H_adm(γ₁) > max{H₁, H₂}. H_adm(γ₁) is a quadratic function of γ₁. We ignore the set of zero volume with H₁ = H₂. In the regions for (p₁₁, p₂₁) in which ${\max }_{{\gamma }_1\in (0,1)}{H}_{\text{adm}}\left({\gamma }_1\right)>\max \left\{H_1,H_2\right\}$ and H₂ > H₁, the interval for γ₁ in which $H_{\text{adm}}\left({\gamma }_1\right)>H_1$ is $\left(0,\frac{1-2p_{21}}{p_{11}-p_{21}}\right)$. In the regions for (p₁₁, p₂₁) in which $m{\mathrm{ax}}_{{\gamma }_1\in (0,1)}{H}_{\text{adm}}\left({\gamma }_1\right)>\max \left\{H_1,H_2\right\}$ and H₁ > H₂, the interval for γ₁ in which $H_{\text{adm}}\left({\gamma }_1\right)>H_1$ is $\left(\frac{p_{21}-1+p_{11}}{p_{21}-p_{11}},1\right)$.

The desired probability is the volume within the unit cube for (p₁₁, p₂₁, γ₁) of the regions in which H_adm(γ₁) > max{H₁, H₂}. The volume is

$$\begin{gathered} {\int }_{1/2}^1{\int }_{1-p_{11}}^{1/2}{\int }_0^{\frac{1-2p_{21}}{p_{11}-p_{21}}}1\text{d}{\gamma }_1\text{d}{p}_{21}\text{d}{p}_{11}+{\int }_{1/2}^1{\int }_0^{1-p_{11}}{\int }_{\frac{p_{21}-1+p_{11}}{p_{21}-p_{11}}}^{1}1\text{d}{\gamma }_1\text{d}{p}_{21}\text{d}{p}_{11} \\ {\int }_0^{1/2}{\int }_{1-p_{11}}^1{\int }_{\frac{p_{21}-1+p_{11}}{p_{21}-p_{11}}}^{1}1\text{d}{\gamma }_1\text{d}{p}_{21}\text{d}{p}_{11}+{\int }_0^{1/2}{\int }_{1/2}^{1-p_{11}}{\int }_0^{\frac{1-2p_{21}}{p_{11}-p_{21}}}1\text{d}{\gamma }_1\text{d}{p}_{21}\text{d}{p}_{11} \\ =4\frac{1-\log 2}{4}. \end{gathered}$$

□