Abstract
Estimated breeding values using best linear unbiased prediction (BLUP) through pedigree relationship can enhance selection efficiency and save time as well as resources in autotetraploid potato breeding program. Here, we used historical preliminary yield evaluation trials data of 469–619 breeding lines for tuber yield and late blight resistance to estimate heritability and BLUP based breeding values modelling auto-tetraploid inheritance in mixed model analysis. The pedigree file had a depth of 3–4 generations with total 370 individuals including 111 founders. Heritability estimates varied from 0.15 for marketable tuber yield to 0.47 for late blight resistance computed using A matrix. The prediction accuracy for total tuber yield, marketable tuber yield and late blight resistance (AUDPC) was 0.53 ± 0.02, 0.44 ± 0.02 and 0.81 ± 0.01, respectively. The prediction accuracy was highest for late blight resistance and moderate for total and marketable tuber yield. The prediction bias measured as regression of observed phenotype values on predicted values for late blight resistance was almost nil in comparison to total and marketable tuber yield. Moderate to high prediction accuracies for tuber yields and late blight resistance suggest the selection of genotypes based on EBVs in Indian potato breeding programme for higher genetic gain.
Keywords: BLUP, EBV, Heritability, Pedigree, Relationship matrix, Agronomy, Horticulture, Plant biology, Plant genetics, Phenology, Bioinformatics, Biocomputational method, Genetics
BLUP; EBV; heritability; pedigree; relationship matrix; Agronomy; Horticulture; Plant Biology; Plant Genetics; Phenology; Bioinformatics; Biocomputational Method; Genetics
1. Introduction
Selection of best individuals is a great challenge in plant breeding. The genetic gain in plant breeding using visual selection has not yielded the desired results in comparison to the results of estimated breeding values in animal breeding programmes. Use of best linear unbiased prediction (BLUP) procedure, which combines phenotypic performance and pedigree relationship is required to maximize the genetic gain in plant breeding programmes including potato. BLUP is the standard selection method in animal breeding where the breeding values of sires are estimated based on progeny performance to select superior genotypes and to breed superior families (Henderson, 1950, 1976). Recently, the method was applied in crop plants (Piepho et al., 2008) and has also been extended in clonal crops, potato (Slater et al., 2014; Ticona-Benavente and da Silva Filho, 2015) and sweet potato (Borges et al., 2010). BLUP uses mixed models with genotypes as random effect.
In animal breeding, pedigree BLUP is in practice and was recently replaced by genomic BLUP, where pedigree relationship is replaced by genomic relationship matrix of marker data (de los Campos et al., 2013). The pedigree based genetic variance-covariance matrix is replaced with genomic variance in genomic BLUP (Slater et al. 2016, 2018; Caruana et al., 2019). The basic requirement for genomic BLUP i.e. dense marker data is limited in most crops, therefore, pedigree BLUP is the most promising strategy for selection of desirable plant genotypes (Slater et al., 2014).
Potato is an important non-grain food crop of the world and is grown and consumed in almost all the countries of the World. The potato breeding programme generally uses phenotypic recurrent selection (Bradshaw and Mackay 1994) and breeding populations are developed by controlled hybridization, followed by selection pressure on progeny to reduce the population size. In the initial clonal generations, the breeding lines/clones are selected based merely on visual selection (Jansky 2009). The fewer clones are multiplied for tuber number and through assessment afterwards (Slater et al., 2014). Visual selection is ineffective in breeding as it leads to the elimination of both superior and inferior individuals and intense phenotypic selection have been found to be ineffective despite 150 years of breeding (Jansky 2009). This is because the expression of most traits is influenced by the environmental factors.
Although progeny testing and phenotypic recurrent selection have demonstrated genetic gains in potato breeding, its adoption is limited and breeding cycle is longer (Jansky 2009; Slater et al., 2014). BLUP prediction of breeding value is a standard practice in animal breeding and animal breeding programs have been benefitted from selection of best individuals based on genetic merit by use of pedigree information in the analysis (Piepho et al., 2008; Slater et al., 2014). Still, BLUP has not gained much popularity in crop breeding in India.
BLUP uses mixed linear models to calculate breeding value derived from pedigree relationships and expected genetic covariances from large datasets. BLUP takes into consideration the information from all relatives in the analysis, resulting in good accuracy, particularly for low heritability traits. It also uses more information from relatives that are more closely related to account for the degree of genotypic similarity. To implement BLUP-based breeding, the heritability values of the target traits are required. The inheritance pattern in potato is more complex than diploids due to its auto-tetraploid nature and thus the analysis must consider the relevant inheritance pattern of auto-tetraploids (Slater et al., 2014). In auto-polyploids, the multiple homologous chromosomes pair to form multivalents during meiosis and the alleles from sister chromatids can be delivered to same gamete, known as double reduction (Slater et al., 2014). Kerr et al. (2012) modified the relationship matrix, which considered this complex inheritance pattern in auto-tetraploids. The present work aims to apply BLUP EBV-based selection in auto-tetraploid potato for tuber yield and late blight resistance for enhanced genetic gain in potato breeding in India for the first time.
2. Materials and methods
Historical data of replicated preliminary yield evaluation trials conducted at Kufri, Shimla, which is a major potato breeding station for late blight resistance breeding in India, were compiled with year wise information of breeding lines evaluated in F1C4 to F1C7 generation from 2000-2018. The number of breeding lines evaluated each year varied from 18 to 56 with an average value of 33 lines per year (Table 1). The plot size varied from 3 to 5 rows of 2m each with a spacing of 60 × 20cm. The common traits observed in these trials were total tuber yield, marketable tuber yield and late blight resistance. The data were cleaned, checked for the uniformity of units and merged in a single excel file.
Table 1.
Year wise total variance for all the three traits (±s.e.).
| Year | Number of breeding lines | Total variance |
||
|---|---|---|---|---|
| Total tuber yield | Marketable tuber yield | Late blight resistance (AUDPC) | ||
| 2000 | 18 | 2355.56 ± 8.68 | 2873.88 ± 6.97 | - |
| 2001 | 19 | 2867.65 ± 9.91 | 2203.17 ± 7.96 | - |
| 2002 | 35 | 4638.53 ± 11.51 | 5141.23 ± 12.12 | - |
| 2003 | 21 | 2747.53 ± 11.44 | 2148.03 ± 10.11 | 16671.08 ± 28.18 |
| 2004 | 31 | 6570.35 ± 14.56 | 5654.12 ± 13.51 | 29828.01 ± 31.02 |
| 2005 | 29 | 3249.40 ± 10.59 | 2761.95 ± 7.79 | 109018.88 ± 61.31 |
| 2006 | 32 | 2820.61 ± 7.54 | 2196.34 ± 6.11 | 38800.84 ± 34.82 |
| 2007 | 31 | 2806.20 ± 7.63 | 2607.38 ± 7.20 | 17759.80 ± 23.94 |
| 2008 | 31 | 2870.62 ± 2.46 | 2162.30 ± 2.29 | 40949.78 ± 36.34 |
| 2009 | 46 | 4236.64 ± 9.60 | 2600.10 ± 7.52 | - |
| 2010 | 53 | 3109.14 ± 7.66 | 2439.46 ± 5.21 | 43550.97 ± 28.67 |
| 2011 | 23 | 2168.61 ± 7.13 | 2392.98 ± 4.13 | 32082.35 ± 37.35 |
| 2012 | 24 | 2852.65 ± 6.62 | 2557.59 ± 4.82 | 303460.62 ± 112.45 |
| 2013 | 32 | 2278.95 ± 8.44 | 2136.77 ± 5.96 | 90855.46 ± 53.29 |
| 2014 | 34 | 2624.60 ± 6.91 | 6486.56 ± 7.90 | 92913.52 ± 52.28 |
| 2015 | 56 | 2707.42 ± 5.52 | 2605.67 ± 3.29 | 61739.91 ± 33.20 |
| 2016 | 35 | 4238.75 ± 11.00 | 2800.66 ± 8.95 | 244382.98 ± 83.56 |
| 2017 | 35 | 4546.55 ± 11.40 | 2254.00 ± 8.02 | 256896.56 ± 85.67 |
| 2018 | 34 | 4514.90 ± 11.52 | 4045.33 ± 10.91 | 88932.38 ± 51.14 |
Total tuber yield and marketable tuber yield was recorded on plot basis and converted into quintals per hectare. Late blight resistance was recorded as AUDPC based on 3–4 readings during the season. The late blight observations were taken on weekly intervals after first appearance of symptoms till 100% disease was observed in susceptible control. The AUDPC was calculated as per the standard formula (Forbes et al., 2014). Kufri is located at an elevation of 2500 m amsl and is a hotspot for field screening of potato lines to late blight resistance. For total and marketable tuber yield, the phenotypic data of 619 entries was used, while the number was 469 for late blight resistance.
Pedigree details i.e. parents, grandparents and great grandparents of each breeding line were searched in the local pedigree database and potato pedigree database (van Berloo et al., 2007) as well as in publications i.e. Potato Journal (Indian Potato Association) and American Journal of Potato Research. The pedigree file covered 3–4 generations for most of the breeding lines except few, where the pedigree could not be traced back. There were total 370 individuals including 111 founders i.e. individuals with no parental information in the pedigree.
Pedigree based best linear unbiased prediction (ABLUP) is a model predicting breeding values using the expected relatedness among individuals (A) (Henderson 1984).
The model
| y = 1nμ + Xb + Zu + e |
was fitted to the data for all the three traits separately as explained previously by Slater et al. (2014).
y is a vector of phenotypic records
μ is the overall mean.
1n is a vector of ones
b is a vector of year effects.
X is a matrix allocating records to year effects.
Z is a matrix allocating records to breeding values
u is a vector of breeding values
e is a residual vector.
The numerator relationship matrix (A matrix or pedigree relationship matrix) was calculated as per Slater et al. (2014) considering 10 per cent double reduction.
Mixed model was used to estimate variance components (REML), predict estimated breeding values (EBV's) for each hybrid, trait and BLUP values. The heritability was calculated as h2 = [genetic variance/(genetic variance + environmental variance)].
Prediction accuracies: The predictive ability of the models was assessed using the Pearson's correlation between the observed phenotypes and EBV's, which is the prediction accuracy. Fifty breeding lines were randomly sampled as a validation set for 50 replicates, while the remaining lines were considered as training set. Year information was fitted as a fixed effect in the model. Bias was investigated as the slope of the regression of phenotypes on EBV, and scatter plot of EBVs vs observed phenotypes.
All the analyses were done in R (R Core Team, 2014) using various packages. The package “AGHmatrix” (Amadeu et al., 2016) was used for construction of A matrix, “Sommer” (Covarrubias-Pazaran 2016) was used for mixed model analysis, estimation of breeding values, BLUP values and heritability. Prediction bias was estimated using ggplot2 library and lm function and heatmap of A matrix was made using package “superheat”.
3. Results
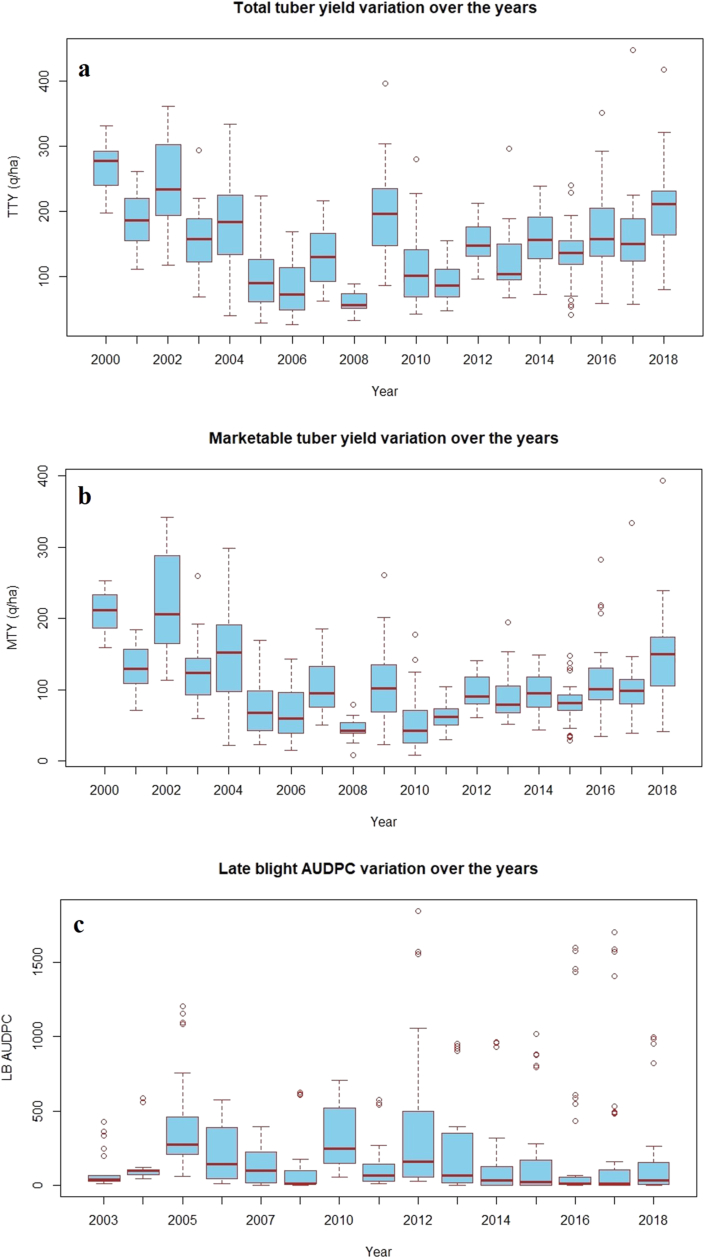
The data on all the three traits under study, i.e. total tuber yield, marketable tuber yield and late blight resistance (AUDPC) showed wide range of variation as depicted in box plots (Figure 1). Total and marketable tuber yield varied from 26.1 q/ha to 448.1 q/ha and 8.30 to 393.90 q/ha, respectively. The average total and marketable total yield was 151.3 and 105.9 q/ha (Table 2). The late blight AUDPC score values varied from 0 to 1846.25 with an average of 209.28. High standard deviation values were observed for all the three traits (Table 2). As per the values of genetic and environmental variance, the heritability estimates computed using A matrix for late blight resistance was moderate (0.47 ± 0.06), while low heritability was recorded for total (0.27 ± 0.06) and marketable tuber yield (0.15 ± 0.05) (Table 3).
Figure 1.
Variation in total tuber yield, marketable tuber yield and late blight resistance over the years a) Total tuber yield b) Marketable tuber yield c) Late blight resistance (AUDPC).
Table 2.
Basic statistics of potato breeding lines evaluated in Kufri, Shimla from 2000-2018.
| Trait | Min | Max | Mean | SD |
|---|---|---|---|---|
| Total Tuber yield (q/ha) | 26.1 | 448.1 | 151.3 | 72.4 |
| Marketable tuber yield (q/ha) | 8.30 | 393.9 | 105.9 | 62.3 |
| Late blight resistance (AUDPC) | 0 | 1846.25 | 209.28 | 323.72 |
Table 3.
Variance components and heritability estimates of different traits (±s.e.).
| Trait | σa2 | σe2 | h2 |
|---|---|---|---|
| Total Tuber yield | 1530 ± 3.10 | 4059 ± 5.05 | 0.27 ± 0.06 |
| Marketable tuber yield | 810 ± 2.26 | 4452 ± 5.29 | 0.15 ± 0.05 |
| Late blight resistance (AUDPC) | 31242 ± 16.0 | 35163 ± 16.98 | 0.47 ± 0.06 |
σa2 – genetic variance; σe2-environmental variance; h2 -Heritability.
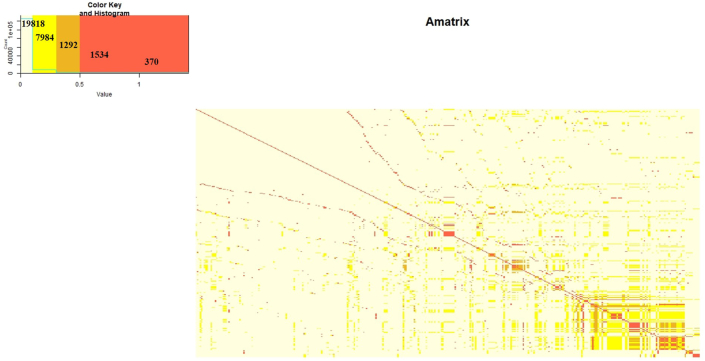
The relationship matrix prepared using pedigree relationship showed the pair wise relationship among individuals (Figure 2). The heatmap of A matrix showed that majority of the relationship was in between 0 - 0.1 (19818), followed by 0.1–0.3 (7984), 0.5–1.0 (1534), 0.3–0.5 (1292) and 1.0–1.5 (370) (Figure 2).
Figure 2.
Heatmap of pedigree relationship matrix (A matrix).
The training population size was 419 for late blight and 569 for total and marketable tuber yield (Table 4). The prediction accuracy for total tuber yield and marketable tuber yield was 0.53 ± 0.02 and 0.44 ± 0.02, respectively, while late blight resistance (AUDPC) observed high prediction accuracy of 0.81 ± 0.01. The prediction accuracy was highest for late blight resistance and moderate for total and marketable tuber yield. The average prediction accuracy was 0.59 ± 0.02 (Table 4).
Table 4.
Training population size and the prediction accuracies for traits.
| Traits | ABLUP Prediction Accuracy |
||
|---|---|---|---|
| Total records | Training population size | rebv:tbv∗ | |
| Total Tuber yield | 619 | 569 | 0.53 ± 0.02 |
| Marketable tuber yield | 619 | 569 | 0.44 ± 0.02 |
| Late blight (AUDPC) | 469 | 419 | 0.81 ± 0.01 |
| Mean | 0.59 ± 0.02 | ||
values are mean ± s.e. for 50 individuals using 50 replicates.
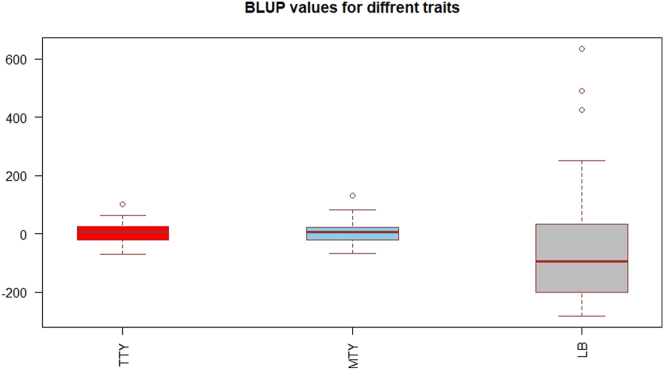
According to BLUP/EBVs for all the breeding lines, the top five lines for total and marketable tuber yield were same with one exception (Table 5, Figure 3). The top lines were SM/11–120, SM/98–106, HB/82–372, SM/93–18, SM/90–45 and SM/91–1515. Based on EBVs, the five best breeding lines for late blight resistance were SM/08–11, SM/09–91, SM/10–239, SM/10–136 and SM/08–01 (Table 5).
Table 5.
EBV/BLUP values of breeding lines for all the traits. The values are arranged in descending order for total and marketable tuber yield, while late blight resistance values were arranged in ascending order.
| Breeding line | Total tuber yield | Breeding line | Marketable tuber yield | Breeding line | Late blight resistance (AUDPC) |
|---|---|---|---|---|---|
| SM/11-120 | 99.94 | SM/11-120 | 130.70 | SM/08-11 | -282.52 |
| SM/98-106 | 61.96 | SM/98-106 | 81.51 | SM/09-91 | -280.53 |
| HB/82-372 | 50.64 | SM/91-1515 | 79.81 | SM/10-239 | -273.63 |
| SM/93-18 | 47.67 | SM/90-45 | 61.87 | SM/10-136 | -271.24 |
| SM/90-45 | 47.50 | HB/82-372 | 61.48 | SM/08-01 | -270.81 |
| SM/10-139 | 47.08 | SM/95-05 | 58.63 | SM/08-04 | -266.42 |
| SM/91-1515 | 46.51 | SM/95-188 | 57.12 | SM/10-139 | -262.74 |
| SM/92-168 | 46.03 | SM/94-38 | 51.41 | SM/10-178A | -261.05 |
| SM/08-11 | 45.76 | SM/98-239 | 50.81 | SM/10-178 | -260.88 |
| SM/93-04 | 43.13 | KS/95-124 | 50.61 | SM/09-99 | -256.61 |
| SM/10-255 | 41.81 | SM/94-44 | 43.58 | SM/10-233 | -254.60 |
| SM/94-44 | 41.45 | SM/93-04 | 43.43 | SM/08-09 | -254.36 |
| SM/08-12 | 41.39 | SM/95-32 | 42.77 | SM/09-94 | -250.29 |
| SM/94-137 | 40.81 | SM/92-168 | 42.45 | SM/09-100 | -244.82 |
| SM/94-38 | 40.71 | SM/08-04 | 42.15 | SM/09-121 | -243.49 |
| SM/09-99 | 40.28 | SM/10-255 | 41.59 | SM/09-136 | -239.72 |
| SM/08-04 | 39.82 | SM/93-237 | 40.77 | SM/08-12 | -236.68 |
| SM/94-133 | 39.26 | SM/93-18 | 40.31 | SM/10-255 | -236.40 |
| SM/93-233 | 39.20 | SM/10-178 | 40.30 | SM/09-161 | -234.33 |
| SM/10-178 | 38.48 | SM/88-343 | 39.99 | SM/09-122 | -234.04 |
| SM/10-103 | 38.11 | SM/08-11 | 38.92 | SM/09-163 | -223.55 |
| SM/09-91 | 37.09 | SM/10-103 | 36.24 | SM/09-84 | -213.96 |
| SM/05-75 | 36.93 | SM/10-139 | 35.83 | Kufri Girdhari | -211.90 |
| VMT 5-1 | 34.97 | SM/09-163 | 33.30 | SM/05-75 | -211.43 |
| SM/93-17 | 34.51 | SM/93-233 | 31.63 | SM/09-10 | -207.36 |
| SM/93-237 | 34.45 | SM/95-43 | 31.55 | SM/03-25 | -206.76 |
| SM/94-134 | 34.22 | SM/09-99 | 29.15 | SM/10-103 | -205.36 |
| SM/95-43 | 33.09 | SM/94-133 | 28.93 | SM/11-120 | -203.23 |
| SM/09-163 | 32.39 | SM/08-12 | 28.22 | SM/10-118 | -203.16 |
| SM/10-118 | 31.32 | SM/09-91 | 28.00 | SM/09-03 | -200.10 |
| SM/94-43 | 30.35 | SM/09-161 | 27.49 | LBY-2 | -199.98 |
| SM/09-121 | 30.31 | SM/93-17 | 25.87 | SM/09-123 | -198.64 |
| SM/09-161 | 29.24 | SM/94-137 | 25.46 | SM/09-24 | -195.86 |
| KS/95-124 | 29.02 | SM/05-75 | 25.28 | SM/09-14 | -195.07 |
| SM/95-188 | 28.18 | SM/09-121 | 25.19 | SM/03-23 | -194.91 |
| SM/09-123 | 27.57 | SM/10-118 | 24.92 | SM/09-01 | -192.43 |
| SM/98-239 | 27.28 | SM/96-127 | 24.44 | SM/09-33 | -192.12 |
| SM/94-11 | 26.60 | SM/03-25 | 22.89 | SM/10-164 | -184.87 |
| SM/10-239 | 25.64 | SM/09-123 | 21.87 | SM/10-102 | -183.17 |
| SM/88-343 | 24.80 | SM/09-10 | 21.70 | SM/03-32 | -179.20 |
| SM/10-178A | 23.53 | SM/98-232 | 20.94 | SM/09-141 | -175.41 |
| SM/95-05 | 23.34 | SM/94-11 | 19.13 | SM/03-45 | -175.06 |
| SM/09-10 | 22.70 | SM/94-43 | 18.35 | SM/09-153 | -173.32 |
| SM/94-31 | 21.98 | VMT 5-1 | 18.23 | SM/03-13 | -170.27 |
| SM/03-25 | 21.17 | SM/94-31 | 17.37 | SM/03-70 | -165.50 |
| KS/96-725 | 20.81 | SM/94-82 | 17.15 | SM/09-57 | -157.44 |
| SM/10-102 | 20.52 | KS/96-725 | 16.53 | SM/10-44 | -145.27 |
| SM/10-233 | 20.21 | SM/10-233 | 16.52 | SM/10-05 | -140.39 |
| SM/10-136 | 20.21 | SM/87-151 | 16.14 | SM/03-17 | -139.86 |
| SM/08-09 | 20.13 | SM/10-136 | 16.05 | SM/09-162 | -139.73 |
| SM/00-43 | 19.08 | SM/10-239 | 15.53 | SM/03-02 | -138.90 |
| SM/09-84 | 19.06 | SM/88-991 | 15.47 | SM/03-49 | -129.58 |
| SM/09-153 | 18.90 | SM/09-153 | 14.66 | SM/09-164 | -128.06 |
| SM/09-57 | 18.62 | SM/92-338 | 14.06 | VMT 5-1 | -127.81 |
| SM/92-338 | 18.34 | SM/10-164 | 12.89 | SM/01-04 | -124.50 |
| SM/09-94 | 18.31 | SM/94-134 | 12.83 | SM/10-116 | -123.89 |
| SM/10-164 | 17.96 | SM/10-178A | 12.83 | SM/03-16 | -119.23 |
| SM/05-170 | 17.57 | Kufri Himalini | 12.22 | LBY-24 | -105.92 |
| SM/96-127 | 17.54 | SM/10-102 | 12.07 | SM/00-42 | -104.66 |
| SM/09-136 | 17.02 | SM/09-136 | 11.61 | SM/01-07 | -101.91 |
| SM/94-82 | 16.15 | SM/99-13 | 10.93 | SM/02-01 | -97.41 |
| LBY-18 | 13.82 | SM/87-55 | 10.44 | SM/02-03 | -91.45 |
| SM/09-122 | 13.29 | SM/96-206 | 10.33 | SM/00-43 | -82.91 |
| SM/09-14 | 12.59 | SM/09-84 | 10.07 | SM/10-67 | -82.11 |
| Kufri Himalini | 12.56 | SM/09-57 | 9.60 | SM/00-72 | -81.51 |
| CP2379 | 12.04 | SM/09-122 | 9.03 | SM/00-191 | -81.17 |
| SM/09-164 | 11.97 | SM/08-09 | 8.59 | SM/05-170 | -79.93 |
| SM/03-23 | 11.32 | SM/09-94 | 8.55 | SM/02-02 | -69.36 |
| SM/00-42 | 11.14 | SM/08-01 | 8.50 | SM/02-07 | -66.83 |
| SM/09-100 | 10.43 | SM/09-164 | 8.49 | SM/02-04 | -66.59 |
| SM/09-03 | 10.41 | SM/05-170 | 8.13 | SM/02-06 | -57.20 |
| SM/98-232 | 10.15 | SM/09-03 | 7.42 | SM/01-03 | -57.09 |
| SM/09-162 | 10.00 | SM/03-23 | 7.33 | SM/00-120 | -53.73 |
| SM/04-20 | 9.93 | SM/00-42 | 7.31 | SM/04-20 | -48.97 |
| SM/08-01 | 9.19 | SM/00-43 | 6.64 | SM/97-50 | -45.88 |
| SM/09-33 | 8.43 | SM/09-162 | 6.48 | VMT 2-5 | -44.83 |
| SM/95-32 | 7.82 | B 4201 | 6.39 | SM/02-08 | -43.87 |
| SM/09-24 | 7.70 | LBY-18 | 6.22 | SM/01-08 | -42.41 |
| Kufri Girdhari | 7.52 | SM/04-20 | 5.80 | SM/97-203 | -33.25 |
| SM/09-01 | 7.29 | SM/09-14 | 5.27 | SM/99-56 | -18.42 |
| SM/94-62 | 5.48 | SM/94-62 | 4.32 | LBY-18 | -18.24 |
| SM/10-05 | 3.87 | SM/87-185 | 3.93 | SM/00-192 | -11.84 |
| SM/05-40 | 3.27 | SM/09-24 | 3.78 | KS/96-919 | -11.71 |
| SM/03-32 | 3.22 | SM/00-191 | 2.66 | KS/97-204 | -7.54 |
| SM/99-13 | 1.67 | Kufri Girdhari | 2.28 | KS/95-124 | -7.16 |
| SM/10-44 | 1.65 | Kufri Giriraj | 2.02 | SM/98-232 | 4.59 |
| KS/96-919 | 1.62 | SM/09-33 | 1.70 | SM/99-67 | 17.76 |
| LBY-24 | 1.06 | KS/96-919 | 0.09 | SM/98-239 | 19.86 |
| SM/94-55 | 0.88 | SM/97-243 | -0.02 | SM/05-40 | 24.63 |
| SM/99-56 | 0.69 | SM/09-100 | -0.43 | SM/98-106 | 27.01 |
| SM/00-191 | -1.25 | SM/10-05 | -1.09 | SM/95-43 | 29.79 |
| SM/96-206 | -1.31 | SM/96-103 | -2.06 | SM/99-71 | 34.55 |
| SM/03-13 | -2.15 | SM/09-01 | -2.10 | SM/00-59 | 41.37 |
| B 4201 | -3.38 | CP2379 | -2.54 | SM/96-104 | 59.62 |
| SM/09-141 | -4.56 | SM/00-120 | -2.60 | SM/98-182 | 62.57 |
| SM/00-72 | -5.44 | SM/94-55 | -3.79 | SM/97-219 | 66.15 |
| SM/03-70 | -6.61 | SM/99-56 | -3.98 | LBY-15 | 68.69 |
| SM/98-182 | -8.02 | SM/05-40 | -5.15 | SM/00-45 | 76.17 |
| SM/00-120 | -8.33 | SM/00-72 | -5.59 | SM/99-33 | 88.75 |
| SM/96-103 | -8.80 | SM/10-44 | -5.84 | KS/96-725 | 89.13 |
| SM/10-116 | -9.07 | SM/03-13 | -7.11 | Kufri Himalini | 89.19 |
| SM/88-991 | -10.02 | SM/98-182 | -8.65 | SM/00-168 | 99.08 |
| SM/03-45 | -10.24 | SM/99-42 | -9.27 | SM/99-02 | 103.72 |
| SM/03-02 | -10.47 | SM/96-145 | -11.40 | HR 9-3 | 119.36 |
| LBY-17 | -11.53 | LBY-24 | -11.89 | SM/00-44 | 121.95 |
| SM/10-67 | -12.94 | KS/96-814 | -12.47 | Kufri Shailja | 123.40 |
| LBY-15 | -13.12 | SM/09-141 | -12.69 | SM/99-11 | 132.63 |
| LBY-2 | -13.78 | SM/99-67 | -12.81 | SM/97-243 | 137.44 |
| KS/96-814 | -14.02 | SM/99-35 | -13.04 | SM/99-13 | 140.14 |
| LBY-19 | -15.85 | SM/10-67 | -13.24 | KS/96-814 | 142.79 |
| Kufri Giriraj | -16.08 | SM/99-33 | -13.82 | SM/05-25 | 157.77 |
| KS/97-204 | -16.90 | SM/10-116 | -14.08 | SM/96-127 | 172.95 |
| SM/87-151 | -17.03 | KS/97-204 | -14.11 | SM/99-42 | 175.48 |
| SM/99-35 | -17.93 | SM/03-70 | -15.07 | LBY-19 | 198.49 |
| SM/99-33 | -18.18 | SM/03-32 | -15.54 | SM/00-63 | 211.93 |
| SM/87-55 | -18.26 | SM/99-11 | -17.29 | HR 5-2 | 212.58 |
| SM/99-42 | -19.19 | SM/03-45 | -17.89 | LBY-17 | 212.90 |
| HR 2-5 | -19.76 | SM/01-07 | -20.08 | SM/00-115 | 229.88 |
| SM/97-243 | -19.89 | Kufri Jyoti | -20.50 | Kufri Giriraj | 250.62 |
| SM/99-67 | -20.21 | SM/97-219 | -21.31 | SM/00-29 | 423.93 |
| SM/97-219 | -21.19 | SM/02-01 | -22.80 | SM/00-18 | 490.21 |
| SM/96-145 | -21.55 | SM/00-192 | -22.80 | Kufri Jyoti | 635.21 |
| SM/99-71 | -21.75 | SM/97-203 | -23.61 | ||
| SM/03-17 | -23.35 | SM/03-02 | -23.65 | ||
| SM/03-16 | -24.10 | LBY-2 | -24.06 | ||
| SM/99-11 | -25.39 | LBY-17 | -24.86 | ||
| HR 9-3 | -25.62 | SM/99-71 | -25.29 | ||
| HR 5-2 | -26.20 | SM/96-104 | -26.27 | ||
| SM/87-185 | -26.28 | LBY-15 | -29.44 | ||
| SM/03-49 | -26.88 | SM/01-04 | -30.91 | ||
| SM/00-192 | -27.86 | VMT 2-5 | -31.28 | ||
| VMT 2-5 | -28.78 | SM/02-06 | -31.98 | ||
| SM/02-01 | -29.00 | SM/00-168 | -32.27 | ||
| SM/05-25 | -29.67 | SM/02-04 | -33.37 | ||
| SM/01-07 | -30.15 | SM/00-29 | -36.12 | ||
| SM/99-39 | -31.35 | LBY-19 | -36.60 | ||
| SM/02-03 | -34.64 | SM/99-39 | -37.03 | ||
| Kufri Jyoti | -34.81 | SM/00-59 | -38.08 | ||
| SM/97-203 | -34.93 | Kufri Shailja | -39.31 | ||
| SM/02-06 | -35.62 | HR 2-5 | -39.36 | ||
| SM/00-168 | -36.12 | SM/03-17 | -40.74 | ||
| SM/00-29 | -36.49 | SM/03-49 | -40.82 | ||
| SM/02-08 | -37.56 | SM/02-02 | -41.71 | ||
| SM/01-04 | -38.07 | HR 5-2 | -42.01 | ||
| SM/96-104 | -38.57 | SM/01-03 | -43.06 | ||
| SM/01-03 | -39.88 | SM/05-25 | -43.88 | ||
| SM/02-04 | -40.87 | SM/02-08 | -44.05 | ||
| SM/02-07 | -41.80 | SM/02-03 | -44.37 | ||
| SM/97-50 | -42.10 | SM/03-16 | -44.84 | ||
| SM/00-59 | -50.25 | HR 9-3 | -45.70 | ||
| SM/02-02 | -50.31 | SM/97-50 | -45.81 | ||
| SM/00-63 | -51.19 | SM/02-07 | -46.31 | ||
| SM/00-115 | -52.09 | SM/00-63 | -50.45 | ||
| SM/01-08 | -55.13 | SM/00-115 | -52.06 | ||
| SM/00-18 | -60.49 | SM/01-08 | -54.92 | ||
| Kufri Shailja | -61.06 | SM/99-02 | -55.83 | ||
| SM/00-44 | -64.42 | SM/00-18 | -58.87 | ||
| SM/99-02 | -65.79 | SM/00-44 | -61.16 | ||
| SM/00-45 | -71.19 | SM/00-45 | -68.27 |
Figure 3.
Variation in BLUP values of breeding lines for total tuber yield, marketable tuber yield and late blight resistance.
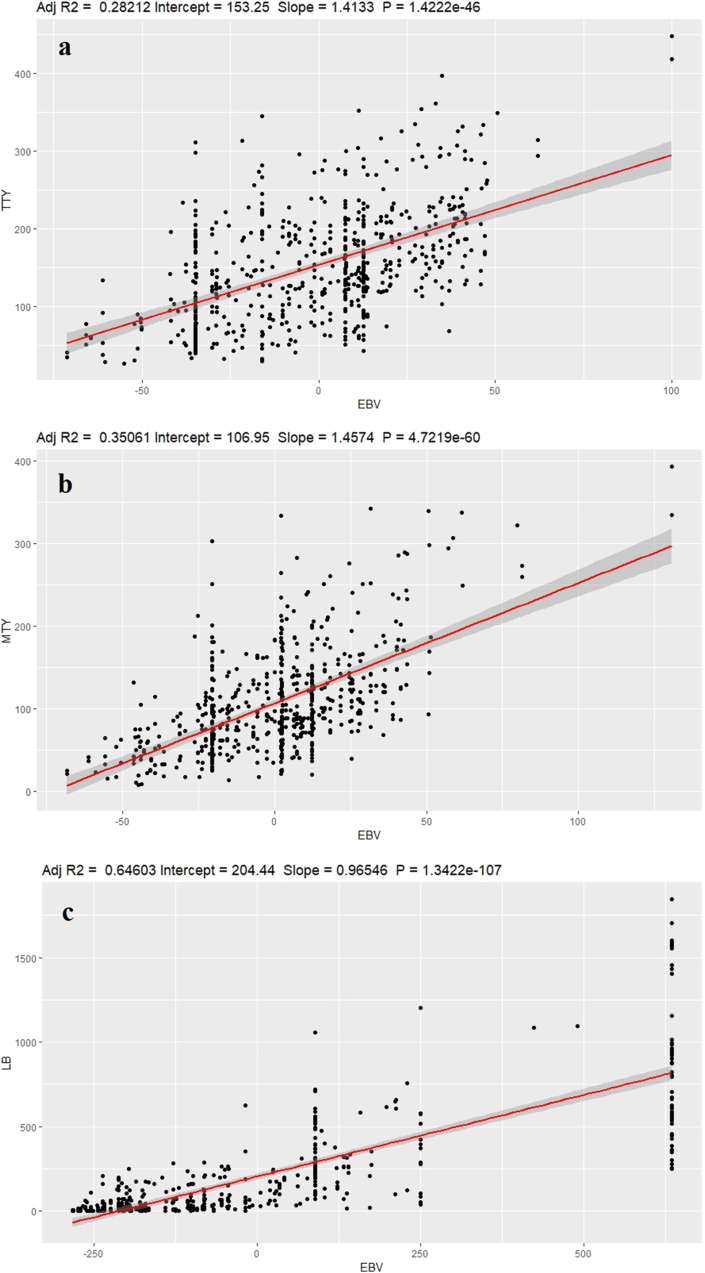
In prediction bias, the deviation from the slope of regression shows the over estimation or underestimation of EBV values in comparison to observed phenotypes. For late blight the regression coefficient was close to one (0.97 ± 0.03), while the deviation for total tuber yield (1.41 ± 0.09) and marketable tuber yield (1.46 ± 0.09) was high (Table 6). The scatter plot of EBVs and observed phenotypes also showed that EBVs are in line with observed phenotypes for late blight resistance (Figure 4). The adjusted R2 value i.e. goodness of fit of linear regression model was 0.65 for late blight resistance (AUDPC), followed by 0.35 for marketable tuber yield and 0.28 for total tuber yield (Figure 4).
Table 6.
Regression coefficients of observed phenotype values on EBVs.
| Traits | Regression coefficient∗ |
|---|---|
| Total Tuber yield | 1.41 ± 0.09 |
| Marketable tuber yield | 1.46 ± 0.08 |
| Late blight (AUDPC) | 0.97 ± 0.03 |
| Mean | 1.28 ± 0.07 |
EBVs of all the breeding lines were used for regression analysis.
Figure 4.
Regression plots of observed phenotype value over estimated breeding value for all the traits a) Total tuber yield b) Marketable tuber yield c) Late blight resistance (AUDPC).
4. Discussion
The improvement in the development of potato varieties with higher yield and resistance to late blight is evident. However, the demand is continuously increasing for further genetic progress in the future. Continuous success in selection programs depends on the use of all improvement strategies available. Selection is the process of identification of genetically superior individuals based on the phenotypic values of the individual and its relatives. Most of the economic traits in potato breeding are complex and controlled by polygenes. The conventional breeding scheme follows recurrent selection and results in slow and steady improvement. The selection based on estimated breeding values using BLUP model could result in faster genetic gains particularly for complex traits with polygenic inheritance. The pedigree details however should be accurate and complete for capturing the total variance through pedigree relationship matrix. The selections based solely on phenotype are misleading and inappropriate (Bradshaw et al., 2009). Thus, use of mixed models for estimation of breeding values of clones or parental lines through best linear unbiased prediction (BLUP) is an appropriate strategy for complex traits with low heritability as the EBVs estimate only the additive genetic effect, the genetic component that is transmitted from parents to progeny.
The breeding lines showed wide variation for all the three traits, which is a prerequisite for any selection programme in crop breeding (Machida-Hirano 2015; Bonierbale et al., 2020). The variation for total and marketable tuber yield was high in comparison to late blight resistance. The reason being all the breeding lines belong to biotic stress resistance breeding programme and have undergone rigorous selection for late blight resistance through artificial inoculation as well as field reaction in initial generations. The material under evaluation also included control varieties which vary from highly resistant to highly susceptible category. High standard deviation for all the three traits indicated that the observations are spread out from the mean value of the data.
Heritability is a key parameter in quantitative genetics because it determines the response to selection. The heritability estimates here are based on pedigree relationship using autotetraploid inheritance. Late blight resistance (AUDPC) showed moderate heritability estimate, while both the tuber yields recorded low estimates for heritability. The results are in line with the genetic control of traits i.e. late blight resistance is an oligogenic trait while yield is a highly complex trait controlled by many genes. Thus, yield has low heritability and is most affected by the environmental variations and late blight resistance is least affected. The selection will be more effective for highly heritable traits. The similar heritability estimates have been observed earlier for late blight (Enciso-Rodriguez et al., 2018). Ticona-Benavente and da Silva Filho (2015) also observed low heritability for tuber yield, while Slater et al. (2014) observed moderate heritability for tuber yield.
This study demonstrated the potential advantage of EBVs using pedigree BLUP in potato breeding for effective selection in all traits in Indian potato breeding programme. As the BLUP uses genetic information of all relatives, the estimation of breeding values is much accurate than progeny mean analysis, which uses only full sibs (Slater et al., 2014). This clearly indicates that selection based on BLUP estimated breeding values is superior to phenotypic selection, especially for low heritability traits like tuber yield. We observed high prediction accuracy for late blight and moderate prediction accuracies for total and marketable tuber yield. High prediction accuracy for late blight could be attributed to robust phenotypic data for late blight as Kufri is a hotspot for late blight occurrence and the disease appears consistently over the years without much deviation. Moreover, the heritability for late blight was moderate and the traits is governed by few genes. The high prediction accuracy for late blight resistance indicates that the estimated breeding values could be used for late blight resistance breeding for selection of resistant genotypes in breeding programme. Although, the training population size was large for total and marketable tuber yield compared to late blight resistance (Table 4), the predictions for tuber yields were moderate. Yield is a complex trait highly influenced by environmental variations. We too observed low heritability and high yearly yield variations for the breeding lines. Although the yield predictions were good for selection of genotypes, a further increase in the training population size of breeding lines could enhance the yield predictions i.e. estimating breeding values. The BLUP values for all the breeding lines were in agreement to the observed phenotype value for all the three traits.
The predictions are also affected by relationship of the individuals in the pedigree which could be observed in the heatmap of A matrix (Figure 2). The prediction accuracy in general increases with the increase in relationships in the matrix. In our pedigree relationship matrix i.e. A matrix (370 × 370), the relationship was observed in 30,628 pairs, while no relationship was found in 105902 pairs. In potato, out of 4,397 cultivars cultivated worldwide, 14.9% have been bred from 15 genotypes (Li et al., 2018), which indicate that common parents have been used in potato breeding across the globe. Therefore, increasing the depth of pedigree could increase the relationship in the matrix, which can capture all the genetic variance for the traits under study.
The regression coefficients for EBV indicated no bias for late blight resistance and high bias for tuber yields based on deviation of regression slope from one. Similar regression coefficients were reported in earlier studies (Sverrisdóttir et al., 2017; Caruana et al., 2019). The scatter plots of EBVs and observed phenotypes also revealed the same results for prediction bias (Figure 4). In general, high adjusted R2 value indicate good fit of the model i.e. smaller differences between the observed data and the fitted values. This can be seen in the late blight resistance plot where the differences between observed phenotype values and EBVs were lower, hence the adjusted R2 value was high. However, total and marketable tuber yield plots had low adjusted R2 values and the residual plots also showed large differences between observed phenotype value and EBVs (Figure 4). The higher R2 values does not always indicate good fit of the model and a good model can have low R2 values also. Similarly, when the variances (scales) for the two variables are different, we don't get 1.0 slope for no bias.
There is a remarkable progress and success of BLUP in animal breeding, which has led to high genetic gains, and consequently resulted in the adoption of methodology in crop plants too (Piepho et al., 2008; Slater et al., 2014). The BLUP analysis provides an individual estimate of EBV for all the lines, the superior lines can therefore be identified from low scoring families also (Molenaar et al., 2018). The BLUP based estimation of breeding values for individuals across multiple traits could also be used to generate a selection index for selection of superior individuals for all the traits together (Xu et al., 2012). We expect the replication of similar results in our potato breeding programme. Our results showed that selection of breeding lines based on EBVs will be more efficient than observed phenotypic values to maximize the genetic gain in potato breeding in India. Moreover, it will save the additional resources required for tuber multiplication and phenotyping large number of breeding clones to select the best lines. However, maintaining accurate and extensive pedigree records for devising relationship matrix to estimate EBVs is an important activity in breeding programs. Nonetheless, the more accurate and efficient approach is DNA markers based genetic relatedness to implement genomic selection (Heffner et al., 2010; Crossa et al., 2010). Pedigree based EBVs could be the most effective breeding strategy until genomic selection can be routinely implemented. Decisions about parent selection based on EBVs and GEBVs will ultimately enable new, improved high yielding disease resistant potato varieties in India.
Declarations
Author contribution statement
Salej Sood: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Vinay Bhardwaj: Performed the experiments; Contributed reagents, materials, analysis tools or data.
Surinder Kumar Kaushik, Sanjeev Sharma: Performed the experiments.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data included in article/supplementary material/referenced in article.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
We are thankful to Director, ICAR-CPRI, Shimla for facilitation during the course of study. Thanks are also due to Sh. Naresh Thakur and Ranjesh Bhardwaj for field maintenance of trials.
References
- Amadeu R.R., Cellon C., Olmstead J.W., Garcia A.A.F., Resende M.F.R., Muñoz P.R. AGHmatrix: R package to construct relationship matrices for autotetraploid and diploid species: a blueberry example. Plant Genome. 2016;9:1–10. doi: 10.3835/plantgenome2016.01.0009. [DOI] [PubMed] [Google Scholar]
- Bonierbale M.W., Amoros W.R., Salas E., de Jong W. Potato breeding. In: Campos H., Ortiz O., editors. The Potato Crop. Springer; Cham: 2020. pp. 163–217. [Google Scholar]
- Borges V., Ferreira P.V., Soares L., Santos G.M., Santos A.M.M. Seleção de clones de batata-doce pelo procedimento REML/BLUP. Acta Sci. Agron. 2010;32:643–649. [Google Scholar]
- Bradshaw J.E., Dale M.F.B., Mackay G.R. Improving the yield, processing quality and disease and pest resistance of potatoes by genotypic recurrent selection. Euphytica. 2009;170(1):215–227. [Google Scholar]
- Bradshaw J.E., Mackay G.R. Breeding strategies for clonally propagated potatoes. In: Bradshaw J.E., Mackay G.R., editors. Potato Genetics. Cab International; Wallingford: 1994. pp. 467–497. [Google Scholar]
- Caruana B.M., Pembleton L.W., Constable F., Rodoni B., Slater A.T., Cogan N.O.I. Validation of genotyping by sequencing using transcriptomics for diversity and application of genomic selection in tetraploid potato. Front. Plant Sci. 2019;10:670. doi: 10.3389/fpls.2019.00670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covarrubias-Pazaran G. Genome-assisted prediction of quantitative traits using the R package sommer. PloS One. 2016;11 doi: 10.1371/journal.pone.0156744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J., de los Campos G., Perez P., Gianola D., Burgueno J., Araus J.L. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics. 2010;186:713–724. doi: 10.1534/genetics.110.118521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G., Hickey J.M., Pong-Wong R., Daetwyler H.D., Calus M.P.L. Whole-Genome regression and prediction methods applied to plant and animal breeding. Genetics. 2013;193:327–345. doi: 10.1534/genetics.112.143313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enciso-Rodriguez F., Douches D., Lopez-Cruz M., Coombs J., de los Campos G. Genomic selection for late blight and common scab resistance in tetraploid potato (Solanum tuberosum) G3. 2018;8:2471–2481. doi: 10.1534/g3.118.200273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forbes G., Pérez W., Andrade Piedra J. International Potato Center (CIP); 2014. Field Assessment of Resistance in Potato to Phytophthora Infestans. Lima (Peru) p. 35. [Google Scholar]
- Heffner E.L., Lorenz A.J., Jannink J.L., Sorrells M.E. Plant breeding with genomic selection: gain per unit time and cost. Crop Sci. 2010;50:1681–1690. [Google Scholar]
- Henderson C.R. Estimation of genetic parameters. Ann. Math. Stat. 1950;21:309–310. [Google Scholar]
- Henderson C.R. University of Guelph; Guelph: 1984. Applications of Linear Models in Animal Breeding. [Google Scholar]
- Henderson C.R. A simple method for computing the inverse of a numerator relationship matrix used in prediction of breeding values. Biometrics. 1976;32:69–83. [Google Scholar]
- Jansky S. Breeding, genetics and cultivar development. In: Singh J., Kaur L., editors. Advances in Potato Chemistry and Technology. Academic Press; New York: 2009. pp. 27–62. [Google Scholar]
- Kerr R., Li L., Tier B., Dutkowski G., McRae T. Use of the numerator relationship matrix in genetic analysis of autopolyploid species. Theor. Appl. Genet. 2012;124:1271–1282. doi: 10.1007/s00122-012-1785-y. [DOI] [PubMed] [Google Scholar]
- Li X., Xu J., Duan S., Bian C., Hu J., Shen H., Li G., Jin L. Pedigree-based deciphering of genome-wide conserved patterns in an elite potato parental line. Front. Plant Sci. 2018;9:690. doi: 10.3389/fpls.2018.00690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machida-Hirano R. Diversity of potato genetic resources. Breed Sci. 2015;65(1):26–40. doi: 10.1270/jsbbs.65.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molenaar H., Boehm R., Piepho H.P. Phenotypic selection in ornamental breeding: it's better to have the BLUPs than to have the BLUEs. Front. Plant Sci. 2018;9:1511. doi: 10.3389/fpls.2018.01511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piepho H., Möhring J., Melchinger A., Büchse A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica. 2008;161:209–228. [Google Scholar]
- R Core Team . R Foundation for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2014. R: A Language and Environment for Statistical Computing.http://www.R-project.org/ [Google Scholar]
- Slater A.T., Wilson G.M., Cogan N.O., Forster J.W., Hayes B.J. Improving the analysis of low heritability complex traits for enhanced genetic gain in potato. Theor. Appl. Genet. 2014;127:809–820. doi: 10.1007/s00122-013-2258-7. [DOI] [PubMed] [Google Scholar]
- Slater A.T., Cogan N.O.I., Rodoni B.C., Daetwyler H.D., Hayes B.J., Caruana B. Breeding differently - the digital revolution: high-throughput phenotyping and genotyping. Potato Res. 2018;60:337–352. [Google Scholar]
- Slater A.T., Cogan N.O.I., Forster J.W., Hayes B.J., Daetwyler H.D. Improving genetic gain with genomic selection in autotetraploid potato. Plant Genome. 2016 doi: 10.3835/plantgenome2016.02.0021. [DOI] [PubMed] [Google Scholar]
- Sverrisdóttir E., Byrne S., Sundmark H.E.R., Johnsen H.O., Kirk H.G., Asp T., Janss L., Nielsen K.L. Genomic prediction of starch content and chipping quality in tetraploid potato using genotyping-by-sequencing. Theor. Appl. Genet. 2017;130:2091–2108. doi: 10.1007/s00122-017-2944-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ticona-Benavente C.A., da Silva Filho D.F. Comparison of BLUE and BLUP/REML in the selection of clones and families of potato (Solanum tuberosum) Genet. Mol. Res. 2015;14(4):18421–18430. doi: 10.4238/2015.December.23.30. [DOI] [PubMed] [Google Scholar]
- van Berloo R., Hutten R., van Eck H., Visser R. An online potato pedigree database resource. Potato Res. 2007;50:45–57. [Google Scholar]
- Xu Y., Lu Y., Xie C., Gao S., Wan J., Prasanna B. Whole-genome strategies for marker-assisted plant breeding. Mol. Breed. 2012;29:833–854. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supplementary material/referenced in article.