Cartilage Segmentation in High-Resolution 3D Micro-CT Images via Uncertainty-Guided Self-training with Very Sparse Annotation

Abstract

Craniofacial syndromes often involve skeletal defects of the head. Studying the development of the chondrocranium (the part of the endoskeleton that protects the brain and other sense organs) is crucial to understanding genotype-phenotype relationships and early detection of skeletal malformation. Our goal is to segment craniofacial cartilages in 3D micro-CT images of embryonic mice stained with phosphotungstic acid. However, due to high image resolution, complex object structures, and low contrast, delineating fine-grained structures in these images is very challenging, even manually. Specifically, only experts can differentiate cartilages, and it is unrealistic to manually label whole volumes for deep learning model training. We propose a new framework to progressively segment cartilages in high-resolution 3D micro-CT images using extremely sparse annotation (e.g., annotating only a few selected slices in a volume). Our model consists of a lightweight fully convolutional network (FCN) to accelerate the training speed and generate pseudo labels (PLs) for unlabeled slices. Meanwhile, we take into account the reliability of PLs using a bootstrap ensemble based uncertainty quantification method. Further, our framework gradually learns from the PLs with the guidance of the uncertainty estimation via self-training. Experiments show that our method achieves high segmentation accuracy compared to prior arts and obtains performance gains by iterative self-training.

1. Introduction

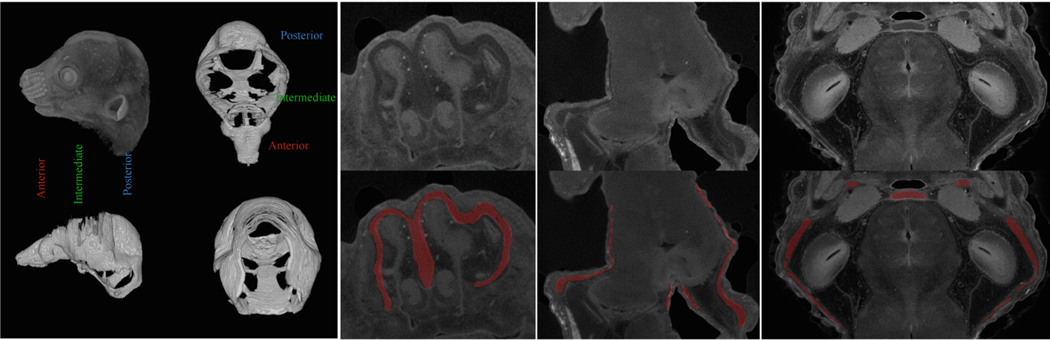
Approximately 1% of babies born with congenital anomalies have syndromes including skull abnormalities [13]. Anomalies of the skull invariably require treatments and care, imposing high financial and emotional burdens on patients and their families. Although prenatal development data are not available for study in humans, the deep conservation of mammalian developmental systems in evolution means that laboratory mice give access to embryonic tissues that can reveal critical molecular and structural components of early skull development [3, 18]. The precise delineation of 3D chondrocranial anatomy is fundamental to understanding dermatocranium development, provides important information to the pathophysiology of numerous craniofacial anomalies, and reveals potential avenues for developing novel therapeutics. An embryonic mouse is tiny (∼2 cm³), and thus we dissect and reconstruct the chondrocranium from 3D micro-computed tomography (micro-CT) images of specially stained mice. However, delineating fine-grained cartilaginous structures in these images is very challenging, even manually (e.g., see Fig. 1).

Fig. 1.

Examples of micro-CT images of stained mice. (a) A raw 3D image and its manual annotation. The shape variations are large: the front nasal cartilage is relatively small (i.e., 300²); the cranial vault is very big (i.e., 900 × 500) but extremely thin like a half-ellipsoid surface. (b) A 2D slice from the nasal cartilage (top) and its associated label (bottom); the image contrast is low and there are many hard mimics in surrounding areas. (c) Two 2D slices from the cranial vault (top) and their associated labels (bottom); the cartilage is very thin. Best viewed in color.

Although deep learning has achieved great success in biomedical image segmentation [11, 12, 19, 20, 22], there are three main challenges when applying existing methods to cartilage segmentation in our high-resolution micro-CT images. (1) The topology variations of craniofacial cartilages are very large in the anterior, intermediate, and posterior of the skull (as shown in Fig. 1(a)). Known methods for segmenting articular cartilages in knees [2, 17] only deal with relatively homogeneous structures. (2) Such methods deal with images of much lower resolutions (e.g., 200×512²), and simple scaling-up would precipitate huge computation requirements. Micro-CT scanners work at the level of one micron (i.e., 1μm), and a typical scan of ours is of size 1500×2000². In Fig. 1(c), the cropped sub-region is of size 400², and the region-of-interest (ROI) is only 5 pixels thick. (3) More importantly, only experts can differentiate cartilages, and it is unrealistic to manually label whole volumes for training fully convolution networks (FCNs) [12]. While some semi-supervised methods [21, 23] were studied very recently, how to acquire and make the most out of very sparse annotation is seldom explored, especially for real-world complex cartilage segmentation tasks.

To address these challenges, we propose a new framework that utilizes FCNs and uncertainty-guided self-training to gradually boost the segmentation accuracy. We start with extremely sparsely annotated 2D slices and train an FCN to predict pseudo labels (PLs) for unseen slices in the training volumes and the associated uncertainty map, which quantifies pixelwise prediction confidence. Guided by the uncertainty, we iteratively train the FCN with PLs and improve the generalization ability of FCN in unseen volumes. Although the above process seems straightforward, we must overcome three difficulties. (1) The FCN should have a sufficiently large receptive field to accommodate such high-resolution images yet needs to be lightweight for efficient training and inference due to the large volumes. (2) Bayesian-based uncertainty quantification requires a linear increase of either space or time during inference. We integrate FCNs into a bootstrap ensemble based uncertainty quantification scheme and devise a K-head FCN to balance efficiency and efficacy. (3) The generated PLs contain noises. We consider the quality of PLs and propose an uncertainty-guided self-training scheme to further refine segmentation results.

Experiments show that our proposed framework achieves an average Dice of 78.98% in segmentation compared to prior arts and obtains performance gains by iterative self-training (from 78.98% to 83.16%).

2. Method

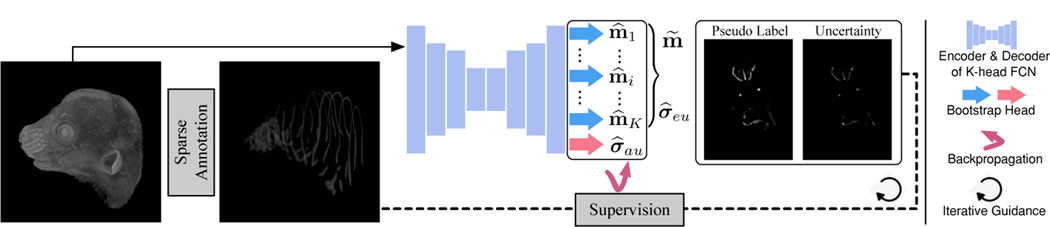
As shown in Fig. 2, our proposed framework contains a new FCN, which can generate PLs and uncertainty estimation at the same time, and an iterative uncertainty-guided self-training strategy to boost the segmentation results.

Fig. 2.

An overview of our proposed framework.

2.1. K-Head FCN

Initial Labeling and PL Generation.

We consider two sets of 3D data, $\mathcal{A}={\left\{{\mathcal{A}}_i\right\}}_{i=1}^L$ and $\mathcal{B}={\left\{{\mathcal{B}}_i\right\}}_{i=1}^U$, for training and testing respectively, where each ${\mathcal{A}}_i$ (or ${\mathcal{B}}_i$) is a 3D volume and L (or U) is the number of volumes in $\mathcal{A}$ (or $\mathcal{B}$). Each 3D volume can be viewed as a series of 2D slices, i.e., ${\mathcal{A}}_i={\{{\mathbf{A}}_i^j\}}_{j=1}^{i_Q}$, where i_Q is the number of slices in ${\mathcal{A}}_i$. To begin with, experts chose representative slices in each ${\mathcal{A}}_i$ from the anterior, intermediate, and posterior of the skull and annotated them at the pixel level. Due to the high resolution of our micro-CT images, the annotation ratio is rather sparse (e.g., 25 out of 1600 slices). Thus, each ${\mathcal{A}}_i$ can be divided into two subsets $\mathcal{A}{l}_i={\{{\mathbf{\text{l}}}_i^j\}}_{j=1}^{i_P}$ and $\mathcal{A}{u}_i={\{{\mathbf{u}}_i^j\}}_{j=1}^{i_R}$, where each slice ${\mathbf{\text{l}}}_i^j$ has its associate label ${\mathbf{m}}_i^j$, and i_Q > i_R ≫ i_P. Conventionally, using such sparse annotation, a trained FCN lacks generalization ability to the unseen volumes B. Hence, a key challenge is how to make the most out of the labeled slices. We will show that an FCN can delineate ROIs in unseen slices of the training volumes (i.e., $\mathcal{A}{u}_i$) with very sparsely labeled slices. For this, we propose to utilize these true labels (TLs) and generate PLs to expand the training data.

Uncertainty Quantification.

Since FCN here is not trained by standard protocol, its predictions may be unreliable and noisy. Thus, we need to consider the reliability of the PLs (which may otherwise lead to meaningless guidance). Bayesian methods [7] provided a straightforward way to measure uncertainty quantitatively by utilizing Monte Carlo sampling in forward propagation to generate multiple predictions. Prohibitively, the computational cost grows linearly (either time or space). Since our data are large volumes, such cost is unbearable. To avoid this issue, we need to design a method that is both time- and space-efficient. Below we illustrate how to design a new FCN for this purpose.

There are two main types of uncertainty in Bayesian modelling [8, 16]: epistemic uncertainty captures uncertainty in the model (i.e., the model parameters are poorly determined due to the lack of data/knowledge); aleatoric uncertainty captures genuine stochasticity in the data (e.g., inherent noises). Without loss of generality, let f_θ(x) be the output of a neural network, where θ is the parameters and x is the input. For segmentation tasks, following the practice in [8], we define pixelwise likelihood by squashing the model output through a softmax function $S:p\left(y\mid f_{\theta }(x),{\sigma }^2\right)=S\left(\frac{1}{{\sigma }^2}{f}_{\theta }(x)\right)$. The magnitude of σ determines how ‘uniform’ (flat) the discrete distribution is. The log likelihood for the output is: $\log \left(p\left(y=c\mid f_{\theta }(x),{\sigma }^2\right)\right)=\frac{1}{{\sigma }^2}{f}_{\theta }^c(x)-\log {\sum }_{c^{\prime }}\exp \left(\frac{1}{{\sigma }^2}{f}_{\theta }^{c^{\prime }}(x)\right)=\frac{1}{{\sigma }^2}\log \frac{\exp \left(f_{\theta }^c(x)\right)}{{\sum }_{c^{\prime }}\exp \left(f_{\theta }^{c^{\prime }}(x)\right)}-\log \frac{{\sum }_{c^{\prime }}\exp \left(\frac{1}{{\sigma }^2}{f}_{\theta }^{c^{\prime }}(x)\right)}{{\left({\sum }_{c^{\prime }}\exp \left(f_{\theta }^{c^{\prime }}(x)\right)\right)}^{\frac{1}{{\sigma }^2}}}\approx \frac{1}{{\sigma }^2}\log S{\left(f_{\theta }(x)\right)}^c-\frac{1}{2}\log {\sigma }^2$, where $f_{\theta }^c(x)$ is the c-th class of output f_θ(x), and we use the explicit simplifying assumption ${\left({\sum }_{c^{\prime }}\exp \left(f_{\theta }^{c^{\prime }}(x)\right)\right)}^{\frac{1}{{\sigma }^2}}\approx \frac{1}{\sigma }{\sum }_{c^{\prime }}\exp \left(\frac{1}{{\sigma }^2}{f}_{\theta }^{c^{\prime }}(x)\right)$. The objective is to minimize the loss given by the negative log likelihood:

$${\mathcal{L}}_{UC}\left(\theta ,{\sigma }^2\right)=-\frac{1}{N}\sum _i^N\sum _m^M{\mathbb{1}}_{m=c}\log \left(p\left(y_i=c\mid f_{\theta }\left(x_i\right),{\sigma }^2\right)\right),$$ (1)

where N is the number of training samples and ${\mathbb{1}}_{m=c}$ is the one-hot vector of class c. In practice, we make the network predict the log variance s := logσ² for numerical stability. Now, the aleatoric uncertainty is estimated by e^−s, and we can quantify the epistemic uncertainty by the predictive variance by $\frac{1}{K}{\sum }_k^K{\widehat{y}}_k^2-{\left(\frac{1}{K}{\sum }_k^K{\widehat{y}}_k\right)}^2$, where ${\widehat{y}}_k$ = f_θ(x) is the k-th sample from the output distribution.

K-Head FCN.

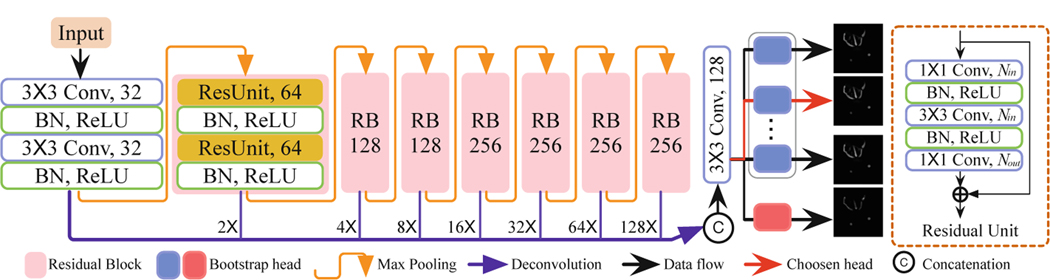
To sample K samples from the output distribution, we adopt the bootstrap method into the FCN design. A naïve way would be to maintain a set of K networks ${\{f_{{\theta }_k}\}}_{k=1}^K$ independently on K different bootstrapped subsets $(\text{i.e.},{\{D_k\}}_{k=1}^K)$ of the whole dataset D and treat each network $f_{{\theta }_k}$ as independent samples from the weight distribution. However, it is computationally expensive, especially when each neural net is large and deep. Hence, we propose a single network that consists of a shared backbone architecture with K lightweight bootstrapped heads branching on/off independently. The shared network learns a joint feature representation across all the data, while each head is trained only on its bootstrapped sub-sample of the data. The training and inference of this type of bootstrap can be conducted in a single forward/backward pass, thus saving both time and space. Besides, in contrast to previous methods where σ² is assumed to be constant for all inputs, we estimate it directly as an output of the network [7, 16]. Thus, our proposed network consists of a total of K + 1 branches—K heads corresponding to the segmentation prediction map and an extra head corresponding to σ². In all the experiments, K is set as 5, and the input image size is 512 × 512.

Figure 3 shows the detailed structure of our new K-head FCN. There are 7 residual blocks (RBs) and max-pooling operations in the encoding-path to deliver larger reception fields, each RB containing 2 cascaded residual units as in ResNet [6]. To save parameters, we maintain the number of channels in each residual unit and a similar number of feature channels at the last 4 scales. Rich contextual and semantic information is extracted in shallower and deeper scales in the encoding-path and is up-sampled to maintain the same size for the input and output and then concatenated to generate the final prediction. The output layer splits near the end of the model for two reasons: (1) ease the training difficulty and improve the convergence speed; (2) incur minimal computation resource increases (both time and space) in training and inference. To train the network, we randomly choose one head in each iteration and compute the cross-entropy loss ${\mathcal{L}}_{CE}$. It is combined with the uncertainty loss ${\mathcal{L}}_{UC}$ to update the parameters in the chosen head branch and the shared backbone only (i.e., freezing the other K − 1 head branches). Specifically, $\mathcal{L}$ = ${\mathcal{L}}_{CE}$ + 0.04${\mathcal{L}}_{UC}$.

Fig. 3.

The network architecture of our proposed method, K-head FCN. The output layer branches out to K bootstrap heads and an extra log-variance output.

2.2. Iterative Uncertainty-Guided Self-Training

Since both $\mathcal{A}{l}_i$ and $\mathcal{A}{u}_i$ come from the same volume ${\mathcal{A}}_i$ and are based on the assumption that the manifolds of the seen/unseen slices (of ${\mathcal{A}}_i$) are smooth in high dimensions [15], our generated PLs bridge the annotation gap. However, the K predictions, ${\{{\widehat{\mathbf{m}}}_i^{j,k}\}}_{k=1}^K$, obtained from the output distribution for each ${\mathbf{u}}_i^j\in \mathcal{A}{u}_i$ could be unreliable and noisy. Thus, we propose an uncertainty-guided scheme to reweight PLs and rule out unreliable (highly uncertain) pixels in subsequent training. Specifically, we calculate the voxel-level cross-entropy loss weighted by the epistemic uncertainty ${\mathit{\sigma }}_i^j$ for ${\mathbf{u}}_i^j:{\mathcal{L}}_{CE}({\overline{\mathbf{m}}}_i^j,{\tilde{\mathbf{m}}}_i^j)=\frac{\sum _v{e}^{-{\sigma }_v}{\mathcal{L}}_{ce}({\overline{m}}_v,{\tilde{m}}_v)}{\sum _v{e}^{-{\sigma }_v}}$, where ${\overline{\mathbf{m}}}_i^j$ is the prediction at the current iteration and ${\tilde{\mathbf{m}}}_i^j={{\sum }_{k=1}^K\widehat{\mathbf{m}}}_i^{j,k};{\overline{m}}_v$ and ${\tilde{m}}_v$ are the values of the v-th pixel (for simplicity, we omit i and j); σ_v is the sum of normalized epistemic and aleatoric uncertainties at the v-th pixel; ${\mathcal{L}}_{ce}$ is the cross-entropy error at each pixel. Note that we do not choose a hard threshold to convert the average probability map ${\tilde{\mathbf{m}}}_i^j$ to a binary mask, as inspired by the “label smoothing” technique [14] which may help prevent the network from becoming over-confident and improve generalization ability.

With the expansion of the training set (TLs ∪ PLs), our FCN can distill more knowledge about the data (e.g., topological structure, intensity variances), thus becoming more robust and generalizing better to unseen data $\mathcal{B}$. However, due to the extreme sparsity of annotation at the very beginning, not all the generated PLs are evenly used (i.e., highly uncertain and assigned with low weights). Hence, we propose to conduct this process iteratively.

Overall, with our iterative uncertainty-guided self-training scheme, we can further refine the PLs and FCN at the same time. In practice, it needs 2 or 3 rounds, but we do not have to train from scratch, incurring not too much cost.

3. Experiments and Results

Data Acquisition.

Mice were produced, sacrificed, and processed in compliance with animal welfare guidelines approved by the Pennsylvania State University (PSU). Embryos were stained with phosphotungstic acid (PTA), as described in [10]. Data were acquired by the PSU Center for Quantitative Imaging using the General Electric v|tom|x L300 nano/micro-CT system with a 180-kV nanofocus tube and were then reconstructed into micro-CT volumes with a resulting average voxel size of 5μm and volume size of 1500 × 2000². Seven volumes are divided into the training set $\mathcal{A}={\{{\mathcal{A}}_i\}}_{i=1}^4$ and test set $\mathcal{B}={\{{\mathcal{B}}_i\}}_{i=1}^3$. Only a very small subset of slices in each ${\mathcal{A}}_i$ is labeled for training (denoted as $\mathcal{A}{l}_i$) and the rest unseen slices $\mathcal{A}{u}_i$ and $\mathcal{B}$ are used for the test. Four scientists with extensive experience in the study of embryonic bones/cartilages were involved in image annotations. They first annotated slices in the 2D plane and then refined the whole annotation by considering 3D information of the neighboring slices.

Evaluation.

In the 3D image regions not considered by the experts, we select 11 3D subregions (7 from $\mathcal{B}$ and 4 from $\mathcal{A}{u}_i$), each of an average size 30×300² and containing at least one piece of cartilages. These subregions are chosen for their representativeness, i.e., they cover all the typical types of cartilages (e.g., nasal capsule, Meckel’s cartilage, lateral wall, braincase floor, etc). Each subregion is manually labeled by experts as ground truth. The segmentation accuracy is measured by Dice-Sørensen Coefficient (DSC).

Implementation Details.

All our networks are implemented with TensorFlow [1], initialized by the strategy in [5], and trained with the Adam optimizer [9] (with β₁ = 0.9, β₂ = 0.999, and ϵ = 1e-10). We adopt the “poly” learning rate policy $L_r\times {\left(1-\frac{iter}{\#iter}\right)}^{0.9}$, where the initial rate L_r = 5e-4 and the max iteration number is set as 60k. To leverage the limited training data and reduce overfitting, we augment the training data with standard operations (e.g., random crop, flip, rotation in 90°, 180°, and 270°). Due to large intensity variance among different images, all images are normalized to have zero mean and unit variance.

Main Results.

The results are summarized in Table 1. To our best knowledge, there is no directly related work on cartilage segmentation from embryonic tissues. We compare our new framework with the following methods. (1) A previous work which utilizes U-Net [19] to automatically segment knee cartilages [2]. We also try another robust FCN model DCN [4]. For a fair comparison, we scale up U-Net [19] and DCN [4] to accommodate images of size 512² as input and match with the number of parameters of our K-head FCN (denoted as U-Net* and DCN*). (2) A semi-supervised method that generates PLs and conducts self-training (i.e., 1-head FCN-R3).

Table 1.

Segmentation results. Top: DSC (%) comparison of cartilages in the anterior, intermediate, and posterior skull, w/annotation ratio of 3.0%. TL: true labels; PL: pseudo labels. Bottom-left: “K-head FCN-R3-U (TL∪PL)” w/annotation ratio of 3.0%. Bottom-right: “K-head FCN-R3-U (TL∪PL)” w/different annotation ratios.

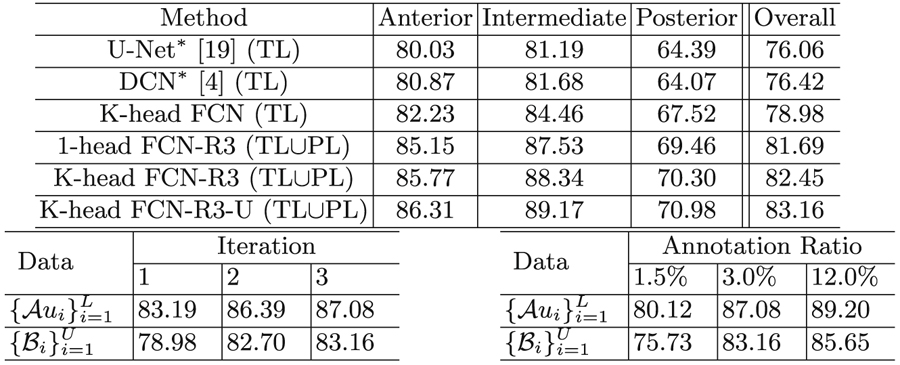First, compared with known FCN-based methods, our K-head FCN yields better performance for cartilages in different positions. We attribute this to its deeper structures and multi-scale extracted feature fusion design, which leads to larger receptive fields and richer spatial and semantic features. Hence, our backbone model can capture significant topology variances in skull cartilages (e.g., relatively small but thick nasal parts, and large but thin shell-like cranial base and vault). Second, to show that our K-head FCN is comparable with Monte Carlo sampling based Bayesian methods, we implement 1-head FCN and conduct sampling K times to obtain PLs. Repeating the training process 3 times (denoted as ‘-R3’), we observe that using PLs, K-head FCN-R3 achieves similar performance as 1-head FCN-R3. However, in each forward pass, we obtain K predictions at once, thus saving ∼ K × the time/space costs. Qualitative results are shown in Fig. 4. Third, we further show that under the guidance of uncertainty, our new method (K-head FCN-R3-U) attains performance gain (from 82.45% to 83.16%). We attribute this to that unreliable PLs are ruled out, and the model optimizes under cleaner supervisions.

Fig. 4.

Qualitative examples: (a) Raw subregions; (b) ground truth; (c) U-Net* (TL); (d) K-head FCN (TL); (e) K-head FCN-R3-U (TL∪PL). (XX) = (trained using XX).

Discussions.

(1) Iteration Numbers. We measure DSC scores on both unseen slices in the training volumes $({\{\mathcal{A}{u}_i\}}_{i=1}^L)$ and unseen slices in the test volumes $({\{{\mathcal{B}}_i\}}_{i=1}^U)$ during the training of “K-head FCN-R3-U” (see Table 1 bottom-left). We notice significant performance gain after expanding the training set (i.e., TLs → TLs ∪ PLs, as Iter-1 → Iter-2). Meanwhile, because the uncertainty of only a small amount of pixels changes during the whole process, the performance gain is not substantial from Iter-2 to Iter-3. (2) Annotation Ratios. As shown in Table 1 bottom-right, the final segmentation results can be improved using more annotation, but the improvement rate decreases when labeling more slices. (3) Uncertainty Estimation. We visualize the samples along with estimated segmentation results and the corresponding epistemic and aleatoric uncertainties from the test data in Fig. 5. It is shown that the model is less confident (i.e., with a higher uncertainty) on the boundaries and hard mimic regions where the epistemic and aleatoric uncertainties are prominent.

Fig. 5.

Visualization of uncertainty. From left to right: a raw image region, ground truth, prediction result, estimated epistemic uncertainty, and estimated aleatoric uncertainty. Brighter white color means higher uncertainty.

4. Conclusions

We presented a new framework for cartilage segmentation in high-resolution 3D micro-CT images with very sparse annotation. Our K-head FCN produces segmentation predictions and uncertainty estimation simultaneously, and the iterative uncertainty-guided self-training strategy gradually refines the segmentation results. Comprehensive experiments showed the efficacy of our new method.