Vapor- and Liquid-Phase Adsorption of Alcohol and Water in Silicalite-1 Synthesized in Fluoride Media

Abstract

In this work, batch-adsorption experiments and molecular simulations are employed to probe the adsorption of binary mixtures containing ethanol or a linear alkane-1,n-diol solvated in water or ethanol onto silicate-1. Since the batch-adsorption experiments require an additional relationship to determine the amount of solute (and solvent adsorbed, as only the bulk liquid reservoir can be probed directly, molecular simulations are used to provide a relationship between solute and solvent adsorption for input to the experimental bulk measurements. The combination of bulk experimental measurements and simulated solute-solvent relationship yields solvent and solute loadings that are self-consistent with simulation alone, and allow for an assessment of the various assumptions made in literature. At low solution concentrations, the solute loading calculated is independent of the assumption made. At high concentrations, a negligent choice of assumption can lead to systematic overestimation or underestimation of calculated solute loading.

1. Introduction

Adsorption from liquid mixtures onto solids is exploited in a wide range of chemical processes, ranging from fixed-bed adsorption and membrane separations to heterogeneous catalysis and their hybrids. A primary characteristic of these processes is their equilibria. However, multicomponent adsorption equilibria are often not available because of inherent challenges in their measurements [1]. As a specific example, the equilibria of diols in zeolites are important for heterogeneous catalysis [2–4] and separation [5–9] applications. Campaigns to produce high-value chemicals by renewable routes [10, 11] are opening up others.

The physical adsorption of both solute and solvent (i.e., the total uptake) from liquid solutions onto solids is difficult to determine in widely-adopted static (i.e., batch) experiments, because only the bulk liquid reservoir can be probed directly. The consequences of this limitation are best explained by the mass balances. The total mass balance for uptake from a binary mixture can be expressed as

$$V_{\mathrm{in}}{\rho }_{\mathrm{in}}=V_{\mathrm{eq}}{\rho }_{\mathrm{eq}}+m_{\mathrm{z}}(Q_{\mathrm{A}}+Q_{\mathrm{S}})$$ (1)

where V_in and V_eq are the initial and equilibrium solution volumes, respectively, ρ_in and ρ_eq are the respective values for the solution (volumetric mass) density, m_z is the mass of the adsorbent, and Q_A and Q_S are the loadings (in mass units) of solute A and solvent S, respectively. The mass balance on the solute is

$$V_{\mathrm{in}}{C}_{\mathrm{A},\mathrm{in}}=V_{\mathrm{eq}}{C}_{\mathrm{A},\mathrm{eq}}+m_{\mathrm{z}}{Q}_{\mathrm{A}}$$ (2)

where C_A,in and C_A,eq are the solute (volumetric mass) concentrations in the initial and equilibrated solutions, respectively. In a typical experiment, V_in, C_A,in, C_A,eq, and m_z are measured. Together, Eqs. 1 and 2 have three unknowns (V_eq, Q_A, Q_S), giving them no unique solution. As a result, an additional approximation must be made in order to estimate the solute and solvent loadings. Different options typically employed in the literature are listed in Table 1.

Table 1:

Common assumptions for the experimental determination of uptake from solution.

Name	Additional Relationa	Eq.	Ref.
Excess adsorption	Vin = Veq	(3)	[9, 12–31]
NS adsorption	QS = 0	(4)	[32, 33]
VC by solute adsorption	Veq = Vin − mzQA/ρA	(5)	[32] a
PF adsorption	Vp = QA/ρA + QS/ρS	(6)	[34–38]b

Abbreviations: CA, coadsorption; NS, no-solvent; PF, pore filling; VC, volume change

^aSome authors used a mass basis instead of the volume basis here.

Here, V_p, ρ_A, and ρ_S are the micropore volume of the adsorbent, the density of the liquid-phase of the solute, and the density of the solvent, respectively. The two simpler approaches are termed excess (XS) adsorption and " no-solvent" (NS) adsorption. The XS adsorption is obtained by assuming that the volume of solution does not change upon adsorption. To address the inherent volume change (VC) of solution upon adsorption, the VC assuming ideal solution can be estimated from the amount of adsorbed solute and its liquid density. A fourth method, the pore filling (PF) model, assumes that the solution adsorbed is ideal with a volume equivalent to V_p. For nanoporous materials that allow for highly selective adsorption, however, the occupiable pore volume depends on the guest molecule used in its determination [39]. The reasons for this dependence are that a certain fraction of smaller pores may only be accessible to smaller guest molecules and that, for nonspherical and/or hydrogen-bonding guest molecules, their packing is influenced by the accessible orientations in elongated channels. For example, the pore volume of silicalite-1 obtained from the saturation loadings of water or nitrogen [40] ranges from 0.125 to 0.186 mL/g (a difference of a factor of 1.5, and alcohol adsorption yields intermediate V_p values, see Table S2 in the Supporting Information, SI). Therefore, it is necessary to assess the significance of the choice of pore volume on the uptake predicted.

More complicated methods of obtaining total uptake exist, but are scarcely used. The addition of another component to the solution phase which does not adsorb in the micropores will allow for closure of mass balances. This is commonly referred to as the nonadsorbing solvent method [42–43]. However, this approach which is commonly used for liquid mixtures of hydrocarbons [44,45] breaks down for nonideal mixtures, since sorbate fugacities can be quite different in the presence of a nonadsorbing solvent component [46]. In addition, it is sometimes difficult to find an inert compound that does not adsorb after long times [35]. Alternatively, Farhapour and Bono [47] designed a special pycnometer to measure the total uptake of ethanol/water mixtures onto silicalite-1 and demonstrated that the PF model is inadequate because it does not account for VCs of mixing (i.e., nonideal solutions) in the micropores. Yu et al. [46] presented the density bottle method, which measures adsorption by the apparent density change of zeolite crystals, and showed that this method exhibits qualitative agreement with ideal adsorbed solution theory [48] (IAST) for acetone/methanol mixtures while the nonadsorbing solvent method does not. However, as the authors state in the paper [46], the density bottle method is highly dependent on the solution density, which could introduce large uncertainties in the calculation of total uptake. Moreover, the method requires a large amount of material, which could represent an issue for assessing the performance of new advantageous materials that cannot yet be synthesized in large scales. In subsequent work, the density bottle method was used to measure adsorption of liquid benzene/hydrocarbon mixtures onto silicalite-1 and NaX zeolites [49]. Bowen and Vane [50] used the density bottle method to determine the total uptake from ethanol/water solutions onto silicalite-1 and ZSM-5. However, they were unable to rationalize the finding that a zeolite with acidic aluminum sites was more selective for ethanol adsorption over water than an all-silica zeolite of the same framework type. Another rarely used approach is to determine the relative or absolute solute and solvent loadings in the porous material by spectroscopic means [51]. While there is no consensus on how to measure total uptake, predicting both solute and solvent adsorption using unary adsorption data and IAST is fraud with error for strongly associating mixtures [52–54]. Molecular simulations are useful, if not necessary, in this regard.

Recently, we reported adsorption equilibria of aqueous solutions of linear alkane-α, ω-diols (diols) with three to six carbons onto silicalite-1, and observed great agreement for solute loading between independently-conducted simulations and experiments [8]. Similar agreement between the two approaches was obtained from single-component gas-phase adsorption of methanol, ethanol, and water in silicalite-1 [53]. We realized that the simulations allow direct observation of the adsorbed phase, and that this information can be supplied to the experiments. For hydrophobic all-silica zeolites, simulations show that water adsorption primarily results from coadsorption with adsorbed alcohols; it reaches a maximum at intermediate alcohol loadings, and then decreases as the diol loading approaches saturation. In that case, an attractive option is to assume that the coadsorption in the experimental system matches that predicted by simulation. Mathematically, this can be expressed for the aqueous mixtures as

$$Q_{\mathrm{S}}=\sum _{k=0}^2{a}_k{Q}_{\mathrm{A}}^k$$ (7)

where {a_k} (with 1 ≤ k ≤ 2) are coefficients determined from simulation, and a₀ is the loading of neat solvent taken either from experiment or simulation. To this point, solutions of ethanol (E), butane-1,4-diol (B), or pentane-1,5-diol (P) in water (W) were considered. To investigate the transferability of the results to solution phases with diverse chemical characters, a solution of P in a strongly adsorbing solvent, E, was also included. The coadsorption method was then used to compare solute and solvent uptakes calculated from various approaches reported in the literature. The results demonstrate that systematic underestimation or overestimation of solute/solvent loadings can be made without careful consideration of the adsorbent and mathematical approach used. This work also opens new opportunities for the simulation of other material frameworks of varied properties, which could aid the integration between computational and experimental research in the field.

2. Methodology

Certain commercially available items may be identified in this paper. This identification does not imply recommendation by NIST, nor does it imply that it is the best available for the purposes described.

2.1. Molecular Simulations

Configurational-bias Monte Carlo simulations [55] in the isobaric-isothermal version of the Gibbs ensemble [56–58] were employed to obtain adsorption equilibria for the P/E mixture from solution at T=323 K and p=1.0 bar with a total of N=100 or 500 molecules (where the larger number was needed at lower solution concentrations to ensure sufficiently large equilibrium box sizes for the solution phase). Sampling of phase transfers was enhanced through identity switch moves [59] between P and E molecules. The interaction of the solute and solvent molecules and the zeolite were described by the TraPPE-UA [60,61] and TraPPE-Zeo [62] models, respectively. The rigid all-silica zeolite framework (silicalite-1) used was based on the structure with orthorhombic symmetry and P nma space group resolved by van Koningsveld et al [63]. Its unit cell was replicated two, two, and three times in a, b, and c, respectively, to obtain the entire simulation box representing the zeolite phase.

Eight independent simulations were carried out at each state point, and the statistical uncertainties are reported as the 95% confidence intervals estimated by multiplying the standard error of the mean by a factor of 2.4. The number of Monte Carlo Cycles (MCCs), each consisting of N_tot randomly selected trial moves, for equilibration ranged from 100,000 to 850,000 MCCs, with longer periods being required for those at low concentrations and/or high loadings. All production periods consisted of 100,000–450,000 MCCs.

The simulation data for the adsorption of the E/W, B/W, and P/W mixtures in silicalite-1 at T = 323 K and p = 1.0 bar with a total of N_tot = 1,100 molecules were taken from prior work [8,54].

2.2. Adsorbent Characterization

All-silica MFI hydrophobic zeolite was synthesized by the fluoride method reported elsewhere, referred herein as MFI-F. Characterization of the material properties can be found in the same reference [32]. All-silica MFI zeolite was synthesized on a large scale using a conventional approach in alkaline medium, referred as MFI-OH. The material had its structural properties characterized. Powder X-ray diffraction (PXRD) patterns were collected using an X'Pert X-ray powder diffractometer with an X'celerator detector. Samples were scanned at 45 kV and 40 mA using Co Kα radiation (λ = 1.789 Å) and a step size of 2θ = 0.02° (50.0 s/step) over a 2θ range of 3 to 50°. Ar adsorption data were collected at T = 87 K using an Autosorb 2 from Quantachrome. Samples were outgassed at T = 573 K overnight before the measurements. Scanning electron microscopy (SEM) images were obtained on a JEOL 6500 instrument at an accelerating voltage of 5 kV. ²⁹Si and ¹H MAS NMR were performed using a Bruker DSX-500 and a Bruker MAS probe. The powder was packed into a 4 mm rotor and was spun at 14 kHz for ¹H and 8 kHz for ²⁹Si MAS NMR at room temperature. The spectral frequencies were 500.2 and 99.5 MHz, for ¹H and ²⁹Si, respectively. NMR signals were collected after 4 microsecond 90 degree pulse for both nuclei. NMR spectra were referenced to TMS for both nuclei. Characterization data can be found in the SI.

2.3. Unary Adsorption Experiments

Water and ethanol unary sorption isotherms were conducted at 298 K. The experiments were conducted on a TA instruments VTI-SA +vapor sorption analyzer located at the Facility for Adsorbent Characterization and Testing at the National Institute of Standards and Technology. The instrument is a dynamic vapor sorption system that obtains the desired relative humidity or partial pressure value by continuously mixing a dry nitrogen flow with a humid nitrogen flow. The sample (≈25 mg) was activated in-situ at 413 K for up to 8 hr under a constant flow of pure nitrogen before starting each experiment.

Batch-adsorption experiments were conducted at T = 323 ± 0.5 K. Solution concentrations were analyzed with an Ailgent 7890B gas chromatograph equipped with a fused silica column (Rtx-VMS, Restek) and a flame ionization detector. The relative signal intensities of the adsorbate and a 1-butanol (99.5%, Aldrich) internal standard were used to determine the concentrations. The reported uncertainties in concentrations represent one standard deviation from multiple GC injections.

The initial diol solution to adsorbent mass was 4 mL/g. Approximately 100 mg of zeolite with appropriate amount of diol solution was added to glass vials (C4011–1, crimp seal, Thermo Scientific™) and then the vials were rotated at 20 r pm in a ProBlot12 hybridization oven until equilibrium was reached. The supernatant solutions were filtered using a Monoject syringe fitted with a 0.2μm hydrophilic polypropylene (GHP) syringe filter to remove the zeolite particles.

To investigate the influence of the choice of pore volume on the calculated uptake, values of pore volumes (V_p) were estimated from nitrogen adsorption [40], the solute saturation loading and liquid density, and the solvent saturation loading and liquid density. Section S1 of the SI provides additional details on the determination of V_p and the equations used to calculate the solute and solvent loadings from Eqs. 1 and 2 and one of Eqs. 3 to 6. The analytical forms of the equations used to calculate the solute loadings and solvent loadings are shown in Section S1.3 of the SI.

The densities of pure components and of aqueous solutions were obtained by extrapolation of the relationships reported in the open literature [64–66] to 323 K (see Figure S2 in the SI), allowing solution nonidealities to be captured. In the absence of reported values, the density of the P/E solutions was calculated assuming ideal solution.

3. Results and Discussion

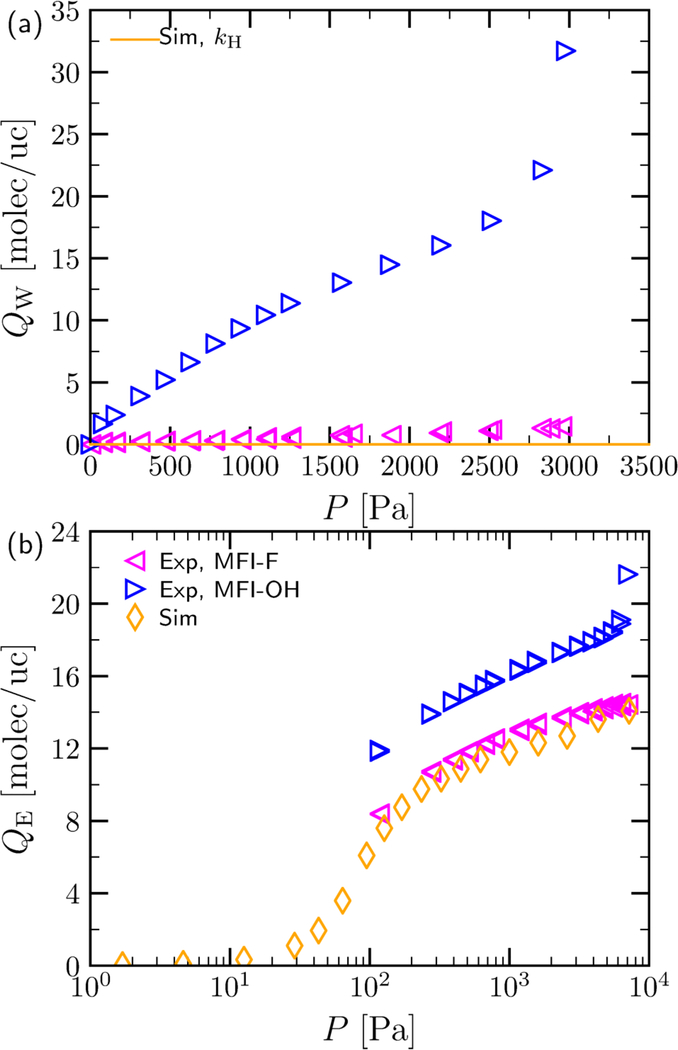
The MFI-F and MFI-OH materials in this work are assigned monoclinic symmetry (see Section S2.1 in the SI). The gas-phase unary water and ethanol adsorption isotherms on these materials at T =298 K are shown in Figure 1 for the MFI-F and MFI-OH materials investigated in this work. The results are compared to the defect-free silicalite-1 simulations reported previously [53]. The very low water adsorption onto defect-free silicalite-1 synthesized via the fluoride route confirms its hydrophobicity. However, unary water adsorption onto MFI-OH shows high adsorption reaching ≈ 32 molecules per unit cell, indicating a very hydrophilic material. Indeed, ²⁹Si Solid-state NMR experiments confirmed the presence of ≈ 8 % Q₃ sites in MFI-OH (see Section S2.1 in the SI). As expected, the use of ethanol as adsorbate leads to stronger adsorption due to the hydrophobic aliphatic chain in the solute. There is great agreement between simulated and experimental isotherms for MFI-F, which gives us confidence that our simulation methodology is accurate.

Figure 1:

Adsorption of (a)water and (b)ethanol at T=298K as a function of pressure obtained by gravimetric adsorption experiments onto the MFI-F and MFI-OH materials studied in this work and by simulation onto a defect-free all-silica MFI material studied in previous work [53]. The Henry's constant, K_H of adsorption for water calculatedby simulation is obtained by fitting to all simulation data points which have a loading below 1 molec/uc.

Next, we focus on the competitive adsorption in binary solutions. As discussed previously, solution-phase batch-adsorption experiments require one assumption to obtain a unique solution to the mass balances. We propose to use the predicted coadsorption by simulation coupled with the bulk solute concentration measurements to determine the solvent loadings in the liquid phase. For most liquid-phase binary systems, this would be challenging to validate. However, the use of ethanol/water solutions is convenient because their isotherms can be obtained independently from vapor-phase experiments.

In Figure 2, we compare the liquid-phase ethanol/water adsorption isotherm onto MFI-F with simulated data. Both solvent and solute adsorption are self-consistent between simulations and our combined approach (referred to as the coadsorption method from now on), which includes experimental bulk measurements and simulated solvent loadings, especially at low concentration. As the ethanol concentration increases, the uncertainty in the measurement of solute concentration by GC increases, leading to a larger relative fluctuation in determined water loading than ethanol loading. As the saturation loading is reached, the ethanol loading calculated by the combined approach becomes ≈ 12 molecules per unit cell experimentally. This saturation loading is in line with the vapor-phase ethanol saturation of ≈ 14 molec/uc.

Figure 2:

Adsorption of (a) ethanol and (b) water at T = 323 K as a function of equilibrium solute concentration obtained by the coadsorption (CA) method onto MFI-F in this work and by simulation reported in previous work [53].

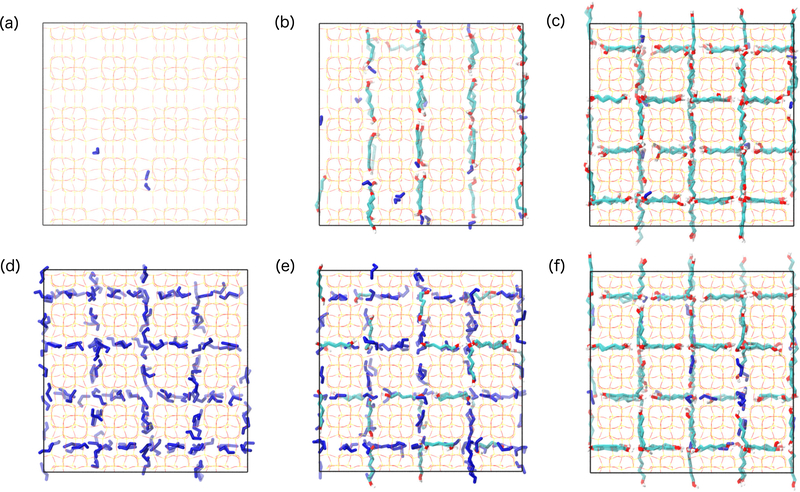
Next, we implement this approach to solutions of high boiling point solutes, specifically linear alkane-α, ω-diols, whose adsorption cannot be easily measured by vapor-phase unary experiments. Liquid-phase adsorption is much different in the presence of a coadsorbing solvent and a strongly adsorbing solvent. The difference lies in the way the pores are filled as a function of increasing solution concentration, as compared between P/W in Figure 3a–c and P/E in Figure 3d–f. At low concentrations, water is scarcely observed in the pores (Figure 3a), while the channels are filled by ethanol (Figure 3d). As the diol concentrations increase, the pores in equilibrium with the P/W mixture become more occupied as the loadings of both P and W increase (Figure 3b), while the occupation of the pores in equilibrium with the P/E mixture does not change significantly (Figure 3e). Instead, the adsorption of diol from the ethanolic mixture is associated with a decrease in solvent adsorption. In this sense, the diol displaces the solvent as the concentration is increased. At high concentrations, where the diol loadings approach saturation, the occupation of the pore volumes is similar, with the smaller differences being a result of different hydrogen-bonding networks and packing efficiencies from the diols with different chain lengths. The contrasting solvent effects on the total uptake of these two mixtures makes them prime candidates for assessment of the adsorption uptakes of solutions with diverse chemical character.

Figure 3:

Snapshots of adsorbed configurations for (a-c, top row) pentane-1,5-diol (P)/ water (W) and (d-f, bottom row) P/ ethanol (E) mixtures at (a,d; left column) low, (b,e; middle column) medium, and (c,f; right column) high concentrations. P is represented with teal carbon backbones, red oxygen atoms, and white hydrogen atoms, while all solvent molecules (W or E) are represented in dark blue. The solution concentrations, diol loadings, and solvent loadings associated with the systems depicted in each subplot are shown inTable 2.

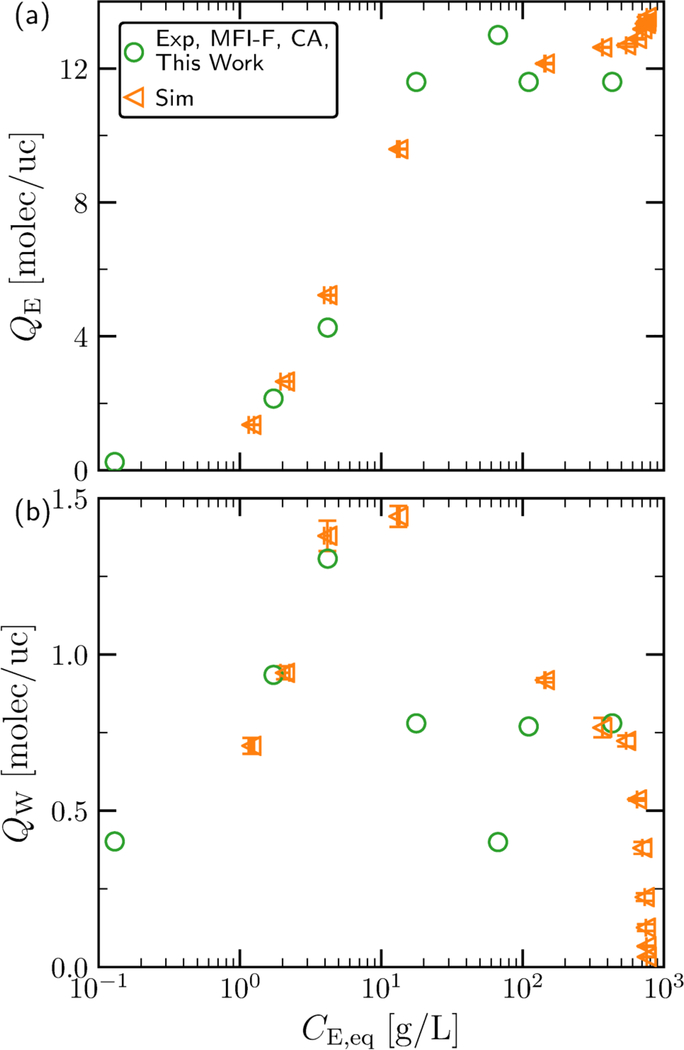
We then applied the coadsorption method to P/W solutions, i.e., we used simulations to obtain a relationship between adsorbed P and adsorbed W, which we used along with the measured P concentrations to solve the mass balance equations. In Figure 4a, the diol loadings obtained by simulation and the coadsorption method are presented as a function of equilibrium solution concentration for P/W mixtures. The two experimental materials were synthesized differently and possess different crystal symmetries. The simulations agree very well with the results measured experimentally for MFI-F. However, the adsorption of P obtained from MFI-OH, which was synthesized in an alkaline medium on a large scale, is different than the obtained for MFI-F. First, the adsorption step is delayed to higher P concentrations. P saturation is somewhat similar to the ones obtained for MFI-F and predicted by simulations. As will be shown in the following sections, the solute loadings calculated at low solution concentrations are independent of the calculation approach. These observations lead to the conclusion that the difference in uptakes at low/intermediate concentrations must be due to the different synthesis protocol, that is, defects introduced by the non-fluoride synthesis route.

Figure 4:

Equilibria of pentane-1,5-diol (P) / water (W) mixtures between solution phases and silicalite-1. (a) Loading of P as a function of equilibrium solution concentration produced by simulation [8] as compared to the MFI-F and MFI-OH materials used in this work as calculated by the coadsorption (CA) method. (b) Loading of W as a function of solution concentration produced by simulation and the coadsorption method (CA).

The water loadings predicted by the coadsorption method and simulation are presented in Figure 4b. The water loadings obtained by simulations exhibit their characteristic peak, [8] which results from exclusion of water at high diol loadings where diol packing is more efficient and water coadsorption requires a larger entropic penalty. Calculation of the water adsorption by the coadsorption method reveals a similar peak for MFI-F, which again represents consistency for the hydrophobic material used in both experiments and simulations. The water loading for MFI-OH shows a broader peak, which could be due to defects in the framework. However, at low diol concentrations, it predicts that very low water amount is adsorbed on MFI-OH. This is not consistent with the unary data presented in Figure 1. The coadsorption coefficients obtained from simulations for a defect-free material can only be used for a self-consistent calculation of adsorbed water for a defect-free MFI-F, and not for MFI-OH with high silanol density. Similar observations can be made for B/W solutions, as shown in Figure S7.

The coadsorption model for predicting the adsorption of P and W onto MFI-OH must be different. Since the water adsorption is relatively large near the saturation pressure of water (see Figure 1a), the coadsorption between P and W is expected to be similar to pore-filling. Therefore, we adopt a coadsorption model with a similar mathematical form to the PF model, with a linear relationship between Q_P and Q_W. We choose two different CA models to investigate the range of loadings thatmay be calculated. The first one (Model H) assumes a high neat solvent loading of 32 molec/uc, while the second (Model L) assumes a low neat solvent loading of 20 molec/uc. For both models, the rate of solvent loading change with increasing solute loading is chosen to be-2.4 molec/uc so that the W loading at P saturation (8 molec/uc) is 0.8 molec/uc for Model L, which is consistent with simulation of the defect-free structure. The resultant isotherms for the two models are shown in Figure S9. Models L and H do not show a considerable difference for the diol isotherm except at high concentration, where a difference of ≈2 molec P/uc can be observed. The associated water loading of Model H is shifted upward from that of Model L by a constant value of ≈ 12 molec/uc at concentrations below ≈ 20 g/L, and by a slightly smaller amount at higher concentrations as the associated diol loadings from the two models begin to deviate from one another. The relatively large deviation in water loading between the two models associated with no deviation in diol loading at concentrations below 400 g/L suggests that a consistent diol loading can be calculated below high concentrations, while the associated water loading remains elusive. Simulations with frameworks containing defects could assist in validating the calculation of water loading, which represent a challenge for future studies.

We then attempted to use the density-bottle method to calculate the total adsorption uptake for P/W onto MFI-OH. The results can be found in Table S3 in the SI. Although the diol loadings agree with the ones obtained by the coadsorption method, the solvent loadings show high uncertainty, probably because they are strongly dependent on the solution density used [46], being inconclusive in our hands.

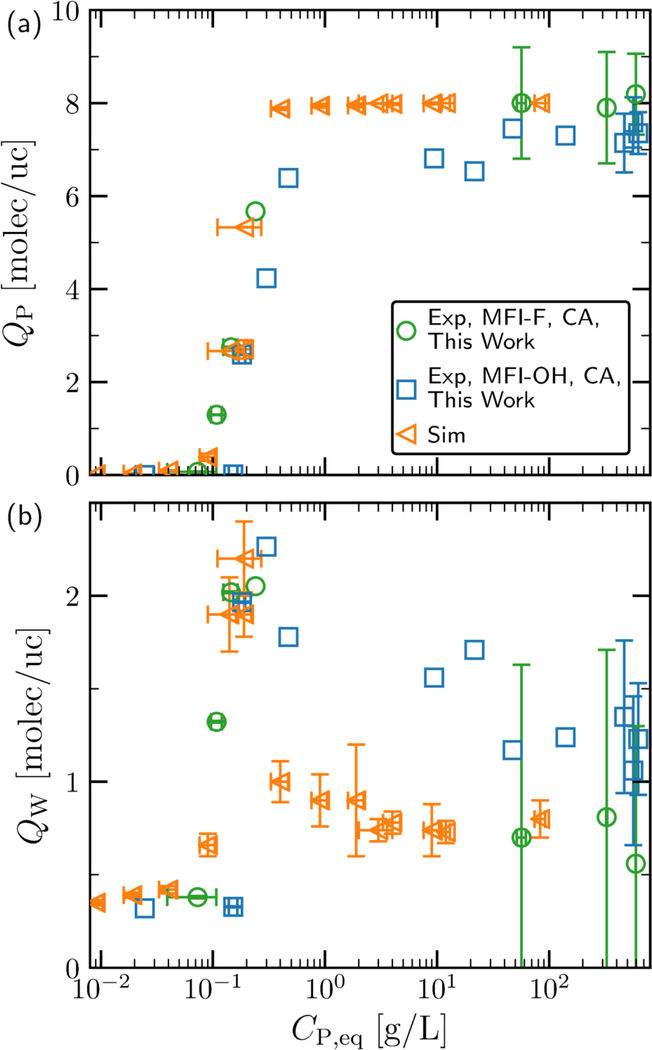
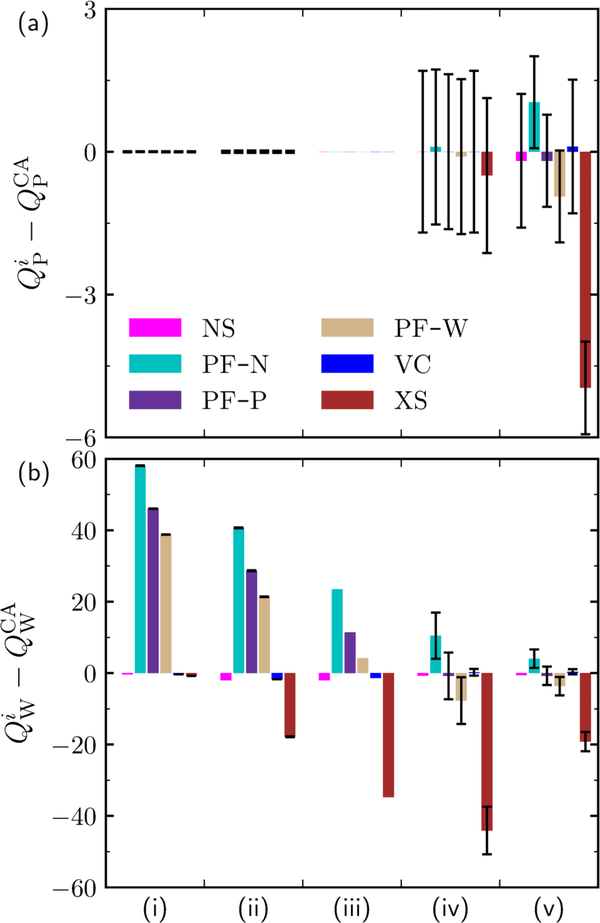
In Figure 5, the coadsorption method is used as a means to assess the performance of conventional methods used in the literature for calculating uptakes. The differences in diol and water loadings between conventional methods and those predicted by the coadsorption method are presented for five characteristic concentrations (increasing from left-to-right) in Figure 5a, b, respectively. The associated equilibrium values for solution concentration and loadings are depicted in Table 3. At low concentrations, the difference in diol loading calculated is immaterial to the calculation approach applied, and all approaches are in agreement with the coadsorption method. However, the corresponding water loadings differ by almost two orders-of-magnitude. The PF models overestimate the water loading by ≈ 40 to ≈ 60 molec/uc. The VC method underpredicts the water adsorption, while the NS and XS adsorption predict unphysical values, as their water adsorption is zero and negative, respectively.

Figure 5:

Difference in loading between NS, PF-B, PF-N, PF-W, VC, or XS (superscript i) (see Table 1) and the coadsorption approach (CA) for (a) pentane-1,5-diol (P) loading, and (b) water (W) loading as a function of increasing solution concentrations (and loadings), increasing in value from left-to-right(i-v). The numerical values of solution concentrations and loadings yielded by the CA method at each point (i-v) are presented in Table 3. All loadings are presented in units of molec/uc. The x-axis ticks marks separate different state points. Error bars (black) are present in the cases where replicate experimental measurements were performed.

Table 3:

Solution Concentrations and Equilibria for the Coadsorption Method at the Points Investigated in Figure 5

	CP,eq [g / L]	QP [molec / uc]	QW [molec / uc]
(i)a	0.073 ± 0.034	0.0661 ± 0.0073	0.3798 ± 0.0066
(ii)a	0.145 ± 0.21	2.745 ± 0.016	2.0192 ± 0.0053
(iii)b	0.24	5.7	2.1
(iv)a	56.8 ± 5.2	8.0 ± 1.2	0.70 ± 0.93
(v)a	594.0 ± 2.0	8.19 ± 0.87	0.56 ± 0.74

^aUncertainty values obtained from replicate experiments and the same initial concentration

^bNo replicate experiments performed.

As the solution concentration (or loading) increases (moving to the right in Figure 5), the deviation in P loading increases in magnitude while the deviation in water loading decreases in magnitude (an exception is the deviation in XS water loading, which reaches a minimum and then continues to be a large, negative value). The sign in the deviation of all terms does not change, except for the water loadings predicted by the PF-W method. This results from the volume which P occupies at saturation in the zeolite being larger than the volume which water can occupy, and also corresponds to negative water loadings (see Table S21 in the SI).

At high concentration, the choice of uptake calculation method can either overestimate or underestimate those obtained from the coadsorption method. Specifically, the NS, PF-P, PF-W, and VC methods perform well, while the PF-N and XS methods perform poorly. The PF-Napproach predicts water loadings and diol loadings which are approximately 10 and 1 molec/uc higher than that yielded by the coadsorption approach, resulting in an underestimation of the ratio water/diol adsorbed. The XS approach, which unfortunately is the most commonly employed method, performs the worst, underestimating the diol loading by almost three molec/uc and the water loading by almost 30 molec/uc.

The coadsorption method was also applied for P/E mixtures. The isotherm is presented in Figure S8. Good agreement is obtained between simulation and experimental data for MFI-F. The diol isotherm obtained from MFI-OH is somewhat similar to MFI-F. However, it underestimates the amount of ethanol adsorbed at low concentrations, indicating the need for simulations using a defects-containing framework. We then compared the coadsorption method for P/E over MFI-F to the other conventional methods in Figure 6. The associated equilibrium values for solution concentration and loadings are depicted in Table 4. Unlike water, ethanol adsorbs strongly at low solute concentrations. As the solute concentration increases, the solute (P) loading increases while the solvent (E) loading decreases (see Figure S8 in the SI). In fact, the number of ethanol molecules per unit cell decreases linearly with increasing number of diol molecules per unit cell (see Figure S1 in the SI). This suggests that the factors contributing to adsorption in ethanolic solutions are much different than those in the aqueous solutions. P molecules cannot adsorb at very low concentrations; instead, they adsorb at higher concentrations where P molecules must displace adsorbed ethanol as the concentration is increased.

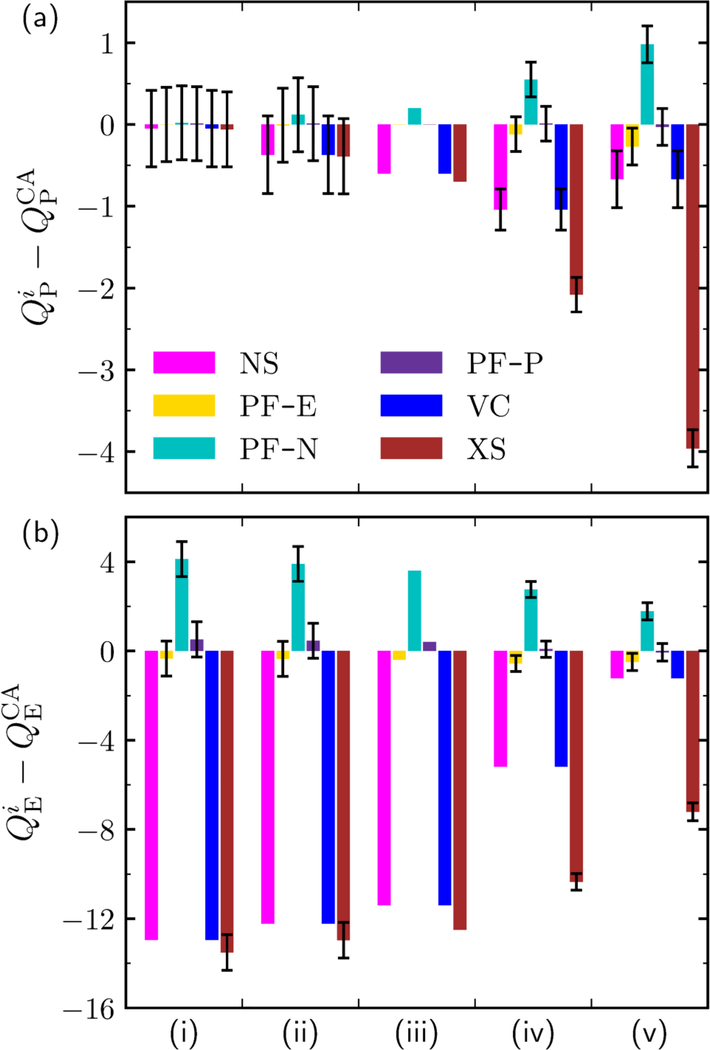
Figure 6:

Difference in loading between NS, PF-B, PF-N, PF-E, VC, or XS (superscript i) (see Table 1) and the CA approach for (a) P loading, and (b) E loading at different solution concentrations (and loadings) increasing from left-to-right (i–v). The solution concentrations and loadings yielded by the CA method at each point (i–v) are presented in Table 4. All loadings are presented in units of molec/uc. The x-axis tick marks separate different state points. Error bars (black) are present in the cases where replicate experimental measurements were performed

Table 4:

Solution Concentrations and Equilibria for the Coadsorption Method at the Points Investigated in Figure 6

	CP,eq [g / L]	QB [molec / uc]	QW [molec / uc]
(i)a	7.6 ± 1.5	0.37 ± 0.32	12.95 ± 0.54
(ii)a	49.5 ± 1.5	0.81 ± 0.32	12.22 ± 0.54
(iii)b	65	1.3	11
(iv)a	171 ± 13	4.99 ± 0.15	5.18 ± 0.25
(v)a	480.09 ± 0.75	7.34 ± 0.16	1.22 ± 0.27

^aUncertainty values obtained from replicate experiments and the same initial concentration

^bNo replicate experiments performed.

The trends for deviation in diol loading for the P/E mixture are shown in Figure 6a. At low concentrations, the choice of calculation method is immaterial to the equilibria predicted. However, the deviations increase in magnitude as the concentrations are increased. The VC and NS methods are equivalent when the total mixture density is assumed to be an ideal solution (see Section S1.5 in the SI); they both slightly underestimate the P loading at intermediate concentrations and above. The most significant deviations are for PF-N (overestimation by ≈ 0.9 molec/uc) and XS (underestimation by ≈ 3.8 molec/uc). At high solution concentrations, the PF-P and PF-E diol loadings are essentially the same as the coadsorption method, with no statistically significant deviations. Less approaches are in agreement with the coadsorption method for the P/E mixture, suggesting that it is more difficult to accurately calculate the diol adsorption from ethanol solution.

The solvent deviation for the ethanolic solution is much different than for the aqueous solution. This is because ethanol saturates the zeolite at low diol solution concentrations. As a result, the pore-filling methods are much more realistic (although PF-N still overestimates by ≈ 5 molec/uc).

Since the VC and NS methods both yield zero solvent loading, and the solvent adsorption predicted by the XS method is always negative, only the PF models predict finite selectivities. The PF-N method slightly underestimates the selectivity at low concentrations, and the extent of underestimation increases as the concentrations increase. At all concentrations observed, the selectivities predicted by PF-P and PF-E are statistically equivalent to those predicted by the coadsorption method. This is expected based off of the `displacement adsorption' mechanism described earlier, and serves as additional validation of the coadsorption approach.

The results for the four different options for calculating the total uptake from liquid solution are summarized in Table 5 for the two different solutions and concentration regimes. At low concentrations the useful result observed is that the solute loading calculated is inconsequential to the method chosen. The solvent loadings can be underestimated or overestimated depending on the approach used. Specifically, the pore-filling model can introduce great uncertainties for aqueous solutions where the co-adsorption mechanism occurs. It may be applicable, however, to solutions where the displacement adsorption mechanism is more favorable, as the case of ethanolic solutions. It is also worthy mentioning that the choice of pore-volume is critical for this type of approach and should be used carefully. At high diol concentrations, different approaches can either underestimate or overestimate the loadings for both solute and solvent.

Table 5:

Summary of Options for Calculation of Total Uptake of Diols from Aqueous or Ethanolic Solutions

	Aqueous		Ethanolic
	QP or QB	QW	QP	QE
Low CA,eq	all methods equivalent	PF >> CA	all methods equivalent	PF ≥ CA
		NS ≡ 0		NS ≡ 0
		VC < CA		VC = NSa
		XS < 0		XS < 0
High CA,eq	PF ≈ CA	PF ≥ CA or PF < CA
	NS ≈ CA	NS ≡ 0	NS < CA	NS ≡ 0
	VC ≈ CA	VC < CA	VC = NSa	VC = NSa
	XS << CA	XS << 0	XS << CA	XS << 0

^aResults from assuming no excess density of solution.

4. Conclusions

In order to predict the total uptake in a solution-phase batch-adsorption experiment, an assumption must be made to close the mass-balance equations. In this work, a new option for closure of the mass balances, referred to as the coadsorption method, is presented. This approach matches the coadsorption of experiment to that yielded by molecular simulation, which can directly relate the uptake of both solute and solvent in the adsorbed phase. The coadsorption method was found to be self-consistent with simulation of defect-free silicalite-1 crystals. In addition, it was validated by comparing the calculated adsorption of ethanol/water mixtures from liquid-phase to that measured independently in single-component adsorption from vapor-phase. The coadsorption method was then used to determine the adsorption of different binary diol solutions and as a basis to assess the accuracy of conventional approaches for the calculation of uptakes and selectivities. This work is, to our knowledge, the first systematic investigation of the effect of different assumptions on the resultant equilibria.

The results demonstrate that the excess adsorption model, while mathematically simple and extremely popular in the literature, is a poor choice for calculating adsorption from solution-phase in batch experiments above low concentrations. It leads to a systematic underestimation of solute adsorption above low concentrations. In addition, using the pore-filling model with a pore volume estimated from the adsorption of a small molecule (e.g., N₂), which is perhaps the second-most-popular approach, leads to a systematic overestimation of solute loading above low concentrations. Using the pore-filling model with a pore volume estimated from the saturated loading and liquid-phase density of the pure solute or solvent leads to more accurate solute loadings. For pentane-1,5-diol/ethanol solutions, this approach also led to accurate solvent loadings. For the adsorption of diols from aqueous solutions onto a hydrophobic, all-silica MFI-type zeolite, batch-adsorption measurements with conventional uptake calculation approaches could not accurately predict the selectivity without input from molecular simulation. Although the coadsorption method with simulation of defect-free MFI did not accurately represent the solvent adsorption onto hydrophilic MFI, the results present new opportunities for the simulation of imperfect crystals as a way to investigate adsorption phenomena from liquid-solutions coupled with experimental data.

Table 2:

Solution Concentrations and Uptakes Associated with Figure 3

Label	Mixture	CD,eq [g/L]	QD [molec/uc]	QS [molec/uc]
(a)	P/W	0.040 ± 0.007	0.087 ± 0.010	0.418 ± 0.015
(b)	P/W	0.14 ± 0.05	2.6629 ± 0.0007	1.9 ± 0.2
(c)	P/W	83 ± 9	7.9997 ± 0.0002	0.8 ± 0.10
(d)	P/E	8.1 ± 1.5	0.117 ± 0.015	13.31 ± 0.16
(e)	P/E	197 ± 11	2.94 ± 0.19	8.9 ± 0.3
(f)	P/E	647 ± 11	7.08 ± 0.09	1.82 ± 0.16