Variation in model performance by data cleanliness and classification methods in the prediction of 30-day ICU mortality, a US nationwide retrospective cohort and simulation study

Abstract

Objective

There has been a proliferation of approaches to statistical methods and missing data imputation as electronic health records become more plentiful; however, the relative performance on real-world problems is unclear.

Materials and methods

Using 355 823 intensive care unit (ICU) hospitalisations at over 100 hospitals in the nationwide Veterans Health Administration system (2014–2017), we systematically varied three approaches: how we extracted and cleaned physiologic variables; how we handled missing data (using mean value imputation, random forest, extremely randomised trees (extra-trees regression), ridge regression, normal value imputation and case-wise deletion) and how we computed risk (using logistic regression, random forest and neural networks). We applied these approaches in a 70% development sample and tested the results in an independent 30% testing sample. Area under the receiver operating characteristic curve (AUROC) was used to quantify model discrimination.

Results

In 355 823 ICU stays, there were 34 867 deaths (9.8%) within 30 days of admission. The highest AUROCs obtained for each primary classification method were very similar: 0.83 (95% CI 0.83 to 0.83) to 0.85 (95% CI 0.84 to 0.85). Likewise, there was relatively little variation within classification method by the missing value imputation method used—except when casewise deletion was applied for missing data.

Conclusion

Variation in discrimination was seen as a function of data cleanliness, with logistic regression suffering the most loss of discrimination in the least clean data. Losses in discrimination were not present in random forest and neural networks even in naively extracted data. Data from a large nationwide health system revealed interactions between missing data imputation techniques, data cleanliness and classification methods for predicting 30-day mortality.

Strengths and limitations of this study.

• This study focuses on a large, real-world data set consisting of 355 823 intensive care unit stays at over 100 different facilities.

• Multiple methods of model fitting and missing data imputation were implemented in standardised ways that reflect common practice.

• The approach we used for each implementation is available in an Appendix or via GitHub to allow transparency and reproducibility, and we encourage validation on other data sets.

• Due to high dimensionality of method combinations, this study only considered one outcome and only considered one standardisation method and decided on an a priori approach within each data set/categorisation model/missingness imputation triad.

Introduction

Risk adjustment plays an increasingly central role in the organisation, care of and science about critically ill patients.^{1 2} Statistical adjustment, including the handling of missing data, is essential for many performance measurements as well as pay-for-performance and shared savings systems. It is used to stratify the care of patients for treatments and track quality improvement efforts over time.³ It is routinely measured, even in clinical trials, to assess confounder balance between arms and may form part of a randomized clinical trial(RCT) enrollment or drug approval criteria.⁴

As a result, there has been a proliferation of risk scores and missing data imputation tools both for the common task of short-term mortality prediction and for more specialised tasks. Many statistical tools have been promoted. Rules of thumb have developed and existed long enough to be critiqued.^5–9 The Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis guidelines offer standardisation of reporting.¹⁰ Textbooks have emerged.¹¹ Yet questions remain on fundamental pragmatic issues: How clean does the data have to be to prevent the so-called ‘garbage in, garbage out (GIGO)’ phenomenon? How sensitive are methods to missing data and how should it be handled? Do these analytic decisions interact?

To address such questions, we compared the performance of an array of methods on a single-standardised problem—the prediction of 30-day mortality based on demographics, day 1 laboratory results, comorbidities and diagnoses among patients admitted to the intensive care unit (ICU) at any hospital in the nationwide Veterans Health Administration system.^12–14 Using the same set of real ICU admissions, we systematically varied three parameters: the approach used to extract and clean physiologic variables from the electronic health record; the approach used to handle missing data and the approach used to compute the risk. We systematically applied these approaches in a 70% development sample and tested the results in an independent 30% testing sample to provide real-world comparisons to inform future pragmatic implementation of risk scores.

Methods

Cohort

Data were drawn from the Veterans Affairs Patient Database (VAPD), which contains daily patient physiology for acute hospitalisations between 1 January 2014 and 31 December 2017. The VAPD includes patient demographics, laboratory results and diagnoses that are commonly used to predict 30-day mortality from the day of admission. Here, we included data from all ICU hospitalisations on day 1 of each hospitalisation. Full details of the VAPD have been published elsewhere.¹⁵

The development of this database was reviewed and approved by the Veterans Ann Arbor Healthcare System’s Institutional Review Board.

Four versions of the data set were created for each hospitalisation on admission: (A) raw lab values extracted using only lab test names, (B) raw lab values extracted using only Logical Observation Identifiers Names and Codes (LOINC), (C) cleaned lab values extracted using both LOINC^{16 17} and searched text lab test names and (D) cleaned lab values converted to Acute Physiology And Chronic Health Evaluation (APACHE) points, extracted using both LOINC and lab test names.

No patient and public involvement

This research was done without patient involvement. Patients were not invited to comment on the study design and were not consulted to develop patient relevant outcomes or interpret the results. Patients were not invited to contribute to the writing or editing of this document for readability or accuracy.

Predictor variables

In our primary analyses, we adjust for 10 laboratory values that were collected within 1 day of hospital admission. Further patient-level adjustments included demographic characteristics (gender, age, race and Hispanic ethnicity), 30 comorbidities and 38 primary diagnoses. The individual comorbidities used in models are defined by methods described in van Walraven’s implementation of the Elixhauser comorbidity score.¹⁸ We adjust for 38 primary diagnoses drawn from the Healthcare Cost and Utilization Clinical Classification Software (CCS),¹⁹ which consist of the top 20 most frequent single-level CCS diagnoses and 18 level-1 multilevel categories of diagnoses (online supplemental appendix A). In secondary analyses, to emphasise the role of data cleanliness, we estimate risk using only the laboratory values since the non-laboratory values do not vary in data cleanliness and curation.

Outcome variable: 30-day mortality

Our primary outcome variable is 30 day all-cause mortality, defined as death within 30 days of the admission date for the index hospitalisation. Mortality is evaluated using the highly reliable Veterans Administration beneficiary death files, which aggregate from multiple sources.^{12 20 21}

Statistical analysis and model development

Random forests is an ensemble machine learning method that aggregates the results of multiple decision trees fit on bootstrap samples of the original data.^{22 23} For each decision tree, the original data are bootstrapped to create a new data set of the same size and the tree is fit to the new data. Instead of considering all predictors to determine the splitting criterion at a node, the split variable is chosen from a random subset of variables in order to reduce the correlation between different trees. Many such trees are grown, creating a ‘forest’. Each observation is classified by each tree, and the majority classification over all trees is the predicted class. The ability of random forests to learn non-linear and complex functions contributes to its predictive performance.

The neural network²⁴ can ‘learn’ to classify samples without manually designed task-specific rules. The algorithm applies different weights to predictors and uses these transformations in subsequent ‘layers’ of the neural net, culminating in the output layer with predictions. We applied the random forest and the neural network on our task. A traditional logistic regression model was also performed and compared.

Statistical analyses were performed with Python and the scikit-learn package.²⁵

Training and testing sets

The data set was randomly split into a 70% training set and a 30% testing set. The same split was used for all classification methods. This process was replicated five times (five different training sets and corresponding testing set were generated), and each time the models were fit on the training set and used to predict the 30-day mortality of the testing set.

Missing data and imputation

We imputed the missing values before training and testing the models, comparing:

• ‘Mean value’: the mean value of each variable in the training set was used to replace missing values.²⁶

• ‘Random forest’: used random forest to impute missing values (missForest).²⁷

• ‘Extremely randomised trees (extra-trees regression)’: this method is similar to random forest but is faster.^{28 29}

• ‘Ridge regression’: used Bayesian ridge regression to impute missing values.³⁰

• ‘Normal value’³¹: normal values were used to impute missing values—this is common in clinical prediction contexts in which it is assumed that clinicians order tests they fear are not normal, and therefore the absence of such a test is a sign that the clinician reviewed other aspects of the patient’s case and judged the odds of physiologic abnormality so low that testing was not indicated.

• ‘No missing’: casewise deletion.³²

Variable importance and partial dependence plots

Predictor variable importance was evaluated for random forests.³³ When classifying a sample using a decision tree, a predictor was used at each node. Predictors that appear more frequently and that reduce the misclassification more substantially are considered more important. By combining all trees in a random forest model, we assessed the variable importance of each predictor. Different values of the same predictor may have different effects on the prediction. We plotted the partial dependence plots³⁰ to show how the value of predictors affects the prediction of 30-day mortality. Partial dependence plots were used to visualise non-linearity among variables.

Results

Cohort description

The cohort comprised 355 823 ICU hospitalisations at over 100 different hospitals, as described elsewhere.¹⁵ The mean age of the cohort was 66.9 years, and there were 34 867 deaths within 30 days of admission, a primary outcome event rate of 9.8% (table 1.)

Table 1.

ICU patient demographics

Variables	ICU only cohort
Hospitalisations, N	355 823
Age, mean (SD), y	66.9 (11.6)
Male, N (%)	341 579 (96.0)
Race, N (%)
White	256 293 (72.0)
Black or African American	73 855 (20.8)
Other	25 675 (7.2)
Hispanic, N (%)	20 532 (5.8)
30-day mortality, N (%)	34 867 (9.8)
Length of stay, mean (SD), days	9.5 (13.0)

ICU, intensive care unit.

Rates of data missingness for each laboratory value in each data set are shown in table 2. Data set A has a high proportion of missing laboratory values for blood urea nitrogen (0.84) and haematocrit (0.85) compared with data sets B and C. This is due to data set A using a single, broad lab test name to identify laboratory values: ‘BUN’ for blood urea nitrogen and ‘HCT’ for haematocrit. In contrast, data sets B and C incorporated LOINC codes for BUN and HCT, which result in fewer missing laboratory values.

Table 2.

Proportion of labs missing

Data set	Albumin (albval)	Bilirubin (bili)	Blood urea nitrogen (BUN)	Creatinine (creat)	Glucose (glucose)	Haematocrit (HCT)	Partial presssure (PaO2)	pH (pa)	Sodium (Na)	White blood cell (WBC)
A	0.39	0.42	0.84	0.13	0.07	0.85	0.66	0.14	0.11	0.13
B	0.38	0.42	0.13	0.13	0.06	0.12	0.65	0.44	0.11	0.13
C	0.39	0.45	0.13	0.12	0.06	0.11	0.69	0.64	0.11	0.13

Using all data for model development

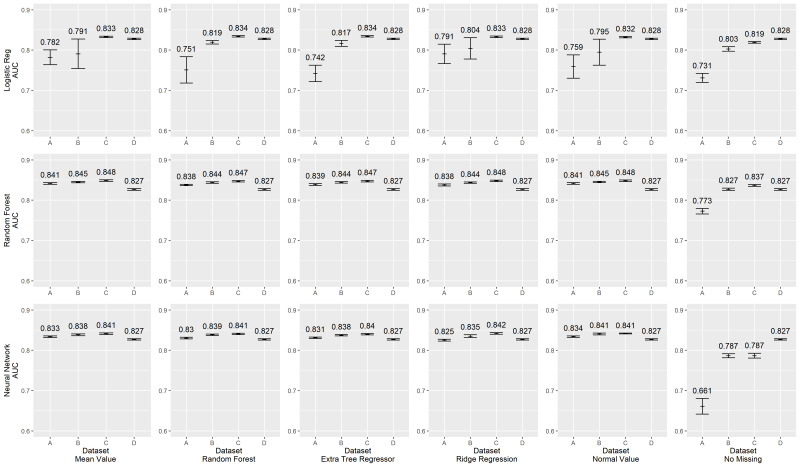
Figure 1 shows the Area Under the Curve (AUC) scores of different classification models and imputation methods in the primary analysis. The highest AUCs obtained for each primary classification method (rows of the figure: logistic regression, random forest or a neural network) were very similar: AUCs of 0.83–0.85. Likewise, there was relatively little variation within classification method by the missing value imputation method used, be it mean value imputation, random forest, extremely randomised trees (extra-trees regression), ridge regression or normal value imputation. All models suffered dramatic losses in discrimination when casewise deletion was used for missing data in the least clean data set (far right columns). Full model performance for each condition are shown in online supplemental appendix B.

Figure 1.

Area Under the Curve (AUC) scores, full Model.

Variation in discrimination was found, however, across classification methods, as a function of data cleanliness (note that the analyst was blinded during the analysis to how each data set was developed, and hence did not know which was ‘cleanest’). In the logistic regression model developed using the least clean data (data set A had raw lab values extracted using only lab test names), performance was always lower than the performance with the more complete and clean data sets—by AUC’s of 0.05 to about 0.1, p value <0.05). Similarly, performance in data set B (extracted using LOINC codes without unit standardisation) was lower and more unstable for mean value imputation and ridge regression. In marked contrast, neither random forests nor neural networks showed such reduced performance when developed in less clean data—in no case did the AUC degradations exceed 0.025 despite similar optimal performance.

Secondary analysis using only laboratory values

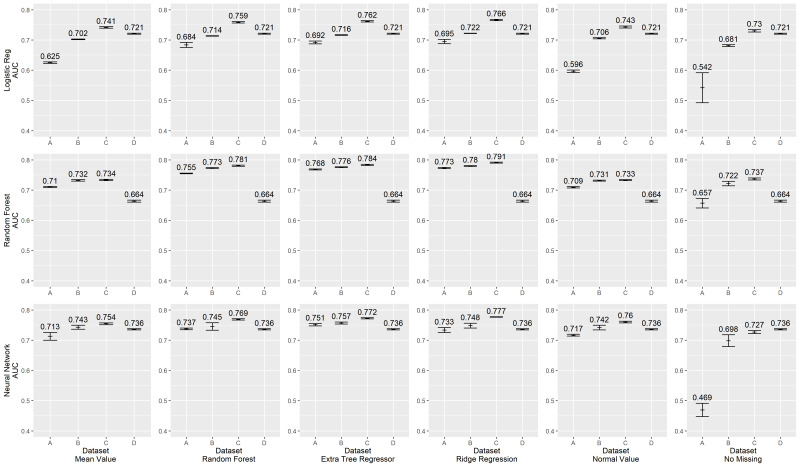
The primary analysis presented above considers the real-world case in which demographics, diagnoses and laboratory values are used in combination with risk model prediction. Yet, of these, only laboratory values were subjected to variation in cleanliness. We, therefore, conducted a secondary analysis using only laboratory values to assess more clearly the impact of data quality. Results are shown in figure 2.

Figure 2.

Area Under the Curve (AUC) scores for lab-only predictors.

Average model performance with this much smaller group of predictors is, as expected, somewhat lower with less data—optimal AUCs typically range from 0.73 to 0.78 across combinations of classification model and missing data imputation. No uniformly superior strategy is evident, save markedly lower performance of casewise deletion in the least clean data set (A). As before, logistic regression shows markedly reduced discrimination when developed in the least clean data set. Neural networks show consistent performance.

Also notable is the marked reduction of discrimination of random forest models and neural network models regardless of the missing data imputation model used within data set D. Data set D has the ‘cleanest’ data, in that it has hand-curated inclusion criteria, standardisation of units and conversion of values from their continuous scale to a semiquantitative set of ‘points’ as is done in the APACHE scoring algorithms. Attempting to work with such standardised point values as inputs consistently resulted in markedly worse discrimination in random forest models and neural network models than using other ‘less clean’ data sets (the difference between data set D and other data sets is significant with a p value <0.05).

Variable importance

The most important predictors of 30-day mortality were age and laboratory values. Age had the highest importance scores, regardless of which data set was used, indicating that age is the most important variable when predicting 30-day mortality. The 10 laboratory values also had high importance scores. For data sets A, B and C, laboratory values fell in the top-13 most important variables, and there were at least 8 laboratory values in the top-10 most important variables. However, for data set D, there were only six laboratory values in the top-10 most important variables, and the variable for white blood cell ranked 20th. This may indicate that transforming laboratory values to APACHE scores results in the loss of information contained in the original values and negatively influences the performance of the random forest model.

Partial dependence plots

As it is hard to visualise the relationship between multiple predictors and the outcome, we created partial dependence plots to show the effect of predictors on the outcome.³⁴ The plots can also show whether the relationship between a specific predictor and the outcome is linear, quadratic, monotonic or more complex. Further analysis can be done by combining the partial dependence plots and medical knowledge. Figures 3 and 4 are the partial dependence plots for the pH score and the PaO₂ score. We will take these as examples to show how the value of predictors in different data sets affects 30-day mortality. The X-axis is the value of the predictor. For each value of the predictor, the Y-axis is the averaged model output for all observations with the corresponding value of the predictor. A higher partial dependence value corresponds to a higher risk of mortality. As we know, the normal value of the pH score is 7.4, and both higher values and lower values are abnormal. Typically, abnormal values lead to a higher risk of death. Therefore, a U-shaped partial dependence plot is to be expected for data sets A, B and C. However, only the plot for data set C is U shaped. This is because data set C is ‘cleaner’ than data sets A and B, and the models can learn the real effect of pH score on 30-day mortality. Data sets A and B are not as clean as data set C, as some other variables are presented in these data sets as pH score. Thus, it is difficult for the models to use the pH score variable in data sets A and B. This result indicates that cleaner variables benefit the classification models. However, not all variables have this problem. For most other variables such as the PaO₂ score, the plots of data sets A, B and C have similar trends.

Figure 3.

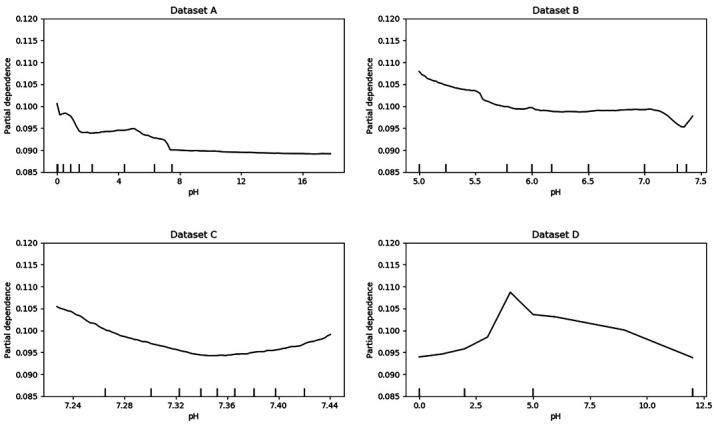
Partial dependence plots for pH.

Figure 4.

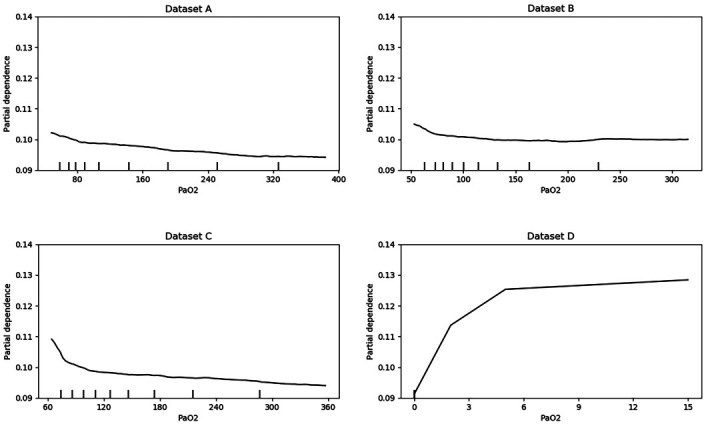
Partial dependence plots for PaO₂.

Discussion

We used real data from a large nationwide health system to explore the interaction between missing data imputation techniques, data cleanliness and classification methods for the common problem of predicting 30-day mortality in a hold-out testing data set. In brief, we found that any of several imputation techniques other than casewise deletion performed equivalently in terms of discrimination, regardless of data cleanliness or classification method used. We found that logistic regression showed worse discrimination with less carefully cleaned data than did random forest or neural networks. Random forest models (and to a degree, neural networks) displayed diminished discrimination when given data that had been too highly cleaned and standardised prior to use.

Relationship to past research

Missing data are ubiquitous in large data sets. Even when missingness is completely at random, missing data lead to significant loss in statistical power and predictive ability.³² We have previously found that the random forest method consistently produced the lowest imputation error compared with commonly used imputation methods.²⁶ Random forest had the smallest prediction difference when 10%–30% of the laboratory data were missing. Our present analysis of real data shows that as more specialised laboratory values are introduced into the prediction setting, much higher levels of missingness may be present. We thereby extend the previous finding that random forest continues to perform well for missing data. Our findings on the poor performance of casewise deletion as an approach to handling missing data are in agreement with mainstream recommendations for more than two decades.³²

Our findings on missing data are of note because of the distinctive, yet real world, way in which missing data were generated. There were two missingness processes. First, clinicians in routine practice only sometimes order any given laboratory, and thus the presence or absence of an order may itself provide prognostic importance.³⁵ Second, an effort to identify all target laboratory values may or may not succeed. Even in a large system with a strong tradition of centralisation, laboratory labelling practices vary over time and clinical insight is often necessary to distinguish valid laboratory tests.³⁶ For any given data pull, it is not trivial to understand which missing values represent failure to find data that exist versus representing true missingness. Past work has rarely explicitly considered these distinct missingness-generating processes (in addition to true missingness at random) for their distinct implications.

The finding of poorer discrimination of random forest in models where the data were fully standardised and cleaned was not anticipated given past literature. The APACHE score was designed to simplify the lab results and to help doctors predict mortality.² Even in its more recent incarnations, APACHE transforms continuous lab results into discrete acute physiology scores.³⁷ Our data suggest that transforming lab results to APACHE scores is not necessary for random forest and may even lead to the loss of information.²³ Remarkably, even standardisation to equivalent units across institutions may not be necessary—but at the same time, this means that sources of variance other than simply the laboratory value may also be subtly incorporated into risk prediction in non-standardised ways. It is a case-specific decision as to whether incorporation of such variance is helpful for a given task or is a source of bias.

Implications

Our findings have implications for both practitioners seeking to implement a given prediction rule and scientists interested in risk prediction generally. For practitioners, no given method yields consistently superior results in terms of discrimination. Therefore, other performance considerations, whether psychometric or implementation ease, may play an important role. They also suggest that missing data imputation approaches other than casewise deletion during development are mandatory.

Our results also note that random forests and neural networks were strikingly robust to even quite naively prepared data, in contrast to logistic regression. This suggests that the truth of the oft-quoted aphorisms about ‘GIGO’ may depend on the categorisation model and missing data imputation method used. In situations where ascertainment and cleaning of data are more costly, random forests may offer pragmatic advantages if these findings are replicable.

Strengths and limitations

Strengths of our analysis include its use of real-world data, with real-world data generation and missingness-generation problems on an established problem encountered by medical researchers and clinicians. We also used multiple methods implemented in standardised ways. The approach we used for each implementation is available in an Appendix or via GitHub to allow transparency and reproducibility.

Limitations of our analysis stem fundamentally from the nearly infinite combinations of analysis factors that might be varied, and our inability to explore such a high dimensional space. Thus, we only considered one outcome and one standardisation method and decided on an a priori approach for each combination of data set, categorisation model and missingness imputation method used. Other outcomes and other possible data structures (such as using trends in data) may yield different answers. We focus on discrimination, as measured by AUC, but other measurement properties are assuredly also important. We also focused on individual-level prediction, as opposed to considering the impact on hospital-level quality assessment or other tasks for which these results may be used.

Conclusion

In sum, our results suggest that there is little variation in discrimination among different statistical classification models in well-cleaned data using modern missing data imputation techniques. As such, the decision about which of the well-performing imputation and adjustment methods to use can be made based on other factors relevant to the particular application—as long as the lower performing methods are avoided. If these findings are replicated in other data with other outcomes, they may help inform pragmatic model selection.