A method for handling the extrapolation of solid crystalline phases to temperatures far above their melting point.

Abstract

Thermodynamic descriptions in databases for applications in computational thermodynamics require representation of the Gibbs energy of stable as well as metastable phases of the pure elements as a basis to model multi-component systems. In the Calphad methodology these representations are usually based on physical models.

Reasonable behavior of the thermodynamic properties of phases extrapolated far outside their stable ranges is necessary in order to avoid that they become stable just because these properties extrapolate badly. This paper proposes a method to prevent crystalline solid phases in multi-component systems to become stable again when extrapolated to temperatures far above their melting temperature.

1. Introduction

The Calphad (CALculation of PHAse Diagrams) method has its strength in the description of multi-component multi-phase systems producing realistic phase diagrams and thermodynamic data. To deliver acceptable results the descriptions of the Gibbs energy functions of most phases must cover the entire composition and temperature space of a system also for regions where the phases are not stable. Many models use polynomials depending on the temperature, pressure and phase composition and this may lead to nonphysical values when extrapolated.

In particular, for most elements in their stable crystalline phase, the heat capacity increases, sometimes steeply, as the temperature approaches the melting temperature. This “pre-melting” phenomenon has several reasons, such as increasing quasi-harmonic vibrations, electronic excitations and amount of thermal vacancies [1]. The resulting heat capacities, C_P, at the melting temperature will often be much larger than the Dulong-Petit value of 3R where R is the universal gas constant.

When the Scientific Group Thermodata Europe (SGTE) assessed the C_P information for the purpose of constructing a thermodynamic database for the elements [2] they were well aware of the fact that an extrapolation to higher temperatures of the heat capacities of the solid phases, fitted to their stable range, would make the solid phase stable again. As a simple solution to avoid this and to have a continuous heat capacity they introduced a break point in the solid heat capacity at the melting temperature. Above this temperature the heat capacity of the metastable solid was modeled with an expression which started from the assessed value at the melting temperature of the solid and is then forced to approach the C_P of the liquid at high temperature as shown in Fig. 1(a). This prevented the solid from reappearing at high temperature but the complete C_P curve for Al in its face centered cubic (fcc) structure was left with a kink at the melting point of Al as shown in Fig. 1(a). The same type of kink was introduced in the functions of most pure elements and, because many compounds have their heat capacities estimated using the Kopp-Neumann rule [3, 4], such kinks are inherited in many compounds or solution phases when this phase is stable above the melting temperature of one or more of its constitutional elements.

Figure 1:

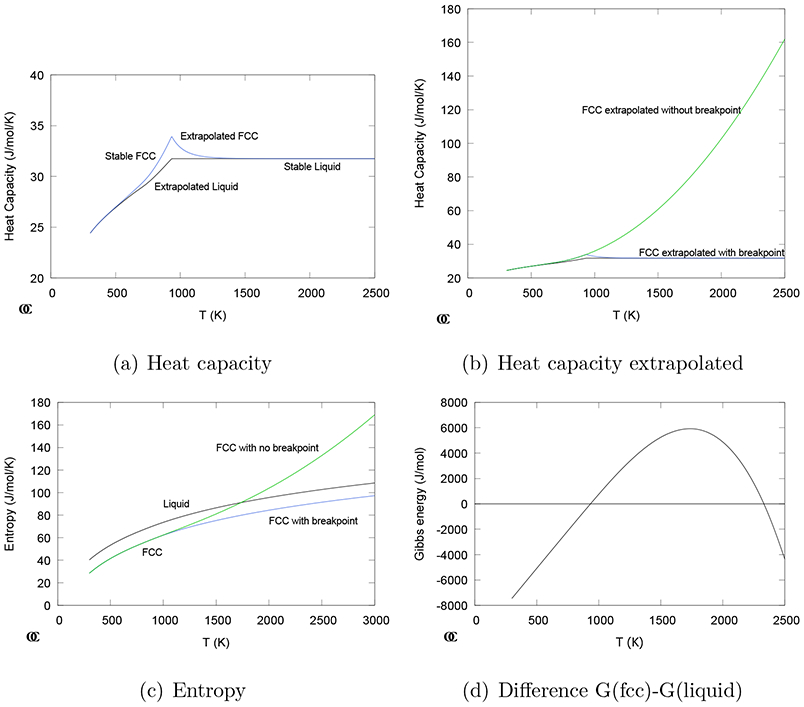
(a) Calculated C_P for pure fcc and liquid Al extrapolated according to the SGTE unary database [2]. (b) A curve has been added extrapolating the C_P fitted to the stable fcc without the break point. (c) The entropy curves for the liquid and the fcc with and without the break point. (d) The difference of the Gibbs energy for the fcc without the break point and the liquid.

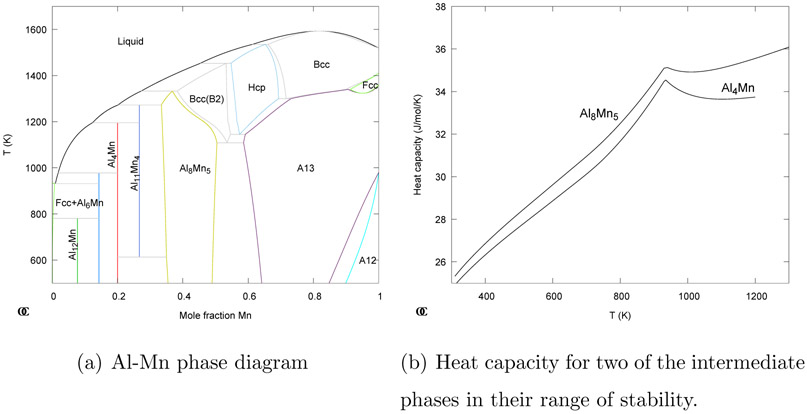
As an example how the kink in the heat capacity for a pure element can be inherited consider the assessment of the phase diagram for Al-Mn in Fig. 2(a) and the heat capacity of two intermediate phases plotted in Fig. 2(b). Both phases have a kink at the melting temperature of Al and for a stoichiometric compound like Al₄Mn the heat capacity can be refitted using experimental data but for a solution phase like Al₈Mn₅ it is necessary to remove the kink already in the description of the pure element.

Figure 2:

(a) The phase diagram for Al-Mn as assessed by [5] with several intermetallic phases. The heat capacities for two of them, Al₄Mn and Al₈Mn₅ are plotted in (b). For the Al₈Mn₅ the composition was selected to be 40 % Mn per mole. Both heat capacities have a kink at the melting temperature of pure Al.

When the C_P expression for the stable fcc Al phase, as fitted by SGTE, is extrapolated beyond the melting temperature to high temperatures, the C_P curve shown in Fig. 1(b) extends to very high values. The C_P of liquid Al was assumed constant by SGTE but larger than 3R, a value recommended for most liquid metals [6, 7] at high temperature when experimental data is missing. In Fig. 1(c) the corresponding entropy curves for liquid and fcc with and without break point are plotted, the latter intersects with the liquid curve around 1600 K where $S_m^{\text{fcc}}=S_m^{\text{liq}}$. This has as consequence that at this temperature the Gibbs energy difference between the fcc and liquid phases has a maximum and starts to decrease as shown in Fig. 1(d), and eventually the fcc phase is predicted to become stable again around 2300 K.

It is contrary to experience that a solid phase, with any composition, can reappear at temperatures far above its melting point. It is evident that the prediction of a solid stable at high temperature is caused by the high C_P values in the extrapolated part of the C_P function for the solid fcc phase without break point because:

$${\left(\frac{\partial (S_m^{\text{fcc}}-S_m^{\text{liq}})}{\partial T}\right)}_{P,N_i}=\frac{C_P^{\text{fcc}}-C_P^{\text{liq}}}{T}$$ (1)

$${\left(\frac{\partial (G_m^{\text{fcc}}-G_m^{\text{liq}})}{\partial T}\right)}_{P,N_i}=-(S_m^{\text{fcc}}-S_m^{\text{liq}})$$ (2)

At the 2013 Ringberg workshop Palumbo et al. [8] discussed several options for removing the kink in C_P to get a smooth transition of the Gibbs energy expression at the melting point for the solid phases. But they could not propose any model.

2. A new method to avoid kinks and reappearing solid phase

The method proposed in this paper is based on the observation that in all systems at equilibrium at sufficiently high temperature no solid phases are stable. From this one can conclude that the liquid must always have a higher entropy than any stable solid phase, independently of the composition of the phase. Thus a solid phase with higher entropy than the liquid at the same temperature should not be allowed to become stable but should be removed from an equilibrium calculation. As illustrated by Fig. 1(d), the Gibbs energy for the solid cannot become lower than the liquid Gibbs energy without first having a point of maximum difference and that is also a point of equal entropies. The entropies of the solid and liquid phases are available during the equilibrium calculation and an equal-entropy criterion, EEC, thus can be tested by the software at each calculation and a solid phase with higher entropy than the liquid can be removed without any loss of time. This criterion is formally identical to the prediction of an entropy catastrophe [9, 10] but is fundamentally different because it is not based on a physical model that could possibly predict an instability. The Gibbs energy expression for the solid is just a mathematical model and the EEC simply reveals when the model makes an incorrect extrapolation. Any solid phase α for which S^α/S^liquid ≥ 1 must be removed and not allowed to be stable and the temperature for S^α/S^liquid = 1 will be called the equal entropy temperature, EET.

In the next section it will be shown how the EEC can be applied to a multi-component system when the solids are metastable and have compositions different from the liquid.

2.1. The EEC applied to a multi-component system

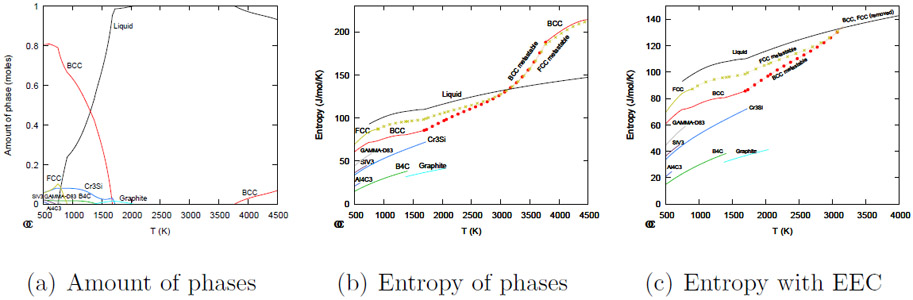
To gain some confidence in the EEC we present in Fig. 3(a) a calculated phase fraction diagram between 500 and 2500 K for an Al-B-C-Cr-Al-Cu-Li-Mn-Si-Sn-V alloy with the major elements 42% Cr and 40% V per mole. The COST 507 database [11] was used for the calculation. This database has 120 phases for this system of which 8 solid phases are predicted to be stable in this alloy. In Fig. 3(b) the molar entropies of the solid and liquid phases are plotted as solid lines in their stable temperature ranges. For the fcc and bcc phases the calculated molar entropy (at the composition closest to becoming stable for each phase, see section 2.4) are plotted with x and dot symbols also in the temperature range where they are metastable. The general expectation, that the liquid should always have higher molar entropy than any of the stable solid phases in the equilibrium, is confirmed, even if the compositions of the phases are very different as shown in Figs. 3(c)-3(e).

Figure 3:

Calculations for varying temperature of an 11-component alloy showing the amount of the phases, their entropy and the composition of liquid, bcc and fcc phases in their range of stability. The entropies of the metastable fcc and bcc in (b) are always lower than the entropy of the liquid because at high temperature they have the same heat capacity as the liquid. See the text for more details.

The COST database uses the SGTE unary data and Fig. 3(a) was calculated keeping the break points at the melting temperatures of the pure elements. The effect of extrapolation to higher temperatures without these break points is illustrated by the phase fraction diagram in Fig. 4(a) where the bcc phase appears with a stable amount above the liquid phase field at temperatures above 4000 K. This is evidently incorrect and must be due to the extrapolation of the Gibbs energy being seriously bad for the metastable bcc. The result should thus be neglected and as bcc is stable at low temperature an automatic procedure related to some property of the bcc phase is needed. The EEC seems to serve well in this role because Fig. 4(b) confirms that the bcc phase now has higher molar entropy than the liquid when it becomes stable and thus violates the EEC. The lines marked with x and dots are the entropies of the metastable extrapolation of bcc and fcc, respectively, as in Fig. 3(b). The removal of the break points has significantly increased the entropies already at 3000 K for fcc and bcc and long before the bcc becomes stable its entropy is higher than the liquid. With an automatic test for the EEC it would be safe to use the database without any break points.

Figure 4:

(a) Effect of removing the break point for the descriptions of the pure elements, the bcc phase reappears below 4000 K. (b) Entropy curves for the phases in their stable ranges and for the bcc and fcc also in their metastable ranges, drawn with dots and x, respectively. Note the sharp increase of the entropy for fcc and bcc at high temperature. In (c) the EEC has removed the phases with an entropy higher than the liquid.

Using the EEC will remove any phase with an entropy higher than the liquid as shown in Fig. 4(c) and thus prevent the bcc or fcc from becoming stable at high temperature and we obtain the same phase fractions as in Fig. 3(a).

The entropy plotted for the extrapolated metastable fcc and bcc phases in Figs. 3(b), 4(b) and 4(c) are for the compositions that are closest to becoming stable, because these are the compositions the computer software will track for all metastable phases as explained in section 2.4. Any metastable phase with an entropy higher than that of the liquid at its calculated composition will be removed according to the EEC. This means the EEC will compare the entropy of solids with different compositions with the entropy of the stable liquid at the same temperature. It is the software, calculating the equilibrium, that must remove phases not satisfying the EEC.

2.2. The EEC applied to the binary Al-Cr

As an example how the EEC can work in a binary system the Al-Cr system was selected because the melting temperatures of Al and Cr differ more than 1000 K. In Fig. 5(a) the phase diagram for Al-Cr has been calculated from the SGTE 1991 unary database without the break points for solid phases at the melting temperatures for Al and Cr. The phases were treated as ideal solutions and all intermetallics ignored and the EEC was not applied. The bcc phase for Al is assumed to have the same C_P as fcc and in combination with a lattice stability: $G_{\text{Al}}^{\text{bcc}}=G_{\text{Al}}^{\text{fcc}}+10083-4.813$ T, the bcc becomes stable at high temperature across the whole composition range.

Figure 5:

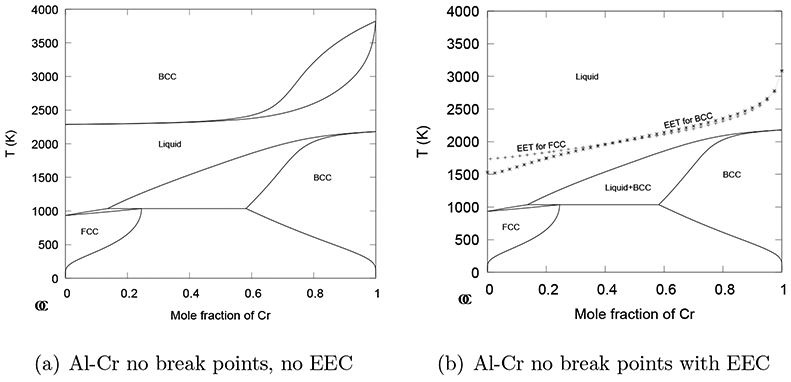
(a) The Al-Cr phase diagram without break points for pure Al and Cr and without the EEC. (b) The same diagram calculated with the EEC and with the EET for fcc (+) and bcc (*) plotted inside the liquid range.

In Fig. 5(b) the diagram has been calculated with the same parameters and applying the EEC. The lines with symbols represents how the EET for fcc and bcc varies with the liquid composition across the system. Above these lines the EEC will remove the bcc and fcc phases and the liquid remains the only stable phase at higher temperatures. Both diagrams in Fig. 5 have been calculated using the heat capacity of the metastable fcc Al shown in Fig. 1(b). This is certainly an extreme extrapolation and may cause other problems but it is possible to obtain a more reasonable extrapolated heat capacity for pure Al without creating any kinks when the EEC can prevent the solid to reappear at high temperatures.

2.3. The EEC applied to the properties of compounds and solutions

Compounds with an independently assessed heat capacity expression always have a melting temperature that was fitted and above this the EEC will prevent the compound from becoming stable again if its heat capacity extrapolates badly.

Entropy contributions from temperature dependent excess parameters should normally have similar magnitudes in both solid and liquid phases and thus should not be any problem. However, if such problems should occur a careful check of the assessment for the model parameters will solve them.

2.4. Implementation of the EEC in software

It will be straightforward to implement the EEC in any thermodynamic software used to calculate the equilibrium and it will not make the equilibrium calculations slower because the entropy of the phases at their current composition are available at each iteration during an equilibrium calculation.

Each software will have its own implementation of the EEC and simply calculates the entropies together with the Gibbs energies of the liquid and solid phases during the equilibrium calculation. It is recommended that the entropies for all of the metastable phases are also calculated at each iteration and the phases are removed if their entropy fails the EEC. In software like Thermo-Calc [12] or OC [13] which use the algorithm proposed by Hillert [14], the metastable phases will always have a well-defined composition which is the one closest for the phase to become stable. In other software there must be some kind of estimate of the compositions of the metastable phases that can be used to remove a metastable solid phase with higher entropy than the liquid. Alternatively, the EEC can be used when a new solid phase is found to be stable in an iteration step or when the equilibrium has been calculated. Though in the latter case the equilibrium must be recalculated with this phase removed and this will take extra time.

There is a small risk that a metastable solid phase will be removed due to the EEC when in fact it could become stable with another composition and with lower entropy than that of the liquid. This should mean that the solid has a miscibility gap and it is the responsibility of the software to detect this and adjust the composition of the phase. If the liquid has a miscibility gap the liquid with the highest entropy should be used for the EEC. The implementation of the EEC in the OC software is available at [15] as this is a free software.

3. Unary database and models

In 1991 the SGTE unary database was a big progress for the Calphad method as it included not only heat capacity descriptions but also a separate model for the magnetic transitions. The heat capacity for the stable phase of an element was applied to for all metastable allotropes for that element. This database gained worldwide acceptance for assessments of many thermodynamic systems and most commercial databases. Agreement on a unary database is essential for creating multi-component databases because it is necessary that the pure elements are modeled in the same way in order to combine assessments from different researchers.

Recently serious work has begun to develop a new unary database with more sophisticated descriptions [16, 17, 18, 19, 20, 21]. The criteria that these new unary descriptions need to fulfill and the functions to mathematically represent them are now being discussed at a series of bi-annual workshops at the KTH Royal Institute of Technology in Stockholm, Sweden. In this new unary database all phases have zero heat capacity at 0 K and all perfectly ordered crystalline phases have zero entropy at 0 K.

One focus of these discussions has been the handling of the thermodynamic properties of metastable solid phases far above their melting temperatures. The discussions on the treatment of the extrapolation of the properties of the metastable solid phases far above their melting temperatures spawned a new need for handling this and this new proposed treatment, the appliaction of the EEC, is described in the present paper. But already when using modifications of the SGTE 1991 unary descriptions, the EEC is useful to detect extrapolations that are nonphysical. In this paper a single example of a multi-component application of the EEC is shown but the EEC has been tested for many other systems with satisfactory results.

4. Conclusion

The assumption made in this paper that the liquid phase in a system should always have higher entropy than any stable solid phase is based on the observation that at high temperature the liquid is the only stable condensed phase. The equi-entropy criterion, EEC, is derived from this and states that a solid with higher entropy than the liquid must not be allowed to be stable.

If a solid phase with higher entropy than the liquid is predicted to be stable in a calculation, it will most certainly depend on a bad extrapolation of the Gibbs energy function of the phase. The result cannot be trusted and, therefore, this phase should be removed from the calculation of this particular equilibrium. By applying the EEC criterion already during the equilibrium calculation, the phase can be identified and removed automatically without noticeable expense of time. This method may decrease the need of the compromise made in the 1991 work which introduced a kink in the heat capacity of the pure elements because the method allows more freedom in the search for better extrapolations of Gibbs energy functions of solid phases of elements when fitting to experimental and theoretical data.