Modeling and forecasting of COVID-19 using a hybrid dynamic model based on SEIRD with ARIMA corrections

Abstract

The outbreak of novel coronavirus (COVID-19) attracted worldwide attention. It has posed a significant challenge for the global economies, especially the healthcare sector. Even with a robust healthcare system, countries were not prepared for the ramifications of COVID-19. Several statistical, dynamic, and mathematical models of the COVID-19 outbreak including the SEIR model have been developed to analyze the infection its transmission dynamics. The objective of this research is to use public data to study the properties associated with the COVID-19 pandemic to develop a dynamic hybrid model based on SEIRD and ascertainment rate with automatically selected parameters. The proposed model consists of two parts: the modified SEIRD dynamic model and ARIMA models. We fit SEIRD model parameters against historical values of infected, recovered and deceased population divided by ascertainment rate, which, in turn, is also a parameter of the model. Residuals of the first model for infected, recovered, and deceased populations are then corrected using ARIMA models. The model can analyze the input data in real-time and provide long- and short-term forecasts with confidence intervals. The model was tested and validated on the US COVID statistics dataset from the COVID Tracking Project. For validation, we use unseen recent statistical data. We use five common measures to estimate model prediction ability: MAE, MSE, MLSE, Normalized MAE, and Normalized MSE. We proved a great model ability to make accurate predictions of infected, recovered, and deceased patients. The output of the model can be used by the government, private sectors, and policymakers to reduce health and economic risks significantly improved consumer credit scoring.

1. Introduction

The outbreak of the COVID-19 epidemic has restored the interest of the research fraternity and political community in the mathematical modeling and forecasting of the epidemic. Lots of research works are coming up with new predictive models to analyze the surge of the outbreak and to predict future outcomes (Anastassopoulou et al., 2020; Cooper et al., 2020; Giordano et al., 2020; Kucharski et al., 2020a; Ndairou et al., 2020; Rafiq et al., 2020; Russo et al., 2020; Silva et al., 2020; Wu et al., 2020b; Zhou et al., 2020). The Covid-19 pandemic outbreak has posed significant challenges to the global economy and the healthcare industry. Several statistical, mathematical, and dynamic models of the Covid-19 outbreak including the SIR, SEIR, and SEIRD have been developed to analyze the transmission dynamics of the outbreak (Cooper et al., 2020). Although these epidemiological models are useful for estimating the dynamics of transmission, when it comes to targeting resources and evaluating the impact of intervention strategies, these models are parametric and depend on many assumptions (Kucharski et al., 2020b; Li et al., 2020; Tuite & Fisman, 2020; Wu et al., 2020b; Zhao et al., 2020). Unlike system identification in engineering, where the parameters in the models are estimated using real data, at the outbreak, estimated parameters using real-time data are not accurate or readily available. Most analyses used manually chosen parameters and hence did not fit the data very well. The accuracy of forecasting the future cases of COVID-19 using these models may not be very high.

The key challenge involved in identifying the transmission of the Covid-19 pandemic is that the true numbers of infected cases. The infected numbers available for mathematical modeling of the dataset are those confirmed by tests. However, there may be many infected people who may never get tested, which makes the confirmed cases to be only a fraction of the true number of actual infections. Bertozzi et al. (Bertozzi et al., 2020) present a detailed study on challenges involved in building a mathematical model for Covid-19 spread, to measure its impact on the economy, and to build policies. The outcome of the study (Bertozzi et al., 2020) shows that the SEIR model may result in over-predicting the reproduction number R₀ and is not well calibrated. In studies (Ge et al., 2020; Qianying, 2020) modifications of SEIRD model was studied with considering under-reporting in early stages of pandemic.

A generalized SEIR model study on the Italian Covid-19 dataset was carried out by Godio et al. (Godio et al., 2020) using Swarm Intelligence Approach. The authors (Godio et al., 2020) claim that the method followed aims to enhance the reliability of predictions. This research is spearheading in the regions of Spain and South Korea, however, has its limitations that include the conditions of partial infections due to exposure (Shi, Cao, & Feng, 2020), or it classifies the category of symptomatic and asymptomatic cases (Shaikh, Shaikh, & Nisar, 2020) due to the nature of the epidemic spread.

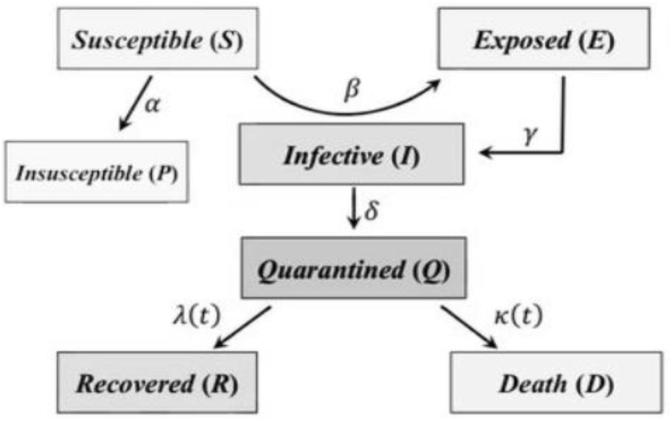
The main objective of this work is to improve the classical SEIR model, using the SEIRD and ARIMA models which will compensate residuals between actual and predicted data. The final broad objective is to provide a reliable approach that predicts the epidemic evolution so that the policymakers could undertake both proper initiatives to reduce the contagion and perform selective actions considering the distinctiveness of each region. A more generalized SEIRD model scheme is presented in Fig. 1.

Fig. 1.

SEIR Model for epidemic outbreak prediction (Korolev, 2020; Wang et al., 2020).

2. Related work

Mathematical modeling concedes rapid computation and estimation of pandemic outbreaks and plays a valuable role in decision making. Simulation techniques, on the other hand, are used when the data collection involves a large number of conditions to test, which leads to increased cost (Siettos & Russo, 2013). Several mathematical and statistical models have been derived recently such as the Multivariate linear regression (Thomson et al., 2006), time series models (Kurbalija et al., 2014), grey forecasting models (Wang et al., 2018a; Zhang et al., 2017), back-propagation neural networks (Liu et al., 2019; Ren et al., 2013; Zhang et al., 2013), and simulation models (Nsoesie et al., 2013; Orbann et al., 2017). The spread of an epidemic is unpredictable and random. Due to this reason, it becomes difficult to build mathematical models to analyze epidemic randomness. Hethcote (1989, pp. 119–144) identifies three basic types of deterministic models – SIS endemic, SIR epidemic, SIR endemic for the mathematical modeling, and predicting the spread of infectious disease. Theorems that consist of “reproduction number R0, contact number σ and replacement number R″ are presented for mathematical models like SEIR and MSEIRS (Hethcote, 1989, pp. 119–144). Compared with statistics methods, mathematical modeling based on dynamical equations receive relatively less attention (Adam et al., 2020), though they can provide a more detailed mechanism for the epidemic dynamics.

The classical susceptible exposed infectious recovered model (SEIR) is one of the most widely adopted methods for characterizing the epidemic of COVID-19 outbreak in both China and other countries (Hethcote, 1989, pp. 119–144). The SEIR model replicates the “time-history” of any epidemic or pandemic outbreak, and it presents the model of dynamic interaction between people with four different health conditions or phases of the pandemic, namely the susceptible (S), exposed (E), infective (I), and recovered (R). SEIRD model contains the 4 basic containers in the SEIR model: Susceptible, Exposed, Infective, Recovered, along with an added container - Dead. A “Formal Characterization and Model Comparison Validation” based on the SEIRD model which uses the data from Korea and Spain is proposed by Casas et al. (Fonseca i Casas et al., 2020). The proposed model showed the predicted parameterization with empirical evidence and a decision support system (DSS) is implemented to study the nature of the pandemic in Catalonia (Fonseca i Casas et al., 2020).

A data-driven model to predict the spread of Covid-19 for an upcoming week using the SEIRD model is studied and tested for datasets obtained from Italy, India, and Russia (Rapolu et al., 2020). The proposed model (Rapolu et al., 2020) produces results in which the parameters are calculated from the data, to plan for the future requirement of PPEs for hospital staff and healthcare devices. Contrarily, the transmission dynamics of Covid-19 were evaluated based on a SEIRD compartmental modeling approach by Mukaddes et al. (Mukaddes et al., 2020). This model was based on the “kinematic parameters” that describe the transmission, recovery, and death rate in Bangladesh. The study also highlights the dynamic factors and two parameters that refer to infection which derives the reproduction number R_0. This study is groundbreaking for research work carried out in developing nations to reopen the businesses and to boost the economy back to the pre-covid period. However, external influences such as weather, herd immunity were not considered as a part of the study (Mukaddes et al., 2020).

The COVID-19 pandemic is very dynamic and spreads rapidly, and hence there is a need to create robust modeling solutions to curb the outbreak. A forced SEIRD model with two different infection rate functions of the Covid-19 spread in Italy was investigated by Piccolomini et al. (LoliPiccolomini & Zama, 2020), in which the “integration time was distributed into sub-intervals” to estimate the model parameters. The study was based on data collected from two regions in Italy, Lombardia and Emilia-Romagna. This model (LoliPiccolomini & Zama, 2020) will be efficient to make predictions about different stages of the epidemic outbreak across various regions in Italy and Europe. Another popular and widely used statistical method for time-series forecasting is the Automatic Regressive Integrated Moving Average (ARIMA) model, which studies the series of temporal structures in time series data. Earlier study on disease management techniques with time series using ARIMA models is proposed by Sato (2013). The author Sato (2013) emphasizes the fact that the options to follow up and spot the difference in data patterns should be given importance in healthcare practices.

Forecasting a disease is essential for the healthcare department and policymakers to strengthen their vigilance and reallocate their resources. ARIMA time series model is a widely accepted method for the pandemic forecasting because of its simplicity and systematic structure (Ceylan, 2020; Wang et al., 2018b). The extent of the outbreak of the Covid-19 pandemic in Italy, Spain, and France was examined with the ARIMA model (Ceylan, 2020). The proposed model consists of 4 steps in modeling which include “assessment, prediction of parameters, characteristic checking, and forecasting”. The outcome of the study can guide policymakers and healthcare authorities in the European nations to effectively allocate resources and plan for the future flare-up of the current situation (Ceylan, 2020).

Alzahrani et al. (Alzahrani et al., 2020) studied the spread of pandemic outbreak using the ARIMA prediction model in Saudi Arabia. The authors have used the “linear parametric model prediction approach”, in which the parameters of the ARIMA model were chosen based on the value of the “Akaike information criterion” (Akaike, 1974; Alzahrani et al., 2020). The dataset was divided into training and testing datasets and four statistical models were employed to predict the spread of Covid-19, by comparing the performance of each model with the evaluation metrics from which good fit is derived (Alzahrani et al., 2020). Other related studies and research work on disease prediction using ARIMA and hybrid ARIMA modeling techniques found in the literature are presented in Table 1.

Table 1.

Research work found in the literature for disease prediction using ARIMA/hybrid models.

Method (s)/Type of Modeling	Pandemic/Epidemic/Endemic	The research found in the literature
ARIMA	Malaria	Gaudart et al., (Gaudart et al., 2009)
ARIMA, Artificial Neural Networks (ANN)	HAV	Guan et al., (Guan et al., 2004)
ARIMA	SARS	Earnest et al., (Earnest et al., 2005)
ARIMA, Seasonal Autoregressive Integrated Moving Average (SARIMA)	Influenza	He et al., (He & Tao, 2018); Chen et al., (Chen et al., 2020)
Multivariate Poisson Regression (MPR), ARIMA, and ANN	Dengue Fever	Polwiang (Polwiang, 2020)
Random Forest (RF), ARIMA/X Models	Infectious Diarrhea	Fang et al., (Fang et al., 2020)
Elman Recurrent Neural Networks (ERNN), ARIMA, and Jordan Neural Networks (JNN)	Brucellosis	Wu et al., (Wu et al., 2019)
ARIMA (or) SARIMA-NAR (Nonlinear Autoregressive Network) (or) hybrid model	Covid −19	Ceylan (Ceylan, 2020); Alzahrani et al. (Alzahrani et al., 2020); Perone (Perone, 2020); Kumar et al. (Kumar et al., 2020); Sato (Sato, 2013); Wang et al. (Wang et al., 2018b); Benvenuto et al. (Benvenuto et al., 2020); Hernandez-Matamoros et al. (Hernandez-Matamoros et al., 2020); Kufel (Kufel, 2020)

This paper aims to build a hybrid model that will allow us to estimate the short and long-term dynamics of COVID disease and build confidence intervals of predictions by using a hybrid dynamic model based on SEIRD with ARIMA corrections. This model will help officials to be prepared for the waves of pandemic and reserve hospital beds in advance.

3. Materials and methods

3.1. Dataset

The proposed method was tested on US statistics from The COVID Tracking Project (COVID Tracking Project, 2020). This volunteer-based organization proved to be a reliable source of information about the COVID-19 outbreak in the US and is used by major research facilities worldwide. The dataset includes daily information on the number of infected, recovered, and deceased individuals for each date. The data is updated daily, enabling researchers to update model parameters frequently to achieve the highest accuracy possible. The first available observation dates to January 22, 2020.

The dataset consists of the following columns:

• ▪Cumulative infected people as of each date (all individuals who were diagnosed till each date).
• ▪Cumulative recovered people from the start of the outbreak;
• ▪Deceased people from the start of the outbreak.

The observed data as of those dates is reported in Table 2, the key dates in the dynamics of the outbreak are major (common for many states) stay-at-home orders or advisories enactments (March 30 and April 04, 2020) and lifts (April 30 and June 02, 2020). Note that the dates differ from state to state because lockdowns are state-regulated, and six states never or enforced lockdowns. The last day of observation used while building this method is September 16. Since the stay-at-home orders and advisories didn’t change the situation dramatically, lockdown isn’t considered in the proposed model, and basic model parameters are proposed to be fixed.

Table 2.

Statistics of the COVID outbreak in the US as of key dates in government responses to the COVID-19 pandemic.

Date∖Key statistics	Infected	Increase in Infected	Recovered	Deceased
March 30	173,442	22,042	4560	3424
April 4	317,434	33,212	12,816	9264
April 30	1,074,764	29,549	154,648	59,580
June 2	1,835,554	20,110	541,976	102,131
September 16	6,597,783	40,021	2,525,573	188,802

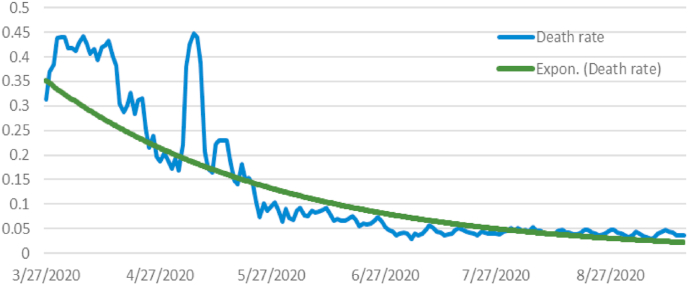
On the other hand, according to Fig. 2, the COVID death rate was decreasing over time, which was reflected in the dynamic model. The death rate is decreasing over time, which can be explained by continuous scientific efforts to cure the disease more efficiently.

Fig. 2.

COVID Death rate dynamics and its trend line.

3.2. The hybrid dynamic model framework

In the investigation, we introduce a hybrid model which is based on an enhanced SEIRD model and ARIMA model.

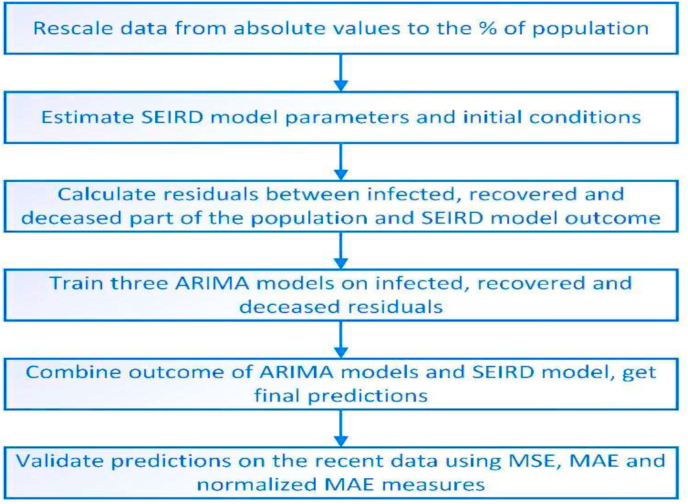
As it is shown in Fig. 3, the method’s core stages are: building a SEIRD compartment model; estimating its parameters; calculating and predicting the difference between SEIRD model solution and observed data using the ARIMA model; adjusting model prediction using this difference.

Fig. 3.

The workflow of the proposed algorithm.

This model consists of the following stages:

• 1.Firstly, we estimate SEIRD model parameters using historical data, trying to make a perfect fit as possible. This model is responsible for long-term prediction.
• 2.Calculate residuals between historical infected, recovered, and deceased percentage of the population, and corresponding solutions of the SEIRD model
• 3.Train three ARIMA models on each of these residuals. Prediction of ARIMA models will compensate residuals between the SEIRD model and historical data and make predictions mode accurate.
• 4.Validate the prediction of the obtained hybrid model using recent data, which was not included in previous stages.

Given that a large proportion of the COVOD-19 infections are asymptomatic or mild asymptomatic and the testing capacity is not always sufficient, not all infected (and therefore recovered and deceased) patients are tested & reported. The observed number of cases constitutes some proportion on of all infections; the ratio of the two is called ascertainment rate (or reporting rate) (Ge et al., 2020; Qianying, 2020), (Ge et al., 2020; Qianying, 2020). When testing capacity is not sufficient, or testing effort is not very high, the reporting rate could be as low as 5% or 10% (Peixoto et al., 2020). In very ideal situation, the reporting rate could be as high as 50–70%, followed by a successful control of the epidemic. If the number of infected patients increases rapidly, it is a sign that the ascertainment rate is low, much more cases were not tested or reported. The true number of infections might only be found through a population level serological study. That is why, during the model parameters estimation we introduce “ascertainment rate” parameter, which is a scaling factor of historical infected, recovered and deceased population.

3.3. SEIRD model with vital dynamics and dynamic mortality rate

A basic compartment model in epidemiology is the SIR model (Harko et al., 2014), (Beckley et al., 2013), which studies the population’s flow between three compartments: Susceptible, Infected, and Recovered. It has already been applied to the recent COVID-19 pandemic and showed good results (Yang et al., 2020). The next level of complexity is introducing vital dynamics (birth and mortality rates) to the model (Shi et al., 2020). Since the coronavirus decease has a quite long incubation period, it is logical to model the pandemic with another compartment – Exposed individuals who already are infected but cannot spread the virus further yet. Such a model is called a SEIR compartment model. One more introduced compartment that completes our compartment structure is Deceased individuals.

A SEIRD model simulates the flow of the population between Susceptible, Exposed, Infected, Recovered, and Deceased groups (or compartments). While traditionally compartment models are built for closed systems, in this method, the total population size is not fixed due to the introduction of birth and mortality rates. This allows us to model the pandemic more accurately. The COVID mortality rate is represented by an inverse exponential function with two parameters, rather than a constant. Based on the analysis shown in Fig. 1, it was proved to be useful to model the mortality rate as an inverse exponential function, which is another heuristic to the proposed method for the same reason.

The compartments of the model are as follows:

S(t): Susceptible individuals - stock of healthy people who may be infected; population inflow due to births is considered.

E(t): Exposed individuals - virus carriers in the latent stage, during which they are not virus spreaders. Usually corresponds to an asymptomatic phase of the disease.

I(t): Infectious individuals - virus carriers able to spread the disease to individuals in contact with them.

R(t): Recovered individuals - stock of healthy people who are immune to COVID-19.

D(t): Deceased individuals - population loss due to the disease, natural deaths included.

The model itself is comprised of a system of differential equations:

$$\{\begin{array}{l}\frac{dS}{dt}=\Lambda N-\mu S-\frac{\beta SI}{N}\hfill \\ \frac{dE}{dt}=\frac{\beta SI}{N}-\left(\mu +\mathrm{\sigma }\right)E\hfill \\ \frac{dI}{dt}=\sigma E-\left(\gamma +\mu \right)I\hfill \\ \frac{dR}{dt}=\gamma \left(1-{\mu }_{COVID}\left(t\right)\right)I-\mu I\hfill \\ \frac{dD}{dt}=\gamma {\mu }_{COVID}\left(t\right)I\hfill \end{array}$$ (1)

with constraints at time t = 0 S = ${\text{S}}_0$, E = ${\text{E}}_0$,I = ${\text{I}}_0$,R = ${\text{R}}_0$, D = ${\text{D}}_0$ and parameters.

• •$\text{Λ}$ – population’s birth rate;
• •$\mu$ – population’s mortality rate;
• •$\beta$ – rate of virus transmission, which is the probability of transmitting disease between a susceptible and an infectious individual;
• •$\mathrm{\sigma }$ – rate of latent individuals becoming infectious (average duration of incubation is $1/\mathrm{\sigma }$);
• •$\gamma$ – recovery rate, which can be initially estimated as $\gamma =1/D$, where $D$ is the average duration of infection;
• •${\mu }_{COVID}\left(t\right)$ – death rate due to COVID-19, which is estimated by an inverse exponential formula ${\mu }_{COVID}\left(t\right)=\alpha e^{-\mathrm{\xi }t}$.

The population size

$$N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)$$ (2)

is not fixed due to its global birth and mortality rates taken into account at any given time t.

3.4. Parameter estimation using basin-hopping algorithm

To use the model proposed in the previous section, firstly, we need to specify its parameters so it will fit the historical data. Moreover, we estimate not only the model parameters but also initial conditions for susceptible and exposed compartments of the model, and ascertainment rate.The reason for this assumption is that we are still uncertain about the percentage of the infected population that is not reported in statistics because of the mild form of illness (who will suffer from the disease in a mild form and do not infect others). Regarding the exposed population, we do not have the exact number of exposed passengers who visted the US at the time of the COVID outbreak. As the dataset consists of cumulative data, we calculated the number of currently infected individuals as a difference between cumulative infected and recovered ones. After this step, data was rescaled from the absolute numbers to the percent of the population.

To fit model parameters and initial conditions, we use the Basin-hopping algorithm (Wales & Doye, 1997). This iterative heuristic algorithm is a generalization of the simulated annealing algorithm, which was inspired by molecular processes that occur in metalwork. The procedure of annealing is used to achieve the optimal molecular arrangements of metal particles. While cooling, heated material comes into shape with minimal system energy - and therefore, less or no defect. After choosing an initial state, the algorithm picks the neighboring state and proceeds to decide on moving to it or staying and then iterates this process until finding the global optimum or reaching the iterations limit. As a generalization to simulated annealing algorithm, Basin-hopping global optimization technique randomly perturbates coordinates and proceeds to find the global optimum similarly.

One of the key reasons for choosing this instrument is the algorithm’s ability to reach global optima even after finding several local ones, as it is not restricted to the best candidates at each step. As a measure of quality between differential equation solution and historical data, we use MAE/mean metrics that were described and investigated in (Kolassa & Schütz, 2007). Thus, as an objective function of the Basin-hopping algorithm, we select the sum of:

$$\frac{MAE(I_A\cdot A_r,I)}{{\overline{I}}_A}+\frac{MAE(R_A\cdot A_r,R)}{{\overline{R}}_A}+\frac{MAE(D_A\cdot A_r,D)}{{\overline{D}}_A},$$ (3)

where $A_r$ is ascertainment rate, $I_A\left(t\right)$ is the actual percentage of the population that stays infected at day $t$, $R_A\left(t\right)$ is the actual percentage of the population that overcame the disease till day $t$, $D_A\left(t\right)$ is the actual percentage of the population that was deceased till day $t$, ${\overline{I}}_A,{\overline{R}}_A$ and ${\overline{D}}_A$ is the average values of infected, recovered, and deceased values over time domain, $MAE(\cdot ,\cdot )$ is calculated according to equation ($4$).

After parameter estimation all trajectories of infected, recovered and deceased population are scaled back by dividing on $A_r$.

3.5. ARIMA model for residual estimation

In this step, the difference between data by SEIRD algorithm and observed data is estimated and corrected using the ARIMA model (stands for Auto-Regressive Integrated Moving Average). The structure of this model includes autoregression and moving average as the main components. The autoregression algorithm uses a certain number of past data instances (also called the number of lagged observations) to predict the variable value at each new point, exploring trends and co-dependencies of observations.

Differentiation of raw data is performed to ensure stationarity of variable: each value at time t is subtracted from the value at time t-1.

The third part, moving average, also makes use of dependencies in the data, but this time between an observation and a residual error from applying the moving average algorithm to several lagged observations.

To each of these parts corresponds a parameter, where each parameter is an integer value:

p: Lag order, or number of past observations considered by the model;

d: Degree of differencing, or how many times raw observations are differenced; q: Order of moving average, or window size for moving average algorithm.

In our case, an algorithm that finds the best set of parameters and runs statistical tests of stationarity and seasonality is used. The obtained prediction of residuals is subtracted from data predicted by the compartment model to increase its performance.

3.6. Validation

During the validation stage, we gather new data that was not used in SEIRD model parameter estimation and ARIMA models fitting. We will use such measures of quality:

(1) Mean average error, given by equation

$$MAE\left(y,\hat{y}\right)=\frac{1}{T}\sum _{t=1}^T\left|y\left(t\right)-\hat{y}\left(t\right)\right|$$ (4)

(2) Mean squared error, given by equation

$$MSE\left(y,\hat{y}\right)=\frac{1}{T}\sum _{t=1}^T{\left(y\left(t\right)-\hat{y}\left(t\right)\right)}^2$$ (5)

(3) Mean squared logarithmic error, given by equation

$$MSE\left(y,\hat{y}\right)=\frac{1}{T}\sum _{t=1}^T{\left(\log (y\left(t\right)+1)-\log (\hat{y}\left(t\right)+1)\right)}^2$$ (6)

(4) Normalized mean average error, given by equation

$$NormMAE\left(y,\hat{y}\right)=\frac{MAE\left(y,\hat{y}\right)}{\overline{\left(y\right)}}$$ (7)

(5) Normalized mean squared error, given by equation

$$NormMAE\left(y,\hat{y}\right)=\frac{MSE\left(y,\hat{y}\right)}{\overline{\left(y\right)}\cdot \overline{\left(\hat{y}\right)}}$$ (8)

where $\overline{\left(x\right)}$ denotes mean value of time series $x$. Moreover, we calculate the maximum deviation between the main prediction line and two scenarios (optimistic and adverse) that are calculated from ARIMA models using a 95% confidence level. The equation of this measure is

$$MaxDev\left(y,\hat{y}\right)=\underset{1\le t\le T}{\max }\frac{\left|y\left(t\right)-\hat{y}\left(t\right)\right|}{y\left(t\right)}$$ (9)

4. Results and discussion

In this section, we will provide results of hybrid model approbation on data from the COVID Tracking Project (COVID Tracking Project, 2020).

4.1. SEIRD model

In this subsection, we estimate some parameters and initial conditions of the SEIRD model using the Basin-hopping algorithm and build rough long-term predictions of pandemic development. We optimize only initial values of susceptible and exposed fraction of the population, whilst infected, recovered, and deceased initial conditions are set to zero. Global birth and death rate are also not optimized and are set according to actual values for the annual 2020 birth and death rate in the US.

In Table 3 it is shown boundaries and optimized values for the SEIRD model parameters and initial values. As we can see from the table, the initial fraction of the susceptible population is estimated at the level of 93%. It can be explained by the fact that by inserting into model $A_r$ parameter, we take into account even mildly ill patients who will never appear in medical statistics. Otherwise, $S_0$ would be much lower. $A_r$ is quite low, which can be explained by the fact of insufficient testing in early stages of pandemic. Interestingly recovery rate is very low, which means that if a person suffers from the disease in a severe form, it takes a lot of time to recover. The value of $\mathrm{\sigma }$ is also very small, which shows that the incubation period of COVID is quite large. Worth noticing that all the above parameters were estimated only using mathematical algorithms and based on available data that might be inaccurate. That is why the values of the incubation period and recovery rate that are estimated in hospitals may differ from those obtained by our research. The pure SEIRD model can be used for the long-term rough predictions of the pandemic dynamic.

Table 3.

Optimized parameters and initial conditions of the SEIRD model.

Parameter	Description	Minimum value	Maximum value	Optimized value
$\mathrm{\sigma }$	Rate of latent individuals becoming infectious	0	0.1	0.00051
$\beta$	Probability of transmitting disease between a susceptible and an infectious individual	0	1	1
$\gamma$	Recovery rate, which can be initially estimated as $\gamma =1/D$, where $D$ is the average duration of infection.	0	0.1	0.0088
$\alpha$	Starting death rate from COVID	0	0.3	0.3
$\mathrm{\xi }$	Decaying speed of death rate due to enhancements in treatment	0	0.1	0.009
$S_0$	The initial fraction of the susceptible population	0.4	1	0.45
$E_0$	The initial fraction of the exposed population	0	0.05	0.035
$A_r$	Ascertainment rate, %	5%	100%	10.6%

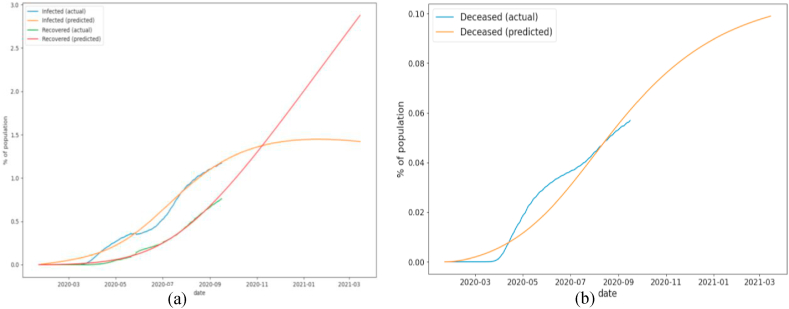
In Fig. 4, long-term predictions for infected, recovered, and deceased fractions of the population are displayed. In this and below figures, results of SEIRD model are scaled back by dividing on $A_r$. To get all infected population (both reported and not reported), corresponding plots should be multiplied by 9.45, which is $1/A_r$. Based on the figures, we can conclude that number of infected people will rise till early 2021, and afterwards will begin to decline.

Fig. 4.

(a) Long-term prediction of the infected and recovered fraction of population (b) Long-term prediction of the deceased fraction of population.

Based on Fig. 4 and Table 4, we can conclude that the SEIRD model fits historical data quite well, the best fit we have on infected and recovered constituents of the model. Un-normalized measures are the lowest for the deceased fraction population. It can be explained by the fact that the fraction of deceased patients comparing to infected and recovered is small.

Table 4.

Quality measures of fitted SEIRD model.

Category/measure	MAE	MSE	MSLE	Normalized MAE	Normalized MSE
Infected	$4.15\cdot {10}^{-4}$	$2.77\cdot {10}^{-7}$	$2.75\cdot {10}^{-7}$	0.099619	0.015101
Recovered	$1.2\cdot {10}^{-4}$	$2.64\cdot {10}^{-8}$	$2.62\cdot {10}^{-8}$	0.059617	0.006346
Deceased	$3.99\cdot {10}^{-5}$	$2.76\cdot {10}^{-9}$	$2.76\cdot {10}^{-9}$	0.167145	0.053079

4.2. ARIMA models

At this step, we calculate residuals between the fitted SEIRD model and historical data and train ARIMA models on the residuals for each category (infected, recovered, deceased). To estimate optimal ARIMA parameters P and Q, we use the Akaike information criterion, and to estimate the optimal D parameter, we use the Augmented Dickey-Fuller test (Dickey, 2015, pp. 192–30).

In Table 5, the estimated parameters of ARIMA models for each category are presented. Worth mentioning that parameters of ARIMA models over different constituents of model are very similar, which is a good sign that tells us that the behavior of residuals time series is the same and can be simulated using similar (or even the same) models. After training ARIMA models, we evaluate predictions for all three categories 60 days ahead.

Table 5.

Parameters of ARIMA models for each category.

Category/parameter	The order of the autoregressive model (P)	The degree of differencing (D)	the order of the moving-average model (Q)
Infected	2	0	2
Recovered	0	2	2
Deceased	2	0	2

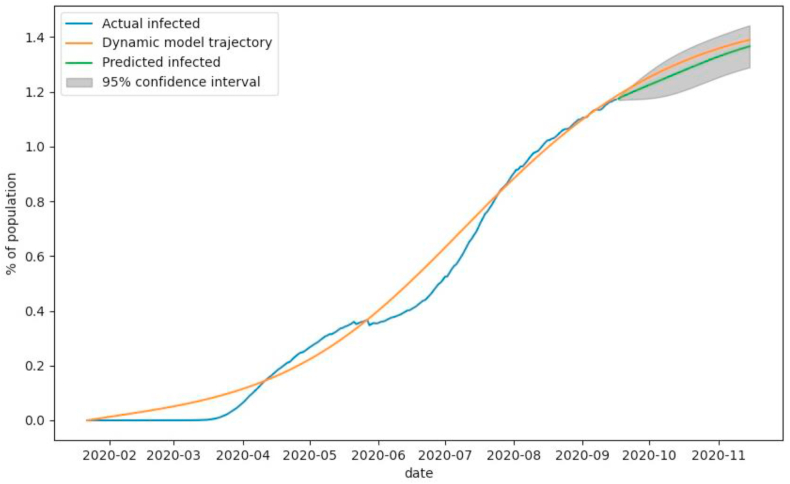
The analysis of modeling and prediction of the number of infected individuals (Fig. 5) shows that the number of observed cases of decease during the early stage of the outbreak (mid-May) is deficient due to the small number of tests performed during this period. The inconsistency in testing and changing levels of quarantine severity explain further fluctuations in deviations of observed data from the output of the SEIRD model. The prediction, corrected by ARIMA residual estimation, steadily increases, with optimistic and pessimistic scenarios (lower and upper bounds of the grey area, respectively) deviating by around 0.1%

Fig. 5.

The observed number of infected individuals (blue), number of infected individuals modeled with SEIRD model (yellow), and predicted number of infected individuals (green) by SEIRD model and corrected by ARIMA residual prediction with 95% confidence interval (grey).

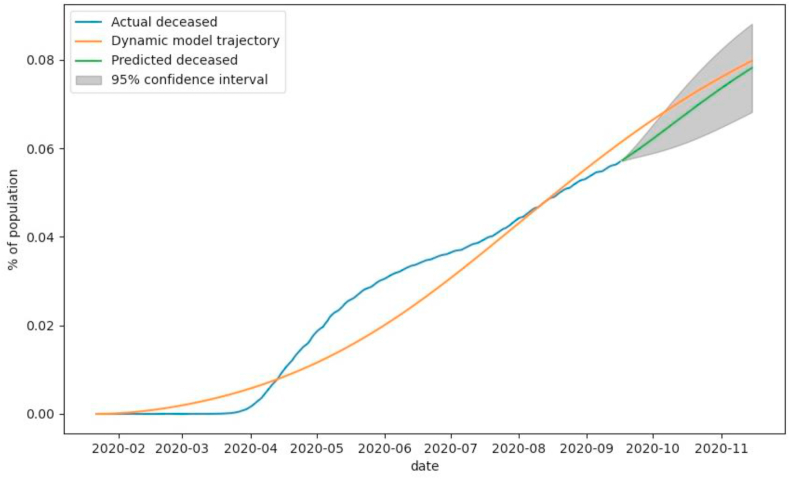
As shown in Fig. 6, until early April, the losses from COVID-19 are close to zero. It is safe to assume that some people who passed away due to the decease were undiagnosed or misdiagnosed, and therefore the data on those cases were not taken into account in COVID statistics. A decline in the COVID death rate observed in August after it has grown for several months presumably occurred by the reason for the development and spreading of treatment protocols and medical research that allowed to select of the most effective medicine. Despite all the measures of previous months, the predicted number of deceased individuals rises quite sharply.

Fig. 6.

The observed number of deceased individuals (blue), number of deceased individuals modeled with SEIRD model (yellow), and predicted number of deceased individuals (green) by SEIRD model and corrected by ARIMA residual prediction with 95% confidence interval (grey).

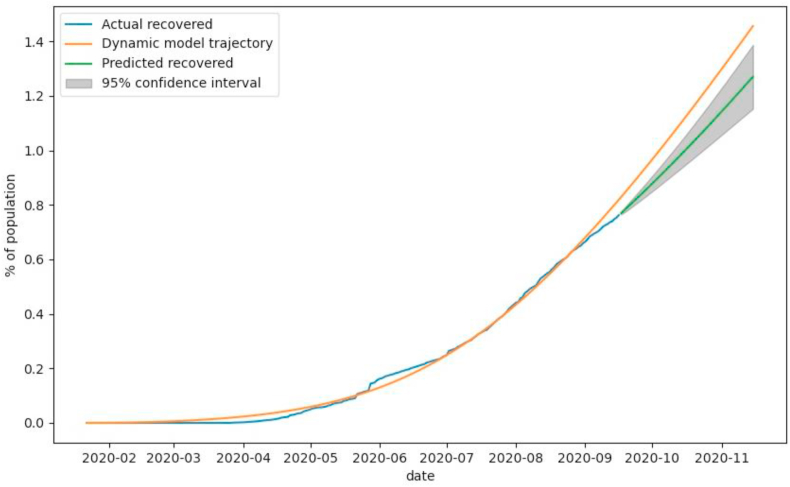
The proposed method describes the changing number of recovered individuals very accurately (Fig. 7), while in the early stages of the outbreak; the number of people recovered is lower than expected. It can be explained by a lack of techniques and materials to treat the patients. However, in the first half of August, we observe a decrease in patients who recovered from the disease, which might be since the number of asymptomatic non-registered cases rose.

Fig. 7.

The observed number of recovered individuals (blue), number of recovered individuals modeled with SEIRD model (yellow), and predicted number of recovered individuals (green) by SEIRD model and corrected by ARIMA residual prediction with 95% confidence interval (grey).

4.3. Validation

Validation of any method is an essential step that helps understand how the final model will perform in the future with new previously unseen data. The method was validated on the most recent data - the last two weeks (from September 16, 2020 to September 29, 2020) of the pandemic. The validation dataset was taken from the same source and therefore has the same structure.

As shown in Table 6, all measures of the prediction quality for the infected, recovered, and deceased fractions of the population are very low. Normalized MAE values show that:

• (a)The average difference between the actual number of infected individuals and predicted one is only 1.6%;
• (b)The average difference between the actual number of recovered individuals and predicted one is only 1%;
• (c)The average difference between the actual number of deceased individuals and predicted one is only 1.3%;

Table 6.

Quality measures of the fitted model for validations set.

	MAE	MSE	MSLE	Normalized MAE	Normalized MSE	Maximum deviation
infected	$2.03\cdot {10}^{-4}$	$4.8\cdot {10}^{-8}$	$4.68\cdot {10}^{-8}$	0.016682	0.000329	5.7%
recovered	$8.46\cdot {10}^{-5}$	$7.94\cdot {10}^{-9}$	$7.81\cdot {10}^{-9}$	0.010481	0.000121	9.2%
deceased	$8.07\cdot {10}^{-6}$	$9\cdot {10}^{-11}$	$9\cdot {10}^{-11}$	0.013795	0.000259	12.7%

Based on the maximum deviation column, we can conclude that for the next 60 days starting from the last day of model training:

• (a)The maximum deviation between the predicted and actual number of infected individuals will not exceed 5.7% with a probability of 95%.
• (b)The maximum deviation between the predicted and actual number of recovered individuals will not exceed 9.2% with the probability of 95%.
• (c)The maximum deviation between the predicted and actual number of deceased individuals will not exceed 12.7% with the probability of 95%.

4.4. Discussion

A generalized SEIRD model with vital dynamics is combined with ARIMA stochastic models to enhance model prediction ability. The parameters of the SEIRD model were fitted using the basin-hopping algorithm. Key method’s standouts include:

• ‐Using a Basin-hopping algorithm to fit parameters and initial conditions of the model for COVID decease
• ‐Including into the SEIRD model exponentially decaying mortality rate, which reflects historic dynamics over the year of 2020.
• ‐Correction of model residuals using the ARIMA model with automatically selected parameters.

Estimated results gives a range of the most probable scenarios selected among the solutions within a 95% probability. Worst- and best-case scenarios differ from the final prediction by 5.7% for the infected population, 9.2% for the recovered population, and 12.7% for the deceased population. During data validation, we used not only MAE, MSE, and MLSE metrics, but also normalized MAE and MSE which give us the ability to compare the prediction of categories that have different scales (percentage of the deceased population is about 100 times less than recovered).

The model has some limitations. We summarize them to highlight possible needs in the further development of the modeling.

• ‐We have currently not sufficient information to say that, after recovery, an individual becomes immune to the disease, but we made this assumption: the model did not allow the transition from the recovered category to the susceptible category.
• ‐The model does not consider that the exposed category may have a partial infection ability, as described in (Shi et al., 2020), nor distinguishes symptomatic from asymptomatic people, as studied in (Shaikh et al., 2020).
• ‐Except for the death rate parameter, the model does not have a strong link to the health resiliency of citizens. The death rate parameter could also be related to external factors like air pollution, which makes people more sensitive to respiratory diseases (Wu et al., 2020a).

However, the quality of model prediction says that most of these additional factors lead to residuals between the SEIRD model and actual data. Hence, in the second step, ARIMA models efficiently compensate these residuals.

5. Conclusion

The proposed hybrid model consists of a dynamic SEIRD model with vital dynamics and decaying COVID mortality rate and three ARIMA models that cancel out dynamic model residuals and enhance prediction quality. Unlike pure dynamics models like SIR, SEIR, and SEIRD, this model allows us to make precise predictions for up to 2 months ahead.

The model was tested on US COVID statistic data. Obtained validation results allow us to conclude that the proposed hybrid model has good prediction ability and decent performance. Obtained long-term predictions reflect the general dynamic of the outbreak and are especially useful for the healthcare system workers and government officials. Obtained short-term predictions allows us not only to forecast the future number of infected, recovered, and deceased patients, but only estimate forecast error under adverse or optimistic circumstances. The proposed method can be used as an effective tool for prediction and analysis of the dynamics of the COVID-19 pandemic.

Here are some perspective ways of further development of the proposed method:

• (a)Parameter estimation with different algorithms and boundaries;
• (b)Testing the method of COVID statistics in other countries;
• (c)Develop alternative methods for residue prediction;

Enhancing of the proposed hybrid model depends on profound research results about COVID-19. That is why monitoring recent research in the field and quickly adjusting the model according to the new data is crucial.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

CRediT authorship contribution statement

Maher Ala’raj: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Updating the model Resources, Software. Munir Majdalawieh: Supervision, Validation, Visualization. Nishara Nizamuddin: Roles/Writing - original draft, Writing - review & editing.

Handling editor: