Comparing Propensity Score Methods Versus Traditional Regression Analysis for the Evaluation of Observational Data: A Case Study Evaluating the Treatment of Gram-Negative Bloodstream Infections

Abstract

Background

Propensity score methods are increasingly being used in the infectious diseases literature to estimate causal effects from observational data. However, there remains a general gap in understanding among clinicians on how to critically review observational studies that have incorporated these analytic techniques.

Methods

Using a cohort of 4967 unique patients with Enterobacterales bloodstream infections, we sought to answer the question “Does transitioning patients with gram-negative bloodstream infections from intravenous to oral therapy impact 30-day mortality?” We conducted separate analyses using traditional multivariable logistic regression, propensity score matching, propensity score inverse probability of treatment weighting, and propensity score stratification using this clinical question as a case study to guide the reader through (1) the pros and cons of each approach, (2) the general steps of each approach, and (3) the interpretation of the results of each approach.

Results

2161 patients met eligibility criteria with 876 (41%) transitioned to oral therapy while 1285 (59%) remained on intravenous therapy. After repeating the analysis using the 4 aforementioned methods, we found that the odds ratios were broadly similar, ranging from 0.84–0.95. However, there were some relevant differences between the interpretations of the findings of each approach.

Conclusions

Propensity score analysis is overall a more favorable approach than traditional regression analysis when estimating causal effects using observational data. However, as with all analytic methods using observational data, residual confounding will remain; only variables that are measured can be accounted for. Moreover, propensity score analysis does not compensate for poor study design or questionable data accuracy.

This article assists clinicians with understanding the relative pros and cons, the general steps involved, and the appropriate interpretation of the results of traditional regression analysis, propensity score matching, propensity score weighting, and propensity score stratification.

The impact of various approaches to administering antibiotic therapy on health outcomes are commonly estimated using observational studies as randomized controlled trials (RCTs) are not always feasible, ethical, or affordable. Numerous factors affect antibiotic treatment strategies and, as such, exposed subjects (ie, strategy A) and unexposed subjects (ie, strategy B) in observational studies tend to differ on a number of both measured and unmeasured characteristics. For example, patients who are severely ill, immunocompromised, or have a history of multidrug-resistant infections have a greater likelihood of receiving more “aggressive” antibiotic therapy (ie, broad-spectrum agents, combination therapy, prolonged durations) than their younger and healthier counterparts (ie, confounding by indication), making fair comparisons between exposed and unexposed patients challenging [1]. Additional characteristics such as the experience and beliefs of the provider or requests from family members also influence both treatment decisions and patient outcomes but are difficult to account for in observational studies. Thus, unmeasured confounding is a perpetual limitation to observational studies. These issues are circumvented by randomizing patients to treatment assignment where both easily measured and unmeasured “confounders” are naturally balanced across treatment groups.

In response to the inherent concerns with observational studies, propensity score methods are increasingly being used to reduce the unwanted effect of treatment selection bias [2]. The goal of propensity score techniques is to optimize the covariate similarity in the exposed and unexposed groups. Several approaches to propensity score analysis have been used in the infectious diseases literature, including matching, weighting, and stratification. However, a general gap in understanding among clinicians on how to critically review observational studies that have incorporated these analytic techniques exists. We previously addressed the question “Does transitioning patients with gram-negative bloodstream infections from intravenous (IV) to oral therapy impact 30-day mortality?” through propensity score matching using a multicenter cohort [3]. Here, we repeat the analysis using multivariable regression, propensity score weighting, and propensity score stratification using this clinical question as a case study to guide clinicians through (1) the pros and cons of each analytic approach, (2) the general steps of each approach, and (3) the appropriate interpretation of the results of each approach. For a more nuanced understanding of approaches to estimate causal effects using observational data that may be more appropriate for those with advanced training in statistics, we refer the reader to several comprehensive review articles on this topic [4–6].

METHODS

Description of Cohort

A detailed description of the cohort used for the current work has been reported previously [3, 7, 8]. The cohort includes manually collected data from 4967 patients with monomicrobial Enterobacterales bloodstream infections from 1 January 2008 to 31 December 2014, hospitalized at The Johns Hopkins Hospital, the Hospital of the University of Pennsylvania, or the University of Maryland Medical Center. Demographic information, pre-existing medical conditions, source of bacteremia, source control, severity of illness, microbiologic data, antibiotic therapy, and patient outcomes were collected. Additional eligibility criteria were imposed on the cohort to specifically address the research question “Does transitioning patients with gram-negative bloodstream infections from IV to oral therapy impact 30-day mortality?” [3].

Patients whose antibiotic treatment was switched from IV to oral therapy were referred to as the “exposed” group, and those who remained on IV therapy for the duration of treatment were referred to as the “unexposed” group. We focused on a single outcome (ie, 30-day all-cause mortality) and estimated the association between being in the exposed or unexposed group and 30-day mortality using odds ratios. Below, we detail the methodology used to evaluate the study question using logistic regression, propensity score matching, propensity score weighting, and propensity score stratification. Typically, either regression analysis or 1 of the 3 propensity score techniques is selected to evaluate the association between the exposure and outcome when estimating causal effects in observational data, but for explanatory purposes, we present the findings using each of the 4 approaches. All analysis were performed using STATA version 15.0 statistical package (Stata Corp).

Logistic Regression

We begin by discussing traditional logistic regression analysis. Logistic regression was employed to estimate the odds of 30-day mortality comparing patients who were transitioned to oral therapy versus those who remained on IV therapy. This association (ie, the unadjusted odds ratio) was estimated using univariable regression analysis where the outcome was “regressed” on the binary variable indicating whether a patient was switched to oral therapy or not. The adjusted odds ratio was then estimated by adding confounders into the model (eg, intensive care unit [ICU] status, immunocompromise, etc). Confounders were defined as variables that likely influenced the decision to switch to oral therapy and also impacted the likelihood of death within 30 days changing the measure of association (ie, the odds ratio) by at least 10% and distorting the true relationship between the exposure and outcome [9, 10]. The general guidance of limiting variable inclusion to 1 variable per 10 outcome events was used [11].

Propensity Score Generation

An alternative approach for the evaluation of observational data involves the generation and incorporation of propensity scores. The propensity score is the probability a patient will receive oral step-down therapy, based on characteristics of the patient, organism, and any other measurable factors that might influence this decision [12]. Propensity scores were estimated using multivariable logistic regression, in which patient and organism characteristics were the predictors in a model of the odds of being allocated to either the oral step-down therapy group or the IV therapy group. Covariates were selected based on a priori hypothesized associations and not analytic methods like stepwise algorithms or using P-value cutoffs [13, 14].

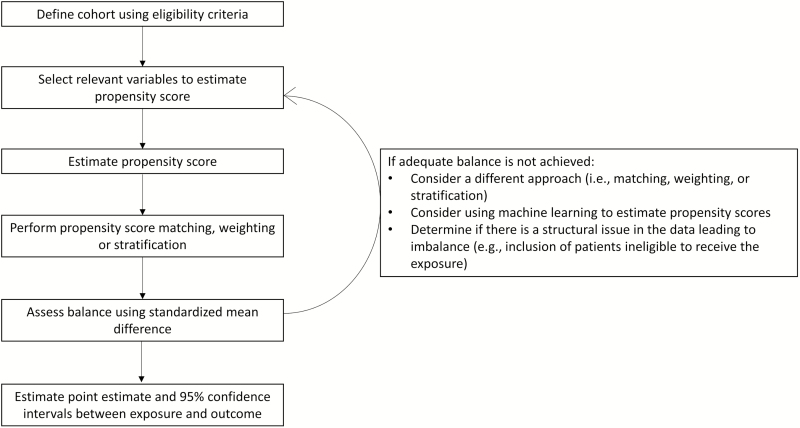
The estimated propensity scores ranged from 0 to 1 for each patient in the study population. The propensity scores were each individual’s predicted probability of receiving oral therapy (generated from the logistic regression model). After calculating propensity scores, the various propensity score methods were used to estimate the odds of death within 30 days comparing patients transitioned to oral therapy with those who remained on IV antibiotics, as described in Figure 1.

Figure 1. .

General steps involved in analytic approaches incorporating propensity score methodology.

Propensity Score Matching

Exposed and unexposed patients were matched based on the proximity of propensity scores. 1:1 nearest neighbor matching without replacement was performed with a caliper size (or distance of) 0.2 standard deviations, meaning that, for each exposed individual, 1 comparison individual was selected as a “match” [5]. The comparison individual (who had not yet been selected as a match [ie, “without replacement”]) was the person with the propensity score closest to the exposed individual’s propensity score. If the “closest” match had a propensity score greater than 0.2 standard deviations away from the exposed patient, the exposed patient was dropped, as no “similar” comparison individual existed. Alternative approaches to propensity score matching include “with replacement,” meaning a comparison group patient could be matched to more than 1 exposed patient, or a more liberal caliper size, which loosens the restrictions of the necessary proximity of a match’s propensity score. Caliper sizes of 0.2 or 0.25 standard deviations are commonly used [5]. Propensity score matching can result in obtaining close (or even exact) matches on a set of key covariates.

A density plot of propensity scores in the exposed and unexposed groups was constructed as a visual inspection of balance. Thirty-day mortality was then compared in the matched cohort using logistic regression with additional adjustment for baseline variables whose standardized mean difference was greater than 10%. Standardized mean differences evaluate for appropriate balance for each measured covariate between patients in the exposed and unexposed groups in the matched sample [15, 16]. Standardized mean differences of less than 10% between the 2 groups indicate reasonable balance in the 2 groups across each variable [15]. Adjustment for any unbalanced (ie, standardized mean differences ≥10%) or relevant variables that impact treatment selection in the propensity score–matched cohort is known as a “doubly robust” estimation [17, 18].

Propensity Score Weighting

After propensity scores were generated, inverse probability of treatment weighting (IPTW) was investigated as an alternative to propensity score matching. Patients transitioned to oral therapy were weighted by the inverse of the propensity score and patients who remained on IV therapy were weighted by the inverse of 1 minus the propensity score [19]. Weighting created a pseudo-population, which increased the influence of patients receiving a treatment they would not be expected to receive [20], improving the ability to conduct comparisons of 30-day mortality between the groups. More specifically, weighting mathematically increases the representation of “rare” patients in each exposure group. Subjects with a high propensity score (ie, calculated to have a high probability of being transitioned to oral therapy) but who, in reality, remained on IV therapy received a higher weight than patients with a low propensity score (ie, calculated to have a low probability to be transitioned to oral therapy) and who—as expected—remained on IV therapy for the remainder of their treatment course. Patients whose propensity scores were higher than the 99th percentile of the IV therapy group and smaller than the first percentile of the oral therapy group were trimmed. Trimming improves the accuracy and precision of estimates by avoiding the influence of patients with extreme outlier weights [21, 22].

Similar to propensity score matching, standardized mean differences were used to evaluate variable balance at baseline between the 2 groups in the weighted cohort. Regression analysis was performed on the weighted sample to compare outcomes between groups, and a doubly robust estimation was used to increase the precision of effect estimate.

Propensity Score Stratification

Propensity score stratification relies on the premise that individuals within a propensity score stratum are more similar to each other than to the general population being investigated [4]. To evaluate the study question, 5 strata were created using quintiles of the propensity score. Although 5 strata are commonly used, the creation of additional strata may further reduce selection bias if the dataset is large [23]. Outcomes were compared among exposed and unexposed patients within each stratum. The odds ratios were estimated for each stratum, adjusting for any variables not balanced within the stratum. Then, the overall odds ratio across all strata was estimated using Mantel-Haenszel pooling [24]. The pooled odds ratio has a similar interpretation as the odds ratio from matching or weighting.

RESULTS

Distribution of Baseline Variables in the Full Cohort

Overall, 2161 patients met the eligibility criteria, with 876 (41%) transitioned to oral therapy while 1285 (59%) remained on IV therapy. Baseline characteristics, stratified by exposure status, in the full cohort are displayed in Table 1.

Table 1.

 Baseline Characteristics of 2161 Hospitalized Adult Patients With Enterobacterales Bloodstream Infections Comparing Patients Transitioned to Oral Antibiotic Therapy Versus Those Who Remained on Intravenous Antibiotic Therapy

Characteristics	Oral Therapy (n = 876; 40.5%)	Intravenous Therapy (n = 1285; 59.5%)	P Value
Age (median, IQR), years	59 (47–69)	59 (48–68)	.928
Female, n (%)	437 (49.9)	579 (45.1)	.027
Race/ethnicity, n (%)
White	423 (48.3)	663 (51.6)	.131
Black	369 (42.1)	493 (38.4)	.80
Asian	30 (3.4)	55 (4.3)	.315
Latino	25 (2.9)	34 (2.6)	.771
Weight (median, IQR), kg	74.9 (63.5–88.3)	73.5 (62.3–88.4)	.597
Pre-existing medical conditions, n (%)
End-stage liver disease	51 (5.8)	87 (6.8)	.376
End-stage renal disease requiring dialysis	41 (4.7)	100 (7.8)	.004
Structural lung diseasea	43 (4.9)	98 (7.6)	.012
Congestive heart failure (ejection fraction <45%)	78 (8.9)	121 (9.4)	.686
Diabetes	228 (26.0)	307 (23.9)	.259
Immunocompromised, n (%)
Human immunodeficiency virus	39 (4.5)	48 (3.7)	.405
Chemotherapy within 6 months	246 (28.1)	355 (27.6)	.816
Absolute neutrophil count <500 cells/mL	59 (6.7)	181 (14.1)	<.001
Immunomodulatory therapy or high-dose steroids within 30 days	33 (3.8)	43 (3.3)	.602
Solid organ transplant	103 (11.8)	114 (8.9)	.028
Hematopoietic stem cell transplant within 12 months	30 (3.4)	97 (7.5)	<.001
Total days of antibiotic therapy (median, IQR)	15 (12–16)	14 (11–15)	<.001
Total days of intravenous therapy (median, IQR)	3 (2–4)	14 (11–15)	<.001
Combination antibiotic therapy for >48 hours, n (%)	54 (6.2)	154 (12.0)	<.001
Source of infection, n (%)
Respiratory	29 (3.3)	117 (9.1)	<.001
Skin and soft tissue	22 (2.5)	50 (3.9)	.079
Urinary tract	405 (46.2)	383 (29.8)	<.001
Biliary	121 (13.8)	148 (11.5)	.113
Intra-abdominal	160 (18.3)	290 (22.6)	.016
Catheter-associated	137 (15.6)	282 (21.9)	<.001
Pitt bacteremia score on day 1 (median, IQR)	1 (0–3)	2 (1–4)	<.001
Intensive care unit on day 1, n (%)	161 (18.4)	415 (32.3)	<.001
Enterobacterales isolated from bloodstream
Citrobacter spp.	21 (2.4)	20 (1.6)	.160
Enterobacter spp.	98 (11.2)	159 (12.4)	.430
Escherichia coli	420 (48.0)	513 (39.9)	<.001
Klebsiella spp.	284 (32.4)	477 (37.1)	.025
Proteus mirabilis	29 (3.3)	63 (4.9)	.072
Serratia marcescens	24 (2.7)	53 (4.1)	.088

Abbreviation: IQR, interquartile range.

^aChronic obstructive pulmonary disease, emphysema, pulmonary fibrosis, tracheostomy dependency.

Standardized mean differences for each variable in the full cohort used for multivariable regression analysis as well as for each of the propensity score–based methods are shown in Table 2. In the full cohort, 13 variables had standardized mean differences greater than 10%, confirming that important differences in baseline patient and microbial characteristics existed between the oral step-down and IV therapy groups. Of note, standardized mean differences are not generally estimated for multivariable regression analysis but were calculated for the current work solely for comparative purposes.

Table 2.

 Standardized Mean Differences of Baseline Characteristics Before and After Propensity Score Matching, Inverse Probability of Treatment Weighting of Propensity Scores, and Propensity Score Stratification (Displayed by Each Quintile) Approaches Between Patients Transitioned to Oral Antibiotic Therapy and Those Remaining on Intravenous Antibiotic Therapy for Enterobacterales Bloodstream Infections

Variable	Full Cohort	Matching	IPTW	Quintile 1	Quintile 2	Quintile 3	Quintile 4	Quintile 5
Age	0.004	−0.011	−0.017	0.216	0.014	0.024	0.120	−0.245
Female	−0.097	−0.011	0.023	0.055	0.163	−0.059	0.070	−0.204
White race	−0.066	0.016	−0.008	−0.054	−0.015	0.015	−0.000	−0.026
Black race	0.077	−0.030	0.020	0.063	0.061	0.023	−0.018	−0.046
Asian race	−0.044	0.021	−0.022	−0.110	−0.036	−0.004	−0.054	0.153
Latino ethnicity	0.013	0.045	−0.014	−0.019	−0.220	0.004	0.187	−0.010
Weight in kilograms	0.023	−0.010	0.019	0.325	−0.128	0.046	0.084	−0.153
End-stage liver disease	−0.039	0.006	−0.021	−0.174	0.129	−0.121	0.063	0.013
End-stage renal disease requiring dialysis	−0.129	0.012	−0.014	−0.096	0.113	0.031	−0.025	−0.145
Structural lung disease	−0.112	0.042	−0.014	0.033	−0.041	0.116	−0.029	−0.148
Congestive heart failure (ejection fraction <45%)	−0.018	0.000	−0.009	0.001	−0.022	0.107	−0.042	−0.029
Diabetes	0.049	0.003	−0.016	0.026	−0.037	−0.002	0.076	−0.021
Human immunodeficiency virus	0.036	0.007	−0.021	−0.247	−0.122	0.134	0.101	−0.055
Chemotherapy within 6 months	0.010	0.021	−0.006	−0.056	−0.113	0.239	0.048	−0.173
Absolute neutrophil count <500 cells/mL	−0.242	0.005	0.042	0.288	−0.075	−0.199	0.062	*
Immunomodulatory therapy or high-dose steroids within 30 days	0.023	0.015	−0.012	−0.108	−0.006	0.005	0.120	−0.052
Solid organ transplant	0.095	−0.018	−0.015	−0.029	−0.140	0.130	−0.055	0.067
Hematopoietic stem cell transplant within 12 months	−0.182	0.007	0.030	0.136	−0.001	−0.204	−0.055	0.085
Total days of antibiotic therapy	0.229	0.023	−0.027	−0.104	−0.028	−0.004	0.102	0.138
Combination antibiotic therapy for >48 hours	−0.204	0.000	−0.015	−0.121	−0.014	0.128	−0.140	0.011
Respiratory source	−0.242	−0.027	−0.044	−0.186	0.051	−0.020	0.027	*
Skin and soft tissue source	−0.078	0.070	−0.019	−0.075	−0.137	0.131	0.018	0.148
Urinary tract source	0.343	−0.030	−0.021	−0.098	−0.069	0.093	0.066	0.045
Biliary source	0.069	0.000	0.010	0.205	−0.035	0.038	−0.101	−0.008
Intra-abdominal source	−0.107	0.030	0.004	−0.018	0.068	−0.127	0.086	−0.068
Catheter-associated source	−0.162	−0.017	0.022	0.185	0.053	−0.100	−0.101	0.027
Pitt bacteremia score on day 1	−0.535	0.048	0.020	−0.453	−0.053	0.036	0.119	−0.012
Intensive care unit on day 1	−0.324	0.013	0.013	−0.047	−0.178	0.125	−0.019	−0.017
Citrobacter spp.	0.060	0.049	0.058	0.198	0.128	−0.011	−0.088	0.086
Enterobacter spp.	−0.037	0.008	0.073	0.174	0.213	−0.099	0.014	−0.146
Escherichia coli	0.162	0.046	0.025	−0.146	−0.037	0.013	0.116	0.194
Klebsiella spp.	−0.099	−0.048	−0.050	0.038	−0.043	0.057	−0.088	−0.184
Proteus mirabilis	−0.080	−0.069	−0.053	0.064	−0.036	−0.051	−0.153	−0.062
Serratia marcescens	−0.076	0.025	−0.063	−0.372	−0.221	0.074	0.144	0.172

Standardized differences could not be computed for variables with an asterisk “*” because neither the exposed nor unexposed groups in the specific quintile had patients with the specific variable.

Abbreviation: IPTW, inverse probability of treatment weighting.

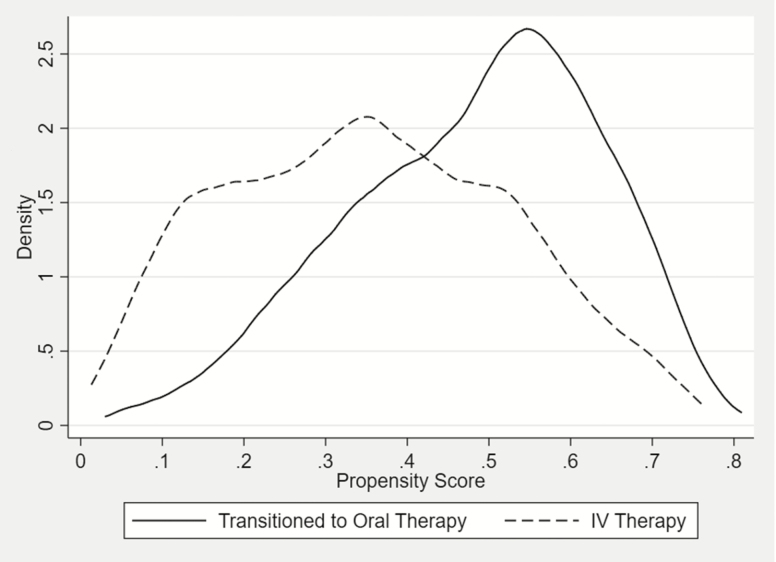
Figure 2 illustrates a propensity score density plot for the oral step-down and IV therapy groups for the full cohort. As predicted, the majority of patients transitioned to oral therapy had elevated propensity scores (ie, a higher expectation to be converted to oral therapy), whereas the majority of patients remaining on IV therapy tended to have lower scores. It is reassuring that there was generally reasonable overlap in the propensity score distributions of the 2 groups.

Figure 2. .

Distribution of propensity scores for oral step-down and intravenous therapy groups in a cohort of adult patients with Enterobacterales bloodstream infections. Abbreviation: IV, intravenous.

Distribution of Baseline Variables in the Propensity Score–Matched Cohort

After matching, 739 propensity score–matched pairs of oral step-down and IV therapy patients were identified (total of 1478 patients) [1]. Propensity score matching led to the exclusion of 683 patients. As standardized mean differences in the matched cohort were less than 10% for all measured variables, matching appeared to successfully reduce selection bias (Table 2).

Distribution of Baseline Variables in the Propensity Score–Weighted Cohort

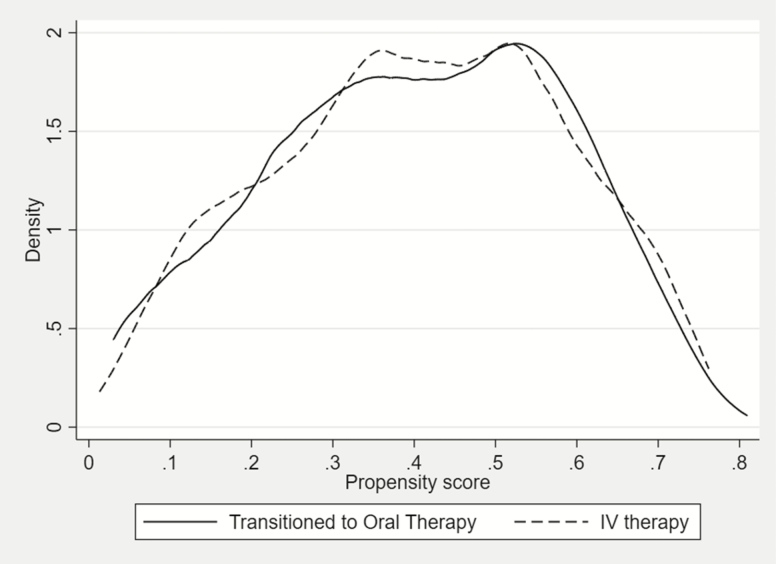
Similar to the propensity score–matched cohort, the IPTW cohort resulted in standardized mean differences of less than 10% for all variables when comparing exposed and unexposed patients. Figure 3 illustrates the density plots of propensity scores for the oral step-down group and IV therapy group in the weighted sample. Compared with Figure 2, the near overlap of graphs in Figure 3 indicates the success of the approach in equating the propensity score distributions between the 2 groups.

Figure 3. .

Distribution of propensity scores for oral-step down and intravenous therapy groups in a propensity score inverse probability of treatment–weighted cohort of patients with Enterobacterales bloodstream infections. Abbreviation: IV, intravenous.

Distribution of Baseline Variables in the Propensity Score–Stratified Cohort

Table 2 shows the standardized mean differences between patients transitioned to oral therapy and the IV therapy group for the 5 quintiles. Imbalances were observed between the 2 treatment groups for several variables within each stratum, suggesting there may be lingering confounding within each stratum.

Thirty-Day Mortality

Traditional regression analysis, propensity score matching, and IPTW showed no difference in 30-day mortality between patients transitioned to oral therapy and those who remained on IV therapy (Table 3). Odds ratios ranged between 0.84 to 0.95 and there was substantial overlap between all 95% confidence intervals. More variability was seen, however, with strata-specific odds ratios, which ranged from 0.35 to 1.43. The lower 2 strata suggested a trend towards reduced mortality for patients transitioned to oral therapy versus those who remained on IV therapy, whereas the upper 3 strata and the pooled odds ratios across strata showed no difference in 30-day mortality between the 2 groups. Some of the variability in the associations across strata may be explained by relatively small sample sizes in the strata.

Table 3.

 Odds ratios for 30-Day Mortality Comparing Patients With Enterobacterales Bloodstream Infections Transitioned to Oral Antibiotic Therapy Versus Those Who Remained on Intravenous Antibiotic Therapy

Analytic Approach	Odds Ratio	95% Confidence Interval	P Value
Multivariable logistic regression	.95	.73–1.23	.681
Propensity score matching	.90	.70–1.21	.495
Propensity score inverse probability of treatment weighting	.91	.65–1.28	.582
Propensity score inverse probability of treatment weighting (with trimming at the first centile)	.84	.64–1.10	.196
Propensity score stratification
First stratum	.35	.14–.88	.026
Second stratum	.53	.27–1.05	.070
Third stratum	1.29	.71–2.36	.401
Fourth stratum	1.08	.59–1.97	.807
Fifth stratum	1.43	.79–2.57	.237
Overall estimate using Mantel-Haenszel pooling of the 5 strata	.90	.69–1.18	.460

DISCUSSION

Using various approaches to analyze observational data including regression analysis, propensity score matching, propensity score IPTW, or propensity score stratification, the odds of 30-day mortality for patients with Enterobacterales bloodstream infections transitioned to oral therapy versus those who remained on IV therapy were similar. The same ultimate conclusions were reached regardless of the approach used, likely because our stringent eligibility criteria for inclusion increased the probability of similarities in the distribution of baseline variables among exposed and unexposed patients; however, this is not always the case. Several published studies have illustrated why propensity score methods are preferred to traditional regression analysis [25–27]. Although results may not significantly differ in a given dataset, there are characteristics of propensity score analysis that make it an overall more appealing approach compared with traditional regression analysis.

Propensity score methods are more likely to achieve a similar distribution of observed baseline variables across exposed and unexposed patients compared with regression analysis, more closely mimicking what would be expected in an RCT [28–30]. A limitation of traditional analysis of observational studies is that, when comparing the outcomes of patients who receive 2 different therapies, the observed differences are the result of both varying patient characteristics as well as differences related to the assigned treatment, making it challenging to distinguish the true impact of one treatment approach versus the alternative treatment approach. For example, if the distribution of patients in the ICU is dissimilar between the 2 treatment groups, it is difficult to determine to what extent differences in outcomes between the exposed and unexposed groups are attributable to the exposure and to what extent are due to ICU status. Unlike traditional regression analysis that limits the number of variables used to adjust for potential confounders when evaluating the relationship between the exposure and outcome and rely on functional form assumptions to essentially extrapolate from 1 group to the other when there is not good covariate balance, propensity score methods allow for the integration of large numbers of variables during the generation of the propensity scores, increasing the likelihood of similar distributions of measured covariates across the groups [31, 32]. The greater reduction in confounding afforded by propensity score methods increases the probability of more valid estimates of the relationship between the exposure and outcome.

An additional benefit to propensity score approaches is the ability to “separate” design and analysis. With propensity score approaches, most of the work is “front-ended” and focused on the development of 2 groups that are similar on all characteristics except for the primary exposure. This reduces the ability to “visualize” the point estimate for the primary outcome during the early analytic phases, potentially reducing the unintentional bias that can occur when regression analysis yields an unexpected odds ratio or P value, prompting the researcher to “add” or “drop” variables in an attempt to obtain a more desirable point estimate and P value.

Although propensity score approaches are generally preferred over conventional regression analysis, there is no clear consensus as to the optimal propensity score approach. Propensity score matching is commonly used in the literature as the notion of matching an exposed and unexposed patient based on similar propensity scores is easy to conceptualize. Some studies have shown matching and weighting to eliminate baseline differences to a greater extent than stratification [33, 34].

In our study, propensity score matching resulted in adequate balance in the exposed and unexposed groups across all baseline covariates, but at the cost of losing one-third of the eligible cohort because of unmatched patients. With propensity score matching, a reduction in the total sample size of the cohort is expected. The external validity of a matched cohort can be limited—especially with small cohorts or strict caliper sizes—as the matched cohort often excludes patients with extreme propensity scores with no match. For example, if all patients with high Pitt bacteremia scores are unmatched, the study findings are no longer generalizable to severely ill patients. Propensity score matching is a reasonable approach when large sample sizes are present and when there are a greater number of subjects in the unexposed group (so as to not exclude exposed subjects as there are generally fewer patients in the exposed group than in the unexposed group). With a large unexposed group, one can explore higher k:1 ratios than 1:1 matching (eg, 2:1, 3:1, etc) to increase the sample size [5].

Propensity score weighting requires a more nuanced understanding of statistics as it can result in a patient being included either as a fraction of a patient or as multiple patients. Underrepresented patients within an exposure group are given an increased weight (eg, “1.5 times a person”). Inverse probability of treatment weighting increases the representation of “rare” patients and decreases the representation of “common” patients in each exposure group. Inverse probability of treatment weighting should be considered when the sample size of the cohort is small or if the control group is either smaller or the same size as the exposed group, making standard matching approaches not practical. Weighting maintains the sample size of the cohort and preserves external validity; however, utilizing additional tools like trimming to exclude the influence of patients with extreme weights may eliminate some observations, although considerably less than with propensity score matching [22].

Propensity score stratification enables the exploration of possible dissimilarities of outcomes within each stratum (essentially, subgroup effects), which could be overlooked with matching and weighting methods [35]. In our cohort, stratification demonstrated that patients in the first and second strata (those unlikely to transition to oral therapy) may receive the greatest benefit from an early transition to oral therapy, and those in the third to fifth strata (eg, a high likelihood of transitioning to oral therapy) will have no difference in outcomes whether transitioned to oral step-down therapy or remaining on IV therapy. Results from the first 2 strata may relate to an earlier return to baseline functional status afforded by oral therapy and could inform additional investigations to identify potential risk modifiers and guide deviations in standard clinical management for select patients.

In conclusion, propensity score methods provide an approach to analyzing observational data that approximates the validity of RCTs to a greater extent than traditional regression approaches. As with all analytic methods using observational data—and propensity score techniques are no exception –residual confounding will always remain and only variables that can be measured can be accounted for. Sensitivity analyses (eg, calculating an E-value) can be considered to better assess how much an effect estimate is subject to unmeasured confounding [36, 37]. Moreover, propensity score analysis does not compensate for poor study design or questionable data accuracy. When RCTs are not feasible, we encourage the consideration of propensity score techniques.

Notes

Disclaimer. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Financial support. This work was supported by the National Institute of Allergy and Infectious Diseases of the National Institutes of Health under award number UM1AI104681. The work was also supported in part by grants K23-AI127935 (to P. D. T.), K24-AI079040 (to A. D. H), and K24-AI080942 (to E. L.), all from the National Institutes of Health.

Potential conflicts of interest. J. H. H. was affiliated with the University of Pennsylvania during the conduct of this research and is an employee of and holds shares in the GlaxoSmithKline group of companies. S. E. C. received consulting fees from Novartis, Theravance, and Basilea. E. L. served on a Data Safety and Monitoring Board for Merck and on an advisory board for Shionogi. All other authors report no potential conflicts. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.