Assessing the Probability That a Positive Report is False: An Approach for Molecular Epidemiology Studies

Abstract

Too many reports of associations between genetic variants and common cancer sites and other complex diseases are false positives. A major reason for this unfortunate situation is the strategy of declaring statistical significance based on a P value alone, particularly, any P value below .05. The false positive report probability (FPRP), the probability of no true association between a genetic variant and disease given a statistically significant finding, depends not only on the observed P value but also on both the prior probability that the association between the genetic variant and the disease is real and the statistical power of the test. In this commentary, we show how to assess the FPRP and how to use it to decide whether a finding is deserving of attention or “noteworthy.” We show how this approach can lead to improvements in the design, analysis, and interpretation of molecular epidemiology studies. Our proposal can help investigators, editors, and readers of research articles to protect themselves from overinterpreting statistically significant findings that are not likely to signify a true association. An FPRP-based criterion for deciding whether to call a finding noteworthy formalizes the process already used informally by investigators—that is, tempering enthusiasm for remarkable study findings with considerations of plausibility.

The genomic revolution presents exciting opportunities to learn about the etiology of cancer and other complex diseases. We now face the daunting task of searching through the staggeringly large number of genetic variants to identify the few among them that are involved in the etiology of these diseases.

The high chance that an initial “statistically significant” finding will turn out to be a false-positive finding, even for large, well-designed, and well-conducted studies (1–8), is one symptom of the problem we face. For example, Colhoun et al. (8) estimated the fraction of false-positive findings in studies of association between a genetic variant and a disease to be at least .95. It is impossible, of course, to know the proportion of apparent false-positive findings that are attributable to poor study design [likely to be moderate (6,9)], population stratification [likely to be low (6,10)], or low statistical power in studies designed to replicate positive findings (7,11); however, even if biases from all sources were completely eliminated, the chance that there is no true association for most reports of association between a genetic variant and disease with a P value just below .05 would remain high (2,5,6,8). We call the probability of no association given a statistically significant finding the false positive report probability (FPRP). The precise definition of FPRP and the simple mathematics used in this article can be found in the Appendix.

In the absence of bias, three factors determine the probability that a statistically significant finding is actually a false-positive finding. First is the magnitude of the P value (2,8,12–14). Second, and less appreciated, is statistical power (2,8,14,15), which is often low because, with few exceptions, the odds ratio for genetic variants that are truly associated with a disease is less than 2 or the genetic variant is uncommon. Third, but of primary importance as we (6,14) and others (2,8,15,16) have noted, is the fraction of tested hypotheses that is true. In this commentary, we show how to 1) calculate FPRP from its three determinants and 2) develop a criterion based on the FPRP for evaluating whether a study finding is noteworthy. We then demonstrate how this approach can be used in the design, analysis, and interpretation of molecular epidemiology studies.

Etiology of False-Positive Findings

Historical Overview of the False-Positive Problem

The earliest molecular epidemiology studies were designed to test promising hypotheses. Although many of these studies were small, most were designed to test hypotheses on the basis of strong biologic evidence of the importance of particular genes and, to a certain extent, on the function of particular genetic variants, such as the role of the GSTM1 null (17) and NAT2 slow acetylation (18) genotypes in bladder cancer. Studying the entire genome, regions of a chromosome, or even multiple genes in a single pathway was not feasible. Now, however, technical advances, including lower cost, reductions in quantity of DNA required, high throughput platforms, and better annotation of fine haplotype structures, are allowing investigators to move beyond testing a handful of hypotheses in the most promising single nucleotide polymorphisms (SNPs) of the most promising candidate genes toward testing several haplotypes and SNPs in thousands of genes whose functions remain obscure or unknown. Even if a single SNP in any given gene is unlikely to be a cause of a complex disease, all the variants in all the genes in toto might still contribute substantially to the etiology of the disease. Thus, the challenge we now face is how to take advantage of these technical opportunities in a way that accelerates the identification and confirmation of the genetic causes of cancer and, at the same time, minimizes the number of false-positive findings and, in turn, their consequences.

Determinants of FPRP

Three factors determine the magnitude of the FPRP (seeequation 1 in Appendix): 1) prior probability π of a true association of the tested genetic variant with a disease, 2) α level or observed P value, and 3) statistical power to detect the odds ratio of the alternative hypothesis at the given α level or P value. Statistical power is in itself based on sample size, frequency of the at-risk genetic variant, and the specified odds ratio for the presumed association under the alternative hypothesis. A high FPRP (e.g., >.5) could be a consequence of any combination of a low prior probability, low statistical power, or a relatively high P value.

FPRP Under Different Scenarios

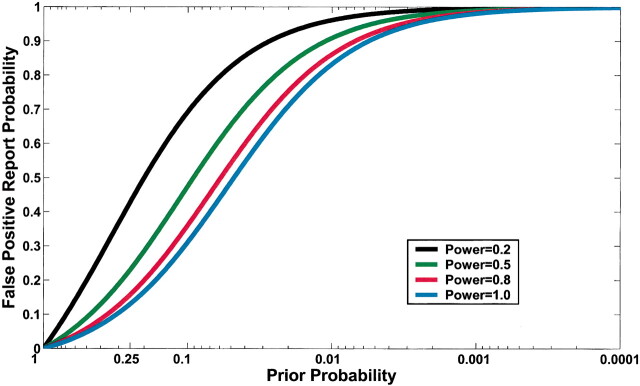
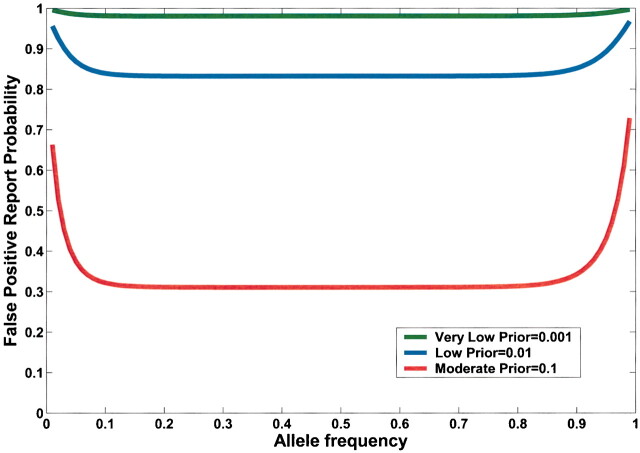
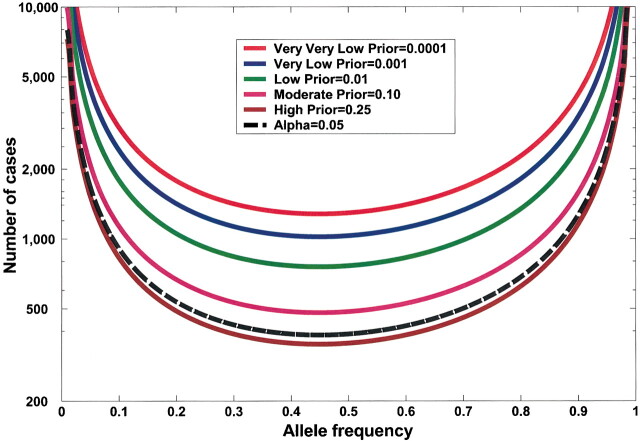
Current practice in molecular epidemiology studies is to set an arbitrary value for the α level, usually .05, and to call an association between a genetic variant and a disease with a P value below α statistically significant. Fig. 1 shows that differences in the prior probability level over the range of three or more orders of magnitude between the most likely and least likely hypotheses that are typically tested have a large effect on FPRP. With a moderate prior probability, FPRP can be high, even for a study with reasonable statistical power, when the observed P value is close to .05. Although a substantial reduction in the FPRP can be achieved for moderate to high prior probabilities (i.e., 0.10–0.25) by increasing statistical power, FPRP will be high for prior probabilities below 0.01, even with the maximum statistical power of 1 (i.e., the blue curve on Fig. 1). The reduction in FPRP is small when statistical power is higher than 0.8 and, accordingly, even when sample size is increased dramatically, especially with low prior probabilities. Therefore, increasing the number of case patients and control subjects can reduce FPRP substantially with high prior probabilities but provides only a marginal benefit when the prior probability is low (Fig. 2). The frequency of the genetic variant also affects statistical power and therefore FPRP. Fig. 3 shows the FPRP in a study with 1500 case patients and 1500 control subjects over a range of allele frequencies for three prior probabilities when α = .05. When considering statistical power against an odds ratio (equivalent to the risk ratio [RR] for a rare disease) of 1.5, a lower statistical power for studying less common genetic variants results in a higher FPRP (see Appendix, step 2 of spreadsheet).

Fig. 1.

Effect of changes in prior probability and statistical power on false positive report probability (FPRP) when the α level is .05. FPRP shown is for a P value at or just below α; FPRP will be lower when the observed P value is substantially below α. A low FPRP is achievable only for high prior probabilities. Moreover, statistical power has an important impact on FPRP, except for particularly high and low prior probabilities. For example, for a prior probability of 0.1, the FPRPs are 0.69, 0.47, 0.36, and 0.31 for statistical powers of 0.2, 0.5, 0.8, and 1.

Fig. 2.

Effect of sample size on false positive report probability (FPRP). In this figure, allele frequency q = .3, α = .05, and statistical power is for detecting an odds ratio of 1.5. FPRP shown is for a P value at or just below α; FPRP will be lower when the observed P value is substantially below α. Prior probability and N (numbers of case patients and control subjects) have a large effect on the FPRP. FPRP remains very high with a low prior probability (.001). Increasing the sample size beyond N = 1500 case patients and control subjects will have only a marginal effect on FPRP because statistical power is already close to 1.

Fig. 3.

False positive report probability (FPRP) as function of allele frequency (q) of a high-risk allele for three prior probabilities. In this figure, α = .05, N = 1500 case patients and control subjects, and statistical power is calculated for detecting an odds ratio of 1.5. FPRP shown is for a P value at or just below α; FPRP will be lower when the observed P value is substantially below α. Allele frequency affects FPRP through its effect on statistical power.

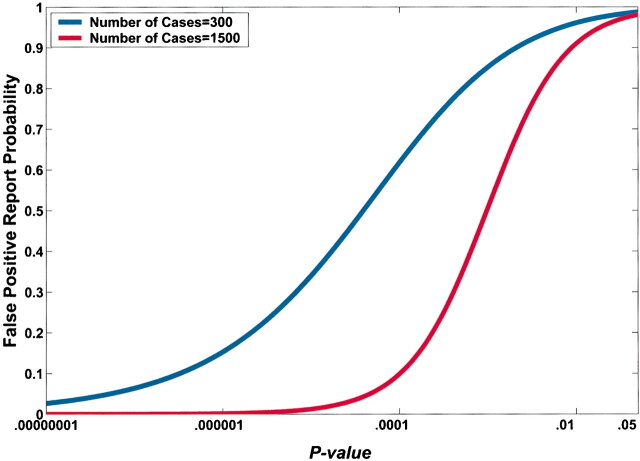
A lower observed P value also reduces FPRP (Fig. 4). However, equal P values can correspond to very different FPRPs because of the influences of prior probability and statistical power on the FPRP. For example, in Fig. 4, a P value of .00024 would achieve an FPRP of 0.2 in a study of 1500 case patients and 1500 control subjects; however, the identical P value in a smaller study of 300 case patients and 300 control subjects would have an FPRP of 0.72.

Fig. 4.

Effect of sample size on the relation between the P value and false-positive report probability (FPRP). FPRP is shown as a function of the P value for two sample sizes, N = 300 and N = 1500, when the prior probability is 0.001, the allele frequency (q) is 0.3, and statistical power is shown to detect an odds ratio of 1.5. The FPRP value can be very different even when the P value and prior probability are the same because of differences in statistical power.

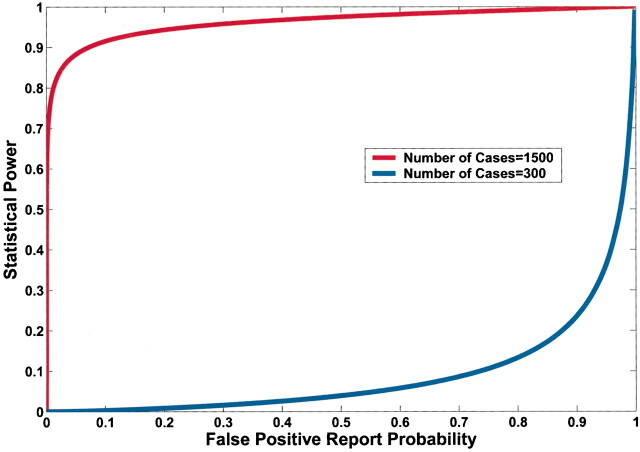
A large study can have much more statistical power than a small study to achieve the FPRP required to declare a finding noteworthy. For example, in Fig. 5, a study of 1500 case patients has much more statistical power than a study of 300 case patients to achieve an FPRP below 0.5.

Fig. 5.

Effect of decreasing the false positive report probability (FPRP) required to declare a finding noteworthy on statistical power. Statistical power is shown to detect an odds ratio of 1.5, with a prior probability of 0.001 and an allele frequency (q) of .3 for 300 and for 1500 case patients and control subjects. Note the trade-off between increased statistical power and a lowered FPRP for a fixed sample size and the potential increase in statistical power with the same FPRP but larger sample size.

The examples above demonstrate that the current practice of a universal criterion for statistical significance based on rejection of the null hypothesis at an α level of .05 is untenable across the range of prior probabilities of a true association, even with a maximum statistical power of 1. Hence, as we test ever less likely hypotheses, even an infinitely large sample size does not, by itself, substantially reduce FPRP.

Using an FPRP Criterion to Test the Association Between a Genetic Variant or Haplotype and Disease Risk

Analysis of a SNP

Above, we explored determinants of FPRP across a range of scenarios. Now, we propose a four-step procedure in which a decision on whether a given association between a SNP and a particular disease is deserving of attention or is noteworthy.

1. Preset an FPRP noteworthiness value for each hypothesis. A universal value for declaring a finding to be noteworthy is probably not appropriate; the stringency of the FPRP value should depend on statistical power (Fig. 5) and the magnitude of the losses (negative consequences) from potentially wrong decisions. Studies of rare tumors (e.g., childhood cancers) or small initial studies of common tumors should probably have an FPRP value of 0.5 or above; given that some estimates of the overall FPRP in the molecular epidemiology literature have been near 0.95 (8), an FPRP value near 0.5 would represent a substantial improvement over current practice. We believe that large studies or pooled analyses that attempt to be more definitive evaluations of a hypothesis should use a more stringent FPRP value, perhaps below 0.2.

2. Determine the prior probability of the hypothesis before viewing study results. The prior probability of a hypothesis can simply be the subjective answer to the question “What is the probability of a meaningful association between a genetic variant (for analysis of a SNP) or gene (for a haplotype analysis) and a disease?” A meaningful elevation in odds ratio might be defined as 1.5 or greater; however, in some situations, a lower odds ratio can be defensible.

In the absence of epidemiologic data, determination of a prior probability should integrate existing information from genomic and functional data on the gene and the specific genetic variant. For example, a SNP that results in a nonconservative change in the coding region of a gene thought to play an important and rate-limiting role in the pathogenesis of a disease would have a higher prior probability than a synonymous SNP in a gene (19) for which there is a redundant mechanism that could, at least in part, compensate for the failure of one component of the system (20). However, the relevance of the gene is usually more important than the type of SNP (16); even synonymous SNPs can alter mRNA stability and gene expression (21) or can be in linkage disequilibrium with a functionally important SNP.

One can use simple assumptions to determine a reasonably low range for the prior probability that a randomly selected nonsynonymous variant located within a gene is truly associated with a complex disease (8). If the number of functional variants in 30 000 known genes is between 50 000 and 250 000, and between one and five SNPs contribute to the disease (22), the prior probability might be set between 0.0001 and 0.00001. In contrast, the prior probability that a variant of a gene with functional data that is suggestive of a possible association, perhaps from a knockout animal or in vitro observation, will be truly associated with disease risk is likely to be in the 0.01–0.001 range.

Existing epidemiologic data on the association or linkage between the SNP or gene and disease should also influence the prior probability. The quality of the studies (23) and the statistical powers and P values of the tests should influence the weight given to the epidemiologic evidence. Data from diseases with possibly related etiologies can also be used. For example, the prior probability for an association between a genetic variant and ovarian cancer might be increased by evidence of an association between the same genetic variant and breast cancer. Data, however, cannot “count” twice; in a meta-analysis, for example, investigators must take special care that specification of the prior probability is independent of the data to be used in the analysis.

Assigning a precise prior probability to a specific hypothesis is neither possible nor, fortunately, required to use this approach. Assigning a genetic variant to one of several ranges of prior probabilities rather than to any specific value should be sufficient to identify those findings that are likely to be robust. For example, the range of each prior probability category could be 10-fold; in fact, simply designating a prior probability as high (≈0.1), moderate (≈0.01), or low (≈0.001) will be adequate for many situations.

Alternatively, investigators who are uncomfortable with the subjectivity of choosing a prior probability have additional options; they can start from empirical evidence of replication rates in similar studies (3,4,7,8) and then increase or decrease the presumed prior probability according to other available information. In addition, investigators who are reluctant to specify a prior probability can perform a simple sensitivity analysis of the effect of a wide range of prior probabilities on FPRP (see Appendix, step 2 of spreadsheet).

The practice of choosing a prior probability may not be quite as unfamiliar as it seems. Investigators already informally use prior probability to decide whether to launch a study, which genes to study, and how to interpret the results. We believe that formally developing prior probabilities before seeing study results can, in itself, lead to a substantial improvement in interpreting study findings over current scientific practice.

3. Specify the odds ratio and mode of inheritance for which statistical power should be calculated. Until more associations between genetic variants and particular diseases are replicated, we advocate using the statistical power to detect an odds ratio of 1.5 for alleles with an elevated risk in FPRP calculations [an odds ratio of 1.5 is a plausible value for important biologic effects (17,18)]. The reduction in FPRP from choosing an odds ratio above 1.5 will be small in situations where increasing statistical power has little effect, such as when the statistical power is already above 0.8 and the prior probability is much smaller than α. Statistical power and FPRP can be adversely affected, however, by specifying an odds ratio closer to 1.

If the SNP has an unknown function and there is no epidemiologic data, there is little basis for specifying the mode of inheritance in the statistical power calculation. Perhaps a dominant mode is most reasonable, on the premise that the difference between carrying one and two copies of the genetic variant is likely to have less effect on the odds ratio than the difference between carrying zero and one copy of the genetic variant. Investigators may wish to evaluate whether changing the assumed mode of inheritance greatly changes FPRP.

4. After completion of the study, determine whether the finding is noteworthy. Using standard software, calculate the odds ratio and 95% confidence interval (or odds ratio and P value) for the association between the genetic variant and the disease. Calculate FPRP from the observed P value, statistical power, and prior probability by using the FPRP calculation spreadsheet (see Appendix). Determine whether the estimated FPRP value is below the prespecified FPRP value. In addition, the reporting of FPRP values over a range of prior probabilities can inform readers who assume a prior probability different from the authors’ and can allow evaluation of the sensitivity of the FPRP value to different assumed prior probabilities.

Calculating FPRP for an SNP From a Reported Odds Ratio and Confidence Interval

The FPRP calculation spreadsheet (see Appendix) can help reviewers, editors, and readers to calculate an FPRP value when the P value or confidence interval for the odds ratio is available, but the FPRP approach is not used. Investigations can use the spreadsheet to determine for themselves whether to consider a finding in the literature to be noteworthy with their own prior probability.

Analysis of a Haplotype

Calculating FPRP when studying haplotypes requires some additional considerations. Without knowledge of the function of the SNPs in one or more haplotypes, the prior probability will apply to the gene or locus as a whole and therefore would be greater than the prior probabilities for each of the individual SNPs (8). Accordingly, the P value can be obtained from an omnibus test (24). In the omnibus test, the null hypothesis is that the risk of the disease is the same for all haplotypes and the alternative hypothesis is that the risk of the disease from at least one haplotype is different from the others. Statistical power can be obtained for an alternative hypothesis, such as an odds ratio of 1.5 for carriers of one of the more frequent haplotypes, with the most common haplotype as the referent.

Design Implications: FPRP and Sample Size

Fig. 6 shows how FPRP considerations can be used to determine sample size. A sample size of several hundred case patients and control subjects will achieve a statistical power of 0.8 to detect an odds ratio of 1.5 for a genetic variant of moderate frequency using an FPRP value of 0.2 when the prior probability is 0.25. Interestingly, the sample sizes needed to achieve a low FPRP with a high prior probability are similar to standard sample size calculations with the same statistical power and an α level of .05. For example, for q = .3 and a statistical power of 0.8 to detect an odds ratio of 1.5, the sample size required for an FPRP of 0.2 with a prior probability of 0.25 is 389 (Fig. 6, brown line), which is very close to 426, the standard sample size when α = .05 (Fig. 6, black broken line).

Fig. 6.

Sample size needed to achieve a false positive report probability (FPRP) value of 0.2 with various prior probabilities or with an α level of .05 (black broken line) for traditional sample size (N) calculations. Sample size is shown for various allele frequencies (q), with statistical power of 0.8 to detect an odds ratio of 1.5.

Example of the Application of the FPRP Approach to a Report in the Literature

Kuschel et al. (25) recently reported results on 16 SNPs in a total of seven genes involved in the repair of double-stranded DNA breaks and breast cancer from a case–control study of 2200 case patients and 1800 control subjects. Their article highlighted two polymorphisms in XRCC3, one polymorphism each in XRCC2 and LIG4, and a haplotype analysis of XRCC3 based on three SNPs. We use data from the Kuschel et al. article to demonstrate application of our FPRP approach. In our analysis of the Kuschel et al. data, we specified the FPRP value to be 0.5 because this value would provide high statistical power to find important SNPs and because other large breast cancer studies in the field will soon provide additional data addressing the contribution of these genes.

To assign a prior probability for these genes, we considered a previous finding that genetic variation in BRCA2, a DNA double-stranded repair gene, is associated with risk of breast cancer (26). On the basis of evidence of an association between genetic variation in the XRCC3 gene and other tumors (27), specifically cutaneous melanoma and bladder cancer, we assigned a relatively high prior probability range (i.e., 0.01–0.1). We then developed a range of prior probabilities for each of four genetic variants (outlined in Table 1) by taking into account previous reports that genetic variants in these specific genes are associated with other cancers, the type of genetic variant and its location in a coding or noncoding region, and functional data, if available. For each genetic variant, the FPRP value was calculated using the estimated prior probability range, the statistical power to detect an odds ratio of 1.5 (or its reciprocal, 0.67), and reported results (using estimated odds ratios and P values). An FPRP calculation spreadsheet for one SNP under a dominant mode of inheritance is shown in the Appendix.

Table 1.

False positive report probability (FPRP) values for four results on associations between 16 variants in genes involved in the repair of double-stranded DNA breaks and breast cancer based on data in Kuschel et al. (25)

Gene/SNP	Odds ratio (95% CI)*	Statistical power under recessive model†	Reported P value‡	Prior probability§
								.25	.1	.01	.001	.0001	.00001
XRCC3 C→T at nt 18067	1.32 (1.08 to 1.60)	1.00	.015	.042	.12	.59	.94	.993	.9993
XRCC3 A→G at nt 17893	0.82 (0.72 to 0.94)‖	.9895	.0075	.022	.064	.43	.88	.987	.9987
LIG4 T→C at nt 1977	0.65 (0.42 to 0.98)	.87	.088	.23	.48	.91	.990	.9990	1.00
XRCC2 G→A at nt 31479	2.60 (1.00 to 6.73)	.17	.071	.56	.79	.98	.998	.9998	1.00
XRCC3 haplotype		1.00¶	.000016#	.000049	.00015	.0016	.016	.14	.62

^*Odds ratios, except as noted, were calculated for the homozygotes with rare genetic variants versus the referents for homozygotes with common genetic variants, as reported in Table 2 of (25). CI = confidence interval. SNP = single-nucleotide polymorphism.

^†Statistical power, except as noted, is the power to detect an odds ratio of 1.5 for the homozygotes with the rare genetic variant (or, 0.67 = 1/1.5 for protective effect) and 1 for the heterozygotes and for the homozygote with the common variant, with an α level equal to the reported P value.

^‡ P values were calculated using the omnibus chi-square test, with two degrees of freedom, as reported in Table 2 of (25). The FPRP values are based on these P values.

^§The most likely range of prior probabilities are in bold type for each gene/SNP or haplotype. The prior probability is for an effect of the gene/SNP in the direction of the observed odds ratio.

^‖Odds ratios were calculated for the heterozygotes with the genetic variants versus the referent for the homozygotes with the common genetic variants, as reported in Table 2 of (25).

^¶Statistical power to reject the null hypothesis using the omnibus chi-square test, when the odds ratio is 1.5 for the second most frequent haplotype and 1 for the other haplotypes, with the most common haplotype as referent.

^# P value was calculated using the omnibus chi-square test, with seven degrees of freedom.

Among the four genetic variants we considered, the FPRP value for the A→G SNP at nt 17893 of XRCC3 was the only FPRP value below .5 for the prior probabilities we chose (Table 1). The C→T SNP at nt 18067 of XRCC3 had a higher P value, similar statistical power, and the same range of prior probabilities as the A→G SNP at nt 17893 of XRCC3; thus, its FPRP value is higher and less likely to represent a true association. We would choose not to highlight the XRCC2 and LIG4 SNPs, despite P values below .1, because of the high FPRP values that would result, given our prior probability range. For high prior probabilities, the LIG4 SNP result would have a much lower FPRP value than the XRCC2 SNP, even though their reported P values are similar. This situation is a consequence of the greater statistical power to detect a noteworthy finding for the LIG4 SNP than the rarer XRCC2 SNP. Using Appendix Table 1, investigators can assign their own range of prior probabilities to the published data, choose an FPRP value for each genetic variant, and perform a sensitivity analysis of the effects of prior probability on FPRP.

Appendix Table 1.

Joint probability of significance of test and truth of hypothesis

Truth of alternative hypothesis	Significance of test			Total
		Significant	Not significant
True association	(1 − β)π [True positive]	βπ [False negative]	π
No association	α(1 − π) [False positive]	(1 − α) (1 − π) [True negative]	1 − π
Total	(1 − β)π + α(1 − π)	βπ + (1 − α) (1 − π)	1

Kuschel et al. (25) also used a haplotype analysis to investigate the effect of the genetic variants in the XRCC3 gene on breast cancer risk. They presented pair-wise odds ratios for seven haplotypes against an arbitrary baseline, but we prefer to analyze the haplotype data with an omnibus chi-square test (24), which gives a value of 34 with seven degrees of freedom for a P value of .000016 (Table 1). The FPRP value is very low for this prior probability range and is quite robust even for low prior probabilities—that is, the FPRP value remains below 0.5 even for a prior probability of 0.0001. This interpretation suggests that the XRCC3 gene may contain one or more genetic variants that increase breast cancer risk.

Discussion

Molecular epidemiology studies are poised to take advantage of cheaper, faster laboratory platforms that enable analysis of many SNPs in more genes. However, continued reliance on the standard P value criterion of .05 to define statistical significance without consideration of power or prior probability will overwhelm us with too many false positives. Clearly, we need a new approach for deciding which findings to highlight among the results. Using a much lower P value based on multiple comparison corrective procedures would result in unnecessarily low power for hypotheses with high prior probabilities and for studies of diseases where collection of large numbers of cases is not feasible. Restricting ourselves to evaluation of the more plausible hypotheses would eliminate the opportunity for new, unpredictable discoveries among thousands of genes and SNPs. By contrast, we propose that the decision about whether to call a finding noteworthy or deserving of attention be made directly on the estimated probability that the finding does not represent a real association. Thus, our approach allows the prior probability of the hypothesis, the power of the study, and the tolerance for a false-positive decision, as well as the P value, to play a role in deciding whether a finding is noteworthy.

The FPRP approach is essentially Bayesian in that it formally integrates data from direct observation of study results with other information about the likelihood of a true association. Most Bayesian approaches focus on the posterior distribution of the odds ratio; however, by contrast, the FPRP approach retains the familiar dichotomy of findings (8,28) into those that are noteworthy and those that are not. Furthermore, unlike most Bayesian approaches, the FPRP approach does not require specification of a prior probability distribution for the odds ratio, which is a more challenging task than specification of only a prior probability, especially when so little is known about many of the SNPs that are studied. In addition, FPRP and the complement of posterior probability (obtained from a Bayesian analysis) are both conditional probabilities of no association; however, they are conditional on different data. That is, FPRP is conditional on the finding meeting a criterion for being called noteworthy and is not defined otherwise, but the complement of the posterior probability is conditional on all the data and is always defined. In addition, our calculation of FPRP is specific to the alternative hypothesis, including mode of inheritance and specific odds ratios, for which statistical power is calculated. In our view, despite some important advantages of the Bayesian approach, evaluation of evidence using the FPRP approach is simpler to understand and requires fewer assumptions and less technical expertise than standard Bayesian approaches; therefore, the FPRP approach seems more likely to be quickly adopted and uesd by investigators.

One potential limitation to the FPRP approach is the challenge of assigning a range for prior probability. However, investigators informally use prior probabilities already to decide which experiments to perform, which studies to field, and which specific hypotheses to test in those studies, and for interpreting results. With more experience, investigators should be better able to determine a prior probability. In the meantime, however, a crude classification of prior probabilities into low, medium, and high or a sensitivity analysis of FPRP across a range of prior probabilities should be an improvement over the current practice of relying entirely on statistical significance. An additional important benefit of considering prior probability is that investigators are forced to evaluate the existing evidence before seeing the results of their own study.

Requiring replication of a first statistically significant association in a second study before a finding is considered to be real can also reduce the percentage of false positives. It is a particularly useful strategy when false positives are likely to be due to bias in design or poor fieldwork. If, however, one assumes that the results from more than one study are all valid and can be combined, then using separate tests of statistical significance is not the optimal way to make a decision based on the available data. The FPRP approach, in contrast, is suitable for results from a pooled analysis or a meta-analysis, just as it is for an individual study.

Several other analytic methods to reduce the numbers of false-positive findings have been used or proposed. Bonferroni correction, discussed by Risch and Merikangas (29), and somewhat more powerful false discovery rate methods (30,31) lower the α level on the basis of the total number of tests performed, so that the probability that any true null hypothesis is rejected is maintained at a specified value, typically .05. Colhoun et al. (8) recently recommended reducing the standard value of statistical significance (i.e., the α level) from .05 to .0005 or .00005 to achieve a ratio of true-positive to false-positive reports of 20 : 1, under the assumption (based on empirical evidence of replication fractions) that .02 is a realistic prior probability. Standard Bayes and empirical Bayes methods yield a posterior distribution. Most empirical Bayes methods use the empirical distribution of odds ratios for each of the SNPs to determine a prior probability without considering that some SNPs are more likely than others to be associated with disease; however, some methods (32) do allow prior probabilities to differ.

The most important advantage of the FPRP approach over alternative non-Bayesian analytic methods is that it directly addresses the concern in the literature over too many false-positive reports (1). Thus, the decision of whether an association between a genetic variant and a disease is noteworthy depends on both prior probability and statistical power, in addition to the P value. We consider setting a low α level to be an indirect and inferior means to achieve the desired end of a low FPRP, because an FPRP can be high even for a low observed P value when the prior probability is low. Moreover, insisting on a very low P value before any finding is considered statistically significant may unnecessarily reduce statistical power when the prior probability is high, thereby constraining research on diseases with rare genetic variants or on diseases for which studies with large sample sizes are unrealistic. By contrast, the FPRP approach allows even relatively small studies or analyses of associations of rare genetic variants and diseases to make contributions to the field by providing a way for their results to be carefully and judiciously considered.

The flexibility of the FPRP approach provides several benefits. First, the FPRP approach is especially helpful for hypotheses with low prior probability, including broad data-mining efforts, such as whole genome scans, subgroup analyses, and tests for gene–gene and gene–environment interactions, because it can lead to more cautious interpretation of surprising findings. Second, an investigator can allow statistical power and loss from false-positive and false-negative decisions to influence the FPRP criterion for noteworthiness. Third, investigators can consider the false-negative report probability (Wacholder S: unpublished data), the probability of a true association between a genetic variant and a disease given a finding that is not considered noteworthy, when deciding whether further investigation is still warranted. Finally, FPRP integrates the evidence for each hypothesis individually, without being influenced by extraneous factors, such as how many (33) or which other hypotheses are also being evaluated. In fact, a generalization allowing correlations between pairs of prior probabilities would allow the effects of genetic variants in the same pathway, such as the repair of double-stranded DNA breaks, to be correlated, thereby increasing or decreasing the FPRP for one genetic variant according to the apparent strength of the association between a disease and another genetic variant in the same pathway.

Focusing on FPRP helps to illuminate issues in the study design, analysis, and interpretation of molecular epidemiology studies. Until now, investigators have almost universally denoted findings as “statistically significant” or “noteworthy,” in the usual senses of the words, on the basis of a statistical test with an α level of .05. Indeed, this strategy is effective when the prior probability of the primary hypothesis of an epidemiologic study or clinical trial is sufficiently high to justify a study on its own. For example, in a study with a statistical power of 0.8, the FPRP values when the P value is just under .05 would be 0.06 (for a prior probability of 0.5) and 0.36 (for a prior probability of 0.1). With recent advances in technology, however, high-throughput, low-cost genotyping can justify initiation of molecular epidemiology studies designed to evaluate many SNPs, even when the prior probabilities for most or all of the individual hypotheses are low.

Most immediately, the FPRP approach offers guidelines for publication and interpretation of study results. It provides a way for editors and readers of articles to protect themselves from being misled by statistically significant findings that do not signify a true association. Furthermore, the FPRP framework for interpreting initial findings can guide investigators’ decisions about whether to attempt to replicate molecular epidemiologic studies or to increase their understanding of the disease mechanism through development of in vitro model systems. Finally, the FPRP approach helps to formalize what investigators have always done informally—that is, tempering enthusiasm for surprising study findings with consideration of plausibility.

Appendix

What Is False Positive Report Probability?

To understand False Positive Report Probability (FPRP), first consider the four joint probabilities defined by the truth or falsity of the null hypothesis (H₀), crossed with the decision resulting from a statistical test T of H₀. We assume that the measure of association, the odds ratio or relative risk (RR), takes on one of two possible values, RR₀ = 1 under the null hypothesis of no association between the genetic variant (G) and disease (D) and RR_A under the alternative hypothesis (H_A).

Classical frequentist statistical theory, which is most commonly taught in applied biostatistics courses, does not specifically address these probabilities. In classical theory, the truth of H₀ and H_A is considered unknown, not random. Therefore, we must go outside classical theory to consider H₀ and H_A probabilistically. We define the prior probability (π) as π = Pr(H_A is true). We use the frequentist concepts of statistical size (i.e., probability of rejection under the null hypothesis) and statistical power in this formulation. A statistical test T has statistical size α for testing H₀ when rejection of H₀ is defined as T>z_α and Pr(T>z_α | H₀ is true) = Pr(rejecting H₀ | H_A is false) = α. Statistical power is denoted by 1 − β, with Pr(T>z_α | H₀ is false) = Pr(rejecting H₀ | H_A is true) = 1 − β or the probability of rejecting when the alternative hypothesis H_A is true. Note that statistical power is reduced when a lower, more stringent statistical size α and a greater z_α are used.

We define FPRP for standard statistical significance testing as Pr(H₀ is true | association is deemed statistically significant) = Pr(H₀ is true | T>z_α), where z_α is the α point of the standard normal distribution. The distinction between α level, statistical size, and FPRP is crucial; α level is the probability of a statistically significant finding, given that the null hypothesis is true, whereas FPRP is the probability that the null hypothesis is true, given that the statistical test is statistically significant.

Appendix Table 1 presents the joint probabilities of statistical significance of a single test of association and truth of the alternative hypothesis when one SNP is chosen randomly for testing.

Thus,

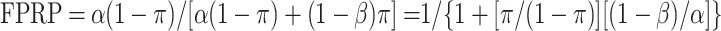One can see from this equation that FPRP is always high when α is much greater than π, and even more so when 1 − β is low.

To illustrate this point, consider the probability that a positive finding is false in an analysis of the association between a disease and a randomly selected SNP from a panel of 1000 SNPs available for testing. Allow the statistical test to have a maximum power of 1 and a standard α level of .05 (Appendix Table 2). If only one of these 1000 SNPs is known to be associated with the disease (i.e., π = .001), then the probability of both a true association and rejection of the test of association is .001 = (.001 × 1), and the probability that there is both no association and rejection of the null hypothesis is .04995 = .999 × .05; the total probability of rejection is .05095 = (.001 + .04995). Thus, there is only a 2% chance that the statistically significant finding will represent a true association—that is, conditional on rejection of the test; there remains a 98% chance that there is no association (FPRP = 0.98 = 0.04995/0.05095). In contrast, if 500 of the 1000 SNPs were known to be associated with the disease (i.e., π = 0.5), then the FPRP would be below 5%, and a statistically significant finding would have a 95% probability of representing a true association.

Appendix Table 2.

Joint probability of rejection of test and truth of hypothesis when π = .001, α = .05, and β = 0

Truth of alternative hypothesis	Significance of test			Total
		Significant	Not significant
True association	0.00100	0.00000	0.00100
No association	0.04995	0.94905	0.99900
Total	0.05095	0.94905	1.00000

Technical Points on Design and Data Analysis Using FPRP Value

In the FPRP-based analytical approach described in this commentary, the FPRP value is calculated from the prior probability, statistical power, and observed P value by substituting the P value in place of α in the right-hand side of equation 1. If the FPRP value is below a preset FPRP value (F), the association between the genetic variant and the disease is deemed noteworthy. Just as the P value is the lowest α level at which a test would be deemed statistically significant, the FPRP value is the lowest FPRP value at which a test would yield a noteworthy finding.

To consider the statistical power of a test of the null hypothesis, where the relative risk is RR = RR₀ = 1 versus the alternative hypothesis RR = RR_A, we first assume that the estimate of RR is normally distributed with a variance σ². We calculate the statistical power (1 − β) of a procedure that determines a finding to be noteworthy (rejects the null hypothesis) when the FPRP value is below the preset FPRP value for a given prior probability (π). To do this calculation, we note that statistical power (1 − β) depends on α and must satisfy the following equation:

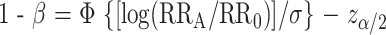where Φ is the cumulative distribution function of the standard normal distribution, and z_α/2 is the α/2 point of the standard cumulative normal distribution. Equation 2 is the standard formula for the statistical power of a test with an alternative hypothesis that the odds ratio equals RR_A. Equation 2 can be re-expressed in terms of genotype frequency and number of case patients and control subjects (N) as 1 − β = Φ[N(q1 − q0)²)/(2(1 − q)q)]^0.5 − z_α/2, where q0 is the fraction of control subjects with a higher-risk genotype, q1 = q0(RR_A)/[1 + q0(RR_A − 1)], the fraction of case patients with a higher-risk genotype, and q = (q1 + q0)/2.

When calculating FPRP value for a report, σ and z_α/2 in equation 2 are replaced by the standard error (SE) of the log–odds ratio estimate and the two-sided P value point of the standard normal distribution, respectively. Even when SE is not available directly, SE can still be obtained when the 1 − α% confidence interval (CI_U to CI_L) for the odds ratio are given: SE = [log(CI_U − CI_L)]/(2z_α/2), where log is the natural logarithm function. For example, the denominator, 2z_α/2, is 2 × 1.96 when α = .05.

Representation of FPRP Calculation Spreadsheet

An Excel spreadsheet to calculate FPRP is included with the online material (seehttp://jncicancerspectrum.oupjournals.org/jnci/content/vol96/issue6). In the representation of the spreadsheet below, input data are used to implement the method. Input data are italicized, and output data are bold. The odds ratio (OR) and confidence interval (CI) in step 4 are from Kuschel et al. (25). Note that the numbers in the commentary and in the FPRP calculation spreadsheet below were obtained by programs written in MatLab (The MathWorks, Natick, MA) and Excel (Microsoft, Redmond, WA), respectively.

Step 1. Preset an FPRP value for noteworthiness.

FPRP value: 0.5

Step 2. Enter up to six values for the prior probability that there is an association between the genetic variant and the disease.

Prior probability 1: .25

Prior probability 2: .1

Prior probability 3: .01

Prior probability 4: .001

Prior probability 5: .0001

Prior probability 6: .00001

Step 3. Enter up to three values of odds ratio that are plausible values for a noteworthy finding, assuming that there is a non-null association under a dominant model. Odds ratio 1: 1.2, statistical power =.179; odds ratio 2: 1.5, statistical power = .904; odds ratio 3: 2.0, statistical power = 1.000.

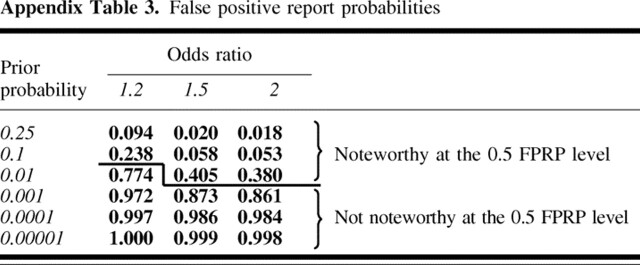
Step 4. Enter odds ratio estimate and 95% confidence interval to obtain FPRP value. OR = 1.316; 95% CI = 1.08 to 1.60; log(OR) = .275; SE[log (OR)] = .100; P value = .006. FPRP values are shown in Appendix Table 3.

Appendix Table 3.

False positive report probabilities