Abstract
Theta oscillations (4-8 Hz) provide an organizing principle of cognitive control, allowing goal-directed behavior. In adults, theta power over medial-frontal cortex (MFC) underlies conflict/error monitoring, whereas theta connectivity between MFC and lateral-frontal regions reflects cognitive control recruitment. However, prior work has not separated theta responses that occur before and immediately after a motor response, nor explained how medial-lateral connectivity drives different kinds of control behaviors. Theta’s role during adolescence, a developmental window characterized by a motivation-control mismatch also remains unclear. As social observation is known to influence motivation, this might be a particularly important context for studying adolescent theta dynamics. Here, adolescents performed a flanker task alone or under social observation. Focusing first on the nonsocial context, we parsed cognitive control into dissociable subprocesses, illustrating how theta indexes distinct components of cognitive control working together dynamically to produce goal-directed behavior. We separated theta power immediately before/after motor responses, identifying behavioral links to conflict monitoring and error monitoring, respectively. MFC connectivity was separated before/after responses and behaviorally-linked to reactive and proactive control, respectively. Finally, distinct forms of post-error control were dissociated, based on connectivity with rostral/caudal frontal cortex. Social observation was found to exclusively upregulate theta measures indexing post-response error monitoring and proactive control, as opposed to conflict monitoring and reactive control. Linking adolescent cognitive control to theta oscillations provides a bridge between non-invasive recordings in humans and mechanistic studies of neural oscillations in animal models; links to social observation provide insight into the motivation-control interactions that occur during adolescence.
Keywords: Theta, Cognitive Control, Medial-Frontal Cortex (MFC), Adolescence, Social Observation, Motivation
Introduction
Goal-directed behavior in humans engages neurocognitive processes—commonly referred to as cognitive control—to coordinate system-level brain activity (Gratton 2018). Cognitive control involves two primary components, including: 1) monitoring for conflict or errors, which indicates that control is needed; 2) control recruitment, further broken down into proactive control, recruited before needed, and reactive control, recruited in a just-in-time manner (i.e., the Dual Mechanisms of Control framework; Braver 2012). In various mammalian species, theta oscillations reflect organizing activity within a cross-level cognitive control system (Cavanagh and Frank 2014; Cohen 2017; Verguts 2017) and time-frequency EEG analyses can map oscillations among brain regions in ways that are missed by other approaches, linking particular cognitive control subprocesses to neural oscillations. For example, in adults, increased theta power over medial-frontal cortex (MFC) underlies monitoring (Ullsperger et al. 2014), whereas theta connectivity between MFC and lateral-frontal regions reflects control recruitment (Cavanagh and Frank 2014). Application of these methods to adolescent data provides a unique opportunity to inform mechanistic understandings of cognitive control during a critical period of development. Cognitive control develops throughout childhood to approach maturity in adolescence (Casey et al. 2001; Luna et al. 2004; Chatham et al. 2009), with motivational processes becoming uniquely salient during this period (Nelson et al. 2005; Casey et al. 2008; Steinberg et al. 2008; Luciana and Collins 2012). Moreover, social observation can increase motivation (Triplett 1898; Zajonc 1965; Chib et al. 2018), particularly during the adolescent period (Nelson et al. 2005; Blakemore 2008; Crone 2014), suggesting that social observation may reflect an important context in which to study motivation-control interactions. Here, we leverage EEG and advanced time-frequency approaches to explore the role of theta oscillations and social observation on the deployment of cognitive control systems during this vital window of human brain development.
Studying interactions between motivational and cognitive control processes could provide a more fundamental understanding of cognitive control (Holroyd and Yeung 2012; Botvinick and Braver 2015; Cools 2016). While links between motivation and cognitive control have been well-studied at the behavioral level, the neuroscience of motivation-control interactions is quite limited (Botvinick and Braver 2015), particularly in relation to social motivation. Social processes, such as observation and evaluation, can increase motivation (Triplett 1898; Zajonc 1965; Chib et al. 2018). Recent work examines the influence of social observation on motivation and cognitive control during adolescence (Crone 2014; Buzzell, Troller-Renfree, et al. 2017; Barker et al. 2018) with a range of neural techniques (fMRI, ERPs). However, few studies dissect the ways that social observation influences specific cognitive control subprocesses. Studying theta oscillations could provide a useful method for examining how distinct subprocesses of cognitive control are impacted by social observation. For example, work in adults suggests that monetary incentives specifically affect proactive control (Botvinick and Braver 2015), but comparable work is needed in adolescents focusing specifically on social observation and motivation.
Regarding cognitive control subprocesses, researchers often study cognitive control by having participants perform speeded visuo-motor tasks, such as the flanker task (Eriksen and Eriksen 1974), which involves a mixture of low conflict (congruent) and high conflict (incongruent) trials that often result in the commission of errors. When performing such tasks, work in adults demonstrates increased MFC theta power in response to conflict (conflict monitoring; Cohen and Donner, 2013) or errors (error monitoring; Cavanagh et al., 2009). Increased theta synchrony within the MFC region (inter-trial phase synchrony) is also typically observed in response to such events (Cavanagh et al. 2009). Together, MFC theta power and MFC theta synchrony may form the equivalent of an “alarm signal” (Cavanagh and Frank 2014) and the initial stages of coordinating neural activity in response to critical events (Verguts 2017). Moreover, MFC appears to recruit lateral-frontal cortex (LFC) to instantiate top-down control (Miller 2000; Miller and Cohen 2001) through theta connectivity between MFC and LFC (inter-channel phase synchrony; connectivity) after errors or in response to conflict (Cavanagh et al. 2009; Bolaños et al. 2013; Cohen and Donner 2013).
However, existing time-frequency work has yet to fully leverage analysis of theta oscillations in an effort to parse cognitive control at finer levels of detail (see Figure 1). In conflict tasks, errors can be prevented through two primary avenues: proactive or reactive control (DMC framework; Braver 2012). For example, error commission (and error monitoring) could drive a transient increase in proactive control to prevent errors on the following trial (i.e. instantiated before the control is required). Thus, one might hypothesize that an increase in MFC theta power and MFC-LFC connectivity after errors, but before the following trial, might reflect error monitoring and proactive control, respectively. In contrast, reactive control, is theorized to reflect the recruitment of control in a reactive and “just-in-time” manner as it is needed (i.e. after a stimulus is presented, but before the response). Thus, one would expect a conflict monitoring process (MFC theta power) to detect conflict and recruit reactive control (MFC-LFC connectivity) following presentation of incongruent trials, but prior to responding. While prior work has shown that MFC theta power, MFC theta synchrony, and MFC-LFC connectivity are generally increased in response to either conflict or errors (Cavanagh and Frank 2014), to the best of our knowledge, prior work has not explicitly dissociated such processes within the same dataset. That is, most work only studies error-related effects within response-locked data, only congruency-related effects within stimulus-locked data, and rarely are both error and congruency effects reported together for the same participants and task. With such an approach, it is difficult to determine whether theta dynamics truly reflect pre-response conflict monitoring and reactive control (to resolve conflict), as opposed to post-response error monitoring and proactive control to prepare for the subsequent trial. In the current study, we isolate both pre- and post-response theta dynamics within the same segments of response-locked data and demonstrate dissociable associations with error/conflict monitoring and proactive/reactive control.
Figure 1.
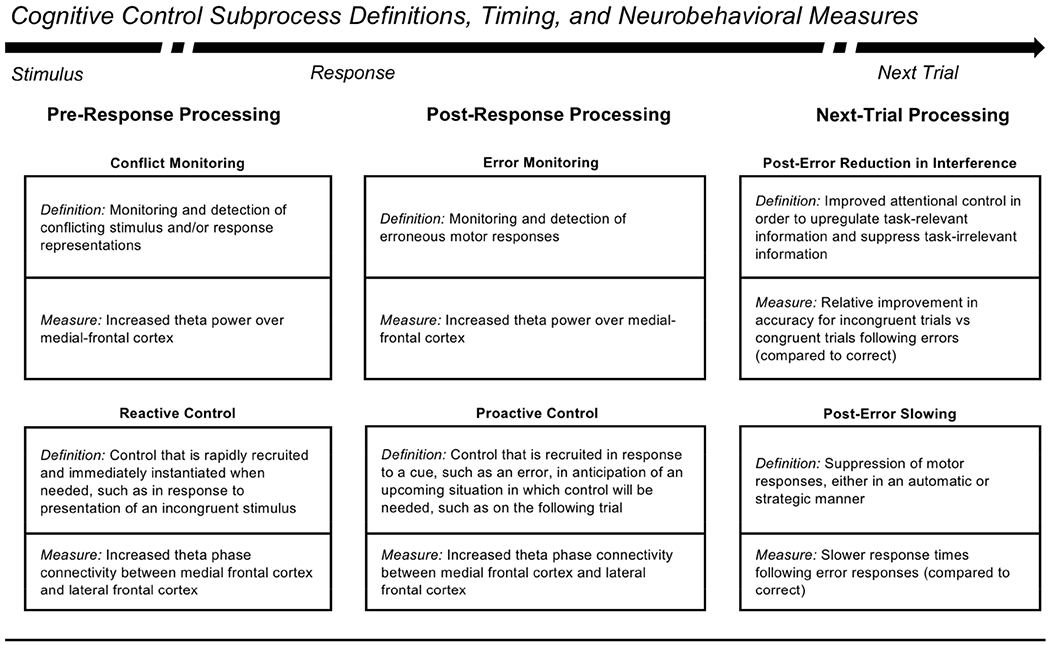
Description of cognitive control subprocesses and neurobehavioral measures. The arrow depicts the flow of time for a single trial on a task requiring cognitive control (e.g. a flanker task). Time begins with stimulus presentation and pre-response processing, followed by response commission and post-response processing, ending with presentation of a subsequent trial and associated neurobehavioral processing. Each box defines a particular cognitive control subprocess and a neural or behavioral measure that can be used to index the subprocess. Note that the use of proactive control here is distinct from the more common study of “tonic proactive control” that occurs at the block level. Instead, our use of proactive control is in line with the notion of “transient proactive control” that can follow an error and prepare control for the subsequent trial in a proactive manner. See Table S1 for definitions.
Beyond separating pre- and post-response theta oscillations, more work is needed to validate the functional significance of theta dynamics via associations with behavior. Towards this end, post-error reduction in interference (PERI; Danielmeier and Ullsperger, 2011) reflects an unequivocal and “ground-truth” behavioral measure of transient proactive control following error commission (Ridderinkhof et al. 2011). PERI reflects increased accuracy on incongruent trials (relative to congruent), associated with proactively (Ridderinkhof et al. 2011) adjusting selective attention (King et al. 2010) on post-error trials. Thus, if post-response MFC-LFC connectivity reflects transient proactive control (for the next trial), then this measure should associate with PERI. Similarly, if pre-response increases in MFC-LFC connectivity reflect recruitment of reactive control in order to prevent an error, then failures of such control should be observable immediately before error responses as a possible cause of such errors. While some work has linked MFC-LFC connectivity to behavior (Cavanagh et al. 2009; Cohen and Donner 2013), the current study provides the first concurrent validation that pre- and post-response MFC-LFC connectivity are dissociated in terms of behavioral correlates of reactive and proactive control, respectively.
Studying theta oscillations may also allow for dissociating general vs. task-specific changes in behavior after errors. Whereas PERI reflects task-specific proactive control (Ridderinkhof et al. 2011), post-error slowing (PES) reflects a general increase in response times following errors and is thought to at least partially reflect a general and automatic inhibition of (pre-)motor cortex following unexpected events like errors (Jentzsch and Dudschig 2009; Notebaert et al. 2009; Danielmeier and Ullsperger 2011; Wessel and Aron 2017; Wessel 2018). fMRI work has demonstrated that more rostral regions of LFC, including dorsolateral prefrontal cortex (DLPFC), more closely relate to post-error changes in selective attention and accuracy rates (PERI), whereas more caudal regions of LFC, including primary and pre-motor regions, links more closely to post-error changes in response times (PES; King et al. 2010). While existing time-frequency work only targets overall levels of MFC-LFC theta connectivity, we would predict that MFC connectivity with rostral-LFC to predict PERI, a deliberative and task-specific form of proactive control; in contrast, we would predict that MFC connectivity with caudal-LFC would link to more automatic and general changes in behavior: PES.
The current study validates these proposed theta-based indices of cognitive control subprocesses and leverages them to investigate the impacts of social observation. Towards this end, we had a large group of adolescents perform a flanker task twice (in a counterbalanced order), once alone and once under social observation. Before investigating the effects of social observation, we utilized the nonsocial condition in order to establish theta-based indices of cognitive control subprocesses. We applied Cohen’s Class reduced interference distributions (RID) and time-frequency principal components analysis (TF-PCA; Bernat et al. 2005) to isolate pre- and post-response theta dynamics within the same epochs of data. In this way, we dissociated pre- and post-response MFC theta power as indices of conflict/error monitoring, respectively, as well as pre- and post-response MFC-LFC connectivity as indices of reactive/proactive control, respectively. For post-error changes, we also dissociated MFC connectivity with rostral/caudal LFC to dissociate task-specific control (PERI) and generalized response slowing (PES) following errors. Moving towards a more mechanistic account of how cognitive control subprocess interrelate to produce post-error changes in behavior, we formalized relations between MFC theta power, MFC theta synchrony (inter-trial phase synchrony) and MFC-LFC theta connectivity (inter-channel phase synchrony) within a structural equation model.
After establishing theta-based indices of cognitive control subprocesses and their interrelations, we investigated how social observation impacted each subprocess individually. One view might suggest that if social observation increases overall levels of arousal, then social observation would yield a non-specific and uniform increase across all subprocesses. However, based on the notion that social observation can increase motivation—particularly during the adolescent period—and previous work in adults linking motivation to increases in proactive control specifically, we hypothesized that social observation would particularly influence proactive control.
Materials & Methods
Participants
The current report focuses on 144 adolescents (M age = 13.12 years, SD = .58, range = 12.11 – 15.29; 73 male) that were part of a larger longitudinal study focused on socio-emotional development. Children were originally selected at 4 months-of-age based on observations of their behavior in the laboratory (Fox et al. 2001). The 144 participants reported here reflect adolescents who returned to the laboratory at approximately 13 years-of-age to perform a flanker task and had valid behavioral data; these participants did not differ from the larger longitudinal study in terms of 4-month reactivity (χ2 = 3.97, p = .265) and a total of 132 of these participants had valid EEG. A series of statistical analyses were performed on subsets of this sample following the removal of condition-specific outliers; EEG plots include all 132 participants with EEG data. Analyses of flanker task ERP data have previously been reported for a largely overlapping subset of these participants (Buzzell, Troller-Renfree, et al. 2017), however, this report reflects the first investigation of time-frequency dynamics in this sample. All procedures were approved by the University of Maryland—College Park institutional review board; all parents provided written informed consent, and children provided assent.
Flanker Task
In a counterbalanced order, participants completed a modified flanker task (Eriksen and Eriksen 1974) twice; once while alone (nonsocial condition) and once while believing they were being observed by peers (social condition). During the nonsocial condition, participants were provided with computer-generated feedback following each block. Prior to completing the flanker task within the social condition participants logged into an intranet chatroom where they created a screen name and uploaded their picture while waiting for two other age-matched peers to also log into the chatroom (see Figure 2B). For the social condition, participants were led to believe that their flanker task performance would be monitored via webcam by these peers and that real-time feedback would be provided after each block. In reality, the peers were fictitious, and the feedback was computer generated. During the nonsocial condition, participants were instructed that no one would observe their performance and that the block-level feedback was simply computer generated (see Figure 2C). Prior work has established the validity of this paradigm and its ability to modulate social motivation (Barker et al. 2018). See the supplement for further details of the social deception protocol, as well as analyses confirming that the counterbalanced design removed the possibility of order effects confounding statistical analyses of interest.
Figure 2.
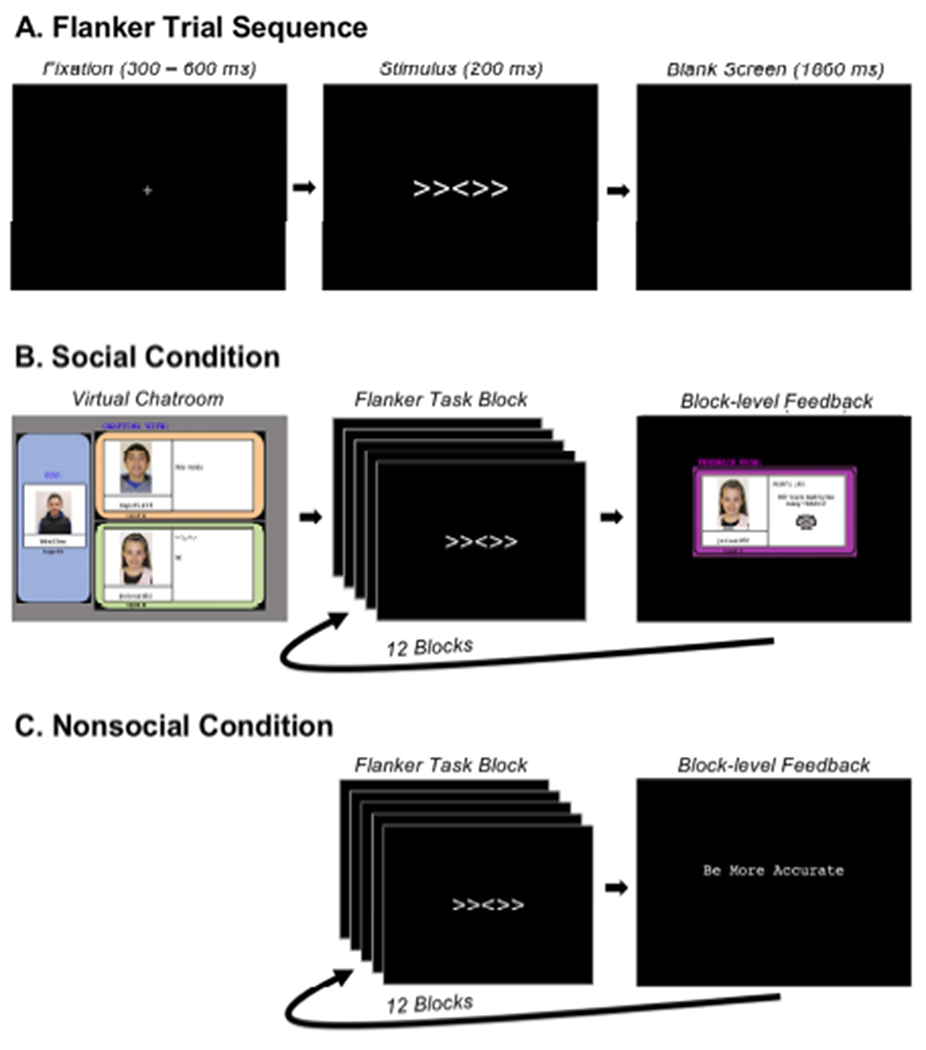
Experimental paradigm. A) Identical trial sequence employed within the social and nonsocial conditions (no trial-level feedback). B) Depiction of the virtual chat room and block-level social feedback employed within the social condition to increase social motivation. C) Depiction of the nonsocial condition in which block-level computer-based feedback was provided.
Within the social and the nonsocial conditions, block-level feedback always consisted of text conveying instructions in one of three categories. Specifically, text either indicated that the adolescent needed to be more accurate, to respond faster, or that they were doing a good job. For the social condition, text consisted of phrases more conversational in nature (e.g, “No! You’re making too many mistakes!”), and text was always accompanied by an emoticon (see Figure 2B), which the participant was led to believe was selected in real time by a peer. Nonsocial condition feedback consisted of text only, in unembellished phrasing (e.g., “be more accurate”). Although the adolescents believed that feedback was either provided by a peer or computer-generated, feedback was always generated based on task performance. If adolescents performed at or below 75% accuracy, they received feedback indicating the need to be more accurate. If performance was at or above 90%, they received feedback indicating the need to respond faster. If performance was between 75% and 90%, they received feedback indicating that they were doing a good job. This feedback procedure is consistent with the recommendations by Gehring and colleagues (2012), which helped maintain accuracy at a level that would ensure an adequate number of errors for subsequent response-locked EEG analyses.
Each trial of the flanker task involved presentation of a central arrowhead flanked by two additional arrowheads on each side and facing in the same (congruent) or opposite (incongruent) direction (see Figure 2A). Participants were instructed to indicate the direction of the central arrowhead via button press and ignore the flanking arrowheads. Incongruent and congruent trials were presented with equal probability. For the social and non-social conditions, participants separately completed 12 blocks, each consisting of 32 trials and all blocks were followed by feedback. No feedback was presented at the trial level. Stimuli were presented on a 17” LCD monitor, using E-Prime 2.0.8.74 (Psychology Software Tools, Pittsburg, PA). Responses were collected using an EGI Response Pad (Model: 4608150-50) button box. The task was completed within a dimly lit, electrically-shielded and sound-attenuated room. Participants were left alone within the experimental room during data collection, with all monitoring of the task and EEG collection being performed within an adjacent room.
While prior work validated that this task modulates social motivation (Barker et al. 2018), we additionally collected subjective reports of motivation from participants as a methods-check of our manipulation. Towards this end, participants were asked to rate on a scale of 1-10 “How hard did you try when you were playing the game that included feedback from the kids?”, as well as “How hard did you try when you were playing the game that included feedback from the computer?” Participants were further asked to provide a free-response explanation for their reported effort level in each condition. Statistical comparison of self-reported motivation between the social and non-social conditions was performed via a paired-samples t-test.
EEG Acquisition and Preprocessing
EEG was acquired using a 128-channel HydroCel Geodesic Sensor Net and EGI software (Electrical Geodesic, Inc., Eugene, OR); EEG analysis was performed using the EEGLAB toolbox (Delorme and Makeig 2004) and custom MATLAB scripts (The MathWorks, Natick, MA). Targeted electrode impedance level during data collection was < 50 kΩ, given that a high input-impedance system was used. Data were sampled online at 250 Hz and referenced to the vertex. Following acquisition, systematic marker offsets were measured and corrected for the EGI system (constant 36 ms offset) and E-Prime computer (constant 15 ms offset). Data were high-pass filtered at .3 Hz and low-pass filtered at 45 Hz. FAST tools (Nolan et al. 2010) were used to identify and remove bad channels. In order to identify and remove artifactual activity from the data, ICA decomposition was run on an identical data set with the addition of a 1 Hz high-pass filter (Viola et al. 2010). This 1 Hz filtered data set was epoched into arbitrary 1000 ms epochs; prior to running ICA, noisy epochs were detected and removed if amplitude was +/− 1000 uV or if power within the 20-40hz band (after Fourier analysis) was greater than 30dB. If a channel led to more than 20% of the data being rejected, this channel was instead rejected. ICA was run on the 1 Hz high-pass filtered dataset and the ICA weights were then copied back to the original (continuous) .3 Hz high-pass filtered dataset (for an overview of this approach, see: Viola et al., 2010); all subsequent processing was performed on the .3 Hz high-pass filtered dataset. Artifactual ICA components were first detected in an automated procedure using the ADJUST toolbox (Mognon et al. 2011), followed by manual inspection of the ICA components (see supplement for further details). All ICA components identified as artifacts (through automated and manual inspection) were subtracted from the data.
For EEG analyses, data were epoched to the response markers from −1000 to 2000 ms. All response-locked epochs were baseline corrected using the −400 to −200 ms period preceding the response. Note that this baseline correction removes the DC offset present in the EEG signal; further baseline normalization procedures were not employed, given the use of time-frequency PCA to separate event-related EEG dynamics from any constant offsets present in the data (see below for further details). A final rejection of +/− 100 uV was used to identify and remove bad epochs in the data that might have been missed by other methods. If greater than 20% of the data were rejected, the channel was rejected instead. All missing channels were then interpolated using a spherical spline interpolation. Following interpolation, data were referenced to the average of all electrodes. Given the focus on theta band activity, data were downsampled to 32 Hz in order to improve computational speed with no loss to the signal of interest (i.e. theta = ~4-8 Hz; Nyquist = 16 Hz).
Subsampling of EEG
All participants included in the EEG analyses had a minimum of 6 artifact-free trials per condition of interest, which has been shown to be suitable for response-locked analyses in either children or adults (Pontifex et al. 2010; Steele et al. 2016). However, the calculation of some EEG metrics (i.e. coherence-based measures) are inherently scaled (and biased) based on the number of trials used in their calculation, requiring a means to equate trial numbers across conditions when they are calculated. Therefore, we implemented a subsampling procedure, selecting a random subsample of 4 trials (without replacement; no trial appeared twice within a given subsample) to equate trial counts between conditions each time an EEG metric of interest was computed. This process of taking a random subsample of 4 trials and calculating EEG metrics with matched trial counts was repeated 25 times (with replacement; trials could appear across more than one subsample, but the same trial never repeated within a subsample) creating 25 estimates of a given EEG metric for each condition. We additionally bootstrapped these 25 subsamples 100 times (with replacement), before taking the mean of the bootstrapped samples as the final mean estimate of a given EEG metric (however, this additional bootstrapping, via the MATLAB bootstrp function, is not critical and is a largely redundant step).
Our subsampling approach retains the same logic as the traditional (single) subsample approach, with the added benefit of incorporating all information available to the researcher when estimating EEG metrics for a given condition. While it is technically only necessary to subsample the condition with a greater number of trials, in order to match trial numbers with the condition having less trials, we applied the same subsampling approach to all conditions for analytic consistency (note that subsampling does not increase the effective number of trials in the condition with less trials and this step is for analytic consistency only). Similarly, while the utility of subsampling is found in appropriate scaling of coherence-based metrics, we applied the subsampling approach when calculating power-related EEG metrics as well to maintain analytic consistency and ensure that the exact same mixture of trials was used for computing all EEG metrics (the index of trials going into each subsample was only generated once, for each condition, for each participant, and then used for calculating all EEG metrics).
Isolation of Pre- and Post-Response Cognitive Control Within the Theta Band
Cohen’s class RID and time-frequency PCA.
The most common approach to studying peri-response MFC theta is to calculate separate time-frequency decompositions, either for stimulus- or response-locked data, separately. However, in studying stimulus-locked congruency effects, it is difficult to ascertain whether any theta dynamics truly reflect pre-response conflict monitoring and reactive control (to resolve conflict), as opposed to post-response error monitoring and proactive control to prepare for the subsequent trial; a similar issue arises when attempting to interpret post-response theta and trying to rule out pre-response theta dynamics. One solution would be to measure both pre- and post-response MFC theta within a single, response-locked time-frequency distribution. However, attempting to separately measure MFC theta dynamics that occur immediately before or after the response, within the same time-frequency distribution, leads to the issue of appropriately separating these theoretically distinct processes that occur close together in time. Without a high level of resolution in both the time and frequency domains it would be difficult to distinguish when pre-response theta ends, and post-response theta begins, as well as the exact theta band that each process presents itself within.
To alleviate this issue, we employed Cohen’s class reduced interference distributions (RID) to decompose a time-frequency representation of response-locked average power (Bernat et al. 2005); delta band activity was filtered out prior to TF decomposition to isolate theta activity. Cohen’s class RID refers to a time-frequency transformation method yielding uniformly high resolution in both the time and frequency domains. Of note, the Cohen’s class RID approach does not require any a priori tailoring in order to achieve high resolution within particular frequency bins and instead produces uniformly high resolution across all frequency bins (Bernat et al. 2005). This feature of Cohen’s class RIDs is particularly useful when studying a population like adolescents where the exact frequency bins capturing theta are not known a priori; similarly, this feature does not bias measurement of pre- or post-response theta if they present at slightly different frequency bins within the theta band.
After decomposing the TF distribution, we employed PCA of the average power time-frequency surface (TF-PCA; Bernat et al., 2005) to isolate separate sources of theta activity pre- and post-response. TF-PCA provides a data-driven approach for separating pre- and post-response theta, as this approach is designed to identify, and then separately measure, unique processes present within the same time-frequency distribution (Bernat et al. 2005; Harper et al. 2014). Specifically, TF-PCA is a data reduction technique that involves application of PCA to the time-frequency surface. Separately, for each participant, for each channel, for all conditions of interest, the 2-dimensional time-frequency average power surfaces (samples x frequency) were reorganized into vectors by concatenating the row of sample data corresponding to each frequency bin into a vector. Therefore, each participant contributed one vector for each channel x condition combination. The PCA was then run on all vectors, from all participants at once, producing a single PCA factor solution (determined via inspection of the scree plot) for all data. The factor loadings for each factor were then transformed back into a 2-dimensional surface and applied to all channels, participants, and conditions, producing the PC-weighted data that was used for plotting and further analyses.
Investigation of the scree plot suggested that a 3-factor solution described the data well. This 3-factor solution identified a clear MFC theta band factor maximal immediately following the response, consistent with prior work investigating post-error theta (Cavanagh et al. 2009), which has also been shown to contribute to the ERN (Luu et al. 2004; Trujillo and Allen 2007). Critically, the 3-factor solution also yielded a pre-response theta factor with maximal activation over MFC and posterior scalp regions, consistent with prior work investigating stimulus-locked theta for conflict (Cohen and Cavanagh 2011; Cohen and Donner 2013), which contributes to the N2 (Harper et al. 2014). A third alpha band factor was also identified, although investigation of this third factor is beyond the scope of the current report. See Figure 3 for a depiction of the pre- and post-response theta factors. These results represent the first evidence separating pre- and post-response MFC theta within the same epoch, removing confounds of pre-response theta on post-response theta, and vice-versa.
Figure 3.
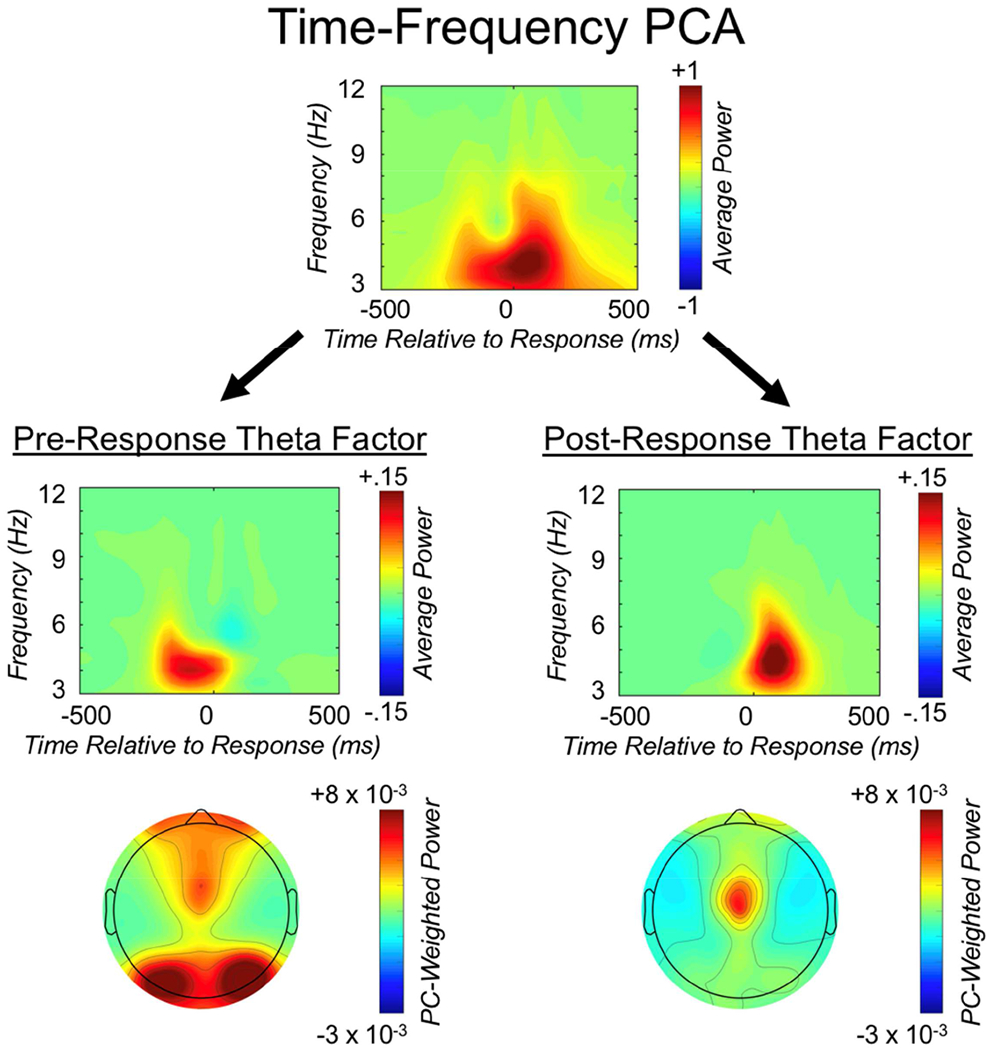
The Time-frequency PCA approach. We isolated separate pre- and post-response theta factors by applying time-frequency principle component analysis (PCA) to average power data. These factor loadings were subsequently applied to total power and also leveraged for inter-channel phase synchrony measurement. The top panel reflects the unweighted average power time-frequency distribution over medial-frontal cortex (MFC), collapsed across all conditions of interest. The second row depicts the same average power distribution weighted by the pre- and post-response theta factors, respectively; the third row displays the corresponding topographic plots.
Total power.
Total power refers to a time-frequency distribution of power values that includes both phase- and non-phase-locked information, and is computed from a time-frequency transformation of trial-level data that is then averaged across trials; in contrast, average power refers to a time-frequency distribution of power values that includes primarily phase-locked information and is computed from a time-frequency transformation of data that has already been averaged across trials of interest. After identifying pre- and post-response theta factors using the average power time-frequency surfaces, we then applied these factor loadings to a time-frequency decomposition of total power, again using Cohen’s Class RID and pre-filtering out delta. This approach allowed us to extract total power within the theta band immediately before, and immediately following the response; these data were used for subsequent analyses. Identifying the factor loadings first within the TF surface for average power improves separation of events occurring distinctly before and after the response; applying these loadings to a TF decomposition of total power incorporates both phase-locked and non-phase-locked data (Cohen 2014), which is the most commonly employed metric for studying MFC monitoring processes and yields a more comprehensive measure of MFC theta (Cohen 2014). Thus, we were able to extract a measure of total power that allowed for more direct comparisons with prior adult work, while still allowing us to retain the high time-frequency resolution afforded by Cohen’s class RID and time-frequency PCA loadings (derived from the average power TF surface). In the text, all subsequent analyses and references to “theta power” refer to the total power measure weighted by the average power TF-PCA loadings. For analyses and plotting, MFC theta power was separately averaged for the pre- and post-response theta factors, within each condition of interest, for a cluster of electrodes that included E6 (approximately equal to FCz in the EGI geodesic sensor net) and the six immediately adjacent electrodes (E12, E5, E112, E106, E7, E13). Topographic plots exclude the outermost ring of electrodes, given that no a priori hypotheses related to these electrodes and they are subject to additional movement artifact; see Figure 4 for a complete map of electrode and cluster locations.
Figure 4.
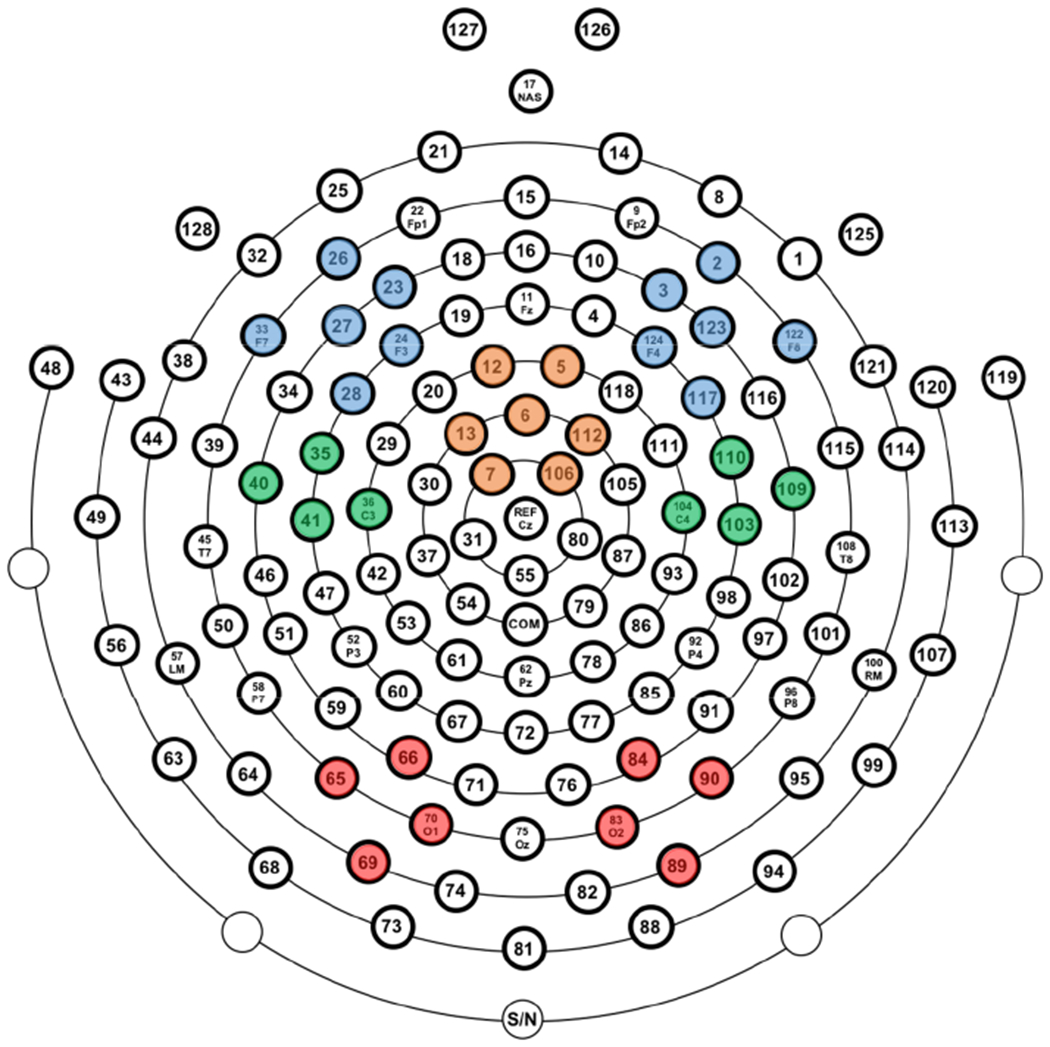
Electrode clusters employed in all EEG analyses. Medial-frontal cortex (orange); left and right rostral-lateral-frontal cortex (blue); right and left caudal-lateral-frontal cortex (green); right and left occipital cortex (red).
Inter-channel phase synchrony.
Inter-channel phase synchrony reflects a measure of consistent phase alignment between channels and is calculated across trials within a given frequency band and time range (here defined by a PCA factor); this measure is thought to index neuronal connectivity and communication between brain regions and therefore we use the term “connectivity” to interchangeably refer to inter-channel phase-synchrony throughout this manuscript. Following the application of a Laplacian transform (current source density; CSD) to improve spatial resolution (Tenke and Kayser 2012), we computed inter-channel phase-synchrony (across trials) to test for connectivity between an MFC seed electrode (FCz/E6) and six clusters over other cortical regions. Of note, raw EEG data is susceptible to volume conduction that degrades spatial resolution. However, a Laplacian transform mitigates volume conduction and enhances spatial resolution (Tenke and Kayser 2012), allowing for the separation of the clusters tested here, and critically, distinguishing between rostral/caudal LFC. Specifically, a Laplacian transform corresponds to the second spatial derivative of the field potential and acts as a spatial filter that works to subtract out spatially distributed (volume-conducted) effects present in the raw EEG. The ability of the Laplacian transform to mitigate volume conduction has been validated using both simulated and real data (Srinivasan et al. 2007; Winter et al. 2007; Tenke and Kayser 2012, 2015; Carvalhaes and de Barros 2015), to include demonstrations of the convergence of the Laplacian transform and other source-modelling approaches for localizing cortical activity (Tenke and Kayser 2012). Moreover, specific validation of this approach as a means to remove volume conduction prior to calculating inter-channel phase-synchrony and yielding unbiased estimates of connectivity has been demonstrated (Srinivasan et al. 2007; Winter et al. 2007).
We applied the same pre- and post-response theta factor loadings to the connectivity surfaces in order to isolate pre- and post-response connectivity. We attempted to move beyond overall tests of MFC-LFC connectivity and take advantage of the improved spatial resolution afforded by a Laplacian transform. Specifically, we tested MFC connectivity with separate rostral and caudal LFC clusters, including: right (E123, E2, E122, E117, E124, E3) and left (E27, E26, E33, E28, E24, E23) rostral-LFC that most closely approximates right/left DLPFC, as well as right (E103, E104, E110, E109) and left (E41, E36, E35, E46) caudal-LFC that most closely approximates right/left primary and pre-motor cortex. We also included right (E90, E89, E83, E84) and left (65, 69, 70, 66) occipital regions in the connectivity analyses to test whether connectivity was indeed stronger for frontal areas relative to other brain regions. Topographic plots excluded the outermost ring of electrodes; see Figure 4 for a complete map of electrode and cluster locations.
Inter-trial phase synchrony.
While our analyses focus primarily on theta power and theta connectivity, we also conducted additional analyses of inter-trial phase synchrony (Cohen 2014), particularly for post-response analyses of error-related theta dynamics over MFC. Inter-trial phase synchrony reflects a measure of consistent phase alignment within a given channel and is calculated across trials within a given frequency band and time range (here defined by a PCA factor). We applied the same post-response theta factor loadings in order to isolate post-response effects and then averaged across the same MFC electrode cluster used to analyze MFC total power (E6, E12, E5, E112, E106, E7, E13), yielding a measure of “MFC theta synchrony”. In the text, all subsequent analyses and references to “MFC theta synchrony” refer to inter-trial phase synchrony weighted by the average power TF-PCA loadings and averaged within the MFC cluster.
Experimental Design and Statistical Analyses
Overview.
Prior research has not fully characterized the performance monitoring system during adolescence utilizing time-frequency analyses of EEG. Thus, we first sought to explore the neurobehavioral dynamics of the cognitive control system in the non-social condition. This supported further analyses probing effects of social observation (in the social condition) and provided results that can be more readily referenced to the broader performance monitoring literature in adults that typically lacks a social manipulation. Additionally, using a structural equation model, we formalized inter-relations between post-error behavior (PERI/PES) and individual differences in error-related MFC theta power, MFC theta synchrony and MFC connectivity. Next, we computed difference scores for all behavioral and neural measures for the social and non-social conditions, separately, and ran an additional series of statistical analyses to probe the effect of social observation on cognitive control.
Statistical analyses.
Data reduction and statistical analyses were performed using a combination of Matlab 2014b (The MathWorks, Natick, MA), R version 3.4.3 (R. Core Team 2017), and SPSS version 24.0 (IBM Corp., Armonk, NY) and Mplus version 7.3 (Muthén & Muthén, 2012). Below, the complete details of each statistical analysis is described. For all analyses, alpha was set to .05; where appropriate, a Greenhouse-Geisser correction was employed for violations of sphericity, however, raw degrees of freedom are reported for ease of interpretation.
Behavioral data.
For all behavioral analyses, response time (RT) analyses were restricted to correct trials and log-transformed prior to averaging. All analyses of RT data were performed on log-transformed data; raw RT values are reported in the text for ease of interpretation. Additionally, outliers (+/− 3 SD) were removed from all conditions for both accuracy and RT measures; following the calculation of difference scores, outliers were again removed based on difference score values. We first calculated the overall accuracy and response times (RT) within the non-social condition. Next, we calculated the behavioral effects of stimulus conflict by calculating difference scores (incongruent minus congruent) for both accuracy and RT; for RT calculations, only correct trials were employed. These measures are referred to as “conflict-effect-accuracy”, and “conflict-effect-RT”, respectively.
In order to investigate behavioral changes following errors, we calculated accuracy rates and RT following error vs correct responses and difference scores were computed. In order to isolate post-error effects, congruency was held constant and only trials following error-incongruent and correct-incongruent trials were analyzed (with no congruency restriction for the post-error trial). We calculated PERI, indexing variation in task-specific proactive control after errors (Danielmeier and Ullsperger, 2011), by subtracting the conflict-effect-accuracy following correct responses from the conflict-effect-accuracy following errors. Next, we calculated PES, indexing general/automatic inhibition of (pre-)motor cortex after errors (Jentzsch and Dudschig 2009; Notebaert et al. 2009; Danielmeier and Ullsperger 2011; Wessel and Aron 2017; Wessel 2018), by subtracting the RT on post-error vs post-correct trials. Note that the deliberative and task-specific nature of PERI is in direct contrast to the more generalized and simple increase in RT (PES) following errors (Ridderinkhof 2002; King et al. 2010; Danielmeier and Ullsperger 2011; Maier et al. 2011). Below, we discuss testing for relations between error-related neural data and these post-error behavioral measures.
Error monitoring and post-error proactive control.
We first tested whether MFC theta power increased following errors. Here, we held congruency constant (analyzing only incongruent trials) and employed a paired-samples t-test to compare error vs. correct differences within the post-response theta factor. Moreover, leveraging this same post-response theta factor and inter-channel phase synchrony (connectivity), we employed an ANOVA model to test whether a seed electrode over medial-frontal cortex (MFC) became more connected with electrode clusters over LFC following errors. For this model investigating post-error control recruitment, hemisphere (right, left), caudality (rostral-LFC, caudal-LFC, occipital) and accuracy (error-incongruent, correct-incongruent) were all entered as within-subjects factors. Collectively, this set of analyses tested whether theta oscillations related to performance monitoring (increased theta power) and control recruitment (increased phase synchrony between MFC and LFC).
To confirm that MFC connectivity with LFC regions reflects the recruitment of transient proactive control for the following trial, we tested whether between-subject variation in MFC-LFC connectivity predicted between-subject changes in PERI. We hypothesized that MFC connectivity with rostral-LFC would predict PERI, a deliberative and task-specific form of proactive control. In contrast, we hypothesized that MFC connectivity with caudal-LFC regions would link to more automatic and general changes in behavior: PES. To test for these brain-behavior relations, post-response connectivity difference scores (error minus correct) were calculated for MFC connectivity with rostral- and caudal-frontal regions, outliers were removed, and we additionally collapsed across hemisphere prior to testing for relations with post-error behavior to reduce the number of comparisons; qualitatively similar relations were identified when not collapsing across hemisphere. Relations between these connectivity measures and both PES/PERI were tested using a family of Pearson’s product-moment correlation tests; a false-discovery rate (FDR) correction for multiple comparisons was applied using the method proposed by Benjamini and Hochberg (1995). We tested specificity in rostral vs. caudal connectivity predicting either PERI or PES via the modified Fisher’s r-to-z test proposed by Steiger (1980), which is appropriate for comparing correlations from the same sample that share one variable in common. Briefly, using the method proposed by Steiger (1980), coefficients of each correlation were converted to a z-score using the standard Fisher’s r-to-z transformation, the asymptotic covariance of the estimates was then computed and these values used in an asymptotic z-test to test for significant differences between the correlations.
Insofar as post-response MFC-LFC connectivity reflects the recruitment of control, it is theoretically plausible that MFC-LFC connectivity more closely associates with post-error changes in behavior (i.e. PERI and PES), as compared to either post-response MFC theta power or MFC theta synchrony predicting behavior. However, in order to confirm that any potential relations between post-response MFC-LFC connectivity and behavior could not be explained by MFC theta power or MFC theta synchrony, we repeated the correlation tests described above when controlling for either MFC theta power or MFC theta synchrony.
While we hypothesized that post-response MFC-LFC connectivity would be more closely linked to post-error behavior, we also hypothesized that post-response MFC theta power and MFC theta synchrony might form the equivalent of an “alarm signal” (Cavanagh and Frank 2014) and the initial stages of coordinating neural activity in response to critical events (Verguts 2017) that must precede control recruitment via MFC-LFC connectivity. Therefore, we hypothesized that post-response MFC theta power and MFC theta synchrony would predict post-response MFC-LFC connectivity. Additionally, we hypothesized that post-response MFC theta power and MFC theta synchrony might predict post-error behavior, but only indirectly and through associations with post-response MFC-LFC connectivity. Note that such hypotheses imply that MFC theta power and MFC theta synchrony are necessary, but not sufficient, for producing changes in post-error behavior, whereas MFC-LFC connectivity is both necessary and sufficient. To formalize these hypotheses, we employed a path-analytic framework to model relations between MFC theta power, MFC theta synchrony, MFC-LFC connectivity, and PERI/PES. We modelled: 1) direct effects of post-response MFC theta power and MFC theta synchrony on rostral/caudal MFC connectivity; 2) direct effects of MFC theta power, MFC theta synchrony and MFC-LFC connectivity on PERI/PES; 3) indirect effects of MFC theta power and MFC theta synchrony on PERI/PES through MFC-LFC connectivity. Model fit was evaluated across several metrics, including: Root mean square error of approximation (RMSEA), comparative fit index (CFI), Standardized root mean square residual (SRMR), Akaike information criterion (AIC), and Bayesian information criterion (BIC). To improve model fit, MFC theta power and MFC theta synchrony were allowed to covary, as well as the two measures of connectivity (MFC connectivity with rostral/caudal LFC), whereas covariance between PERI and PES was set to zero. All effects were tested using a maximum likelihood (ML) estimator, and significance evaluated across 10,000 bootstrap samples using bias-corrected confidence intervals (CI), at both the 90% and 95% levels.
Conflict monitoring and pre-response reactive control.
As described above, we utilized the improved resolution of Cohen’s Class RID and time-frequency PCA to perform a separate test of pre-response monitoring and control, isolated from post-response cognitive control, all within the same epochs; this approach goes beyond prior analyses of peri-response theta in adults or adolescents. A conflict monitoring effect within the pre-response theta factor was tested via a paired-samples t-test comparing congruent-correct and incongruent-correct trials; we hypothesized that MFC theta power would be increased for incongruent-correct (vs. congruent-correct) trials.
An ANOVA model with hemisphere (right, left), caudality (rostral-LFC, caudal-LFC, occipital) and congruency (incongruent-correct, congruent-correct) as within-subjects factors investigated reactive control within the pre-response theta factor. Here, accuracy was held constant to isolate congruency effects. We hypothesized that incongruent-correct trials would be associated with increased pre-response connectivity between MFC and LFC, reflecting increased instantiation of reactive control in order to resolve the conflict associated with incongruent trials. Additionally, if pre-response increases in MFC-LFC connectivity reflect the recruitment of reactive control in order to prevent an error, then failures of such control should be observable prior to error responses as a possible cause of the incorrect response. To test this claim, we investigated whether MFC-LFC connectivity within the pre-response theta factor was reduced prior to error responses using an ANOVA with hemisphere (right, left), caudality (rostral-LFC, caudal-LFC, occipital) and accuracy (error-incongruent, correct-incongruent) as within-subject factors. Here, we held congruency constant, and analyzed only incongruent trials that are thought to require reactive control to resolve conflict and respond correctly. We hypothesized that pre-response MFC-LFC connectivity would be reduced prior to error-incongruent (vs. correct-incongruent) responses.
Testing effects of social observation on cognitive control.
Following analyses of the nonsocial condition characterizing theta band cognitive control dynamics during adolescence, we investigated how each of these processes were influenced by social observation. Critically, identification of several distinct subprocesses underlying cognitive control allowed us to investigate possible heterogeneity in how social observation influences particular subprocesses, as opposed to a monolithic influence. To reduce the number of comparisons and to avoid potential four-way interactions, we approached analyses of social observation using difference scores for the behavioral and neural measures described above. Relevant difference scores were calculated based on accuracy or congruency for all behavioral and neural measures with outliers (+/− 3 SD) being removed.
A series of paired-samples t-tests were employed to investigate behavioral differences as a function of social context. Similarly, separate paired-samples t-tests explored whether pre-response MFC theta power (conflict monitoring), or post-response MFC theta power (error monitoring) were influenced by social observation. Finally, separate ANOVA models were employed to test whether pre- or post-response MFC-LFC connectivity was influenced by social observation, as measures of reactive and proactive control, respectively. These ANOVA models were similar to those described above, with hemisphere (right, left) and caudality (rostral-LFC, caudal-LFC, occipital) as within-subjects factors, but also including social context (nonsocial, social) as a within-subject factor and employing connectivity difference scores as the dependent variable.
Results
Non-Social Condition
Behavior.
For all analyses (behavioral and EEG), outliers (+/− 3 SD) for specific conditions were removed where appropriate; each statistical analysis was performed using as much data as possible as opposed to listwise deletion across all analyses. Within the non-social condition, accuracy rates for congruent and incongruent trials were 95.11% and 74.47%, respectively; a one sample t-test for the conflict-effect-accuracy (incongruent minus congruent) was significant [t(1,143) = −26.91, p < .001]. Similarly, RTs for correct-congruent and correct-incongruent trials were 380.16 ms (SE = 3.77) and 454.22 ms (SE = 5.33), respectively; a one sample t-test for the conflict-effect-RT (incongruent minus congruent) was also significant [t(1,142) = 31.02, p <.001]. Collectively, this pattern of findings for both RT and accuracy resembles results in prior research in both adolescents (Hogan et al. 2005) and adults (Botvinick et al. 2001). PES and PERI-accuracy were in the expected direction and above zero, although on average, there were no significant group-level effects of PES [t(1,141) = 1.27, p = .207] or PERI-accuracy [t(1,142) = .9, p = .369], as indicated by a pair of one-sample t-tests. However, such null effects at the group-level could arise from opposing individual differences in activation of post-response proactive control (MFC-LFC connectivity). That is, PES and PERI might still be present at the subject-level, but only emerge for individuals exhibiting stronger MFC-LFC connectivity following errors; indeed, the following section reports significant relations between individual differences in post-response MFC-LFC connectivity and individual differences in post-error behavioral metrics that were hypothesized a priori.
Error monitoring and post-error proactive control.
A paired-samples t-test investigated post-response MFC theta power as a correlate of error monitoring; this test revealed an increase in total power for errors [t(1,127) = 11.48, p < .001]. The ANOVA investigating MFC connectivity within this same post-response theta factor revealed a main effect of accuracy [F(1,116) = 50.5, p < .001], caudality [F(2,232) = 99.45, p < .001] and a caudality-by-accuracy interaction [F(2,232) = 5.63, p = .004]. Follow-up comparisons, collapsing across hemisphere, demonstrated significantly stronger post-error connectivity between MFC and rostral-LFC regions, in comparison to occipital [t(1,116) = 3.29, p = .001]. MFC connectivity with caudal-LFC was also significantly stronger than occipital [t(1,116) = 2.39, p = .018], whereas connectivity magnitude did not differ between rostral- and caudal-LFC regions [t(1,116) = .62, p = .539]. This pattern of results is consistent with MFC-related monitoring (theta power) recruiting LFC-related control (MFC-LFC connectivity) following error commission. Figure 5 depicts the error/correct post-response theta power and connectivity results.
Figure 5.
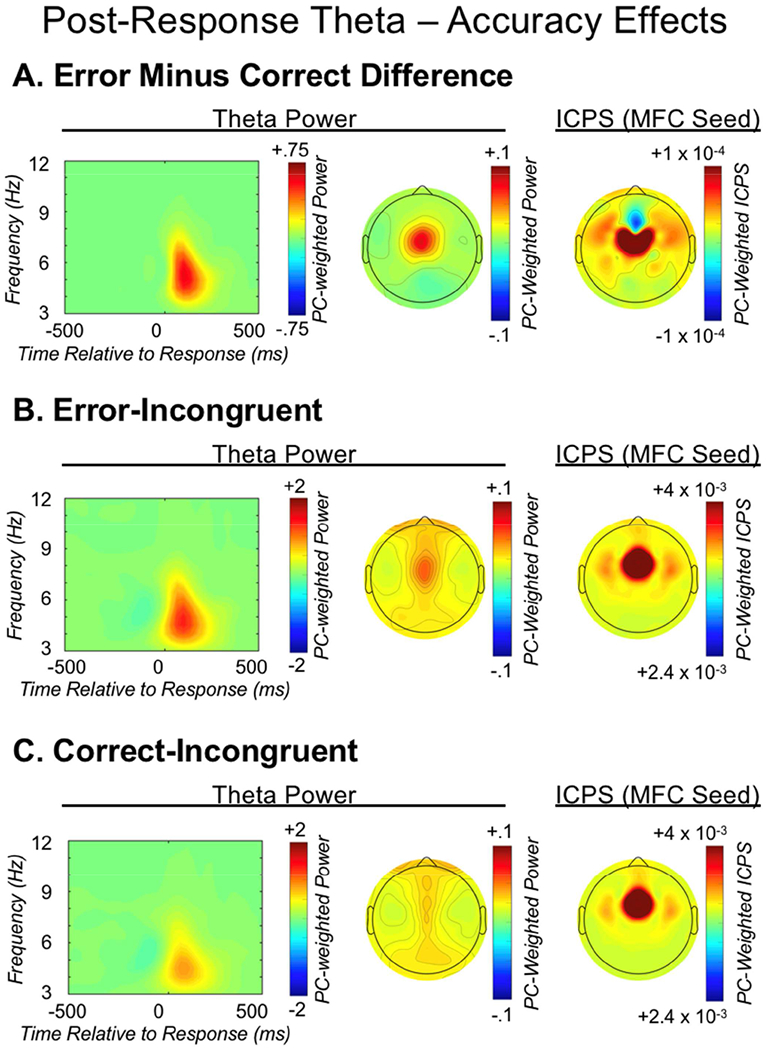
Post-response theta dynamics. From left to right, each row depicts: the medial-frontal cortex (MFC) total power time-frequency distribution weighted by the post-response theta factor; the corresponding topographic plot; MFC-seeded inter-channel phase synchrony (ICPS) within the post-response theta factor. The three rows present: A) the difference between error-incongruent and correct-incongruent activity; B) error-incongruent activity; C) correct-incongruent activity.
Task-specific improvement in accuracy following errors (PERI) was significantly predicted by connectivity with rostral-LFC regions [r(130) = .245, p = .005], confirming a link to proactive control, whereas caudal-LFC connectivity did not relate to PERI (see Table 1 and Figure S3). A modified Fisher’s r-to-z transformation (Steiger 1980) demonstrated that the correlation coefficient associating rostral-LFC and PERI was significantly different from the coefficient for caudal-LFC and PERI, (Z = 2.04, p = .041), suggesting PERI was exclusively predicted by rostral-LFC connectivity. In contrast, the more simple and automatic form of post-error behavior, PES, was significantly predicted by caudal-LFC connectivity [r(130) = .244, p = .005], whereas rostral-LFC connectivity did not significantly relate to PES (see Table 2 and Figure 6), albeit the correlation coefficients for PES and caudal/rostral LFC did not significantly differ from each other (Z = 1.09 p = .278). Table 1 reports correlation test statistics; all significant correlations survived an FDR correction for multiple comparisons and qualitatively similar results were obtained when not collapsing across hemisphere. Additionally, correlation coefficients did not qualitatively differ when controlling for either MFC theta power or MFC theta synchrony.
Table 1.
Important terms and definitions.
A list of relevant terms and their corresponding definitions.
| Cohen’s class reduced interference distribution (RID) | A time-frequency transformation method yielding improved time-frequency resolution without requiring a priori tailoring of the transformation. Cohen’s class RID, particularly in combination with TF-PCA, has proven superiority in resolving time-frequency dynamics of human EEG. |
| Time-frequency Principle Components Analysis (TF-PCA) | A data reduction technique that allows for isolating distinct processes in the time-frequency surface. TF-PCA involves application of principal component analysis to the time-frequency surface after first converting the 3-dimensional time-frequency surface to a 2-dimensional vector by “stacking” each frequency bin across time. |
| Laplacian transform (Current source density; CSD) | A method of improving the spatial resolution of scalp-recorded EEG by removing volume conduction; corresponds to the second spatial derivative of the field potential. |
| Average power | A power measure that includes primarily phase-locked information and is computed from a time-frequency transformation of data that has already been averaged across trials of interest. |
| Total power | A power measure that includes both phase- and non-phase-locked information and is computed from a time-frequency transformation of trial-level data that is then averaged across trials. |
| Inter-channel phase synchrony (ICPS; connectivity) | An index of neuronal connectivity and communication between brain regions. Reflects a measure of consistent phase alignment between channels and is calculated across trials within a given frequency band and time range (here defined by PCA factor). |
| Post-error reduction in interference (PERI) | A task-specific index of proactive control influencing selective attention for the trial following an error. Computed by first calculating the difference in accuracy on incongruent vs. congruent trials after error and correct trials, then subsequently subtracting these difference scores such that increases in PERI reflect improved performance after errors. |
| Post-error slowing (PES) | A general index of response slowing and motor inhibition on trials follow an error. Computed by subtracting the log-RT on correct trials that follow correct responses from the log-RT of correct trials following errors; greater PES reflects a general slowing after errors. |
Table 2.
Post-error connectivity and post-error behavior
Pearson product-moment correlation test statistics, their significance (superscript), and corresponding sample size (italics), for a series of correlation tests between rostral/caudal lateral-frontal cortex (LFC) connectivity and either post-error reduction in interference (PERI) or post-error slowing (PES). Connectivity measures reflect MFC-seeded inter-channel phase synchrony within the post-response theta factor for the error minus correct contrast.
Denotes p < .05 after FDR correction for multiple comparisons; Post-error reduction in interference (PERI); Post-error slowing (PES); lateral-frontal cortex (LFC)
Figure 6.
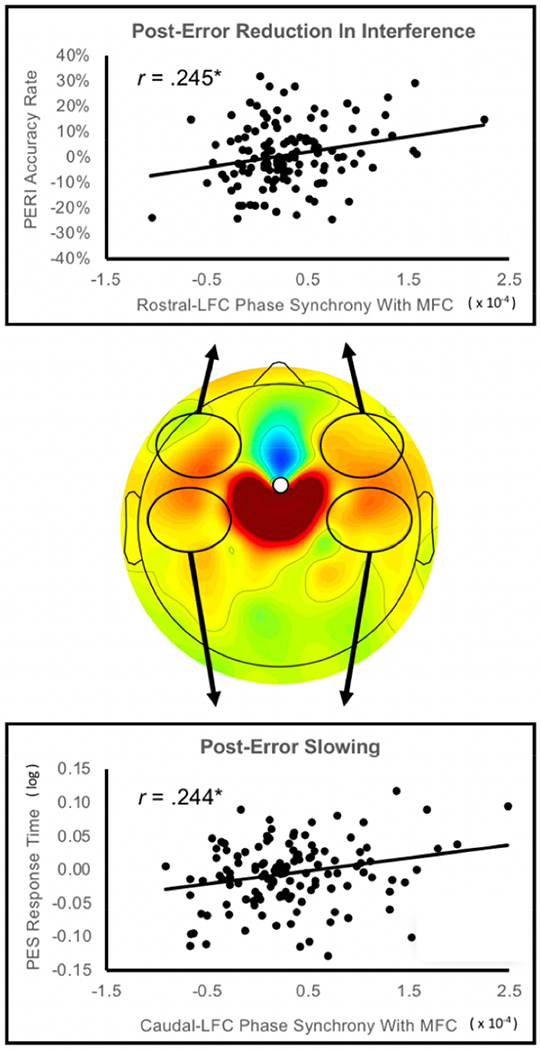
Relations between post-error MFC-LFC connectivity and next-trial behavior. The central plot depicts the increase in medial-frontal cortex (MFC) to lateral-frontal cortex (LFC) connectivity within the post-response theta factor (MFC seed; error minus correct difference); black ellipses indicate the location of electrode clusters used to quantify MFC connectivity with rostral/caudal LFC. The top scatterplot depicts relations between bilateral rostral-LFC connectivity and post-error reduction in interference (PERI); the bottom scatterplot depicts relations between bilateral caudal-LFC connectivity and post-error slowing (PES).
Results of the best fitting structural equation model (RMSE = 0.000, CFI = 1, SRMR = .005; see Figure 7 and Table 3) demonstrated that post-response MFC theta power and MFC theta synchrony directly predicted increases in post-response MFC connectivity with either rostral or caudal LFC, albeit the effect of MFC theta synchrony on MFC connectivity with caudal-LFC was only significant using a 90% CI (other effects significant using 95% CI). Moreover, consistent with the correlational results presented above, post-response MFC connectivity with rostral-LFC uniquely predicted PERI (95% CI), but was not significantly related to PES; conversely, post-response MFC connectivity with caudal-LFC uniquely predicted PES (90% CI) but was not significantly related to PERI. Post-response MFC theta power and MFC theta synchrony did not exhibit significant direct effects on either PERI or PES. However, post-response MFC theta power indirectly predicted PES, through post-response MFC connectivity with caudal-LFC (90% CI), and indirectly predicted PERI, through post-response MFC connectivity with rostral-LFC (95% CI). Additionally, MFC theta synchrony indirectly predicted PERI, through MFC connectivity with rostral-LFC (95% CI). All other direct and indirect effects were not significant. Collectively, results of the structural equation model are consistent with the notion that post-response MFC theta power and MFC theta synchrony form the equivalent of an “alarm signal” (Cavanagh and Frank 2014) and the initial stages of coordinating neural activity in response to critical events (Verguts 2017), which influence post-response MFC-LFC connectivity, and such connectivity is directly associated with post-error behavioral changes.
Figure 7.
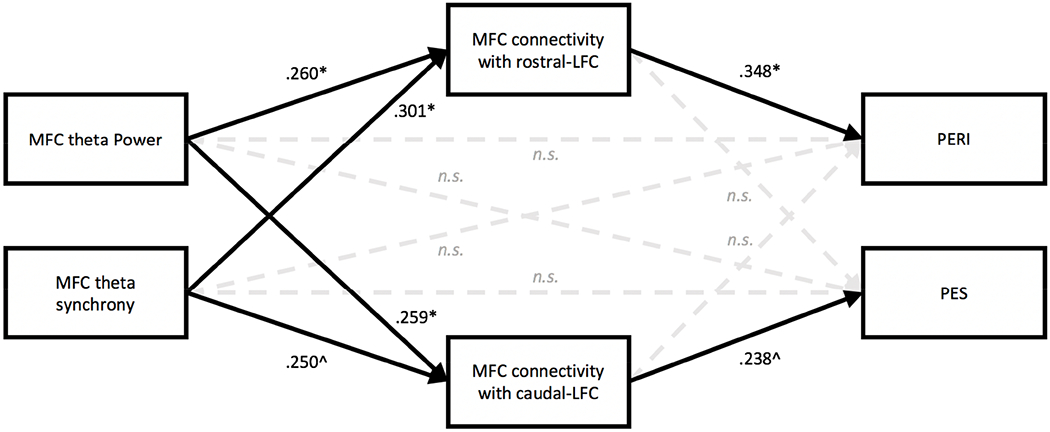
Standardized effects of theta power, synchrony and connectivity on post-error behavior. All neural measures reflect error-minus-correct difference scores weighted by the post-response theta factor. Medial frontal cortex (MFC); Lateral frontal cortex (LFC); Post-error reduction in interference (PERI); Post-error slowing (PES). Solid lines indicate significant paths and dashed lines indicate nonsignificant paths. Standardized direct effects are reported for ease of interpretation; significance was determined using bootstrapped unstandardized effects and their confidence intervals (see Table 3); * Indicates significance using a 95% confidence interval and ^ indicates significance using a 90% confidence interval. Significant indirect effects of MFC theta power or MFC theta synchrony on PERI/PES are reported in the main text and in Table 3.
Table 3.
Unstandardized direct and indirect effects for the structural equation model
| Direct effects. | LL 2.5% | LL 5% | Estimate | UL 5% | UL 2.5% |
|---|---|---|---|---|---|
| Connectivity with caudal-LFC | |||||
| *MFC theta power | 0.080 | 0.403 | 1.956 | 3.605 | 3.994 |
| ^MFC theta synchrony | −0.003 | 0.013 | 0.090 | 0.161 | 0.176 |
| Connectivity with rostral-LFC | |||||
| *MFC theta power | 0.010 | 0.232 | 1.555 | 2.848 | 3.087 |
| *MFC theta synchrony | 0.004 | 0.018 | 0.086 | 0.161 | 0.174 |
| PES | |||||
| ^Connectivity with caudal-LFC | −0.001 | 0.003 | 0.020 | 0.037 | 0.040 |
| Connectivity with rostral-LFC | −0.022 | −0.018 | 0.003 | 0.024 | 0.028 |
| MFC theta power | −0.313 | −0.274 | −0.099 | 0.043 | 0.071 |
| MFC theta synchrony | −0.003 | −0.002 | 0.005 | 0.012 | 0.013 |
| PERI | |||||
| *Connectivity with caudal-LFC | 0.031 | 0.041 | 0.090 | 0.136 | 0.145 |
| Connectivity with rostral-LFC | −0.054 | −0.048 | −0.011 | 0.022 | 0.029 |
| MFC theta power | −0.424 | −0.362 | −0.033 | 0.304 | 0.369 |
| MFC theta synchrony | −0.027 | −0.024 | −0.007 | 0.009 | 0.012 |
| Indirect effects | LL 2.5% | LL 5% | Estimate | UL 5% | UL 2.5% |
|
^MFC theta power -> Caudal-LFC connectivity -> PES | |||||
| 0.000 | 0.004 | 0.039 | 0.116 | 0.134 | |
| MFC theta power -> Rostral-LFC connectivity -> PES | |||||
| −0.035 | −0.025 | 0.005 | 0.049 | 0.060 | |
| MFC theta synchrony -> Caudal-LFC connectivity -> PES | |||||
| 0.000 | 0.000 | 0.002 | 0.005 | 0.006 | |
| MFC theta synchrony -> Rostral-LFC connectivity -> PES | |||||
| −0.001 | −0.001 | 0.000 | 0.003 | 0.004 | |
| MFC theta power -> Caudal-LFC connectivity -> PERI | |||||
| −0.143 | −0.120 | −0.022 | 0.033 | 0.051 | |
|
*MFC theta power -> Rostral-LFC connectivity -> PERI | |||||
| 0.015 | 0.035 | 0.140 | 0.323 | 0.360 | |
| MFC theta synchrony -> Caudal-LFC connectivity -> PERI | |||||
| −0.007 | −0.006 | −0.001 | 0.001 | 0.002 | |
|
*MFC theta synchrony -> Rostral-LFC connectivity -> PERI | |||||
| 0.000 | 0.001 | 0.008 | 0.019 | 0.021 | |
Indicates significance using a 95% confidence interval and
indicates significance using 90% confidence interval. All neural measures reflect error-minus-correct difference scores weighted by the post-response theta factor. Medial frontal cortex (MFC); Lateral frontal cortex (LFC); Post-error reduction in interference (PERI); Post-error slowing (PES).
Conflict monitoring and pre-response reactive control.
A paired-samples t-test investigating the pre-response theta factor revealed an increase in MFC total power[t(1,128) = 3.34 p = .001] prior to incongruent-correct compared to congruent-correct responses, consistent with a role in conflict monitoring. The ANOVA model investigating connectivity within this same pre-response theta factor yielded a main effect of caudality [F(2,236) = 54.08, p < .001], as well as a caudality-by-congruency interaction [F(2,236) = 10.47, p < .001]. Follow-up comparisons, collapsing across hemisphere, demonstrated significantly stronger connectivity between MFC and caudal-LFC regions, in comparison to occipital [t(1,116) = 2.19, p = .03], whereas connectivity magnitude for caudal-LFC did not significantly differ from rostral-LFC [t(1,116) = 1.41, p = .161]; connectivity strength did not differ for rostro-LFC and occipital [t(1,116) = 1.05, p = .298]. An interaction between hemisphere and congruency was also identified [F(1,118) = 4.14, p = .044], such that stronger MFC connectivity with the right hemisphere overall was observed prior to incongruent-correct responses. Collectively, this pattern of results is consistent with MFC-related conflict monitoring (theta power) recruiting LFC-related reactive control (MFC-LFC connectivity) to resolve conflict, with an emphasis on the role of more caudal-LFC regions and a right-lateralized network. Figure 8 depicts the congruent/incongruent pre-response theta power and connectivity results.
Figure 8.
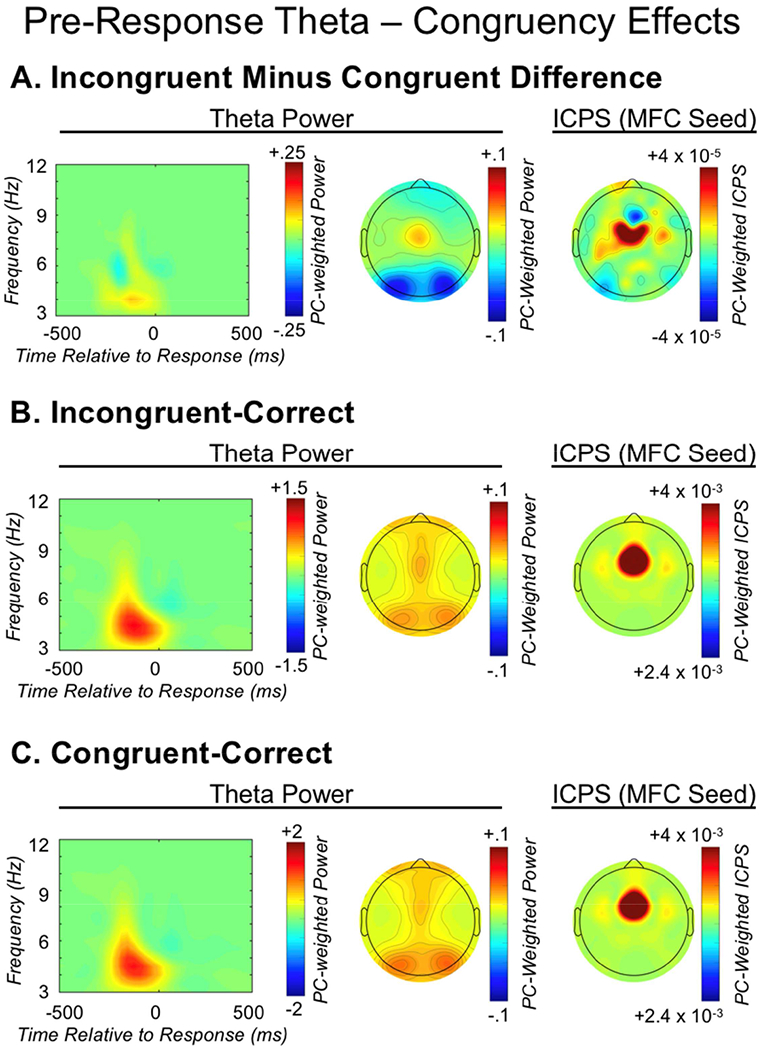
Pre-response theta dynamics. From left to right, each row depicts: the medial-frontal cortex (MFC) total power time-frequency distribution weighted by the pre-response theta factor; the corresponding topographic plot; MFC-seeded inter-channel phase synchrony (ICPS) within the pre-response theta factor. The three rows present: A) the difference between incongruent-correct and congruent-correct activity; B) incongruent-correct activity; congruent-correct activity.
To provide further evidence that pre-response MFC-LFC connectivity reflects reactive control, we tested whether such connectivity was weaker on error-incongruent trials (in comparison to correct-incongruent trials), suggesting a failure of reactive control leading to errors. This ANOVA model revealed a main effect of accuracy [F(1,120) = 27.33, p < .001], caudality [F(2,240) = 52.37, p < .001], and a caudality-by-accuracy interaction [F(2,240) = 9.02, p < .001]. Follow-up comparisons, collapsing across hemisphere, demonstrated that the MFC region exhibited a significant decrease in connectivity prior to error responses for rostral-LFC [t(1,120) = −4.72, p < .001] and caudal-LFC regions [t(1,120) = −4.87, p < .001], but did not differ for occipital regions [t(1,120) = −.56, p = .58]. These data provide further support for pre-response MFC-LFC connectivity as an index of reactive control, with reduced reactive control recruitment associating with error responses. Figure 9 depicts the error/correct pre-response theta connectivity results. Also note the inverse pattern of control recruitment before and after response execution: reduced reactive control before the response leads to errors and post-response increases in proactive control (for the next trial), whereas increased reactive control before the response leads to correct responses and reduced post-response proactive control (for the next trial). This complete cascade of cognitive control processing is depicted in Figure 10.
Figure 9.
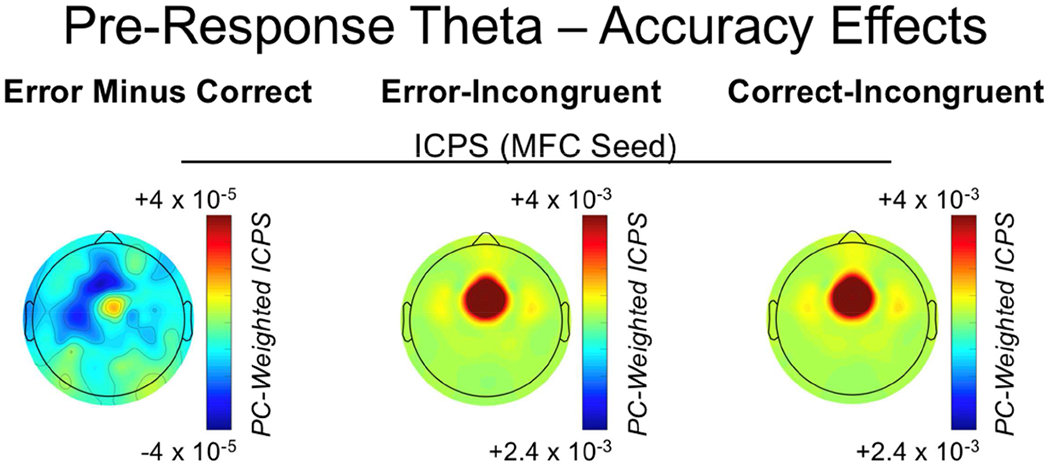
Pre-response theta dynamics as a function of response accuracy. From left to right, plots reflect medial-frontal cortex (MFC) seeded inter-channel phase synchrony (ICPS) within the pre-response theta factor for: the difference between error-incongruent and correct-incongruent activity; error-incongruent activity; correct-incongruent activity.
Figure 10.
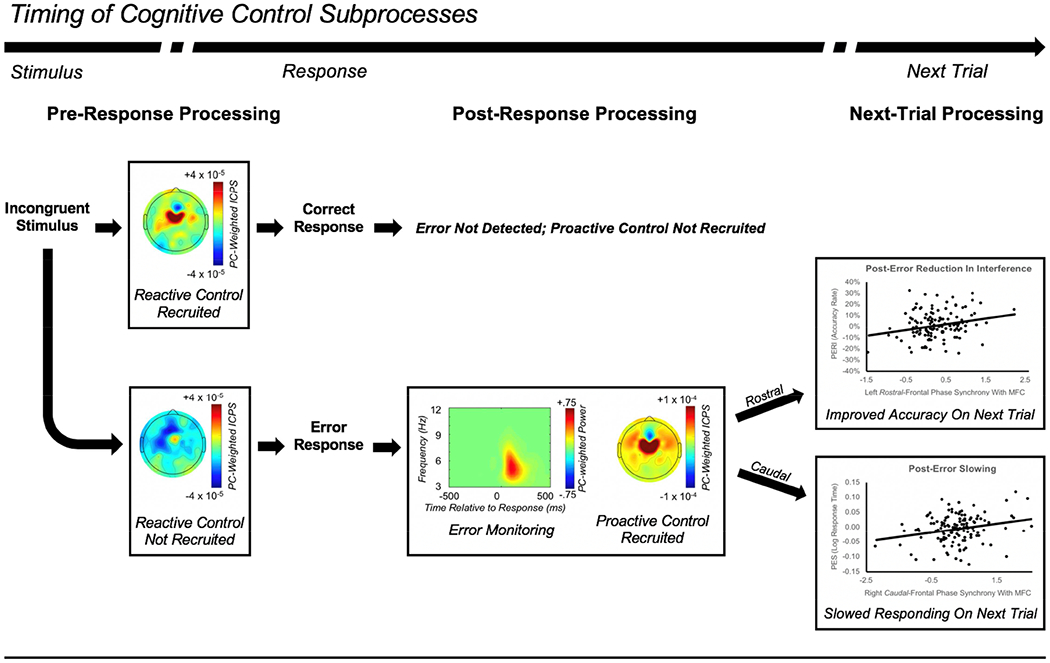
Cascade of processes involved in cognitive control. Progressing from left to right, the image depicts the relative timing of a cascade of cognitive control subprocesses. Following the presentation of a stimulus requiring control (e.g. an incongruent stimulus), if reactive control is properly recruited prior to the response then a correct response will be made; this results in post-response error monitoring not detecting the presence of an error, and as a result, no subsequent increase in proactive control (for the next trial) will be observed (top panel). In contrast, if reactive control is not properly recruited prior to the response then an error will be made, leading error monitoring to detect the presence of an error, further leading to an increase in proactive control processes (bottom panel). In turn, proactive control will influence behavior on the following trial, with more rostral-lateral-frontal cortex (LFC) regions driving post-error reduction in interference (PERI: top scatterplot), and more caudal-LFC regions driving post-error slowing (PES; bottom scatterplot).
Effects of Social Observation
Subjective reports of motivation.
Consistent with our previously published study (Barker et al. 2018), participants reported significantly higher levels of effort during the social, compared to non-social, condition [t(1,143) = 7.353, p < .001]. Moreover, increased effort within the social condition was commonly attributed to social factors in the free-response explanations of effort; for example: “I tried hard because other people were giving me feedback.” Collectively, the subjective reports of motivation confirm that the social manipulation successfully increased motivation.
Behavior.
For all analyses (behavioral and EEG), outliers (+/− 3 SD) for specific conditions were removed where appropriate; each statistical analysis was performed using as much data as possible as opposed to listwise deletion across all analyses. Social observation improved task performance, with a reduced conflict effect for accuracy in the social (compared to nonsocial) condition [t(1,142) = −2.65, p = .009]. Improved performance did not occur at the cost of a speed-accuracy trade-off, given that conflict-effect-RT did not differ between the social and nonsocial conditions [t(1,142) = 1.17, p = .243]. Similarly, social observation did not significantly influence post-error behavior for either PERI [t(1,140) = −.23, p = .816] or PES [t(1,138) = .72, p = .474].
Error detection and post-error proactive control.
Social observation yielded an increase in error monitoring, with post-response MFC theta power for errors being greater in the social condition, [t(1,127) = 3.1, p = .002]. Additionally, an ANOVA model investigating post-response error-related connectivity revealed a main effect of social context, with social observation driving an overall increase in connectivity with the MFC region [F(1,115) = 4.92, p = .028]. A main effect of caudality was also identified, with connectivity being stronger at more rostral locations [F(2,230) = 12.7, p < .001]. Finally, a post-hoc contrast identified a significant linear caudality-by-social-context interaction, such that social observation was associated with increasingly stronger connectivity between MFC and more anterior regions (i.e. rostral- and caudal-LFC, relative to occipital) [F(1,115) = 4.23, p = .042]. Collectively, this pattern of results demonstrates that social observation yields increases in error monitoring and post-response proactive control. The right side of Figure 11 depicts the effects of social observation on post-response theta power and connectivity.
Figure 11.
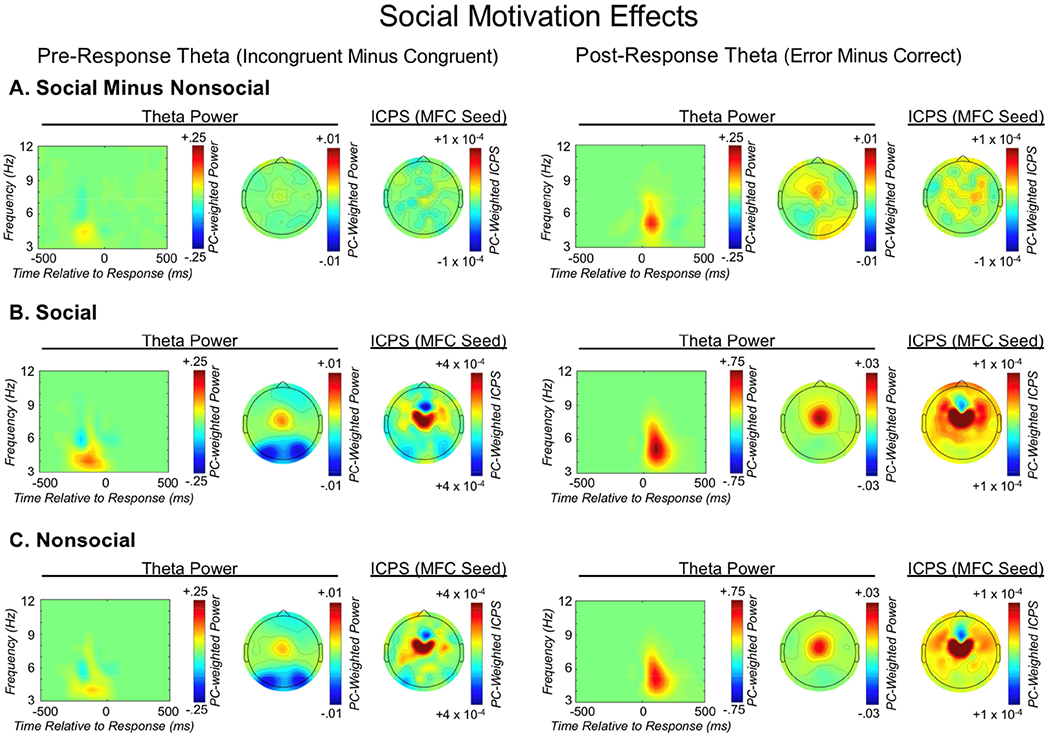
The effects of social observation on pre- and post-response theta dynamics. From left to right, each row depicts: the medial-frontal cortex (MFC) total power time-frequency distribution weighted by the pre-response theta factor; the corresponding topographic plot; MFC-seeded inter-channel phase synchrony (ICPS) within the pre-response theta factor; the MFC total power time-frequency distribution weighted by the post-response theta factor; the corresponding topographic plot; MFC-seeded ICPS within the post-response theta factor. From top to bottom, each row depicts: A) the difference between social and nonsocial congruency-related and error-related difference scores of neural activity; B) social congruency-related and error-related difference scores of neural activity; C) nonsocial congruency-related and error-related difference scores of neural activity.
Conflict monitoring and pre-response reactive control.
In contrast to an effect of social observation on error monitoring, a paired samples t-test identified no effect of social observation on conflict monitoring, as measured by pre-response and congruency-related MFC theta power [t(1,127) = .499, p = .618]. Similarly, social observation did not influence pre-response reactive control, as an ANOVA model investigating congruency-related pre-response connectivity with MFC only exhibited the already described main effect of caudality [F(2,240) = 17.34, p < .001], as well as a main effect of hemisphere [F(1,120) = 5.46, p = .021] such that connectivity was increased for the right hemisphere, but this did not interact with social context. Null relations were also identified when probing pre-response connectivity as a function of accuracy, with the only significant result being the already described main effect of caudality [F(2,242) = 7.8, p = .001]. The left side of Figure 11 depicts the effects of social observation on pre-response theta power and connectivity. Collectively these data suggest that social observation exclusively influences post-response error monitoring and proactive control, not pre-response conflict monitoring or reactive control.
Discussion
The current study provides a detailed characterization of cognitive control subprocess supported by theta oscillations during adolescence. Leveraging Cohen’s Class RID, time-frequency PCA, and a Laplacian transform, we elucidated novel theta dynamics not previously observed in adolescents or adults. We dissociated pre- and post-response theta, linking greater pre-response MFC-LFC connectivity to reactive control and correct responding on the current trial. Post-response MFC-LFC connectivity exhibited the opposite pattern, being increased after errors and reflecting proactive control for the following trial. We further characterized differences in post-response MFC connectivity with rostral/caudal LFC after errors: MFC connectivity with rostral-LFC predicted post-error reduction in interference (PERI), whereas connectivity with caudal-LFC predicted post-error slowing (PES). Moreover, a structural equation model revealed that MFC theta power and MFC theta synchrony predicted post-response MFC-LFC connectivity, and indirectly predicted post-error behavior through their associations with MFC-LFC connectivity. Turning to the effects of social observation, we took advantage of an improved characterization of cognitive control—afforded by time-frequency EEG—to distinguish how social observation influences adolescent cognitive control. Social observation exclusively upregulated post-response error monitoring (MFC theta power) and proactive control (MFC-LFC connectivity), but not pre-response conflict monitoring and reactive control. Collectively, the current study details the role of theta oscillations and social observation in adolescent cognitive control, while informing research on cognitive control more generally.
In adults, evidence suggests MFC neurons subserve performance monitoring (Ridderinkhof et al. 2004), with LFC instantiating top-down control (Kerns et al. 2004). fMRI has confirmed similar MFC and LFC roles during adolescence (Crone and Steinbeis 2017). However, adult studies use measures of theta to index unique organizing properties of cognitive control (Cavanagh and Frank 2014; Verguts 2017). The current results extend such work to adolescence and finds that, at a broad level, adolescent theta dynamics appear qualitatively similar to findings in adults. Conflict and error monitoring were associated with increased MFC theta power, and control recruitment relied on MFC-LFC theta connectivity (inter-channel phase synchrony). Crucially, we demonstrated theta’s behavioral relevance, with accurate responses linked to pre-response MFC-LFC theta connectivity, and post-error behavioral changes linked to post-response MFC-LFC theta connectivity. These findings are consistent with prior results in adult humans, non-human primates (Tsujimoto et al. 2006) and other mammals (Narayanan et al. 2013), but also provide novel insights regarding the distinction between pre- and post-response theta dynamics and link them to the concept of reactive/proactive control.
Using a between-subjects structural equation modelling approach, we formalized relations between distinct post-response theta measures (power, synchrony and connectivity) and behavioral correlates of control on post-error trials. Results of the structural equation model were consistent with the notion that post-response MFC theta power and MFC theta synchrony form the equivalent of an “alarm signal” (Cavanagh and Frank 2014) and the initial stages of coordinating neural activity in response to critical events (Verguts 2017), which influence post-response MFC-LFC connectivity. In line with the notion that recruitment of LFC is necessary in order to instantiate control and adapt behavior (Miller 2000; Miller and Cohen 2001; Kerns et al. 2004), post-response MFC-LFC connectivity directly related to post-error behavioral changes, but MFC theta power and MFC theta synchrony only exhibited indirect effects on post-error behavior through associations with MFC-LFC connectivity. Taken together, this work provides a foundation for mechanistic accounts of adolescent cognitive control and the effects of social observation during a critical window of human development.
Although the current study did not directly assess developmental changes in theta oscillations and cognitive control, when considered in relation to developmental studies (e.g., Uhlhaas et al. 2009; Marek et al. 2018), and prior work in adults (Cavanagh and Frank 2014; Gratton 2018), the current findings provide insight into how control-related theta oscillations might develop. Across childhood and adolescence, increasing age predicts greater theta-band decoupling of brain networks while at rest, particularly for frontal brain regions involved in cognitive control (Marek et al. 2018; but also see: Schäfer et al. 2014). These age-related changes in theta-band decoupling are theorized to reflect increased cognitive flexibility and an improved ability to rapidly activate cognitive control networks, as needed, when performing tasks that require cognitive control (Marek et al. 2018). Directly supporting this notion, other work demonstrates that across childhood and adolescence, increasing age broadly predicts greater theta synchronization and connectivity over frontal brain regions in response to task events that require cognitive control (Müller et al. 2009; Uhlhaas et al. 2009; Crowley et al. 2014; Chorlian et al. 2015; Bowers et al. 2018). The nascent but emerging view is that theta-based brain networks associated with cognitive control exhibit protracted development across childhood and adolescence, with development of these theta-based networks underlying an improved ability to flexibly deploy cognitive control exactly when and how it is needed. Along this developmental backdrop, the current study demonstrates that at least the basic patterns of theta power, synchrony and connectivity associated with cognitive control are in place by early adolescence. Moreover, the current study suggests that the ability to instantiate reactive control, as well as distinct forms of proactive control, all reliant on theta dynamics, are present by early adolescence. Observation of these theta oscillation patterns in early adolescence, and their links to task behavior, are consistent with reports that adolescents already exhibit a majority of medial-lateral frontal connections similar to those of adults (Hwang et al. 2010) and that across adolescence there is an absence of changes in the core error-monitoring system and its relations with post-error control (Buzzell, Richards, et al. 2017).
Although the current study provides evidence that the basic patterns of adult-like cognitive control are present by early adolescence, we were unable to directly test for further developmental changes across the adolescent period. In line with the general pattern of protracted theta development across childhood and adolescence (described above), more subtle and nuanced patterns of theta development may occur between early adolescence and adulthood. Thus, additional work is needed to determine how theta oscillations and the specific cognitive control subprocess described here might further change during mid-to-late adolescence, and moreover, whether effects of social motivation change across the adolescent period. Whereas adolescent cognitive control can appear adult-like in some contexts (Casey et al. 2001; Luna et al. 2004), motivational factors may disproportionately affect adolescents due to an overactivation of the limbic system during this developmental period (Nelson et al. 2005; Casey et al. 2008; Steinberg et al. 2008; Luciana and Collins 2012; Luna et al. 2015). Indeed, while incentives can facilitate adolescent performance in some contexts (e.g., reward-contingent inhibitory control: Padmanabhan et al. 2011), motivation effects can also obscure adult-like functions if arousal or cognitive load are too high (Luciana and Collins 2012), which has been suggested to underlie the increase in risk-taking typically observed during adolescence (e.g., Shulman et al. 2016; but also see: Pfeifer and Allen 2012). To the extent that social observation also increases motivation, the current results illustrate novel features of motivation-control relations by parsing cognitive control into particular subprocesses. Social observation (motivation) exclusively influenced post-response error monitoring (theta power) and proactive control (post-response MFC-LFC connectivity). Similarly, social observation (motivation) yielded task-specific accuracy improvements (a reduced behavioral conflict-effect). This pattern matches effects induced by monetary incentives on proactive control in adults (Botvinick and Braver 2015) and may explain other findings on motivational influences during adolescence (Luciana et al. 2012). It is possible that the effects of social observation and motivation on control-related theta dynamics exhibit an additional period of more nuanced development during mid-to-late adolescence, before returning to adult-like levels. In line with such predictions, at least two studies have reported a reduction in task-related theta synchronization during late adolescence (Uhlhaas et al. 2009; Crowley et al. 2014), before increasing again to reach adult levels (Uhlhaas et al. 2009). However, these studies did not parse cognitive control and associated theta dynamics into specific subprocesses, nor assess the effects of social observation. Critically, the current study provides a framework and set of metrics that can be leveraged by future studies to better characterize how cognitive control subprocesses might change across the adolescent period, particularly in relation to motivational factors such as social observation. However, it is also worth noting that although participants reported increased motivation while under social observation in the current study, such assessments remain inherently subjective and demand characteristics cannot be completely ruled out. Additionally, block-level feedback differed between the social and nonsocial conditions in the current study; future work might seek to control for such differences.
The current report provides several critical extensions of prior adult work regarding the neural mechanisms involved in cognitive control. fMRI studies suggest a rostro-caudal order regarding LFC control function (Koechlin 2003; Badre and Wagner 2004; Badre 2008), with caudal regions associated with simpler forms of control, including motor inhibition, and rostral regions linked to more complex forms of control (Koechlin 2003; Badre and Wagner 2004). However, different forms of control are known to follow errors (Danielmeier and Ullsperger 2011), and yet, rostral-caudal theories have not previously been applied to explain such findings. Here, we use MFC theta connectivity (inter-channel phase synchrony) to distinguish between divergent forms of post-error behavioral control related to rostral/caudal LFC. MFC connectivity with caudal-LFC predicted PES, a relatively automatic and general change in behavior associated with motor inhibition (Notebaert et al. 2009; King et al. 2010; Wessel and Aron 2017), whereas MFC connectivity with rostral-LFC predicted PERI, a more deliberative and task-specific form of proactive control linked to selective attention (Ridderinkhof 2002; King et al. 2010; Maier et al. 2011). Clearly, these findings require replication in adults. Nevertheless, these findings suggest a way to integrate understandings in prior research on distinct features of cognitive control across three levels of analysis: 1) theory-based distinctions between MFC for monitoring and LFC for control (MacDonald et al. 2000), 2) anatomy-based distinctions based on rostral-caudal LFC organization (Badre 2008), and 3) neurophysiology-based distinctions based on theta as an organizing rhythm for cognitive control (Cavanagh and Frank 2014).
These data also inform debates regarding whether error processing is adaptive (Jentzsch and Dudschig 2009; Notebaert et al. 2009; Danielmeier and Ullsperger 2011; Wessel 2018). PES is the most widely reported post-error behavioral phenomenon and traditionally viewed as an adaptive response reflecting increased cautiousness after errors (Botvinick et al. 2001). However, this view has been challenged, as PES often does not always relate to improved accuracy or attention (Jentzsch and Dudschig 2009; Notebaert et al. 2009; Buzzell, Beatty, et al. 2017). Even when adaptive, PES reflects a general response to all post-error trials, contrasting with PERI, which is task-specific and an unequivocal correlate of adaptive behavior and proactive control (Ridderinkhof 2002; King et al. 2010; Danielmeier and Ullsperger 2011; Maier et al. 2011). An emerging view is that both adaptive and non-adaptive responses can be observed following errors (Danielmeier and Ullsperger 2011; Purcell and Kiani 2016; Wessel 2018). The current data support this view by demonstrating how two distinct forms of post-error behavior can emerge in parallel after errors: simultaneous communication between a common MFC node and separate LFC subregions through communication channels supported by synchronized theta oscillations.
A combination of Cohen’s class RID and time-frequency PCA (Bernat et al. 2005) allowed isolation of explicitly pre- and post-response theta dynamics within the same epochs. This separation removed a confound present in fMRI studies, where pre- and post-response cognitive control likely blends together due to the slower time course of the BOLD signal. The current study details separation of pre- and post-response theta dynamics and their differential relations with task behavior, demonstrating the functional importance of isolating these processes. Whereas pre-response connectivity was related to correct responses on the current trial (reactive control), post-response connectivity related to improved performance on the following—post-error—trial (proactive control). Critically, we also demonstrate that pre- and post-response control are inversely related. Pre-response failures of reactive control (reduced MFC-LFC connectivity) were associated with error responses, followed by post-response connectivity increases reflecting transient proactive control to adapt future behavior. Conversely, successful pre-response reactive control yielded correct responses, followed by reduced post-response connectivity. The Cascade of Control Model (Banich 2009) proposes similar inverse relations before/after stimulus presentation, with pre-stimulus control reducing the need for reactive control after stimulus presentation. However, the current results present the first evidence for similar inverse relations before/after response execution. Thus, separation of pre- and post-response theta allowed for galvanizing the notion of inverse control relations into a more general principle of the cognitive control system. However, similar observations in adults are needed.
Collectively, the current report provides a detailed account of theta oscillations in adolescent cognitive control, elucidates the nuanced effects of social observation, and identifies several novel mechanisms of cognitive control more broadly. Linking adolescent cognitive control to theta dynamics opens the door to theoretical integration across developmental stages and even species, complementing existing fMRI/ERP studies of adolescent cognitive control. Identifying dissociations in how social observation influences control can inform future investigations into motivation-control relations during this critical period of human development. Finally, the methodology employed here can be employed in future studies to more broadly characterize typical and atypical cognitive control dynamics across age.
Supplementary Material
Acknowledgments
Funding
This work was supported by grants from the National Institute of Mental Health (U01MH093349 and U01MH093349-S to NAF; P01HD064653 supporting EMB), the National Science Foundation (DGE1322106 to SVT), the Eunice Kennedy Shriver National Institute of Child Health and Human Development (1F32HD097921 supporting TVB), and the NIMH-Intramural Research Program (ZIAMH-002782 supporting DSP). The authors declare no competing interests, financial or otherwise.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests: none
References
- Badre D 2008. Cognitive control, hierarchy, and the rostro–caudal organization of the frontal lobes. Trends Cogn Sci. 12:193–200. [DOI] [PubMed] [Google Scholar]
- Badre D, Wagner AD. 2004. Selection, Integration, and Conflict Monitoring: Assessing the Nature and Generality of Prefrontal Cognitive Control Mechanisms. Neuron. 41:473–487. [DOI] [PubMed] [Google Scholar]
- Banich MT. 2009. Executive Function: The Search for an Integrated Account. Curr Dir Psychol Sci. 18:89–94. [Google Scholar]
- Barker TV, Troller-Renfree SV, Bowman LC, Pine DS, Fox NA. 2018. Social influences of error monitoring in adolescent girls. Psychophysiology. 0:e13089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. 1995. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J R Stat Soc Ser B Methodol. 57:289–300. [Google Scholar]
- Bernat EM, Williams WJ, Gehring WJ. 2005. Decomposing ERP time–frequency energy using PCA. Clin Neurophysiol. 116:1314–1334. [DOI] [PubMed] [Google Scholar]
- Blakemore S-J. 2008. The social brain in adolescence. Nat Rev Neurosci. 9:267. [DOI] [PubMed] [Google Scholar]
- Bolaños M, Bernat EM, He B, Aviyente S. 2013. A weighted small world network measure for assessing functional connectivity. J Neurosci Methods. 212:133–142. [DOI] [PubMed] [Google Scholar]
- Botvinick M, Braver T. 2015. Motivation and Cognitive Control: From Behavior to Neural Mechanism. Annu Rev Psychol. 66:83–113. [DOI] [PubMed] [Google Scholar]
- Botvinick MM, Braver TS, Barch DM, Carter CS, Cohen JD. 2001. Conflict monitoring and cognitive control. Psychol Rev. 108:624. [DOI] [PubMed] [Google Scholar]
- Bowers ME, Buzzell GA, Bernat EM, Fox NA, Barker TV. 2018. Time-frequency approaches to investigating changes in feedback processing during childhood and adolescence. Psychophysiology. 55:e13208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braver TS. 2012. The variable nature of cognitive control: a dual mechanisms framework. Trends Cogn Sci. 16:106–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzzell GA, Beatty PJ, Paquette NA, Roberts DM, McDonald CG. 2017. Error-induced blindness: error detection leads to impaired sensory processing and lower accuracy at short response–stimulus intervals. J Neurosci. 37:2895–2903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzzell GA, Richards JE, White LK, Barker TV, Pine DS, Fox NA. 2017. Development of the error-monitoring system from ages 9–35: Unique insight provided by MRI-constrained source localization of EEG. Neuroimage. 157:13–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzzell GA, Troller-Renfree SV, Barker TV, Bowman LC, Chronis-Tuscano A, Henderson HA, Kagan J, Pine DS, Fox NA. 2017. A Neurobehavioral Mechanism Linking Behaviorally Inhibited Temperament and Later Adolescent Social Anxiety. J Am Acad Child Adolesc Psychiatry. 56:1097–1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalhaes C, de Barros JA. 2015. The surface Laplacian technique in EEG: Theory and methods. Int J Psychophysiol, On the benefits of using surface Laplacian (current source density) methodology in electrophysiology. 97:174–188. [DOI] [PubMed] [Google Scholar]
- Casey BJ, Durston S, Fossella JA. 2001. Evidence for a mechanistic model of cognitive control. Clin Neurosci Res. 1:267–282. [Google Scholar]
- Casey BJ, Jones RM, Hare TA. 2008. The adolescent brain. Ann N Y Acad Sci. 1124:111–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh JF, Cohen MX, Allen JJ. 2009. Prelude to and resolution of an error: EEG phase synchrony reveals cognitive control dynamics during action monitoring. J Neurosci. 29:98–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh JF, Frank MJ. 2014. Frontal theta as a mechanism for cognitive control. Trends Cogn Sci. 18:414–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatham CH, Frank MJ, Munakata Y. 2009. Pupillometric and behavioral markers of a developmental shift in the temporal dynamics of cognitive control. Proc Natl Acad Sci. 106:5529–5533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chib VS, Adachi R, O’Doherty JP. 2018. Neural substrates of social facilitation effects on incentive-based performance. Soc Cogn Affect Neurosci. 13:391–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chorlian DB, Rangaswamy M, Manz N, Kamarajan C, Pandey AK, Edenberg H, Kuperman S, Porjesz B. 2015. Gender modulates the development of Theta Event Related Oscillations in Adolescents and Young Adults. Behav Brain Res. 292:342–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MX. 2014. Analyzing neural time series data: theory and practice. MIT press. [Google Scholar]
- Cohen MX. 2017. Where Does EEG Come From and What Does It Mean? Trends Neurosci. 40:208–218. [DOI] [PubMed] [Google Scholar]
- Cohen MX, Cavanagh JF. 2011. Single-trial regression elucidates the role of prefrontal theta oscillations in response conflict. Front Psychol. 2:30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MX, Donner TH. 2013. Midfrontal conflict-related theta-band power reflects neural oscillations that predict behavior. J Neurophysiol. 110:2752–2763. [DOI] [PubMed] [Google Scholar]
- Cools R 2016. The costs and benefits of brain dopamine for cognitive control. Wiley Interdiscip Rev Cogn Sci. 7:317–329. [DOI] [PubMed] [Google Scholar]
- Crone EA. 2014. The role of the medial frontal cortex in the development of cognitive and social-affective performance monitoring: Performance monitoring in adolescence. Psychophysiology. 51:943–950. [DOI] [PubMed] [Google Scholar]
- Crone EA, Steinbeis N. 2017. Neural Perspectives on Cognitive Control Development during Childhood and Adolescence. Trends Cogn Sci. 21:205–215. [DOI] [PubMed] [Google Scholar]
- Crowley MJ, van Noordt SJR, Wu J, Hommer RE, South M, Fearon RMP, Mayes LC. 2014. Reward feedback processing in children and adolescents: Medial frontal theta oscillations. Brain Cogn. 89:79–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danielmeier C, Ullsperger M. 2011. Post-error adjustments. Front Psychol. 2:233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, Makeig S. 2004. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 134:9–21. [DOI] [PubMed] [Google Scholar]
- Eriksen BA, Eriksen CW. 1974. Effects of noise letters upon the identification of a target letter in a nonsearch task. Percept Psychophys. 16:143–149. [Google Scholar]
- Fox NA, Henderson HA, Rubin KH, Calkins SD, Schmidt LA. 2001. Continuity and discontinuity of behavioral inhibition and exuberance: psychophysiological and behavioral influences across the first four years of life. Child Dev. 72:1–21. [DOI] [PubMed] [Google Scholar]
- Gehring WJ, Liu Y, Orr JM, Carp J. 2012. The error-related negativity (ERN/Ne). Oxf Handb Event-Relat Potential Compon. 231–291. [Google Scholar]
- Gratton G 2018. Brain reflections: A circuit-based framework for understanding information processing and cognitive control. Psychophysiology. 55:e13038. [DOI] [PubMed] [Google Scholar]
- Harper J, Malone SM, Bernat EM. 2014. Theta and delta band activity explain N2 and P3 ERP component activity in a go/no-go task. Clin Neurophysiol. 125:124–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogan AM, Vargha-Khadem F, Kirkham FJ, Baldeweg T. 2005. Maturation of action monitoring from adolescence to adulthood: an ERP study. Dev Sci. 8:525–534. [DOI] [PubMed] [Google Scholar]
- Holroyd CB, Yeung N. 2012. Motivation of extended behaviors by anterior cingulate cortex. Trends Cogn Sci. 16:122–128. [DOI] [PubMed] [Google Scholar]
- Hwang K, Velanova K, Luna B. 2010. Strengthening of top-down frontal cognitive control networks underlying the development of inhibitory control: a functional magnetic resonance imaging effective connectivity study. J Neurosci Off J Soc Neurosci. 30:15535–15545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jentzsch I, Dudschig C. 2009. Short Article: Why do we slow down after an error? Mechanisms underlying the effects of posterror slowing. Q J Exp Psychol. 62:209–218. [DOI] [PubMed] [Google Scholar]
- Kerns JG, Cohen JD, MacDonald AW, Cho RY, Stenger VA, Carter CS. 2004. Anterior cingulate conflict monitoring and adjustments in control. Science. 303:1023–1026. [DOI] [PubMed] [Google Scholar]
- King JA, Korb FM, von Cramon DY, Ullsperger M. 2010. Post-Error Behavioral Adjustments Are Facilitated by Activation and Suppression of Task-Relevant and Task-Irrelevant Information Processing. J Neurosci. 30:12759–12769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koechlin E 2003. The Architecture of Cognitive Control in the Human Prefrontal Cortex. Science. 302:1181–1185. [DOI] [PubMed] [Google Scholar]
- Luciana M, Collins PF. 2012. Incentive Motivation, Cognitive Control, and the Adolescent Brain: Is It Time for a Paradigm Shift? Child Dev Perspect. 6:392–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luciana M, Wahlstrom D, Porter JN, Collins PF. 2012. Dopaminergic modulation of incentive motivation in adolescence: Age-related changes in signaling, individual differences, and implications for the development of self-regulation. Dev Psychol. 48:844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luna B, Garver KE, Urban TA, Lazar NA, Sweeney JA. 2004. Maturation of Cognitive Processes From Late Childhood to Adulthood. Child Dev. 75:1357–1372. [DOI] [PubMed] [Google Scholar]
- Luna B, Marek S, Larsen B, Tervo-Clemmens B, Chahal R. 2015. An Integrative Model of the Maturation of Cognitive Control. Annu Rev Neurosci. 38:151–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luu P, Tucker DM, Makeig S. 2004. Frontal midline theta and the error-related negativity: neurophysiological mechanisms of action regulation. Clin Neurophysiol. 115:1821–1835. [DOI] [PubMed] [Google Scholar]
- MacDonald AW, Cohen JD, Stenger VA, Carter CS. 2000. Dissociating the role of the dorsolateral prefrontal and anterior cingulate cortex in cognitive control. Science. 288:1835–1838. [DOI] [PubMed] [Google Scholar]
- Maier ME, Yeung N, Steinhauser M. 2011. Error-related brain activity and adjustments of selective attention following errors. Neuroimage. 56:2339–2347. [DOI] [PubMed] [Google Scholar]
- Marek S, Tervo-Clemmens B, Klein N, Foran W, Ghuman AS, Luna B. 2018. Adolescent development of cortical oscillations: Power, phase, and support of cognitive maturation. PLOS Biol. 16:e2004188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK. 2000. The prefontral cortex and cognitive control. Nat Rev Neurosci. 1:59. [DOI] [PubMed] [Google Scholar]
- Miller EK, Cohen JD. 2001. An Integrative Theory of Prefrontal Cortex Function. Annu Rev Neurosci. 24:167–202. [DOI] [PubMed] [Google Scholar]
- Mognon A, Jovicich J, Bruzzone L, Buiatti M. 2011. ADJUST: An automatic EEG artifact detector based on the joint use of spatial and temporal features. Psychophysiology. 48:229–240. [DOI] [PubMed] [Google Scholar]
- Müller V, Gruber W, Klimesch W, Lindenberger U. 2009. Lifespan differences in cortical dynamics of auditory perception: Lifespan differences in cortical dynamics. Dev Sci. 12:839–853. [DOI] [PubMed] [Google Scholar]
- Muthñn LK, Muthñn BO. 2012. Mplus. Stat Anal Latent Var Users Guide Seventh Ed Los Angel CA Muthñn Muthñn.
- Narayanan NS, Cavanagh JF, Frank MJ, Laubach M. 2013. Common medial frontal mechanisms of adaptive control in humans and rodents. Nat Neurosci. 16:1888–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson EE, Leibenluft E, McClure EB, Pine DS. 2005. The social re-orientation of adolescence: a neuroscience perspective on the process and its relation to psychopathology. Psychol Med. 35:163–174. [DOI] [PubMed] [Google Scholar]
- Nolan H, Whelan R, Reilly RB. 2010. FASTER: Fully Automated Statistical Thresholding for EEG artifact Rejection. J Neurosci Methods. 192:152–162. [DOI] [PubMed] [Google Scholar]
- Notebaert W, Houtman F, Van Opstal F, Gevers W, Fias W, Verguts T. 2009. Post-error slowing: an orienting account. Cognition. 111:275–279. [DOI] [PubMed] [Google Scholar]
- Padmanabhan A, Geier CF, Ordaz SJ, Teslovich T, Luna B. 2011. Developmental changes in brain function underlying the influence of reward processing on inhibitory control. Dev Cogn Neurosci. 1:517–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeifer JH, Allen NB. 2012. Arrested development? Reconsidering dual-systems models of brain function in adolescence and disorders. Trends Cogn Sci. 16:322–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pontifex MB, Scudder MR, Brown ML, O’Leary KC, Wu C-T, Themanson JR, Hillman CH. 2010. On the number of trials necessary for stabilization of error-related brain activity across the life span. Psychophysiology. 47:767–773. [DOI] [PubMed] [Google Scholar]
- Purcell BA, Kiani R. 2016. Neural mechanisms of post-error adjustments of decision policy in parietal cortex. Neuron. 89:658–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R. Core Team. 2017. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2017; ISBN3-900051-07-0 https://www.R-project.org. [Google Scholar]
- Ridderinkhof KR, Forstmann BU, Wylie SA, Burle B, van den Wildenberg WPM. 2011. Neurocognitive mechanisms of action control: resisting the call of the Sirens. Wiley Interdiscip Rev Cogn Sci. 2:174–192. [DOI] [PubMed] [Google Scholar]
- Ridderinkhof KR, Ullsperger M, Crone EA, Nieuwenhuis S. 2004. The role of the medial frontal cortex in cognitive control. science. 306:443–447. [DOI] [PubMed] [Google Scholar]
- Ridderinkhof RK. 2002. Micro- and macro-adjustments of task set: activation and suppression in conflict tasks. Psychol Res. 66:312–323. [DOI] [PubMed] [Google Scholar]
- Schäfer CB, Morgan BR, Ye AX, Taylor MJ, Doesburg SM. 2014. Oscillations, networks, and their development: MEG connectivity changes with age: MEG Network Oscillations Change with Age. Hum Brain Mapp. 35:5249–5261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shulman EP, Smith AR, Silva K, Icenogle G, Duell N, Chein J, Steinberg L. 2016. The dual systems model: Review, reappraisal, and reaffirmation. Dev Cogn Neurosci. 17:103–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan R, Winter WR, Ding J, Nunez PL. 2007. EEG and MEG coherence: measures of functional connectivity at distinct spatial scales of neocortical dynamics. J Neurosci Methods. 166:41–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele VR, Anderson NE, Claus ED, Bernat EM, Rao V, Assaf M, Pearlson GD, Calhoun VD, Kiehl KA. 2016. Neuroimaging measures of error-processing: Extracting reliable signals from event-related potentials and functional magnetic resonance imaging. Neuroimage. 132:247–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiger JH. 1980. Tests for comparing elements of a correlation matrix. Psychol Bull. 87:245–251. [Google Scholar]
- Steinberg L, Albert D, Cauffman E, Banich M, Graham S, Woolard J. 2008. Age differences in sensation seeking and impulsivity as indexed by behavior and self-report: evidence for a dual systems model. Dev Psychol. 44:1764. [DOI] [PubMed] [Google Scholar]
- Tenke CE, Kayser J. 2012. Generator localization by current source density (CSD): Implications of volume conduction and field closure at intracranial and scalp resolutions. Clin Neurophysiol. 123:2328–2345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenke CE, Kayser J. 2015. Surface Laplacians (SL) and phase properties of EEG rhythms: simulated generators in a volume-conduction model. Int J Psychophysiol Off J Int Organ Psychophysiol. 97:285–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Triplett N 1898. The Dynamogenic Factors in Pacemaking and Competition. Am J Psychol. 9:507–533. [Google Scholar]
- Trujillo LT, Allen JJ. 2007. Theta EEG dynamics of the error-related negativity. Clin Neurophysiol. 118:645–668. [DOI] [PubMed] [Google Scholar]
- Tsujimoto T, Shimazu H, Isomura Y. 2006. Direct Recording of Theta Oscillations in Primate Prefrontal and Anterior Cingulate Cortices. J Neurophysiol. 95:2987–3000. [DOI] [PubMed] [Google Scholar]
- Uhlhaas PJ, Roux F, Singer W, Haenschel C, Sireteanu R, Rodriguez E. 2009. The development of neural synchrony reflects late maturation and restructuring of functional networks in humans. Proc Natl Acad Sci. 106:9866–9871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullsperger M, Fischer AG, Nigbur R, Endrass T. 2014. Neural mechanisms and temporal dynamics of performance monitoring. Trends Cogn Sci. 18:259–267. [DOI] [PubMed] [Google Scholar]
- Verguts T 2017. Binding by random bursts: A computational model of cognitive control. J Cogn Neurosci. 29:1103–1118. [DOI] [PubMed] [Google Scholar]
- Viola FC, Debener S, Thorne J, Schneider TR. 2010. Using ICA for the analysis of multi-channel EEG data. Simultaneous EEG FMRI Rec Anal Appl Rec Anal Appl. 121–133. [Google Scholar]
- Wessel JR. 2018. An adaptive orienting theory of error processing. Psychophysiology. 55:e13041. [DOI] [PubMed] [Google Scholar]
- Wessel JR, Aron AR. 2017. On the globality of motor suppression: Unexpected events and their influence on behavior and cognition. Neuron. 93:259–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winter WR, Nunez PL, Ding J, Srinivasan R. 2007. Comparison of the effect of volume conduction on EEG coherence with the effect of field spread on MEG coherence. Stat Med. 26:3946–3957. [DOI] [PubMed] [Google Scholar]
- Zajonc RB. 1965. Social Facilitation. Science. 149:269–274. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


