Abstract
It is widely accepted that biomechanics plays an important role in glaucoma pathophysiology, but the mechanisms involved are largely unknown. Rats are a common animal model of glaucoma, and finite element models are being developed to provide much-needed insight into the biomechanical environment of the posterior rat eye. However, material properties of rat ocular tissues, including the sclera, are currently unknown. Since the sclera plays a major role in posterior ocular biomechanics, our goal was to use inverse finite element modeling to extract rat scleral material properties. We first used digital image correlation to measure scleral surface displacement during whole-globe inflation testing. We modeled the sclera as a nonlinear material with embedded collagen fibers, then fit modeled displacements to experimental data using a differential evolution algorithm. Subject-specific models were constructed in which 3 parameters described the stiffness of the ground substance and collagen fibers in the posterior eye, and 16 parameters defined the primary orientation and alignment of fibers within eight scleral sub-regions. We successfully extracted scleral material properties for eight rat eyes. Model displacements recreated general patterns of the experimental displacements but did not always match local patterns. The fiber directions and fiber concentration parameters were highly variable, but on average, fibers were aligned circumferentially and were more aligned in the peripapillary sclera than in the peripheral sclera. The material properties determined here will be used to inform future finite element models of the rat posterior eye with the goal of elucidating the role of biomechanics in glaucoma pathophysiology.
Keywords: inverse finite element modeling, material properties, sclera, rat, glaucoma
1. Introduction
Glaucoma is the second most prevalent cause of blindness worldwide (Tham et al. 2014). Although it is widely accepted that biomechanics plays an important role in glaucoma, the specifics of this role are not well understood (Campbell et al. 2014). Elevated intraocular pressure (IOP) is a key risk factor in glaucoma, and computational modeling studies have shown that high IOP results in increased mechanical stress and strain in ocular tissues, particularly in the optic nerve head (ONH) region, a main and early site of glaucomatous damage (Quigley et al. 1981; Sigal et al. 2004, 2007; Hua et al. 2018). However, it is not known exactly how biomechanical insult leads to axonal degeneration in the ONH, which is the cause of glaucomatous vision loss (Quigley 1999; Alqawlaq et al. 2018).
Rodent models of glaucomatous optic neuropathy, such as the rat, have proven useful for mechanistic studies and also have certain advantages over monkey models because of their lower cost, ease of animal husbandry, and low genetic variability between individuals. However, rat ocular biomechanics have not been well characterized; in fact, our previous study is the only attempt to-date to perform computational modeling of rat ONH biomechanics (Schwaner et al. 2018). Computational modeling has the potential to provide the detailed biomechanical information necessary to investigate the relationships between biomechanical insult and ONH pathophysiology, but to be accurate, this approach requires ONH tissue material property information. This information is not currently available for the rat. Previous work has shown that scleral stiffness is the most influential material property on ONH biomechanics in human modeling studies (Sigal et al. 2005; Hua et al. 2018), and our preliminary studies have supported a similar finding in the rat (not published). Therefore, the purpose of this study was to determine material properties of the rat sclera. To do so, we carried out mechanical testing of rat sclera followed by inverse finite element modeling (FEM) to extract material parameter values from experimental data.
The sclera is a tough connective tissue with a complex organization of collagen fibers (Gogola et al. 2018). Although it has been represented in some modeling studies as an isotropic solid (Sigal et al. 2004; Hua et al. 2018), in an effort to be true to the physiology, other studies have implemented material models that consist of an isotropic matrix reinforced by collagen fibers (Coudrillier et al. 2013; Wang et al. 2016; Feola et al. 2018). Previous studies characterizing scleral biomechanics have utilized a variety of methods including uniaxial strip testing (Chen et al. 2014), biaxial testing of scleral samples (Eilaghi et al. 2010), and whole globe inflation testing (Girard et al. 2009a; Myers et al. 2010; Coudrillier et al. 2015a). Whole globe inflation testing was used in the present study because it is the most physiologically relevant form of loading, because it allowed us to interrogate an intact sclera rather than excised samples, and because it is the most feasible method to perform on the small rat eye. We utilized inverse FEM to extract material properties from experimental scleral deformation data because it allowed us to assess regional scleral properties, account for local scleral thickness variation, and employ a fiber-reinforced material model. The properties reported by this study will inform future efforts to model rat ONH biomechanics.
2. Methods
2.1. Experimental Method
2.1.1. Animals
Twenty male Brown Norway rats (10–13 months old; Charles River Laboratories, Inc., Wilmington, MA) were used for this study. All procedures were approved by the Institutional Animal Care and Use Committee at the Georgia Institute of Technology. Some rats were removed from this study according to exclusion criteria discussed below.
2.1.2. Optical Coherence Tomography Scanning
The thickness of the sclera varies with position, and thus it was necessary to determine scleral thickness for inverse FEM (Norman et al. 2010); we accomplished this by performing in vivo spatial-domain optical coherence tomography (SD-OCT; Envisu R4300; Leica Microsystems, Buffalo Grove, IL) volume scans (Fig. 1). Before SD-OCT, animals were anesthetized with ketamine (60 mg) and xylazine (7.5 mg/kg) and a drop of topical tetracaine (1%) was applied to the eye. After induction of anesthesia, eyes were dilated with a topical drop of tropicamide (1%). We used SD-OCT to obtain five image volumes of the posterior region of each eye near the ONH. The first volume was centered on the ONH and then subsequent images were taken of the superior, inferior, temporal, and nasal regions adjacent to the ONH. All volumes included the ONH to aid in later image registration. Each image volume was a 2.7 mm by 2.7 mm rectangular scan consisting of 100 b-scans with 1000 a-scans per b-scan. Note that the scans shown in Fig. 1 do not appear rectangular because the rays outside of a 2.7 mm diameter circle are blocked by the edges of the imaging lens holder. Before each scan, the reference arm of the SD-OCT system was adjusted until the image of the sclera appeared “flat” on the screen, as is standard practice. This corresponds to the situation in which all rays emitted by the SD-OCT probe pass through a convergence point in the eye, ensuring that each ray travels the same distance before reaching the sclera. This in turn, allows accurate thickness measurements to be made. After SD-OCT, IOP was measured in each eye using a Tonolab tonometer (Icare, Raleigh, NC) previously calibrated in-house by elevating IOP between 5–50 mmHg using a hydrostatic column (data not shown). An average of six IOP measurements was taken to be the anesthetized IOP of the rat.
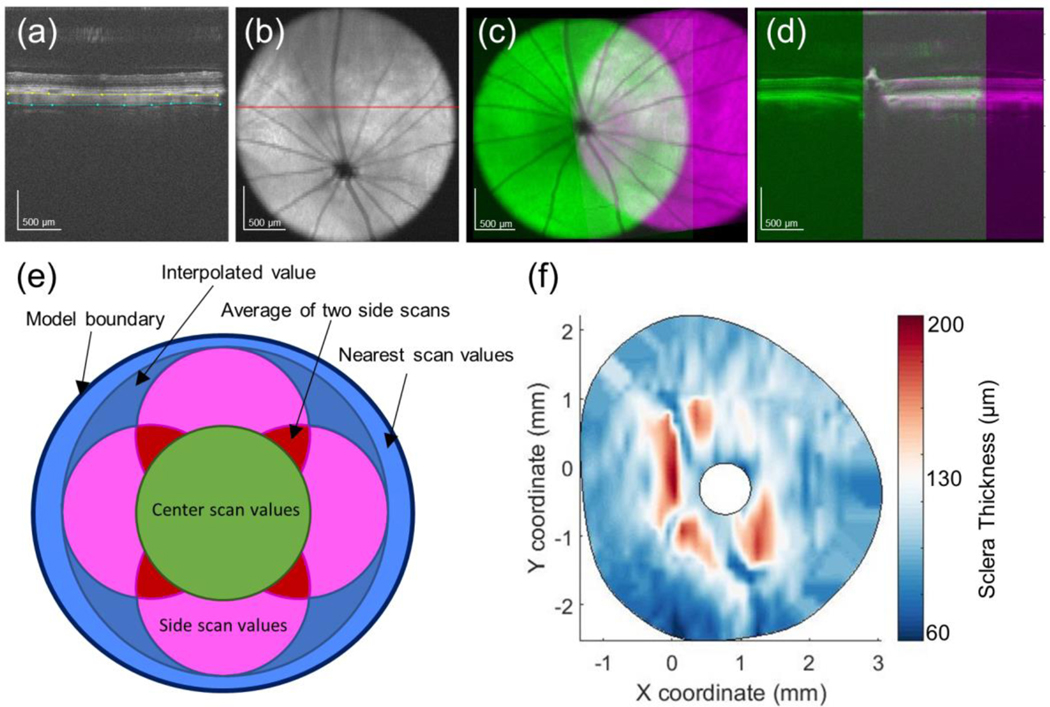
Fig. 1.
Measuring scleral thickness from SD-OCT scans. a SD-OCT B-scan with the anterior (yellow) and posterior (cyan) scleral surfaces delineated. b Average intensity projection through the sclera, choroid, and retina. Red line indicates b-scan in panel a. c Registration of two SD-OCT volume scans, obtained by aligning the ONH and retinal vessels as seen in two average intensity projection images. d Registration of the same two SD-OCT volume scans in the axial direction by aligning the anterior scleral surface as seen in two b-scans passing through the ONH. The colors in this panel are identical to those in panel C. e Schematic detailing how thickness data from five SD-OCT volumes was combined into a single thickness map. f Typical final thickness map for a rat sclera
2.1.3. Whole-Globe Inflation Testing
We implemented an established inflation testing method described elsewhere (Hannon et al. 2019). Briefly, after animals were euthanized by CO2 asphyxiation, their eyes were removed and cleaned of extra-orbital tissue. It was necessary to leave a small amount of tissue surrounding the ONH to prevent leaking during inflation testing. After cutting a hole in the cornea, the eye was secured, cornea side down, to a testing apparatus using superglue, and a speckle pattern was applied to the posterior scleral surface using graphite powder (#970 PG, General Pencil Company, Inc., Redwood City, CA). The rig was filled with baby oil to prevent drying of the eye and attached to an inflation testing setup via Luer connections (Fig. 2). IOP was controlled by changing the height of a reservoir containing 1X phosphate buffered saline (PBS) in series with the eye.
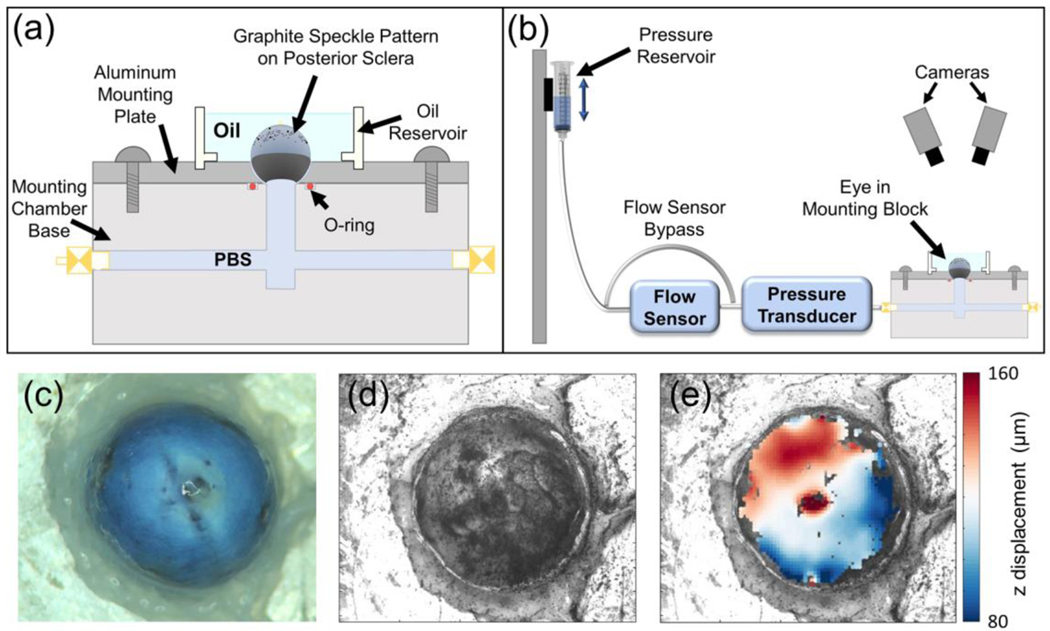
Fig. 2.
Whole-globe inflation testing setup. a Schematic of the testing rig. b Schematic of the whole globe inflation testing apparatus. c Overhead view of the sclera before graphite speckle pattern was applied. d DIC camera view of the sclera after application of graphite speckle pattern. e Facet overlay displaying z displacement (toward the camera) of the scleral surface at the end of an inflation test. a and b from (Hannon et al. 2019)
All measurement equipment was calibrated regularly before testing. The pressure transducer was calibrated by raising the reservoir through a series of pressure steps to correlate sensor voltage with known pressures. Weekly intrinsic and daily extrinsic calibrations of two stereo cameras (Dantec Dynamics, Holtsville, NY) were performed with a calibration target according to manufacturer protocols. During extrinsic calibration, the calibration target was submerged in mineral oil at the level of the eye to ensure compensation for the refractive index of mineral oil. The eye was imaged during the inflation test with a 100 ms exposure time.
Preconditioning was carried out by first ramping IOP to 15 mmHg and holding for 5 minutes, and then performing 10 load-unload cycles from 3 to 15 mmHg at a rate of 0.5 mmHg/second. The eye was allowed to reach a steady state at 3 mmHg (see below), and then subjected to a series of pressure steps: 3 – 6 mmHg, 6 – 9 mmHg, 9 – 12 mmHg, 12 – 20 mmHg, and 20 – 30 mmHg. IOP and flow rate of PBS into the eye were monitored using a gage pressure transducer (142PC01G; Honeywell, Charlotte, NC) and an in-line flow sensor (SLG64–0075; Sensiron, Stafa, Switzerland). Before each pressure step, the eye was allowed to creep until it reached a steady state, as determined by monitoring the flow rate into the eye over time. Note that since the flow sensor acted as a resistor in series between the fluid reservoir and the eye, IOP at steady state was always slightly below the pressure applied to the system. iPerfusion software was used to record IOP and flow data and to control the fluid reservoir (Sherwood et al. 2016). During the test, the two stereo cameras captured images of the scleral surface at a frame rate of one image every 30 seconds. In some eyes, PBS leakage occurred either through the ONH region, through vessels in the sclera, or through the glue securing the eye to the testing rig. These eyes (32 of 40) were excluded from the study. The remaining eight eyes were from eight rats.
2.1.4. Digital Image Correlation
Istra 4D digital image correlation (DIC) software (v2.5.1, Dantec Dynamics, Holtsville, NY), was used to calculate the shape and deformation of the surface of the sclera from images taken during testing. The algorithm produced a 3D facet map overlaying the surface of the eye. The correlation parameters used were as follows: facet size of 45 pixels, grid spacing of 28 pixels, maximum permissible start point accuracy of 0.2 pixels, residuum of 30 grey values, and 3D residuum of 1.1 pixels. In 3D space, the resulting facet grid spacing was approximately 150 μm.
Displacement data was smoothed using parameters recommended by Dantec Dynamics: a grid reduction factor (minimizing the difference between the data point and the spline function) of 2 for displacement and contours, and a smoothness factor (straightens filtered data) of −0.5 for displacement and 0 for contours. Further postprocessing was accomplished using custom MATLAB (2017a; MathWorks, Natick, MA) scripts, as follows.
The image taken one minute before the first pressure step, during which the eye was at an IOP of approximately 3 mmHg, was selected as the reference state. The x, y, and z displacements of each correlated facet were averaged over the last five images after reaching equilibrium at each pressure step. This average displacement was taken as the displacement of each facet at the given pressure. Only facets that were correlated in all of the last five images at the end of each of the five pressure steps were used for analysis. Facets that were obvious outliers, e.g. had displacement values that far exceeded those of immediately neighboring facets, were removed by manual inspection.
The displacement “noise floor” of the DIC system was estimated by applying a speckle pattern to a glass bead that was approximately the size of a rat eye. Ideally, we would have imaged a naïve (unpunctured) eye, but we were concerned that tissue swelling, viscoelastic relaxation, and aqueous humor drainage from the eye would have added additional noise and given an incorrect estimate of the intrinsic DIC noise floor. We mounted the glass bead in the testing apparatus and oil bath and imaged the bead with the stereo cameras at a frame rate of one image every 30 seconds over the course of six hours. We used the DIC algorithm to calculate displacements on the surface of the static bead over the six hours. The noise in the total displacement was 0.3 μm. We found that the z-component of displacement dominated the noise in the other two directions, and as a result, the noise in the z-component was approximately the same as the noise in the total displacement. Thus, the estimated noise floor was 0.3 μm.
2.1.5. Scleral Thickness Measurements
We measured sclera thickness from the SD-OCT volume scans using a custom MATLAB script to view and make delineations on b-scans throughout the volumes. In brief, we delineated the boundaries of the sclera, the optic nerve, and the long posterior ciliary arteries (LPCAs) throughout each of the five SD-OCT scan volumes for each eye. Since the SD-OCT system did not track the relative locations of scan volumes from the same eye, the five volume scans had to be co-registered, as follows. An average intensity projection that clearly showed the retinal vessels and a b-scan passing through the ONH center were exported for each volume. The image slices for the intensity projections were selected such that each resulting image clearly showed the retinal vessels. We used a custom MATLAB script to register adjacent volumes (images of the superior, inferior, temporal, and nasal regions) with the central volume (image of the ONH) by aligning the ONH and retinal vessels in the intensity projection images, and by aligning the anterior scleral boundary at the ONH in the b-scans. A separate custom MATLAB script was used to measure scleral thickness by fitting splines to the delineation points on the anterior and posterior scleral surfaces, and by then extracting the axial distance (distance along an ascan) between them at 0.1 mm intervals.
Since the five SD-OCT volumes overlapped and did not usually fully encompass the region visualized by DIC imaging, the following approach was used to generate a thickness map (Fig. 1E). All locations within the central SD-OCT volume were given a thickness value directly from that SD-OCT scan, while locations within overlapping regions between two peripheral (i.e. non-central) SD-OCT volumes were given an average of the thickness values from those scans. For locations that were not contained within an SD-OCT volume scan but were contained within the convex hull of SD-OCT volume scans, an interpolated thickness value was assigned. Locations that were outside of the SD-OCT volumes’ convex hull were assigned the thickness value of the nearest SD-OCT measurement or interpolated value.
2.2. Finite Element Modeling
2.2.1. Building the model geometry
The 3D facet coordinates from the reference image were imported into Rhino (v5 SR14; Robert McNeel and Associates, Seattle, WA) where the model geometry was created. Note that in the following, all described surfaces are non-uniform rational basis spline surfaces, and all curves are Bezier curves. The DIC facets were fit with a surface using the Rhino “Patch” command to represent the posterior scleral surface. The outer boundary edge (farthest from the ONH) of the model anterior surface was then defined by fitting a curve through facets near the outer edges of the facet map. This approach allowed us to exclude artifacts that often existed at the facet map edges due to factors such as glare. We next imported thickness data into the model, which required registering the SD-OCT volumes with the DIC images (Fig. 3). The LPCAs and the optic nerve were used as landmarks for this registration because they were visible in the DIC images and in the SD-OCT scans. In more detail, the outlines of the LPCAs and the optic nerve were manually traced in the DIC reference image, and their pixel coordinates were mapped onto the 3D facet map using a custom MATLAB script. After the sclera, LPCA, and optic nerve point clouds from SD-OCT delineations were imported into Rhino, the SD-OCT thickness data was manually registered with the DIC data by aligning the optic nerve and LPCA point clouds from the SD-OCT scans with the tracings of the optic nerve and LPCAs from the DIC images.
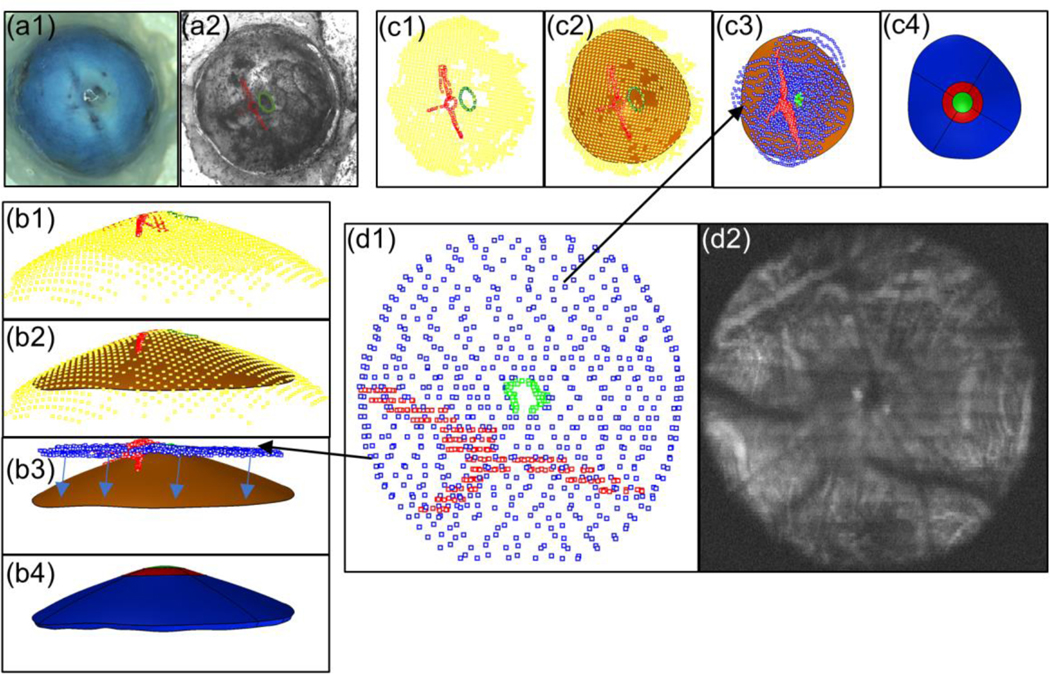
Fig. 3.
Registration of thickness data with DIC data. a1. Image of eye without speckle pattern applied. a2 Eye with speckle pattern applied and LPCAs (red) and optic nerve (green) delineated. Panel c (top view) and panel b (side view) show the same steps from different viewpoints. b1 and c1 Optic nerve (green) and LPCA (red) delineations from DIC image mapped to 3D coordinates using DIC facet map (yellow). b2 and c2 Surface (orange) fit through the DIC facets forming the posterior surface of the sclera model. b3 and c3 SD-OCT delineations of the sclera (blue), LPCAs (red), and optic nerve (green) manually registered to DIC data. Arrows in b3 indicate how the thickness map was projected to the posterior model surface. b4 and c4 Model after thickness data was applied and the model was split up into eight regions. The ONH region is shown in green, the peripapillary regions are shown in red, and the peripheral regions are in blue. d1 SD-OCT delineations of the sclera (blue), LPCAs (red), and optic nerve (green). d2 Average intensity projection of slices from an SD-OCT volume in which the LPCAs and optic nerve are visible
A custom Rhino.Python script was used to apply the thickness data to the existing scleral surface. First, the thickness map was projected onto the scleral surface, and at each map location, a point was offset in the direction of the local scleral surface normal by its associated thickness value. The resulting point cloud was then fit with a surface that represented the anterior scleral surface. The anterior surface was connected to the posterior surface by generating a third surface connecting their outer (farthest from the ONH) edges, to create the scleral model geometry. The model was then divided into nine regions so that regional fiber organization parameters could be calculated by the inverse method. First, the model was divided into an ONH region, a peripapillary sclera region, and a peripheral sclera region. The ONH region was a disc of diameter 0.75 mm centered on the ONH, the peripapillary region was an annulus of internal diameter 0.75 mm and external diameter of 1.5 mm, and the peripheral scleral region was the remainder of the model. We chose these diameters from observations of rat ONH histomorphometric reconstructions (Pazos et al. 2015; Schwaner et al. 2018) and a polarized light microscopy image of the rat sclera (kindly provided by Dr. Ian Sigal). The ONH region contained a combination of sclera, vascular, and nerve tissues (among others), but it was considered to be one homogeneous solid in the model because it was not feasible to model individual structures in the ONH region, and each individual structure alone likely did not have large effects on the deformation of the sclera. The peripapillary (pp) and peripheral (pr) sclera regions were further divided into superior (ppS and prS), inferior (ppI and prI), nasal (ppN and prN), and temporal (ppT and prT) sectors.
2.2.2. Modeling Details: Mesh, Boundary Conditions, and Material Model
The model geometry was imported into Trelis (Computational Simulation Software, LLC; American Fork, UT) and meshed with 8-node hexahedral elements. Measured displacements (from DIC imaging) were interpolated from the facet map to the nodes on the outer boundary edge of the posterior scleral surface and applied as boundary conditions. It was assumed that nodes lying on the boundary surface (connecting the anterior and posterior surfaces) shared the same displacements as the nearest posterior boundary edge node (Fig. 4). Pressure was applied to the anterior scleral surface in a series of steps that matched the recorded IOP levels during the inflation test. For simplicity, it was assumed that a zero-stress state existed at the reference pressure; thus, all pressure increases applied to the model were relative to the reference pressure value.
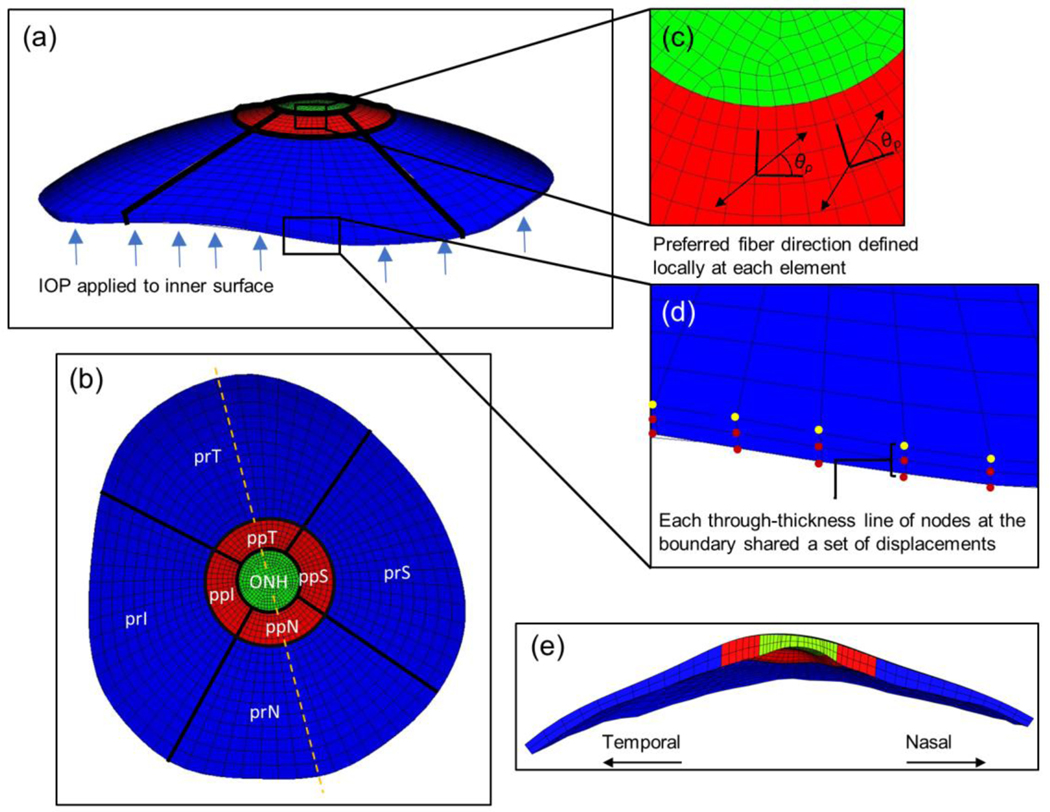
Fig. 4.
FEM details. a Side view of a finite element model mesh. IOP was applied to the anterior surface as indicated by the blue arrows. b Top view of the meshed model with regions labelled. Orientation is the same as in the top view from Fig. 3. Dashed line indicates cross-sectional cut shown in (e). c Zoomed in view of the mesh in the peripapillary and ONH regions. The preferred fiber direction was defined locally at each element. d Zoomed in view of the model outer edges (furthest from the ONH). Displacements from the DIC facet map were interpolated and applied as boundary conditions to nodes on the posterior boundary edge (yellow dots). Each through-thickness line of nodes (red dots) on the boundary surface shared displacements with the closest posterior boundary edge node, i.e. with the nearest yellow dot. e Temporal-Nasal cross-sectional view of the model. Abbreviations: optic nerve head (ONH); peripapillary superior, temporal, inferior, and nasal regions (ppS, ppT, ppI, ppN); and peripheral superior, temporal, inferior, and nasal regions (prS, prT, prI, prN)
The ONH was modelled as a nearly incompressible neo-Hookean solid, for which the strain energy density function takes the form:
| (1) |
where μ is the shear modulus, I1 is the first invariant of the right Cauchy-Green deformation tensor, J is the determinant of the deformation gradient tensor, and λ is Lame’s first parameter. Since neo-Hookean materials reduce to the linear elastic model at small strains, it is common to present their material parameter values in the form of a Young’s modulus, E, and Poisson’s ratio ν using the conversion:
| (2) |
| (3) |
The material model chosen to represent the sclera was a Mooney-Rivlin ground substance reinforced by fibers lying within the plane tangent to the posterior scleral surface and with orientations following a Von Mises distribution (Girard et al. 2009a). The strain energy density function for sclera was thus given by:
| (4) |
where Wgs is the contribution of the ground substance and Wfiber represents the contribution of the collagen fibers. Further,
| (5) |
| (6) |
where c1 is the first Mooney-Rivlin coefficient, c2 is the second Mooney-Rivlin coefficient, I2 is the second invariant of the right Cauchy-Green deformation tensor, and K is the bulk modulus. The sclera was assumed to be incompressible and thus K was set as K = 1 GPa (Girard et al. 2009a). P(θ) is the distribution function of the fibers, θp is the preferred fiber orientation relative to a local material coordinate system, and F2(λ[θ]) represents the response of the collagen fibers. The semi-circular von Mises distribution is given by:
| (7) |
where I0 is the modified Bessel function of the first kind of order 0 and kf is the fiber concentration factor. The fiber response is given by:
| (8) |
where c3 is the exponential fiber stress coefficient, c4 is the fiber uncrimping coefficient, Ei(∙) is the exponential integral function, λm is the fiber stretch for straightened fibers, and c5 is the modulus of straightened fibers. In all simulations, we took c2 = 0 MPa, causing the ground substance to behave as a neo-Hookean solid. Based on previous data demonstrating that the rat sclera behaves nonlinearly in the IOP range of 3 mmHg to 30 mmHg (Hannon et al. 2019), we assumed that the collagen fibers never fully straightened (λ >λm), eliminating the need for the coefficients c5, c6, and λm.
The anisotropic behavior of the sclera was determined by the values of kf and θp. The term kf dictates the degree of anisotropy; specifically, kf = 0 results in an isotropic distribution of fibers within the material plane, while kf = ∞ results in all the fibers lying aligned along a preferred direction dictated by θp. The material coordinate system of each element was defined as follows: the plane of fibers was locally tangent to the posterior scleral surface, while a value of θp = 0° corresponded to a fiber axis in the circumferential direction, and θp = 90° corresponded to a fiber axis in the meridional direction. It was assumed that the entire sclera shared common values for the coefficients c1, c3, and c4 (Girard et al. 2009a), but each region was described by its own values of kf (kf_ppS, kf_ppI, etc.) and θp (θp_ppS, θp_ppI, etc.), resulting in a set of 19 unknown parameters for inverse FEM calculations, namely: c1, c3, c4, kf_prS kf_prI, kf_prT, kfprN, kf_ppS, kf_ppI, kf_ppT, kf_ppN, θp_prS, θp_prI, θp_prT, θp_prN, θp_ppS, θp_ppI, θp_ppT, θp_ppN. The process of defining the model was accomplished using a combination of custom MATLAB and Rhino.Python scripts. All were solved using FEBio (v. 2.8.2; Salt Lake City, UT) (Maas et al. 2012).
2.3. Inverse Modeling and Differential Evolution
To describe the material behavior of the rat sclera, we adjusted the values of the 19 unknown material parameters to minimize the error between computed and experimental (DIC) displacements. Experimental displacement values were interpolated from the facet map at node locations on the scleral surface using a custom MATLAB script and the error was calculated using the following cost function (Girard et al. 2009a):
| (9) |
where are the components of the experimental (e) displacements and are the three components of the model (m) displacements at node n and IOP level p. The total number of interrogated scleral surface nodes is N, and P is the total number of IOP levels. Since there were gaps in the facet map where some facets did not correlate, only the closest node to each correlated facet was used in the cost function calculation.
We used a differential evolution (DE) optimization algorithm to minimize the cost function, which was implemented by making modifications to a MATLAB package obtained from the MATLAB file exchange (Buehren 2017). DE has been used in inverse FEM studies on the monkey eye and has several advantages for this type of problem (Girard et al. 2009a, b, 2011b): it does not require the optimized problem to be differentiable, it can accommodate but does not require a starting guess, and it can be effective in avoiding local minima. To understand how the DE algorithm works, one can think of each trial set of parameter values as the member of a “population”. Each algorithm iteration consists of a series of steps that includes mating between population members to produce offspring, mutation of offspring, and competition between parents and offspring. The winning member of each contest is the parameter set that produces the lowest cost function value, and the winners comprise the population for the next iteration. The particular DE package that we used allows the user to select different strategies or variations on the DE algorithm, set bounds on each parameter, and set the resolution of each parameter. There are a few important settings associated with the algorithm, including strategy, population size (NP), weighting factor (F), and crossover constant (CR). A more in-depth discussion can be found at (Price et al. 2005).
2.4. Two-Step Optimization Strategy
Determining material parameters, as we seek to do here, is a challenging computational problem. After empirical testing, it was determined that a two-step optimization strategy worked well for this problem. In step one, the set of optimized parameters was “compressed” to reduce the dimensionality of the parameter space. Specifically, in this step we sought parameter values for c1, c3, c4, and a “bin” parameter for each scleral region that mapped to both a kf value and θp value, resulting in a total of 11 parameters to be optimized. We found that using 72 “bins” worked well, with each bin representing a kf and θp value as illustrated in Table 1. The search ranges for the c terms were set as 0.001 ≤ c1 ≤ 1 MPa, 0.0001 ≤ c3 ≤0.1 MPa, and 1 ≤ c4 ≤ 1000. The algorithm settings were strategy = rand/bin/1, NP = 50, F = 0.5, and CR = 0.9, and the algorithm was allowed to run for 250 iterations, a total of 12,500 model simulations. The goal of this step was to accomplish a broad and conservative sampling of the parameter space to prevent convergence on local minima while identifying the area that contained the global minimum cost function value.
Table 1.
θp and kf value associated with each bin value.
| Bin Number | θp (°) | kf |
|---|---|---|
| 1 | 15 | 0.5 |
| 2 | 15 | 1.5 |
| 3 | 15 | 2.5 |
| 4 | 15 | 3.5 |
| 5 | 15 | 4.5 |
| 6 | 15 | 5.5 |
| 7 | 30 | 0.5 |
| 8 | 30 | 1.5 |
| : | : | : |
| 71 | 180 | 4.5 |
| 72 | 180 | 5.5 |
In step two, the full set of 19 parameters was optimized, with settings as follows: strategy = best/bin/1, NP = 90, F = 0.5, and CR = 0.5. The search ranges remained the same for the c terms, but kf and θp search ranges were set to 0 ≤ kf ≤ 10 and 0 ≤ θp ≤ 179 degrees. The best parameter set from step one was provided as a starting guess, and the algorithm was allowed to run for 450 iterations, at total of 40,500 model simulations. Selecting the “best/bin/1” strategy resulted in a more aggressive sampling of the parameter space in which the current best population member was involved in all 90 “mating” interactions during a given iteration (Price et al. 2005).
The optimization process was parallelized by running models on 38 cores spread out over eight different computers. The process was directed by a MATLAB package obtained from the MATLAB file exchange (Buehren 2017). A typical model took about 50 seconds to solve and the entire optimization process took about 3.5 days per eye to complete all iterations.
2.5. Proof-of-Concept Testing
Proof-of-concept testing was performed to assess the efficacy of the optimization strategy. A set of arbitrary material properties were input into a rat sclera model and a forward calculation was performed to generate a test set of “pseudo-experimental” displacement data. The optimization protocol was tested against this data set to determine whether it could retrieve the known set of arbitrary properties. This was repeated for two different sets of material properties to ensure we could accurately determine the material properties.
2.6. Mesh Convergence
A numerical mesh convergence study was performed by systematically increasing the number of elements in the circumferential, meridional, and thickness directions and evaluating the z displacement at eight nodes located on the ONH and peripapillary region boundaries. However, we found that using the mesh that produced mesh-independent results (“the converged mesh”) in the optimization protocol described above would have resulted in computation times that were too long (on the order of a week or more per eye). To justify using a lower density mesh, a variation of the proof-of-concept test was repeated. Specifically, an arbitrary material parameter set was input into the converged mesh and used to generate a set of “pseudo-experimental” displacement data. A lower density mesh was then used in the optimization protocol to retrieve the known material parameters.
2.7. Sensitivity to ONH stiffness
It was necessary to specify a value for ONH stiffness in the calculations, which was unknown and could not be determined by optimization due to inconsistent facet correlation (i.e. poor experimental data) in this region. Therefore, we assumed an ONH stiffness (see below) and assessed the sensitivity of model displacements to ONH stiffness by performing forward calculations with a sclera model. Because the ONH regions in the rat sclera models encompassed an area of the rat eye that contains a combination of neural, scleral, and vascular tissue, it was estimated that the Young’s modulus of the ONH region lies within a range of 0.03 MPa to 1 MPa (Sigal et al. 2004). The ONH modulus was varied within this range, and the average total displacement for nodes in the peripapillary region was calculated for each modulus value.
3. Results
3.1. Proof-of-Concept Testing
We performed proof-of-concept testing to determine whether the optimization strategy provided acceptable solutions to the inverse problem. In testing, the cost function reached values of 0.021 μm and 0.005 μm for the two sets of specified material parameters, which is very small compared to the DIC “noise floor”. In set one, the values for c1 and c3 were retrieved exactly and the value for c4 had an error of only 0.2%. All but two θp values were retrieved exactly, and those two had errors of only 7° and 2°. All kf values but one had errors of less than 5%, and the last had an error of 10.1%. In set two, the ci values all had errors of less than 5%. All θp values but one were retrieved exactly, and that value had an error of only 1°. All kf values but one had errors lower than 10%, and that one had an error of 10.1%. We conclude that the optimization strategy converges and provides an answer of sufficiently low error after the selected number of iterations (250 in step 1 and 450 in step 2).
3.2. Mesh Convergence
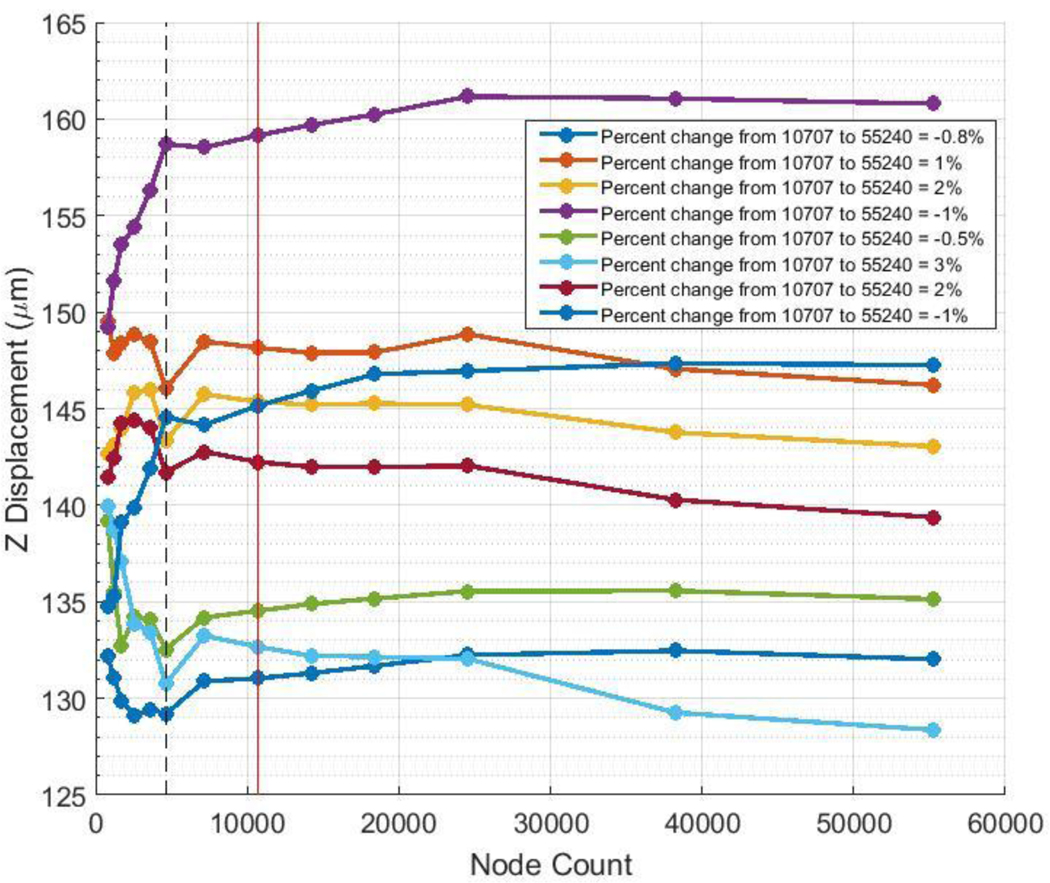
The mesh convergence study showed that mesh independence was reached with a mesh consisting of 10,707 nodes and 6900 elements with two elements through the thickness (Fig. 5). As mentioned, this mesh density would have been infeasible for use in the inverse method due to overly long computation times, so further testing was performed to determine whether a lower density mesh would be acceptable for use. The converged mesh was used to generate a set of “pseudo-experimental” data with an arbitrary parameter set, and a mesh containing 4626 nodes and 3018 elements with two elements through the thickness was used to retrieve the known parameters. We judged that numerical accuracy would be considered as acceptable if the error in the retrieved parameter values was comparable to that seen in proof-of-concept testing. Using the 4626-node mesh, the cost function value was 0.218 μm. The retrieved value for c1 had an error of 4%, c3 had an error of 10%, and c4 had an error of 2.5%. All θp values had errors of 1°, except for one which had an error of 6°. All kf values had errors of 8% or less. Although the cost function value was an order of magnitude higher than that seen in proof-of-concept testing, all the other parameters had comparable relative error. Thus, we considered the mesh with 4626 nodes, 3018 elements, and two elements through the thickness to have sufficient numerical accuracy for the inverse FEM work and used this as the production mesh going forward. Total node and element counts varied slightly between models (on the order of 1%) because the ONH surface was meshed with a “pave” algorithm, producing an unstructured mesh on that surface. However, the scleral regions all had the same number of nodes and elements from model to model.
Fig. 5.
Mesh convergence study. Each colored line indicates the total z displacement of a particular node. The legend details the relative error between the mesh considered to be converged (10,707 nodes, indicated by the vertical red line) and the most dense mesh with 55,240 nodes. The production mesh (4626 nodes) that was determined to have sufficient numerical accuracy is indicated by the dashed black line
It should be noted that in this test, the arbitrary set of kf values were randomly generated, but forced to lie between 1 and 6, based on previous inverse FEM studies on the monkey eye (Girard et al. 2009b). In an earlier proof-of-concept test, a large proportion (4 out of 8) of the randomly generated kf values were less than 1. That test was not successful, as the error of the retrieved θp and kf values was too high, although the retrieved c values all had errors less than 5%. This showed that if the overall degree of fiber alignment is too low, the method is not sensitive enough to resolve fiber directions accurately. This result is intuitive, because as kf, decreases, the effect of θp on model behavior also decreases.
3.3. Sensitivity to ONH Young’s Modulus
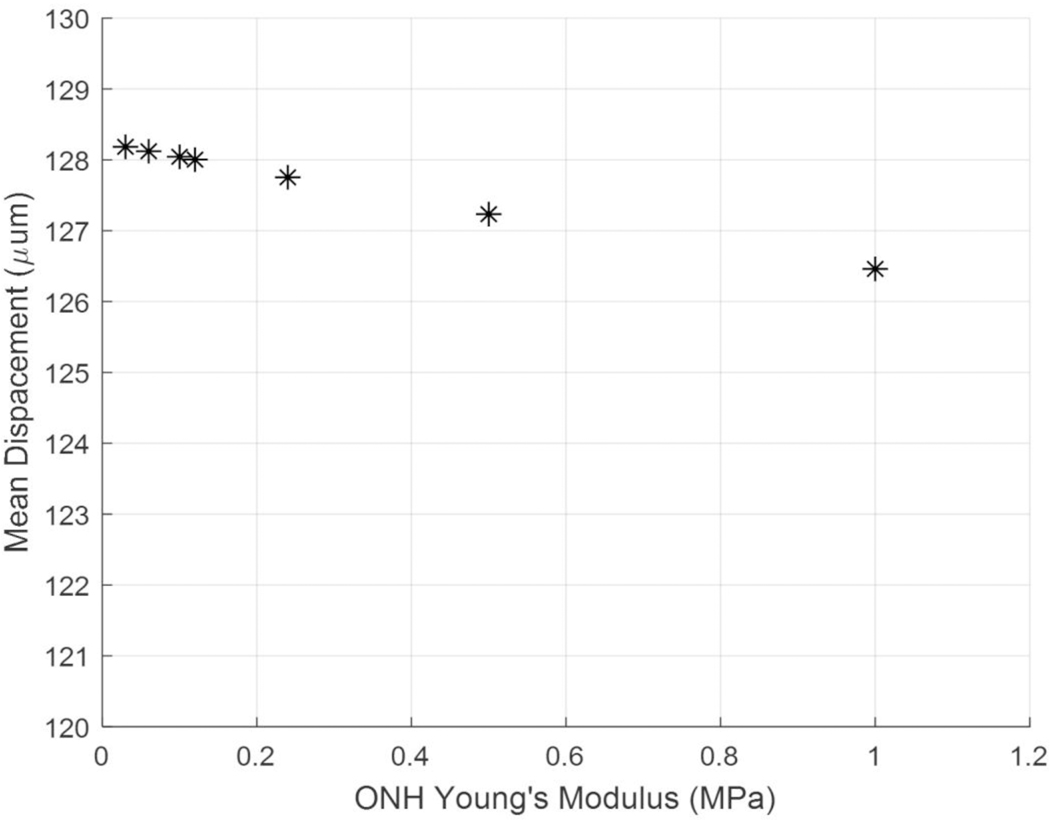
To help select a suitable value for ONH Young’s modulus, we investigated the sensitivity of peripapillary sclera displacement to changes in ONH stiffness. Varying the assumed ONH Young’s modulus value from 0.03 to 1 MPa resulted in a 1.72 μm difference in mean peripapillary scleral nodal displacement (Fig. 6). This shows that the model had a low sensitivity to ONH stiffness, since 1.72 μm is far below the experimental peripapillary sclera displacements, which were on the order of 140 μm. We estimated that the ONH modulus was near 0.1 MPa and used this as the ONH modulus value in all simulations.
Fig. 6.
Model sensitivity to assumed ONH Young’s modulus. As the modulus of the ONH was increased, the mean nodal displacement of the peripapillary sclera decreased. The difference in displacement between the ONH Young’s modulus values of 0.03 MPa and 1 MPa was 1.72 μm
3.4. Inverse Finite Element Modeling
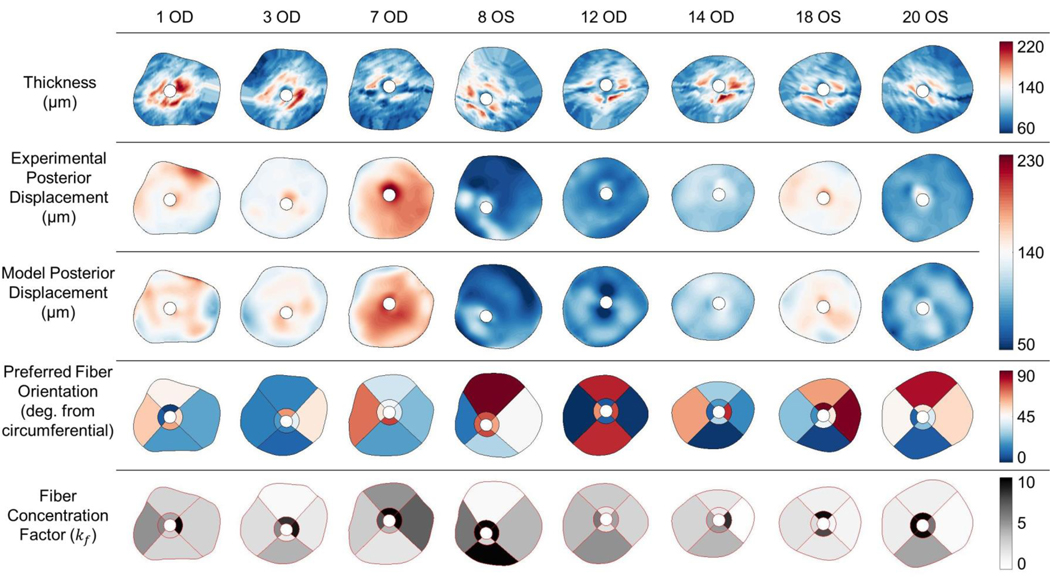
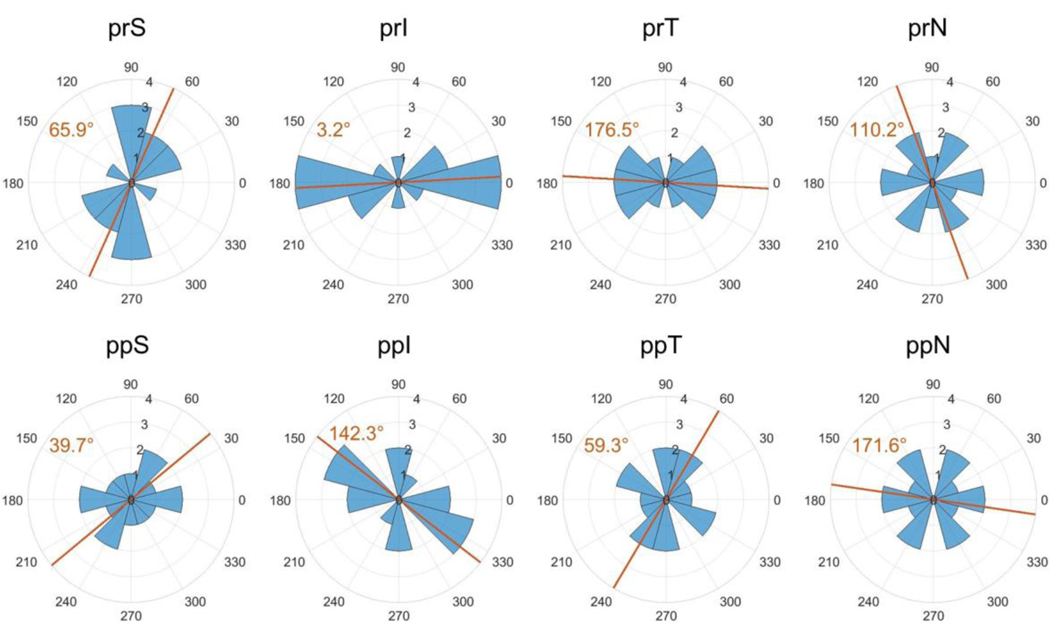
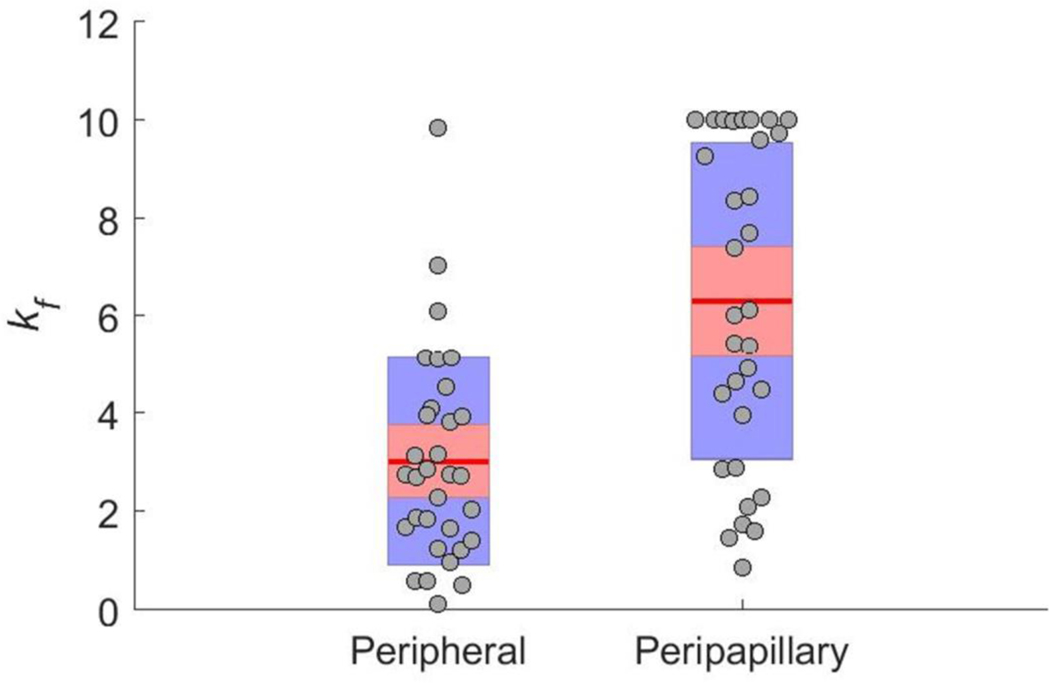
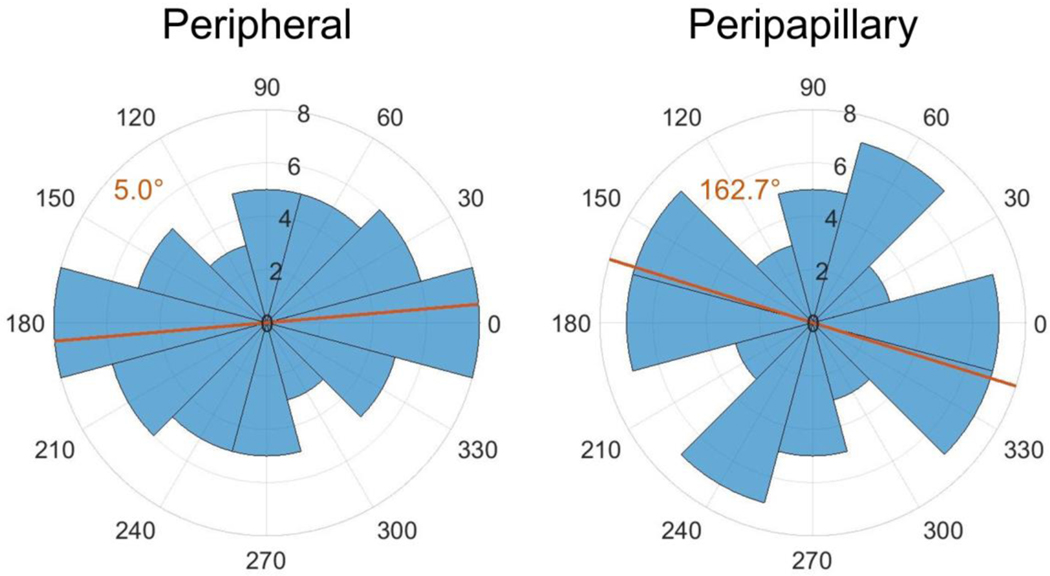
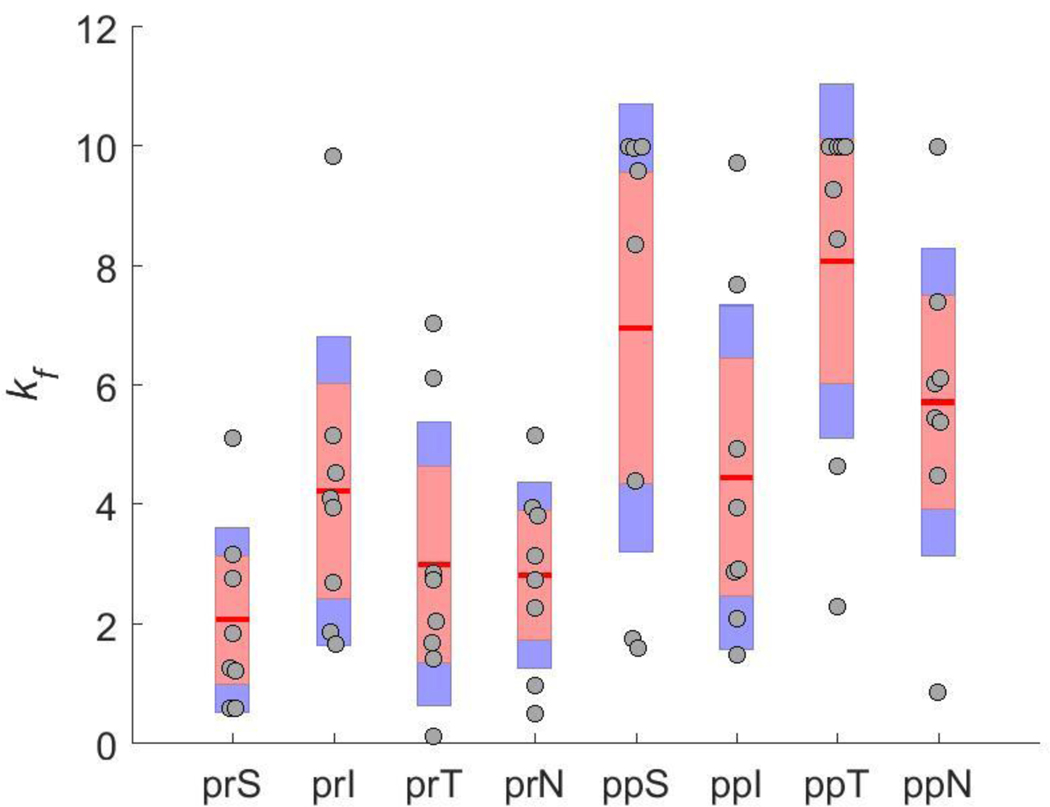
Using the inverse method, scleral material parameter values were successfully calculated for a total of eight eyes. The average cost function value for all eyes was 5.8 μm (Table 2), which is much lower than the experimental displacement values ranging from approximately 50 μm to 230 μm. Although the models failed to match highly localized details of the experimentally-measured displacements in most eyes, they did exhibit good agreement with the overall experimentally-measured displacement patterns (Fig. 7). This was also true when comparing the model and experimental displacements at different pressure steps (not shown). The spread of c1 and c4 values was small, but there was high variability in c3, with three of the values being an order of magnitude higher than the other five (Table 2). Note that three of the low c3 values reached the specified lower boundary limit of 0.0001 MPa, and 7 kf values reached the specified upper boundary limit of 10. The θp and kf values were also highly variable (Fig. 7–Fig. 11). However, a few patterns did emerge. Specifically, the peripapillary kf values were significantly higher than those in the peripheral sclera (Wilcoxon; p < 0.0001) (Fig. 8). The mean fiber direction was calculated for all eight scleral regions (Fig. 11) as well as the peripheral and peripapillary sclera (Fig. 10) according to circular statistics methods implemented in a MATLAB package obtained from the MATLAB file exchange (Berens 2009). The fiber orientation was circumferential on average in the peripheral sclera, and to a lesser degree in the peripapillary sclera (Fig. 10). Interestingly, the prI, prT, and prS regions displayed less variability in θp than did other regions (Fig. 11). The prI and prT regions trended toward circumferential alignment (mean fiber directions of 3.2° and 176.5°), and the prS region trended toward near meridional alignment (mean fiber direction of 65.9°).
Table 2.
c, kf, and cost function values obtained from inverse FEM
| 1 OD | 3 OD | 7 OD | 8 OS | 12 OD | 14 OD | 18 OS | 20 OS | Mean (SD) | |
|---|---|---|---|---|---|---|---|---|---|
| c1 (MPa) | 0.04 | 0.03 | 0.043 | 0.051 | 0.043 | 0.045 | 0.031 | 0.019 | 0.0378 (0.0097) |
| c3 (MPa) | 0.0022 | 0.0002 | 0.0054 | 0.0044 | 0.0004 | 0.0001 | 0.0001 | 0.0001 | 0.0016 (0.002) |
| c4 | 243 | 342 | 312 | 274 | 312 | 433 | 349 | 363 | 329 (54) |
| kf_prS | 2.76 | 0.60 | 5.11 | 0.60 | 3.17 | 1.85 | 1.26 | 1.22 | 2.07 (1.44) |
| kf_prI | 2.70 | 4.10 | 1.87 | 9.84 | 5.15 | 3.95 | 1.67 | 4.54 | 4.23 (2.42) |
| kf_prT | 2.86 | 1.68 | 7.03 | 6.12 | 2.75 | 0.13 | 2.04 | 1.41 | 3.00 (2.22) |
| kf_prN | 5.16 | 2.28 | 3.14 | 3.96 | 3.82 | 2.73 | 0.97 | 0.51 | 2.82 (1.45) |
| kf_ppS | 4.40 | 8.37 | 10.00 | 9.98 | 1.75 | 1.61 | 9.60 | 10.00 | 6.96 (3.52) |
| kf_ppI | 2.88 | 1.48 | 3.96 | 2.91 | 2.10 | 4.94 | 7.70 | 9.73 | 4.46 (2.69) |
| kf_ppT | 10.00 | 9.27 | 10.00 | 10.00 | 4.65 | 8.45 | 2.30 | 10.00 | 8.08 (2.77) |
| kf_ppN | 5.45 | 5.39 | 7.41 | 10.00 | 6.04 | 4.48 | 0.86 | 6.13 | 5.72 (2.42) |
| Cost (μm) | 6.3 | 4.6 | 6.5 | 7.1 | 7.2 | 3.4 | 4.4 | 6.6 | 5.8 (1.3) |
| Age (months) | 13 | 13 | 11 | 11 | 11 | 11 | 10 | 10 | 11.3 (1.2) |
| IOP at OCT (mmHg) | NA | NA | 15.0 | 13.3 | 10 | 9.8 | 10.8 | 10 | 11.5 (2.2) |
Also shown are age of animal and IOP reading at SD-OCT scan. OD indicates right eye and OS indicates left eye. IOP readings were not taken for rats 1 and 3.
Fig. 7.
Comparison of scleral thickness (top row), experimental posterior displacement at the last pressure step as measured by DIC (second row), posterior displacement at the last pressure step of the finite element model (third row), preferred fiber orientation (fourth row), and fiber concentration factor (fifth row) for 8 rat eyes. In all cases, the superior direction is up and inferior direction is down. For OD eyes, the temporal direction is to the right and nasal is to the left. These directions are reversed in OS eyes. The preferred fiber orientation is displayed as the angle from a circumferential orientation. Note that a θp of either 45° or 135° is displayed as white. Scleral thickness was highest within and near the peripapillary region. Model displacements matched the overall pattern of experimental displacements but failed to match all local displacement patterns. The preferred fiber orientation was highly variable, but exhibited a general trend toward circumferential alignment. Fiber concentration factor was generally higher in the peripapillary sclera than the peripheral sclera
Fig. 11.
Symmetric rose plots of the θp values for each scleral region. Symbols and figure interpretation are the same as in Fig. 10. Mean fiber directions in the prI and prT regions suggest a trend toward circumferential alignment. The mean direction in prS was near meridional. Although the mean direction is plotted for all other regions, clear trends did not arise due to high variability. Abbreviations as in Fig. 4
Fig. 8.
Peripheral and peripapillary scleral fiber concentration factor (kf) values as determined by inverse FEM. Circles indicate raw values, the red line indicates the mean, the red box indicates the 95% confidence interval, and the blue box indicates the standard deviation. The fiber concentration factor was higher (on average) in the peripapillary region (Wilcoxon; p < 0.0001)
Fig. 10.
Symmetric rose plots (circular histograms) of the fiber orientations in the peripheral and peripapillary scleral regions. Each blue wedge represents a bin of width 30°. The radius of each wedge indicates the number of θp values in that bin. Note that since the plot is symmetric, the number of θp values plotted is 64 rather than 32. The orange lines indicate the mean preferred fiber direction which is also given in the orange text. Both mean directions suggest an overall circumferential alignment in the peripheral and peripapillary sclera
4. Discussion
This study provides the first quantification of rat scleral biomechanical material properties. Inverse FEM was used to fit experimentally measured displacement data obtained from whole globe inflation testing paired with DIC. The inverse method determined three parameters that dictated the nonlinear stiffening behavior of the entire posterior rat sclera (c1, c3, and c4) and 16 parameters that dictated the anisotropy of eight scleral regions (kf and θp). The parameter c1 describes the mechanical behavior of the ground substance in the sclera, while c3 and c4 describe the behavior of a collagen bundle.
Several inverse FEM studies have been carried out on human and monkey eyes, but many of these studies used different approaches or material models for the sclera, which makes comparisons to the present work challenging (Coudrillier et al. 2012, 2015a, b; Grytz et al. 2014a, b). However, Girard et al. (2009b, a, 2011b) used a similar inflation approach and the same material model to characterize the material properties of monkey eyes. Compared to these previous inverse FEM studies, the c1 values that we obtained were an order of magnitude lower, while the c3 and the c4 values were comparable (Girard et al. 2009b, 2011b). In the monkey studies, only two kf values were assigned per eye (one for the peripapillary region and one for the peripheral region), and they ranged from ~0.5 to ~5.8. The peripheral kf values from the present study largely lay within that range, but our peripapillary kf values were higher (Fig. 8). These higher values could indicate a greater degree of alignment in the peripapillary rat sclera than in the monkey, or they could be due to the fact that we assigned a separate kf value to each of the four peripapillary regions. However, as in the monkey study, the peripapillary kf values were higher than those of the peripheral sclera (on average). This indicates that the fibers in the peripapillary region were more aligned along the preferred axes, making these regions more anisotropic than those in the periphery.
A high fiber alignment in the peripapillary sclera relative to the surrounding posterior sclera has been reported from experimental measurements on several species including the rat (Girard et al. 2011a; Pijanka et al. 2012, 2019; Coudrillier et al. 2015a). Specifically, the rat eye study by Girard et al., used small angle light scattering (SALS) to measure fiber organization and reported a “degree of fiber alignment” and “degree of circumferentiality” for regions throughout the rat sclera. Although Girard et al. report the same alignment trends that we found, our kf values generally indicated a much higher degree of alignment than those experimentally determined by SALS. Specifically, near the scleral canal, the area with the highest fiber alignment in the posterior sclera, Girard et al. reported a median degree of alignment of 0.16, corresponding to a kf value of approximately 0.26 (see Appendix), while our inverse FEM predicted a mean kf value of 6.31. The source of this discrepancy is unclear: it could be due to overestimation of kf by our inverse FEM method, spatial averaging in the SALS data, or limitations of the von Mises distribution used to describe collagen fiber orientation in the sclera. Indeed, a subsequent publication (Gouget et al. 2012) noted that collagen fiber distributions in sclera were better fit by an extension of the von Mises distribution, albeit at the cost of significant complexity. Future inverse FEM studies should consider a more complex and realistic fiber distribution function.
In the present study, fiber alignment in the peripheral sclera was circumferential on average in both the peripheral and peripapillary sclera, which is the same trend as was found in the inverse FEM monkey studies (Girard et al. 2009b, 2011b). At least two studies using experimental measurements of fiber organization have observed this pattern in the rat as well (Girard et al. 2011a; Baumann et al. 2014). Note that Girard et al. (the study using SALS) defined a larger peripapillary sclera region than we did here, which is necessary to keep in mind while comparing their results with ours. Girard and colleagues did not report any trends in fiber direction by location around the ONH (i.e. superior, inferior, temporal, or nasal regions) as opposed to the trends we saw in regions prI, prT, and prS (Fig. 11).
As is evident from Fig. 7, there was a large range of total posterior displacement between eyes, and different eyes displayed different local patterns of displacement. The models closely matched overall levels of displacement for each eye, leading us to conclude that the retrieved values for parameters determining the overall stiffness of the sclera (c1, c3, and c4) were accurate. The low variability exhibited by these parameters supports this conclusion. However, it is possible that these values were overestimated due to the assumption that the eye was at a stress-free state at the reference pressure (see below). This inverse FEM approach also did not perfectly mimic all areas of particularly low or high displacement, indicating that the regionally-specific parameters (kf and θp) may not have accurately described true fiber organization within each region. This is consistent with the large inter-eye variability in kf and θp. Based on the proof-of-concept results, the material parameter values returned for each eye were likely the best set (or close to the best set) of values to match the experimental displacement patterns within the given modeling assumptions; however, those assumptions may have been too limiting to resolve true fiber parameters. This will be discussed further below.
4.1. Limitations
4.1.1. Modeling Assumptions
Several modeling assumptions may have affected the results of this study. One major assumption made in the models was that the sclera only has one layer of collagen fibers. Studies in other species have shown quite clearly that there are several layers of collagen fibers through the thickness of the sclera and that they often have different preferred fiber directions and degrees of alignment (Pijanka et al. 2015; Gogola et al. 2018). In some cases, such as the scenario where a layer of isotropic fiber orientation underlies that of a highly aligned layer, a Von Mises distribution does not accurately describe the true probability density function of fiber orientations (Gouget et al. 2012). Thus, the values for kf and θp that we extracted should be interpreted as through-thickness average values for each scleral region. Further, we assumed that fiber stiffness and density did not vary by location in the sclera by optimizing a single c3 value for the entire sclera. We did so to prevent the list of parameters in our optimization procedure from growing too large, as this may have resulted in infeasibly long convergence times or non-unique solutions. We also assumed that the size and arrangement of the eight scleral model regions were suitable for extracting fiber organization, but this may not have been the case. The patterns of fiber organization in the rat sclera may occur at a smaller scale than the size of the regions we chose. Both of these assumptions decreased the sensitivity of the sclera models, and probably contributed to their inability to recreate highly localized patterns of displacement seen in the experimental data.
Other than incorporating location-specific scleral thickness, we did not account for geometric complexities in the sclera immediately surrounding the optic nerve. One example of such complexity in the rat eye is the existence of a second scleral canal (which allows several blood vessels to exit the globe) just inferior to the main canal through which the optic nerve passes. Instead, these structures were contained within the ONH region of the model, which was represented as an isotropic solid. Further, we assumed a single Young’s modulus value for the ONH region in all models. This may have affected the resulting retrieved parameters, particularly in the peripapillary region, although our sensitivity study indicated that this effect was likely small. The chosen search limits for optimized parameters may also have affected results. In three eyes, the kf values in one or two regions reached the specified upper boundary limit of 10, and in three eyes, the c3 values reached the specified lower boundary limit of 0.0001 MPa, meaning that these seven kf values may have been underestimated and these three c3 values may have been overestimated. Alternatively, reaching the specified limits for these parameters may reflect the overall difficulty/complexity of the inverse FEM procedure.
Finally, we used a simplistic method, “the relative pressure approach”, to account for the effects of prestress. Inflation tests require a non-zero reference pressure to prevent buckling of the ocular to shell from affecting results. We assumed that the sclera was in a stress-free state at the reference pressure for each eye and applied loads in the sclera models that were relative to each eye’s reference pressure. This is a common approach taken in the field (Girard et al. 2009a; Coudrillier et al. 2012) but it is associated with error. Grytz et al. (2013) previously estimated that the error associated with this method could overestimate the ground substance and fiber stiffness by 54% and 15%, respectively, although the error in fiber orientation was less than 1°. They presented two alternative methods that lowered this error. The first is a complex approach that involves computing the prestress using an iterative method and is not feasible for use in inverse FEM due to the additional computation time it would require. The second is called the “relative displacement approach” and is much simpler to implement. Briefly, it involves adding an extra pressure step (equal to the experimental reference pressure) to the beginning of the FE simulation. The resulting deformed geometry is taken as the reference state for all displacement and strain calculations but has a non-zero stress state. Unfortunately, this second approach was incompatible with our models because of the prescribed displacement boundary conditions that we applied. Grytz et al. had the advantage of using a 3D digitizer to extract scleral surface geometry that included the edge clamped by the testing rig, which allowed them to apply fixed and spring boundary conditions to the model edges. However, it should also be noted Grytz et al. estimated the error for a preload of 5 mmHg, whereas the preload pressures in our study were lower (2.2 mmHg to 2.9 mmHg). Therefore, the error associated with prestress in the current study would be less than Grytz et al. previously reported. Future iterations of the method presented here should include a better way to account for prestress if possible.
4.1.2. Methodological Limitations
There were other limitations with the method that may have affected our results. First, the DIC method can produce artifacts due to optical issues such as glare or poor speckling. Although we made efforts to minimize these artifacts, it is possible that some remained and affected the results. Such artifacts probably did not significantly affect overall trends but could have introduced error into the kf and θp values, especially in the small peripapillary regions. Further, there were several sources of error associated with SD-OCT thickness measurement location, although not with the thickness measurements themselves. First, there was error associated with projecting the thickness map to the posterior surface of the sclera model, since the SD-OCT images are artificially “flattened” but cannot easily be warped back to the actual shape of the sclera. We estimate that this location error was nearly 0 for locations close to the ONH, and on the order of 150 μm near the edges of the SD-OCT scans. However, we note that the largest variation in scleral thickness occurred near the ONH (Fig. 7), so thickness measurement location accuracy in this region was most important. Second, there is error in the horizontal distance within b-scans reported by the SD-OCT system. The horizontal distance is an indirect measure derived from the angle of the rays, the optical power of the rat eye, and the size of the rat eye. Thus, error is introduced if differences between eyes are not accounted for. We can gain an estimate of the horizontal scaling error by comparing the axial length of an imaged eye with that of the standard eye used to calibrate the SD-OCT system by Leica, which was 6.29 mm (information provided by Leica). Assuming a variation in axial length of 6 to 7.5 mm for brown Norway rats around 14 months of age (Lozano and Twa 2013), the scaling error ranges from 4.6% to −19.2%. Note that again, the absolute error in horizontal distance will be smaller near the ONH in the central SD-OCT scan compared to the edges, and thus this error likely did not significantly affect the most critical regions of our models. Lastly, the steps of delineating the sclera in SD-OCT scans and manually registering SD-OCT delineations with DIC data both had a certain level of subjectivity.
A few other limitations and assumptions are worth mentioning but likely did not significantly affect results. First, the actual IOP at each pressure step varied between eyes. This occurred because the flow rate entering each eye can differ, making the pressure drop across the flow sensor eye-specific. However, we accounted for this by directly recording IOP throughout the inflation test and including eye-specific IOP data in the inverse FEM framework. Second, we assumed that the choroid did not have a significant effect on scleral deformation. As these were enucleated eyes without blood flow this is a reasonable assumption. Lastly, since only displacements at the posterior scleral surface were recorded, it was assumed that nodes on the model boundary surface shared displacements with the nearest node on the outer boundary edge of the posterior scleral surface.
4.2. Future Work
In the future, we plan to implement the results from this study in forward FE models of the rat posterior eye. Although it is not clear how accurately the fiber organization parameters describe true fiber directions, the experimental displacements were matched well by the inverse FEM, meaning that the retrieved material parameter sets can be used to inform improved models of the sclera. The FE models that implement the parameter values found in this study will be used to investigate the link between biomechanical insult to the ONH and glaucoma.
In future studies using this method, a combined imaging and inverse modeling approach, similar to that in (Coudrillier et al. 2015b), is recommended. Recent studies using polarized light microscopy have provided invaluable information about scleral collagen organization in several species (Gogola et al. 2018). Since the posterior rat eye has the advantage of containing LPCAs that are visible from the outer surface, DIC data could be registered with fiber organization data obtained from polarized light microscopy. This would provide excellent fiber organization information that could be fed into the model at a much higher resolution than in the current study, and a more complex and realistic fiber distribution function could be implemented without adding unknown parameters. In addition, including experimentally determined fiber orientation data would greatly reduce computation time because the DE algorithm would only have to optimize stiffness parameters. If possible, it would also be helpful to perform non-invasive thickness measurements on the eye while it is mounted in the inflation setup. SD-OCT with a telecentric lens may be able to accomplish this, but we were unable to do so with our existing SD-OCT machine. As mentioned, a better approach for including the effects of prestress should be utilized in future work. The relative displacement approach developed by Grytz et al. (2013) could be used if the geometry of the fixed (glued) scleral edges is recorded during testing. It may be possible obtain this data from an SD-OCT scan as mentioned above.
4.3. Conclusion
This study is the first to quantify rat scleral biomechanical properties. We implemented an inverse modeling approach that optimized material parameters in subject-specific sclera models to match displacement data acquired from whole globe inflation testing paired with DIC. The chosen material model accounted for the nonlinear and anisotropic properties of the sclera due to collagen fibers. Stiffness parameters for the entire posterior sclera and fiber organization parameters for several regions throughout the posterior sclera were calculated. There was extremely high variability in the regional fiber organization parameters, indicating that the method was likely not sensitive enough to resolve detailed fiber orientation data from specific regions within the sclera, especially within the peripapillary sclera. However, modelled displacements matched experimental displacements well, indicating that the method successfully retrieved scleral stiffness parameters, and the overall trends in the fiber data were consistent with what has been previously reported. Namely, fiber directions in the peripheral and peripapillary sclera were circumferential on average, and the degree of fiber alignment in the peripapillary sclera was higher than in the peripheral sclera. These stiffness parameters and trends in fiber organization data can be used to inform modeling efforts of the rat ONH, particularly in the context of glaucoma biomechanics research.
Fig. 9.
Scleral fiber concentration factor (kf) values, broken down by scleral region. Symbols indicate the same quantities as in Fig. 8. There was a high variability in kf and no clear trends were apparent across individual regions. Abbreviations as in Fig. 4
Acknowledgements:
Supported by National Institutes of Health [R01EY025286 (CRE) 5T32 EY007092-32 (BGH), F31 EY028832 (SAS)], Georgia Research Alliance (CRE), and Department of Veterans Affairs RX002342 (AJF).
The authors would like to thank Dr. Ian Sigal for providing an image of the posterior rat sclera as well as Dr. Anthony Kuo and Don Vanderlaan for advice on optical coherence topography.
Appendix: Relationship between fiber concentration factor (kf) and degree of alignment
We wished to compare our extracted kf values with the experimental data on degree of fiber alignment (DA) reported by Girard et al. (2011a) in the rat sclera, for which it was necessary to relate kf and DA. The DA parameter reported by Girard et al. (2011a) is defined by (note typographic error in that publication)
| (10) |
where the orientation index (Sacks et al. 1997), 01, is defined as
| (11) |
where P(θ) is the probability density function of fiber directions and satisfies
| (12) |
In other words, half of all fiber directions lie within −01 to +01 about a preferred direction, θp. For DA, a value of 0 means that fiber direction is isotropic within a plane, and a value of 1 means that all fibers have an orientation of θp. The von Mises distribution is defined as
| (13) |
where I0 is the modified Bessel function of the first kind of order zero and kf is the fiber concentration factor. By substituting Equation 13 into Equation 11, and substituting φ = θp − θ, we obtain
| (14) |
which can be rearranged to obtain an implicit relationship between kf and 01
| (15) |
Although obtaining an analytical solution to equation (15) is difficult, one can iteratively find the value of 01 that satisfies Equation 15 for a given kf by plugging a value for kf into the term on the right and numerically evaluating the integral on the left with different values for 01 until the equation is satisfied.
Footnotes
Conflict of Interest: The authors declare that they have no conflict of interest.
Contributor Information
Stephen A. Schwaner, George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 315 Ferst Drive, 2116 IBB, Atlanta, GA 30332
Bailey G. Hannon, George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 315 Ferst Drive, 2116 IBB, Atlanta, GA 30332
Andrew J. Feola, Center for Visual and Neurocognitive Rehabilitation, Atlanta VA Healthcare System, Atlanta, GA
C. Ross Ethier, Coulter Department of Biomedical Engineering, Georgia Institute of Technology/Emory University, 315 Ferst Drive, 2306 IBB, Atlanta, GA 30332.
References
- Alqawlaq S, Flanagan JG, Sivak JM (2018) All roads lead to glaucoma: Induced retinal injury cascades contribute to a common neurodegenerative outcome. Exp Eye Res 0–1. 10.1016/j.exer.2018.11.005 [DOI] [PubMed] [Google Scholar]
- Baumann B, Rauscher S, Gl M, et al. (2014) Peripapillary Rat Sclera Investigated In Vivo With Polarization-Sensitive Optical Coherence Tomography. Invest Ophthalmol Vis Sci 55:7686–7696. 10.1167/iovs.14-15037 [DOI] [PubMed] [Google Scholar]
- Berens P (2009) CircStat : A MATLAB Toolbox for Circular Statistics. J Stat Softw 31:. 10.18637/jss.v031.i10 [DOI] [Google Scholar]
- Buehren M (2017) Differential Evolution. In Matlab Cent. File Exch. http://www.mathworks.com/matlabcentral/fileexchange/authors/12286. Accessed 5 Jan 2018 [Google Scholar]
- Campbell IC, Coudrillier B, Ross Ethier C (2014) Biomechanics of the Posterior Eye: A Critical Role in Health and Disease. J Biomech Eng 136:021005 10.1115/1.4026286 [DOI] [PubMed] [Google Scholar]
- Chen K, Rowley AP, Weiland JD, Humayun MS (2014) Elastic properties of human posterior eye. J Biomed Mater Res A 102:2001–7. 10.1002/jbm.a.34858 [DOI] [PubMed] [Google Scholar]
- Coudrillier B, Boote C, Quigley HA, Nguyen TD (2013) Scleral anisotropy and its effects on the mechanical response of the optic nerve head. Biomech Model Mechanobiol 12:941–963. 10.1007/s10237-012-0455-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coudrillier B, Pijanka J, Jefferys J, et al. (2015a) Collagen Structure and Mechanical Properties of the Human Sclera: Analysis for the Effects of Age. J Biomech Eng 137:041006 10.1115/1.4029430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coudrillier B, Pijanka JK, Jefferys JL, et al. (2015b) Glaucoma-related Changes in the Mechanical Properties and Collagen Micro-architecture of the Human Sclera. PLoS One 10:e0131396 10.1371/journal.pone.0131396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coudrillier B, Tian J, Alexander S, et al. (2012) Biomechanics of the human posterior sclera: age- and glaucoma-related changes measured using inflation testing. Invest Ophthalmol Vis Sci 53:1714–28. 10.1167/iovs.11-8009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eilaghi A, Flanagan JG, Tertinegg I, et al. (2010) Biaxial mechanical testing of human sclera. J Biomech 43:1696–1701. 10.1016/j.jbiomech.2010.02.031 [DOI] [PubMed] [Google Scholar]
- Feola AJ, Nelson ES, Myers J, et al. (2018) The impact of choroidal swelling on optic nerve head deformation. Investig Opthalmology Vis Sci 59:4172 10.1167/iovs.18-24463 [DOI] [PubMed] [Google Scholar]
- Girard MJA, Dahlmann-Noor A, Rayapureddi S, et al. (2011a) Quantitative mapping of scleral fiber orientation in normal rat eyes. Invest Ophthalmol Vis Sci 52:9684–93. 10.1167/iovs.11-7894 [DOI] [PubMed] [Google Scholar]
- Girard MJA, Downs JC, Bottlang M, et al. (2009a) Peripapillary and Posterior Scleral Mechanics—Part II: Experimental and Inverse Finite Element Characterization. J Biomech Eng 131:051012 10.1115/1.3113683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard MJA, Francis Suh JK, Bottlang M, et al. (2011b) Biomechanical changes in the sclera of monkey eyes exposed to chronic IOP elevations. Investig Ophthalmol Vis Sci 52:5656–5669. 10.1167/iovs.10-6927 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard MJA, Suh JKF, Bottlang M, et al. (2009b) Scleral biomechanics in the aging monkey eye. Investig Ophthalmol Vis Sci 50:5226–5237. 10.1167/iovs.08-3363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogola A, Jan N, Lathrop KL, Sigal IA (2018) Radial and Circumferential Collagen Fibers Are a Feature of the Peripapillary Sclera of Human, Monkey, Pig, Cow, Goat, and Sheep. Investig Opthalmology Vis Sci 59:4763 10.1167/iovs.18-25025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouget CLM, Girard MJ, Ethier CR (2012) A constrained von Mises distribution to describe fiber organization in thin soft tissues. Biomech Model Mechanobiol 11:475–482. 10.1007/s10237-011-0326-y [DOI] [PubMed] [Google Scholar]
- Grytz R, Downs JC (2013) A forward incremental prestressing method with application to inverse parameter estimations and eye-specific simulations of posterior scleral shells. Comput Methods Biomech Biomed Engin 16:768–780. 10.1080/10255842.2011.641119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grytz R, Fazio M a., Libertiaux V, et al. (2014a) Age- and Race-Related Differences in Human Scleral Material Properties. Invest Ophthalmol Vis Sci 55:8163–8172. 10.1167/iovs.14-14029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grytz R, Fazio MA, Girard MJA, et al. (2014b) Material properties of the posterior human sclera. J Mech Behav Biomed Mater 29:602–617. 10.1016/j.jmbbm.2013.03.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannon BG, Schwaner SA, Boazak EM, et al. (2019) Sustained scleral stiffening in rats after a single genipin treatment. J R Soc Interface 16:20190427 10.1098/rsif.2019.0427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua Y, Voorhees AP, Sigal IA (2018) Cerebrospinal fluid pressure: Revisiting factors influencing optic nerve head biomechanics. Investig Ophthalmol Vis Sci 59:154–165. 10.1167/iovs.17-22488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lozano DC, Twa MD (2013) Development of a rat schematic eye from in vivo biometry and the correction of lateral magnification in SD-OCT imaging. Investig Ophthalmol Vis Sci 54:6446–6455. 10.1167/iovs.13-12575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maas SA, Ellis BJ, Ateshian GA, Weiss JA (2012) FEBio: Finite Elements for Biomechanics. J Biomech Eng 134:011005 10.1115/1.4005694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers KM, Cone FE, Quigley H a., et al. (2010) The in vitro inflation response of mouse sclera. Exp Eye Res 91:866–875. 10.1016/j.exer.2010.09.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman RE, Flanagan JG, Rausch SMK, et al. (2010) Dimensions of the human sclera: Thickness measurement and regional changes with axial length. Exp Eye Res 90:277–284. 10.1016/j.exer.2009.11.001 [DOI] [PubMed] [Google Scholar]
- Pazos M, Yang H, Gardiner SK, et al. (2015) Rat optic nerve head anatomy within 3D histomorphometric reconstructions of normal control eyes. Exp Eye Res 139:1–12. 10.1016/j.exer.2015.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pijanka JK, Coudrillier B, Ziegler K, et al. (2012) Quantitative Mapping of Collagen Fiber Orientation in Non-glaucoma and Glaucoma Posterior Human Sclerae. Investig Opthalmology Vis Sci 53:5258 10.1167/iovs.12-9705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pijanka JK, Markov PP, Midgett D, et al. (2019) Quantification of collagen fiber structure using second harmonic generation imaging and two-dimensional discrete Fourier transform analysis: Application to the human optic nerve head. J Biophotonics e201800376 10.1002/jbio.201800376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pijanka JK, Spang MT, Sorensen T, et al. (2015) Depth-dependent changes in collagen organization in the human peripapillary sclera. PLoS One 10:1–17. 10.1371/journal.pone.0118648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price KV, Storn RM, Lampinen JA (2005) Differential Evolution: A Practical Approach to Global Optimization. Springer, Berlin [Google Scholar]
- Quigley H a (1999) Neuronal death in glaucoma. Prog Retin Eye Res 18:39–57 [DOI] [PubMed] [Google Scholar]
- Quigley HA, Addicks EM, Green WR, Maumenee AE (1981) Optic Nerve Damage in Human Glaucoma. II. The site of injury and susceptibility to damage. Arch Ophthalmol 99:635–49. 10.1001/archopht.1981.03930010635009 [DOI] [PubMed] [Google Scholar]
- Sacks MS, Smith DB, Hiester ED (1997) A small angle light scattering device for planar connective tissue microstructural analysis. Ann Biomed Eng 25:678–689. 10.1007/BF02684845 [DOI] [PubMed] [Google Scholar]
- Schwaner SA, Kight AM, Perry RN, et al. (2018) A Methodology for Individual-Specific Modeling of Rat Optic Nerve Head Biomechanics in Glaucoma. J Biomech Eng 140:084501-1–084501-10. 10.1115/1.4039998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherwood JM, Reina-Torres E, Bertrand JA, et al. (2016) Measurement of Outflow Facility Using iPerfusion. PLoS One 11:e0150694 10.1371/journal.pone.0150694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal I a, Flanagan JG, Ethier CR (2005) Factors influencing optic nerve head biomechanics. Invest Ophthalmol Vis Sci 46:4189–99. 10.1167/iovs.05-0541 [DOI] [PubMed] [Google Scholar]
- Sigal I a, Flanagan JG, Tertinegg I, Ethier CR (2004) Finite element modeling of optic nerve head biomechanics. Invest Ophthalmol Vis Sci 45:4378–87. 10.1167/iovs.04-0133 [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR (2007) Predicted extension, compression and shearing of optic nerve head tissues. Exp Eye Res 85:312–322. 10.1016/j.exer.2007.05.005 [DOI] [PubMed] [Google Scholar]
- Tham YC, Li X, Wong TY, et al. (2014) Global prevalence of glaucoma and projections of glaucoma burden through 2040: A systematic review and meta-analysis. Ophthalmology 121:2081–2090. 10.1016/j.ophtha.2014.05.013 [DOI] [PubMed] [Google Scholar]
- Wang X, Rumpe H, Lim WEH, et al. (2016) Finite element analysis predicts large optic nerve head strains during horizontal eye movements. Investig Ophthalmol Vis Sci 57:2452–2462. 10.1167/iovs.15-18986 [DOI] [PubMed] [Google Scholar]