Full Law Identification in Graphical Models of Missing Data: Completeness Results

Abstract

Missing data has the potential to affect analyses conducted in all fields of scientific study including healthcare, economics, and the social sciences. Several approaches to unbiased inference in the presence of non-ignorable missingness rely on the specification of the target distribution and its missingness process as a probability distribution that factorizes with respect to a directed acyclic graph. In this paper, we address the longstanding question of the characterization of models that are identifiable within this class of missing data distributions. We provide the first completeness result in this field of study – necessary and sufficient graphical conditions under which, the full data distribution can be recovered from the observed data distribution. We then simultaneously address issues that may arise due to the presence of both missing data and unmeasured confounding, by extending these graphical conditions and proofs of completeness, to settings where some variables are not just missing, but completely unobserved.

1. Introduction

Missing data has the potential to affect analyses conducted in all fields of scientific study, including healthcare, economics, and the social sciences. Strategies to cope with missingness that depends only on the observed data, known as the missing at random (MAR) mechanism, are well-studied (Dempster et al., 1977; Cheng, 1994; Robins et al., 1994; Tsiatis, 2006). However, the setting where missingness depends on covariates that may themselves be missing, known as the missing not at random (MNAR) mechanism, is substantially more difficult and under-studied (Fielding et al., 2008; Marston et al., 2010). MNAR mechanisms are expected to occur quite often in practice, for example, in longitudinal studies with complex patterns of dropout and re-enrollment, or in studies where social stigma may prompt non-response to questions pertaining to drug-use, or sexual activity and orientation, in a way that depends on other imperfectly collected or censored covariates (Robins & Gill, 1997; Vansteelandt et al., 2007; Marra et al., 2017).

Previous work on MNAR models has proceeded by imposing a set of restrictions on the full data distribution (the target distribution and its missingness mechanism) that are sufficient to yield identification of the parameter of interest. While there exist MNAR models whose restrictions cannot be represented graphically (Tchetgen Tchetgen et al., 2018), the restrictions posed in several popular MNAR models such as the permutation model (Robins & Gill, 1997), the block-sequential MAR model (Zhou et al., 2010), the itemwise conditionally independent nonresponse (ICIN) model (Shpitser, 2016; Sadinle & Reiter, 2017), and those in (Daniel et al., 2012; Thoemmes & Rose, 2013; Martel Garćıa, 2013; Mohan et al., 2013; Mohan & Pearl, 2014; Saadati & Tian, 2019) are either explicitly graphical or can be interpreted as such.

Despite the popularity of graphical modeling approaches for missing data problems, characterization of the class of missing data distributions identified as functionals of the observed data distribution has remained an open question (Bhattacharya et al., 2019). Several algorithms for the identification of the target distribution have been proposed (Mohan & Pearl, 2014; Shpitser et al., 2015; Tian, 2017; Bhattacharya et al., 2019). We show that even the most general algorithm currently published (Bhattacharya et al., 2019) still retains a significant gap in that there exist target distributions that are identified which the algorithm fails to identify. We then present what is, to our knowledge, the first completeness result for missing data models representable as directed acyclic graphs (DAGs) – a necessary and sufficient graphical condition under which the full data distribution is identified as a function of the observed data distribution. For any given field of study, such a characterization is one of the most powerful results that identification theory can offer, as it comes with the guarantee that if these conditions do not hold, the model is provably not identified.

We further generalize these graphical conditions to settings where some variables are not just missing, but completely unobserved. Such distributions are typically summarized using acyclic directed mixed graphs (ADMGs) (Richardson et al., 2017). We prove, once again, that our graphical criteria are sound and complete for the identification of full laws that are Markov relative to a hidden variable DAG and the resulting summary ADMG. This new result allows us to address two of the most critical issues in practical data analyses simultaneously, those of missingness and unmeasured confounding.

Finally, in the course of proving our results on completeness, we show that the proposed graphical conditions also imply that all missing data models of directed acyclic graphs or acyclic directed mixed graphs that meet these conditions, are in fact sub-models of the MNAR models in (Shpitser, 2016; Sadinle & Reiter, 2017). This simple, yet powerful result implies that the joint density of these models may be identified using an odds ratio parameterization that also ensures congenial specification of various components of the likelihood (Chen, 2007; Malinsky et al., 2019). Our results serve as an important precondition for the development of score-based model selection methods for graphical models of missing data, as an alternative to the constraint-based approaches proposed in (Strobl et al., 2018; Gain & Shpitser, 2018; Tu et al., 2019), and directly yield semi-parametric estimators using results in (Malinsky et al., 2019).

2. Preliminaries

A directed acyclic graph (DAG) $\mathcal{G}(V)$ consists of a set of nodes V connected through directed edges such that there are no directed cycles. We will abbreviate $\mathcal{G}(V)$ as simply $\mathcal{G}$, when the vertex set is clear from the given context. Statistical models of a DAG $\mathcal{G}$ are sets of distributions that factorize as $p(V)={\prod }_{V_i\in V}p(V_i|{\text{pa}}_{\mathcal{G}}(V_i))$, where ${\text{pa}}_{\mathcal{G}}(V_i)$ are the parents of V_i in $\mathcal{G}$. The absence of edges between variables in $\mathcal{G}$, relative to a complete DAG entails conditional independence facts in p(V ). These can be directly read off from the DAG $\mathcal{G}$ by the well-known d-separation criterion (Pearl, 2009). That is, for disjoint sets X, Y,Z, the following global Markov property holds: ${(X{⫫}_{\text{d-sep}}Y|Z)}_{\mathcal{G}}\Rightarrow {(X⫫Y|Z)}_{p(V)}$. When the context is clear, we will simply use X ⫫ Y | Z to denote the conditional independence between X and Y given Z.

In practice, some variables on the DAG may be unmeasured or hidden. In such cases, the distribution p(V ∪ U) is Markov relative to a hidden variable DAG $\mathcal{G}(V\cup U)$, where variables in U are unobserved. There may be infinitely many hidden variable DAGs that imply the same set of conditional independences on the observed margin. Hence, it is typical to utilize a single acyclic directed mixed graph (ADMG) consisting of directed and bidirected edges that entails the same set of equality constraints as this infinite class (Evans, 2018). Such an ADMG $\mathcal{G}(V)$ is obtained from a hidden variable DAG $\mathcal{G}(V\cup U)$ via the latent projection operator (Verma & Pearl, 1990) as follows. A → B exists in $\mathcal{G}(V)$ if there exists a directed path from A to B in $\mathcal{G}(V\cup U)$ with all intermediate vertices in U. An edge A ↔ B exists in $\mathcal{G}(V)$ if there exists a collider-free path (i.e., there are no consecutive edges of the form → ◦ ←) from A to B in $\mathcal{G}(V\cup U)$ with all intermediate vertices in U, such that the first edge on the path is an incoming edge into A and the final edge is an incoming edge into B.

Given a distribution p(V ∪ U) that is Markov relative to a hidden variable DAG $\mathcal{G}(V,U)$, conditional independence facts pertaining to the observed margin p(V ) can be read off from the ADMG $\mathcal{G}(V)$ by a simple analogue of the d-separation criterion, known as m-separation (Richardson, 2003), that generalizes the notion of a collider to include mixed edges of the form → ◦ ↔,↔ ◦ ←, and ↔ ◦ ↔.

3. Missing Data Models

A missing data model is a set of distributions defined over a set of random variables {O,X⁽¹⁾,R,X}, where O denotes the set of variables that are always observed, X⁽¹⁾ denotes the set of variables that are potentially missing, R denotes the set of missingness indicators of the variables in X⁽¹⁾, and X denotes the set of the observed proxies of the variables in X⁽¹⁾. By definition missingness indicators are binary random variables; however, the state space of variables in X⁽¹⁾ and O are unrestricted. Given $X_i^{(1)}\in X^{(1)}$ and its corresponding missingness indicator R_i ∈ R, the observed proxy X_i is defined as $X_i\equiv X_i^{(1)}$ if R_i = 1, and X_i =? if R_i = 0. Hence, p(X | R,X⁽¹⁾) is deterministically defined. We call the non-deterministic part of a missing data distribution, i.e, p(O,X⁽¹⁾,R), the full law, and partition it into two pieces: the target law p(O,X⁽¹⁾) and the missingness mechanism p(R | X⁽¹⁾,O). The censored version of the full law p(O,R,X), that the analyst actually has access to is known as the observed data distribution.

Following the convention in (Mohan et al., 2013), let $\mathcal{G}(V)$ be a missing data DAG, where V = {O ∪ X⁽¹⁾ ∪ R ∪ X}. In addition to acyclicity, edges of a missing data DAG are subject to other restrictions: outgoing edges from variables in R cannot point to variables in {X⁽¹⁾,O}, each X_i ∈ X has only two parents in $\mathcal{G}$, i.e., R_i and $X_i^{(1)}$ (these edges represent the deterministic function above that defines X_i, and are shown in gray in all the figures below), and there are no outgoing edges from X_i (i.e., the proxy X_i does not cause any variable on the DAG, however the corresponding full data variable $X_i^{(1)}$ may cause other variables.) A missing data model associated with a missing data DAG $\mathcal{G}$ is the set of distributions p(O,X⁽¹⁾,R,X) that factorizes as,

$$\prod _{V_i\in O\cup X^{(1)}\cup R}p(V_i|{\text{pa}}_{\mathcal{G}}(V_i))\prod _{X_i\in X}p(X_i|X_i^{(1)},R_i).$$

By standard results on DAG models, conditional independences in p(X⁽¹⁾,O,R) can still be read off from $\mathcal{G}$ by the d-separation criterion (Pearl, 2009). For convenience, we will drop the deterministic terms of the form $p(X_i|X_i^{(1)},R_i)$ from the identification analyses in the following sections since these terms are always identified by construction.

As an extension, we also consider a hidden variable DAG $\mathcal{G}(V\cup U)$, where V = {O,X⁽¹⁾,R,X} and variables in U are unobserved, to encode missing data models in the presence of unmeasured confounders. In such cases, the full law would obey the nested Markov factorization (Richardson et al., 2017) with respect to a missing data ADMG $\mathcal{G}(V)$, obtained by applying the latent projection operator (Verma & Pearl, 1990) to the hidden variable DAG $\mathcal{G}(V\cup U)$. As a result of marginalization of latents U, there might exist bi-directed edges (to encode the hidden common causes) between variables in V (bi-directed edges are shown in red in all the figures below). It is straightforward to see that a missing data ADMG obtained via projection of a hidden variable missing data DAG follows the exact same restrictions as stated in the previous paragraph (i.e., no directed cycles, ${\text{pa}}_{\mathcal{G}}(X_i)=\{X_i^{(1)},R_i\}$, every X_i ∈ X is childless, and there are no outgoing edges from R_i to any variables in {X⁽¹⁾,O}.)

3.1. Identification in Missing Data Models

The goal of non-parametric identification in missing data models is twofold: identification of the target law p(O,X⁽¹⁾) or functions of it f(p(O,X⁽¹⁾)), and identification of the full law p(O,X⁽¹⁾,R), in terms of the observed data distribution p(O,R,X).

A compelling reason to study the problem of identification of the full law in and of itself, is due to the fact that many popular methods for model selection or causal discovery, rely on the specification of a well-defined and congenial joint distribution (Chickering, 2002; Ramsey, 2015; Ogarrio et al., 2016). A complete theory of the characterization of missing data full laws that are identified opens up the possibility of adapting such methods to settings involving non-ignorable missingness, in order to learn not only substantive relationships between variables of interest in the target distribution, but also the processes that drive their missingness. This is in contrast to previous approaches to model selection under missing data that are restricted to submodels of a single fixed identified model (Strobl et al., 2018; Gain & Shpitser, 2018; Tu et al., 2019). Such an assumption may be impractical in complex healthcare settings, for example, where discovering the factors that lead to missingness or study-dropout may be just as important as discovering substantive relations in the underlying data.

Though the focus of this paper is on identification of the full law of missing data models that can be represented by a DAG (or a hidden variable DAG), some of our results naturally extend to identification of the target law (and functionals therein) due to the fact that the target law can be derived from the full law as ${\sum }_{R}p(O,X^{(1)},R)$.

Remark 1.

By chain rule of probability, the target law p(O,X⁽¹⁾) is identified if and only if p(R = 1 | O,X⁽¹⁾) is identified. The identifying functional is given by

$$p(O,X^{(1)})=\frac{p(O,X^{(1)},R=1)}{p(R=1|O,X^{(1)})}.$$

(the numerator is a function of observed data by noting that X⁽¹⁾ = X, and is observed when R = 1).

Remark 2.

The full law p(O,X⁽¹⁾,R) is identified if and only if p(R | O,X⁽¹⁾) is identified. According to Remark 1, the identifying functional is given by

$$p(O,X^{(1)},R)=\frac{p(O,X^{(1)},R=1)}{p(R=1|O,X^{(1)})}\times p(R|O,X^{(1)}).$$

The rest of the paper is organized as follows. In Section 4, we explain, through examples, why none of the existing identification algorithms put forward in the literature are complete in the sense that there exist missing data DAGs whose full law and target law are identified but these algorithms fail to derive an identifying functional for them. In Section 5, we provide a complete algorithm for full law identification. In Section 6, we further extend our identification results to models where unmeasured confounders are present. We defer all proofs to the Appendix.

4. Incompleteness of Current Methods

In this section, we show that even the most general methods proposed for identification in missing data DAG models remain incomplete. In other words, we show that there exist identified MNAR models that are representable by DAGs, however all existing algorithms fail to identify both the full and target law for these models. For brevity, we use the procedure proposed in (Bhattacharya et al., 2019) as an exemplar. However, as it is the most general procedure in the current literature, failure to identify via this procedure would imply failure by all other existing ones. For each example, we also provide alternate arguments for identification that eventually lead to the general theory in Sections 5 and 6.

The algorithm proposed by (Bhattacharya et al., 2019) proceeds as follows. For each missingness indicator R_i, the algorithm tries to identify the distribution ${p(R_i|{\text{pa}}_{\mathcal{G}}(R_i))|}_{R=1}$, sometimes referred to as the propensity score of R_i. It does so by checking if R_i is conditionally independent (given its parents) of the corresponding missingness indicators of its parents that are potentially missing. If this is the case, the propensity score is identified by a simple conditional independence argument (d-separation). Otherwise, the algorithm checks if this condition holds in post-fixing distributions obtained through recursive application of the fixing operator, which roughly corresponds to inverse weighting the current distribution by the propensity score of the variable being fixed (Richardson et al., 2017) (a more formal definition is provided in the Appendix.) If the algorithm succeeds in identifying the propensity score for each missingness indicator in this manner, then it succeeds in identifying the target law as Remark 1 suggests, since $p(R=1|O,X^{(1)})={{\prod }_{R_i\in R}p(R_i|{\text{pa}}_{\mathcal{G}}(R))|}_{R=1}$. Additionally, if it is the case that in the course of execution, the propensity score $p(R_i|{\text{pa}}_{\mathcal{G}}(R_i))$ for each missingness indicator is also identified at all levels of its parents, then the algorithm also succeeds in identifying the full law (due to Remark 2).

In order to ground our theory in reality, we now describe a series of hypotheses that may arise during the course of a data analysis that seeks to study the link between the effects of smoking on bronchitis, through the deposition of tar or other particulate matter in the lungs. For each hypothesis, we ask if the investigator is able to evaluate the goodness of fit of the proposed model, typically expressed as a function of the full data likelihood, as a function of just the observed data. In other words, we ask if the full law is identified as a function of the observed data distribution. If it is, this enables the analyst to compare and contrast different hypotheses and select one that fits the data the best.

Setup.

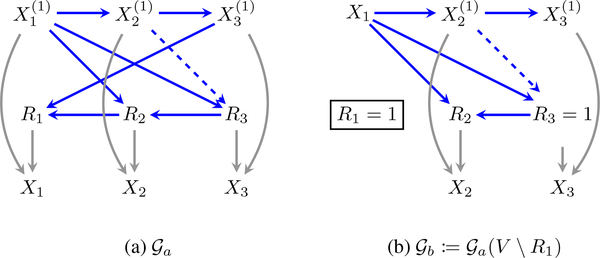
To start, the investigator consults a large observational database containing the smoking habits, measurements of particulate matter in the lungs, and results of diagnostic tests for bronchitis on individuals across a city. She notices however, that several entries in the database are missing. This leads her to propose a model like the one shown in Fig. 1(a), where $X_1^{(1)}$, $X_2^{(1)}$, and $X_3^{(1)}$ correspond to smoking, particulate matter, and bronchitis respectively, and R₁,R₂, and R₃ are the corresponding missingness indicators.

Figure 1.

(a) The missing data DAG used in scenario 1 (without the dashed edge $X_2^{(1)}\to R_3$) and scenario 2 (with the dashed edge $X_2^{(1)}\to R_3$) (b) Conditional DAG corresponding to the missing data DAG in (a) after fixing R₁, i.e., inverse weighting by the propensity score of R₁.

For the target distribution p(X⁽¹⁾), she proposes a simple mechanism that smoking leads to increased deposits of tar in the lungs, which in turn leads to bronchitis $(X_1^{(1)}\to X_2^{(1)}\to X_3^{(1)})$. For the missingness process, she proposes that a suspected diagnosis of bronchitis is likely to lead to an inquiry about the smoking status of the patient $(X_3^{(1)}\to R_1)$, smokers are more likely to get tested for tar and bronchitis ($X_1^{(1)}\to R_2$, $X_1^{(1)}\to R_3$), and ordering a diagnostic test for bronchitis, increases the likelihood of ordering a test for tar, which in turn increases the likelihood of inquiry about smoking status (R₁ ← R₂ ← R₃).

We now show that for this preliminary hypothesis, if the investigator were to utilize the procedure described in (Bhattacharya et al., 2019) she may conclude that it is not possible to identify the full law. We go on to show that such a conclusion would be incorrect, as the full law is, in fact, identified, and provide an alternative means of identification.

Scenario 1.

Consider the missing data DAG model in Fig. 1(a) by excluding the edge $X_2^{(1)}\to R_3$, corresponding to the first hypothesis put forth by the investigator. The propensity score for R₁ can be obtained by simple conditioning, noting that $R_1⫫R_3|X_3^{(1)}$, R₂ by d-separation. Hence, $p(R_1|{\text{pa}}_{\mathcal{G}}(R_1))=p(R_1|X_3^{(1)},R_2)=p(R_1|X_3,R_2,R_3=1)$.

Conditioning is not sufficient in order to identify the propensity score for R₂, as $R_2\cancel{⫫}{R}_1|X_1^{(1)}$, R₃. However, it can be shown that in the distribution $q(V\backslash R_1|R_1=1)\equiv \frac{p(V)}{p(R_1=1|{\text{pa}}_{\mathcal{G}}(R_1))}$, R₂ ⫫ R₁ | X₁,R₃ = 1, since this distribution is Markov relative to the graph in Fig. 1(b) (see the Appendix for details). We use the notation q(· | ·) to indicate that while q acts in most respects as a conditional distribution, it was not obtained from p(V ) by a conditioning operation. This implies that the propensity score for R₂ (evaluated at R = 1) is identified as q(R₂ | X₁,R₃ = 1,R₁ = 1).

Finally, we show that the algorithm in (Bhattacharya et al., 2019) is unable to identify the propensity score for R₃. We first note that $R_3\cancel{⫫}{R}_1|X_1^{(1)}$ in the original problem. Furthermore, as shown in Fig. 1(b), fixing R₁ leads to a distribution where R₃ is necessarily selected on as the propensity score $p(R_1|{\mathrm{pa}}_{\mathcal{G}}(R_1))$ is identified by restricting the data to cases where R₃ = 1. It is thus impossible to identify the propensity score for R₃ in this post-fixing distribution. The same holds if we try to fix R₂ as identification of the propensity score for R₂ required us to first fix R₁, which we have seen introduces selection bias on R₃.

Hence, the procedure in (Bhattacharya et al., 2019) fails to identify both the target law and the full law for the problem posed in Fig. 1(a). However, both these distributions are, in fact, identified as we now demonstrate.

A key observation is that even though the identification of $p(R_3|X_1^{(1)})$ might not be so straightforward, $p(R_3|X_1^{(1)},R_2)$ is indeed identified, because by d-separation $R_3⫫R_1|X_1^{(1)}$, R₂, and therefore $p(R_3|X_1^{(1)},R_2)=p(R_3|X_1,R_2,R_1=1)$. Given that $p(R_3|X_1^{(1)},R_2)$ and $p(R_2|X_1^{(1)},R_3=1)$ are both identified (the latter is obtained through as described earlier), we consider exploiting an odds ratio parameterization of the joint density $p(R_2,R_3|{\text{pa}}_{\mathcal{G}}(R_2,R_3))=p(R_2,R_3|X_1^{(1)})$. As we show below, such a parameterization immediately implies the identifiability of this density and consequently, the individual propensity scores for R₂ and R₃.

Given disjoint sets of variables A,B,C and reference values A = a₀,B = b₀, the odds ratio parameterization of p(A,B | C), given in (Chen, 2007), is as follows:

$$\frac{1}{Z}\times p(A|b_0,C)\times p(B|a_0,C)\times \mathrm{OR}(A,B|C),$$ (1)

where

$$\begin{gathered} \mathrm{OR}(A=a,B=b|C) \\ =\frac{p(A=a|B=b,C)}{p(A=a_0|B=b,C)}\times \frac{p(A=a_0|B=b_0,C)}{p(A=a|B=b_0,C)}, \end{gathered}$$

and Z is the normalizing term and is equal to

$$\sum _{A,B}p(A|B=b_0,C)\times p(B|A=a_0,C)\times \mathrm{OR}(A,B|C).$$

Note that OR(A,B | C) = OR(B,A | C), i.e., the odds ratio is symmetric; see (Chen, 2007).

A convenient choice of reference value for the odds ratio in missing data problems is the value R_i = 1. Given this reference level and the parameterization of the joint in Eq. (1), we know that $p(R_2,R_3|X_1^{(1)})=\frac{1}{Z}\times p(R_2|R_3=1,X_1^{(1)})\times p(R_3|R_2=1,X_1^{(1)})\times \mathrm{OR}(R_2,R_3|X_1^{(1)})$, where Z is the normalizing term, and

$$\begin{gathered} \text{OR}(R_2=r_2,R_3=r_3|X_1^{(1)}) \\ =\frac{p(R_3=r_3|R_2=r_2,X_1^{(1)})}{p(R_3=1|R_2=r_2,X_1^{(1)})}\times \frac{p(R_3=1|R_2=1,X_1^{(1)})}{p(R_3=r_3|R_2=1,X_1^{(1)})}. \end{gathered}$$

The conditional pieces $p(R_2|R_3=1,X_1^{(1)})$ and $p(R_3|R_2=1,X_1^{(1)})$ are already shown to be functions of the observed data. To see that the odds ratio is also a function of observables, recall that $R_3⫫R_1|R_2,X_1^{(1)}$. This means that R₁ = 1 can be introduced into each individual piece of the odds ratio functional above, making it so that the entire functional depends only on observed quantities. Since all pieces of the odds ratio parameterization are identified as functions of the observed data, we can conclude that $p(R_2,R_3|X_1^{(1)})$ is identified as the normalizing term is always identified if all the conditional pieces and the odds ratio are identified. This result, in addition to the fact that $p(R_1|R_2,X_3^{(1)})$ is identified as before, leads us to the identification of both the target law and the full law, as the missingness process p(R | X⁽¹⁾) is identified.

Scenario 2.

Suppose the investigator is interested in testing an alternate hypothesis to see whether detecting high levels of particulate matter in the lungs, also serves as an indicator to physicians that a diagnostic test for bronchitis should be ordered. This corresponds to the missing data DAG model in Fig. 1(a) by including the edge $X_2^{(1)}\to R_3$. Since this is a strict super model of the previous example, the procedure in (Bhattacharya et al., 2019) still fails to identify the target and full laws in a similar manner as before.

However, it is still the case that both the target and full laws are identified. The justification for why the odds ratio parameterization of the joint density $p(R_2,R_3|{\text{pa}}_{\mathcal{G}}(R_2,R_3))=p(R_2,R_3|X_1^{(1)},X_2^{(1)})$ is identified in this scenario, is more subtle. We have,

$$\begin{gathered} p(R_2,R_3|X_1^{(1)},X_2^{(1)})=\frac{1}{Z}\times p(R_2|R_3=1,X_1^{(1)},X_2^{(1)}) \\ \times p(R_3|R_2=1,X_1^{(1)},X_2^{(1)})\times \mathrm{OR}(R_2,R_3|X_1^{(1)},X_2^{(1)}). \end{gathered}$$

Note that $R_2⫫X_2^{(1)}|R_3$, $X_1^{(1)}$, and R₃ ⫫ R₁ | R₂, $X_1^{(1)}$, $X_2^{(1)}$. Therefore, $p(R_2|R_3=1,X_1^{(1)},X_2^{(1)})=p(R_2|R_3=1,X_1^{(1)})$ is identified the same way as described in Scenario 1, and $p(R_3|R_2=1,X_1^{(1)},X_2^{(1)})=p(R_3|R_1=1,R_2=1,X_1,X_2)$ is a function of the observed data and hence is identified. Now the identification of the joint density $p(R_2{R}_3|X_1^{(1)},X_2^{(1)})$ boils down to identifiability of the odds ratio term. By symmetry, we can express the odds ratio $\text{OR}(R_2,R_3|X_1^{(1)},X_2^{(1)})$ in two different ways,

$$\begin{gathered} \mathrm{OR}(R_2,R_3|X_1^{(1)},X_2^{(1)}) \\ =\frac{p(R_2|R_3,X_1^{(1)})}{p(R_2=1|R_3,X_1^{(1)})}\times \frac{p(R_2=1|R_3=1,X_1^{(1)})}{p(R_2|R_3=1,X_1^{(1)})} \\ =\frac{p(R_3|R_2,X_1^{(1)},X_2^{(1)})}{p(R_3=1|R_2,X_1^{(1)},X_2^{(1)})}\times \frac{p(R_3=1|R_2=1,X_1^{(1)},X_2^{(1)})}{p(R_3|R_2=1,X_1^{(1)},X_2^{(1)})}. \end{gathered}$$

The first equality holds by d-separation $(R_2⫫X_2^{(1)}|R_3,X_1^{(1)})$. This implies that $\text{OR}(R_2,R_3|X_1^{(1)},X_2^{(1)})$ is not a function of $X_2^{(1)}$. Let us denote this functional by $f_1(R_2,R_3,X_1^{(1)})$. On the other hand, we can plug-in R₁ = 1 to pieces in the second equality since $R_3\perp \perp R_1|R_2,X_1^{(1)}$, $X_2^{(1)}$ (by d-separation.) This implies that $\text{OR}(R_2,R_3|X_1^{(1)},X_2^{(1)})$ is a function of $X_1^{(1)}$ only through its observed values (i.e. X₁). Let us denote this functional by $f_2(R_2,R_3,X_1,X_2^{(1)},R_1=1)$. Since odds ratio is symmetric (by definition), then it must be the case that $f_1(R_2,R_3,X_1^{(1)})=f_2(R_2,R_3,X_1,X_2^{(1)},R_1=1)$; concluding that f₂ cannot be a function of $X_2^{(1)}$, as the left hand side of the equation does not depend on $X_2^{(1)}$. This renders f₂ to be a function of only observed quantities, i.e. f₂ = f₂(R₂,R₃,X₁,R₁ = 1). This leads to the conclusion that $p(R_2,R_3|X_1^{(1)},X_2^{(1)})$ is identified and consequently the missingness process p(R | X⁽¹⁾) in Fig. 1(a) is identified. According to Remarks 1 and 2, both the target and full laws are identified.

Adding any directed edge to Fig. 1(a) (including the dashed edge) allowed by missing data DAGs results in either a self-censoring edge $(X_i^{(1)}\to R_i)$ or a special kind of collider structure called the colluder $(X_j^{(1)}\to R_i\leftarrow R_j)$ in (Bhattacharya et al., 2019). We discuss in detail, the link between identification of missing data models of a DAG and the absence of these structures in Section 5.

Scenario 3.

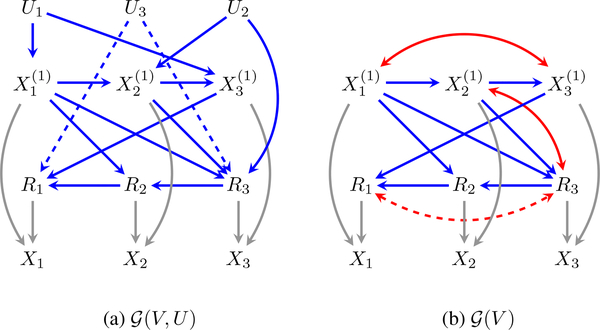
So far, the investigator has conducted preliminary analyses of the problem while ignoring the issue of unmeasured confounding. In order to address this issue, she first posits an unmeasured confounder U₁, corresponding to genotypic traits that may predispose certain individuals to both smoke and develop bronchitis. She posits another unmeasured confounder U₂, corresponding to the occupation of an individual, that may affect both the deposits of tar found in their lungs (for e.g., construction workers may accumulate more tar than an accountant due to occupational hazards) as well as limit an individual’s access to proper healthcare, leading to the absence of a diagnostic test for bronchitis.

The missing data DAG with unmeasured confounders, corresponding to the aforementioned hypothesis is shown in Fig. 2(a) (excluding the dashed edges). The corresponding missing data ADMG, obtained by latent projection is shown in Fig. 2(b) (excluding the dashed bidirected edge). A procedure to identify the full law of such an MNAR model, that is nested Markov with respect to a missing data ADMG, is absent from the current literature. The question that arises, is whether it is possible to adapt the odds ratio parameterization from the previous scenarios, to this setting.

Figure 2.

(a) The missing data DAG with unobserved confounders used in scenario 3 (without the dashed edges) and scenario 4 (with the dashed edges). (b) The corresponding missing data ADMGs obtained by applying the latent projection rules to the hidden variable DAG in (a).

We first note that by application of the chain rule of probability and Markov restrictions, the missingness mechanism still factorizes in the same way as in Scenario 2, i.e., $p(R|X^{(1)})=p(R_1|R_2,X_3^{(1)})\times p(R_2,R_3|X_1^{(1)},X_2^{(1)})$ (Tian & Pearl, 2002). Despite the addition of the bidirected edges $X_1^{(1)}\leftrightarrow X_3^{(1)}$ and $X_2^{(1)}\leftrightarrow R_3$, corresponding to unmeasured confounding, it is easy to see that the propensity score for R₁ is still identified via simple conditioning. That is, $p(R_1|{\text{pa}}_{\mathcal{G}}(R_1))=p(R_1|X_3,R_2,R_3=1)$ as $R_1⫫R_3|X_3^{(1)}$, R₂ by m-separation. Furthermore, it can also be shown that the two key conditional independences that were exploited in the odds ratio parameterization of p(R₂,R₃ | X⁽¹⁾), still hold in the presence of these additional edges. In particular, $R_2⫫X_3^{(1)}|R_3$, $X_1^{(1)}$ and $R_3⫫R_1|R_2,X_1^{(1)}$, $X_2^{(1)}$ by m-separation. Thus, the same odds ratio parameterization used for identification of the full law in Scenario 2, is also valid for Scenario 3. The full odds ratio parameterization of the MNAR models in Scenarios 2 and 3 is provided in Appendix B.

Scenario 4.

Finally, the investigator notices that a disproportionate number of missing entries for smoking status and diagnosis of bronchitis, correspond to individuals from certain neighborhoods in the city. She posits that such missingness may be explained by systematic biases in the healthcare system, where certain ethnic minorities may not be treated with the same level of care. This corresponds to adding a third unmeasured confounder U₃, which affects the ordering of a diagnostic test for bronchitis as well as inquiry about smoking habits, as shown in Fig. 2(a) (including the dashed edges.) The corresponding missing data ADMG is shown in Fig. 2(b) (including the bidirected dashed edge.) Once again, we investigate if the full law is identified, in the presence of an additional unmeasured confounder U₃, and the corresponding bidirected edge R₁ ↔ R₃.

The missingness mechanism p(R | X⁽¹⁾) in Fig. 2(b) (including the dashed edge) no longer follows the same factorization as the one described in Scenarios 2 and 3, due to the presence of a direct connection between R₁ and R₃. According to (Tian & Pearl, 2002), this factorization is given as $p(R|X^{(1)})=p(R_1|R_2,R_3,X_1^{(1)},X_2^{(1)},X_3^{(1)})\times p(R_2|R_3,X_1^{(1)})\times p(R_3|X_1^{(1)},X_2^{(1)})$. Unlike the previous scenarios, the propensity score of R₁, $p(R_1|R_2,R_3,X_1^{(1)},X_2^{(1)},X_3^{(1)})$, includes $X_1^{(1)}$, $X_2^{(1)}$, and R₃ past the conditioning bar. Thus, the propensity score of R₁ seems to be not identified, since there is no clear way of breaking down the dependency between R₁ and $X_1^{(1)}$. The problematic structure is the path $X_1^{(1)}\to R_3\leftrightarrow R_1$ which contains a collider at R₃ that opens up when we condition on R₃ in the propensity score of R₁.

In light of the discussion in previous scenarios, another possibility for identifying p(R | X⁽¹⁾) is through analysis of the odds ratio parameterization of the entire missingness mechanism. In Section 5, we provide a description of the general odds ratio parameterization on an arbitrary number of missingness indicators. For brevity, we avoid re-writing the formula here. We simply point out that the first step in identifying the missingness mechanism via the odds ratio parameterization is arguing whether conditional densities of the form p(R_i | R \ R_i = 1,X⁽¹⁾) are identified, which is true if $R_i⫫X_i^{(1)}|R\backslash R_i$, $X^{(1)}\backslash X_i^{(1)}$.

Such independencies do not hold in Fig. 2(b) (including the dashed edge) for any of the Rs, since there exist collider paths between every pair ($X_i^{(1)}$, R_i) that render the two variables dependent when we condition on everything outside $X_i^{(1)}$, R_i (by m-separation). Examples of such paths are $X_1^{(1)}\to R_3\leftrightarrow R_1$ and $X_2^{(1)}\leftrightarrow R_3\leftrightarrow R_1\leftarrow R_2$ and $X_3^{(1)}\to R_1\leftrightarrow R_3$.

In Section 6, we show that the structures arising in the missing data ADMG presented in Fig. 2(b) (including the dashed edge), give rise to MNAR models that are provably not identified without further assumptions.

5. Full Law Identification in DAGs

(Bhattacharya et al., 2019) proved that two graphical structures, namely the self-censoring edge $(X_i^{(1)}\to R_i)$ and the colluder $(X_j^{(1)}\to R_i\leftarrow R_j)$, prevent the identification of full laws in missing data models of a DAG. In this section we exploit an odds ratio parameterization of the missing data process to prove that these two structures are, in fact, the only structures that prevent identification, thus yielding a complete characterization of identification for the full law in missing data DAG models.

We formally introduce the odds ratio parameterization of the missing data process introduced in (Chen, 2007), as a more general version of the simpler form mentioned earlier in Eq. (1). Assuming we have K missingness indicators, p(R | X⁽¹⁾,O) can be expressed as follows.

$$\begin{gathered} p(R|X^{(1)},O)=\frac{1}{Z}\times \prod _{k=1}^{K}p(R_k|R_{-k}=1,X^{(1)},O) \\ \times \prod _{k=2}^K\text{OR}(R_k,R_{\prec k}|R_{\succ k}=1,X^{(1)},O) \end{gathered}$$ (2)

where R_−k = R \ R_k,R_≺k = {R₁, …, R_k−1},R_≻k = {R_k+1, …, R_K}, and

$$\begin{gathered} \mathrm{OR}(R_k,R_{\prec k}|R_{\succ k}=1,X^{(1)},O) \\ =\frac{p(R_k|R_{\succ k}=1,R_{\prec k},X^{(1)},O)}{p(R_k=1|R_{\succ k}=1,R_{\prec k},X^{(1)},O)} \\ \times \frac{p(R_k=1|R_{-k}=1,X^{(1)},O)}{p(R_k|R_{-k}=1,X^{(1)},O)}. \end{gathered}$$

Z in Eq. (2) is the normalizing term and is equal to ${\sum }_r\{{\prod }_{k=1}^{K}p(r_k|R_{-k}=1,X^{(1)},O)\times {\prod }_{k=2}^K\mathrm{OR}(r_k,r_{\prec k}|R_{\succ k}=1,X^{(1)},O)\}$.

Using the odds ratio reparameterization given in Eq. (2), we now show that under a standard positivity assumption, stating that p(R | X⁽¹⁾,O) > δ > 0, with probability one for some constant δ, the full law p(R, X⁽¹⁾,O) of a missing data DAG is identified in the absence of self-censoring edges and colluders. Moreover, if any of these conditions are violated, the full law is no longer identified. We formalize this result below.

Theorem 1.

A full law p(R, X⁽¹⁾,O) that is Markov relative to a missing data DAG $\mathcal{G}$ is identified if $\mathcal{G}$ does not contain edges of the form $X_i^{(1)}\to R_i$ (no self-censoring) and structures of the form $X_j^{(1)}\to R_i\leftarrow R_j$ (no colluders), and the stated positivity assumption holds. Moreover, the resulting identifying functional for the missingness mechanism p(R | X⁽¹⁾,O) is given by the odds ratio parameterization provided in Eq. 2, and the identifying functionals for the target law and full law are given by Remarks 1 and 2.

In what follows, we show that the identification theory that we have proposed for the full law in missing data models of a DAG is sound and complete. Soundness implies that when our procedure succeeds, the model is in fact identified, and the identifying functional is correct. Completeness implies that when our procedure fails, the model is provably not identified (non-parametrically). These two properties allow us to derive a precise boundary for what is and is not identified in the space of missing data models that can be represented by a DAG.

Theorem 2.

The graphical condition of no self-censoring and no colluders, put forward in Theorem 1, is sound and complete for the identification of full laws p(R,O, X⁽¹⁾) that are Markov relative to a missing data DAG $\mathcal{G}$.

We now state an important result that draws a connection between missing data models of a DAG $\mathcal{G}$ that are devoid of self-censoring and colluders, and the itemwise conditionally independent nonresponse (ICIN) model described in (Shpitser, 2016; Sadinle & Reiter, 2017). As a substantive model, the ICIN model implies that no partially observed variable directly determines its own missingness, and is defined by the restrictions that for every pair $X_i^{(1)}$, R_i, it is the case that $X_i^{(1)}⫫R_i|R_{-i}$ $X_{-i}^{(1)}$, O. We utilize this result in the course of proving Theorem 2.

Lemma 1.

A missing data model of a DAG $\mathcal{G}$ that contains no self-censoring edges and no colluders, is a submodel of the ICIN model.

6. Full Law Identification in the Presence of Unmeasured Confounders

We now generalize identification theory of the full law to scenarios where some variables are not just missing, but completely unobserved, corresponding to the issues faced by the analyst in Scenarios 3 and 4 of Section 4. That is, we shift our focus to the identification of full data laws that are (nested) Markov with respect to a missing data ADMG $\mathcal{G}$.

Previously, we exploited the fact that the absence of colluders and self-censoring edges in a missing data DAG $\mathcal{G}$, imply a set of conditional independence restrictions of the form $X_i^{(1)}⫫R_i|R_{-i}$, $X_{-i}^{(1)}$, O, for any pair $X_i^{(1)}\in X^{(1)}$ and R_i ∈ R (see Lemma 1). We now describe necessary and sufficient graphical conditions that must hold in a missing data ADMG $\mathcal{G}$ to imply this same set of conditional independences. Going forward, we ignore (without loss of generality), the deterministic factors p(X | X⁽¹⁾,R), and the corresponding deterministic edges in $\mathcal{G}$, in the process of defining this graphical criterion.

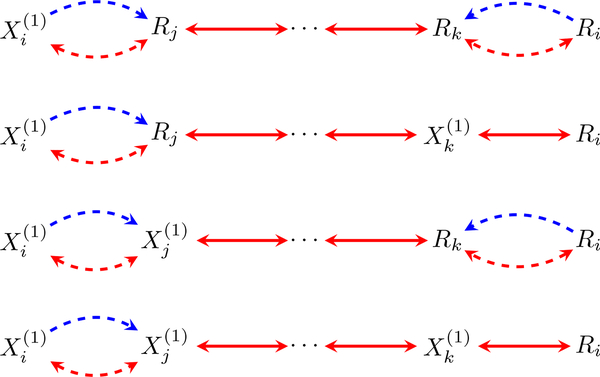
A colliding path between two vertices A and B is a path on which every non-endpoint node is a collider. We adopt the convention that A → B and A ↔ B are trivially collider paths. We say there exists a colluding path between the pair $(X_i^{(1)},R_i)$ if $X_i^{(1)}$ and R_i are connected through at least one non-deterministic colliding path i.e., one which does not pass through (using deterministic edges) variables in X.

We enumerate all possible colluding paths between a vertex $X_i^{(1)}$ and its corresponding missingness indicator R_i in Fig. 3. Note that both the self-censoring structure and the colluding structure introduced in (Bhattacharya et al., 2019) are special cases of a colluding path. Using the m-separation criterion for ADMGs, it is possible to show that a missing data model of an ADMG $\mathcal{G}$ that contains no colluding paths of the form shown in Fig. 3, is also a submodel of the ICIN model in (Shpitser, 2016; Sadinle & Reiter, 2017).

Figure 3.

All possible colluding paths between $X_i^{(1)}$ and R_i. Each pair of dashed edges imply that the presence of either (or both) result in formation of a colluding path.

Lemma 2.

A missing data model of an ADMG $\mathcal{G}$ that contains no colluding paths is a submodel of the ICIN model.

This directly yields a sound criterion for identification of the full law of missing data models of an ADMG $\mathcal{G}$ using the odds ratio parameterization as before.

Theorem 3.

A full law p(R,X⁽¹⁾,O) that is Markov relative to a missing data ADMG $\mathcal{G}$ is identified if $\mathcal{G}$ does not contain any colluding paths and the stated positivity assumption in Section 5 holds. Moreover, the resulting identifying functional for the missingness mechanism p(R | X⁽¹⁾,O) is given by the odds ratio parametrization provided in Eq. 2.

We now address the question as to whether there exist missing data ADMGs which contain colluding paths but whose full laws are nevertheless identified. We show (see Appendix for proofs), that the presence of a single colluding path of any of the forms shown in Fig. 3, results in a missing data ADMG $\mathcal{G}$ whose full law p(X⁽¹⁾, R,O) cannot be identified as a function of the observed data distribution p(X,R,O).

Lemma 3.

A full law p(R,X⁽¹⁾,O) that is Markov relative to a missing data ADMG $\mathcal{G}$ containing a colluding path between any pair $X_i^{(1)}\in X^{(1)}$ and R_i ∈ R is not identified.

Revisiting our example in scenario 4, we note that every $(R_i,X_i^{(1)})$ pair is connected through at least one colluding path. Therefore, according to Lemma 3, the full law in Fig. 2(a) including the dashed edge, is not identified. It is worth emphasizing that the existence of at least one colluding path between any pair $(R_i,X_i^{(1)})$ is sufficient to conclude that the full law is not identified.

In what follows, we present a result on the soundness and completeness of our graphical condition that represents a powerful unification of non-parametric identification theory in the presence of non-ignorable missingness and unmeasured confounding. To our knowledge, such a result is the first of its kind. We present the theorem below.

Theorem 4.

The graphical condition of the absence of colluding paths, put forward in Theorem 3, is sound and complete for the identification of full laws p(X⁽¹⁾,R,O) that are Markov relative to a missing data ADMG.

Throughout the paper, we have focused on identification of the full law which, according to Remark 1, directly yields identification for the target law. However, identification of the full law is a sufficient but not necessary condition for identification of the target law. In other words, the target law may still be identified despite the presence of colluding paths. Fig. 4(a) in (Bhattacharya et al., 2019) is an example of such a case where the full law is not identified due to the colluder structure at R₂; however, as the authors argue the target law remains identified.

7. Conclusion

In this paper, we concluded an important chapter in the non-parametric identification theory of missing data models represented via directed acyclic graphs, possibly in the presence of unmeasured confounders. We provided a simple graphical condition to check if the full law, Markov relative to a (hidden variable) missing data DAG, is identified. We further proved that these criteria are sound and complete. Moreover, we provided an identifying functional for the missingness process, through an odds ratio parameterization that allows for congenial specification of components of the likelihood. Our results serve as an important precondition for the development of score-based model selection methods that consider a broader class of missing data distributions than the ones considered in prior works. An interesting avenue for future work is exploration of the estimation theory of functionals derived from the identified full data law. To conclude, we note that while identification of the full law is sufficient to identify the target law, there exist identified target laws where the corresponding full law is not identified. We leave a complete characterization of target law identification to future work.