Linear Regression in Medical Research

Related Article, see p 110

KEY POINT:

Linear regression is used to quantify the relationship between ≥1 independent (predictor) variables and a continuous dependent (outcome) variable.

In this issue of Anesthesia & Analgesia, Müller-Wirtz et al¹ report results of a study in which they used linear regression to assess the relationship in a rat model between tissue propofol concentrations and exhaled propofol concentrations (Figure.

Figure.

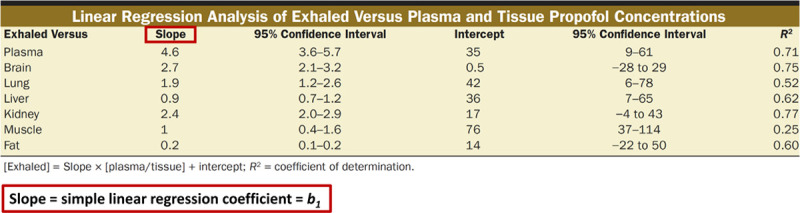
Table 2 given in Müller-Wirtz et al,¹ showing the estimated relationships between tissue (or plasma) propofol concentrations and exhaled propofol concentrations. The authors appropriately report the 95% confidence intervals as a measure of the precision of their estimates, as well as the coefficient of determination (R²). The presented values indicate, for example, that (1) the exhaled propofol concentrations are estimated to increase on average by 4.6 units, equal to the slope (regression) coefficient, for each 1-unit increase of plasma propofol concentration; (2) the “true” mean increase could plausibly be expected to lie anywhere between 3.6 and 5.7 units as indicated by the slope coefficient’s confidence interval; and (3) the R² suggests that about 71% of the variability in the exhaled concentration can be explained by its relationship with plasma propofol concentrations.

Linear regression is used to estimate the association of ≥1 independent (predictor) variables with a continuous dependent (outcome) variable.² In the most simple case, thus referred to as “simple linear regression,” there is only one independent variable. Simple linear regression fits a straight line to the data points that best characterizes the relationship

between the dependent (Y) variable and the independent (X) variable, with the y-axis intercept (b₀), and the regression coefficient being the slope (b₁) of this line:

A model that includes several independent variables is referred to as “multiple linear regression” or “multivariable linear regression.” Even though the term linear regression suggests otherwise, it can also be used to model curved relationships.

Linear regression is an extremely versatile technique that can be used to address a variety of research questions and study aims. Researchers may want to test whether there is evidence for a relationship between a categorical (grouping) variable (eg, treatment group or patient sex) and a quantitative outcome (eg, blood pressure). The 2-sample t test and analysis of variance,³ which are commonly used for this purpose, are essentially special cases of linear regression. However, linear regression is more flexible, allowing for >1 independent variable and allowing for continuous independent variables. Moreover, when there is >1 independent variable, researchers can also test for the interaction of variables—in other words, whether the effect of 1 independent variable depends on the value or level of another independent variable.

Linear regression not only tests for relationships but also quantifies their direction and strength. The regression coefficient describes the average (expected) change in the dependent variable for each 1-unit change in the independent variable for continuous independent variables or the expected difference versus a reference category for categorical independent variables. The coefficient of determination, commonly referred to as R², describes the proportion of the variability in the outcome variable that can be explained by the independent variables. With simple linear regression, the coefficient of determination is also equal to the square of the Pearson correlation between the x and y values.

When including several independent variables, the regression model estimates the effect of each independent variable while holding the values of all other independent variables constant.⁴ Thus, linear regression is useful (1) to distinguish the effects of different variables on the outcome and (2) to control for other variables—like systematic confounding in observational studies or baseline imbalances due to chance in a randomized controlled trial. Ultimately, linear regression can be used to predict the value of the dependent outcome variable based on the value(s) of the independent predictor variable(s).

Valid inferences from linear regression rely on its assumptions being met, including

• the residuals are the differences between the observed values and the values predicted by the regression model, and the residuals must be approximately normally distributed and have approximately the same variance over the range of predicted values;

• the residuals are also assumed to be uncorrelated. In simple language, the observations must be independent of each other; for example, there must not be repeated measurements within the same subjects. Other techniques like linear mixed-effects models are required for correlated data⁵; and

• the model must be correctly specified, as explained in more detail in the next paragraph.

Whereas Müller-Wirtz et al¹ used simple linear regression to address their research question, researchers often need to specify a multivariable model and make choices on which independent variables to include and on how to model the functional relationship between variables (eg, straight line versus curve; inclusion of interaction terms).

Variable selection is a much-debated topic, and the details are beyond the scope of this Statistical Minute. Basically, variable selection depends on whether the purpose of the model is to understand the relationship between variables or to make predictions. This is also predicated on whether there is informed a priori theory to guide variable selection and on whether the model needs to control for variables that are not of primary interest but are confounders that could distort the relationship between other variables.

Omitting important variables or interactions can lead to biased estimates and a model that poorly describes the true underlying relationships, whereas including too many variables leads to modeling the noise (sampling error) in the data and reduces the precision of the estimates. Various statistics and plots, including adjusted R², Mallows C_p, and residual plots are available to assess the goodness of fit of the chosen linear regression model.