Multi-contact 3C reveals that the human genome during interphase is largely not entangled

Abstract

During interphase the eukaryotic genome is organized into chromosome territories that are spatially segregated into compartment domains. The extent to which interacting domains or chromosomes are entangled is not known. We analyze series of co-occurring chromatin interactions using multi-contact 3C (MC-3C) in human cells to provide insights into the topological entanglement of chromatin. Multi-contact interactions represent percolation paths (C-walks) through 3D chromatin space. We find that the order of interactions within C-walks that occur across interfaces where chromosomes or compartment domains interact is not random. Polymer simulations show that such C-walks are consistent with distal domains being topologically insulated, i.e. not catenated. Simulations show that even low levels of random strand passage, e.g. by topoisomerase II, would result in entanglements, increased mixing at domain interfaces and an order of interactions within C-walks not consistent with experimental MC-3C data. Our results indicate that during interphase entanglements between chromosomes and chromosomal domains are rare.

INTRODUCTION

As cells exit mitosis the nucleus reforms and individual chromosomes decondense while maintaining their territorial organization ¹. Within each territory chromosomes become spatially compartmentalized: domains of active and inactive chromatin cluster together to form euchromatic A and heterochromatic B compartments, respectively. Interactions between chromosomes also develop where individual chromosome territories interact and where some level of apparent intermingling can be observed ². Similar to intra-chromosomal associations, inter-chromosomal contacts are enriched for interactions between domains of the same type (A-A and B-B interactions).

In the crowded chromatin environment of the nucleus any locally acting topoisomerase II enzymes could randomly pass strands through each other, which would lead to topological entanglements between chromatin from different chromosomes or from different domains within chromosomes producing catenations. Given sufficient time, this could lead to complete mixing of chromosomes reaching an equilibrium state ^3,4. Considerable theoretical analyses have explored how chromosomes can maintain individual and largely separate territories. In a simulation study by Rosa et al ⁴, segregation and unmixing of chromosomal domains were associated with two generic polymer effects: nuclear confinement (i.e. chromatin density) and topological disentanglement. It was suggested that the topologically disentangled state is the result of slow kinetics of chromatin relaxation after cells exit metaphase ⁴. The assumption was that the interphase nuclei is not equilibrated and behaves like a semi-dilute solution of unentangled ring polymers which are known to segregate due to topological constraints ^3-7. The enormous length of mammalian chromosomes makes the reptation time, i.e. the time for the ends of the linear chromosome to explore the nucleus, extremely long so that chromosomes, and chromosomal sub-domains, can effectively be treated as though they are ring polymers.

Despite the fact that nucleus-wide equilibration and mixing of chromosomes is prohibitively slow, localized Topoisomerase II – mediated interlinking between chromosomes and sub-chromosomal domains could still occur leading to increased mixing. Imaging experiments have shown that neighboring chromosome territories overlap to some extent at their borders and at these locations chromatin from different chromosomes appears to mix ⁸. However, it is not known whether this mingling is the result of formation of local entanglements due to topoisomerase II activity, or whether this level of mixing is consistent with the expected level of intermixing at the interface of two topologically closed chromosomes. Similarly, active and inactive compartment domains that can be located far apart along chromosomes cluster together to form euchromatic and heterochromatic compartments. Interactions between such distal domains are readily detected by chromosome conformation capture based methods ^9,10, but whether this involves or leads to topological entanglements and extensive mixing of the domains is not known.

Topological entanglements of chromatin fibers could create complications for any process acting on the genome including transcription, replication and chromosome condensation and segregation. However, the extent to which chromosome entanglements form during interphase is not known because experimentally detecting such topological features of chromosomes has not been technically possible. Here we show that detection of strings of co-occurring chromatin interactions in single cells using Multi-Contact 3C (MC-3C) can reveal the extent to which catenations between chromosomes and between chromosomal domains occur. Comparing experimental MC-3C data with polymer simulations we find that chromosomes and chromosomal compartments are consistent with a model of the genome in which the genome is largely devoid of entanglements.

RESULTS

Multi-contact 3C

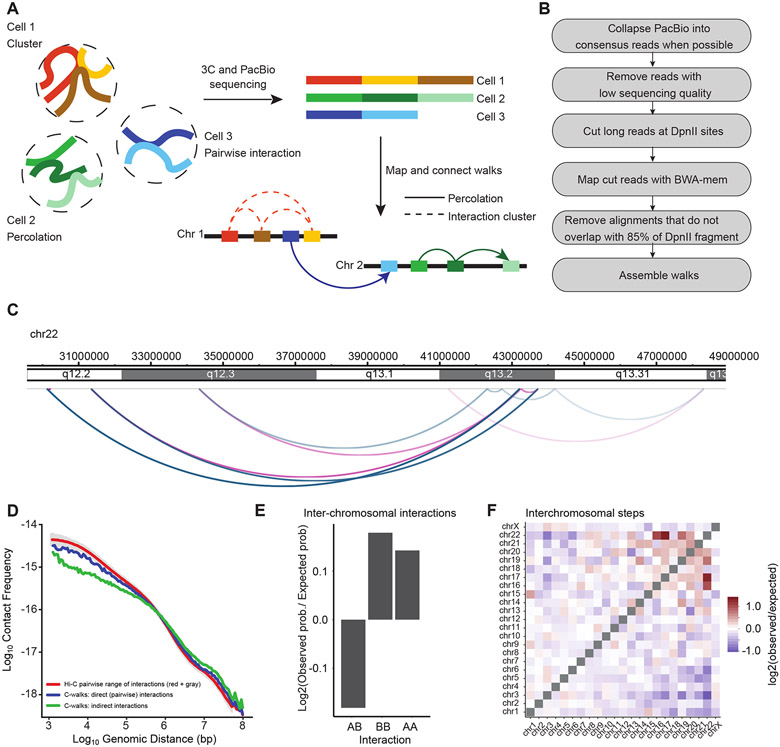
We implemented Multi-contact 3C (MC-3C) an experimental method and corresponding polymer simulations to detect and analyze sets of multi-contact chromatin interactions that occur in single cells. The method is based on conventional chromosome conformation capture (3C) ¹¹ and the C-walk and multi-contact 4C approaches developed earlier ^12-14. 3C performed with the restriction enzyme DpnII produces long ligation products where multiple restriction fragments become ligated together to form DNA molecules that can be >6 kb long, and that are mostly linear (Extended Data Figure 1). Such long linear strings of ligation products (referred to as C-walks ¹³) can represent clusters of loci that interact simultaneously with each other in single cells (“clusters”, Figure 1A). C-walks can also represent connected paths of pairwise interactions where fragment 1 interacts with fragment 2, which in turn interacts with fragment 3 while fragments 1 and 3 do not directly interact (Figure 1A). Such connectivity can occur in highly connected interaction networks where each pair of loci can be linked through any number of indirect interactions, referred to as interaction or bond percolation ¹⁵. Here we will treat C-walks as “percolation paths” to reflect the fact that they can, and often do (see below) represent series of linked fragments.

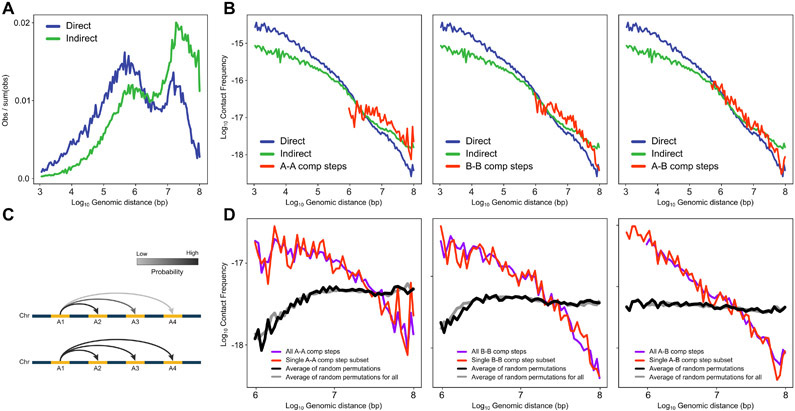
Figure 1:

Outline of MC-3C. A: Schematic of the MC-3C approach. By performing PacBio sequencing on the products of a 3C experiment fragments that belong to the same interaction cluster or percolation path are captured as chimeric long reads. B: Computational pipeline used to process PacBio reading reads to generate C-walks. C: Example of a C-walk. Red arcs represent steps in the positive direction (in the direction of the right telomere of the chromosome) and blue arcs represent steps in the negative direction (in the direction of the left telomere of the chromosome). The steps get darker during the walk. D: Interaction frequency as a function of genomic distance for direct contacts in C-walks (26,603 interactions), indirect contacts in C-walks (32,244 interactions), and down sampled Hi-C (26,603 interactions). Grey shade represents the variance in the Hi-C data when P(s) is calculated for diferente samples of 26,603 Hi-C interactions. E. Comparison of inter-chromosomal A-A, B-B and A-B interactions. An expected probability of A-A, B-B and A-B interactions was calculated from all detected fragments that participate in inter-chromosomal interactions and compared to the observed proportion of interactions and converted to a base-2 logarithm. The positions of A and B compartments were calculated by principal component analysis of Hi-C data binned at 250 kb resolution ¹⁰. The expected A-A, B-B and A-B interactions that would occur by random chance were calculated by multiplying the proportion of A and B fragments present in the observed C-walks. F. Observed/expected number of inter-chromosomal steps. Small chromosomes preferentially interact. The expected values were calculated in the same manner as panel E but considering only inter-chromosomal interactions. Source date for panels d and e are available online.

To identify the restriction fragments that make up each string of ligation products, DNA generated with 3C was sequenced on a Pacific Biosciences RS II DNA sequencer. Sequence reads were split in individual restriction fragments by computationally splitting reads at DpnII sites. Individual sections were then mapped to the human genome sequence hg19 (¹⁶, Figure 1B). The result is a set of C-walks similar to the one depicted in Figure 1C. For details on the mapping procedure and filtration of the multi-contact fragments see Methods. Each walk is an ordered set of interactions – here named steps – that connect fragments that are located on the same chromosome or on different chromosomes. The physical dimensions of such paths within the cell nucleus are probably in the range of up to several hundred nm: a C-walk where fragments interact end-to-end and combined is 6 kb would maximally be around several hundred nm long (assuming a contour length of the chromatin fiber of 40 nm/kb ¹⁷) but will likely occupy a volume with a smaller diameter.

We applied MC-3C to exponentially growing HeLa S3 cells that are mostly in interphase. After processing and pooling data obtained from 2 independent biological replicates, we obtained a set of 118,154 interphase C-walks. To verify the quality of the data we first treated the interactions as pairwise data including only direct interactions that are between adjacent fragments within the C-walks. We plotted their interaction frequency (P) as a function of genomic distance (s, in bp) between the loci (Figure 1D). P(s) for direct C-walk interactions is similar to that obtained from a conventional Hi-C dataset. Interestingly, P(s) for indirect interactions within C-walks, where all pairwise combinations of fragments within a C-walk are considered an interaction, deviates from the P(s) of direct interactions in C-walks and pairwise Hi-C data (Figure 1D). There is generally a shift to longer-range interactions, and a reduction in shorter-range interactions. This observation indicates that indirect interactions are not equivalent to direct interactions and therefore that the order of fragments in C-walks is not random. This implies that C-walks are not reflecting sets of chromatin segments that all interact with each other simultaneously as in the cluster model.

Interaction interfaces between chromosomes are relatively smooth

We first explored the subset of C-walks that include interactions between two different chromosomes, as these sets of co-occurring interactions could provide insights into the structure of the interface where two chromosome territories touch. Similar to previous analyses of C-walks ¹³, and to be conservative, we removed C-walks that include interactions between more than 2 chromosomes because some of these could be the result of random ligation events (48% of inter-chromosomal C-walks). The remaining inter-chromosomal C-walks (42,851 in total) reproduce known features of inter-chromosomal interactions such as enrichment of interactions between A and between B compartments (Figure 1E) and of inter-chromosomal interactions between small, gene-rich chromosomes, as previously described in Hi-C experiments ¹⁰ (Figure 1F).

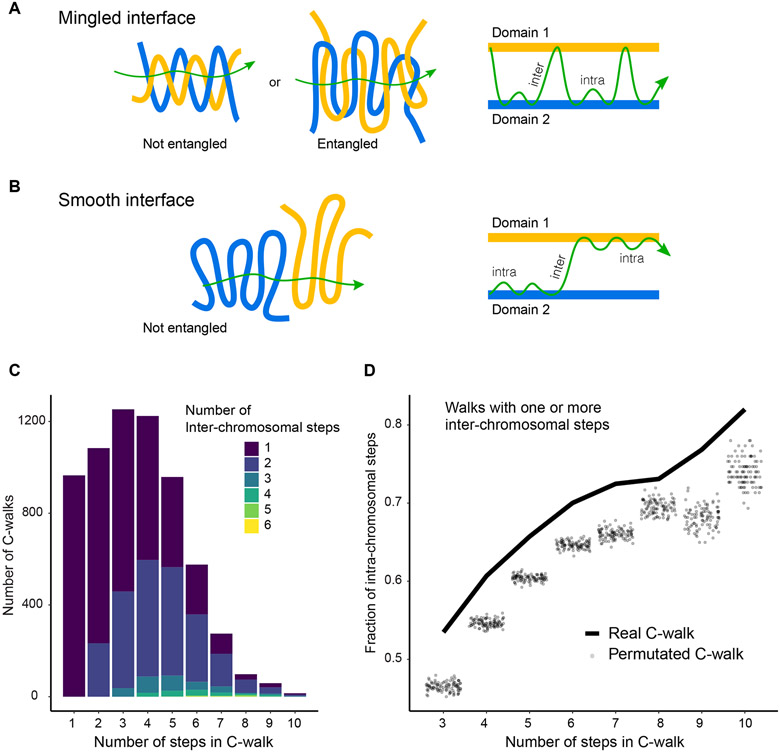
We were interested to determine whether the string of ligation products forming inter-chromosomal C-walks would provide information about the nature, structure and roughness of the interface of two chromosome territories. If at the interface of two territories loci from each chromosome freely mix, we expect to see multiple inter-chromosomal steps within each C-walk, and loci from the two chromosomes could potentially be ligated in any order (Figure 2A). Two types of intermingling are possible and highlighted in Figure 2A. In one case the two domains are entangled and in the other, two separate domains could extensively invade the same connected volume region without being topologically entangled. Indeed, polymer interfaces can have a very large surface area relative to their volume without being topologically linked. In contrast when the two territories are proximal but do not locally mix or interlink, e.g. there is a rather smooth interface, we would expect far fewer steps between the two chromosomes per inter-chromosomal C-walk, while observing many intra-chromosomal steps connecting loci within each of the territories (Figure 2B).

Figure 2:

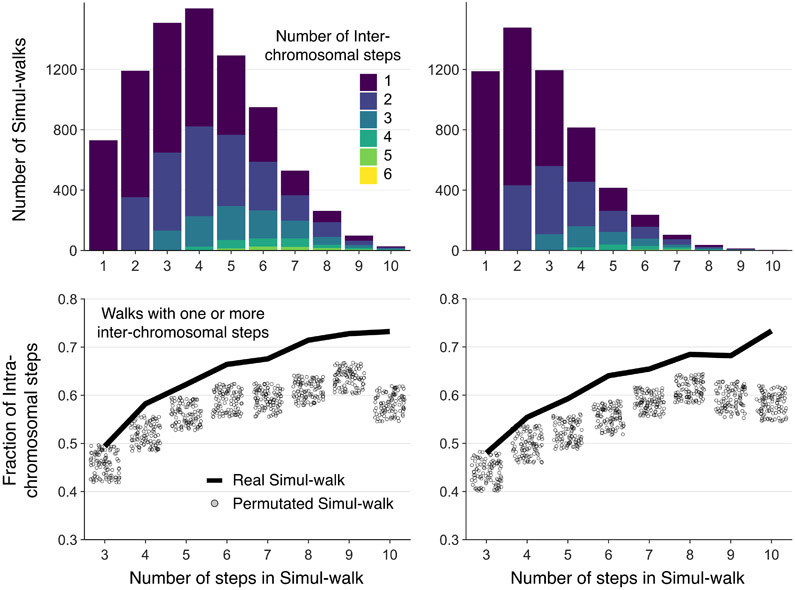
Inter-chromosomal interfaces show limited mixing. A, B: Schematic of how mingled and smooth interfaces would be captured in multi-contact data. In a mingled interface (top row) a C-walk would contain many steps between the two domains, as schematically indicated on the right. In a smooth interface the C-walk would contain series of steps within one domain and only occasionally contain a step between the two. Here, domains are any two distinct chromosomes or two distal A and/or B compartments located on the same chromosome. In general, any two chromatin regions which are not neighbors along the linear genome but are spatially proximal would qualify as (interacting) domains in this picture. C: Stacked barplots with the number of C-walks containing at least one inter-chromosomal step separated by the number of steps between two chromosomes (in colors) and the number of steps (along the x-axis) that they contain. Most inter-chromosomal C-walks contain only one or two inter-chromosomal step. D: Proportion of intra-chromosomal steps in the set of C-walks with one or more inter-chromosomal steps, separated by the total number of steps in each C-walk. The solid line shows the proportion for real C-walks. The dots correspond to the same proportion in 100 sets of permutated walks. The observed C-walks have a higher proportion of intra-chromosomal steps than would expected if the order of the steps was random. Sum of p-values is less than 10⁻⁷. Source data for panels c and d area available online.

We performed two analyses to distinguish between these possibilities. First, we determined the number of inter-chromosomal steps that occur within each inter-chromosomal C-walk (Figure 2C). Interestingly, most inter-chromosomal C-walks only have 1 or 2 inter-chromosomal steps, even for long C-walks, with the remaining steps before or after this step occurring between fragments contained within either territory. C-walks of increasing length tend to add mostly intra-chromosomal steps, and as a result the percentage of intra-chromosomal steps per C-walk increases as compared to shorter C-walks (Figure 2D). Second, we explored whether the order of the fragments within each C-walk mattered. For this analysis we only used inter-chromosomal C-walks for which all fragments could be mapped. We created 100 sets of permutations (for each set of C-walks of length n (number of steps)) in which we randomized the order of DpnII fragments within observed inter-chromosomal C-walks, and then for each permutated set again calculated the percentage of intra-chromosomal steps per C-walk. We find that real C-walks have more intra-chromosomal steps than permutated walks, for C-walks of all lengths (Figure 2D). The same phenomenon is observed when C-walks were analyzed separately for inter-chromosomal interfaces between two A domains, two B domains or between an A and a B domain (Extended Data Figure 2). Importantly, one implication of this result is that the order of fragments in C-walk ligation strings is meaningful and that they do not simply represent clusters of fragments that all interact with each other at the same time. Instead, C-walks likely represent percolation paths. We call all C-walks between chromosomes or domains with only one inter-chain crossing a “pure” percolation path. Fraction of such walks in the MC-3C datasets is given in Supplementary Table 1. The statistical significance of the deviation in the order of walks between the experimental C-walks (observed) as compared to the permutated sets (expected for random mixing) is measured by a non-parametric chi-square goodness of fit test and shown by sum of p-values for walks of different sizes. The smaller the sum of p-values, the smaller the extent to which chromosomes are mixed (Supplementary Table 1).

The explanation for the observation that randomizing the order of steps within inter-chromosomal C-walks leads to lower numbers of intra-chromosomal steps is that in real C-walks steps within each chromosome are clustered together to form continuous intra-chromosomal sub-walks, and the C-walk only infrequently crosses from one chromosome territory to another. This suggests a rather smooth interface between chromosomes.

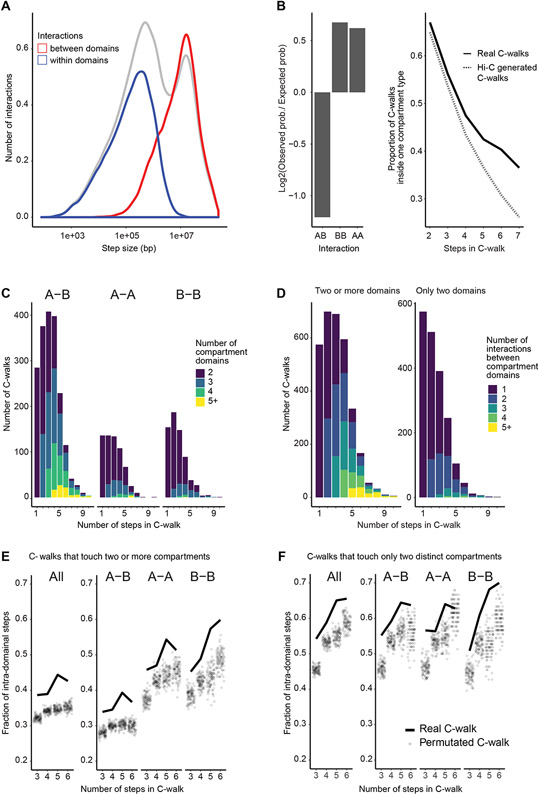
Within chromosomes distal compartment domains interact but mingle less than expected

Next, we explored properties of C-walks that occur entirely within chromosomes. We find a bimodal distribution in step sizes, with enrichment of steps in the range of hundreds of kb, and in the range of several Mb (Figure 3A, gray line). Such distribution has been observed before ¹³. The shorter-range steps involve interactions between fragments located within a single compartment domain (either A or B; Figure 3A, blue line), while the longer-range steps involve interactions between loci located in different compartment domains (either A-A, B-B, or A-B interactions; Figure 3A, red line). 43.4% of all intra-chromosomal steps involve interactions between fragments located in different compartmental domains, and 87% of all intra-chromosomal C-walks involve more than one compartmental domain, indicating extensive contact between distal compartment domains. As expected, we find that interactions between two A compartment domains or two B compartment domains occur more frequently than interactions between an A and a B compartment (Figure 3B).

Figure 3:

Intra-chromosomal interfaces between compartment domains show limited mixing. A: Density plot of the distance of all (gray line), intra-domain (blue line) and inter-domain interactions (red line, including A-A, B-B and A-B interactions). The area under the gray curve of all interactions has been adjusted so that it is double of the area under the curve of the each of the red and blue lines. B: Left panel: Comparison of A-A, B-B and A-B interactions. An expected probability of A-A, B-B and A-B interactions was calculated from all detected fragments that participate in intra-chromosomal interactions and compared to the observed proportion of interactions and converted to a base-2 logarithm. Right panel: For each number of steps, the proportion of C-walks that only contact domains of one compartment type (A or B) was calculated for experimental multi-contact data (full line) and for a set of computationally generated C-walks that was produced from sampling pairwise Hi-C data (dotted line). C: Stacked barplots with the number of compartment domains traversed by intra-chromosomal C-walks that visit 2 or more domains. These are separated by the number of steps in the C-walk on the x-axis and further separated into subplots that show C-walks that traverse both A and B domains (A-B), only A domains (A-A) and only B domains (B-B). D: Stacked barplots showing the number of intra-chromosomal C-walks that visit exactly two distinct domains (right subplot) and for intra-chromosomal walks that visit two or more distinct domains (left subplot) with 1, 2, 3, 4 and five or more inter-domain steps, separated on the x-axis by the total number of steps in a C-walk. E: Proportion of intra-domain steps in C- walks that visit two or more domains, separated on the x-axis by the total number of steps in each C-walk (solid line) compared to the same calculation done on 100 sets of permutated walks (semi-opaque dots). This was done for all the C-walks that touch two or more domains (on the left), and separately for those that visit both A and B domains (A-B), those that visit only A domains (A-A) and those that visit only B domains (B-B). F: Same as panel E but using the set of C-walks (and corresponding permutations) that visit only two compartment domains. Sum of p-values is less than 10⁻⁵. Source data are available online.

We computationally generated a comparable set of intra-chromosomal walks by sampling from pairwise Hi-C data (see Methods). We find that for any given number of steps, C-walks are more likely to stay within the same compartment type – visiting just A or just B compartment territories – than the Hi-C derived C-walks (Figure 3B, right panel). This again indicates that steps in C-walks are inter-dependent, consistent with previous comparisons between multi-contact data and pairwise data ¹³.

C-walks that involve interactions between two compartmental domains represent sets of interactions at the interface where two or more of these domains touch. We first determined the number of distinct compartment domains that are captured within the subset of intra-chromosomal C-walks that involve interactions between at least 2 distinct compartment domains. We find that such C-walks can involve interactions between up to as many as 11 distinct compartment domains (Figure 3C). Such C-walks often are between sets of either A or B domains, as would be expected, but with one or a few steps in a compartment domain of opposite type mixed in. We noticed that such domains of opposite type tend to be located directly adjacent in the linear genome to one of the other compartment domains of concordant type that are part of the same C-walk. This indicates these are likely not random ligation events. When we analyze C-walks that exclusively involve only A or only B compartment domains, we find that such inter-compartment C-walks typically contain fragments from up to 4 distinct domains (Figure 3C).

To test whether the order of fragments in intra-chromosomal C-walks matters we again employed permutations. We randomized the order of fragments within C-walks that involve at least two compartment domains along the same chromosome (irrespective of compartment type, Figure 3D left plot) and calculated the number of steps that occur within individual compartment domains (Figure 3E). We find that real C-walks have more intra-compartment domain steps than randomized C-walks. This was found for C-walks that include fragments from both A and B compartments, only A compartments or only B compartments (Figure 3E). Similar results were found when we restricted our analysis to C-walks that involve only two compartment domains (A-A, B-B and A-B interactions; Figure 3F). In the Extended Data Figure 3 we rule out the possibility that the relatively infrequent inter-domain steps are the result of random ligation events.

The fact that real C-walks display more intra-compartment domain steps suggests limited mixing of chromatin at the interface of two interacting compartment domains so that for each locus the nearest neighbor tends to be located within the same compartment domain, similar to what we observed for chromosomal interfaces.

Simulations show MC-3C data are consistent with unentangled chromosome and domain interfaces

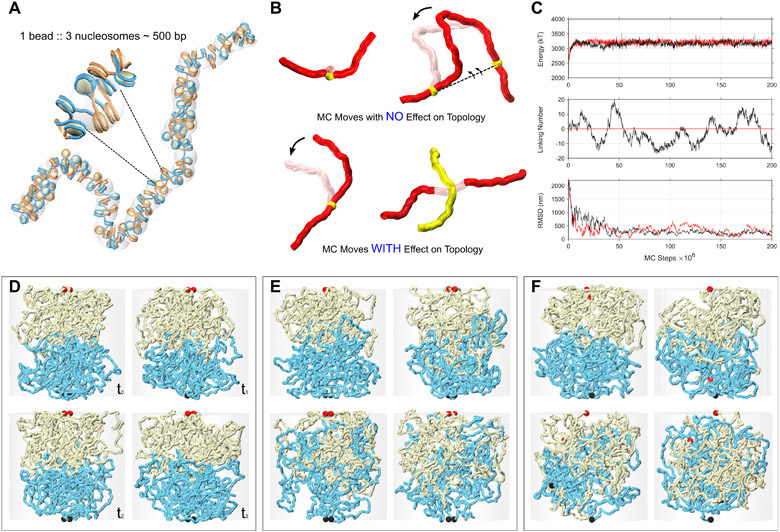
The limited mixing of chromatin from different chromosomes or sub-chromosomal domains could reflect a lack of topological entanglement. Topological entanglement would increase the mixing at the interface ^3,18. To test this hypothesis, we performed coarse-grained simulations of chromosome and domain interaction interfaces with and without topological entanglements and then determined how topological differences at the interface affect chromatin mixing and the composition of C-walks.

We first simulated chromatin domains as topologically closed polymers (Extended Data Figure 4). In these simulations the ends of each polymer, each representing a chromosomal domain located on the same or on different chromosomes, were held together making them effectively rings. For sufficiently long polymers, local sub-chains can be treated as topologically closed systems ¹⁹. Weak attractions between monomers were included to simulate the attractive forces leading the A and B compartment formation ^20,21, although including these did not affect the results (Extended Data Figure 5). We also tested the effect of chromatin density (from dilute to crowded) but found that this did not affect the results either (Extended Data Figure 5). Simulations included sufficient numbers of Monte Carlo steps to reach equilibrium (Extended Data Figure 4-C). Figure 4A shows the interface between two topologically closed polymers in yellow and cyan, reflecting two interacting chromosomal domains that can be located along the same chromosome or on different chromosomes. Unlinking is guaranteed by keeping the domain ends, shown in red and black ball pairs, fixed and proximate. This snapshot shows that after millions of Monte Carlo steps, the two domains remain largely unmixed.

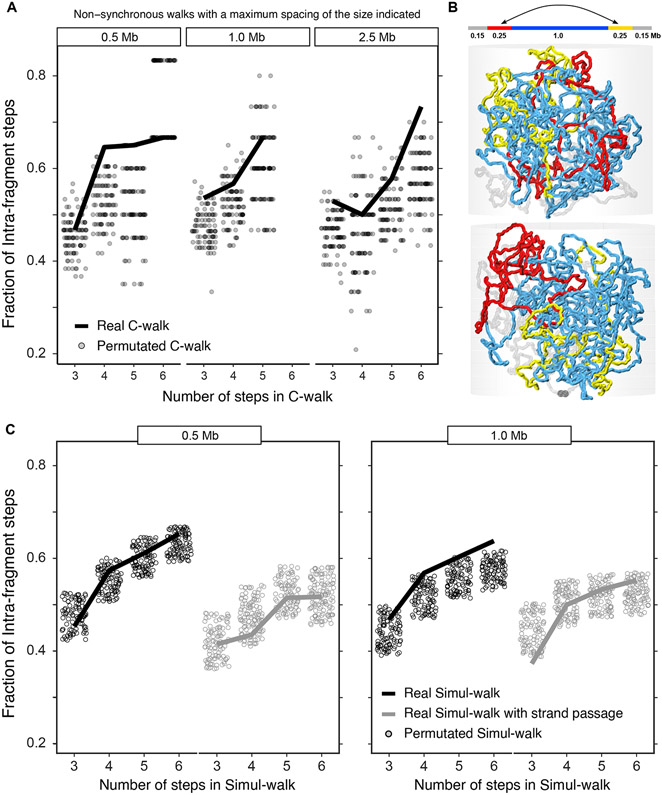
Figure 5:

Distal parts within the same compartment domain can show considerable mixing but may also have low levels of strand crossing. A. Analysis of C-walks connecting two segments of 250 kb each, spaced by 0.5, 1.0 and 2.5 Mb, that are contained within a single compartment domain. The proportion of intra-segment steps in this set of C-walks is shown, separated by the total number of steps in each C-walk. Very few C-walks had more than 6 steps and are left out. The solid line shows the proportion for experimental C-walks. Grey dots correspond to the same proportion in 100 sets of permutated walks. B. (Top) Schematic depiction of the polymer chain used for simulations in the middle and lower panels. (Middle, Bottom) Snapshots of the system. C. Analysis of simul-walks obtained with polymer simulations depicted in B with and without strand passage. The statistics of simul-walks without strand passage most resemble experimental C-walks shown in A. Sum of p-values for each individual subplot is given in Supplementary Table 1. Source data are available online.

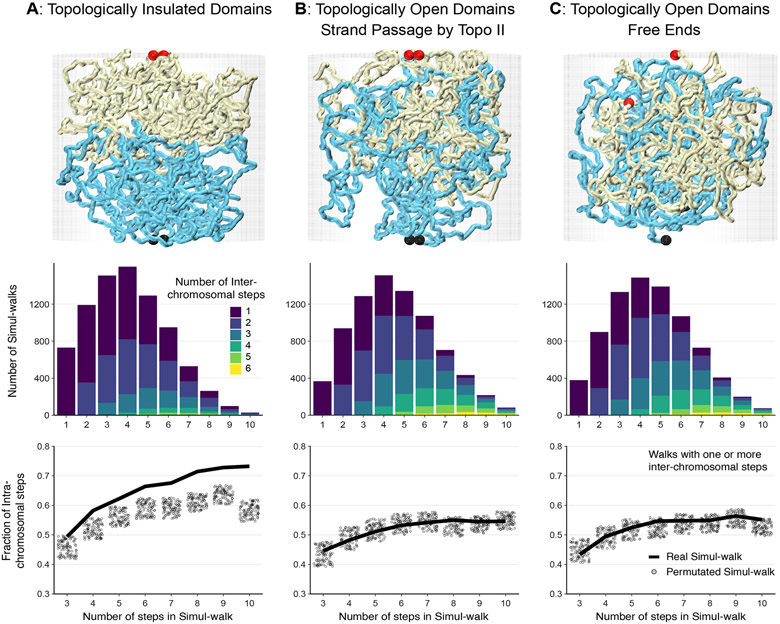
Figure 4:

Impact of topological linking and entanglement on mixing at compartment domains or chromosomal interfaces. (Top) Simulations were performed on three types of interfaces: (A) Topologically unlinked domains, (B) Topologically linked domains via strand-passage, and (C) Topologically open domains via free-end movements. Chains are shown in yellow and cyan with ends highlighted by the red and black balls. The interface remains smooth and unmixed for the topologically insulated domains in panel A, while the two topologically open domains in panels B and C exhibit considerable mingling. The interface mixing of the simulated chains is quantified by computationally generating percolation paths (simul-walks) similar to the C-walks obtained by MC-3C. (Middle) The number of inter-chomosomal (or inter-domain) steps that occur within each inter-chain simul-walk is presented. . (Bottom) The fraction of intra-domain steps in simul-walks with at least one inter-domain interaction is shown in solid black lines (compare to Figure 2D and Figure 3E, F for C-walks). The unmixed interfaces in simulation A demonstrate a higher fraction of intra-domain steps in simul-walks with at least one inter-domian crossing. Randomly permutating those same simul-walks results in a lower fraction of intra-domain steps shown by gray dots. In contrast, for the mixed and catenated interfaces in simulations in panels B and C, the fraction of intra-domain steps in simul-walks is indistinguishable from permutated simul-walks indicating extensive mixing. Sum of p-values for the unmixed interfaces in simulation A is <10⁻⁸ while in B and C it is 1.15 and 0.45 respectively. Source data are available online.

Next we simulated C-walks as percolation paths through the simulated polymer systems (see Methods). Briefly, we randomly chose a location along either of the two polymers and then stepped with a given step size (r_cutoff = 75 nm) to a proximal polymer section. We generated a collection of simulated C-walks (simul-walks) in this manner and selected the subset that contained at least one inter-domain step. We then performed the same set of analyses and permutations on this sub-set of inter-domain (or inter-chromosomal) simul-walks as we did for experimental C-walks (Figures 2 and 3). The number of inter-domain steps that occur within inter-domain simul-walks are shown in the middle row in Figure 4. Interestingly, most inter-domain simul-walks contain only 1 or 2 inter-domains steps, very similar to what we found in the experimental C-walks between chromosomes and between compartment domains within chromosomes (Figures 2 and 3). When we permutated the steps within this set of simul-walks we observed a reduction in the number of intra-domains steps, corresponding to more inter-domain steps (Figure 4A, bottom). This simulation reproduces very closely what we observed when we permutated experimental C-walks (Figure 2 and Figure 3). The results from the simulations did not change when we used different sizes of the steps (r_cutoff) for calculating simul-walks (Extended Data Figure 6).

When we performed this analysis for polymer systems that were topologically open (Figure 4B and 4C) we obtained very different results. First, in the presence of strand passage or free movement of ends of the interacting domains, we observed extensive mixing and catenation of the two interacting polymers (Figure 4B, 4C, top row; Extended Data Figure 4-C) ²². Second, simul-walks generated under these conditions displayed features very different from experimental C-walks. The number of simul-walks with 1 inter-domain step decreased, while walks with 3, 4, 5 and 6 inter-domain steps increased dramatically (Figure 4B and 4C, middle row). Permutating steps within these simul-walks did not change the number of intra-domain steps, consistent with the observation that the domains are extensively mixed (Figure 4B and 4C, top row). Combined these analyses indicate that experimental C-walks are most consistent with data predicted from models without entanglements between chromosomes or between compartment domains.

Analysis of C-walks contained within compartment domains

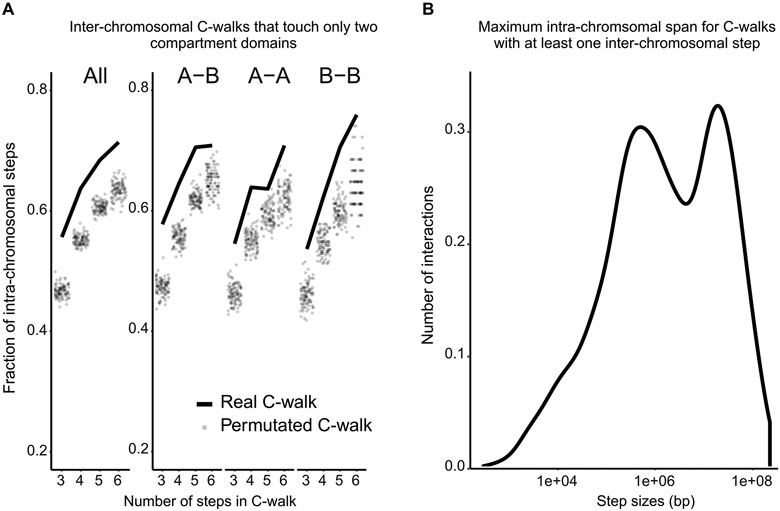
To measure the level of mixing of chromatin within compartment domains we analyzed C-walks that involve interactions between two segments of 250 kb each that are separated by 0.5, 1.0 and 2.5 Mb, and that are both contained within the same compartment domain. This analysis allows investigation of the extent to which two distal chromatin segments within a single compartment domain mix. In Figure 5, we plotted the fraction of intra-segmental steps as a function of the length of the C-walk and compared this to permutated C-walks, exactly as we did for intra-chromosomal C-walks that connect different compartment domains. We observed that the fraction of intra-segmental steps in the majority of permutated C-walks is lower than for experimental C-walks, but that there is overlap as well. This indicates that segments separated by 0.5 – 1.5 Mb but located within the same compartment domain display considerable mixing as previously suggested by super-resolution microscopy for neighboring domains and subdomains of a few hundred kb in size ²³.

To determine the extent to which mixing is expected to occur at this length scale, and how this depends on allowing strand passage, we performed the following simulations. Compartment domains were simulated as circular molecules within a confined space (semi-dilute regime, Extended Data Figure 5). We performed Monte Carlo simulations with (topologically open) or without (topologically closed) strand passage. Figure 5B shows simulation snapshots in the absence of strand passage with the two 250 kb segments highlighted in red and yellow and the middle 1.0 Mb region in cyan. Snapshots show that inside a domain the chromatin is mixed and that the two 250 kb segments are not long enough to produce blob-like conformations that would make them impenetrable with respect to each other. On the other hand, the 1.0 Mb cyan region produces a topological blob and barrier for mixing with the rest of the chromatin. These simulations show that chromatin at short length scales (hundred of kb) is a random polymer chain which readily mingles while at larger scales (Mb) chromatin resembles a collection of unmixed neighboring blobs with their surfaces in smooth contact.

We then calculated simul-walks through these polymer conformations and selected simul-walks that involved at least one step between the two distal segments of 250 kb that are separated by 0.5 or 1.0 Mb (red and yellow domains, separated by cyan segment in Figure 5B). We then calculated the fraction of such intra-segmental steps in these simul-walks and compared that to the fraction of intra-domain steps observed after permutating the simul-walks (Figure 5C). We observe that for domains separated by 0.5 Mb the fraction of intra-segmental steps in simul-walks is comparable to that for permutated simul-walks, both in the absence or presence of strand passage. This indicates that domains that are separated by relatively small distances (0.5 Mb) readily mingle even in the absence of strand passage.

Next, we analyzed simul-walks and permutated simul-walks that involve interactions between segments separated by 1.0 Mb. As expected, in the presence of strand passage the fraction of intra-segmental steps in simul-walks is comparable to that of permutated simul-walks, indicating extensive mixing of the segments. However, in the absence of strand passage, the fraction of intra-segmental steps for permutated simul-walks is in the majority of cases lower than for the simul-walks. This indicates that segments separated by 1.0 Mb can mix to some extent even in the absence of strand passage, but that strand passage leads to more extensive mixing. Comparing the results from the simul-walks to those for experimental C-walks we note that the observations with experimental C-walks (including for segments separated by 0.5 Mb) most resemble those of the simul-walks obtained from simulations for domains separated by 1.0 Mb in the absence of strand passage. This suggests that distal regions within compartment domains mix to some extent but less than expected from simulations where loci can mix freely as a result of strand passage.

DISCUSSION

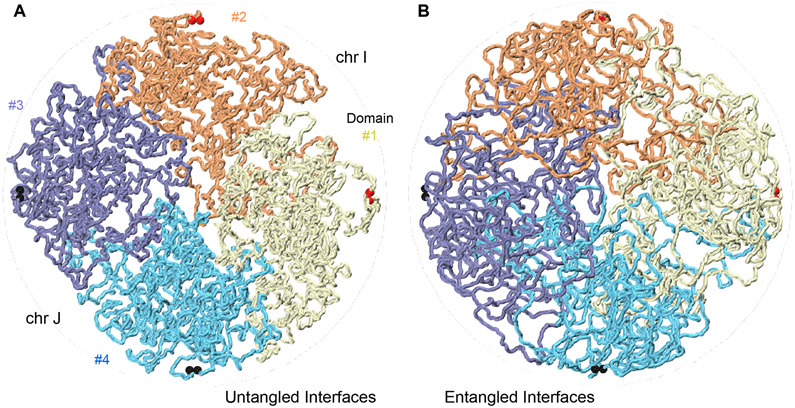
We present experimental data that show that the interphase genome is largely not topologically entangled. A summary of our findings is depicted in Figure 6. Figure 6A portrays chromatin as an organization of largely unentangled blob-like domains in a semi-crowded condition with rather smooth interfaces. Figure 6B illustrates the same domains with a large degree of entanglement, such that the boundaries between domains and between chromosomes fade away. Experimental inter-chromosomal and inter-compartment domain C-walks are consistent with a picture of the genome where topological entanglements between chromosomes and between compartment domains are rare, as illustrated in Figure 6A. At shorter length scale, e.g. within compartment domains and in the absence of active mechanisms, we found that chromatin becomes mixed to some extent even without allowing strand passage. These findings are consistent with prior models of fractal globules ¹⁰, and blob-like globular domains ²⁴.

Figure 6:

Chromatin is an organization of largely untangled blob-like domains squeezed together under a semi-crowded condition with rather smooth interfaces. A. A simulation snapshot of four domains #1 to #4, two pairs from different chromosomes I and J, pushed together in a cylindrical container under semi-dilute conditions. The interfaces are smooth and untangled. Panel B shows the same system, allowing strand passage. Chromatin domains diffuse and fuse into each other and distinct chromosomal and domain interfaces, visible in A, fade away.

Although theoretical considerations and polymer simulations had suggested that chromosomes would display low levels of entanglement in cycling cells for kinetic reasons, it has proven difficult to experimentally assess the topological state of the genome in cells directly. Previous studies employed multi-contact data to explore the presence of sub-nuclear compartments ²⁵, and to test whether interactions between genes and regulatory elements occur in hubs or in pairs ^12-14. Here we find that the overall statistics of the composition and order of multi-contact data can also provide insights into the topological nature of the interfaces between chromosomes and chromosomal domains revealing that chromosomal entanglements are rare. Similarity of the statistics between experimental C-walks and the simul-walks shows that the two major factors responsible for the smooth interfaces between domains and chromosomes are nuclear crowding (confinement) and topological disentanglement. However, unlike previous reports ⁴, we observe these phenomena even under well-equilibrated conditions for the typical domain sizes in contact. Similar to previous reports, the unmixing applies to a wide range of domain sizes ⁷.

Lack of entanglements within contiguous domains of up to several Mb was recently reported by Goundaroulis and co-workers using an entirely independent approach: their re-analysis of oligo-paint serial fluorescent labeling data from Bintu and colleagues ^26,27 indicates chromatin domains can be largely knot free, at least for the relatively small subset of cells where the chromatin fiber could be reliably traced ²⁷. They did not investigate the extent to which different chromosomes or different compartments domains are entangled.

Previous imaging studies found that chromosome territories overlap at least partially ^2,8. Combined with our data these observations indicate that chromatin fibers, or chromosomal domains from one chromosome can locally invade another territory to some extent, but apparently without becoming topologically linked. The overlap between chromosome territories observed microscopically occurs at a length-scale of several microns, while percolation paths studied here are probably in the range of hundreds of nanometers. It will be interesting to acquire much longer C-walks that cover up to microns in 3D space to determine whether any additional architectural features of territory boundaries can be detected. This will require isolating much longer 3C ligation products, combined with very long read sequencing platforms such as nanopore sequencing.

In a crowded environment of the nucleus, and with topoisomerase II acting locally to randomly pass strands, chromosomes would form a highly entangled and knotted state, at least at their interfaces ²⁸. Our data support a very different state during interphase in which entanglements between chromosomes and compartment domains are rare. How is frequent entanglement prevented when topoisomerase II is abundantly present? One possibility is that topoisomerase II is acting only rarely throughout the genome during interphase. During mitosis entanglements between sister chromatids, that are naturally formed during DNA replication, and any interlinks between different chromosomes must be removed to facilitate accurate chromosome segregation and this requires extensive topoisomerase II activity ²⁹. As a result, as cells exit mitosis the genome is initially largely disentangled. If topoisomerase II activity is greatly reduced as cell enter G1 then reformation of the interphase genome conformation in the absence of strand passage would prevent entanglements from forming. However, there is evidence that Topoisomerase II is acting throughout the genome in interphase. Topoisomerase II-mediated breaks can readily be detected at CTCF sites and gene promoters ^30,31. Thus, it appears other processes must act to ensure that entanglements are prevented or are selectively removed, possibly by making topoisomerase II act not randomly so that it is directed towards disentanglement. Recent theoretical analyses have demonstrated that a process of loop formation through chromatin extrusion that strictly acts in cis will lead to a largely disentangled genome ^32-34. Polymer simulations have shown that formation of arrays of loops during mitosis will drive segregation and decatenation of sister chromatids ^35,36. Similar extrusion processes in interphase are predicted to position linkages and crossings between and along chromosomes such that topoisomerase II action will remove these links leading to topological simplification ^33,34.

Cohesin complexes have been proposed to extrude loops in vivo during interphase, while condensin complexes generate dense arrays of extruded loops in mitosis. The process of loop extrusion in interphase was first proposed based on patterns of Hi-C data representing topologically associating domains (TADs) and detection of loops between convergent CTCF sites ^37-41, while loop extrusion has been a logical mechanism for generating arrays of loops observed along mitotic chromosomes ^42-46. Recent in vitro experiments have demonstrated that cohesin and condensin complexes indeed can extrude ^47-50. These observations provide support for the model in which loop extrusion events can guide topoisomerase II activity to generate and maintain a largely decatenated genome. MC-3C combined with polymer simulations can provide a powerful experimental approach to assess the topological state of chromosomes, e.g. as cells progress through the cell cycle, and in cases where cells display a variety of chromosome folding defects.

METHODS

Cell Culture

Hela S3 cells (ATCC CCL-2.2; tested and found to be mycoplasma free) were cultured in Dulbecco’s Modified Eagle Medium (DMEM, Gibco, 10569044) supplemented with 10% Fetal Bovine Serum (Gibco, 16000), 100 U/ml penicillin (Gibco, 15140) and 100 μg/ml streptomycin (Gibco, 15140) at 37°C and 5% CO2.

Multi-contact 3C protocol

In situ Chromosome conformation capture (3C) was performed as previously described ¹¹, with modifications described in Belaghzal et al. ⁵¹. In this in situ variant digestion and ligation occurs within permeabilized cells. Briefly, cells were washed with HBSS (Gibco, 14025092), cross-linked with 1% formaldehyde (Fisher, BP531) for 10 minutes at room temperature. Crosslinking was quenched by addition of glycine to a final concentration of 125 mM and cells were incubated for 5 minutes at room temperature, followed by incubation on ice for 15 minutes. Aliquots of 5 million cross-linked cells were lysed by incubation in lysis buffer (10 mM Tris-HCl (pH=8.0), 10 mM NaCl, 0.2% Igepal CA-630) supplemented with Halt protease inhibitor (Thermo Fisher, 78429) for 15 minutes on ice. Cells were disrupted with a dounce homogenizer using pestle A (2× 30 strokes). A final concentration of 0.1% SDS was added and extracts were incubated at 65°C for 10 minutes. SDS was quenched by addition of with Triton X-100 to a final concentration of 1%. Chromatin was then digested with 400 U DpnII (NEB, R0543) at 37°C overnight. After enzyme inactivation by incubation at 65°C for 20 minutes, DNA ligation was performed by addition of 10 μL T4 DNA ligase (NEB, M0202) and incubation at 16°C for 4 hours. Crosslinking was reversed by addition of 50 μl proteinase K (10mg/ml) (Invitrogen, 25530031) followed by incubation at 65°C for 2 hours, followed by another addition of 50 μL proteinase K (10mg/ml) and overnight incubation at 65°C. DNA was isolated by 1:1 phenol/chloroform (Fisher, BP1750I) extraction followed by ethanol precipitation. RNA was removed by addition of and 1 μL RNase (1 mg/ml; Sigma, 10109169001) and incubation at 37°C for 30 minutes. Prior to sequencing on Pacbio RS II the 3C library was size-selected with Bluepippin.

Determination of topology of 3C ligation products

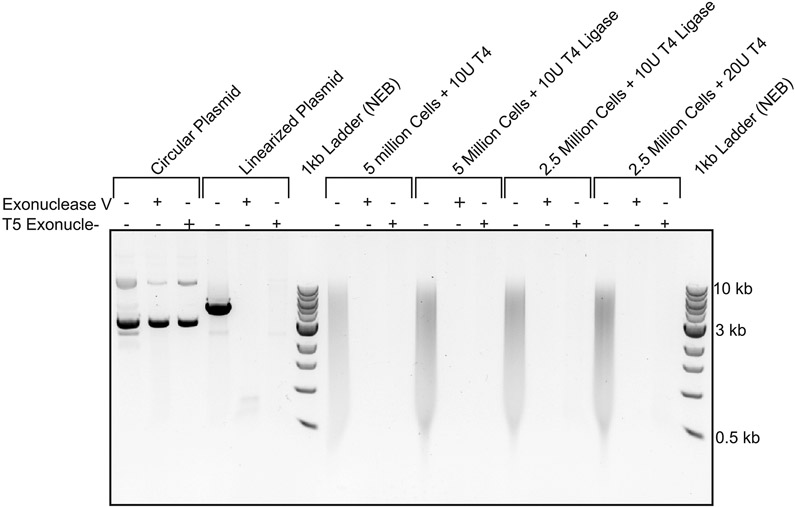
Pacbio sequencing relies on adapter ligation and therefore any circular ligation products in 3C libraries could not be sequenced. To assess whether strings of 3C ligation products are linear or circular we treated 3C libraries with exonuclease V (NEB, M0345) or T5 exonuclease (NEB, M0363). These nucleases only degrade linear DNA. As a control plasmid pCMV6 plasmid (4.6kb) was linearized by digestion with NdeI (NEB, RO111). 180 ng control linearized plasmid DNA and 180 ng of 3C library was treated with either 0.5 Unit exonuclease V (NEB, M0345) or 0.5 Unit T5 exonuclease (NEB, M0363) at 37°C for 30 minutes. Degradation of DNA was then analyzed by running samples on a 0.8% Agarose gel. Both exonucleases degraded the linearized plasmid and the 3C ligation product library indicating 3C products are linear. Circular plasmid DNA was not degraded (Extended Data Figure 1).

PacBio library preparation

Samples for PacBio library preparation were size selected into two groups of small (3-6 kb) and large (6 kb) molecules. Libraries were constructed using the PB Express 2.0 Kit according to the manufacturer’s instructions and sequenced in a PacBio RSII instrument.

Data processing

Extract consensus reads of insert and quality filter

To identify the restriction fragments that make up each string of ligation products, DNA generated with 3C was sequenced on a Pacific Biosciences RS II DNA sequencer. To improve the quality of sequencing error-prone PacBio reads we used the SMRT Analysis v 2.2.0 package (PacBiosciences) to obtain consensus sequences when the same molecule was sequenced more than once and to remove reads with low quality. Only reads of insert with a quality threshold over 80 were selected. Sequence reads were split in individual restriction fragments by computationally splitting reads at DpnII sites. Individual sections were then mapped to the human genome sequence (hg19) using BWA-mem. Two adjacent fragments within one C-walk that map to two adjacent restriction fragments in the genome were merged and treated as a single fragment as they are likely partial digestion products. We further excluded reads that map to <85% of a restriction fragment or that visit the same fragment more than once. Fragments that could not be uniquely mapped were kept as steps in the C-walk. This is because C-walks can contain fragments that are not unique in the genome, e.g. a fragment from a LINE or SINE element. Such fragments cannot be uniquely mapped, but they still represent interactions. The result is a set of C-walks.

Virtually digest reads at GATC sites

The extracted reads of insert were virtually cut at the sequence sites recognized by DpnII (GATC) using BioPython scripts.

Map reads with BWA-MEM

Cut reads were mapped using bwa-mem ¹⁶, with default parameters. Pairs of reads that are consecutive on the PacBio molecule and that align with 85% of a genomic DpnII fragment are counted as a direct interaction, or a step. When two adjacent fragments map to two adjacent DpnII fragments in the genome they were merged as these may represent partial digestion products. The different steps that come from a single PacBio molecule constitute a walk. If there was an unmapped cut read in the middle of a walk, a NA was inserted. Walks that visit the same DpnII genomic fragment more than once were filtered out. For downstream analysis two sets of walks were used: those with NA fragments and those without. The number of walks that visit each chromosome and compartment type are shown in the Supplementary Table 2.

It is known that the HeLa genome contains numerous translocations and chromosomal fusions. To rule out that results are affected by chromosomal rearrangements, we have repeated all analyses using only the subset of chromosomes that are structurally intact (as we did in Naumova et al. ⁵²). This reduces the number of C-walks greatly, but all results are unaffected.

C-Walks generated from Hi-C data

C-walks were computationally generated from non-synchronous HeLa S3 pairwise Hi-C data. The Hi-C experiment was performed as described ^51,53. For each computationally generated walk, one 1 kb bin from chromosome 4 was selected at random. Then, a new fragment was randomly selected from the set of cis interactions of that bin in the Hi-C dataset, excluding the immediate neighbors. From this second fragment the same selection was done, and so on until walks with the desired number of steps were generated. Computationally generated walks were made so that they had the same number of step distribution as the experimental C-walks.

Permutated C-walks

Permutated walks were generated by taking all the fragments involved in a C-walk and randomly rearranging the order of the fragments in the walk. One hundred permutations were done per walk. Only C-walks with no NAs were used.

Contact Probability for C-walks and down- sampled Hi-C data

To calculate the contact frequency (P) as a function of genomic distance s we used pair of interacting loci mapped to autosomal chromosomes only. As comparison, HeLa S3 Hi-C data was down-sampled for autosomal chromosomes only for 200 times to obtain sets of equal number of interactions as number of directed by MC-3C (Direct interactions: 101,521; indirect interactions: 219,966). Interactions were selected for genomic distances starting at 1 kb up to 100 Mb using log-binning. The observed number of interactions in each genomic distance bin was divided by total number of possible interactions for in each genomic distance bin.

Compartment calls

A-B-compartmentalization profile was calculated by principle component analysis of Hi-C dataset obtained from non-synchronized HeLa S3 cultures binned at 250 kb resolution. The first eigenvector represents the A-B-compartmentalization.

Statistical significance

The distribution of inter-chromosomal steps that occur within each inter-chromosomal C-walk (Figure 2C) is quite different for experimental C-walks (observed) as compared to the permutated sets (expected for random mixing). The significance of this difference can be measured by a non-parametric chi-square goodness of fit test. The number of inter-chain crossings that occur within each C-walk of a given number of steps, are the categories in the chi-square test. For example, in Figure 2C, the number of observed inter-chain crossings for all walks of size 6 are {1:217, 2:294, 3:35, 4:25, 5:4, 6:1}; in which the first number is the number of crossings and the second one is their abundance (shown by stacked bar in the figure). In the permutated (expected) set, the distribution becomes {1:131, 2:325, 3:59, 4:44, 5:14, 6:3}. A chi-square test reveals that the significance of this difference is less than p₆ = 10⁻¹⁰. The sum of p-values for all step sizes greater than 2 (Σ_i>2 p_i) is considered as the statistical significance of our observation and the degree of unmixing between domains. The smaller the sum of p-values, the smaller the extent to which chromosomes are mixed. The sum of p-values for all the data presented in this manuscript is given in Supplementary Table 1.

Polymer simulations and generation of simul-walks

To better understand the geometry and mixing at the interface of two interacting compartment domains (within or between chromosomes), we simulated the interaction of two domains of length 1.5 Mb using polymer modeling. Polymers were represented as a chain of monomers with harmonic bonds and a bending persistence length of 40 nm, a repulsive excluded volume potential, and an additional small short-range repulsion/attraction (representative of good versus bad solvent conditions) between and across both domains. We typically simulated two 3,000 monomer chains, with one monomer corresponding to 0.5 kb (~3 nucleosomes), with the width of 30 nm and the bead to bead distances corresponding to an average nucleosome density of 2.5 nucleosomes per 11 nm ¹⁷. The main simulator is written in Python with the intensive potential function calculations being done through a FORTRAN to Python interface wrapper. The details of coarse-graining, energy terms, Monte Carlo moves, and equilibration tests are given in Extended Data Figure 4.

Three types of domain-domain interfaces were simulated. (1) Topologically insulated domains with fixed-ends and no strand-passage allowed. (2) Topologically open domains with fixed-ends but with strand-passage allowed. This mimics the activity of the Topoisomerase II enzyme, and (3) topologically open domains with no strand-passage but with freely moving ends. All simulations were started from a non-mingled state with the two domains being pushed towards each other along a cylindrical axis of symmetry.

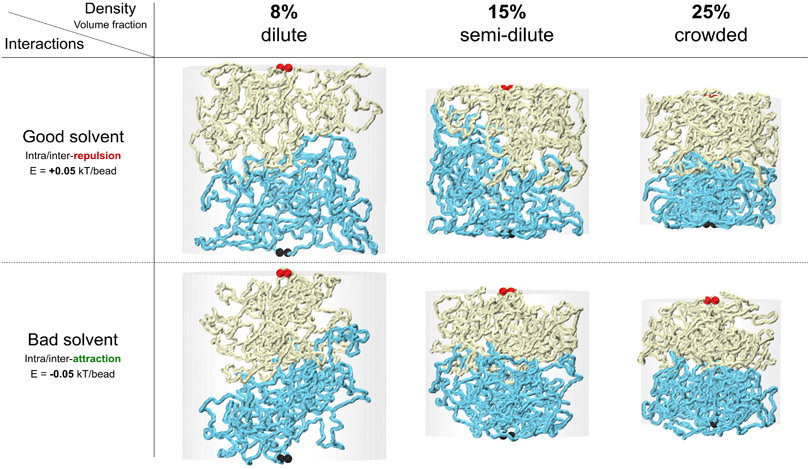
For every condition, 200 million Monte Carlo steps were performed. From the final 150 million equilibrated steps, 1,000 uncorrelated snapshots of the system were used for statistical averaging and analysis of interaction simul-walks. The results shown, in the main figures, correspond to semi-dilute conditions with a chromatin-chromatin self-interaction energy of E_attraction = – 0.05 k_BT/bead. This weak self-attraction (or bad solvent condition) can give rise to compartmentalization ²¹. Using good solvent conditions along with the different levels of crowding produced similar interface mixing behavior as shown in Extended Data Figure 5.

To generate an ensemble of multi-contact walks from the simulations, referred to as simul-walks, the following steps were performed: Step 1: from a random snapshot of the Monte Carlo ensemble choose one random position on a random chain. Step 2: from the spatially close neighbors to this point, within a cut off distance (r_cutoff) and NOT from the nearest neighbors along the same chain, choose one interaction partner. Step 3: continue step 2 until no new neighbor is available within r_cutoff to interact with. This is considered one simul-walk. Step 4: Repeat from step 1. From this simul-walk ensemble, histogram of the inter-chromosomal or inter-domain steps and the fraction of intra-chromosomal or intra-domain steps in the walks with at least one inter-chromosomal or inter-domain crossing, are calculated. We checked that the statistics of simul-walks are independent of the parameters such as r_cutoff (Extended Data Figure 6). Note that two adjacent fragments within an experimental C-walk that map to two adjacent restriction fragments in the genome were merged and treated as a single fragment. Similarly, ignoring the neighboring fragments in making the simul-walks in step 2, was done to mimic this merger step. Moreover, in the 3C procedure, it is protein-DNA complexes that are being ligated together. The size of the protein complexes can vary and on average the contact radius in 3C is thought to be ~50–100 nm. This again limits the ligation of the immediate neighbors in the genome.

Reporting Summary statement:

Further information on experimental design is available in the Nature Research Reporting Summary linked to this article

CODE AVAILABILITY

The C-walk assembly pipeline and scripts necessary to generate all plots are available on https://github.com/dekkerlab/MC-3C_scripts

DATA AVAILABILITY

The PacBio dataset is available on GEO under accession number GSE146945. Source data are available with the paper online.

Extended Data

Extended Data Fig. 1. Analysis of DNA sizes in control circular DNA, control linear DNA and 3C library DNA before and after exonuclease digestion.

Agarose gel analysis (0.8% agarose) of DNA size of control circular plasmid DNA, control linear plasmid DNA and of 3C library DNA before and after exonuclease digestion. 3C library and control plasmid DNA were digested with Exonuclease V and T5 exonuclease to determine whether 3C ligation products are linear or circular. In the presence of either exonuclease dsDNA will be digested, and circular DNA will remain present. As control both exonucleases are shown not to digest circular plasmid (pCMV6, 4.6kb) (lane 1-3), whereas linearized plasmid was digested (lane 4-6). Different concentration of 3C library and ligase did not result in detection of circular ligation products as no DNA was detected after exonuclease treatment (lanes 7-18). Markers: 1 kb ladder (New England Biolabs).

Extended Data Fig. 2. Statistics of the inter-chromosomal C-walks.

Additional analyses of inter-chromosomal C-walks. A. Proportion of inter-chromosomal steps for C- walks that visit only two distinct compartment domains, separated on the x-axis by the total number of steps in each C-walk (solid line). These are compared to the inter-chromosomal steps after permutating this set of C-walks (dots). This was done for all the walks that touch two domains (on the left), and separately for those that visit one A and one B domain (A-B), those that visit two A domains (A-A) and those that visit two B domains (B-B). B. Density plot of the maximum intra-chromosomal span (largest intra-chromosomal distance between fragments that make up a C-walk) for inter-chromosomal C-walks.

Extended Data Fig. 3. Ruling out the impact of random ligation events.

Frequency of intra- and inter-domain interactions as a function of the genomic distance. Most long-range interactions are inter-domain steps. We considered the possibility that the inter-domain steps are experimental noise due to random ligation events that do occur with some frequency in 3C-based experiments. To investigate this, here, we determined whether inter-domain steps display the expected inverse relationship with genomic distance that separates the loci. We find that the frequency of inter-domain steps decays rapidly. Such distance-dependent decay would not be expected if these interactions were the result of random ligation. A. Density of interactions corresponding to Figure 1D with logarithmic binning similar to Bonev et al. (54). This graph shows clearly that indirect interactions are more long range. B. Contact probability profiles for steps in walks with single inter-compartment step (A-A, B-B, A-B). These steps follow a similar distance decay as direct and indirect interactions. This shows that inter-compartment steps are not random ligation events. C. Schematic of inter-domain interactions with (upper) or without (lower) distance decay. D. Observed distance decay scaling for C-walks with inter-compartment steps and the permutated versions of those walks. Left Panel (A-A): All inter-compartment A-A steps (purple; 2,980 interactions from all C-walks that contain one or more inter-compartment steps) and single inter-compartment A-A (red; 936 interactions from C-walks that contain only a single inter-compartment step). Middle Panel (B-B): All B-B steps (purple; 2,720 interactions) and single B-B (red; 882 interactions). Right Panel (A-B): All A-B steps (purple; 5,655 interactions) and single A-B (red; 1,392 interactions). The permutated walks mimic the effect of random ligation between distal domains. Randomized walks generate flat scaling profiles not consistent with the observations.

Extended Data Fig. 4. Details of the polymer simulations.

Details of the Monte-Carlo approach used to study the interface of interacting chromosomal domains in contact. A. Coarse-graining is done at the level of chromatin fibers with the diameter of ~25 – 30 nm. Every ~3 nucleosomes are considered one bead with the bead to bead bond distance of ~15 nm at equilibrium and the bending persistence length of 40 nm ⁵⁵. A hard-core excluded volume and a short-range pairwise interaction with the form E_pairwise = q × exp[−2(r - σ)² / σ²)] is considered, in which, σ is the diameter of the beads and “q” is a small negative/positive charge depending on the attraction/repulsion between the beads. B. Monte Carlo is used because it is much more effective in sampling the phase space of possible conformations. Two types of Monte Carlo moves are possible. Those which don’t change the topology (i.e. the linking or knotting state) of the system and those which do. Top two moves, i.e. a single bead random movement and a crank-shaft rotation between two randomly chosen points along the chain, do not cause strand passage and do not move the relative position of the chain ends, hence do not affect the topology. Random rotations around a single point and/or brief random ghosting (no excluded volume) of parts of the chromatin fiber allow for relative movement of the ends and/or strand-passage, and thereby affect the topology. C. Equilibration for the case with topologically closed domains is presented in red. Equilibration for the case with topologically open domains with fixed-ends but with strand-passage is presented in black. Energy and linking number approach equilibrium after a few millions Monte Carlo steps. Linking number or number of entanglements is always an integer and remains zero for the case with topologically closed domains. RMSD values measured between two distal parts of a chain are shown. It takes up to ~50 million steps for the system to relax in a dynamic-globule structure. We call this a dynamic-globule because even at equilibrium, fluctuations in the distance between two regions on the same chain remain considerable (≈±100 nm). D. Simulation snapshots for the case of topologically closed domains with fixed-ends and no strand-passage in “Monte Carlo” time from t₀ to t₃. The interface between the two domains remains unmixed. E. Simulation snapshots for the case of topologically open domains with fixed-ends but with strand-passage allowed. This mimics the activity of the Topo II enzyme. Mixing increases gradually as a function of the Monte Carlo time. Note that the domain ends, highlighted with red and black ball pairs, do not move. F. Simulation snapshots for the case of topologically open domains with no strand-passage but with freely moving ends. Domains mingle gradually as a function of the Monte Carlo time.

Extended Data Fig. 5. Simulation snapshots for domain interfaces at different solution conditions.

Equilibrated simulation snapshots for domain interfaces at different solution conditions. Two major determinants of polymer mixing are (1) whether polymer prefers to interact with the solvent (good solvent) or to interact with itself (bad solvent). This can be simulated effectively by a repulsive/attractive short-range interaction between the chain’s beads. Both conditions might be present in the nucleus leading to microphase separation of chromatin into euchromatin versus heterochromatin domains; and (2) the density of the polymer mixture, here simulated by the confining cylindrical walls surrounding the two chains. Our simulations at different solvent and under different crowding conditions still show that domains that are topologically unlinked will barely mix and retain their smooth interfaces. The result might be different for the good solvent in ultra-dilute condition, in which, domains will barely touch and won’t generate measurable multi-contact walks. We believe this condition is not relevant to the chromatin in vivo and would not be consistent with our MC-3C data.

Extended Data Fig. 6. Simul-walks statistics not dependent on the selected percolation parameters.

Simul-walks statistics do not change considerably by changing the selected percolation parameter r_cutoff (Left: r_cutoff = 75 nm, Right: r_cutoff = 60 nm). The left panel is shown in the main Figure 4 because the r_cutoff is chosen in such a way that the maximum number of steps in simul-walks in the histogram is ~3-4 which is similar to the peak in the histogram of C-walks in Figure 2C. Regardless, the top two histograms show that most walks still involve only 1 or 2 inter-chromosomal or inter-domain interactions. At the bottom, the shift between the simul-walks (black solid lines) and randomly permutated versions (circles) remains the same as well. The r_cutoff value cannot be changed much more than this, because the minimum center to center distance of two touching beads is ~50-60 nm and choosing larger cutoffs will result in skipping some neighboring chains in the percolation path search. Therefore, our results are independent of the parameters we used to find the simul-walks.

Supplementary Material

1

Supplementary Table 1 Sum of p-values of a chi-square statistics test on the significance of “number of inter-chain steps in walks” versus their “permutated versions” as a measure for degree of mixing in C-walks or simul-walks. Stacked bar plots (e.g. main Figures 2 and 4) represent the distribution of number of inter-chain steps in walks (observed). These distributions change considerably when the walks are randomized (expected) as described in the Methods. Chi-Square goodness of fit test is a non-parametric test that is used to find how the observed value is significantly different from the expected value. It is a good test specially when the sample data is divided into categories. In this test the numbers of points that fall into each category (here each category is defined by the number of inter-domain or inter-chromosomal steps) are compared with the expected numbers of points in each category. Analysis is done for all the walks containing at least 3 steps and the calculated p-values are summed up for all possible steps (usually maximum 6 or 10 steps are counted). The smaller the sum of p-values the more significant the degree of unmixing is. The sum of p-values for the inter-chromosomal C-walks of Figure 2, <10⁻⁷, the topologically insulated simul-walks of Figure 4, <10⁻⁸, and the inter-domain walks of Figure 3F, <10⁻⁵, show considerable unmixing. Simul-walks with strand passage or free ends have large p-values, i.e. considerable mixing. The p-values corresponding to the distal parts within the same compartment domain (related to Figure 5 data) are in the intermediate range. Overall the distal parts within the same domain are mixed, and mixing increases if strand-passage is allowed. The sum of p-values for the experimental C-walks of Figure 5A do not indicate strand passage (Abbreviations: “StPs” for strand passage and “Ins” for topologically insulated). Percentage of walks that represent pure percolation paths are shown for the inter-chromosomal C-walks of Figure 2 and the simul-walks of Figure 4. Pure percolations are walks with only one inter-chain crossing. Note that even for the long walks of length 6 to 10, ~30% of the walks correspond to pure percolation paths rather than clusters of loci. The numbers are consistent between the inter-chromosomal C-walks and the topologically insulated simul-walks. This table quantifies the degree of mixing/unmixing and demonstrates the statistical significance of our findings.

2

Supplementary Table 2 Number of walks that visit each chromosome and compartment type. As the tables make clear, all chromosomes are represented in our data, with larger chromosomes being generally visited more often. A and B compartments are visited by a similar number of walks.