Abstract
In the context of tissue engineering, chitosan hydrogels are attractive biomaterials because they represent a family of natural polymers exhibiting several suitable features (cytocompatibility, bioresorbability, wound healing, bacteriostatic and fungistatic properties, structural similarity with glycosaminoglycans), and tunable mechanical properties. Optimizing the design of these biomaterials requires fine knowledge of its physical characteristics prior to assessment of the cell–biomaterial interactions. In this work, using atomic force microscopy (AFM), we report a characterization of mechanical and topographical properties at the submicron range of chitosan hydrogels, depending on physico-chemical parameters such as their polymer concentration (1.5%, 2.5% and 3.5%), their degree of acetylation (4% and 38.5%), and the conditions of the gelation process. Well-known polyacrylamide gels were used to validate the methodology approach for the determination and analysis of elastic modulus (i.e., Young’s modulus) distribution at the gel surface. We present elastic modulus distribution and topographical and stiffness maps for different chitosan hydrogels. For each chitosan hydrogel formulation, AFM analyses reveal a specific asymmetric elastic modulus distribution that constitutes a useful hallmark for chitosan hydrogel characterization. Our results regarding the local mechanical properties and the topography of chitosan hydrogels initiate new possibilities for an interpretation of the behavior of cells in contact with such soft materials.
Electronic supplementary material
The online version of this article (10.1007/s40204-020-00141-4) contains supplementary material, which is available to authorized users.
Keywords: Atomic force microscopy, Chitosan hydrogel gelation, Young’s modulus distribution
Introduction
Regenerative medicine aims at restoring the function of lost, damaged, or diseased tissue through its replacement or regeneration. The development and use of biomaterials to achieve these objectives is a founding paradigm of tissue engineering and a fast-growing research axis (Kumar 2018; Meco and Lampe 2018; Rami et al. 2014). Following this, it is well established that cell responses and functions are critically influenced by not only biological, but also topological and biomechanical interactions between cells and biomaterials (Glass et al. 2014; Zhou and Groth 2018). Such interactions are partly regulated by cell adhesion sites in adherent cells, thus implying cell–material interactions at the subcellular level (Fereol et al. 2009; Ladoux and Nicolas 2012; Skoog et al. 2018).
Among the various biomaterials used for tissue engineering, hydrogels are of interest because they are highly hydrated, ‘tissue-like’ materials, potentially providing a favorable medium for cell growth and differentiation. In particular, chitosan hydrogels with cavities are of specific interest for cell maturation, preserving paracrine cell signaling (Perrard et al. 2016). Furthermore, their physical and biochemical properties, including stiffness, morphology, microstructure and composition, can be controlled (Lee 2018; Li et al. 2012; Rami et al. 2014). Chitosan hydrogels are currently used as medical device (e.g., the Novashield nasal stent marketed by Medtronic company (Medtronic 2017)), but are also envisioned for water treatment, cell/tissue maturation, crop and food preservation (Gutiérrez 2017; López-Velázquez et al. 2019; Mohammadzadeh Pakdel and Peighambardoust 2018; Perrard et al. 2016). The choice of this natural polymer family is founded by a number of suitable properties (biocompatibility, bioresorbability, bioactivity for tissue regeneration, haemostatic, bacteriostatic and fungistatic properties (Crini et al. 2007; Kim et al. 2008; Yang 2011)). Chitosans are linear polysaccharides consisting of N-acetyl d-glucosamine and d-glucosamine residues linked by a β(1 4) glycosidic linkage. d-Glucosamine residues can be protonated at acidic pH, whereas N-acetyl glucosamine residues stay neutral. Polymers in the chitosan family differ by their degree of acetylation (DA, i.e., the fraction of N-acetyl glucosamine units), their molecular mass distributions and, at a finer scale, the intramolecular repartition of glucosamine and N-acetyl glucosamine residues. Our recent studies suggested that chitosan hydrogels are promising candidates as supporting material for various tissue engineering applications (Aussel et al. 2017; Montembault et al. 2006). Notably, the implantation of low-DA chitosan hydrogels in a fragmented form can be used as scaffolds for spinal cord injury and axon regeneration by preventing formation of a mature glial scar. This facilitates functional tissue regeneration and modulates the inflammatory response (Chedly et al. 2017). Regarding the latter point, our results are consistent with the study of Vasconcelos et al. (2013) which reported that subcutaneous implantation in mice of a chitosan 3D porous scaffold with DA 5% induced an anti-inflammatory macrophage response (M2 polarization), whereas chitosan scaffolds with DA 15% favored a pro-inflammatory macrophagic phenotype (M1) (Vasconcelos et al. 2013). Such phenotypic transitions of macrophages are believed to be involved in tissue repair (Novak and Koh 2013). However, the underlying cellular mechanisms by which the properties of chitosan hydrogels modulate the macrophagic response remain unclear. These include biomechanical, topographical, composition and processing parameters. In order to better understand these mechanisms, it is important to determine the mechanical, topographical and structural properties of chitosan hydrogels at a pertinent scale, i.e., at the cellular scale, and more specifically at the cell adhesion site scale.
Thus, the aim of this present study is to connect the mechanical and topographical properties of chitosan hydrogels at sub-micron-range, depending on their polymer concentration Cp (% w/w), their DA, and their preparation route. For this, we used the atomic force microscopy (AFM). Indeed, AFM is recognized to be a suitable device to characterize the surface properties of gels (Denisin and Pruitt 2016; Elosegui-Artola et al. 2014; Schillers et al. 2017), although a correct characterization by AFM of soft materials with surface rugosity is a challenge (Dokukin and Sokolov 2015; Notbohm et al. 2012; Piner et al. 1999).
In order to validate our experimental protocol and AFM data analysis performed with specifically designed software, a comparative study of the mechanical properties of reference (flat) polyacrylamide gels with various elastic moduli, based on the work of Elosegui-Artola et al. (2014), was carried out.
Here, we present elastic modulus and surface topography maps at different depths in chitosan hydrogels and at 66.7 nm resolution (within the local plane of the surface), with three different polymer concentrations Cp (1.5%, 2.5%, 3.5%), two different DAs (4%, 38.5%), and two gelation routes: the first preparation route involves the gelation of a chitosan solution in contact with gaseous ammonia (Montembault et al. 2005b) (‘ammonia vapor route’); the second one results from the gelation of a chitosan solution with sodium hydroxide aqueous solution (‘NaOH solution route’). Our analysis highlights that these physico-chemical parameters modulate the mechanical properties at the local scale, as well as the multi-layered structure of the hydrogels. Such local AFM mechanical characterizations are compared to macroscopic shear rheological analyses.
Materials and methods
Polyacrylamide gel preparation
Polyacrylamide gels were prepared according to the method previously described by Elosegui-Artola (2014). Briefly, glass cover slips (30 mm diam.) were activated to enhance gel adhesion, by immersion in a solution (25 mL) of 3-methacryloxypropyl trimethoxysilane (75 µL, Bind-Silane, Sigma), 10% acetic acid aqueous solution (750 µL) and qs 100% ethanol during 3 min, before being washed three times with ethanol, and air-dried for 10 min. Thin sheets of polyacrylamide gel were prepared from different concentrations of acrylamide (5.5%; 7.52%; 12%) and bisacrylamide (respectively, 0.03%; 0.16%; 0.15%) by addition of a solution of 0.5% ammonium persulfate and 0.05% tetramethyl ethylenediamine (Sigma), to generate gels of different elastic properties, i.e., acrylamide 5.5% + bisacrylamide 0.03% (noted Acr 5.5%/bis 0.03%), acrylamide 7.52% + bisacrylamide 0.16% (Acr 7.52%/bis 0.16%) and acrylamide 12.0% + bisacrylamide 0.15% (Acr 12.0%/bis 0.15%) (Elosegui-Artola et al. 2014). Twenty-five microliters of these mixtures were placed onto the surface of a circular activated glass coverslip and covered with circular top coverslip (22 mm diam.) previously treated with Repel-Silane ES, 2% solution of dimethyldichlorosilane dissolved in octa methyl cyclooctasilane (Sigma). After gel polymerization, the top coverslips were removed; the gels were rinsed three times with phosphate buffer saline solution (PBS, 1 ×) and were stored at 4 °C in PBS. During AFM experiments, polyacrylamide gels were immersed in PBS at room temperature.
Chitosan hydrogel preparation
Highly deacetylated chitosan produced from squid pen was purchased from Mahtani Chitosan (batch type 114, DA 4%) and was filtered in solution as described in a previous work (Montembault et al. 2005b). A part of this polymer batch was then N-reacetylated, using acetic anhydride in hydro-alcoholic media (Vachoud et al. 1997). Briefly, anhydro-alcoholic chitosan solution was prepared at a concentration of 0.5% (w/v) (with a water/1,2-propanediol ratio of 1/1 [v/v]). Acetic anhydride was then diluted in 1,2-propanediol, and this resulting acetylating mix was added dropwise to the chitosan solution. The amount of acetic anhydride added in the chitosan solution corresponded to the number of moles of amine sites to be reacetylated. After stirring for 3 h, the N-reacetylated chitosan was isolated by precipitation with aqueous ammonia, thoroughly washed with deionized water until neutral pH, and freeze-dried. The DA was analyzed by 1H NMR spectroscopy, according to the method of Hirai (1991). The DAs of the initial chitosan and the N-reacetylated chitosan were 4% and 38.5%, respectively.
The number average and weight average molar masses (Mn and Mw) of chitosans were determined by size exclusion chromatography coupled online with a differential refractometer (Wyatt Optilab T-rEx) and a multi-angle laser light scattering detector (Wyatt HELEOS), according to our previous works (Montembault et al. 2005b). The weight average molar masses were around 550 kg/mol for the two chitosans and the dispersity ratio Mw/Mn was close to 1.5. The reacetylation step did not change significantly the degree of polymerization of the chitosan (DPw ~ 3400).
Chitosan physical hydrogels were prepared using two different gelation routes. The first is the ammonia vapor route, which corresponds to a neutralization process performed by placing an aqueous chitosan solution in contact with ammonia vapors (generated by 200 mL of a 1 M ammonia solution in the volume of a closed reactor of 5L) for 15 h. Different gels were obtained by varying the DA (4%, 38.5%) and polymer concentration Cp (1.5%, 2.5%, 3.5% w/w). A second gelation route consists of neutralizing chitosan aqueous solutions with a sodium hydroxide solution (2 M for 2 h), using a chitosan with a DA 4% at a concentration Cp 2.5%. All chitosan hydrogels were prepared following our published works (Chedly et al. 2017; Fiamingo et al. 2016; Montembault et al. 2005a, b) and then sterilized by autoclaving at 121 °C for 20 min.
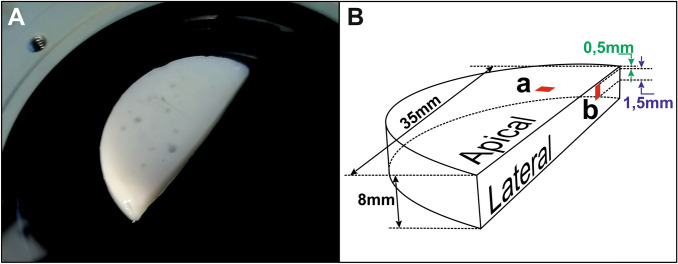
At the end of the hydrogel gelation process, in particular for hydrogels issued from the ammonia vapor neutralization route, a rigid and thin membrane covers the apical surface of the chitosan hydrogel (Fiamingo et al. 2016; Sereni et al. 2017). In order to characterize mechanically this apical membrane and the lateral surface, we manufactured our chitosan hydrogels within 8-mm-thick molds with a half circle shape with 35 mm diameter (Fig. 1) using a Petri dish and a Teflon insert. During gelation with ammonia vapors, the lateral surface of the half disk was not in direct contact with the base, preventing formation of the thin and dense layer.
Fig. 1.
a Image of chitosan hydrogel top view (: 4%, : 3.5%), neutralized with ammonia vapor b sketch of the chitosan hydrogel half circle shape, red squares represent zones assessed by AFM. «a» is the assessed area located at the level of the thin layer formed at the first neutralized surface of the hydrogel, i.e., apical surface, ‘b’ is the assessed area located between 0.5 and 2 mm from the surface on the lateral surface of the hydrogel
In practice, our half-moon chitosan hydrogels were cut in smaller pieces (~ 1.5 × 1.5 × 1.5 mm) using a scalpel. For AFM measurements, the sample is fixed on a glass coverslip with a double-sided adhesive in such a way as to orient toward the top the unaltered hydrogel surface to be assessed by AFM. AFM experiments were performed in water at room temperature.
AFM measurements
We used two different AFM devices, i.e., AFM ASYLUM MFP-3D-BIO, provided by Inc. Oxford Instruments Asylum Research (USA), and JPK bioafm NanoWizard®3 and 4 (Germany). These different AFM benches were used to assess the force–distance curves with non-coated n-type silicon cantilevers (CSC38) provided by MikroMasch® (Sofia, Bulgaria). The tips used were pyramidal probes with 20° half angle aperture and 350 µm cantilever length. The same calibration procedure was systematically performed to calculate the nominal spring constant k, based on the thermal noise approach (Hutter 1993). The mean nominal spring constant was about 0.072 ± 0.026 N/m.
Measurements on polyacrylamide gels were achieved considering a measuring point grid with 2 µm mesh over a 18 × 18 µm2 surface in the gel center, i.e., with grid mesh size in the same range as used by Elosegui-Artola (2014). For each acrylamide/bisacrylamide sample, three different zones of measurement at the gel surface were arbitrarily chosen, thus leading to the analysis of 300 spectroscopy force curves per sample.
Concerning chitosan hydrogel surfaces, AFM force spectroscopy measurements, including apical and lateral surfaces, were performed with a measurement point grid with 66.7 nm mesh size over an area of 1 × 1 µm2 at the hydrogel surface. The analysis was carried out on 512–2560 force-spectroscopy curves per hydrogel sample area.
According to Bilodeau (1992), for quadrilateral pyramid probe, the force-indentation depth relation is given by the following Hertz-based equation:
| 1 |
where is the applied force, the elastic modulus, the half angle aperture and the indentation depth; is the Poisson's ratio assumed to be close to 0.4 for polyacrylamide gels according to values reported in the literature (Alcaraz et al. 2003; Gross and Kress 2017; Hutter 1993), and 0.5 for chitosan hydrogels.
In addition, the contact point can be found according to the following equation:
| 2 |
where is the sensor position, and are the deflection and the spring constant of the cantilever, respectively (figure SM1 in supplementary materials).
Using (1) and (2), we obtained the following equation:
| 3 |
The elastic modulus and the contact point are calculated by fitting the experimental curve with Eq. (3) (figures SM2 and SM3 in supplementary materials).
As we previously described in Féréol et al. (2017), we have checked that the elastic modulus remained constant as indentation increased, to ensure that both polyacrylamide gels, and chitosan hydrogels behave like an elastic material with a purely linear behavior.
Due to the wide dispersion of elastic modulus values observed notably for chitosan hydrogels, we present our results with smoothed functions for elastic moduli distributions. Thus, a ‘nonparametric probability density function’ (NPPDF) using a kernel density estimation based on a normal (Gaussian) function was determined with the MATLAB® built-in function (fitdist()) to fit the elastic modulus occurrence distribution (Mathworks 2020). For each gel, i.e., polyacrylamide gels and chitosan hydrogels, the bandwidth of kernel smoothing window or Kernel smoothing parameter Ker was set following this formula:
| 4 |
where Emax is the maximum value of the elastic modulus measured for each gel.
Rheometry measurements
Dynamic rheological measurements were taken on different chitosan hydrogels following the same procedure as described in Fiamingo et al. (2016). Briefly, rheological measurements were taken at room temperature using an ARES rheometer (TA Instruments) operating with a plate–plate geometry (diameter 25 mm). The shear strain amplitude was monitored to ensure that the measurements were taken within the linear viscoelastic domain at a strain amplitude of 0.5%, resulting in storage modulus (G′) and loss modulus (G″) independent of the strain amplitude (figure SM4 in supplementary materials). Angular frequency sweep measurements were taken in the range from 100 rad/s down to 0.05 rad/s. G′ is fairly constant with frequency in this range, as expected for gels, thus the values used hereafter were determined in the low-angular frequency range. Rheometry measurements were repeated three times for each hydrogel type.
Results
Methodological validation with reference polyacrylamide gel
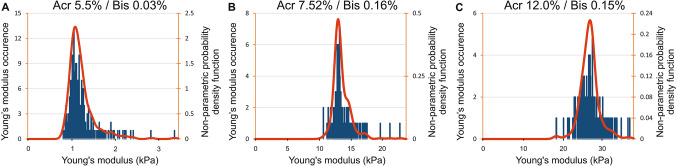
In order to validate both our experimental approach to characterize soft materials, and the analysis of AFM results with our data analysis software, we prepared and studied three different polyacrylamide gels following the protocol described by Elosegui-Artola et al. (2014), i.e., with following predicted elastic modulus values () 1.99 ± 0.13 kPa (Acr 5.5%/Bis 0.03%), 13.69 ± 2.84 kPa (Acr 7.52%/Bis 0.16%) and 29.01 ± 6.18 kPa (Acr 12.0%/Bis 0.15%) (Elosegui-Artola et al. 2014). Figure 2a–c presents the distributions of elastic modulus for these three conditions. The red curves represent the continuous estimations of distribution functions (NPPDF) that fit and smooth the histograms of elastic modulus values.
Fig. 2.
Histograms of elastic modulus occurrence distributions versus elastic modulus values for three polyacrylamide gels assessed by AFM varying concentration of acrylamide (Acr) and bis-acrylamide (Bis). Red curve represents the nonparametric probability density function (NPPDF) using a kernel density estimation based on a normal distribution to fit and smooth the occurrence distribution of elastic modulus values
For each polyacrylamide gel, we calculated the mean elastic modulus value noted , and the modal modulus value defined as the maximum of the distribution function and noted . In all cases, we observed that the modal value is rather close to the mean value , indeed, the differences vary between − 0.4 and 11.3% (Table 1). These results also compare well with the reference data obtained by Elosegui-Artola et al. (Table 1) (Elosegui-Artola et al. 2014). The relative differences in the values of elastic moduli (%) for (Acr 5.5%/Bis 0.03%), (Acr 7.52%/Bis 0.16%) and (Acr 12.0%/Bis 0.15%) are − 37.8%, 0.2%, and − 6.4%, respectively (Table 1). For the softest gel, i.e., (Acr 5.5%/Bis 0.03%), the discrepancy found can be explained as described by Schillers et al. (2017), invoking an uncertainty in cantilever calibration and instrumental errors. Additional elements concerning the methodological validation are provided in supplementary materials.
Table 1.
Elastic modulus of three different polyacrylamide gels assessed by AFM and compared to those obtained by AFM in Elosegui-Alberto et al. (2014) for the same formulations
| Acr 5.5%/Bis 0.03% | Acr 7.52%/Bis 0.16% | Acr 12.0%/Bis 0.15% | |
|---|---|---|---|
| Number of data | 300 | 300 | 300 |
| Maximum value () (kPa) | 3.41 | 23.01 | 37.34 |
| Mean value () ± SD (kPa) | 1.24 ± 0.32 | 13.71 ± 1.39 | 27.14 ± 2.40 |
| Peak modal value () (kPa) | 1.10 | 13.18 | 27.24 |
| Skewness | 2.6 | 2.4 | 0.4 |
| (%) | 11.3 | 3.9 | − 0.4 |
| Kernel size parameter (kPa) | 0.05 | 0.63 | 0.88 |
|
Mean value () ± SD (kPa) (Elosegui-Artola et al.) |
1.99 ± 0.13 | 13.69 ± 2.84 | 29.01 ± 6.18 |
| (%) | − 37.8 | 0.2 | − 6.4 |
In conclusion, our results are in good agreement with various data found in the literature (Denisin and Pruitt 2016; Elosegui-Artola et al. 2014), validating our experimental protocol, as well as our AFM data analysis.
AFM study of Chitosan hydrogels
We performed the AFM analysis of elastic modulus values at both the lateral surface, and the apical surface of the chitosan hydrogels for three different polymer concentrations (Cp = 1.5%, 2.5%, 3.5% w/w), for two different DAs (4%, 38.5%), and for two different gelation routes (ammonia vapor neutralization or sodium hydroxide solution neutralization) (Fiamingo et al. 2016). The specific sample with a concentration Cp = 2.5% and a DA of 4%, gelled with gaseous ammonia was used in a previous work and showed remarkable regenerative properties in the form of a suspension of a fragmented (micron-range) hydrogel, inducing a robust axonal regeneration after implantation in a rat spinal cord lesion model (Chedly et al. 2017). In this work, we added two similar chitosan hydrogel samples by varying the concentration, i.e., 1.5% and 3.5%. It is expected that the topographical, structural, and mechanical properties of chitosan hydrogel will be impacted by the chitosan concentration. Moreover, we also analyzed a sample with a higher DA of 38.5%, investigated previously in the same study (Chedly et al. 2017). As previously reported increasing the DAs of chitosan strongly impacts the biological response of macrophages in vivo (Chedly et al. 2017; Vasconcelos et al. 2013). Finally, we used a comparable sample to examine the individual effect of the gelation method on the chitosan hydrogel mechanical properties, i.e., gelation of the chitosan solution in contact with sodium hydroxide aqueous solution vs gelation in a closed reactor in presence of ammonia vapor.
Due to the known differences (Fiamingo et al. 2016) in structural and mechanical properties of chitosan hydrogels between the apical surface and the lateral surface (representative of bulk properties), we compared these two hydrogel regions by AFM. In the following, analyses and results are presented in order to distinguish between the bulk properties, those assessed on the lateral surface, and those of the apical surface of chitosan hydrogels.
Characterization of local mechanical properties on the lateral surface of chitosan hydrogels
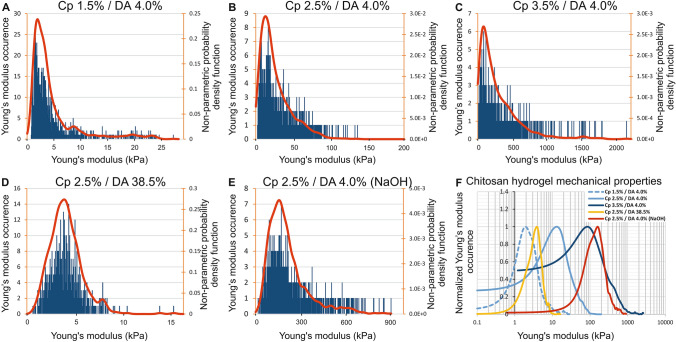
Figure 3 shows, for each chitosan hydrogel sample, the elastic modulus distribution histograms superimposed with the NPPDF distributions (red lines), calculated as described previously. Whatever the tested sample, the elastic modulus distributions present a wide dispersion (Fig. 3a–e) with standard deviations close to the mean values (Table 2). Figure 3a–d also highlights an asymmetric distribution extended towards high modulus values, characterized by positive skewness values, s > 1 (Table 2), where the skewness is given by the following formula:
| 5 |
where n is the number of data.
Fig. 3.
a–e Histogram of elastic modulus and distribution functions for five chitosan hydrogels, varying their concentration Cp, DA and route of gelation assessed by AFM on their lateral surface (measurements performed at a depth between 0.5 and 2 mm from the surface). The red curve represents the nonparametric probability density function (NPPDF) using a kernel density estimation to smooth the histograms. f Comparison of the normalized elastic modulus occurrence corresponding to these five hydrogels
Table 2.
Young modulus and associated parameters of five chitosan hydrogels assessed by AFM on lateral surface and by rheometer device
| Lateral surface | Cp 1.5%/DA 4.0% | Cp 2.5%/DA 4.0% | Cp 3.5%/DA 4.0% | Cp 2.5%/DA 38.5% | Cp 2.5%/DA 4.0% (NaOH) | |
|---|---|---|---|---|---|---|
| AFM device | Number of data | 1280 | 1587 | 768 | 584 | 1280 |
| Maximum value () (kPa) | 27.4 | 237.6 | 2,603.4 | 15.3 | 916.1 | |
| Mean value () (kPa) | 4.7 | 26.3 | 317.0 | 4.1 | 213.3 | |
| Standard deviation (kPa) | 4.7 | 21.4 | 376 | 1.7 | 135.8 | |
| Peak value () (kPa) | 1.9 | 13.0 | 85.0 | 3.9 | 158.8 | |
| Skewness | 2.4 | 2.0 | 3.1 | 1.3 | 1.7 | |
| (%) | 58.9 | 50.7 | 73.2 | 4.6 | 25.6 | |
| 14.2 | 18.3 | 30.6 | 4.0 | 5.8 | ||
| Kernel size (kPa) | 0.6 | 5.3 | 58.3 | 0.3 | 20.5 | |
| Rheometer device | Storage shear modulus () (kPa) 0.2 (kPa) | 0.25 | 1.1 | 2.45 | 2.54 | 1.95 |
| Equivalent elastic modulus (kPa) 0.6 (kPa) | 0.75 | 3.3 | 7.35 | 7.62 | 5.85 |
Again, data processing provides the modal value and the mean value . As a result of asymmetric distribution functions, we can observe significant differences between and (>); the ratio ()/ varying between 25 and 75% for the tested sample on the lateral surface except for the sample Cp = 2.5% /DA 38.5% where the relative discrepancy between and is only 5%, in agreement with a more symmetrical distribution, skewness = 1.3 (Table 2). As a result, chitosan hydrogels generally exhibit broad and asymmetric modulus distributions that could be associated with a submicron range heterogeneous structure at low DAs (Popa-Nita et al. 2010) (Fig. 3a–c and e)). To go further, we assessed the macroscopic mechanical properties of all chitosan hydrogel samples with a plate–plate shear rheometer device (Table 2). The real part of the complex shear modulus G′ is used to calculate the equivalent elastic modulus obtained with the rheometer device, ~ 3G’ and can be compared with and obtained with AFM (Table 2). The values of elastic modulus obtained by AFM ( and ) are generally higher than those obtained from rheology, except for the high DA (38.5%) sample. This could be related to the multi-layered structure of chitosan hydrogels, associated with the gradual slowing down in the neutralization kinetics with diffusion depth (Enache et al. 2018; Sereni et al. 2017). At low DAs, the chitosan chain conformations in solution are strongly impacted by their charge density; thus, a slow neutralization kinetics will yield a softer (disentangled) hydrogel. In-plane shear rheometry induces a series-type mechanical coupling of all layers with an apparent macroscopic modulus ideally related to the moduli of all layers according to:
| 6 |
where and are the thickness and shear modulus of the layer and is the width of the gel sample. From this ‘inverse rule of mixture’ or Reuss law (Reuss 1929), the impact of the softer layers should dominate the rheological response, resulting in lower values. Actually, since the hydrogels exhibit a multilayered morphology with a dense and rigid external apical layer on top of softer internal layers, the AFM evaluation of the elastic modulus should yield a lower estimation of the elastic modulus of the dense membrane, since softer layers may also contribute to the indentation. In spite of this lower estimation, the elastic modulus of the apical surface stays in order of magnitudes higher than the rheology estimation that is representative of softer internal layers.
Influence of polymer concentration Cp
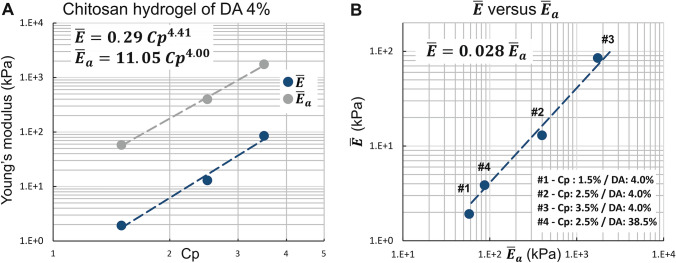
As expected, for the samples prepared through the ammonia route with a DA of 4%, the values of and increase with the mass concentration Cp. In the same way, we observe that the ratio also increases with Cp, evidencing that the modulus distribution becomes more asymmetric at high Cp (Table 2). In addition, the values of can be related to chitosan concentration Cp (w/w) according to a power law function, , where is close to 4.4 (Fig. 6a). Such values are significantly higher than in homogeneous polyacrylamide gels ( ~ 3–3.5) (Abidine et al. 2015; Adibnia 2016; Oyen 2014), which could result from the specific physical gel structure of chitosan hydrogels (Popa-Nita et al. 2010), implying the role of entanglements (Popa-Nita et al. 2009; Sereni et al. 2017), inherited from the polyelectrolyte chitosan solution in the mechanical properties of hydrogels. Increasing polymer concentration would thus result in an increase in multiple physical interaction sites and entrapped entanglements, leading to a ‘multiple’ physical network with various interaction types.
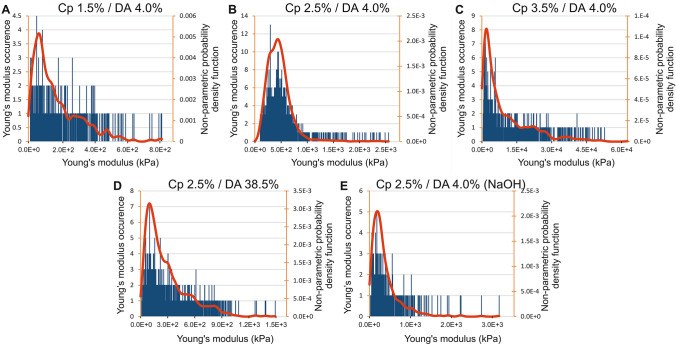
Fig. 6.
Histograms of elastic modulus assessed by AFM for apical surfaces of five chitosan hydrogel types. The red curves represent the estimation of probability density function using a kernel density estimation
Influence of the gelation route
Figure 3f and columns 2 and 5 in Table 3 allow comparing the modulus distribution functions of hydrogel samples at the same polymer concentration Cp = 2.5% and DA of 4.0%, but with different gelation conditions (NaOH solution vs ammonia vapor).
Table 3.
Analysis of Young’s modulus assessed by AFM at the apical surface of five chitosan hydrogels and associated methodological parameters
| Apical surface | Cp 1.5%/DA 4.0% | Cp 2.5%/DA 4.0% | Cp 3.5%/DA 4.0% | Cp 2.5%/DA 38.5% | Cp 2.5%/DA 4.0% (NaOH) | |
|---|---|---|---|---|---|---|
| AFM device | Number of data | 512 | 2560 | 1024 | 1280 | 512 |
| Maximum measured value () (kPa) | 734.4 | 2,325.3 | 56,269.8 | 1,323.4 | 2,881.8 | |
| Mean value (Eam) (kPa) | 154.7 | 425.1 | 8,812.3 | 248.0 | 338.4 | |
| Standard deviation (kPa) | 133.5 | 237.9 | 9,490.8 | 205.2 | 333.8 | |
| Peak (modal) value () (kPa) | 57.9 | 398.7 | 1,747.9 | 87.2 | 174.2 | |
| Skewness | 1.48 | 2.93 | 1.64 | 1.46 | 2.96 | |
| Kernel size (kPa) | 14.7 | 46.5 | 1,125.4 | 26.5 | 57.6 |
We observe significantly higher values for the elastic moduli and resulting from the sodium hydroxide neutralization route, in comparison with the series of samples neutralized with ammonia vapor ( and are increased by a factor of 8 and 12, respectively). Thus, the sodium hydroxide solution route yields hydrogels with a higher modulus, i.e., more cohesive structure. The difference between hydrogels obtained by one or the other gelation route is due to different gelation kinetics. Indeed, neutralization with ammonia vapors requires the formation of vapors and condensation onto the chitosan solution surface, whereas neutralization with NaOH solution is followed by direct and fast diffusion through the formed hydrogel and the solution (Enache et al. 2018). Thus, neutralization with NaOH solution is faster and could yield a more entangled hydrogel from the highly entangled polyelectrolyte chitosan parent solution (Sereni et al. 2017). Supplementary figures SM5 and SM6 display examples of the evolution of the gel width (e) during gelation of chitosan acetate solutions. Tables TSM2 and TSM3 show the comparative characterization of gelation kinetics in terms of reaction parameter .
Influence of the degree of acetylation DA
The impact of the degree of acetylation on the modulus distributions can be observed comparing Fig. 3b and d obtained at the same polymer concentration Cp = 2.5%, using the same neutralization conditions (ammonia route), with chitosan of similar molar masses, but at two different DAs, i.e., 4% and 38.5%. An increase in the DA is related with a decrease in the modulus deduced from AFM spectroscopy. In solution, at a DA of 4%, chitosan is a strong polyelectrolyte (Popa-Nita et al. 2009; Schatz et al. 2003) with a high entanglement density and high hydrophilicity. At a DA of 38.5%, the density of charge is lower, thus the entanglement density also decreases, although the persistence length is partly preserved due to the steric contribution of acetyl groups (Lamarque et al. 2005). Consequently, in the neutralized state, low DA hydrogels will preserve a higher entanglement density, formed by interchain interactions from a highly entangled solution. Moreover, we previously showed that low DA chitosan in the neutralized state was in the most hydrophobic conditions (Becerra et al. 2017). Thus, low DA chitosan hydrogels could entrap a higher entanglement density in a physical network formed with a higher density of hydrophobic junctions, resulting in a higher modulus for the hydrogels (Table 2 and Fig. 3F).
Chitosan hydrogel family identification by their mechanical properties
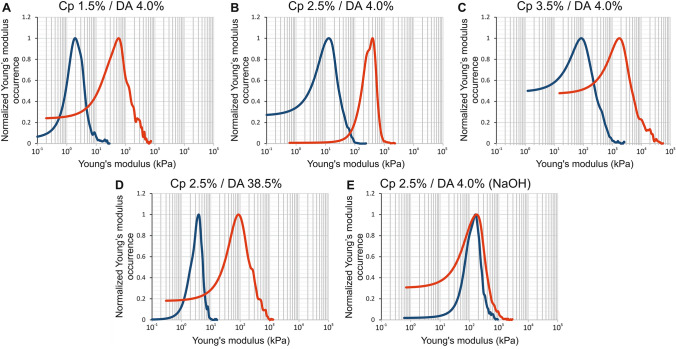
In order to compare the characteristic mechanical behavior of chitosan hydrogels depending on three parameters, namely concentration, gelation route, and DA, we have reported the normalized nonparametric probability density function versus the normalized Young modulus distribution for each condition (Fig. 4).
Fig. 4.

Normalized nonparametric probability density functions versus normalized young’s modulus distribution ( of five chitosan hydrogels assessed by AFM on lateral surfaces
This graph highlights that gelation route or DA values seem to impact the shape of the Young modulus distribution, while parameter Cp associated with low DAs results in limited effect, and tends to preserve a similar shape of the normalized curves (Fig. 4).
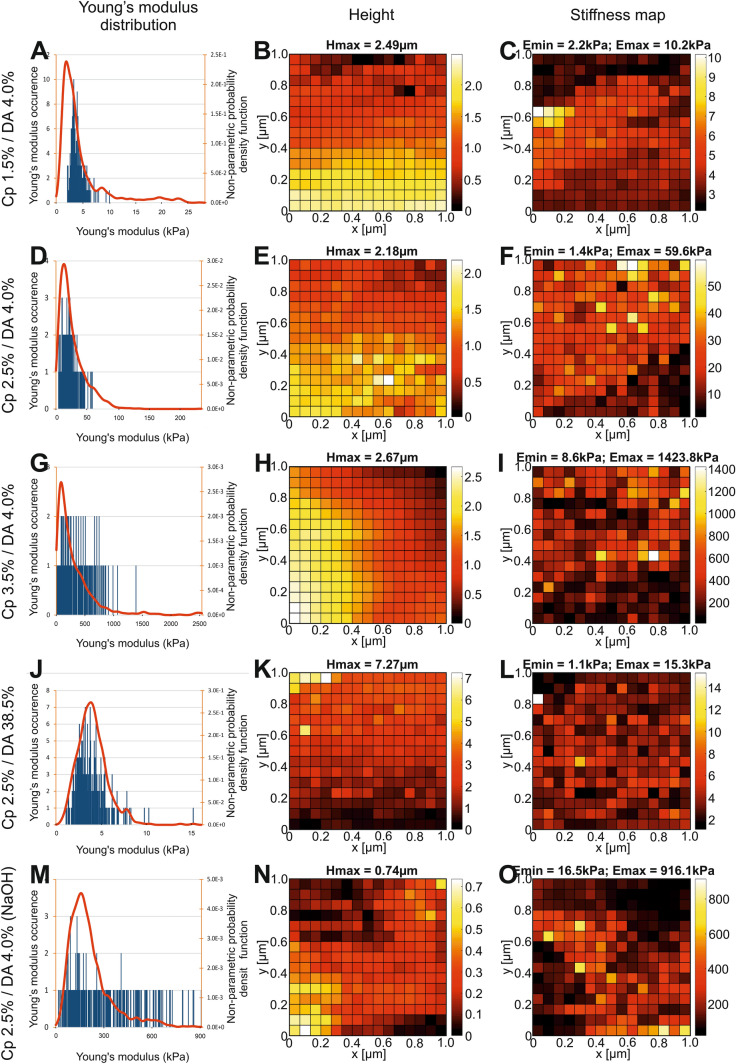
Young’s modulus and topography maps
In order to complete the previous mechanical characterization and assess the characteristic sizes of the hydrogel microstructure, we report in Fig. 5 the Young modulus distribution maps over a 1 × 1 µm2 surface together with the corresponding topographical maps of each chitosan hydrogel. In Fig. 5a, d, g, j and m, the Young modulus distribution histograms calculated from their corresponding maps are in agreement with the Young modulus NPPDF calculated from all samples of the same condition (red curves) as shown in Fig. 3. The topography map of each sample is shown in Fig. 5b, e, h, k and n, and the Young modulus distribution maps are shown in Fig. 5c, f, i, l and o. Variations in height and elastic modulus maps do not appear to be correlated.
Fig. 5.
Topological and mechanical property maps of chitosan hydrogels (Lateral surfaces). a, d, g, j and m Histograms of elastic modulus distributions for a given region (in blue), superimposed with the elastic modulus estimation of density probability functions performed with all studied samples (in red). b, e, h, k and n Topography (relative height) of the hydrogel surface. c, f, i, l and o Elastic modulus distribution map on the hydrogel surface
Characterization of local mechanical properties on the apical surface of chitosan hydrogels
The apical surface of hydrogel chitosan samples (i.e., the surfaces formed at first contact with the gaseous or liquid base) was analyzed by AFM following the same method described above for the lateral surfaces. Thus, Fig. 6a–e shows, for each sample, the elastic modulus distribution histograms superimposed with the continuous estimation of the probability distribution functions (NPPDF, red lines). As we already observed for the lateral surface, the elastic modulus distribution of chitosan hydrogels presents a wide dispersion (Fig. 6a–e) with standard deviation values close to the mean values and skewness values > 1 (Table 3). Again, all the samples studied on the apical surface show an asymmetric distribution extended toward high elastic modulus values of the histogram (Fig. 6). The elastic modulus corresponding to NPPDF peak values is reported in Table 3. Considering low DA chitosan (4%) samples neutralized with ammonia vapor, the polymer concentration impacts the elastic modulus following a power law as observed for the lateral surface, although the absolute values are significantly higher at the apical surface (Fig. 7a). When the DA increased from 4% to 38.5%, the elastic modulus decreased by a factor of 4.6 (Table 3), while for the lateral surface analyses the factor was close to 3.3. In order to compare apical and lateral surfaces, we have reported on the same graphs the normalized elastic modulus occurrence curves (NPPDF) from both surface type analyses in Fig. 8. The apical surfaces exhibit higher elastic moduli, in agreement with the formation of a dense layer in contact with the base. Surprisingly, in the case of hydrogels neutralized with NaOH aqueous solutions, the apical surface modulus value is close to the value on the lateral surface, suggesting that the microstructure in the apical and lateral surfaces is similar, at least in the investigated depth range. Visually, or through an optical stereomicroscope it was possible to observe a clear apical membrane after slow neutralization with ammonia vapor, whereas this membrane was more difficult to exhibit in fast neutralization conditions (NaOH), possibly because the hard surface membrane could be much thicker and more diffuse (in this case, the lateral surface investigation could still be located in the dense superficial membrane).
Fig. 7.
a Elastic modulus peak values versus polymer concentration after ammonia vapors neutralization. b Relation between elastic modulus peak values at the lateral surface and elastic modulus peak values at the apical surface
Fig. 8.
Comparison between the normalized elastic modulus occurrence assessed by AFM of the chitosan hydrogel apical surfaces (red curve) and chitosan hydrogel bulk (blue curve)
In case of neutralization with ammonia vapor, we observe that the elastic modulus of the lateral surface and of the apical surface follow a linear relation, i.e., ~ Fig. 7b and Fig. 8a–d, whereas the NaOH route gelation yields close to (Fig. 8e). These results suggest that the gelation route and the gelation kinetics are key parameters in the formation of the layered organization of chitosan hydrogels, allowing to modulate the hydrogel homogeneity and induce mechanical gradients between the bulk and the surface layer.
Discussion
An atomic force spectroscopy at 66.7 nm resolution was carried out to examine the physical properties of chitosan hydrogels. The optimization of their mechanical properties requires the control of the gelation method, of the molecular parameters of chitosan (ex: degree of acetylation), and of the formulation parameters of the initial chitosan solution (ex: chitosan concentration).
Our contribution is a local characterization approach, which allowed us to exhibit various, measurable structural heterogeneities in chitosan hydrogels at multiple length scales, as revealed by our normalized curves and modulus maps obtained with AFM. The differences observed in the modulus values obtained with AFM and rheology may arise from the multi-layered structure of chitosan hydrogels (Sereni et al. 2017), and the precise location of AFM analysis with respect to the hydrogel surface. In this regard, a high ratio of can be interpreted as reflecting a high modulus gradient of hydrogels. Thus, AFM is clearly shown to be a unique technique able to reveal heterogeneities and gradients in the mechanical properties of chitosan hydrogels at the nanometer to micron scales, a characterization that cannot be assessed through the rheological behavior of macroscopic hydrogels. Specifically, at the micron-range area, the neutralization route impacts the breadth of the distribution of elastic moduli: Ammonia vapor neutralization of low DA chitosan solutions yields hydrogels with a higher heterogeneity parameter (), in comparison with sodium hydroxide solution neutralization of gels at the same concentrations. An increase in the DA strongly reduces such sub-micron scale heterogeneities, an indication that the observed modulus fluctuations for low DA hydrogels could be related to entanglement density fluctuations entrapped in the hydrogels. Indeed, during neutralization, chitosan chains switch from an extended conformation in the polyelectrolyte state to a more compact and disentangled conformation in the neutralized state. Gel formation only occurs if an entanglement network can persist entrapped in the gel. Thus, at low DA, a high charge density in chitosan solutions could favor strong conformation changes and disentanglements during neutralization, whereas the conformation of chitosan of a higher acetylation degree chitosan would be less sensitive to the neutralization state, maintaining a persistence length due to the steric hindrances of acetyl moieties.
Another important consequence of our nano-localized mechanical measurements is our ability to estimate the impact of the various parameters of chitosan formulations on the formation of different zones in the multi-layered hydrogels, at micron scale and/or higher length scales. Thus, we were able to characterize and compare the first-formed surface (apical), and the bulk (lateral surface) of hydrogels. A stiffer membrane is formed at the apical surface, as was previously observed, although this was never quantified before (Fiamingo et al. 2016; Sereni et al. 2017). We have found a scaling relation relating the mechanical properties of the bulk versus apical layer for hydrogel neutralization with ammonia vapor, for all investigated concentrations and DAs. Our results also show that the polymer concentration impacts the bulk and apical surface moduli of different hydrogel layers with a similar power law.
Further, an increase in the acetylation degree was found to induce a decrease in the chitosan hydrogel elastic moduli. Although a higher DA results in a more hydrophobic polymer in acidic solutions (Popa-Nita et al. 2009), an opposite trend is expected in the neutralized state, where a low DA yields a more hydrophobic hydrogel (Becerra et al. 2017). Thus, in the neutralized state, a low DA chitosan should favor hydrophobic interactions, also entrapping a higher entanglement density, thus resulting in a higher modulus.
Finally, our AFM-based mechanical characterization approach is pertinent to better understand hydrogel–cell interactions. Indeed, we have shown previously that alveolar macrophages are impacted, in terms of shape, spreading, height and cytoskeletal stiffness, by the mechanical properties of the substrate with elastic modulus values close to 10 kPa, 40 kPa, 160 kPa up to nearly infinite rigidity (Féréol et al. 2006). This sensitivity is regulated by the formation of macrophage adhesion sites (Fereol et al. 2009). Concerning chitosan-based materials, several studies have shown that a change in DA is correlated with a change in the macrophage phenotype invading the hydrogel (Chedly et al. 2017; Vasconcelos et al. 2013). From our present results on chitosan hydrogel materials, changes in the DA are related to a change in mechanical properties in a range from 4 to 13 kPa, i.e., the range of sensibility of macrophages to substrate mechanical properties (Féréol et al. 2006; Sridharan et al. 2019). This could at least partly explain the macrophage polarization mechanism in contact with chitosan hydrogels with different degrees of acetylation. In order to establish the specific impact of the mechanical properties of the substrate on macrophage polarization, further cellular studies are planned, varying the type of hydrogels, and the type of surface (apical or lateral) used for cell culture.
Conclusion
Atomic force spectroscopy is shown to be an ideal tool for the characterization of soft complex materials. In this work, we have developed a methodological approach and applied it to the characterization of multi-layered hydrogels obtained by neutralization of chitosan acetate aqueous solutions. At a sub-micron scale, we thus clearly demonstrate that the neutralization conditions (with ammonia vapors or NaOH liquid solutions), the molecular parameters of chitosan (degree of acetylation), and the processing parameters (chitosan concentration) affect the hydrogel local mechanical properties. We have interpreted this by invoking the dynamic effects related to disentanglement time during neutralization and gelation kinetics.
In addition, we characterized for the first time the elastic modulus of the thin membrane covering the apical surface of samples elaborated through ammonia route. In contrast, for gels obtained by NaOH neutralization the elastic modulus value of the apical surface was not substantially different from that of the chitosan hydrogel bulk. The results of our micro-scale mechanical characterization of various formulations of chitosan hydrogels should initiate new possibilities for an interpretation of the behavior of cells in contact with such soft materials.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
We would like to acknowledge the « Ministère de l'Enseignement Supérieur et de la Recherche Scientifique » of Algeria for PhD funding attributed to AB, Satt-Lutech (financial support for MV salary) and Prof. Hugues Talbot, Université Paris-Saclay, for the helpful discussions.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Research resource identifiers (RRID)
Software: MATLAB, RRID:SCR_001622. Software: AMIRA 5.2, Advanced 3D Visualization and Volume Modeling, RRID:SCR_007353.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
R. Fodil and S. Féréol are contributing authors.
Contributor Information
R. Fodil, Email: redouane.fodil@u-pec.fr
S. Féréol, Email: sophie.fereol@u-pec.fr
References
- Abidine Y, Laurent VM, Michel R, Duperray A, Palade LI, Verdier C. Physical properties of polyacrylamide gels probed by AFM and rheology. EPL (Europhys Lett) 2015;109:38003. doi: 10.1209/0295-5075/109/38003. [DOI] [Google Scholar]
- Adibnia V, Hill RJ. Universal aspects of hydrogel gelation kinetics, percolation and viscoelasticity from PA-hydrogel rheology. J Rheol. 2016 doi: 10.1122/1.4948428. [DOI] [Google Scholar]
- Alcaraz J, Buscemi L, Grabulosa M, Trepat X, Fabry B, Farre R, Navajas D. Microrheology of human lung epithelial cells measured by atomic force microscopy. Biophys J. 2003;84:2071–2079. doi: 10.1016/S0006-3495(03)75014-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aussel A, Thébaud NB, Bérard X, Brizzi V, Delmond S, Bareille R, Siadous R, James C, Ripoche J, Durand M, Montembault A, Burdin B, Letourneur D, L'Heureux N, David L, Bordenave L. Chitosan-based hydrogels for developing a small-diameter vascular graft: in vitro and in vivo evaluation. Biomed Mater. 2017;12:065003. doi: 10.1088/1748-605X/aa78d0. [DOI] [PubMed] [Google Scholar]
- Becerra J, Sudre G, Royaud I, Montserret R, Verrier B, Rochas C, Delair T, David L. Tuning the hydrophilic/hydrophobic balance to control the structure of chitosan films and their protein release behavior. AAPS Pharm Sci Tech. 2017;18:1070–1083. doi: 10.1208/s12249-016-0678-9. [DOI] [PubMed] [Google Scholar]
- Bilodeau GG. Regular pyramid punch problem. J Appl Mech. 1992;59:519–523. doi: 10.1115/1.2893754. [DOI] [Google Scholar]
- Chedly J, Soares S, Montembault A, von Boxberg Y, Veron-Ravaille M, Mouffle C, Benassy MN, Taxi J, David L, Nothias F. Physical chitosan microhydrogels as scaffolds for spinal cord injury restoration and axon regeneration. Biomaterials. 2017;138:91–107. doi: 10.1016/j.biomaterials.2017.05.024. [DOI] [PubMed] [Google Scholar]
- Crini G, Badot PM, Guibal E. Chitine et chitosane: du biopolymère à l'application. Franche-Comté: Presses Univ; 2007. [Google Scholar]
- Denisin AK, Pruitt BL. Tuning the range of polyacrylamide gel stiffness for mechanobiology applications. ACS Appl Mater Interfaces. 2016;8:21893–21902. doi: 10.1021/acsami.5b09344. [DOI] [PubMed] [Google Scholar]
- Dokukin M, Sokolov I. High-resolution high-speed dynamic mechanical spectroscopy of cells and other soft materials with the help of atomic force microscopy. Sci Rep. 2015;5:12630. doi: 10.1038/srep12630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elosegui-Artola A, Bazellières E, Allen MD, Andreu I, Oria R, Sunyer R, Gomm JJ, Marshall JF, Jones JL, Trepat X, Roca-Cusachs P. Rigidity sensing and adaptation through regulation of integrin types. Nat Mater. 2014;13:631–637. doi: 10.1038/nmat3960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enache AA, David L, Puaux J-P, Banu I, Bozga G. Kinetics of chitosan coagulation from aqueous solutions. J Appl Polym Sci. 2018;135:46062. doi: 10.1002/app.46062. [DOI] [Google Scholar]
- Fereol S, Fodil R. Effect of cholesterol depletion on the viscoelastic properties of alveolar epithelial cells assessed by atomic force microscopy in large deformation. Revue de composites et des matréiaux avancés. 2017;28:57–72. doi: 10.3166/rcma.2017.00004. [DOI] [Google Scholar]
- Fereol S, Fodil R, Laurent VM, Balland M, Louis B, Pelle G, Henon S, Planus E, Isabey D. Prestress and adhesion site dynamics control cell sensitivity to extracellular stiffness. Biophys J. 2009;96:2009–2022. doi: 10.1016/j.bpj.2008.10.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Féréol S, Fodil R, Labat B, Galiacy S, Laurent VM, Louis B, Isabey D, Planus E. Sensitivity of alveolar macrophages to substrate mechanical and adhesive properties. Cell Motil Cytoskelet. 2006;63:321–340. doi: 10.1002/cm.20130. [DOI] [PubMed] [Google Scholar]
- Fiamingo A, Montembault A, Boitard SE, Naemetalla H, Agbulut O, Delair T, Campana-Filho SP, Menasche P, David L. Chitosan hydrogels for the regeneration of infarcted myocardium: preparation, physicochemical characterization, and biological evaluation. Biomacromol. 2016;17:1662–1672. doi: 10.1021/acs.biomac.6b00075. [DOI] [PubMed] [Google Scholar]
- Glass KA, Link JM, Brunger JM, Moutos FT, Gersbach CA, Guilak F. Tissue-engineered cartilage with inducible and tunable immunomodulatory properties. Biomaterials. 2014 doi: 10.1016/j.biomaterials.2014.03.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross W, Kress H. Simultaneous measurement of the Young's modulus and the Poisson ratio of thin elastic layers. Soft Matter. 2017;13:1048–1055. doi: 10.1039/C6SM02470J. [DOI] [PubMed] [Google Scholar]
- Gutiérrez TJ. Chitosan applications for the food industry. Chitosan. 2017 doi: 10.1002/9781119364849.ch8. [DOI] [Google Scholar]
- Hirai AOH, Nakajima A. Determination of degree of deacetylation of chitosan by 1H NMR spectroscopy. Polym Bull. 1991;26:87–94. doi: 10.1007/BF00299352. [DOI] [Google Scholar]
- Hutter JLBJ. Characterization of atomic-force microscope tips. Rev Sci Instrum. 1993;64:1868–1873. doi: 10.1063/1.1143970. [DOI] [Google Scholar]
- Kim IY, Seo SJ, Moon HS, Yoo MK, Park IY, Kim BC, Cho CS. Chitosan and its derivatives for tissue engineering applications. Biotechnol Adv. 2008;26:1–21. doi: 10.1016/j.biotechadv.2007.07.009. [DOI] [PubMed] [Google Scholar]
- Kumar P. Future biomaterials for enhanced cell–substrate communication in spinal cord injury intervention. Future Sci OA. 2018;4:FSO68. doi: 10.4155/fsoa-2017-0130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ladoux B, Nicolas A. Physically based principles of cell adhesion mechanosensitivity in tissues. Rep Prog Phys. 2012;75:116601. doi: 10.1088/0034-4885/75/11/116601. [DOI] [PubMed] [Google Scholar]
- Lamarque G, Lucas JM, Viton C, Domard A. Physicochemical behavior of homogeneous series of acetylated chitosans in aqueous solution: role of various structural parameters. Biomacromol. 2005;6:131–142. doi: 10.1021/bm0496357. [DOI] [PubMed] [Google Scholar]
- Lee JH. Injectable hydrogels delivering therapeutic agents for disease treatment and tissue engineering. Biomater Res. 2018;22:27. doi: 10.1186/s40824-018-0138-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Katsanevakisa E, Liu X, Zhanga N. Engineering neural stem cell fates with hydrogel design for central nervous system regeneration. Prog Polym Sci. 2012;37:1105–1129. doi: 10.1016/j.progpolymsci.2012.02.004. [DOI] [Google Scholar]
- López-Velázquez JC, et al. Gelatin–chitosan—PVA hydrogels and their application in agriculture. J Chem Technol Biotechnol. 2019;94:3495–3504. doi: 10.1002/jctb.5961. [DOI] [Google Scholar]
- Mathworks (2020). https://it.mathworks.com/help/stats/fitdist.html
- Meco E, Lampe KJ. Microscale architecture in biomaterial scaffolds for spatial control of neural cell behavior. Front Mater. 2018 doi: 10.3389/fmats.2018.00002. [DOI] [Google Scholar]
- Medtronic (2017) Chitosan as a biomaterial. https://www.medtronic.com/se-sv/healthcare-professionals/products/ear-nose-throat/bio-packing/bio-nasal-packing/novashield.html. Accessed 2017.
- Mohammadzadeh Pakdel P, Peighambardoust SJ. Review on recent progress in chitosan-based hydrogels for wastewater treatment application. Carbohydr Polym. 2018;201:264–279. doi: 10.1016/j.carbpol.2018.08.070. [DOI] [PubMed] [Google Scholar]
- Montembault A, Viton C, Domard A. Rheometric study of the gelation of chitosan in aqueous solution without cross-linking agent. Biomacromol. 2005;6:653–662. doi: 10.1021/bm049593m. [DOI] [PubMed] [Google Scholar]
- Montembault A, Viton C, Domard A. Rheometric study of the gelation of chitosan in a hydroalcoholic medium. Biomaterials. 2005;26:1633–1643. doi: 10.1016/j.biomaterials.2004.06.029. [DOI] [PubMed] [Google Scholar]
- Montembault A, Tahiri K, Korwin-Zmijowska C, Chevalier X, Corvol MT, Domard A. A material decoy of biological media based on chitosan physical hydrogels: application to cartilage tissue engineering. Biochimie. 2006;88:551–564. doi: 10.1016/j.biochi.2006.03.002. [DOI] [PubMed] [Google Scholar]
- Notbohm J, Poon B, Ravichandran G. Analysis of nanoindentation of soft materials with an atomic force microscope. J Mater Res. 2012;27:229–237. doi: 10.1557/jmr.2011.252. [DOI] [Google Scholar]
- Novak ML, Koh TJ. Phenotypic transitions of macrophages orchestrate tissue repair. Am J Pathol. 2013;183:1352–1363. doi: 10.1016/j.ajpath.2013.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oyen ML. Mechanical characterisation of hydrogel materials. Int Mater Rev. 2014;59:44–59. doi: 10.1179/1743280413Y.0000000022. [DOI] [Google Scholar]
- Perrard MH, Sereni N, Schluth-Bolard C, Blondet A, d’Estaing SG, Plotton I, Morel-Journel N, Lejeune H, David L, Durand P. Complete human and rat ex vivo spermatogenesis from fresh or frozen testicular tissue. Biol Reprod. 2016;95:89. doi: 10.1095/biolreprod.116.142802. [DOI] [PubMed] [Google Scholar]
- Piner RD, Hong S, Mirkin CA. Improved Imaging of soft materials with modified AFM tips. Langmuir. 1999;15:5457–5460. doi: 10.1021/la990408d. [DOI] [Google Scholar]
- Popa-Nita S, Rochas C, David L, Domard A. Structure of natural polyelectrolyte solutions: role of the hydrophilic/hydrophobic interaction balance. Langmuir. 2009;25:6460–6468. doi: 10.1021/la900061n. [DOI] [PubMed] [Google Scholar]
- Popa-Nita S, Alcouffe P, Rochas C, David L, Domard A. Continuum of structural organization from chitosan solutions to derived physical forms. Biomacromol. 2010;11:6–12. doi: 10.1021/bm9012138. [DOI] [PubMed] [Google Scholar]
- Rami L, Malaise S, Delmond S, Fricain J-C, Siadous R, Schlaubitz S, Laurichesse E, Amédée J, Montembault A, David L, Bordenave L. Physicochemical modulation of chitosan-based hydrogels induces different biological responses: interest for tissue engineering. J Biomed Mater Res Part A. 2014;102A:3666–3676. doi: 10.1002/jbm.a.35035. [DOI] [PubMed] [Google Scholar]
- Reuss A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J Appl Math Mech Zeitschrift für Angewandte Mathematik und Mechanik. 1929;9:49–58. doi: 10.1002/zamm.19290090104. [DOI] [Google Scholar]
- Schatz C, Viton C, Delair T, Pichot C, Domard A. Typical physicochemical behaviors of chitosan in aqueous solution. Biomacromol. 2003;4:641–648. doi: 10.1021/bm025724c. [DOI] [PubMed] [Google Scholar]
- Schillers H, et al. Standardized nanomechanical atomic force microscopy procedure (SNAP) for measuring soft and biological samples. Sci Rep. 2017;7:5117. doi: 10.1038/s41598-017-05383-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sereni N, Enache A, Sudre G, Montembault A, Rochas C, Durand P, Perrard MH, Bozga G, Puaux JP, Delair T, David L. Dynamic structuration of physical chitosan. Hydrogels Langmuir. 2017;33:12697–12707. doi: 10.1021/acs.langmuir.7b02997. [DOI] [PubMed] [Google Scholar]
- Skoog SA, Kumar G, Narayan RJ, Goering PL. Biological responses to immobilized microscale and nanoscale surface topographies. Pharmacol Ther. 2018;182:33–55. doi: 10.1016/j.pharmthera.2017.07.009. [DOI] [PubMed] [Google Scholar]
- Sridharan R, Cavanagh B, Cameron AR, Kelly DJ, O'Brien FJ. Material stiffness influences the polarization state, function and migration mode of macrophages. Acta Biomater. 2019;89:47–59. doi: 10.1016/j.actbio.2019.02.048. [DOI] [PubMed] [Google Scholar]
- Vachoud L, Zydowicz N, Domard A. Formation and characterisation of a physical chitin gel. Carbohydr Res. 1997;302:169–177. doi: 10.1016/S0008-6215(97)00126-2. [DOI] [Google Scholar]
- Vasconcelos DP, Fonseca AC, Costa M, Amaral IF, Barbosa MA, Aguas AP, Barbosa JN. Macrophage polarization following chitosan implantation. Biomaterials. 2013;34:9952–9959. doi: 10.1016/j.biomaterials.2013.09.012. [DOI] [PubMed] [Google Scholar]
- Yang TL. Chitin-based materials in tissue engineering: applications in soft tissue and epithelial organ. Int J Mol Sci. 2011;12:1936–1963. doi: 10.3390/ijms12031936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou G, Groth T. Host responses to biomaterials and anti-inflammatory design-a brief review. Macromol Biosci. 2018;18:e1800112. doi: 10.1002/mabi.201800112. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.