Dynamic distortion correction for functional MRI using FID navigators

Abstract

Purpose:

To develop a method for slice-wise dynamic distortion correction for EPI using rapid spatiotemporal B₀ field measurements from FID navigators (FIDnavs) and to evaluate the efficacy of this new approach relative to an established data-driven technique.

Methods:

A low-resolution reference image was used to create a forward model of FIDnav signal changes to enable estimation of spatiotemporal B₀ inhomogeneity variations up to second order from measured FIDnavs. Five volunteers were scanned at 3T using a 64-channel coil with FID-navigated EPI. The accuracy of voxel shift measurements and geometric distortion correction was assessed for experimentally induced magnetic field perturbations. The temporal signal-to-noise ratio (tSNR) was evaluated in EPI time-series acquired at rest and with a continuous nose touching action, before and after image realignment.

Results:

Field inhomogeneity coefficients and voxel shift maps measured using FIDnavs were in excellent agreement with multi-echo EPI measurements. FID-navigated distortion correction accurately corrected image geometry in the presence of induced magnetic field perturbations, outperforming the data-driven approach in regions with large field offsets. In fMRI scans with nose touching, FIDnav-based correction yielded tSNR gains of 30% in gray matter. Following image realignment, which accounted for global image shifts, tSNR gains of 3% were achieved.

Conclusions:

Our proposed application of FIDnavs enables slice-wise dynamic distortion correction with high temporal efficiency. We achieved improved signal stability by leveraging the encoding information from multi-channel coils. This approach can be easily adapted to other EPI-based sequences to improve temporal SNR for a variety of clinical and research applications.

Introduction

Single-shot EPI forms the basis of most fMRI studies as it facilitates measurement of BOLD signal fluctuations related to neuronal activity with high temporal resolution. However, given its low effective bandwidth in the phase-encoding direction, EPI is highly sensitive to magnetic field (B₀) inhomogeneities that occur at interfaces between materials with different magnetic susceptibilities and due to hardware imperfections. Uncompensated variations in the encoding field produce non-linear geometric distortions and regions of signal “pile-up”, while intra-voxel dephasing creates signal voids in regions with high inhomogeneity. These susceptibility-induced effects increase linearly with field strength, and lead to a loss in BOLD sensitivity (1), as well as difficulties in co-localizing functional data with anatomical information (2).

Active shimming is typically performed prior to imaging to help offset inhomogeneities induced by the subject-specific susceptibility distribution by superimposing an optimal set of low-spatial-order spherical harmonic (SH) fields on the static magnetic field. The EPI readout time can also be reduced by employing ramp sampling and/or parallel imaging acceleration to minimize artifacts, but residual distortions remain a problem (3). Static distortions may be corrected in post-processing by computing voxel displacements from a low-resolution map of field offsets, usually measured from a separate multi-gradient-echo (MGRE) acquisition (4). Alternatively, the displacement field may be estimated from two sets of images acquired with reversed phase encoding directions (“blip-up” and “blip-down”), which exhibit equal magnitude distortions in opposite directions (5). These methods fail, however, to capture dynamic changes that occur over time due to physiological mechanisms such as respiration (6,7), subject motion (8,9), and imperfections in the gradient system, including eddy current effects and gradient heating (10,11). These spatially-dependent field fluctuations result in residual non-linear geometric distortions and signal variations. As most fMRI studies attempt to detect BOLD contrast changes on the order of 1%, even small signal instabilities degrade temporal SNR and reduce sensitivity to detect true neural activity, yielding spurious results (12).

The issues associated with dynamic field perturbations have motivated the development of various strategies to measure B₀ fluctuations during fMRI, usually at the cost of modifying the sequence and timing of acquisition. Dynamic spatially-resolved field maps may be estimated from the phase evolution of each EPI volume if a second echo is acquired using accelerated readouts (dynamic off-resonance correction with multi-echo acquisition [DOCMA]) (3); however, acquiring two volumes per TR places a limit on spatial resolution. This spatiotemporal constraint can be avoided by jittering the echo time (13) or alternating the spatial encoding direction (14) for consecutive time points. However, these modifications fundamentally alter the fMRI acquisition, potentially inducing additional BOLD contrast variations, and are not rapid enough to accurately characterize respiration-induced B₀ changes (15). Alternatively, coil-dependent phase offsets may be measured in a separate reference scan and subtracted from EPI data, which enables generation of dynamic field maps from single-echo EPI (16,17). In general, data-driven methods are limited by signal dropout, geometric distortions, and phase unwrapping, particularly at ultra-high fields and in highly heterogeneous regions such as air-tissue interfaces and post-operative sites.

Ideally, optimal shim parameters should be calculated for each slice, to enable correction for continuous physiological effects (18). Currently, the only existing solution for real-time field monitoring is external NMR field probes, which allows independent field measurements to be sampled concurrently with the imaging process at discrete locations around the object (19). Multiple studies have demonstrated that physiological and hardware-related temporal B₀ variations can be effectively modeled by a series of low-spatial-order expansions (9,20,21). Thus, fitting SH functions to field probe measurements allows correction for field fluctuations that occur due to both hardware imperfections (21) and physiological mechanisms (22). Correction can be performed either retrospectively (23), or prospectively by dynamically updating the scanner shim currents in real time (24). Van Gelderen et al demonstrated real-time shimming capability to compensate for respiration-induced B₀ fluctuations (25); however, this approach requires subject-specific training to calibrate phase changes related to chest motion and cannot correct for other sources of field perturbations.

Navigator methods offer a more efficient solution for measuring these low-spatial-order B₀ variations by sampling a small additional amount of k-space data, while circumventing the need for additional instrumentation. Double volumetric navigators (DvNavs), based on a pair of highly-accelerated, low-resolution 3D EPI acquisitions interleaved with the host sequence, may also be used to generate a spatially resolved field map for each volume (26); however, the time required for DvNav encoding would place a substantial burden on the fMRI acquisition. Ward et al. first proposed measuring linear B₀ inhomogeneities from the phase difference between orthogonal projections with different TEs to enable real-time shimming (8). Cloverleaf navigators combine motion and shim measurement in a single trajectory and measure B₀ inhomogeneities directly from shifts in the k-space domain (27). However, as spatial encoding takes time, most navigator solutions increase the minimum TE or decrease acquisition efficiency if interleaved with the host sequence. Furthermore, most of these prior navigator methods cannot resolve higher-order spatial field patterns. Versluis et al. used a combination of one-dimensional navigators and sensitivity encoding to approximate the spatially-resolved B₀ field, although this requires explicit knowledge of the coil sensitivity profiles (28).

FID navigators (FIDnavs) measure the signal from each receiver coil without any spatial encoding and thus can be acquired extremely rapidly with minimal impact on the sequence (29). Measuring the phase evolution between two FID signals can compensate for global respiratory-induced frequency fluctuations and system frequency drifts in EPI time series (7,10,30); however, this is insufficient to correct for non-linear geometrical distortions that arise from more localized B₀ field variations. In this work, we propose a new method for dynamic distortion correction in EPI time series that leverages the spatial encoding information provided by the multi-channel coil arrays to enable characterization of spatiotemporal B₀ fluctuations from FIDnavs embedded in each slice (31,32). This approach overcomes the limitations of previous MR-based solutions by enabling fast calculation of higher-order shim parameters, without the need for spatial encoding, image reconstruction or phase unwrapping algorithms, or explicit calculation of coil sensitivity profiles. In this work we evaluate the accuracy of FIDnav-based voxel shift measurements and assess the improvement in BOLD time-series stability that can be achieved using FID-navigated slice-wise dynamic distortion correction in fMRI. Preliminary results of this study have been presented in abstract form (33).

Methods

B₀ field measurements from FIDnavs

As described in Wallace et al. (2020), FIDnavs measure the signal integral over the excited slice of the underlying spin density distribution, modulated by the B₀ inhomogeneities and receive coil sensitivities at each spatial location. This may be approximated by the discrete summation of a complex-valued multi-channel reference image with matched contrast properties. Dynamic B₀ field changes may be expressed as a series of low-spatial-order basis functions: ΔB_0,n(r) = ΔB_0,0(r) + β(r)b_n, where r denotes the spatial coordinate and n indexes time. A forward model can be generated by simulating the effect of changes in these inhomogeneity coefficients on the complex-valued FIDnav signals (y_j,n), with spatial encoding provided by a multi-channel reference image:

$$\left[\begin{array}{c}{y}_{1,n}\\ y_{2,n}\\ .\\ .\\ .\\ y_{N_c,n}\end{array}\right]=\left[\begin{array}{c}{S}_{1,0}\\ S_{2,0}\\ .\\ .\\ .\\ S_{N_c,0}\end{array}\right]exp\left(i\gamma {\tau }_{NAV}\beta b_n\right)$$ [1]

where y_j,n is the measured FIDnav from coil j at acquisition n; each S_j,0 is a 1 × N_p vector of the complex pixel intensities of a reference image with N_p pixels, measured by coil j; γ is the gyromagnetic ratio (in rad/s); τ is the echo time of the reference image (designed to match the sampling time of the FIDnav); β is an N_p × N_b matrix representing the N_b basis functions and b_n is an N_b × 1 vector representing the inhomogeneity coefficients at acquisition n. In-plane SH functions up to second order are represented by five inhomogeneity coefficients $b=\left[b_0,b_x,b_y,b_{x^2-y^2},b_{xy}\right]$. These unknown coefficients at each time point can be computed using a non-linear algorithm that minimizes the residual sum-of-squares error between the forward model and the measured FIDnavs at each excitation:

$${\widehat{b}}_n=arg\underset{b_n}{min}{\Vert y_n-f\left(b_n\right)\Vert }^2$$ [2]

Theoretically, the central k-space point of the single-shot EPI trajectory may yield similar information to an FIDnav. However, in practice, gradient delays, eddy currents, and B₀ inhomogeneities (which may all be considered as background field gradients) deflect the EPI trajectory from its prescribed path. Thus, in the presence of system imperfections and local B₀ offsets, the EPI readout no longer passes through the center of k-space, and a simple forward model cannot accurately predict the measured signal at the assumed center of k-space (Supporting Figure S1). An accurate forward model would require exact knowledge of the trajectory error, which is not available to us because many of these gradient errors vary dynamically. In contrast, the FIDnav is acquired without any gradient encoding and thus the FID signal is not affected by gradient delays or dynamically varying trajectory errors. Changes in the FIDnav signal reflect changes in the local B₀ field, as well as eddy currents from preceding gradients, which may be modeled by low-spatial-order SH functions.

Reference image for EPI

The FIDnav signal model requires multi-channel GRE reference image data with matched contrast properties to be acquired for each subject (32). Acquiring two datasets with reversed gradient polarities eliminates phase errors arising from gradient delays and other system imperfections (34). One challenge of this approach is that, to achieve full brain coverage, TRs for single-shot EPI acquisitions are typically on the order of 2–3 seconds. For a matrix size of 64×64 and TR of 2 s, acquisition of reference data for model calibration would take ~4 minutes. In this work, we accelerate reference data acquisition using a segmented EPI reference image with three encoding lines per shot (Fig. 1A), and blip-up and blip-down encoding, to provide self-referencing compensation for the effects of gradient imperfections on the encoded signal. We also assess the minimal resolution requirements for the reference image data to further reduce the time required for forward model generation.

Figure 1.

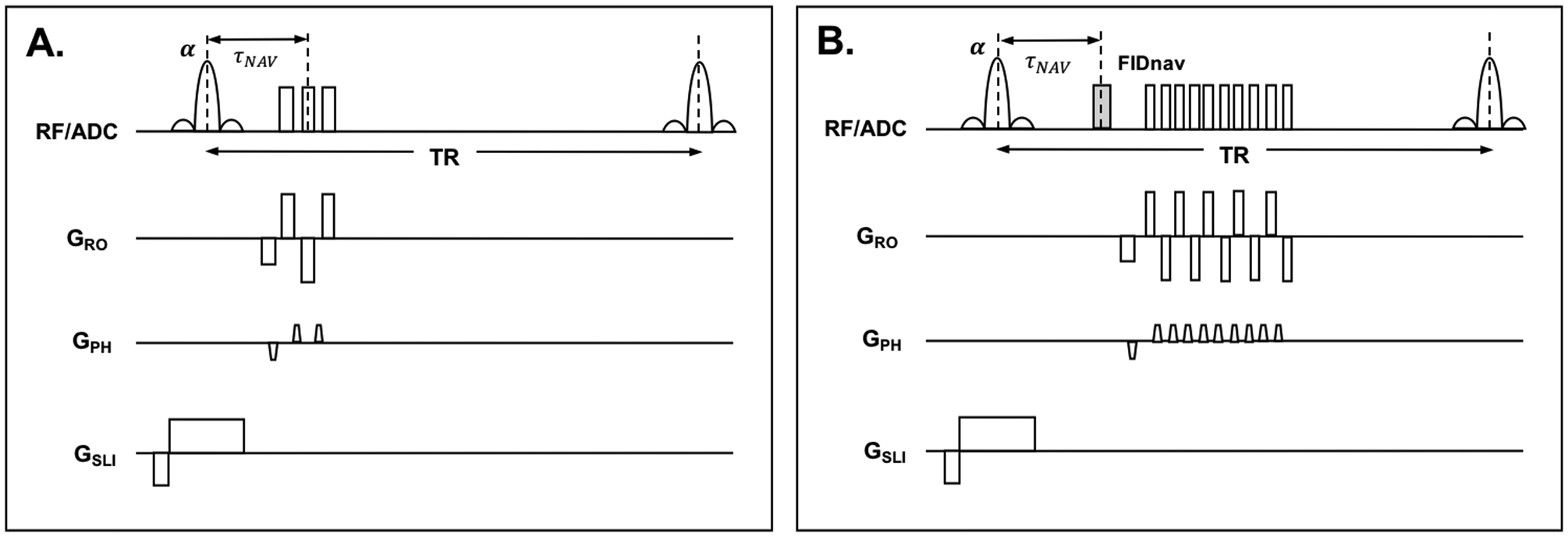
Pulse timing diagram showing segmented EPI reference scan (A) and FID-navigated EPI time series scan (B).

MRI Experiments

All imaging experiments were performed at 3T (MAGNETOM Skyra; Siemens, Erlangen, Germany) using the vendor-supplied 64-channel head coil. Five volunteers were scanned after providing written informed consent in accordance with the institutional IRB-approved protocol. An FIDnav module was inserted into a gradient-echo EPI sequence between each slice-selective excitation and EPI readout (Fig. 1B). A schematic of the experimental design is shown in Figure 2.

Figure 2.

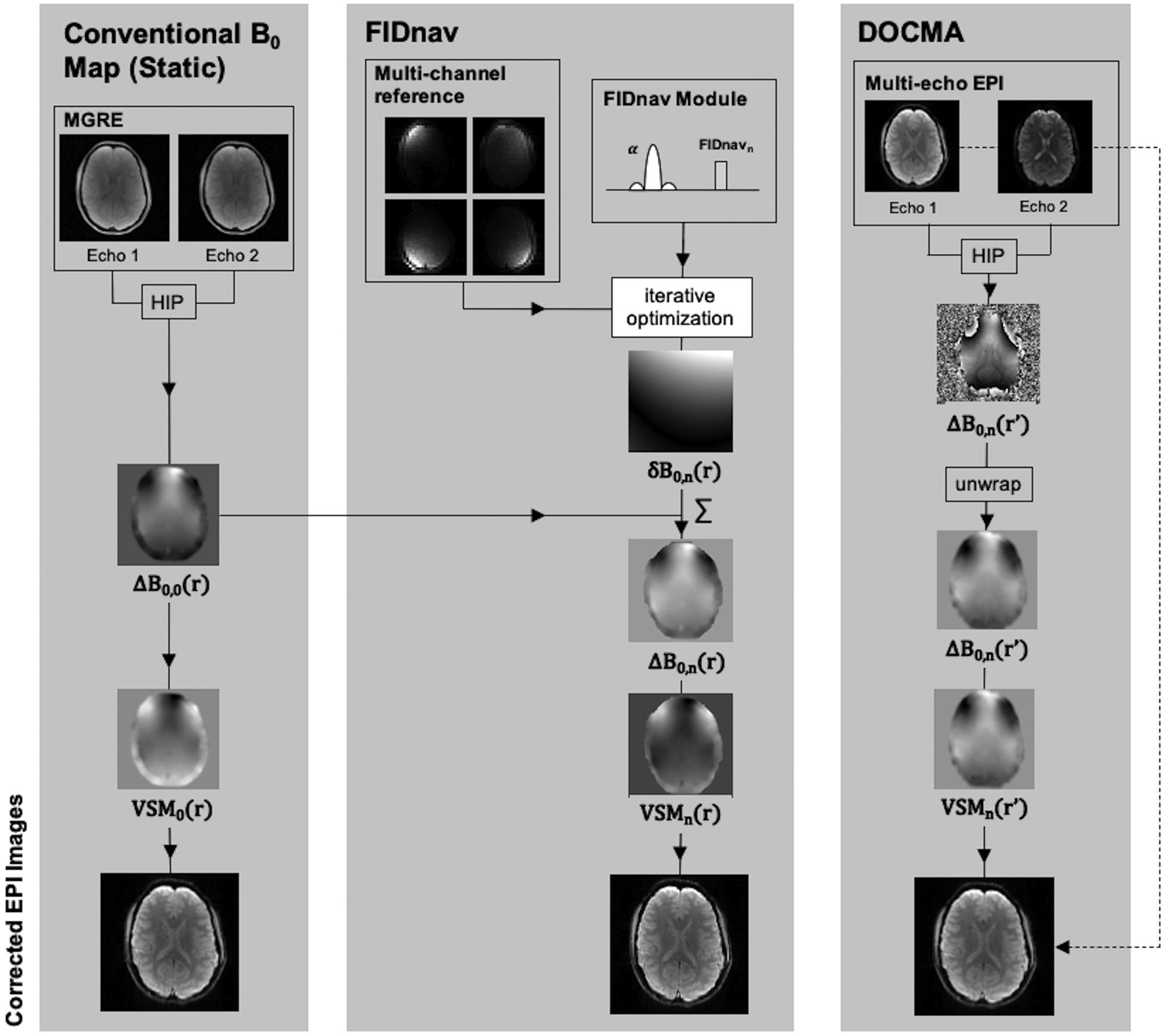
Experimental design to compare geometric distortion correction using voxel shift maps (VSMs) computed from conventional static ΔB₀ field measurements from a multi-gradient-echo (MGRE) scan, and from dynamic FIDnav- and DOCMA-based field offsets. Static ΔB₀ field maps were calculated by taking the Hermitian inner product (HIP) over channels of the phase difference between multi echo images and scaling to obtain ΔB_0,0(r). Coefficients describing the change in B₀ were estimated from FIDnavs and used to compute maps of δB_0,n(r). These were superposed with the static ΔB₀ map to compute ΔB_0,n(r) at each time point n. For the DOCMA approach, maps of ΔB_0,n(r’) were computed in distorted image space from the HIP of multi-echo EPI images. VSMs were computed from each ΔB₀ measurement and used to unwarp the first-echo EPI image.

Experiment 1: Phantom validation

To validate the accuracy of FIDnav-based B₀ measurements in an EPI sequence and assess the minimal requirements for forward model generation, a cylindrical water bottle was scanned with manual adjustment of the scanner shim settings. A segmented EPI reference image was acquired with TE 5 ms, TR 1000 ms, EPI factor 3 and blip-up and blip-down encoding (total acquisition time 22 s). Axial FID-navigated multi-echo EPI scans were acquired with the following parameters: TE₁/TE₂ 16.0/33.8 ms, TR 1000 ms, 10 repetitions, GRAPPA acceleration factor 2. The FIDnav module sampled 64 points in 0.4 ms, centered on T_NAV 5 ms. Both reference and FID-navigated scans were acquired with flip angle 90°, receiver bandwidth 2232 Hz/pixel, FOV 192 mm, voxel size 3 mm isotropic, 16 slices with 20% inter-slice gap, centered at the isocenter of the magnet. First and second-order shim settings were manually adjusted up to ±10 μT/m and ±100 μT/m² in increments of 2.5 μT/m and 25 μT/m², respectively. EPI images were reconstructed using Dual-Polarity GRAPPA (DPG), which incorporates Nyquist ghost correction into the parallel imaging reconstruction (35). Acquisition of two echoes per TR enabled calculation of spatially-resolved field maps using the DOCMA approach (3). Specifically, the phase evolution between echoes was obtained via a weighted sum over channels of the Hermitian inner product and used to compute ΔB₀.

Unwrapped field maps were computed in SPM (Statistical Parametric Mapping v12, Wellcome Trust Centre for Neuroimaging, London, UK, www.fil.ion.ucl.ac.uk/spm/) and smoothed with a 5-mm FWHM kernel. SH functions were fit to the measured pixel-wise field maps in the foreground region, masked using intensity thresholding. Field inhomogeneity coefficients up to second order were estimated from each FIDnav measurement and compared to those measured using multi-echo EPI. This analysis was repeated following retrospective down-sampling of the reference image data to assess the impact of image resolution on the accuracy of model-based FIDnav shim parameter estimation. Field estimates were converted into voxel-shift maps (VSMs):

$$d_{PE}\left(x\right)=\frac{\gamma \Delta B_0\left(x\right)}{B{W}_{pp}}$$ [3]

where BW_pp is the effective bandwidth per pixel along the phase-encoding direction. VSMs were applied to the reconstructed EPI data using SPM.

Experiment 2: Geometric distortion correction in volunteers

To compare the performance of FIDnav-based VSMs to the reference data-driven method, FID-navigated multi-echo EPI images were acquired in five volunteers with the following conditions: 1) resting position, standard shim settings; 2) applied field offset in the phase-encoding (Y) direction of ±10 μT/m; and 3) with subjects touching their nose. Scan parameters for the FID-navigated multi-echo EPI scans were as follows: T_NAV 5 ms, TE₁/TE₂ 18/48.1 ms, TR 2000 ms, receiver bandwidth 1860 Hz/pixel, in-plane resolution 2 mm, GRAPPA factor 2 and 6/8 partial Fourier. Posterior-anterior phase-encoding was used to avoid signal pileup in the frontal cortex (36). Segmented EPI reference images with blip-up and blip-down encoding were acquired for forward model generation with TE 5 ms, TR 2000 ms, receiver bandwidth 2232 Hz/pixel and matrix size 32×32, yielding an in-plane resolution of 7 mm (total acquisition time 44 s). Both sets of scans were acquired with flip angle 70°, FOV 224 mm, 20 slices with 2.5 mm slice thickness and 20% inter-slice gap, and fat suppression. In addition, a multi-echo GRE field map was acquired for static distortion correction (TE₁/TE₂ 4.92/7.38 ms, TR 250 ms, flip angle 25°, receiver bandwidth 800 Hz/pixel, in-plane resolution 2 mm; matched FOV, slice thickness and spacing). An axial T₂-weighted fast-spin-echo (FSE) image (TR 7360 ms, TE 78 ms, receiver bandwidth 220 Hz/pixel, in-plane resolution 0.9 mm, with matched FOV, slice thickness and spacing) was acquired to provide an anatomical reference.

Multi-channel EPI images were reconstructed using DPG and combined using sum-of-squares. B₀ inhomogeneity coefficients up to second order were measured from FIDnavs in each slice. Estimated field difference maps were superposed onto the static field map and converted into VSMs to correct for geometrical distortions. VSMs estimated using the reference DOCMA method were also applied for comparison. Static, FIDnav-based and DOCMA distortion corrected images were compared to FSE images, assuming these have minimal distortion. In one volunteer, VSMs were also calculated from the first EPI echo image using the method proposed in (17). Structural images were masked using FSL’s BET tool (FMRIB, Oxford, UK, www.fmrib.ox.c.uk/fsl/). Normalized root-mean-square error (NRMSE) was calculated within the brain region for EPI images with induced geometric distortions corrected using each method, relative to a reference EPI image with static distortion correction. Differences in NRMSE were assessed using two-sided paired Wilcoxon rank sum tests with α=0.05.

Experiment 3: Temporal stability of BOLD signal in volunteers

To evaluate the improvement in BOLD signal stability with the proposed approach, fMRI scans were acquired at rest and while the volunteer performed a continuous nose-touching action. Scan parameters were identical to those used in Experiment 2, with 120 EPI volumes acquired in each series, resulting in a total acquisition time of ~4 minutes. Static distortion correction was applied using field measurements from a MGRE acquisition. Dynamic distortion correction was applied by superimposing second-order field changes estimated from FIDnavs on the static field map for each time point (Fig. 2). DOCMA-based correction was also applied for comparison. Distortion-corrected images were aligned to the first image in each series using rigid-body registration in SPM. Temporal SNR (tSNR) was computed as the ratio of the mean and standard deviation of each voxel time-course for the first echo image in each series as a measure of BOLD signal stability for static and dynamic distortion correction, with and without rigid-body realignment (37). Improvement in mean tSNR associated with dynamic distortion correction was characterized by comparing to images reconstructed using the static distortion correction scheme. The relative tSNR gain was calculated as follows:

$$\Delta tSNR\left(\text{\%}\right)=100\frac{\langle tSN{R}_{\mathit{\text{dynamic}}}\left(r\right)\rangle -\langle tSN{R}_{\mathit{\text{static}}}\left(r\right)\rangle }{\langle tSN{R}_{\mathit{\text{static}}}\left(r\right)\rangle }$$ [4]

where 〈tsNR(r)〉 denotes the mean tSNR over all voxels within the whole-brain mask or gray matter regions (segmented in SPM). Significance of the one-sided Wilcoxon signed rank test for median tSNR gain above zero was tested.

Functional MRI data analysis was performed on the first echo image series using SPM. Functional images were slice-time corrected; no additional registration was applied as our preprocessing pipeline includes realignment. The data were smoothed spatially with a Gaussian kernel (FWHM 4 mm) to improve SNR. For the nose touching experiment, arm motion events were modeled using a general linear model. These events were modeled as boxcars representing the duration of each block, and were convolved with the canonical hemodynamic response function included with SPM. Differences in brain activation with this condition and rest condition were compared using paired t-tests within SPM. An uncorrected threshold of P<0.001 was considered statistically significant.

Results

Experiment 1: Phantom validation

A comparison between field coefficients measured using the proposed approach and the reference EPI-based method for applied shim changes is shown in Figure 3. FIDnav measurements were computed using a reference image matrix size of 32×32, as this provided a good trade-off between the efficiency of both reference data acquisition and shim parameter computation and the accuracy of field measurements (Supporting Table S1). The proposed approach accurately characterized shim changes, with mean absolute errors of 0.49 ± 0.06 μT/m (first-order) and 1.22 ± 0.37 μT/m² (second-order) relative to the reference data-driven approach for maximum changes of 10 μT/m and 100μT/m², respectively. Maps of normalized signal intensity before and after correction for first- and second-order shim changes are shown in Supporting Figure S2.

Figure 3.

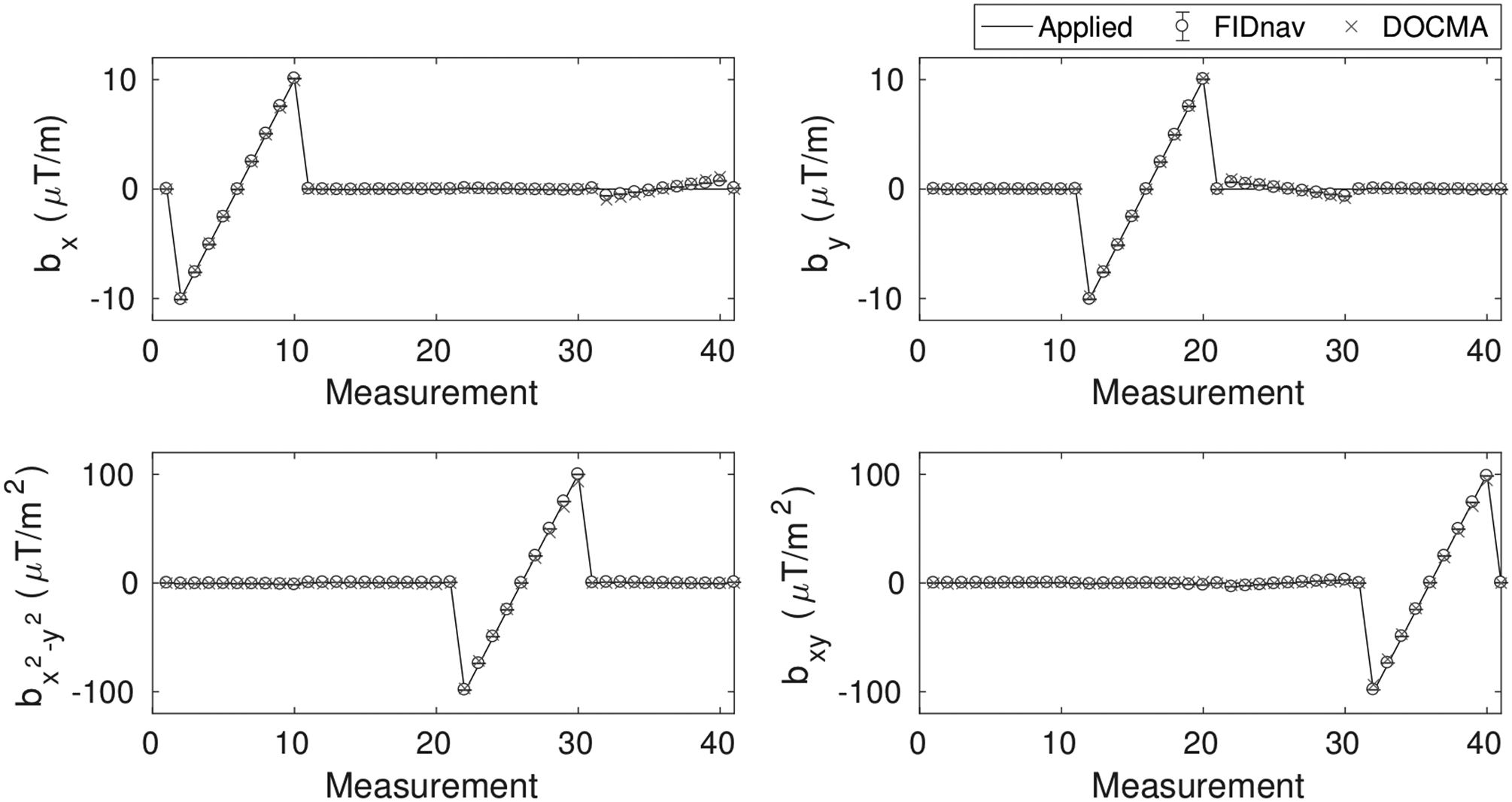
Applied first- and second-order field offsets in a phantom showing field inhomogeneity coefficients estimated from the proposed FIDnav-based approach and the reference DOCMA method. FIDnav measurements accurately characterized field changes up to second order in the phantom study.

Experiment 2: Geometric distortion correction in volunteers

Figure 4 shows a comparison of the voxel shifts induced by modifying the shim settings along the phase-encoding direction and by the volunteer touching their nose, computed with the proposed FIDnav-based approach and the reference DOCMA method. Increasing the Y-shim gradient resulted in negative voxel shifts in the frontal brain region (stretching) with respect to the posterior-anterior phase-encoding direction, while nose touching in volunteers led to positive voxel shifts in this region. Difference maps confirm that these two measures are in good agreement. Relative to the spatially-resolved EPI-based VSMs, correction with FIDnav field estimates led to a substantial reduction in the residual voxel shift (Fig. 4C–D). The mean absolute error of voxel shifts reduced from 1.01 ± 0.67 mm to 0.06 ± 0.10 mm (Y-shim) and 0.25 ± 0.25 mm to 0.09 ± 0.17 mm (nose touching) following correction with FIDnav estimates. Figure 5 illustrates geometric distortion correction results in a representative volunteer following an adjustment in Y-shim and during nose touching. Comparison with anatomical image data shows that static distortion correction resulted in residual unwarping errors, which are most easily observed in the frontal brain regions. FIDnav field estimates accurately compensated for geometric distortions induced by both changing shim settings and the nose-touching action, while residual unwarping errors are present in the DOCMA method. Table 1 lists the mean NRMSE values calculated in each EPI image relative to the reference EPI image, which confirms that accuracy of geometric distortion correction is improved following FIDnav correction. Distortion correction results using phase maps derived from single-echo EPI are also shown for comparison in Supporting Figure S3. Both data-driven approaches produced unreliable field estimates in regions of high inhomogeneity, which exhibit large geometric distortions and signal dropout at longer echo times.

Figure 4.

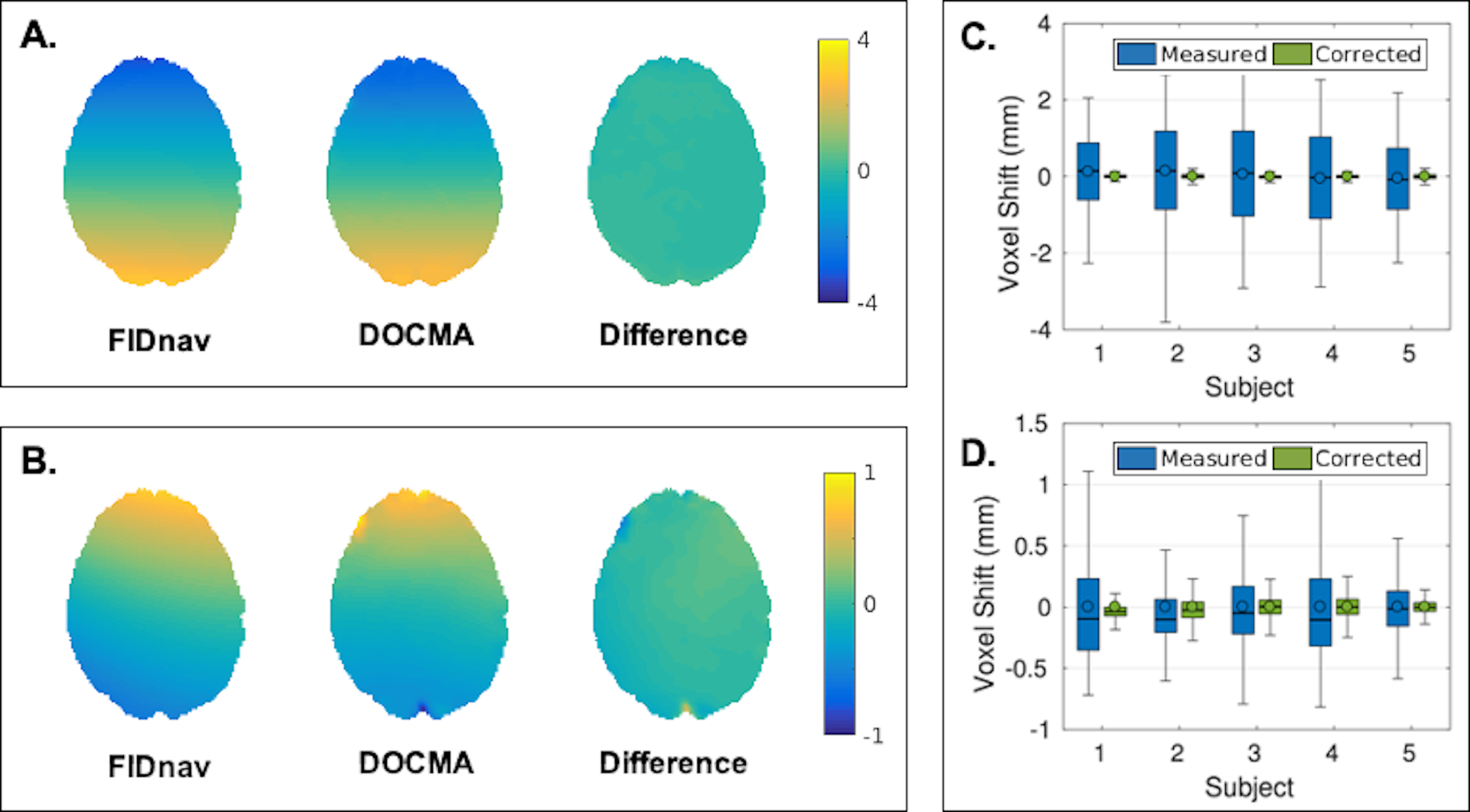
Comparison of voxel shift maps (VSMs) in an axial slice showing the residual geometric distortion in the brain induced by +10μT/m change in the Y-shim gradient (A) and nose touching (B) in a representative volunteer, measured from FIDnavs and the reference DOCMA method. Voxel shifts measured using DOCMA (“measured”) and after subtraction of voxel shifts modelled using the proposed FIDnav method (“corrected”) for all subjects in the brain region with applied Y-shim gradient (C) and with nose touching (D). Boxes delineate 25^th and 75^th quantiles, with whiskers extending to the maximum voxel shifts; median and mean are denoted by solid lines and open circles, respectively. Difference maps and residual voxel shifts confirm that spatial field offsets estimated by the proposed FIDnav-based approach are in good agreement with pixel-wise estimates from multi-echo EPI.

Figure 5.

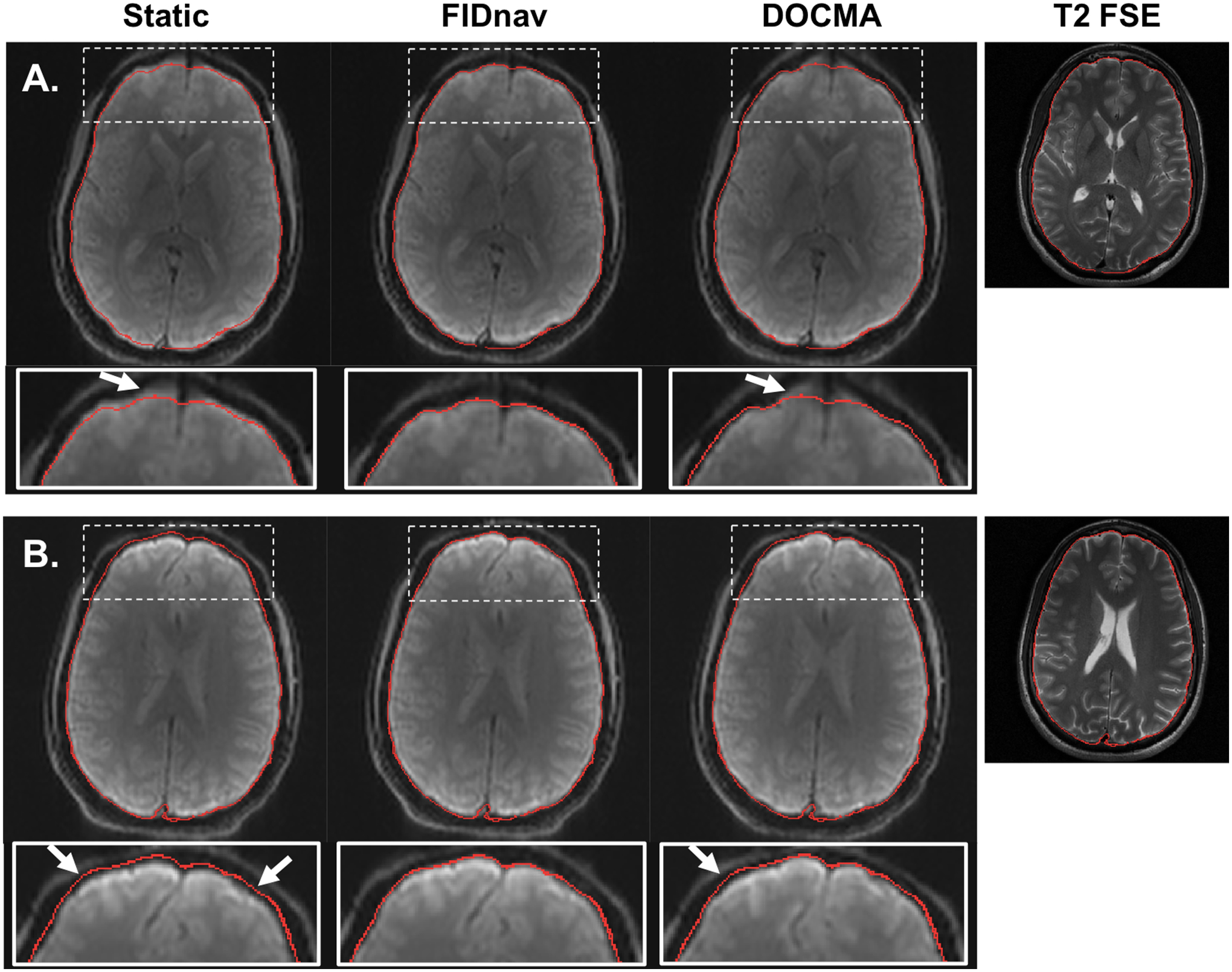
Distortion correction results in a representative volunteer following correction with a static voxel shift map (VSM) and with VSMs obtained from FIDnav and DOCMA field measurements for changing Y-shim (A) and nose touching (B). The brain boundary extracted from T2 FSE (shown on the right for comparison) is overlaid on each corrected image. Arrows denote regions with residual unwarping errors, observed with both static and DOCMA correction. FIDnavs enable reliable geometric distortion correction for both shim changes and nose touching.

Table 1.

Normalized root-mean-square error (NRMSE) in percent after change in Y-shim gradient and with nose touching following distortion correction with static GRE, FIDnav and DOCMA voxel shift maps, respectively. Significance of paired Wilcoxon rank sum test is indicated by *.

NRMSE (%)	Y-Shim			Nose Touching
Subject No.	Static	FIDnav	DOCMA	Static	FIDnav	DOCMA
1	5.2	2.3	2.4	4.0	2.5	2.6
2	5.0	1.5	1.6	1.7	1.3	1.4
3	4.8	1.4	1.5	2.2	1.4	1.3
4	5.3	2.0	0.5	1.4	1.6	1.6
5	6.7	2.6	6.3	3.1	1.5	1.7
Mean	5.5	2.0*	2.14*	2.49	1.7	1.7
SD	1.0	0.6	1.59	1.05	0.5	0.5

Experiment 3: Temporal stability of BOLD signal in volunteers

Figure 6A shows the difference in standard deviation (SD) with static and FIDnav-based dynamic distortion correction for no motion and nose touching, before and after rigid-body realignment. Prior to realignment, the image series with static correction exhibited substantially higher SD than the FIDnav-corrected images for both no motion and nose touching. Rigid-body realignment accounted for global field changes, resulting in highly similar SD maps for static and dynamic distortion correction in the no motion case. Residual differences can be observed in the frontal brain region for nose touching, as changing geometric distortions are accounted for by FIDnav field correction, but not by image realignment. Figure 6B shows a comparison of the signal intensity in this region with static and dynamic distortion correction; signal fluctuations induced by nose touching are successfully removed by FID-navigated correction. The tSNR distribution for each correction scheme is summarized in Table 2. Figure 7 shows the tSNR gains within the whole brain and segmented gray matter across all subjects. Before realignment, FIDnav correction resulted in significant median tSNR increase of 30% and 24% within the brain for no motion and nose touching, respectively. After realignment, tSNR gains for the nose-touching paradigm were 1.6% and 2.8% in whole-brain and gray matter regions, respectively, while there was no gain in tSNR for cases without intentional field perturbations. Results from DOCMA correction were more variable (Fig. 7C).

Figure 6.

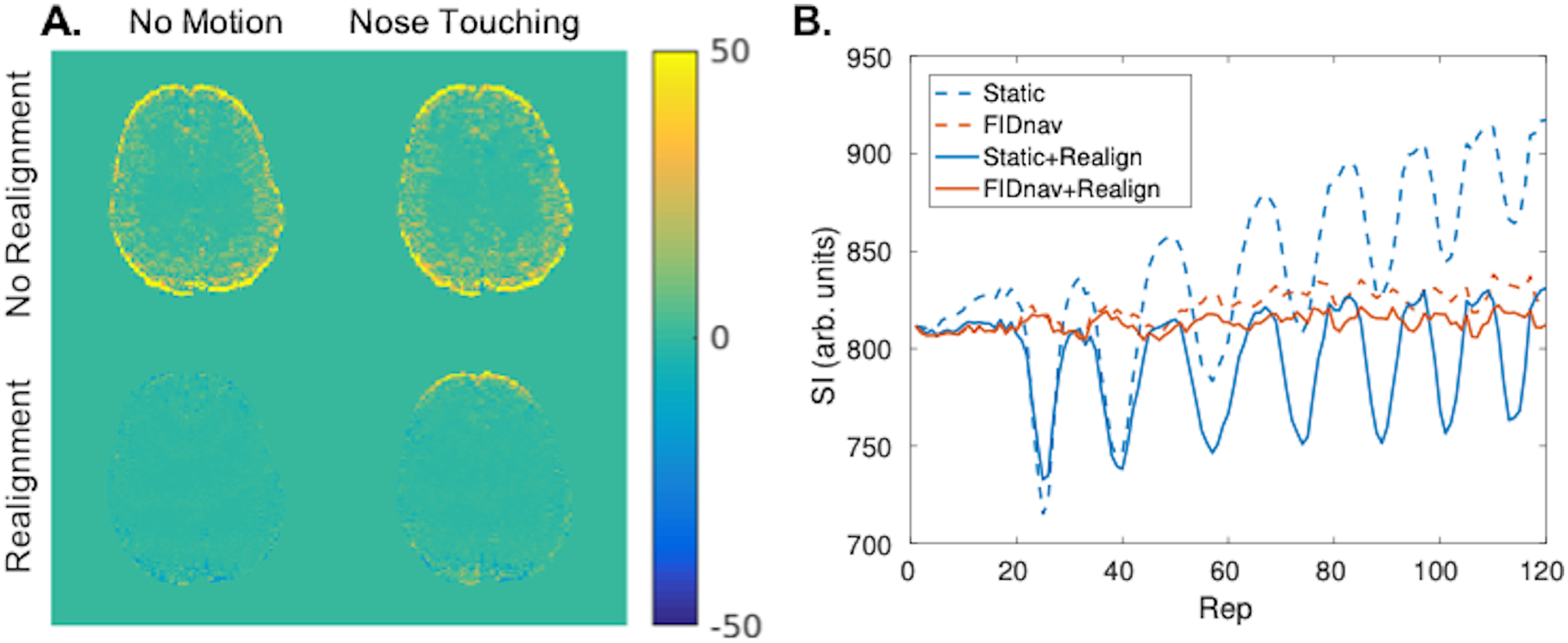
Maps showing difference in standard deviation (SD) between static distortion correction and FID-navigated distortion correction for no motion and nose touching paradigms, with and without rigid-body realignment (A). FIDnavs improved the SD of the raw image series by accounting for field changes over the course of the scan. Image realignment accounted for image drift due to global field changes; however, was insufficient to compensate for geometric distortions induced by nose touching in the frontal brain region. Signal within a ROI in the frontal brain region is shown for static and FIDnav-based distortion correction, with and without image realignment (B). FIDnav-based correction successfully removed signal fluctuations due to dynamically changing distortions.

Table 2.

Summary of the tSNR distribution with static and FIDnav-based dynamic distortion correction, reported as the mean ± standard deviation of the tSNR within each ROI across all five subjects.

	Without Image Realignment				With Image Realignment
	No Motion		Nose Touching		No Motion		Nose Touching
	Static	FIDnav	Static	FIDnav	Static	FIDnav	Static	FIDnav
Whole Brain	51 ± 23	64 ± 26	45 ± 21	53 ± 23	67 ± 26	65 ± 26	56 ± 23	57 ± 23
Gray Matter	49 ± 27	66 ± 30	42 ± 23	51 ± 26	68 ± 30	66 ± 30	55 ± 26	56 ± 26

Figure 7.

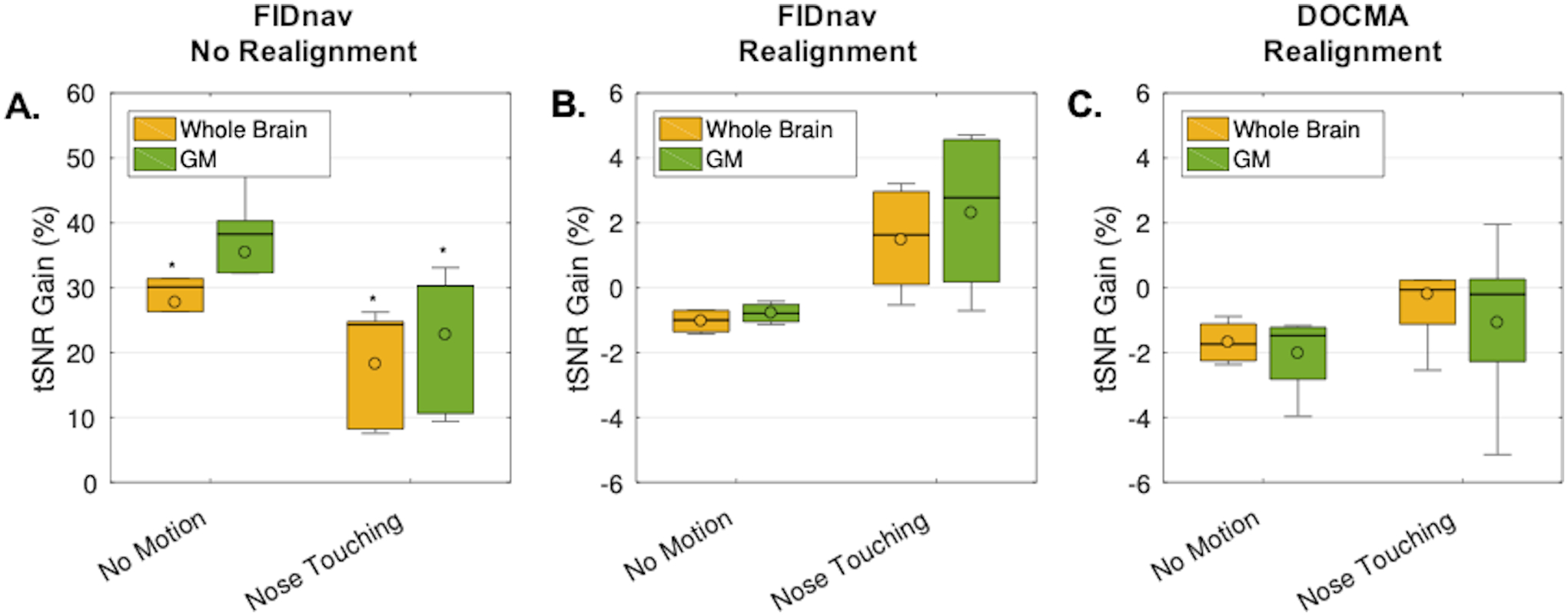
Boxplots showing the tSNR gains across volunteers for the no motion and nose touching paradigms for FIDnav-based dynamic distortion correction, without (A) and with (B) rigid-body realignment, and DOCMA-based dynamic distortion correction with rigid-body realignment (C). The tSNR gain was evaluated relative to static distortion correction in the whole-brain and in gray matter (GM) for each subject and scan. In the raw image series, FIDnavs resulted in a significant tSNR gain. Following rigid-body realignment, FID-navigated dynamic distortion correction results in a small tSNR improvement relative to static correction. DOCMA results were more variable. Boxes delineate 25^th and 75^th quantiles, with whiskers extending to the most extreme points. Median and mean are denoted by solid lines and open circles, respectively. Results of one-sided Wilcoxon signed rank test denoted by *.

Maps of brain activation detected during nose touching are displayed in Figure 8 for static and FIDnav-based dynamic distortion correction. In both cases, activation is detected in the motor cortex; however, with static distortion correction, regions of false positive activation are also detected near the edges of the brain due to geometric distortion patterns that correlate with the motor task. These false positive activations are successfully removed with FIDnav-based correction.

Figure 8.

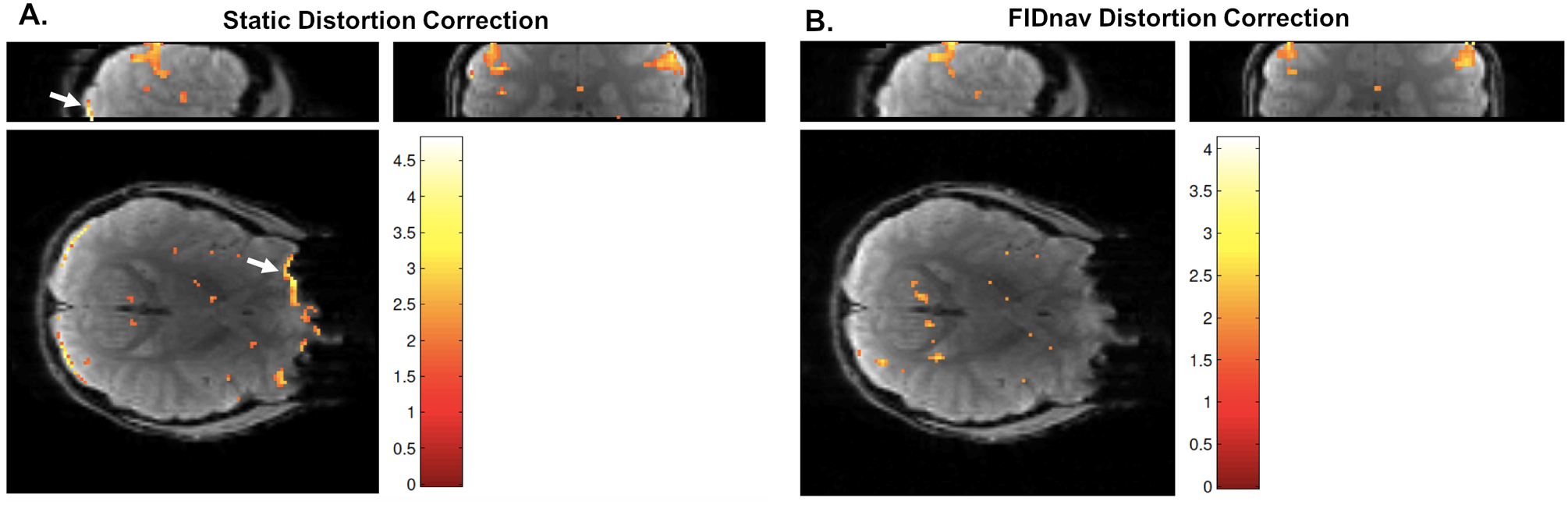
Activation detected during nose touching in a volunteer, following image realignment, with static distortion correction (A) and FID-navigated distortion correction (B). Activation is detected in the motor cortex, as expected with this paradigm. With static distortion correction, false positive activations are also detected in the frontal and posterior brain regions due to residual unwarping errors. FIDnav distortion correction successfully removes these false positive activations.

Discussion

We have proposed a new approach for slice-wise dynamic distortion correction in fMRI using ultra-short FIDnavs and spatial encoding provided by multi-channel array coils. To our knowledge, this is the first study to perform dynamic distortion correction in EPI using FIDnavs. Our results in phantom and volunteer experiments demonstrate that field changes up to second order can be accurately characterized by FIDnavs embedded in each slice of an EPI sequence using information from a low-resolution reference image. In single-shot EPI, dynamic magnetic field perturbations result in shifts and geometric distortion of the reconstructed images. Comparison with a reference anatomical scan confirms that geometric distortion correction with FIDnavs improves image fidelity in the presence of spatiotemporally-varying magnetic field changes.

In fMRI, field variations give rise to intensity fluctuations within each voxel, adversely impacting the tSNR of the BOLD signal time-course. The dominant impact of field fluctuations in this study was a shift in image space, which was corrected by both FIDnav-based dynamic distortion correction and conventional realignment in image space. However, the nose-touching paradigm also induced higher-order field changes, which could not adequately be compensated by rigid-body realignment, resulting in spurious signal fluctuations and false positive activations. These were successfully removed by the proposed FIDnav correction, with a small gain in tSNR observed across the whole brain region. These results demonstrate that our proposed method can improve BOLD sensitivity by compensating for residual geometric distortions in the reconstructed images.

Overall, the proposed FIDnav-based method was comparable to, or in some cases, outperformed the reference DOCMA approach with respect to both geometric distortion correction and improvement in BOLD signal stability. Reliable phase unwrapping and the invertibility of distortion are both crucial for EPI-based field mapping approaches. We used an accelerated acquisition to minimize ΔTE; however, we found that even with shorter TEs facilitated by acceleration, signal dropout in the second echo led to unreliable phase correction in regions of high inhomogeneity. Figure 5 illustrates that FIDnav correction outperformed DOCMA in the frontal brain cortex, where field inhomogeneity is higher. Although reliable measurement of activation in brain regions with high B₀ inhomogeneity remains challenging, we believe that our method represents an improvement over existing techniques for obtaining reliable distortion correction in the presence of dynamic field perturbations. Unwrapping errors led to temporal instability in field measurements in some subjects, which may help explain why DOCMA failed to improve tSNR. While previous studies have demonstrated it is possible to estimate field changes from the phase information in single-echo EPI (16,17), our proposed method has several key advantages over data-driven dynamic distortion correction approaches, as these require reconstruction and phase unwrapping of image data to perform field correction. This limits their suitability and utility for real-time applications or for correcting phase inconsistencies between segments in multi-shot EPI.

Our proposed FIDnav-based solution also has several advantages over other shim navigator approaches. One-dimensional navigator signals have previously been used to measure linear field changes from the phase difference between projections with different TEs in image space (8) or shifts in k-space (27). These methods assume that inhomogeneities along each axis can be measured independently; however, dephasing effects mean the phase evolution of the projection data is not necessarily linearly related to B₀ inhomogeneities in that direction (38). Thus, projection data alone is insufficient to resolve field changes in multiple directions without a priori information provided by a reference scan (39). Also, the time required for spatial encoding may substantially increase the minimal TE or limit the frequency of shim updates. Subsequent studies demonstrated that encoding information provided by multi-channel coil arrays allows low-spatial-order B₀ information to be recovered from an unencoded FIDnav signal. The first realization of this approach considered the temporal evolution of the FID signal to estimate ΔB₀ at each time point (31); however, R₂* relaxation and ΔB₀-induced dephasing contribute to non-linear phase evolution, limiting application of this technique in vivo. Changes in ΔB₀ can be more reliably estimated relative to a reference time point using an FIDnav sampled at the echo time of the reference image, as this approach makes no assumption that the FID signal evolves linearly as a function of ΔB₀ (32). An advantage of this method is that no explicit calculation of coil sensitivity profiles is required as this information is inherently encoded within the reference image. As the minimal TE/TR is extended only by the duration of the FIDnav (0.4 ms) with encoding provided by the reference image, our method enables slice-wise dynamic distortion correction without compromising spatiotemporal resolution.

To enable spatially-resolved field measurements from FIDnavs, a multi-channel reference image is required to create a forward model of the FIDnav signals from each receiver coil. We minimized the time needed to acquire this reference data by using a low-resolution (7 mm in-plane) multi-shot EPI sequence, rather than a GRE sequence used in previous work (32). As most fMRI studies already acquire a static field map, model calibration could be integrated in a single step using a multi-echo reference scan. The effect of respiration-induced field perturbations on the reference image is assumed to be minimal at 3T. Future work could investigate reordering reference data segments to minimize sensitivity to phase errors using the fast low-angle excitation echo-planar technique (FLEET) (40). In this work, we estimated field changes up to second order, which enabled validation in a controlled phantom study with modification of the scanner shim settings. With a 64-channel head coil, it is possible to solve for B₀ inhomogeneity coefficients up to third order; however, we previously did not find any significant differences between fitting second- and third-order inhomogeneity coefficients at 3T (32), and increasing the number of coefficients may make the system more sensitive to noise. The value of third-order correction may be more evident at higher field strengths, which will be the subject of future work. Like most navigator methods, our proposed approach assumes that the measured field does not change within the EPI readout and thus cannot correct for higher-frequency field changes. Currently field probes are the only method that can simultaneously monitor field changes during the EPI readout itself to compensate for trajectory deviations due to eddy currents and other hardware-related instabilities (21).

We used accelerated, multi-echo EPI to provide a reference VSM for each volume using the DOCMA approach. Acceleration limited the amount of geometric distortion by reducing the total readout time. Adjusting the scanner shim settings and nose touching in volunteers induced small, but measurable distortions in the images. All images were unwarped in SPM using either static or dynamic field estimates and aligned using rigid-body registration. As well as correcting for inter-volume head motion, global frequency changes are also compensated by image realignment. Thus, differences in tSNR following realignment represent residual unwarping errors, slice-wise shifts, realignment errors and BOLD contrast changes.

Motion is another major source of magnetic field perturbations due to the changing orientation of the susceptibility distribution as the head moves within the static magnetic field (9). We minimized head motion using foam padding, and it was assumed that the relative position of the underlying spin density distribution and the coil sensitivities remained fixed. Measurement of rigid-body head pose information using FIDnavs in 2D sequences is non-trivial as it is difficult to model the effect of out-of-plane motion (41). Our proposed approach could be combined with optical tracking (42) or other motion measurement approaches (43,44) to measure motion-induced field changes.

This work presents a proof of principle of the ability of FID navigators to correct for geometric distortions in single-shot EPI at 3T, although this method is readily extendable to other EPI-based sequences and field strengths. The tSNR gains realized with FID-navigated dynamic distortion correction are expected to be even higher at 7T as susceptibility effects scale with field strength. FIDnav-based field measurements are highly applicable in both 2D multi-shot and 3D EPI as the proposed approach does not require formation of an image and minimally impacts the sequence timing. This would enable correction for physiological and hardware-related phase variations between shots, which can corrupt individual image volumes and reduce the signal stability of the BOLD time course (45). Extension to simultaneous multi-slice (SMS) acquisitions is also feasible. In SMS acquisitions, the measured FIDnav represents the sum of the excited spins in each slice and captures shim changes across all simultaneously excited slices. A 3D spherical harmonics model may be used to compute shim changes across the volume from FIDnav measurements following each multi-band excitation, using a forward model generated from multi-slice reference data (Supporting Figure S4).

In this work, higher-order field perturbations were corrected retrospectively by updating the VSM used to unwarp each EPI image. Shim changes measured from FIDnavs could also be used to update the transmit frequency and first-order shim fields in real time. Prospective correction of higher-order field changes is becoming feasible using custom-built shim array coils (18). Real-time shimming would enable correction for the effects of magnetic field perturbations on RF excitation, fat suppression and intra-voxel dephasing, in addition to changing geometric distortions. FID-navigated dynamic distortion correction is expected to translate to improved BOLD sensitivity in fMRI studies, which could help improve localization for presurgical planning in epilepsy patients (46), the reliability of fMRI in patients with Parkinson’s and Alzheimer’s disease, and in research studies utilizing high-resolution fMRI to measure neuronal activation with sub-millimeter spatial resolution (47). This technique could also be translated to other EPI applications, such as perfusion and diffusion-weighted imaging and non-BOLD fMRI.

Conclusion

We have evaluated a new approach for slice-wise dynamic distortion correction using FIDnavs embedded in each slice of a single-shot EPI sequence. FIDnav-based dynamic distortion correction improved geometric accuracy of images acquired with magnetic field perturbations and improved tSNR of the EPI time series by accounting for global and higher-order field fluctuations. Our proposed FIDnav-based approach has several key advantages over data-driven methods: it does not fundamentally alter the acquisition and can be implemented without compromising spatiotemporal resolution. Furthermore it does not require computationally expensive image reconstruction and phase unwrapping, making it more amenable to real-time shimming applications. FID-navigated dynamic distortion correction is widely applicable and is expected to improve BOLD sensitivity in fMRI experiments at field strengths of 3T and above.