Abstract
Reducing airborne infectious risk is crucial for controlling infectious respiratory diseases (e.g., COVID-19). The airborne transmissibility of COVID-19 is high so that the common ventilation rate may be insufficient to dilute the airborne pathogens, particularly in public buildings with a relatively large occupancy density. Reducing occupancy can reduce the pathogen load thereby reducing airborne infection risk. However, reduced occupancy deteriorates work productivity due to the lost hours of work. This study proposes an occupancy-aided ventilation strategy for constraining the airborne infection risk and minimizing the loss of work productivity. Firstly, two mechanisms of occupancy schedule (alternative changeovers between normal occupancy and reduced occupancy) for reducing the airborne infection risk and loss of work productivity are revealed based on analyzing features of the indoor concentration profile of exhaled aerosols. Secondly, optimization of the occupancy schedule is developed to maximize the total time length of normal occupancy for the minimum loss in work productivity while satisfying the constraint on airborne infection risk (e.g., with the reproduction number less than one). The airborne infection risk is evaluated with the rebreathed fraction model. Case studies on COVID-19 in a classroom demonstrate that the proposed occupancy-aided ventilation is effective with an earning ratio of 1.67 (the ratio of the improvement in health outcome to the loss in work productivity) and is robust to the variable occupancy loads and occupancy flexibilities.
Keywords: Occupancy-aided ventilation, Occupancy schedule, Airborne infection risk, Rebreathed fraction, Work productivity
Graphical abstract
1. Introduction
COVID-19, caused by SARS-CoV-2, is causing substantial damages to public health. Up to September 2020, COVID-19 has caused mortality over 900,000 worldwide. As an infectious respiratory disease, COVID-19 primarily affects the respiratory tract [1], including the transmission routes of large droplets, contact, and fomite [2]. Also, more and more evidence supports that COVID-19 is spread via aerosol transmission [3]. SARS-CoV-2 survives in aerosols for multiple hours [4], causing airborne infectious risk. A possible case of COVID-19 due to airborne transmission in a restaurant in Guangzhou (China) was reported to have an airborne infection risk of 45% with 1-h exposure, and another possible case at a choir rehearsal in Skagit (USA) was reported to have an airborne infection risk of 53% with 2.5 h exposure [5].
Engineering and administrative controls (which separate the people and pathogens) are effective interventions to flatten the epidemic curve for reducing morbidity and mortality [6]. Since the transmission routes of large droplets, contact, and fomite can be effectively reduced by administrative controls of quarantine, stopping mass gathering, studying and working from home, social distancing, handwashing, surface disinfection, etc., airborne transmission becomes relatively outstanding, particularly for public buildings [7]. Ventilation, as one of engineering controls, plays a crucial role in reducing airborne infection risk [3]. Ventilation (natural ventilation or mechanical ventilation) is widely used for thermal comfort [8] and indoor air quality [9]. Regarding indoor air quality, ventilation replaces contaminated indoor air with clean air to dilute the pathogens in aerosols and lower the inhaled dose [9]. However, the ventilation rate in public buildings (e.g., offices, schools, shops, restaurants, cruise ships, etc.) is significantly lower than that in hospitals for saving energy and cost. Because of the relatively low ventilation rate and large occupancy density in public buildings, it is highly possible for the susceptible to breathe in the aerosols exhaled by infectors, resulting in high airborne infection risk.
The large asymptomatic proportion and high airborne transmissibility of COVID-19 increase its airborne infection risk in public buildings. Lauer et al. [10] estimated that the mild or asymptomatic cases accounted for about 80% of the total cases of COVID-19. Mizumoto et al. [11] estimated the asymptomatic cases accounted for 15.5–20.2% of total cases of COVID-19. The asymptomatic infectors have infectivity comparable to the symptomatic infectors [12]. He et al. [13] found that the asymptomatic infectors were responsible for 25–69% secondary cases of COVID-19. The large proportion and high infectivity of asymptomatic infectors of COVID-19 increase the infection risk, particularly when the relaxed lockdown measures bring a large number of occupants back to public buildings. Moreover, the airborne transmissibility of COVID-19 is high, with the quantum generation rate of 970 ± 390 quanta/h in the outbreak of a choir rehearsal in Skagit (USA) [14], while the quantum generation rate of Tuberculosis is merely 1–50 [15]. Dai and Zhao [15] estimated the airborne infection risk of COVID-19 with the quantum generation rate inferred from the basic reproduction number, and found that the common ventilation rate in public indoor spaces was generally insufficient for airborne infection risk control of COVID-19 [15].
A bundle of multiple interventions is suggested for airborne infection risk control rather than a single one [7]. Zhang [16] integrated source control (e.g., face masks and local air exhaust) and air cleaning (e.g., standalone room air cleaners and filters) with ventilation to reduce airborne infection risk. Reducing occupancy is also an effective supplement of ventilation for airborne infection risk control [3,16]. On the one hand, reducing occupancy in a shared space of public buildings has the possibility to reduce the number of asymptomatic occupants, thereby reducing the pathogens in aerosols. In this regard, reducing occupancy is one type of source control interventions. On the other hand, reducing occupancy can reduce the number of susceptible, thereby reducing secondary cases. Another advantage is that reducing occupancy does not require modifications to the existing ventilation system. Melikov et al. [17] proposed to combine intermittent occupancy with ventilation, and demonstrated the potential of this strategy for airborne infection risk control. However, reducing occupancy means that occupants shorten their time in their shared working space, thereby reducing work productivity due to the lost work hours from the workers who would otherwise have fully occupied the room and worked for the entire period of each shift. Thus, it requires a new strategy to effectively combine reducing occupancy with ventilation, which reasonably balances the reduction in airborne infection risk and the loss in work productivity, particularly for public buildings.
This study proposes an occupancy-aided ventilation strategy for the desired airborne infection risk control with minimum work productivity loss. Two mechanisms of occupancy schedule of the occupancy-aided ventilation are revealed and the optimization of the occupancy schedule is developed (Section 2). Case studies for airborne infection control of COVID-19 in a classroom are conducted to demonstrate the effectiveness of the proposed occupancy-aided ventilation, and application issues and robustness of the proposed occupancy-aided ventilation are further discussed (Sections 3, 4).
2. Methodology
The general process of the occupancy-aided ventilation proposed is introduced first, from which it can be seen that the occupancy schedule is the core of the occupancy-aided ventilation (Section 2.1). Then, mechanisms of scheduling the occupancy are revealed for good overall performance regarding controlling the airborne infection risk and reducing the loss in work productivity (Section 2.2). Furthermore, an optimization of the occupancy schedule is developed based on the genetic algorithm (an optimization algorithm) to maximize the work productivity while satisfying the constraint on the airborne infection risk control (Section 2.3).
2.1. General introduction on occupancy-aided ventilation proposed
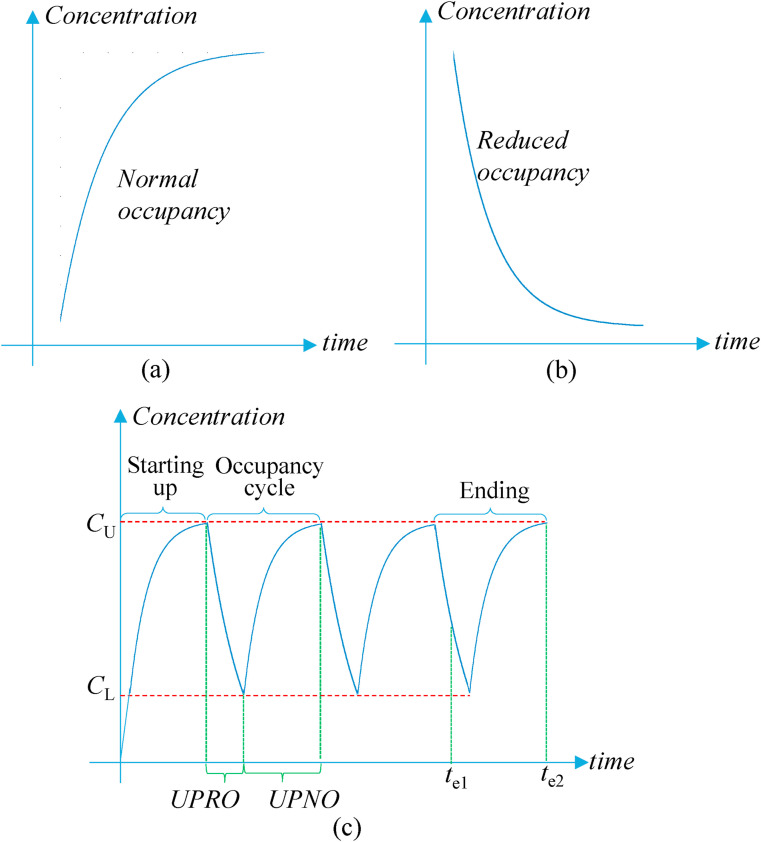
The occupancy-aided ventilation operates the ventilation system at the maximal ventilation rate with reduced occupancy. Given that the maximal ventilation rate is insufficient to dilute and remove indoor exhaled aerosols for airborne infection risk control [15], the occupancy is reduced, as a supplementary measure, to reduce the indoor exhaled aerosols. The proposed occupancy-aided ventilation serves normal and reduced occupancies. The indoor concentration of exhaled aerosols increases and decreases during the normal occupancy and reduced occupancy respectively (Fig. 1 (a) and (b)). The entire ventilation process (e.g., determined by office hours or school hours) includes several changeovers between the normal and reduced occupancies. Thus, with the occupancy-aided ventilation, the ventilation system operates at its maximal capacity, and the occupancy alternatively shifts between reduced and normal occupancies. The ventilation system can be natural ventilation or mechanical ventilation. For public buildings, mechanical ventilation may be more common. The changeover is controlled by the upper and lower limits of indoor exhaled aerosol concentration. When the indoor exhaled aerosol concentration reaches the upper limit, the normal occupancy is changed to the reduced occupancy. The corresponding period is defined as the unit period of normal occupancy (UPNO) (Fig. 1(c)). When the indoor exhaled aerosol concentration reduces to the lower limit, the reduced occupancy is changed to the normal occupancy. The corresponding period is defined as the unit period of reduced occupancy (UPRO) (Fig. 1(c)).
Fig. 1.
Variations of indoor exhaled aerosol concentration of (a) normal occupancy; (b) reduced occupancy; and (c) entire ventilation process.
Note: The variation of indoor exhaled aerosol concentration is obtained according to Equation (4). UPRO and UPNO are the unit periods of reduced occupancy and normal occupancy respectively; te is the ending time of the entire ventilation process.
However, using the upper and lower limits of indoor concentration of exhaled aerosols to schedule the occupancy has two disadvantages. First, it could be costly to monitor the indoor concentration of exhaled aerosols accurately. Second, the period of normal occupancy or reduced occupancy could be variable, which might cause inconvenience to the work arrangement. For example, the starting-up stage of the entire ventilation process has normal occupancy, and its period could be longer than that of normal occupancy in the occupancy cycle, because the initial indoor exhaled aerosol concentration of the starting-up stage could be lower than the lower limit of indoor exhaled aerosol concentration (Fig. 1(c)). To address these disadvantages, this study firstly calculates the unit periods of normal occupancy and reduced occupancy in the occupancy cycle from the upper and lower limits of indoor exhaled aerosol concentration, and then determines the occupancy schedule by the two unit periods. That is that the occupancy schedule consists of the unit period of normal occupancy and the unit period of reduced occupancy alternatively until the end of the entire ventilation process.
2.2. Mechanisms for occupancy schedule of occupancy-aided ventilation
Fig. 1(a) shows that during the normal occupancy, the indoor concentration of exhaled aerosols firstly increases fast and then tends to stay at a high level. The rising momentum of the indoor exhaled aerosol concentration decreases because the aerosols removed by ventilation increase with the growing difference between the indoor exhaled aerosol concentration and the outdoor concentration. This indicates that the unit period of normal occupancy should not be too long (i.e., the upper limit of indoor exhaled aerosol concentration should not be too high). Otherwise, the occupants would stay in an environment with a high concentration of exhaled aerosols for a long time. However, the accumulative period of normal occupancy should be sufficiently long for work productivity. The accumulative period of normal occupancy refers to the time length of normal occupancy in the entire occupancy schedule, which is determined by the unit period and number of normal occupancy. Thus, the accumulative period of normal occupancy should be divided into as many units of normal occupancy as possible. This indicates that a smaller unit period of normal occupancy is preferred for airborne infection risk control.
On the other hand, Fig. 1(b) shows that during the reduced occupancy, the indoor concentration of exhaled aerosols firstly reduces fast and then tends to be steady. The decline of the indoor exhaled aerosol concentration slows down because the aerosols removed by ventilation decrease with the reducing difference between the indoor exhaled aerosol concentration and the outdoor concentration. This indicates that the unit period of reduced occupancy should not be too long (i.e., the lower limit of indoor exhaled aerosol concentration should not be too small). Otherwise, the average contribution of the reduced occupancy to lowering airborne infection risk weakens. However, the accumulative period of reduced occupancy should not be too short for airborne infection risk control. The accumulative period of reduced occupancy refers to the time length of reduced occupancy in the entire occupancy schedule, which is determined by the unit period and number of reduced occupancy. Thus, the accumulative period of reduced occupancy should be broken into as many units of reduced occupancy as possible, i.e., a smaller unit period of reduced occupancy is preferred for airborne infection risk control.
Moreover, the ending stage should be effectively utilized for work productivity. As shown in Fig. 1(c), the entire ventilation process can end at t e1 when the indoor exhaled aerosol concentration is low due to the reduced occupancy. The low indoor exhaled aerosol concentration at the ending point is a waste because all occupants are supposed to leave the shared space when the entire ventilation process ends (i.e., the working period is over). This indicates that the ending stage has not been effectively utilized for work productivity. The entire ventilation process also may end at t e2 when the indoor exhaled aerosol concentration is high (close to the upper limit of indoor concentration of exhaled aerosols) due to the normal occupancy. The high indoor exhaled aerosol concentration at the ending point indicates that the ending stage has been effectively utilized for work productivity. Thus, the unit periods of normal and reduced occupancies should be co-determined to make the entire ventilation process end close to the upper limit of indoor exhaled aerosol concentration.
From the above explanations, two mechanisms of scheduling normal occupancy and reduced occupancy can be summarized. First, a smaller unit period of normal occupancy and a smaller unit period of reduced occupancy are preferred for airborne infection risk control. Second, the unit periods of normal and reduced occupancies should be co-determined to ensure that the entire ventilation process ends close to the upper limit of indoor exhaled aerosol concentration for work productivity. It should be noted that a shorter unit period of normal occupancy also indicates more disturbance to work. Thus, the unit period of normal occupancy should be limited by the work nature, which can be predefined by users (e.g., employers or managers). The unit period of reduced occupancy should not be too short because it takes time for occupants to leave and come back to the shared space.
2.3. Optimization of occupancy schedule of occupancy-aided ventilation
The airborne infection risk in this study is evaluated by the rebreathed fraction. The rebreathed fraction is defined as the proportion of the air exhaled by others in the inhaled air, which equals the ratio of the volume of exhaled air by all occupants in the room to the room volume (Equation (1)) [18]. The smaller the rebreathed fraction, the lower the airborne infection risk [19]. According to the mass conservation law, the CO2 exhaled into the room equals the CO2 increase in the room (Equation (2)) [18]. Based on Equations (1), (2), the rebreathed fraction is calculated as the ratio of the CO2 concentration difference in indoor air and outdoor air to the CO2 concentration in the exhaled air (Equation (3)) [18]. The CO2 concentrations in the outdoor air and exhaled air are relatively stable [20,21]. Thus, the indoor CO2 concentration is the core of the calculation of the rebreathed fraction. The indoor CO2 concentration is calculated by Equation (4) according to the mass conservation law for well-mixed conditions, which is mainly determined by the CO2 generation rate and the ventilation rate [19]. The ventilation rate is determined such that the maximal indoor CO2 concentration for the designed occupancy capacity should not exceed the value stipulated by indoor air quality standards, e.g., 800 ppm above the outdoor CO2 concentration for air quality of Category II according to ISO 17772 [22]. The CO2 generation rate of a typical person is calculated by Equation (5) [23]. Thus, the occupancy schedule determines the CO2 generation rate, thereby determining the rebreathed fraction.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Where f is the rebreathed fraction; V is the room volume (m3); V b is the volume of exhaled air into the room (m3), which is the net exhaled air into the room while part of the exhaled air is removed to outdoors by ventilation; C in, C o, and C a are the CO2 concentrations in indoor air, outdoor air, and exhaled air respectively (ppm); is the indoor CO2 generation rate by all occupants (ml/s); Q is the ventilation rate (m3/s); t is the time interval (s) and i is the ith time interval; is the CO2 generation rate of a typical person (ml/s); e is the correction factor, which is 0.85 and 0.75 for Chinese males and females respectively; RQ is the molar ratio of the exhaled CO2 to the inhaled O2, which is 0.83 for a typical adult at light/sedentary activities; H is the height (m); M is the metabolic rate (W/m2); W is the mass (kg).
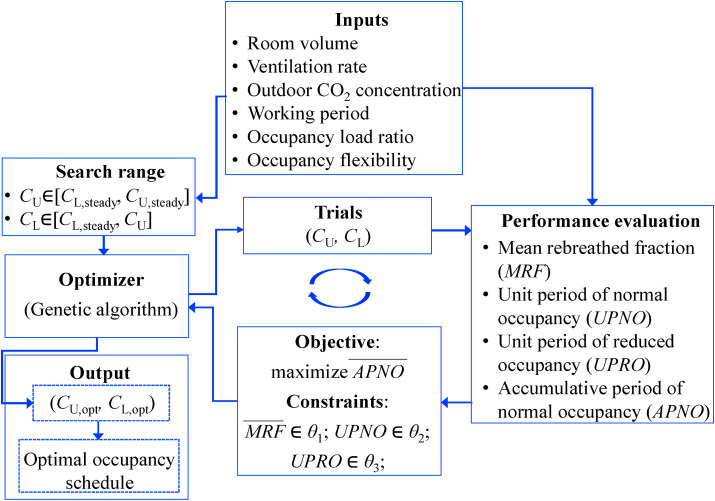
In the proposed optimization, an optimization algorithm is used to search the trials of upper and lower limits of indoor exhaled aerosol concentration. The genetic algorithm is adopted in this study, which is a search heuristic mimicking Charles Darwin's theory of natural selection (i.e., selection, crossover, and mutation) [24], and has been widely used to search the optimal trials [25]. Since the airborne infection risk is evaluated by the rebreathed fraction which is calculated from the CO2 concentration (Equation (3)), CO2 is used as the biomarker of the exhaled aerosols. The search range of the upper limit of indoor CO2 concentration is between the lower and upper steady values of indoor CO2 concentration (Equations (6), (7)). The upper limit of indoor CO2 concentration can be lower than the stipulated one by indoor air standards because the occupancy load can be smaller than the designed occupancy capacity (Equation (7)). The search range of the lower limit of indoor CO2 concentration is between the lower steady value of indoor CO2 concentration (Equation (6)) and the upper limit of indoor CO2 concentration. Given the trials of the upper and lower limits from the genetic algorithm, the profile of the indoor CO2 concentration is calculated by Equation (4) with the inputs of the room volume, ventilation rate, outdoor CO2 concentration, working period, occupancy load ratio and occupancy flexibility. The occupancy flexibility determines how many occupants leave the shared space for reduced occupancy. Limited by the work nature, it might be impractical for all occupants to leave the shared space for reduced occupancy. For example, in a shared space designed for 25 occupants of which the occupancy load ratio is 80% and the occupancy flexibility is 60%, the number of occupants for normal occupancy is 20 (i.e., 25 × 80%) and the number of occupants for reduced occupancy is 8 (i.e., 20–20 × 60%). With the profile of indoor CO2 concentration, the mean rebreathed fraction (Equation (3)), unit periods of normal and reduced occupancies (Fig. 1(c)), and accumulative period of normal occupancy are calculated.
| (6) |
| (7) |
Where C L,steady and C U,steady are the lower and upper steady values of indoor CO2 concentration; is the designed occupancy capacity; OLR is the occupancy load ratio; OF is the occupancy flexibility.
The objective of the optimization is to maximize the normalized accumulative period of normal occupancy. The accumulative period of normal occupancy is normalized to be between 0 and 1 (Equation (8)). A longer normalized accumulative period of normal occupancy indicates higher work productivity. For example, a normalized accumulative period of normal occupancy of 0.9 indicates that 10% (i.e., 1–0.9) of work productivity is sacrificed because of the reduced occupancy for airborne infection risk control compared with the conventional ventilation strategy with normal occupancy merely. The optimization subjects to the condition that the normalized mean rebreathed fraction (Equation (9)) is not greater than a predefined value for airborne infection risk control. The mean rebreathed fraction is normalized to be between 0 and 1, and a smaller normalized mean rebreathed fraction denotes a lower airborne infection risk (i.e., larger health outcome). For example, a normalized mean rebreathed fraction of 0.8 indicates that the mean rebreathed fraction is reduced by 20% (i.e., 1–0.8) compared with the conventional ventilation strategy with normal occupancy merely. Moreover, the optimization is also subject to the constraints on the unit periods of normal and reduced occupancies as explained in Section 2.2. The genetic algorithm iteratively updates the trials of the upper and lower limits of indoor CO2 concentration. The trials failing to satisfy the constraints are ruled out, and the iteration stops until the objective function (i.e., the normalized accumulative period of normal occupancy) converges. The details of the genetic algorithm can be found in Konak et al. [26]. The final trials are optimal, and the corresponding unit periods of normal and reduced occupancies determine the occupancy schedule of the occupancy-aided ventilation (Section 2.1).
| (8) |
| (9) |
Where APNO and are the accumulative period of normal occupancy and the normalized one respectively; WP is the working period (i.e., the period of the entire ventilation process); MRF and are the mean rebreathed fraction and the normalized one of the proposed occupancy-aided ventilation respectively; MRF c is the mean rebreathed fraction of the conventional ventilation strategy.
3. Result
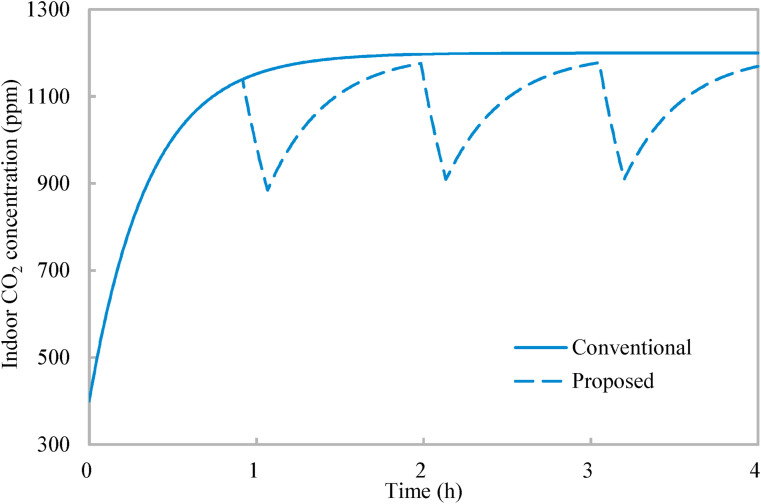
Case studies are conducted in a classroom to demonstrate the application and effectiveness of the proposed occupancy-aided ventilation. The classroom is served by mixing ventilation so that Equation (4) applies. The classroom has dimensions of 8.8 m (length) × 6.1 m (width) × 2.4 m, which is designed for 25 occupants. The working period is 4 h (a morning/afternoon session). The outdoor CO2 concentration is 400 ppm [21], and the CO2 concentration in the exhaled air is 37,500 ppm [18]. The unit period of normal occupancy is limited to be within 30 min–90 min, and the unit period of reduced occupancy is limited to be larger than 5 min. When the occupancy load ratio and occupancy flexibility are both 100% and the normalized mean rebreathed fraction is limited to less than 0.8, Fig. 3 shows the indoor CO2 concentration profiles of the conventional ventilation strategy and the proposed occupancy-aided ventilation. With the conventional ventilation strategy (which has normal occupancy merely), the indoor CO2 concentration increases from 400 ppm and tends to converge to 1200 ppm (i.e., 800 ppm above the outdoor CO2 concentration [22]). The developed optimization (Fig. 2 ) determines the upper and lower limits of indoor CO2 concentration as 1178 ppm and 918 ppm respectively, and the corresponding unit periods of normal occupancy and reduced occupancy are 55 min and 9 min respectively. The entire ventilation process is interrupted by two units of reduced occupancy, and the indoor CO2 concentration is effectively reduced. The entire ventilation process ends at a concentration of indoor CO2 concentration close to the upper limit of indoor CO2 concentration. Thus, the occupancy schedule from the developed optimization follows the mechanisms of the occupancy schedule (Section 2.2).
Fig. 3.
Variations of indoor CO2 concentration with time: Conventional ventilation strategy and proposed occupancy-aided ventilation.
Fig. 2.
Optimization of occupancy schedule of occupancy-aided ventilation.
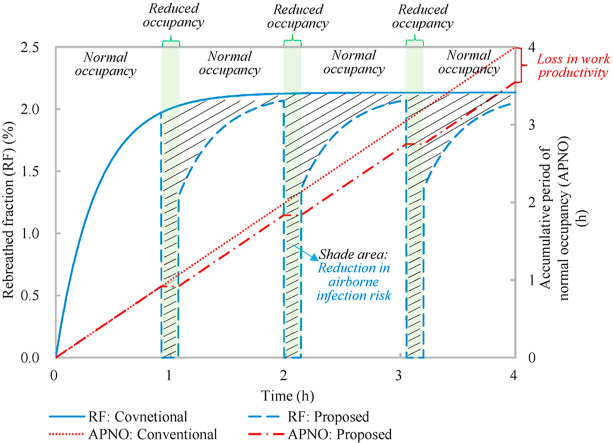
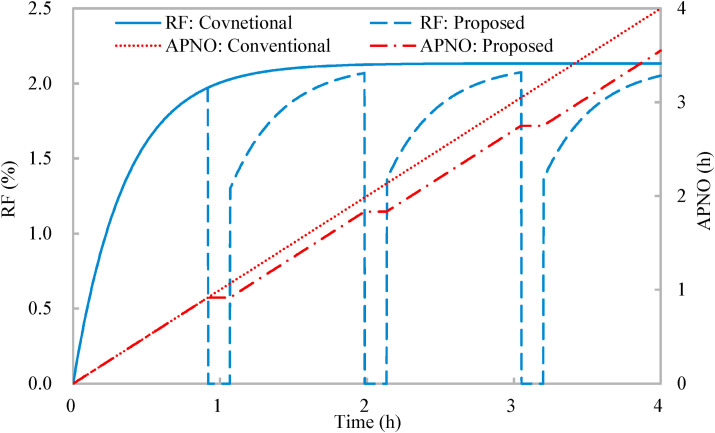
Fig. 4 shows that the rebreathed fraction of the conventional ventilation strategy increases from 0 and converges to 2.13%, and the mean rebreathed fraction is 1.94%. The accumulative period of normal occupancy of the entire ventilation process equals the working period (4 h) since the conventional ventilation strategy consists of normal occupancy merely. With the proposed occupancy-aided ventilation, when the rebreathed fraction increases to 1.97%, the occupancy is reduced. Since the occupancy flexibility is 100% which indicates all occupants leave the shared space for reduced occupancy, the rebreathed fraction for reduced occupancy is nil. When the reduced occupancy changes to the normal occupancy, the rebreathed fraction jumps to 1.30% (determined by the lower limit of the indoor CO2 concentration (Equation (3)) and increases. The mean rebreathed fraction is 1.53%. The normalized mean rebreathed fraction is 0.78 which satisfies the constraint on airborne infection risk control that the normalized mean rebreathed fraction should be less than 0.8 as predefined. The accumulative period of normal occupancy linearly increases at normal occupancy and keeps invariable at reduced occupancy (Fig. 4). The accumulative period of normal occupancy for the entire ventilation process is 213 min and the normalized one is 0.89. In other words, compared with the conventional ventilation strategy, the proposed occupancy-aided ventilation has a loss of 11% in work productivity, but improves health outcome by 22%, which demonstrates the effectiveness of the proposed occupancy-aided ventilation.
Fig. 4.
Variations of rebreathed fraction (RF) and accumulative period of normal occupancy (APNO) with time: Conventional ventilation strategy and proposed occupancy-aided ventilation.
4. Discussion
Reducing occupancy has been recommended for airborne infection risk control [3,16]. Under some urgent scenarios, even the lockdown of a whole city is adopted [30]. Reducing occupancy is particularly useful when other practical measures cannot effectively control airborne infection risk, such as airborne infection risk control of COVID-19 when the schools, office, etc. are re-opened after the lockdown [17]. However, reducing occupancy inevitably shortens the working time length, resulting in the loss of work productivity. The occupancy-aided ventilation is proposed to minimize the loss of work productivity while controlling the airborne infection risk. The proposed occupancy-aided ventilation applies to the types of work where the workers are required to work on-site in shared indoor environments. Several practical issues of the proposed occupancy-aided ventilation are discussed as follows, as well as the limitations of this study.
4.1. How to set constraint on airborne infection risk
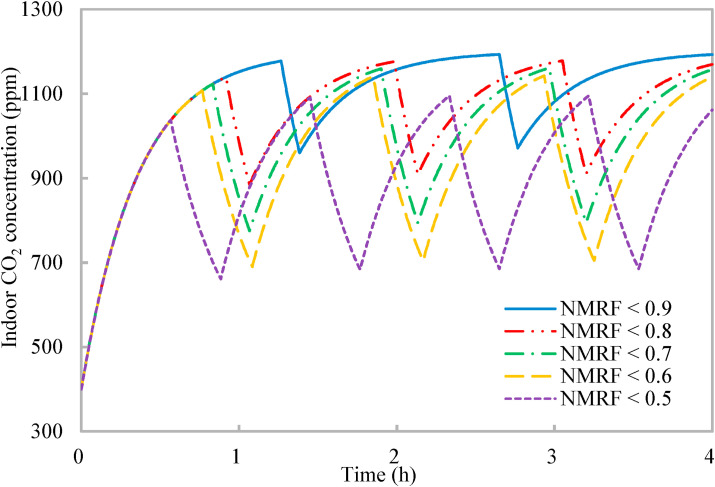
The three constraints in the developed optimization require to be predefined by users (Fig. 2). The two constraints on the unit periods of normal occupancy and reduced occupancy are determined mainly according to the work requirements and the environment (Section 2.1), and the effects of the constraint on airborne infection risk (i.e., the normalized mean rebreathed fraction) are further investigated to provide guidelines for users. Fig. 5 shows that when the requirement on airborne infection risk improves (with a reduced normalized mean rebreathed fraction), the entire ventilation process is broken by more units of reduced occupancy, which is explained as follows. The reduced normalized mean rebreathed fraction indicates the accumulative period of reduced occupancy needs to be prolonged. According to the mechanism of the occupancy schedule (Section 2.2), a short unit period of reduced occupancy is preferred for airborne infection risk control. Thus, with the prolonged accumulative period of reduced occupancy, it is broken into more units to achieve a short unit period of reduced occupancy (not greater than 19 min in Fig. 5). Moreover, it can be observed from Fig. 5 that for the different constraints on the normalized mean rebreathed fraction, the entire ventilation process always ends at a high indoor CO2 concentration close to the upper limit of indoor CO2 concentration, which again is consistent with the mechanism of occupancy schedule for work productivity (Section 2.2).
Fig. 5.
Variations of indoor CO2 concentration with time of proposed occupancy-aided ventilation: Different constraints on normalized mean rebreathed fraction (NMRF).
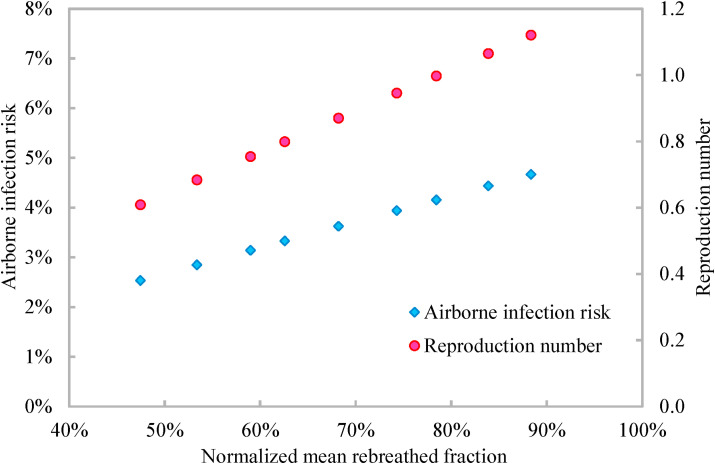
When the airborne transmissibility (i.e., the quantum generation rate) of the concerned infectious respiratory disease is known, the airborne infection risk can be calculated by Equation (10) from the rebreathed fraction [18]. One inhaled quantum indicates an infection risk of 63% and might involve a large number of organisms [27], which implicitly considers the infectious source strength, infectivity, biological decay of pathogens, etc. [28]. The rebreathed fraction based airborne infection risk evaluation (Equation (10)) has been validated to provide the same result as the well-recognized Wells-Riley model, but is more convenient to implement than the Wells-Riley model because the rebreathed fraction can be conveniently calculated from CO2 concentration (Equation (3)) [18]. The rebreathed fraction based airborne infection risk evaluation can account for the pathogen removal effects of filters, masks, air cleaner, etc. via the removal efficiency of pathogens (i.e., ϕ in Equation (10)). Dai and Zhao [15] suggested that the airborne infection risk should be constrained to be less 1% or even be less than 0.1%, and the corresponding constrain on the mean rebreathed fraction can be inversely calculated from Equation (10). Rudnick and Milton [18] suggested that the mean rebreathed fraction should be controlled to make the reproduction number less than one (Equations (11), (12)). With the airborne infection risk, the production number is calculated by Equation (11), which is the number of the susceptible will be infected due to airborne transmission. The method suggested by Rudnick and Milton [18] is more reasonable because a reproduction number less than one indicates that there are no new infection cases. The quantum generation rate of a speaking COVID-19 infector at a slight activity level is reported to be 142 quanta/h [29]. When all occupants wear a mask with an efficiency of 65% and there is one asymptomatic infector among the 25 occupants, the airborne infection risk increases from 2.54% to 4.67% with the increasing normalized mean rebreathed fraction (Fig. 6 ). The corresponding reproduction number increases from 0.61 to 1.12 (Fig. 6). To make the reproduction number less than one, the normalized mean rebreathed fraction should be less than 80%.
| (10) |
| (11) |
| (12) |
Where P is the airborne infection risk; f is the mean rebreathed fraction; I is the number of infectors; q is the quantum generation rate (h−1); t is the exposure time (h); n is the number of occupants; R is the reproduction number; is the removal efficiency of pathogens by filters, masks, air cleaners, etc.
Fig. 6.
Variations of airborne infection risk and reproduction number with normalized mean rebreathed fraction.
Note: The data are calculated from Equations (10), (11) with the quantum generation rate of 142 quanta/h and the mask efficiency of 65%.
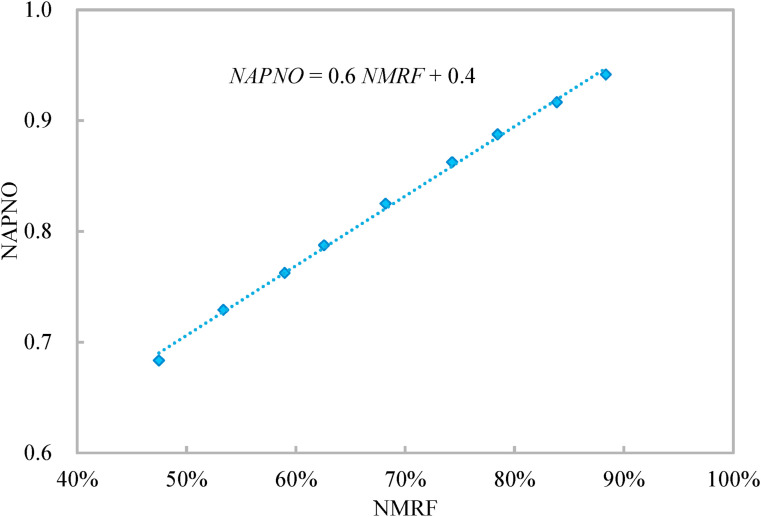
Fig. 7 shows that for the entire ventilation process, the normalized accumulative period of normal occupancy linearly increases with the normalized mean rebreathed fraction with the coefficient of determination of 0.998. This indicates the work productivity linearly reduces with the improving health outcome. The slope of the linear relationship of 0.6 indicates the earning ratio of the proposed occupancy-aided ventilation is 1.67 (1/0.6). The earning ratio is the ratio of the improvement in health outcome to the loss in work productivity, which is calculated as the ratio of the reduction in the normalized mean rebreathed fraction to the reduction in the normalized accumulative period of normal occupancy. Thus, the constraint on the normalized mean rebreathed fraction does not affect the effectiveness of the proposed occupancy-aided ventilation (i.e., the earning ratio). When the airborne transmissibility of the concerned infectious respiratory disease is unknown, the users can determine the constraint on the normalized mean rebreathed fraction according to Fig. 7 to balance the health outcome and work productivity.
Fig. 7.
Variation of normalized accumulative period of normal occupancy (NAPNO) of entire ventilation process with normalized mean rebreathed fraction (NMRF).
4.2. Effects of occupancy load ratio
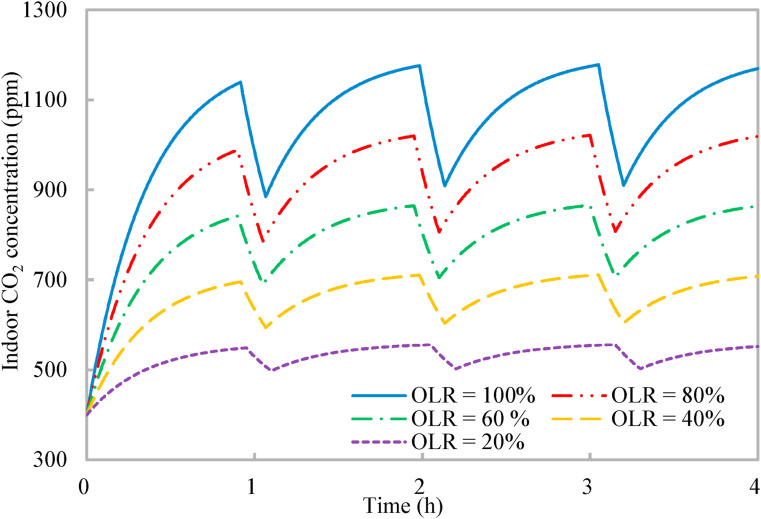
The ventilation system is designed for 25 occupants, but the classroom might have less than 25 occupants during the normal occupancy with the occupancy load ratio less than 100%. With a decreasing occupancy load ratio, the ventilation rate per occupant in the shared space increases and the indoor CO2 concentration decreases [16]. Fig. 8 shows that the maximal indoor CO2 concentration decreases from around 1140 ppm–550 ppm when the occupancy load ratio reduces from 100% to 20%. Again, the entire ventilation process ends at an indoor CO2 concentration close to the respective upper limit of indoor CO2 concentration with the varying occupancy load ratios, which further validates the mechanisms of occupancy schedule revealed in Section 2.2. The normalized mean rebreathed fraction under different occupancy load ratios maintains around 0.78, which satisfies that the normalized mean rebreathed fraction should be less than 0.8 for the reproduction number of COVID-19 in this classroom less than one (Fig. 6). The entire ventilation process is divided by three units of reduced occupancy, and the unit period of reduced occupancy maintains at 9 min. The corresponding normalized accumulative period of normal occupancy is 0.89. Thus, the proposed occupancy-aided ventilation is effective and robust with the effectiveness insensitive to the occupancy load ratio.
Fig. 8.
Variations of indoor CO2 concentration with time of proposed occupancy-aided ventilation: Different occupancy load ratios (OLR).
4.3. Effects of occupancy flexibility
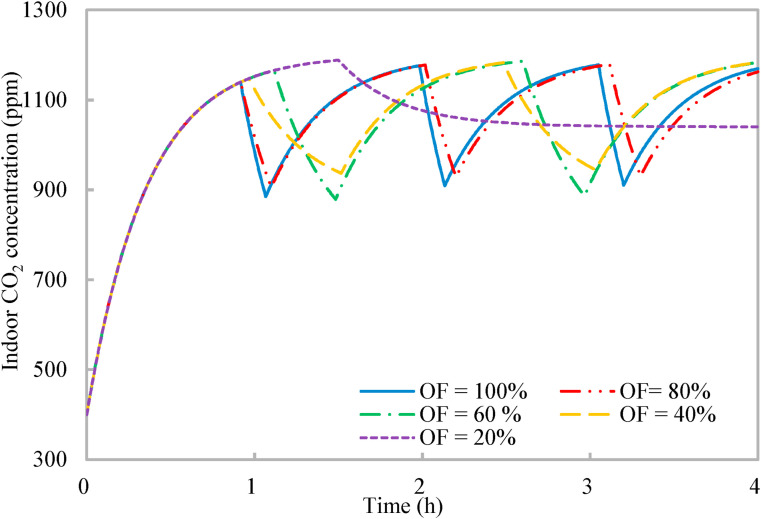
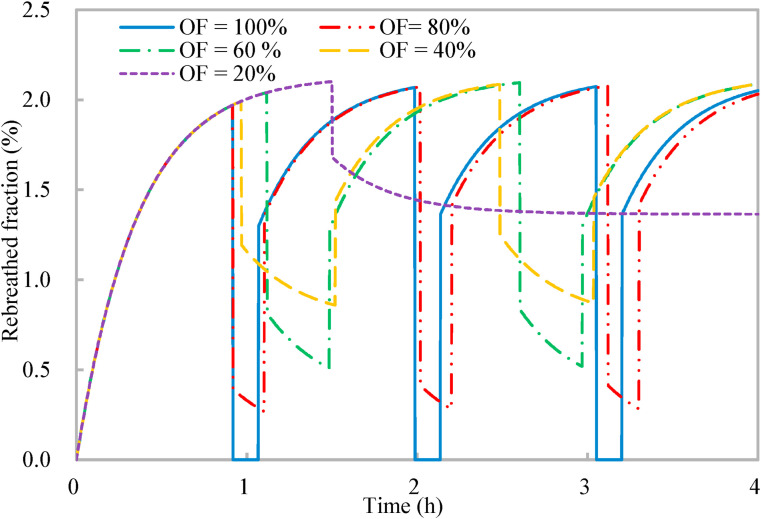
As discussed in Section 2.3, it might be impractical for all occupants to leave the shared space for reduced occupancy limited by the work nature, and the effects of the occupancy flexibility on the effectiveness of the proposed occupancy-aided ventilation are investigated. Lower occupancy flexibility indicates fewer occupants would leave the shared space for reduced occupancy. As a result, the reduction effects of the reduced occupancy on indoor CO2 concentration and rebreathed fraction deteriorate (Fig. 9, Fig. 10 ). The rebreathed fraction is weighted by the occupancy flexibility (Equation (13)). The occupancy flexibility is nil for the normal occupancy, indicating that all occupants are in the shared space. When the occupancy flexibility is less than 100% for reduced occupancy, the rebreathed fraction sharply reduces first due to the reduced number of occupants and then reduces gradually due to the reduced indoor CO2 concentration (Fig. 10). With the occupancy flexibilities of 40%, 60%, 80%, and 100%, the entire ventilation process always ends at an indoor CO2 concentration close to the upper limit of indoor CO2 concentration for work productivity (Section 2.2). However, when the occupancy flexibility is 20%, the reduced occupancy has to last for 150 min until the end of the entire ventilation process to satisfy that the normalized mean rebreathed fraction should be less than 0.8. The contribution of the reduced occupancy to the work productivity is also taken into account, because some occupants are working during the reduced occupancy when the occupancy flexibility is less than 100% (Equation (14)). For all the five occupancy flexibilities, the normalized mean rebreathed fraction is less than 0.8 (around 0.78) and the work productivity (Equation (14)) maintains around 0.89. Thus, the proposed occupancy-aided ventilation is effective and robust with the effectiveness insensitive to the occupancy flexibility.
| (13) |
| (14) |
Where NAPRO is the normalized accumulative period of reduced occupancy.
Fig. 9.
Variations of indoor CO2 concentration with time of proposed occupancy-aided ventilation: Different occupancy flexibilities (OF).
Fig. 10.
Variations of rebreathed fraction with time of proposed occupancy-aided ventilation: Different occupancy flexibilities (OF).
4.4. Limitations of this study
1, 2, 3, 4 have discussed several practical issues of the proposed occupancy-aided ventilation, which provides guidelines on the applications of the proposed occupancy-aided ventilation. However, some practical issues have not been accounted for, e.g., the potential congestion of corridors caused by the changeover between the normal and reduced occupancies and the exit/entry ways of leaving/entering the shared indoor environments. Furthermore, the evaluations of the airborne infection risk and work productivity in this study are simplified to some extent. It is challenging to evaluate work productivity accurately because it is affected by multiple factors in complicated manners (e.g., the mental and physiological conditions and the quality of indoor thermal environments [31]). This study evaluates the work productivity from the accumulative period of normal occupancy in a simplified manner, which follows the logic that a longer accumulative period of normal occupancy indicates a prolonged working time length, thereby increasing the work productivity.
The rebreathed fraction based airborne infection risk evaluation is developed based on the assumption that the pathogen distribution in the indoor air is uniform (Equations (2), (4)). However, the pathogen distribution is inevitably non-uniform [9]. This assumption has been widely used and is regarded as acceptable for mixing ventilation [18]. When the ventilation system employs advanced air distribution which delivers fresh and clean air effectively to the breathing zone, e.g., displacement ventilation and stratum ventilation [9,21], the assumption of uniform distribution of airborne pathogens might cause large errors, and new evaluation methods are required to account for the effects of the non-uniformly distributed airborne pathogens on the airborne infection risk [32]. Moreover, the airborne infection risk evaluation requires the number of infectors, while it is challenging to deterministically obtain the number of infectors unless the epidemical data are available. During the design of proper interventions fighting severe infectious diseases, the number of infectors is generally assumed to a small number (e.g., 1 or 2) [15,18,19,29]. This assumption is relatively reasonable for severe infectious diseases in public buildings, because symptomatic infectors of severe infectious diseases are generally quarantined and not allowed to attend public buildings. In the future study, probability analysis will be developed to include the effects of the number of infectors.
5. Conclusions
Given that ventilation rates commonly encountered may be insufficient for airborne infection risk control of COVID-19 (particularly for public buildings), the occupancy-aided ventilation proposed in this study schedules the occupancy with normal and reduced occupancy, and uses the reduced occupancy as a supplement to ventilation for airborne infection risk control. Two mechanisms of scheduling normal occupancy and reduced occupancy are revealed and optimization of the occupancy schedule is developed for the desired airborne infection risk control and the minimal loss of work productivity. Case studies of COVID-19 in a classroom are conducted to demonstrate the application and effectiveness of the proposed occupancy-aided ventilation. The main findings are as follows.
-
(1)
Shorter unit periods of normal and reduced occupancies are preferred for airborne infection risk control.
-
(2)
The unit periods of normal and reduced occupancies should be co-determined to make the entire ventilation process end at an indoor exhaled aerosol concentration close to the upper health limit for work productivity.
-
(3)
The proposed occupancy-aided ventilation is effective with an earning ratio of 1.67 (i.e., the ratio of the improvement in health outcome to the loss in work productivity).
-
(4)
The proposed occupancy-aided ventilation is robust, with the effectiveness insensitive to the occupancy load ratio and occupancy flexibility.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
The work described in this paper is supported by National Natural Science Foundation of China (Project No. 51878585 and No. 51908203).
References
- 1.Zhang W., Du R.H., Li B., Zheng X.S., Yang X.L., Hu B., Wang Y.Y., Xiao G.F., Yan B., Shi Z.L., Zhou P. Molecular and serological investigation of 2019-nCoV infected patients: implication of multiple shedding routes. Emerging Microbes & Infections. 2020;9(1):386–389. doi: 10.1080/22221751.2020.1729071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tang S., Mao Y., Jones R.M., Tan Q., Ji J.S., Li N., Shen J. Aerosol transmission of SARS-CoV-2? Evidence, prevention and control. Environment International. 2020;144:106039. doi: 10.1016/j.envint.2020.106039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Morawska L., Tang J.W., Bahnfleth W., et al. How can airborne transmission of COVID-19 indoors be minimised? Environment International. 2020;142:105832. doi: 10.1016/j.envint.2020.105832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.van Doremalen N., Bushmaker T., Morris D.H., et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. New England Journal of Medicine. 2020;382(16):1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Buonanno G., Morawska L., Stabile L. Quantitative assessment of the risk of airborne transmission of SARS-CoV-2 infection: prospective and retrospective applications. Environment International. 2020;145:106112. doi: 10.1016/j.envint.2020.106112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? The Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.ASHRAE . Reaffirmed by the Technology Council; 2020. Position Document on Airborne Infectious Diseases, Approved by the Board of Directors, January 19, 2014. [Google Scholar]
- 8.Zhang S., Lin Z. Predicted Mean Vote with skin wettedness from standard effective temperature model. Building and Environment. 2021;183:107412. [Google Scholar]
- 9.Lu Y., Oladokun M., Lin Z. Reducing the exposure risk in hospital wards by applying stratum ventilation system. Building and Environment. 2020;183:107204. [Google Scholar]
- 10.Lauer S.A., Grantz K.H., Bi Q., et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Annals of Internal Medicine. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mizumoto K., Kagaya K., Zarebski A., Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance. 2020;25(10):2000180. doi: 10.2807/1560-7917.ES.2020.25.10.2000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen Y., Wang A., Yi B., Ding K., Wang H., Wang J., Xu G. The epidemiological characteristics of infection in close contacts of COVID-19 in Ningbo city. Chinese Journal of Epidemiology. 2020;41(5):668–672. doi: 10.3760/cma.j.cn112338-20200304-00251. [DOI] [PubMed] [Google Scholar]
- 13.He X., Lau E.H., Wu P., et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nature Medicine. 2020;26(5):672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- 14.Miller S.L., Nazaroff W.W., Jimenez J.L., Boerstra A., Buonanno G., Dancer S.J., Kurnitski J., Marr L.C., Morawska L., Noakes C. Transmission of SARS‐CoV‐2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event. Indoor Air. 2020 doi: 10.1111/ina.12751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dai H., Zhao B. Association of the infection probability of COVID-19 with ventilation rates in confined spaces. Building Simulation. 2020;13:1321–1327. doi: 10.1007/s12273-020-0703-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang J. Integrating IAQ control strategies to reduce the risk of asymptomatic SARS CoV-2 infections in classrooms and open plan offices. Science and Technology for the Built Environment. 2020;26:1013–1018. [Google Scholar]
- 17.Melikov A.K., Ai Z.T., Markov D.G. Intermittent occupancy combined with ventilation: an efficient strategy for the reduction of airborne transmission indoors. Science of The Total Environment. 2020;744:140908. doi: 10.1016/j.scitotenv.2020.140908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rudnick S.N., Milton D.K. Risk of indoor airborne infection transmission estimated from carbon dioxide concentration. Indoor Air. 2003;13(3):237–245. doi: 10.1034/j.1600-0668.2003.00189.x. [DOI] [PubMed] [Google Scholar]
- 19.Issarow C.M., Mulder N., Wood R. Modelling the risk of airborne infectious disease using exhaled air. Journal of Theoretical Biology. 2015;372:100–106. doi: 10.1016/j.jtbi.2015.02.010. [DOI] [PubMed] [Google Scholar]
- 20.Ai Z.T., Mak C.M., Cui D.J., Xue P. Ventilation of air-conditioned residential buildings: a case study in Hong Kong. Energy and Buildings. 2016;127:116–127. [Google Scholar]
- 21.Cheng Y., Zhang S., Huan C., Oladokun M.O., Lin Z. Optimization on fresh outdoor air ratio of air conditioning system with stratum ventilation for both targeted indoor air quality and maximal energy saving. Building and Environment. 2019;147:11–22. [Google Scholar]
- 22.ISO/TR 17772-2 . ISO; Geneva: 2018. Guideline for Using Indoor Environmental Input Parameters for the Design and Assessment of Energy Performance of Buildings. [Google Scholar]
- 23.Qi M.W., Li X.F., Weschler L.B., Sundell J. CO2 generation rate in Chinese people. Indoor Air. 2014;24(6):559–566. doi: 10.1111/ina.12110. [DOI] [PubMed] [Google Scholar]
- 24.Yu Z.J., Chen J., Sun Y., Zhang G. A GA-based system sizing method for net-zero energy buildings considering multi-criteria performance requirements under parameter uncertainties. Energy and Buildings. 2016;129:524–534. [Google Scholar]
- 25.Nguyen A.T., Reiter S., Rigo P. A review on simulation-based optimization methods applied to building performance analysis. Applied Energy. 2014;113:1043–1058. [Google Scholar]
- 26.Konak A., Coit D.W., Smith A.E. Multi-objective optimization using genetic algorithms: a tutorial. Reliability Engineering & System Safety. 2006;91(9):992–1007. [Google Scholar]
- 27.Wells W.F. Cambridge University Press; Cambridge MA: 1955. Airborne Contagion and Air Hygiene; pp. 117–122. [Google Scholar]
- 28.Sze To G.N., Chao C.Y.H. Review and comparison between the Wells–Riley and dose‐response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20(1):2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: quanta emission rate of SARS-CoV-2 for infection risk assessment. Environment International. 2020;141:105794. doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Martorell-Marugán J., Villatoro-García J.A., García-Moreno A., López-Domínguez R., Requena F., Merelo J.J., Lacasaña M., Luna J., Díaz-Mochón J., Lorente J., Carmona-Sáez P. DatAC: a visual analytics platform to explore climate and air quality indicators associated with the COVID-19 pandemic in Spain. Science of The Total Environment. 2020;750:141424. doi: 10.1016/j.scitotenv.2020.141424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang F., de Dear R., Hancock P. Effects of moderate thermal environments on cognitive performance: a multidisciplinary review. Applied Energy. 2019;236:760–777. [Google Scholar]
- 32.Zhang S., Lin Z. medRxiv; 2020. Dilution-based Evaluation of Airborne Infection Risk-Thorough Expansion of Wells-Riley Model. [DOI] [PMC free article] [PubMed] [Google Scholar]