Influence of windowing and metal artefact reduction algorithms on the volumetric dimensions of five different high-density materials: a cone-beam CT study

Abstract

Objective:

To assess the influence of windowing and metal artefact reduction (MAR) algorithms on the volumetric dimensions of high-density materials using two CBCT systems.

Methods:

Four cylinders of amalgam, cobalt-chromium, gutta-percha, titanium and zirconium, were manufactured and their physical volumes (PV) were measured. A polymethyl methacrylate phantom containing the cylinders was submitted to CBCT acquisitions with Picasso Trio and OP300 units with their MAR enabled and disabled. The tomographic volume (TV) of all the cylinders was obtained by semi-automatic segmentation using two windowing adjustments: W1—large window width and upper window level; W2—narrow window width and low window level. Volumetric distortion was expressed as the difference between TV and PV. Statistics comprised intraclass correlation coefficient (ICC) and analysis of variance (ANOVA) for repeated measures with Tukey post hoc test (α = 5%).

Results:

The ICC values ​​indicated excellent reproducibility of TV. Gutta-percha and titanium resulted in the smallest volumetric distortion. Using W1 provided less volumetric distortion for almost all experimental conditions (p < 0.05). Activating MAR algorithm of Picasso Trio underestimated gutta-percha and titanium TV (p < 0.05) and was inefficient in significantly reducing the volumetric distortion of the other materials (p > 0.05). Disabling MAR algorithm of OP300 resulted in smaller volumetric distortion for almost all experimental conditions (p < 0.05).

Conclusions:

The TV of gutta-percha and titanium were closer to the PV. In general, the MAR algorithms of both systems were inefficient in significantly reducing the volumetric distortion of high-density materials. We encourage the use of large window width and upper window level to evaluate high-density materials.

Introduction

Although CBCT is a very precise and useful imaging method in dentistry, artefacts are considered one of its main disadvantages. An artefact can be defined as an error that appears on the reconstructed image and that does not represent the physical object.¹ The presence of high-density materials in the patient scanned—such as those used for the manufacturing of dental implants, restorations, intracanal materials and metal posts—generates artefacts in the final CBCT volume due to beam hardening, scattering and partial volume effects.¹

Volumetric distortion is one of the artefacts associated with high-density materials, that is, the volume of the scanned object is larger than its physical volume (PV).^2,3 The CBCT device, the material type and some technical factors, such as voxel size and field of view, can influence this overestimation of the object’s volume.⁴ Volumetric distortion (also known as blooming) can negatively affect CBCT analysis because the dimensional alteration of an object can interfere with the surrounding voxels and annul important information. Clinically, volumetric distortion may impair the evaluation of endodontically treated teeth⁵ and of peri-implant bone.⁶

One approach to reduce metal-related artefacts without increasing the radiation dose to the patient is to activate metal artefact reduction (MAR) algorithms available in some CBCT devices. Supposedly, during reconstruction, the activation of MAR assigns to the image a threshold that is equivalent to its regular grey values in order to minimize any extreme values produced by artefacts, decreasing grey value variability and homogenizing them.^7–10 However, the activation of these algorithms requires a longer reconstruction time and there is no consensus on whether it improves diagnostic tasks.^11–16

Windowing is a process used to adjust the grey tones in tomographical images during their visualization. These adjustments are usually applied to multidetector CT to select between soft and bone tissue visualization. In this regard, the amount of grey tones available for selection is defined by the system’s contrast resolution, that is, bit depth. The literature has shown that windowing may subjectively influence bone limits and consequently bone measurements,¹⁷ objectively influence tooth segmentation,¹⁸ and subjectively affect visualization of implant abutments.¹⁹ Within this context, little information is available regarding standardized conditions in which high-density dental materials are present. Therefore, the aim of this study was to assess the influence of windowing and MAR algorithms on the volumetric dimensions of five high-density materials using two CBCT systems.

Material and methods

This in vitro experimental study was previously approved by the local Ethics Committee (protocol number CAAE 95920918.1.0000.5418, 2.965.934).

Sample preparation

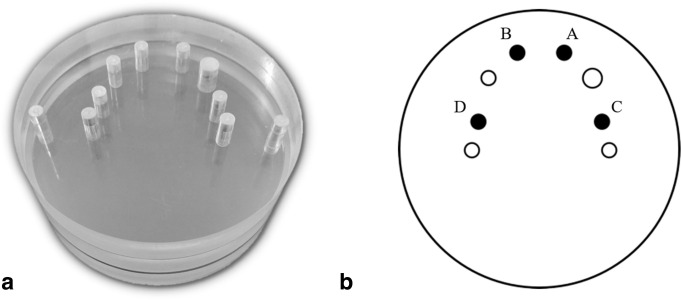
A polymethyl methacrylate (PMMA) phantom (diameter: 100 mm; height: 43.5 mm) with perforations to mimic a lower dental arch was used in this study (Figure 1A).²⁰ The following five high-density materials were studied: amalgam dental alloy (Southern Dental Industries Ltd., SDI, Australia); cobalt-chromium (Scardua Laboratory, Vila Velha, Brazil); gutta-percha (Dentsply, Petrópolis, Rio de Janeiro, Brazil); titanium (S.I.N. Implantes, São Paulo, Brazil); and zirconium (Scardua Laboratory, Vila Velha, Brazil). Amalgam and gutta-percha were manufactured from a silicone-made matrix, while cobalt-chromium, titanium and zirconium were milled by CAD-CAM system. According to the Archimedes’ Principle, the PV of each cylinder was measured using an analytical scale (Adventurer Pro, OHAUS, Parsippany, USA). The height and diameter of each cylinder were measured using a digital caliper. These measures were repeated three times to ensure high accuracy. The physical dimensions of each cylinder are displayed in Table 1.

Figure 1.

(A) PMMA phantom. (B) Schematic axial view of the phantom showing the positions A-B-C-D, where cylinders were inserted (highlighted in black).

Table 1.

Physical dimensions of each cylinder considering all materials

Material	Cylinder	Height, mm	Diameter, mm	PV, mm³
Am	A	5.5	5.4	124.81
	B	5.5	5.4	114.8
	C	5.5	5.4	121.12
	D	5.5	5.4	119.67
CoCr	A	5.5	5.4	128.48
	B	5.5	5.4	127.02
	C	5.5	5.4	127.64
	D	5.5	5.4	130.1
Gu	A	5.5	5.5	131.36
	B	5.5	5.5	132.51
	C	5.5	5.5	127.57
	D	5.5	5.5	135.33
Ti	A	5.5	5.5	130.88
	B	5.5	5.5	131.08
	C	5.5	5.5	131.09
	D	5.5	5.5	130.79
Zi	A	5.5	5.4	124.34
	B	5.5	5.4	126.91
	C	5.5	5.4	125.62
	D	5.5	5.4	122.56

Am, amalgamalloy; CoCr, cobalt-chromium; Gu, gutta-percha; PV, physical volume; Ti, titanium; Zi, zirconium.

Image acquisition

Four cylinders of the same material were placed inside two anterior and two posterior perforations of the phantom (Figure 1B) in order to simulate a more clinical situation since the presence of more than one high-density material is usual. The other perforations were completely filled with PMMA cylinders.

CBCT scans were acquired with the Picasso Trio (E-Woo Technology Co., Ltd./Vatech, Giheung-gu, Korea) and OP300 Maxio (Instrumentarium Dental, Tuusula, Finland) units. The exposure parameters of each system were fixed for all acquisitions, except for the MAR algorithm, which was off and on (Table 2). Each combination of material (5), CBCT unit (2) and MAR algorithm (2), was considered as an experimental condition for scanning. Each scan was acquired three times, resulting in 60 CBCT scans. Then, all CBCT images were exported in the DICOM format and randomized using RANDOM.ORG (Randomness and Integrity Services Ltd., Dublin, Ireland).

Table 2.

Exposure parameters for each CBCT device

CBCT device	FOV, cm	Voxel, mm	kVp	mA	Scanning time, s	Number of basis images	Contrast resolution, bit	MAR algorithm
Picasso Trio	8.5 × 12	0.200	90	5	24	424	16	Off	On
OP300	8 × 15	0.250	90	5	24.3	312	13	Off	On

CBCT, cone-beam computed tomography; FOV, field of view; MAR, metal artefact reduction; kVp, kilovoltage peak; mA, milliamperage.

Image evaluation

Two oral radiologists, who were blinded to the experimental conditions, received instructions regarding the software tools and the segmentation method using images that were not included in the study. Then, the evaluators independently segmented the cylinders’ volumes in CBCT by means of a semi-automatic method using the ITK-SNAP V.3.6 software.²¹ During segmentation, the smallest region of interest (ROI) involving the entire cylinder was selected individually. All ROIs measured 40×40×40 voxel. After selecting the “Lower Threshold” option, the observers could decrease or increase the threshold value to comprise the greyscale corresponding to the dimension and morphology of the cylinder. The next step consisted of tracing the volume within the selected threshold using the “Add Bubbles” tool, and then automatically filling in the volume from these bubbles. Finally, fine tuning was accomplished by manually removing or adding pixels, if necessary. At the end of segmentation, the segmented volumes expressed in mm³ were tabulated in Microsoft Office Excel spreadsheets (Microsoft Corporation, Redmond, Washington, USA).

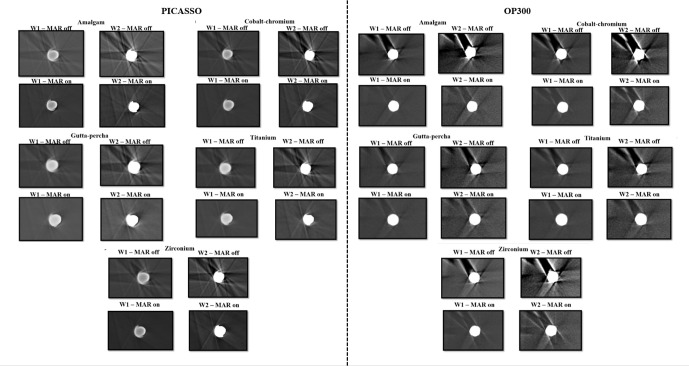
The segmentation of all of the cylinders occurred considering two windowing adjustments (Figure 2). Windowing adjustment 1 (W1): large width and upper level using the automatic windowing adjustment of ITK-SNAP. Each image had its own width and level values, applied automatically by the software when opening the image. Windowing adjustment 2 (W2): narrow width and low level, by reducing these to one-third from the automatic values of each image. Additional post-processing adjustments, such as filter, brightness and contrast, were not allowed during the segmentations.Considering all experimental conditions, 960 segmentations were obtained.

Figure 2.

Images of the cylinders (cylinder at position C) in each experimental condition obtained with the two CBCT units.

The W1 and W2 evaluations were performed at an interval of 30 days in order to reduce bias associated with the evaluators’ memorization. 30 days after the segmentations, 30% of the whole sample was randomly selected through a stratified randomization to comprehend all variables studied and then it was reevaluated to calculate intraexaminer reproducibility.

Statistical analysis

The numerical differences between the segmented and the PV of each cylinder were calculated as a measure of volumetric distortion, also expressed in mm³ (continuous quantitative variable). Data were explored using descriptive analysis to better understand the trend of volumetric distortion for each factor studied (material, windowing and MAR algorithm). The Shapiro-Wilk test confirmed parametric distribution. The percentage of volumetric distortion was calculated by the volumetric distortion divided by the PV.

Data were submitted to repeated measures ANOVA with Tukey post hoc test at a significance level of 5% to verify if the factors studied and their interactions influence the expression of volumetric distortion. The intraclass correlation coefficient (ICC) was used to calculate intraexaminer and interexaminer reproducibility according to the interpretation of Szklo and Nieto.²²

Our hypotheses were that materials with the lowest atomic number and physical density (gutta-percha and titanium) would exhibit less volumetric distortion than the other materials and that a large window width and upper window level would reduce volumetric distortion. Regarding MAR, our hypothesis was that the algorithms would be effective in decreasing volumetric distortion.

Results

The ICC for interexaminer reproducibility was 0.9994. The ICC for intraexaminer reproducibility was 0.9973 for observer 1 and 0.9981 for observer 2. These ICC values demonstrated excellent reproducibility of the volumetric measurements performed in our study.

Table 3 shows the mean, standard deviation, percentage and confidence interval of volumetric distortion according to the factors studied for the two CBCT systems. In general, the dimensions of the volumes segmented in Picasso Trio images were closer to the physical ones, as for gutta-percha, titanium and the use of large window width and upper level ​(W1) for both CBCT units. Activation of the Picasso Trio MAR algorithm resulted in lower percentages (1.17%) than its non-activation (10.58%). Disabling the MAR algorithm of the OP300 system estimated the volumetric dimensions ​​closer to the physical ones (29.20%) when compared to activation of the algorithm (37.79%).

Table 3.

Mean, standard deviation, percentage and confidence interval of volumetric distortion according to material, MAR activation. and windowing adjustment obtained for the two CBCT units

CBCT unit			Mean (SD), mm³	Percentage, %	95% CI
Picasso Trio	Material	Am	17.82 (6.7)	14.58	(15.87–19.87)
		CoCr	11.17 (5.79)	8.64	(9.49–12.86)
		Gu	−0.04 (13.57)	0.03	(-3.98–3.89)
		Ti	1.12 (12.99)	0.86	(-2.64–4.9)
		Zi	13.31 (7.68)	10.78	(11.08–15.55)
	MAR	Off	13.53 (9.66)	10.58	(11.57–15.49)
		On	1.50 (11.16)	1.17	(-1.03–4.04)
	Windowing	W1	3.96 (10.27)	3.10	(2.10–5.81)
		W2	13.4 (11.91)	10.48	(11.24–15.55)
OP300	Material	Am	52.32 (10.5)	42.80	(49.27–55.37)
		CoCr	47.47 (11.58)	36.72	(44.1–50.83)
		Gu	33.56 (7.82)	25.17	(31.29–35.83)
		Ti	37.93 (10.82)	28.99	(34.79–41.07)
		Zi	49.62 (10.47)	40.19	(46.58–52.66)
	MAR	Off	37.33 (7.58)	29.20	(35.79–38.87)
		On	48.31 (14.23)	37.79	(45.42–51.19)
	Windowing	W1	38.81 (11.24)	30.36	(36.78–40.85)
		W2	49.54 (11.4)	38.75	(47.48–51.61)

Am, amalgam alloy; CBCT, cone-beam computed tomography; CI, confidence interval; CoCr, cobalt-chromium; Gu, gutta-percha; MAR, metal artefact reduction; SD, standard deviation; Ti, titanium; W1, large window width and upper window level; W2, narrow window width and low window level; Zi, zirconium.

Bold numbers indicate the lowest descriptive values of volumetric distortion considering each condition.

Repeated measures ANOVA (Table 4) showed that all factors studied and their interactions influenced the volumetric dimensions for Picasso Trio (p < 0.05). For OP300, there were significant differences in almost all factors and their interactions (p < 0.05), except for “MAR algorithm-Material” and “Material-MAR algorithm-Windowing” interactions.

Table 4.

Repeated measures ANOVA for material, MAR activation and windowing adjustment obtained for the two CBCT units

CBCT unit	Factors and interactions	p-value
Picasso Trio	Material	0.001
	MAR algorithm	0.001
	MAR algorithm-Material	0.001
	Windowing	0.001
	Windowing-Material	0.001
	MAR algorithm-Windowing	0.001
	Material-MAR algorithm-Windowing	0.023
OP300	Material	0.001
	MAR algorithm	0.001
	MAR algorithm-Material	0.063
	Windowing	0.001
	Windowing-Material	0.001
	MAR algorithm-Windowing	0.008
	Material-MAR algorithm-Windowing	0.642

CBCT, cone-beam computed tomography; MAR, metal artefact reduction.

Bold p-values indicate statistically significant differences (p < 0.05).

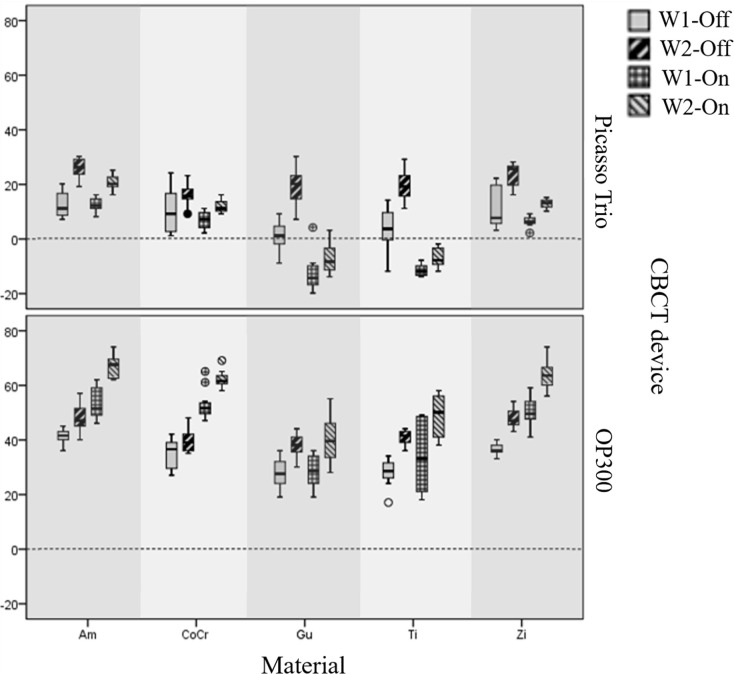
Table 5 shows the estimated means and standard deviations of volumetric distortion for each factor studied using the Tukey post hoc test. The use of W1 adjustments provided less volumetric distortions for almost all materials and MAR conditions (p < 0.05). The MAR algorithm of Picasso Trio was inefficient in significantly reducing the volumetric distortions of amalgam, cobalt-chromium and zirconium in both windowing adjustments (p > 0.05). Enabling the algorithm of Picasso Trio underestimated the measured volumes of gutta-percha and titanium (p < 0.05), that is, the mean measured volumes were smaller than the physical ones. Disabling the MAR algorithm of OP300 resulted in smaller volumetric distortion than enabling it for almost all materials and windowing adjustment conditions (p < 0.05), except for titanium in W1 adjustment and gutta-percha in both windowing adjustments. Box plots illustrating the data are shown in Figure 3.

Table 5.

Estimated means and standard deviations of volumetric distortion according to MAR algorithm and windowing adjustment obtained for the two CBCT units

CBCT unit	Material	MAR	Windowing
			W1 (SD)	W2 (SD)	p valuea
Picasso	Am	Off	12.45 (4.73)	26.04 (3.41)	p < 0.01
		On	12.28 (2.48)	20.52 (2.47)	p < 0.01
		p valueb	1.00	0.14
	CoCr	Off	10.37 (8.38)	15.79 (4.06)	0.16
		On	6.96 (2.79)	11.58 (2.4)	0.43
		p valueb	0.9	0.62
	Gu	Off	1.15 (4.87)	19.28 (6.76)	p < 0.01
		On	−12.88 (6.33)	−7.73 (5.03)	0.23
		p valueb	p < 0.05	p < 0.05
	Ti	Off	3.84 (7.85)	19.35 (4.97)	p < 0.01
		On	−11.58 (2)	−7.1 (3.24)	0.5
		p valueb	p < 0.01	p < 0.01
	Zi	Off	10.9 (7.46)	23.44 (4.12)	p < 0.01
		On	6.12 (1.76)	12.81 (1.29)	p < 0.05
		p valueb	0.37	1.00
OP300	Am	Off	41.01 (2.42)	47.93 (4.7)	0.14
		On	53.37 (5.65)	66.99 (3.85)	p < 0.01
		p valueb	p < 0.01	p < 0.01
	CoCr	Off	35.22 (5.29)	39.74 (5.29)	0.86
		On	52.84 (5.03)	62.09 (2.97)	p < 0.01
		p valueb	p < 0.01	p < 0.01
	Gu	Off	27.81 (5.34)	37.86 (4.35)	p < 0.01
		On	28.68 (5.35)	39.91 (7.69)	p < 0.01
		p valueb	1.00	1.00
	Ti	Off	28.31 (4.57)	40.8 (2.49)	p < 0.01
		On	33.83 (12.67)	48.79 (7.47)	p < 0.01
		p valueb	0.54	p < 0.01
	Zi	Off	36.78 (2.02)	47.81 (3.51)	p < 0.01
		On	50.34 (5.28)	63.56 (5.35)	p < 0.01
		p valueb	p < 0.01	p < 0.01

Am, amalgam alloy; CBCT, cone-beam computed tomography; CoCr, cobalt-chromium; Gu, gutta-percha; MAR, metal artefact reduction; SD, standard deviation; Ti, titanium; W1, large window width and upper window level; W2, narrow window width and low window level; Zi, zirconium.

Bold p-values indicate statistically significant differences (p < 0.05).

^ap-value corresponding to comparisons between W1 and W2 considering the same MAR condition.

^bpvalue corresponding to comparisons between MAR algorithm conditions considering the same windowing adjustment.

Figure 3.

Boxplots of volumetric distortions considering windowing adjustments (W1 and W2) and MAR condition (Off – without MAR; On – with MAR) obtained for each material and CBCT unit. Am—amalgam alloy; CoCr—cobalt-chromium; Gu—gutta-percha; Ti—titanium; Zi—zirconium. Outliers are highlighted. The black dotted line at zero represents the absence of volumetric alteration.

Table 6 displays the p-values from Tukey post hoc test considering the comparisons among materials. Volumetric distortion values were statistically different in almost all comparisons, except the ones between cobalt-chromium/zirconium (p = 0.45) and gutta-percha/titanium (p = 0.89), for Picasso Trio; and amalgam/zirconium (p = 0.21) and cobalt-chromium/zirconium (p = 0.43), for OP300.

Table 6.

P-values from Tukey post hoc test considering comparisons among materials for the two CBCT units

		p values
CBCT unit		Am	CoCr	Gu	Ti
Picasso Trio	Am	--	--	--	--
	CoCr	<0.01	--	--	--
	Gu	<0.01	<0.01	--	--
	Ti	<0.01	<0.01	0.89	--
	Zi	<0.01	0.45	<0.01	<0.01
OP300	Am	--	--	--	--
	CoCr	<0.01	--	--	--
	Gu	<0.01	<0.01	--	--
	Ti	<0.01	<0.01	<0.01	--
	Zi	0.21	0.43	<0.01	<0.01

CBCT–cone-beam computed tomography. Am–amalgam alloy; CoCr–cobalt-chromium; Gu–gutta-percha; Ti–titanium; Zi–zirconium.

Bold p-values indicate statistically significant differences (p < 0.05).

Discussion

Windowing adjustments

Different window widths and levels can influence the representation of grey values and some studies have attempted to identify a better windowing protocol for evaluating bone¹⁷ and for segmenting teeth.¹⁸ Additionally, subjective brightness and contrast adjustments have been shown to improve the visualization of implant-abutment joints.¹⁹ In our study, the windowing adjustments were standardized considering the automatic adjustment made by the ITK-SNAP software (W1). During pilot tests, reducing window values in W2 to one-third of the automatic values (W1) was chosen because it subjectively changed the dimensions of the cylinders in a greater extent than other. Only two types of opposite windowing adjustments were selected as a first step in identifying whether these would objectively influence on volumetric dimensions, since there were already other factors under study.

The W1 protocol resulted in significantly lower volumetric distortion compared to W2 for almost all conditions (Table 5). A wider window width implies a larger greyscale, thus we believe that W1 permits more accurate distribution of the grey tones in order to better represent the high-density cylinders. It is worth mentioning that the automatic windowing adjustment of ITK-SNAP (W1) was the one that most reduced volumetric distortion in our study, but this is not a general rule for all CBCT viewer softwares. Additionally, we might say that windowing, brightness, contrast and γ adjustments are equivalent grey-level transformations. Therefore, when aiming to reduce volumetric distortion, low brightness and low contrast adjustments shall be applied when windowing adjustments are not available in a given software.^23,24

MAR algorithms

The MAR algorithm is currently a hot topic in the literature. Some studies with designs that differ from ours evaluated the effectiveness of MAR algorithms in objectively reducing artefacts other than volumetric distortion.^{7,9,10,13,25,26} In other studies, the algorithm did not improve diagnostic tasks when considering other types of artefacts that were not volumetric distortions,^12–16 neither did it reduce artefacts arising from exomass.²⁷ Another study evaluating other types of artefacts reported a reduction in the diagnostic accuracy of root fracture detection.¹¹

Vasconcelos et al. (2015)³ showed that the MAR algorithm with EndoMode function of Cranex 3D did not reduce volumetric distortion expression and even made it worse according to a subjective analysis. Our results corroborate these findings since neither Picasso Trio nor OP300 MAR was efficient in significantly reducing volumetric distortion in objective analysis. In addition, the activation of MAR resulted in higher volumetric distortion for gutta-percha and titanium in Picasso Trio and for all materials in OP300. Both algorithms may have been helpful in decreasing other artefacts existing in the images, such as hyperdense streaks and hypodense bands,^{7,9,10,13,25,26} but not volumetric distortion.

Although the MAR algorithm of Picasso Trio was inefficient in significantly reducing volumetric distortion, most descriptive values were lower when MAR was enabled (Table 5, Figure 3). In addition, to the best of our knowledge, this study demonstrates for the first time that this algorithm significantly underestimated the PV of gutta-percha and titanium. Subjectively, the cylinders in Picasso Trio images exhibited a discrete shape distortion with a prominent border (Figure 2). Such distortion may be the cause of this underestimation since the volumetric distortions of gutta-percha and titanium were already very small in the mode without MAR. We believe that the MAR algorithm misinterpreted the extreme grey values of the cylinders as artefacts when homogenizing grey values.

Materials

We evaluated five high-density materials with different atomic numbers (Z) and densities. Amalgam alloy is composed of mercury (Z = 80), silver (Z = 47) and zinc (Z = 30) and the cylinders had a density of 10.9 g/cm³. The cylinders made of cobalt (Z = 24)–chromium (Z = 27) alloy had a density of 7.8 g/cm³. Gutta-percha is composed mainly of isoprene rubber with a very low atomic number, as well as zinc oxide (Z = 30) and its density was 2.6 g/cm³. Titanium has an atomic number of Z = 22 and density of 6 g/cm³. Finally, the atomic number of zirconium is Z = 40 and its density was 6.1 g/cm³.

Gutta-percha and titanium demonstrated volumetric dimensions closer to their physical ones compared to the other materials studied herein. This result can be explained by their smaller atomic number and density compared to amalgam, cobalt-chromium and zirconium, considering that the higher the atomic number and physical density, the higher is the expression of artefacts.^5,8,9,28 Likewise, titanium also demonstrated the least volumetric distortion when compared to amalgam and copper-aluminum alloys in another study.⁴ The non-significant differences between some materials (Table 6) might be due to resemblances they present regarding atomic number, physical density and volumetric distortions values. In this sense, gutta-percha did not differ from titanium (for Picasso Trio) because both materials present low atomic number and physical density and they both demonstrated smaller volumetric distortions. Meanwhile, cobalt-chromium/zirconium (for both CBCT systems) and amalgam/zirconium (for OP300) comparisons were not significant because these materials have high atomic number and physical density.

Repeated measures ANOVA

When considering Picasso Trio, volumetric distortion was significantly influenced by all factors and interactions. For OP300, the “MAR algorithm-Material” and “Material-MAR algorithm-Windowing” interactions did not significantly influence volumetric distortion. These interactions were not significant since the trend of OP300 MAR did not vary depending on the material, in contrast to the findings for gutta-percha and titanium in Picasso Trio. Unfortunately, manufacturers do not provide information about how exactly MAR algorithms work. Thus, further studies are necessary to better understand this tool, particularly its impact on volumetric distortion.

CBCT units

Since some studies have shown that acquisition parameters can influence the expression of artefacts,^1,3 these parameters were kept fixed in all acquisitions with each CBCT system and as similar as possible between the two devices studied. Considering that both systems possess different protocols and characteristics, the volumes measured with Picasso Trio were closer to the PV. We believe that one of the main reasons to explain such finding is the different contrast resolution settings of the two devices (Picasso Trio: 16-bit resolution; OP300: 13-bit resolution). Higher contrast resolution increases the possibility of grey values in the final image, resulting in more representative grey tones for the object.²⁹ In addition, the slight difference between voxel sizes (Picasso Trio: 0.2 mm; OP300: 0.25 mm) may reduce expression of the partial volume effect in Picasso Trio since smaller voxel sizes better represent the dimensions of an object.^2,30

Clinical considerations

The aim of positioning four cylinders inside the phantom in the same acquisition was to simulate a more clinical situation since the presence of more than one high-density material in a patient’s dental arch is common. Nevertheless, in addition to volumetric distortion, photon starvation, beam hardening and scattering induced artefacts were also observed in the CBCT scans. However, this condition (i.e., four cylinders inside the phantom) was kept the same for each combination of material, CBCT device and MAR algorithm.

Usually, CBCT reconstructed volumes have a lower spatial resolution than base images, due to an undersampling in digital images which results in reconstruction errors (artefacts).³¹ CBCT images might be considered a good representation of the scanned object, although this method is not entirely accurate since it is always susceptible to many sources of artefacts. When considering the objects’ dimensions, both volume and shape distortions have an impact on CBCT images since these types of artefacts will add more error to the representation of the scanned object.

The present study assessed the influence of windowing adjustments and MAR algorithms on the volumetric distortion of different high-density materials by volume segmentation. Although the influence of artefacts on measurements around implants are not always statistically relevant,^32–35 it may be clinically relevant since fine details are crucial for periodontal, peri-implant and endodontic evaluation and any slight distortion makes a difference.³¹ Moreover, volumetric distortion may impair the evaluation of thin cortical bone, that is smaller than 0.5 mm, and when peri-implant bone defects are at early stage.^6,36 Furthermore, root canal sealers can induce volumetric distortion in CBCT and their effect on root evaluation should be further investigated since evaluating the quality of canal fillings is important in cases in which the professional is investigating relapsing lesions.⁵ Besides, the detection of root fractures^11,37 and mesio-buccal canals³⁸ are challenging diagnostic tasks. Since volumetric distortion modifies the object’s representation, we could infer that the tomographical representation of an endodontic pin can be compromised, for example. Nonetheless, we do not have strong subsidies yet to categorically point out specific clinical conditions that volumetric distortion could affect, because this topic needs to be further elucidated and explored.

Limitations

Our study presents some limitations that must be discussed. The slight differences between the volumes of cylinders of the same material were inherent to the manufacturing technique, although it was the most precise as possible. In addition, the fact that each material had different physical density contributed to their cylinders demonstrating different PV when using the Archimedes Principle. Nevertheless, these differences did not impact our results, since the data submitted to the statistical analysis were the volumetric differences (i.e., the subtraction of the measured volume and the PV of each cylinder) in each CBCT acquisition.

Although human jaws and teeth are preferred for simulating clinical situations, future studies including diagnostic tasks and volumetric and shape distortions need to be conducted to contribute to a greater clinical relevance of the present study. In this initial study, some aspects that could refer to a more controlled in vitro technical approach (i.e., use of homogeneous cylinders with known PV and a phantom that would guarantee that the cylinders would always be placed in the same position) were needed to enable standardization and control of all variables under study. We therefore reinforce the relevance of our study because of its controlled design and because more information about factors that influence volumetric dimensions is required.

Conclusions

Gutta-percha and titanium showed volumetric dimensions closer to their PV when compared to the other materials. In general, the MAR algorithms of the two systems were inefficient in significantly reducing the volumetric distortion of high-atomic number and high-density materials. For clinical practice, larger window width and upper levels might be considered for reducing volumetric distortion of high-density materials, although possible implications of this procedure for image quality and for the accuracy of a given diagnostic task should be further investigated.