The frontier of simulation-based inference

Abstract

Many domains of science have developed complex simulations to describe phenomena of interest. While these simulations provide high-fidelity models, they are poorly suited for inference and lead to challenging inverse problems. We review the rapidly developing field of simulation-based inference and identify the forces giving additional momentum to the field. Finally, we describe how the frontier is expanding so that a broad audience can appreciate the profound influence these developments may have on science.

Mechanistic models can be used to predict how systems will behave in a variety of circumstances. These run the gamut of distance scales, with notable examples including particle physics, molecular dynamics, protein folding, population genetics, neuroscience, epidemiology, economics, ecology, climate science, astrophysics, and cosmology. The expressiveness of programming languages facilitates the development of complex, high-fidelity simulations and the power of modern computing provides the ability to generate synthetic data from them. Unfortunately, these simulators are poorly suited for statistical inference. The source of the challenge is that the probability density (or likelihood) for a given observation—an essential ingredient for both frequentist and Bayesian inference methods—is typically intractable. Such models are often referred to as implicit models and contrasted against prescribed models where the likelihood for an observation can be explicitly calculated (1). The problem setting of statistical inference under intractable likelihoods has been dubbed likelihood-free inference—although it is a bit of a misnomer as typically one attempts to estimate the intractable likelihood, so we feel the term simulation-based inference is more apt.

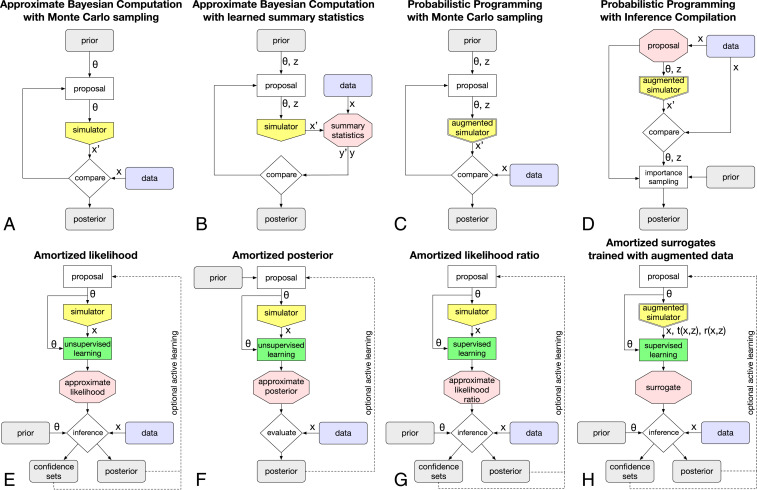
The intractability of the likelihood is an obstruction for scientific progress as statistical inference is a key component of the scientific method. In areas where this obstruction has appeared, scientists have developed various ad hoc or field-specific methods to overcome it. In particular, two common traditional approaches rely on scientists to use their insight into the system to construct powerful summary statistics and then compare the observed data to the simulated data. In the first one, density estimation methods are used to approximate the distribution of the summary statistics from samples generated by the simulator (1). This approach was used for the discovery of the Higgs boson in a frequentist paradigm and is illustrated in Fig. 1E). Alternatively, a technique known as approximate Bayesian computation (ABC) (2, 3) compares the observed and simulated data based on some distance measure involving the summary statistics. ABC is widely used in population biology, computational neuroscience, and cosmology and is depicted in Fig. 1A. Both techniques have served a large and diverse segment of the scientific community.

Fig. 1.

(A–H) Overview of different approaches to simulation-based inference.

Recently, the toolbox of simulation-based inference has experienced an accelerated expansion. Broadly speaking, three forces are giving new momentum to the field. First, there has been a significant cross-pollination between those studying simulation-based inference and those studying probabilistic models in machine learning (ML) (4), and the impressive growth of ML capabilities enables new approaches. Second, active learning—the idea of continuously using the acquired knowledge to guide the simulator—is being recognized as a key idea to improve the sample efficiency of various inference methods. A third direction of research has stopped treating the simulator as a black box and focused on integrations that allow the inference engine to tap into the internal details of the simulator directly.

Amidst this ongoing revolution, the landscape of simulation-based inference is changing rapidly. In this review we aim to provide the reader with a high-level overview of the basic ideas behind both old and new inference techniques. Rather than discussing the algorithms in technical detail, we focus on the current frontiers of research and comment on some ongoing developments that we deem particularly exciting.

Simulation-Based Inference

Simulators.

Statistical inference is performed within the context of a statistical model, and in simulation-based inference the simulator itself defines the statistical model. For the purpose of this paper, a simulator is a computer program that takes as input a vector of parameters $\theta$, samples a series of internal states or latent variables $z_i\sim p_i\left(z_i|\theta ,z_{<i}\right)$, and finally produces a data vector $x\sim p\left(x|\theta ,z\right)$ as output. Programs that involve random samplings and are interpreted as statistical models are known as probabilistic programs, and simulators are an example. Within this general formulation, real-life simulators can vary substantially:

• •The parameters $\theta$ describe the underlying mechanistic model and thus affect the transition probabilities $p_i\left(z_i|\theta ,z_{<i}\right)$. Typically the mechanistic model is interpretable by a domain scientist and $\theta$ has relatively few components and a fixed dimensionality. Examples include coefficients found in the Hamiltonian of a physical system, the virulence and incubation rate of a pathogen, or fundamental constants of Nature.
• •The latent variables $z$ that appear in the data-generating process may directly or indirectly correspond to a physically meaningful state of a system, but typically this state is unobservable in practice. The structure of the latent space varies substantially between simulators. The latent variables may be continuous or discrete and the dimensionality of the latent space may be fixed or may vary, depending on the control flow of the simulator. The simulation can freely combine deterministic and stochastic steps. The deterministic components of the simulator may be differentiable or may involve discontinuous control flow elements. In practice, some simulators may provide convenient access to the latent variables, while others are effectively black boxes. Any given simulator may combine these different aspects in almost any way.
• •Finally, the output data $x$ correspond to the observations. They can range from a few unstructured numbers to high-dimensional and highly structured data, such as images or geospatial information.

For instance, particle physics processes often depend only on a small number of parameters of interest such as particle masses or coupling strengths. The latent process combines a high-energy interaction, rigorously described by a quantum-field theory, with the passage of the resulting particles through an incredibly complex detector, most accurately modeled with stochastic simulations with billions of latent variables. Epidemiological simulations can be based on a network structure with geospatial properties, and the latent process consists of many repeated structurally identical stochastic time steps. In contrast, cosmological simulations of the evolution of the Universe may consist of a highly structured stochastic initial state followed by a smooth, deterministic time evolution.

These differences lead to an absence of a one-size-fits-all inference method. In this review we aim to clarify the considerations needed to choose the most appropriate approach for a given problem.

Inference.

Scientific inference tasks differ by what is being inferred: Given observed data $x$, is the goal to infer the input parameters $\theta$, or the latent variables $z$, or both? We will focus on the common problem of inferring $\theta$ in a parametric setting, we will comment on methods that allow inference on $z$, and we will not focus on nonparametric inverse problems. Sometimes only a subset of the parameters is of interest, while the rest are nuisance parameters.

Inference may be performed either in a frequentist or in a Bayesian approach and may be limited to point estimates $\widehat{\theta }\left(x\right)$ or extended to include a probabilistic notion of uncertainty. In the frequentist case, confidence sets are often formed from inverting hypothesis tests based on the likelihood-ratio test statistic. In Bayesian inference, the goal is typically to calculate the posterior $p\left(\theta |x\right)=p\left(x|\theta \right)p\left(\theta \right)/\int \hspace{0.17em}\hspace{0.17em}\mathrm{d}{\theta }^{\prime }p\left(x|{\theta }^{\prime }\right)p\left({\theta }^{\prime }\right)$ for observed data $x$ and a given prior $p\left(\theta \right)$. In both cases the likelihood function $p\left(x|\theta \right)$ is a key ingredient.

The fundamental challenge for simulation-based inference problems is that the likelihood function $p\left(x|\theta \right)$ implicitly defined by the simulator is typically not tractable, as it corresponds to an integral over all possible trajectories through the latent space (i.e., all possible execution traces of the simulator). That is,

$$p\left(x|\theta \right)=\int \hspace{0.17em}\mathrm{d}z\hspace{0.17em}p\left(x,z|\theta \right),$$ [1]

where $p\left(x,z|\theta \right)$ is the joint probability density of data $x$ and latent variables $z$. For real-life simulators with large latent spaces, it is clearly impossible to compute this integral explicitly. Since the likelihood function is the central ingredient in both frequentist and Bayesian inference, this is a major challenge for inference in many fields. This paper reviews simulation-based or likelihood-free inference techniques that enable frequentist or Bayesian inference despite this intractability. These methods can be seen as a specialization of inverse uncertainty quantification (UQ) on the model parameters in situations with accurate, stochastic simulators.

In practice, an important distinction is that between inference based on a single observation and that based on multiple independent and identically distributed (i.i.d.) observations. In the second case, the likelihood factorizes into individual likelihood terms for each i.i.d. observation, as $p\left(x|\theta \right)={\prod }_i{p}_{\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}}\left(x_i|\theta \right)$. For example, time-series data are typically non-i.i.d. and must be treated as a single high-dimensional observation, whereas the analysis of collision data in the search for the Higgs boson constitutes a dataset with many i.i.d. measurements. This distinction is important when it comes to the computational cost of an inference technique, as inference in the i.i.d. case will necessitate many repeated evaluations of the individual likelihood $p_{\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}}\left(x_i|\theta \right)$.

Traditional Methods.

The problem of inference without tractable likelihoods is not a new one, and two major approaches have been developed to address it. Arguably the most well known is ABC (2, 3). Until recently, it was so established that the terms “likelihood-free inference” and “ABC” were often used interchangeably. In the simplest form of rejection ABC, the parameters $\theta$ are drawn from the prior, the simulator is run with those values to sample $x_{\text{sim}}\sim p\left(\cdot |\theta \right)$, and $\theta$ is retained as the posterior sample if the simulated data are sufficiently close to the observed data. In essence, the likelihood is approximated by the probability that the condition $\rho \left(x_{\text{sim}},x_{\text{obs}}\right)<ϵ$ is satisfied, where $\rho$ is some distance measure and $ϵ$ is a tolerance. The accepted samples then follow an approximate version of the posterior. We show a schematic workflow of this algorithm in Fig. 1A (for a more elaborate Markov chain Monte Carlo algorithm with a proposal function).

In the limit $ϵ\to 0$, inference with ABC becomes exact, but for continuous data the acceptance probability vanishes. In practice, small values of $ϵ$ require unfeasibly many simulations. For large $ϵ$, sample efficiency is increased at the expense of inference quality. Similarly, the sample efficiency of ABC scales poorly to high-dimensional data $x$. Since the data immediately affect the rejection process (and in more advanced ABC algorithms the proposal distribution), inference for new observations requires repeating the entire inference algorithm. ABC is thus best suited for the case of a single observation or at most a few i.i.d. data points. Lacking space to do the vast ABC literature justice, we refer the reader to a review of ABC methods, see ref. 5, and highlight the combination with Markov chain Monte Carlo (MCMC) (6) and sequential Monte Carlo (SMC) (7, 8).

The second classical approach to simulation-based inference is based on creating a model for the likelihood by estimating the distribution of simulated data with histograms or kernel density estimation (1). Frequentist and Bayesian inference then proceeds as if the likelihood were tractable. We sketch this algorithm in Fig. 1E (replacing the green learning step with a classical density estimation method). This approach has enough similarities to ABC to be dubbed “approximate frequentist computation” by the authors of ref. 9. One advantage over ABC is that it is amortized: After an upfront computational cost at the simulation and density estimation stage, new data points can be evaluated efficiently. In Fig. 1E this is depicted by the blue “data” box entering only at the inference stage and not affecting the simulation step. This property makes density estimation-based inference particularly well suited for problems with many i.i.d. observations, a key reason for its widespread use in particle physics measurements.

Both of the traditional approaches suffer from the curse of dimensionality: In the worst case, the required number of simulations increases exponentially with the dimension of the data $x$. Therefore both approaches rely on low-dimensional summary statistics $y\left(x\right)$ and the quality of inference is tied to how well those summaries retain information about the parameters $\theta$. Traditionally, the development of powerful summary statistics has been the task of a domain expert, and the summary statistics have been prescribed prior to inference.

Frontiers of Simulation-Based Inference.

These traditional simulation-based inference techniques have played a key role in several fields for years. However, they suffer from shortcomings in three crucial aspects:

• •Sample efficiency: The number of simulated samples needed to provide a good estimate of the likelihood or posterior can be prohibitively expensive.
• •Quality of inference: The reduction of the data to low-dimensional summary statistics invariably discards some of the information in the data about $\theta$, which results in a loss in statistical power. Large values of the $ϵ$ parameter in ABC or the bandwidth parameter for kernel density estimation lead to poor approximations of the true likelihood. Both reduce the overall quality of inference.
• •Amortization: Performing inference with ABC for a new set of observed data requires repeating most steps of the inference chain, in particular if the proposal distribution depends on the observed data. The method scales poorly when applied to large numbers of observations. On the other hand, inference based on density estimation is amortized: The computationally expensive steps do not have to repeated for new observations. This is particularly desirable for the case with i.i.d. observations.

In recent years, new capabilities have become available that let us improve all three of these aspects. We loosely group them into three main directions of progress:

• 1)The ML revolution allows us to work with higher-dimensional data, which can improve the quality of inference. Inference methods based on neural network surrogates are directly benefiting from the impressive rate of progress in deep learning.
• 2)Active learning methods can systematically improve sample efficiency, letting us tackle more computationally expensive simulators.
• 3)The deep integration of automatic differentiation and probabilistic programming into the simulation code, as well as the augmentation of training data with information that can be extracted from the simulator, is changing the way the simulator is treated in inference: It is no longer a black box, but exposed to the inference workflow.

A Revolution in Machine Learning.

Over the last decade, ML techniques, in particular deep neural networks, have turned into versatile, powerful, and popular tools for a variety of problems (10). Neural networks initially demonstrated breakthroughs in supervised learning tasks such as classification and regression. They can easily be composed to solve higher-level tasks, lending themselves to problems with a hierarchical or compositional structure. Architectures tailored to various data structures have been developed, including dense or fully connected networks aimed at unstructured data, convolutional neural networks that leverage spatial structure for instance in image data, recurrent neural networks for variable-length sequences, and graph neural networks for graph-structured data. Choosing an architecture well suited for a specific data structure is an example of inductive bias, which more generally refers to the assumptions inherent in a learning algorithm independent of the data. Inductive bias is one of the key ingredients behind most successful applications of deep learning, although it is difficult to characterize its role precisely.

One area where neural networks are being actively developed is density estimation in high dimensions: Given a set of points $\left\{x\right\}\sim p\left(x\right)$, the goal is to estimate the probability density $p\left(x\right)$. As there are no explicit labels, this is usually considered an unsupervised learning task. We have already discussed that classical methods based for instance on histograms or kernel density estimation do not scale well to high-dimensional data. In this regime, density estimation techniques based on neural networks are becoming more and more popular. One class of these neural density estimation techniques is normalizing flows (11–26), in which variables described by a simple base distribution $p\left(u\right)$ such as a multivariate Gaussian are transformed through a parameterized invertible transformation $x=g_{\varphi }\left(u\right)$ that has a tractable Jacobian. The target density $p_g\left(x\right)$ is then given by the change-of-variables formula as a product of the base density and the determinant of the transformation’s Jacobian. Several such steps can be stacked, with the probability density “flowing” through the successive variable transformations. The parameters $\varphi$ of the transformations are trained by maximizing the likelihood of the observed data under the model $p_g\left(x_{\mathrm{o}\mathrm{b}\mathrm{s}}\right)$, resulting in a model density that approximates the true, unknown density $p\left(x\right)$. In addition to having a tractable density, it is possible to generate data from the model by drawing the hidden variables $u$ from the base distribution and applying the flow transformations. Neural density estimators have been generalized to model the dependency on additional inputs, i.e., to model a conditional density such as the likelihood $p\left(x|\theta \right)$ or posterior $p\left(\theta |x\right)$.

Generative adversarial networks (GANs) are an alternative type of generative model based on neural networks. Unlike in normalizing flows, the transformation implemented by the generator is not restricted to be invertible. While this allows for more expressiveness, the density defined by the generator is intractable. Since maximum likelihood is not a possible training objective, the generator is pitted against an adversary, whose role is to distinguish the generated data from the target distribution. We will later discuss how the same idea can be used for simulation-based inference, using an idea known as the “likelihood-ratio trick.”

Active Learning.

A simple, but very impactful idea is to run the simulator at parameter points $\theta$ that are expected to increase our knowledge the most. This can be done iteratively such that after each simulation the knowledge resulting from all previous runs is used to guide which parameter point should be used next. There are multiple technical realizations of this idea of active learning. It is commonly applied in a Bayesian setting, where the posterior can be continuously updated and used to steer the proposal distribution of simulator parameters (27–33). But it applies equally well to efficiently calculating frequentist confidence sets (34–36). Even simple implementations can lead to a substantial improvement in sample efficiency.

Similar ideas are discussed in the context of decision making, experimental design, and reinforcement learning, and we expect further improvements in inference algorithms from the cross-pollination between these fields. For instance, a question that is occasionally discussed in the context of reinforcement learning (37, 38) or Bayesian optimization (39), but has not yet been applied to the likelihood-free setting, is how to make use of multifidelity simulators offering multiple levels of precision or approximations.

Integration and Augmentation.

Both ML and active learning can substantially improve quality of inference and sample efficiency compared to classical methods. However, overall they do not change the basic approach to simulation-based inference dramatically: They still treat the simulator as a generative black box that takes parameters as input and provides data as output, with a clear separation between the simulator and the inference engine. A third direction of research is changing this perspective, by opening the black box and integrating inference and simulation more tightly.

One example of this shift is the probabilistic programming paradigm. Gordon et al. (40) describe probabilistic programs as the usual functional or imperative programs with two added constructs: 1) the ability to draw values at random from distributions and 2) the ability to condition values of variables in a program via observations. We have already described simulators as probabilistic programs focusing on the first construct, which does not require opening the black box. However, conditioning on the observations requires a deeper integration as it involves controlling the randomness in the generative process. This approach abstracts the capabilities needed to implement particle filters and SMC (41). Previously, this required writing the program in a special-purpose language; however, recent work allows these capabilities to be added to existing simulators with minimal changes to their codebase (42). Ultimately, probabilistic programming aims at providing the tools to infer the incredibly complex space of all execution traces of the simulator conditioned on the observation.

A complementary development is the observation that additional information that characterizes the latent data-generating process can be extracted from the simulator and used to augment the data used to train surrogates. Those developing inference algorithms and those familiar with the details of the simulator should consider whether, in addition to the sole ability to sample $x\sim p\left(x|\theta \right)$, the following quantities are well defined and tractable:

• 1)$p\left(x|z,\theta \right)$
• 2)$t\left(x,z|\theta \right)\equiv {\nabla }_{\theta }\log p\left(x,z|\theta \right)$
• 3)${\nabla }_z\log p\left(x,z|\theta \right)$
• 4)$r\left(x,z|\theta ,{\theta }^{\prime }\right)\equiv p\left(x,z|\theta \right)/p\left(x,z|{\theta }^{\prime }\right)$
• 5)${\nabla }_{\theta }\left(x,z\right)$
• 6)${\nabla }_{z}x$.

These quantities can then be used to augment the usual output $x$ from the simulator and can be exploited in supervised learning objectives and can dramatically increase the sample efficiency for surrogate training (43–45), as we will detail later.

Many of the quantities above involve derivatives, which can now be efficiently calculated using automatic differentiation (often referred to simply as autodiff) (46). Autodiff is a family of techniques similar to but more general than the backpropagation algorithm that is ubiquitous in deep learning. Automatic differentiation, like probabilistic programming, involves nonstandard interpretations of the simulation code and has been developed by a small but established field of computer science. In recent years several researchers have advocated that deep learning would be better described as differential programming (47, 48). With this view, incorporating autodiff into existing simulation codes is a more direct way to exploit the advances in deep learning than trying to incorporate domain knowledge into an entirely foreign substrate such as a deep neural network.

Extracting the necessary information from the simulator again requires integration deep in the code. While technologies to incorporate the probabilistic programming paradigm into existing code bases are just emerging, the development of tools to enable autodiff in the most commonly used scientific programming languages is well advanced. We highlight that two of the quantities listed above (quantities 2 and 3) involve both autodiff and probabilistic programming. The integration of inference and simulation as well as the idea of augmenting the training data with additional quantities has the potential to change the way we think about simulation-based inference. In particular, this perspective can influence the way simulation codes are developed to provide these new capabilities.

Workflows for Simulation-Based Inference

This wide array of capabilities can be combined in different inference workflows. As a guideline through this array of different workflows, let us first discuss common building blocks and the different approaches that can be taken in each of these components. In Fig. 1 and the following sections we will then piece these blocks together into different inference algorithms.

An integral part of all inference methods is running the simulator, visualized as a yellow pentagon in Fig. 1. The parameters at which the simulator is run are drawn from some proposal distribution, which may or may not depend on the prior in a Bayesian setting, and can be chosen either statically or iteratively with an active learning method. Next, the potentially high-dimensional output from the simulator may be used directly as input to the inference method or reduced to low-dimensional summary statistics.

The inference techniques can be broadly separated into those which, like ABC, use the simulator itself during inference and methods which construct a surrogate model and use that for inference. In the first case, the output of the simulator is directly compared to data (Fig. 1 A–D). In the latter case, the output of the simulator is used as training data for an estimation or ML stage, shown as the green boxes in Fig. 1 E–H. The resulting surrogate models, shown as red hexagons, are then used for inference.

The algorithms address the intractability of the true likelihood in different ways: Some methods construct a tractable surrogate for the likelihood function and others that for the likelihood-ratio function, both of which make frequentist inference straightforward. In other methods, the likelihood function never appears explicitly, for instance when it is implicitly replaced by rejection probability.

The final target for Bayesian inference is the posterior. Methods differ in whether they provide access to samples of parameter points sampled from the posterior, for instance from MCMC or ABC, or a tractable function that approximates the posterior function. Similarly, some methods require specifying which quantities are to be inferred early on in the workflow, while others allow this decision to be postponed.

Using the Simulator Directly during Inference.

Let us now discuss how these blocks and computational capabilities can be combined into inference techniques, beginning with those which, like ABC, use the simulator directly during inference. We sketch some of these algorithms in Fig. 1 A–D.

A reason for the poor sample efficiency of the original rejection ABC algorithm is that the simulator is run at parameter points drawn from the prior, which may have a large mass in regions that are in strong disagreement with the observed data. Different algorithms have been proposed that instead run the simulator at parameter points that are expected to improve the knowledge on the posterior the most (27–31). Compared to vanilla ABC, these techniques improve sample efficiency, although they still require the choice of summary statistics, distance measure $\rho$, and tolerance $ϵ$.

In the case where the final stage of the simulator is tractable or the simulator is differentiable (respectively, properties 1 and 6 from the list in Integration and Augmentation), asymptotically exact Bayesian inference is possible (43) without relying on a distance tolerance or summary statistics, removing ABC’s main limitations in terms of quality of inference.

The probabilistic programming paradigm presents a more fundamental change to how inference is performed. First, it requires the simulator to be written in a probabilistic programming language, although recent work allows these capabilities to be added to existing simulators with minimal changes to their codebase (42). In addition, probabilistic programming requires either a tractable likelihood for the final step $p\left(x|z,\theta \right)$ (quantity 1) or the introduction of an ABC-like comparison. When these criteria are satisfied, several inference algorithms exist that can draw samples from the posterior $p\left(\theta ,z|x\right)$ of the input parameters $\theta$ and the latent variables $z$ given some observed data $x$. These techniques are based either on MCMC (Fig. 1C) or on training a neural network to provide proposal distributions (49) as shown in Fig. 1D. The key difference from ABC is that the inference engine controls all steps in the program execution and can bias each draw of random latent variables to make the simulation more likely to match the observed data, improving sample efficiency.

A strength of these algorithms is that they allow us to infer not only the input parameters into the simulator, but also the entire latent process leading to a particular observation. This allows us to answer entirely different questions about scientific processes, adding a particular kind of physical interpretability that methods based on surrogates do not possess. While standard ABC algorithms in principle allow for inference on $z$, probabilistic programming solves this task more efficiently.

Surrogate Models.

A key disadvantage of using the simulator directly during inference is the lack of amortization. When new observed data become available, the whole inference chain has to be repeated. By training a tractable surrogate or emulator for the simulator, inference is amortized: After an upfront simulation and training phase, new data can be evaluated very efficiently. This approach scales particularly well to data consisting of many i.i.d. observations. As discussed in Traditional Methods, this is not a new idea, and well-established methods use classical density estimation techniques to create a surrogate model for the likelihood function. But the new computational capabilities discussed in Simulation-Based Inference have given new momentum to this class of inference techniques, some of which are visualized in Fig. 1 E–H.

A powerful probabilistic approach is to train neural conditional density estimators such as normalizing flows as a surrogate for the simulator. The conditional density can be defined in two directions: The network can learn either the posterior $p\left(\theta |x\right)$ (32, 50–54) or the likelihood $p\left(x|\theta \right)$ (33, 55–57). We show these three techniques in Fig. 1 E and F; note that the likelihood surrogate algorithm is structurally identical to the classical density estimation-based approach, but uses more powerful density estimation techniques.

Relatedly, neural networks can be trained to learn the likelihood-ratio function $p\left(x|{\theta }_0\right)/p\left(x|{\theta }_1\right)$ or $p\left(x|{\theta }_0\right)/p\left(x\right)$, where in the latter case the denominator is given by a marginal model integrated over a proposal or the prior (4, 58–65). We sketch this approach in Fig. 1G. The key idea is closely related to the discriminator network in GANs mentioned above: A classifier is trained using supervised learning to discriminate two sets of data, although in this case both sets come from the simulator and are generated for different parameter points ${\theta }_0$ and ${\theta }_1$. The classifier output function can be converted into an approximation of the likelihood ratio between ${\theta }_0$ and ${\theta }_1$! This manifestation of the Neyman–Pearson lemma in an ML setting is often called the likelihood-ratio trick.

These three surrogate-based approaches are all amortized: After an upfront simulation and training phase, the surrogates can be evaluated efficiently for arbitrary data and parameter points. They require an upfront specification of the parameters of interest, and the network then implicitly marginalizes over all other (latent) variables in the simulator. All three classes of algorithms can employ active learning elements such as an iteratively updated proposal distribution to guide the simulator parameters $\theta$ toward the relevant parameter region, improving sample efficiency. Using neural networks eliminates the requirement of low-dimensional summary statistics, leaving it to the employed model to learn the structures in high-dimensional data and potentially improving quality of inference.

Despite these fundamental similarities, there are some differences between emulating the likelihood, the likelihood ratio, and the posterior. Learning the posterior directly provides the main target quantity in Bayesian inference but induces a prior dependence at every stage of the inference method. Learning the likelihood or the likelihood ratio enables frequentist inference or model comparisons, although for Bayesian inference an additional MCMC or quantity 6 step is necessary to generate samples from the posterior. The prior independence of likelihood or likelihood-ratio estimators also leads to extra flexibility to change the prior during inference. An advantage of training a generative model to approximate the likelihood or posterior over learning the likelihood-ratio function is the added functionality of being able to sample from the surrogate model. On the other hand, learning the likelihood or posterior is an unsupervised learning problem, whereas estimating the likelihood ratio through a classifier is an example of supervised learning and often a simpler task. Since for the higher-level inference goal the likelihood and the likelihood ratio can be used interchangeably, learning a surrogate for the likelihood-ratio function may often be more efficient.

Another strategy that allows us to leverage supervised learning is based on extracting additional quantities from the simulator that characterize the likelihood of the latent process (e.g., quantities 2 and 4 from the list in Integration and Augmentation). This additional information can be used to augment the training data for surrogate models. The resulting supervised learning task can often be solved more efficiently, ultimately improving the sample efficiency in the inference task (9, 44, 45, 66).

Surrogate-based approaches benefit from imposing suitable inductive bias for a given problem. It is widely acknowledged that the network architecture of a neural surrogate should be chosen according to the data structure (e.g., images, sequences, or graphs). Another, potentially more consequential, way of imposing inductive bias is to have the surrogate model reflect the causal structure of the simulator. Manually identifying the relevant structures and designing appropriate surrogate architectures is very domain specific, although has been shown to improve the performance on some problems (67–69). Recently attempts have been made to automate the process of creating surrogates that mimic the simulation (70). Looking farther ahead, we would like to learn surrogates that reflect the causal structure of a coarse-grained system. If this is possible, it would allow the surrogate to model only the relevant degrees of freedom for the phenomena that emerge from the underlying mechanistic model.

Preprocessing and Postprocessing.

There are a number of additional steps that can surround these core inference algorithms, either in the form of preprocessing steps that precede the main inference stage or as an afterburner following the main inference step.

One preprocessing step is to learn powerful summaries $y\left(x\right)$. Because of the curse of dimensionality, both ABC and classical density estimation-based inference methods require a compression of the data into low-dimensional summary statistics. They are usually prescribed (i.e., hand chosen by domain scientists based on their intuition and knowledge of the problem at hand), but the resulting summaries will generally lose some information compared to the original data. A minimally invasive extension of these algorithms is to first learn summary statistics that have certain optimality properties, before running a standard inference algorithm such as ABC. We sketch this approach in Fig. 1B for ABC, but it applies equally to inference based on density estimation.

The score $t\left(x|\theta \right)\equiv {\nabla }_{\theta }p\left(x|\theta \right)$, the gradient of the log (marginal) likelihood with respect to the parameters of interest, defines such a vector of optimal summary statistics: In a neighborhood of $\theta$, the score components are sufficient statistics, and they can be used for inference without loss of information. Just like the likelihood, the score itself is generally intractable, but it can be estimated based on quantity 5 and an exponential family approximation (71, 72). If quantity 2 is available, augmented data extracted from the simulator can instead be used to train a neural network to estimate the score (44) without requiring such an approximation. Learned summaries can also be made robust with respect to nuisance parameters (73, 74).

Even if it is not necessary to reduce the data to low-dimensional summary statistics, in some fields the measured raw or “low-level” data can be very high dimensional. It is then common practice to compress them to a more manageable set of “high-level” features of moderate dimensionality and to use these compressed data as input to the inference workflow.

Inference compilation (49) is a preprocessing step for probabilistic programming algorithms, shown in Fig. 1D. Initial runs of the simulator are used to train a neural network used for sequential importance sampling of both $\theta$ and $z$.

After the completion of the core inference workflow, an important question is whether the results are reliable: Can the outcome be trusted in the presence of imperfections such as limited sample size, insufficient network capacity, or inefficient optimization?

One solution is to calibrate the inference results. Using the ability of the simulator to generate data for any parameter point, we can use a parametric bootstrap approach to calculate the distribution of any quantity involved in the inference workflow. These distributions can be used to calibrate the inference procedure to provide confidence sets and posteriors with proper coverage and credibility (9, 60). While possible in principle, such procedures may require a large number of simulations. Other diagnostic tools that can be applied at the end of the inference stage involve training classifiers to distinguish data from the surrogate model and the true simulator (60), self-consistency checks (9, 60), ensemble methods, and comparing distributions of network output against known asymptotic properties (75–77). Some of these methods may be used for uncertainty estimation, although the statistical interpretation of such error bars is not always obvious.

None of these diagnostics address the issues encountered if the model is misspecified and the simulator is not an accurate description of the system being studied. Model misspecification is a problem that plagues inference with both prescribed and implicit models equally. Usually this is addressed by expanding the model to have more flexibility and introducing additional nuisance parameters.

Recommendations.

The considerations needed to choose which of the approaches described above is best for a given problem will include the inference goals, the dimensionality of model parameters, the latent variables, and the data; whether good summary statistics are available; the internal structure of the simulator; the computational cost of the simulator; the level of control over how the simulator is run; and whether the simulator is a black box or whether any of the quantities discussed in Integration and Augmentation can be extracted from it. Nevertheless, we believe that the existing body of research lets us provide a few general guidelines.

First, if any of the quantities discussed in Frontiers of Simulation-Based Inference are available, they should be leveraged. Powerful algorithms are available for the case with differentiable simulators (43), for simulators for which the joint likelihood of data and latent variables is accessible (44), and for simulators explicitly written as a probabilistic model in a probabilistic programming framework (78). Probabilistic programming is also the most versatile approach when the goal is not only inference on the parameters $\theta$, but also inference on the latent variables $z$.

If powerful low-dimensional summary statistics are established, traditional techniques can still offer a reasonable performance. In most cases, however, we recommend trying methods based on training a neural network surrogate for the likelihood (33, 56) or the likelihood ratio (60, 62, 64). If generating synthetic data from the surrogate is not important, learning the likelihood ratio rather than the likelihood allows us to leverage powerful supervised learning methods.

Finally, active learning techniques can improve the sample efficiency for all inference techniques. There is a tradeoff between active learning, which tailors the efficiency to a particular observed dataset, and amortization, which benefits from surrogates that are agnostic about the observed data. A good compromise here will depend on the number of observations and the sharpness of the posterior compared to the prior.

Discussion

Until recently, scientists confronted with inverse problems and a complex simulator as a forward model had little recourse other than to choose ABC or methods based on classical density estimation techniques. While these approaches have served some domains of science quite well, they have relied heavily on the labor-intensive process of experts providing powerful summary statistics. As a result, there is a frontier beyond which these traditional methods are less useful and new techniques are needed.

The term likelihood-free inference has served as a point of convergence for what were previously disparate communities, and a new lingua franca has emerged. This has catalyzed significant cross-pollination and led to a renaissance in simulation-based inference. The advent of powerful ML methods is enabling practitioners to work directly with high-dimensional data and to reduce the reliance on expert-crafted summary statistics. New programming paradigms such as probabilistic programming and differentiable programming provide new capabilities that enable entirely new approaches to simulation-based inference. Finally, taking a more systems-level view of simulation-based inference that brings together the statistical and computational considerations has taken root. Here active learning is leading the way, but we expect more advances like this as simulation-based inference matures.

The rapidly advancing frontier means that several domains of science should expect either a significant improvement in inference quality or the transition from heuristic approaches to those grounded in statistical terms tied to the underlying mechanistic model. It is not unreasonable to expect that this transition may have a profound impact on science.

Data Availability.

There are no data associated with this paper.