Markov state modeling reveals alternative unbinding pathways for peptide–MHC complexes

Significance

Peptide binding to MHC receptors is part of a central biological process that enables our immune system to attack diseased cells. We use molecular simulations to illuminate the mechanisms driving stable peptide–MHC binding. Our simulation framework produces an atomistic model of the unbinding dynamics for a given peptide–MHC, which quantifies transitions between the major states of the system (bound, intermediate, and unbound). We applied this framework to study the binding of a SARS-CoV peptide to the HLA-A*24:02 receptor. This work revealed the unexpected importance of peptide’s position 4 in driving the stability of the complex, a finding with broader biomedical implications. Our methods can be applied to other peptide–MHC complexes, requiring only a 3D model as input.

Abstract

Peptide binding to major histocompatibility complexes (MHCs) is a central component of the immune system, and understanding the mechanism behind stable peptide–MHC binding will aid the development of immunotherapies. While MHC binding is mostly influenced by the identity of the so-called anchor positions of the peptide, secondary interactions from nonanchor positions are known to play a role in complex stability. However, current MHC-binding prediction methods lack an analysis of the major conformational states and might underestimate the impact of secondary interactions. In this work, we present an atomically detailed analysis of peptide–MHC binding that can reveal the contributions of any interaction toward stability. We propose a simulation framework that uses both umbrella sampling and adaptive sampling to generate a Markov state model (MSM) for a coronavirus-derived peptide (QFKDNVILL), bound to one of the most prevalent MHC receptors in humans (HLA-A24:02). While our model reaffirms the importance of the anchor positions of the peptide in establishing stable interactions, our model also reveals the underestimated importance of position 4 (p4), a nonanchor position. We confirmed our results by simulating the impact of specific peptide mutations and validated these predictions through competitive binding assays. By comparing the MSM of the wild-type system with those of the D4A and D4P mutations, our modeling reveals stark differences in unbinding pathways. The analysis presented here can be applied to any peptide–MHC complex of interest with a structural model as input, representing an important step toward comprehensive modeling of the MHC class I pathway.

Class I major histocompatibility complexes (MHCs), also known as human leukocyte antigens (HLAs) in humans, are proteins that bind to intracellular peptides and present them at the cellular surface (1). In the endoplasmic reticulum, MHCs are loaded with peptides of length 8 to 11 amino acids derived from cleaved intracellular proteins. Then the combined peptide–MHC complex is transported to the cell surface to be inspected by surveilling T cells. T cell activation normally occurs when a cell presents peptides not found in healthy cells, triggering an immune response. Current efforts in immunotherapy aim to amplify this mechanism to target diseased cells (i.e., infected or tumoral). Since every patient has a different set of MHCs, this problem must be addressed in a personalized manner, i.e., by identifying disease-specific peptides that can bind to the MHCs of a particular patient or to MHCs that will provide broad population coverage.

Therefore, a prerequisite for T cell activation, or immunogenicity, is stable binding to occur between a given peptide and MHC (2). Peptides bound to MHCs on the cell surface can be identified directly using mass spectrometry, and experiments have been curated into databases such as SysteMHC Atlas (3). Additionally, the binding affinities of peptides can be measured with competitive binding assays, for example, which can provide half maximal inhibitory concentration (IC50) values. In turn, results from binding assay experiments have been curated into databases such as the Immune Epitope Database (IEDB) (4). This accumulation of experimental data has led to the popularity of sequence-based methods for peptide–MHC binding prediction. These methods are based on machine learning, typically with neural networks, trained on sequences of known peptide–MHC pairs and can rapidly predict binding affinity (5–8).

Moving beyond a simple measurement or prediction of binding, uncovering the molecular mechanisms for strong binding usually starts with an analysis of a structure of the bound complex. Structures can be from one of the few hundred crystal structures available at the Protein Data Bank (PDB) or modeled with a docking-based approach (9–14). However, an analysis of a single conformation may be misleading due to the flexibility of the structure (15), and the dynamics of peptide–MHC binding must be probed. Along this direction, experimental methods such as NMR (16, 17), hydrogen/deuterium exchange (18), and fluorescence anisotropy (19) have been used to gain insight into the flexibility of peptide–MHC complexes. However, these experimental methods have particular limitations regarding the cost, the size of the system, and the resolution of the results.

As an alternative, molecular simulations can be used to analyze the stability and dynamics of peptide–MHC binding. Such analysis can cover the major conformational states of the process, while providing atomistic details that cannot be currently achieved with experimental methods. In this context, many simulation studies have focused on bound peptide–MHC complexes (20). Going even further, Ayres et al. (21) built a simplified model for peptide flexibility in the binding site of a particular MHC, and Wan et al. (22) used the Molecular Mechanics Poisson–Boltzmann Surface Area continuum solvation method to compute binding free energy estimates from molecular dynamics (MD). For that, they simulated both bound peptide–MHC conformations and fully unbound conformations (22). While simulating bound/unbound states may be enough for accurate binding affinity prediction, information on the intermediate states and the transition between states is lacking. In another study, a coarse-grained Monte Carlo-based framework was developed for generating detachment pathways of peptides exiting the MHC binding site (23). These detachment pathways allow some analysis of the transition between bound and unbound states. However, the use of coarse graining prevents atomic-level predictions of peptide–MHC interactions that could characterize the major states along the binding/unbinding pathways.

Here we propose an analysis that goes beyond previous simulation studies, capable of revealing all of the molecular interactions that are driving the stability of a peptide–MHC complex. In other words, we provide a model that can capture all of the major conformational states along the binding/unbinding pathway, as well as the transitions between those states, using atomistic MD. Such models are known as Markov state models (MSMs) (24) and allow for the quantification of both binding affinity and stability for a given peptide–MHC complex (25–27). However, building MSMs of the whole binding process for peptide–MHCs, in atomic-level detail, is computationally challenging. MHCs are large systems composed of about 380 residues, which contribute to the high computational cost of MD. More importantly, the typical timescales involved in the binding process are significantly longer than current MD simulations are capable of reaching within a reasonable timeframe. For instance, while the timesteps of typical full-atom MD simulations are on the order of femtoseconds, the half-life of the more stable peptide–MHC complexes reaches tens of hours (2).

To address the computational challenges, we propose a simulation framework for peptide–MHCs that splits the problem into two stages: an exploration stage and a connection stage. The exploration stage makes use of umbrella sampling (28), which is a well-known technique that can accelerate the sampling along an appropriate reaction coordinate. The connection stage makes extensive use of the relatively newer class of methods called adaptive sampling (27, 29–33). Adaptive sampling works by iteratively performing short MD simulations in parallel. At each iteration, the next round of MD simulations is initialized using conformations that aim to optimize exploration using a restart strategy. The restart strategy selects the conformations using all of the simulation data already performed up to the given iteration. Adaptive sampling methods are typically performed in conjunction with MSMs (30, 32). MSMs are built by defining states and counting transitions between states, producing a transition matrix that contains the transition probabilities. Thus, MSMs do not require each individual simulation to be long for construction, only long enough to be able to count transitions. Adaptive sampling methods combined with MSMs are becoming increasingly popular as a way to accelerate the sampling of MD, and recent studies have been investigating how to optimize its use (32–35).

As an example case, we focus this work on studying the binding of the viral peptide QFKDNVILL with the human MHC receptor HLA-A*24:02. The choice of this system is interesting in multiple regards. First, a crystal structure is available for this system (36), which we use to begin our modeling. Second, HLA-A*24:02 is one of the most prevalent HLA allotypes in the human population (4), being therefore highly relevant for several biomedical applications. Third, the displayed peptide is derived from the nucleocapsid protein of severe acute respiratory syndrome coronavirus (SARS-CoV), and this protein has over 90% sequence similarity with that of SARS-CoV-2, the coronavirus that causes COVID-19 (37). Therefore, insights from this system may be relevant for the current and/or future coronavirus epidemics. Finally, the popular sequence-based predictor NetMHC4.0 (5) fails to correctly predict the binding affinity of this peptide, potentially neglecting the role of key secondary interactions.

Class I MHCs usually bind peptides through dominant intermolecular interactions that typically involve the residues at both ends of the peptide (so-called anchor residues). The chemical properties of deeper pockets in the MHC binding cleft determine the “identity” of the preferred anchor residues. As a consequence, we can usually summarize the binding profile of a particular MHC allotype by specifying the types of residues found in the anchor positions. For instance, IEDB data indicate that the anchor residues for peptides binding to HLA-A*24:02 are position 2 (p2 anchor) and the last residue (C-term anchor), with a preference for hydrophobic residues in both positions (4). In particular, the p2 anchor is preferentially a tryptophan (W) or tyrosine (Y), but the corresponding pocket can tolerate a phenylalanine (F). The C-term anchor is preferentially a phenylalanine (F), isoleucine (I), or tryptophan (W), but the corresponding pocket can also tolerate a leucine (L) or methionine (M). Note that the amino acid binding chart at IEDB does not indicate any relevant preferences for peptide positions p3 to p6. Although anchor residues vary depending on the MHC allotype, middle positions are usually considered to be more exposed to T cell interaction and less relevant for peptide–MHC binding (38). Interestingly, the viral peptide QFKDNVILL, called WT in this work as the “wild type”, has both anchor positions as “tolerated” residues. The lack of any preferred anchors might explain the very low binding affinity predicted by NetMHC4.0 for this complex (7,769.11 nM). While the strongest contacts in the WT system are likely to still be formed by the anchor residues, we are interested in the role of secondary interactions involving the other nonanchor peptide positions, which may play a larger role in the absence of strong primary anchors.

Thus, the objective of this work is to investigate the role of secondary interactions in the binding of QFKDNVILL to HLA-A*24:02. Using our proposed simulation framework (Fig. 1), we generate over 150 $\mathrm{\mu }$s of MD data to build a MSM of the entire binding/unbinding process. Our model predicts that QFKDNVILL is capable of binding to HLA-A*24:02, and mutational analysis based on reweighting of this WT system reveals the importance of the nonanchor residue in position 4. Additional MSMs of two mutated peptide variants (D4A and D4P), generated using around 500 $\mathrm{\mu }$s of total MD data, were used to predict the relative ranking of these three systems, and this ranking was confirmed using competitive binding assays. Detailed analysis of the MSMs for the three different systems has revealed alternative peptide-unbinding pathways, as well as alternative ways in which position 4 (p4) can affect peptide–MHC stability. Structural analysis of MHC binders that lack canonical primary anchors, as the one described here, may provide the key to identify valuable peptide targets that are being currently missed in vaccine development and T cell-based immunotherapy efforts.

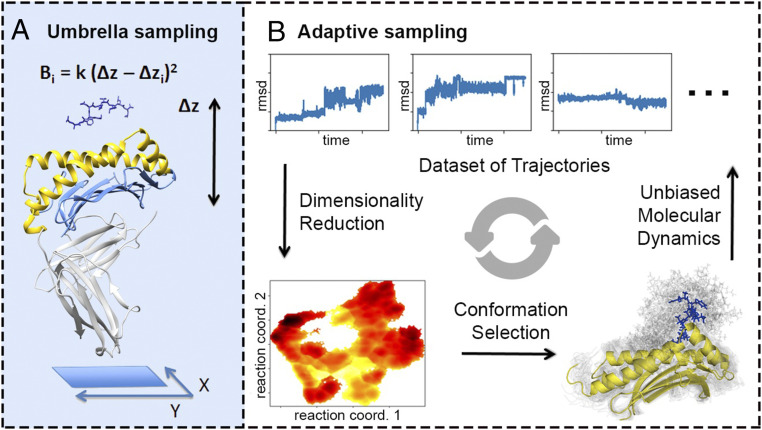
Fig. 1.

Overview of the simulation framework. (A) The exploration stage involves running umbrella-sampling simulations along the z-dist reaction coordinate, which approximates the unbinding direction. $B_i$ is the energy bias, while $k$ is the force constant. The $\beta$-sheet floor of the MHC (light blue) is aligned to the XY plane, and then the Z coordinate is used to define z-dist. The truncated portion of the MHC (light gray) is not included in any of the simulations. (B) The connection stage involves running unbiased simulations in an adaptive sampling fashion until most of the states are connected. Restarting conformations are chosen by analyzing the trajectories in a dimensionality-reduced space using TICA that adequately captures the binding/unbinding pathway. Then the selection of conformations is biased toward the less densely sampled regions of the TICA space.

Results

Simulation Framework Enables Building MSMs for Peptide–MHC Binding/Unbinding.

A simulation framework (Fig. 1) is used to generate MD data to build an MSM of the WT system. Characteristics of the exploration and connection stages for the WT system can be found in SI Appendix, Fig. S1. A total of 160 $\mathrm{\mu }$s of aggregate simulation data were generated, where each simulation takes ∼15 h on a single Tesla V100 graphics processing unit (GPU), taking about 2,600 GPU-hours total. Time-lagged independent components analysis (TICA) was performed to reduce the dimensionality of the conformations (39, 40). We keep the top two independent components, which adequately capture two different detachment pathways that the peptide takes to go from the native state to the unbound state (SI Appendix, Figs. S2 and S3). One component roughly represents the detachment of the N-term while the second one represents the detachment of the C-term. After discretization of the TICA space into microstates, the discrete transition-based reweighting analysis method (dTRAM) (41) was used to combine the biased and unbiased trajectories from the two stages of the simulation framework into a final MSM (Materials and Methods and SI Appendix, Figs. S2–S4).

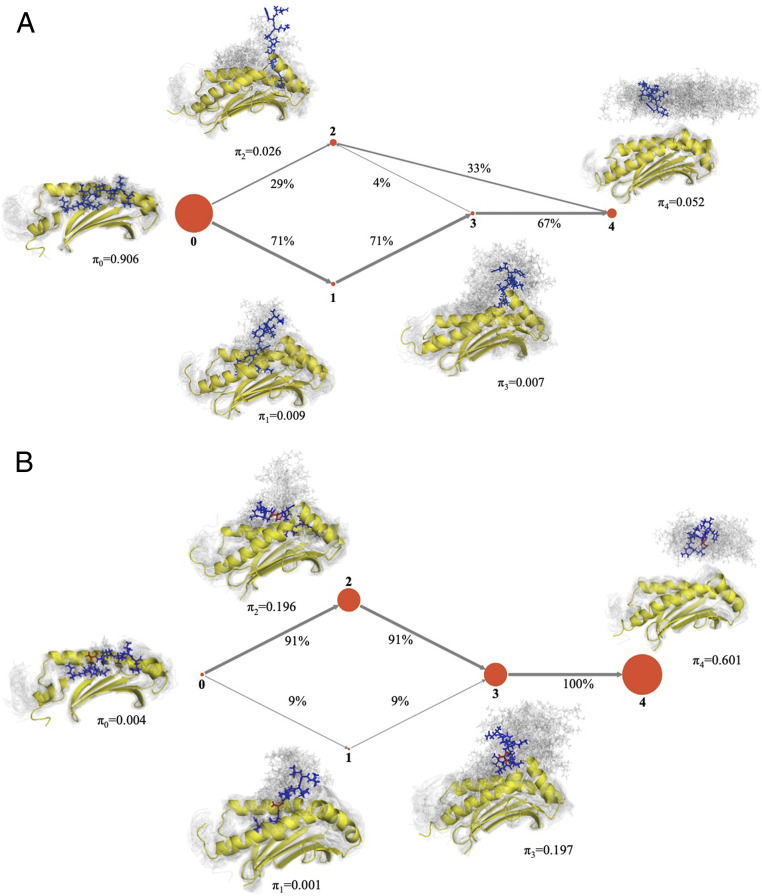
We partition the microstates into five states, which were defined to distinguish between the major metastable states along the binding pathway based on a previous study of detachment pathways (23). Detachment pathways are mainly distinguished by the order in which the anchor residues detach from the corresponding MHC pocket (23), which we captured in the MSM through TICA. The two endpoints of binding are the native state (state 0) and the unbound or dissociated state (state 4). The native state (state 0) is defined as the set of all microstates with an average all-atom rmsd of below 0.2 nm from the crystal structure. The unbound/dissociated state (state 4) is defined as the set of microstates where the minimum distance between the peptide and MHC is greater than 0.5 nm. The next two states define partially bound states where only a single anchor of the peptide is in the corresponding MHC pocket. The N-term bound state (state 1) is defined as the set of nonnative microstates where the center of mass of position 2 in the peptide is below 0.2 nm from the center of mass of the native position 2 location. The C-term bound state (state 2) is defined as the set of nonnative microstates where the center of mass of position 9 in the peptide is below 0.2 nm from the center of mass native position 9 location. State 3 defines all of the other associated microstates which have the peptide in contact with the MHC. Typical conformations can be found within each of the five states (see Fig. 4).

Fig. 4.

Flux network of unbinding trajectories for the WT system. States 0, 1, 2, and 3 denote the set of associated states that have the peptide in contact to the MHC. State 4 represents the dissociated or unbound state. Size of the nodes (depicted in red) indicates the equilibrium probabilities of each state (${\pi }_i$). (A) The WT system prefers to unbind through detaching first on the C-term end (state 0 to state 1 transition) due to the stronger interactions on the N-term end, which include the aspartic acid in position 4. (B) With a single mutation, the D4A system prefers to unbind through detaching first on the N-term end (state 0 to state 2 transition), and the accessibility of both detachment pathways favors the instability of the D4A system. Note that the MSM model includes all transitions between nodes, in all directions. However, this flux network depicts only trajectories starting from state 0 and reaching state 4 (i.e., unbinding pathways).

The MSM for WT predicts that the native state is the most probable state ($P\left(\text{native state}\right)={\pi }_0=0.906$), despite the lack of strong primary anchors. Therefore, our model predicts the stable binding of QFKDNVILL to HLA-A*24:02, which is in line with crystallographic evidence (36). The predicted free energy of binding was $\mathrm{\Delta }{G}_{WT}=-7.19\pm 1.02$ kJ/mol.

Mutational Analysis of the WT MSM Reveals the Importance of Peptide’s Position 4 toward Binding.

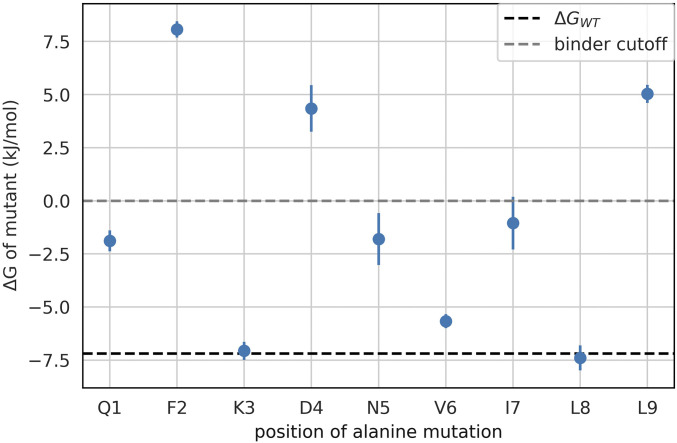
We used the MSM of the WT system to perform mutational analysis based on reweighting the state probabilities computed from the MSM and predict the change to the binding affinity upon alanine mutation (Fig. 2). Unsurprisingly, the F2A and L9A mutations were predicted to be most disruptive to binding, as positions 2 and 9 are the primary anchor residues for this peptide. However, the D4A mutation was also predicted to be remarkably disruptive to peptide binding (Fig. 2). This implies that secondary interactions involving p4 must be particularly relevant for the binding of WT.

Fig. 2.

$\mathrm{\Delta }\mathrm{\Delta }G$ predictions from the mutational analysis. The black dashed line represents the predicted $\mathrm{\Delta }{G}_{WT}$ of $-7.19$ kJ/mol. The gray dashed line represents the separation between predicted binders and nonbinders. Alanine mutations in positions 2, 4, and 9 are all predicted to significantly impair binding, while alanine mutations in positions 1, 5, and 7 are predicted to reduce the binding affinity.

We can decompose the effect of the alanine exchanges across the different associated states (i.e., states 0, 1, 2, and 3) (Table 1). Mutating the anchor residues (i.e., p2 and p9) has the expected effect of destabilizing the states associated with the presence of these respective positions in the corresponding MHC pockets. In other words, for the F2A mutation, the native state (state 0) and the N-term bound state (state 1) are most destabilized, while for the L9A mutation, the native state and the C-term bound state (state 2) are most destabilized. The native state (state 0) and the N-term bound state (state 1) are also most destabilized for the D4A mutation. Given that this peptide is a 9-mer, position 4 is closer to the N-term side and is likely playing a role in stabilizing the interactions from that end.

Table 1.

Destabilization of the metastable states upon alanine mutation

Mutation$\backslash$state	0	1	2	3
F2A	38.7	37.7	7.3	6.7
D4A	14.9	17.5	3.5	4.6
L9A	19.8	1.1	15.9	8.7

Shown are the values $RT\left[\text{ln}\left(Z_{wt}^{S_i}/Z_{wt}^{dissociated}\right)-\text{ln}\left(Z_{mut}^{S_i}/Z_{mut}^{dissociated}\right)\right]$ in kJ/mol (Materials and Methods) for all associated states $S_i$. Computed values are all in reference to the dissociated state, so the values for state 4 would all be zero.

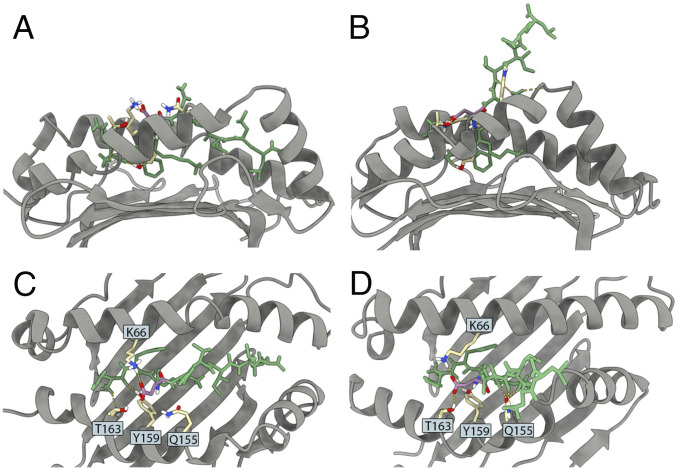
We can use the WT MSM to analyze the relevant intermolecular contacts by computing the probability that a given contact exists while the system is within a particular state (SI Appendix, Figs. S5–S8). In the native state (state 0), the aspartic acid in position 4 of the peptide (D4) was more likely to interact with MHC residues K66, Q155, Y159, and T163 (SI Appendix, Fig. S5). Given the three-dimensional (3D) arrangement of the binding cleft (see Fig. 5), the D4-K66 and D4-T163 interactions are not surprising. On the other hand, the contributions of Q155 and Y159 are less obvious, despite being predicted to be even more important for the N-term bound state (SI Appendix, Fig. S5).

Fig. 5.

Representative conformations in the WT system from state 0 (native state) and state 1 (N-term bound state). A and B depict the side views of states 0 and 1, respectively. These states can be distinguished by the location of the C-term of the peptide relative to the MHC binding cleft (i.e., proximity to the F pocket). C and D depict the top views of states 0 and 1, respectively. Peptide’s p4 residue (aspartic acid, D) is depicted in magenta (carbon atoms in magenta; oxygen atoms depicted in red). Other peptide positions are depicted in green. Key MHC residues predicted to interact with p4 are depicted in yellow (carbon atoms in yellow; oxygen atoms depicted in red; nitrogen atoms in blue; hydrogen atoms in white), including lysine 66 (K66), threonine 163 (T163), tyrosine 159 (Y159), and glutamine 155 (Q155). Hydrogen bonds involving any of these residues are depicted in yellow dashed lines.

The mutational analysis can be performed on the MHC side as well, and we used the MSM of the WT system to evaluate the impact of mutations Q155A and Y159A. Interestingly, the MSM predicts Y159A to have a similar detrimental impact on binding ($\mathrm{\Delta }{G}_{Y159}=4.86\pm 0.77$ kJ/mol) to that observed for the D4A mutation. The same impact was not predicted for Q155A ($\mathrm{\Delta }{G}_{Q155A}=-7.52\pm 0.37$ kJ/mol). Visual inspection of conformations obtained from states 0 and 1 indicates a network of hydrogen bonds involving D4 and MHC residues K66 and T163. Due to the side chain flexibility of D4, direct hydrogen bonds between D4-Q155 and D4-Y159 can also be observed in some conformations.

MSMs of D4A and D4P Indicate Alternative Roles for p4.

To confirm the dominant role of hydrogen bonds on the beneficial role of p4 for peptide binding, we created MSMs with two peptide variants: D4A and D4P. Characteristics of the exploration and connection stages for the D4A system can be found in SI Appendix, Fig. S9. A total of 213 $\mathrm{\mu }$s of aggregate simulation data were used to build the MSM (Materials and Methods and SI Appendix, Figs. S10–S12), taking approximately 3,000 GPU-hours to complete. Our model for D4A predicts that the unbound state is the most probable state ($P\left(\text{unbound state}\right)={\pi }_4=0.601$). We predict $\mathrm{\Delta }{G}_{D4A}=1.02\pm 1.01$ kJ/mol, thus corroborating the mutational analysis prediction based on the WT network (Fig. 2) and predicting QFKANVILL to be a much weaker binder to HLA-A*24:02.

Characteristics of the exploration and connection stages for the D4P system can be found in SI Appendix, Fig. S13. A total of 293 $\mathrm{\mu }$s of aggregate simulation data were used to build the MSM (Materials and Methods and SI Appendix, Figs. S14–S16), taking approximately 4,300 GPU-hours to complete. By replacing the flexible polar D4 with a rigid nonpolar P4, we expected to observe similar results to that of D4A. Surprisingly, the resulting MSM predicted D4P to be a stronger binder ($\mathrm{\Delta }{G}_{D4P}=-8.01\pm 0.18$ kJ/mol) than WT. We also evaluated the impact of the MHC mutations Q155A and Y159A using the MSM of D4P, but these mutations were not predicted to affect the binding of the peptide. Taken together, these results indicate that P4 benefits peptide–MHC binding through a mechanism that is different from that observed for D4 (i.e., does not rely on hydrogen bonds with the aforementioned MHC residues).

Competitive Binding Assays Confirm Predicted Ranking of Relative Binding Affinities.

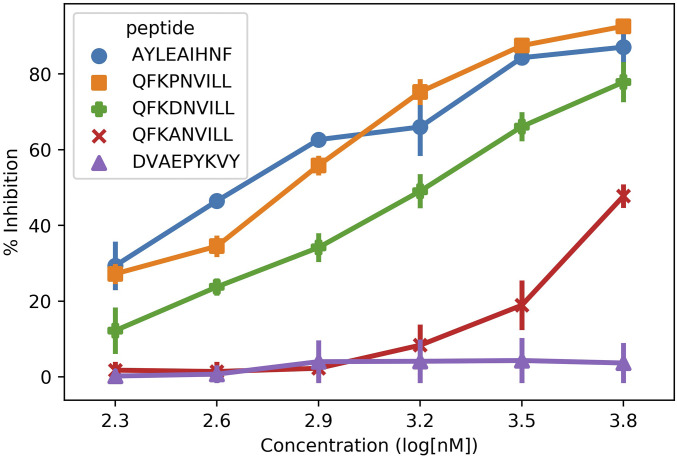
To validate our MSM-derived predictions we performed competitive binding assays with WT, D4A, and D4P (Fig. 3). First, QFKDNVILL (WT) shows partial inhibition across a variety of concentrations (${\text{IC}50}_{\text{WT}}\hspace{0.17em}=\hspace{0.17em}$1,600 nM), but does not reach the level of the positive control. This confirms the MSM prediction of weak yet stable binding of WT toward HLA-A*24:02. Note that NetMHC4.0 not only predicts this peptide to be a much weaker binder (7,769 nM), but also predicts D4A to be a stronger binder (4,154 nM). However, our binding assay with D4A shows little to no inhibition across concentrations (${\text{IC}50}_{\text{D}4\text{A}}\hspace{0.17em}>\hspace{0.17em}$6,000 nM), thus confirming the MSM prediction that this mutation significantly impairs binding to HLA-A*24:02. Finally, the binding assay of D4P confirmed the MSM prediction that this mutation in fact enhances binding to HLA-A*24:02 (${\text{IC}50}_{\text{D}4\text{P}}\hspace{0.17em}=\hspace{0.17em}$600 nM).

Fig. 3.

Competitive binding assays to determine the ranking of WT, D4A, and D4P. Based on the relative position of the WT curve (green plus) versus the positive control (blue circle), we see that QFKDNVILL is indeed a weak binder to HLA-A*24:02 (${\text{IC}50}_{\text{WT}}\hspace{0.17em}=\hspace{0.17em}$1,600 nM). Upon mutation of D4 to an alanine, inhibition is significantly reduced (${\text{IC}50}_{\text{D}4\text{A}}\hspace{0.17em}>\hspace{0.17em}$6,000 nM) as the D4A curve (red cross) is most similar to the negative control (purple triangle). Upon mutation of D4 to a proline, inhibition is increased (${\text{IC}50}_{\text{D}4\text{P}}\hspace{0.17em}=\hspace{0.17em}$600 nM) as the D4P curve (orange square) is most similar to the positive control.

MSM Flux Analysis Reveals Alternative Unbinding Pathways.

By comparing the WT MSM with the MSM of the mutants (D4A and D4P), we can identify differences in unbinding pathways. This analysis was done by computing the percentage of flux that goes from the native state (state 0) to the unbound state (state 4). Fig. 4A shows that the majority of WT unbinding pathways first detach from the C-term end. However, upon D4A mutation, the majority of unbinding pathways detach first from the N-term end (Fig. 4B). Note that both pathways are accessible for the D4A system, but the lack of stabilizing interactions involving position 4 allows for the alternate unbinding route. In addition, D4A prefers to stay in the unbound state (state 4), as opposed to WT’s preference of staying in the bound state (state 0). The stabilizing effect of D4 on WT seems primarily related to the interaction with MHC positions K66, T163, Y159, and Q155, respectively. Interestingly, these positions are mostly conserved across HLA allotypes (SI Appendix, Fig. S17). In particular, D4 interactions with K66 and T163 can be easily observed both in state 0 and in state 1 (Fig. 5), which is consistent with the role of stabilizing the N-term portion of the peptide.

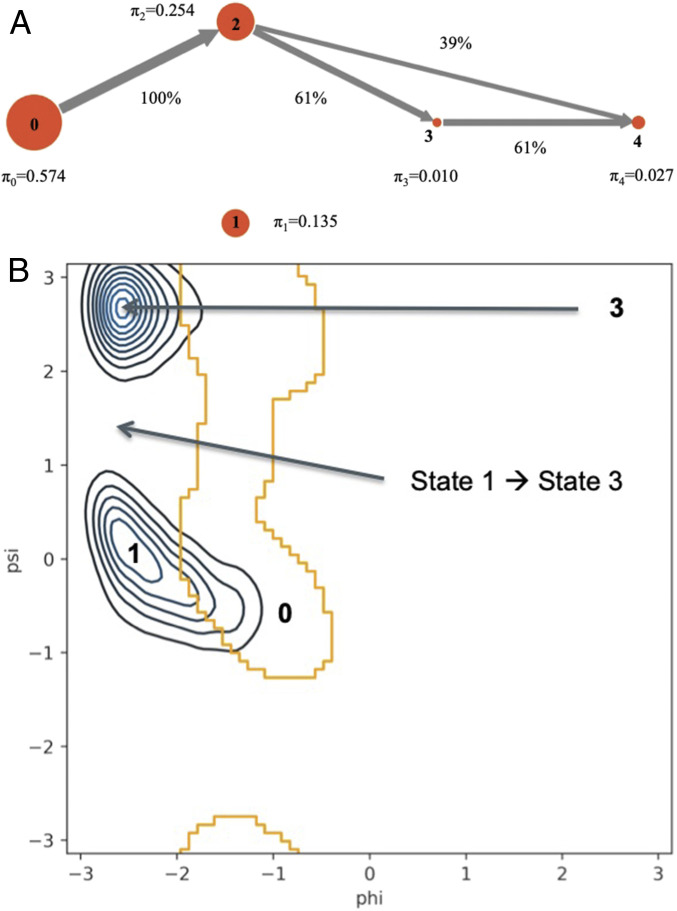
The D4P mutation revealed a different picture. Like D4A, the D4P system has a preference to unbind from the N-term first. In fact, all sampled unbinding trajectories for the D4P system showed the N-term detaching first, and there were zero trajectories sampled where the C-term detaches first (i.e., although the MSM included transitions from state 0 to state 1, and from state 1 back to state 0, none of the trajectories included transitions from state 1 to states 3 and 4). However, unlike D4A, D4P is a more stable binder, and the various bound states (states 0, 1, and 2) have higher equilibrium probabilities (Fig. 6A). Therefore, the inability of D4P to detach first from the C-term side represents a decrease in unbinding options of the system, even offsetting any destabilizing effect from the lack of a salt bridge with p4.

Fig. 6.

(A) Flux network of unbinding trajectories for the D4P system. The introduction of a proline forces the unbinding starting from the N-term side (state 2). (B) (Blue contour) Phi/psi angles (in radians) of position 4 from WT/D4A unbinding trajectories where the C-term side unbinds first. The bottom region covers states 0 and 1, while the top region covers state 3. (Orange border) Ramachandran plot of accessible phi/psi angles of proline. Unbinding trajectories during the transition from state 1 to state 3 lie in regions that do not overlap with the accessible phi/psi angle of proline. Thus, the unbinding trajectories adopt backbone conformations of p4 that are incompatible with the rigidity of proline. Note that the MSM of D4P (A) includes transitions from state 0 to state 1 and from state 1 back to state 0. However, these transitions are not depicted in the flux network, since none of the paths passing by state 1 were able to progress to state 4.

Finally, Fig. 6A shows that the native state for the D4P system appears to be relatively less stable than other intermediate states compared to the WT system, despite being a stronger binder. Currently, it is not known whether QFKPNVILL is immunogenic. In addition to the lack of a charged residue in the T cell receptor binding interface, T cell recognition of this complex may be impaired by a less stable peptide–MHC native state. However, further experiments are needed to investigate the immunogenicity of the D4P system.

Proline’s Rigid Backbone Prevents Torsions that Would Facilitate Unbinding.

The D4P system has a strong preference to unbind from the N-term side first. While it is possible for the D4P system to be in a state with the C-term unbound (state 1, Fig. 6A), our sampling suggests that it is difficult for conformations to then progress to a state in which the N-term is subsequently unbound (state 3). To investigate why, the backbone torsions of position 4 were extracted from the unbinding trajectories of WT and D4A where the C-term unbinds first and compared with the Ramachandran plot of prolines (42). In Fig. 6B, we see that trajectories starting in the native state (state 0) lie in regions overlapping with the possible phi/psi angles for prolines. However, as the WT/D4A transitions to having the C-term unbind first (state 1), p4 adopts a backbone conformation that is inaccessible for prolines. Unbinding trajectories continue to be outside the accessible region of prolines as WT/D4A transitions from state 1 to state 3 (anchors unbound, but peptide in contact with MHC). Therefore, the rigidity of the proline backbone in D4P prevents transitions from state 1 to state 3 and subsequently from becoming fully unbound.

Discussion

In this work, we studied the mechanism behind stable binding of QFKDNVILL to HLA-A*24:02. We proposed a simulation framework that makes it feasible to generate MD data to build an MSM of the entire binding/unbinding process. As expected, our model predicted the importance of the anchor residues in positions 2 and 9, as demonstrated by mutational analysis. Interestingly, these analyses also singled out the contribution of the nonanchor position 4 to the stability of the system. To further explore the role of this position on peptide binding, we used our model to estimate the impact of two different mutations over the peptide’s binding affinity and later confirmed our prediction with competitive binding assays. While D4A significantly impairs peptide binding, D4P leads to stronger binding.

In addition, by building the MSMs for each of these systems we were able to observe alternative unbinding pathways. While the WT system is more likely to start unbinding from the C-term end, both D4A and D4P are more likely to unbind the N-term first. This behavior is consistent with the loss of key interactions observed in the WT system, particularly between p4 and MHC residues K66, Q155, Y159, and T163. Interaction with K66 is not surprising, since a D4-K66 salt bridge can be observed on the original crystal structure (PDB code 3I6L), as well as in other conformations corresponding to the bound state (Fig. 5C). In particular, K66 and T163 seem to be able to keep D4 in place, even when the peptide is already partially unbound from the C-term end (Fig. 5D). Visual inspection also suggests other roles for these MHC residues, notably interactions between p1-Y159 and p5/p6-Q155 (Fig. 5).

Interestingly, our model also predicts direct interactions between D4 and both Q155 and Y159 (SI Appendix, Figs. S5 and S6). In fact, the Y159A exchange had a negative impact on the binding of the WT, similar to that observed for D4A. The same impact was not detected when introducing Y159A on the D4P system. Taken together these results suggest two different mechanisms through which p4 can contribute to peptide–MHC stability. Polar residues, particularly negatively charged residues, such as aspartic acid, can benefit from a network of conserved interactions that help stabilize the N-term end of the peptides. On the other hand, having a proline at p4 makes it harder for the peptide backbone to bend in ways that would favor peptide detachment (Fig. 6). Although our analysis was limited to a few peptide–MHCs of interest, we believe the two binding mechanisms involving p4 might be of broader relevance to peptide–MHC binding in general. Two interesting observations provide additional support to this hypothesis. First, all of the aforementioned MHC residues, that are potential p4 contacts, are present in the consensus sequence produced by aligning over 10,000 protein sequences including HLA-As, HLA-Bs, and HLA-Cs (SI Appendix, Fig. S17). The prevalence of K66 is not very high, about 40% across all types, being often replaced with N in HLA-As and I in HLA-Bs. T163 is particularly high among HLA-A sequences (74%). Most notably, Q155 and Y159 are present in over 99.9% of the sequences for all HLA types, and the peptide-binding contribution of these specific MHC positions has been observed in previous studies (43, 44). Second, across sequences of HLA binders, the observed frequencies of aspartic acid and proline were shown to be 2.2 times more frequent than expected relative to the proteome (7). Another negatively charged residue, glutamic acid, was also found to be 1.6 times more frequent than expected (7). Further experimental studies will be needed to investigate the differential contribution of these interactions on the binding of different peptides and across different HLA allotypes.

This work applies MSMs to describe the preferred unbinding pathways for peptide–MHC complexes. In addition, to the best of our knowledge, this is also the largest computational exploration of peptide–MHC dynamics to date (over 650 $\mathrm{\mu }$s). This unique combination of methods provided a wealth of information on the studied systems, including the contributions of particular interactions to peptide binding and complex stability. Such analysis can also be done for any other peptide–MHC of interest, providing an initial 3D structure of the complex. In the absence of a crystal structure, an appropriate 3D model could be used, and our group has also contributed tools for this particular task (13, 14). The computational cost to build the MSMs was manageable and was done using local GPU computing clusters (about 10,000 GPU-hours compared to 115,000 GPU-hours in ref. 26).

While this work demonstrates the feasibility of using MD and MSMs to study peptide–MHC dynamics, it is important to note that the approximations performed here could have an impact on obtained results. The use of an implicit solvent, for instance, can have an effect on the dynamics of the system and artificially accelerate the time for events to occur. In addition, hydrophobic interactions are typically the major contributions of peptide–MHC binding, particularly for the anchor residues, and the finite size of water molecules may need to be accounted for. Finally, there is evidence of allostery where peptide binding affected the dynamics of remote regions in HLA-A2, including the ${\alpha }_3$ and $\beta$-2 microglobulin domains (45). While we used positional restraints on the $\beta$-sheet floor to minimize the potential impact, the full effect of the MHC truncation in our simulations is unknown.

Future work can focus on ways to improve the accuracy of the final MSM. This is likely in the form of including more atoms into the system, such as the $\beta$-2 microglobulin portion of the MHC, explicit water molecules, or even the other proteins involved in keeping MHCs in the peptide-receptive state (46). However, the simulation output similarly needs to be kept high for enough statistics to be generated. Other enhanced sampling approaches (47) could conceivably be done as long as there is a way to produce an unbiased MSM in the end. The use of coarse graining is also promising; however, it is highly nontrivial to perform in such a way that does not negatively influence the computation of kinetic quantities (48, 49).

Finally, it is worth noting that the peptide studied here (QFKDNVILL) was derived from the nucleocapsid protein of SARS-CoV, and a highly similar peptide exists in the nucleocapsid protein of SARS-CoV-2 (NFKDQVILL). The differences between the two peptides do not appear to be significant, as asparagine and glutamine are both polar, uncharged residues. More importantly, both peptides share the same residues in positions 2, 4, and 9, which means that the analysis we have performed here likely applies to both systems. Finally, given that D4 and K66 are exposed for the recognition by T cells, this conserved interaction could be the focus of cross-reactive T cell responses (i.e., T cells primed with QFKDNVILL may also recognize NFKDQVILL). In fact, cross-reactivities involving D4 in other viral peptides have already been predicted (50) and confirmed experimentally (51). Regardless of its role in T cell recognition, the alternative roles of p4 in peptide–MHC binding and stability highlight the importance of structure-based methods in the analysis of peptide–MHC binding and the discovery of peptide targets for several immunotherapy applications.

Materials and Methods

Molecular Dynamics Protocol.

In this work, we simulate only the binding site of the MHC to make the whole framework more computationally tractable. While the entire peptide–MHC complex is a large system of around 380 residues total, we exclude the $\beta$-2 microglobulin and portions of the $\alpha$ chain ($\alpha$-3) of the MHC, leaving two $\alpha$-helices ($\alpha$-1 and $\alpha$-2 in yellow; Fig 1A) and the $\beta$-sheet floor (in light blue; Fig 1A) that enclose the bound peptide. This roughly results in a system half the size of the original (around 190 residues total). The MHC portion that was truncated is likely important for overall stability of the MHC, so in all simulations we include a positional restraint on the $C_{\alpha }$ atoms of the $\beta$-sheet floor (force constant: 100 kJ$\cdot$mol$\cdot {\mathrm{n}\mathrm{m}}^{-2}$), which include the main contacts formed between the simulated binding site and the truncated portion.

In all simulations, the AMBER99sbildn (52) force field was used with implicit solvent (GBSA OBC) (53). Simulations were performed at 300 K with the Langevin integrator (friction coefficient: 0.1 ${\mathrm{p}\mathrm{s}}^{-1}$). The hydrogen masses were artificially increased to 4 amu to allow a 4-fs timestep. Starting conformations were equilibrated for 500 ns with the positional restraints on the $C_{\alpha }$ atoms of the whole system.

Exploration Stage: Umbrella Sampling.

Umbrella sampling is used to accelerate the exploration of the relevant states of the binding process. Biased sampling is needed here since the half-life of peptide–MHC binding can be on the order of seconds or greater (2). Starting with the crystal structure of WT (PDB code 3I6L), we generate detachment/unbinding pathways of the peptide.

The geometry of the MHC allows us to define a convenient reaction coordinate for the umbrella sampling. Bound peptides are enclosed between two $\alpha$-helices atop a $\beta$-sheet floor. To detach, peptides must essentially unbind in a direction that is approximately normal to the $\beta$-sheet floor (23), which is roughly planar (50). We can see from Fig. 1A that the principal axis of the (nontruncated) system happens to roughly align with this direction. Thus, if the principal axis is aligned to the Z direction in Euclidean space, the $\beta$-sheet floor becomes approximately aligned to the XY plane, and a bias along the Z direction can be used to accelerate sampling along the binding/unbinding pathway. The biases for the umbrella-sampling simulations are based on the distance between the center of masses of the peptide and the MHC along the Z coordinate. We call this distance the z-dist. We use the $C_{\alpha }$ atoms of the $\beta$-sheet floor as a stable set of atoms to compute the center of mass for the MHC; these are the same atoms from which we add positional restraints.

Given the description of the reaction coordinate above, we run umbrella-sampling simulations across z-dist umbrellas centered from 1.0 to 3.0 nm (in increments of 0.1 nm) with a force constant of 100 kJ$\cdot$mol$\cdot {\mathrm{n}\mathrm{m}}^{-2}$, where the the z-dist of the native state is approximately 1.0 nm. Each simulation was run for approximately 1 $\mathrm{\mu }$s, producing many detachment trajectories across the runs. Additional umbrella-sampling simulations were done for D4A with a looser force constant (10 kJ$\cdot$mol$\cdot {\mathrm{n}\mathrm{m}}^{-2}$) given that the peptide is known to be a nonbinder and is less stable. Several replicates were performed, particularly for umbrellas centered in the 2.0- to 3.0-nm range to sample more association/dissociation events.

Connection Stage: Generating Transition Statistics with Adaptive Sampling.

In this stage, we use adaptive sampling to run enough unbiased molecular dynamics to produce a final MSM that connects most of the states generated (Fig. 1B). At each iteration, a new set of about 20 unbiased molecular dynamics simulations is spawned from starting conformations chosen from less densely sampled regions of the conformational space. The conformations are chosen based on the analysis of the set of trajectories that have already been generated. Trajectories are first featurized using residue–residue contacts (defined as the closest heavy atom distance) between peptide with MHC and peptide with itself. Then the conformations are mapped to the two leading independent components using TICA (39, 40) (lag 10 ns), and the space is discretized into microstates with K means (100 clusters). Next, microstates are chosen with probability inversely proportional to the number of conformations mapped to it, and a conformation is uniformly randomly chosen from the microstate as a starting point for the next round of simulations. We repeat the adaptive sampling iterations until a MSM can be built using more than 90% of the microstates (SI Appendix, Figs. S1, S9, and S13). All simulations were run using CUDA and OpenMM (54) and performed on NOTS as part of Rice University’s Center of Research Computing.

Building the MSMs.

Similar to the adaptive sampling process, the trajectories were featurized using residue–residue contacts between peptide with MHC and peptide with itself, resulting in 1,692 contacts. We extract two independent components using TICA using a lag time of 10 ns based on the convergence of timescales (SI Appendix, Figs. S2A, S10A, and S14A). The two leading independent components adequately capture the transition to and from the native and unbound states (SI Appendix, Figs. S3, S11, and S15). This space was discretized into microstates using K means with 100 clusters. From the trajectories on the discretized space, discrete dTRAM was used to build a Markov state model (41), taking into account the biases introduced with the umbrella-sampling simulations. A final MSM was constructed using a lag time based on the convergence of timescales (SI Appendix, Figs. S2B, S10B, and S14B). Error bars are computed based on a moving block procedure for bootstrapping (55). The final MSMs are self-consistent based on the Chapman–Kolmogorov test (SI Appendix, Figs. S4, S12, and S16). All analysis was performed using MDTraj (56) and Pyemma (57).

Mutational Analysis.

We can estimate the changes in the free energy of binding upon mutation ($\mathrm{\Delta }\mathrm{\Delta }G$) for residues in the peptide or MHC. We do this with free energy perturbation theory (58, 59). The change in binding free energy is computed as

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathrm{\Delta }G& =\mathrm{\Delta }{G}_{mut}-\mathrm{\Delta }{G}_{wt}\hfill \\ \hfill & =\left(G_{mut}^{\text{associated}}-G_{mut}^{\text{dissociated}}\right)-\left(G_{wt}^{\text{associated}}-G_{wt}^{\text{dissociated}}\right)\hfill \\ \hfill & =\left(G_{mut}^{\text{associated}}-G_{wt}^{\text{associated}}\right)-\left(G_{mut}^{\text{dissociated}}-G_{wt}^{\text{dissociated}}\right)\hfill \\ \hfill & =-RT\text{ln}\left(\frac{Z_{mut}^{\text{associated}}}{Z_{wt}^{\text{associated}}}\right)+RT\text{ln}\left(\frac{Z_{mut}^{\text{dissociated}}}{Z_{wt}^{\text{dissociated}}}\right),\hfill \end{array}$$ [1]

where $RT=2.479\frac{\text{kJ}}{\text{mol}}$ at temperature $T=298$ K, and $Z$ is the configurational partition function for the corresponding system. The last two terms represent $\mathrm{\Delta }{G}_{wt->mut}^{\text{associated}}$ and $-\mathrm{\Delta }{G}_{wt->mut}^{\text{dissociated}}$, thus completing the free energy cycle. Positive values of $\mathrm{\Delta }\mathrm{\Delta }G$ indicate that the mutant is a weaker binder, while negative values of $\mathrm{\Delta }\mathrm{\Delta }G$ indicate that the mutant is a stronger binder.

The ratio of configurational partition functions over a state $S$ can be manipulated as

$$\begin{array}{cc}\hfill \frac{Z_{mut}^S}{Z_{wt}^S}& =\frac{1}{Z_{wt}^S}{\int }_S{e}^{-\beta U_{mut}\left(x\right)}dx\hfill \\ \hfill & =\frac{1}{Z_{wt}^S}{\int }_S{e}^{-\beta U_{mut}\left(x\right)}{e}^{\beta U_{wt}\left(x\right)}{e}^{-\beta U_{wt}\left(x\right)}dx\hfill \\ \hfill & =\frac{1}{Z_{wt}^S}{⟨e^{-\beta \left(U_{mut}\left(x\right)-U_{wt}\left(x\right)\right)}⟩}_{S,wt},\hfill \end{array}$$ [2]

where $U\left(x\right)$ is the potential energy. The average is taken using the stationary probabilities, $\mu \left(x\right)$, of the WT system computed from the MSM/dTRAM analysis. Thus, the following ratios can be finally computed as

$$\begin{array}{cc}\hfill \frac{Z_{mut}^{\text{dissociated}}}{Z_{wt}^{\text{dissociated}}}& =\frac{{\sum }_{x\in S_D}{e}^{-\beta \left(U_{mut}\left(x\right)-U_{wt}\left(x\right)\right)}\mu \left(x\right)}{{\sum }_{x\in S_D}\mu \left(x\right)}\hfill \\ \hfill \frac{Z_{mut}^{\text{associated}}}{Z_{wt}^{\text{associated}}}& =\frac{{\sum }_{x\in S_A}{e}^{-\beta \left(U_{mut}\left(x\right)-U_{wt}\left(x\right)\right)}\mu \left(x\right)}{{\sum }_{x\in S_A}\mu \left(x\right)},\hfill \end{array}$$ [3]

where a configuration, $x$, is in $S_D$, the dissociated state, if the minimum distance between the peptide and MHC is greater than 0.5 nm. Otherwise, $x$ is in $S_A$, the associated state.

The original and mutation energies are computed using the same force field from the molecular dynamics simulations [AMBER99sbildn force field (52) with GBSA OBC implicit solvent (53)] but only nonbonded terms were considered. Mutated structures were generated with PyMOL where the original amino acid was cut back to the $C_{\beta }$-atom and hydrogen atoms were added, resulting in an alanine structure. The value of the dihedral angle $C-C_{\alpha }-C_{\beta }-H_{\beta 1}$ was taken to be the dihedral angle of the original residue, $C-C_{\alpha }-C_{\beta }-C_{\gamma }$ (or $C-C_{\alpha }-C_{\beta }-C_{\gamma 1}$ for the valine in position 6 and isoleucine in position 7).

Competitive Binding Assays.

We run competitive binding assays to find the binding affinities of QFKDNVILL (WT), QFKANVILL (D4A), and QFKPNVILL (D4P) with HLA-A*24:02. Fluorescent and unlabeled peptides were synthesized by BioSynthesis, Inc. EBC-1 cells used for assay were transduced with HLA-A*2402 for increased expression. The competition peptide assay followed protocol established by Kessler et al. (60). In brief, EBC-1 cells were washed with elution buffer and then incubated overnight in the dark with a fixed concentration of a known HLA-A*24:02 binding peptide tagged with GFP and varying concentrations of test peptides. Cells were analyzed on a FACs CANTO II analyzer and median fluorescence intensity was measured. IC50 values were determined using nonlinear regression from GraphPad Prism 8.0.

Multiple-Sequence Alignment.

A total of 19,689 protein sequences were downloaded from IMGT/HLA (61), corresponding to the three classical class I HLA genes (HLA-A, HLA-B, HLA-C). Since many sequences did not cover the entire protein length, we removed entries with less than three-quarters of the complete sequence, resulting in a total of 10,435 sequences (HLA-A, 3,160; HLA-B, 3,788; HLA-C, 3,487). A multiple-sequence alignment was performed with MUSCLE (62), and the visual inspection was performed with Jaview (63).

Data Availability.

Code for umbrella sampling, adaptive sampling, and MSM analysis, as well as representative structures, can be found in Github at https://github.com/KavrakiLab/adaptive-samplingpmhc. Simulation data are available upon request.