Significance
We are experiencing the accelerated loss and reconfiguration of biological diversity. Meanwhile, those charged with natural resource management are struggling to meet the challenges of monitoring and managing wildlife populations across vast areas crisscrossed by political borders. What if, akin to weather maps, we could track and forecast the dynamics of wildlife populations across space and time? Using the world’s most extensive large carnivore monitoring program, we showcase the application of an effective tool for spatially explicit quantification of wildlife population dynamics at scales that are relevant to management and conservation.
Keywords: spatial capture–recapture, imperfect detection, noninvasive monitoring of large carnivores, density surface, vital rates
Abstract
The ongoing recovery of terrestrial large carnivores in North America and Europe is accompanied by intense controversy. On the one hand, reestablishment of large carnivores entails a recovery of their most important ecological role, predation. On the other hand, societies are struggling to relearn how to live with apex predators that kill livestock, compete for game species, and occasionally injure or kill people. Those responsible for managing these species and mitigating conflict often lack fundamental information due to a long-standing challenge in ecology: How do we draw robust population-level inferences for elusive animals spread over immense areas? Here we showcase the application of an effective tool for spatially explicit tracking and forecasting of wildlife population dynamics at scales that are relevant to management and conservation. We analyzed the world’s largest dataset on carnivores comprising more than 35,000 noninvasively obtained DNA samples from over 6,000 individual brown bears (Ursus arctos), gray wolves (Canis lupus), and wolverines (Gulo gulo). Our analyses took into account that not all individuals are detected and, even if detected, their fates are not always known. We show unequivocal quantitative evidence of large carnivore recovery in northern Europe, juxtaposed with the finding that humans are the single-most important factor driving the dynamics of these apex predators. We present maps and forecasts of the spatiotemporal dynamics of large carnivore populations, transcending national boundaries and management regimes.
Few topics in conservation and wildlife management are as controversial as large carnivores. Predation is both the most important ecosystem service provided by predators (1, 2) and the primary source of conflict with humans, e.g., via livestock loss, competition for game species, and risk to people (1, 3). The ongoing recovery of large carnivores in North America (4) and Europe (5) has brought this conflict to the forefront of public debate as societies grapple with relearning how to live with apex predators. Stakeholders face each other across a polarized spectrum with some lobbying for carnivore recovery and protection while others advocate fiercely against it (6). Meanwhile wildlife managers find themselves navigating an often hostile political landscape, as they attempt to follow national and international mandates of sustainable natural resource management (7).
Regardless of their position in the dispute, stakeholders generally agree that reliable estimates conveying the state and dynamics of carnivore populations are urgently needed to inform debate, policy, and management. Unfortunately, large carnivores are notoriously difficult to monitor due to their elusiveness and because their populations tend to spread over vast areas and multiple jurisdictions. In general, comprehensive population-level assessments are highly sought after in ecology but remain elusive. As a consequence, ecologists often resort to minimum counts and much-criticized proxies (8–10) or piece together estimates from local studies that are difficult to scale up. For example, conservation of the endangered tiger (Panthera tigris) would clearly benefit from monitoring and assessment at large spatial scales (10) but efforts in this direction have only just begun (11).
In this study, we provide the most comprehensive assessment of the distribution, status, and population dynamics of three sympatric apex predators to date. Using a unified analytical approach (Fig. 1), we mapped the densities and measured vital rates of brown bears (Ursus arctos), gray wolves (Canis lupus), and wolverines (Gulo gulo) across more than half a million square kilometers. We utilized the world’s most extensive individual-based monitoring dataset on large carnivores collected annually by Norwegian and Swedish authorities and volunteers (Rovbase 3.0) (12). We analyzed data collected between 2012 and 2019 consisting of DNA genotypes from 35,578 noninvasively collected samples associated with 2,824 individual bears, 1,092 wolves, and 2,118 wolverines (SI Appendix, Figs. S1–S3). In addition, we integrated information associated with known deaths of 2,246 bears, 457 wolves, and 596 wolverines (SI Appendix, Figs. S4–S6). Dead recoveries are not only evidence of human impact but also an important source of information on individual fates in these hunted populations.
Fig. 1.
The process of turning long-term monitoring data, such as noninvasive genetic samples and dead recoveries, into population density maps and vital rate estimates. The OPSCR model combines submodels for the ecological and observation processes. The model produces estimates of parameters describing individual space use (home range size and movements), abundance and density, and population dynamics. The model can be used further to generate spatially explicit projections of abundance for user-defined scenarios (see also Fig. 4).
Populations as Changing Surfaces
We analyzed the data using a Bayesian open-population spatial capture–recapture (OPSCR) model (13–15) (Fig. 1), which addresses three challenges associated with population-level wildlife inventories: 1) Detection is imperfect and sampling effort heterogeneous in space and time; not all individuals present in the study area are detected (16). 2) Individuals that reside primarily outside the surveyed area may be detected within it. Without an explicit link between the population size parameter and geographic space or area, density cannot be estimated and population size is ill-defined (17). 3) Nonspatial population dynamic models often estimate “apparent” survival and recruitment, as these parameters include the probability of permanent emigration and immigration, respectively. By explicitly modeling movement of individuals between years, the OPSCR model can return unbiased estimates of demographic parameters (13, 18).
The OPSCR-derived annual density maps and abundance estimates are direct expressions of the status of the population (Fig. 2 and SI Appendix, Tables S1–S3) and show that, depending on species and year, between 8 and 95% of the individuals remain undetected during annual noninvasive genetic sampling. Similarly, around 12% of bear deaths, 59% of wolf deaths, and 64% of wolverine deaths go undetected. This underscores how the use of minimum counts as proxies for population size or vital rates can be misleading and does not allow users to disentangle the effects of population dynamics from those of spatially and temporally varying detection and recovery probability (19, 20). We estimate that 2,757 (95% credible interval [CrI]: 2,636 to 2,877) bears, 375 (CrI: 352 to 402) wolves, and 1,035 (CrI: 985 to 1,088) wolverines lived in Scandinavia during the final monitoring season of our study (Fig. 2). These population-level abundance estimates underline the magnitude of recovery following eradication policies and intense persecution that had led to local extinction or severe reduction to small remnant populations of large carnivores by the early 1900s (21–23).
Fig. 2.
Annual density maps for brown bears (U. arctos), gray wolves (C. lupus), and wolverines (G. gulo) in Norway and Sweden between 2012 and 2019, with corresponding population estimates (black violins, total; blue violins, Sweden; red violins, Norway). Gray bars in the violin plots indicate the total number of individual carnivores detected during noninvasive genetic sampling. Time series are labeled with the season or year during which the majority of samples were collected for each species (SI Appendix). Bear image credit: Staffan Widstrand Photography. Wolf image credit: Shutterstock/Kjetil Kolbjørnsrud. Wolverine image credit: Shutterstock/Karel Bartik.
Wildlife in a Politically Divided World
Large carnivores are highly mobile and often occur in transboundary populations (24, 25). This is also the case in Scandinavia where home ranges of many individuals straddle the border of the European Union between Norway and Sweden (14, 26, 27). Like in other transboundary populations, this has ecological, management, and legal implications. Coordinated monitoring and a population-level analysis allowed estimation of density and abundance at various spatial scales and for different administrative units within a single model (Fig. 3 and SI Appendix, Tables S1–S3). Our study revealed that while the wolf population occurs primarily in Sweden (SI Appendix, Fig. S7), the number of wolves in Norway has been growing (posterior linear slope: 4 individuals per year, CrI: 2.2 to 5.7; Fig. 2). This positive trend cannot be explained solely by the interplay of recruitment and survival (see Spatial Population Dynamics), but is likely a result of movement and source–sink dynamics with neighboring Sweden. By far the most skewed in terms of the national share in these populations is the bear (SI Appendix, Fig. S8). The Scandinavian brown bear population currently spreads over three core areas (23, 28) centered in Sweden (Fig. 2) where 95% of the Scandinavian population resides according to our estimates for 2018. Like wolves, bears in Norway are at the fringe of these core areas and management on the Swedish side of the border is liable to play a substantial role in the current state and future of the Norwegian portion of the bear population (14).
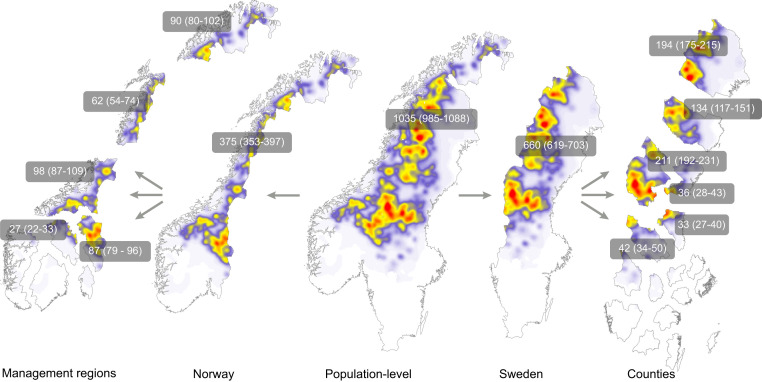
Fig. 3.
The OPSCR model generates population-level density (color scale in Fig. 2) and abundance estimates (with 95% credible intervals), as shown here for wolverines on the Scandinavian Peninsula in 2019. These can be broken down into estimates for the national or local jurisdictions at the scale at which carnivore management takes place (e.g., large carnivore management regions in Norway and counties in Sweden). This top–down approach is preferable to methods that piece together estimates derived locally because they risk biased estimates by double counting animals that are shared by multiple jurisdictions (14). Abundance estimates are not shown for all regions on the map; for a complete tally across all jurisdictions and scales see SI Appendix, Table S3. Equivalent maps for wolves and bears can be found in SI Appendix, Figs. S7 and S8.
Spatial Population Dynamics
The OPSCR model includes a population dynamic submodel (also estimating movements; Materials and Methods and SI Appendix, Tables S4–S12) that integrates both live detections through noninvasive genetic sampling (NGS) (based on feces, hair, saliva, and urine) and dead recoveries (Fig. 1). For all three species, we considered two competing sources of mortality: 1) legal culling, which is always detected (e.g., legal hunting, management kills, defense of life and property), and 2) all other mortalities, which are not always detected (e.g., natural deaths, vehicle and train collisions, illegal hunting). By distinguishing these two main causes of death and accounting for imperfect detection, the model can produce estimates of total mortality, as well as separate estimates for each mortality cause (29, 30). Humans are the dominant force driving the dynamics of all three species. Legal culling alone made up 70% of estimated total mortality for bears and 28% for wolves and wolverines during the study period (SI Appendix, Figs. S9–S11). Male bears and wolverines experienced on average higher mortality than females (SI Appendix, Figs. S9 and S11), contributing to female-biased populations. At least for bears, higher male mortality is most likely driven by regulations that protect females with dependent young from legal hunting (31). By contrast, wolves form cohesive family groups (packs) and showed substantially less sex-specific differentiation in key parameters, such as abundance and vital rates (SI Appendix, Fig. S10 and Table S9).
Norwegian and Swedish management programs cull from the same carnivore populations, but, as shown here, do so at different intensities (SI Appendix, Fig. S12). This can at least in part be explained by different legal and regulatory constraints: Whereas both countries are signatories to the Council of Europe Bern Convention for the protection of European Wildlife and Habitats (32), only Sweden is bound by the rules of the European Habitat Directive (33) regarding the conditions under which wildlife species may be killed. Thus, despite lower overall carnivore numbers, Norway’s legal culling rates are as high as or higher than those in Sweden (SI Appendix, Fig. S12). Wolverines experience the most pronounced difference in national culling pressures: In most years wolverines in Norway are culled at more than twice the rate of those in Sweden (SI Appendix, Fig. S12). This is the likely cause for the apparent decline in wolverine abundance in Norway (posterior linear slope: −10.3 individuals per year, 95% CrI: −15.3 to −5.5; Fig. 2), compared with an increase in Sweden (posterior linear slope: 21.6 individuals per year, 95% CrI: 12.4 to 30.6; Fig. 2). Differences in management are also manifested in the truncated national distribution of wolves and bears: To limit conflict with livestock husbandry (mostly domestic sheep and semidomestic reindeer), Norway delineates zones where wolves and bears are allowed to exist, as opposed to areas where they are not tolerated (34).
Into the Future
What if, akin to weather maps, we could forecast the dynamics of wildlife populations across space and time? The OPSCR model can be used to project density and abundance under different conditions and intervention scenarios (35, 36) (Fig. 4). This is a powerful tool to aid adaptive management of natural resources and to test hypotheses about spatial ecology and population dynamics. For example, maintaining current levels of adult culling mortality of female wolverines during the coming years (and assuming that it is additive to all other mortality sources) would lead to a predicted 6% probability of decline in the number of female wolverines in Scandinavia by 2022 compared with the average population size during 2013 to 2019. A 50% increase in culling mortality would result in a 61% probability of decline, whereas the probability of a decline would shrink to 4% if culling mortality were to decrease by 50% compared with pre-2020 levels.
Fig. 4.
Estimated (white background) and projected (hatched background) size of the female wolverine population in Scandinavia. Abundance estimates were obtained through OPSCR analysis of 7 y of noninvasive genetic sampling and dead recoveries. Forecasting was accomplished through posterior sampling from the same model. Forecasts are shown for five different levels of culling pressure, compared to the average annual adult culling mortality between 2013 and 2019. The approach also captures the increase in uncertainty (longer violins) as predictions are made farther into the future.
Human interference is the main driver of the dynamics of many wildlife populations. Robust quantitative estimates and projections are thus essential for decision making and should consider populations, not only parts thereof. Isolationist approaches to monitoring and inference are still the norm today and lead to management decisions that ignore essential factors influencing populations, such as transboundary source–sink dynamics (37). Whereas management interventions can be constrained to jurisdictions, their implications cannot.
Materials and Methods
Large Carnivore Monitoring.
We used data from the Scandinavian large carnivore database Rovbase 3.0 (12). This database is used jointly by Norway and Sweden to record information obtained during large carnivore monitoring, NGS data, GPS search tracks, and dead recovery data. Detailed information about each of these components is provided in SI Appendix.
Open-Population Spatial Capture–Recapture Analysis.
The OPSCR model (13–15) is composed of three submodels described in the following sections: 1) a model for population dynamics and population size (Population dynamics), 2) a model for density and movements (Density and movement), and 3) a model for detections during DNA searches (Detections).
Population dynamics.
We used a multistate formulation for the population dynamics model (38). Following this framework, each individual life history is represented by a succession of discrete states that arise from a Markov process. Between two consecutive years, an individual at time can either remain in its current state or transition to another one, with transition probabilities corresponding to vital rates (e.g., recruitment and mortality). For the bear and wolverine models, we considered four different states (SI Appendix, Fig. S13A): 1) “unborn” if the individual has not yet been recruited in the population; 2) “alive” if the individual is alive at the start of the current monitoring season; 3) “dead legal” if the individual has died from legal culling between the start of the previous and current monitoring seasons; and 4) “dead” if the individual has a) died from any other cause of mortality between the start of the previous and current monitoring seasons or b) died earlier, regardless of the cause.
At the first occasion, individuals can only be in the unborn or alive states so that , where is the probability to be in state alive at the first occasion. In subsequent years (), the individual state is modeled as a Markov process, i.e., conditional on the state of the individual at as follows:
-
If , an individual can be recruited by transitioning from state unborn to state alive with probability . This parameter has to be time specific, as it depends on the number of individuals that are left in the departure state (i.e., the unborn state) which necessarily decreases with time. Note that the per capita recruitment rate can be derived as the number of new recruits at time , divided by the number of individuals alive at .
-
If , the individual can survive and remain in state alive with probability , die from legal culling () with probability , or die from all other causes and transition to with probability , where .
-
Finally, all individuals in dead states ( or 4) transition to , the absorbing state, with probability 1.
Population size in each year is derived as the sum of all individuals in the alive state,
| [1] |
where is the total augmented population size and the indicator function. This approach uses data augmentation, whereby additional, undetected individuals are provided and are available for inclusion in the population in each time step (39). A slightly different population dynamics submodel was used for wolves (SI Appendix, Fig. S13B) to account for social behavior.
For all three species, we considered two competing sources of mortality: legal culling (), which is always detected (e.g., legal hunting, management kills, defense of life and property), and all other mortalities (), which may not always be detected (e.g., natural deaths, vehicle and train collisions, illegal hunting). By distinguishing between these two causes of mortality in the model and accounting for imperfect detection, the OPSCR model can produce estimates of total mortality, as well as separate estimates for each mortality cause (29, 30). For wolves and wolverines, vital rates were allowed to vary between years, yielding annual estimates of recruitment and cause-specific mortality. For bears, the patchy configuration and large spatiotemporal gaps in sampling in Sweden (SI Appendix) did not allow us to estimate fully time-dependent vital rates; instead we split the total time into two periods (2012 to 2014 and 2015 to 2018) and allowed recruitment and “other” mortalities to differ between periods, while assuming that they were constant within each period. However, even for bears, mortality due to legal culling was allowed to vary annually, as dead recoveries were available every year in both Sweden and Norway. Although compensation between mortality sources was not modeled explicitly, estimates of and can reflect mutual influences, including compensation, of the associated true vital rates as these parameters are estimated independently between years (or multiyear periods for bear).
Vital rate parameters were time, sex, species, and state specific. Spatial variation in density and fates was also partially accounted for in the model. Perfect detectability of legal culling deaths, together with estimates of spatially explicit abundance, allowed direct estimation of annual legal culling mortality for any desired spatial unit, including country-specific estimates. Spatial variation in legal culling mortality and recruitment emerged phenomenologically because the OPSCR model is ultimately an agent-based model that allows realizations of individual life histories (including transitions to live and dead states) while taking into account the existing data. Because large carnivore NGS and dead recovery data are so extensive in Norway and Sweden, realization of individual life histories (and movement; see Density and movement) can lead to spatially varying population trends without explicit integration of country/region-specific vital rates.
Density and movement.
In OPSCR, the location of an individual is described by its activity center (AC). The distribution of individual ACs is modeled using a spatial point process. Here, we used an inhomogeneous binomial point process (40). This formulation allows the density of ACs to vary according to a spatial intensity function, (where is a vector of spatial coordinates). Then , the expected number of ACs falling within an area , follows
| [2] |
where is the entire habitat and M is the total number of ACs (including unborn individuals) within and
| [3] |
In this study, we define the intensity function of the inhomogeneous binomial point process to condition the initial AC locations (index for individual omitted for readability) on a spatial covariate (the species-specific proxies for density in our analysis),
| [4] |
where is the value of the spatial covariate at coordinates .
To distinguish between emigration and mortality, we integrated AC movement into the OPSCR model by allowing shifts of individual ACs between years. To account for the fact that individual movements are the result of both the attractiveness of the habitat at the arrival location (habitat selection) and the distance from the previous location, individual movements were modeled as a Markovian inhomogeneous binomial point process. The probability density of an individual’s AC at time , , was conditional on 1) the distance to the AC location in the previous year, with coordinates , and 2) a species-specific spatial covariate :
| [5] |
Eq. 5 represents the prior distribution of latent variable , where is the SD of a bivariate normal distribution centered on . Under this specification, movement is described as an isotropic Gaussian random walk (41) weighted by the spatial covariate . The SD therefore regulates the distance that individuals are likely to move between time periods.
The distribution of carnivores in Norway and Sweden likely depends on many different spatial covariates (e.g., prey density, human density, land cover type, terrain, elevation, latitude). Due to the computational challenge associated with a very large habitat and an already complex model, it was not feasible within the scope of this study to test for and select covariates and their interactions from the large pool of candidate variables. Instead, we chose to use coarse species-specific proxies that reflect the species distributions. Finally, for bears, we used data on the location of dead animals to capture the distribution of core areas; we constructed the coarse spatial density covariate based on all dead recovery locations for bears between 2012 and 2018 (SI Appendix, Fig. S14). For wolves, we used the locations of pack observations by the authorities, to which we applied a smoothing kernel to create a coarse year-specific spatial covariate representing the number of observed packs per habitat cell (SI Appendix, Fig. S15). For wolverines, we used the locations of known dens (from den visits conducted by authorities in their effort to document reproductions) to generate a spatial covariate representing the number of known dens per habitat cell (SI Appendix, Fig. S16). These density covariates were not the sole drivers of patterns in density; spatiotemporal patterns in density emerge as a result of individual-based system dynamics in the model (i.e., realizations of observed and latent individual life histories). For example, despite using single (not time-dependent) density covariates for wolverine and bear, we obtained substantial fluctuations in model-estimated density surfaces across years. We note that the density covariates used here do not mirror our covariates for modeling spatial variation in detection probability (including search effort; SI Appendix, Figs. S17–S20). Density covariates were standardized for computational efficiency during model fitting.
Detections.
In spatial capture–recapture (SCR), detection is closely linked with the home range concept in that the probability of detecting an individual is modeled as a function of the distance to its AC. Most SCR models, including the ones used here, consider the half-normal model to represent the decline in detection probability (42) with increasing distance from the AC. Following this formulation, the probability to detect individual at detector and time is
| [6] |
where represents the baseline detection probability at the location of the AC; , the scale parameter, represents the width of the detection distribution; and is the distance between detector and the AC of individual at time (Fig. 1). For individuals in state alive, the frequency of subdetectors with at least one detection is then modeled as , where , the number of subdetectors associated with detector at occasion , is the number of trials.
Both the baseline probability () and scale parameter () of the detection function can be under the influence of various individual, spatial, and detector-specific factors. These, as well as the spatial configuration of the detector grid, are described in SI Appendix. The detection function in SCR models reflects animal space use and is thus closely linked with the home range concept. As a coarse validation of the spatial assumptions of the model, we calculated sex- and species-specific circular home range sizes (area encompassed by the 95% vertex of the utilization distribution) from the scale parameter using the distribution with two degrees of freedom (43) and report the results in SI Appendix.
The detection process described above concerns detections via NGS. Information contributed by dead recoveries was integrated differently, with the goal to 1) enforce perfect detection of the deaths of individuals legally culled (as reporting is a legal requirement) and 2) inform the model about the fates and locations of individuals that had been recovered regardless of the cause of death. Dead recovery was realized as a binary process where all individuals legally culled were recovered with a probability of 1 and individuals had a recovery probability of zero if they died from other causes: , where is an indicator function returning 1 if and 0 otherwise. Although detection probability of deaths due to other causes was fixed at zero, all known deaths, regardless of cause, were incorporated in the state matrix . States of individuals recovered dead (and thus transitions) following the last live detection were thus no longer latent, even in the absence of further live detections. Dead recovery locations were used as the coordinates of the AC of the recovered individual in the year following its death, thus informing (through the movement model described above) the AC location during the last time step that the animal was alive.
Analysis.
We fitted our Bayesian OPSCR models using Markov chain Monte Carlo (MCMC) simulation with Numerical Inference for Statistical Models Using Bayesian and Likelihood Estimation (NIMBLE) (44–46) in R version 3.6.1 (47). NIMBLE provides an alternative implementation of the Bayesian Inference Using Gibbs Sampling (BUGS) model language coupled with the capability to add custom functions, distributions, and MCMC samplers to improve computing performance. OPSCR models represent a significant computational challenge due to their complexity. This challenge is amplified in our analysis due to the size of the problem (number of individuals, spatial and temporal extent). For this reason, we implemented additional approaches to substantially reduce computation time, including 1) a binomial observation model that allowed substantial reduction of the number of detectors (and therefore runtime) without compromising the precision and accuracy of model estimates (48) and 2) removing unnecessary evaluation of the likelihood whenever the distance between a detector and a predicted AC location was larger than a distance threshold (49). This distance was adjusted for each species and sex to maximize the efficiency of the local evaluation. Model implementation in NIMBLE (46), in combination with the aforementioned developments, yielded a roughly 100-fold improvement in MCMC efficiency (50) compared to that in ref. 51, ultimately enabling us to run the different OPSCR models presented here in a few days or weeks, instead of months. We implemented separate OPSCR models for males and females to account for sex-specific traits such as detection probability, survival, home range size, and dispersal distance. For all six models (three species, two sexes), we ran multiple chains (wolf and wolverine, 4; bear, 8), each with 15,000 iterations (thinned by a factor of 10 for bears and 5 for wolves and wolverines), including a 5,000-iteration burn-in period. We used computing clusters for running multiple MCMC chains on separate cores, enabling us to run many chains simultaneously thereby reducing the total runtime. We considered models as converged when the Gelman–Rubin diagnostic (Rhat) (52) was <1.1 for all parameters and by visually inspecting the trace plots.
We performed several simulation-based assessments of SCR/OPSCR model performance and reliability throughout the development process that led to the models used in the analysis. This included assessing robustness to nonindependence between observations (53), spatial aggregation of detection information (48), interruptions in data collection (including an empirical test of the OPSCR model’s ability to make reliable predictions for years with artificial data removal) (54), and integration of multiple data sources (55). However, while goodness-of-fit (GOF) tests for nonspatial CR models are relatively mature (56), GOF testing for SCR and especially OPSCR is still in its infancy and development is needed.
Data and model code for performing the analysis described here are available in ref. 57. We refer interested readers to our R package nimbleSCR (50, 58), which includes functions for fitting SCR models using NIMBLE. The package includes a collection of methods that drastically improve MCMC estimation, thereby enabling application of SCR to large-scale problems.
Parameter estimation.
The OPSCR is a hierarchical model with many parameters and latent variables directly estimated or derived (SI Appendix, Tables S4–S6). Unless otherwise indicated, we summarized posterior distributions using their median and 95% CrI. To obtain abundance estimates, we summed the number of OPSCR-predicted AC locations of alive individuals that fell within each geographic region of interest (Scandinavia-wide, country specific, or local administrative unit) for each iteration of the MCMC chains, thus generating a posterior distribution of the density in that spatial unit. In this fashion, abundance estimates and the associated uncertainty can be extracted for any desired spatial unit (Fig. 3). To ensure that abundance estimates of spatial subunits add up to overall abundance estimates, we used the mean and the associated 95% credible interval to summarize posterior distributions of abundance. Combined (female/male) parameter estimates were obtained by summing the posterior samples obtained from the sex-specific models. We used both the distribution of model-estimated AC positions and the scale parameter of the detection function to construct density maps that not only are based on the position of the center of an individual’s home range, but also take into account the area over which that individual’s activity is spread (space use). To do so, we constructed raster maps of individual utilization distributions (using the half-normal kernel with the model-estimated scale parameter ), scaled values in each raster to sum to one, and then aggregated rasters across all individuals for a given model iteration into a single raster map. This was repeated for every iteration and an overall density map was derived by calculating the average of the posterior utilization density (i.e., across iterations) in each cell. We obtained posterior trend estimates for parameters by calculating the least-squares slope across years for each iteration. We reported trends as such if the 95% CrI of the posterior slope did not include zero. Note that these trend estimates should be interpreted as the result of assumption-free calculation and not linear regression analysis (which makes assumptions about linearity and normally distributed errors).
Forecasting.
To illustrate OPSCR-based forecasting, we generated predictions from the fitted wolverine OPSCR model using posterior predictions. We created a NIMBLE custom function (45) that takes as input a set of parameter values from the posterior MCMC samples and generates new MCMC samples (for and ) based on the fitted OPSCR model for future years for which no data (NGS and dead recoveries) are yet available. Here, we expanded the model structure for 5 y without data (2020 to 2024) and simulated model node values for these years based on parameter values of 500 randomly selected MCMC iterations. Uncertainty is propagated during simulations as it is during model fitting. For the years 2020 to 2024, we fixed and per-capita recruitment to their mean values during the preceding 7 y (2013 to 2019). To explore the impact of alternative hunting pressures, we repeated the posterior sampling process for five different levels of relative to the average adult legal culling mortality during 2013 to 2019, i.e., , , (status quo), , and . For demonstration purposes, we did not consider the possibility for compensatory mortality but instead assumed that all hunting-related mortality was additive. Results from the posterior sampling procedure were processed like those from the original model fitting. We provide only a simple illustration of the potential of OPSCR for making forecasts. Actionable predictions should take into account that different sources of mortality are mutually influenced by their magnitude and timing. Furthermore, our example relies on the same density covariates that were used during the period with data. These covariates would have to be updated if extensive distributional change (e.g., range expansion or contraction) is to be expected in the future.
Supplementary Material
Acknowledgments
This work was made possible by the large carnivore monitoring programs and the extensive monitoring data collected by Swedish (Länstyrelsena) and Norwegian (Statens naturoppsyn) wildlife management authorities, as well as the public in both countries. Genetic analyses were conducted by the laboratory personnel at the DNA laboratories at the Swedish University of Agricultural Sciences, Uppsala University, the Swedish Museum of Natural History, the Norwegian Institute for Nature Research, and the Norwegian Institute of Bioeconomy Research. Computations/simulations were performed on resources provided by computing cluster “Orion,” administered by the Center for Integrative Genetics at the Norwegian University of Life Sciences and by Uninett Sigma2—the National Infrastructure for High Performance Computing and Data Storage in Norway. We thank both Swedish and Norwegian wildlife managers for constructive discussions during the study and J. Swenson, D. Sheil, and three anonymous referees for helpful comments on earlier versions of this manuscript. This study was funded by the Norwegian Environment Agency (Miljødirektoratet), the Swedish Environmental Protection Agency (Naturvårdsverket), the Research Council of Norway (NFR 286886; project WildMap), and the Peder Sather Grant. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the US Government.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2011383117/-/DCSupplemental.
Data Availability.
The .RData file with input data for OPSCR model fitting and carnivore density raster files have been deposited in Github (https://github.com/richbi/WildThings) (57).
References
- 1.Ordiz A., Bischof R., Swenson J. E., Saving large carnivores, but losing the apex predator? Biol. Conserv. 168, 128–133 (2013). [Google Scholar]
- 2.Ripple W. J., et al. , Status and ecological effects of the world’s largest carnivores. Science 343, 1241484 (2014). [DOI] [PubMed] [Google Scholar]
- 3.Lamb C. T., et al. , The ecology of human–carnivore coexistence. Proc. Natl. Acad. Sci. U.S.A. 117, 17876–17883 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bruskotter J. T., Shelby L. B., Human dimensions of large carnivore conservation and management: Introduction to the special issue. Hum. Dimens. Wildl. 15, 311–314 (2010). [Google Scholar]
- 5.Chapron G., et al. , Recovery of large carnivores in Europe’s modern human-dominated landscapes. Science 346, 1517–1519 (2014). [DOI] [PubMed] [Google Scholar]
- 6.Enserink M., Vogel G., The carnivore comeback. Science 314, 746–749 (2006). [DOI] [PubMed] [Google Scholar]
- 7.Trouwborst A., Fleurke F. M., Linnell J. D. C., Norway’s wolf policy and the Bern convention on European wildlife: Avoiding the “manifestly absurd”. J. Int. Wildl. Law Pol. 20, 155–167 (2017). [Google Scholar]
- 8.Pollock K. H., et al. , Large scale wildlife monitoring studies: Statistical methods for design and analysis. Environmetrics 13, 105–119 (2002). [Google Scholar]
- 9.Stephens P. A., Pettorelli N., Barlow J., Whittingham M. J., Cadotte M. W., Management by proxy? The use of indices in applied ecology. J. Appl. Ecol. 52, 1–6 (2015). [Google Scholar]
- 10.Gopalaswamy A. M., Karanth K. U., Delampady M., Stenseth N. C.. How sampling-based overdispersion reveals India’s tiger monitoring orthodoxy. Conserv. Sci. Practice, 1, e128 (2019). [Google Scholar]
- 11.Tempa T., et al. , The spatial distribution and population density of tigers in mountainous terrain of Bhutan. Biol. Conserv. 238, 108192 (2019). [Google Scholar]
- 12.Miljødirektoratet, Naturvårdsverket, Rovbase 3.0. https://rovbase30.miljodirektoratet.no. Accessed 8 October 2019.
- 13.Ergon T., Gardner B., Separating mortality and emigration: Modeling space use, dispersal and survival with robust-design spatial capture–recapture data. Methods Ecol. Evol. 5, 1327–1336 (2014). [Google Scholar]
- 14.Bischof R., Brøseth H., Gimenez O., Wildlife in a politically divided world: Insularism inflates estimates of brown bear abundance. Conserv. Lett. 9, 122–130 (2016). [Google Scholar]
- 15.Chandler R. B., Hepinstall-Cymerman J., Merker S., Abernathy-Conners H., Cooper R. J., Characterizing spatio-temporal variation in survival and recruitment with integrated population models. Auk 135, 409–426 (2018). [Google Scholar]
- 16.Kéry M., Schaub M., Bayesian Population Analysis Using WinBUGS: A Hierarchical Perspective (Academic Press, Waltham, MA, 2012). [Google Scholar]
- 17.Efford M., Density estimation in live-trapping studies. Oikos 106, 598–610 (2004). [Google Scholar]
- 18.Schaub M., Royle J. A., Estimating true instead of apparent survival using spatial Cormack–Jolly–Seber models. Methods Ecol. Evol. 5, 1316–1326 (2014). [Google Scholar]
- 19.Scott C., et al. , Questionable policy for large carnivore hunting. Science 350, 1473–1475 (2015). [DOI] [PubMed] [Google Scholar]
- 20.Mitchell M. S., et al. , Distinguishing values from science in decision making: Setting harvest quotas for mountain lions in Montana. Wildl. Soc. Bull. 42, 13–21 (2018). [Google Scholar]
- 21.Wabakken P., Sand H., Liberg O., Anders B., The recovery, distribution, and population dynamics of wolves on the Scandinavian peninsula, 1978-1998. Can. J. Zool. 79, 710–725 (2001). [Google Scholar]
- 22.Flagstad Ø., et al. , Colonization history and noninvasive monitoring of a reestablished wolverine population. Conserv. Biol. 18, 676–688 (2004). [Google Scholar]
- 23.Swenson J. E., et al. , Challenges of managing a European brown bear population; lessons from Sweden, 1943–2013. Wildl. Biol. 1, wlb.00251 (2017). [Google Scholar]
- 24.Liu J., Yong D. L., Choi C.-Y., Gibson L., Transboundary frontiers: An emerging priority for biodiversity conservation. Trends Ecol. Evol. 35, 679–690 (2020). [DOI] [PubMed] [Google Scholar]
- 25.Morehouse A. T., Boyce M. S., Grizzly bears without borders: Spatially explicit capture–recapture in southwestern Alberta. Jour. Wild. Mgmt. 80, 1152–1166 (2016). [Google Scholar]
- 26.Gilroy J. J., Ordiz A., Bischof R., Carnivore coexistence: Value the wilderness. Science 347, 381 (2015). [DOI] [PubMed] [Google Scholar]
- 27.Gervasi V., et al. , Sharing data improves monitoring of trans-boundary populations: The case of wolverines in central Scandinavia. Wildl. Biol. 22, 95–106 (2016). [Google Scholar]
- 28.Schregel J., et al. , Limited gene flow among brown bear populations in far northern Europe? Genetic analysis of the east–west border population in the Pasvik valley. Mol. Ecol. 21, 3474–3488 (2012). [DOI] [PubMed] [Google Scholar]
- 29.Bischof R., Swenson J. E., Yoccoz N. G., Mysterud A., Gimenez O., The magnitude and selectivity of natural and multiple anthropogenic mortality causes in hunted brown bears. J. Anim. Ecol. 78, 656–665 (2009). [DOI] [PubMed] [Google Scholar]
- 30.Bischof R., et al. , Regulated hunting re-shapes the life history of brown bears. Nat. Ecol. Evol. 2, 116–123 (2018). [DOI] [PubMed] [Google Scholar]
- 31.Bischof R., Fujita R., Zedrosser A., Söderberg A., Swenson J. E., Hunting patterns, the ban on baiting, and harvest demographics of brown bears in Sweden. J. Wildl. Manag. 72, 79–88 (2008). [Google Scholar]
- 32.Council of Europe , Convention on the conservation of European wildlife and natural heritage. https://www.coe.int/en/web/conventions/full-list/-/conventions/treaty/104. Accessed 5 August 2020.
- 33.Council of Europe , Council Directive 92/43/EEC of 21 May 1992 on the conservation of natural habitats and of wild fauna and flora. http://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:31992L0043. Accessed 5 August 2020.
- 34.Ministry of Environment , “Rovvilt I Norsk Natur, St.Meld. Nr [in Norwegan]” (Government white paper nr. 15, Oslo, 2003–2004; https://www.regjeringen.no/no/dokumenter/stmeld-nr-15-2003-2004-/id403693/). Accessed 5 August 2020.
- 35.Chandler R. B., Clark J. D., Spatially explicit integrated population models. Methods Ecol. Evol. 5, 1351–1360 (2014). [Google Scholar]
- 36.Augustine B. C., et al. , Sex-specific population dynamics and demography of capercaillie (Tetrao urogallus L.) in a patchy environment. Popul. Ecol. 62, 80–90 (2020). [Google Scholar]
- 37.Gervasi V., Linnell J. D. C., Brøseth H., Gimenez O., Failure to coordinate management in transboundary populations hinders the achievement of national management goals: The case of wolverines in Scandinavia. J. Appl. Ecol. 56, 1905–1915 (2019). [Google Scholar]
- 38.Lebreton J.-D., Pradel R., Multistate recapture models: Modeling incomplete individual histories. J. Appl. Stat. 29, 353–369 (2002). [Google Scholar]
- 39.Royle J. A., Dorazio R. M., Parameter-expanded data augmentation for Bayesian analysis of capture–recapture models. J. Ornithol. 152, 521–537 (2012). [Google Scholar]
- 40.Illian J., Penttinen A., Stoyan H., Dietrich S., Statistical Analysis and Modeling of Spatial Point Patterns (Wiley, 2008). [Google Scholar]
- 41.Gardner B., Sollmann R., Samba Kumar N., Jathanna D., Karanth K. U., State space and movement specification in open population spatial capture-recapture models. Ecol. Evol. 8, 10336–10344 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Royle J. A., Converse S. J., Hierarchical spatial capture-recapture models: Modeling population density in stratified populations. Methods Ecol. Evol. 5, 37–43 (2014). [Google Scholar]
- 43.Royle J. A., Chandler R. B., Sollmann R., Gardner. B., Spatial Capture-Recapture (Elsevier/Academic Press, Amsterdam, The Netherlands, 2013). [Google Scholar]
- 44.Turek D., de Valpine P., Paciorek C. J., Efficient Markov chain Monte Carlo sampling for hierarchical hidden Markov models. Environ. Ecol. Stat. 23, 549–564 (2016). [Google Scholar]
- 45.de Valpine P., et al. , Programming with models: Writing statistical algorithms for general model structures with NIMBLE. J. Comput. Graph Stat. 26, 403–413 (2017). [Google Scholar]
- 46.NIMBLE Development Team , NIMBLE: MCMC, particle filtering, and programmable hierarchical modeling. https://cran.r-project.org/package=nimble. Accessed 5 August 2020.
- 47.R Core Team , R: A language and environment for statistical computing (R Version 3.6.1). https://www.r-project.org/. Accessed 27 November 2019.
- 48.Milleret C., et al. , Using partial aggregation in spatial capture recapture. Methods Ecol. Evol. 9, 1896–1907 (2018). [Google Scholar]
- 49.Milleret C., et al. , A local evaluation of the individual state-space to scale up Bayesian spatial capture-recapture. Ecol. Evol. 9, 352–363 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Turek D., et al. , Efficient estimation of large-scale spatial capture-recapture models. Ecosphere, in press. [Google Scholar]
- 51.Plummer M., “JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling” in Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003), Hornik K., Leisch F., Zeileis A., eds. (Technische Universität Wien, Vienna, Austria, 2003), pp. 1–10. [Google Scholar]
- 52.Gelman A. “Inference and monitoring convergence” in Markov Chain Monte Carlo in Practice, Gilks W. R., Richardson S., Spiegelhalter D. J., Eds. (Chapman and Hall, London, UK, 1996), pp. 131–143. [Google Scholar]
- 53.Bischof R., Dupont P., Milleret C., Joseph C., Royle J. A., Consequences of ignoring group association in spatial capture–recapture analysis. Wildl. Biol. 2020, wlb.00649 (2020). [Google Scholar]
- 54.Milleret C., et al. , Estimating abundance with interruptions in data collection using open population spatial capture-recapture models. Ecosphere 11, e03172 (2020). [Google Scholar]
- 55.Tourani M., Dupont P., Ali Nawaz M., Bischof R., Multiple observation processes in spatial capture–recapture models: How much do we gain?. Ecology 101, e03030 (2020). [DOI] [PubMed] [Google Scholar]
- 56.Pradel R., Gimenez O., Lebreton J.-D., Principles and interest of GOF tests for multistate capture-recapture models. Anim. Biodivers. Conserv. 28, 189–204 (2005). [Google Scholar]
- 57.Bischof R., Milleret C., Dupont P., Carnivore open-population spatial recapture in Nimble, input data, and density rasters. https://github.com/richbi/WildThings. Deposited 20 August 2020.
- 58.Bischof R., et al. , NimbleSCR: Spatial capture-recapture in SCR methods using ‘nimble’ (R Package Version 0.1.0, 2020). https://cran.r-project.org/web/packages/nimbleSCR/index.html. Accessed 26 October 2020.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The .RData file with input data for OPSCR model fitting and carnivore density raster files have been deposited in Github (https://github.com/richbi/WildThings) (57).