Significance
Decision making involves the evaluation of the options, and the current popular theory puts the orbitofrontal cortex (OFC) in a central role in this process. However, by using a sophisticated task design in which the decision making requires both evidence accumulation over time and a stimulus-to-action transformation, we found that the OFC neuronal activity reflected neither. Both processes were instead represented in the dorsolateral prefrontal cortex (DLPFC), and the stimulus-to-action transformation occurred before the evidence accumulation. Our study argued for a more limited role of the OFC in value-based decision making than previously proposed and indicated how the OFC and the DLPFC may work together to compute value during decision making.
Keywords: decision making, value, prefrontal cortex
Abstract
A key step of decision making is to determine the value associated with each option. The evaluation process often depends on the accumulation of evidence from multiple sources, which may arrive at different times. How evidence is accumulated for value computation in the brain during decision making has not been well studied. To address this problem, we trained rhesus monkeys to perform a decision-making task in which they had to make eye movement choices between two targets, whose reward probabilities had to be determined with the combined evidence from four sequentially presented visual stimuli. We studied the encoding of the reward probabilities associated with the stimuli and the eye movements in the orbitofrontal (OFC) and the dorsolateral prefrontal (DLPFC) cortices during the decision process. We found that the OFC neurons encoded the reward probability associated with individual pieces of evidence in the stimulus domain. Importantly, the representation of the reward probability in the OFC was transient, and the OFC did not encode the reward probability associated with the combined evidence from multiple stimuli. The computation of the combined reward probabilities was observed only in the DLPFC and only in the action domain. Furthermore, the reward probability encoding in the DLPFC exhibited an asymmetric pattern of mixed selectivity that supported the computation of the stimulus-to-action transition of reward information. Our results reveal that the OFC and the DLPFC play distinct roles in the value computation during evidence accumulation.
We often have to choose between different options based on each option’s value. In many cases, the evaluation of each option is a complex process in which one has to combine multiple pieces of information. Our subjective experience is often that we carry out the action that substantiates a decision only after it has been made. Accordingly, it has been proposed that there is an intermediate stage in the brain where the value computation and decision-making process are completely dissociated from their motor contingency (1–4). In particular, the orbitofrontal cortex (OFC) has been proposed to play that role (5, 6). In a series of studies, Padoa-Schioppa and coworkers (3, 4, 7) reported that some OFC neurons encoded the value of the chosen option regardless of the direction of the eye movement used by the animals to indicate their choice. In addition, OFC lesions have been shown to lead to deficits in stimulus-value updating but not action-value updating (8). Researchers have further suggested that the dorsolateral prefrontal cortex (DLPFC) receives the input from the OFC and transforms stimulus-based decisions into actions (1, 3, 9–11).
However, much of the evidence for a central role of the OFC in computing an action-independent decision derives from experiments that employed rather simple stimulus–reward associations (1, 3, 4, 12, 13). Such experimental designs may not be ideal for teasing apart the stimulus, value, decision making, and action signals in the brain. A task in which decisions have to be calculated in an extended process as the ones investigated in many perceptual decision-making studies (9, 14–16) may help us to find out how the value computation unfolds in the brain, whether the OFC is where the good-based decision making occurs, and where the stimulus-to-action transition happens in the brain.
Therefore, we studied the neuronal responses in the OFC and the DLPFC using a probabilistic reasoning task that required an extended decision-making process. Two monkeys were trained to make choices between two colored targets by integrating probabilistic evidence across time. The reward probability of each color was indicated by a sequence of simple shape pictures that served as visual cues. The monkeys had to combine information from these shapes to calculate the reward probabilities and determine which color was more rewarding. Their choices were indicated with saccadic eye movements. Critically, both red and green targets could appear on either the left or the right, randomly chosen by the computer in each trial. The evidence was provided in regard to the target color, independent from eye movement directions. We investigated how the value information regarding colors (stimulus based) is transformed into the value information regarding spatial locations (action based) in the brain to form decisions. We recorded single-unit activities from the DLPFC and the OFC. We found that the OFC neurons encoded evidence associated with each shape in the shape sequence, but only transiently and only in the stimulus domain. The accumulation of evidence was represented only in the DLPFC and only in the action domain. These results suggest that the OFC and the DLPFC encode value information differently during decision making.
Results
Behavior.
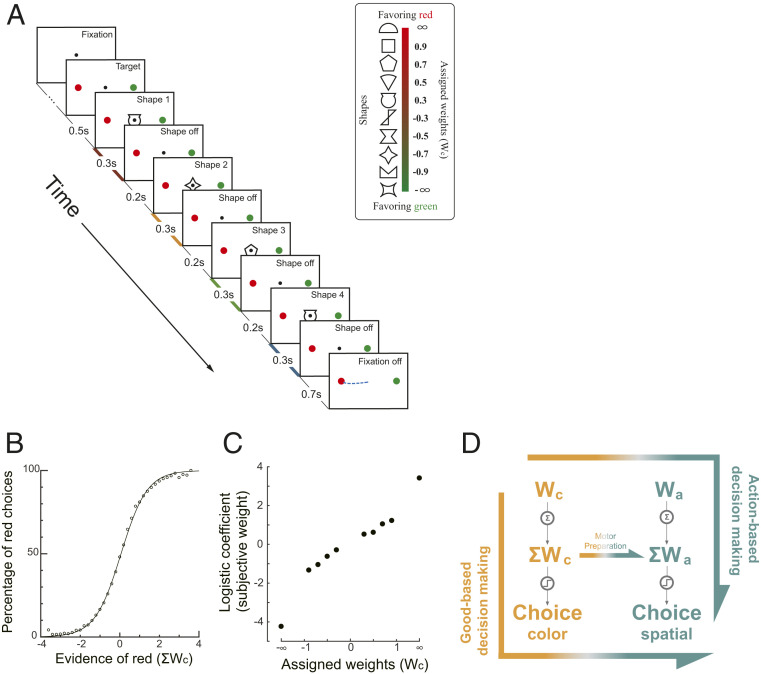
We trained the monkeys to perform a probabilistic reasoning task (Fig. 1A). The task was slightly modified from a previous study (17). In each trial, the animals watched a sequence of 4 shapes, drawn randomly with replacement from a pool of 10 shapes. Each shape was assigned a weight. The sum of the weights was the log odds between the reward probabilities of the red target and the green target (Eqs. 1 and 2). Thus, the shapes with positive weights indicated that the red target had a larger reward probability, whereas the shapes with negative weights indicated that the green target had a larger reward probability. The monkeys reported their choice with a saccadic eye movement toward the chosen target. The reward was delivered probabilistically based on the summed weight of the shapes in the sequence. There were no correct or error choices in the absolute sense, and the monkeys received a probabilistic reward associated with either choice. A rational choice should be for the target with a larger reward probability. Importantly, the red and the green targets were randomly placed either on the left or on the right side of the screen, which allows us to dissociate the choice of target color from the choice of saccade direction.
Fig. 1.
(A) Task design. Four shapes were presented sequentially on the computer screen while the monkey fixated at the FP. After the FP was turned off, the monkey made a saccade to either the red or the green choice target. The shapes were selected randomly with replacement in each trial from a set of 10. Each of them was assigned a unique weight (Inset). The reward probability was calculated with the sum of the weights associated with the four shapes. Positive weights indicated that the red target had a higher reward probability than the green one. The red, yellow, green, and blue shadings on the time axis indicate the four stimulus representation periods. (B) Monkey performance. The percentage of red choices is plotted against the summed weight of the four shapes. Each dot indicates the percentage of red choice in trials with the same grouped summed weights. The curve is a logistic function fitted to all trials. (C) Subjective weights. We used logistic regression to assess the leverage of each shape on the monkeys’ choices and defined the coefficients as the subjective weights. Positive subjective weights indicate a tendency to choose the red target. (D) Two competing decision-making hypotheses. In stimulus-based decision making, the evidence regarding color (Wc) is first accumulated into the ΣWc, which is then used to generate the action-independent color choice and finally forms the action. In contrast, the action-based decision-making hypothesis assumes that the Wc is first transformed into the action domain (Wa), which is then accumulated into the ΣWa and used to form the action. In addition, the stimulus-based decision making may be complemented by a motor preparation process, in which the ΣWa is calculated from the ΣWc during decision making.
Both monkeys learned to perform the task (Fig. 1B and SI Appendix, Fig. S1 A and B). The monkeys chose the green target more often when the summed color weight was negative and the red target more often when the summed weight was positive. To assess how each shape affected the monkeys’ choices, we applied a logistic regression with the number of appearances of each shape as the regressors (Eq. 4). The regression coefficients showed the same rank order as the assigned weights, indicating the monkey assigned appropriate weights to the shapes (Fig. 1C and SI Appendix, Fig. S1 C and D). This rank order was preserved in all epochs (SI Appendix, Fig. S2), although the early epochs were weighted slightly less (SI Appendix, Fig. S1 E and F). The monkeys treated the two shapes with infinite weights as if they had large but finite weights (Fig. 1C); they could be canceled by other shapes, and the monkeys did not stop integrating information when the infinitive shapes appeared early in a trial (SI Appendix, Fig. S3).
The task design allowed us to study the stimulus-to-action transition in the brain. The shape weights indicated the reward probability in the stimulus domain (target color). Both colors could appear on the left or the right. Thus, the reward probability associated with the red and the green target is orthogonal to the reward probability associated with the left or right eye movement direction. Because the eye movement circuitry in the brain carries out the motor commands using spatial coordinates, the decision has to be transformed into the action domain. The critical question is when the value information in the stimulus domain is transformed into the action domain. If the transition occurs before the evidence accumulation, the evidence associated with each shape is first transformed into the action domain and then accumulated. Thus, the representation of the accumulated evidence in the brain should be found only in the action domain. Alternatively, if the transition happens after the decision regarding color is made, the evidence must first be accumulated in the stimulus domain. As a result, we would observe the representation of the accumulated evidence in the stimulus domain but not the single piece of evidence in the action domain (Fig. 1D). An additional scenario in the stimulus-based decision making is that there may be a separate motor preparation process accompanying the ongoing stimulus-based evidence accumulation, in which the action value is calculated from the stimulus value (horizontal arrow in Fig. 1D, Middle). In this scenario, the transition occurs before the end of the evidence accumulation. We may observe the representation of the accumulated evidence in both the stimulus and the action domains in the brain, but not the representation of the individual piece of evidence in the action domain.
Therefore, with this behavior paradigm, we may study how the decision making unfolds in the brain by investigating in which domain neurons in the prefrontal circuitry encode value information associated with either the individual shapes or the combination of shapes. For mathematical convenience, in our analyses, we used weights, which are monotonically related to value, as a proxy to illustrate how value is encoded in the brain (SI Appendix, Fig. S5). We use Wc to refer to the weight associated with the particular shape appearing in an epoch in the stimulus domain, Wa for the weight associated with the shape in the action domain, ΣWc for the sum of the weights of the shapes that have appeared so far in the stimulus domain, and ΣWa for the sum of the weights of the shapes that have appeared in the action domain.
Example Neurons.
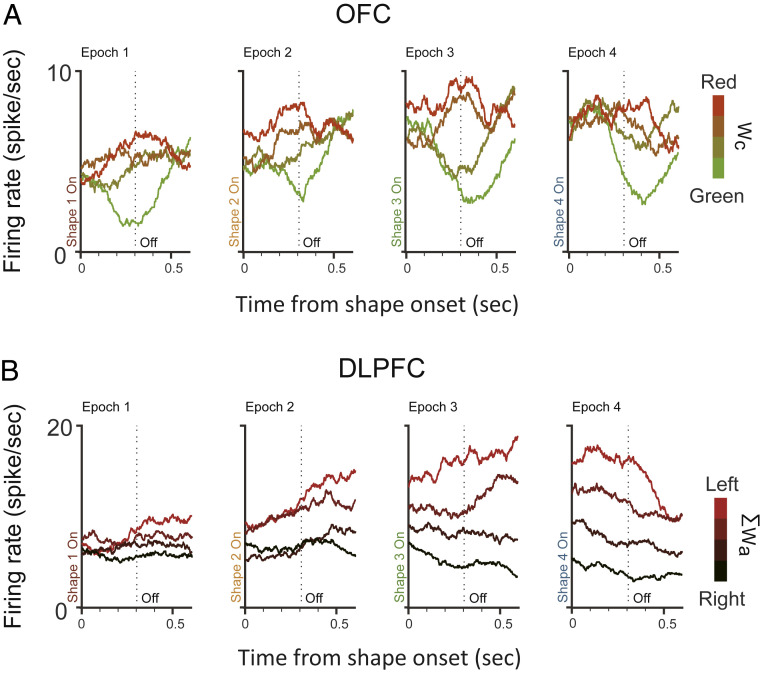
We recorded single-unit activities from the OFC and the DLPFC. Fig. 2 and SI Appendix, Fig. S6 show two representative example units from each area, respectively. The example neuron from the DLPFC exhibited a response pattern similar to that of the neurons in the lateral intraparietal cortex (LIP) (17, 18). Its responses ramped up or down as the evidence grew in favor of or against the target associated with its preferred eye movement direction. When we sorted the trials into quartiles by the ΣWa in each epoch, we observed greater responses when the ΣWa was larger (Fig. 2B). Its responses, however, did not reflect the weights associated with color (SI Appendix, Fig. S6A). In contrast, the example neuron from the OFC did not have a clear ramping activity pattern that encoded either Wa or ΣWa (SI Appendix, Fig. S6 G and H). Its responses were instead modulated by the Wc. The neuron’s responses were greater when the evidence associated with the particular shape presented in the epoch was in favor of the red target (Fig. 2A).
Fig. 2.
Example neurons. (A) The activity of an OFC neuron encoded the Wc. Response averages are aligned to the shape onsets and extended 100 ms into the next shape period. The trials are divided into quartiles by the Wc (indicated by the color), and the neuron’s response averages are computed. The dashed vertical lines indicate the shape offset at 300 ms. (B) The activity of a DLPFC neuron encoded the ΣWa. The trials are divided into quartiles by the ΣWa (indicated by the redness), and the neuron’s response averages are computed. Other conventions are the same as in A. See also SI Appendix, Fig. S6 for the neurons’ selectivities to the other variables.
Population Analyses: Choices.
The example neurons showed that the neurons in both the OFC and the DLPFC encoded relevant information for decision making. To fully understand the roles that the two areas play in decision making, we recorded the activities of 277 cells from the OFC (121 and 156 from monkeys K and E, respectively) and of 384 cells from the DLPFC (170 and 214 from monkeys K and E, respectively) and studied their response patterns when the monkeys were performing the task.
First, we asked the question of whether the choice outcome was encoded in the two areas. This would provide us clues to whether they were involved in decision making. Just as the weights, the choice outcome can also be either in the stimulus domain or in the action domain. We looked at them separately.
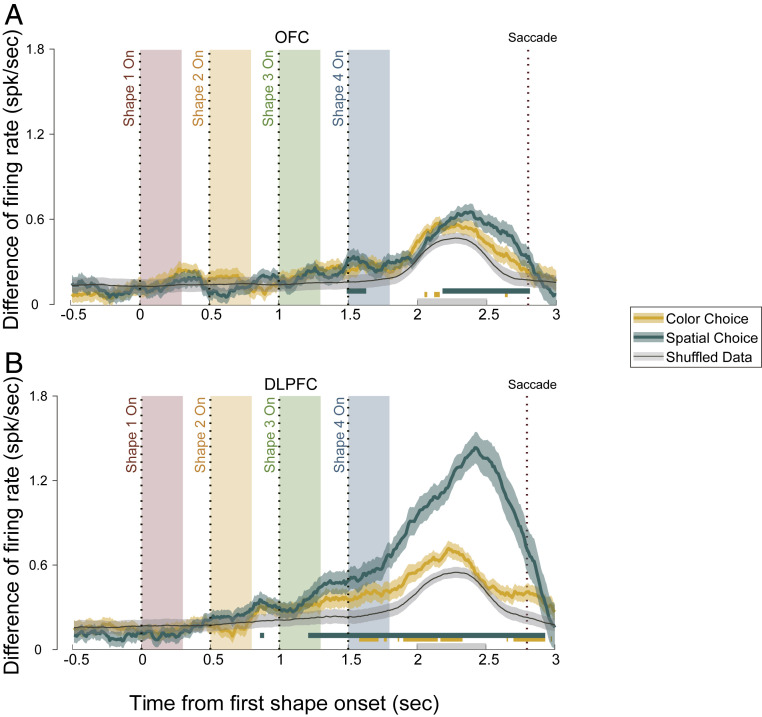
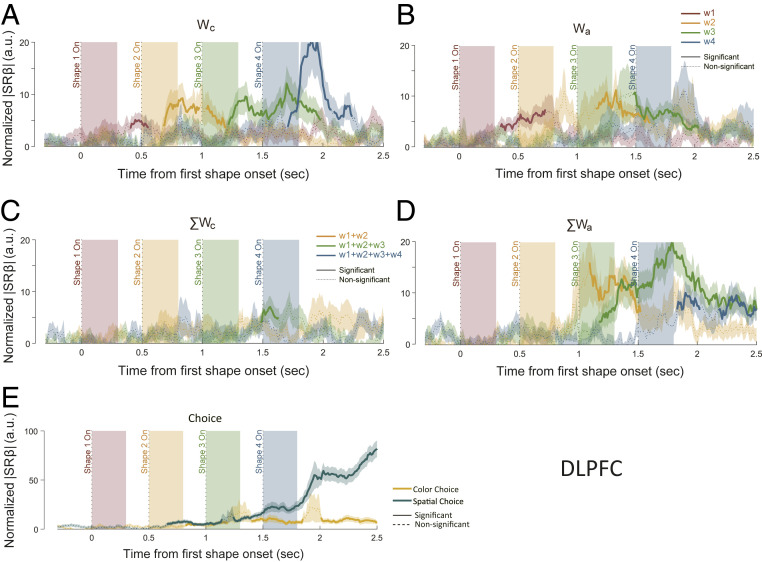
We sorted all trials according to each neuron’s preference of either color or eye movement direction during a 500-ms time window starting at 200 ms after the last shape’s offset. We calculated the neurons’ responses difference between the preferred and the nonpreferred choice outcomes (Fig. 3). Because of the way that the neurons’ preferences were determined (Methods), the calculated response difference would be larger than 0, even if there was only noise. Therefore, we determined the significance of the response difference by comparing the actual data against the shuffled data. The OFC neurons barely signaled the monkeys’ choice in either the stimulus or the action domain during the stimulus presentation period (Fig. 3A). There was, interestingly, a significant representation of the spatial choice in the OFC before the saccade. The DLPFC neurons, however, were strongly modulated by the monkeys’ choice outcome regarding the eye movement direction (Fig. 3B). The modulation became significant (ANOVA, P < 0.01) at 210 ms after the third shape epoch and was maintained until the end of the trial. The DLPFC neurons also showed a difference between their responses to the two color choices, although in a much more modest and less consistent manner. The representation of the color choice in the DLPFC did not precede that of the spatial choice.
Fig. 3.
Choice representations in (A) the OFC and (B) the DLPFC. The average firing rate difference of the neurons between trials with different spatial and color choices are shown. Green, spatial choice; yellow, color choice; black, shuffled data. The green and yellow shaded areas indicate the SEM, and the gray shaded area indicates the SD of the 1,000 shuffles. The green and yellow horizontal lines mark the periods in which the spatial or color choice curve is significantly different from the shuffled data (P < 0.01, one-way ANOVA). The four color-shaded boxes indicate the shape presentation period in the four epochs, with the dashed lines indicating the shape onset. The rightmost dashed line marks the average saccade time. The gray bar on the horizontal axis represents the period from which the mean firing rates were calculated to define the neurons’ preferred choices (Methods).
Population Analyses: Stimulus Weights.
We further studied whether the neuronal responses in the two areas captured different stages of decision making. To understand the complete picture of how neurons in the OFC and the DLPFC contributed to the task, we looked at how each relevant variable in the task may explain the populational responses in each area. More specifically, we looked at how neurons’ responses may be explained with the Wc, Wa, ΣWc, and ΣWa in each of the four epochs in a trial with a linear model containing all four weight variables in all four epochs (ΣWc and ΣWa were not considered in the first epoch). We also included two choice variables in the model: one for the color and one for the eye movement direction. Although the variables in the stimulus domain are orthogonal to those in the action domain, the variables within the same domain—single weight and sum weight—are linearly dependent. To alleviate the multicollinearity problem, we fitted the model via least absolute shrinkage and selection operator (LASSO). We calculated the absolute value of standard regression coefficients to evaluate the effect size of each variable. is analogous to the more commonly used but not sensitive to linearly dependent predictors (Methods). We normalized the following a previously described procedure to compare the results from different neuron populations (3). The results are plotted in Fig. 4 for the OFC and in Fig. 5 for the DLPFC and in SI Appendix, Figs. S7 and S8 for individual monkeys.
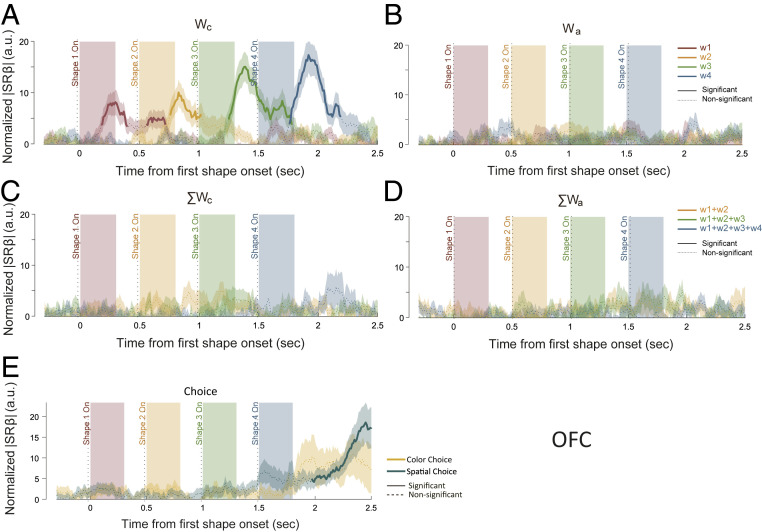
Fig. 4.
Representations of the single weights and the summed weights in the OFC with LASSO. The effect sizes of (A) Wc, (B) Wa, (C) ΣWc, (D) ΣWa, and (E) choice were quantified using normalized |SRβ|. (A–D) The red, yellow, green, and blue traces indicate the weights associated with the first, second, third, and fourth epochs, respectively. (E) Green and yellow traces indicate spatial choice and color choice, respectively. The solid sections of each curve indicate significance (P < 0.01 for at least a consecutive 150 ms), and the dashed sections are not significant. Shaded areas along the curves stand for the SEM. The traces of the ΣWc and ΣWa of the first epoch were omitted in C and D (Methods).
Fig. 5.
Representations of the single weights and the summed weights in the DLPFC with LASSO. The effect sizes of (A) Wc, (B) Wa, (C) ΣWc, (D) ΣWa, and (E) choice were quantified using normalized |SRβ|. (A–D) The red, yellow, green, and blue traces indicate the weights associated with the first, second, third, and fourth epochs, respectively. (E) Green and yellow traces indicate spatial choice and color choice, respectively. The solid sections of each curve indicate significance (required P < 0.01 for at least a consecutive 150 ms), and the dashed sections are not significant. Shaded areas along the curves stand for the SEM. The traces of the ΣWc and ΣWa of the first epoch were omitted in C and D (Methods).
Among the four variables, OFC prominently encoded the Wc (Fig. 4A). The encoding for each shape was, however, not sustained. It disappeared shortly after the next shape appeared. There was only a slight overlapping between the consecutive shapes, suggesting a lack of information accumulation. Consistently, the representation of ΣWc was very weak (Fig. 4C), which also explains the finding that the OFC did not encode the color choice outcome. In addition, the encoding of the weights was restricted to the stimulus domain and not observed in the action domain (Fig. 4 B and D). Consistent with Fig. 3A, the choice signals were lacking during the shape presentation epochs, although the spatial choice was significantly encoded by the OFC late in a trial (Fig. 4E). This late spatial choice signal most likely did not arise from within the OFC, because there were no significant representations of either the color choice or the ΣWa.
In contrast, the DLPFC neurons exhibited a different encoding pattern (Fig. 5). First of all, both variables in the action domain (Wa and ΣWa), as well as the spatial choice, were strongly represented in the DLPFC (Fig. 5 B, D, and E). The DLPFC neurons were also found to encode the Wc (Fig. 5A). As in the OFC, the encoding of the ΣWc in the DLPFC was weak and inconsistent, if it existed at all (Fig. 5C). The results suggest a lack of accumulation in the stimulus domain in the DLPFC also.
The absence of the representations of ΣWc in either area was surprising. One possible explanation is that the LASSO was too stringent for detecting a weak signal. Therefore, we further performed separate linear regression analyses in which the neurons’ responses were regressed against each individual variable. We estimated the variance explained by each factor at the population level by calculating the normalized ∆R2 (3). By doing regression separately for each parameter, we can achieve a larger statistical power and argue more convincingly for the absence of encoding. The regression results confirmed the results based on the LASSO. Both the ∆R2 (SI Appendix, Figs. S10 and S12) and the percentage of neurons (SI Appendix, Figs. S11 and S13) showed only very weak representations of ΣWc in both the OFC and the DLPFC, which may be explained away by the correlation between Wc and ΣWc. In addition, the regressions did not find any representations of the weight information in the action domain in the OFC (SI Appendix, Figs. S10 and S11).
In contrast to the weak representations of ΣWc in both area, the regression analyses revealed strong representations of the weights in the action domain in the DLPFC, even more so than those indicated by the LASSO (SI Appendix, Fig. S12). With the regression analyses, we observed a ramping pattern in the DLPFC’s representations of ΣWa, which was similar to what has been reported previously in neurons in the DLPFC and the LIP during decision making (9, 17, 18). Such a ramping pattern was missing in the LASSO analyses. After a transient phase in which the neurons’ activities had to be accounted for by the ΣWa in addition to the eye movements, the extra explanation power of the ΣWa disappeared. This was not an artifact of the particular parameter searching procedure we used in LASSO analyses. We confirmed the results with a different scaling parameter that minimizes the potential underestimation of the ΣWa in the late trial period (SI Appendix, Fig. S9). Such dynamics indicate that the representation of ΣWa in the DLPFC was replaced by that of a binary choice variable in the later period of decision making.
The negative findings cannot be explained by the use of the weights instead of the value in our analyses. We further performed the regression analyses directly based on value, which was calculated as the probability of receiving a reward of a red-or-green (stimulus domain) or left-or-right (action domain) choice given the appearance of a given shape or sequence. The results were also similar and confirmed the findings (SI Appendix, Figs. S14 and S15).
Finally, we asked the question of whether the OFC and DLPFC neurons encoded the reward probability of the chosen target, which is analogous to the chosen value that was defined by Padoa-Schioppa and coworkers (3, 4) and was a critical piece of evidence in support of the proposed OFC’s role in good-based decision making (6). In our task, because the monkeys almost always chose the option with the larger reward probability, the chosen value can be quantified with the larger reward probability between the two options. Therefore, we regressed the OFC and DLPFC neurons’ responses against the larger reward probability between the two targets in each epoch. Note that this quantity is neither in the stimulus nor in the action domain. It is nevertheless independent of any action contingencies. Again, the encoding of the chosen reward probability was very weak in either area (SI Appendix, Fig. S16). Therefore, the representations of reward probability in an action-independent form were absent in both areas.
Stimulus-to-Action Transition.
The above analyses suggested that the transition between the stimulus-based signal and the action-based signal occurred at the single-weight stage before evidence accumulation. Next, we looked for evidence of whether this transition occurred in the OFC or the DLPFC. The computation involved in this transition is not trivial. Because the Wc and the Wa are orthogonal to each other, a nonlinear transformation is required. It has been suggested that a network with neurons with nonlinear mixed selectivity may allow the transition to be implemented via a simple linear readout (19). Thus, we studied whether neurons in the OFC and the DLPFC exhibited nonlinear mixed selectivity regarding Wc.
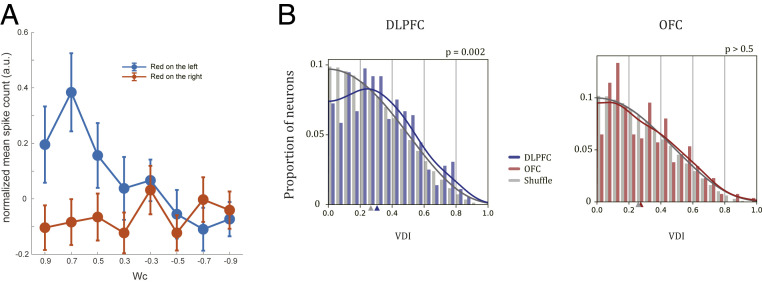
One signature of mixed selectivity is that a neuron’s Wc selectivity may vary under different target configurations. For instance, the example DLPFC neuron in Fig. 6A was selective to Wc when the red target was on the left but not when it was on the right (Fig. 6A). To quantify this selectivity difference between different target spatial configurations, we defined the variance difference index (VDI) to measure the response variance difference (Methods). Neurons with the same selectivities under different target configurations can be considered as pure Wc neurons, and those with the opposite selectivities are pure Wa neurons. The VDIs of both types of neurons are 0. Neurons with large VDIs exhibit different but not opposite Wc selectivities under two target configurations and may play a role in the computation of the transition from Wc to Wa.
Fig. 6.
Mixed selectivity. (A) An example DLPFC neuron showing nonlinear mixed selectivity to the spatial configuration and the color weights. A multiple-regression analysis indicated that the effect on spike counts induced by the interaction term of configuration and weight was significant (P = 0.002, t test). (B) The distribution of the VDI of the DLPFC (Left, blue) and the OFC (Right, red) neurons and their corresponding shuffled distributions (gray). Solid lines indicate fitted probability distributions based on KDE (Methods). Colored triangles on the x axes indicate the medians of the corresponding distributions. The VDIs of DLPFC neurons are significantly larger than the shuffled data (P = 0.002, Kolmogorov–Smirnov test), while the VDIs of OFC neurons are not (P = 0.567, Kolmogorov–Smirnov test).
We calculated the VDIs of all neurons in the DLPFC and the OFC. The VDIs of the DLPFC neurons were significantly larger than the VDIs of the distribution obtained after we shuffled the spatial configuration labels in the original data (P = 2.16e-3, Kolmogorov–Smirnov test; Fig. 6 B, Left). The OFC neurons’ VDIs did not differ from those of the shuffled data (P = 0.567, Kolmogorov–Smirnov test; Fig. 6 B, Right). We also counted the number of the neurons whose VDI exceeded a certain threshold. The number of the DLPFC neurons that satisfied the criterion was consistently significantly more than expected by chance for a large range of thresholds. The number of the OFC neurons was not significantly different from the chance level (SI Appendix, Fig. S17). In conclusion, although both the DLPFC and the OFC neurons encoded Wc, only the DLPFC neurons exhibited a nonlinear mixture pattern that may support the computation of the stimulus-to-action transition at the single-weight stage.
Discussion
Here, we have shown how the stimulus-based and action-based decision-making signals were represented in the OFC and the DLPFC. These results indicated that there is a lack of information accumulation in the OFC necessary for calculating the value of the choices in either the stimulus or the action domain. Within the DLPFC, we demonstrated that decisions for actions were computed in the action domain, and the transition between the stimulus-based and action-based value information occurred at the stage of the single piece of evidence before accumulation.
OFC and Value-Based Decision Making.
Although it has been widely accepted that the OFC neurons encode the value, our study suggests that such a view does not extend to the case when the value has to be determined from multiple pieces of evidence presented sequentially. We found that the OFC neurons encoded only value information associated with individual stimuli. The encoding was transient, and the information was not accumulated over time.
One may argue that our task design may favor a solution with which the brain may have performed the entire task in the action domain without computing value at all, which would explain the absence of the accumulated value signal in the OFC. This is, however, unlikely. First, unlike in typical perceptual decision-making tasks, the evidence associated with the shapes used in the current study was defined by and learned through their reward associations. In addition, even in the most typical perceptual decision-making tasks, it has been shown that value is still being computed during decision making. For example, the midbrain dopamine neurons’ activities signaled reward predictions during the motion viewing period when monkeys were doing the random dots task, further suggesting that the brain is actively calculating value during even very typical perceptual decision-making tasks (20). Furthermore, the reward circuitry, including the ventromedial prefrontal cortex and the DLPFC, was shown to be underlying the choice bias in the random dots task when the two choices were unevenly rewarded (21). In fact, perceptual tasks in the animal studies always involve animals learning the association between perceptions and rewards. Value cannot be excluded from these tasks.
Several studies have suggested that the information processing in the OFC is sequential (22, 23). Our study further indicates that the integration of information across time does not occur within the OFC. We did observe a representation of the choice, and thus the accumulated information, in the action domain around the time of choice. Given the late appearance of this signal, it probably reflected computation from somewhere else in the brain, including the DLPFC.
In particular, in a recent paper (7), monkeys were trained to make choices between two sequentially presented offers. Very few neurons were found to encode the value difference between the two offers. Similar to the in our study, the computation of value difference requires the integration of information across time. Therefore, consistent with our study, the study suggested that the OFC does not integrate value information across time. In addition, the authors proposed a circuit inhibition mechanism that involves an unidentified circuitry in addition to the OFC, which likely involves the DLPFC.
Motor Preparation.
A stimulus-based model does not necessarily mean that the representation of the action-based decision variable has to be completely absent from the brain before the stimulus-based decision is complete. A variant of the stimulus-based model may account for the observed representations of variables in the action domain (ΣWa) during decision making (Fig. 1D). In this scenario, ΣWa is not calculated from the accumulation of the Wa. Instead, the information accumulation occurs in an action-independent way (ΣWc), and the ongoing computation of ΣWc is accompanied by its transformation into ΣWa during decision making. Having ΣWa early in the decision process may serve the purpose of motor preparation.
Our results do not support this scenario. For that to be true, we should have observed the representation of ΣWc in the brain, and the representation of Wa would be unnecessary. However, we did not find evidence that either the OFC or the DLPFC neurons encoded the ΣWc during decision making. The accumulation of information happened only in the action domain in the DLPFC, and it did not arise from an intermediate stimulus-based stage in the DLPFC.
Action-Based Decision Making.
Many studies have shown that the neurons at different levels of the motor pathway may reflect the decisions in the action domain long before the decisions are made (9, 14–16, 24–26). These studies inspired the hypothesis that decision making may be implemented in the brain as an action selection process in which the values of competing actions are calculated and compared. Our findings in the DLPFC provided further evidence that the brain may compute action decisions entirely in the action domain even when the stimulus-based strategy may appear to align with our subjective experience better. This would allow actions to be executed as soon as the decisions are made, which makes sense as humans and animals in the real world need to make responses quickly to survive.
The finding of only action-based decision-making signals in the DLPFC may be due to the task design. The monkeys knew the eye movement target configuration from the trial beginning and had a strong motivation to perform the task quickly. We will find a different result if this information becomes available only after the stimulus sequence is presented, such as in several previous studies (3, 27). Nevertheless, with both the stimulus-based and action-based solutions available, our task design is fair for studying how the brain carries out decision making. By providing evidence in the stimulus domain, stimulus-based computations could happen naturally, and the brain is free to choose when and how the stimulus-to-action transition occurs. Thereby, we may study how evidence is transformed into actions in the brain, whether the transition occurs at an early or a late stage during decision making, and whether there is a stage where the decision is computed independently of motor contingencies. It is, however, reasonable to suspect that our finding is applicable only when speedy actions are desired, and the brain may take a different route otherwise.
We cannot exclude the possibility that other brain areas besides the OFC and the DLPFC may accumulate value information in the stimulus domain and carry out stimulus-based decision making. Analogous to the dichotomy of the ventral and dorsal pathways in the visual systems, the brain may also have two separate pathways for decision making (28). Several lines of evidence suggested that the ventral PFC areas contain a stimulus-based attention system (29, 30). Given the close relationship between attention and decision making, it would be interesting to find out whether the VLPFC accumulates value information in the stimulus domain in this task.
DLPFC vs. LIP.
Previous studies using a similar behavior paradigm showed that the LIP neurons also encoded the combined evidence (17, 18). The similarities between the DLPFC and the LIP were also observed in experiments using random dot motion discrimination tasks (9, 31). The present results again raise the question of the relative roles that the DLPFC and the LIP play in decision making.
Here, we reported that the DLPFC neurons encoded single weights in both the color and the action domain as well as the summed weights in the action domain. On the surface, the DLPFC by itself seems to possess all of the necessary pieces for the stimulus-to-action computation. If this is true, the decision-making signal found in the LIP may be inherited from the DLPFC. However, the choice signal that we observed in the DLPFC first reached statistical significance 1,210 ms after the first shape onset (Fig. 3B). This latency was much larger than what was found in the LIP, which was reported to be around 150 ms after the shape onset in a study that used a very similar behavior paradigm (17). The prolonged latency of the choice signal in the DLPFC would be too late to contribute to decision making. Moreover, the LIP neurons are far less heterogeneous and encode decision variables much more consistently than the DLPFC neurons. Given the extensive connections between the DLPFC and the LIP, it is entirely possible that the LIP is where the accumulation first occurs, and the DLPFC inherits the results for motor preparation. Future investigations are still needed to determine the roles that the two areas play in decision making.
Summary.
Our study explored the roles of the OFC and the DLPFC in decision making. We showed that the OFC encoded the value in a transient manner and did not accumulate information across time. Furthermore, the decisions were computed entirely in the action domain in the DLPFC, and the stimulus-to-action transition occurred before the evidence accumulation. These results, taken together, showed that the OFC and the DLPFC play distinct roles in value computation during decision making.
Methods
Subjects and Materials.
Two naive male rhesus monkeys (Macaca mulatta) were used in this study (K and E). They weighed, on average, 6 to 7 kg during the experiments. All procedures followed the protocol approved by the Animal Care Committee of Shanghai Institutes for Biological Sciences, Chinese Academy of Sciences (Shanghai, China).
In each experimental session, the monkeys were seated in a primate chair, viewing a 23.6-inch video monitor, which was placed at 60 cm distance. An infrared oculometer system (EyeLink 1000) was used to monitor the eye positions at a sampling rate of 500 Hz. Juice or water reward was given to the monkeys based on their preference. The liquid delivery was controlled by a computer-controlled solenoid. The monkeys drank ∼150 to 250 mL per experimental session.
Behavioral Task.
We trained the monkeys to perform a probabilistic reasoning task. The monkeys started each trial by fixating and maintaining their gaze on a central fixation point (FP) (0.2° in diameter) on a computer monitor. After the monkeys acquired fixation for 500 ms, a green and a red target showed up on the left and the right side of the FP at the eccentricity of 6°. Both colors could appear on either side, which was randomly selected from trial to trial. After another 500 ms, four shapes were shown sequentially near the FP. For monkey E, the center of the shapes was the same as the FP, while for monkey K, the center of the shapes was at a random location chosen from the four vertices of an invisible 1° × 1° grid centered on the FP. The shapes were white line drawings and ∼1.5° × 1.5°. Each shape was presented for 300 ms. Between two consecutive shape presentations, there was a 200-ms delay in which only the FP and the targets were on the screen. Thus, each shape epoch was 500 ms long. The FP disappeared 700 ms after the offset of the fourth shape, instructing the monkeys to report their choice. The monkeys had to make a saccadic eye movement toward one of the targets within 1 s and hold their fixation on it for another 510 ms. The juice reward would be delivered at the end of the fixation of the target.
The reward was determined probabilistically. The probabilities of getting a reward by choosing the red and the green target were
| [1] |
and
| [2] |
where represents the shape shown in the ith epoch, represents the weight assigned to and and are the reward probabilities of the red target and the green target, given the shape sequence respectively. and add up to 1. The infinitive weights with opposite signs may cancel each other. The reward probability for the red target is 1 with noncanceled +∞ shape sequences and is 0 with noncanceled −∞ shape sequences. The same weights were used for the two monkeys, although the shapes were shuffled between them.
Training.
After the monkeys learned to perform a delay saccade task, they were trained to learn a one-shape version of the probabilistic reasoning task, starting with the easiest shape pair (weight = ±∞). New shapes were added into the training once the performance of the existing shape set reached 70% (judged by whether the choice is consistent with the weight sign). The reward was given probabilistically according to each shape’s weight. Once all shapes were learned, we started to train the monkeys with two-shape sequences. This version of the task was similar to the final task, except that the shapes did not disappear until the start of the delay period. Once the monkeys’ performance reached 70%, we extended the shape sequence to three shapes and then to four shapes. At the last stage of the training, after the monkeys were able to perform the task with four shapes, we started to turn off each shape in the sequence at 300 ms after its onset. The full training took 18 mo for monkey E and 10 mo for monkey K.
Surgery.
The monkeys received a chronic implant of a titanium headpost with standard procedures before the training. After their performance reached a satisfactory level, we performed a second surgery to implant an acrylic recording chamber over the prefrontal region, inside of which a craniotomy was made. The chamber had an inner size of 19.5 × 24 mm and was centered over the left principal sulcus. All surgery procedures were done under aseptic conditions. The monkeys were sedated with ketamine hydrochloride (5 to 15 mg/kg, intramuscularly [i.m.]) and anesthetized with isoflurane gas (1.5 to 2%, to effect). Their body temperature, heart rate, blood pressure, and CO2 were monitored during the surgeries.
MRI.
Before and after the recording chamber was implanted, we scanned the monkeys with a Siemens 3T scanner to identify and verify recording locations. The monkeys were sedated with ketamine hydrochloride (5 to 15 mg/kg, i.m.) and anesthetized with isoflurane gas (1.5 to 2%, to effect) during the scanning.
Behavioral Analyses.
We computed the percentage of choosing the red target for all possible total log likelihood ratio values and fitted the psychometric curve with the least-squares method (Fig. 1B)
| [3] |
where Trials with the shapes of infinite weights were excluded. Unless otherwise mentioned, these trials were also excluded in all of the electrophysiology analyses.
To test the effects of individual shapes on the monkeys’ choices, we applied a logistic regression using individual trials, where the regressors were the appearance counts of each shape presented in each trial (Fig. 1C),
| [4] |
where and is the appearance count for the ith shape. We defined the fitted coefficients as the subjective weights. All 10 shapes were included in this analysis.
The behavior analyses were based on the same sessions of the electrophysiology recordings used in the analyses below.
Electrophysiology.
The recording procedures are described in our previous study (23). Briefly, neuronal responses were recorded using single electrodes (FHC or AlphaOmega) with an AlphaLab SnR System (AlphaOmega). Only units with reasonably isolated waveforms were recorded. Offline sorting was used to improve data quality (NeuroExplorer). Two to four single electrodes were used in each session. The microelectrodes were driven by a multichannel micromanipulator (Alpha Omega EPS).
We recorded single-unit activities from 277 cells in the OFC (121 and 156 from monkeys K and E, respectively) and 384 cells in the DLPFC (170 and 214 from monkeys K and E, respectively). According to MRI results and the neural activities observed during penetrations, the OFC recording locations were on the ventral surface of the frontal lobe between the lateral and medial orbital sulci, roughly corresponding to Walker’s areas 11 and 13 (SI Appendix, Fig. S4A). The DLPFC recordings were from both banks of the posterior portion of the principal sulcus in the Brodmann areas 9 and 46d (SI Appendix, Fig. S4B).
Example Neuron Peristimulus Time Histogram.
The firing rate of the example neurons was calculated with a 200-ms sliding window with 10-ms steps. The same setting was also used in all of the other analyses involving sliding windows. The trials were sorted into four quartiles by the variable under discussion (ΣWa in Fig. 2B and Wc in Fig. 2A) in each epoch.
Choice Analyses.
To find out how the neuronal activities in the DLPFC and OFC reflected the monkeys’ choices, we calculated the mean firing rate difference between trials of opposite choice outcomes as follows. For each neuron, we determined its spatial and color choice preference using their mean response in a 500-ms time window after the fourth shape offset (2 to 2.5 s from the first shape onset). Then, we calculated the mean firing rate difference of each region between the preferred choice condition and the nonpreferred choice condition for both the spatial and the color choice.
To determine the significance, we shuffled the choice labels in each neuron’s data and computed the population average following the same procedure. Repeating the procedure 1,000 times gave us a null distribution of mean firing rate differences, to which we compared the actual mean firing rate differences using a one-way ANOVA at every time point. The P-value threshold was 0.01, and no corrections for multiple comparisons were made. The latency of the choice signal was defined as the first time point when a significant choice signal lasted for more than 100 ms continuously.
We included all neurons regardless of the significance of their selectivity to achieve a larger statistical power. Because of how we defined the choice preference, even for the shuffled data, the difference between the preferred and the nonpreferred choices was larger than 0.
LASSO.
To alleviate the variables’ interdependency problem in simple linear regressions, we created a model using LASSO (32) that contained the single weight, the summed weight, and the choice regressors,
| [5] |
where is the firing rate of the neuron at time t; are the fitted coefficients at time t; and represent the single weight associated with the shape in the ith epoch in the color and the action domain, respectively; and and represent the summed weight in the ith epoch in the color and the action domain, respectively. Thus, and Note that and therefore we did not include in the model. and are the choice in the color (red = 1, green = 0) and the action domain (left = 1, right = 0), respectively.
While the summed weights are entirely dependent on the single weights, adding an L1-norm penalty of the coefficients in the loss function encourages the fitting algorithm to use a smaller number of regressors. Thus, the LASSO model biases toward the summed weights and against the single weights when they may both explain the data.
The LASSO model was fitted independently for each neuron at each time point. All of the vectors of regressor samples were normalized into unit vectors before model fitting. We used the built-in function of MATLAB, lasso, to fit our data. A 10-fold cross-validation procedure was used to determine the regularization parameter Specifically, we grid-searched in the log space, from 10−2 to 100.6, with the step set at 100.2. For each neuron, we found the that achieved the smallest mean-squared error for the most time bins and used it as the regularization parameter of this neuron. To verify whether some of our conclusions were due to the choice of the which may underestimate variables late in a trial, we also tested with a based on a late trial period between 1.8 and 2.5 s after the trial onset. The results were similar (SI Appendix, Fig. S9).
We cannot use ∆R2 directly as in the regression model to estimate a factor’s effect. This is because the factors we are testing are not independent. The effects explained by a removed factor may be accounted for by the other factors, and the R2 of the reduced model may stay the same. To estimate the effect size of each factor correctly, we used the absolute value of the standard regression coefficient computed with the equation
| [6] |
where is the SD of the ith regressor, and is the SD of FR(t). Intuitively, represents the proportion of variance that is contributed by a single factor.
To compare the between different neuronal populations, we followed the normalization procedure described by Cai and Padoa-Schioppa (3). An 800-ms time window before the first shape onset was used as the baseline period, in which each trial’s stimulus labels were shuffled 100 times so that the distribution for the baseline could be obtained. The mean and the variance of the distribution were then used in calculating the normalized For each neuron and each factor i, the normalized was
| [7] |
where and are the mean and the SD of respectively. Following the same procedure, we calculated the normalized population average of by further normalizing the
| [8] |
where N is the number of neurons. Thus, the normalized population has an expected value of 0 and a SD of 1 at the chance level and is comparable across different populations or brain areas.
A one-tailed t test was used to test whether the normalized population was significantly different from 0. A cluster-size–based thresholding method was used to address the multicomparison problem (33). A continuous period of is considered significant if and only if the P value computed from the t test at every time point in this period is smaller than 0.01 and the length of this period exceeds 150 ms. The two thresholds together determine the false detection rate. To determine the false detection rate, we computed a maximum null distribution by first computing the size of the largest cluster (the duration of the longest continuous “active” period) in a label-shuffled dataset and then repeating this computation 100 times. We applied the same procedure separately for each subject and for each brain area. The false detection rate was then estimated as the percentage of shuffles that had the maximum cluster size larger than 150 ms. As a result, the possibility of falsely detecting a significant cluster from the shuffled dataset was 0.05 for DLPFC data combined from both subjects and smaller than 0.01 for all of the other subjects and brain areas.
Mixed Selectivity Analysis.
We used the response variances under two target spatial configurations to quantify neurons’ asymmetric selectivity. We defined the variance difference index VDIi of neuron i as
| [9] |
where is the variance of the normalized response of neuron i to the 10 shape cues when the target configuration equals respectively.
To compute the of a neuron, we first calculated its response to each of the 10 shapes within an 800-ms time window after the shape’s onset under the respective target configuration. We normalized the responses by subtracting the minimal response and dividing them by the range
| [10] |
where is the averaged response of neuron to shape j and under configuration is the normalized response, and and are the minimum and maximum values across all combinations of shapes and configurations.
The variance of neuron i under configuration k is then computed as
| [11] |
where indicates the variance calculated across the shapes.
With we computed for each neuron with Eq. 9. A large indicates a large strong mixed selectivity. Trials with infinitive weights were excluded from this analysis.
The two-sample Kolmogorov–Smirnov test was applied to examine the significance of the difference between the DLPFC and OFC neurons’ VDI distributions and their corresponding shuffled distributions. The smooth curve reflecting the estimation of probability density was obtained by kernel density estimation (KDE). We used python package KDEpy with a Gaussian kernel and mirroring to correct the boundary bias around zero.
We computed the proportion of the neurons whose VDIs were larger than 0.2, 0.3, 0.4, 0.5, and 0.6 (SI Appendix, Fig. S17). We shuffled the spatial configurations before computing the VDIs 1,000 times to obtain the distribution of the shuffled data.
Supplementary Material
Acknowledgments
We thank Yang Xie, Zhewei Zhang, Wenyi Zhang, and Wei Kong for their help in all phases of the study and Xinying Cai for providing comments and advice. Funding for this work was provided by the National Natural Science Foundation of China (Grant 31771179), the Shanghai Municipal Science and Technology Major Project (Grant 2018SHZDZX05), and the Strategic Priority Research Program of the Chinese Academy of Science (Grant XDB32070100).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2019077117/-/DCSupplemental.
Data Availability.
The sorted spike train and neural data have been deposited in Mendeley: https://data.mendeley.com/datasets/pxjkztdhvr/1.
References
- 1.Wallis J. D., Miller E. K., Neuronal activity in primate dorsolateral and orbital prefrontal cortex during performance of a reward preference task. Eur. J. Neurosci. 18, 2069–2081 (2003). [DOI] [PubMed] [Google Scholar]
- 2.Chen X., Stuphorn V., Sequential selection of economic good and action in medial frontal cortex of macaques during value-based decisions. eLife 4, e09418 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cai X., Padoa-Schioppa C., Contributions of orbitofrontal and lateral prefrontal cortices to economic choice and the good-to-action transformation. Neuron 81, 1140–1151 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Padoa-Schioppa C., Assad J. A., Neurons in the orbitofrontal cortex encode economic value. Nature 441, 223–226 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Padoa-Schioppa C., Orbitofrontal cortex and the computation of economic value. Ann. N. Y. Acad. Sci. 1121, 232–253 (2007). [DOI] [PubMed] [Google Scholar]
- 6.Padoa-Schioppa C., Conen K. E., Orbitofrontal cortex: A neural circuit for economic decisions. Neuron 96, 736–754 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ballesta S., Padoa-Schioppa C., Economic decisions through circuit inhibition. Curr. Biol. 29, 3814–3824.e5 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rudebeck P. H., et al. , Frontal cortex subregions play distinct roles in choices between actions and stimuli. J. Neurosci. 28, 13775–13785 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kim J.-N., Shadlen M. N., Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat. Neurosci. 2, 176–185 (1999). [DOI] [PubMed] [Google Scholar]
- 10.Kennerley S. W., Wallis J. D., Evaluating choices by single neurons in the frontal lobe: Outcome value encoded across multiple decision variables. Eur. J. Neurosci. 29, 2061–2073 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wallis J. D., Orbitofrontal cortex and its contribution to decision-making. Annu. Rev. Neurosci. 30, 31–56 (2007). [DOI] [PubMed] [Google Scholar]
- 12.Raghuraman A. P., Padoa-Schioppa C., Integration of multiple determinants in the neuronal computation of economic values. J. Neurosci. 34, 11583–11603 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kennerley S. W., Behrens T. E. J., Wallis J. D., Double dissociation of value computations in orbitofrontal and anterior cingulate neurons. Nat. Neurosci. 14, 1581–1589 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shadlen M. N., Newsome W. T., Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol. 86, 1916–1936 (2001). [DOI] [PubMed] [Google Scholar]
- 15.Hernández A., Zainos A., Romo R., Temporal evolution of a decision-making process in medial premotor cortex. Neuron 33, 959–972 (2002). [DOI] [PubMed] [Google Scholar]
- 16.Gold J. I., Shadlen M. N., Representation of a perceptual decision in developing oculomotor commands. Nature 404, 390–394 (2000). [DOI] [PubMed] [Google Scholar]
- 17.Yang T., Shadlen M. N., Probabilistic reasoning by neurons. Nature 447, 1075–1080 (2007). [DOI] [PubMed] [Google Scholar]
- 18.Kira S., Yang T., Shadlen M. N. N., A neural implementation of Wald’s sequential probability ratio test. Neuron 85, 861–873 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rigotti M., et al. , The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nomoto K., Schultz W., Watanabe T., Sakagami M., Temporally extended dopamine responses to perceptually demanding reward-predictive stimuli. J. Neurosci. 30, 10692–10702 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen M. Y., Jimura K., White C. N., Maddox W. T., Poldrack R. A., Multiple brain networks contribute to the acquisition of bias in perceptual decision-making. Front. Neurosci. 9, 63 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rich E. L., Wallis J. D., Decoding subjective decisions from orbitofrontal cortex. Nat. Neurosci. 19, 973–980 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Xie Y., Nie C., Yang T., Covert shift of attention modulates the value encoding in the orbitofrontal cortex. eLife 7, e31507 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cisek P., Kalaska J. F., Neural correlates of reaching decisions in dorsal premotor cortex: Specification of multiple direction choices and final selection of action. Neuron 45, 801–814 (2005). [DOI] [PubMed] [Google Scholar]
- 25.Basso M. A., Wurtz R. H., Modulation of neuronal activity in superior colliculus by changes in target probability. J. Neurosci. 18, 7519–7534 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Romo R., Hernández A., Zainos A., Neuronal correlates of a perceptual decision in ventral premotor cortex. Neuron 41, 165–173 (2004). [DOI] [PubMed] [Google Scholar]
- 27.Bennur S., Gold J. I., Distinct representations of a perceptual decision and the associated oculomotor plan in the monkey lateral intraparietal area. J. Neurosci. 31, 913–921 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rushworth M. F. S., Kolling N., Sallet J., Mars R. B., Valuation and decision-making in frontal cortex: One or many serial or parallel systems? Curr. Opin. Neurobiol. 22, 946–955 (2012). [DOI] [PubMed] [Google Scholar]
- 29.Wardak C., Vanduffel W., Orban G. A., Searching for a salient target involves frontal regions. Cereb. Cortex 20, 2464–2477 (2010). [DOI] [PubMed] [Google Scholar]
- 30.Bichot N. P., Heard M. T., DeGennaro E. M., Desimone R., A source for feature-based attention in the prefrontal cortex. Neuron 88, 832–844 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Roitman J. D., Shadlen M. N., Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci. 22, 9475–9489 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tibshirani R., Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 58, 267–288 (1996). [Google Scholar]
- 33.Nichols T., Holmes A., Nonparametric permutation tests for functional neuroimaging. Hum. Brain Mapp. 15, 1–25 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The sorted spike train and neural data have been deposited in Mendeley: https://data.mendeley.com/datasets/pxjkztdhvr/1.