Theoretical issues in deep networks

Abstract

While deep learning is successful in a number of applications, it is not yet well understood theoretically. A theoretical characterization of deep learning should answer questions about their approximation power, the dynamics of optimization, and good out-of-sample performance, despite overparameterization and the absence of explicit regularization. We review our recent results toward this goal. In approximation theory both shallow and deep networks are known to approximate any continuous functions at an exponential cost. However, we proved that for certain types of compositional functions, deep networks of the convolutional type (even without weight sharing) can avoid the curse of dimensionality. In characterizing minimization of the empirical exponential loss we consider the gradient flow of the weight directions rather than the weights themselves, since the relevant function underlying classification corresponds to normalized networks. The dynamics of normalized weights turn out to be equivalent to those of the constrained problem of minimizing the loss subject to a unit norm constraint. In particular, the dynamics of typical gradient descent have the same critical points as the constrained problem. Thus there is implicit regularization in training deep networks under exponential-type loss functions during gradient flow. As a consequence, the critical points correspond to minimum norm infima of the loss. This result is especially relevant because it has been recently shown that, for overparameterized models, selection of a minimum norm solution optimizes cross-validation leave-one-out stability and thereby the expected error. Thus our results imply that gradient descent in deep networks minimize the expected error.

1. Introduction

A satisfactory theoretical characterization of deep learning should begin by addressing several questions that are natural in the area of machine-learning techniques based on empirical risk minimization (see for instance refs. 1 and 2). They include issues such as the approximation power of deep networks, the dynamics of the empirical risk minimization by gradient flow, and the generalization properties of gradient descent techniques—Why does the expected error not suffer, despite the absence of explicit regularization, when the networks are overparameterized? In this paper we review briefly our work on approximation and describe recent results in characterizing complexity control in training deep networks. The first part, about approximation power of deep versus shallow architectures, is a brief summary of our main results described in published papers (3) and references there. The second part describes a recent characterization (details in ref. 4 with a short announcement in ref. 5) of the optimization process used to train deep networks and in particular of the properties of the dynamical system corresponding to the gradient flow, which is the continuous equivalent of the gradient descent algorithms in common use (we study gradient flow and leave to others the extension to gradient descent). One of these results, about the equivalence of constrained and unconstrained optimization, implies a classical form of complexity control by gradient descent with respect to the exponential loss.

2. Approximation

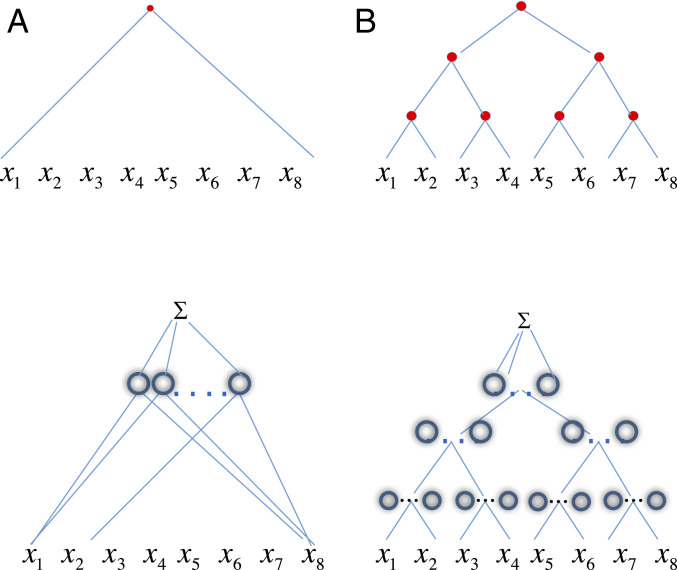
We start with the first set of questions, summarizing results in refs. 3 and 6–9. The main result is that deep networks have the theoretical guarantee, which shallow networks do not have, that they can avoid the curse of dimensionality for an important class of problems, corresponding to a certain type of compositional functions, that is, functions of functions. An especially interesting subset of compositional functions is the ones that can be written as hierarchically local compositional functions where all of the constituent functions are local—in the sense of bounded small dimensionality. The deep networks that can approximate them without the curse of dimensionality are of the deep convolutional type as shown in Fig. 1—although, importantly, weight sharing is not necessary.

Fig. 1.

Top graphs are associated to functions. Each Bottom diagram (Insets) depicts the ideal network approximating the function above. (Inset A) A shallow universal network in 8 variables and $N$ units approximates a generic function of 8 variables $f\left(x_1,\dots ,x_8\right)$. (Inset B) A hierarchical network at the bottom in $n=8$ variables, which approximates well functions of the form $f\left(x_1,\dots ,x_8\right)=h_3\left(h_{21}\left(h_{11}\left(x_1,x_2\right),h_{12}\left(x_3,x_4\right)\right),h_{22}\left(h_{13}\left(x_5,x_6\right),h_{14}\left(x_7,x_8\right)\right)\right)$ as represented by the binary graph above. In the approximating network each of the $n-1$ nodes in the graph of the function corresponds to a set of ReLU units. Similar to the shallow network, a hierarchical network is universal; that is, it can approximate any continuous function; the text discusses how it can approximate a subclass of compositional functions exponentially better than a shallow network. Redrawn from ref. 23.

Implications of results likely to be relevant in practice are 1) deep convolutional architectures have the theoretical guarantee that they can be much better than one-layer architectures such as kernel machines for certain classes of problems, 2) the problems for which certain deep networks are guaranteed to avoid the curse of dimensionality (see for a nice review ref. 10) correspond to input–output mappings that are compositional with local constituent functions, and 3) the key aspect of convolutional networks that can give them an exponential advantage is not weight sharing but locality at each level of the hierarchy.

A. Related Work.

Several papers in the 1980s focused on the approximation power and learning properties of one-hidden-layer networks (called shallow networks here). Very little appeared on multilayer networks (but see refs. 11–15). By now, many publications (for instance refs. 16–18) characterize approximation properties of generic multilayer networks. Much interest has focused on separation results, that is, on the fact that specific functions cannot be represented efficiently by shallow networks (19) (see also refs. 14, 20, and 21). An interesting review of approximation of univariate functions by deep rectified linear unit (ReLU) networks has recently appeared (22). Unlike all these papers, we focus on the approximation by deep networks of certain important classes of multivariate functions which avoid the curse of dimensionality. We think that our results are especially interesting because they represent a potential explanation for one of the greatest puzzles that has emerged from the field of deep learning, that is, the unreasonable effectiveness of convolutional deep networks in a number of sensory problems.

B. Shallow and Deep Networks.

The general paradigm is as follows. We are interested in determining how complex a network, denoted as a function $f\left(x\right)$, ought to be to theoretically guarantee approximation of an unknown target function $g$ up to a given accuracy $ϵ>0$. In particular, this section characterizes conditions under which deep networks are “better” than shallow networks in approximating functions. Both types of networks use the same small set of operations—dot products, linear combinations, a fixed nonlinear function of one variable, possibly convolution, and pooling. Each node in the networks corresponds to a node in the graph of the function to be approximated, as shown in Fig. 1.

We define a deep network with $K$ layers with the usual coordinate-wise scalar activation functions $\sigma \left(z\right):\hspace{1em}\mathbf{R}\to \mathbf{R}$ as the set of functions $f\left(W;x\right)=\sigma \left(W^K\sigma \left(W^{K-1}\cdots \sigma \left(W^{1}x\right)\right)\right)$, where the input is $x\in {\mathbf{R}}^d$, and the weights are given by the matrices $W^k$, one per layer, with matching dimensions. We sometime use the symbol $W$ as a shorthand for the set of $W^k$ matrices $k=1,\dots ,K$. There are no bias terms: The bias is instantiated in the input layer by one of the input dimensions being a constant. A shallow network is a deep network with $K=1$.

We approximate functions with networks in which the activation nonlinearity is a ReLU, given by $\sigma \left(x\right)=x_{+}=max\left(0,x\right)$. The architecture of the deep networks reflects the function graph, with each node $h_i$ being a ridge function, comprising one or more neurons.

Note that in our main example (Fig. 1) of a network corresponding to a function with a binary tree graph, the resulting architecture is an idealized version of deep convolutional neural networks described in the literature. In particular, it has only one output at the top unlike most of the deep architectures with many channels and many top-level outputs. Correspondingly, each node computes a single value instead of multiple channels, using the combination of several units. However, our results hold also for these more complex networks (see corollary 4 in ref. 21).

The sequence of results is as follows:

• Both shallow (Fig. 1, Inset A) and deep (Fig. 1, Inset B) networks are universal; that is, they can approximate arbitrarily well any continuous function of $n$ variables on a compact domain. The result for shallow networks is classical.

• We consider a special class of functions of $n$ variables on a compact domain that are hierarchical compositions of local functions, such as $g\left(x_1,\dots ,x_8\right)=h_3\left(h_{21}\left(h_{11}\left(x_1,x_2\right),h_{12}\left(x_3,x_4\right)\right),h_{22}\left(h_{13}\left(x_5,x_6\right),h_{14}\left(x_7,x_8\right)\right)\right)$.

• The structure of the function in Fig. 1B is represented by a graph of the binary tree type, reflecting dimensionality $d=2$ for the constituent functions $h$. In general, $d$ is arbitrary but fixed and independent of the dimensionality $n$ of the function $g$. Ref. 21 formalizes the more general compositional case using directed acyclic graphs.

• The approximation of functions with such a specific compositional structure can be achieved with the same degree of accuracy by deep and shallow networks but the number of parameters is in general much lower for the deep networks than for the shallow network for the same approximation accuracy.

The two main theorems (3) are one about shallow networks (originally due to ref. 24) and the second one about deep networks with smooth activation function (7–9). They can be condensed in the following informal statement, where complexity is measured in terms of number $N$ of units:

Theorem 1 (Informal).

For a continuous target function $g\left(x\right)$ with $x\in {\mathbb{R}}^n$ the complexity of a shallow network that provides accuracy at least $ϵ$ is $\mathcal{O}\left({ϵ}^{-n}\right)$. If $g\left(x\right)$ has a graph representation in terms of a binary tree, consider a deep network with the same compositional architecture and with an activation function $\sigma :\mathbb{R}\to \mathbb{R}$ which is infinitely differentiable and not a polynomial. Then the complexity of the network to provide approximation with accuracy at least $ϵ$ is $\mathcal{O}\left(\left(n-1\right){ϵ}^{-2}\right)$.

The exponential dependence of the number of parameters required for an accuracy $\mathcal{O}\left(ϵ\right)$ on the dimension $n$ is known as the curse of dimensionality. The precise statement of the result in ref. 3 shows that the curse of dimensionality can be reduced by smoothness of the target functions. Of course, the binary tree case of the theorem is the simplest case: The extension to more complex trees is obvious.

The result of Theorem 1 can be extended to nonsmooth ReLU for the case of deep networks in a number of ways, one of which, suggested by Mhaskar (25), is as follows. The first step is to recall theorem 3.2 in ref. 25 that applies to smooth activation functions such as the “square” of the ReLU, that is, the function $x_{+}^2$ defined as $=x^2$ if $x\ge 0$ and otherwise $=0$. Loosely speaking, theorem 3.2 implies that for such activation functions deep networks with a sufficient number of neurons and layers can approximate continuous functions as well as free knots splines. The second step is to use theorem 1 in ref. 26 on approximating ${\left(x_{+}\right)}^2$ with ReLU networks.

The intuition of why hierarchical compositional functions can be approximated by deep networks without incurring the curse of dimensionality can be best explained in the following way.

Consider the space of polynomials, which is of course a smaller space than spaces of Sobolev functions, but which can approximate arbitrarily well continuous functions. Let us call $P_k^n$ the linear space of polynomials of degree at most $k$ in $n$ variables and $T_k^n$ the subset of the space $P_k^n$ which consists of compositional polynomials with a binary tree graph and constituent polynomial functions of degree $k$ (in two variables). Then the following theorems hold (3):

Theorem 2.

Let $\sigma :\mathbb{R}\to \mathbb{R}$ be infinitely differentiable and not a polynomial. Every $g\in P_k^n$ can be realized with an arbitrary accuracy by a shallow network with $r$ units, $r=\left(\genfrac{}{}{0.0pt}{}{n+k}{k}\right)\approx k^n$.

Theorem 3.

Let $\sigma :\mathbb{R}\to \mathbb{R}$ be infinitely differentiable and not a polynomial. Let $n=2^{\ell }$. Then $f\in T_k^n$ can be realized by a deep network with a binary tree graph and a total of $r$ units with $r=\left(n-1\right)\left(\genfrac{}{}{0.0pt}{}{2+k}{2}\right)\approx \left(n-1\right)k^2$.

Theorems 2 and 3 make clear that a hierarchical compositional polynomial corresponding to a binary graph is a very sparse polynomial—among the polynomials of the same degree in the same number of variables. It is possible to show (3) that this intuition extends from polynomials to Sobolev functions. Of course the target function graph in Fig. 1, Top Right is just one of the directed acyclic graphs (DAGs) (23) that can describe different forms of compositionality. Prior knowledge of the DAG underlying a learning problem can be exploited to a great advantage by an appropriate deep-learning architecture.

3. Optimization and Complexity Control

It has been known for a long time that the key to predictivity in machine learning is controlling the complexity of the network and not simply the raw number of its parameters. This is usually done during optimization by imposing a constraint, often under the form of a regularization penalty, on the norm of the weights, since relevant complexity measures, such as the Rademacher complexity, depend on it. The problem is that there is no obvious control of complexity in the training of deep networks!

Recent results by ref. 27 illuminate the apparent absence of “overfitting” in the special case of linear networks for binary classification. They prove that minimization of loss functions such as the logistic, the cross-entropy, and the exponential loss yields asymptotic convergence to the maximum margin solution for linearly separable datasets, independently of the initial conditions and without explicit regularization. Here we discuss the case of nonlinear multilayer deep neural networks (DNNs) under exponential-type losses (Fig. 2). We first outline related work. We then describe our main results, summarized in Theorem 4 (4, 28).

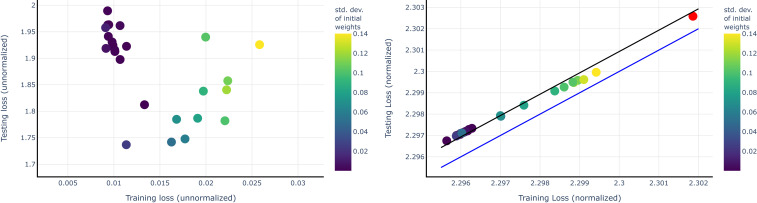
Fig. 2.

Empirical evidence of a small generalization gap by normalized networks with respect to the cross-entropy loss. Left graph shows testing vs. training cross-entropy loss for networks each trained on the same datasets (CIFAR-10) (46) but with different initializations, yielding zero classification error on the training set but different testing errors. Right graph shows the same data, that is, testing vs. training loss for the same networks, now normalized by dividing each weight by the Frobenius norm of its layer. Note that all points have zero classification error at training. The red circle on the top right refers to a network trained on the same CIFAR-10 dataset but with randomized labels. It shows zero classification error at training and test error at chance level. The top line is a square-loss regression of slope 1 with positive intercept. The bottom line is the diagonal at which training and test loss are equal. The networks are three-layer convolutional networks. Left graph can be considered as a visualization of generalization bounds when the Rademacher complexity is not controlled. Right graph is a visualization of the same relation for normalized networks that is $L\left(\rho f\left(V;x\right)\right)\le \widehat{L}\left(\rho f\left(V;x\right)\right)+c_1\rho {\mathbb{R}}_N\left(\stackrel{\sim }{\mathbb{F}}\right)+c_2\sqrt{\ln \left(\frac{1}{\delta }\right)/2N}$ for $\rho =1$. Under our conditions for $N$ and for the architecture of the network the terms $c_1{\mathbb{R}}_N\left(\stackrel{\sim }{\mathbb{F}}\right)+c_2\sqrt{\ln \left(\frac{1}{\delta }\right)/2N}$ represent a small offset. Note that the exponential loss is not a better proxy for the classification loss for large $\rho$. Empirically for these datasets, the test exponential loss with $\rho =1$ provides a ranking that approximately agrees with the test classification ranking. From ref. 35.

A. Related Work

A number of papers have studied gradient descent for deep networks (29–31). Close to the approach of refs. 4 and 28 reviewed here is ref. 32. Its authors study generalization assuming a regularizer because they are—like us—interested in normalized margin. Unlike their assumption of an explicit regularization, we show here that commonly used techniques, such as weight and batch normalization, in fact minimize the surrogate loss margin while controlling the complexity of the classifier without the need to add a regularizer or to use weight decay. Two very recent papers (33, 34) develop an elegant margin maximization-based approach which leads to some of the same results of this section (and others). Our goal here is to review where the complexity control is hiding in the training of deep networks under exponential-type loss functions and how it leads to the selection by gradient descent of minimum norm solutions.

B. The Dynamics of Optimization.

We begin by some notation and basic properties that we need in this optimization section.

We consider, for simplicity, the case in which $f$ takes scalar values, implying that the last layer matrix $W^K$ has size $1\times h_{K-1}$, where $h_k$ denotes the size of layer $k$. The weights of hidden layer $k$ have size $h_k\times h_{k-1}$. In the case of binary classification which we consider here the labels are $y\in \left\{-\mathrm{1,1}\right\}$. The activation function in this section is the ReLU activation.

For ReLU activations the following important positive one-homogeneity property holds: $\forall z,\forall a\ge 0,\sigma \left(\alpha z\right)=\alpha \sigma \left(z\right)$. Thus, $\sigma \left(z\right)=\frac{\partial \sigma \left(z\right)}{\partial z}z$. A consequence of one-homogeneity is a structural lemma (lemma 2.1 of ref. 36, closely related to Euler’s theorem for homogeneous functions) ${\sum }_{i,j}{W}_k^{i,j}\left(\frac{\partial f\left(W;x\right)}{\partial W_k^{i,j}}\right)=f\left(W;x\right)$, where $W_k$ is here the vectorized representation of the weight matrices $W_k$ for layer $k$.

For the network, homogeneity of the ReLU implies $f\left(W;x\right)={\prod }_{k=1}^K{\rho }_{k}f\left(V_1,\dots ,V_K;x\right)$, where $W_k={\rho }_k{V}_k$ with the matrix norm ${\Vert V_k\Vert }_p=1$. Note that $\frac{\partial f\left(W;x\right)}{\partial {\rho }_k}=\frac{\rho }{{\rho }_k}f\left(V;x\right)$ and that the definitions of ${\rho }_k$ and $V_k$ all depend on the choice of the norm used in normalization.

We will assume that for some $t>T_0$ the gradient flow converges to an $f$ that separates the data; that is, $f\left(x_n\right)y_n>0\hspace{0.17em}\forall n=1,\dots ,N$. The assumption of separability, which is very strong in the case of linear networks, is much weaker in the case of overparameterized deep networks that typically can “fit the training set”; that is, they can separate the training data after a relatively small number of gradient descent iterations.

We conjecture that the hypothesis of smooth activations we use here is a technicality due to the necessary conditions for existence and uniqueness of solutions to ordinary differential equations (ODEs). Generalizing to differential inclusions and nonsmooth dynamical systems should allow for these conditions to be satisfied in the Filippov sense (37). The Clarke subdifferential is supposed to deal appropriately with functions such as ReLU (34).

The standard approach to training deep networks is to use stochastic gradient descent to find the weights $W_k$ that minimize the empirical exponential loss $L=\frac{1}{N}{\sum }_n{e}^{-y_{n}f\left(x_n\right)}$ by computing

$$\stackrel{\cdot }{W_k}=-\frac{\partial L}{\partial W_k}=\frac{1}{N}\sum _{n=1}^N{y}_n\frac{\partial f\left(W;x_n\right)}{\partial W_k}{e}^{-y_{n}f\left(W;x_n\right)}$$ [1]

on a given dataset $\left\{x_n,y_n\right\}\hspace{1em}\forall n=1,\dots ,N$ with $y$ binary. Since the goal is binary classification, we are interested in $f\left(V;x\right)$ (remember $signf\left(V;x\right)=signf\left(W;x\right)$). We want to study the dynamics of $f\left(V;x\right)$ implied by Eq. 1. With this goal we study three related versions of this problem:

• 1)Minimization of $L=\frac{1}{N}{\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}$ under the constraint $\Vert V_k\Vert =1$ with respect to (wrt) $V_k$ for fixed $\rho$;
• 2)Minimization of $L=\frac{1}{N}{\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}$ under the constraint $\Vert V_k\Vert =1$ wrt $V_k$ and $\rho$;
• 3)Minimization of $L\hspace{0.17em}=\hspace{0.17em}\frac{1}{N}{\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}\hspace{0.17em}=\hspace{0.17em}\frac{1}{N}{\sum }_n{e}^{-y_{n}f\left(W;x_n\right)}$ wrt $V_k,\rho$, which is equivalent to typical training, Eq. 1.

B.1. Constrained minimization.

Constrained optimization of the exponential loss, using Lagrange multipliers, minimizes $L=\frac{1}{N}{\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}$ under the constraint $\Vert V_k\Vert =1$ which leads us to minimize

$$\mathcal{L}=\frac{1}{N}\sum _n{e}^{-\rho y_{n}f\left(V;x_n\right)}+\sum _k{\lambda }_k{\Vert V_k\Vert }^2$$ [2]

with ${\lambda }_k$ such that the constraint $\Vert V_k\Vert =1$ is satisfied. We note that this would be the natural approach for training deep networks while controlling complexity—based on classical generalization bounds (4).

B.2. Fixed $\rho$: minima.

Gradient descent on $\mathcal{L}$ for fixed $\rho$ wrt $V_k$ yields then the dynamical system

$$\stackrel{\cdot }{V_k}=\rho \frac{1}{N}\sum _n{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_n\left(\frac{\partial f\left(V;x_n\right)}{\partial V_k}-V_{k}f\left(V;x_n\right)\right)$$ [3]

because ${\lambda }_k=\frac{1}{2}\rho \frac{1}{N}{\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_{n}f\left(V;x_n\right)$, since $V_k^T\stackrel{\cdot }{V_k}=0$, which in turn follows from ${\Vert V_k\Vert }^2=1$.

Since for fixed $\rho$ the domain is compact, some of the stationary points $\stackrel{\cdot }{V_k}=0$ of the constrained optimization problem must correspond to one or more minima. Assuming data separation is achieved (that is, $y_{n}f\left(V;x_n\right)>0\hspace{1em}\forall n$), they satisfy

$$\sum _n{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_n\frac{\partial f\left(V;x_n\right)}{\partial V_k}=\sum _n{e}^{-\rho y_{n}f\left(V;x_n\right)}{V}_k{y}_{n}f\left(V;x_n\right).$$ [4]

Of course the infimum of the exponential loss $L$ is zero only for the limit $\rho =\infty$; for any finite $\rho$ the minimum of $L$ is at the boundary of the compact domain. For any finite, sufficiently large $\rho$ the minimum is the critical point of the gradient with a positive semidefinite Hessian. In general it is not unique; it is unique in the case of one-hidden-layer linear networks.

B.3. $\rho \to \infty$ has the same stationary points as the full dynamical system.

Consider the limit of $\rho \to \infty$ in Eq. 4. The asymptotic stationary points of the flow of $V_k$ then satisfy

$$\sum _n{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_n\left(\frac{\partial f\left(V;x_n\right)}{\partial V_k}-V_{k}f\left(V;x_n\right)\right)=0$$ [5]

also in the limit $\underset{\rho \to \infty }{lim}$, that is, for any large $\rho$. So the stationary $V_k$ points for any large $\rho =R$ satisfy Eq. 5 with $\rho =R$.

Consider now gradient descent for the full system obtained with Lagrange multipliers, that is, on $\mathcal{L}={\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}+{\sum }_k{\lambda }_k{\Vert V_k\Vert }^2$ wrt $V_k$ and ${\rho }_k$, with ${\lambda }_k$ chosen (as before) to implement the unit norm constraint. The full gradient dynamical system is

$$\stackrel{\cdot }{{\rho }_k}=\frac{\rho }{{\rho }_k}\frac{1}{N}\sum _n{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_{n}f\left(V;x_n\right)$$ [6]

$$\stackrel{\cdot }{V_k}=\rho \frac{1}{N}\sum _n{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_n\left(\frac{\partial f\left(V;x_n\right)}{\partial V_k}-V_{k}f\left(V;x_n\right)\right).$$ [7]

Observe that after onset of separability $\stackrel{\cdot }{{\rho }_k}>0$ with $\underset{t\to \infty }{lim}\stackrel{\cdot }{{\rho }_k}=0$, $\underset{t\to \infty }{lim}\rho \left(t\right)=\infty$ (for one layer $\rho \propto \log t$) (4). Thus $\rho \left(t\right)$ is a monotonically increasing function from $t_0$ to $t=\infty$. Furthermore, ${\rho }_k$ grows at a rate which is independent of the layer $k$ (4). In fact, Eq. 1 via the relation $\stackrel{\cdot }{\Vert W_k\Vert }=\frac{\partial \Vert W_k\Vert }{\partial W_k}\frac{\partial W_k}{\partial t}=\frac{W_k}{\Vert W_k\Vert }\stackrel{\cdot }{W_k}$ implies $\stackrel{\cdot }{{\Vert W_k\Vert }^2}=2{\sum }_{n=1}^N{y}_{n}f\left(W;x_n\right)e^{-y_{n}f\left(W;x_n\right)}$, which shows that the rate of growth of ${\Vert W_k\Vert }^2$ is independent of $k$. This observation (38) is summarized as follows:

Lemma 1.

During gradient descent, the rate of change of the squares of the Frobenius norms of the weights is the same for each layer; that is, $\frac{\partial {\rho }_k^2}{\partial t}=2\frac{1}{N}{\sum }_{n=1}^N\rho y_{n}f\left(V;x_n\right)e^{-\rho y_{n}f\left(V;x_n\right)}$.

Because $\rho \left(t\right)$ grows monotonically in $t$, there exists $T$ such that $\rho \left(T\right)=R$. At time $T$ then, the condition for a stationary point of $V_k$ in Eq. 7 coincides with Eq. 5. This leads to the following:

Lemma 2.

The full dynamical system 7 in the limit of $t\to \infty$ converges to the same limit to which the dynamical system 3 converges for $\rho \to \infty$, in the sense of having the same sets of stationary points.

B.4. Asymptotic stationary points coincide with maximum margin.

Here we show that the limit for the two systems exists, is not trivial, and corresponds to maximum margin/minimum norm solutions. We start from Eq. 5. Without loss of generality let us assume that the training data $f\left(V;x_n\right)$ are ranked at $t=T_0$ according to increasing normalized margin; that is, $f\left(V;x_1\right)\le f\left(V;x_2\right)\le \cdots \le f\left(V;x_N\right)$. Let us call $B_k\left(V;x_n\right)=y_n\left(\frac{\partial f\left(V;x_n\right)}{\partial V_k}-V_{k}f\left(V;x_n\right)\right)$. Then the equilibrium condition of Eq. 5 becomes

$$\begin{array}{cc}\hfill & \sum _n^N{e}^{-\rho \left(T_0\right)y_{n}f\left(V;x_n\right)}{B}_k\left(V;x_n\right)\hfill \\ \hfill & \hspace{1em}=e^{-R{y}_{1}f\left(V;x_1\right)}\left(B_1+B_2{e}^{-R{\mathrm{\Delta }}_2}+\cdots +B_N{e}^{-R{\mathrm{\Delta }}_N}\right)=0,\hfill \end{array}$$ [8]

where ${\mathrm{\Delta }}_1=y_{1}f\left(V;x_1\right)-y_{1}f\left(V;x_1\right)=0$, ${\mathrm{\Delta }}_2=y_{2}f\left(V;x_n\right)-y_{1}f\left(V;x_1\right)\ge 0$, ${\mathrm{\Delta }}_3=y_{3}f\left(V;x_n\right)-y_{1}f\left(V;x_1\right)\ge 0$, and all ${\mathrm{\Delta }}_n\ge 0$ increase with $n$. Eq. 8 can be rewritten then as

$$e^{-\rho \left(T_0\right)y_{1}f\left(V;x_1\right)}\left({\alpha }_1{B}_1+{\alpha }_2{B}_2+\cdots +{\alpha }_N{B}_N\right)=0,$$ [9]

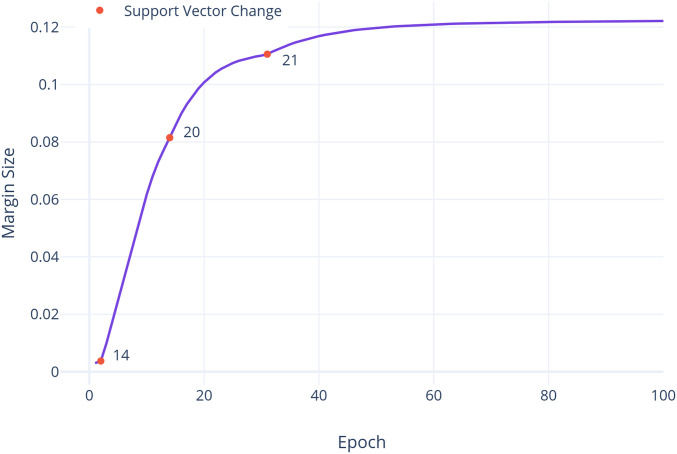
where the ${\alpha }_n$ are all positive (${\alpha }_1=1$) and decreasing with $n$. The left-hand side of the stationary point equation has the form $ϵ\left(B_1+{ϵ}^{\prime }B\right)=0$, with $B={\sum }_{n=2}^N{\alpha }_n{B}_n$, with both $ϵ$ and ${ϵ}^{\prime }$ going to zero for $T_0\to \infty$. Thus $\underset{T_0\to \infty }{lim}ϵ\left(B_1+{ϵ}^{\prime }B\right)=\underset{T_0\to \infty }{lim}ϵB_1=0$ can be satisfied for sufficiently large $T_0$ by $B_1=0$, that is, by $\frac{\partial f\left(V;x_1\right)}{\partial V_k}-V_{k}f\left(V;x_1\right)=0$. This is the condition in which the stationary point corresponding to $x_1$ provides the maximum, or more precisely, supremum of the margin. Before that limit is reached, the solution $V_k$ changes with increasing $\rho \left(t\right)$. Thus the asymptotic stationary points coincide with maximum margin. The following lemma (4) shows that the margin is increasing with $t$, after separability is reached and after a single support vector dominates (Fig. 3):

Fig. 3.

Monotonic increase of the margin: the growth of the margin ${\text{min}}_n{y}_{n}f\left(V;x_n\right)$ in the binary case. The network converges to 100% training accuracy in epoch 3 and changes the support vectors three times (red circles—the numbers above them correspond to the index of the datapoint that becomes the support vector) before stabilizing. As predicted by theory, the margin is nondecreasing. As the support vectors change, note that the rate of margin growth accelerates.

Lemma 3.

There exists a $\rho \left(T_{*}\right)$ such that for $\rho >\rho \left(T_{*}\right)$ the sum ${\sum }_{n=1}^N{e}^{-\rho y_{n}f\left(V;x_n\right)}\propto e^{-\rho y_{1}f\left(V;x_1\right)}$. For $\rho >\rho \left(T_{*}\right)$ then the margin increases $y_1\frac{\partial f\left(V;x_1\right)}{\partial t}\ge 0$ (even if $\rho$ is kept fixed).

Proof:

$y_{1}f\left(V;x_1\right)$ increases monotonically or is constant because

$$\begin{array}{cc}\hfill & y_{*}\frac{\partial f\left(V;x_1\right)}{\partial t}=\sum _k{\left(\frac{\partial y_{1}f\left(V;x_1\right)}{\partial V_k}\right)}^T\stackrel{\cdot }{V_k}\hfill \\ \hfill & \hspace{1em}=\sum _k\frac{\rho }{{\rho }_k^2}{e}^{-\rho y_{1}f\left(V;x_1\right)}\left({‖\frac{\partial f\left(V;x_1\right)}{\partial V_k}‖}_F^2-{f\left(V;x_1\right)}^2\right).\hfill \end{array}$$ [10]

Eq. 10 implies $\frac{\partial y_{1}f\left(V,x_1\right)}{\partial t}\ge 0$ because ${\Vert f\left(V;x_1\right)\Vert }_F={\Vert V_k^T\frac{\partial f\left(V;x_1\right)}{\partial V_k}\Vert }_F\le {\Vert \frac{\partial f\left(V;x_1\right)}{\partial V_k}\Vert }_F$, since the Frobenius norm is submultiplicative and $V_k$ has unit norm.

We finally note that the maximum margin solution in terms of $f\left(V;x\right)$ and $V_k$ is equivalent to a minimum norm solution in terms of $W_k$ under the condition of the margin being at least 1. This is stated in the following lemma (4):

Lemma 4.

The maximum margin problem

$$\underset{W_K,\dots ,W_1}{max}\underset{n}{min}{y}_{n}f\left(W;x_n\right),\hspace{1em}\mathit{subj.to}\hspace{1em}\Vert W_k\Vert =1,\hspace{1em}\forall k$$ [11]

is equivalent to

$$\underset{W_k}{min}\frac{1}{2}{\Vert W_k\Vert }^2,\hspace{0.17em}\mathit{subj.to}\hspace{0.17em}{y}_{n}f\left(W;x_n\right)\ge 1,\hspace{1em}\forall k,\hspace{0.17em}n=1,\dots ,N.$$ [12]

B.5. Unconstrained gradient descent for deep networks: implicit norm control.

Empirically it appears that gradient descent (GD) and stochastic gradient descent (SGD) converge to solutions that can generalize even without any explicit capacity control such as a regularization term or a constraint on the norm of the weights. How is this possible? The answer is provided by the fact—trivial or surprising—that the unit vector $\frac{W\left(T\right)}{{\Vert W\left(T\right)\Vert }_2}$ computed from the solution $W\left(T\right)$ of gradient descent $\stackrel{\cdot }{W}=-{\nabla }_{W}L$ at time $T$ is the same, irrespective of whether the constraint ${\Vert V\Vert }_2=1$ is enforced during gradient descent. This confirms Srebro results for linear networks and throws some light on the nature of the implicit bias or hidden complexity control. We show this result next.

We study the new dynamical system induced by the dynamical system in ${\stackrel{\cdot }{W_k}}^{i,j}$ under the reparameterization $W_k^{i,j}={\rho }_k{V}_k^{i,j}$ with ${\Vert V_k\Vert }_2=1$. This is equivalent to changing coordinates from $W_k$ to $V_k$ and ${\rho }_k={\Vert W_k\Vert }_2$. For simplicity of notation we consider here for each weight matrix $V_k$ the corresponding “vectorized” representation in terms of vectors $W_k^{i,j}=W_k$.

We use the following definitions and properties (for a vector $w$): Define $\frac{w}{\rho }=v$; thus $w=\rho v$ with ${\Vert v\Vert }_2=1$ and $\rho ={\Vert w\Vert }_2$. The following relations are easy to check:

• 1)Define $S=I-v{v}^T=I-\frac{w{w}^T}{{\Vert w\Vert }_2^2}$; $\frac{\partial v}{\partial w}=\frac{S}{\rho }$.
• 2)$Sw=Sv=0$ and $S^2=S$.
• 3)In the multilayer case $\frac{\partial f\left(W;x_n\right)}{\partial W_k}=\frac{\rho }{{\rho }_k}\frac{\partial f\left(V;x_n\right)}{\partial V_k}$.

The unconstrained gradient descent dynamic system used in training deep networks for the exponential loss is given in Eq. 1; that is,

$$\stackrel{\cdot }{W_k}=-\frac{\partial L}{\partial W_k}=\frac{1}{N}\sum _{n=1}^N{y}_n\frac{\partial f\left(W;x_n\right)}{\partial W_k}{e}^{-y_{n}f\left(W;x_n\right)}.$$ [13]

Following the chain rule for the time derivatives, the dynamics for $W_k$ induce the following dynamics for $\Vert W_k\Vert ={\rho }_k$ and $V_k$ by using relations 1) to 3) above,

$$\begin{array}{cc}\hfill \stackrel{\cdot }{{\rho }_k}& =\frac{\partial \Vert W_k\Vert }{\partial W_k}\frac{\partial W_k}{\partial t}=V_k^T\stackrel{\cdot }{W_k}\hfill \\ \hfill \stackrel{\cdot }{V_k}& =\frac{\partial V_k}{\partial W_k}\frac{\partial W_k}{\partial t}=\frac{S_k}{{\rho }_k}\stackrel{\cdot }{W_k},\hfill \end{array}$$ [14]

where $S_k=I-V_k{V}_k^T$. Thus, unconstrained gradient descent coincides with the dynamical system

$$\begin{array}{cc}\hfill \stackrel{\cdot }{{\rho }_k}& =\frac{\rho }{{\rho }_k}\frac{1}{N}\sum _{n=1}^N{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_{n}f\left(V;x_n\right)\hfill \\ \hfill \stackrel{\cdot }{V_k}& =\frac{\rho }{{\rho }_k^2}\frac{1}{N}\sum _{n=1}^N{e}^{-\rho y_{n}f\left(V;x_n\right)}{y}_n\left(\frac{\partial f\left(V;x_n\right)}{\partial V_k}-V_{k}f\left(V;x_n\right)\right)\hfill \end{array}$$

where we use the structural lemma to write $V_k^T\frac{\partial f\left(V;x_n\right)}{\partial V_k}=f\left(V;x_n\right)$.

Clearly the dynamics of unconstrained gradient descent and the dynamics of constrained gradient descent are very similar since they differ only by a ${\rho }^2$ factor in the $\stackrel{\cdot }{V}$ equations. The conditions for the stationary points of the gradient for the $V$ vectors—that is, the values for which $\stackrel{\cdot }{V}=0$—are the same in both cases, since for any $t>0$ we have $\rho \left(t\right)>0$. This is summarized as follows:

Lemma 5.

Constrained and unconstrained gradient descents have the same set of minima or infima.

In ref. 4 we show that the dynamics of the constrained gradient descent Eq. 7 are the same as those of the well-known and much used algorithm called “weight normalization” (39).

Actual convergence for the constrained case happens if

$$\frac{\partial f\left(V;x_{*}\right)}{\partial V_k}-V_{k}f\left(V;x_{*}\right)=0$$ [15]

which corresponds to a long but finite time and thus a large but finite $\rho$ and a small but nonzero $\lambda$. Eq. 15 is thus the solution that corresponds to a regularization problem with a nonzero but vanishing $\lambda$.

Note that Eq. 15 gives immediately the solution in the one-layer linear case of $f\left(V;x\right)=V^{T}x$. The stationary points of the gradient are given by $\sum {\alpha }_n\rho \left(t\right)\left(x_n-V{V}^T{x}_n\right)$. The Lagrange multiplier case is similar, giving $\sum {\alpha }_n\rho \left(t\right)x_n-\lambda V=0$, with $\lambda$ satisfying ${\lambda }^2=\frac{1}{N}{\sum }_n{e}^{2\rho y_n{V}^T{x}_n}{\rho }^2{y}_n{x}_n$. Thus $\lambda \to 0$ for $\rho \to \infty$. In this case, if $f\left(x_1\right)=1$, the solution is $V=x_1$. In the two-layer linear case, the equations provide a direct relation between $V_1$ and $V_2$, which can be extended to the nonlinear, ReLU case.

C. Summary

There are several additional results on the dynamics of $\rho$ and on the different convergence times for linear networks in the case of weight normalization vs. unconstrained gradient descent, weight normalization showing a faster convergence. For these additional results we refer to ref. 4. We describe here a few implications about the loss landscape.

C.1. Landscape and minima.

ReLU networks with exponential-type loss functions do not have zeros of the gradient (wrt the unnormalized $W_k$) that separate the data. The stationary points of the gradient of $f$ in the nonlinear multilayer separable case under exponential loss are given by ${\sum }_{n=1}^N{y}_n\frac{\partial f\left(W;x_n\right)}{\partial W_k^{i,j}}{e}^{-y_{n}f\left(W;x_n\right)}=0$. Thus, the only stationary points of the gradient that separate the data are for $\rho =\infty$. If other stationary points were to exist for a value $W^{*}$ of the weights, they would be given by zero-valued linear combinations with positive coefficients of $\frac{\partial f\left(W;x_n\right)}{\partial W_k^{i,j}}$. Use of the structural lemma shows that $\frac{\partial f\left(W;x\right)}{\partial W_k^{i,j}}=0,\forall i,j,k$ implies $f\left(W^{*};x\right)=0$. So stationary points of the gradient wrt $W_k$ that are data separating do not exist for any finite $\rho$. The situation is quite different if we consider stationary points wrt $V_k$. Note that minima arbitrarily close to zero loss exist for any finite, large $\rho$. For $\rho \to \infty$, the Hessian becomes arbitrarily close to zero, with all eigenvalues close to zero. On the other hand, any point of the loss at a finite $\rho$ has a Hessian wrt $W_k$ which is not identically zero, since it has at least some positive eigenvalues (4).

Clearly, it would be interesting to characterize better the degeneracy of the local minima (we conjecture that the loss function of a deep network is a Morse–Bott function). For the goals of this section, however, the fact that they cannot be completely degenerate is sufficient. As shown in ref. 4, under the exponential loss, zero loss (at infinite $\rho$) corresponds to a degenerate infimum, with all eigenvalues of the Hessian being zero. The other stationary points of the gradient are less degenerate, with at least one nonzero eigenvalue.

C.2. Summary theorem.

The following theorem (informal statement) summarizes the main results on minimization of the exponential loss in deep ReLU networks:

Theorem 4.

Assume that separability is reached at time $T_0$ during gradient descent on the exponential loss; that is, $y_{n}f\left(W;x_n\right)>0,\hspace{0.17em}\forall n$. Then unconstrained gradient descent converges in terms of the normalized weights to a solution that is under complexity control for any finite time. In addition, the following properties hold:

• 1)Consider the dynamics (A) resulting from using Lagrange multipliers on the constrained optimization problem: “Minimize $L={\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}$ under the constraint $\Vert V_k\Vert =1$ wrt $V_k$.” The dynamics converge for any fixed $\rho$ to stationary points of the $V_k$ flow that are minima with a positive semidefinite Hessian.
• 2)Consider the dynamics (B) resulting from using Lagrange multipliers on the constrained optimization problem: “Minimize $L=\frac{1}{N}{\sum }_n{e}^{-\rho y_{n}f\left(V;x_n\right)}$ under the constraint $\Vert V_k\Vert =1$ wrt $V_k$ and ${\rho }_k$.” The stationary points of $V_k$ in (B) in the limit of $t\to \infty$coincide with the limit $\rho \to \infty$ in the dynamics (A) and they are maxima of the margin.
• 3)The unconstrained gradient descent dynamics converge to the same stationary points of the flow of $V_k$ as (A) and (B).
• 4)Weight normalization (39) corresponds to dynamics (B).
• 5)For each layer $\frac{\partial {\rho }_k^2}{\partial t}$ is the same irrespective of $k$.
• 6)In the one-layer network case $\rho \approx \log t$ asymptotically. For deeper networks, the product of weights at each layer diverges faster than logarithmically, but each individual layer diverges slower than in the one-layer case.
• 7)Gradient flow converges for infinite time to directions given by a set of support vectors with the same value $y_{1}f\left(V;x_1\right)$ that satisfy the set of $K$ coupled vector equations $\left(\frac{\partial f\left(V;x_1\right)}{\partial V_k}=V_{k}f\left(V;x_1\right)\right)$.

In summary, there is an implicit regularization in deep networks trained on exponential-type loss functions, originating in the gradient descent technique used for optimization. The solutions are in fact the same as those that are obtained by regularized optimization. Convergence to a specific solution instead of another of course depends on the trajectory of gradient flow and corresponds to one of multiple infima of the loss (linear networks will have a unique minimum), each one being a margin maximizer. In general, each solution will show a different test performance. Characterizing the conditions that lead to the best among the margin maximizers is an open problem.

4. Discussion

A main difference between shallow and deep networks is in terms of approximation power or, in equivalent words, of the ability to learn good representations from data based on the specific compositional structure of certain tasks. Unlike shallow networks, deep local networks—in particular, convolutional networks—can avoid the curse of dimensionality in approximating the class of hierarchically local compositional functions. This means that for such class of functions deep local networks represent an appropriate hypothesis class that allows good approximation with a minimum number of parameters. It is not clear, of course, why many problems encountered in practice can be represented in this way. Although we and others have argued that the explanation may be in either the physics or the neuroscience of the brain, these arguments are not rigorous. Our conjecture at present is that local hierarchical compositionality is imposed by the wiring of our sensory cortex and, critically, is reflected in language. Thus the specific compositionality of some of the most common visual tasks may simply reflect the way our brain works. From a general point of view, it is clear that there are many different forms of compositionality that translate in different DAGs (3).

Optimization turns out to be surprisingly easy to perform for overparameterized deep networks because SGD will converge with high probability to global infima that are typically more degenerate (for the exponential loss) than other local critical points.

The gradient flow on the appropriately normalized network corresponding to gradient descent is under complexity control, despite overparameterization and even in the absence of explicit regularization, because in the case of exponential-type losses, the directions of the weights converge to one of several minima for finite times (and to a minimum norm solution for time going to infinity). This implicit complexity control mechanism—implicit regularization—however, does not by itself fully explain the behavior of overparameterized deep networks, which fit the training data and perform well on out-of-sample points.

Remember that the classical analysis of empirical risk minimization (ERM) algorithms studies their asymptotic behavior for the number of data $N$ going to infinity. In this limiting regime, $N>D$, where $D$ is the fixed number of weights; consistency (informally the expected error of the empirical minimizer converges to the best in the class) and generalization (the empirical error of the minimizer converges to the expected error of the minimizer) are equivalent. Empirically we know that for a nonasymptotic regime with $N<D$ deep networks can yield good expected error in the absence of generalization. This is similar to the regression case for some linear kernel methods (40–44). This phenomenon suggests that under certain conditions, the pseudoinverse may perform well in terms of expected error while the generalization gap (difference between expected and empirical loss) is large. We note that is not surprising that complexity control is a prerequisite for good performance even in an overparameterized regime in which the classical analysis via generalization does not apply. The minimum-norm pseudoinverse solution is unique and continuous, satisfying the key conditions—including stability with respect to noise in the data—of a well-posed problem. In fact, a recent paper (45) shows that solutions of overparameterized deep networks that optimize cross-validation leave-one-out stability minimize the expected error. Furthermore they suggest that maximum stability corresponds to minimum norm solutions. Thus the main results of this paper imply that gradient flow in deep networks with an exponential-type loss does (locally) minimize the expected error because it selects minimum norm solutions.

5. Materials and Data Availability

All data and code associated with this paper are accessible publicly at GitHub, https://github.com/liaoq/pnas2019.