Network interventions for managing the COVID-19 pandemic and sustaining economy

Significance

It has been challenging to identify nonpharmaceutical intervention strategies that reconcile two conflicting aims: Reducing the spread of infections while maintaining economic activities amid the coronavirus disease 2019 (COVID-19) pandemic. Commonly implemented strategies such as lockdowns or stay-at-home orders involve a significant restriction of economic activities. Using agent-based simulations, we show that two network intervention strategies that divide or balance social groups can substantially reduce transmission while sustaining economic activities. When the two strategies are jointly implemented without any additional measures, they can keep the effective reproduction number of COVID-19 around 1.0 in most cases.

Abstract

Sustaining economic activities while curbing the number of new coronavirus disease 2019 (COVID-19) cases until effective vaccines or treatments become available is a major public health and policy challenge. In this paper, we use agent-based simulations of a network-based susceptible−exposed−infectious−recovered (SEIR) model to investigate two network intervention strategies for mitigating the spread of transmission while maintaining economic activities. In the simulations, we assume that people engage in group activities in multiple sectors (e.g., going to work, going to a local grocery store), where they interact with others in the same group and potentially become infected. In the first strategy, each group is divided into two subgroups (e.g., a group of customers can only go to the grocery store in the morning, while another separate group of customers can only go in the afternoon). In the second strategy, we balance the number of group members across different groups within the same sector (e.g., every grocery store has the same number of customers). The simulation results show that the dividing groups strategy substantially reduces transmission, and the joint implementation of the two strategies could effectively bring the spread of transmission under control (i.e., effective reproduction number ≈ 1.0).

Alteration of established network structures is one form of Valente’s framework of network interventions (1, 2). “Lockdowns” (or shelter-in-place orders, curfews, or mass quarantines) under the coronavirus disease 2019 (COVID-19) pandemic are an extreme case of alteration, in which all nonessential economic activities that require physical interactions are suspended and corresponding network ties are effectively dissolved (3). Although nonpharmaceutical interventions (NPIs), including lockdowns, have been shown to reduce the speed of the spread of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) (4–8), these interventions are not sustainable for a prolonged period of time due to their detrimental impact on population health and economies (9). Lockdowns have been shown to be associated with physical inactivity (10), increased depression (10, 11), increased domestic violence (12), and reduced access to healthcare (13). Moreover, the main strategies employed in lockdowns [i.e., closing schools, prohibiting gatherings, requiring people to stay at home, closing nonessential businesses (7, 8, 14)] have a significant negative impact on economies (15). For example, in the United States, 20.5 million jobs were lost in April 2020, peaking at an unemployment rate of 14.7% (16, 17); moreover, the increases in unemployment are associated with negative mental health outcomes (18). Although lockdown and shelter-in-place policies have been shown to be effective in lowering the number of cases and deaths due to COVID-19 (4–8, 19), governments in many countries are confronted by significant political, economic, and social pressure to reopen their economies and remove the restrictions imposed by lockdown orders (19, 20).

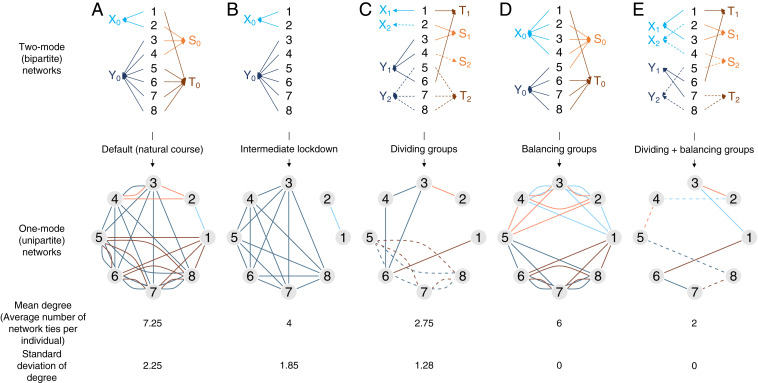
As a result of this pressure, many governments are currently looking for strategies that can achieve two conflicting goals: To reopen economies while reducing and preventing transmission of COVID-19 infections (i.e., keeping the effective reproduction number [R_eff: the average number of secondary transmissions caused by a single primary case] of COVID-19 low). Here, we illustrate two network intervention strategies for managing the spread of transmission while allowing individuals to remain economically active (Fig. 1 C and D). The primary goal of each strategy is to reduce the overall number of direct network ties by reducing contacts between individuals and decreasing transmission of the infectious agent.

Fig. 1.

The two network intervention strategies (dividing groups and balancing groups). The flow is A → B, A → C, A → D, and C → E. We display a hypothetical network of eight people across two sectors (groups X and Y are in the same sector, and groups S and T are in the same sector). In the simulation, we used a network of 10,000 people across eight sectors. The two-mode networks (Top) show the distribution of group activities and sectors in which each subject (IDs 1 to 8) participates. For example, ID1 belongs to X₀ (e.g., go to workplace X₀) and T₀ (e.g., go to supermarket T₀) and regularly engages in his or her activities (e.g., working and shopping, respectively) at the appropriate locations (X₀ and T₀). The two-mode networks can be converted to one-mode networks (Bottom), in which a shared group connects two individuals. For example, ID1 and ID2 may be involved in transmission at X₀ and the network tie between ID1 and ID2. A network tie in one-mode networks represents a chance of transmission, while an arrow in two-mode networks represents an individual going to a location and engaging in economic activities. In this example, the mean degree (number of the network ties per individual) and its variation (SD) are smaller when dividing groups (A → C) and balancing groups (A → D).

In the first strategy (“dividing groups”), a group is split into two distinct subgroups such that individuals in different subgroups no longer physically interact (Fig. 1C). Here, we define a group as a set of people who engage in the same activity (e.g., shopping) in a single sector at one specific location, which creates the potential for physical contact and chance of transmissions. Members of a subgroup engage in the same economic activities, and each subgroup retains the same function as the original undivided group. For example, a cohort of 100 college students that originally operated from 9 AM to 3 PM may be divided into two subgroups: one subgroup of 60 students operating from 7 AM to 1 PM, and the other subgroup of the 40 remaining students operating from 2 PM to 8 PM (21). Alternatively, the two subgroups could operate simultaneously, but would be physically separated and served by different staff [otherwise, staff may mediate transmissions between members of different groups (22, 23)]. Upon reopening schools, France plans to cap class sizes at 15 people (24), while South Korea and Japan separated student groups into morning and afternoon classes (25, 26). Additionally, some supermarkets reserve a specific day and time for at-risk individuals (seniors, immunocompromised individuals, expectant mothers, etc.) to shop (27). These policies, while primarily enacted to achieve an appropriate level of physical distancing, can contribute to the separation of networks [dividing groups by age or susceptibility (28)] if the employees or environments do not mediate transmission between groups.

In the second strategy (“balancing groups”), some number of individuals approaching a destination are redirected to a different location with the same functionality to equalize the number of people at each location (Fig. 1D). For example, consider a group of customers and two supermarkets run by the same franchise within a community where one store is usually full, while the other is not. Some customers heading to one store would need to go to the other store to ensure that the number of customers at each location is equal. Such redirection is often observed when some stores are more crowded than others. If a large number of people head to popular stores at a specific time of day, stores may exhibit peak-time crowdedness, which may lead to a higher concentration of infected individuals in a single location (29). In order to achieve physical distancing, many supermarkets have set limits on the number of people who can shop at the same time (30), which may incidentally contribute to balancing the number of customers across multiple supermarkets. Akin to this phenomenon in stores, emergency departments prevent patient overflow by diverting ambulances to hospitals with fewer patients (31, 32). These “balancing groups” strategies have the potential to reduce the total number of physical interactions between individuals that represent a chance for transmission without compromising their level of economic activity (i.e., before and after implementation, the total number of shopping customers remains unchanged).

To illustrate the potential consequences of these strategies, we implemented agent-based simulations of the susceptible−exposed−infectious−recovered (SEIR) model (20, 33–37) (network-based SEIR model without vital dynamics) using parameters of SARS-CoV-2 (38). We assumed that, once a virus is transmitted, exposed individuals experience a latent period of 3 d and become infectious for an average of 3 d (an infectious period for each individual is randomly drawn from a geometric distribution) (39). After the infectious period, all infected individuals recover with immunity. We assume that the acquired immunity persists until the end of the simulation (300 d) (see Materials and Methods).

We set up a network of 10,000 individuals with dispersed degree distributions representative of an actual social network (Fig. 2C, default scenario), in which we aimed to mimic past social mixing surveys (40–42). The median degree of the network (number of contacts) is 15.55 (95% quantile range [QR]: 15.06 to 16.28). The network consists of three types of network ties with differing probabilities of transmissions (differing weights): family ties having the highest probability of transmission, nonfamily close ties having an intermediate probability of transmission, and weak ties having the lowest probability of transmission (where transmissibility varies by sector). These ties are nested in one of the eight sectors (families, workplaces, educational institutions, healthcare institutions, grocery stores, restaurants and cafés, sports/leisure groups, and other groups) (see Parameters of the Agent-Based Simulations and Constructing the Social Network Structure with Edge Weights).

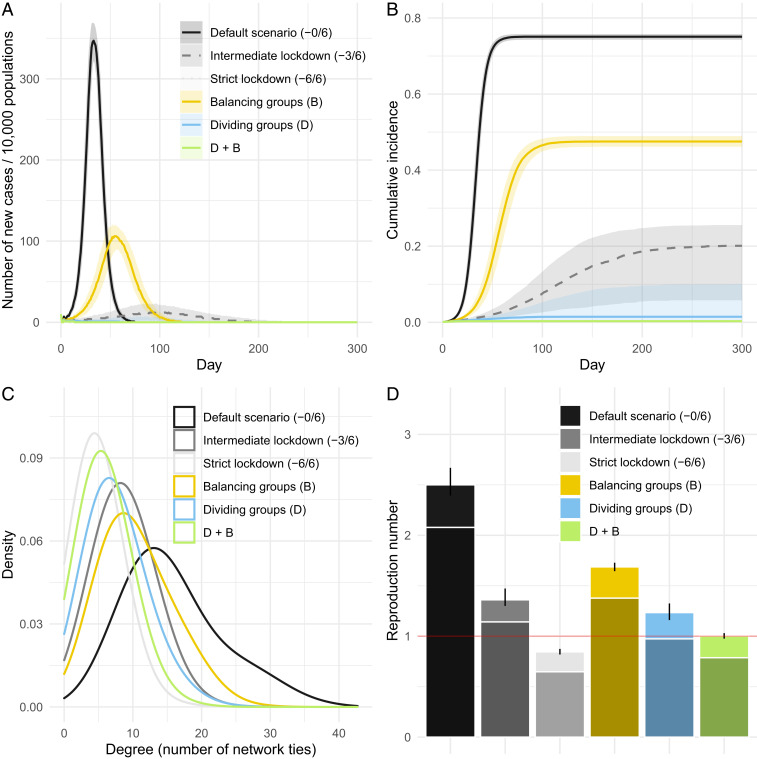
Fig. 2.

The results of agent-based simulations. (A) Incidence dynamics over 300 d. The lines and shades represent medians and interquartile ranges for 1,000 iterations of our simulation. The curves for the strict lockdown scenario and others are invisible because they are located near the x axis (this also occurs in B). The legend for A is shared with B. (B) Cumulative incidence dynamics over 300 d. (C) Degree distributions (density plots) in each scenario. Distributions are drawn using a single random seed for illustration purposes. (D) The network-based reproduction number in each scenario. Error bars represent the 95% QRs obtained from 1,000 simulations. The top, light parts of the bars show the increment effect due to the SD in the degree distribution (see Converting R₀ to β for Agent-Based Simulations for details). The red horizontal line represents a reproduction number of 1.

We simulated the spread of infections over the network constructed as above for the duration of 300 d. We assumed density-dependent mixing during the simulation (43): Group members had a constant possibility of interacting with one another and of transmitting the virus of 4.458% (β = 0.04458) per day per network tie with a weight of 1 (family tie). Transmissibility (β) was calculated from the conversion formula between β and the basic reproduction number (R₀) for network-based models (44) to ensure that R₀ reflecting the network structure is consistent with 2.5, which is estimated elsewhere (38, 45) (see Converting R₀ to β for Agent-Based Simulations). This means that, on average, a single case causes 2.5 secondary cases over the course of infection. β of 0.04458 roughly corresponds to a level of transmissibility reported elsewhere (e.g., 0.0463 in ref. 46).

Individuals may share groups in multiple sectors (e.g., two people work at the same place and shop at the same grocery store); in such cases, the possibility of transmission was assumed to multiply. We randomly infected 10 individuals on day 0. We implemented this simulation 1,000 times per scenario. Each ith simulation (i = 1, 2, …, 1,000) over the different scenarios used the same random seed. Medians and ranges were calculated over the 1,000 iterations of the simulation. The social network structures and group assignments were randomly drawn for every iteration.

We examined the effectiveness of six different network intervention scenarios by comparing the epidemic curves, the final cumulative incidence (overall attack rate), and R_eff among the six scenarios. The first scenario was a default scenario in which no intervention was implemented (“natural course”). The second scenario was a 3/6 activity restriction, in which ties for three activities (educational institutions, restaurants/cafés, and sports/leisure) were removed out of a set of six activities (family ties or ties in medical institutions were not removed) (“intermediate lockdown”). This level of lockdown might be less strict than one shown in a previous paper (28) and the level of actual lockdown in the states of New York (47) and California (48). The third scenario was a 6/6 activity restriction, in which ties for all six activities (the three activities above plus those in workplaces, grocery stores, and other groups) were removed (“strict lockdown”). The replicating lockdown strategies involve a commensurate sacrifice of economic activities. The final three scenarios demonstrate the “dividing groups” strategy, the “balancing groups” strategy, and the strategy combining the two strategies, in which group sizes of all postdivision subgroups in each sector are balanced (D + B) (Fig. 1E). Each scenario is presented as if each strategy was implemented independently of any other intervention (e.g., physical distancing or the use of facial coverings) to enable a pure comparison between different strategies. As a result, the effects reported here may be smaller than what would be expected in a real-world situation where multiple interventions are implemented at the same time.

In robustness tests, we aimed to confirm the potential effects of the dividing and balancing groups strategies in various settings and specifications. Therefore, we further manipulated our settings regarding group and network tie formation, transmissibility and infectiousness period, and behavioral and environmental changes. Additionally, we applied a more complex network structure (social consolidation). We also examined alternative strategies employed as part of lockdowns (avoiding large gatherings) (see Robustness Tests for details).

Results

The “dividing groups” scenario exhibited a median cumulative incidence of 0.014 (95% QR: 0.002 to 0.191) on day 300 (Fig. 2B, light blue). The median cumulative incidence ratio of the “dividing groups” scenario as compared to that of the default scenario was 0.014 (95% QR: 0.002 to 0.191). The median R_eff of the dividing groups strategy was 1.234 (95% QR: 1.160 to 1.325). Doubling the number of groups almost halved the mean degree and its SD (SI Appendix, Fig. S1 B and C), which is almost comparable to the intermediate lockdown (−3/6) scenario (Fig. 2C, sky-blue vs. gray).

The “balancing groups” scenario exhibited a median cumulative incidence (or attack rate) of 0.475 (95% QR: 0.428 to 0.514) on day 300 (Fig. 2B, orange), which was lower than that of the default scenario (median of 0.728) (Fig. 2B, the darkest gray). The median cumulative incidence ratio of the “balancing groups” scenario as compared to the default scenario was 0.751 (95% QR: 0.729 to 0.775) (or median of the relative reduction in the attack rate is 63.4%). The median estimate for R_eff of the balancing groups strategy was 1.687 (95% QR: 1.645 to 1.728). The mechanism behind the reduction of infection in the “balancing groups” is simple: Balancing groups reduced the number of network ties (and thus the mean degree) and reduced the variation in degree (SI Appendix, Figs. S1 B and C and S2). This means that, after the sizes (the count of group members) of groups in each sector were equalized, individuals with higher connectivity, who could contribute more to the spread of transmission, lost a substantial number of network ties. The degree distribution of the balancing groups strategy shows that a high degree of mixing in the default setting (i.e., high connectivity mostly by close ties in some sectors) has been mitigated (Fig. 2C, orange vs. dark gray). Some of the close and weak ties are dissolved because the two individuals in the ties no longer belong to the same group.

The “dividing groups with balancing groups (D + B)” scenario achieved a median cumulative incidence of 0.003 (95% QR: 0.001 to 0.012) (Fig. 2B, green), which is almost at the same level as the strict lockdown scenario (median cumulative incidence of 0.003 (95% QR: 0.001 to 0.012) (Fig. 2B, the light gray—the two relevant bars overlap). The median cumulative incidence ratio of the D + B scenario as compared to that of the default scenario was 0.002 (95% QR: 0.001 to 0.004). While the number of infections increases overall (the number of those who experience the infection tripled [a total of 30 cases at day 300 as compared with a total of 10 seed cases at day 0]), the spread of the virus over social networks was slow. Although R_eff of the D + B scenario (median = 1.004, 95% QR: 0.976 to 1.030) was not as low as that of the strict lockdown scenario (median: 0.845, 95% QR: 0.819 to 0.874), the D + B strategy alone can contribute to managing the virus almost at a “control” level (R_eff ≈ 1.0) (Fig. 2D).

Our findings remained qualitatively unchanged as a result of the 11 different types of robustness tests we conducted (see Materials and Methods and SI Appendix, Figs. S3–S21). Most importantly, strictly enforcing self-isolation of symptomatic patients achieves further reduction in R_eff, bringing the estimated R_eff below 1 (median: 0.948 [95% QR: 0.921 to 0.975) if combined with the D + B scenario. Simulation results were consistent with R_eff values provided by mathematical predictions (see Converting R₀ to β for Agent-Based Simulations). Restricting the gathering of groups of more than five members can manage the infection toward a controlled state (R_eff ≈ 1.0) (SI Appendix, Fig. S21).

For the dividing groups strategy, we also investigated whether the original even split (where we designated a 50% chance of being assigned to the first and second subgroups) maximized the effect of the division. In the real world, even divisions may not be feasible in some cases. For example, some supermarkets in the United States reserve morning hours for seniors (27), but seniors do not represent one half of the US population. Alternatively, even if people are asked to separate into subgroups that are evenly populated, a majority of people may prefer to choose a specific group (limited adherence to the policy). We found that, even if the division were not even, there would be some effects in lowering transmissions (e.g., when the probabilities are 0.2 and 0.8, median R_eff is 1.448 [95% QR: 1.339 to 1.580]). However, as predicted, we found the median R_eff takes a minimum value of 1.234 (95% QR: 1.162 to 1.314) when the probabilities are 0.5 and 0.5 (SI Appendix, Fig. S5).

Discussion

In summary, we have identified network intervention strategies that provide some insight into how we can reconcile two conflicting aims: Reducing the spread of infections over social networks while maintaining economic activities. When the dividing and balancing strategies (i.e., D + B strategy) are jointly implemented, they will be effective enough to keep R_eff around 1.0 in most cases without any additional measures. Although the detrimental impacts on health (e.g., emotional well-being) and economies (e.g., recession) caused by lockdowns can be largely avoided, these strategies have rarely been discussed in public or political debates (21).

Can some of these strategies replace the lockdown strategies for addressing the current or potential future waves of the COVID-19 outbreak? A direct comparison is difficult since there are many types of lockdown strategies. However, our results indicate that our intermediate lockdown strategy (−3/6) alone, in which many network ties rooted in workplaces and essential services stay intact, does not reduce the reproduction number sufficiently. The median R_eff (1.361, 95% QR: 1.300 to 1.473) of the intermediate lockdown strategy is substantially above 1, and our simulation indicates up to 20% of the population could be infected. Indeed, in the real world, such partial lockdown strategies have been used in conjunction with other measures such as isolating symptomatic and/or diagnosed individuals, quarantining family members of isolated individuals, promoting physical distancing, and mandating the use of facial coverings in public spaces. The result of this combined strategy was the reduction of the reproduction number to around 1 (e.g., from the 2.5 to 3.0 range to the 0.75 to 1.25 range in the state of California between March and May 2020) (19). Therefore, as long as we can closely monitor the implementation of these interventions as they are applied to the public, both the dividing and the D + B strategies can be considered as alternatives to currently implemented strategies. Their effect sizes were larger than those of our intermediate lockdown strategy. In combination with other measures such as self-isolation and physical distancing, the institution of our strategies would result in R_eff below 1. Such a joint approach will also be effective when R₀ is very high [e.g., R₀ in the state of New York was estimated to be 5.7 or greater (45)]. Otherwise, we would need to recommend dividing groups into five or more subgroups.

The dividing groups and D + B strategies can also act as promising alternatives to a gradual reopening of economic activities after a peak of the outbreak has passed, in advance of a secondary or tertiary wave of the outbreak. Since reopening the economy represents a step-by-step transition from more-strict lockdown strategies to milder ones (e.g., from −6/6 to −3/6), the rate of transmission may increase again unless the virus becomes extinct from a community, herd immunity is achieved, or other measures such as physical distancing are sufficient to control its transmission. On the other hand, if the economy is reopened while people remain divided into subgroups, a lower number of new cases will arise compared to an undivided population, and new peaks may be avoided.

Like other simulation studies, a key limitation to this analysis is that we only explored agent-based simulations with specific parameter spaces and with specific assumptions. In reality, there are hundreds or thousands of “sectors” of daily life, the number of sectors that each individual belongs to varies, the transmission probability would change based on the symptoms and other factors of the host, and the possibility of virus subtypes would affect the rate of infection among other factors (49, 50). Nevertheless, we believe that our model captures the salient features of the problem. Although we believe that we used realistic network structures in our simulations, the predicted effects of the proposed strategies should be interpreted with caution, due to the simplistic and demography-specific nature of our model. Particularly, our model needs to be tailored and calibrated with relevant parameters and data to reliably assess the potential impacts of these strategies in specific settings and contexts. Once digital contact tracing data of large sections of populations becomes available, network sampling and other techniques should allow for more precise predictions of the effect size of each NPI (51–53).

Our simulations also assumed that, once the network interventions are implemented, agents will repeat their actions (aside from the simulation where symptomatic individuals were required to self-isolate) and thus will not contribute to further mixing of populations (e.g., members of a group who are diverted to store Y away from store X will continue to go to store Y and not attempt to return to store X). However, people in the real world may not be very consistent or rational. Most importantly, we assumed that our simulations primarily followed a density-dependent mixing model (43), where increases in group size correspond to proportional increases in the number of contacts, potentially causing a viral transmission. In other words, in addition to a small number of close contacts (close school friends), a classroom of 20 college students is twice as likely as a classroom of 10 college students to experience a transmission event; however, this assumption may be reasonable in the context of the COVID-19 pandemic, given a number of recent cluster events originating from large social gatherings (54).

Nevertheless, in addition to sustaining the economy, there are several advantages to the proposed strategies. First, we anticipate several spillover effects that will result in benefits for populations where these strategies are implemented. The dividing groups strategy requires each sector to manage more than one subgroup and to secure the human resources to do so separately and independently. Such strategies may not only sustain the economy when implemented but may also function as an economic stimulus and lower the unemployment rate (e.g., part-time jobs become full-time jobs and new jobs are created to account for the need for multiple sets of staff). Moreover, if the dividing strategy is implemented using division by time frame (e.g., from 7 AM to 1 PM and from 2 PM to 8 PM), “rush hours” and corresponding increases in road and business traffic may wane, leading to possible increases in the sustainability in major cities. Second, prior surveys or contact tracing (digital or nondigital) (55) are not required in advance of the implementation of these strategies. Compared with previously proposed network interventions (1, 28, 56), which require intensive efforts in advance (e.g., establishing network graphs, identifying important network bridges or hubs, and intervening on such bridges or hubs), our strategies involve less preparation and could be more readily implemented.

One of the critical considerations for implementing either of these network intervention strategies is the acceptability by the public (57). The demonstrated strategies will be emotionally taxing because they require individuals to drastically alter their daily routines [endowment effect (58)]. Individuals may no longer be allowed to go to certain places at certain times; the balancing groups strategy may determine whether businesses are open or closed for particular individuals, while the dividing groups strategy may place time constraints on when businesses are available for particular individuals. However, compliance with both the dividing or balancing groups strategies may be higher than compliance with lockdown strategies, as they do not completely prohibit visiting specific types of businesses or utilizing certain services (as lockdowns do). Neither the dividing strategy nor the balancing strategy requires people to stay home all day, potentially preventing the development of “quarantine fatigue” (a phenomenon in which people loosen up and travel more during the lockdowns) (59). Other considerations include the cost and feasibility of implementing these kinds of network interventions. Even if they are acceptable, these interventions may be difficult to implement if they are costly. For example, financial constraints may prevent administrators in the education sectors from expanding school premises to facilitate the need for additional physical space (i.e., classrooms). Additionally, in specialized industries or other sectors where the choices for personnel are limited due to the need for specialized training, network intervention strategies may not be feasible.

Historically, people in the United States and other countries have accepted such strategies, which restricted individual freedoms in the face of an economic or social crisis. In the 1973 oil crisis, gasoline was scarce, and rationing strategies were implemented (60). For example, people with a vehicle with a license plate ending in an odd number could only purchase gasoline on odd-numbered days. Consolidation of the demonstrated strategies into culturally acceptable interventions may be discussed in different phases of the COVID-19 pandemic in different sociopolitical contexts.

Materials and Methods

Parameters of the Agent-Based Simulations.

We used a total of 60 parameters in our model (Table 1). In addition, we numerically labeled each of the three lockdown strategies as well as the dividing groups, balancing groups, and combination (D + B) strategies.

Table 1.

Parameter values for agent-based simulations

Parameters	Values	Notes	Robustness test number
Network structure (environment), overall
Number of agents (humans)	10,000
Number of sectors	8
Number of categories in network ties	3	Family, close, and weak ties	5
Consideration of family ties	Yes	All of the time
Consideration of close ties in nonfamily sectors	Yes	No in a robustness test	5
Consideration of weak ties in nonfamily sectors	Yes	No in a robustness test	5
Consideration of the consolidation of social space	No	Yes in a robustness test	11
Social network model for family ties	Complete
Social network model for close ties	Small-world (61)	Addressing consolidation in social space
Rewiring probability in the small-world model	0.2		4
Social network model of weak ties	Complete	See the edge weight below
Detailed parameters for the eight sectors (for the edge weights)
Numbers of groups in families, workplaces, educational institutions, healthcare institutions, grocery stores, restaurants/cafés, sports/leisure, and the other sectors	(3,000, 1,000, 25, 25, 10, 25, 500, 500)	Based on a sample city	1
Enrollment rates for families, workplaces, educational institutions, healthcare institutions, grocery stores, restaurants/cafés, sports/leisure, and the other sectors	(1, 0.4, 0.25, 0.5, 0.5, 0.5, 0.7, 0.5)	Workplace: 40% of individuals engage in working (62, 63); Sports/leisure (64)
Distribution used for the group assignment	Uniform	Geometric distribution in robustness tests	3
Number of close ties in workplaces, educational institutions, healthcare institutions, grocery stores, restaurants/cafés, sports/leisure, and the other sectors	(Up to 6, up to 4, 0, 0, 0, up to 8, up to 4)	Based on refs. 40 and 42; vary due to the group size and rewiring of network ties; when group size is smaller than the number (e.g., six for workplaces), all of the possible network ties were made
Edge weight of families	1	Default value
Edge weight of close ties in nonfamily sectors	0.5	Transmissibility of close ties is a half of that of family members [intensity of 0.5 (46) × encounter frequency of 1]	5
Edge weights of weak ties in workplaces, educational institutions, healthcare institutions, grocery stores, restaurants/cafés, sports/leisure, and the other sectors	(0.075, 0.075, 0.0025, 0.005, 0.01, 0.025, 0.025)	Intensity of 0.1 (46) × encounter frequency of (0.75, 0.75, 0.025, 0.05, 0.1, 0.25, 0.25)	5
Strategy-specific settings
Exceptions in the lockdown strategies, sector	Healthcare	Healthcare sector is not closed
Exceptions in the lockdown strategies, group size	No	Only in a robustness test: groups with a small group size are not closed (avoid large gatherings)	10
Fraction in division in the dividing strategy	0.5 (even)	A robustness test for the noneven split	2
Infectious disease dynamics
Initial number of infections on day 0	10	The number of initially infected individuals, located randomly in the social networks
Number of spontaneous infections on week X	0	New infections at day 7, 14, 21, …	9
Per-contact transmissibility (β)	0.04458	Converted from R0 of 2.5 (see Converting R0 to β for Agent-Based Simulations) (38, 45)	6
Latent period (duration in the days in the “Exposed” compartment)	3 d (39)
Infectious period (mean duration in the “Infectious” compartment) (τ)	3 d (38, 39)	Used as the mean of a geometric distribution	7
Observation period in the simulation	300 d
Symptoms and behavior (agents)
Behavioral strategy updates	None	Considered in a robustness test	8
Contacts during self-isolation of symptomatic cases	Family only	Considered in a robustness test	8
Asymptomatic ratio	0.45 (65)	Considered in a robustness test	8
Viral shedding and transmissibility of asymptomatic cases	Same as symptomatic cases (0.04458)	Constant; see refs. 66 and 67
Presymptomatic period	0.5 (half of the infectious period) (68)	Considered in a robustness test; 0.5 is used as a parameter for p in a binominal distribution	8

To determine the number of groups in each sector, we referenced random cities in the United States with around the same population as our simulation (n = 10,000) and used the distribution of businesses, households, and other services as a template for our simulation groups. More specifically, we focused on Sierra Madre, CA (population 10,793) as our sample city. Sierra Madre is a suburb of Pasadena, CA, located 13 miles away from downtown Los Angeles. Using data from the US Census (69) and the American Community Survey (70), we determined that there were 2,862 families, 1,812 businesses, 8 grocery stores, 21 educational institutions, 30 healthcare institutions (e.g., medical and dental clinics), and 22 restaurants and cafés in the city. After some adjustment to account for variation in the distribution of sectors across different cities and to account for inactiveness of some of the registered activities, we determined the group numbers listed in the table above. For the workplace sector, we assumed that 20% of registered businesses were dormant and another 20% were owned by a parent company or shared an owner with another registered business (and therefore should not count as an additional business for the simulation). However, our choice of the number of groups would not substantially affect our conclusion, as shown in the robustness check (see Robustness Tests). In addition, as shown in the mathematical prediction (see Converting R₀ to β for Agent-Based Simulations), the reproduction number would decrease proportionally regardless of the number of groups in sectors.

Constructing the Social Network Structure with Edge Weights.

In our modeled network structure, we aimed to incorporate the characteristics of SARS-CoV-2; new COVID-19 cases not only occur via family ties and nonfamily close contacts (e.g., a close friend sharing a karaoke room), but they have also been found to occur via nonclose contacts (e.g., coattendants at a church service or individuals near an index case in a waiting room at a hospital (71)—group members may not necessarily know each other). Such transmissions may come from direct contact, droplet transmission, aerosol transmission, or other forms (64). Therefore, we created multiple sectors (n = 8) with varying numbers of groups (see Parameters of the Agent-Based Simulations). A detailed description of how the simulation social network was constructed is below.

To generate family ties, we created 3,000 families where the number of family members varied. All individuals in the simulation belonged to a family. The sizes of each family were probabilistically determined based on the total number of groups in each sector. For example, it was possible for a family to have either 1 or 10 individuals. We assumed that all members of a single family comprised a complete network, where all possible network ties were drawn to other family members within the family. Then, we set a network tie strength (edge weight), which represents the intensity of a possible transmission over family ties to be one as a default (46, 61). A typical individual has four or five family ties.

Next, we constructed weak ties by assuming that individuals belong to social groups in which they have a chance to physically interact with others. Groups are classified into seven sectors representing different social settings. In more concrete terms, we created 1,000 workplaces, 25 educational institutions, 25 medical institutions, 10 grocery stores, 25 restaurants and cafés, 500 sports/leisure groups, and 500 other small groups (e.g., friend and neighbor groups). The number of groups that individuals belonged to varied; some had network ties only with family members (i.e., belong to only the family sector). We assumed that individuals could not belong to more than one group from the same sector; therefore, the maximum number of groups an individual could belong to is seven (one group from each of the sectors). The sizes of each group were probabilistically determined based on the total number of groups in each sector.

First, once the groups and sectors were constructed, we determined the enrollment rate (or active limit) of each sector (Table 1). All of the 10,000 individuals do not necessarily belong to all of the sectors. For example, that of the workplace sector is 40%, which is obtained by the product of the employment−population ratio (the number of people employed by the number of people of working age), which was 61% (United States) in January 2020 (72) and the fraction of ages 15 y and 64 y in the population pyramid in the state of California (63%) (73). For the education sector, we assumed that everybody between the ages of 0 y and 19 y goes to school and everybody outside of that age range does not and used 25% as the enrollment rate of the education sector. For the sports/leisure sector, we referred to the information that ∼70% of the people in the United States are physically active (74). When the data were not available, we used a default enrollment rate of 50%.

Second, for each sector (including family ties), we determined the probability of assigning individuals to each of these groups, by generating weights using a uniform distribution. For example, suppose that there are 10 individuals with two groups in a sector and that two values (weights for each group) are randomly drawn from a uniform distribution (e.g., 0.6 and 0.9). The weights are adjusted so that the sum of all weights is 1 (i.e., 0.4 and 0.6, respectively). Using the adjusted weights, we randomly assign the 10 people into two groups. On average, the first group may get four people, and the second group may get around six people, but the assignments are not deterministic.

Third, we considered the encounter frequency (a chance of sharing an indoor environment) of weak ties in different sectors. For example, the encounter frequency of a workplace (e.g., two employees occupy the same room or floor of a building for 30 h per week out of 40 possible business hours) would be higher than the encounter frequency of a medical institution (e.g., two patients of the same primary care physician may occupy the physician’s clinic for 2 h per week, and, most likely, one patient will not encounter the other). We assumed a certain number of open hours each week for the different sectors (40 h for workplace, education, healthcare, grocery, and restaurant/café [weekdays and weekends], and 16 h for sports/leisure and other [mainly weekends only]) and the hours per week when people engage (30 h for workplace and education, 1 h for healthcare, 2 h for grocery, and 4 h for restaurant/café, sports/leisure, and other). The division of values for each sector represents the chance that two random individuals are in the same place at the same time when they belong to the same group in a sector. Incorporating the encounter frequency can allow us to weaken the strength of weak ties created in a sector in which there are groups with large group sizes but people do not stay for an extended period of time (such as medical and dental clinics).

Fourth, we considered the intensity of each tie in regards to the possibility of transmission. From past literature (46), we know that the secondary attack rate (or the possibility of transmission more broadly) of family ties is 10 times as high as that of weak ties (made from sharing the same environment, which may cause various forms of transmission), and the secondary attack rate of close ties is 5 times as high as that of weak ties.

Lastly, we multiplied the encounter frequency coefficient and the intensity coefficient (of possible transmission) to calculate the edge weight (the network tie strength). When there were two or more different weak ties from two or more sectors, we summed them to calculate the weight. When there were two or more different family, close, and weak ties, we chose the stronger ones (family ties or otherwise close ties). Ultimately, the network tie strength of weak ties ranged from 0.0025 (medical institutions) to 0.075 (workplaces and educational institutions). A typical individual has six or seven weak ties (647 before considering the network tie strength).

For close ties [physical contact or two-way conversation without physical distancing (40)], we assumed that these ties arise only in some of the sectors (workplaces, educational institutions, sports/leisure groups, and other groups). Based on the fraction of close ties previously reported (40, 42), we assumed that a typical individual has up to eight close ties in sports/leisure sectors, six close ties in workplaces, and four close ties in the educational institutions other sectors. Therefore, in these sectors, people may have both close ties and weak ties. To reflect human nature on the consolidation of social space, we randomly established close ties among all of the weak ties in the four sectors using a Watts−Strogatz small-world model (75) with a rewiring probability of 0.2. This means that a friend of a friend (i.e., a close contact of a close contact) is very likely to be a friend, while some close contacts may play a role in bridging communities in social networks. The median transitivity (global clustering coefficient) of close ties in the default setting is 0.228 (95% QR: 0.223 to 0.232), which is comparable to transitivity figures previously reported (65, 76).

Then, we set the network tie strength of close ties to be 0.5, as the secondary attack rate of close ties is around a half of the tie strength of family ties (46). A typical individual has five close ties (10 before considering the network tie strength). No new close ties are newly made after the balancing and/or dividing strategies are implemented [no network recovery (68) is allowed], while close ties of two individuals are not dissolved when they move to the same new group as a result of the balancing strategy or when they belong to the same subgroup as a result of the dividing strategy.

Consequently, using density-dependent mixing (43), we assumed that all group members in each group in each sector had a constant possibility of interacting with each other (which are counted as network ties), regardless of overall group size. However, the probabilities of transmission vary. This method allowed us to create a degree distribution of each of the 1,000 social networks (randomly drawn from 1,000 iterations), in which a network tie is weighted (family ties: 1, close ties: 0.5, and weak ties: 0.005 to 0.075). From this method, we obtained the median mean degree of 15.6, which is comparable to the number of contacts in past social mixing surveys (42) [e.g., 13.4 in the POLYMOD study (40)], and the median of the SD of degree of 7.0.

Converting R₀ to β for Agent-Based Simulations.

We determined the parameter value for transmissibility (β; the probability of transmitting the virus per day per network tie) as follows for our network-based SEIR model. The basic reproduction number (R₀) for the SEIR model is given by (66)

$$R_0=\beta \times N\times \tau .$$ [1]

Eq. 1 shows that the average number of infections caused by a single infection (R₀) is determined by the transmission probability (transmissibility) in a single network tie between an individual in the “I” compartment (i.e., infectious) and one in the “S” compartment (i.e., susceptible) multiplied by the average duration of infectiousness (τ) and the number of network ties per infectious individual (N).

We used the reported R₀ of 2.5 (38, 45) and τ of 3 (38, 39). In the homogeneous mixing model, the population size serves as the average number of network ties linked to an individual, because the network is assumed to be complete (all individuals are connected to every other individual) (33). In this case, the population size itself will be used for the value of N. However, in the network-based models, network ties are assumed to represent potential interactions which may cause a viral transmission. Therefore, individuals are not connected to every other individual, and N is typically smaller than the population size. It is known that the average degree of cases (the number of network ties that infected individuals have) is typically higher than the mean degree of the network (m: the average number of network ties that individuals have over the entire social networks); as individuals with a higher degree have a larger risk of infection, they account for a larger fraction of primary cases than their population ratio. This can be generally considered by using the SD (s), which is derived from the second moment of distributions. It has been shown that N is given as below when the model employs a structured social network as its framework (44),

$$N=m+\frac{s^2}{m}.$$ [2]

The “network N” here incorporates the mean degree (m) as well as the SD (s) of the degree distributions. Eq. 2 shows that the reproduction number can be disproportionately larger than expected from the mean degree when the degree distribution has large tails. For example, when a social network has a mean degree of 15 with an SD of 0 (all individuals connect with 15 others), there are no hubs [i.e., potential superspreaders if they become infectious (67)]. Then, the network N is simply 15. On the other hand, a social network with a mean degree of 15 with an SD of 8 has a substantial number of hubs, and, therefore, the adjusted network N will be inflated according to the level of variation.

Using Eq. 2 as well as m and s obtained in Constructing the Social Network Structure with Edge Weights, we obtained the network N of 18.7. Then, using Eq. 1, we obtained β of 0.04458, which roughly corresponds to β previously reported (0.043) (46). Since the network N varies by the social network structure randomly drawn across the 1,000 iterations, the predicted R₀ (of the default setting) for each iteration would increase or decrease based on the number of large social groups generated in the specific iteration (Fig. 2D).

Quality Assurance of Our Simulations.

We checked the quality of our simulations from three different perspectives. First, since we converted R₀ (2.5) to β (0.04458) using the median mean and the median SD for the 1,000 degree distributions, a typical social network structure exhibiting a mean close to the median mean and an SD close to the median SD was expected to exhibit R₀ of 2.5 in our simulations. The box plot in Fig. 2D (default scenario) shows that the median of R₀ over 1,000 iterations is almost 2.5 (2.499939). Therefore, we confirmed that the generation of social network structures and the simulations worked as intended. Second, we compared the result of our null model (default scenario with R₀ of 2.5) with prior simulation studies. For example, the peak cumulative incidence of a prior study with R₀ of 2.2 (38) was around 65%, while that of our null model was 75.1%. Although the prior study (38) used the ordinary differential equation-based SEIR model, the result should not differ substantially using the network-based SEIR model. Since we used a slightly higher R₀, the peak cumulative incidence became slightly higher, which is understandable. Third and finally, G.D. and S.K.I. reproduced the R code (originally written by A.N.) and confirmed the simulation results (see Data Availability).

Robustness Tests.

We performed 11 robustness test simulations embedded in 11 different approaches to evaluate whether different parameter choices alter our findings (200 iterations were completed for each setting described below).

First, we modified the number of the groups to “3,000, 2,000, 50, 50, 20, 50, 700, 1,250” (larger numbers of groups and smaller group sizes than the original “3,000, 1,000, 25, 25, 10, 25, 500, 500”) and “3,000, 500, 10, 10, 5, 10, 250, 250” (smaller numbers of groups and larger group sizes) (see SI Appendix, Figs. S3 and S4 for the results).

Second, for the dividing strategy, a probability of the split into two subgroups was manipulated within the range between 0.0 and 0.5 (six settings by steps of 0.1), where the defaults are 0.0 (the original default scenario) and 0.5 (the original dividing groups strategy) (SI Appendix, Fig. S5).

Third, we used geometric distributions with two parameters (0.2 and 0.8) instead of a uniform distribution, to draw probabilities for group assignment (SI Appendix, Figs. S6 and S7). For example, a geometric distribution with a parameter (success probability) of 0.2 is more right-skewed than that of one with a parameter of 0.8. Since the geometric distribution with the parameter of 0.2 would create a larger number of people acting as hubs who belong to groups with a larger number of group members and have a larger number of network ties, the effects of balancing groups are expected to be amplified.

Fourth, we used the Watts−Strogatz small-world model (75) with three different parameters for the rewiring probability (0.0, 0.5 and 1.0) instead of using 0.2 (SI Appendix, Figs. S8–S10). When the rewiring probability is higher, the mean distance of social networks for each group is lower.

Fifth, we used family ties and weak ties in one setting (SI Appendix, Fig. S11) and family ties and close ties in the other setting (SI Appendix, Fig. S12), in addition to the primary analysis with family ties, close ties, and weak ties. In other words, the edge weight of close ties turns out to be 0 in the first setting, while that of weak ties turns out to be 0 in the second setting. We aimed to do so to illustrate that our network intervention strategies do not rely on either weak ties (drawn from complete graphs of groups) or close ties (drawn from the small-world model).

Sixth, we altered the transmissibility (β from 0.04458 to 0.0357, 0.0535, 0.0713, and 0.0892), which corresponds to R₀ of 2.0, 3.0, 4.0, and 5.0, respectively (SI Appendix, Figs. S13–S16).

Seventh, we also altered the period of infectiousness, which was originally 3 d (as the parameter of a geometric distribution) and used 7 d and 10 d (SI Appendix, Figs. S17 and S18).

Eighth, we allowed individuals (agents of agent-based simulations) to update their behavioral strategies during the simulations to adjust for transmission across the social network. In more concrete terms, when individuals develop symptoms (after the presymptomatic period), they stay home until they recover (i.e., go to the “R” phase) and do not interact with individuals other than family members (SI Appendix, Fig. S19). This self-isolation procedure has been the most frequently implemented intervention against COVID-19 across the world, and is likely the most acceptable intervention across different cultures. We used an asymptomatic ratio of 45% (77), and assumed that the presymptomatic period and the postsymptomatic period both extend to half of the duration of the infectious period (78). The presymptomatic period of each individual is randomly determined by a binomial distribution with parameters n (the determined infectious period) and p (0.5). We also assumed that transmissibility of asymptomatic cases was the same as that of symptomatic cases (β of 0.04458 was used) (62, 63).

Ninth, we introduced 10 new cases spontaneously from outside of the simulated community every week until day 300 (SI Appendix, Fig. S20). The 10 new cases were randomly chosen from the pool of individuals in the S (susceptible) phase at the start of the week.

Tenth, we relaxed the condition of strict lockdown strategies, in which all network ties in the six sectors were dissolved. This is not a robustness test of our network intervention strategies, but of that of lockdown strategies. In more concrete terms, we set up exceptions for groups of smaller sizes (5, 20, 50) to continue interacting after a lockdown is implemented (SI Appendix, Fig. S21). While large gatherings are avoided, activities within groups with a small group size are permitted. Restricting large gatherings is a frequently used NPI implemented as a lockdown-type strategy; however, this approach also restricts activities of people who belong to large groups. For reference, in Texas, the order (as of July 2020) has limited outdoor gatherings of 10 or more people (79); an indoor gathering of up to 100 has been permitted in California (as of July 2020) (80).

Lastly, we considered consolidation of social space based on peoples’ attributes (e.g., socioeconomic position and race/ethnicity) (73). In more concrete terms, people with similar attributes may choose and prefer to use the same facilities or be members of the same groups (in contrast to random mixing). To confirm the reported effect of the proposed strategies in the case of such nonrandom mixing, we randomly assigned an attribute A to randomly selected families (50%) and an attribute B to the nonselected families (50%). In this setup, individuals with attribute A were more likely to be assigned to a random half of available groups, while those with attribute B were more likely to be assigned to the other half of the groups. Those with A occupied a majority in a half of all groups in the 7 sectors (A/B ratio is roughly 3), while those with the attribute B occupied a majority in the other half (A/B ratio is roughly 1/3). Therefore, network ties (both close ties and weak ties) between two individuals with the same attribute were more likely to occur (assortativity coefficient (81) = 0.177). The results are displayed in SI Appendix, Fig. S22.

Data Availability.

All simulation and analysis code has been deposited on A.N.'s COVID-19 Github page (https://github.com/akihironishi/covid19_pnas) (82).