Dynamic frontostriatal functional peak connectivity (in alcohol use disorder)

Abstract

Alcohol use disorder (AUD) is associated with changes in frontostriatal connectivity, but functional magnetic resonance imaging (fMRI) functional connectivity (FC) approaches are usually not adapted to these circuits. We developed a circuit‐specific fMRI analysis approach to detect dynamic changes in frontostriatal FC inspired by medial‐ventral‐rostral to lateral‐dorsal‐caudal frontostriatal gradients originally identified in nonhuman primate tract‐tracing data. In our PeaCoG (“peak connectivity on a gradient”) approach we use information about the location of strongest FC on empirical frontostriatal connectivity gradients. We have recently described a basic PeaCoG version with conventional FC, and now developed a dynamic PeaCoG approach with sliding‐window FC. In resting state data of n = 66 AUD participants and n = 40 healthy controls we continue here the analyses that we began with the basic version. Our former result of an AUD‐associated ventral shift in right orbitofrontal cortex PeaCoG is consistently detected in the dynamic approach. Temporospatial variability of dynamic PeaCoG in the left dorsolateral prefrontal cortex is reduced in AUD and associated with self‐efficacy to abstain and days of abstinence. Our method has the potential to provide insight into the dynamics of frontostriatal circuits, which has so far been relatively unexplored, and into their role in mental disorders and normal cognition.

We have recently described a basic PeaCoG version with conventional FC, and now developed a dynamic PeaCoG approach with sliding‐window FC. In resting state data of participants with alcohol use disorder (AUD) and healthy controls we continue here the analyses that we began with the basic version. We find that temporospatial variability of dynamic PeaCoG in the left dorsolateral prefrontal cortex is reduced in AUD and associated with self‐efficacy to abstain and days of abstinence.

1. INTRODUCTION

Alcohol use disorder (AUD) is characterized by a loss of control over drinking behavior which leads to diverse and severe negative consequences for affected individuals and their social environment (Bora & Zorlu, 2017; Kendler, Ohlsson, Karriker‐Jaffe, Sundquist, & Sundquist, 2017). One of the central neural systems involved in controlling behavior by stabilizing and destabilizing behavioral plans and neural representations in the cortex consists of cortical‐basal ganglia‐thalamus‐cortical loops which constitute a functional hierarchy from reward over cognitive to motor processes (Haber, 2003, 2016; Shipp, 2017). With their central role for controlling overt and covert behavior, these loops, and especially their initial frontostriatal segment, play a prominent role in normal cognitive functions (Balleine, Delgado, & Hikosaka, 2007; MacLean, 1972; Marquand, Haak, & Beckmann, 2017; Samejima, Ueda, Doya, & Kimura, 2005; Takikawa, Kawagoe, & Hikosaka, 2002) and mental disorders, where they have for example been implicated in alcohol addiction (Becker, Kirsch, Gerchen, Kiefer, & Kirsch, 2017; Courtney, Ghahremani, & Ray, 2013; Galandra et al., 2019; Park et al., 2010), in other addictions (Ersche et al., 2011; Morein‐Zamir & Robbins, 2015; Wilcox, Teshiba, Merideth, Ling, & Mayer, 2011; Yuan et al., 2017), as well as in disorders like schizophrenia (Fornito et al., 2013) or attention deficit hyperactivity disorder (Naaijen et al., 2018).

While the classical model of cortical‐basal ganglia‐thalamus‐cortical loops assumes that a cortical region projects to a part of the striatum that ultimately projects back to the original cortical site (“closed loop”), it is well established that cortical regions have widespread and distributed projection profiles in the striatum and that patches of the striatum receive overlapping projections from different cortical areas (Averbeck, Lehman, Jacobson, & Haber, 2014; Choi, Yeo, & Buckner, 2012; Jarbo & Verstynen, 2015; Ogawa et al., 2018; Selemon & Goldman‐Rakic, 1985; Yeterian & Van Hoesen, 1978). Already very early, it had been recognized that the projection fields of different cortical areas are convergent if the cortical areas are anatomically connected (Yeterian & Van Hoesen, 1978), which might represent an underlying anatomical mechanism that controls the dynamic formation of networks of interacting cortex areas.

In a comprehensive review of the literature on cortical‐basal ganglia‐thalamus‐cortical circuits Shipp (2017) discusses the structure and function of “closed” and “open loops” that are formed by different frontostriatal projections. “Open loop” projections go from the cortex to parts of the striatum that finally project to other cortical sites, and can provide an interface of cortical areas to influence the function of distant closed cortical‐basal ganglia‐thalamus‐cortical loops and thus the respective brain networks.

However, these models are mainly based on nonhuman primate tract‐tracing data, and the functional relevance of connectivity changes in these “closed loop” and “open loop” frontostriatal projections and their implications for normal and pathological cognition and behavior are so far only incompletely understood.

While the functional dynamics of these circuits are almost impossible to assess with other neuroscientific methods, with its capability for simultaneous data acquisition over the cortex as well as subcortical regions with relatively precise spatial resolution, functional MRI (fMRI) is ideally suited to assess such changes in frontostriatal circuit function. However, the most relevant fMRI analysis method at hand, functional connectivity (FC) analysis, is usually not tailored for circuit‐specific analysis and might in its standard form only provide a perspective on the processes in frontostriatal circuits that might be difficult to interpret with respect to this question.

Therefore, we have developed an fMRI data functional connectivity (FC) analysis approach that aims at assessing information about the relative spatial distribution of frontostriatal connectivity in fMRI resting state data (Gerchen, Rentsch, Kirsch, Kiefer, & Kirsch, 2019). For simplification and for increased interpretability of the results we have based our method on the model of medial‐ventral‐rostral to lateral‐dorsal‐caudal frontostriatal gradients by Haber (2003). It is well established from non‐human primate tract tracing studies (Averbeck et al., 2014; Haber, 2003) and has been confirmed in human magnetic resonance imaging (MRI) studies (Choi et al., 2012; Di Martino et al., 2008; Draganski et al., 2008; Jeon, Anwander, & Friederici, 2014; Jung et al., 2014; Marquand et al., 2017) that the topography of frontostriatal projections follows a medial‐ventral‐rostral to lateral‐dorsal‐caudal organization, where more ventral and rostral frontal areas project to more ventral and rostral striatal regions, while more dorsal and caudal frontal areas project to more dorsal and caudal striatal regions (Haber, 2003, 2016), which has been described as a frontostriatal connectivity gradient in a model by Haber (2003).

In our fMRI analysis approach we depart from the conventional point‐to‐point (for example seed‐to‐voxel or region of interest [ROI]‐to‐ROI) analyses usually applied in FC studies and base our analyses on the spatial localization of maximal connectivity of seed voxels in a target area. Specifically, we use voxels in the frontal cortex as seeds and identify the location of the voxel in the striatum with maximal FC, which we call “peak connectivity.” This frontostriatal peak connectivity marks the striatal area a frontal cortical region is most strongly interacting with, and should be relatively close to the anatomical and electrophysiological information the Haber model is based on.

To obtain a frontostriatal gradient we then apply principle component analysis (PCA) over the empirically estimated peak connectivity locations of all frontal voxels, and extract the first principle component as the representative axis. The projection of the striatal peak connectivity locations on this gradient provides what we call PeaCoG (“peak connectivity on a gradient”) values, which are then used for further analyses (please see the Materials & Methods Section 2.3.3 for more details).

With this approach we were able to identify a region in the right orbitofrontal cortex (rOFC) where striatal peak connectivity location was shifted ventrally in patients with AUD in comparison to healthy controls (HC; Gerchen et al., 2019; see inlay in Figure 2a). Interestingly, the patient group showed a reduction in PeaCoG variability, suggesting a “clamping” of the rOFC to ventral striatal regions in alcohol addiction, or, in other terms, a bias towards the closed‐loop recurrent rOFC‐striatum circuit mode. In addition, we identified associations of PeaCoG values with self‐report questionnaires reflecting different aspects of alcohol addiction like craving or ability to control drinking behavior in the superior frontal gyrus, medial frontal and dorsolateral prefrontal cortex, and the inferior frontal gyrus (Gerchen et al., 2019).

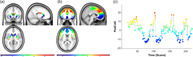
FIGURE 2.

rOFC cluster dynamic PeaCoG spatial distribution. (a) Number of time points the right OFC cluster (small inlay) dynamic peak connectivity fell into spatial bins in the striatum during the resting state session averaged over groups. The results demonstrate a ventral shift of dynamic rOFC‐striatal connectivity in the AUD group. The x‐axis corresponds to striatal locations in Figure 1a. Small asterisks mark bins where the number of time points was significantly different between the groups (p < .05 Bonferroni corrected for the number of bins [20]). Shaded areas represent the SEM. (b) Area in the striatum (blue) corresponding to the bin of the gradient where more connectivity in the AUD group was consistently detected over the different window sizes

Importantly, these analyses were based on conventional FC measures estimated over the whole time series of a resting state fMRI measurement. So far, it remained unclear whether frontostriatal peak connectivity also exhibits variability within individual subjects over the time course of an fMRI scanning session, and whether this variability is changed in AUD or is associated with clinical variables.

In this article we now describe a novel dynamic PeaCoG approach that assesses time‐varying peak connectivity locations along the same gradient as in the former approach with sliding‐window functional connectivity analysis and continue the analysis of the resting state data set begun in Gerchen et al. (2019) with this newly developed methodology.

2. MATERIALS AND METHODS

2.1. Participants

Data were acquired in the baseline session of an intervention study (Becker et al., 2017; Becker et al., 2018), and the results are based on exploratory analyses which were not preregistered as goals of the original study. We analyzed data of n = 66 participants diagnosed with alcohol addiction based on ICD‐10 criteria (age: 46.8 ± 9.16 years (mean ± SD; range 25–65 years; 16 female) and n = 40 healthy control participants (age: 47.28 ± 9.21 years, range 22–64 years; 17 female). All participants were eligible for MRI scanning and did not have further neurological or mental disorders. The patient group was recruited from the Central Institute of Mental Health inpatient addiction clinic. Patients abstained from alcohol for at least 5 days before scanning (10.12 ± 4.69 days [mean ± SD]) and were free of any detoxification medication for at least 3 days.

The study was approved by the local ethics committee of the Medical Faculty Mannheim at the University of Heidelberg, Germany (2011‐303 NMA) and all procedures complied with the WHO's Declaration of Helsinki. Before participation, all participants were informed about the study and provided written informed consent. After completion, participants received €50 compensation.

The originally acquired sample comprised 123 data sets, of which 2 were excluded due to incidental anatomical findings, 5 due to missing or corrupt physiological recordings, 4 due to excessive head motion, and 6 due to restricted brain coverage of the normalized functional images.

2.2. Data acquisition

Before scanning, the participants completed the Obsessive Compulsive Drinking Scale (OCDS; Anton, 2000), the Alcohol Abstinence Self‐Efficacy Scale (AASE; DiClemente, Carbonari, Montgomery, & Hughes, 1994), the Alcohol Dependence Scale (ADS; Skinner & Horn, 1984), and the Alcohol Urge Questionnaire (AUQ; Bohn, Krahn, & Staehler, 1995).

MRI measurements were conducted on a 3 T Siemens Trio TiM scanner (Siemens Healthineers, Erlangen, Germany) at the CIMH. Anatomical MPRAGE images were acquired with repetition time TR = 2.3 s, echo time TE = 3.03 ms, flip angle 9°, and resolution of 1 × 1 × 1 mm. During the resting state measurement 220 functional echo planar imaging (EPI) images were acquired with TR = 1.5 s, TE = 28 ms, flip angle 80° in 24 4 mm slices with 1 mm gap and 3 × 3 mm in‐plane resolution. During functional scanning, heart rate and respiration signals were monitored and saved.

2.3. Data analysis

Data analysis was conducted with MATLAB (R2011b; MathWorks Inc., Sherborn, Massachusetts, United States). Imaging analysis was conducted with SPM12 (v6685; Wellcome Department of Cognitive Neurology, London, United Kingdom).

2.3.1. Preprocessing

Anatomical images were segmented and normalized to the SPM12 TPM MNI template and the forward and inverse transformation matrices of the normalization were saved. The functional resting state images were corrected for heart rate and respiration with AZTEC (van Buuren et al., 2009), slice‐time corrected, realigned to the mean image of the run, co‐registered to the anatomical image, normalized by applying the estimated forward normalization matrix, resampled to a resolution of 2 × 2 × 2 mm, and smoothed with a Gaussian kernel with full width at half maximum FWHM = 6 mm.

2.3.2. Anatomical masks

Hemisphere‐specific masks of the striatum and of the frontal cortex combined with the anterior insula and the anterior cingulate cortex (called “frontal masks” afterwards) were constructed from the Neuromorphometrics atlas accompanying SPM12. All analyses were conducted within these masks.

The individual inverse normalization matrices were used to project the masks from MNI space to the individual subject space and estimate the size of these regions in each subject. These estimates were used as covariates in the respective second level analyses in normalized space to control for a possible confounding influence of anatomical differences in the target structures on our results.

2.3.3. First level analyses

First level models were set up in SPM12 that included the six standard motion regressors, a cerebrospinal fluid (CSF) signal, a white matter (WM) signal, the global gray matter signal, and dummy nuisance regressors of volumes affected by head motion (movement threshold = 1 mm; global intensity change threshold z = 5) estimated with the ART toolbox (http://www.nitrc.org/projects/artifact_detect). From this first level analysis the residual images corrected for the covariates were saved. Nuisance regressors were estimated in a prior first level analysis without autocorrelation correction (“first” first level).

Voxel time courses of the voxels contained in the defined masks were then extracted from the residual images and saved.

PeaCoG

All analyses were conducted separately in the left and right hemisphere. For each voxel in the frontal masks, Pearson correlations were used to estimate functional connectivity with all voxels in the striatum, and the MNI coordinates of the striatal voxel with the highest correlation were extracted (“peak connectivity”). Further analyses are then based on this spatial information extracted from the data.

To reduce these three‐dimensional values to a single representative dimension that is straightforward to analyze, the peak connectivity positions of each frontal voxel were averaged over all subjects, a principal component analysis was conducted over this data, and the first principle component was extracted. This component is the representative spatial gradient (Figure 1a) along which frontal peak connectivity is maximally distributed in the striatum. It is now possible to project the individual peak connectivity location of each frontal voxel onto this gradient (PeaCoG) and map these PeaCoG values on the frontal cortex (Figure 1b). When subject‐specific peak connectivity values are projected onto the representative gradient, individual PeaCoG maps can be obtained that can then be used for second level analyses (see also Gerchen et al. (2019)).

FIGURE 1.

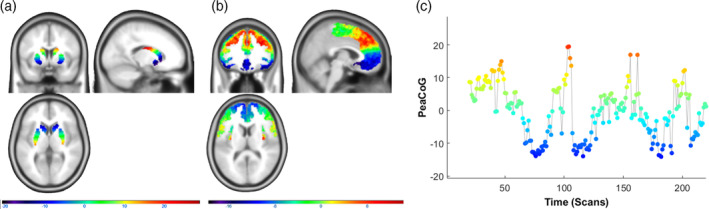
Frontostriatal connectivity gradient and dynamic PeaCoG time course. (a) Locations of striatal voxels projected on the empirically estimated striatal gradient. (b) Striatal peak connectivity locations on the gradient of frontal voxels (PeaCoG maps) averaged over the whole sample. A medial‐ventral‐rostral to lateral‐dorsal‐caudal organizational pattern of frontostriatal connectivity is clearly visible. Please note that the scale of the colors in display B is more restricted than in display A, which presumably is due to a regression to the mean effect related to the averaging. (c) Dynamic striatal peak connectivity of a voxel in the left dlPFC (Figure 3) during the resting state session in a single patient with AUD that was not specifically selected (first participant of the sample). The y‐axis and the colors correspond to striatal locations in Figure 1a. We conducted dynamic PeaCoG analyses based on sliding window dynamic functional connectivity with window sizes of 15, 20, 30, and 45 volumes, the example time course is shown for a window size of 20 volumes

Dynamic PeaCoG

To assess intraindividual variability of the PeaCoG estimate over time we developed a dynamic PeaCoG approach based on sliding‐window functional connectivity analysis. In this procedure we estimate the position of the peak connectivity position from a chunk of the time course with a defined number of data points (window) and project this position onto the general gradient to obtain a PeaCoG value. Then, the window is moved ahead one time point by one time point and the procedure is repeated to construct a time course of PeaCoG values (Figure 1c). As the results of dynamic functional connectivity analyses depend on the chosen window size, we conducted analyses with four different window sizes of 15, 20, 30, and 45 volumes (24.6 s, 32.8 s, 49.2 s, and 73.8 s, respectively) and consider the results together. We selected window sizes that span the range from ~ 20 to 60 s that is often used in sliding window FC studies, and increased the step size for longer windows. We did not specifically select or optimize the exact numbers, but arbitrarily started with a window size of 15 volumes (=22.5 s), increased the window size by 5 volumes, and added 5 additional volumes to the increase at every step (15 + 5 = 20; 20 + 10 = 30; 30 + 15 = 45) up to a window size of 45 (= 67.5 s).

2.3.4. Second level analyses

With the obtained time‐dependent PeaCoG values it is then possible to conduct analyses based on the intraindividual variability of frontostriatal peak connectivity and compare it between subjects. For this we focused on two measures: The distribution of peak connectivity locations in the striatum over time, and the SD of the dynamic PeaCoG time course on the frontal maps. All reported second level analyses included age, gender, and the estimated individual size of the striatum and frontal masks as covariates.

Right OFC ROI analyses

We used the first measure for a ROI analysis to test whether the shift of frontostriatal peak connectivity towards ventral striatal regions that we identified in the right OFC with PeaCoG analyses based on conventional functional connectivity over the whole time series (Gerchen et al., 2019; see inlay in Figure 2a) could also be demonstrated based on the spatial distribution of dynamic PeaCoG values in the striatum over time. For this we split the striatal gradient into 20 bins and counted the time points peak connectivity fell into these bins (i.e., similar to a histogram). The number of bins was arbitrarily chosen at a relatively high even number. The bin size (2.5 mm) is slightly higher than the original length of voxel edges (2 mm). We then compared the counts of each bin between groups with two‐sample t tests with a significance threshold of p = .05 Bonferroni corrected for the number of bins (nominal threshold p = .05/20 = .0025).

Dynamic PeaCoG SD

We used the second measure, the PeaCoG SD, to conduct exploratory analyses over the whole frontal masks and identify regions where the variability of dynamic frontostriatal peak connectivity differed between groups. Here we used mass‐univariate two‐sample t tests to test for group differences in each voxel and used a cluster‐level corrected significance threshold of p = .025 (p = .05 Bonferroni corrected for the number of hemispheres: nominal threshold p = .05/2 = 0.025) with a cluster‐defining threshold (CDT) of p < .001 uncorrected. In our analyses, we did not correct for the number of different window sizes here, but only consider results that were consistently detected with at least two window sizes.

Association with clinical variables

We further tested the association of the frontal PeaCoG SD maps with nine clinical variables (3 scores of the OCDS, 3 scores of the AASE, the ADS sum score, the AUQ sum score, and the number of abstinent days before scanning) within the clinical group. In these tests we applied the same nominal cluster‐corrected threshold of p = 0.05/2 = 0.025 and report only results that were obtained with more than one window size. Please note that we chose this relatively relaxed threshold for our exploratory analyses, and that we did not correct for the number of clinical variables here.

Further we conducted partial correlation analyses of the nine clinical variables with the mean dynamic PeaCoG SD from the cluster in the left dorsolateral prefrontal cortex (dlPFC) identified in the dynamic PeaCoG SD group comparison (Figure 3). Here, we also report results at a nominal threshold of p < .05 that were detected with at least two window sizes. Again we chose a relatively relaxed discovery threshold for these exploratory analyses, and did not correct for the number of clinical variables.

FIGURE 3.

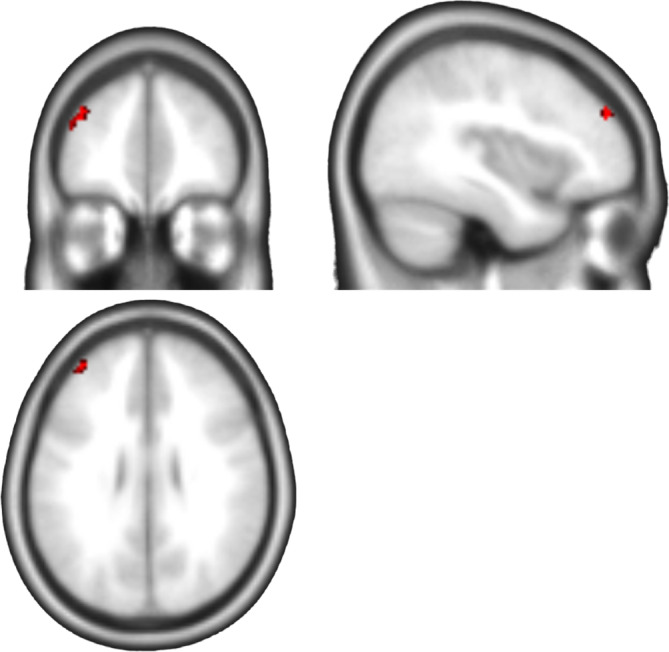
Group comparison of dynamic PeaCoG SD. Cluster in the left dorsolateral prefrontal cortex (dlPFC) with higher dynamic PeaCoG variability (SD) in healthy controls in comparison to participants with AUD (cluster‐level p < .025 corr., CDT = 0.001 unc.). The cluster was detected with three of four window sizes. Brighter colors indicate higher overlap (max 3)

3. RESULTS

The estimated frontostriatal peak connectivity gradients (Figure 1a,b) are the same as in Gerchen et al. (2019). They are largely consistent with the model of a medial‐ventral‐rostral to lateral‐dorsal‐caudal gradient striatal connectivity in the frontal cortex, except for the most dorsal and caudal parts, where connectivity seems to be oriented toward more middle striatal parts of the striatum in our data (Figure 1b).

An example of a frontostriatal peak connectivity time course obtained with the dynamic PeaCoG approach is shown in Figure 1c. In this exemplary and not specifically selected participant with AUD (the first participant of the whole sample) it can be seen that the peak connectivity location on the striatal gradient is exhibiting dynamic changes over time within a single participant. Such dynamic PeaCoG time courses are available for each single voxel in the frontal cortex, and are the basis for our further analyses.

3.1. Right OFC ROI analyses

First, we used this information to assess and compare the spatial distribution of striatal peak connectivity in the right OFC cluster that differed between AUD and HC participants in our former analyses based on conventional FC. Plots of the average distribution of dynamic PeaCoG values in the right OFC ROI are shown for the four window sizes in Figure 2a. With all four window sizes a clear shift in the dynamic spatial peak connectivity distribution in the AUD group toward more ventral striatal regions is evident. We identified bins in all four analyses where the number of time points of peak connectivity with these bins was significantly different between the groups (nominal threshold p = .05/20 = .0025; marked with asterisks in Figure 2a; see Supplementary Table S1 for detailed results). Over all four window sizes, two bins in the mid striatum had lower connectivity and one bin in the ventral striatum had increased connectivity in the AUD group. The bin with increased connectivity is plotted in Figure 2b as a demonstration how our approach can be used to obtain insight into the temporospatial function of frontostriatal connectivity.

3.2. Dynamic PeaCoG SD

We then proceeded our analyses by assessing the SD over time of the dynamic PeaCoG time courses. In our exploratory analyses over the whole frontal masks we identified several clusters where dynamic PeaCoG SD was lower in the AUD group compared with the HC group (Table 1). A cluster in the right frontopolar cortex was detected with the 15 and 20 volume windows sizes (cluster bb in Table 1), and a cluster in the left lateral orbital gyrus was detected with the 30 and 45 volume window sizes (cluster cc in Table 1). The most consistent effect over the window sizes was a cluster in the left dorsolateral PFC (left dlPFC; cluster aaa in Table 1; Figure 3) that was consistently detected with three of our four sliding‐window sizes (15, 20, and 45 volumes; effect sizes of Cohen's d = 0.77, 0.79, 0.72, respectively) and where the effect was not much smaller (Cohen's d = 0.7) although not significant in the fourth (30 volumes).

TABLE 1.

SPM results of the dynamic PeaCoG SD group comparison

	Cluster‐level		Peak‐level			Overlapping clusters
	pFWE‐corr	kE	pFWE‐corr	t	MNI (mm; x, y, z)
15 vols
Left	0.013	31	0.004	5.37	−44, 46, 24	aaa
			0.376	4.20	−38, 48, 30
	0.017	29	0.504	4.07	−24, 22, −20
			0.945	3.58	−28, 30, 22
Right	0.004	43	0.013	5.12	26, 64, 2	bb
			0.767	3.81	22, 54, −2
			0.965	3.51	28, 52, 6
	0.001	56	0.059	4.74	10, 50, 8
			0.246	4.15	8, 48, 20
			0.744	3.83	4, 42, 14
20 vols
Left	0.015	30	0.093	4.63	−38, 46, 30	aaa
			0.107	4.59	−44, 46, 22
Right	0.004	41	0.024	5.02	26, 64, 2	bb
			0.741	3.84	24, 52, −2
30 vols
Left	0.004	37	0.029	4.91	−44, 36, −18	cc
			0.837	3.77	−42, 46, −14
			0.996	3.25	−50, 36, −10
45 vols
Left	0.005	32	0.142	4.52	−46, 34, −16	cc
			0.498	4.14	−44, 48, −16
	0.022	23	0.251	4.37	−38, 48, 28	aaa
	0.013	26	0.294	4.33	−36, 28, 46

Note: Results are presented for the contrast HC > AUD. For the contrast AUD > HC no significant cluster was detected with any window size. Clusters that were consistently found with different window sizes are marked as overlapping clusters with small letters. Table shows 3 local maxima more than 8 mm apart.

We did not identify any significant clusters in any of the analyses where dynamic PeaCoG SD was increased in the AUD group in comparison to the HC group.

3.3. Association with clinical variables

The exploratory analyses testing associations of dynamic PeaCoG SD with the nine clinical variables over the whole frontal cortex maps did not detect significant associations at the nominal cluster‐level threshold of p = .025 for any single window size.

When we conducted the ROI association analyses specifically for the left dlPFC cluster (Figure 3) we detected positive associations of the averaged dynamic PeaCoG SD at the nominal significance level with the AASE self‐efficacy to abstain (AASE‐S) scale for all four window sizes (15 volumes: rho = 0.3047, p = .0212; 20 volumes: rho = 0.3384, p = .01; 30 volumes: rho = 0.2994, p = .0237; 45 volumes: rho = 0.3107, p = .0187; Figure 4a) and with the number of days of abstinence before scanning for three window sizes (15 volumes: rho = 0.2434, p = .0791; 20 volumes: rho = 0.2775, p = .0442; 30 volumes: rho = 0.3051, p = .0263; 45 volumes: rho = 0.3032, p = .0273; Figure 4b).

FIGURE 4.

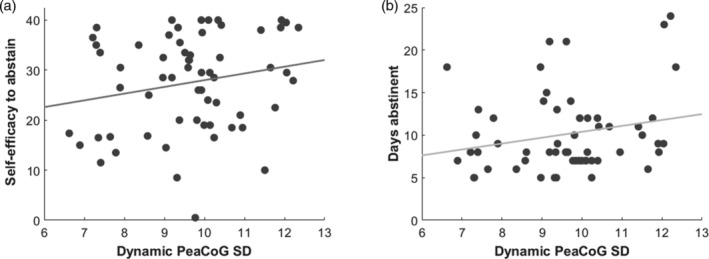
Association of dynamic PeaCoG SD in the left dlPFC cluster with clinical variables. (a) Positive association of left dlPFC dynamic PeaCoG SD with self‐efficacy to abstain from alcohol assessed with the Alcohol Abstinence Self‐Efficacy Scale (rho = 0.3384, p = .01). The association was nominally significant with all four window sizes. (b) Positive association of left dlPFC PeaCoG SD with days of abstinence before scanning (rho = 0.2775, p = .0442). The association was nominally significant with three of four window sizes. Scatter plots for the 20 volume window size are shown

4. DISCUSSION

In this article we have established a novel fMRI analysis method to assess the spatial dynamics of peak functional connectivity of frontal voxels in the striatum. Our dynamic PeaCoG approach provides a window into fast functional reorganization of frontostriatal circuits, and allows to test hypotheses about their dynamic function.

Our PeaCoG approach abstracts from the exact strength of functional connectivity at specific voxels or ROIs, which so far has been the target of the vast majority of functional connectivity studies, and instead uses information about the relative spatial distribution of connectivity values in the target structure. It is worthwhile to note that this information would be much more difficult to obtain with other neuroscientific methods like direct electrophysiological recordings, but is straightforward to assess in fMRI, which is due to the specific strength of fMRI in simultaneous large‐scale measurements of cortical and subcortical sites despite its relatively low temporal resolution and susceptibility for noise from diverse sources. Nonetheless, it would be important to substantiate the effects described here with less indirect neuroscientific methods.

Importantly, we focus our PeaCoG analyses on the single most representative data point that should best reflect the functional state of a specific frontostriatal circuit, the peak connectivity location on a frontostriatal connectivity gradient. Analyzing only this peak connectivity location reduces the amount of information that is potentially available with fMRI, but strongly enhances the practicability and interpretability of the approach.

To directly demonstrate the applicability of our method and already use it to obtain insight into relevant pathological processes, we continued our analyses of an AUD resting state data set which we have begun with the conventional FC PeaCoG approach in Gerchen et al. (2019).

Here, we first focused on the rOFC cluster that we obtained with the conventional FC approach. It is important to note that we interpreted this effect as a “clamping” of the OFC to the ventral striatum, but that this was based on group effects, and not on a representation of the dynamics of the connectivity, which would be a more appropriate test for this conclusion. In principle, conventional FC is a special case of dynamic FC using a single window with the length of the complete time course. Therefore, it is lying at an extreme end of the spectrum of representations of the signal, and it is important to test whether an effect detected here would generalize to analyses based on more dynamic representations, which is exactly the case here. While larger window sizes seem to show stronger peaks in our data, we are able to demonstrate the ventral shift of rOFC striatal peak connectivity consistently for all four window sizes we assessed (Figure 2a), supporting the interpretation of our original finding as a disease‐related change in the function of the system. Furthermore, we now demonstrate how our procedures can be used to map the involved parts of the striatum (Figure 2b) to provide results with a straightforward interpretation.

We then focused our analyses on the variability (SD) of the dynamic PeaCoG signal, and found a cluster in the left dlPFC with decreased SD in AUD. To limit the dependency of our results on the assumptions of the applied parametric test statistics we have repeated our main analyses on the dynamic PeaCoG SD maps with a permutation approach (threshold‐free cluster enhancement (TFCE) implemented in FSL's “randomize” function) that constructs a test statistic by randomly assigning participants to the experimental groups while taking nuisance variables into account (Winkler, Ridgway, Webster, Smith, & Nichols, 2014). With this nonparametric approach we identify the same overlapping cluster in the left DLPFC again with the same three window sizes (Supplementary Figure 1), demonstrating that our results are robustly detected with parametric and nonparametric statistical methods.

While our PeaCoG measures might appear rather abstract, they have a straightforward interpretation that is reflecting a potential core functionality of frontostriatal circuits. If, for example, the DLPFC really influences other brain regions by striatal projections to their “closed” cortical‐basal ganglia‐thalamus‐cortical loops as suggested by Shipp (2017), the variability of DLPFC dynamic PeaCoG would reflect how flexible this executive control mechanism is exerted over networks within an individual. A less dynamic system might thus reflect a pathological state that is associated with less behavioral control, like in AUD.

Over the last decade dynamic, or time‐varying, FC has been increasingly adapted in fMRI research, and a large variety of methodological choices for estimating dynamic FC are now available (see for example, Lurie et al., 2019; Preti, Bolton, & Van De Ville, 2017; Savva, Mitsis, & Matsopoulos, 2019). A central aspect that concerns all methods is that the existence of dynamic fluctuations in functional connectivity should optimally be tested for with appropriate null models (Chang & Glover, 2010; Hindriks et al., 2016; Liegeois, Laumann, Snyder, Zhou, & Yeo, 2017; Savva et al., 2019; Zalesky & Breakspear, 2015). Constructing such models and supporting the existence of dynamic fluctuations statistically is, however, challenging (Hindriks et al., 2016; Liegeois et al., 2017). For example, Hindriks et al. (2016) found that it is rather impossible to identify time‐varying FC in short data sets of individual participants, while averaging over subjects or sessions clearly increased the power and allowed establishing the existence of dynamic FC.

Importantly, here we did not yet rigorously test for the existence of dynamic changes in the topography of frontostriatal peak functional connectivity with an appropriate spatiotemporal null model. Such a null model for the dynamic PeaCoG approach should implement the underlying assumption that frontal voxels are constantly linked to a specific location in the striatum and do not exhibit dynamical changes in their maximal connectivity location. The data derived from such a model should be combined with the complex noise present in fMRI modeled under realistic assumptions, and the real data should be tested against the modeled data. While it is nontrivial to implement such an approach, it will be a crucial step for future research to test for the existence of dynamic PeaCoG changes.

Another potential concern is the stability of the peak voxel selection, which might be susceptible to noise. In our former paper we have conducted a control analysis in which we restricted the peak voxel selection to clusters of k = 5 voxels with maximal connectivity (Gerchen et al., 2019). While it was computationally infeasible to repeat our whole dynamic PeaCoG analyses with this additional cluster criterion, we have tested the effect of this control analysis in the DLPFC cluster that was consistently showing a group difference in dynamic PeaCoG SD in three of the four window sizes (Figure 3). The original results in the cluster were: 15 vols: t = 4.20, p = 2.9090e−05; 20 vols: t = 4.56, p = 7.3478e−06; 30 vols: t = 3.98, p = 6.6386e−05; 45 vols: t = 3.64, p = 2.1907e−04 and the corrected results were: 15 vols: t = 2.90, p = .0023; 20 vols: t = 3.46, p = 3.9817e−04; 30 vols: t = 3.22, p = 8.6714e−04; 45 vols: t = 2.79, p = .0031). While the group difference was still highly significant, this shows that peak voxel stability is a concern in the applied methodology and should be taken into account in future implementations of the approach.

Interestingly, the SD in the left dlPFC cluster was positively associated with self‐perceived efficacy to abstain from alcohol as well as days of abstinence before scanning in the AUD group. Thus, this phenotype might reflect the recovery process during the treatment of AUD and abstinence. The clinical associations that we found suggest that our novel fMRI analysis method is able to detect meaningful results that contain relevant information about pathological brain processes. However, all our analyses were of an exploratory nature and we applied relatively relaxed statistical thresholds in the analyses assessing clinical associations. Therefore, our results should only be taken as a first hint on the role of frontostriatal peak connectivity in these processes and need to be replicated.

Besides the use case in AUD demonstrated here, the established method has the potential to allow insights into the flexible and distributed dynamic function of frontostriatal circuits in other disorders as well as normal cognition.

An interesting further general question is how changes in frontostriatal circuits relate to dynamical interactions in typical resting‐state networks such as the default‐mode network, salience, and the cognitive control network. While this question is far beyond the scope of this paper, our approach is in principle well suited to also address this kind of questions.

Furthermore, the dynamic PeaCoG approach could directly be translated into a real‐time fMRI neurofeedback approach that could aim at increasing the SD of lateral PFC‐striatal peak connectivity and might be applied as an add‐on therapy for AUD, but potentially also other disorders where frontostriatal circuits are centrally involved.

5. CONCLUSIONS

We have established a novel fMRI analysis method based on sliding‐window functional peak connectivity of frontal regions in the striatum. The method allows obtaining insight into the dynamic function of frontostriatal circuits, which has so far been relatively unexplored. Our results suggest that connectivity in these circuits is exhibiting spatial dynamics, and that changes in these dynamics might play a role in AUD.

CONFLICT OF INTEREST

The authors declare no conflicts of interest.

AUTHOR CONTRIBUTIONS

P.K., F.K., and M.K. were responsible for the concept and design of the study the data were taken from. A.R. and M.K. collected the data. M.F.G. developed the analysis approach and M.F.G., F.W., and P.H. analyzed the data. M.F.G., F.W., and P.K. drafted the manuscript. F.K., A.R., P.H., and M.K. provided critical revision of the manuscript for important intellectual content. All authors critically reviewed content and approved the final version for publication.

Supporting information

Supplementary Figure 1 Group comparison of dynamic PeaCoG standard deviation with non‐parametric permutation tests. Non‐parametric permutation tests identified the same cluster (centered at MNI coordinates −38, 48, 30) in the left dorsolateral prefrontal cortex (dlPFC) with higher dynamic PeaCoG variability (SD) in healthy controls than in participants with AUD. Effects were estimated with FSL's “randomize” function and threshold free cluster enhancement (TFCE) at a statistical threshold of p < 0.025. The cluster was again detected with the same three window sizes. Brighter colors indicate higher overlap (max 3).

Supplementary Table 1. Numerical Results of the group comparison of rOFC cluster dynamic PeaCoG spatial distribution presented in Figure 2a. *: p < 0.05 Bonferroni corrected for the number of bins (p < 0.05/20 = 0.0025); **p < 0.05 Bonferroni corrected for the number of bins and window sizes (p < 0.05/[20 x 4] = 0.000625). Degrees of freedom DoF = 100 for all analyses.

Gerchen MF, Weiss F, Kirsch M, et al. Dynamic frontostriatal functional peak connectivity (in alcohol use disorder). Hum Brain Mapp. 2021;42:36–46. 10.1002/hbm.25201

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy and ethical restrictions.