Abstract
Purpose
Estimation of the amount of waste to be generated in the coming years is critical for the evaluation of existing waste treatment service capacities. This study was conducted to evaluate the performance of various mathematical modeling methods to forecast medical waste generation of Istanbul, the largest city in Turkey.
Methods
Autoregressive Integrated Moving Average (ARIMA), Support Vector Regression (SVR), Grey Modeling (1,1) and Linear Regression (LR) analysis were used to estimate annual medical waste generation from 2018 to 2023. A 23-year data from 1995 to 2017 provided from the Istanbul Metropolitan Municipality’s affiliated environmental company ISTAC Company were utilized to examine the forecasting accuracy of methods. Different performance measures such as mean absolute deviation (MAD), mean absolute percentage error (MAPE), root mean square error (RMSE) and coefficient of determination (R2) were used to evaluate the performance of these models.
Results
ARIMA (0,1,2) model with the lowest RMSE (763.6852), MAD (588.4712), and MAPE (11.7595) values and the highest R2 (0.9888) value showed a superior prediction performance compared to SVR, Grey Modeling (1,1), and LR analysis. The results obtained from the models indicated that the total amount of annual medical waste to be generated will increase from about 26,400 tons in 2017 to 35,600 tons in 2023.
Conclusions
ARIMA (0,1,2) model developed in this study can help decision-makers to take better measures and develop policies regarding waste management practices in the future.
Keywords: ARIMA; Grey modeling (1,1); Medical waste; Prediction; SVR; Grid search; Optimization
Introduction
The rapid increase in population and industrialization, and consequently developing economy and urban growth have led to an increase in the number of hospitals, clinics, and other health facilities [1]. This increase in the number of health institutions causes large amounts of medical waste (MW). Although MW constitutes a small part of all waste, it is hazardous in terms of its potential for damaging living things. It can cause several health problems such as infectious diseases. For example, equipment such as syringes or needles used for life-threatening diseases such as typhoid, cholera, hepatitis, and AIDS can lead to the spread of these epidemic diseases.
According to the World Health Organization (WHO), 15% of MW is accepted as hazardous waste that must be handled carefully and need to be managed properly [2, 3]. The proper treatment and management of MW are critical for human health and the environment [4–7]. Inefficient and inappropriate MW management can cause serious environmental pollution such as unpleasant odor, and growth and multiplication of various microorganisms [8]. Thus, MW must be properly processed and disposed of in order to prevent potential risks. In this context, planning the future capacity of the treatment facilities and the determination of proper strategies are very important for managing the amount of waste to be generated. This can only be achieved with the estimation of the MW amount that will occur in the future. Also, the accurate estimation of the MW generation can be useful in the planning of recycling, storage, transportation, and disposal operation capacities.
In previous studies, various mathematical tools such as time series models, data mining, and artificial intelligence techniques were used to estimate the amount of MW to be generated in the future (Table 1). For example, in order to determine the generation rates and physical properties of MW, Bdour et al. (2007) evaluated the quantity and quality of waste produced in the Irbid city of Jordan. The statistical analysis of the study demonstrated that the number of bed-patient (occupancy rate) at the hospital, kind and size of departments, and type of specialization are the most important factors affecting the generation rates [9]. Sabour et al. (2007) developed a mathematical model to predict the composition and generation of hospital waste using the number of hospitals and the number of active beds in Iran [10]. Jahandideh et al. (2009) used the artificial neural network (ANN) and multiple linear regression (MLR) models to predict the MW generation rate in Iran [11]. Eleyan et al. (2013) used the System Dynamics Model for hospital waste characterization and generation using data from Jenin District hospitals, Palestine [12]. Idowu et al. (2013) evaluated the management practices for MW in selected healthcare facilities in Lagos, Nigeria. The results of the study indicated that the current MW management practices and strategies in Lagos are weak. As a result of the study, they stated that low volume MW was generated from health institutions in Lagos and this was probably due to the poor management of MW streams [13]. Karpušenkaitė et al. (2016) evaluated and compared the performance of partial least squares, support vector machines, ANN, MLR and four non-parametric regression methods to estimate Lithuania’s annual MW generation [14]. Tesfahun et al. (2016) developed predictive models for the estimation of a healthcare waste generation rate [15]. Al-Khatib et al. (2016) developed three different MLR models to estimate the daily total hospital waste, general hospital waste, and total hazardous waste in Nablus City using the number of inpatients, number of total patients, and number of beds [16]. Chauhan and Singh (2017) tested different autoregressive integrated moving average (ARIMA) models to predict MW generation of the Garhwal region of Uttarakhand, India. Based on the results based on statistical parameters, they realized that the ARMA(1,1) model is the best model for estimation MW [17]. Minoglou and Komilis (2018) investigated the correlation between socio-economic factors and the MW generation rate using the MLR and principal component analysis [18]. Adamovic et al. (2018) used general regression neural network models to estimate the annual amounts of dangerous chemicals and healthcare waste for various European Union countries. They utilized various social, economic, industrial and agricultural indicators as input variables [19]. Karpušenkaitė et al. (2018) proposed a time-series-based hybrid mathematical model to predict the annual automotive waste amount, including hazardous types [20]. Thakur and Ramesh (2018) investigated the composition and production rates of biomedical waste using MLR and ANN techniques in selected hospitals in Uttarakhand, India. As a result of the analysis, they noticed that the amount of MW depends on the seasons of the year [21]. Golbaz et al. (2019) used MLR and several Neuron-and Kernel-based machine learning methods were employed to the estimation of MW generation rates of Karaj metropolis. According to the results of the study, they found that the performance of Neuron and Kernel-based machine learning methods is satisfactory and the number of staff and hospital ownership variables are the most effective variables in predicting the MW generation rate [22]. Hao et al. (2019) addressed the problem of predicting multiple factors for the recycling of healthcare waste in Shanghai, China. In order to improve the accuracy of healthcare waste recovery prediction, they proposed a hybrid neural network based on the grey model, triple exponential smoothing, and particle swarm optimization [23]. Çetinkaya et al. (2019) developed a regression model to estimate the amount of MW generated by the hospitals in Aksaray city, Turkey. They used the number of patients in three different age classes (0–15; 15–65; 65 +) and gross domestic product per capita as input variables [24]. Al-Khatib et al. (2020) analyzed and evaluated the current status of MW management in Jenin city in light of MW control regulations proposed by the WHO. The results of the study showed that the average hazardous MW generation rate range from 0.54 to 1.82 kg/bed/day with a weighted average of 0.78 kg/bed/day [25].
Table 1.
The performance of the previous studies on the prediction of MW generation
| Author(s) | Province(s)/Country | Methods | Best Model Performance (R, R2) |
|---|---|---|---|
| Bdour et al. [9] | Irbid, Jordan | MLR | R2 = 0.918 |
| Sabour et al. [10] | Gilan, Iran | Linear Regression | Not available |
| Jahandideh et al. [11] | Fars, Iran | MLR, ANN | R2 = 0.990 (ANN) |
| Eleyan et al. [12] | Jenin, Palestine | System Dynamics Models | Not available |
| Idowu et al. [13] | Lagos, Nigeria | MLR Models | R2 = 0.998 |
| Karpušenkaite et al. [14] | Lithuania | ANN, MLR, SVM, and different non-parametric regression methods |
R2 = 0.905 (with GANPR using regional dataset) R2 = 0.986 (with SSNPR using long annual dataset) |
| Tesfahun et al. [15] | Ethiopian | Mathematical predictive models from the available literatures. |
R2 = 0.965 (with the number of inpatients) R2 = 0.424 (with the number of outpatients) |
| Al-Khatib et al. [16] | Nablus, Palestine | MLR | R2 = 0.984 |
| Chauhan and Singh [17] | Uttarakhand, India | ARIMA models | R2 = 0.832 with ARMA(1,1) model |
| Minoglou and Komilis [18] | 41 Countries | MLR and Principal Component Analysis (PCA) | R2 = 0.8473 |
| Adamović et al. [19] |
European countries |
General Regression Neural Network (GRNNs) Models |
R2 = 0.999 (for the prediction of chemical hazardous waste) R2 = 0.975 (for healthcare and biological hazardous waste) |
| Karpušenkaitė et al. [20] | Lithuania | Time Series Moving Average, Time Series Holt’s Exponential Smoothing, Hybrid Model | Not available |
| Thakur and Ramesh [21] | Uttarakhand, India |
MLR, ANN, and Polynomial Regression |
R2 = 0.954 (ANN for total waste) |
| Golbaz et al. [22] | Karaj, Iran | MLR and several Neuron and Kernel based machine earning methods |
R2 = 0.82 – 0.86 (Kernel-based models) R2 = 0.68 – 0.74 (Neuron-based models) |
| Hao et al. [23] | Shanghai, China | GM (1,1), Triple Exponential Smoothing (TES), Particle Swarm Optimization (PSO) Optimized Back Propagation (BP) Neural Network, and Hybrid Model | Not available |
| Çetinkaya et al. [24] | Aksaray, Turkey | MLR | R2 = 0.979 |
*SSNPR: Smoothing splines non-parametric regression
*GANPR: Generalized additive non-parametric regression
Megacity Istanbul is the main economy and social activity center of Turkey. It is also the most populous city with a population of over 15 million. In Istanbul, MW is collected regularly from around different points of the city by ISTAC company. Approximately 22,000 tons of MW have collected annually with the latest technology equipment and special garments. In addition, waste with epidemic disease risks such as infectious and pathological is eliminated by incineration instead of sterilization. It is important to accurate estimation of the amount of MW to effectively manage this hazardous waste generated to determine appropriate disposal methods and to improve waste management [26]. Thus, the main aim of this study is to apply and compare different techniques to achieve an accurate estimation of the MW amount will be generated in the near future of Istanbul, Turkey. For this purpose, Grey Modeling (1,1), Autoregressive Integrated Moving Average (ARIMA), and Support Vector Regression (SVR) models were used as powerful forecasting techniques. Few studies have focused on regional health waste management in Turkey. Istanbul with an increasing population must be investigated closely due to possible critical impacts on both health and the environment. However, most of the studies on estimating the generated MW quantities in the literature are based on temporary surveys, questionnaires and field works [9, 12, 21, 25]. This can cause differences in estimated MW generation rates. Therefore, in order to fulfill a more accurate, robust, and consistent forecasting study, it is necessary to focus on the actual quantities of MW generated in hospitals and healthcare institutions rather than data obtained from surveys, questionnaires. In this context, a 23-year historical dataset for the MW amount collected from about 9000 healthcare points such as hospitals and healthcare institutions in Istanbul was used.
Materials and methods
Data collection
A 23-year MW data was supplied from ISTAC Company, which is one of the leading waste management companies in Turkey (www.istac.com.tr). ISTAC is the solely responsible company for the MW collection and waste treatment company in Istanbul. It provides services to approximately 307 health institutions and 8000 MW health points in Istanbul. The trend of MW data generated between the years 1995–2017 is shown in Fig. 1. It is clear that the amount of MW has increased consistently.
Fig. 1.
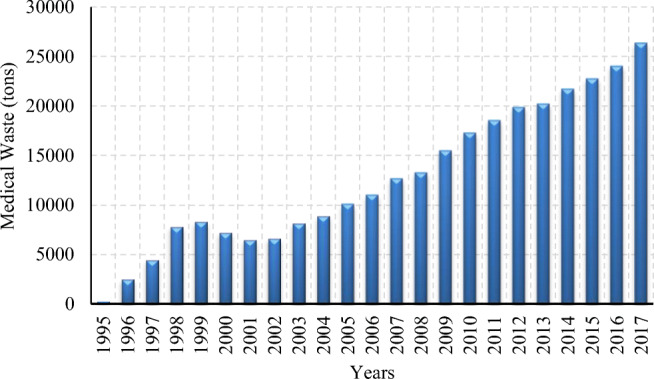
Annual MW generation of Istanbul (ISTAC Company)
Grey modeling (1,1)
Grey system theory (GST), an interdisciplinary approach, was introduced by Deng in the early 1980s as an alternative method to digitize uncertainty [27]. GST is designed to examine uncertain systems that focus on incomplete information caused by small samples [28, 29]. The GST is classified according to the “colors” of the systems. Black indicates unknown information and white indicates known information, while grey indicates partially known information. GST has been successfully applied in many areas such as agriculture, industry, traffic, economics, and engineering and etc. Several grey prediction models have been developed in previous studies. GM (1,1) is the basis of other grey prediction models and has a different principle than classical methods for estimating time series. In the GM (1,1) model, a system is easily identified by a first-order differential equation, and the template is updated whenever new data is available. GM (1,1) model has many advantages such as high accuracy, simplicity and easy calculation even in small datasets (usually 5–10 samples). Therefore, it can be used for short-term prediction activities. However, like other forecasting models, the GM (1,1) model also has some limitations. The GM (1,1) model has a prerequisite for modeling that follows the monotonic exponential prediction approach [30]. In addition, it models and predicts all data, but ignores new information and cannot accurately reflect the characteristics of the current situation. Also, the model can only be used for positive values and time series must have the same frequency as daily, weekly, monthly and yearly.
There are four main steps for the calculation of the GM (1,1) model. A brief summary of the GM (1,1) model is represented below:
Step 1. The positive original data sequence and accumulated generating operation (AGO) time series with n samples are given in Eq. (1,2):
| 1 |
| 2 |
Here,
| 3 |
Step 2. A first -order grey differential equation is formed to obtain the GM (1,1) forecasting model:
| 4 |
where,
| 5 |
where t is time point, θ is horizontal adjustment coefficient, which takes a value between 0 and 1. Choosing the right value of θ minimizes the estimation error. In Eq. (6), a is the development coefficient, b is the control variable. These are two parameters of the GM (1,1) model, and they can be predicted by using the least square method given below:
| 6 |
where,
| 7 |
The whitenization is shown in Eq. (8):
| 8 |
Step 3: After calculating the a and b parameter values, the predicted values of the accumulated sequence are obtained by using Eq. (9):
| 9 |
where denotes AGO prediction of x(t).
Step 4: In order to reverse the forecasting value, the inverse accumulated generation operation (IAGO) is used. This is because the grey prediction model is formulated using AGO data instead of the original data set.
| 10 |
Eq. (11) is obtained using Eqs. (10) and (9):
| 11 |
The reliability of GM (1,1) models needs to be checked with various criteria to confirm whether they satisfy the accuracy requirements. In the literature, two popular test criteria, such as posterior error rate (C) and small error probability (p) are generally used to test the precision of the GM (1,1) model. The test criteria are determined by the following equations:
| 12 |
| 13 |
| 14 |
where is the sequence of actual data, S12 is the variance of the x0, and x¯ is the mean value of x0.
| 15 |
| 16 |
where S22 is the variance of errors and is the mean error.
| 17 |
Table 2 gives the reference values of the forecasting accuracy levels. As far as C and p stay in the allowed scope, the GM (1,1) model can be used for estimation. Small C value means that the discreteness of the prediction errors is small, while a higher p value indicates a higher probability of small error. Therefore, the low value of the C value and the high value of the p value means that the developed model has higher precision.
Table 2.
Prediction accuracy levels of GM (1,1) model
| Accuracy Level | Accuracy Class | Test Criteria | |
|---|---|---|---|
| Posterior Error Ratio, C | Small Error Probability, p | ||
| 1st level | Excellent | C ≤ 0.35 | p ≥ 0.95 |
| 2nd level | Qualified | 0.35 < C ≤ 0.50 | 0.95 > p ≥ 0.80 |
| 3rd level | Marginal | 0.50 < C ≤ 0.65 | 0.80 > p ≥ 0.70 |
| 4th level | Unqualified | 0.65 < C | 0.70 > p |
Autoregressive integrated moving average (ARIMA)
The general Autoregressive Integrated Moving Average (ARIMA) model was introduced by Box and Jenkins [31]. ARIMA is a popular and widely applied stochastic time series model in the literature. It predicts the future values of a time series using a linear combination of past values and a series of errors. This method performs well when the data is stationary or non-stationary. ARIMA is suitable for all kinds of data such as level/trend/seasonality/cyclicality. The main advantages of the ARIMA model can be said as its simplicity and systematic structure to search for a suitable model [32]. However, the model has some drawbacks that limit its scope of application. For example, the model considers that there is a linear relationship between the dependent and independent variables, but the actual data are generally non-linear.
ARIMA model can be denoted with three parameters; ARIMA (p, d, q); where p is the order of the autoregressive components, d is the order of the differencing, and q is the order of the moving average term. A zero value can be applied to the parameter that will not be used in the model. This way, the ARIMA model can be modified to fulfill the function of an ARMA model, and also a simple AR, I, or MA model. Briefly, the general form of the ARIMA model can be expressed with backward operator B which runs on the time index of a data value such as BjYt = Yt − j. Using this operator, the model becomes as given in the below Eqs. (18–20):
| 18 |
| 19 |
| 20 |
where Zt = Yt − μ and a1 represents random error at time t. ∅ (B) and Θ(B) shows the polynomials as expressed in Eqs. (21) and (22):
| 21 |
| 22 |
SVR model with the sequential minimal optimization (SMO) algorithm
Support vector machine (SVM) was first introduced by Cortes and Vapnik in 1995 [33]. SVM can be used to solve many complex problems in engineering, including prediction (or regression analysis), decision making (or classification tasks) processes, and real-life engineering problems. When used for classification problems, the SVM model is called support vector classification (SVC) and when used for regression problems, the SVM model is called support vector regression (SVR). SVR is a useful method, even if there is no prior knowledge about the data [34]. It is also advantageous compared to traditional models such as linear regressions due to its robustness to prevent overfitting.
The solution for regression problems using SVR can be performed by a recursive algorithm named as Sequential Minimal Optimization (SMO). SMO is a simple and effective algorithm that solves the smallest possible optimization problem at each step with two Lagrange multipliers [35]. The calculation speed and ease of application are positive features of this algorithm. Its main advantage is that it is based on the principle of structural risk minimization [36–38]. Furthermore, it provides a unique solution and predicts the regression using a set of basic functions defined in a high-dimensional area.
The regularization constant (called box constraint or cost function) and insensitive loss function are the main parameters of the SVR model. The regularization constant (C) and the insensitive loss function (ε) are used to determine and control the complexity of the model. The accurate selection of these values can increase the performance of the model. However, it is not always easy to choose a suitable SVR parameter to achieve high accuracy. Because, an excessively large value for parameters in the SVR causes overfitting, while a very small value causes underfitting. Therefore, different parameter settings can cause significant differences in performance [39, 40].
In addition, the kernel function directly affects the performance of the SVR model. The kernel function enables needed computations to be carried out directly in the input space. The selection of a kernel function to convert the non-linear input space into a linear space depends on the characteristics of the data. Therefore, to provide a necessary adaptation for many data types, different kernel functions should be searched and their parameters adjusted appropriately. Some common kernel functions are listed in the Eqs. (23–26):
Linear
| 23 |
(Polynomial)
| 24 |
Radial Basis Function (RBF):
| 25 |
Pearson VII kernel function (PUK):
| 26 |
where K(xi, xj) is the kernel function, d is the polynomial degree, γ is the width of RBF kernel, ω and σ are the actual shape and the width of the PUK function, respectively.
LR analysis
The simple linear regression applies the least-squares method to search the line of best fit for a set of data. It allows estimating dependent variable (y) with the aid of a given independent variable (x).The line of best fit can be defined by the equation Y = bx + a, where b represents the slope of the line and a is the intercept. The values of b and a can be determined for a set of data comprising two variables and can be used to predict the value of y for any specified value of x.
Evaluation of model performances
The performance of the models was evaluated using different performance criteria such as root mean square error (RMSE), mean absolute deviation (MAD), mean absolute percentage error (MAPE%), and coefficient of determination (R2). Related equations for calculation of RMSE, MAD, MAPE and R2 values are given in Eq. (27–29):
| 27 |
| 28 |
| 29 |
| 30 |
where and M represent the actual and predicted value of ith data point, respectively. and are the average of the actual and predicted value of ith data point, respectively. Also, n shows the total number of data points. The performance of the models can be measured by calculating R2 value. It takes values between 0 and 1, and values close to 1 means better fitting.
Results and discussion
Forecasting using GM (1,1) model
In order to implement the GM (1,1) model for predicting MW generation, MATLAB version 2018b software was used. It is important to select the suitable value of the horizontal adjustment coefficient (θ) between 0 and 1 to ensure the lowest estimation error. Since different values of this parameter affected the predictive performance of the GM (1,1) model, the different GM (1,1) models were performed using different θ values. As shown in Table 2, two popular test criteria such as posterior error ratio and small error probability were used to compare the accuracy of the GM (1,1) models. The goodness of fit test showed that the precision of the GM (1,1) model was excellent (1st level) with 0.5 horizontal value (θ). The posterior-test ratio (C) and small error probability (p) values were calculated as 0.1616 and 1, respectively. This means that the GM (1,1) model has a higher degree of prediction performance. The development coefficient (α) and the control variable (b) values of the GM (1,1) model were calculated by the least square method. According to the estimation standards of the GTS, when the development coefficient is -α < 0.3, the GM (1,1) model can be applied in mid-long-term forecasting [29]. The development coefficient of this model is −α = 0.07697 < 0.3, which means that we can use the GM (1,1) model to predict the future MW generation of Istanbul.
Forecasting using SVR model with SMO algorithm
Different SMOreg based SVR models were constructed using WEKA software developed by the University of Waikato, New Zealand. Since the correct determination of the parameters had a critical effect on the success of the model, the parameters of the SVR model were adjusted using the grid search optimization approach. This approach searches the best possible values of SVR model parameters such as the regularization constant (C), insensitive loss margin (ε). As mentioned earlier, kernel functions can be used in various types in the SVR model. Therefore, it is also necessary to properly adjust the kernel function parameters such as degree of the polynomial kernel, the width of the RBF kernel, and the actual shape and the width of PUK kernel function [41].
It is seen from Table 3 that the best performance is achieved by using the SVR model with the PUK kernel function. The optimal values of the parameters σ, ω, and C were calculated as 1.0, 1.0 and 100, respectively. On the other hand, the highest values of RMSE and MAD values were calculated by using the SVR model based on the polynomial kernel. The correlation of the determination value of the SVR model based on the RBF kernel function (R2 = 0.9526) was lower than the SVR model based on the PUK kernel function (R2 = 0.9857). This comparison showed that the developed SVR models based on polynomial, RBF, and PUK functions are different in terms of the performance measurements. According to these results, it was concluded that the PUK function is robust and best compared to the polynomial and RBF kernel functions. This is mainly due to the flexibility of the PUK function to change the parameters ω and σ. This flexibility provides a higher predictive ability for the PUK function compared to the other kernel functions [41, 42].
Table 3.
Performance of different kernel functions
| Model | RMSE | MAD | MAPE | R2 |
|---|---|---|---|---|
| Polynomial Kernel | 1622.2923 | 1335.9223 | 34.6421 | 0.9499 |
| RBF Kernel | 1581.2785 | 1117.3358 | 57.6599 | 0.9526 |
| PUK Kernel | 882.5870 | 599.5386 | 12.6760 | 0.9857 |
Forecasting using ARIMA model
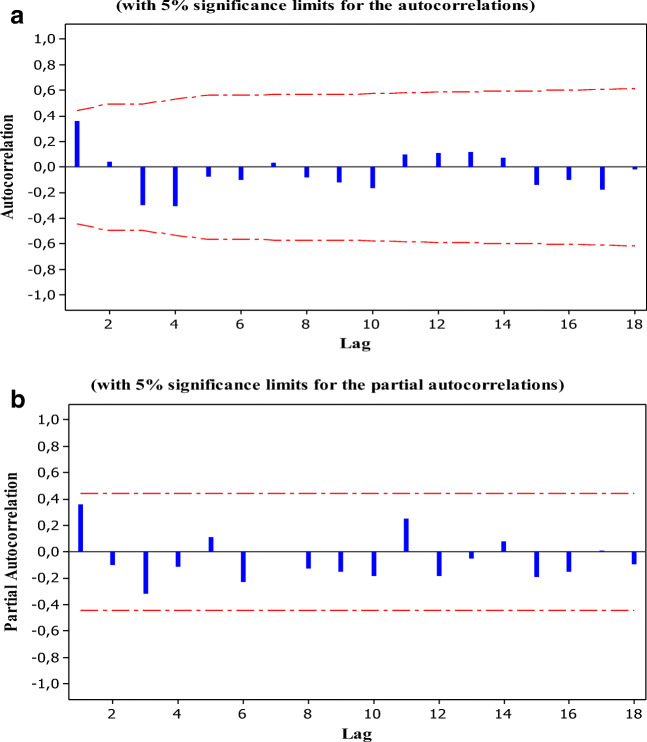
Based on past MW data, the ARIMA model was used to estimate the future trend. The analysis was carried out using STATGRAPHICS Centurion XVI.I software. Because the ARIMA model requires the stationary sequence for the determination of the AR and MA components, the data should be examined for the existence of any trend. Since the series is not stationary, first-order differencing (d = 1) was applied. Autocorrelation function (ACF) plot in Fig. 2a indicated that the series is stationary after first differencing at 5% the significance level.
Fig. 2.
Estimated (a) autocorrelations and (b) partial autocorrelations after first differencing
The patterns of the ACF and partial autocorrelation function (PACF) plots of the differenced series were examined for the tentative determination of the components of the autoregressive (p) and moving average orders (q) in ARMA(p,q) model. Several alternative ARIMA models were also generated for the model selection and their performances were evaluated according to the various statistical tools. As seen from Table 4, the ARIMA (0,1,2) model has the highest R2 (0.9888) and lowest RMSE (763.6852), MAD (588.4712), and MAPE (11.7595) values. Thus, it was selected as the best model and considered a potential prediction model. Table 5 summarizes the statistical significance of the terms in the forecasting model. The p values of the associated with the parameters are less than 0.05, so the terms are significantly different from zero at the 95.0% confidence level.
Table 4.
Model comparison
| Model | RMSE | MAD | MAPE | R2 |
|---|---|---|---|---|
| ARIMA (1,0,2) | 863.4984 | 675.5712 | 11,8660 | 0.9867 |
| ARIMA (0,1,0) | 970.2076 | 729.0000 | 13.6850 | 0.9790 |
| ARIMA (1,2,1) | 1056.3368 | 788.6365 | 15.4074 | 0.9794 |
| ARIMA (0,1,2) | 763.6852 | 588.4712 | 11,7595 | 0.9888 |
| ARIMA (1,1,0) | 893.2460 | 705.4143 | 12.4617 | 0.9822 |
Table 5.
Performance indices of the models
| Model | RMSE | MAD | MAPE | R2 |
|---|---|---|---|---|
| LR | 1462.1266 | 1185.9415 | 26.5966 | 0.9587 |
| ARIMA (0,1,2) | 763.6852 | 588.4712 | 11.7595 | 0.9888 |
| SVR PUK Kernel | 882.5870 | 599.5386 | 12.6760 | 0.9857 |
| GM (1,1) | 1555.8831 | 1298.5890 | 14.0223 | 0.9739 |
Forecasting using LR analysis
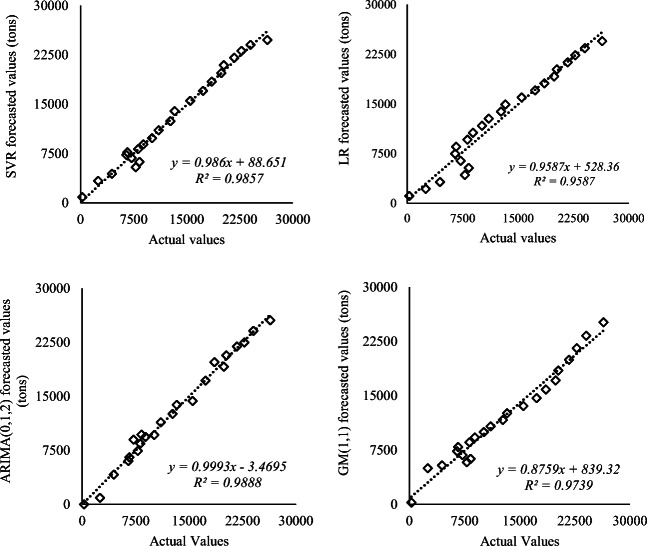
The annual MW data from 1995 to 2017 was used to create the LR model. As shown in Fig. 4, the LR model was fitted to the MW data. The values of R2, RMSE, MAD, and MAPE were calculated as 0.9587, 1462.1266, 1185.9415, and 25.5966, respectively.
Fig. 4.
The scatter plots of the models
Comparison of forecasting models
Figure 3 shows a comparison of the error distribution of different methods in the box plot, , where |FE| is the absolute value of forecasted error statistics. In terms of the maximum absolute error, it can be said that the ARIMA (0,1,2) model performed better than other methods. When the median errors were compared, the SVR model with PUK kernel function performed slightly better than the ARIMA (0,1,2) but significantly lower than the LR and GM (1,1) model. Table 6 presents the summarization of the error analysis in terms of RMSE, MAD, MAPE, and R2 values. It is clear that ARIMA (0,1,2) model performs better than other methods in terms of all error measurements.
Fig. 3.
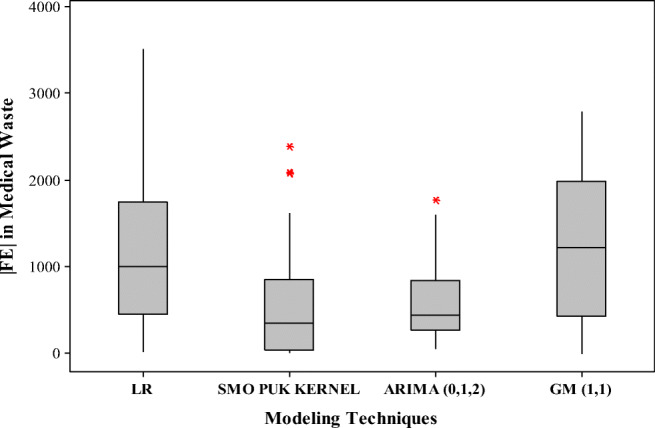
Box plot of the absolute forecasted errors of the models
Table 6.
Parameter estimates of the ARIMA (0,1,2) model
| Parameter | Estimate | Std. Error | t | p value |
|---|---|---|---|---|
| MA (1) | −0.72742 | 0.121841 | −5.97022 | 0.000010 |
| MA (2) | −0.90289 | 0.0876436 | −10.3019 | 0.000000 |
| Mean | 1313.25 | 462.68 | 2.83836 | 0.010507 |
| Constant | 1313.25 |
Figure 4 shows the scatter plots representing the comparison between the actual values and the predicted MW generation for the years using SVR, LR, GM (1,1), and ARIMA (0,1,2) models. Because of higher forecasting accuracy, ARIMA (0,1,2) was applied to estimate the MW amounts of Istanbul from 2018 to 2023. Figure 5 shows the future prediction for MW generation using time series and residual plots for ARIMA (0,1,2) model. It is seen from Table 7 that the total amount of MW in Istanbul will show a relatively stable rising trend in the following six years, and will reach approximately 35,600 tons by the year 2023.
Fig. 5.
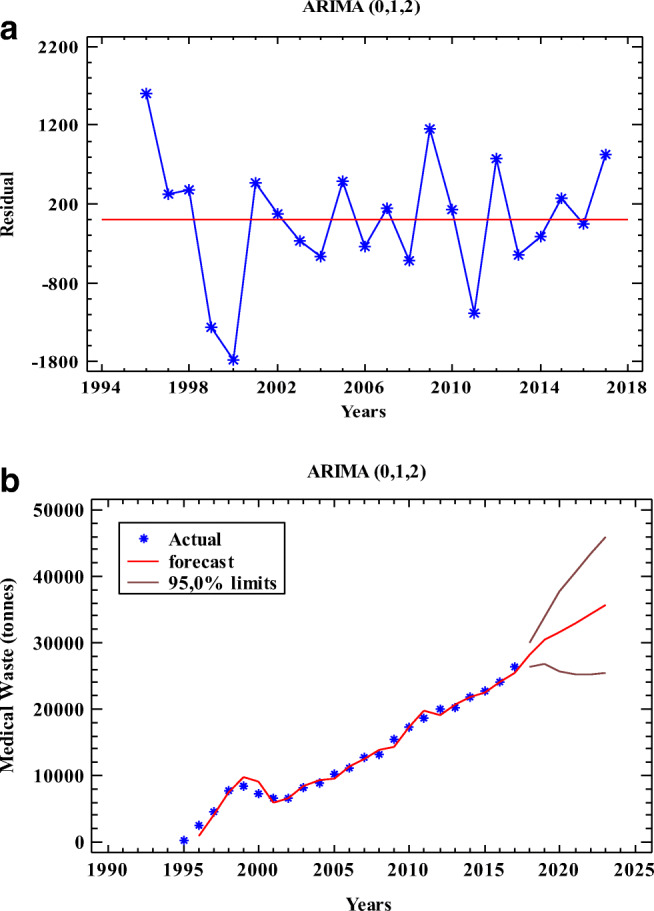
(a) Residual plot (b) time series plot for ARIMA (0,1,2) model
Table 7.
Prediction of MW generation of Istanbul with ARIMA (0,1,2) model
| Year | Forecast | Lower 95.0% Limit | Upper 95.0% Limit |
|---|---|---|---|
| 2018 | 28,279 | 26,467 | 30,091 |
| 2019 | 30,347 | 26,731 | 33,964 |
| 2020 | 31,661 | 25,678 | 37,644 |
| 2021 | 32,974 | 25,325 | 40,623 |
| 2022 | 34,287 | 25,274 | 43,300 |
| 2023 | 35,600 | 25,405 | 45,796 |
Discussion
It is critical to determine future MW generation for an effective MW management system. This information is important to determine the size of storage facilities, the number and type of collection equipment, and future treatment and disposal capacity needs. In recent years, despite an increase in the number and variety of treatment facilities in Turkey, problems with MW management is continued. The increasing population and socio-economic development in Turkey cause a significant increase in the MW generation amount. The city of Istanbul, with its population of approximately 16 million, generates much more MW than other cities of the country. Therefore, research on a suitable model that explains MW generation data is a significant step for ensuring successful MW management in metropolitan cities such as Istanbul. For this purpose, three widely applied models were compared and their performances tested in estimation for the annual MW generation of Istanbul. Statistical tools were employed for the results from models to evaluate forecasting performances for future trends. Depending on the principles of the models, forecasting performances varied. The highest R2 value (0.9888) was obtained with ARIMA (0,1,2) model, and this model was used to estimate the future MW generation amount. ARIMA is a simple, fast and robust time series model to forecast values. Structured modeling ability and acceptable forecasting performance made the ARIMA model best in this study.
Conclusion
It is important to provide appropriate MW management to control and improve the current situation in the increasingly populated city of Istanbul. Sustainable management of MW can only be achieved with accurate waste estimation. Therefore, the aim of this research is to provide a suitable model to estimate the amount of MW generated. In this context, four different methods, such as LR, GM (1,1), ARIMA, and SVR were used. ARIMA (0,1,2) was selected as the best model and used to predict the MW generation of Istanbul between 2018 and 2023. It was concluded that the total amount of MW of Istanbul will show a relatively stable rising trend in the following six years, and will reach approximately 35,600 tons by the year 2023. The results of the study can help authorities to create a reliable MW prediction model, which can be an important source of information for Istanbul. In addition, prior knowledge about the amount of MW generated can be used for both the planning and design of future facilities.
Compliance with ethical standards
Conflict of interest
The authors declare no conflict of interest.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Malekahmadi F, Yunesian M, Yaghmaeian K, Nadafi K. Analysis of the healthcare waste management status in Tehran hospitals. J Environ Heal Sci Eng. 2014;12:116. doi: 10.1186/s40201-014-0116-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.WHO, UNICEF. Water, sanitation and hygiene in health care facilities: status in low- and middle-income countries and way forward. J Chem Inf Model 2015:1–52. doi:10.1017/CBO9781107415324.004.
- 3.Pépin J, Abou Chakra CN, Pépin E, Nault V, Valiquette L. Evolution of the global burden of viral infections from unsafe medical injections, 2000-2010. PLoS One. 2014;9:e99677–7. 10.1371/journal.pone.0099677. [DOI] [PMC free article] [PubMed]
- 4.Alshraideh H, Abu QH. Stochastic modeling and optimization of medical waste collection in northern Jordan. J Mater Cycles Waste Manag. 2017;19:743–753. doi: 10.1007/s10163-016-0474-3. [DOI] [Google Scholar]
- 5.da Paz DHF, Lafayette KPV, de Holanda MJO, do Sobral MCM, de Costa LARC. Assessment of environmental impact risks arising from the illegal dumping of construction waste in Brazil. Environ Dev Sustain 2018. doi:10.1007/s10668-018-0289-6
- 6.Omran A, Altawati M, Davis G. Identifying municipal solid waste management opportunities in Al-Bayda City, Libya. Environ Dev Sustain. 2018;20:1597–1613. doi: 10.1007/s10668-017-9955-3. [DOI] [Google Scholar]
- 7.Rathore P, Sarmah SP, Singh A. Location–allocation of bins in urban solid waste management: a case study of Bilaspur city. India Environ Dev Sustain. 2019;22:3309–3331. doi: 10.1007/s10668-019-00347-y. [DOI] [Google Scholar]
- 8.Awad AR, Obeidat M, Al-Shareef M. Mathematical-statistical models of generated hazardous hospital solid waste. J Environ Sci Heal Part A. 2004;39:315–327. doi: 10.1081/ESE-120027524. [DOI] [PubMed] [Google Scholar]
- 9.Bdour A, Altrabsheh B, Hadadin N, Al-Shareif M. Assessment of medical wastes management practice: a case study of the northern part of Jordan. Waste Manag. 2007;27:746–759. doi: 10.1016/J.WASMAN.2006.03.004. [DOI] [PubMed] [Google Scholar]
- 10.Sabour MR, Mohamedifard A, Kamalan H. A mathematical model to predict the composition and generation of hospital wastes in Iran. Waste Manag. 2007;27:584–587. doi: 10.1016/J.WASMAN.2006.05.010. [DOI] [PubMed] [Google Scholar]
- 11.Jahandideh S, Jahandideh S, Asadabadi EB, Askarian M, Movahedi MM, Hosseini S, et al. The use of artificial neural networks and multiple linear regression to predict rate of medical waste generation. Waste Manag. 2009;29:2874–9. 10.1016/J.WASMAN.2009.06.027. [DOI] [PubMed]
- 12.Eleyan D, Al-Khatib IA, Garfield J. System dynamics model for hospital waste characterization and generation in developing countries. Waste Manag Res. 2013;31:986–995. doi: 10.1177/0734242X13490981. [DOI] [PubMed] [Google Scholar]
- 13.Idowu I, Alo B, Atherton W, Al KR. Profile of medical waste management in two healthcare facilities in Lagos, Nigeria: a case study. Waste Manag Res. 2013;31:494–501. doi: 10.1177/0734242X13479429. [DOI] [PubMed] [Google Scholar]
- 14.Karpušenkaite A, Ruzgas T, Denafas G. Forecasting medical waste generation using short and extra short datasets: case study of Lithuania. Waste Manag Res. 2016;34:378–387. doi: 10.1177/0734242X16628977. [DOI] [PubMed] [Google Scholar]
- 15.Tesfahun E, Kumie A, Beyene A. Developing models for the prediction of hospital healthcare waste generation rate. Waste Manag Res. 2016;34:75–80. doi: 10.1177/0734242X15607422. [DOI] [PubMed] [Google Scholar]
- 16.Al-Khatib IA, Abu Fkhidah I, Khatib JI, Kontogianni S. Implementation of a multi-variable regression analysis in the assessment of the generation rate and composition of hospital solid waste for the design of a sustainable management system in developing countries. Waste Manag Res. 2016;34:225–234. doi: 10.1177/0734242X15622813. [DOI] [PubMed] [Google Scholar]
- 17.Chauhan A, Singh A. An ARIMA model for the forecasting of healthcare waste generation in the Garhwal region of Uttarakhand. India Int J Serv Oper Informatics. 2017;8:352. doi: 10.1504/ijsoi.2017.086587. [DOI] [Google Scholar]
- 18.Minoglou M, Komilis D. Describing health care waste generation rates using regression modeling and principal component analysis. Waste Manag. 2018;78:811–818. doi: 10.1016/J.WASMAN.2018.06.053. [DOI] [PubMed] [Google Scholar]
- 19.Adamović VM, Antanasijević DZ, Ristić M, Perić-Grujić AA, Pocajt VV. An optimized artificial neural network model for the prediction of rate of hazardous chemical and healthcare waste generation at the national level. J Mater Cycles Waste Manag. 2018;20:1736–1750. doi: 10.1007/s10163-018-0741-6. [DOI] [Google Scholar]
- 20.Karpušenkaitė A, Ruzgas T, Denafas G. Time-series-based hybrid mathematical modelling method adapted to forecast automotive and medical waste generation: case study of Lithuania. Waste Manag Res. 2018;36:454–462. doi: 10.1177/0734242X18767308. [DOI] [PubMed] [Google Scholar]
- 21.Thakur V, Ramesh A. Analyzing composition and generation rates of biomedical waste in selected hospitals of Uttarakhand, India. J Mater Cycles Waste Manag. 2018;20:877–890. doi: 10.1007/s10163-017-0648-7. [DOI] [Google Scholar]
- 22.Golbaz S, Nabizadeh R, Sajadi HS. Comparative study of predicting hospital solid waste generation using multiple linear regression and artificial intelligence. J Environ Heal Sci Eng. 2019;17:41–51. doi: 10.1007/s40201-018-00324-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hao H, Zhang J, Zhang Q, Yao L, Sun Y. Improved gray neural network model for healthcare waste recycling forecasting. J Comb Optim 2019; 1–18. 10.1007/s10878-019-00482-2.
- 24.Çetinkaya AY, Kuzu SL, Demir A. Medical waste management in a mid-populated Turkish city and development of medical waste prediction model. Environ Dev Sustain 2019; 1–12. 10.1007/s10668-019-00474-6.
- 25.Al-Khatib IA, Khalaf A, Al-Sari MI, Anayah M. Medical waste management at three hospitals in Jenin district, Palestine. Environ Monit Assess 2020; 192(10):1–16. 10.1007/s10661-019-7992-0. [DOI] [PubMed]
- 26.Uysal F, Tınmaz E. Medical waste management in trachea region of Turkey: suggested remedial action. Waste Manag Res. 2004;22(5):403–407. doi: 10.1177/0734242X04045690. [DOI] [PubMed] [Google Scholar]
- 27.Deng JL. Control problems of grey systems. Syst Control Lett. 1982;1:288e94. [Google Scholar]
- 28.Dai S, Niu D, Han Y. Forecasting of energy-related CO2 emissions in China based on GM(1,1) and least squares support vector machine optimized by modified shuffled frog leaping algorithm for sustainability. Sustain. 2018;10. 10.3390/su10040958.
- 29.Jiang F, Yang X, Li S. Comparison of forecasting India’s energy demand using an MGM, ARIMA model, MGM-ARIMA model, and BP neural network model. Sustain. 2018;10. 10.3390/su10072225.
- 30.Zhou W, Zhang D. An improved metabolism grey model for predicting small samples with a singular datum and its application to sulfur dioxide emissions in China. Discrete Dyn Nat Soc 2016: 1–11. 10.1155/2016/1045057.
- 31.Box GE, Jenkins GM, Reinsel GC, Ljung GM. Time series analysis: forecasting and control. John Wiley & Sons 2015.
- 32.Zafra C, Ángel Y, Torres E. ARIMA analysis of the effect of land surface coverage on PM10 concentrations in a high-altitude megacity. Atmos Pollut Res. 2017;8:660–668. doi: 10.1016/j.apr.2017.01.002. [DOI] [Google Scholar]
- 33.Cortes C, Vapnik V. Support-vector networks. Mach Learn. 1995;20(3):273–297. [Google Scholar]
- 34.Ceylan Z. Estimation of municipal waste generation of Turkey using socio-economic indicators by Bayesian optimization tuned Gaussian process regression. Waste Manag Res 2020: 1–11. 10.1177/0734242X20906877. [DOI] [PubMed]
- 35.Platt J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv Large Margin Classifiers. 1999;10(3):61–74. [Google Scholar]
- 36.Smola AJ, Schölkopf B. A tutorial on support vector regression. Stat Comput. 2004;14:199–222. doi: 10.1023/B:STCO.0000035301.49549.88. [DOI] [Google Scholar]
- 37.Cheng C-S, Chen P-W, Huang K-K. Estimating the shift size in the process mean with support vector regression and neural networks. Expert Syst Appl. 2011;38:10624–10630. doi: 10.1016/J.ESWA.2011.02.121. [DOI] [Google Scholar]
- 38.da Silva MBP, Francisco Escobedo J, Juliana Rossi T, dos Santos CM, da Silva SHMG. Performance of the angstrom-Prescott model (A-P) and SVM and ANN techniques to estimate daily global solar irradiation in Botucatu/SP/Brazil. J Atmos Solar-Terrestrial Phys. 2017;160:11–23. doi: 10.1016/J.JASTP.2017.04.001. [DOI] [Google Scholar]
- 39.Alade IO, Abd Rahman MA, Saleh TA. Predicting the specific heat capacity of alumina/ethylene glycol nanofluids using support vector regression model optimized with Bayesian algorithm. Sol Energy. 2019;183:74–82. doi: 10.1016/j.solener.2019.02.060. [DOI] [Google Scholar]
- 40.Ceylan Z. Assessment of agricultural energy consumption of Turkey by MLR and Bayesian optimized SVR and GPR models. J. Forecast 2020:1–13. 10.1002/for.2673.
- 41.Abakar KAA, Yu C. Performance of SVM based on PUK kernel in comparison to SVM based on RBF kernel in prediction of yarn tenacity. Indian J Fibre Text Res. 2014;39:55–59. [Google Scholar]
- 42.Zendehboudi A, Baseer MA, Saidur R. Application of support vector machine models for forecasting solar and wind energy resources: a review. J Clean Prod. 2018;199:272–285. doi: 10.1016/j.jclepro.2018.07.164. [DOI] [Google Scholar]