Fully Automated Multi-Organ Segmentation in Abdominal Magnetic Resonance Imaging with Deep Neural Networks

Abstract

Purpose

Segmentation of multiple organs-at-risk (OARs) is essential for MR-only radiation therapy treatment planning and MR-guided adaptive radiotherapy of abdominal cancers. Current practice requires manual delineation that is labor-intensive, time-consuming, and prone to intra- and inter-observer variations. We developed a deep learning (DL) technique for fully automated segmentation of multiple OARs on clinical abdominal MR images with high accuracy, reliability, and efficiency.

Methods

We developed Automated deep Learning-based Abdominal Multi-Organ segmentation (ALAMO) technique based on 2D U-net and a densely connected network structure with tailored design in data augmentation and training procedures such as deep connection, auxiliary supervision, and multi-view. The model takes in multi-slice MR images and generates the output of segmentation results. 3.0-Tesla T1 VIBE (Volumetric Interpolated Breath-hold Examination) images of 102 subjects were used in our study and split into 66 for training, 16 for validation, and 20 for testing. Ten OARs were studied, including the liver, spleen, pancreas, left/right kidneys, stomach, duodenum, small intestine, spinal cord, and vertebral bodies. An experienced radiologist manually labeled each OAR, followed by reediting, if necessary, by a senior radiologist, to create the ground-truth. The performance was measured using volume overlapping and surface distance.

Results

The ALAMO technique generated segmentation labels in good agreement with the manual results. Specifically, among the 10 OARs, 9 achieved high Dice Similarity Coefficients (DSCs) in the range of 0.87–0.96, except for the duodenum with a DSC of 0.80. The inference completed within one minute for a 3D volume of 320×288×180. Overall, the ALAMO model matched the state-of-the-art techniques in performance.

Conclusion

The proposed ALAMO technique allows for fully automated abdominal MR segmentation with high accuracy and practical memory and computation time demands.

1. INTRODUCTION

Over the past few years, there is a keen interest in the integration of magnetic resonance (MR) alone into radiation treatment planning and even the therapy workflow, i.e., MR-guided adaptive radiotherapy, to leverage its superior soft-tissue contrast [1–3]. The abdomen, however, represents a challenging treatment site for pursuing these applications, in part due to the presence of many organs-at-risk (OARs) and challenges in contouring them. Contouring OARs on abdominal MR images still heavily relies on manual, tedious procedures that are time-consuming and intra-/inter-observer variation-prone [4–6]. Computer-aided automated multi-organ segmentation would be a compelling approach to the roadblock [7].

Early research on automated segmentation algorithms focused on mathematical modeling of the morphological information of organs. For instance, level-set [8], SNAKE [9], and graph cut [10] focus on attracting descriptors to organ boundaries, driven by intensity gradient and neighborhood structures. However, these models usually rely on the consistent appearance of edges and intensity patterns as well as specific scale tradeoffs. Thus, they have limited applicability to MR datasets that commonly exhibit heterogeneous image quality due to the variations in system models and manufacturers, sequence parameter settings, or field shimming conditions [11]. Atlas-based approaches [12] were investigated as an alternative solution. However, their heavy dependence on the quality and size of atlas and the consistency between the target and atlas samples, along with relatively long processing time needed for performing multiple registrations (for example, 7 minutes in [13]), have impeded widespread use in clinics.

Recently, data-driven approaches, particularly deep learning developments have gained intense popularity. Deep networks incorporate representation as part of the learning, in contrast to hand crafted features in conventional regression methods [7]. In medical segmentation problems, it is common to adopt a supervised learning setting, where images and the corresponding clinical manual labels are used during training, and the resultant network is used to infer the labels automatically on new images. Their superior ability to model the complexity in multi-organ shapes, context information, and the inter-subject varieties has been demonstrated on several benchmark datasets [14, 15]. [16, 17] have made very good reviews on using deep learning (DL) and artificial intelligence techniques for segmentation in medical images. Especially, MR image segmentation for the brain [18], heart [19], and breast [20] have been investigated. However, there are few studies focused on abdominal MR segmentation [21–24]. Despite substantial improvement over the years, the performance in automated abdominal MR segmentation still does not match up to the human performance, particularly in complex-structure organs such as the stomach and duodenum [23]. Most of the previous studies utilized 2D neural networks for organ segmentation. However, single-channel 2D models that analyzes one slice at a time are insufficient to analyze 3D complex structures in volumetric medical images. 3D networks may be more suitable [25]. However, the high computation cost and memory consumption limit the size and field of view of a 3D network, which may drastically compromise the performance of a 3D network in a segmentation task that requires sufficient contextual information [26]. This motivates our investigation of a multi-slice setting with multi-channel network structure. Another challenge for the application of DL in abdominal MR is overfitting, primarily caused by the small data size. With a sample size in the order of hundreds or less, increasing the network complexity may not lead to a performance gain. We hypothesize that a meticulously designed network structure with more effective use of the existing nodes, such as skip connections [27], is likely to be beneficial for expanding the representation power without risking overfitting. Moreover, improvement in training procedures, such as utilizing data augmentation and deeply supervised learning [28] may be helpful.

In this work, we proposed a convolutional neural network (CNN) based fully automated multi-organ MR segmentation technique, namely ALAMO (Automated deep Learning-based Abdominal Multi-Organ segmentation). This technique builds on a multi-slice 2D neural network to account for the correlative and complementary information between adjacent slices in the intrinsic 3D space while avoiding the heavy computation burden associated with 3D neural networks. Novel multi-view training and inference were developed to effectively alleviate outliers in the preliminary segmentation predictions. To improve robustness and reduce overfitting risk, we also investigated the value of various setup options, including network normalization, data augmentation, and deeply supervised learning, which have not been explored together in the particular context - the whole-abdomen multi-organ MR segmentation problem. The thorough technical investigation and assessment would provide insights into DL network optimization in solving this problem. The ALAMO technique, with optimized supervised learning, is intended to possess the potential to serve as a clinically practical and highly accurate, robust automated segmentation system in the settings of MR simulation as well as MR-guided adaptive radiotherapy of abdominal cancers.

2. METHODS

2.1. MR Data

This work was built on the water-phase images from a routinely used breath-hold 3D abdominal MR sequence - DIXON T1-VIBE (Volumetric Interpolated Breath-hold Examination) [29]. All images were acquired using 3.0-Tesla systems (MEGNETOM Skyra/Prisma and Biograph mMR, Siemens Healthineers, Erlangen, Germany) equipped with 18-channel body matrix coils. A total of 102 cases with the diagnosis of no or <2cm abdominal lesions were retrospectively enrolled by reviewing our Picture Archiving and Communication System (PACS) with Institutional Review Board approval and inclusion (adult of all ages; had abdominal MR for clinical indications between Jan 01, 2008 and Jun 01, 2019; had a T1-VIBE scan) and exclusion (T1-VIBE images corrupted by motion artifacts; focal lesion size > 2cm; history of diffusive abdominal disease; major surgery previously performed in the abdomen) criteria. They were split into 66 for training, 16 for validation, and 20 for testing. Each original T1-VIBE image set consisted of 72–80 transversal slices with a spatial resolution of 1.1–1.3 mm in each 2D transversal slice and 2.0–4.0 mm in slice thickness. All 3D image sets were pre-processed with their spatial resolution interpolated into 1.2 mm isotropic. Note that the abdominal MR examination of each patient may involve other sequences, such as half-Fourier single-shot turbo spin-echo (HASTE), short-TI inversion recovery (STIR), and diffusion weighted imaging (DWI), but they were not used in the current segmentation task.

Human labeling was performed by two experienced and board-certified radiologists. Before initiating the labeling process, a training session with 5 additional cases was used to discuss segmentation routines and consensus criteria. During the labeling process, the radiologist with 5 years of experience labeled 10 organs (liver, spleen, pancreas, left/right kidneys, stomach, duodenum, small intestine, spinal cord, and vertebral bodies) using an open-source software application, ITK-SNAP [30]. The senior radiologist specializing in body imaging (with >15 years of experience) reviewed the raw images and contour sets and made necessary adjustments to finalize contours. Adjustment occurred in approximately 20% cases, mostly at the interface of the duodenum and small intestine.

2.2. Deep Learning Models and Framework

The ALAMO technique adopts the popular U-net structure to capture both high-resolution local textures and low-resolution context information with the encoder-decoder multi-scale structure [25, 31].

To capture the third-dimension information in a 2D network, we introduced a multi-slice input with a multi-channel 2D network structure. Twenty contiguous slices obtained from the whole 3D volume serve as the input at the first layer, a multi-channel convolutional layer, of the network. The ALAMO structure is illustrated in Figure 1.

Figure 1.

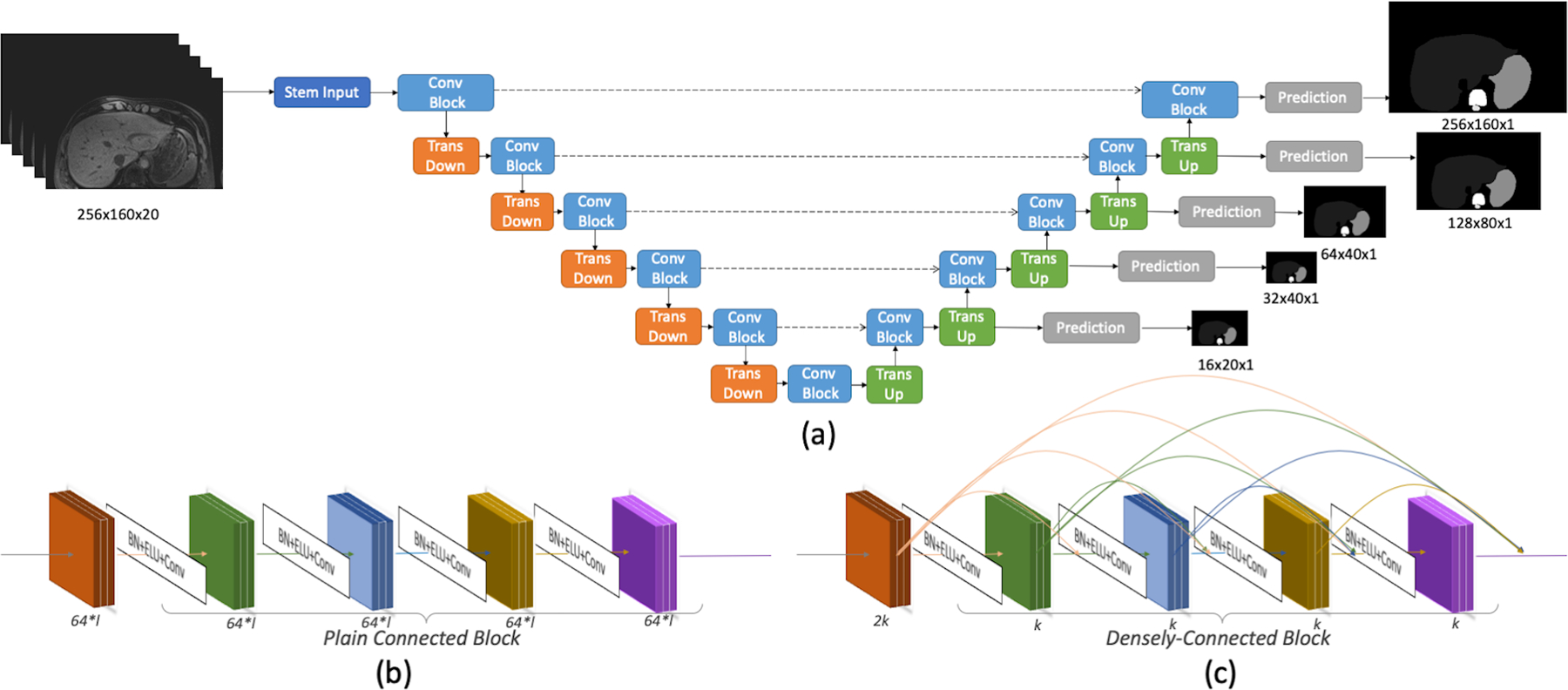
Network structure: (a) The overall U-net structure with two convolution block options: (b) Plain Connected Block in PlainUnet or (c) Densely Connected Block in DenseUnet. In DenseUnet, the filter number (growth-rate) k=48; in the PlainUnet setting, the filter number starts at f=64 and doubles after pooling. Stem input is a single 3×3 convolutional layer with 2k or f filters. Normalizations are applied before the Exponential Linear Units (ELU) and 3×3 convolutional layers. 2×2 average pooling is used in the Transition Down, and a transposed-convolutional layer with 2×2 kernel and stride size of 2 is applied in the Transition Up. A 1×1 convolutional layer and softmax activation output the predictions for 11 classes (background + 10 organs). At each resolution, the auxiliary prediction is used for deeply supervised training.

To prepare the input data, we first performed pixel-wise dataset standardization (i.e., subtracting the mean signal intensity of the 3D dataset from each voxel followed by division by the standard deviation of the signal intensity of the 3D dataset). Stacks of 20 contiguous transversal slices in a matrix size of 256×160 were then randomly sampled from the whole 3D volume that was typically 320×288×180. Random up-down or left-right flipping was finally applied at a probability of 50% for standard data augmentation.

2.3. Evaluation Metrics

Four metrics were used to evaluate the segmentation accuracy against the ground truth (i.e., human annotation), including Dice Similarity Coefficient (DSC) [32], Jaccard Index [33], Mean Surface Distance (MSD), and 95% Hausdorff Distance (95HD) [34]. We use Python’s scipy.stats.ttest_rel for all paired, two-tailed t-test comparisons. Bonferroni correction was used to account for multiple comparisons when applicable.

2.4. Investigation of Structure and Implementation Variations

Thorough technical investigation and assessment were performed step by step here with the goal of achieving a clinically practical and highly accurate, robust automated segmentation system. With all these steps finished, we further performed experiments comparing our multi-slice input (20 slices and 40 slices) approaches to the single-slice input approach and an experiment evaluating the finalized technique against a reference.

2.4.1. Dense Connections in Convolutional Blocks

Our network blocks were configured as either plainly-stacked layers or densely-connected layers, corresponding to PlainUnet and DenseUnet, respectively. Previous work [26, 27, 35] have shown that DenseNet is less prone to overfitting and also helps to alleviate vanishing gradient issues in backpropagation. In this work, we investigated its impact by optimizing a DenseUnet and evaluating it against the PlainUnet [31]. Setup parameters, including the number of filters, f, in the first resolution level in PlainUnet and the growth-rate, k, in DenseUnet, underwent investigations.

2.4.2. Network Normalization

On top of image data standardization, we also explored different methods of network normalization on the feature maps. Network normalization is a widely used approach to help accelerate convergence, stabilize gradients, and alleviate overfitting to training data. Specific implementation options include batch normalization (BN) [23, 25, 26, 36], Instance normalization (IN) [37], and layer normalization (LN) [38]. However, recent studies have shown that the batch size heavily affects the normalization performance [36, 38]. In this work, we can only fit a single sample per batch due to large image matrix size and memory limitations (11 GB), which is a common scenario in whole-abdomen image segmentation. Therefore, we expect a moderate role of BN, with simple sample-driven statistics. Specifically, we investigated the effect of using BN, using BN with the training mode during testing [25], as well as IN and LN.

2.4.3. Further Augmentation

We investigated the effect of random projective deformation as additional options for data augmentation, where the image was transformed by a projection matrix (rotation angle: −0.05 -- + 0.05 rad, shearing scale: −0.3 -- +0.3, projective scale: −0.003 -- + 0.003) at a probability of 50.

2.4.4. Auxiliary Prediction in Deeply Supervised Training

To address the vanishing gradient issue in the backpropagation process, it would be beneficial to direct gradients for optimizing the layers at each resolution level. Deeply supervised training [28] is an approach to add auxiliary side predictions to down-sampled labels directly from the output of each resolution. Therefore, we explored this option by adding extra layers for low-resolution predictions in the decoder branches, as illustrated in Figure 1. The network was optimized to produce not only full-resolution segmentation masks but also multiple low-resolution masks. During the testing phase, the model only computed the final full-resolution output with no additional computation burden for the auxiliary prediction.

2.4.5. Multi-view Training, Inference, and Majority Voting

Processing 2D slices [31, 39] from a single fixed view lacks intrinsic consideration of 3D structure information. Even the stack formulation may still be sensitive to the specific slice orientation. Multi-view may help to leverage the information more effectively [26]. Existing work utilizes multi-view by training independent filters on each view. However, we observed overfitting due to the introduction of additional parameters in this setting. We rationalize that organs may be oriented slightly differently for the imaging coordinates during acquisition and propose to use the same set of filters in different views to be invariant to the digital coordinates. Specifically, we trained the network on transversal, coronal, and sagittal views at a ratio of 4:1:1. Each view provided a 3D segmentation prediction, and a simple majority voting strategy was applied to combine the three predictions into the final segmentation as shown in Figure 2. Three GPUs were used in parallel for this purpose.

Figure 2.

An example of the probability maps from three different view inferences. We fused three probability maps into one final segmentation result by the majority voting strategy.

2.5. Network Implementation

The network was implemented from ground-up in Tensorflow (v1.15) [40] deep learning packages and trained with ADAM [41] optimizer. The learning rate was set to be 1e-4, and a decay rate of 0.9 was applied after every 50k iterations. Our models converged well at 1000k steps (roughly 700 epochs) and we used those checkpoints for evaluation. A workstation equipped with multiple Nvidia RTX 2080 TI Graphis Process Units (GPUs), was used for both training and testing.

3. RESULTS

3.1. Impact of Dense Connections and Network Size

As shown in Table 1, when the network size increased, the runtime and parameter number increased in both DenseUnet and PlainUnet. In general, the PlainUnets were outperformed by DenseUnet by a notable margin, while the latter only used a fraction of the parameters thanks to its more efficient architecture. Furthermore, merely adding more parameters in PlainUnet did not considerably improve the performance. The DenseUnet with k=48 provided the best results in a reasonable runtime. Therefore, we use it as the baseline in our later experiments.

Table 1.

(a) Dice Similarity Coefficient (DSC) and (b) Mean Surface Distance (MSD) between different network sizes of DenseUnet and PlainUnet on the test set. K is the growth rate of Densely Connected Block in DenseUnet, and f is the filter number of the first layer in PlainUnet. DenseUnet (k=32) runs faster than 100× larger PlainUnet (f=64) but still has comparable performance, showing the advanced densely connections help in overall performance. DenseUnet (k=48) gains the best performance while still maintains a fast run time. Best performances are highlighted in bold.

(a)
DenseUnet
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	Parameter Number	Runtime(s)
k24	0.956±0.013	0.791±0.082	0.947±0.006	0.941±0.013	0.868±0.048	0.686±0.083	0.780±0.135	0.873±0.028	0.834±0.037	0.931±0.030	0.861±0.084	1.55M	13.179
k32	0.955±0.011	0.772±0.107	0.939±0.012	0.941±0.011	0.871±0.052	0.696±0.093	0.789±0.105	0.884±0.019	0.887±0.018	0.936±0.021	0.867±0.083	2.74M	13.977
k48	0.960±0.009	0.828±0.074	0.940±0.009	0.951±0.008	0.889±0.046	0.732±0.076	0.790±0.103	0.866±0.028	0.889±0.017	0.934±0.018	0.878±0.071	6.12M	18.052
k64	0.959±0.012	0.799±0.086	0.952±0.008	0.950±0.009	0.889±0.046	0.708±0.091	0.796±0.107	0.886±0.024	0.882±0.026	0.929±0.025	0.875±0.079	10.83M	21.040
PlainUnet
f64	0.957±0.012	0.740±0.131	0.943±0.010	0.943±0.012	0.870±0.045	0.695±0.075	0.792±0.098	0.888±0.024	0.884±0.016	0.908±0.037	0.862±0.086	229M	15.903
f80	0.953±0.013	0.774±0.106	0.945±0.007	0.943±0.013	0.851±0.055	0.711±0.072	0.765±0.106	0.853±0.028	0.875±0.025	0.901±0.043	0.857±0.080	358M	30.623
f96	0.953±0.009	0.793±0.073	0.938±0.016	0.933±0.023	0.861±0.051	0.717±0.077	0.766±0.132	0.876±0.020	0.884±0.017	0.927±0.025	0.865±0.077	515M	38.859
(b)
DenseUnet
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	Parameter Number	Runtime (s)
k24	1.329±0.433	2.750±1.319	0.800±0.181	0.973±0.578	3.326±1.546	4.315±1.457	4.177±3.421	0.795±0.143	1.655±0.359	1.273±0.842	2.139±1.314	1.55M	13.179
k32	1.266±0.233	3.006±1.805	1.398±0.999	1.379±0.972	2.481±1.603	4.249±2.043	4.871±3.331	1.350±1.049	1.026±0.148	1.578±1.117	2.260±1.292	2.74M	13.977
k48	1.188±0.269	2.270±1.167	1.212±0.893	0.934±0.493	2.732±1.241	2.931±1.295	5.081±3.932	0.875±0.219	1.097±0.200	1.180±0.632	1.950±1.269	6.12M	18.052
k64	1.218±0.367	3.324±2.849	0.738±0.165	0.743±0.205	2.367±0.976	4.275±1.832	4.604±3.441	0.738±0.110	1.461±1.523	1.433±0.978	2.090±1.405	10.83M	21.040
PlainUnet
f64	1.318±0.367	2.664±1.395	1.212±0.796	1.121±0.669	2.799±1.100	4.352±2.010	4.760±2.888	0.811±0.264	1.089±0.219	1.666±1.042	2.179±1.346	229M	15.903
f80	1.459±0.376	2.603±1.201	1.069±0.584	1.332±0.962	3.070±1.225	3.708±1.607	5.161±3.245	0.977±0.184	1.257±0.271	2.041±1.487	2.268±1.300	358M	30.623
f96	1.470±0.283	2.792±1.307	2.576±1.865	1.822±1.263	3.130±0.941	4.332±1.767	5.122±4.012	1.211±0.488	1.743±1.340	1.667±0.859	2.586±1.228	515M	38.859

3.2. The Effect of Different Normalization Methods

Table 2 reports the effect of different normalization methods, including a) no normalization, b) BN with the training mode in inference phase, c) BN with the testing mode in inference phase, d) LN, and e) IN. It turned out that “no normalization” provided the best results (DSC = 0.897±0.059; MSD = 1.353±0.669) and the fastest inference time (8.3 seconds).

Table 2.

(a) Dice Similarity Coefficient (DSC) and (b) Mean Surface Distance (MSD) (in units of mm) between different normalization methods (No Normalization [NoNorm], Batch Normalization [BN] in Train/Test mode, Instance Normalization [IN], and Layer Normalization [LN]) in DenseUnet (k=48) on the test set. “*” indicates significant difference (p < 0.05/8 = 6.25e-3 considering Bonferroni correction) when comparing each of the other scenarios to the NoNorm network. Without normalization, the network not only runs fastest but also obtains the best performance. Also, it is worth noting that using the training mode of BN during inference obtains a large performance improvement over using the testing mode of BN. We highlight the best performances in bold.

(a)
DenseUnet
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value	Runtime (s)
NoNorm	0.961±0.008	0.860±0.042	0.954±0.006	0.952±0.009	0.907±0.024	0.766±0.066	0.839±0.085	0.898±0.021	0.886±0.015	0.944±0.013	0.897±0.059	-	8.307
BN_TrainMode	0.960±0.009	0.828±0.074	0.940±0.009	0.951±0.008	0.889±0.046	0.732±0.076	0.790±0.103	0.866±0.028	0.889±0.017	0.934±0.018	0.878±0.071*	5.336e-07	18.052
BN_TestMode	0.957±0.011	0.801±0.105	0.935±0.023	0.923±0.040	0.861±0.059	0.626±0.117	0.734±0.159	0.857±0.042	0.871±0.014	0.883±0.096	0.845±0.096*	1.451e-06	9.703
IN	0.960±0.009	0.826±0.068	0.944±0.007	0.948±0.010	0.888±0.042	0.726±0.078	0.782±0.116	0.851±0.039	0.874±0.028	0.935±0.023	0.874±0.074*	8.155e-06	13.216
LN	0.960±0.011	0.818±0.076	0.950±0.007	0.951±0.007	0.884±0.055	0.704±0.112	0.834±0.071	0.896±0.016	0.898±0.012	0.940±0.013	0.883±0.076*	7.014e-04	13.503
(b)
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value	Runtime (s)
NoNorm	1.135±0.204	1.307±0.472	0.693±0.083	0.812±0.377	1.905±0.698	2.189±0.865	2.771±2.608	0.678±0.098	0.994±0.200	1.047±0.436	1.353±0.669	-	8.307
BN_TrainMode	1.188±0.269	2.270±1.167	1.212±0.893	0.934±0.493	2.732±1.241	2.931 ±1.295	5.081±3.932	0.875±0.219	1.097±0.200	1.180±0.632	1.950±1.269*	4.297e-07	18.052
BN_TestMode	1.370±0.290	2.265±1.153	1.006±0.449	1.058±0.572	3.420±2.691	4.192±2.462	3.890±2.526	0.933±0.254	1.211±0.340	2.129±2.216	2.147±1. 196*	1.951e-07	9.703
IN	1.211±0.263	2.946±1.734	1.262±1.104	1.003±0.586	2.808±1.612	3.773±1.640	5.743±4.552	0.905±0.211	1.656±1.208	1.276±0.788	2.258±1.485*	4.803e-06	13.216
LN	1.179±0.282	1.726±0.841	0.714±0.138	0.808±0.218	2.078±0.882	2.653±1.144	3.476±3.081	0.691±0.140	0.922±0.142	1.259±0.740	1.550±0.886*	2.853e-04	13.503

3.3. The Effect of Additional Augmentation, Deep Supervision, and Multiview.

Table 3 reports the impact of progressively introducing 1) further augmentation with projective deformation (PD), 2) deep-supervised training (DS), 3) multi-view training (MTT), and 4) multi-view inference (MTI) with a majority voting in this experiment. After incorporating all the above techniques, significant performance improvement was observed over the baseline model. The parallel GPU implementation for inference with a subsequent majority voting resulted in an inference time determined by the slowest runtime among three views, which was just slightly longer than single-view inference.

Table 3.

(a) Dice Similarity Coefficient (DSC) and (b) Mean Surface Distance (MSD) (in units of mm) for progressively adding different training and testing settings: projective deformation (PD), deep-supervised training (DS), multi-view training (MTT), and multi-view inference (MTI). “*” indicates significant difference (p < 0.05/8 = 6.25e-3 considering Bonferroni correction) when comparing each of the other scenarios to the baseline model - the non-normalized DenseUnet (k=48) network. Best performances are highlighted in bold.

(a)
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value	Time (s)
Baseline	0.961±0.008	0.860±0.042	0.954±0.006	0.952±0.009	0.907±0.024	0.766±0.066	0.839±0.085	0.898±0.021	0.886±0.015	0.944±0.013	0.897±0.059	-	8.31
+PD	0.962±0.008	0.864±0.034	0.953±0.007	0.952±0.007	0.913±0.027	0.775±0.055	0.846±0.091	0.898±0.024	0.895±0.016	0.944±0.011	0.900±0.056	7.377e-02	8.37
+PD+DS	0.960±0.010	0.869±0.038	0.953±0.007	0.952±0.008	0.916±0.019	0.771±0.074	0.850±0.077	0.897±0.022	0.893±0.014	0.945±0.013	0.901±0.056	1.811e-02	8.32
+PD+DS +MTT	0.961±0.011	0.870±0.042	0.954±0.007	0.954±0.009	0.913±0.022	0.782±0.069	0.860±0.063	0.895±0.017	0.895±0.011	0.945±0.014	0.903±0.053*	4.604e-03	8.33
+PD+DS +MTT+MTI	0.963±0.010	0.880±0.035	0.954±0.007	0.954±0.008	0.923±0.020	0.801±0.065	0.870±0.060	0.904±0.014	0.900±0.010	0.946±0.013	0.909±0.048*	7.801e-06	12.25
(b)
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value	Time (s)
Baseline	1.135±0.204	1.307±0.472	0.693±0.083	0.812±0.377	1.905±0.698	2.189±0.865	2.771±2.608	0.678±0.098	0.994±0.200	1.047±0.436	1.353±0.669	-	8.31
+PD	1.117±0.248	1.215±0.303	0.685±0.118	0.693±0.137	1.736±0.590	2.128±0.759	2.593±2.942	0.663±0.102	0.938±0.196	1.063±0.645	1.283±0.627	6.927e-02	8.37
+PD+DS	1.194±0.296	1.169±0.368	0.681±0.103	0.734±0.180	1.618±0.429	2.262±1.007	2.744±2.860	0.667±0.088	0.948±0.119	1.221±0.869	1.324±0.661	1.654e-02	8.32
+PD+DS +MTT	1.137±0.303	1.167±0.363	0.657±0.084	0.655±0.094	1.618±0.505	2.254±0.924	1.959±1.709	0.675±0.076	0.939±0.106	1.027±0.505	1.209±0.532*	2.939e-03	8.33
+PD+DS +MTT+MTI	1.072±0.268	1.027±0.273	0.655±0.087	0.645±0.090	1.338±0.308	1.831±0.873	1.960±2.671	0.630±0.070	0.892±0.098	0.941±0.321	1.099±0.451*	2.493e-06	12.25

3.4. The Effect of Multi-Slice Training

Table 4 reports the performance when a different number of 2D slices are used in multi-slice input. The DenseUnet trained with the 20-slice input has significantly improved the segmentation results in both DSC and MSD metrics compared to that with the single-slice input. However, with adding more slices, the 40-slice DenseUnet did not obtain significant improvement over the 20-slice input counterpart.

Table 4.

(a) Dice Similarity Coefficient (DSC) and (b) Mean Surface Distance (MSD) (in units of mm) of a different number of 2D stacked slice as input to the 2D DenseUnet. “*” indicates significant difference (p < 0.05/4 =1.25e-2 considering Bonferroni correction) when comparing each of the other scenarios to the 20-slice setting. Multiple-slice input consistently provides better performance than single slice input; however, adding more slices does not significantly improve the results under the current network setting.

(a) Dice similarity coefficient (DSC)
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value
Single Slice	0.963±0.012	0.871±0.038	0.953±0.007	0.955±0.008	0.920±0.021	0.771±0.051	0.870±0.066	0.902±0.017	0.898±0.014	0.941±0.019	0.904±0.055*	1.638e-04
20 Slices	0.963±0.010	0.880±0.035	0.954±0.007	0.954±0.008	0.923±0.020	0.801±0.065	0.870±0.060	0.904±0.014	0.900±0.010	0.946±0.013	0.909±0.048	-
40 Slices	0.964±0.009	0.871±0.041	0.953±0.008	0.955±0.008	0.921±0.021	0.788±0.074	0.873±0.062	0.904±0.018	0.899±0.011	0.943±0.022	0.907±0.051	2.678e-02
(b) Mean surface Distance (MSD)
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value
Single Slice	1.073±0.343	1.140±0.415	0.685±0.091	0.635±0.092	1.403±0.310	1.948±0.902	2.140±2.506	0.637±0.081	0.903±0.117	1.926±3.119	1.249±0.547*	1.632e-04
20 Slices	1.072±0.268	1.027±0.273	0.655±0.087	0.645±0.090	1.338±0.308	1.831±0.873	1.960±2.671	0.630±0.070	0.892±0.098	0.941±0.321	1.099±0.451	0.909±0.048
40 Slices	1.032±0.226	1.099±0.338	0.669±0.092	0.641±0.085	1.390±0.300	1.935±0.915	1.840±2.472	0.636±0.088	0.917±0.117	0.984±0.468	1. 114±0.446	3.014e-02

3.5. The performance of the finalized ALAMO method

Our finalized ALAMO method incorporated all above determined training & testing techniques in a non-normalized DenseUnet with 20-slice 2D data input. The performance of the proposed DenseUnet and popular PlainUnet are summarized in Table 5. The proposed DenseUnet significantly (p<<0.001) outperformed the PlainUnet in terms of DSC, Jaccard Index, MSD, and 95HD. DSC > 0.90 was obtained in most of the organs except for the duodenum (0.80) and the small intestine (0.87). A randomly selected test case is shown in Figure 3. The multi-view DenseUnet provided the best segmentation quality than both the PlainUnet and the single-view DenseUnet, particularly in the challenging organs such as the small intestine and duodenum. Their per-organ performance measured by DSC and MSD are illustrated with box plots in Figure 4.

Table 5.

Quantitative numbers of Dice Similarity Coefficient (DSC), Jaccard Index (Jacc), Mean Surface Distance (MSD), and 95 Hausdorff Distance (95HD) of our final ALAMO model (a) vs. best PlainUnet (b) (f=96) on the test set (n=20). “*” indicates a significant difference (p < 0.05/4 =1.25e-2 considering Bonferroni correction) when comparing the two models

(a) Proposed DenseUnet
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value
DSC	0.963±0.010	0.880±0.035	0.954±0.007	0.954±0.008	0.923±0.020	0.801±0.065	0.870±0.060	0.904±0.014	0.900±0.010	0.946±0.013	0.909±0.048
Jacc	0.929±0.018	0.787±0.054	0.912±0.013	0.913±0.015	0.858±0.034	0.672±0.087	0.775±0.091	0.825±0.024	0.818±0.016	0.898±0.024	0.839±0.076
MSD	1.072±0.268	1.027±0.273	0.655±0.087	0.645±0.090	1.338±0.308	1.831±0.873	1.960±2.671	0.630±0.070	0.892±0.098	0.941±0.321	1.099±0.451
95HD	3.035±0.916	3.235±1.859	1.791±0.332	1.760±0.275	4.079±1.374	8.225±5.784	9.092±16.361	1.473±0.254	2.444±0.281	2.267±0.654	3.740±2.576
(b) PlainUnet (f=96)
	Liver	Pancreas	Right Kidney	Left Kidney	Stomach	Duodenum	Small Intestine	Spinal Cord	Vertebral Body	Spleen	Mean	P-value
DSC	0.953±0.009	0.793±0.073	0.938±0.016	0.933±0.023	0.861±0.051	0.717±0.077	0.766±0.132	0.876±0.020	0.884±0.017	0.927±0.025	0.865±0.077*	2.297e-09
Jacc	0.911±0.016*	0.663±0.099*	0.883±0.028*	0.875±0.039*	0.760±0.076*	0.564±0.093*	0.636±0.154*	0.780±0.032*	0.792±0.027*	0.865±0.042*	0.773±0.112*	1.150e-10
MSD	1.470±0.283	2.792±1.307	2.576±1.865	1.822±1.263	3.130±0.941	4.332±1.767	5.122±4.012	1.211±0.488	1.743±1.340	1.667±0.859	2.586±1.228*	5.413e-09
95HD	4.054±1.020	10.632±6.746	11.841±15.260	6.282±8.723	11.203±5.735	18.540±9.063	27.558±25.731	2.029±0.374	6.639±17.105	4.296±4.685	10.308±7.362*	6.739e-06

Figure 3.

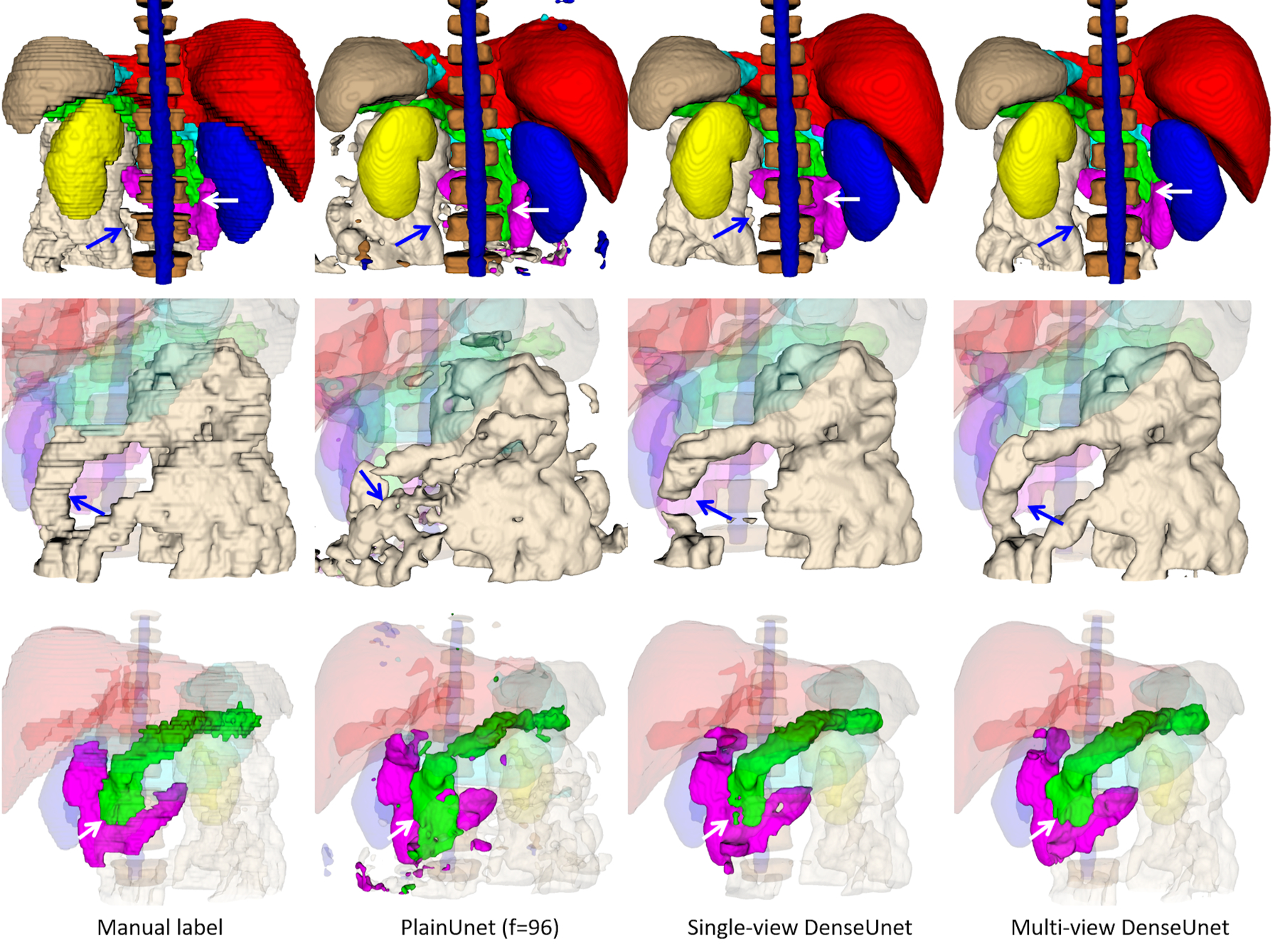
Segmentation results on a random test case with manual label, PlainUnet (f=96), single-view (transversal) version of DenseUnet, and multi-view inference with majority voting: liver(red), spleen(gray), pancreas(green), right kidney(blue), left kidney(yellow), stomach(cyan), duodenum(purple), small intestine(white), spinal cord (blue) and vertebral bodies (dark brown). The first row shows the overall segmentation results, while the 2nd and 3rd row show the zoom-in view of small intestine and pancreas and duodenum in better angels. The multi-view inference correctly segments the small intestine that is missed in single-view inference, as pointed by the blue arrow. Additionally, it produces a more accurate boundary of the pancreas and duodenum, as pointed by the white arrow. Both proposed DenseUnets provide better segmentation quality than the popular PlainUnet.

Figure 4.

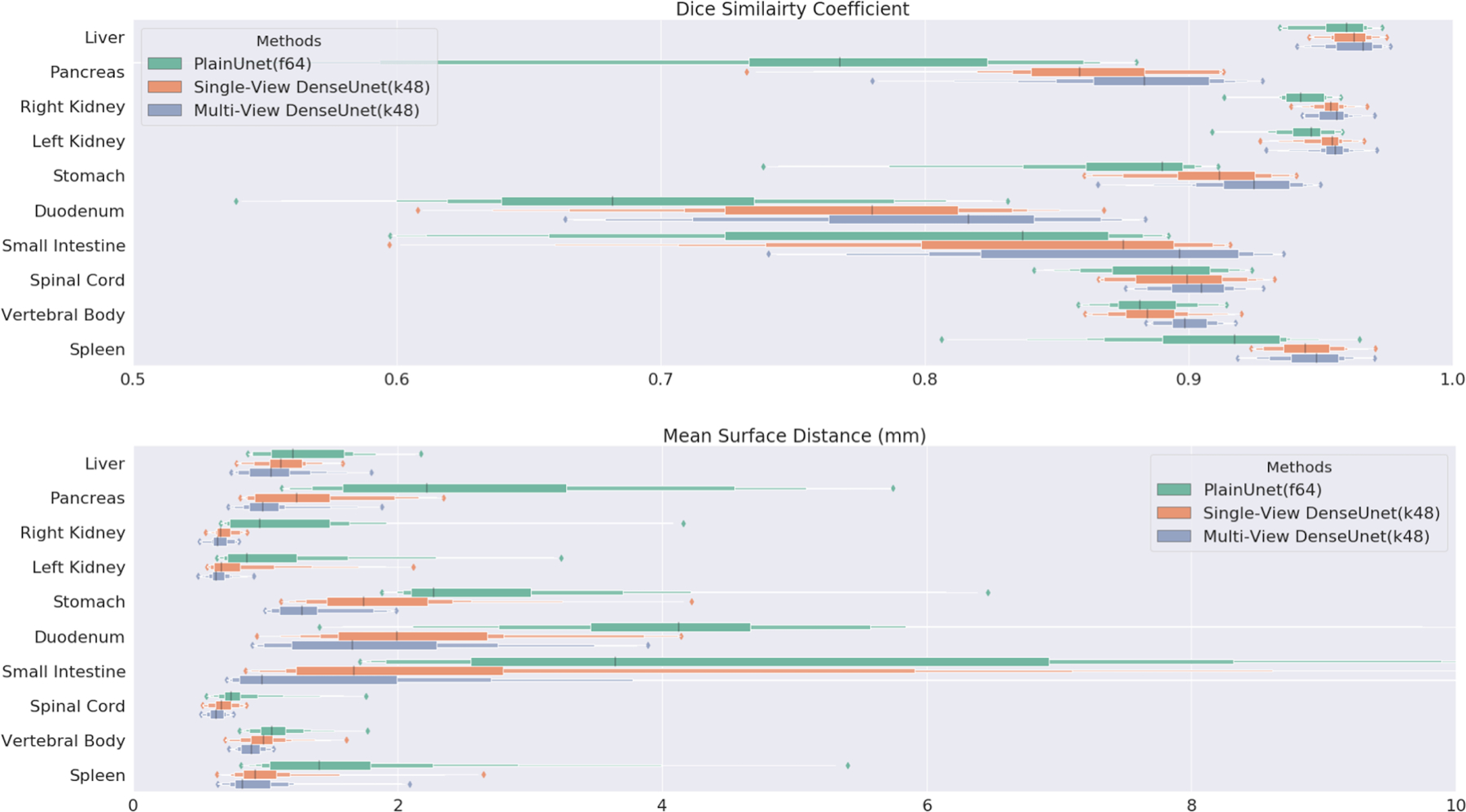
Per-organ Dice similarity coefficient and mean surface distance box plot in test set (n=20) for PlainUnet (f=64), Single-View DenseUnet (k=48) and Multi-View Inference DenseUnet (k=48).

4. DISCUSSION

In this work, we presented a deep learning-based technique ALAMO for fully automated multi-organ segmentation on abdominal MR. ALAMO builds on 2D DenseUnet and incorporates tailored design in data augmentation and training procedures, utilizing multi-slice input, deep connection, auxiliary supervision, and multi-view. Our results showed that ALAMO might be a strong candidate to provide state-of-the-art performance. The major novelty and contribution of this work lies in two aspects. On the methodology aspect, we have introduced a novel multi-view approach to enhance the segmentation quality and robustness of the 2.5D (2D stack) Unet modules. In contrast to existing work with multipath approaches [42], we propose to use shared filter coefficients in our multi-view settings, which also has the benefit of being economical in the number of free parameters. On the practical aspect, this study offers an unprecedented extensive investigation on the roles of various structure optimization and parameter optimization to address this important clinical task of organ segmentation. Statistical tests are performed along the way and practical recommendations are provided. Overall, this study offers an effective, robust, and feasible pipeline that can be reproduced in a practical clinical system without much hardware/software burdens.

While a 3D network may better suit the nature of medical imaging [43, 44], it is also associated with a much higher risk of overfitting and prohibitive demands in memory and computation time. Moreover, the variations in the size of the organs and their relative geometric locations also make it necessary to have both high-resolution and large-space support in the network configuration, which is challenging to achieve with a 3D network. Even though it is possible to address such demands with a multi-resolution or hierarchical scheme, further complexity in the overall pipeline will be introduced. In this work, we demonstrated that a multi-slice-multi-scale 2D network, when carefully designed and optimized, provided a clinically viable alternative.

Two popular networks, PlainUnet and DenseUnet, were compared. We showed that DenseUnet used much fewer parameters and offered more accurate segmentation results and slightly reduced computation time compared to PlainUnet. By adding multiple skip connections within the convolutional blocks, we forced the network to reuse its weights, thus dramatically reducing the number of parameters for a similar performance. A smaller network size not only makes training easier but also makes the model less prone to overfitting to the training data and more robust on unseen test data. This is critically important for MR-based DL applications due to typically limited data size.

The use of normalization resulted in an insignificant performance gain in the single-sample batch setup. This is in accordance with the recent study that suggested the dependence of the normalization performance on the batch size [25, 38]. In time-sensitive applications, such as adaptive planning in MRgRT, non-normalization would be an appropriate choice that comes with a small computation burden and thus dramatically fast speed.

Combining three different views further boosted up our network’s performance. Forcing the network to train on different 2D views and then fusing them can remove certain misclassified regions otherwise appeared in the single-view output. Especially for the small intestine and duodenum that have irregular shapes and are difficult to distinguish from complicated backgrounds, the multi-view network has a better performance compared to the single-view network. Additionally, since we used the same model across different views, the network has fewer parameters than those where multiple models are used in parallel with independent filters. The reduction in parameters is theoretically beneficial for mitigating the overfitting problem and thus potentially important for this particular DL application.

Our last experiment also validated the hypothesis that a multi-channel 2D network with multi-slice (both 20-slice and 40-slice) data input performs better than a 2D network with single-slice data input. However, with the current network design, using 40 slices as input did not improve the final accuracy, and the 20-slice input appeared to be a good fit for the DenseUnet (k=48). Moreover, it is noteworthy that DSC, when already close to 1, may not be a sensitive enough metric to the improvement in performance by multi-slice input. When it comes to the “error rate” (1 - DSC), however, the difference between the single-slice and 20-slice inputs, calculated as (0.909–0.904) / (1–0.904), has a 5.2% difference, even though the absolute difference in DSC is simply 0.005.

There are not many studies on the multi-organ segmentation in abdominal MR with DL. Our work demonstrated a better or similar DSC in the abdominal organs to the limited number of existing studies on 0.35-Tesla TrueFISP images [23] and 3.0-Tesla T2-weighted images [24], especially in challenging organs such as the stomach and the duodenum. Despite a much lower resolution (1.2 mm vs. 0.5mm), our results are still very competitive compared to multi-organ segmentation on CT images that have better signal to noise ratio and spatial resolution [22]. Our segmentation of the organs like the duodenum and small intestine is much better than their CT-base segmentation (DSC: 0.80 vs. 0.75 in the duodenum, 0.87 vs. 0.80 in the small intestine). For the most studied single organ - pancreas, our DSC of 0.88 is still on par with recent state-of-the-art deep learning-based segmentation works [45–48].

We believe there is still room to improve in our network, particularly for organs like the small intestine and duodenum. First, to strike a good balance between computational complexity in 2D and richer geometry context in 3D networks, we will explore the hierarchical multi-resolution 3D approach. Second, the current T1-weighted data has poor boundary conspicuity in some organs, leading to some uncertainties in expert labeling and potentially unstable network performance. Adding other contrast weightings such as T1-weighted fat phase and T2-weighted images as multi-channel input to a re-configured network might further improve the segmentation.

There are some limitations in our work. First, the quantity of image data is limited and particularly we had only 20 cases for testing. Further validation with a more large-scale cohort dataset would be highly needed. Second, our ground truth was generated by human-labeling from one reader followed by reediting, if necessary, from a senior reader. Inter- and intra-observer variability analyses were not possible, which should be addressed in future studies. Additionally, ground truth can be highly improved by, for example, having more experienced readers to reach consensus contours. Last, because of constraints by long training time, we were not able to perform multiple-folds cross validation experiments. However, as a pilot experiments, our ALAMO has shown promising results despite all the limitations and will provide insights into future studies.

5. CONCLUSION

The proposed ALAMO technique allows for fully automated abdominal MR segmentation with high accuracy, and practical memory and computation time demands. This is an important first step to incorporate MRI-based simulation and daily MRI-based adaptive treatment planning in radiotherapy.