Abstract
Purpose
To develop and evaluate a fast and effective method for deblurring spiral real-time magnetic resonance imaging (RT-MRI) using convolutional neural networks (CNN).
Methods
We demonstrate a 3-layer residual CNN to correct image domain off-resonance artifacts in speech production spiral RT-MRI without the knowledge of field maps. The architecture is motivated by the traditional deblurring approaches. Spatially varying off-resonance blur is synthetically generated by using discrete object approximation and field maps with data augmentation from a large database of 2D human speech production RT-MRI. The effect of off-resonance range, shift-invariance of blur, and readout durations on deblurring performance are investigated. The proposed method is validated using synthetic and real data with longer readouts, quantitatively using image quality metrics and qualitatively via visual inspection, and with a comparison to conventional deblurring methods.
Results
Deblurring performance was found superior to a current auto-calibrated method for in vivo data and only slightly worse than an ideal reconstruction with perfect knowledge of the field map for synthetic test data. CNN deblurring made it possible to visualize articulator boundaries with readouts up to 8 ms at 1.5 T, which is 3-fold longer than the current standard practice. The computation time was 12.3 ± 2.2 ms per-frame, enabling low-latency processing for RT-MRI applications.
Conclusion
CNN-deblurring is a practical, efficient, and field-map-free approach for the deblurring of spiral RT-MRI. In the context of speech production imaging this can enable 1.7-fold improvement in scan efficiency and the use of spiral readouts at higher field strengths such as 3 T.
Keywords: artifact correction, convolutional neural networks, deblurring, off-resonance, real-time MRI, speech production
INTRODUCTION
Spiral data sampling is used in a variety of MRI applications due to its favorable properties. It requires only few TRs to achieve Nyquist sampling of k-space, provides excellent velocity point spread function (PSF) (1,2), and reduces motion artifacts due to its natural oversampling at the k-space center (3,4). Spiral sampling is well-suited for advanced reconstruction algorithms such as compressed sensing when combined with strategies such as under sampling and golden angle scheme (5,6). Spiral imaging is also widely used for real-time MRI (RT-MRI) where the capability of capturing rapid motion is crucial such as in cardiac imaging and speech production imaging (6–12).
One major limitation of spiral sampling is image blurring due to off-resonance (13). Off-resonance causes the accumulation of phase error along the readout in k-space domain, resulting in blurring and/or signal loss in the image domain. To date, this artifact remains the predominant challenge for several RT-MRI applications: In speech RT-MRI it degrades image quality primarily at the air-tissue boundaries which include the vocal tract articulators of interest (14–16). In cardiac RT-MRI, it degrades image quality in the lateral wall and adjacent to draining veins, and around implanted metal (e.g., valve clips, etc) (10,17). In interventional RT-MRI, it may degrade image quality around the tools used to perform intervention (depending on the precise composition of the tools) (18). These artifacts are most pronounced with long readout durations which is precisely when spiral provides the greatest efficiency. In speech production RT-MRI, the convention is to use extremely short readouts (≤ 2.5 ms at 1.5 T) (15).
Many spiral off-resonance correction methods have been proposed in the literature. Most existing methods require prior information about the spatial distribution of the off-resonance, also called the field map, Δf(x,y) (19–25). For RT-MRI, this field map needs to be updated frequently throughout the acquisition window because of local off-resonance changes as motion occurs. Several research groups have proposed to estimate the dynamic field maps either from interleaved two-TE acquisition using the conventional phase difference method (14,23,26) or from single-TE acquisition after coil phase compensation (16). Common limitations of these approaches are field map estimation errors due to off-resonance induced image distortion and/or reduced scan efficiency which is undesirable for RT-MRI.
Given a field map, the conventional approach to deblur the image is conjugate phase reconstruction (CPR) (19,20) or one of its several variants (21,22,27). One such variant is frequency-segmentation which reconstructs basis images at demodulation frequencies and applies spatially-varying masks to the basis images to form a desired sharp image. While it is an efficient approximation to assume off-resonance to be spatially varying smoothly, the assumptions are typically violated at air-tissue interfaces. Alternatively, iterative approaches (28,29) are known to be effective at resolving abruptly varying off-resonance at the cost of increased computation complexity. Note that neither iterative nor non-iterative approaches are able to overcome the performance dependence on the quality of the estimated field maps.
Recently, convolutional neural networks (CNN) have shown promise in solving this deblurring task. Zeng et al (30) have proposed a 3D residual CNN architecture to correct off-resonance artifacts from long-readout 3D cone scans. Specifically, off-resonance was framed as a spatially varying deconvolution problem. Synthetic data was generated by simulating zeroth-order global off-resonance at a certain range of demodulation frequency. The trained network was applied successfully to long-readout pediatric body MRA scans. Is there an underlying principle that explains why and how CNNs work well in this deblurring task? Perhaps it is the combinatorial nature of nonlinearities such as the rectified linear unit (ReLU) in CNN models. Traditional methods require field maps (19–25) or focus metrics (31–33) to estimate the spatially-varying mask. In contrast, CNNs utilize prior information about characteristics of off-resonance in the synthesized training data, while ReLU nonlinearities provide the mask to the convolutional filters, which enables spatially-varying convolution (34). Once the network is trained, the feedforward operation of CNNs generates a desired sharp image given a blurry image input in an end-to-end manner, without explicit knowledge of field maps.
In this work, we attempt to establish a connection between the CNN architecture and traditional deblurring methods. We utilize a compact 3-layer residual CNN architecture to learn the mapping between distorted and distortion-free images for 2D spiral RT-MRI of human speech production. We consider this application (15,35,36) because off-resonance appears as spatially (and temporally) abruptly varying blur, degrades image quality at the vocal tract articulators of interest, and therefore is a fundamental limitation to address. We leverage field maps estimated from a previously proposed dynamic off-resonance correction method (16). Specifically, we synthesize spatially varying off-resonance by using the estimated field maps with various augmentation strategies. We test the impact of the augmentation strategies on deblurring performance and generalization in terms of several image quality metrics. We evaluate the proposed method using synthesized and real test data sets and compare its performance quantitatively using metrics and qualitatively via visual inspection against conventional deblurring methods.
THEORY
Image Distortion due to Off-resonance
In spiral MRI, off-resonance results in a spatially varying blur that can be characterized by a PSF (31). Off-resonance causes the local phase accumulation in the k-space signal. In the spatial domain, this can be viewed as an object being convolved with spatially varying filter kernel (PSF) that is determined by the local off-resonance and trajectory-specific parameters such as a readout time map. Here, we briefly introduce this representation in the discrete domain, which we use throughout this paper.
In the presence of off-resonance effects, the signal equation after discretization approximation (28,29) can be expressed as:
| [1] |
where ki and rj represent the k-space and spatial coordinates for i = 1,…,Nd and j = 1,…,Np, respectively; yi is the complex k-space measurement at time ti ∈ [TE,TE + Tread] defining t1 = TE as the start of the readout, TE as echo time, and Tread as the readout duration. xj is the transverse magnetization of an object at a location rj. fj is the off-resonance frequency present at rj. Here is the local phase error that is induced by off-resonance present at rj and is multiplied to the k-space signal at ki. Note that Eq.[1] can be expressed in a matrix vector form as y = Afx where , and with . In the absence of off-resonance effects (i.e., f = 0), Af is reduced to the conventional (non-uniform) Fourier basis matrix A0 with .
Without considering the off-resonance effect, we could reconstruct a blurry image by applying A0TW to y as follows:
| [2] |
where T denotes the conjugate transpose of a matrix. is a diagonal matrix defining [W]i,i = wi where wi denotes a density compensation weight at ki. Here, is a blurring operator matrix defining . The k-th column of Hf corresponds to the discretized PSF for a point-source located at rk. The effect of off-resonance can be seen as a spatially varying convolution since the PSF is shift-variant due to with non-zero fk. Whether the PSF is sharp or blurred is dependent on the off-resonance frequency (fk) given the trajectory-specific parameters – trajectory ki and time map ti. Likewise, the readout duration (Tread) determines the shape of the PSF given fk. For example, the larger fk and/or the longer Tread are, the more phase error of is accrued, therefore increasing the spread of the PSF.
Approximation of Spatially Varying Blur
The blurring operation is described in Eq. [2] as a matrix vector multiplication. An approximate analytical solution to the deblurring problem is therefore:
| [3] |
where and + denotes the pseudo-inverse. Noll et al. have shown that HfTHf can be approximated well by an identity matrix under the condition that the phase term due to off-resonance is sufficiently small (i.e., ) (27). This is the underlying principle behind CPR and its variants. This condition is met whenever the off-resonance f(x,y) due to B0 inhomogeneity and susceptibility exhibits smooth spatial variation (37). Under this assumption, the deblurred image can be obtained by projecting the blurred image onto the column space of HfT:
| [4] |
Note that CPR performs these projections in the frequency domain while other approaches (25,38) including Eq. [4] perform them in the spatial domain.
Next, we approximate of Eq. [1] by . This approximation is supported by literature (29) for general choices of bil and clk. For instance, time-segmentation approximates bil = bl(ti) and for a predetermined set of time points tl while frequency-segmentation approximates and clk = cl(fk) for a predetermined set of frequencies fl. Substituting such an approximation into Hf yields . In matrix form, this can be expressed as:
| [5] |
where and are diagonal matrices with [Bl]i,i = bil and [Cl]k,k = clk, respectively. Eq. [5] can be viewed as a decomposition of the shift-variant blurring operator Hf as a sum of L (L << Np; Np = the number of pixels) convolutions Hl (i.e., approximately shift-invariant blurring operators) with prior weightings Cl. In frequency-segmentation (27), Hl can be given by PSFs at a set of L equally spaced off-resonance frequencies and Cl is a spatially varying mask that has a diagonal element of 1 if a corresponding pixel needs to be assigned to the l-th off-resonance frequency or 0 otherwise. Other types of decomposition can be found in both MR and non-MR literature (29,39,40).
Substituting Eq. [5] into Eq. [4] yields
| [6] |
where , , and . is an identity matrix. Eq. [6] can be interpreted as a blurred image being convolved by H with spatially varying weighting (C), followed by summation (S) along the dimension corresponding to L basis images.
Spatially Varying Deblurring using CNN
Interestingly, the solution described in Eq. [6] resembles the feedforward operation of a simple two-layer CNN. Let us consider a two-layer CNN:
| [7] |
where , , and is a diagonal matrix with 0 and 1 elements that are determined by the nonlinear ReLU activation output (i.e., if , otherwise 0). El and Dl refer to convolution matrices associated with the l-th channel output and input at the first and second layers, respectively. With 1×1 convolutions in the second layer, D reduces to with channel-wise trainable weights dl for l = 1,…,L.
D in the second layer and E of the first layer of the CNN perform frequency summation S and input filtering H in Eq. [6], respectively. The convolution matrices D and E are learned from the training data, whereas the convolution matrix H and spatially-varying mask C are determined by field maps f. More importantly, the zero-one switching behavior of the elementwise ReLU induced nonlinear operator Λ can derive the spatially-varying weight adaptively from the different filtered inputs and analogously achieve the spatially varying weighting of the matrix C in Eq. [6]. Rather than relying on measuring the exam-specific field maps, the CNN would learn from training samples to recognize and undo characteristic effects of off-resonance.
While the implementation of Eq. [7] would be a direct replication of traditional off-resonance deblurring methods, we take this starting point and build on the following recent advances in machine learning to arrive at the proposed network architecture shown in Figure 1. First, we increase the CNN architecture from two to three layers by replacing the single convolutional layer E with two convolutional layers with a ReLU operation in between. When using a single convolutional layer, there exist maximum 2L distinct combinations of different convolution kernels. This is because there are L convolutional filter outputs for each spatial location, and summing up these L coefficients at the second layer yields 2L possible combinations due to the binary selection of the element-wise ReLU. Increasing the number of cascaded layers from one to two increases the number of combinations from 2L to . A similar increase in the number of combinations was derived for encoder-decoder CNNs by Ye et al (34). Second, we consider residual learning by adding a skip connection between input and output. Residual learning is widely used for medical image restoration (41–44) and we experimentally found that it improves deblurring performance (comparison not shown).
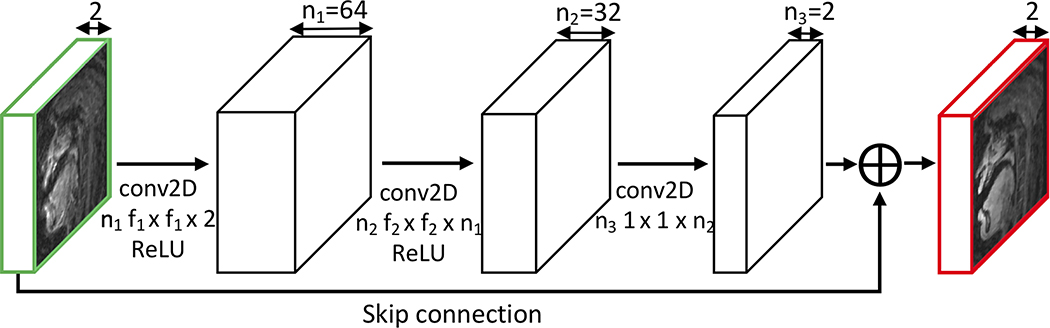
Figure 1. Proposed network architecture.
The input is distorted complex images, and the output is distortion-free complex images, each consisting of two channels (real and imaginary). The first convolutional layer takes the input distorted image of size 84 × 84 × 2 and applies n1 2D convolutions with filter size f1 × f1 × 2 (the last dimension 2 equaling the depth of the input), followed by the ReLU operation. The second layer takes the output of the first layer of size 84 × 84 × n1 and applies n2 2D convolutions with filter size f2 × f2 × n1, followed by the ReLU operation. The third layer takes the output of the second layer of size 84 × 84 × n2 and applies 2 2D convolutions with filter size 1 × 1 × n2. The output of the third layer is added to the input images via the skip connection to generate the final distortion-corrected image of size 84 × 84 × 2.
METHODS
Network Implementation Details
The convolutional neural network (Figure 1) is comprised of 3 convolutional layers. The network architecture is practically implemented with real-valued operations. Although both the input and output of the networks consist of two channels (real and imaginary components), we do not explicitly separate the real and imaginary image processing into separate streams and therefore information between the real and imaginary images is shared between the intermediate layers.
The filter widths are set to n1 = 64, n2 = 32, n3 = 2. We choose f1 = 9, f2 = 5, and f3 = 1. We experimentally determined convolutional filter sizes of f1 and f2 that give the best deblurring performance in terms of image quality metric described in the following section (Supporting Information Figure S1).
We train the model in a combination of Lp loss and gradient difference loss (45) between the prediction and ground truth x:
| [8] |
where and . We choose to use p=1 (i.e., L1 loss) and λ = 1. We report the experimental results on the performance of choosing the different values of λ and choosing between L1 and L2 in Supporting Information Figure S2.
For training the model, we use the ADAM optimizer (46) with a learning rate of 0.001, a mini-batch size of 64, and 200 epochs. We implement the network with Keras using Tensorflow backend. The network is trained using a 16-core Intel Xeon E5–2698 v3 CPU and a graphical processing unit of Nvidia Tesla K80.
Generation of Training Data
We acquired the data from 33 subjects on a 1.5T scanner (Signa Excite, GE Healthcare, Waukesha, WI) at our institution using a standard vocal-tract protocol (6). The imaging protocol was approved by our Institutional Review Board. A 13-interleaf spiral-out spoiled gradient echo pulse sequence was used with the body coil for RF transmission and a custom 8-channel upper airway coil for signal reception. Imaging was performed in the mid-sagittal plane while the subjects being scanned followed a wide variety of speech tasks to capture various articulatory postures. Imaging parameters used included: TR/TE = 6.004/0.8 ms, Tread = 2.52 ms, spatial resolution = 2.4 × 2.4 mm2, slice thickness = 6 mm, FOV = 200 × 200 mm2, receiver bandwidth = ±125 kHz, and flip angle = 15°.
Although this protocol uses a short spiral readout (2.52 ms), we found the off-resonance in this data corpus to be diverse and necessary to be corrected to obtain high-quality images. We adopted a recent dynamic off-resonance correction method (DORC)(16) to estimate dynamic field maps and to reconstruct dynamic images in conjunction with the off-resonance correction. The resultant dynamic images (and field maps) were of size 84 × 84 × 400 (time) for each subject. We regarded these images (x) and estimated field maps (f) as ground truth. We split 33 subjects into 23, 5, and 5 subjects for the training, validation, and test sets, respectively. The validation set was used for choosing network parameters and performing validation experiments. The test set was used for evaluating the performance of the proposed method.
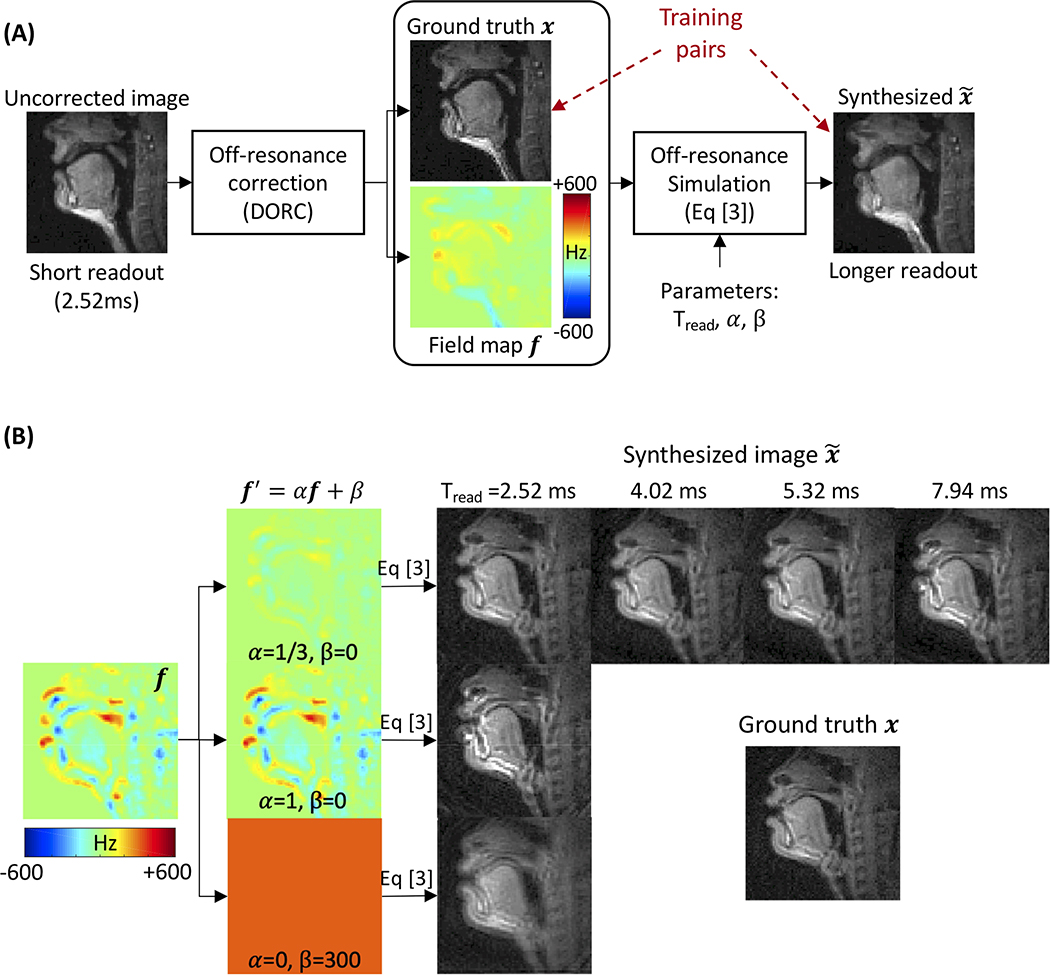
Blurred images were simulated from the ground truth x with augmented field maps f′ by employing Eq. [2] frame by frame as illustrated in Figure 2A. Augmentation included a scale α and an offset β to the field map f such that f′ = αf + β and synthesizing blurred images was based on the augmented field map. Note that α ≠ 0 would inherit original spatially varying off-resonance blur from the field maps f up to scale, whereas α = 0 leads to spatially uniform blur analogous to the work of Zeng et al (30). We added the offset β to simulate the zeroth-order frequency offsets in image space. Such offsets are a typical result of imperfect shimming. We considered four different spiral trajectories (Supporting Information Figure S3). Those correspond to 13-, 8-, 6-, 4-interleaf spiral-out samplings, with readout times (Tread) of 2.52, 4.02, 5.32, and 7.94 ms, respectively, with the same field of view and in-plane resolution. Figure 2B contains examples of synthetic images. During the implementation of Af in Eq. [2], we approximated as described earlier and executed Af with L=6 times non-uniform FFT (47) calls.
Figure 2. Generation of training data.
(A) The ground truth image x and field map f are obtained from short readout (2.52 ms) data with off-resonance estimation and correction. Blurred images are synthesized via simulating Eq. [3] using the ground truth image x and field map f′ augmented by α and β and different spiral readout durations (Tread). (B) The field maps are augmented by f′ = αf + β with scale α ranging from 0 to 1 and constant offset β from −300 to 300 Hz. We also consider four different spiral readout durations (Tread = 2.52, 4.02, 5.32, and 7.94 ms). Those correspond to 13-, 8-, 6-, 4-interleaf spiral-out trajectories, respectively, with the same field of view and in-plane resolution.
Validation Experiments
Here, we evaluated the impact of various data augmentation strategies (for f) on deblurring performance and generalization. Specifically, we trained the same network architecture using reference data from 23 subjects synthesized with different combinations of the scale factor α, frequency offset β, readout duration Tread (spiral trajectories), and the training data size as summarized in Table 1. We then measured the effectiveness of the different configurations by using the validation set (5 subjects) listed in Table 1.
Table 1.
Summary of the parameters used to generate training and validation sets for validation experiments.
| Train |
Validation |
|||||||
|---|---|---|---|---|---|---|---|---|
| α | β (Hz) | Tread (ms) | # of samples | α | β (Hz) | Tread (ms) | ||
| EXP I | A | 1/6 1/3 2/3 1 |
{0} | 2.52 | N* | 1/6 1/3 2/3 1 |
{0} | 2.52 |
| B | 1 | {0} {−300, −200, …, 300} {−300, −200, …, 300} {−300, −200, …, 300} |
2.52 | N N 3.5N 7N |
1 | {0} | 2.52 | |
| EXP II | 1 0 |
{−300, −200, …, 300} {−600, −550, …, 600} |
2.52 | 3.5N 4N |
1 0 |
{0} {−300, −200, …, 300} |
2.52 | |
| EXP III | 1 | {−300, −200, …, 300} | 2.52 4.02 5.32 7.94 |
7N | 1 | {−300, −200, …, 300} | 2.52 4.02 5.32 7.94 |
|
Each row represents a configuration set of α, β, Tread, and # of samples for train set or α, β, Tread for validation set.
Here, N (# of samples) = 9200 84×84 image pairs of distorted and distortion-free complex images.
EXP I–A. Off-resonance range
The off-resonance frequency range is typically unknown. We examined the impact of off-resonance frequency range (fmax denoting the maximum frequency value) in training data on deblurring performance. We trained the network on training data simulated with 4 different values of fmax using , resulting in four trained networks, and compared their model performance on validation data with varying fmax as listed in Table 1. We considered β = 0 and Tread = 2.52 ms for both training and validation sets. Note that the frequency ranges from −625 to 625 Hz (fmax=625 Hz) for the original field maps (i.e., when α = 1 and β = 0).
EXP I–B. Frequency offset and training set size
We added a frequency offset β when synthesizing the training data. This is equivalent to simulating a constant frequency offset over an image space. We considered two training configurations; one with β = 0 and one with β ∈ {−300,−200,…,300}. The former had N (=9200) samples, while the latter had different sample sizes from N to 7N. The range of β from −300 to 300 Hz is deliberately chosen broad to cover the maximum center frequency error that could be expected.
EXP II. Spatially varying versus spatially uniform blur
Recent work by Zeng et al (30) generated training data by simulating off-resonance at evenly spaced frequencies between ± 500 Hz. This approach, if generalized to spatially varying blur, could benefit situations where the field map is not available for synthesizing spatially varying blur. To test the generalizability of this approach and more importantly the necessity of the field maps for the spatially variant blur, we generated synthetic data of spatially invariant blur by setting α = 0 and β ∈ {−600,−550,…,600} and of spatially variant blur by using α = 1 and β ∈ {−300,−200,…,300}, the same setting as in EXP I–B. We then tested each trained network to another configuration setting by considering two validation configurations of spatially variant and invariant blur listed in Table 1.
EXP III. Readout duration
We investigated whether a network trained on a particular Tread (spiral trajectory) can be generalized to the unseen Tread in test time. We used 13-, 8-, 6-, 4-arms trajectories corresponding to Tread of 2.52, 4.02, 5.32, 7.94 ms to synthesize blur data, while setting α = 1 and β ∈ {−300,−200,…,300}.
For all experiments, the accuracy and robustness of deblurring performance were evaluated using multiple image quality metrics. We used the high-frequency normalized error norm (HFEN) (48), due to the expectation that high spatial frequency features would be restored after the blurred boundary is recovered. We also used common metrics, such as peak-signal-to-noise ratio (PSNR) and structural similarity index (SSIM) (49).
Evaluation using Synthetic Test Data
We tested the model on unseen synthetic test data from 5 subjects (independent from training and validation datasets). We used the model trained in EXP III. The test data were simulated from all spiral trajectories without any augmentation (i.e., α = 1,β = 0). For comparison, we applied 1) frequency-segmentation-based multi-frequency interpolation (MFI) (22) and 2) model-based iterative reconstruction (IR) (28) into the synthetically generated test k-space data (y). For MFI, we obtained a deblurred image by . For IR, we obtained a deblurred image by solving iteratively by using conjugate gradient with 16 iterations. In both methods, we used the ground truth field map f to construct Af. HFEN, PSNR, and SSIM metrics were used for evaluation.
It is worth noting that the IR method is known to provide more accurate results than the non-IR method for abruptly varying off-resonance in space. This IR approach could provide the best achievable deblurring performance given the ground truth field map f, although it is not available in practice.
Evaluation using Real Experimental Data
We applied the trained network to real data. We acquired spiral RT-MRI data with four readout durations (2.52, 4.02, 5.32, and 7.94 ms) from two subjects and performed image reconstruction as described by Lingala et al (6). We performed the deblurring on the reconstructed images frame by frame by using the trained network. We compared results with DORC (16). This auto-calibrated method estimates dynamic field maps from single-TE blurred image itself after coil phase compensation, with no scan time penalty, and iteratively reconstructs off-resonance-corrected image using the estimated field map.
RESULTS
Validation Experiments
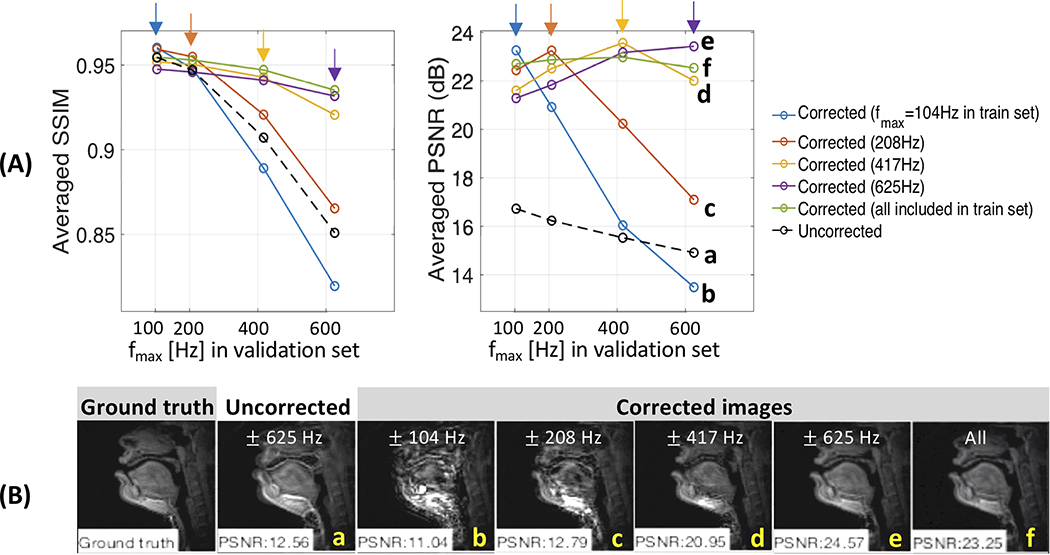
Figure 3A shows deblurring performance (SSIM and PSNR) as a function of the range of off-resonance (fmax) in the train and validation sets (EXP I-A). For the corrected images, each curve represents a separate network trained with different fmax. For no correction (a, black dashed curve), the values of SSIM and PSNR gradually decrease as fmax increases in the validation sets, which is likely due to worsened blurring artifact. All but the network trained with fmax of 104 Hz (b, blue curve) improve image quality for all fmax tested compared with the uncorrected case. Each network is shown to exhibit the highest values of SSIM and PSNR for validation data fmax, with which the network is trained. The performance then quickly degrades for fmax greater than that of its best performance (see c, orange curve). In Figure 3B, representative frames are shown. The uncorrected image presents fmax=625 Hz as shown in (a) and model trained with fmax of 625 Hz shown in (e) exhibits the best deblurring performance qualitatively against the other models shown in (b-d, f). We observe that it is essential for the frequency range of the training set to be a superset of the validation data.
Figure 3. Performance depends on the Training Set (EXP I-A).
(A) Averaged SSIM and PSNR as a function of frequency range (fmax denoting the maximum frequency value) for the uncorrected (black dotted) and corrected (non-black solid) images in the validation set. Color (non-black) represents a separate network trained with different fmax. Note that higher SSIM and PSNR correspond to better performance. The best performance is achieved when the training and validation datasets share the same range of off-resonance (arrows). When severe off-resonance appears in the validation data as off-resonance range is increased, performance for the network trained with fmax less than that of the validation data quickly degrades. (B) Representative example of the ground truth, uncorrected, and corrected images. The uncorrected image had fmax = 625 Hz and was deblurred using models trained with fmax of 104, 208, 417, 625 Hz, and all of them. We observe that it is essential for the frequency range of the training set to be a superset of the validation set.
We also found that adding frequency offsets when synthesizing the training data helps the network perform better, which is shown in Table 2 (EXP I-B). In addition, as the training samples increase from N to 7N, a performance improvement of 2.1, 0.003, and 0.022 can be found in PSNR, SSIM, and HFEN, respectively.
Table 2.
Quantitative evaluation of model performance in terms of the PSNR, SSIM, and HFEN, without and with offset β, and as a function of the number of training samples (EXP I-B).
| Training data | PSNR | SSIM | HFEN (x1000) | |
|---|---|---|---|---|
| Without offset β (= 0) | # of samples = N* | 32.75 | 0.979 | 0.274 |
| With offset β {−300, −200, …, 300} | N | 33.43 | 0.980 | 0.125 |
| 3.5N | 34.40 | 0.983 | 0.094 | |
| 7N | 34.53 | 0.983 | 0.103 | |
| No correction | 26.82 | 0.951 | 0.890 | |
Here, N = 9200 84×84 image pairs of distorted and distortion-free complex images.
Table 3 presents the quantitative comparison of model performance on spatially invariant and variant blur (EXP II). The network trained on spatially variant blur has superior PSNR, SSIM, and HFEN values for both validation data of spatially invariant and variant when compared to no correction and the network trained on spatially invariant blur. The network trained on spatially invariant blur improves all the image metrics for the validation data of spatially invariant blur compared to no correction, but when applied to spatially variant blur, it presents even lower values in all the metrics than with no correction, indicating it fails to deblur spatially varying off-resonance.
Table 3.
Quantitative evaluation of model performance on spatially invariant and variant blur in terms of the PSNR, SSIM, and HFEN (EXP II).
| Validation data | Training data | PSNR | SSIM | HFEN (x1000) |
|---|---|---|---|---|
|
Spatially variant blur
(α = 1 and β = 0) |
no correction | 26.82 | 0.951 | 0.890 |
| Spatially variant blur α = 1 β ∈ {−300, −200, …, 300} |
34.40 | 0.983 | 0.094 | |
| Spatially invariant blur α = 0 β ∈ {−600, −550, …, 600} |
26.53 | 0.934 | 1.414 | |
|
Spatially invariant blur
(α = 0 and β ∈ {−300, −200, …, 300}) |
no correction | 27.01 | 0.897 | 0.346 |
| Spatially variant blur α = 1 β ∈ {−300, −200, …, 300} |
35.60 | 0.986 | 0.037 | |
| Spatially invariant blur α = 0 β ∈ {−600, −550, …, 600} |
35.54 | 0.986 | 0.046 |
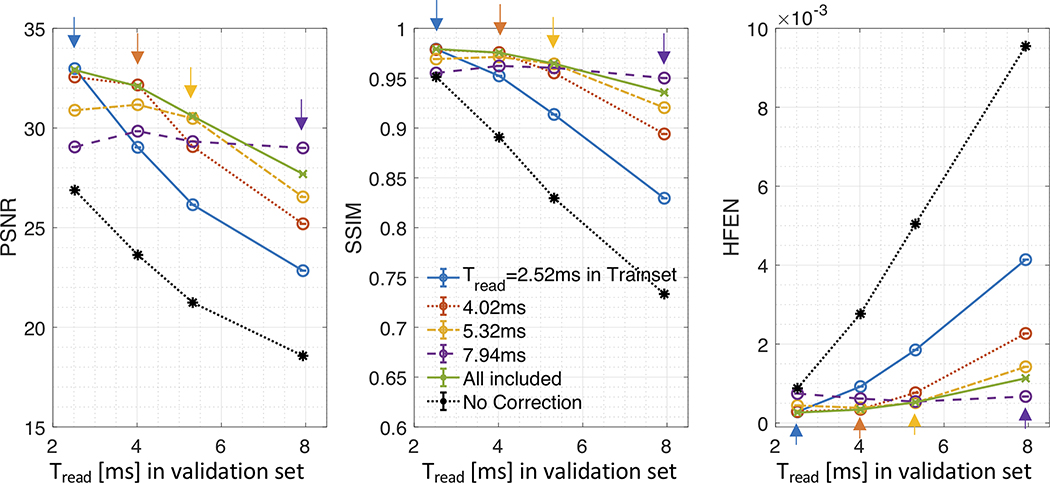
Figure 4 presents image metrics as a function of the readout duration (Tread) in the train and validation sets (EXP III). For each of the Tread tested, the network trained with the corresponding Tread has superior PSNR, SSIM, and HFEN compared to no correction and networks trained with other Tread (see arrows). For each trained network, the performance then quickly degrades for Tread longer than that of its best performance. In contrast to the individually trained networks, the network trained using all the Tread (see green, “All included”) exhibits consistent improvement over the Tread.
Figure 4. Impact of Readout Duration (EXP III).
Image Quality Metrics (PSNR, SSIM, and HFEN) as a function of readout duration (2.52, 4.02, 5.32, and 7.94 ms) for the uncorrected (black) and corrected (non-black) images are shown. For corrected images, color represents a separate network trained with different readout durations; “All included” (green) indicates all of four readout durations are used during training. All metrics are averaged across time and subjects. Note that higher PSNR and SSIM and lower HFEN correspond to better performance. The best performance is almost always achieved when the training and validation datasets share the same readout duration as indicated by arrows in each panel of the image metrics. The performance then quickly degrades for longer readout durations in the validation set than that with which the network was trained.
Evaluation using Synthetic Data
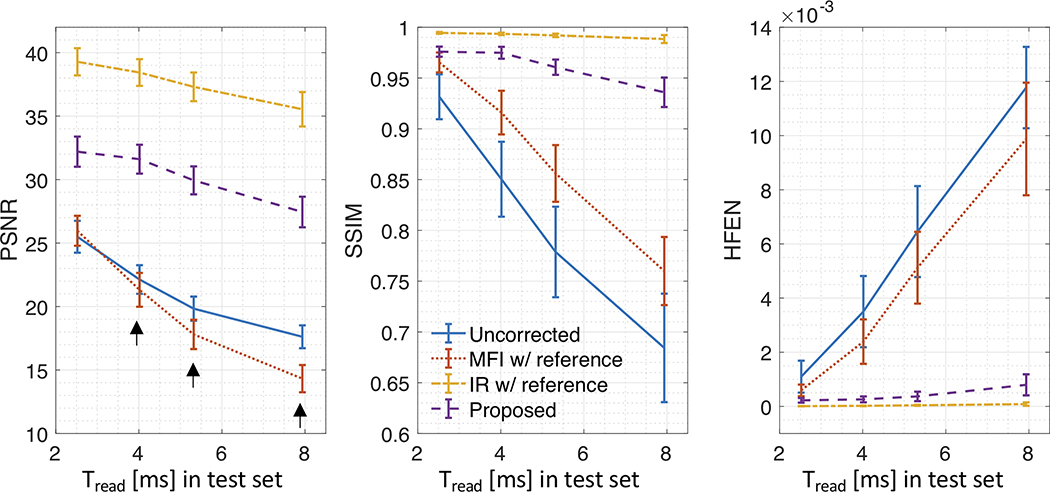
Figure 5 compares image metric results as a function of Tread for images with no correction and after correction using various methods applied to synthetic test data of 5 subjects. The proposed method (purple) is compared against no correction (blue), MFI (red), and IR (orange). For all methods, performance gradually degrades as readout duration increases. Overall, IR has superior PSNR, SSIM, and HFEN values for all readout durations, followed by the proposed method, MFI, and no correction. MFI had an even lower PSNR than that for no correction for Tread≥2.52 ms (black arrows).
Figure 5. Quantitative comparison of deblurring performance for comparison methods using synthetic test data.
Image Quality Metrics (PSNR, SSIM, and HFEN) are shown as a function of readout duration (2.52, 4.02, 5.32, and 7.94 ms). All metrics are averaged across time and subjects and error bars were calculated as the standard deviation. Note that higher PSNR and SSIM and lower HFEN correspond to better performance. The proposed method (purple) is compared against no correction (blue), multi-frequency interpolation (MFI, red), and iterative reconstruction (IR, orange). For all methods, performance gradually degrades as readout duration increases. IR performs best for all readout durations, followed by the proposed method, MFI, and no correction. Note that MFI had lower PSNR than that for no correction for readout duration > 2.52 ms (black arrows).
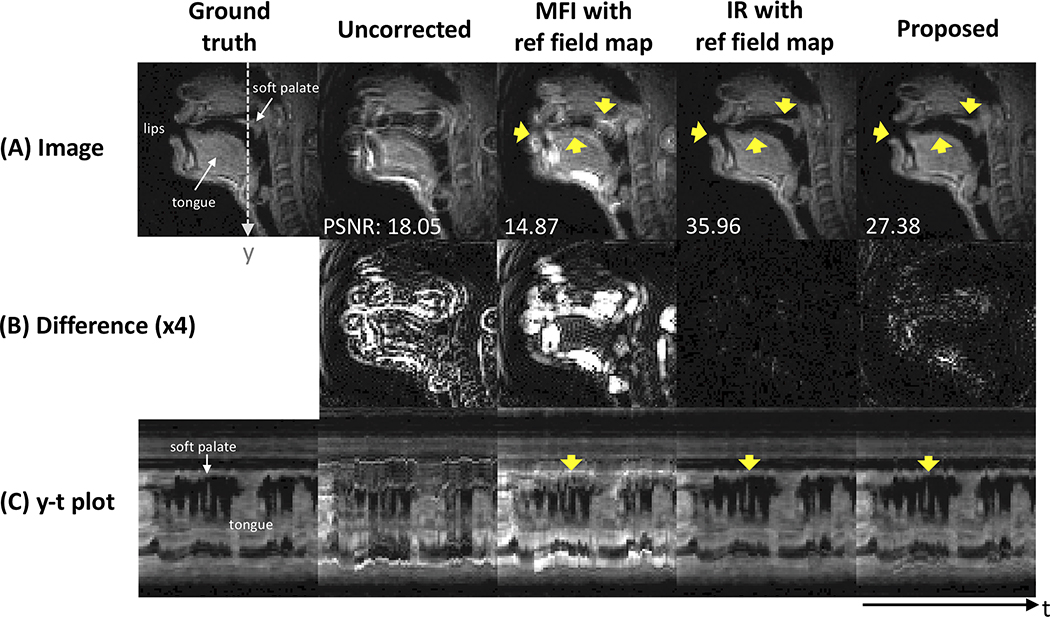
Figure 6 contains representative image frames of the ground truth, uncorrected image, and images corrected by various comparison methods. In Figure 6A, blurring is clearly seen around the lips, tongue surface, and soft palate in the uncorrected image (yellow arrows). After correction, MFI even deteriorates the delineation of the boundaries in those regions, whereas the IR method almost perfectly resolves the blurring artifact as also clearly observed in the difference images (see Fig. 6B). The proposed method successfully resolves the blurring artifact in those regions, which is visually comparable to the result from the IR. Figure 6C shows the intensity time profiles that are extracted at the dotted line marked in the ground truth. Both IR and the proposed methods exhibit sharp boundaries between the tongue and air and around the soft palate, which is consistent over time frames.
Figure 6. Qualitative comparison of deblurred images for comparison methods using synthetic test data.
Left to right: the ground truth, uncorrected, multi-frequency interpolation (MFI), model-based iterative reconstruction (IR), and the proposed method. (A) images before and after deblurring with various methods, (B) absolute difference images (amplified by a factor of 4 for better visualization) with respect to the ground truth, and (C) an intensity vs time (y-t) plot marked by dotted white line in (A). Yellow arrows point out the regions that are most affected by off-resonance blurring and that present contrast in deblurring performance for various methods. The proposed method successfully resolves the blurring artifact, which is superior to uncorrected image and image using MFI, and is visually comparable to IR method that presents the best performance over all others.
Evaluation using Real Experimental Data
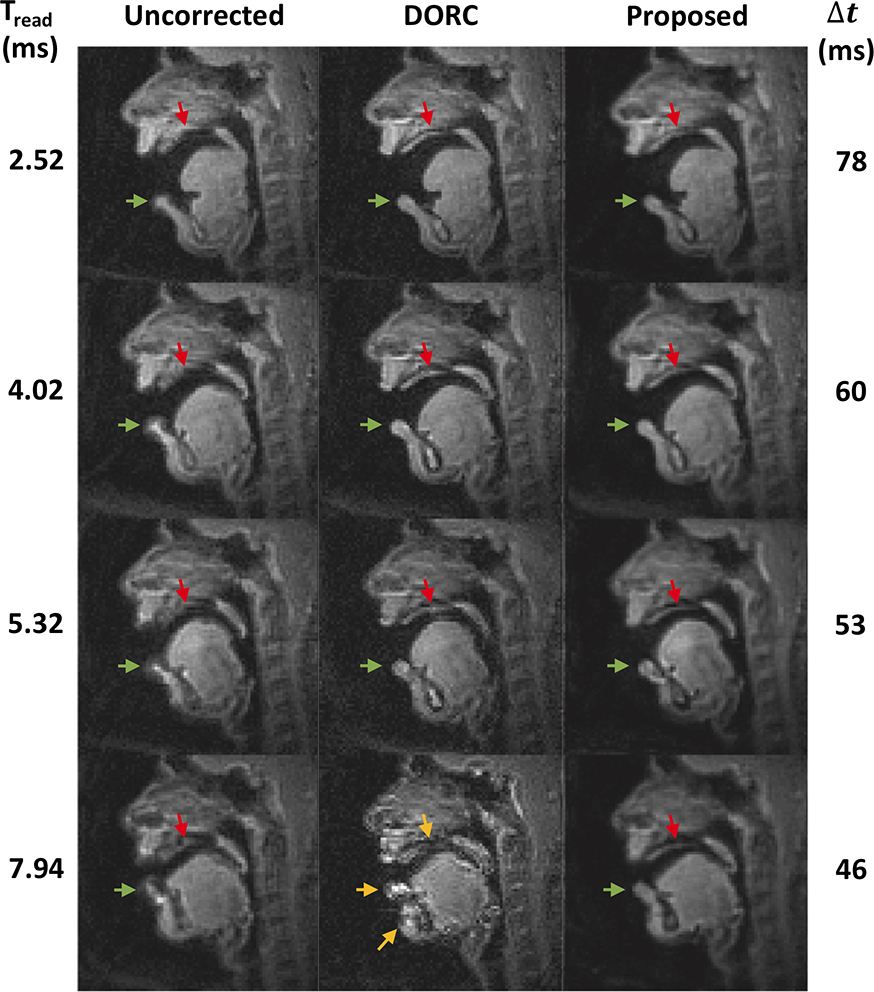
Figure 7 contains representative experimental data using different spiral readout durations. The image is reconstructed with no off-resonance correction and using the DORC (16). The proposed method took the uncorrected images (left column) as an input to the trained network and performed deblurring frame-by-frame. In the uncorrected image, off-resonance blurring is most clearly observed at the lower lip (green arrows) and hard palate (red arrows) and becomes severe with the longer readouts. The proposed method can improve the delineation of boundaries in those locations; the lower lip becomes sharper and the structure of the hard plate becomes visible after correction using the proposed method (see red arrows), which is consistent for all readout durations considered. The DORC exhibits an improved depiction of the air-tissue boundaries for short readouts (≤5.32 ms) but the signal intensity in several regions becomes spuriously amplified, and the blurred anatomic structures still remain unresolved for longer spiral readouts (7.94 ms) (see yellow arrows).
Figure 7. Representative experimental results using long readout spirals.
Left to right: Image reconstruction with no off-resonance correction, image reconstruction using a previous auto-calibrated dynamic off-resonance correction (DORC), and image deblurred by the proposed method. Top to bottom: readout duration from 2.52 to 7.94 ms and temporal resolution of 78 (13-interleaf) to 46 ms (4-interleaf). Green (lower lip) and red (hard palate) arrows point out the regions that are most affected by off-resonance blurring and corrected by the DORC and proposed methods. The proposed method provides improved delineation of the boundaries, which is consistent for all readout durations considered, whereas DORC fails to resolve the blurred boundaries for longer readout duration of 7.94 ms (yellow arrows). See also Supporting Information Videos S1.
DISCUSSION and CONCLUSION
We have demonstrated a machine learning method for correcting off-resonance artifacts in 2D spiral RT-MRI of human speech production without exam-specific field maps. We trained the CNN model using spatially varying off-resonance blur synthetically generated by using the discrete object approximation and field maps. Once the network is trained, the proposed method is computationally fast (12.3 ± 2.2 ms per frame on a single GPU) and effective at resolving spatially varying blur that occurs predominantly at the vocal tract air-tissue boundaries of interest. The performance was superior to the current state-of-the-art auto-calibrated method and only slightly inferior to an ideal reconstruction with perfect knowledge of the field map.
We utilized a simple 3-layer residual CNN to learn the deblurring operation based on the training set of paired blurred and ground truth images. The network with the learned parameters is applied to different subjects with different speech patterns and spatio-temporal off-resonance patterns. The results indicate that frame-by-frame blurring is resolved in a matter that is far superior to the correction of the temporal average blur. The CNN performance is invariant to rotation/flipping (see Supporting Information Table S1), despite the fact that some of learned convolution kernels lack circular symmetry (see Supporting Information Figure S4). Our interpretation is that the CNN estimates local deblurring from the features of the input image while allowing for adaptation to the changing off-resonances. Even in blurred images, the necessary information for deblurring remains local (cf., local imaginary components exploited by Noll et al (31)). We speculate that the convolutional filters are able to pick up information from surrounding pixels and use nonlinearities such as the ReLU operation to preserve only the filter outputs that are relevant to deblurring for each spatial location.
To train the proposed network architecture, we synthetically generated spatially varying off-resonance blur using reference data with field maps estimated from the auto-calibrated method (16) with affine linear data augmentation of the field maps (f′ = αf + β). This is different from the approach taken by Zeng et al (30) where spatially invariant off-resonance was simulated at a range of off-resonance frequencies. We experimentally found that our network architecture trained for spatially invariant blur would not be able to resolve the spatially varying blur, and the usage of spatially-varying field maps is valuable (EXP II). This is consistent with one of the critical underlying assumptions pertaining to machine learning that unseen test data comes from the same distribution as training data. We also investigated generalizability for readout duration. We found that the readout duration of the training and test sets should be the same for the network to correct off-resonance without performance degradation (EXP III). This is consistent with expectation, because each readout (trajectory) presents a unique PSF for a given off-resonance frequency, which might not be generalized by the other readouts unless data from the other readouts are also present during the training phase. One exception would be spiral imaging with extremely short echo time.
We compared the proposed method with several conventional methods. For the synthetic test data, MFI exhibited the worst performance (see Fig. 5). This is likely due to the air-tissue boundary presenting abrupt spatially-varying off-resonance that would not fulfill the assumption of smooth spatial off-resonance variation. Model-based IR with knowledge of the true field map was superior to all others in terms of PSNR, SSIM, and HFEN. However, these two approaches are impractical as they require knowledge of the field map and are therefore limited by the quality of field map estimates. This is a practical limitation of conventional methods. One such case is shown in Figure 7, where auto-calibrated methods do not reliably work at longer readout duration (7.94 ms). This is because the field maps are estimated from the severely distorted images and this error propagates to the estimated field maps and the iterative off-resonance correction procedure. The proposed method avoids this issue and provides superior performance even at a longer spiral readout than the iterative approach.
We used a simple 3-layer CNN architecture, which is motivated by an analogy to traditional deblurring procedures. With the continually growing number of state-of-the-art network architectures, many of which are much deeper, we expect that there is further room for improvement. Nevertheless, there should be a balance between performance and the ability to explain such performance. The purpose of this study was to demonstrate the feasibility of spatially varying off-resonance correction using a simple CNN architecture, and this was achieved. We only examined a single contrast and a single region of the body from the midsagittal imaging plane. A larger study encompassing multiple body regions with different imaging parameters would be valuable in future work.
We considered the speech production application because off-resonance artifacts significantly hamper the detailed speech scientific and linguistic analyses using the dynamic imaging data. The proposed method has shown to provide sharp delineation of articulator boundary with readouts up to ~8 ms at 1.5T, which is 3-fold longer than the current standard practice (15) and would provide 1.7-fold improvement in scan efficiency. This would allow for improved accuracy and precision of speech analysis beginning with boundary segmentation (50–52) that is often impaired by blurring artifact (16). It would also potentially be feasible to achieve higher temporal resolution using a longer readout with image quality comparable to a short readout (see Fig. 7) or to use spiral readouts at higher field strengths such as 3T which is available on more sites and provides higher SNR. The low-latency processing of off-resonance deblurring (12.3 ± 2.2 ms per frame) without field map would also be valuable for other RT-MRI applications such as cardiac studies and interventional RT-MRI where off-resonance at the lateral wall, adjacent to draining veins, or around metal implants and tools impedes diagnostic use of RT-MRI.
Supplementary Material
Supporting Information Video S1. Movie display of comparison of representative experimental results using long readout spirals. Left to right: Image reconstruction with no off-resonance correction, image reconstruction using a previous auto-calibrated dynamic off-resonance correction, and image deblurred by the proposed method. Top to bottom: readout duration from 2.52 to 7.94 ms. This supporting information video corresponds to Figure 7.
Supporting Information Figure S1. Quantitative comparison of deblurring performance for different filter sizes. Image Quality Metrics (PSNR, SSIM, and HFEN) are shown as a function of filter sizes. Each curve with the corresponding color represents a trained network with different filter size of f1, whereas the horizontal axis represents filter size of f2. The filter size of the first and second convolutional layers (f1 and f2, respectively) were varied from 3 to 27 and from 1 to 5, respectively whereas f3 = 1 was kept constant. We choose f1 = 9, f2= 5, and f3= 1 (f1-f2-f3=9–5-1).
Supporting Information Figure S2. Combination of Lp loss and gradient difference loss in the model training. (A) Image Quality Metrics (PSNR, SSIM, and HFEN) are shown. L1 loss in a combination with gradient difference loss with λ = 1 exhibits the highest values of PSNR and SSIM over other combinations. (B) Representative image results for combinations of Lp loss and gradient difference loss. For L2 loss, as gradient difference loss penalty λ increases from 0.01 to 1 (3rd and 4th columns), image sharpness is improved visually. Compared to L2 loss, L1 loss with the same value of λ visually improves the sharpness at the soft palate (4th and 5th columns), although visual difference might not be observed as clearly as that can be observed when increasing λ from 0.01 to 1. We choose to use p = 1 and λ = 1.
Supporting Information Figure S3. Time maps for four different spiral trajectories. Left to right: 13-, 8-, 6-, 4-interleaf spiral-out samplings, with readout times (Tread) of 2.52, 4.02, 5.32, and 7.94 ms, respectively, with the same field of view and in-plane resolution. Only one spiral interleave out of fully sampled interleaves is shown here. Here, TE = 0.8 ms.
Supporting Information Figure S4. Representative examples of learned convolution kernels at the first and second convolutional layers. (A) Kernels shown at the left and right are respectively corresponding to 64 9 × 9 × 1 kernel weights applied to real and imaginary input channels in the first layer. The majority of kernels exhibit circular symmetry which corresponds to the expected shape of off-resonance PSFs in spiral MRI. (B) 18 5 × 5 × 1 kernels are visualized out of 32 convolutional kernels of size 5 × 5 × 64 in the second layer. The kernels in the first 8 columns represent structured patterns whereas the kernels shown in the last column represent unstructured pattern.
Supporting Information Table S1. Quantitative comparison of deblurring performance on blurred input images with image transformations. The deblurring was performed using the network trained for the training data (without any image transform) described in EXP III in Table 1. The synthetic test data with Tread = 2.52 ms, α = 1, and β = 0 was used for this evaluation with image transformation: 1) rotation by 90, 180, or 270 degree, or 2) flip along the left-right or the up-down direction. The slight performance degradation is observed when the input image is rotated or flipped -- at worst 0.51dB in PSNR, 0.002 in SSIM, and 0.047 in HFEN compared to those from the original input image without transformation.
ACKNOWLEDGEMENTS
This work was supported by NIH Grant R01DC007124 and NSF Grant 1514544. We acknowledge the support and collaboration of the Speech Production and Articulation kNowledge (SPAN) group at the University of Southern California, Los Angeles, CA, USA. We thank Andrew York and Samarth Kamle for proofreading the manuscript.
REFERENCES
- 1.Ahn CB, Kim JH, Cho ZH. High-Speed Spiral-Scan Echo Planar NMR Imaging-I. IEEE Trans Med Imaging. 1986;5:2–7. [DOI] [PubMed] [Google Scholar]
- 2.Meyer CH, Hu BS, Nishimura DG, Macovski A. Fast spiral coronary artery imaging. Magn Reson Med. 1992;28:202–13. [DOI] [PubMed] [Google Scholar]
- 3.Nishimura DG, Irarrazabal P, Meyer CH. A velocity k‐space analysis of flow effects in echo‐planar and spiral imaging. Magn Reson Med. 1995;33:549–56. [DOI] [PubMed] [Google Scholar]
- 4.Gatehouse PD, Firmin DN. Flow distortion and signal loss in spiral imaging. Magn Reson Med. 1999;41:1023–31. [DOI] [PubMed] [Google Scholar]
- 5.Kim YC, Narayanan SS, Nayak KS. Flexible retrospective selection of temporal resolution in real-time speech MRI using a golden-ratio spiral view order. Magn Reson Med. 2011;65:1365–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lingala SG, Zhu Y, Kim Y, Toutios A, Narayanan SS, Nayak KS. A fast and flexible MRI system for the study of dynamic vocal tract shaping. Magn Reson Med. 2017;77:112–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kerr AB, Pauly JM, Hu BS, Li KC, Hardy CJ, Meyer CH, et al. Real-time interactive MRI on a conventional scanner. Magn Reson Med. 1997;38:355–67. [DOI] [PubMed] [Google Scholar]
- 8.Yang PC, Kerr AB, Liu AC, Liang DH, Hardy C, Meyer CH, Macovski A, Pauly JM, Hu BS. New real-time interactive cardiac magnetic resonance imaging system complements echocardiography. J Am Coll Cardiol. 1998;32:2049–56. [DOI] [PubMed] [Google Scholar]
- 9.Nayak KS, Pauly JM, Kerr AB, Hu BS, Nishimura DG. Real-time color flow MRI. Magn Reson Med. 2000;43:251–8. [DOI] [PubMed] [Google Scholar]
- 10.Nayak KS, Cunningham CH, Santos JM, Pauly JM. Real-Time Cardiac MRI at 3 Tesla. Magn Reson Med. 2004;51:655–60. [DOI] [PubMed] [Google Scholar]
- 11.Narayanan SS, Nayak KS, Lee S, Sethy A, Byrd D. An approach to real-time magnetic resonance imaging for speech production. J Acoust Soc Am. 2004;115:1771–6. [DOI] [PubMed] [Google Scholar]
- 12.Steeden JA, Kowalik GT, Tann O, Hughes M, Mortensen KH, Muthurangu V. Real-time assessment of right and left ventricular volumes and function in children using high spatiotemporal resolution spiral bSSFP with compressed sensing. J Cardiovasc Magn Reson. 2018;20:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Block KT, Frahm J. Spiral imaging: a critical appraisal. J Magn Reson Imag. 2005;21:657–668. [DOI] [PubMed] [Google Scholar]
- 14.Sutton BP, Conway CA, Bae Y, Seethamraju R, Kuehn DP. Faster dynamic imaging of speech with field inhomogeneity corrected spiral fast low angle shot (FLASH) at 3 T. J Magn Reson Imaging. 2010;32:1228–37. [DOI] [PubMed] [Google Scholar]
- 15.Lingala SG, Sutton BP, Miquel ME, Nayak KS. Recommendations for real-time speech MRI. J Magn Reson Imaging. 2016;43:28–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lim Y, Lingala SG, Narayanan SS, Nayak KS. Dynamic off-resonance correction for spiral real-time MRI of speech. Magn Reson Med. 2019;81:234–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reeder SB, Hu HH, Sirlin CB, Group LI, Diego S. Non-Cartesian Balanced SSFP Pulse Sequences for Real-Time Cardiac MRI. Magn Reson Med. 2016;75:1546–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu H, Martin AJ, Truwit CL. Interventional MRI at high-field (1.5 T): needle artifacts. J Magn Reson Imag. 1998;8:214–9. [DOI] [PubMed] [Google Scholar]
- 19.Shenberg I, Macovski A. Inhomogeneity and multiple dimension considerations in magnetic resonance imaging with time-varying gradients. IEEE Trans Med Imaging. 1985;4:165–74. [DOI] [PubMed] [Google Scholar]
- 20.Maeda A, Sano K, Yokoyama T. Reconstruction by weighted correlation for MRI with time-varying gradients. IEEE Trans Med Imaging. 1988;7:26–31. [DOI] [PubMed] [Google Scholar]
- 21.Noll DC, Meyer CH, Pauly JM, Nishimura DG, Macovski A. A homogeneity correction method for magnetic resonance imaging with time-varying gradients. IEEE Trans Med Imaging. 1991;10:629–637. [DOI] [PubMed] [Google Scholar]
- 22.Man LC, Pauly JM, Macovski A. Multifrequency interpolation for fast off-resonance correction. Magn Reson Med. 1997;37:785–92. [DOI] [PubMed] [Google Scholar]
- 23.Nayak KS, Tsai CM, Meyer CH, Nishimura DG. Efficient off-resonance correction for spiral imaging. Magn Reson Med. 2001;45:521–4. [DOI] [PubMed] [Google Scholar]
- 24.Chen W, Meyer CH. Semiautomatic off-resonance correction in spiral imaging. Magn Reson Med. 2008;59:1212–9. [DOI] [PubMed] [Google Scholar]
- 25.Makhijani MK, Nayak KS. Exact correction of sharply varying off-resonance effects in spiral MRI Proc IEEE Int Symp Biomed Imaging. Arlington, VA, 2006, pp. 730–733. [Google Scholar]
- 26.Nayak KS, Nishimura DG. Automatic field map generation and off-resonance correction for projection reconstruction imaging. Magn Reson Med. 2000;43:151–4. [DOI] [PubMed] [Google Scholar]
- 27.Noll DC. Reconstruction techniques for magnetic resonance imaging. Ph.D. thesis, Stanford University. 1991. [Google Scholar]
- 28.Sutton BP, Noll DC, Fessler JA. Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans Med Imaging. 2003;22:178–88. [DOI] [PubMed] [Google Scholar]
- 29.Fessler JA, Lee S, Olafsson VT, Shi HR, Noll DC. Toeplitz-based iterative image reconstruction for MRI with correction for magnetic field inhomogeneity. IEEE Trans Signal Process. 2005;53:3393–402. [Google Scholar]
- 30.Zeng DY, Shaikh J, Holmes S, Brunsing RL, Pauly JM, Nishimura DG, Vasanawala SS, Cheng JY. Deep residual network for off-resonance artifact correction with application to pediatric body MRA with 3D cones. Magn Reson Med. 2019;82:1398–1411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Noll DC, Pauly JM, Meyer CH, Nishimura DG, Macovski A. Deblurring for non-2D Fourier transform magnetic resonance imaging. Magn Reson Med. 1992;25:319–333. [DOI] [PubMed] [Google Scholar]
- 32.Man LC, Pauly JM, Macovski A. Improved automatic off-resonance correction without a field map in spiral imaging. Magn Reson Med. 1997;37:906–13. [DOI] [PubMed] [Google Scholar]
- 33.Lim Y, Lingala SG, Narayanan S, Nayak KS, Angeles L. Improved depiction of tissue boundaries in vocal tract real-time MRI using automatic off-resonance correction Proc INTERSPEECH, San Francisco, CA, USA, 2016. pp. 1765–1769 [Google Scholar]
- 34.Ye JC, Sung WK. Understanding geometry of encoder-decoder CNNs. arXiv:1901.07647; 2019. [Google Scholar]
- 35.Bresch E, Kim YC, Nayak KS, Byrd D, Narayanan SS. Seeing speech: Capturing vocal tract shaping using real-time magnetic resonance imaging. IEEE Signal Process Mag. 2008;25:123–129. [Google Scholar]
- 36.Scott AD, Wylezinska M, Birch MJ, Miquel ME. Speech MRI: Morphology and function. Phys Medica. 2014;30:604–18. [DOI] [PubMed] [Google Scholar]
- 37.Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996;23:815–50. [DOI] [PubMed] [Google Scholar]
- 38.Ahunbay E, Pipe JG. Rapid method for deblurring spiral MR images. Magn Reson Med. 2000;44:491–4. [DOI] [PubMed] [Google Scholar]
- 39.Denis L, Thiébaut E, Soulez F, Becker JM, Mourya R. Fast approximations of shift-variant blur. Int J Comput Vis. 2015;115:253–278. [Google Scholar]
- 40.Miraut D, Portilla J. Efficient shift-variant image restoration using deformable filtering (Part I). EURASIP J Adv Signal Process. 2012;2012:1–20. [Google Scholar]
- 41.Jin KH, McCann MT, Froustey E, Unser M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans Image Process. 2016;26:1–20. [DOI] [PubMed] [Google Scholar]
- 42.Lee D, Yoo J, Tak S, Ye J. Deep residual learning for accelerated MRI using magnitude and phase networks. IEEE Trans Biomed Eng. 2018;65:1985–1995. [DOI] [PubMed] [Google Scholar]
- 43.Han YS, Yoo J, Ye JC. Deep residual learning for compressed sensing CT reconstruction via persistent homology analysis. arXiv:161106391. 2016; [Google Scholar]
- 44.Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, et al. Low-dose CT with a residual encoder-decoder convolutional neural network. IEEE Trans Med Imaging. 2017;36:2524–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mathieu M, Couprie C, LeCun Y. Deep multi-scale video prediction beyond mean square error. arXiv:1511.05440; 2016. [Google Scholar]
- 46.Kingma DP, Ba J. Adam: a method for stochastic optimization. arXiv:1412.6980; 2014. [Google Scholar]
- 47.Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Signal Process. 2003;51:560–74. [Google Scholar]
- 48.Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans Med Imaging. 2011;30:1028–1041. [DOI] [PubMed] [Google Scholar]
- 49.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 2004;13:600–612. [DOI] [PubMed] [Google Scholar]
- 50.Bresch E, Narayanan S. Region segmentation in the frequency domain applied to upper airway real-time magnetic resonance images. IEEE Trans Med Imaging. 2009;28:323–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kim J, Kumar N, Lee S, Narayanan SS. Enhanced airway-tissue boundary segmentation for real-time magnetic resonance imaging data Proc Int Seminar on Speech Production (ISSP), Cologne, Germany, 2014. pp. 222–225. [Google Scholar]
- 52.Somandepalli K, Toutios A, Narayanan SS. Semantic edge detection for tracking vocal tract air-tissue boundaries in real-time magnetic resonance images Proc INTERSPEECH, Stockholm, Sweden, 2017. pp. 631–635. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Video S1. Movie display of comparison of representative experimental results using long readout spirals. Left to right: Image reconstruction with no off-resonance correction, image reconstruction using a previous auto-calibrated dynamic off-resonance correction, and image deblurred by the proposed method. Top to bottom: readout duration from 2.52 to 7.94 ms. This supporting information video corresponds to Figure 7.
Supporting Information Figure S1. Quantitative comparison of deblurring performance for different filter sizes. Image Quality Metrics (PSNR, SSIM, and HFEN) are shown as a function of filter sizes. Each curve with the corresponding color represents a trained network with different filter size of f1, whereas the horizontal axis represents filter size of f2. The filter size of the first and second convolutional layers (f1 and f2, respectively) were varied from 3 to 27 and from 1 to 5, respectively whereas f3 = 1 was kept constant. We choose f1 = 9, f2= 5, and f3= 1 (f1-f2-f3=9–5-1).
Supporting Information Figure S2. Combination of Lp loss and gradient difference loss in the model training. (A) Image Quality Metrics (PSNR, SSIM, and HFEN) are shown. L1 loss in a combination with gradient difference loss with λ = 1 exhibits the highest values of PSNR and SSIM over other combinations. (B) Representative image results for combinations of Lp loss and gradient difference loss. For L2 loss, as gradient difference loss penalty λ increases from 0.01 to 1 (3rd and 4th columns), image sharpness is improved visually. Compared to L2 loss, L1 loss with the same value of λ visually improves the sharpness at the soft palate (4th and 5th columns), although visual difference might not be observed as clearly as that can be observed when increasing λ from 0.01 to 1. We choose to use p = 1 and λ = 1.
Supporting Information Figure S3. Time maps for four different spiral trajectories. Left to right: 13-, 8-, 6-, 4-interleaf spiral-out samplings, with readout times (Tread) of 2.52, 4.02, 5.32, and 7.94 ms, respectively, with the same field of view and in-plane resolution. Only one spiral interleave out of fully sampled interleaves is shown here. Here, TE = 0.8 ms.
Supporting Information Figure S4. Representative examples of learned convolution kernels at the first and second convolutional layers. (A) Kernels shown at the left and right are respectively corresponding to 64 9 × 9 × 1 kernel weights applied to real and imaginary input channels in the first layer. The majority of kernels exhibit circular symmetry which corresponds to the expected shape of off-resonance PSFs in spiral MRI. (B) 18 5 × 5 × 1 kernels are visualized out of 32 convolutional kernels of size 5 × 5 × 64 in the second layer. The kernels in the first 8 columns represent structured patterns whereas the kernels shown in the last column represent unstructured pattern.
Supporting Information Table S1. Quantitative comparison of deblurring performance on blurred input images with image transformations. The deblurring was performed using the network trained for the training data (without any image transform) described in EXP III in Table 1. The synthetic test data with Tread = 2.52 ms, α = 1, and β = 0 was used for this evaluation with image transformation: 1) rotation by 90, 180, or 270 degree, or 2) flip along the left-right or the up-down direction. The slight performance degradation is observed when the input image is rotated or flipped -- at worst 0.51dB in PSNR, 0.002 in SSIM, and 0.047 in HFEN compared to those from the original input image without transformation.