MRI-Cytometry: Mapping non-parametric cell size distributions using diffusion MRI

Abstract

Purpose:

This report introduces and validates a new diffusion MRI based method termed MRI-Cytometry that can non-invasively map intravoxel, non-parametric cell size distributions in tissues.

Methods:

MRI was used to acquire diffusion-weighted signals with a range of diffusion times and gradient factors, and a model was fit to these data to derive estimates of cell size distributions. We implemented a two-step fitting method to avoid noise-induced artificial peaks and provide reliable estimates of tumor cell size distributions. Computer simulations in silico and experimental measurements on cultured cells in vitro and animal xenografts in vivo were used to validate the accuracy and precision of the method. Tumors in seven patients with breast cancer were also imaged and analyzed using this MRI-Cytometry approach on a clinical 3T MRI scanner.

Results:

Simulations and experimental results confirm MRI-Cytometry can reliably map intravoxel, non-parametric cell size distributions and has the potential to discriminate smaller and larger cells. The application in breast cancer patients demonstrates the feasibility of direct translation of MRI-Cytometry to clinical applications.

Conclusion:

The proposed MRI-Cytometry method can characterize non-parametric cell size distributions in human tumors, which potentially provides a practical imaging approach to derive specific histopathological information on biological tissues.

INTRODUCTION

Cell size is one of the fundamental properties of living cells and plays an important role in metabolism(1), proliferation (2), and cell death (3). At the organ level, biological tissues contain a large variety of cells with different sizes. Most epithelial tissues show a “striking regularity” in cell size, and size heterogeneity often indicates neoplastic growth (4). Therefore, quantifying cell size distributions may provide important information on the state of tissues for diagnosis or monitoring responses to interventions. Currently, cell size information is widely used in blood analyses of anemia (5,6) and cancer (7) but its full potential has not been realized in solid tumors. Biopsy is the standard-of-care method for cell size measurements, but it is invasive, especially for tumors in critical organs. Therefore, it would be valuable to characterize cell size information using non-invasive imaging methods.

Several attempts have been made to acquire cell size information using Diffusion-weighted magnetic resonance imaging (DWI); however, it remains challenging to accurately estimate cell size distributions non-invasively. Two approaches have been reported to overcome this challenge: measuring mean cell size and pre-defining a parametric distribution function for cell size. The first approach measures mean cell size only, simplifying the problem and retaining the most important histopathological information. Mean axon sizes have been measured using q-space imaging (8), AxActive (9), DDE (double diffusion encoding) (10), and qTDS (quantitative temporal diffusion spectroscopy) (11) methods. Mean cell sizes in tumors have been measured using VERDICT (vascular, extracellular and restricted diffusion for cytometry in tumors) (12,13), IMPULSED (imaging microstructural parameters using limited spectrally edited diffusion) (14,15), and POMACE (pulsed and oscillating gradient MRI for assessment of cell size and extracellular space) methods (16). However, these methods do not characterize cell size heterogeneity, which may itself be a diagnostic biomarker. The second approach pre-defines a parametric distribution function for cell size, such as a gamma distribution (17). This analysis provides information on the heterogeneity of cell sizes while adding only one more fitting parameter compared with the first approach. However, cell size distributions likely change during disease progression and in response to treatment (4) making it is inappropriate to pre-define a specific functional form of cell size distributions. Therefore, there is a need to develop an imaging method that can characterize cell size distribution without any pre-defined functional forms.

Estimating non-parametric compartment size distributions without a priori knowledge of the distribution function has been performed to estimate: (i). pore size distribution of glass capillaries (18); (ii) non-parametric axon size distributions in fixed tissues using PGSE (pulse gradient spin echo) (19), NOGSE (non-uniform oscillating gradient spin echo) (20), or DDE (21); and (iii) cell size distributions in asparagus and animal allografts (22). All of these methods addressed the complex optimization problems without assuming any specific distribution forms, ensuring the generalizability of both normal and abnormal tissues. However, these approaches either used special preclinical hardware or focused on animal applications only.

Here, we introduce a new framework, MRI-Cytometry, that estimates cell size distribution without a priori knowledge using clinical MRI scanners. We report the theoretical basis that links DWI signals to cell size distributions and provide validation of MRI-Cytometry using computer simulations in silico, cell culture experiments in vitro, and animal xenograft experiments in vivo. We also show its clinical applicability in patients with breast cancer.

THEORY

Assumptions

Similar to previous studies (12,14,16,23), MRI-Cytometry assumes DWI signals arise from two compartments, i.e., intra- and extracellular spaces without transcytolemmal water exchange. The following assumptions were made.

1. Intracellular diffusion: Cells are modeled as spheres (12,14,16,23). Each spherical cell has a cell size, i.e., diameter d and an intracellular diffusion coefficient D_in, both of which can differ from cell to cell. For example, a cell in an early apoptotic stage may have both smaller d and D_in than a normal cell (24). Therefore, each image voxel contains cells characterized by P(d) and P(D_in), the distributions of d and D_in, respectively. This is more realistic than the assumption of a mean cell size $\overline{d}$ and a single $\overline{D_{in}}$ for all cells.

2. Extracellular diffusion: We adapt the concept of spin packets (25) for extracellular diffusion. The extracellular DWI signals are described as a sum of signals from a large number of individual spin packets originating from different positions in the extracellular spaces within the voxel. Each spin packet has its own diffusion time-dependent diffusion coefficient which can be approximated as (14) D_ex = D_ex0 + β_exf when a narrow frequency range is used, where f is the gradient frequency, D_ex0 represents D_ex at very long diffusion time, and β_ex is the diffusion dispersion rate. Because spin packets originate from different positions, diffuse through different pathways, and encounter different restrictions and hindrances, a voxel contains both P(D_ex0) and P(β_ex), the distributions of D_ex0 and β_ex, respectively. This is different from previous studies that assumed a single extracellular diffusion coefficient (12).

3. Transcytolemmal exchange: Transcytolemmal water exchange is ignored here. This assumption has been widely used in other cell size measurements such as IMPULSED (14,24) and VERDICT (12). This could bias the estimation of intracellular volume fraction but may not affect the estimation of mean cell size (26).

Basic equation

The DWI signals of a voxel can be written as

$$S=\stackrel{\text{intracellular}\text{diffusion}}{\overbrace{\underset{D_{in}}{\int }\underset{d}{\int }{\rho }_{in}{P}_{in}\left(d,D_{in}\right)v\left(d\right)s_{in}\left(d,D_{in}\right)ddd{D}_{in}}}+\stackrel{\text{extracellular}\text{diffusion}}{\overbrace{\underset{{\beta }_{ex}}{\int }\underset{D_{ex0}}{\int }{\rho }_{ex}{P}_{ex}\left(D_{ex0},{\beta }_{ex}\right)exp\left[-b\left(D_{ex0}+{\beta }_{ex}f\right)\right]d{D}_{ex0}d{\beta }_{ex}}}$$ [1]

and $S_0=S\left(b=0\right)={\int }_{D_{in}}{\int }_d{\rho }_{in}{P}_{in}\left(d,D_{in}\right)v\left(d\right)ddd{D}_{in}+{\int }_{{\beta }_{ex}}{\int }_{D_{ex0}}{\rho }_{ex}{P}_{ex}\left(D_{ex0},{\beta }_{ex}\right)d{D}_{ex0}d{\beta }_{ex}$, v(d) = πd³/6 is cell volume, P_in(d, D_in) is the normalized distribution function of the number of cells with a diameter d and an intracellular diffusivity D_in, P_ex(D_ex0, β_ex) is the normalized distribution function of the number of spin packets with D_ex0 and β_ex, ρ_in and ρ_ex are the T2-weighted intra- and extracellular DWI signals per unit volume, respectively, and s_in is intracellular signal attenuation of an impermeable spherical cell. The analytical equations for s_in linking geometric features (d and D_in) to DWI signals have been reported for sine- and cosine-modulated gradient waveforms (27) and cosine-modulated trapezoidal OGSE waveforms (23). Unlike previous studies that enforced a known distribution function (28), Eq. [1] does not assume any specific distribution function for any microstructural parameters.

A general fit of Eq. [1] to data is a complex non-linear optimization problem, especially with the inclusion of variable cell volumes (see below). To address the difficulty of directly fitting Eq.[1] to data reliably, we propose the following two-step fitting approach.

MRI-Cytometry fitting – step#1

Discretization of signal equation

First, we define two weighting parameters: $w_{in}^{\prime }={\rho }_{in}{P}_{in}\left(d,D_{in}\right)v\left(d\right)$ is proportional to the cell-volume-weighted distribution of the number of cells with d and D_in and w_ex = ρ_exP_ex(D_ex0, β_ex) is proportional to the distribution of spin packet volumes with D_ex0 and β_ex. Second, Eq. [1] can be discretized based on physiologically relevant parameter ranges, i.e., 0 ≤ d ≤ d_max, 0 ≤ D_in, D_ex0 ≤ D_free, and 0 ≤ β_ex ≤ β_ex,max. d_max denotes the largest cell size that can be reliably fit depending on the longest diffusion time used in acquisition e.g. in this study d_max is set as 25 μm because the root-mean-square displacement of free water diffusion for t_diff = 70 ms is ~21 μm. The β_ex,max = 10 μm² was determined by previous simulations and animal studies in vivo (24). We empirically discretize d, D_in, D_ex0, and β_ex with N = 50, M = 16, P = 16, and Q = 21 possible values, respectively. Larger numbers of possible parameter values can increase the “resolution” in the parameter space but will significantly increase the computing time. Therefore, for a number of K measurements (each with a combination of experimental parameters such as t_diff and b value), Eq. [1] can be discretized as the k^th measurement becomes

$$S_k=\sum _{n=1}^N\sum _{m=1}^M{w}_{in\left(n,m\right)}^{\prime }{s}_{in}\left(d_{\left(n\right)},D_{in\left(m\right)}|b_k,f_k\right)+\sum _{p=1}^P\sum _{q=1}^Q{w}_{ex\left(p,q\right)}exp\left[-b_k\left(D_{ex0\left(p\right)}+{\beta }_{ex\left(q\right)}\cdot f\right)\right]$$ [2]

here $S_0={\sum }_{n=1}^N{\sum }_{m=1}^M{w}_{in\left(n,m\right)}^{\prime }+{\sum }_{p=1}^P{\sum }_{q=1}^Q{w}_{ex\left(p,q\right)}$ $w_{in\left(n,m\right)}^{\prime }$ and s_in(d_(n), D_in(m)|b_k, f_k) are the intracellular signal fraction and signal arising from a combination of d_(n) and D_in(m), respectively, and w_ex(p,q) is the extracellular signal fraction arising from spin packets with a combination of D_ex0(p), and β_ex(q).

Construction of a dictionary (signal basis matrix)

We create a dictionary containing all possible intra- and extracellular signal forms. Specifically, Eq.[2] can be rewritten as

$$S=\left[\begin{array}{c}{S}_1\\ \\ ⋮\\ \\ S_K\end{array}\right]=\stackrel{\text{intracellular}}{\overbrace{[\begin{array}{ccc}{m}_{in(1|1)}& \cdots & m_{in\left(N\times M|1\right)}\\ & & \\ ⋮& \ddots & ⋮\\ & & \\ m_{in(1|K)}& \cdots & m_{in\left(N\times M|K\right)}\end{array}}}\stackrel{\text{extracellular}}{\overbrace{\begin{array}{ccc}{m}_{ex(1|1)}& \cdots & m_{ex\left(P\times Q|1\right)}\\ & & \\ ⋮& \ddots & ⋮\\ & & \\ m_{ex(1|K)}& \cdots & m_{ex\left(P\times Q|K\right)}\end{array}]}}\times \left[\begin{array}{c}{w}_{in\left(1\right)}^{\prime }\\ ⋮\\ w_{in\left(N\times M\right)}^{\prime }\\ w_{ex\left(1\right)}\\ ⋮\\ w_{ex\left(P\times Q\right)}\end{array}\right]=M\cdot w^{\prime }$$ [3]

Where M is the basis signal matrix (dictionary) containing both intra- and extracellular signal forms: m_in(n,m|k) = s_in(d_(n), D_in(m)|b_k, f_k), and m_ex(p,q|k) = exp[−b_k(D_ex0(p) + β_ex(q) f)]. Note that any $w_{in(\dots )}^{\prime }$, w_ex(…) ≥ 0.

Fitting

We use a regularized non-negative least-squares (NNLS) analysis (29–31) to fit Eq.[3] to data. This approach incorporates a priori information of non-negative signal intensities and finite signal energy to prevent the non-negative least-squares analysis from over-fitting the noisy data while retaining the numerical accuracy of the solution. The resulting regularized non-negative least-squares problem formulation is given as

$$\underset{w^{\prime }\ge 0}{\text{argmin}}\Vert \left[\begin{array}{c}M\\ \xi I\end{array}\right]w^{\prime }-\left[\begin{array}{c}S\\ 0\end{array}\right]{\Vert }_2^2,$$ [4]

Where I is a unity matrix with a size of N × M + P × Q and ξ is a regularization penalty parameter. Of note, larger values of ξ result in more regularization but increase fitting errors, while smaller ξ may decrease fitting errors while increasing the risk of overfitting. We used computer simulations to empirically determine ξ = 0.01 to achieve reasonable fits in the presence of experimental noise with SNR < 150 on T2w images.

Fitting results – step#1

After the regularized NNLS fitting, the vector w′ can be split and converted into two matrices, i.e., a N × M matrix $w_{in}^{\prime }$ for intracellular and a P × Q w_ex matrix for extracellular spaces. The projection of each matrix to each dimension provides a distribution. Namely, the cell-volume-weighted cell size distribution can be obtained as

$$P_{vw}\left(d_{\left(n\right)}\right)=\left(\sum _{m=1}^M{w}_{in\left(n,m\right)}^{\prime }\right)/\left(\sum _{n=1}^N\sum _{m=1}^M{w}_{in\left(n,m\right)}^{\prime }\right)$$ [5]

the distribution function for extracellular diffusion coefficient at long diffusion times as

$$P\left(D_{ex0\left(p\right)}\right)=\left(\sum _{q=1}^Q{w}_{ex\left(p,q\right)}\right)/\left(\sum _{p=1}^P\sum _{q=1}^Q{w}_{ex\left(p,q\right)}\right)$$ [6]

and the distribution of β_ex as

$$P\left({\beta }_{ex\left(q\right)}\right)=\left(\sum _{p=1}^P{w}_{ex\left(p,q\right)}\right)/\left(\sum _{p=1}^P\sum _{q=1}^Q{w}_{ex\left(p,q\right)}\right)$$ [7]

Note that P(D_in), the distribution of D_in, will be obtained in step#2 (see below). In addition to the distributions of microstructural parameters, some other parameters can also be estimated using MRI-Cytometry. For example, the apparent intracellular volume fraction can be calculated as

$$v_{in}=\sum _{n=1}^N\sum _{m=1}^M{w}_{in\left(n,m\right)}^{\prime }$$ [8]

and the cell-volume-weighted mean cell size

$$\overline{d_{vw}}=\left(\sum _{n=1}^N\sum _{m=1}^M{d}_{\left(n\right)}{w}_{in\left(n,m\right)}^{\prime }\right)/\left(\sum _{n=1}^N\sum _{m=1}^M{w}_{in\left(n,m\right)}^{\prime }\right)$$ [9]

MRI-Cytometry fitting – step#2

The fitted P_vw(d) is cell-volume-weighted, which may not meet the needs of many biological and clinical studies that require true cell size distribution (5). A natural approach to convert cell-volume-weighted cell size distributions to cell size distributions is

$$P_{cal}\left(d_{\left(n\right)}\right)=\left(\sum _{n=1}^N\frac{P_{vw}\left(d_{\left(n\right)}\right)}{d_{\left(n\right)}^3}\right)/\left(\sum _{n=1}^N\frac{1}{d_{\left(n\right)}^3}\right)$$ [10]

However, this is usually not optimal in practice because this conversion serves as a low-pass filter that could amplify noise-induced artificial peaks in the distribution which appear at small cell sizes. To overcome this problem, we adopt a second fitting step.

Based on the $w_{in}^{\prime }$ obtained in step#1, the fitted intracellular signals S_in can be obtained as

$$S_{in}=\left[\begin{array}{c}{S}_{in\left(1\right)}\\ ⋮\\ S_{in\left(K\right)}\end{array}\right]=\left[\begin{array}{ccc}{m}_{in(1|1)}& \cdots & m_{in\left(N\times M|1\right)}\\ ⋮& \ddots & ⋮\\ m_{in(1|K)}& \cdots & m_{in\left(N\times M|K\right)}\end{array}\right]\times \left[\begin{array}{c}{w}_{in\left(1\right)}^{\prime }\\ ⋮\\ w_{in\left(N\times M\right)}^{\prime }\end{array}\right]$$ [11]

We then generate another basis matrix (dictionary) for intracellular diffusion only, namely,

$$S_{in}=\left[\begin{array}{ccc}{d}_{\left(1\right)}^3{m}_{in(1|1)}& \cdots & d_{\left(N\right)}^3{m}_{in\left(N\times M|1\right)}\\ ⋮& \ddots & ⋮\\ d_{\left(1\right)}^3{m}_{in(1|K)}& \cdots & d_{\left(N\right)}^3{m}_{in\left(N\times M|K\right)}\end{array}\right]/\left(\sum _{n=1}^N{d}_{\left(n\right)}^3\right)\times \left[\begin{array}{c}{w}_{in\left(1\right)}\\ ⋮\\ w_{in\left(N\times M\right)}\end{array}\right]=M_{in}{w}_{in}$$ [12]

Where M_in is the intracellular signal basis matrix and w_in(n,m) is proportional to the distribution of the number of cells with a combination of d_n and D_in(m). Like the fittings in step#1, we perform another regularized NNLS fitting as

$$\underset{w_{in}\ge 0}{\text{argmin}}{\Vert \left[\begin{array}{c}{M}_{in}\\ {\xi }_2{I}_{in}\end{array}\right]w_{in}-\left[\begin{array}{c}{S}_{in}\\ 0\end{array}\right]\Vert }_2^2$$ [13]

Where I_in is a unity matrix with a size of N ×M and ξ₂ is a regularization penalty parameter usually different from ξ in step#1. We used computer simulations to find ξ₂ in the range of 0.0001 to 0.001 could provide reasonable estimations and empirically determine ξ₂ = 0.0005 throughout this work. Finally, the fitted w_in can be converted to a N × M matrix and the projections to each dimension provide the distributions of d and D_in, respectively. Namely,

$$P\left(d_{\left(n\right)}\right)=\left(\sum _{m=1}^M{w}_{in\left(n,m\right)}\right)/\left(\sum _{n=1}^N\sum _{m=1}^M{w}_{in\left(n,m\right)}\right)$$ [14]

and

$$P\left(D_{in\left(m\right)}\right)=\left(\sum _{n=1}^N{w}_{in\left(n,m\right)}\right)/\left(\sum _{n=1}^N\sum _{m=1}^M{w}_{in\left(n,m\right)}\right)$$ [15]

Moreover, the overall mean cell size can be obtained as

$$\overline{d}=\left(\sum _{n=1}^N{d}_{\left(n\right)}P\left(d_{\left(n\right)}\right)\right)/\left(\sum _{n=1}^{N}P\left(d_{\left(n\right)}\right)\right)$$ [16]

mean intracellular diffusivity as

$$\overline{D_{in}}=\left(\sum _{m=1}^M{D}_{in\left(m\right)}P\left(D_{in\left(m\right)}\right)\right)/\left(\sum _{m=1}^{M}P\left(D_{in\left(m\right)}\right)\right)$$ [17]

and the standard deviation of cell sizes as

$${\sigma }_d=\sqrt{\left(\sum _{n=1}^{N}P\left(d_{\left(n\right)}\right){\left(d_{\left(n\right)}-\overline{d}\right)}^2\right)}/\left(\sum _{n=1}^{N}P\left(d_{\left(n\right)}\right)\right)$$ [18]

Figure 1 shows the diagram of the two-step MRI-Cytometry fitting of a simulated tissue with a Gaussian cell size distribution (actual mean cell size $\overline{d}=16$ μm with a standard deviation σ_d = 3 μm). Details of all other simulation parameters can be found in the Simulation section.

Figure 1.

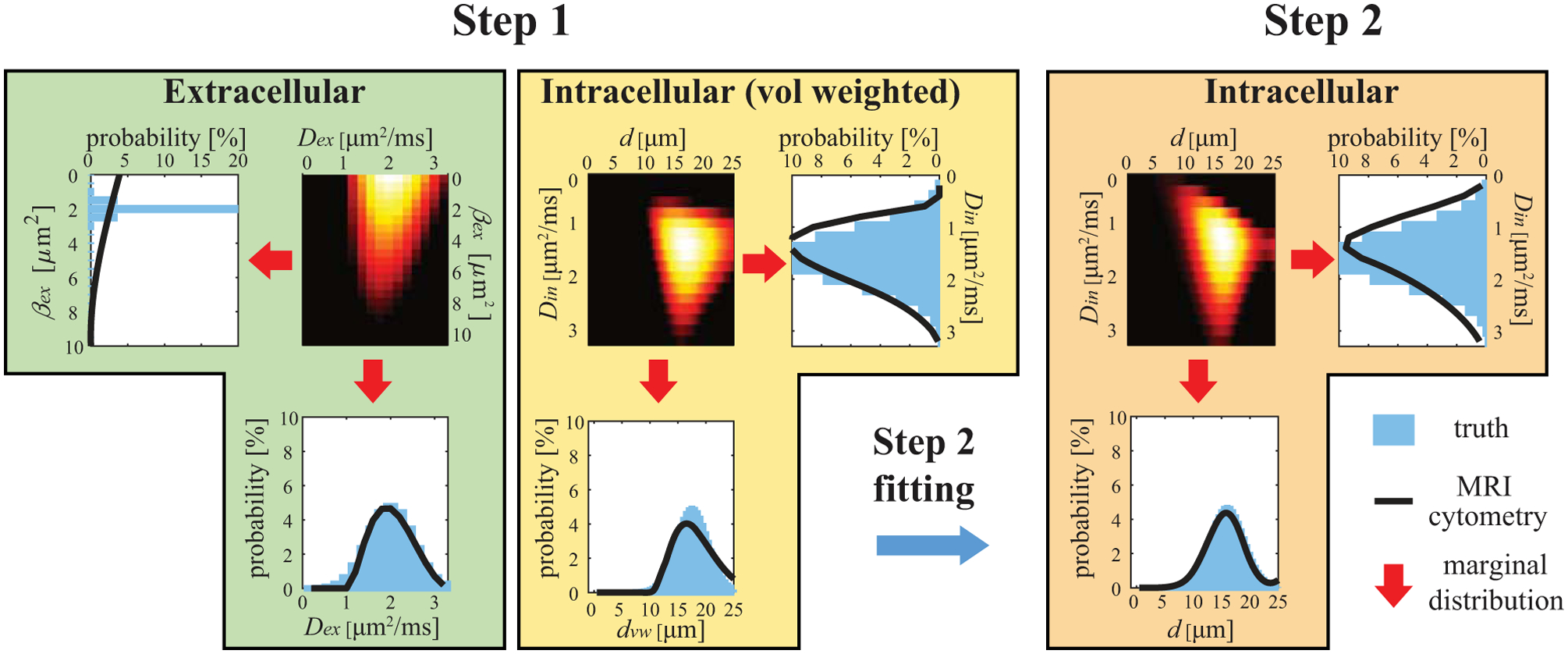
Diagram of two-step MRI-Cytometry fitting of a simulated tissue with a Gaussian cell size distribution. The calculations of marginal distributions are shown in Eqs.[5], [6], [7], [10], [14], and [15].

METHODS

Because MRI-Cytometry is a general framework, we used the data acquired previously for IMPULSED (23), including validation data using cultured cells, animal xenografts, and in vivo data from patients with breast cancer; however, we use the analyses described above. We generated new simulation data, in which the ground-truth microstructural parameters followed distributions of values, in contrast to the single values used in the IMPULSED simulations. All acquisition details for experiments in cultured cells, animal xenografts, and breast cancer patients have been reported previously (23). Brief descriptions are provided below.

Acquisition protocol

All studies in this work, including computer simulations, cultured cells, animal xenografts, and cancer patients, used the same protocols as in (23). Briefly, three acquisitions with effective diffusion times 70, 10, and 5 ms, respectively, were used with the highest b values of 1800 s/mm², 1000 s/mm², and 300 s/mm², respectively. The highest gradient strength was 80 mT/m, gradient rise time 0.9 ms, and the total scan time ~7 mins.

Computer simulations in silico

DWI signals were generated using Eq.[2] with distributions of d, D_in, D_ex0, and β_ex and noise at different signal-to-noise ratios (SNR). Each simulation was repeated 100 times each with different noise but at the same SNR level to investigate the accuracy and precision of MRI-Cytometry. For simplicity, all input parameters were selected to obey Gaussian distributions. Unless otherwise specified, the distributions used in terms of (mean, STD, discretization step) were (16, 2, 0.5) μm, (1.58, 0.5, 0.2) μm²/ms, (2, 0.5, 0.2) μm²/ms, and (2, 0.25, 0.25) μm² for of d, D_in, D_ex0, and β_ex, respectively. These values were determined from our previous fittings of solid tumors (15,32,33). The input v_in was 70%. Four specific simulations were performed:

1. Influence of SNR. Six SNRs (20, 40, 60, 80, 150, and ∞) were simulated to investigate how SNR affects MRI-Cytometry results.

2. Influence of distribution median. Five medians (d_cen = 4, 8, 12, 16, and 20 μm) with the same σ_d = 2 μm were simulated.

3. Influence of distribution width. Five standard deviations (σ_d = 1, 2, 3, 4, and 5 μm) with the same median cell size of d_cen = 16 μm were simulated.

4. Influence of bi-modal distribution. A bi-model distribution consisting of two peaks (8(2) and 16(2) μm in terms of median(STD)) with five different v_d,small values, i.e., cell number fractions of the small cells were simulated at SNR = 40. d = 10 μm was used as the threshold to separate small and large cells.

Validation using cultured cells in vitro

Three types of breast cancer cell lines (MDA-MB-231, MCF7, and MDA-MB-453), one acute T cell leukemia (Jurkat) cell line (all purchased from American Type Culture Collection (Manassas, Virginia, USA)) and the mixture of primary lymphocytes (extracted from human peripheral blood) were prepared from either culture or separation, and then pelleted for MRI experiments. Light microscopy was used to estimate the true cell size distribution.

Validations using animal xenografts in vivo

All procedures were approved by the Institutional Animal Care and Usage Committee at Vanderbilt University Medical Center. MDA-MB-231 (n = 6) and two MCF7 (n = 4) subcutaneous xenografts in the hind limbs were developed in female Athymic nude mice (Harlan Laboratories, Inc., Indianapolis, IN). Animals were scanned on a Varian/Agilent 4.7T MRI when tumor sizes reached 200 – 300 mm³ and then euthanized for histology using H&E staining for cellularity and Na⁺/K⁺-ATPase (ab76020, Abcam) staining for cell size. Histology images were analyzed using CellProfiler™ to obtain quantitative information on cell sizes.

Applications in patients

The human imaging study was approved by the Institutional Review Board at Vanderbilt University Medical Center. Following written informed consent, seven female patients with breast cancer (age 55.3±8.0 years) with tumors ≥ 1 cm were recruited. All human imaging was performed on a Philips 3T Achieva MRI scanner using a 16-channel breast coil.

Data analyses

All DWIs were co-registered to T2-weighted b = 0 images using FSL (34,35) to reduce motion-induced artifacts. Regions-of-interest (ROIs) were manually drawn on PGSE DWIs with b = 1000 s/mm². MRI-Cytometry data fittings were performed using in-house code with Matlab (Mathworks, Natick, Massachusetts) inside ROIs only. As a means of validation, MRI-Cytometry derived cell size distributions were compared with light-microscopy or histology derived distributions in the cultured cells and animal xenografts studies, respectively.

RESULTS

Computer simulations in silico

Figure 2 shows the influence of SNR on the MRI-Cytometry fits. Except for β_ex, the mean distributions of 100 repeats of all other parameters match the ground-truth distributions, suggesting reasonably good accuracy of MRI-Cytometry. Even without noise, MRI-Cytometry still cannot fit P(β_ex) accurately, indicating MRI-Cytometry has very low sensitivity to β_ex. Recall that P_cal(d) is the cell size distribution calculated directly from the cell-volume-weighted size distribution P_vw(d) using Eq.[10]. Because Eq.[10] serves as a low-pass filter, P_cal(d) shows large artificial peaks at small cell sizes, which are presumably caused by noise. These artificial peaks are removed in P(d) obtained by the step#2 MRI-Cytometry.

Figure 2.

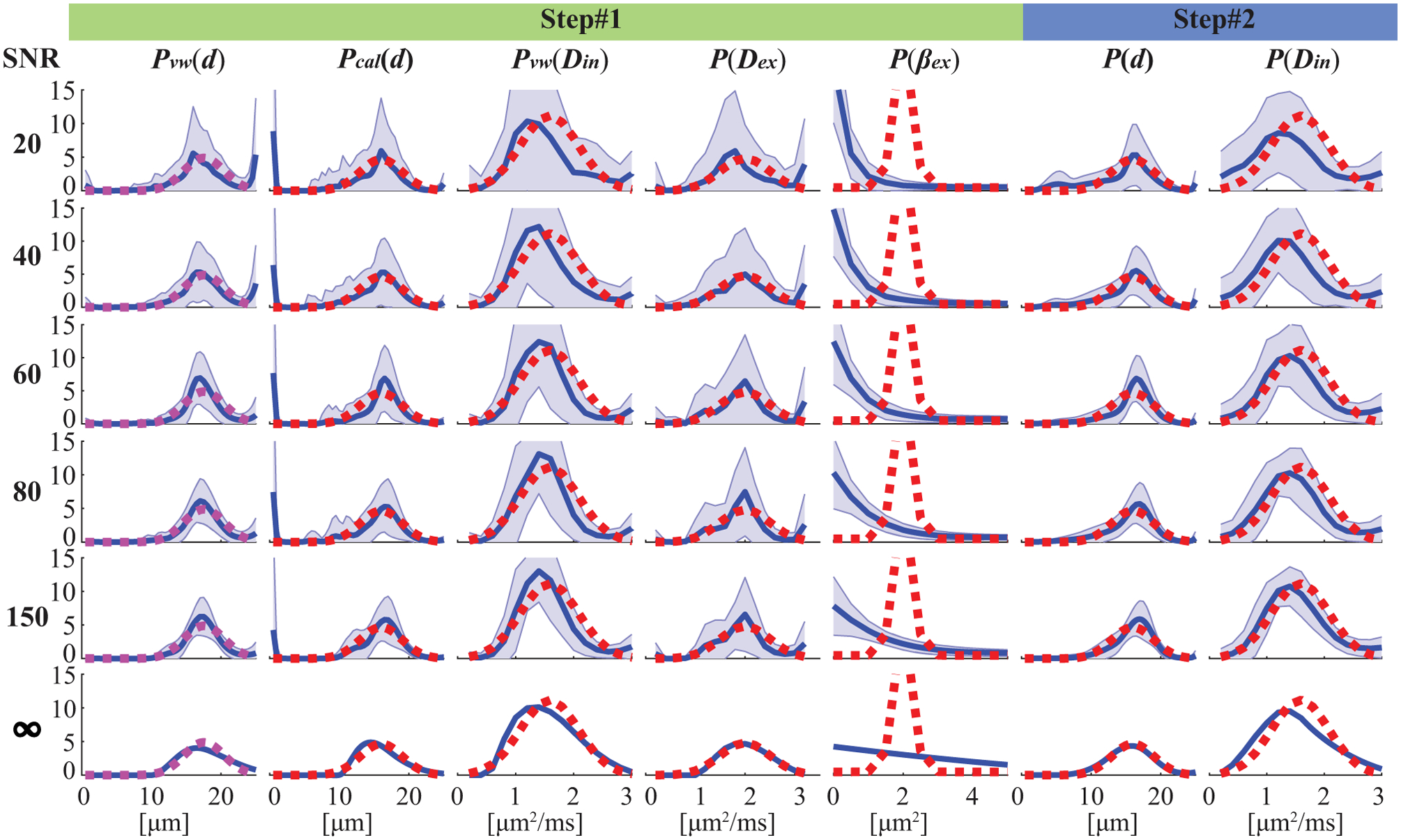
Simulated influence of noise at different SNR levels on MRI-Cytometry fitted distributions of microstructural parameters. For each SNR, the fittings were repeated 100 times each with different noise but at the same SNR level. The red dash lines represent the ground truth, blue solid lines represent the mean fitted distributions of 100 repeats, and the shaded areas represent standard deviations.

The shaded areas in Figure 2 are standard deviations of 100 repeated fits, representing fitting precisions. SNR has a very strong impact on fitting precisions of all distributions obtained with MRI-Cytometry. For typical SNRs such as from 20 to 60 on human scanners, the precisions are relatively low. For SNR=150, the precision is significantly improved, especially for P(d) and P(D_in), and their corresponding coefficients of variation are less or around 10%, indicating reasonably accurate fittings. This is encouraging because a recent report (36) has shown that voxel-wise SNR=150 is achievable in DWI on clinical MRI scanners. It does, however, result in increased scan times (4 acquisitions) and decreased spatial resolution (2.5×2.5×5 mm). Note that P(d) and P(D_in) obtained by step#2 above show much higher precisions than those of P_cal(d) and P_vw(D_in) obtained in step#1, indicating the regularization in step#2 further minimizes the influence of noise. This is another benefit of the two-step approach, in addition to improving accuracy by removing artificial peaks at small cell sizes.

Figure 3 shows the influences of mean cell sizes $\overline{d}$ on MRI-Cytometry fits at SNR=40, a typical SNR achievable in our human breast cancer scans. MRI-Cytometry overestimates P(d) at smaller $\overline{d}=4$ μm, while providing more accurate estimations of P(d) for larger $\overline{d}$. Similarly, estimates of P(D_in) are significantly biased at smaller $\overline{d}$ and the accuracy increases at larger $\overline{d}$. This is expected because the detection sensitivity to cell size and intracellular diffusivity decreases at smaller restriction sizes. Figure 3b summarizes the accuracy and precision of MRI-Cytometry derived parameters dependent on $\overline{d}$. The estimated v_in seems independent of $\overline{d}$. Both $\overline{d_{vw}}$ and $\overline{d}$ reflect the change in $\overline{d}$. The large standard deviations of $\overline{D_{in}}$ suggest that it is hard to estimate reliably, consistent with our previous findings in IMPULSED (23). The fitted σ_d (standard deviations of each fitted P(d)) shows good accuracy but lower precision. The coefficient of variation of d (COV(d)) decreases to ~ 10% only when $\overline{d}>16$ μm, indicating P(d) width can be reliably fit only with larger $\overline{d}$ using the current acquisitions.

Figure 3.

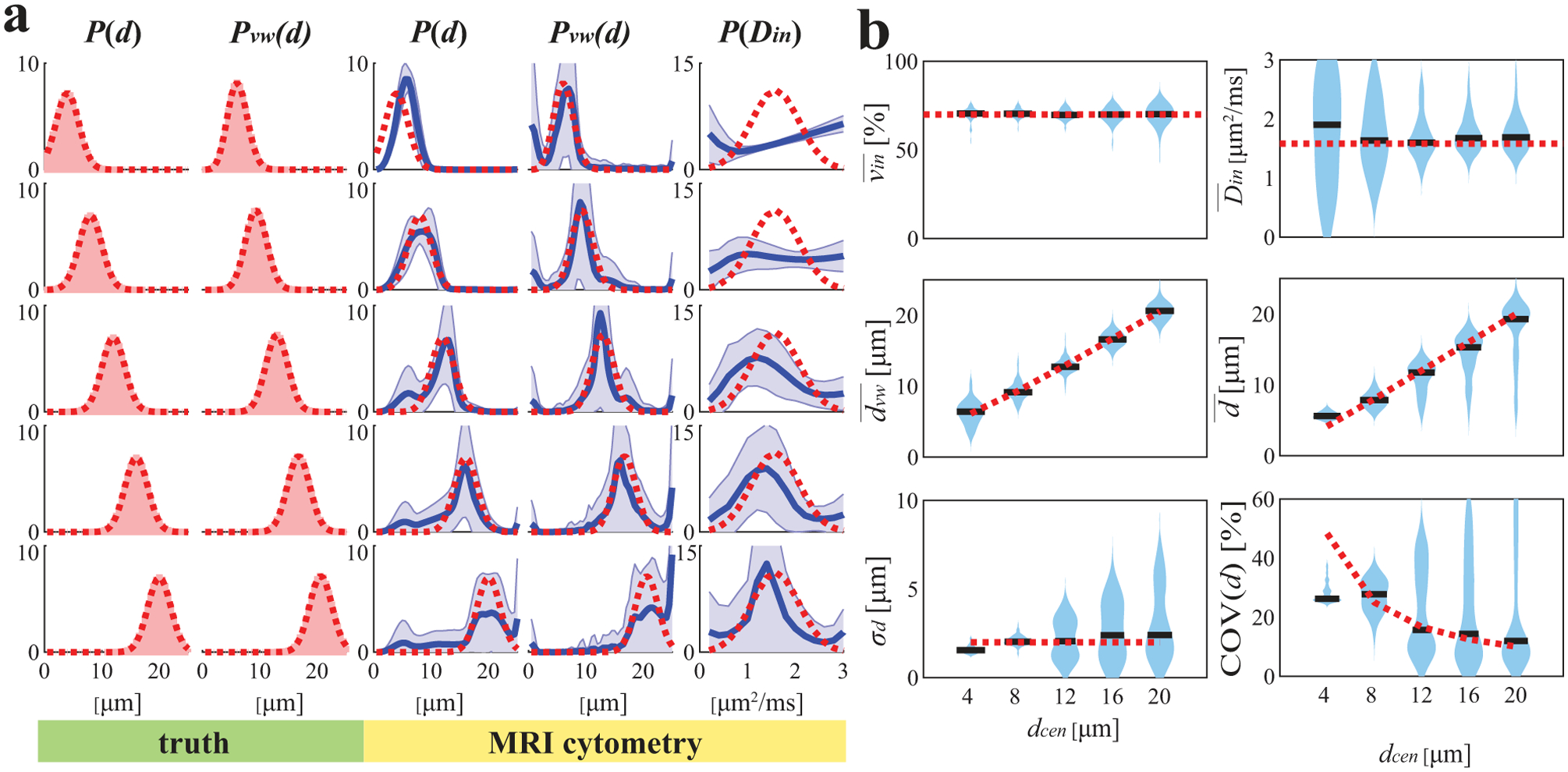
Simulated influence of true median cell size on MRI-Cytometry fitted (a) distributions of microstructural parameters and (b) MRI-Cytometry derived parameters. Figure legends are the same in Figure 2.

Figure 4 shows the influences of the width of P(d) (in terms of STD) on MRI-Cytometry fits when $\overline{d}=16$ μm. Although v_in, $\overline{d_{vw}}$, $\overline{d}$, and $\overline{D_{in}}$ can be fit with reasonable accuracy, MRI-Cytometry derived σ_d overestimates the width of P(d) when ground-truth σ_d is < 2 μm. On the other hand, it underestimates the width of P(d) when ground-truth σ_d > 3 μm. COV(d) is larger than 10%, indicating it is challenging to fit P(d) width reliably at SNR = 40. Therefore, MRI-Cytometry provides higher accuracy to estimate $\overline{d}$ than σ_d.

Figure 4.

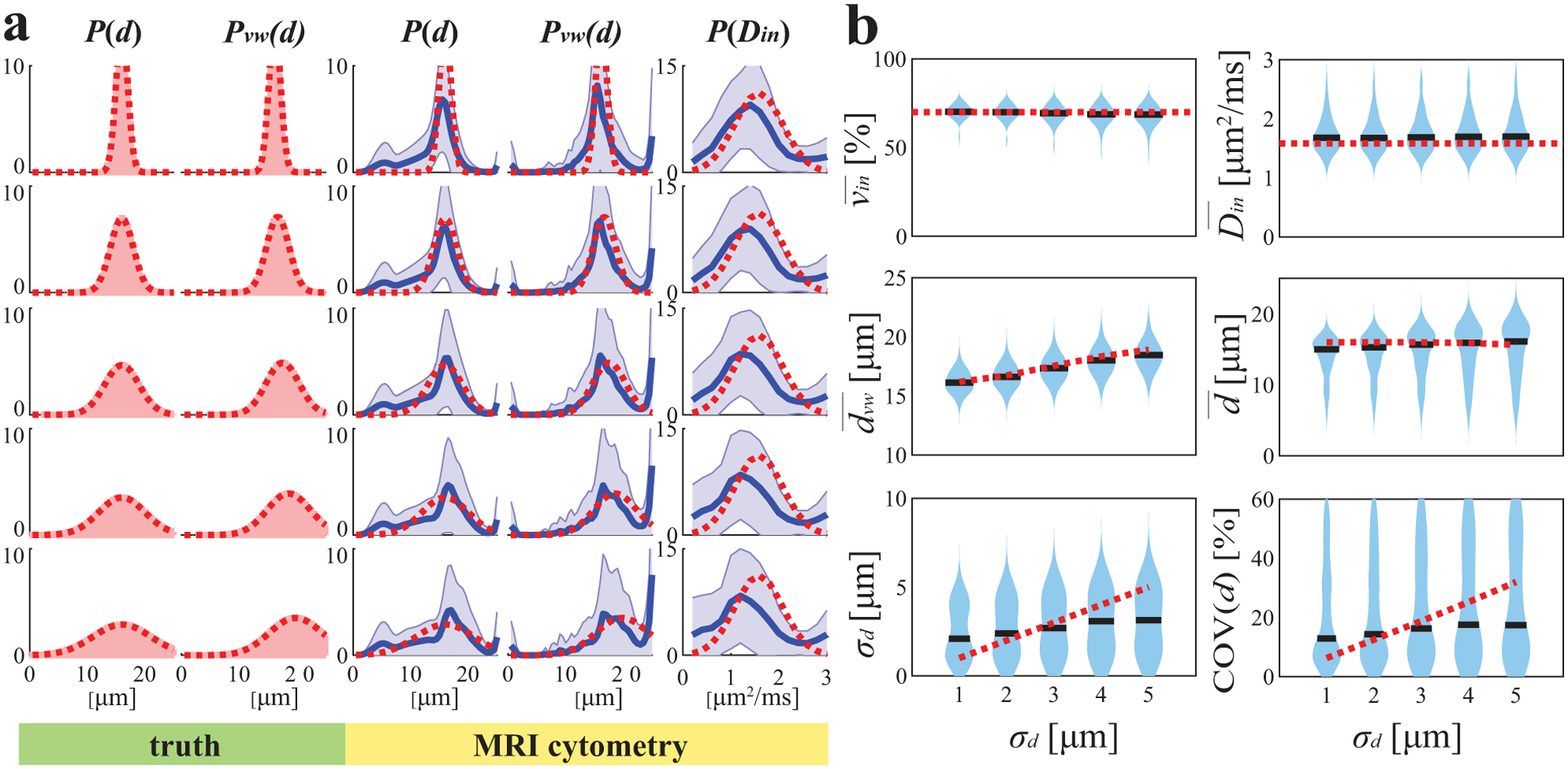
Simulated influence of the standard variation of true mean cell size distribution on MRI-Cytometry fitted (a) distributions of microstructural parameters and (b) MRI-Cytometry derived parameters. Figure legends are the same in Figure 2.

Figure 5 shows how MRI-Cytometry fits bi-modal distributions of d. Recall that the bi-modal distributions consist of two peaks, one of small cells (8 μm) and one of large cells (17 μm), and their relative cell number fractions vary. Note P_vw(d) (i.e., cell-volume-weighted size distributions) barely show bi-modal patterns even if the cell number fraction of small cells reaches 50% (i.e. half of the cells are small). This is because small cells have much smaller cell volumes, so their signal contributions are much smaller than those of larger cells. As a result, P_vw(d) is more sensitive to large cells. As shown in Figure 5b, MRI-Cytometry derived $\overline{d_{vw}}$ shows good accuracy for all combinations of small and large cells, but $\overline{d}$ is slightly overestimated when both small and large cells are present. The MRI-Cytometry derived apparent fractions of cells smaller than 10 μm, $v_{d,\mathit{\text{small}}}$, shows a monotonic dependence on ground-truth values, suggesting MRI-Cytometry can characterize the cell number fractions of small cells. This information cannot be obtained using previous methods that report mean cell sizes (12,14,16).

Figure 5.

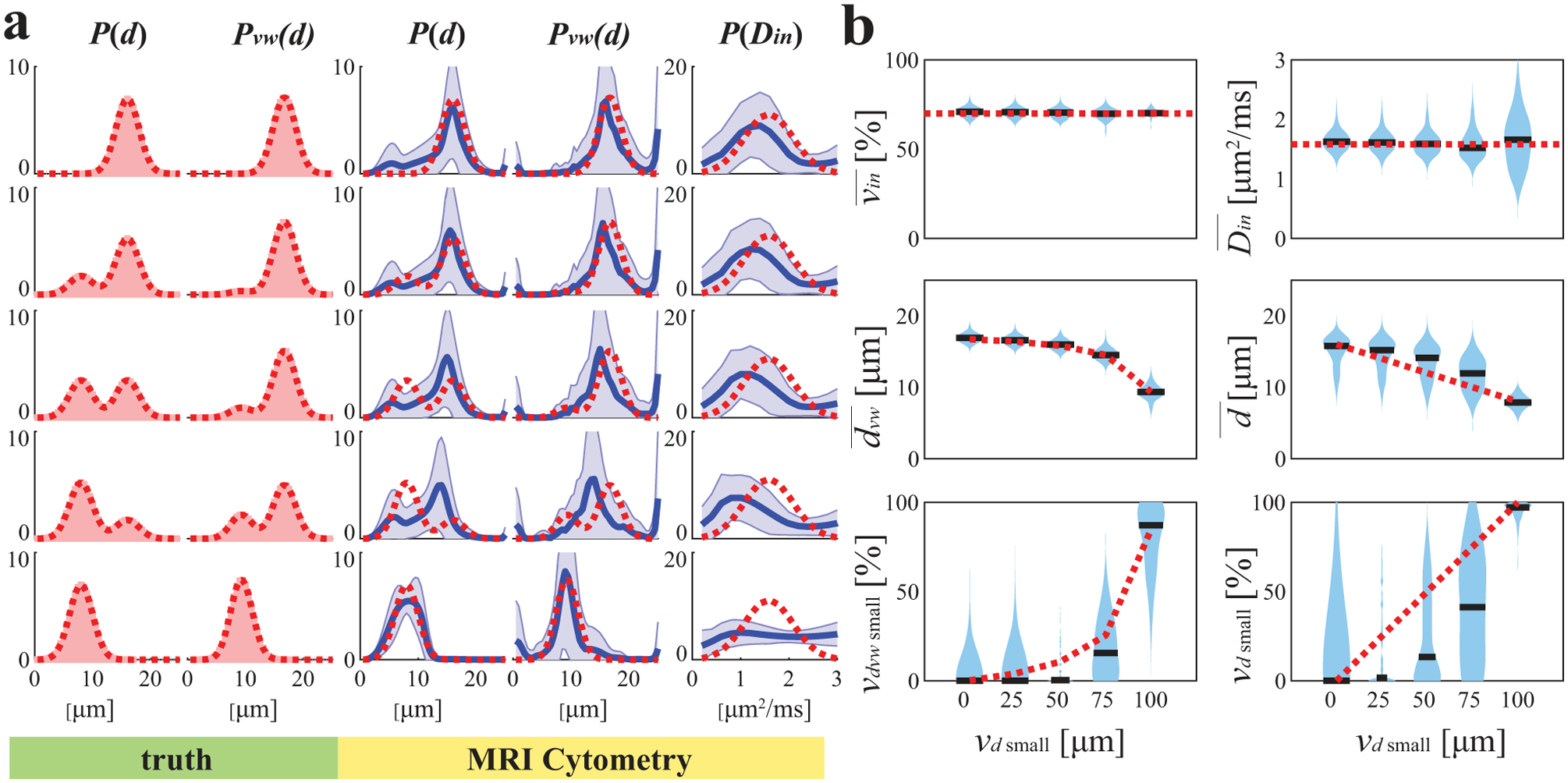
Simulated influence of small cell fractions on MRI-Cytometry fitted (a) distributions of microstructural parameters and (b) MRI-Cytometry derived parameters. Figure legends are the same in Figure 2.

Cultured cells in vitro

Figure 6 shows comparisons of MRI-Cytometry and light microscopy derived cell size distributions P(d) using cultured cells in vitro. For the three breast cancer cell lines (MDA-MB-231, MCF-7, and MDA-MB-453) and Jurkat leukemia cancer cells, P(d) obtained using MRI-Cytometry matched those from light microscopy. For the smallest lymphocytes, MRI-Cytometry found accurate mean values for P(d) but with a broader width. Figure 6b shows the correlation between MRI-Cytometry and light microscopy derived mean cell size $\overline{d}$ and standard deviation σ_d. Although there is a good correlation in $\overline{d}$, there are discrepancies in σ_d which is consistent with simulated results that MRI-Cytometry provides more accurate estimates of $\overline{d}$ than those of σ_d.

Figure 6.

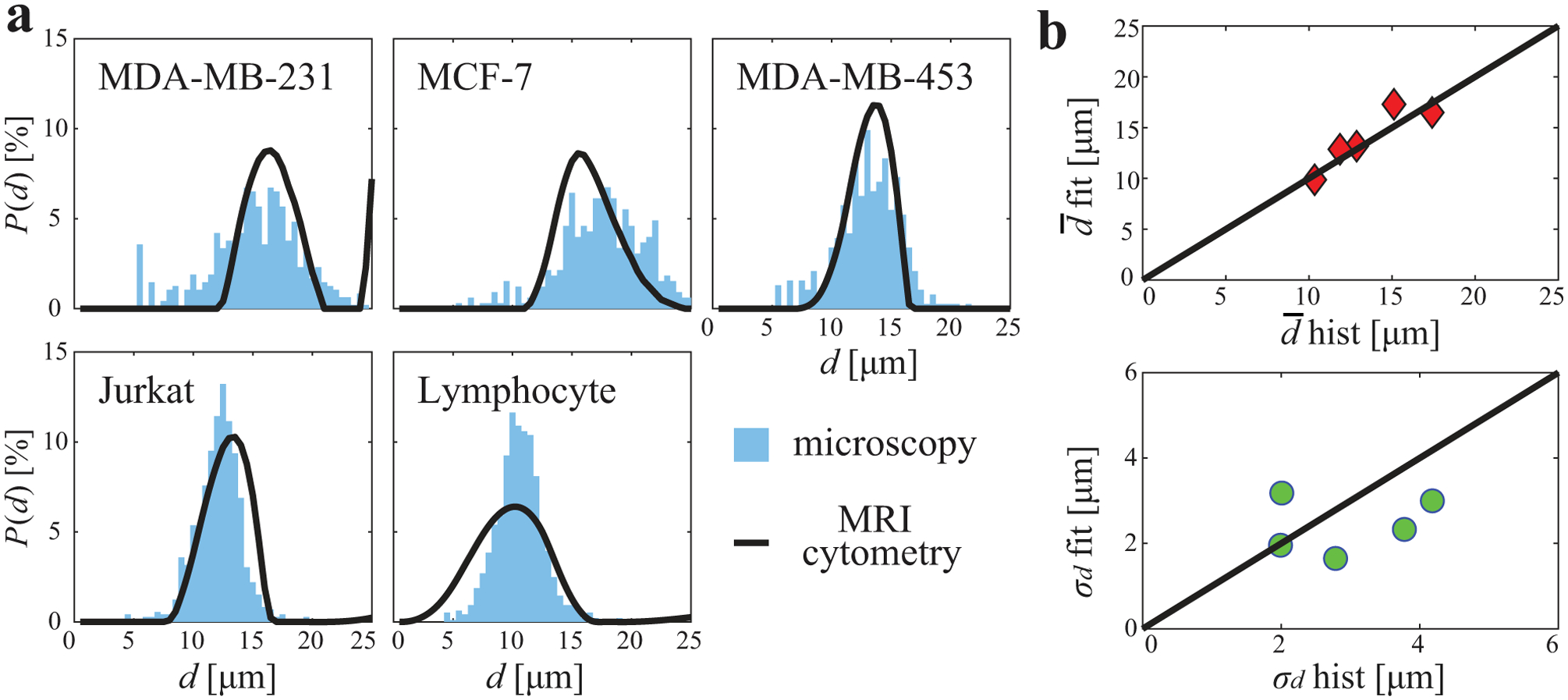
Comparison of MRI-Cytometry and light microscopy derived cell size distribution P(d) using cultured cells in vitro. (a) comparison of distributions of five different cell samples. (b) correlations of MRI-Cytometry and light microscopy derived mean cell size $\overline{d}$ and standard deviation σ_d.

Animal xenografts in vivo

Figure 7a shows comparisons of MRI-Cytometry and histology derived cell size distribution of two types of mouse xenografts (MDA-MB-231 and MCF-7) in vivo. There is a good match in all five representative animals. Because it is challenging to distinguish small cells from other small structures such as cell debris, cells only with a size larger than a threshold of 5.5 μm were included. Note this exclusion did not affect our overall results significantly because the fractions of very small cells (< 5.5 μm) are low, and hence they make minor contributions to overall signals. Figure 7b shows the agreement between MRI-Cytometry and histology derived mean cell size $\overline{d}$ and standard deviation σ_d. The 95% limits of agreement are 1.6 μm and 1.4 μm for $\overline{d}$ and σ_d, respectively, suggesting good agreements.

Figure 7.

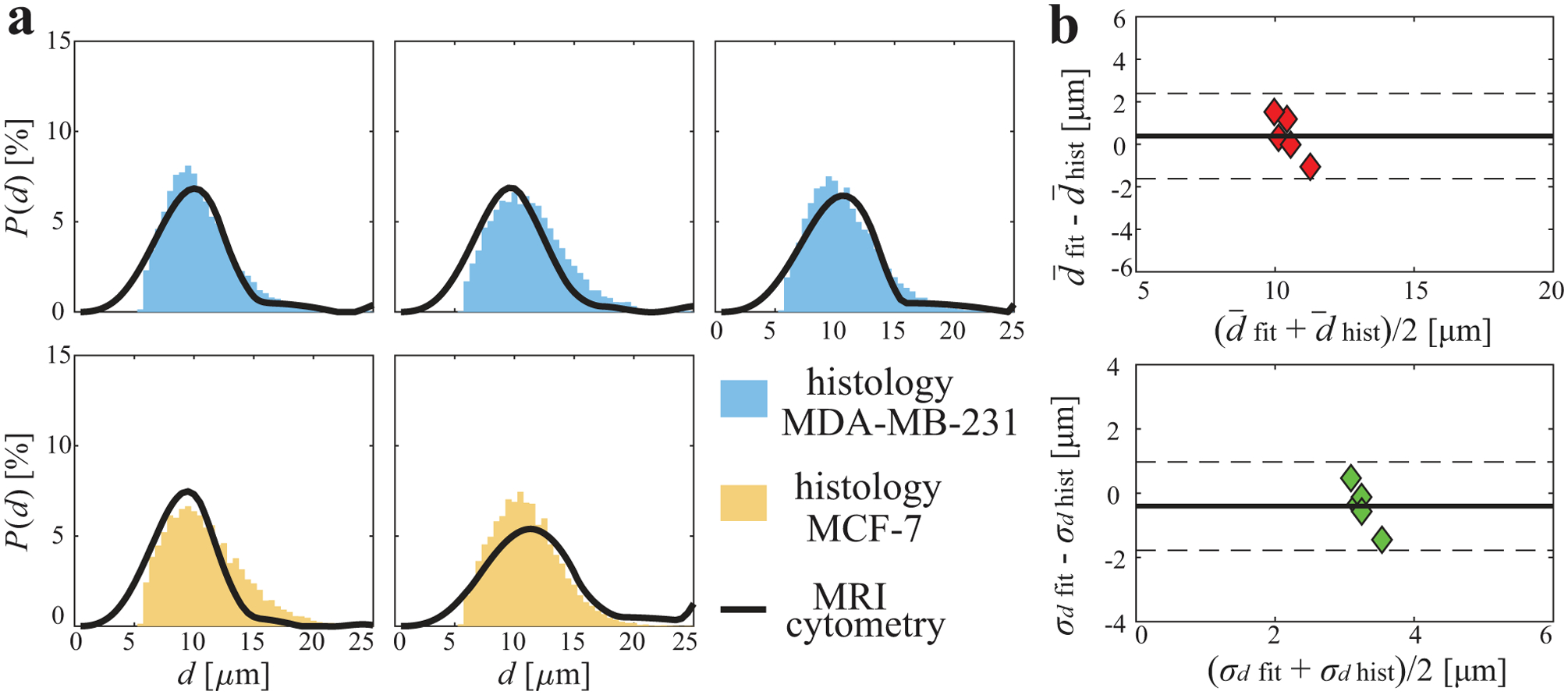
Comparison of MRI-Cytometry and histology derived cell size distribution P(d) of mouse tumors in vivo. (a) comparison of distributions of five tumors (top: MDA-MB-231. Bottom: MCF-7). (b) Bland-Altman plots show the agreement of MRI-Cytometry and light microscopy derived mean cell size $\overline{d}$ and standard deviation σ_d

Breast Cancer patients in vivo

Figure 8 shows representative cell size distributions P(d) and MRI-Cytometry derived v_in and $\overline{d}$ parametric maps of a human breast tumor. SNR was ~45 on T2w images. Four examples of cell size distributions from four representative image voxels are provided. For the voxels in the viable tumors (#1, #2, and #4 shown in Figure 8a, e, and g), the shapes of P(d) are similar to each other. However, voxel #2 shows hyperintensity on the T2-weighted b = 0 image and reduced v_in. This might be due to increased extracellular water. By contrast, P(d) appears very differently as a small peak at large cell sizes (> 20 μm) for the voxel #3 in the necrotic region. This is because the necrotic core consists of mainly fluid and cell debris with few restrictions. This leads to a small fitted intracellular volume fraction v_in (< 10%) and large fitted cell sizes ≥ 20.5 μm, the root-mean-square-displacement of free water at body temperature 37°. Figure 8d and h demonstrate the MRI-Cytometry derived v_in and $\overline{d}$ parametric maps, which show low v_in and high $\overline{d}$ in the necrotic core compared with viable tumors. Note that transcytolemmal water exchange may be responsible for the underestimation of v_in, but it may have minor influence on $\overline{d}$, as we reported previously (26).

Figure 8.

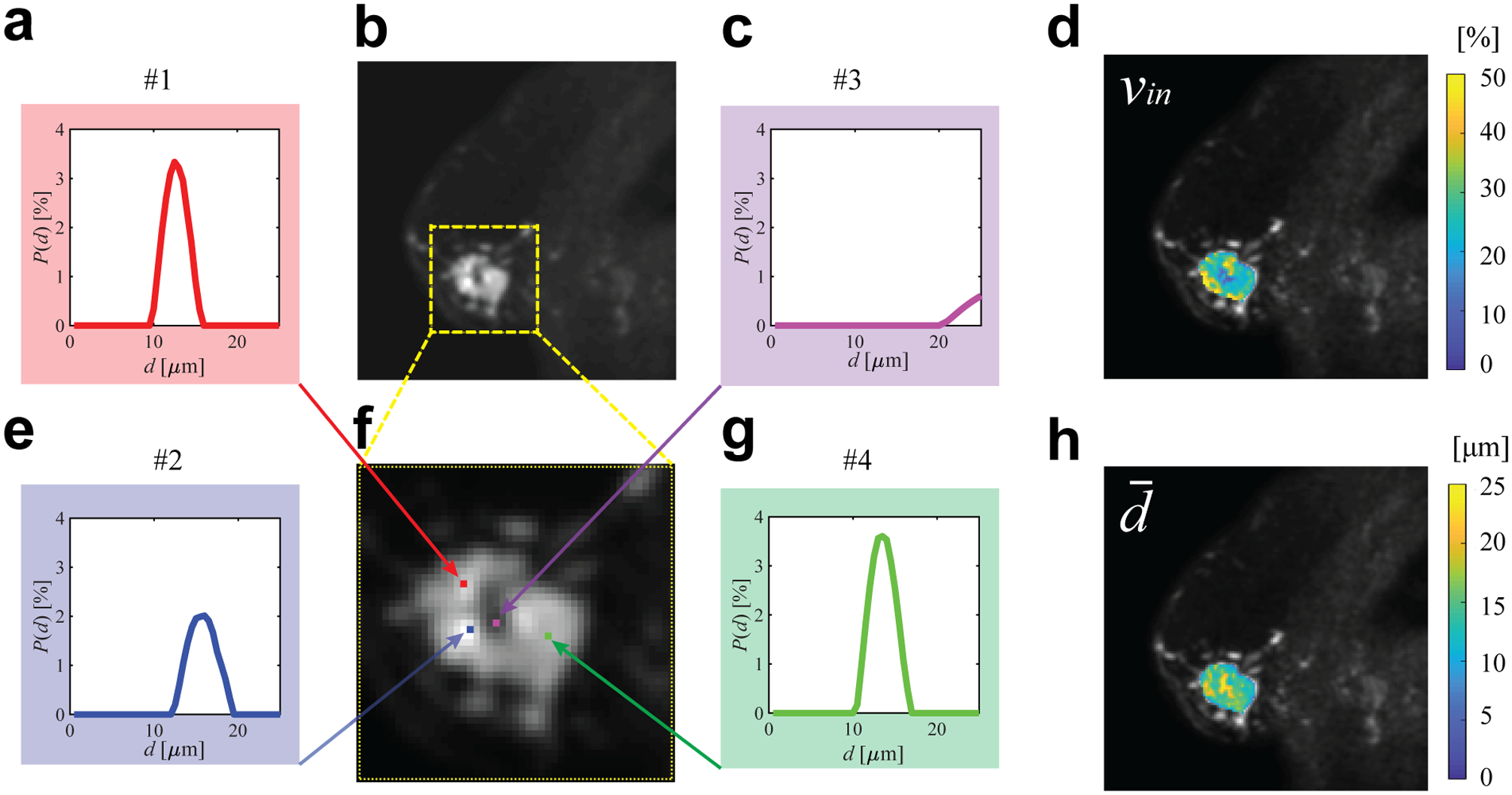
Representative cell size distributions and MRI-Cytometry derived parametric maps of a breast tumor. (b) is T2-weighted b = 0 image of the tumor and (f) is an enlarged view. (a,c,e,g) are four examples of cell size distributions. (d) and (h) are MRI-Cytometry derived v_in and $\overline{d}$ maps of the same tumor.

In addition to the voxel-wise fitting shown above, MRI-Cytometry was also fitted to the whole-tumor signals to investigate the overall cell size distribution of each tumor as shown in Figure 9a. P(d) displays different locations and widths of distributions in different breast tumors. This finding is consistent with previous reports that human breast tumors have large variations in cell sizes (37). For a direct comparison, the averaged cell size distributions from voxel-wise spectra were also provided. The latter shows broader spectra and peaks close to large d indicating voxels in the necrotic regions. Note that the whole tumor data had a much higher SNR than the voxel-wise data, which may contribute to the discrepencies between two results. Unfortunately, the current study lacks histopathological analysis in breast cancer patients to validate the fitted P(d) directly. All fitted distributions are smooth, presumably due to the regularization effect. Figure 9b shows the comparison of MRI-Cytometry and IMPULSED derived cell-volume-weighted mean cell size $\overline{d_{vw}}$. Pearson’s correlation coefficient is r = 0.83 and p < 0.02. This is consistent with previous reports that NNLS fitted results agree well with those fitted using non-linear procedures (31), suggesting the information on mean cell size from IMPULSED can be provided by MRI-Cytometry as well. Figure 10 shows a direct comparison of the mean cell size maps of seven patients obtained using IMPULSED and MRI-Cytometry. The maps are slightly different from each other. Notably, IMPULSED provides more high fitted $\overline{d}$ values > 20 μm especially at tumor boundaries, indicating MRI-Cytometry might be more robust and less sensitive to partial volume effects.

Figure 9.

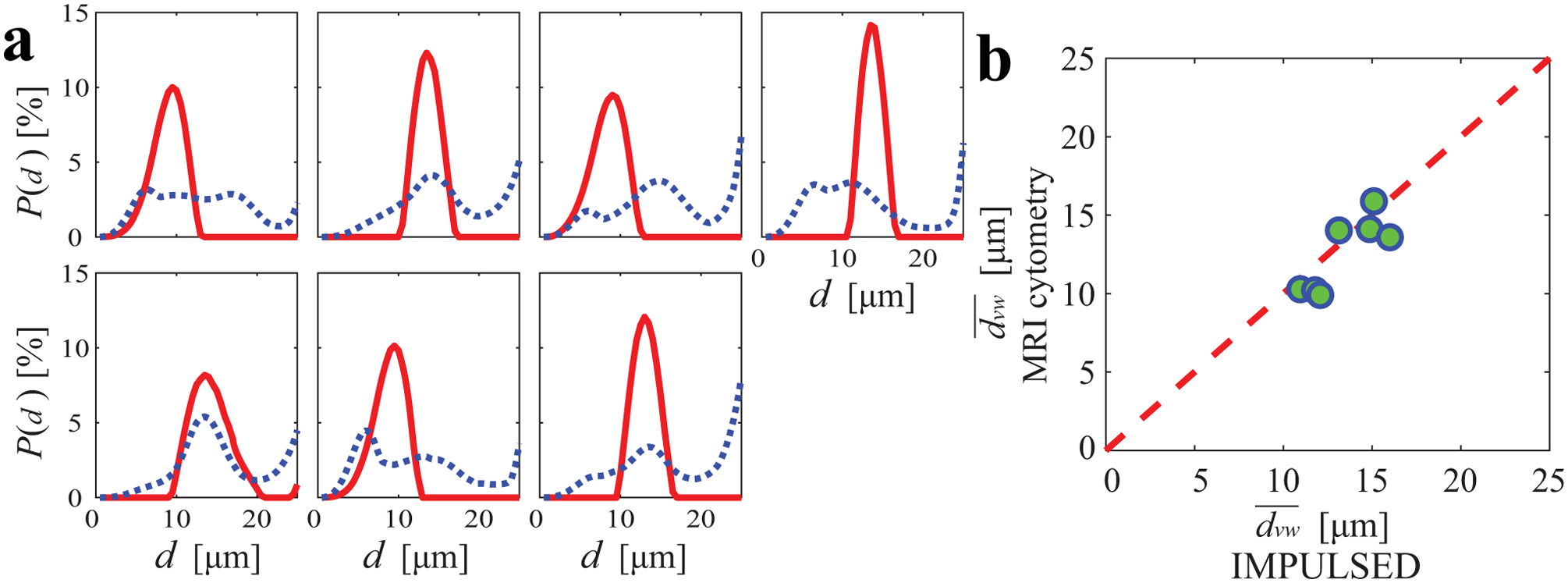
(a) MRI-Cytometry derived cell size distributions of all seven breast cancer patients. Red solid lines and blue dashed lines represent the distributions fitted from the whole tumor data and the averaged voxel-wise spectra, respectively. (b) the comparison of MRI-Cytometry and IMPULSED derived cell-volume-weighted mean cell size $\overline{d_{vw}}$. The Pearson’s correlation provides r = 0.83 and p < 0.02. The red dash line represents identity.

Figure 10.

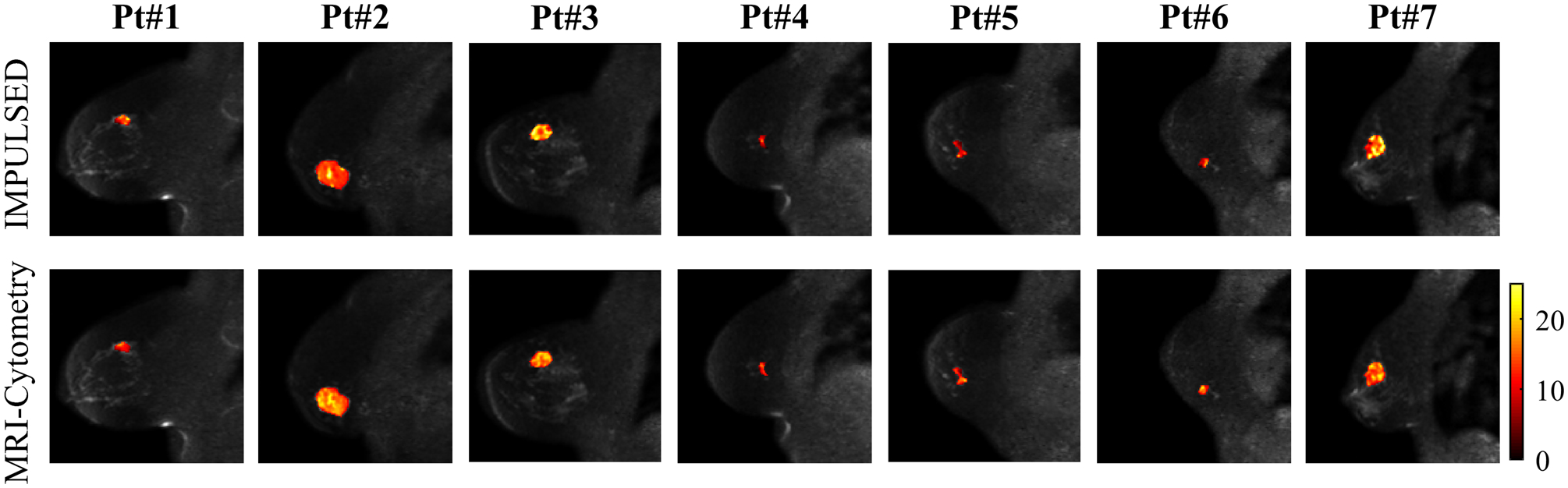
Comparison of mean cell size maps obtained by IMPULSED (top) and MRI-Cytometry (bottom). Each column is a representative slice from a patient.

DISCUSSION

The two-step MRI-Cytometry method is a framework for mapping arbitrary cell size distributions without assuming any parametric distribution. As a general framework, MRI-Cytometry can incorporate combinations of any DWI acquisition methods with appropriate adjustments of fitting basis matrices (dictionaries) as long as the measurements are sensitive to changes in restriction size. We chose data acquisitions used in the IMPULSED method because it is clinically feasible (23). Future directions include using the same MRI-Cytometry framework but with different diffusion acquisition methods (such as PGSE, OGSE, and DDE) and compare the results with the same hardware limitations.

An attractive potential application of mapping cell size distribution is to distinguish different cell populations. For example, immunotherapy provides cutting-edge anti-cancer treatments usually associated with T cell infiltration in tumors (38). Because T cell sizes (7 – 9 μm) are usually smaller than relatively larger cancer cells (10 – 25 μm) (39), mapping cell fractions at different cell sizes may provide an opportunity to characterize T cell infiltration, which is currently not achievable using conventional MRI. Our simulations (Figure 5) suggest that MRI-Cytometry can separate the fractions of small (< 10 μm) cells from relatively larger cancer cells. This may provide an indirect means to probe T cell infiltration in tumors. However, many confounding effects may make this characterization challenging, such as the presence of macrophage and the much smaller contributions of small cells to DWI signals. Stronger gradient coils would improve the ability of MRI-Cytometry to detect smaller cells, which may provide more accurate estimates of T cell infiltration. The current work used a gradient strength up to 80 mT/m and a slew rate < 100 mT/m/sec, both of which limit the shortest diffusion time to be ≈ 5 ms with a corresponding maximum b = 300 s/mm². Such a diffusion time range decreases the detection sensitivity to small cell sizes and intracellular diffusivities, leading to lower fitting precision for MRI-Cytometry derived distributions and parameters such as ${\overline{v_d}}_{’\mathit{\text{small}}}$ and $\overline{D_{in}}$. If stronger gradients such as the Human Connectome coil with 300 mT/m (40) can be used, the detection sensitivity of MRI-Cytometry to smaller cell sizes and intracellular diffusivities may significantly increase. For example, our previous animal study (15) could achieve ≈ 1.7 ms (b = 600 s/mm²) and ≈ 2.5 ms (b = 1320 s/mm²) with a gradient strength up to 360 mT/m. Importantly, intracellular diffusivity D_in of cancer cells can be fit reliably with these much shorter diffusion times. We have recently demonstrated success with this approach using the stronger gradients available on animal scanning systems (15,24).

MRI-Cytometry is based on a two-compartment (intra- and extracellular) model with free water naturally included in the extracellular compartment with D_ex0 = D_free and β_ex = 0. However, the peak corresponding to free water on the D_ex spectra may not be resolved independently due to the regularization used in the MRI-Cytometry fittings, but the free water alters the estimated distribution of extracellular diffusivities P(D_ex0). Fitting multiparametric diffusion models to data is an ill-posted problem and the influence of free water on DWI signals may be similar to having different distributions of extracellular diffusivities, leading to the possibility of multiple solutions. The inclusion of another dimension of measurements using, e.g., varying echo times, may provide additional information to assist in solving this problem. Moreover, the influences of free water fraction and cell membrane permeability, amongst other factors, on MRI-Cytometry fitting need further investigation.

Due to the limited long t_diff ranges used in the current work, our results suggest MRI-Cytometry has a low sensitivity to β_ex. This is consistent with our previous findings in patients (23) that D_ex could be assumed to be a constant, which enhances fitting precisions of other parameters. As a general framework, MRI-Cytometry should not be limited by the practical parameters and it could fit β_ex reliably if a broader range of frequencies can be used, such as up to 150 Hz suggested in a previous animal study (24). However, if only limited frequency ranges are used, it is possible to simply MRI-Cytometry by removing β_ex from the free fitting parameters.

MRI-Cytometry was implemented voxel-wisely on images obtained from breast cancer patients. However, as shown in Figure 8c, it may not be a suitable model for necrotic regions of the tumor, where water is less restricted. A similar example has been reported that suggests models such as IMPULSED may not always be appropriate in very heterogeneous brain tumors (33). A possible solution is to perform a model selection first to determine the suitability of each model before any data fitting is performed (33).

CONCLUSIONS

A novel and fast MRI-Cytometry imaging method is introduced for mapping intravoxel, non-parametric cell size distributions using diffusion MRI. With validations using computer simulations in silico, cultured cells in vitro, and animal xenografts in vivo, we demonstrate the accuracy and precision of MRI-Cytometry. The applications in breast cancer patients in vivo suggest MRI-Cytometry may be translated to clinical applications.