Analysis of the Effects of Finite Element Type within a 3D Biomechanical Model of a Human Optic Nerve Head and Posterior Pole

Abstract

Background and objective:

Biomechanical stresses and strains can be simulated in the optic nerve head (ONH) using the finite element (FE) method, and various element types have been used. This study aims to investigate the effects of element type on the resulting ONH stresses and strains.

Methods:

A single eye-specific model was constructed using 3D delineations of anatomic surfaces in a high-resolution, fluorescent, 3D reconstruction of a human posterior eye, then meshed using our simple meshing algorithm at various densities using 4- and 10-noded tetrahedral elements, as well as 8- and 20-noded hexahedral elements. A mesh-free approach was used to assign heterogeneous, anisotropic, hyperelastic material properties to the lamina cribrosa, sclera and pia. The models were subjected to elevated IOP of 45 mmHg after pre-stressing from 0 to 10 mmHg, and solved in the open-source FE package Calculix; results were then interpreted in relation to computational time and simulation accuracy, using the quadratic hexahedral model as the reference standard.

Results:

The 10-noded tetrahedral and 20R-noded hexahedral elements exhibited similar scleral canal and laminar deformations, as well as laminar and scleral stress and strain distributions; the quadratic tetrahedral models ran significantly faster than the quadratic hexahedral models. The linear tetrahedral and hexahedral elements were stiffer compared to the quadratic element types, yielding much lower stresses and strains in the lamina cribrosa.

Conclusions:

Prior studies have shown that 20-noded hexahedral elements yield the most accurate results in complex models. Results show that 10-noded tetrahedral elements yield very similar results to 20-noded hexahedral elements and so they can be used interchangeably, with significantly lower computational time. Linear element types did not yield acceptable results.

1. Introduction

Elevated intraocular pressure (IOP) is a known risk factor in the development and progression of glaucomatous optic neuropathy, a leading cause of irreversible vision loss [1]. It is known that IOP elevation induces mechanical stresses and strains within the lamina cribrosa (LC) that are thought to play a critical role in glaucomatous axon damage [2, 3]. To assess the precise role of mechanical stresses and strains in glaucoma, an understanding of the biomechanics of the optic nerve head (ONH) is required. Due to the difficulty of directly measuring the biomechanical response of the ONH, many studies estimate ONH biomechanical behavior using numerical simulations. Relatively few analytical simulation studies have been conducted [4], as the complex geometry and material properties of the ONH are not amenable to generalization [5]. Hence, the application of the finite element method (FEM), a powerful numerical approach that is ideal for complex geometries and material properties, has been widely used to simulate stresses and strains in the ONH in both normal and glaucoma eyes [6–9].

The first major challenge in FE modeling is obtaining and translating the geometry of the organ’s macro-structure into an anatomically accurate FE model, which then incorporates realistic material and micro-structural properties to accurately represent the tissues’ mechanical responses [10]. Representation of fibrillar collagen fibrils with preferential orientation into the eye’s connective tissues is important, as they are responsible for the tissues’ heterogeneous, highly nonlinear, anisotropic mechanical properties. Finally, meshing is a substantial challenge for biomechanical simulations, particularly in the eye, due to its compound geometry.

While various element types can be used for meshing an eye model, e.g., tetrahedral, hexahedral, prism, and pyramid, it has been shown that the choice of element type plays a significant role in the stress and strain estimates of biomechanical simulations [11]. Various element types, including 8-noded hexahedral [10, 12–19], 10-noded tetrahedral [5, 20–22], 4-noded tetrahedral [23–26], hex-dominant hybrid (8-noded hexahedral and 6-noded pentahedral element types, or 20-noded hexahedral and 10-noded tetrahedral elements) [27–30], 6-noded prism [31], and 8-noded planar [5, 32, 33], have been used in ocular biomechanics simulations to date. This implies that there is no consensus on the appropriate element type(s) and as a result, the important role that element type plays in the resultant stresses and strains has been largely neglected.

Tetrahedral elements, whether 4-noded or 10-noded, are the most typical element type for meshing, as tetrahedral meshes (or tet meshes) are easier to generate than meshes with other element types [34]. However, meshes consisting of hexahedral elements often exhibit better mechanical performance compared with a tetrahedral mesh, as tetrahedral elements can “lock” [35]. Several automated tetrahedral mesh generation methods have been proposed in the computer-aided engineering (CAE) industry and available algorithms can generate more than 400,000 tetrahedra per minute [36]. However, all-hexahedra meshing methods have difficulty meshing complex geometries like the eye [37, 38] although engineers have preference for hexahedral elements over tetrahedra [39]. Automated hexahedral mesh generation algorithms are available for a more limited class of geometries, which is why a significant amount of time is devoted to decomposing a model into pieces for which hexahedral mesh generation algorithms will succeed [40]. Prior studies suggest that hexahedral meshes yield more accurate solutions than their tetrahedral counterparts for the same number of edges [41].There are ongoing efforts to generate automatic meshing of complicated geometries with unstructured hexahedral elements. Many algorithms, such as sweeping, whisker weaving, H-Morph, and hex-tet plastering have been proposed to generate hex-dominant meshes. However, none of these algorithms guarantee that the resulting mesh will not contain inverted or tangled elements that render the mesh unusable for computer simulation [42]. Therefore, designing robust algorithms that generate error-free hexahedral meshes of complex geometries remains an open problem [43]. Although the convergence behavior of tetrahedral and hexahedral elements has also been compared [44], to the best of our knowledge, no studies to date have examined the relative mechanical performance of tetrahedral and hexahedral elements when combined with material and geometric nonlinearities, such as incompressible materials with highly anisotropic micro-structure, and large deformations. In addition, meshing an eye-specific 3D model for FE simulation is a labor-intensive task due to both the complex geometries and distinct boundaries between constituent tissues. While tet meshes can be easily generated for such a compound structure using various commercially available CAE software packages and FE preprocessing tools, the same cannot be easily accomplished for hex meshes. Hence, this study also proposes a simple meshing algorithm that enables the user to generate pure unstructured hex meshes from a single parent tet mesh, and analyzes the effects of element type on the resultant stresses and strains using a complex human eye-specific FE model.

2. Materials and Methods

2.1. Eye-specific model

The macro-architecture of the model is first defined by 3D delineation of anatomic surfaces within the high-resolution, fluorescent 3D reconstruction of the posterior eye and ONH obtained from a 68-year-old donor of European descent with normality confirmed by ophthalmic clinical record review. The fluorescent 3D reconstruction device employs an episcopic fluorescent microscope fitted with a 16-megapixel, monochrome CCD camera to image the paraffin-embedded tissue block face of an ONH that was fixed at 100 mmHg IOP as it is being serially sectioned on a microtome. The automated system takes an image of the exposed block face after each of 1.5-μm-thickness section is taken with microscope zoom set such that camera resolution is 1.5 × 1.5 μm/pixel. Approximately 1200 images are precisely aligned and stacked to build a 3D reconstruction of an ONH using data from a laser displacement sensor that records the specimen position for each image. Once the autofluorescent images are aligned and stacked to create a volume[45], custom delineation software (MultiView, courtesy of Dr. Claude F. Burgoyne) was used to slice the volume on 40 radial sagittal planes centered on the ONH [46]. Within each radial section, the anatomic surfaces were delineated using 2D Bezier curves to define the morphology of the LC, peripapillary sclera, and pia [47–50]. 3D surfaces are fit to the families of Bezier curves defining each anatomic surface and the resulting eye-specific geometries of the ONH and peripapillary sclera are then fit into a larger generic posterior scleral shell with anatomic shape and thickness. Finally, a parameterized, anatomic surface defining the prelaminar neural tissues, retina and choroid is added [51]. These surfaces are then utilized to build the high-fidelity eye-specific FE surface mesh of the human posterior eye. The final model includes the sclera, LC, pre- and retro-laminar tissues, retina, and pia as presented in Fig. 1. Node sets representing the anterior laminar insertion (ALI), posterior laminar insertion (PLI), and posterior scleral canal opening (PSCO) in the scleral canal, as well as the anterior laminar surface (ALS), were defined on the eye models as illustrated in Fig. 2. A custom Matlab (Mathworks, Natick, Massachusetts, US) program was written to calculate the average radial displacement of the scleral canal at the ALI, PLI, and PSCO as well as the average depth in the ALS as follows. First, a plane was fitted to the ALI, PLI, and PSCO node set (Fig. 3a), and the node locations were then projected to the fitted plane along a vector normal to the plane. The centroid of the projected node locations on the plane was calculated (Fig. 3b) and the distance from the centroid to each projected nodal location was quantified; the difference in the average radial distance from the centroid to the nodal location for the model at IOPs of 10 and 45 mmHg was reported as the average radial displacement of the scleral canal at the ALI, PLI, and PSCO. To calculate the average depth in the ALS, the distance from each ALS node to the ALI plane was calculated along the vector normal to the plane (Fig. 3c); the difference in the average distance of the ALS nodal locations to the ALI plane at IOPs of 10 and 45 mmHg was reported as the average depth in the ALS.

Fig. 1.

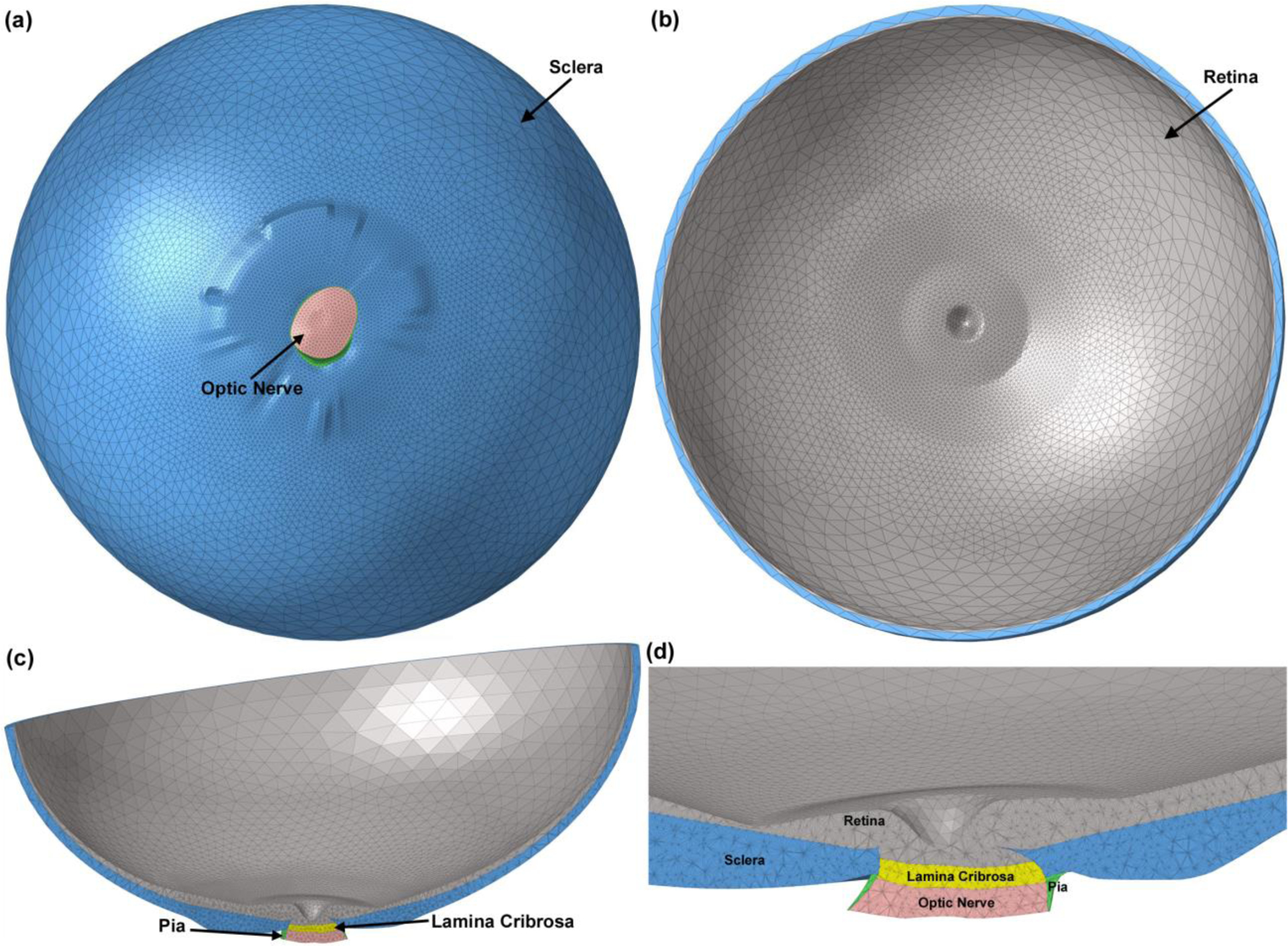
The 3D human eye-specific FE model. A coarser mesh was selected for the anterior section of the sclera and retina while a finer mesh was generated for the posterior part of the globe where the peripapillary sclera, scleral flange, LC, optic nerve, and pia are located. The eye model viewed from (a) the posterior and (b) anterior sides. Cross sections through nasal-inferior axis of (c) the full eye model and (d) the detailed structure of the ONH are presented.

Fig. 2.

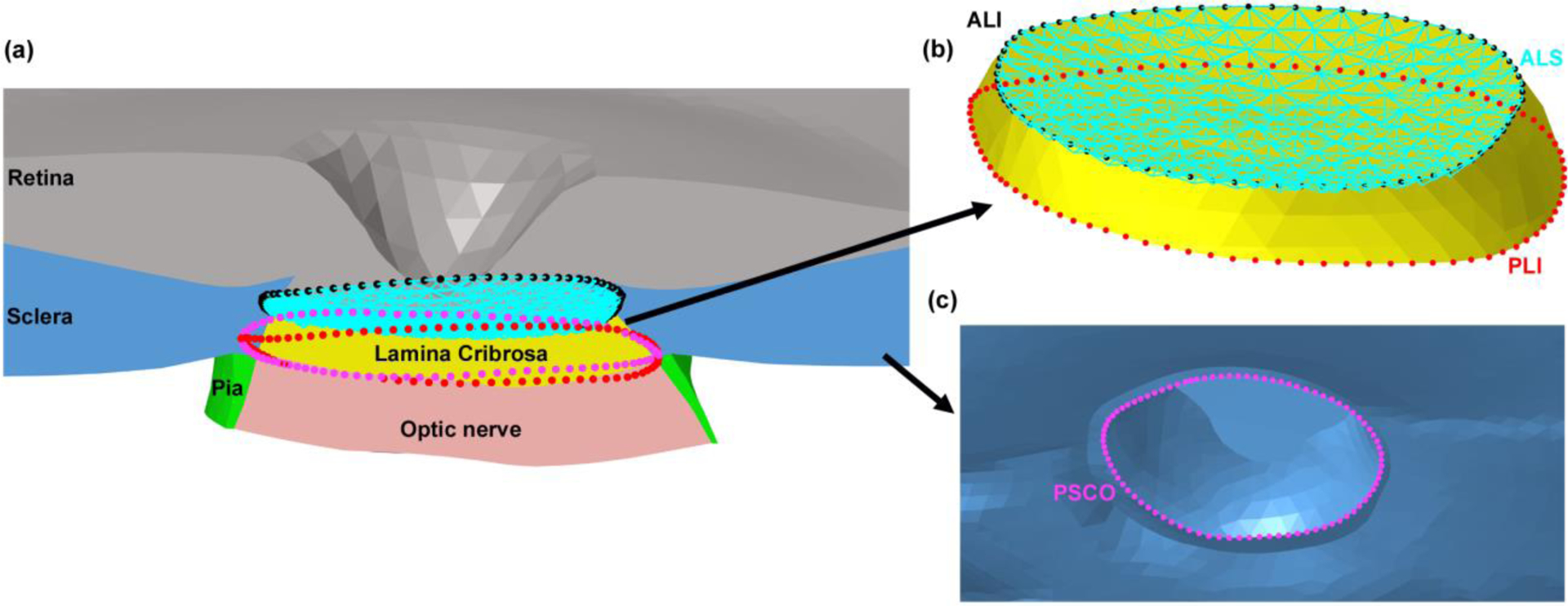
The (a) node sets in the eye model used for landmarks in the scleral canal and the anterior laminar surface (ALS). (b) The node sets were defined in the scleral canal at the anterior laminar insertion (ALI), posterior laminar insertion (PLI), and ALS, as well as (c) the posterior scleral canal opening (PSC.

Fig. 3.

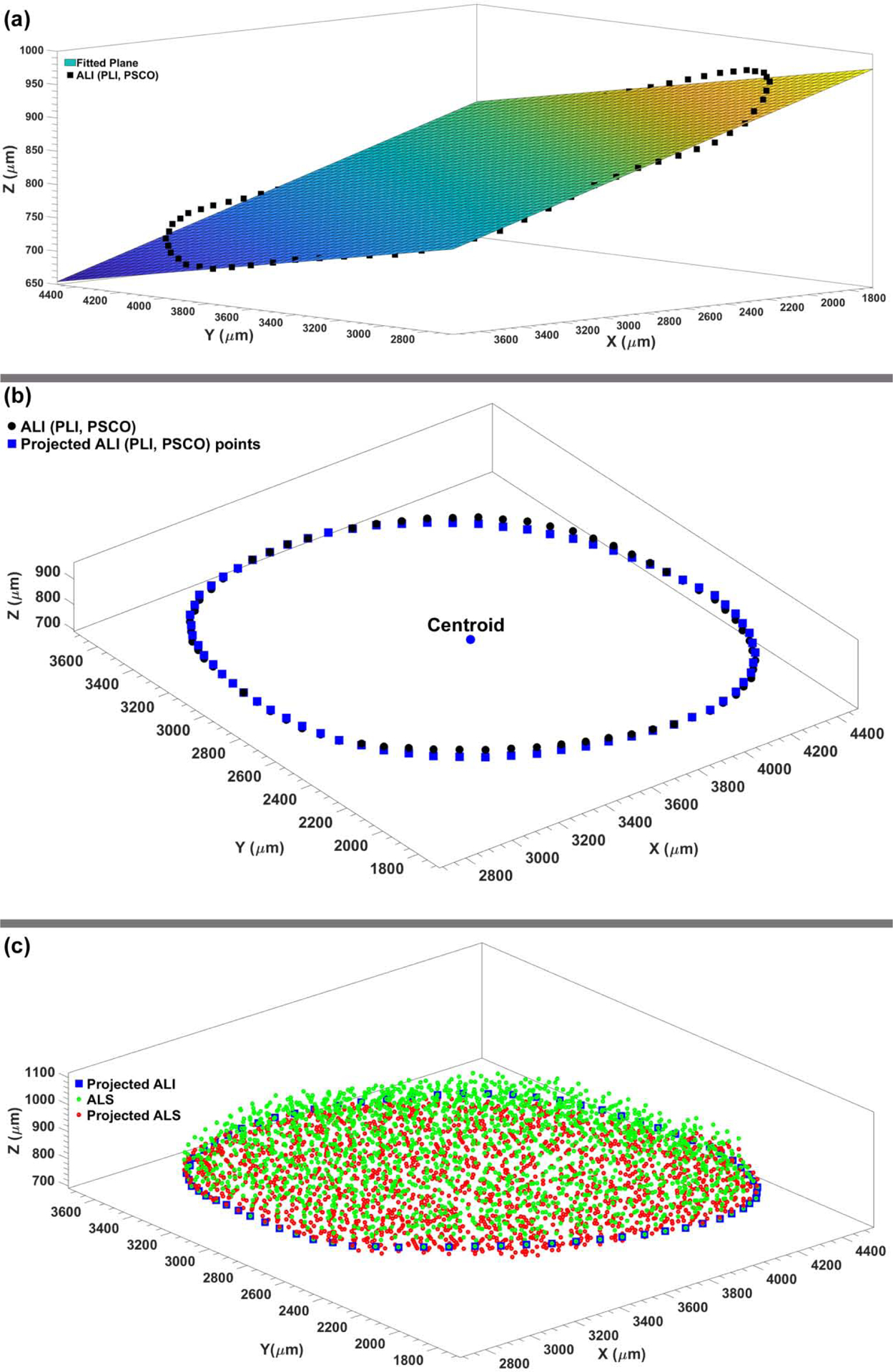
The (a) best-fit plane to the ALI (PLI, PSCO) node sets. (b) The ALI (PLI, PSCO) nodes were projected onto the best-fit plane to calculate the average radial displacement of the scleral canal at the ALI (PLI, PSCO). (c) The average perpendicular distance from the ALS nodes to the best fit plane through the ALI nodes was used to calculate the average depth of the ALS.

2.2. Material properties, boundary conditions, and loading

A mesh-free approach was employed to define the heterogeneous mechanical properties of the ocular connective tissues, as described in detail in our recent publication [51]. Briefly, we took advantage of the assumption that material parameters can be measured or approximated at discrete locations, which are arbitrary and independent of the FE mesh. This is reasonable given that material properties in biologic structures tend to change in a smooth manner within tissues, and change rapidly only at discrete tissue boundaries such as the transition between the LC and the adjacent sclera that are separate solids in the model. To solve a boundary value problem using FEM, knowledge of the material parameters is needed at the Gauss points of each FE. Alternatively, the material parameters can be approximated and stored at the nodal locations of the mesh. In the latter case, the standard shape functions can be used to interpolate the nodal values to obtain the material parameters at the Gauss points. We implemented our mesh-free approach into the open-source FEM package Calculix [52]. The 3D-reconstructed volume of the ONH has an isotropic voxel size of 1.50 μm, providing sufficient resolution to extract anisotropic features of the collagenous micro-structure of the LC, the fenestrated connective tissue structure in the ONH that supports the axons as they leave the eye. Our mesh-free approach allows us to approximate the local laminar connective tissue volume fraction, as well as the direction and strength of the predominant laminar beam orientation via a 3D fabric tensor at the Gauss points of the FE mesh. Using the mesh-free approach proposed herein decouples the material definition from the mesh definition and provides smooth transitions of connective tissue volume fraction and the fabric tensor across the elements of the LC as presented in Fig. 4. A spherical coordinate system was used to define the circumferential, meridional, and normal directions in the sclera. We defined characteristic material directions at convenient locations in the scleral model, namely the anterior and posterior scleral surfaces, which are defined by delineation within the 3D eye reconstruction. While the scleral canal geometry is complex, possessing a more elliptical than circular cross section, traversing the sclera at an oblique angle, and is generally much larger at the posterior scleral boundary compared to the anterior scleral boundary, the circumferential direction can be defined as the tangential direction at scleral canal wall. Similarly, the normal direction can be easily computed at the anterior and posterior scleral surfaces. Control points were seeded on the anterior and posterior scleral surfaces and we used the local surface geometries to calculate a normal orientation at each control point. The circumferential orientation was obtained at the scleral canal by fitting an ellipse to the anterior insertion points of the LC into the scleral canal wall. The tangential direction of this ellipse was projected to each control point on the sclera surface and used to define the circumferential orientation. The meridional direction was obtained from the orthonormality condition. To the best of our knowledge, our recent study [51] is the first to incorporate eye-specific ONH models with realistic nonlinear, anisotropic mechanical properties of the sclera, including the meridional or thickness-dependent width of circumferential fibers that were recently identified by Gogola et al. [53]. We used three layers of control points to define the region parameter across the peripapillary sclera as displayed in Fig. 4. One of the main advantages of using our mesh-free approach for the material definition is that it is independent of the definition of the FE mesh itself, so the same control points can be used for different mesh densities or element types. This makes the method very convenient when studying the effect of mesh density and element type on model results, or optimizing mesh densities in areas of large stress/strain gradients and/or material or geometric discontinuities. The material parameters of the eye-specific FE model are listed in Table 1.

Fig. 4.

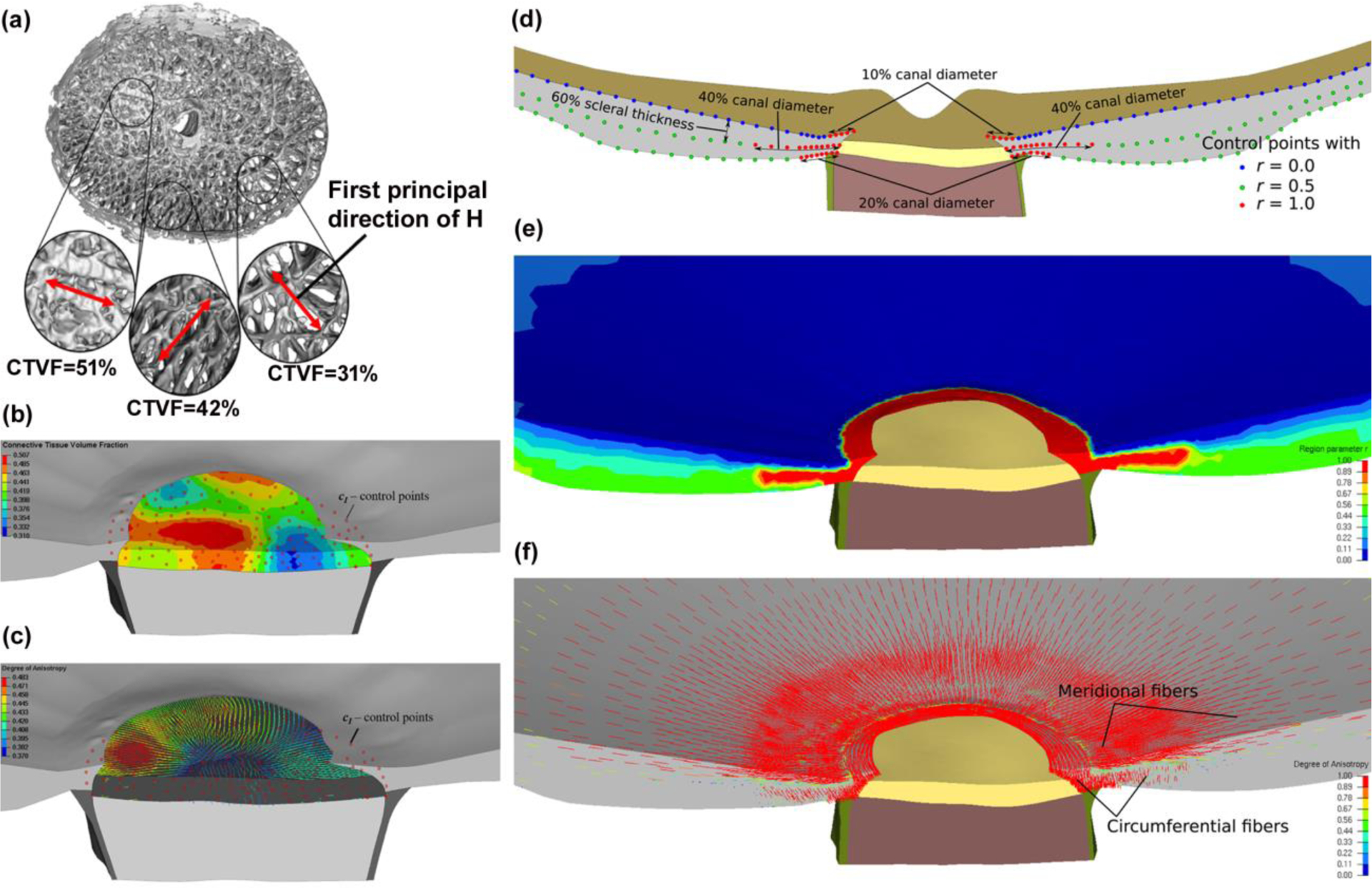
(a) A 3D, segmented LC reconstruction of a human eye, showing large variation in local connective tissue volume fraction (CTVF) and predominant laminar beam orientations; local CTVF and the fabric tensor were calculated from overlapping conical volumes with discrete center locations, which serve as control points for the mesh-free approach. (b) Contour plot of the CTVF in the FE model of the LC. Red dots represent the control points at which the micro-structure was evaluated. (c) First principal directions of the fabric tensor, where the color of the principal directions represents the local degree of anisotropy; The mesh-free approach leads to a smooth approximation of both the material parameter and the fabric tensor across the LC region; (d) Illustration of three layers of control points, with the region parameter, r = 0, 0.5, and 1 representing the meridional, isotropic, and circumferential region in the model, respectively. (e) Contour plot showing the distribution of the region parameter r across the sclera; (f) The first principal direction of the structure tensor representing predominant fiber orientations in the sclera; the mesh-free approach effectively approximated the circumferential and meridional fiber regions. Adapted from Grytz, et al. with permission [51].

Table 1.

The material parameters of the eye-specific FE model. The scleral properties were estimated based on the age (68 years) and ethnicity (European decent) of the donor [78]. The bulk modulus was set to κ=100μ for all tissues.

Tissue	Shear modulus (μ) in MPa	Elastic modulus of collagen fibers (Efib) in MPa	Crimp angle of collagen fibers (θ0)	Crimp parameter (R0/r0)
Retina	0.005	-	-	-
Sclera	0.215	99.83	5.35	4.54
Lamina cribrosa	0.185	20.94	5.35	4.54
Pia	0.215	99.83	5.35	4.54
Optic nerve	0.005	-	-	-

Regarding the applied boundary conditions, the nodes of the sclera and retina along the cut face of the globe at the equator were selected and assigned to the anti-symmetry about a plane with Z = constant (U_x=U_y=UR_z=0) condition. The inner surface of the retina was also selected to apply the pre-stressing load of 10 mmHg with no deformation [54] following by an IOP elevation to 45 mmHg. The contact was not defined between the tissue components, as our fully automatic meshing program could map the surface of the components onto each other and maintain the connectivity of the nodes at the components’ interfaces. A 40-core Intel® Xeon® CPU E7–4870@2.40 GHz computer with 512GB RAM was used to run the simulations in the open-source FE package Calculix. The simulations were conducted in two steps: pre-stressing from 0 to 10 mmHg IOP with no deformation (1 sec) and then IOP elevation from 10 mmHg to 45 mmHg (1 sec) with time steps of 0.10 sec (20 time steps).

2.3. Element types and meshing

Hexahedral elements have been shown to perform well for bending loads. Hexahedral elements also do well for nearly incompressible materials, which make them highly reliable and accurate for biomechanical simulations, particularly in ocular tissues that have these features [55]. The idea of establishing a hexahedral element by subdividing a parent tetrahedral element was proposed years ago but it has never been developed, coded, and used to create robust hexahedral meshes [56]. The advantage of this method would be substantial when a mesh with a higher number of degrees-of-freedom (DOF) is needed [57].

The meshing program was developed in Matlab (Mathworks, Natick, Massachusetts, US). The surface mesh that was produced by the reconstruction algorithm for our eye-specific model was first re-meshed to generate a coarser mesh at the anterior areas of the retina and sclera, and a denser mesh in the posterior portion of the eye model where the peripapillary sclera, scleral flange, optic nerve, LC, and pia are located (Fig. 1). This helped minimize simulation time by distributing a denser mesh at the locations where more accurate estimates of stresses and strains were needed. The volume tetrahedral mesh, composed of either 4-noded or 10-noded elements, was generated using our program, included as Supplementary Material. The connectivity of the elements across tissue/geometric boundaries was maintained at their nodal interfaces using an automated mapping algorithm, which allowed us to avoid defining contacts between the model components, minimizing simulation time. Each tetrahedral element was then decomposed into four unstructured hexahedral elements as presented in Fig. 5 and both 8-noded and 20R-noded hexahedral mesh files were generated. The original tetrahedral elements were also decomposed into four tetrahedral elements each (Fig. 5) to keep the number of elements the same as the hexahedral mesh for comparative simulations. Consequently, the number of active DOF is exactly the same as this is necessary to make a meaningful comparison [58]. Briefly, the proposed algorithm is composed of four main steps, including a) data-gathering, b) defining new nodes, c) splitting, and d) merging the duplicate nodes. The data-gathering step extracts mesh information from the mesh surface file, namely stereolithography (STL) surface definitions; it is assumed that the original tetrahedral mesh adequately captures the necessary geometric features. The step of defining new nodes adds extra nodes on each mid-edge, mid-face, as well as an interior node at the center of tetrahedron to create new elements by a specific division of each parent tetrahedral element. The splitting step transforms each tetrahedral element into four hexahedral elements by choosing the proper sequence of nodes. The merging step removes the duplicate nodes produced in the process of adding new nodes for neighbor elements. The meshing algorithm uses input and output files that are based on the Abaqus *.inp ASCII file format. The meshing algorithm, programmed in Matlab, including the original triangle surface-mesh file reader (STL), parent tet volume mesh generator, and the child hex mesh generator, is attached in the supplementary material section. It has been shown that reduced-integration elements result in more accurate results than the corresponding fully-integrated elements. However, fully integrated 8-noded hexahedral elements may exhibit better mechanical performance under high shear and bending loads due to a single Gauss point at the center of the element. As a result, both the 8-noded fully integrated and 8R-noded reduced integration hexahedral elements were employed and compared in this study. It should be noted that reduced integration uses a lesser number of Gaussian coordinates when solving the integral, which is why it is advisable to use reduced integration instead of full integration for 20-noded hexahedral elements in nonlinear problems, such as plasticity, creep or incompressible materials [59].

Fig. 5.

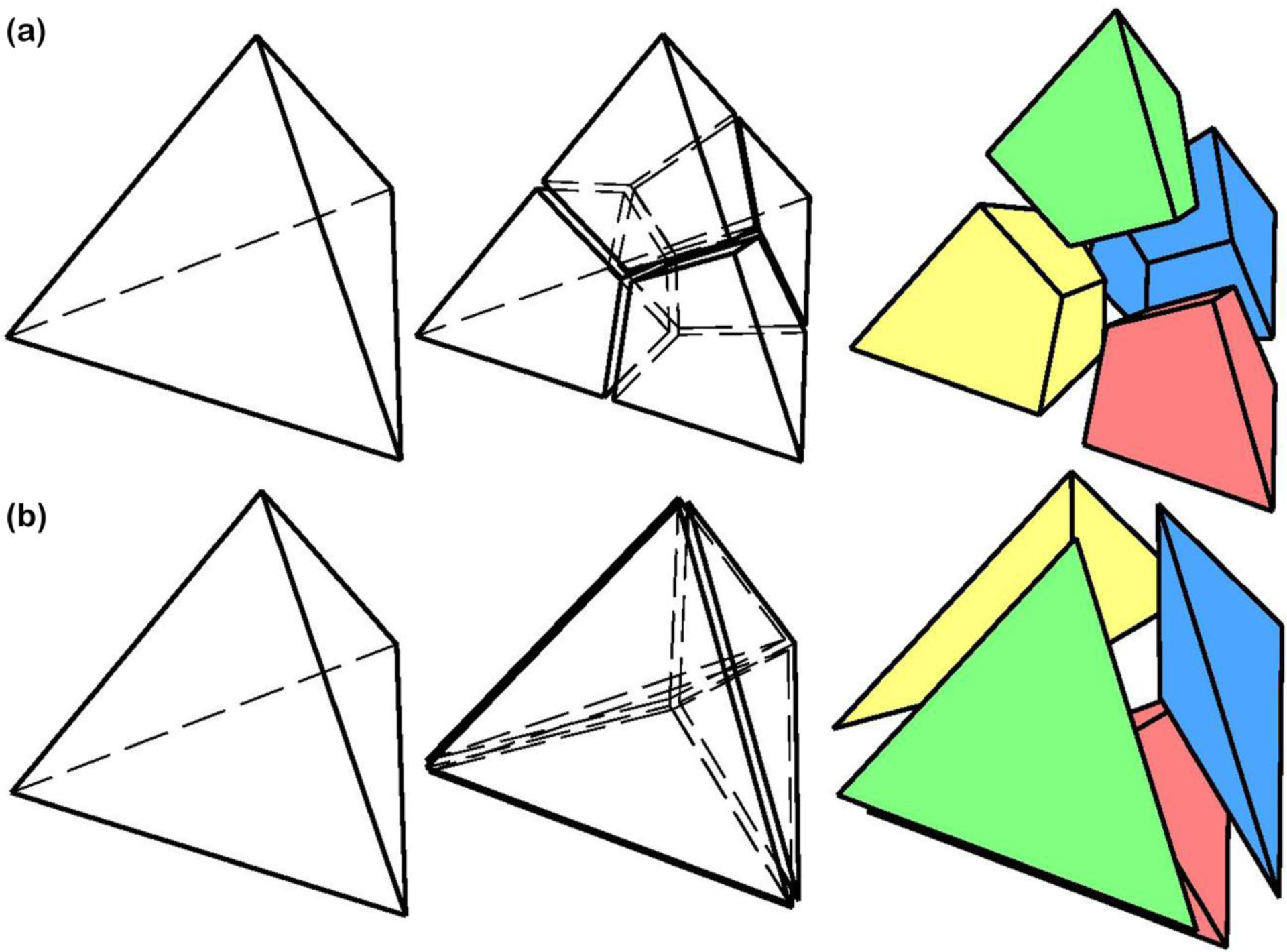
A 4-noded tetrahedral element was breakdown into (a) four 8-noded hexahedral and (b) four 4-noded tetrahedral elements.

3. Results

3.1. Element quality assessment

Element quality assessment is a critical step in verifying the mesh prior to simulation. However, this step is rather complicated because the quality is relative and the solution, by definition, is approximate. In this study, mesh quality assessment was conducted on all tet and hex element meshes using Ansys 2020R1 (Ansys, Inc, Canonsburg, PA, US) and the contours for the sclera and pia, which have the most complex geometries in our eye model, were computed and presented as an example.

The element quality assessment provides a composite quality metric that ranges between 0 and 1 and is based on the ratio of the volume to the sum of the square root of the cube of the sum of the square of the edge lengths for 3D elements. A value of 1 shows a perfect element while a value of 0 indicates that the element has a zero or negative volume [60].

This can also be expressed as follows:

$$\mathit{\text{Quality}}=C\left[\frac{\mathit{\text{volume}}}{\sqrt{{\left[\sum {\left(\mathit{\text{Edge}}\mathit{\text{length}}\right)}^2\right]}^3}}\right]$$ (1)

The parameter C is element type-specific and has been calculated for tet (C_tet = 12.7) and hex elements (C_hex = 41.6). The contours of the element quality index for the sclera and pia meshes of different element types are demonstrated in Fig. 6. The results revealed that all the generated meshes have an element quality > 0.04 implying that even the most complicated biomechanical geometries in the model (sclera and pia) exhibit the quality of the mesh is sufficient to run a reliable simulation. The lowest quality ratio of 0.04 was observed at Bruch’s membrane opening (BMO) of the sclera, which has a very complex structure with a thin tissue of various thicknesses coming to a sharp edge.

Fig. 6.

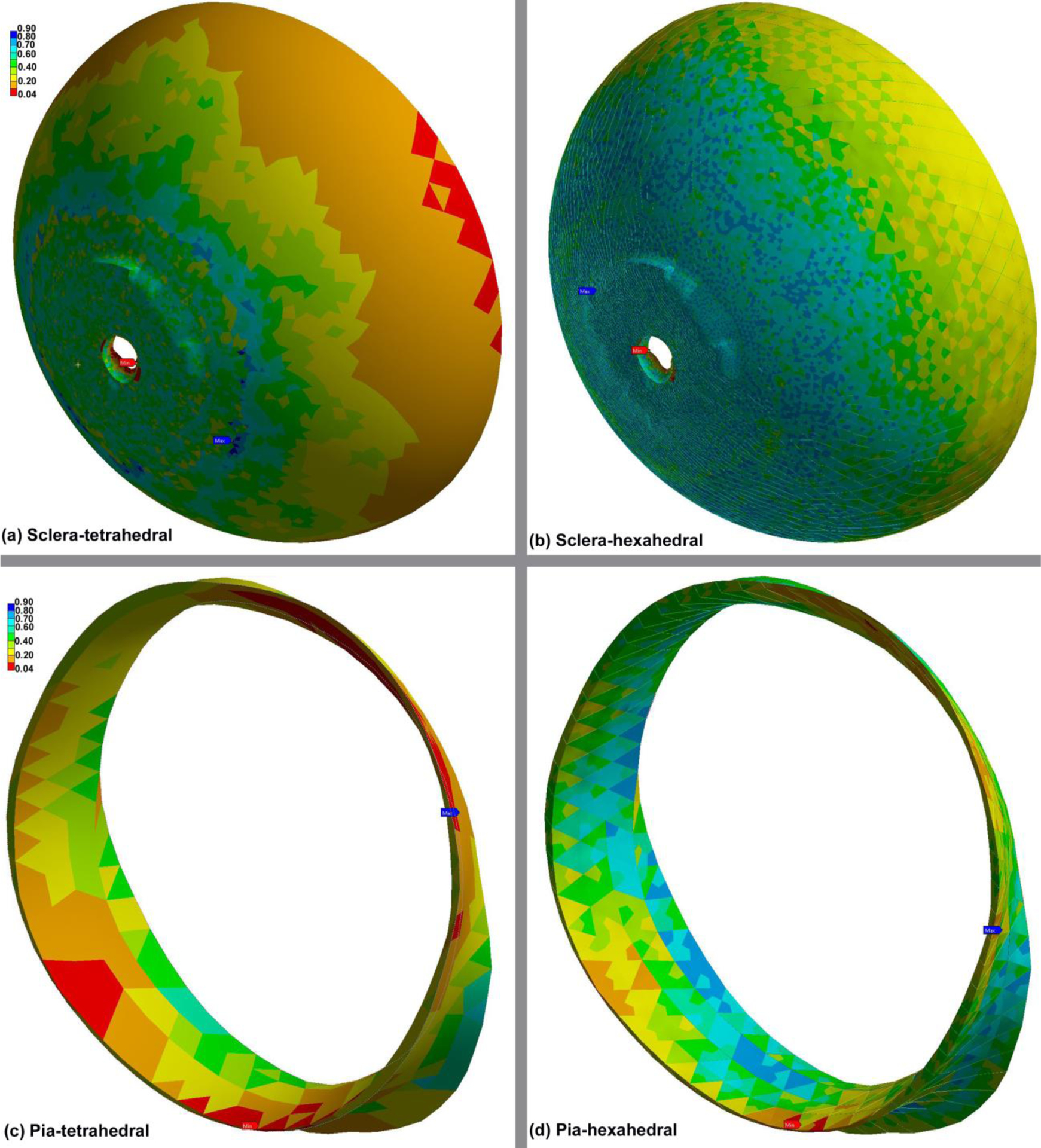
Contour plots of the element quality index computed by Ansys in the (a) scleratetrahedral, (b) sclera-hexahedral, (c) pia-tetrahedral, and (d) pia-hexahedral. A value of 1 indicates a perfect element while a value of 0 indicates that the element has a zero or negative volume.

Other mesh-quality metrics, such as the Jacobian ratio, skewness, and aspect ratio were also calculated for the all components of the eye model: the retina, sclera, pia, optic nerve, and LC. The Jacobian ratio is a measurement of the shape of a given element compared to that of an ideal element. If an element has a poor Jacobian ratio, the element may not map well from element space to real space, thereby making computations based on the element shape less reliable. The Jacobian value ranges from −1.0 to 1.0, where 1.0 represents a perfectly shaped element; the ideal shape depends on the element type. The check is performed by mapping an ideal element in parametric coordinates onto the actual element defined in global coordinates. Here, we calculated the Jacobian ratio at each of the element’s integration points, namely Gauss points, and reported the ratio. As the element becomes more distorted, the Jacobian value approaches zero. A Jacobian value of less than zero represents a concave element, which most analysis codes do not allow. Here, the unstructured hex elements generated by our algorithm exhibited an average Jacobian ratio of > 0.3. Skewness is another quality metric for meshes that quantifies how close a face or cell is to ideal (i.e., equilateral or equiangular). According to the Ansys mesh-quality criteria, the skewness value of 1, 0.75–0.90, 0.50–0.75, 0.25–0.50, 0–0.25, and 0 represent degenerate, poor, fair, good, excellent, and equilateral, respectively. The unstructured hex element mesh generated by our algorithm yielded elements in the fair to excellent range for skewness, again sufficient for reliable simulations. The aspect ratio is a measure of the stretching of a cell, computed as the ratio of the maximum value to the minimum value of either the distances between the cell centroid and face centroids, or the distances between the cell centroid and its nodes. Detailed information on the number of elements/nodes, element length, aspect ratio, skewness, and simulation time for the models using different element types are summarized in Table 2.

Table 2.

The number of elements/nodes, element length, aspect ratio, skewness, and simulation time for various element types.

Element type	Number of elements	Number of nodes	Element length (μm) Min/Max	Aspect ratio	Skewness	Simulation time (hr)
4-noded tetrahedral	363,384	108,867	102.98/264.87	1.677	0.213	0.2520
	371,992	113,690	48.02/172.21	1.883	0.469	0.2630
	485,956	147,900	48.80/161.59	1.845	0.421	0.3419
	506,324	153,875	47.52/151.59	1.569	0.388	0.3536
10-noded tetrahedral	363,384	584,626	102.98/264.87	1.677	0.213	1.7075
	371,992	609,506	48.02/172.21	1.883	0.469	1.9730
	485,956	793,784	48.80/161.59	1.845	0.421	2.2300
	506,324	826,176	53.52/151.59	1.569	0.388	2.4280
8-noded hexahedral	363,384	422,259	24.13/159.12	2.725	0.395	2.1480
	371,992	433,645	25.90/146.64	2.84	0.409	1.9320
	485,956	562,835	25.67/122.22	2.93	0.419	3.0738
	506,324	585,117	21.68/108.25	2.658	0.482	4.6330
8R-noded hexahedral	363,384	422,259	24.13/159.12	2.725	0.395	2.3247
	371,992	433,645	25.90/166.64	2.84	0.409	2.4716
	485,956	562,835	25.67/122.22	2.93	0.419	3.2630
	506,324	585,117	21.68/108.25	2.658	0.482	3.5990
20R-noded hexahedral	363,384	1,599,605	24.13/159.12	2.725	0.395	19.8490
	371,992	1,641,678	25.90/166.64	2.84	0.409	22.0352
	485,956	2,133,368	25.67/122.22	2.93	0.419	32.5591
	506,324	2,219,190	21.68/108.25	2.658	0.482	36.2233

3.2. Computational results

Since the computational cost and accuracy of results from FE simulations depend on the mesh size, mesh density was increased in steps to determine an adequate element count for each element type that provided consistent model simulations (a convergence test). The eye-specific models, therefore, were meshed using our algorithm at four different densities from very coarse to very fine, taking special care to keep the geometry of the models consistent, particularly at the vertices and edges. To evaluate the effects of the mesh density on different element types, the models were simulated and the results compared in terms of the average radial displacement of the scleral canal at the ALI, PLI, and PSCO, average depth in the ALS, volumetric average 1^st principal strain in the LC, and maximum von Mises stress in the LC as shown in Fig. 7. The average radial displacement in the PSCO was of 4.1, 3.7, and 4.3 μm on average for the 10-noded tetrahedral, 8-noded and 20R-noded hexahedral element types, respectively. The 10-noded tetrahedral and 20R-noded hexahedral elements showed the same trend in terms of the average radial displacement of the scleral canal at the ALI, PLI, and PSCO, average depth in the ALS, volumetric average 1^st principal strain, and maximum von Mises stress. The 4-noded tetrahedral and 8R-noded hexahedral elements showed the same pattern of volumetric average 1^st principal strain and maximum von Mises stress while the 4-noded tetrahedral element was behaved randomly at different number of elements when it comes to the average radial displacement of the scleral canal at the ALI, PLI, PSCO and average depth in the ALS. The fully integration 8-noded hexahedral element showed the same pattern as 10-noded tetrahedral and 20R-noded hexahedral of average radial displacement in the ALI while some differences were observed in the average radial displacement in the PLI, PSCO, average depth in the ALS, volumetric average 1^st principal strain, and maximum von Mises stress.

Fig. 7.

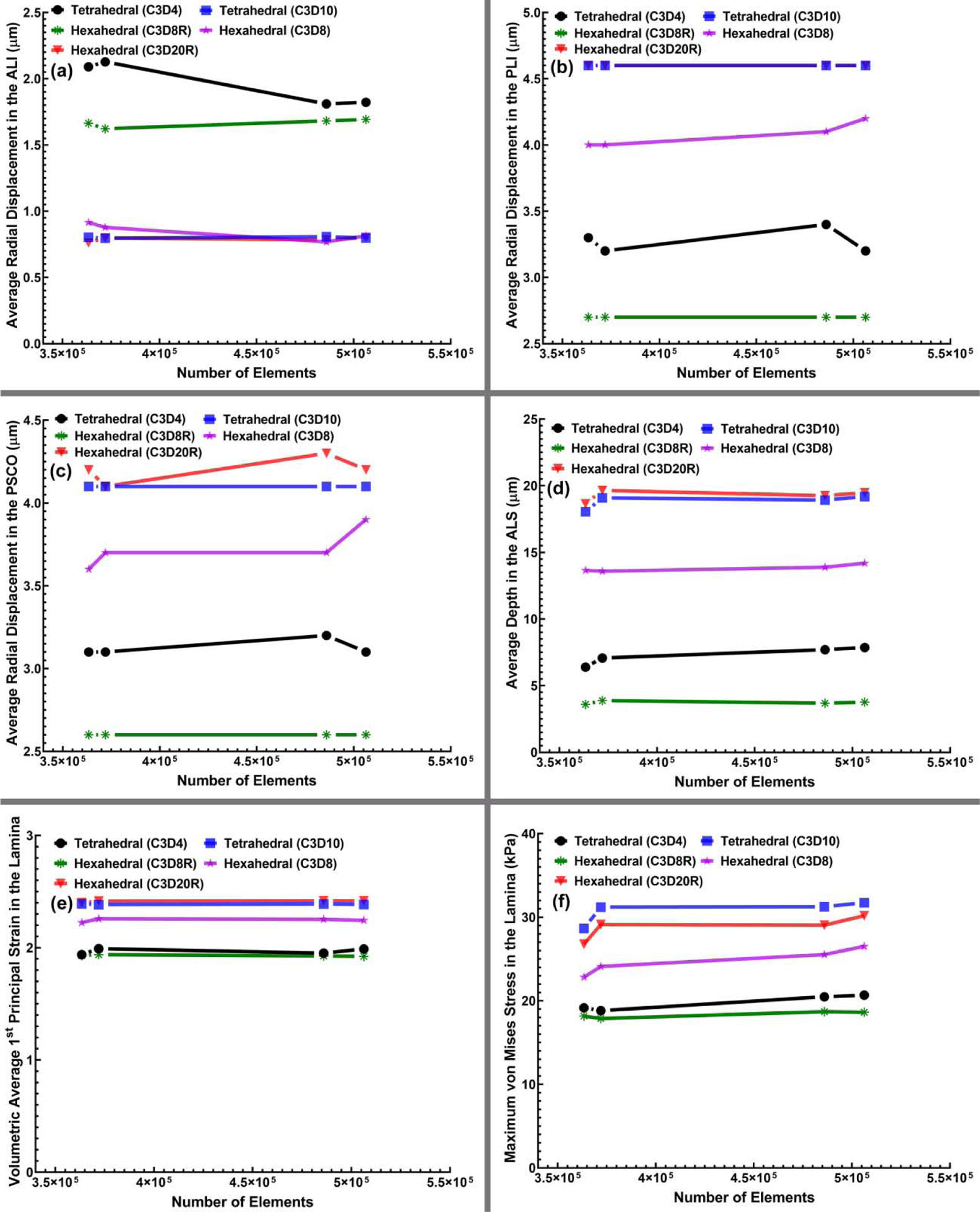
The (a) average radial displacement of the scleral canal at the ALI, (b) PLI, (c) PSCO, (d) average depth in the ALS, (e) volumetric average 1^st principal strain in LC, and (f) maximum von Mises stress in LC versus the number of elements for all four mesh densities and different element types, including 4-noded and 10-noded tetrahedra, as well as 8-noded/8R-noded and 20R-noded hexahedra.

A convergence test with an error tolerance of <5% compared to a denser mesh showed that 485,956 elements was as accurate as denser meshes and was therefore selected as a suitable mesh size for further analyses. Unfortunately, the complex geometries of the eye cannot be meshed too coarsely without severely distorting the geometry, thereby rendering a mesh convergence test unreliable, so we were forced to begin the test with a sufficient number of elements to accurately represent the geometry itself. Figure 7 shows that the target displacements of relevant node sets, as well as volumetric stresses and strains, change less than ~ 5% in models with 363,384 elements compared to those with 506,324 elements. Hence, all the meshes were effectively converged at the lowest element count that we could use to reliably represent the model geometry. We used 485,956 elements for all the final model runs for which data are represented. The maximum von Mises stress, as well as the 1^st, 2^nd, and 3^rd principal strain contour maps for the eye-specific models having 485,956 elements from the superior-inferior and nasal-inferior cutting views were computed as shown in Figs. 8 and 9, respectively. The results showed the same pattern of stresses and strains when using 10-noded tetrahedral and 20R-noded hexahedral element types, while 4-noded tetrahedral element showed the stiffest mechanical response at the lower magnitudes of stress.

Fig. 8.

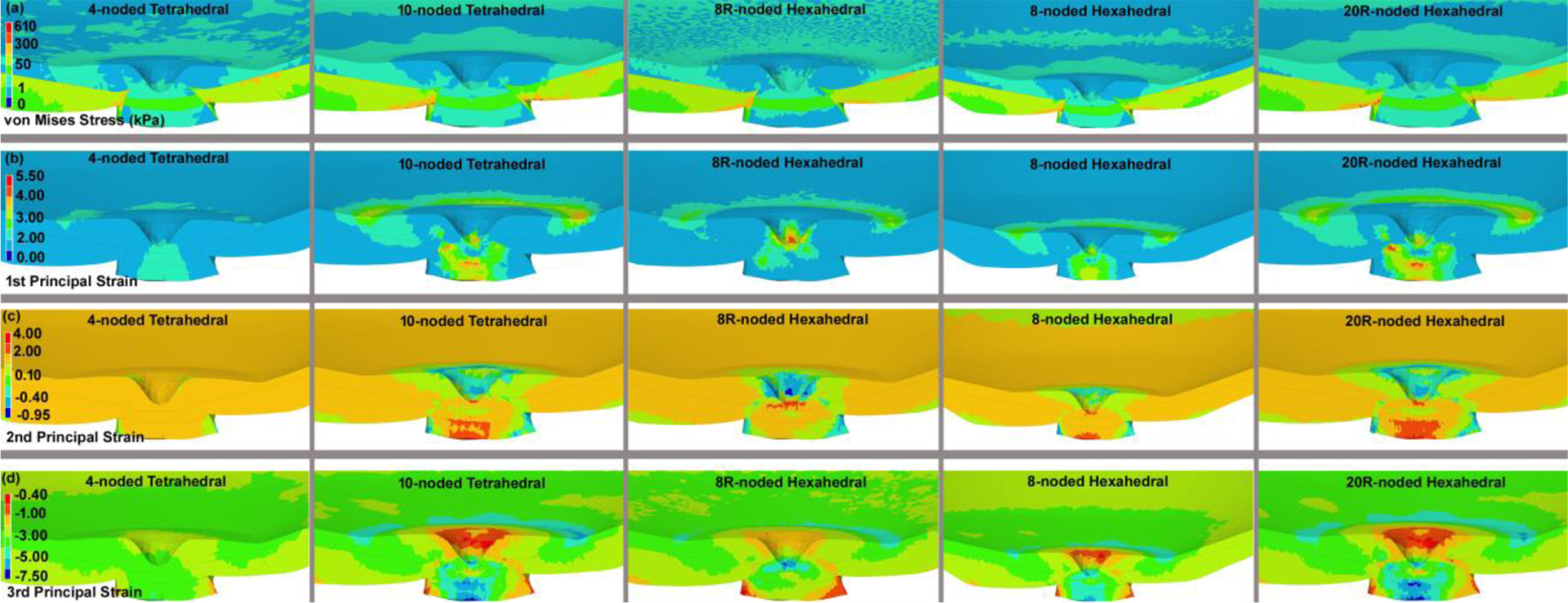
The contours of the (a) maximum von Mises stress, (b) maximum 1^st, (c) 2^nd, and (d) 3^rd principal strain through the superior-nasal section at the posterior side of the eye globe for different element types, including 4-noded and 10-noded tetrahedra, as well as 8-noded/8R-noded and 20R-noded hexahedra. The results here are presented based on the eye model meshed with 485,956 elements.

Fig. 9.

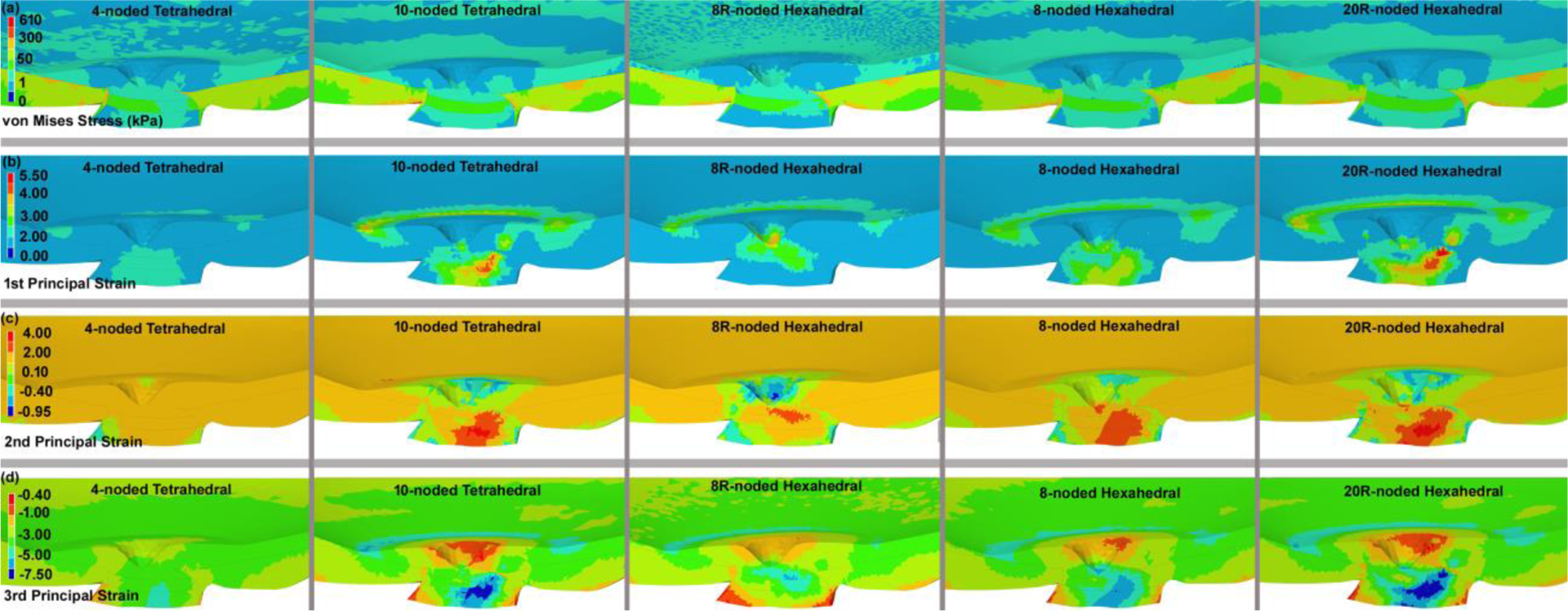
The contours of the (a) maximum von Mises stress, (b) maximum 1^st, (c) 2^nd, and (d) 3^rd principal strain through the nasal-inferior section at the posterior of the eye globe for different element types, including 4-noded and 10-noded tetrahedra, as well as 8-noded/8R-noded and 20R-noded hexahedra. The results here are presented based on the eye model meshed with 485,956 elements.

The volumetric average von Mises stresses and 1^st, 2^nd, and 3^rd principal strains in the LC and peripapillary sclera for the 4-noded and 10-noded tetrahedral and 8-noded and 20R-noded hexahedral element types were calculated and plotted in Figs. 10 and 11, respectively. As in the contour plots of the peripapillary sclera, the volume average von Mises stress showed similar results in the quadratic hex and tet element models (Figure 10), but the linear hex and tet models yielded lower stresses. Volume average strains in the peripapillary sclera were generally similar between all element types, although the linear 4-noded tets exhibited larger strains in the 2^nd and 3^rd principal components. In the lamina, the results were much clearer, in that the quadratic 20-noded hex and 10-noded tet models were nearly identical, while both stress and strain were lower with all the linear element types.

Fig. 10.

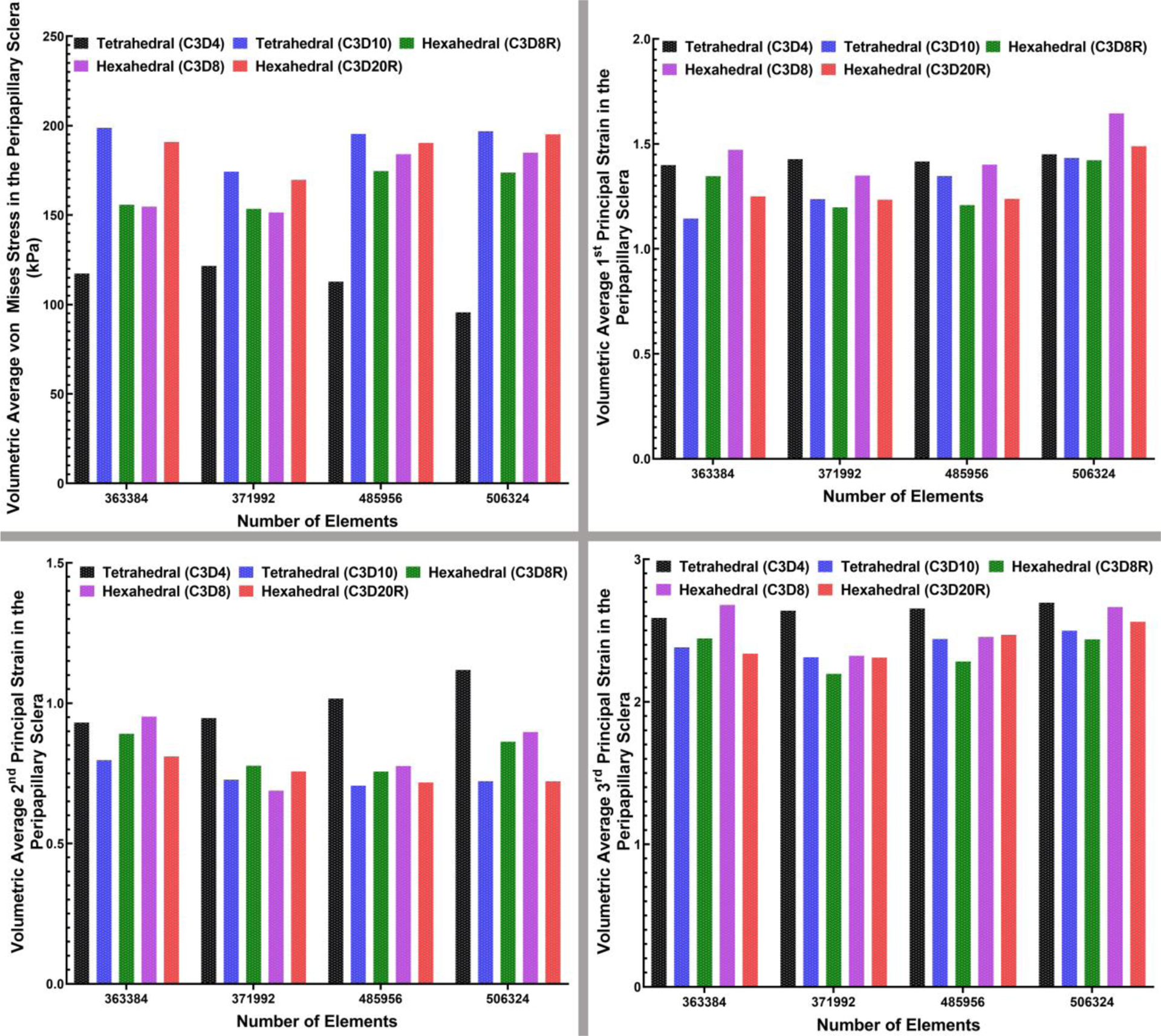
The bar-plot representation of the (a) volumetric average maximum von Mises stress, (b) volumetric average 1^st, (c) 2^nd, and (d) 3^rd principal strain in the peripapillary sclera for all four mesh densities and two different element types, including 4-noded and 10-noded tetrahedra, as well as 8-noded/8R-noded and 20R-noded hexahedra.

Fig. 11.

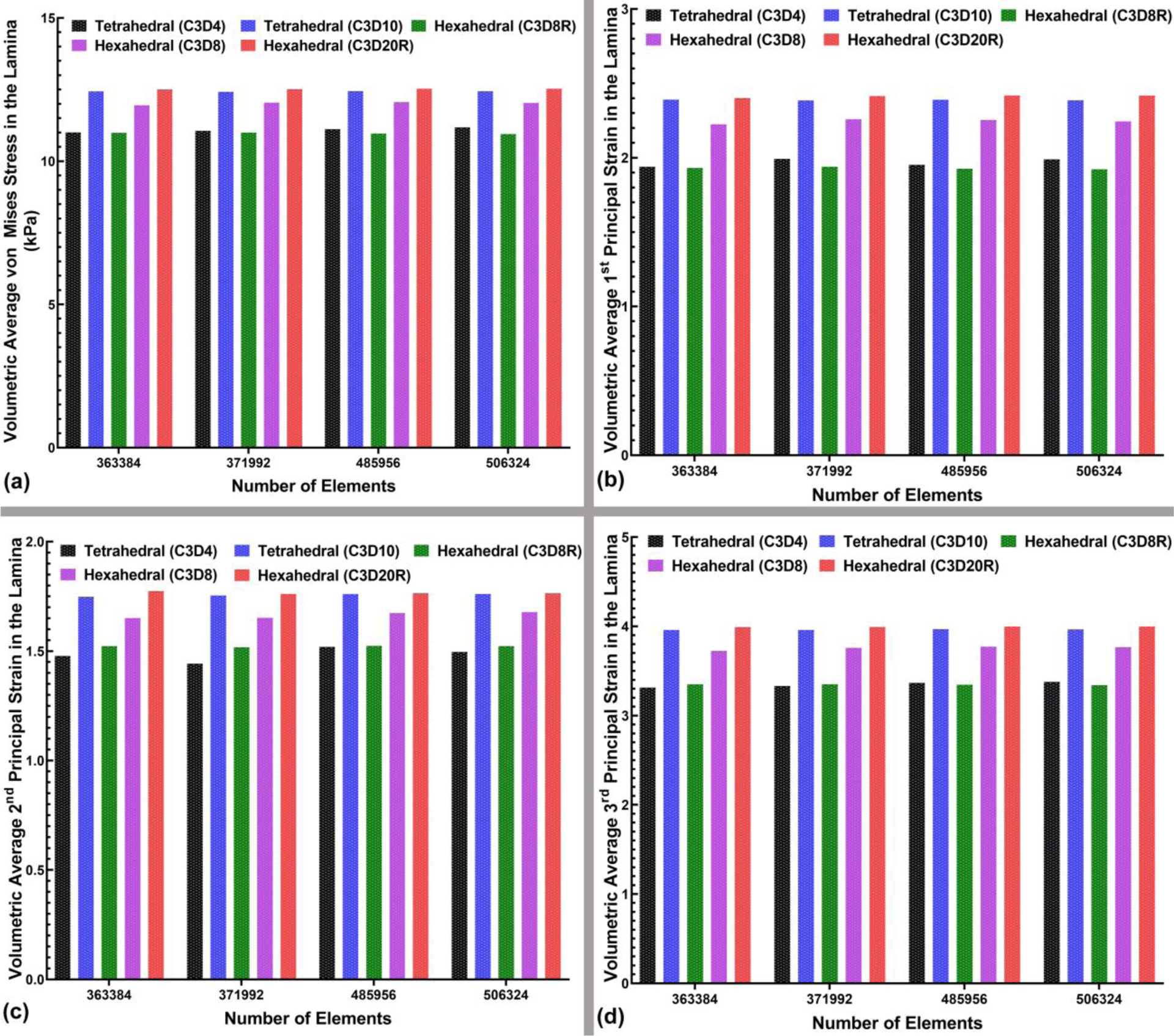
The bar-plot representation of the (a) volumetric average von Mises stress, (b) volumetric average 1^st, (c) 2^nd, and (d) 3^rd principal strain in the LC for all four mesh densities and different element types, including 4-noded and 10-noded tetrahedra, as well as 8-noded/8R-noded and 20R-noded hexahedra.

4. Discussion

Pure hexahedral or hex-dominant meshes are generally preferred over tetrahedral meshes in certain applications and situations because tet meshes normally require 4–10 times more elements than a hexahedral mesh with a similar number of DOF to attain the same level of accuracy [61]. In addition, in some forms of FE simulations, such as those with large-deformations with linear elements, tetrahedral elements have been shown to be mathematically ‘stiffer’ because of its reduced number of DOF; this phenomenon is known as ‘tet-locking’ [62]. Prior work has shown that quadratic hexahedral elements are the most reliable and accurate element type in FE modeling [62–65], so quadratic hexahedral elements were used as the reference element type in this study, with the results from other element types assessed in comparison. Quadratic hexahedral elements are very robust and reliable [66–69], and 20-noded hexahedral elements are particularly suitable for incompressible materials under the bending loads typical of intraocular pressure loading of the optic nerve head of the eye [62]. Hex meshes also have the advantage that they can be repeatedly subdivided anisotropically without deteriorating the element quality [41]. Here, an automatic meshing algorithm that generates unstructured linear and quadratic hexahedral meshes directly from a parent tetrahedral mesh was used to create the meshes with different element types, ensuring that both the geometry and number of elements of each mesh was identical.

Ocular and ONH biomechanics is one of the most active areas of glaucoma research [70]. Various computational stress/strain analyses have been performed, but there is a paucity of knowledge on the accuracy of the simulation results due to the different meshing approaches that have been used. It has been shown that element type plays a significant role in the stress and strain results from biomechanical simulations [11], and thus it is important to devise a set of comparative numerical simulations to elucidate the effects of element type on the FE results from eye models. To accomplish that, an eye-specific model was constructed (Fig. 1) having different node sets (Figs. 2 & 3) based on the high-resolution 3D reconstruction of a donor eye from a 68-year-old patient of European descent without known eye disease and our complex material model was assigned to that (Fig. 4). Thereafter, the model was meshed at four different densities using 4-noded and 10-noded tetrahedral elements and 8-noded/8R-noded and 20R-noded hexahedral elements (Fig. 5). The mesh quality assessment was also carried out to reflect the reliability of our proposed meshing algorithm (Fig. 6). The models were subjected to pre-stressing of 10 mmHg followed by an IOP elevation to 45 mmHg. The FE results were then analyzed to verify the convergence of the mesh according to the number of elements.

Analysis of the average radial displacement of the scleral canal at the ALI, PLI, PSCO, average depth in the ALS, volumetric average strain, and von Mises stress in the LC and sclera revealed that 485,956 4-noded tetrahedral, 10-noded tetrahedral, and 8-noded/8R-noded/20R-noded hexahedral elements resulted in <5% difference in these parameters compared to a denser mesh of 506,324, and therefore this mesh was considered converged and all final results used this mesh density (Fig. 7). It should be noted that linear elements, such as 4-noded tetrahedra and 8-noded hexahedra (fully-integrated), capture bending with shear-like distortion in the element, and generally these elements tend to be stiffer in bending. This can be overcome with reduced-integration elements, but at the expense of an hourglass effect. The 8R-noded hexahedral element is a linear brick element with one integration point, while the shape functions are the same as for the 8-noded hexahedral element. The main advantage of using reduced-integration is that the locking phenomena observed in the 8-noded hexahedral element is not as pronounced. However, the reduced integration element displays other weaknesses, such as it tends to be too compliant in bending. Thus, small elements are required to accurately simulate stress concentrations at the boundary of a structure [71], which are common in eye models. The stresses and strains are most accurate in the integration points and the integration point of the 8R-noded hexahedral element is located in the middle of the element. Hence, low numbers of Gauss points result in a checkerboard-like deformation map, which might be misleading, and as a result, stress and strain values might converge even with a stiff mesh although local accuracy is not guaranteed [71]. In practice, the 8R-noded hexahedral element is not very useful without hourglass control, which was not used in this study, and hence the deformation pattern of the 8R-noded hexahedral elements tended to be out of range of the results from the other element types [62].

Unlike the other element types, results with 4-noded tetrahedral elements did not exhibit typical convergence results for the average radial displacement of the scleral canal at the ALI, PLI, and PSCO (Fig. 7). Generally, 4-noded tetrahedral elements exhibit inaccurate displacement predictions compared to analytical results for a beam under bending or torsion loadings due to shear locking, leading to an unsuitable displacement pattern [66, 72, 73]. Prior comparisons of analytical solutions to linear static bending simulations using linear tetrahedral elements also revealed errors between 10 to 70 percent in both displacement and stress calculations, particularly when using a nearly incompressible material (~0.49) [62, 74]. However, the stiffness matrix eigenvalues for linear tetrahedral elements are generally larger than those for linear hexahedral elements, which is why the linear hexahedra can generally deform in a lower strain energy state, making them more accurate than linear tetrahedrons in most situations [74].

The contours of the stresses and strains at the converged mesh size (485,956) were then computed and compared (Figs. 8 & 9). The results for the remainder of the mesh densities were also calculated for all element types as illustrated in Figs. 10 & 11. Our numerical results showed the volumetric average von Mises stresses of 126.3, 93.7, 100.4, 90, and 89.9 kPa for the scleral shell when using 4-noded and 10-noded tetrahedral elements, and 8R-noded, 8-noded, and 20R-noded hexahedral elements, respectively. Our results are in good agreement with Bellezza et al., [10] which showed that IOP-generated stress would be 10–17 times IOP (here 59.99–101.83 kPa) within the tissues of the scleral shell at points distant from the ONH although the linear tet model results were outside this range for reasons discussed above. When it comes to the peripapillary sclera, the volumetric average von Mises stresses were 112.5, 180.3, 163.4, 172.5, and 179.7 kPa when using 4-noded and 10-noded tetrahedral elements, and 8R-noded, 8-noded, and 20R-noded hexahedral elements, respectively, which is in agreement with 30 times IOP (179.70 kPa) [10]. At the scleral flange, the volumetric average stresses within 30–100 times IOP [10] (180–599 kPa) were observed and here we found the values of 272.5, 249, 293.2, 261.5, and 254.2 kPa for the 4-noded and 10-noded tetrahedral elements, and 8R-noded, 8-noded, and 20R-noded hexahedral elements, respectively. While the reported stresses in all our test cases were generally in the range of the reported stresses by Bellezza et al., [10]), it is well-documented [39] that 4-noded tetrahedral elements tend to be overly stiff, performing poorly in structural applications. The linear tet models were by far the stiffest in our simulations, so results presented herein are consistent with this notion. Noisy contours with locally elevated peak stresses were evident with linear tetrahedral and hexahedral elements compared to the smooth and uniform distributions predicted by quadratic tetrahedral and hexahedral elements [67]. This has also been confirmed when simulating ONH biomechanics, as 10-noded tetrahedral elements produced more accurate solutions than 4-noded tetrahedral elements [23, 24]. Under applied IOP, the LC and/or peripapillary sclera bows posteriorly in most eyes, which demonstrates the importance of using an element that performs well under bending load. In prior studies, hexahedral elements often showed better performance under the bending load, while tetrahedral elements tend to perform poorly under bending conditions [75]. However, our results showed that both 10-noded tetrahedral elements and 20R-noded hexahedral element perform equally well under applied IOP in eye models. This has also been tested in prior studies, as Cifuentes, et al. [39] compared the performance of linear and quadratic tetrahedral and hexahedral elements in various structures under bending, shear, torsion, and axial loadings; they found no significant advantage for the quadratic hexahedral elements over quadratic tetrahedral elements in terms of either accuracy or CPU time. Another group, however, found linear hexahedral meshes are superior to linear tetrahedral meshes [62].

In medical applications, convergence tests with 8- and 20-noded hexahedral and 4- and 10-noded tetrahedral elements were analyzed by comparing the von Mises stresses and principal strains at a selected point of the femur [44]. Results showed that linear tetrahedral elements produced results that more closely matched theoretical solutions, but quadratic hexahedral elements seem to be more stable and less influenced by the degree of mesh refinement. We also observed that in our study (Fig. 7). In a kidney model [76], results showed that both linear and quadratic tetrahedral meshes are slightly stiffer than hexahedral meshes, but are more stable when high impact energies are present in the simulation. For heart mechanics and electrophysiology [74], quadratic hexahedral elements perform slightly better than quadratic tetrahedral elements in the mechanical regime, while linear tetrahedral meshes are the best choice for the electrophysiology problem. When it comes to the fluid-structure interaction (FSI) simulations, hexahedral meshes showed an advantage, as they yield more accurate flow field solutions than their tetrahedral counterparts for the same number of edges [77]. It was also found that tetrahedral grids need roughly double the storage and CPU time than hexahedral tessellations of the same vertices because tetrahedral meshes have more edges. These additional edges, however, may not contribute to the accuracy of the simulation results. Simulation time is a critical factor in any FE study, and hence researchers devote substantial effort to adjust various parameters, such as contacts, mesh density and material properties to minimize the simulation cost. When it comes to our ocular biomechanics simulations, results showed a significantly higher simulation time for 20R-noded hexahedral elements compared to the same number of elements of different types (Table. 2). The highest and the lowest simulation times of ~ 36 hours and ~ 0.25 hour were related to the densest 20R-noded hexahedral and the coarsest 4-noded tetrahedral meshes, respectively. Considering the simulation time, and more importantly, the stress and strain results of 10-noded tetrahedral models compared to 20R-noded hexahedral models, it would be acceptable to use a quadratic tetrahedral element meshes for complex ocular biomechanics simulations to minimize simulation time.

In our study, mesh quality analysis was performed using a robust commercially available CAE software, Ansys 2020R1. Analyses results showed acceptable mesh-quality indices for tet and hex element types (Fig. 6). Our meshing algorithm is based on a parent tet-mesh, so it can quickly generate unstructured hex-meshes from an input file containing a triangular surface mesh of the geometry (STL). This is important, as there are many commercial packages available that can generate high-quality tet-meshes regardless of the complexity of the geometry. Furthermore, commercially available hex-meshing software is expensive, while our meshing algorithm is freely available and can be run in Matlab.

The study is limited by the following considerations. First, there is no experimentally validated gold standard we can use as a reference for the deformations, stresses and strains presented in the analysis. Experimental strain and displacement data are unavailable for the posterior eye due to the difficulty in directly measuring these quantities either in vivo or under controlled experimental conditions. Analytical solutions are out of reach due to the complexity of the geometry, tissue boundaries, and material properties. Thus, we must make some assumptions about the gold standard for comparison of the presented FE analyses. It is widely accepted in the FE literature that quadratic hexahedral elements are the most reliable, robust, and accurate element type compared to tetrahedral, prism, and pyramid elements. Hence, it is reasonable to assume that the quadratic hexahedron is the most accurate element type and use this element as the reference standard and basis of comparison for our study. Second, we used elemental decomposition to create the hexahedral meshes from a parent tetrahedral mesh, and so we could not precisely control and match the mesh quality metrics between the various models. However, all simulations converged with no errors on the initial attempt, and the Jacobians, Skewness, Aspect Ratios, and Ansys Quality metrics were within reasonable limits for all models. As noted, there are some differences in mesh quality between the various mesh types, but this cannot be avoided, and it is important to note that element geometries were identical in the linear and quadratic meshes of the same element type because only mid-side nodes were added. Finally, we generated all of our FE meshes from a single eye-specific geometry and parent tetrahedral mesh with fixed material properties, using elemental decomposition to change element types without altering the model geometry itself. Although this could be considered as a weakness, this approach allows us to isolate the differences in the results due to only element type, which is the focus of the study. In addition, the similarity in results from the quadratic tet and hex elements, in contrast to the other element types, reinforces the reliability of our findings.

5. Conclusions

This study analyzed the effects of element type on the stresses and strains predicted in a 3D human eye FE model. The models yielded similar results for the 10-noded tetrahedral and 20R-noded hexahedral element types, while 10-noded tetrahedral models had significantly lower computational cost and, thus, will be preferred for future eye simulations. Linear tetrahedral elements were the stiffest element type, having lower strains at higher stresses. We also proposed a simple meshing algorithm to automatically generate unstructured hex meshes based on a single parent tet mesh (Matlab code included as Supplementary Material). The robustness of the algorithm was verified by meshing and simulating an eye-specific 3D model of the human ONH with complex geometry and discrete part connectivity. Commercially-available hex-meshing packages are expensive, while our meshing algorithm is freely available and can be run in Matlab. The findings of this study improve our understanding of the effects of element choice on the resultant stresses and strains of computer simulations in ocular biomechanics.

Highlights.

• For complex eye models, 10-noded tetrahedral elements yield very similar results to 20-noded hexahedral elements and so they can be used interchangeably

• Tetrahedral models ran significantly faster than hexahedral models, so they are more computationally efficient

• Linear elements did not yield satisfactory results