Deep brain stimulation of terminating axons

Abstract

Background:

Deep brain stimulation (DBS) of the subthalamic region is an established treatment for the motor symptoms of Parkinson’s disease. Several types of neural elements reside in the subthalamic region, including subthalamic nucleus (STN) neurons, fibers of passage, and terminating afferents. Recent studies suggest that direct activation of a specific population of subthalamic afferents, known as the hyperdirect pathway, may be responsible for some of the therapeutic effects of subthalamic DBS.

Objective:

The goal of this study was to quantify how axon termination affects neural excitability from DBS. We evaluated how adjusting different stimulation parameters influenced the relative excitability of terminating axons (TAs) compared to fibers of passage (FOPs).

Methods:

We used finite element electric field models of DBS, coupled to multi-compartment cable models of axons, to calculate activation thresholds for populations of TAs and FOPs. These generalized models were used to evaluate the response to anodic vs. cathodic stimulation, with short vs. long stimulus pulses.

Results:

Terminating axons generally exhibited lower thresholds than fibers of passage across all tested parameters. Short pulse widths accentuated the relative excitability of TAs over FOPs.

Conclusion(s):

Our computational results demonstrate a hyperexcitability of terminating axons to DBS that is robust to variation in the stimulation parameters, as well as the axon model parameters.

Introduction

Deep brain stimulation (DBS) of the subthalamic region is an established treatment for the motor symptoms of Parkinson’s disease (PD), but the therapeutic mechanisms of action remains unclear. Numerous cell types and neural elements exist in the subthalamic region. These include subthalamic nucleus (STN) neurons with their cell body in the nucleus, afferent inputs to the STN which make synaptic connections onto the STN neurons, and fibers of passage coursing past the STN en route to their terminal locations. This neural diversity complicates interpretation of the neural response to subthalamic DBS, as these various neural elements have different levels of excitability to electrical stimulation¹.

Computational modeling has been used extensively in DBS research to inform our theoretical understanding of the action potential signaling induced by DBS². The neuron models used in those studies are based on mathematical descriptions of the membrane dynamics and neural structure, which can be individually tailored to specific neural populations to estimate their response to stimulation. However, the vast majority of DBS modeling studies have focused on characterizing the activation of fibers of passage because of their generally high level of excitability and ease of simulating³. Nonetheless, studies that have considered the response of terminating axons (TAs) to electrical stimulation have noted that they are often more excitable than fibers of passage (FOPs)^4,5,6.

Several recent DBS studies suggest that activation of a specific population of STN terminating afferents, known as the hyperdirect pathway, may be responsible for some of the therapeutic effects of subthalamic DBS^7,8,9. The hyperdirect pathway is a monosynaptic connection between cortex and the STN¹⁰. Hyperdirect axons arise from layer V pyramidal cells in widespread cortical regions, with large contributions from sensorimotor cortex^11,12. Their descending corticofugal fibers, within the internal capsule, project axon collaterals to the subthalamic region¹³. This creates an interesting targeting opportunity for subthalamic DBS, because if TAs are indeed more excitable than FOPs, then hyperdirect axons may be preferentially recruited when using low stimulus amplitudes^14,15.

The goal of this study was to evaluate the hypothesis that terminating axons are more excitable than fibers of passage during DBS. Given the relatively limited exploration of this topic thus far, we elected to use generalized models of the DBS electric field and idealized axon geometries, in hopes of establishing basic principles on the activation of terminating axons. We then systematically adjusted key model parameters of the axon models, as well as the DBS parameter settings, to quantify the relative excitability of terminating axons versus fibers of passage.

Methods

Axon Models

The goal of this study was to quantify the response of terminating axons (TAs) to deep brain stimulation (DBS) and compare those results to DBS of fibers of passage (FOPs). We created multi-compartment cable models of structurally idealized axons¹⁶ and simulated their response to DBS using NEURON¹⁷. The terminating axon model was designed to generally imitate hyperdirect afferent inputs to the STN (Figure 1). The TA model consisted of two main structural components. A corticofugal fiber, coursing from motor cortex to the brainstem, and the axon collateral, which branched from the corticofugal fiber at the level of the STN and terminated in the subthalamic region¹³. The idealized TA model was aligned to the center of the active contact and oriented such that the axon collateral projected toward the electrode. To evaluate the effects of axonal arbor complexity, four distinct TA model geometries were created with various levels of branching in the axon collateral arbor, referred to as the branch degree (BD) (Figure 2). The fiber diameter decreased at each branch point following Rall’s 2/3 power law¹⁸. The terminal end of each TA model was fixed at 2 μm in diameter. The overall length of the collateral arbor was standardized across branch degrees to ensure that corticofugal axons in each of the different branch degree representations were effectively equidistant from the electrode.

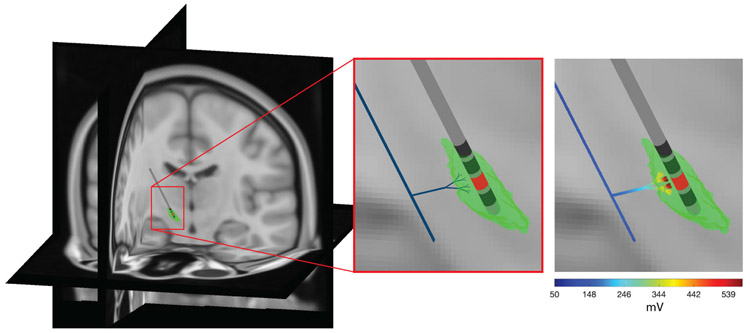
Figure 1.

DBS model of terminating afferents. The generalized terminating axon model was designed to be representative of human subthalamic DBS of the hyperdirect pathway. The parent axon (thick black line in the middle panel) gave rise to a branching collateral that projected toward the DBS electrode. A model of the subthalamic nucleus (green volume) is provided for anatomical reference. The extracellular voltage distribution generated by DBS from the red electrode contact is applied to the axon model in the far right panel. The DBS induced membrane polarization was then used to calculate the thresholds for action potential initiation.

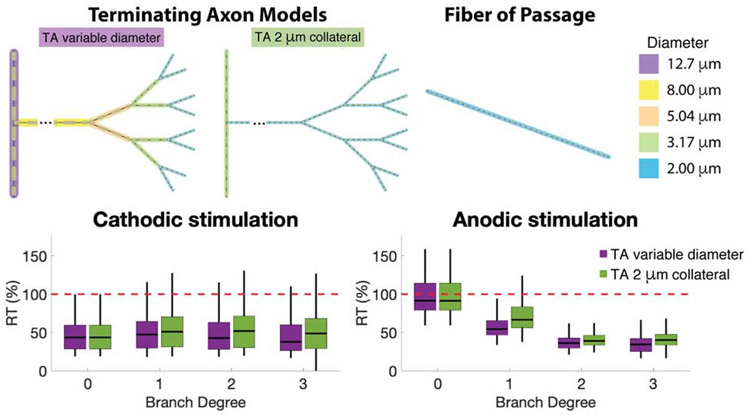
Figure 2.

Axon models. Four different terminating axon (TA) models were generated, each with a different degree of branch complexity in the axonal arbor. Branch diameter decreases at each branch point, but all models terminate with a 2 μm diameter segment. A fiber of passage (FOP) model was diameter-matched to the distal-most fibers of the terminating axon models.

Perfectly straight FOP models were also created for comparison with the TA models. The vast majority of DBS simulation work available in the literature has focused on the activation of straight FOPs to provide a computational proxy for the estimated spread of stimulation¹⁹. Therefore, our FOP model was diameter-matched to the distal-most components of the TA model (2 μm) (Figure 2). The FOP model was oriented perpendicular to the electrode with the central node of Ranvier perfectly aligned to the axis of the DBS electrode. This FOP orientation represents the current standard practice for the creation of DBS volume of tissue activated (VTA) estimates¹⁹.

Prior work suggests that terminating axons should be more excitable than fibers of passage under certain stimulation conditions²⁰. This general hypothesis is drawn from derivations of the cable equation designed to represent extracellular stimulation of a terminating axon. Polarization of the terminating compartment of the axon becomes driven by the first derivative of the extracellular voltage distribution, instead of the typical second derivative. Therefore, terminating axon compartments can be more strongly polarized by the DBS electric field, than if those same compartments were situated in the middle of a cable. As such, definition of the terminating compartment in an axon model becomes an especially important variable in any analysis of TA stimulation²¹. Our default representation of the axon terminals included active membrane dynamics, incorporating the same biophysics as the nodal segments of the axon (voltage-gated fast Na⁺, persistent Na⁺, slow K⁺, as well as passive leak channels)¹⁶. However, we also evaluated a wide range of different representations for the terminating axon.

A goal of this study was to identify the effect of different model parameters on the activation of terminating axons with DBS. Activation thresholds necessary to generate a propagating action potential were calculated for four different stimulation pulse widths (30, 60, 90, and 120 μs) at four different axon-electrode distances (500, 1000, 1500, and 2000 μm) (Figure 3A). We also perturbed the default TA model by modifying various aspects of the axon and quantifying the effect on activation threshold. Overall, our analyses evaluated the roles of stimulation polarity, axon position and orientation relative to the electrode, terminal node membrane properties, and the extent of myelination in the collateral arbor.

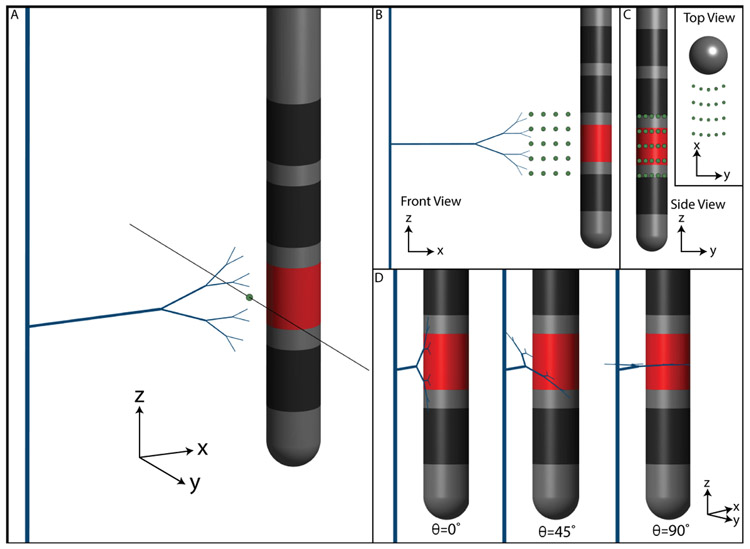
Figure 3.

Axon positions relative to the electrode. (a) Axon-electrode distance is defined as the distance between the axon and the surface of the electrode. The TA model shown is placed at an axon-electrode distance of 2 mm. The three other tested distances are shown with green circles (1.5 mm, 1.0 mm, and 0.5 mm). (b) Populations of TA models were created for each axon-electrode distance. TA models were centered at each of 25 different points, represented by green circles. The inset shows these same points from above the electrode. (c) The TA collaterals were also rotated in the y-z plane by θ=0°, 45°, or 90°.

To study the effects of axon position, the TA and FOP models were shifted in space relative to the DBS electrode (Figure 3). Twenty-five different points in the y-z plane, evaluated at 4 different distances in the x-z plane, were used in the analysis (Figure 3B). Therefore, each axon population result presented in the figures consisted of 100 activation thresholds. To study the effects of axon orientation, TA collaterals were rotated by 0°, 45°, and 90°, relative to the electrode orientation (i.e. in the y-z plane, as defined in Figure 3C). Terminals were also modeled as either active nodes or as purely passive elements (sealed end with passive membrane resistance).

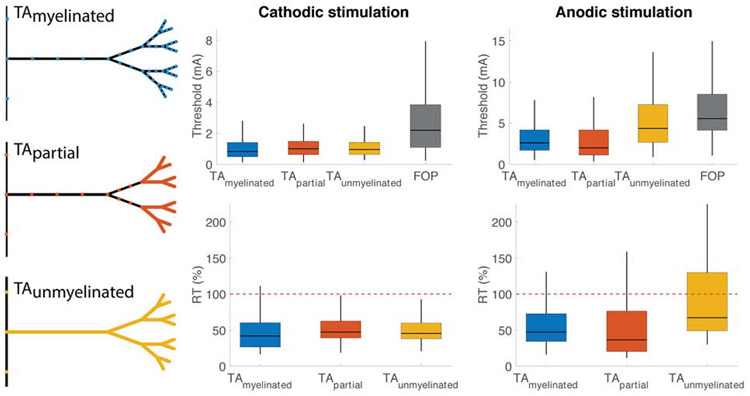
Although tracing studies have identified the general trajectory of hyperdirect axons¹³, little conclusive data exists on the extent of myelination along the axon collaterals. To evaluate the effects of myelination, the axon collaterals of the TA models were simulated as either fully myelinated, partially myelinated, or unmyelinated fibers. Membrane biophysics for unmyelinated regions were drawn from Shu et al.²² (Table S4).

Volume Conductor Model

A finite element volume conductor model of the DBS electrode in a human head was used to calculate the potential distribution from stimulation. The head shape was defined from an image-based anatomical representation of the human head and neck, known as the multimodal imaging-based detailed anatomical (MIDA) model²³ (Figure 1). The electrical model processing steps followed the methodology outlined in Howell and McIntyre²⁴ for MIDA₁. The head was considered an isotropic and homogeneous volume with a conductivity of 0.2 S/m.

Model Analysis

The potential distribution from a unit stimulus (1 mA) was scaled by the time-varying stimulus waveform (i.e. multiplied by the stimulus amplitude for the given pulse width) to create a representation of DBS for the specified stimulation parameter settings. A monophasic rectangular stimulus pulse was used in this study. For each axon position, relative to the DBS electrode, the extracellular potential at each compartment of each axon model was defined via interpolation. These extracellular potentials provided a driving force that induced transmembrane current flow in the axon model²⁵ (Figure 1). We analyzed the response of the axon models to both cathodic and anodic stimulation. Activation thresholds were defined as lowest stimulus amplitude that elicited a propagating action potential in the axon model. For the TA model, it should also be noted that at all identified thresholds, action potentials successfully back-propagated throughout the entire axonal structure.

We compared the activation thresholds of terminating axons (TH_TA) to that of fibers of passage (TH_FOP). FOPs were oriented perpendicular to the electrode, as this represents the lowest threshold orientation for these fibers²⁶. Boxplots were generated to summarize the relative threshold (RT) of TAs vs. FOPs. The relative threshold was calculated by normalizing each terminating axon threshold by the corresponding fiber of passage threshold:

$$RT=100\%\times \frac{T{H}_{TA}(polarity,pw,D,\theta ,xyzshift,terminaltype,BD)}{T{H}_{FOP}(polarity,pw,D,xyzshift)}$$

where TH = activation threshold, PW = pulse width, D = axon-electrode distance, θ = axon collateral rotation in the x-y plane, xyz-shift = 1 of 25 points that the axon model is shifted to for a given D, and BD = branch degree. A RT value equal to 100% suggests that the populations of TAs and FOPs were activated at the same threshold. A RT value less than 100% suggests that TAs had lower thresholds than the FOPs. A RT value greater than 100% suggests that the TAs had higher thresholds than the FOPs. Activation thresholds of TAs were compared to FOPs using a paired Wilcoxon signed-rank test.

Results

Cathodic Stimulation

The first step in our analysis evaluated cathodic activation thresholds of FOPs compared to fully myelinated TAs with active axon terminals. Strength-duration curves and box plots illustrating activation thresholds and relative threshold (RT) are summarized in Figure 4, and elaborated on in the supplemental material (Table S1; Figure S1). Across pulse width and axon-electrode distance, TAs had significantly lower median activation thresholds than FOPs, with an overall RT value of 29% [IQR = 24-36] (p<0.001). This was true across all branch degrees (BD0: 29% [IQR = 24-36], BD1: 30% [IQR = 25-37], BD2: 29% [IQR = 25-36], BD3: 28% [IQR = 24-36], p<0.001, Figure 4). In summary, terminating axons were activated at significantly lower thresholds than corresponding fibers of passage when using cathodic stimulation.

Figure 4.

Cathodic thresholds. (Left) Strength-duration curves of FOP and TA models. Median values are plotted and shaded regions represent the interquartile range. (Middle) Median thresholds across all pulse widths and distances for each axon model. (Right) Relative excitability of terminating axon models. Outliers have been removed. Medians and inter-quartile ranges are listed in Table S1.

Cathodic vs. Anodic Stimulation

Figure 5 presents the effects of adjusting a wide range of model parameters on the relative threshold measure. Summarized across all model parameters, terminating axons were generally more excitable than fibers of passage using both cathodic stimulation (median cathodic RT = 43%, [IQR=28-62], p<0.001) and anodic stimulation (median anodic RT = 48%, [IQR=35-73], p<0.001). Median relative threshold remained below 100% across all tested distances. Larger distances better targeted activation to TAs over FOPs for cathodic but not anodic stimulation (Figure 5). At a 500 μm distance, the median cathodic relative threshold was 62% [IQR=43-98], whereas at a 2000 μm distance the median relative threshold is 26% [IQR=23-44] (p<0.001). Using anodic stimulation, a 1000 μm distance best targeted activation to TAs over FOPs (RE = 39% [IQR=31-60] p<0.001).

Figure 5.

Effects of model parameters on relative excitability for myelinated terminating axons. Results for cathodic stimulation are shown on the left, and results for anodic stimulation are shown on the right. Red dashed lines show a relative excitability of 100%. Outliers have been removed. Medians and inter-quartile ranges are listed in Table S2.

Median relative threshold remained below 100% across all pulse widths using both cathodic and anodic stimulation (Figure 5). Shorter pulse widths better targeted activation to TAs over FOPs. At a 30 μs cathodic pulse, the median relative threshold was 37% [IQR=24-55] (p<0.001), whereas at a 120 μs cathodic pulse the median relative threshold was 47% [IQR=31-66] (p<0.001). Similarly, with a 30 μs anodic pulse, the median relative threshold was 39% [IQR=23-66] (p<0.001), whereas with a 120 μs anodic pulse the median relative threshold was 52% [IQR=42-77] (p<0.001).

Under cathodic stimulation conditions, branch degree did not dramatically affect relative threshold (RT_BD0: 44% [IQR=29-60], RT_BD1: 47% [IQR=30-64], RT_BD2: 43% [IQR=28-63], RT_BD3: 38% [IQR=26-60], p<0.001) (Figure 5). In contrast, larger branch degrees elicited lower relative threshold using anodic stimulation (RT_BD0: 91% [IQR=79-115], RT_BD1: 54% [IQR=47-66], RT_BD2: 36% [IQR=30-43], RT_BD3: 34% [IQR=25-42], p<0.001) (Figure 5). Models with branch degree 0 had a significantly higher median relative threshold than other branch degrees when using anodic stimulation. The site of action potential initiation in the different TA model variants for cathodic (Figure S2) and anodic (Figure S3) is provided in the supplemental material.

Rotation of the TA collateral arbor relative to the electrode only had a small effect on relative threshold. Under both cathodic and anodic stimulation, relative threshold was lowest when the axon collaterals were oriented parallel to the electrode (cathodic: RT_0°=42% [IQR=27-61], RT_45°=42% [IQR=28-62], RT_90°=44% [IQR=30-64], p<0.001, anodic: RT_0°=48% [IQR=34-73], RT_45°=48% [IQR=35-73], RT_90°=48% [IQR=36-73], p<0.001) (Figure 5).

Axon terminals were modeled as either active nodes (containing voltage-gated ion channels, identical to nodes of Ranvier) or as purely passive elements (containing only a passive membrane resistance). During cathodic stimulation, modeling the axon terminals as purely passive elements significantly increased relative threshold, but TAs remained generally more excitable than FOPs (RT_active=29% [IQR=24-36], RT_passive=61% [IQR=49-78], p<0.001). During anodic stimulation, the representation of terminal node model had minimal effect on relative threshold (RT_active=48% [IQR=35-73], RT_passive=48% [IQR=35-73], p<0.001). In addition, increasing the diameter of the terminal compartment of the TA model, to simulate the effect of a large bouton, did not have a dramatic effect on the activation thresholds (Figure S4).

Effect of Collateral Fiber Diameter

The distal most branches of our terminating axon models were all diameter matched at 2 μm. However, due to the selected geometric ratio for the branching of our TA models, examples with a high branch degree also had larger fiber diameters in the more proximal regions of the axon arbor (Figure 2). For example, the proximal branches of collaterals were as high as 8 μm for the BD3 model, while those TA models were still compared to 2 μm FOPs (Figure 4). To evaluate if those proximal branches were effecting the TA activation thresholds, we created a new set of TA models, identical in shape to the original TA models, but with a constant axon diameter of 2 μm throughout the entire axon collateral structure (Figure 6). Median activation thresholds did exhibit a small increase when the diameters of the axon collateral arbor were held at a constant 2 μm. However, TAs remained more excitable than FOPs regardless of which TA model was used (Figure 6).

Figure 6.

Effect of axon diameter on relative threshold of terminating axons compared to fibers of passage. Pictorial representations of the axon models used in this figure are displayed above the results. Only branch degree 3 is displayed in the picture, but the analyses were performed for all branch degrees. TAs with a constant (2 μm) diameter collateral are shown in green. TAs with a variable diameter collateral are shown in purple. Note that branch degree 0 is identical for both model variants, and the resulting relative thresholds are also identical.

Extent of Myelination

The extent of myelination within terminating axon collaterals is typically an unknown parameter in both the anatomy literature, as well as modeling studies. Therefore, we developed TA model variants that had unmyelinated sections to evaluate if myelination was effecting the TA activation thresholds. TAs had lower median thresholds than FOPs across all myelination extents modeled (Figure 7, Table S3). This included model variants that had fully myelinated, partially myelinated, and unmyelinated collaterals. The myelinated TAs were more excitable than FOPs using both cathodic (RT_myelinated=42% [IQR=27-61] p<0.001) and anodic (RT_myelinated=48% [IQR=34-73] p<0.001) stimulation. Using cathodic stimulation, myelinated TAs had the lowest relative threshold, while partially myelinated TAs had the highest relative threshold (RT_partial=48% [IQR=39-63] p<0.001). Using anodic stimulation, partially myelinated TAs had the lowest relative threshold (RT_partial=37% [IQR=20-77] p<0.001), while unmyelinated TAs had the highest relative threshold (RT_unmyelinated=68% [IQR=49-130] p<0.001).

Figure 7.

Effect of myelination. Pictorial representation of myelination extent is displayed on the left. Colored areas represent unmyelinated, exposed membrane. Black areas represent myelin. Activation thresholds (top) and relative threshold (bottom) are shown for axon models of varying myelination. Results for cathodic stimulation are shown on the left, while results for anodic stimulation are shown on the right.

Discussion

The desire to understand the neural response to DBS, as well as its therapeutic mechanisms of action, has existed since inception of the clinical therapy. However, dissecting the specific responses of fibers of passage, local neurons, or afferent inputs to electrical stimulation has long puzzled experimentalists, theoreticians, and clinicians¹. The electric field generated by an extracellular electrode is non-discriminately applied to all of the neural processes that surround the electrode, making truly selective stimulation of a specific neuron type very difficult to achieve²⁷. As a result, subthalamic DBS likely activates a wide range of different neuron types^28,29, and it remains unclear which of those different neural populations are the most important for therapeutic benefit. The goal of this study was to provide a theoretical foundation for characterizing the response of terminating afferent inputs to DBS. Our results demonstrate that terminating axons are generally more excitable than diameter-matched fibers of passage.

The earliest computational models of DBS actually suggested that afferent inputs were the lowest threshold neural elements to the stimulation³⁰. Nonetheless, DBS models gravitated toward characterizing the response of fibers of passage because of their relatively high excitability and simplicity to model³. However, the work of Gradinaru et al.³¹ challenged that simplifying assumption in DBS models when they showed that selectively activating the hyperdirect pathway with optogenetic stimulation was directly linked to therapeutic benefit in rodent models. It should be noted that recent animal work suggests that hyperdirect pathway activation is only sufficient (not necessary) for a positive effect on symptoms [Yu et al., 2020; Johnson et al., 2020]. Nonetheless, an ever growing literature base strongly supports the importance of stimulating the hyperdirect pathway in clinical subthalamic DBS³². As such, DBS models that explicitly account for the neural response of terminating afferent inputs are needed to better evaluate the brain connections that are being modulated by DBS¹⁴.

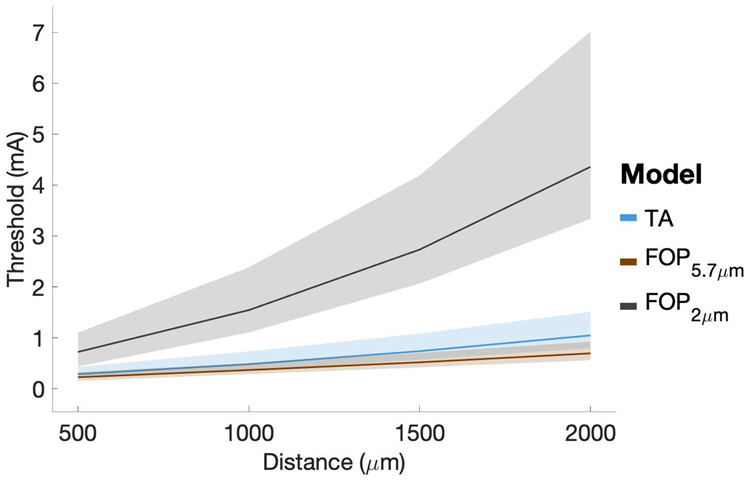
The results of this study suggest that typical VTA models¹⁹, which are based on only FOP activation, likely underestimate the spatial extent of diameter-matched TA activation by a substantial margin (Figure 5). However, the most commonly used VTA model was originally parameterized to predict the activation of large diameter axons (5.7 μm) to provide a “worst-case” scenario for the spread of stimulation to side-effect regions such as the internal capsule³³. Serendipitously, the DBS current-distance relationships of 5.7 μm diameter FOPs actually correspond relatively well with the 2.0 μm diameter TA models that we used to emulate the hyperdirect pathway (Figure 8). As such, the use of an appropriately parameterized VTA model¹⁹ in recent connectomic DBS studies has probably generated reasonable estimates for hyperdirect pathway activation²⁹. Nonetheless, this general topic requires greater attention to detail in future studies attempting to identify clinical correlations between estimated pathway activation and behavioral outcome measures.

Figure 8.

Current-Distance relationships. Cathodic DBS with 60 μs stimuli. The black line represents FOPs with a 2 μm diameter, while the orange line represents FOPs with a 5.7 μm diameter. The blue line represents TA models with a branch degree = 3. Median values are plotted and shaded regions represent the interquartile range.

This study choose to simulate DBS of an idealized representation of the hyperdirect pathway. However, given that action potential initiation in the TA models almost always took place in the collateral arbor (Figures S2, S3), the results are likely generalizable and independent of the neural origin of the terminating arbor. As such, we propose that the findings of this study are also relevant to the activation of globus pallidus inputs to the STN. We found that neither the degree of branching nor the rotational orientation of the collateral branches had a major effect on the TA thresholds from DBS (Figure 5). These conclusions are less robust when considering a non-branching (BD0) terminating axon and anodic stimulation. Figure 6 demonstrates that this feature of anodic stimulation is not primarily dependent on axon diameter, but instead more related to the presence of branch points. Branch points represent opportunities for increased polarization from extracellular stimulation, and given the more proximal site of action potential initiation in TAs from anodic stimulation (Figure S3), help to lower activation thresholds.

The results of this study supports the notion that the presence of terminating afferents in the vicinity of the electrode increases the relative excitability of that neuron to DBS. In addition, if that neuron has an extensive TA arbor there is an increased likelihood that at least one of those axonal processes would be in close proximity to the DBS electrode, which makes it even easier to activate. It then only takes activation of a single axon branch for the action potential to faithfully propagate throughout the entire neural structure³⁴, and subsequently generate the release of neurotransmitters at all of the synaptic connections of that neuron³⁵. In turn, the next layer of neurophysiology questions revolve around understanding the effects of those DBS-induced synaptic inputs on the connected neurons that are local (i.e. STN neurons) or distant (i.e. cortical neurons) from the site of stimulation.

Possibly the two most difficult aspects of parameterizing terminating afferent models for DBS simulations are defining the extent of myelination on the TA arbor, and the membrane properties of the axon terminations^20,21,36. This is because the experimental data needed to define those aspects of the model are not readily available. For example, tract-tracing anatomical techniques are able to characterize the trajectory of the axon and its collaterals, but the intracellular stains do not label the myelin¹³. However, our results demonstrate that the extent of myelination in these small diameter axons did not have a major impact on the activation thresholds for TAs (Figure 7). Another difficult aspect of modeling DBS of terminating afferents is representing the axon terminations. They are generally assumed to be synaptic boutons, but the voltage-gated ion channels, and their membrane conductivity properties, can only be indirectly inferred^37,38. Therefore, we examined two extremes of membrane excitability in our analyses (Figure 5). The default model assumed that the termination had membrane dynamics that matched the nodes of Ranvier (i.e. high excitability - active). The alternate model removed all active membrane dynamics from termination (i.e. low excitability - passive). Not surprisingly, for cathodic stimulation the presence of active membrane dynamics in the termination substantially reduced the activation thresholds. However, our relative excitability measure showed that even with passive membrane dynamics in the termination, TAs were still more excitable than FOPs (Figure 5).

An important motivation for this study was to provide a better understanding of the excitability of terminating axons during anodic stimulation. While anodic stimulation is not typically employed in clinical DBS applications, there have long been theoretical suggestions that it might help facilitate stimulation selectivity between different neural populations^27,39. In addition, recent clinical experiments with anodic DBS in the subthalamic region suggest that there may be therapeutic benefits in the treatment of bradykinesia and rigidity symptoms, compared to cathodic DBS⁴⁰. Our results show that TAs are preferentially activated during anodic DBS, especially when the afferent input has an extensive axonal arbor (Figure 5). Therefore, this topic warrants further investigation with more detailed patient-specific models of subthalamic DBS that better account for the electric field generated by therapeutic stimulation²⁹, as well as anatomically detailed reconstructions of the hyperdirect afferent inputs^12,13.

The models used in this study were intentionally developed with highly simplified representations of the DBS electric field and axonal processes to help us identify general trends in the response of TAs to stimulation. Conceivably, these simple TA models could also be used to generate a new class of VTA predictor functions⁴¹ that may be useful in large-scale probabilistic DBS mapping studies⁴². However, the simplifying assumptions used in this study are known to introduce substantial errors in the DBS voltage distribution²⁴ and calculated neural response to DBS²⁹. Therefore, we concentrated our analyses on the relative excitability of TAs and FOPs. Both neural populations were evaluated within the same simplified DBS context, so while their absolute threshold calculations are inaccurate, the basic biophysics underlying their relative excitability should be preserved. Therefore, the robust preferential TA activation results documented in this study provide motivation for expanded scientific characterization of TA responses using more realistic models of clinical DBS with patient-specific analyses.

HIGHLIGHTS.

• DBS of afferent inputs may contribute to the therapeutic mechanisms

• Terminating axons have unique biophysical responses to DBS

• Terminating axons are more excitable than diameter matched fibers of passage