Training a neural network for Gibbs and noise removal in diffusion MRI

Abstract

Purpose

To develop and evaluate a neural network–based method for Gibbs artifact and noise removal.

Methods

A convolutional neural network (CNN) was designed for artifact removal in diffusion-weighted imaging data. Two implementations were considered: one for magnitude images and one for complex images. Both models were based on the same encoder-decoder structure and were trained by simulating MRI acquisitions on synthetic non-MRI images.

Results

Both machine learning methods were able to mitigate artifacts in diffusion-weighted images and diffusion parameter maps. The CNN for complex images was also able to reduce artifacts in partial Fourier acquisitions.

Conclusions

The proposed CNNs extend the ability of artifact correction in diffusion MRI. The machine learning method described here can be applied on each imaging slice independently, allowing it to be used flexibly in clinical applications.

1 |. INTRODUCTION

The Gibbs phenomenon^1,2 and noise are artifacts that affect all magnetic resonance imaging scans. The traditional solution for both low signal-to-noise ratio (SNR) and Gibbs artifacts has been to apply a smoothing filter to the image. Although smoothing can reduce the variance of noise, it cannot directly correct for the Rician-biased signal present in low-SNR regimes, nor can it accurately reproduce images that are Gibbs-artifact-free. Methods using Gegenbauer polynomials have been shown to be able to detect edges and accurately estimate images up to the edge for the purpose of Gibbs removal.³ Subvoxel shifting is another method that can substantially reduce Gibbs ringing in acquisitions without partial Fourier encoding.⁴ Model-based reconstruction methods^5–8 can improve SNR and/or reduce Gibbs ringing. In parametric protocols with repetitive acquisitions such as diffusion MRI, correlations across the diffusion directions can be used for denoising. Recently, a random matrix theory-based marchenko-pastur principle components analysis (MP-PCA) method has been developed that takes advantage of these correlations for noise estimation⁹ and removal.¹⁰ Also for diffusion, the DESIGNER pipeline¹¹ based on MP-PCA and subvoxel shifting has been demonstrated and validated.

A drawback of many of these methods is that they rely on models that are not fully general. MP-PCA requires the distribution of the noise to be unaltered by processing, as well as many diffusion directions in order to take advantage of the corresponding correlations,^9,10 but many clinical protocols only use a small number of diffusion directions. Meanwhile, subvoxel shifting does not perform well on partial Fourier acquisitions.⁴ Partial Fourier imaging is a complex case due to the interaction between blurring effects from the undersampling and ringing effects from the Fourier series approximation of the image. The combination of these effects is difficult to model explicitly due to the presence of ringing artifacts of varying frequency and phase.⁴ As a result, some groups refrain from applying partial Fourier in diffusion imaging.

Machine learning offers a framework for building models that can be applied to simultaneously remove a variety of artifacts in an acquisition-flexible manner. One potential class of models suitable for these tasks would be convolutional neural networks (CNNs).^12,13 CNNs are models composed of simple building blocks—often convolution kernels only 3 pixels wide followed by an activation function. When many convolution kernels are used together, they can approximate highly nonlinear functions of many variables. The use of simple components makes training such models ideally suited for parallelization and efficient implementation on modern computer architectures. Several recent papers have demonstrated the applicability of CNNs for medical imaging in areas including image reconstruction,^14–18 image quality transfer,¹⁹ super-resolution,²⁰ segmentation,²¹ and artifact correction.²²

Diffusion MRI is an intriguing test application for Gibbs and noise removal models. Both effects can have drastic effects on diffusion parameter maps. The calculation of higher order diffusion parameters can require the application of b-values up to b = 2500 s/mm²,²³ which, coupled with strong diffusion gradients and long echo times, leads to low SNR.24 The well-known ≤9% intensity variation due to Gibbs ringing^1,2 may translate into ~100% errors in the estimated signal moments or cumulants, in particular leading to the so-called “black voxels” (masked outliers) in kurtosis maps.⁶ Thus, systemic defects—such as Gibbs or effects from machine learning-based processing—are substantially amplified in the corresponding parameter maps.

Here, our aim is to develop and evaluate a machine learning approach for Gibbs and noise removal. We show that the framework of CNNs allows the simultaneous removal of these artifact sources in an acquisition-flexible manner—specifically, we extend the ability for Gibbs artifact removal to the partial Fourier setting and noise removal to the setting with few diffusion directions. We accomplish this by training the model entirely on simulations of MRI acquisitions with images from the ImageNet data set.²⁵ Prior to the evaluation stage of our experiments, networks trained this way have never seen an MR image, mitigating overfitting risk. Our results suggest that, with CNN processing, high-quality parameter maps can be calculated from abbreviated acquisitions with a little more than half of the encoding time required for traditional full acquisitions, opening up new possibilities for diffusion MRI. The method can be applied independently to each imaging slice, allowing application to clinical protocols with few repetitive scans.

2 |. METHODS

In MRI, images are reconstructed by sampling a Fourier series at a discrete set of locations where the Fourier series coefficients are the acquired k-space points. This suffers from the Fourier series approximation error that manifests as the Gibbs phenomenon.^1,2 In practice, the MRI scanner does not produce the true, noise-free Fourier series coefficients, but a noise-corrupted version of them. Here, we denote the true image at a given resolution as m_d and its noisy, Gibbs-corrupted version as x_d, where d is an integer that indicates the dth image. Our goal is to learn a functional, f_θ(·), that estimates m_d from x_d where θ are the parameters of the functional. We accomplish this by solving the following optimization problem:

$$\widehat{\theta }={\mathrm{argmin}}_{\theta }\sum _{d=1}^D{\Vert {\mathbf{m}}_d-f_{\theta }\left({\mathbf{x}}_d\right)\Vert }_2^2,$$ (1)

where D is the size of the training data set.

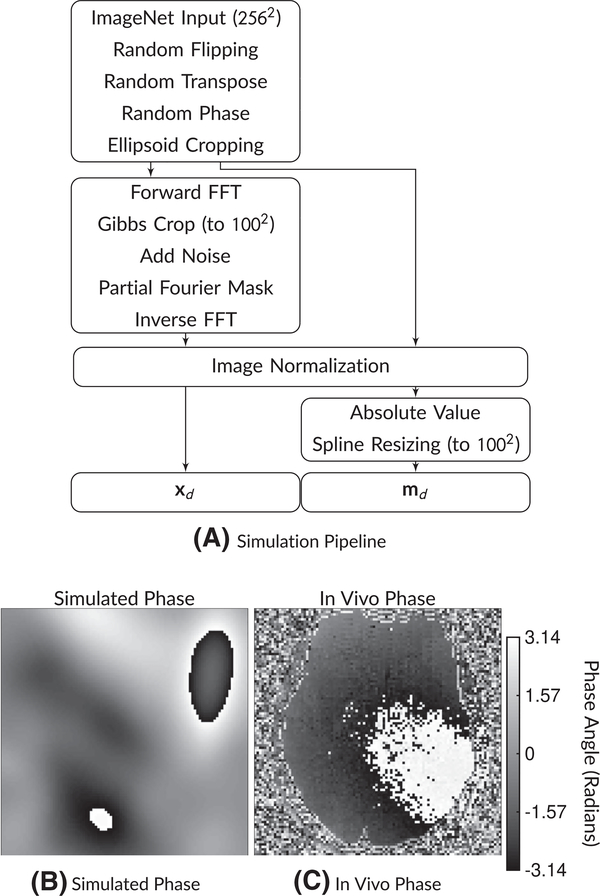
Solving (1) requires a data set of image pairs (m_d, x_d), d ∈ [1, …, D] or a means of generating them. We choose to simulate both m_d and x_d from a latent, high-resolution image that comes from the ImageNet data set.²⁵ This restricts the method to operating independently on 2D images. Figure 1 shows our simulation pipeline. We describe the details of the steps in Section 2.2.1. Section 2.1 describes the model architecture for f_θ(·). In Section 2.3.2, we describe test experiments that were conducted on data sets completely separate from that used for training, including gold standard segmented EPI, prospective diffusion data on healthy and subjects with pathology, and cervical spine imaging. In these real-world diffusion validation experiments, we test the performance of two different networks and compare to state-of-the-art (SoA) methods across partial Fourier factors. We show results from these experiments in Section 3.

FIGURE 1.

A, Simulation pipeline and (B,C) example phase maps. The simulation pipeline begins with a 256 × 256 ImageNet image. Then, after random flipping and transposing, random phase and random ellipsoid cropping are applied. Then, the network input x_d has Gibbs ringing simulated along with noise and partial Fourier masking, followed by normalization. The target m_d images have the absolute value operation applied followed by spline resizing to the target image matrix size. An example of a phase map from this simulation is shown in (B), while a comparison in vivo phase map is shown in (C). Phase maps can have substantial variations that must be considered when applying partial Fourier imaging

2.1 |. Model architecture

There are many potential model architectures for accomplishing deGibbsing. Architectures such as variational¹⁴ and cascaded¹⁵ networks offer the most flexibility for modeling system physics. However, these models often require access to the raw data and system parameters, for tasks such as sensitivity map estimation. Use of such models may require accessing proprietary information or signing research agreements with vendors. Furthermore, the use of models that rely on raw data can incur substantial data storage requirements. Finally, they preclude the use of the model on previously acquired image data sets where the raw data has been discarded.

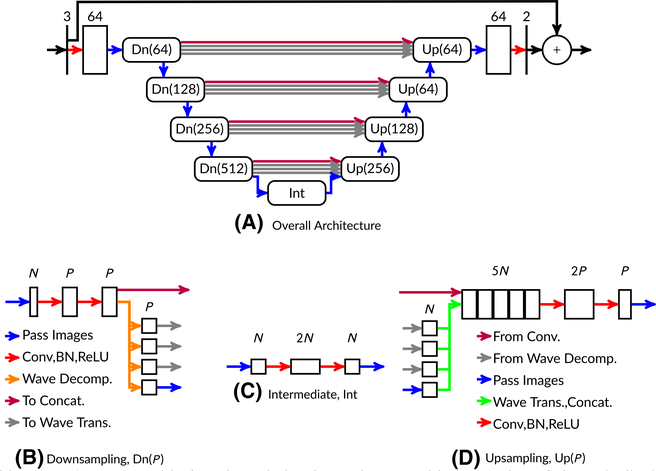
Due to these considerations, we address the Gibbs phenomenon with an image-to-image architecture. Our model comes from the class of U-Net²⁶ architectures. Figure 2 shows a diagram of the architecture. At the midpoint of the U-Net (shown as the bottom of the U in Figure 2), convolution operations affect almost the entire image, enabling the network to learn global features such as conjugate k-space symmetry. We process complex images by inputting the real and imaginary components into the network as two separate channels.¹⁵ After each convolution layer, we apply batch normalization.²⁷ After batch normalization, we apply rectified linear unit (ReLU) activation functions, as is standard practice.²⁸ Unlike the standard U-Net, our model includes wavelet transforms for downsampling and upsampling. The theoretical properties of these modifications were analyzed previously¹⁶ and demonstrated to better-preserve high-resolution features. Based on the intuition that it is easier to learn residuals rather than signals,²⁹ we use a skipped connection over the entire architecture for the real and imaginary channels. For cases with complex inputs, we apply the magnitude operation as a final step after the skipped connection.

FIGURE 2.

Model architecture (A). Boxes with sharp boundaries denote images with the number of channels displayed above the box. Boxes with rounded boundaries are submodules. Also shown are example downsampling (B), upsampling (D), and intermediate (C) submodules at a constant network depth. The model as shown here has 31,646,338 parameters

2.2 |. Training

Code for training our models is available on Github at https://github.com/mmuckley/dldegibbs. All models were trained and tested using the PyTorch package. Links to trained models will be included in the GitHub repository. We trained the network by simulating MRI acquisitions on photographs from the ImageNet data base,²⁵ using resized, noise-free versions of the original photographs as target images m_d. The data set contained 1 281 167 images in the training set and 50 000 images in the validation set. The “best” model was selected based on the minimal loss over the validation data set during the training epochs. Use of ImageNet for training requires specification of (a) an encoding simulation pipeline (Section 2.2.1) and (b) an optimization procedure (Section 2.2.2).

Although the images in ImageNet are not true MR images, we take this approach due to the fact that it is impossible to acquire large volumes of high-resolution diffusion images for the purpose of simulating Gibbs artifacts. Larger data sets are generally believed to be beneficial for learning,^30,31 and the benefits of larger data sets for denoising have been directly demonstrated.³² An alternative would be to train from high-resolution anatomical data, but diffusion-weighted images (DWIs) can have substantially different features from their high-resolution anatomical counterparts. Thus, training a network on simulated Gibbs artifacts from high-resolution anatomical data runs the risk of having the network reconstruct signals that would not be present in the corresponding diffusion data. Furthermore, an anatomical data set would be highly homogeneous, limiting the generalizability of the resulting network. Conversely, ImageNet is a highly heterogeneous data set, enabling the network to learn more generic features and potentially enabling application of this approach in other MRI modalities that suffer from Gibbs artifacts. A key determinant of the feasibility of this approach is the simulation of encoding operations as they occur in vivo, which we discuss below.

2.2.1 |. Simulation

The simplest Gibbs simulation could be accomplished by cropping the k-space representation of a high-resolution image. However, in practice, MR acquisitions are affected by many factors other than the Gibbs phenomenon. We simulate a subset of these effects. Figure 1 shows a flowchart of the simulation pipeline. Figure S1 of the Supporting Information shows diagrams with the effects of key steps on images. The simulation begins with raw grayscale ImageNet image (converted via BT.601 color standards), resized to a standard size of 256 × 256 using bilinear interpolation.³³ The simulation then randomly flips and/or transposes the image, each with a 50% probability. After flipping and transposing, the simulation proceeds to the random phase step. The random phase simulation generates a random set of Gaussian radial basis functions for each simulated image—this is described in detail in Appendix A. An example of simulated phase compared to a true in vivo phase case is shown in Figure 1B,C. The random phase simulation requires a number of probabilistic parameters for specifying the distribution of the simulated phase—these are reported in the appendix.

Since most images have a no-signal background, following random phase simulation we apply random ellipsoid cropping to the images. We also include a 10% probability that no ellipsoid cropping occurs to handle cases that may not have a no-signal background. After image-domain cropping, the processing pipelines split. For the data, x_d, we apply the FFT and crop the image from a 256 × 256 grid to a 100 × 100 grid in k-space to simulate the Fourier series truncation effect. The simulation adds noise at levels from 1 to 32 times the mean absolute k-space value, varying the noise level within this range on a uniform base-2 logarithmic scale (average noise ratio of 10).

After the inverse FFT, both processing pipelines are merged into an image normalization layer where both images are divided by the maximum absolute value in x_d. The absolute value operation is then applied to m_d. To simulate an artifact-free target, m_d, we interpolate m_d from a 256 × 256 grid to a 100 × 100 grid using cubic splines. Finally, to provide the complex-valued CNN with more information, we concatenate a standard partial Fourier reconstruction method³⁴ to the complex-valued x_d output in the channel dimension prior to input to the neural network.

When magnitude images are used, the inputs have Rician noise rather than Gaussian. We maintain most of the above processing stream aside from three modifications. (a) The absolute value operation is applied after inverse FFT in the x_d stream, and (b) followed by dividing by the maximum value of the x_d image for both the m_d and x_d final images. This implicitly builds Rician bias correction into the network training.

2.2.2 |. Optimization

Our optimization routine followed standard practice. We used the ImageNet data set²⁵ with standard training and validation splits. Our convolution weights were initialized with a uniform distribution.³⁵ ReLUs were initialized with zero parameters. We used the Adam algorithm³⁶ with a learning rate of 1 × 10⁻³ over 10 epochs to minimize the mean-squared error cost function in (1). At each epoch, we calculated the loss over the entire validation data set and saved the model with the best validation loss for the in vivo test experiments. Each model was trained independently on each partial Fourier factor. We implemented our models in the PyTorch deep learning framework.³³ Training was performed on an IBM GPU computing cluster with Power9 8335-GTH compute nodes. Each node in the compute cluster had four Nvidia V100 GPUs with 16 GB of memory. Our specific trainings utilized one GPU with a batch size of 55. Training time took approximately 10 days.

2.3 |. Testing

In the test phase, we evaluated the proposed CNN methods for their ability to process DWIs on different data sets. In all our test experiments, we define “SNR” to be the mean absolute image value divided by the complex Gaussian standard deviation. Note that this is different from the k-space ratio used during training. We conducted canonical signal processing experiments and in vivo experiments. To provide context for the performance of the CNN methods, we also processed the DWIs with a SoA method,¹¹ as well as a method designed for partial Fourier imaging.³⁴ In all cases with diffusion parameter maps, the raw DWIs were first processed by the designated method prior to parameter map estimation. To clearly show that our test data sets are distinct from our training data sets, we index test signals with t instead of d.

Raw

These parameter maps were calculated from the raw DWIs with no extra processing before the parameter estimation stage.

State-of-the-art¹¹

Prior to parameter map estimation, the images were denoised using the random matrix theory-based MP-PCA method.¹⁰ The MP-PCA method applies low-rank denoising using a cutoff based on the Marchenko-Pastur law.³⁷ We applied MP-PCA using a 5 × 5 × 5 voxel kernel extent with Rician bias correction,¹⁰ followed by Gibbs removal via subvoxel shifting⁴ where each voxel was discretized into 20 subvoxel elements. The subvoxel shifting method searches in a subvoxel neighborhood for the minimum Gibbs distortion given by the sinc function and interpolates to that subvoxel location. Unlike the CNN methods, the SoA method is able to use information from low-b DWIs to denoise images from high-b diffusion gradients.

Magnitude-input CNN (MCNN)

The raw diffusion images after the magnitude operation, x_t, are processed by a neural network trained with the simulation pipeline in Figure 1 with the target image m_t being a magnitude, deGibbsed image without PF. This particular network attempts to restore the missing partial Fourier information. This network has 31 646 338 parameters.

Standard Partial Fourier (Standard PF)

The raw diffusion images are processed by using a standard partial Fourier reconstruction method that utilizes the phase maps from the symmetric region of k-space³⁴ prior to parameter estimation.

Complex-input CNN (CCNN)

The raw complex-valued diffusion images, x_t, are processed by a neural network trained with the simulation pipeline in Figure 1 with the target image m_t being a magnitude, deGibbsed image without PF. This particular network attempts to restore the missing partial Fourier information. This network has 31 646 338 parameters.

2.3.1 |. Canonical experiments

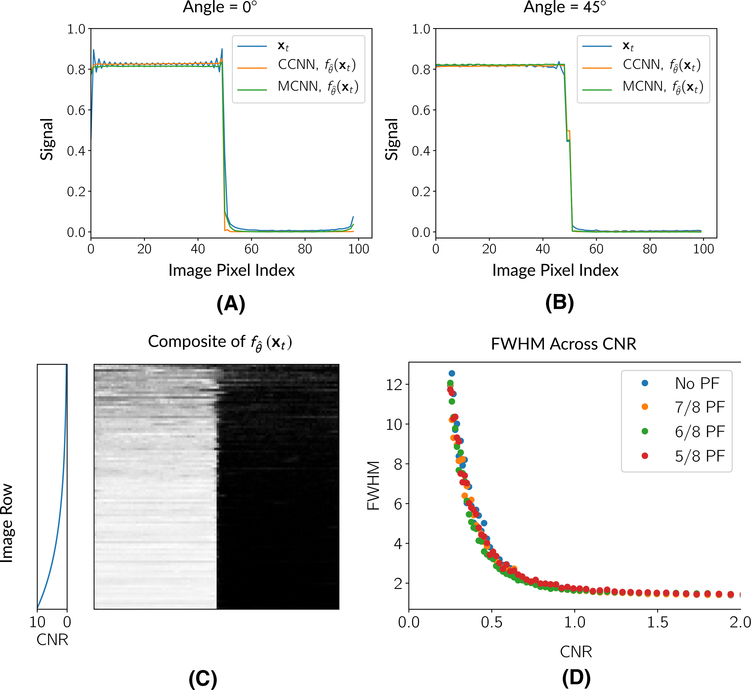
To characterize the deGibbsing and denoising performance of the network, we performed a set of canonical signal processing experiments with two data sets. The first data set consisted of a simple edge phantom, while the second data set consisted of the test split of the 2013 ImageNet challenge.³⁸ Edge-spread function: Edge-spread functions are routinely used to study the resolution properties of image processing methods. Toward the goal of identifying when the network blur small lesions, we conducted tests with a digital edge phantom across a variety of contrast-to-noise ratios. The edge phantom consisted of a 2D digital image with half of the image filled with 1s and the other half filled with 0s. This image was generated at a 1024 × 1024 matrix size (cropped to a 100 × 100 matrix size during simulation). The location of the edge was varied by rotating it. Figure 3 includes a composite image of the phantom generated from $f_{\widehat{\theta }}\left({\mathbf{x}}_t\right)$ at many different SNR levels. We performed two sets of experiments with the edge phantom: contrast-to-noise (CNR) and deGibbsing experiments. In a previous study,⁴ it was noted that deGibbsing performance could vary depending on the angle of the edge. To assess the performance of the method on removing Gibbs artifacts at different angles, we generated the phantom at a set of angles beetween 0 and 45 degrees at a 1024 SNR level and computed the CCNN deGibbsed image.

FIGURE 3.

Responses of CNN models to the edge phantom at different angles and across CNR levels. (A) and (B) show profiles across the edge phantom for the raw, Gibbs-corrupted data, x_t, and the CCNN/MCNN models, $f_{\widehat{\theta }}\left({\mathbf{x}}_t\right)$, for edges at different angles. Both the CCNN and the MCNN method reduce the Gibbs artifacts. (C) shows a composite image of CCNN network estimates across a variety of CNRs from 0.25 to 10, while (D) shows the change in estimated FWHM as a function of CNR for the CCNN model. Above a CNR of 1, CNN performance is fairly stable. Below a CNR of 1, the FWHM increases as the CNR approaches 0

We also performed CNR experiments. The goal of the CNR experiments was to quantify the full-width-half-maximum (FWHM) of the network’s line-spread function across a variety of noise levels (analogous to a point-spread function in 1D). We accomplished this by applying the simulation pipeline in Figure 1 without random flipping and transposing at a variety of CNRs between 0 and 10, resulting in images at 100 × 100 matrix sizes. For each CNR, we applied both the CCNN model and the MCNN model (generating $f_{\widehat{\theta }}\left({\mathbf{x}}_t\right)$ realizations for each one). This resulted in a series of edge-spread function images. To compensate for noise in calculating the FWHM values, for each row of the resulting image, we fit a summation of logistic functions³⁹:

$$l(s)=c+\sum _{i=1}^3\frac{{\alpha }_i}{1+\exp \left(\frac{s-{\beta }_i}{{\gamma }_i}\right)},$$ (2)

where c, α_i, β_i, and γ_i, i ∈ [1, 2, 3] are fitting parameters. We computed the derivative of this function and used it to calculate a line-spread function for each row of the image. From the line-spread functions, we calculated the FWHMs and averaged across the rows. For each CNR level, we repeated and averaged this experiment 50 times.

ImageNet test data

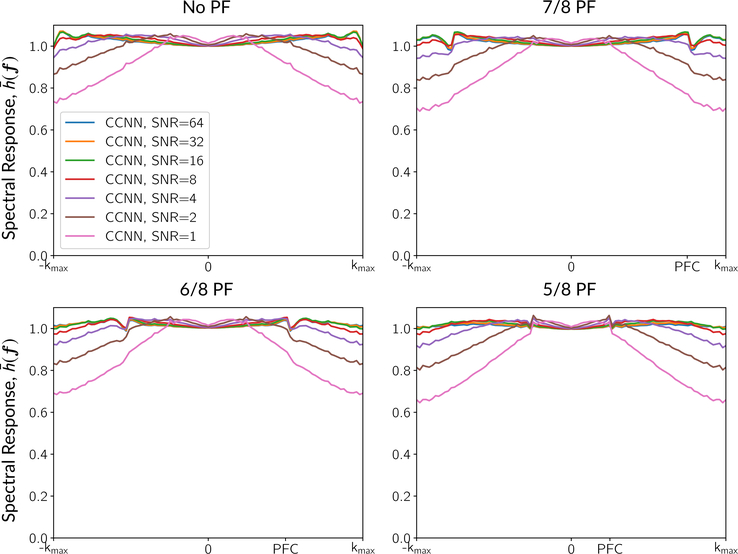
The goal of the tests on the ImageNet data was to assess the network’s performance across a broad variety of signals. For this, we used the test split from the 2013 ImageNet challenge.³⁸ This data was not used at all in training and is distinct from the validation data set. The test set included 40 152 images. We applied the simulation pipeline in Figure 1 and computed the power spectral ratio on the resulting images.⁶ Let S(·) be the operator that computes the power spectral density of the image. For each image-target pair in the validation data set, (x_t, m_t), we computed

$$h_t(\mathit{f})=\sqrt{\frac{\mathcal{S}\left(f_{\widehat{\theta }}\left({\mathbf{x}}_t\right)\right)}{\mathcal{S}\left({\mathbf{m}}_t\right)}}.$$ (3)

Then, we averaged over all t ∈ [1, …, n_test] to compute a mean $\overline{h}(\mathit{f})$ for each partial Fourier factor and SNR level and computed profiles across f in the partial Fourier direction to assess resolution performance. As a last test, we calculated image metrics of MSE, SSIM, and PSNR over this simulated test set. The results are described in the Supporting Information and shown in Table S1.

2.3.2 |. In vivo experiments

For our in vivo tests, we conducted four experiments:

1. A “gold standard” segmented EPI experiment. This was used to achieve a higher matrix size and produce reference diffusion images with almost no Gibbs artifact.

2. A prospective diffusion experiment. This tested the method vs the current SoA in a standard acquisition.

3. A pathology experiment. We acquired diffusion pathology data from a previous study and assessed stability of the MCNN model in the presence of MS lesions.

4. A cervical spine experiment. In addition to diffusion, Gibbs artifacts can confound clinical evaluations.^40,41 In this experiment, we evaluated the method in an alternative anatomy.

“Gold standard” segmented EPI

We acquired segmented EPI data for the purpose of simulating realistic diffusion data that is nearly Gibbs-free. In many cases, segmented EPI scans are not practical due to time limitations and difficulties with reconstruction, but here we use this sequence for the purpose of creating a diffusion reference at a 100 × 100 matrix size using a segmented EPI acquisition at a 128 × 128 matrix size. A volunteer was scanned with a diffusion-weighted imaging protocol under IRB approval. The scan was done after all model and training parameters were complete, so that these data qualify as a true prospective test set. The sequence was applied on a 3T Prisma scanner with a 16-channel head coil (Siemens Healthineers, Erlangen, Germany). Using a segmented EPI readout, we were able to acquire images at a 128 × 128 matrix size with a 2 mm isotropic resolution. The images were acquired at b-values of 500, 1000, and 2000 s/mm² in 39 isotropic directions. The acquisition had TE of 64 ms and a TR of 3 seconds. Reconstruction was accomplished with Siemens software via adaptive combine,⁴² saving the resulting magnitude and phase images.

For the “gold standard” processing, we applied MP-PCA, apodized the 128 × 128 k-space data, applied the inverse FFT, and interpolated to a 100 × 100 image grid. This produced DWIs that were essentially noise and Gibbs-free. For the experimental data sets, we cropped the 128 × 128 k-space to 100 × 100 and added noise to simulate an SNR of 10 at b = 0 s/mm². Then we applied partial Fourier masks at PF factors of 5/8ths, 6/8ths, 7/8ths, and fully sampled, prior to inverse FFT.

To process the experimental data, we applied the CCNN, MCNN, and SoA processing methods to the images with simulated Gibbs. Parameter map estimation for all methods was performed on the processed image using a constrained weighted linear least squares approach.⁴³ Since the complex CNN can take into account smooth variations in the phase of the image to recover high-resolution information, we also included as a comparison a reconstruction using a standard partial Fourier method that estimates smooth phase from the symmetric region of k-space³⁴ applied with our own custom software to the raw data.

Prospective in vivo diffusion

The prospective in vivo diffusion experiments mirrors the in vivo segmented EPI experiments with the absence of the “gold standard” 100 × 100 parameter maps. DWIs were acquired with a spin-echo EPI sequence at a 100 × 100 matrix size with a 2-mm in-plane isotropic resolution over 38 slices and along 66 isotropically distributed directions at b-values of 0, 1000, and 1500 s/mm². We applied the diffusion-weighted acquisition four times: once for each PF factor of 5/8ths, 6/8ths, 7/8ths, and fully sampled, with the intention that the fully sampled DWIs with current SoA processing serve as a gold standard. The acquisition parameters were set based on the shortest values we could achieve for the fully sampled acquisition, leading to a TR of 9 seconds and a TE of 105 ms. The partial Fourier acquisitions used a standard protocol. For this data set, we did not apply any other corrections such as eddy current correction or motion correction, only using the adaptive combine method⁴² outside of the vendor reconstruction software. As with the gold standard experiments, parameter map estimation was done with a weighted linear least squares approach.⁴³

Diffusion pathology

To assess the method in the presence of pathology, we obtained data from a previous study of a patient with multiple sclerosis. For this, we had access to vendor-reconstructed DICOMs, so we were only able to process non-PF images with the MCNN and SoA models. The images were acquired using parallel imaging with an in-plane acceleration factor of 2 and a multiband factor of 2 with b-values of 0, 1000, and 2000 s/mm² over 89 isotropic directions with a TE of 100 ms and a TR of 3.5 seconds. The images were reconstructed at a 130 × 130 matrix size with a 1.69 mm isotropic resolution. This required retraining the MCNN model for the new target matrix size. After processing with the MCNN and SoA methods, we estimated parameter maps with a weighted linear least squares approach⁴³ after processing with the MCNN and SoA models.

Cervical spine experiments

To assess the performance of the method on other anatomies, we also acquired T2-weighted cervical spine data. The cervical spine data set was acquired with a standard clinical protocol that involved a 2D tubo spin-echo acquisition with 75% phase undersampling 240 × 320 acquisition matrix size with a TE of 103 ms and a TR of 3.8 seconds. The reconstructed images had a 0.625 isotropic resolution in the sagittal plane. The frequency-encoding direction was in the A/P direction. For performing deGibbsing at this resolution, we retrained the network, adjusting the MCNN model to produce a target image that included the 75% phase undersampling, but with Gibbs artifacts removed. This was accomplished by applying a phase undersampling mask in the simulation and altering the target resolution to 320 × 320. This adjustment discourages the network from trying to fill in the missing high-resolution information. We applied mild dithering to the resulting image—a practice applied in previous works with CNN-based models.⁴⁴

3 |. RESULTS

3.1 |. Canonical experimental results

Figure 3A,B shows the performance of the network in a canonical deGibbsing experiment with a hard edge with the edge oriented at 0 and 45 degrees, respectively. Both the CCNN and the MCNN methods performed similarly at both angles, with the main difference being the sharpness of the edges with the MCNN method both at the simulated edge and the image boundaries. These image boundary residual artifacts do not appear in the 45° plot since this profile does not reach the image boundaries.

Figure 3C,D shows the response of the CCNN in the edge experiments across a range of contrast-to-noise ratios. Above a CNR of 1, the CNN FWHM rapidly converges toward 1. Below a CNR ratio of 1, the network’s FWHM increases as the CNR approaches 0. Figure 3 also shows a composite image of CNN image estimates, $f_{\widehat{\theta }}\left({\mathbf{x}}_t\right)$, across CNR factors. Figure 3 shows visually how as the CNR decreases, the edge begins to blur.

Figure 4 shows profiles of the mean spectral response, $\overline{h}(\mathit{f})$, in the partial Fourier direction of the CCNN model across different partial Fourier factors and SNR levels over the entire test set. The spectral responses were calculated from the 2013 test split of ImageNet as described in Section 2.3.1. As the SNR decreases, the network applies more smoothing, resulting in a decrease of the spectral magnitude at high frequencies of about 30% at an SNR value of 1. The MCNN method exhibited similar profiles, but with more smoothing at low SNR—the MCNN smoothing without partial Fourier at an SNR of 1 led to about 50% attenuation of the high frequencies. In all cases, we observed features in the spectral responses around spectral cutoff points—this included the ripples at the edge of the sampled k-space in the No PF setting, with further cusps developing near the PF cutoff points in the PF settings.

FIGURE 4.

Spectral responses in the partial Fourier direction across different partial Fourier factors and SNR levels for the CCNN model. “PFC” indicates the partial Fourier cutoff. Ripples can be seen that are related to the Gibbs effect and the PF cutoffs. In the partial Fourier cases, the CCNN response has a cusp in the frequency response at the level of the partial Fourier factor. The response beyond the PFC characterizes the ability to restore the missing Fourier harmonics. At lower SNRs, the PFC singularity gradually disappears, and the CCNN model becomes a low-pass filter, applying more smoothing to compensate for the increased noise. Profiles for the MCNN method were similar, but resulted in smoothing at the lower SNR levels

Quantitative results on the ImageNet test set are shown in Table S1 in the Supporting Information. For MSE, the CCNN model performed better than the MCNN model at equivalent partial Fourier factors, and performance generally decreased with increased acceleration. This trend was repeated for PSNR, but MCNN models displayed higher SSIM values.

3.2 |. In vivo results

“Gold standard” segmented EPI

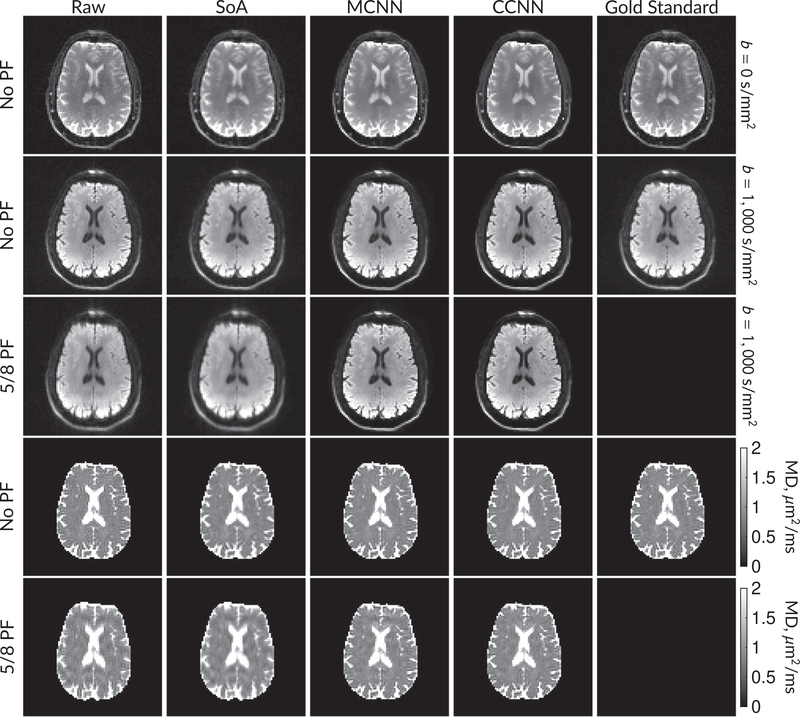
Figure 5 shows b = 0 s/mm² images, average b = 1000 s/mm² images, and mean diffusivity (MD) images without partial Fourier (No PF) and with 5/8ths partial Fourier (5/8 PF) calculated from the segmented EPI experiments. The far right column shows the “gold standard” segmented EPI diffusion processing results. This data has minimal Gibbs artifacts. The other columns consist of experimental data processing methods that should approach the “gold standard” column.

FIGURE 5.

DW and MD images from various methods performed on segmented EPI data. At the top are shown the b = 0 s/mm² and averaged b = 1000 s/mm² images from Raw, SoA, MCNN, and CCNN methods. The final column shows the “gold standard,” results from apodizing the full segmented EPI data set and cropping. Comparisons with and without partial Fourier are shown for b = 1000 s/mm² images and mean diffusivity images. Partial Fourier artifacts are mitigated in the CNN methods

Mean diffusivities calculated from the raw DWI data (Raw) show notable noise and Gibbs ringing artifacts, while this is removed with the SoA method. However, the SoA method begins to lose its ability to compensate for the Gibbs ringing and resolution loss when partial Fourier is utilized in the acquisition. Partial Fourier artifacts are reduced in the CNN methods. Other slices from this data are shown in the Supporting Information in Figures S7–S11.

Prospective in vivo diffusion

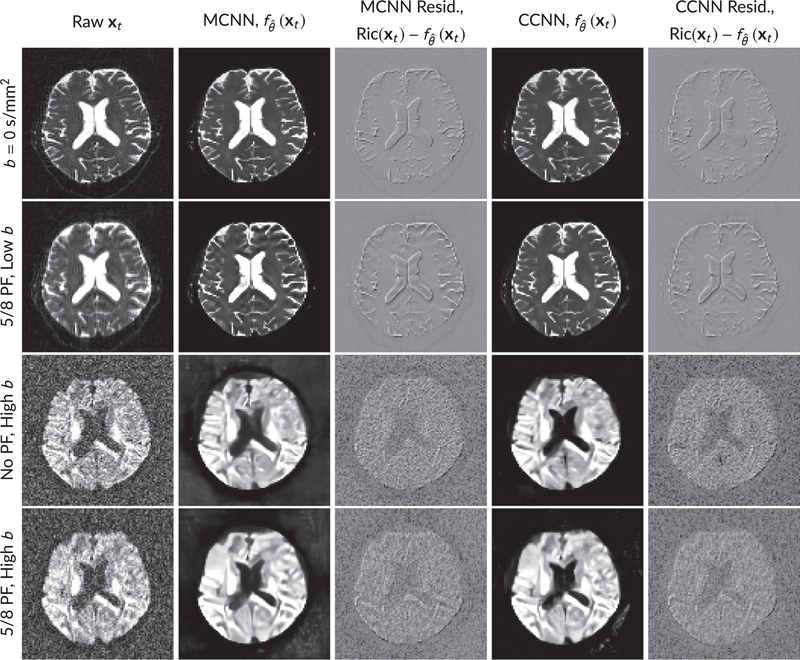
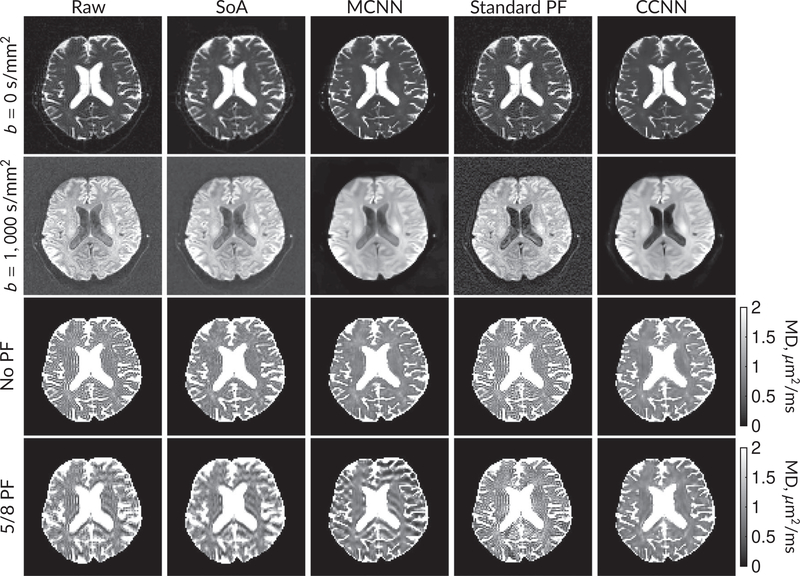
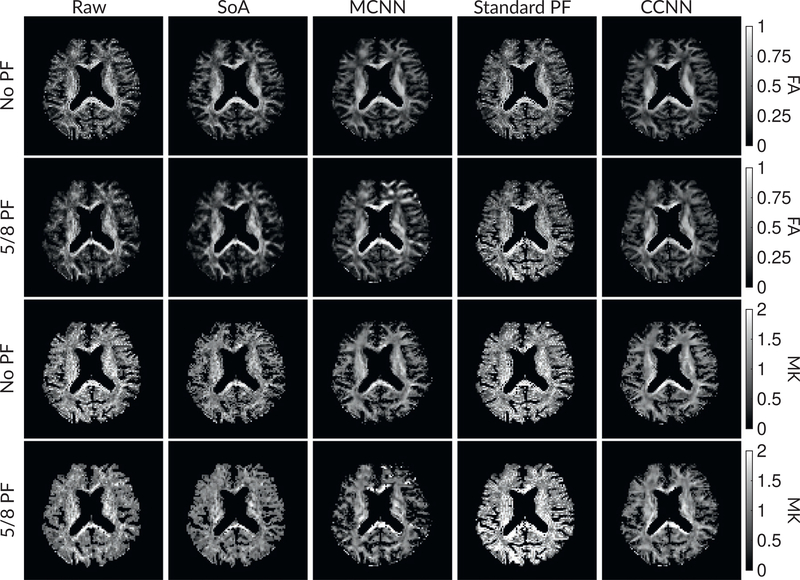
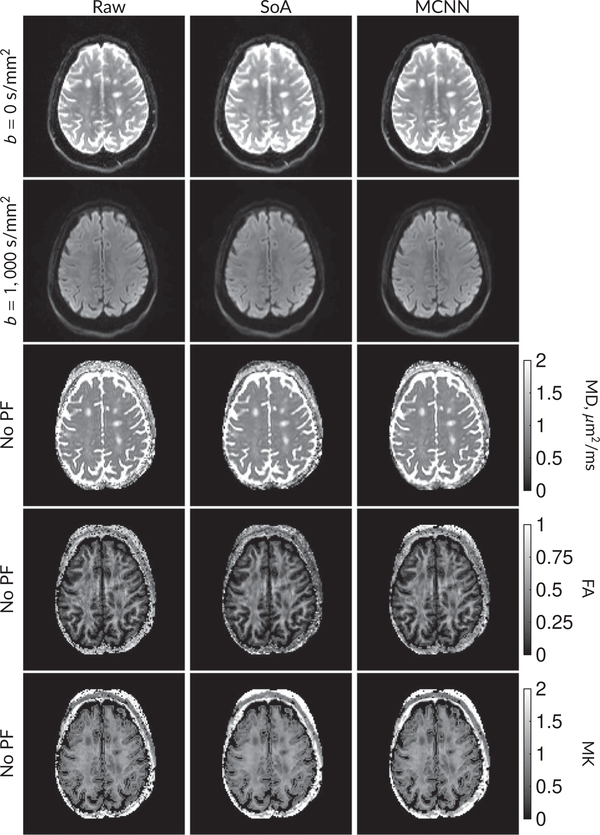
Figure 6 shows examples of images from the prospective data before and after processing at low (b = 0 s/mm²) and high (b = 1 500 s/mm²) diffusion gradient strengths. The raw images (Raw) served as the input for the magnitude deep learning (MCNN) and complex deep learning (CCNN) methods. Figures 7 and 8 show parameter maps for prospective diffusion data. Figure 7 shows DWIs and mean diffusivity, whereas Figure 8 shows fractional anisotropy and mean kurtosis. Aside from the MCNN method, results are similar to those shown in Figure 6, with the SoA, MCNN, and CCNN methods all removing artifacts without partial Fourier, whereas the CCNN method is the only method able to remove artifacts at 5/8 partial Fourier. This is most obvious in the MD parameter maps. Similar trends are observed in the other diffusion parameter maps. The effects of denoising are primarily visible in the mean kurtosis images, where SoA, MCNN, and CCNN achieve substantial noise reduction.

FIGURE 6.

Examples of images from in vivo data at low b (b = 0 s/mm²) and high b (b = 1500 s/mm²). Artifacts in the Raw image, x_t, are corrected by the MCNN and CCNN models, $f_{\widehat{\theta }}\left({\mathbf{x}}_t\right)$. Also shown are the residuals between the CNN corrections and the original Raw image with Rician bias correction Ric(x_t).¹⁰ The Gibbs and noise artifacts removed by the methods are observed in the residuals. Gibbs removal is prevalent at b = 0 s/mm², whereas noise removal is more prevalent at b = 1500 s/mm²

FIGURE 7.

DW and MD images from various methods performed on prospective diffusion data. At the top are shown the b = 0 s/mm² and average b = 1000 s/mm² images from Raw, SoA, MCNN, standard partial Fourier, and CCNN methods. Rows 3 and 4 show results for mean diffusivity. The SoA method and both deep learning methods perform well without partial Fourier acceleration; however, at the 5/8ths partial Fourier factor, artifacts are present for all methods other than the CCNN method

FIGURE 8.

Parameter maps from various methods with CSF masks. Rows 1 and 2 show the FA images from Raw, SoA, MCNN, standard partial Fourier, and CCNN methods, with MK images being in rows 3 and 4. Succeeding rows alternate the inclusion of partial Fourier encoding

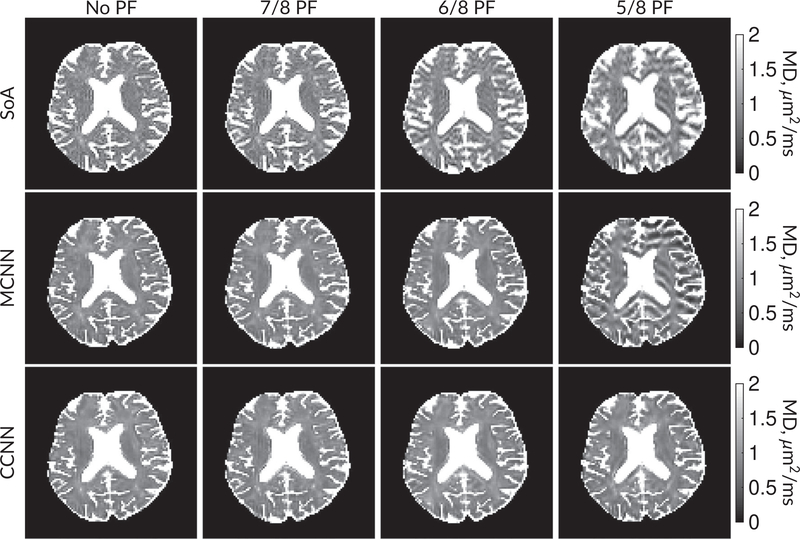
Figure 9 compares MD maps across various partial Fourier factors between the MCNN, CCNN and SoA methods. The methods perform similarly without partial Fourier acceleration, but as partial Fourier acceleration increases, the image is continually degraded in the SoA method, with “black voxels” appearing around the lateral ventricles. The CCNN method mitigates the appearance of these artifacts in the parameter maps. Other slices from this data set are shown in the Supporting Information in Figures S12–S16.

FIGURE 9.

Comparison of mean diffusivity (MD) parameter maps across PF factors of 5/8ths, 6/8ths, 7/8ths, and without PF (No PF). The methods include SoA, MCNN, and CCNN methods. Without partial Fourier, all methods are similar; however, as the PF factor increases, substantial artifacts are introduced in the SoA and MCNN methods. The CCNN method is able to reduce the introduction of artifacts

Diffusion pathology

Figure 10 shows results from in vivo diffusion pathology. In this case, we only had access to magnitude DICOMs with iPaT acceleration, so only the MCNN method was used. We observed similar artifact characteristics as in the previous Figures 5, 7, and 8. In this case, all three methods provide similar diffusion parameter maps for MD, FA, and MK. Other slices from this data set, including zoomed images of pathology, are shown in the Supporting Information in Figures S17–S22.

FIGURE 10.

Parameter maps calculated for a patient with multiple sclerosis. MS lesions are visible in all three parameter maps. Both the SoA and magnitude-input CNN (MCNN) methods are able to denoise parameter maps relative to the original (Raw) data. Images zoomed on the lesions are shown in the Supporting Information

Cervical spine experiments

We show cervical spine results in the Supporting Information in Figure S24.

4 |. DISCUSSION

Our results indicate that with carefully crafted simulations, it is possible to train CNN models based solely on MR encoding operators that can be applied to in vivo MR imaging data. We characterized the performance of this method with canonical experiments, showing Gibbs removal capability with hard edges, as well as providing evidence that the network’s denoising capability depends on signal-adaptive smoothing, and that this smoothing largely takes place at contrast-to-noise ratios below 1. In principle, there are no restrictions on applying the method in new applications other than retraining based on the application image matrix size. When reconstruction and preprocessing steps failed to remove artifacts, the network also generally preserved them.

4.1 |. Effects of in vivo reconstruction method

The results diverged depending on the reconstruction method between the segmented EPI and prospective diffusion experiments. This could be due to the ordering of partial Fourier versus adaptive coil combination. In the segmented EPI experiment, the partial Fourier masking was done after coil combination (as coil combination was done by the vendor reconstruction software). This exactly matched the partial Fourier masking of the simulation. In the prospective diffusion experiment, coil combination was done after partial Fourier masking, which did not match the simulation. This may be the reason for the failure of MCNN for prospective diffusion at extreme partial Fourier factors. The effect seems to have been benign for MCNN method at lower partial Fourier accelerations. The effect was also benign for the CCNN method, as it was trained to use smooth phase. As the prospective diffusion experiment is more representative, we would only recommend the CCNN method out of the methods we tested when using extreme partial Fourier acceleration. For other balanced accelerations like parallel imaging (eg, the pathology data), we did not observe effects on either model. The in vivo results here should be considered an initial demonstration of the potential of the method. Validation studies, particularly those studying the effects of reconstruction method, are necessary before adoption in target applications.

4.2 |. Data set considerations

Practically, the success of the approach can be attributed to (a) having a sufficiently deep neural network able to adequately capture the difference between Gibbs-corrupted and ground-truth images and (b) to the heterogeneity of the synthetic training set and the richness of the encoding simulations providing ample training data. During training, the models saw over 10 million candidate phase maps simulated on over 1 million baseline images. Data sets of this size are difficult to acquire in medical imaging, and impossible to acquire for the purpose of simulating Gibbs artifacts in diffusion-weighted imaging. We ran one experiment on a smaller data set size, using 1% of ImageNet (about 12 000 images). Although the resulting models performed reasonably on ImageNet validation data, they failed on in vivo data, producing diffusion parameter maps outside of physiological ranges (shown in Figure S23 of the Supporting Information). This suggests that the proposed approach overfits on 1% of ImageNet, but this overfitting is mitigated when using the full ImageNet data set. Training such a model requires careful consideration of the simulation process and its relationship with the test data set. As we see in Figures 6 and 7, subtle or benign artifacts in the DWIs are substantially magnified in the corresponding parameter maps. To consider the effects of overfitting, we designed our experiments to have not only separate training, validation, and test data sets as different groups of images, but to have the test phase of the experiments consider images of a different class. Prior to our diffusion imaging experiments, we did not use MR images. In principle, this would allow detection of overfitting errors when testing on healthy subjects. As shown in Figure 10, we did not detect issues using the model on patients with pathology.

4.3 |. Future directions

Our results were achieved by processing each DWI separately, which could be advantageous in that the processing of each image is independent of artifacts that may be present in other images. However, a disadvantage is that the proposed methods do not fully leverage the repetitive correlations present in applications such as diffusion MRI. It is difficult to denoise images at high b-values without access to information from low b-value images. Such relations are considered in the random matrix denoising method.¹⁰ This suggests that one avenue to explore in the future for diffusion would be to combine the random matrix theory-based denoising¹⁰ as a preprocessing step, able to incorporate the correlations between different DWIs, with the subsequently improved performance of CCNN-based removal of Gibbs and other artifacts.

Lastly, we note that an independent work recently appeared on the topic of Gibbs removal in MRI.⁴⁵ Although this and the present paper share target applications, they differ fundamentally in approach, with ours focusing on simulations and the effects of Gibbs on higher-order diffusion parameters such as mean kurtosis, while the cited work uses a k-space masking framework on in vivo MR data. Both these methods represent interesting approaches, with an item of future work being to explore relative benefits and tradeoffs in target applications.

5 |. CONCLUSION

We have shown that Gibbs artifacts and noise can be substantially reduced by training a convolutional neural network with simulations of the image acquisitions. We demonstrated our method on canonical experiments and in vivo data that includes healthy subjects and those with pathology, and showed its potential for artifact removal. The method can be applied independently on each slice of the imaging data set, enabling its use in many clinical settings such as clinical diffusion MRI where few diffusion directions may be available. In the future, we will examine possible extensions, including consideration of 3D anatomical structures, correlations across repetitive acquisitions, explicit incorporation of physics into the model, and validation on other clinical applications.

Supplementary Material

Subinfo

FIGURE S1 Diagram showing key simulation steps. A latent, high-resolution image from ImageNet has the Gibbs effect simulated via k-space cropping. Then, noise is added. After noise addition, a partial Fourier mask is applied that leads to some blurring of the image. This serves as the input image, x_d. The target image is obtained by interpolatin the high-resolution image to a lower resolution without the Gibbs artifact

TABLE S1 Table of metrics for CCNN and MCNN models at 100 × 100 and 130 × 130 matrix sizes for the ImageNet test set. Metrics were averaged between images of the ImageNet test split and are shown ± standard deviations

FIGURE S2 Activations across PF factors. (top) Original x_t input to the neural network at an SNR of 1024. (bottom) Activations from one channel prior to first wavelet transform. The activations in early layers enhance the Gibbs artifact, which is then subtracted from the image in the final step

FIGURE S3 Images of activations from all 64 channels prior to the first wavelet transform. Some activations enhance Gibbs artifacts, while others smooth the image or detect alterations in the phase. The overall characteristics of the network are an integration of the activations

FIGURE S4 Mean-squared difference metrics between various processing methods and the gold standard segmented EPI reference with 95% confidence intervals. All metrics were calculated slice-by-slice and then averaged across slices

FIGURE S5 Structural similarity metrics between various processing methods and the gold standard segmented EPI reference with 95% confidence intervals. All metrics were calculated slice-by-slice and then averaged across slices

FIGURE S6 PSNR metrics between various processing methods and the gold standard segmented EPI reference with 95% confidence intervals. All metrics were calculated slice-by-slice and then averaged across slices

FIGURE S7 b = 0 s/mm² images corresponding to slices 3, 6, and 9 (out of 10) for the segmented EPI experiment in the main body

FIGURE S8 Average b = 1000 s/mm² images corresponding to slices 3, 6, and 9 (out of 10) for the segmented EPI experiment in the main body

FIGURE S9 Mean diffusivity images corresponding to slices 3, 6, and 9 (out of 10) for the segmented EPI experiment in the main body

FIGURE S10 Fractional anisotropy images corresponding to slices 3, 6, and 9 (out of 10) for the segmented EPI experiment in the main body

FIGURE S11 Mean kurtosis images corresponding to slices 3, 6, and 9 (out of 10) for the segmented EPI experiment in the main body

FIGURE S12b = 0 s/mm² images corresponding to slices 10, 20, and 30 (out of 38) for the prospective in vivo data from the main body

FIGURE S13 Average b = 1000 s/mm² images corresponding to slices 10, 20, and 30 (out of 38) for the prospective in vivo data from the main body

FIGURE S14 Mean diffusivity images corresponding to slices 10, 20, and 30 (out of 38) for the prospective in vivo data from the main body

FIGURE S15 Fractional anisotropy images corresponding to slices 10, 20, and 30 (out of 38) for the prospective in vivo data from the main body

FIGURE S16 Mean kurtosis images corresponding to slices 10, 20, and 30 (out of 38) for the prospective in vivo data from the main body

FIGURE S17 b = 0 s/mm² images corresponding to slices 15, 25, and 35 (out of 50) for the MS pathology data set in the main body

FIGURE S18 Average b = 1000 s/mm² images corresponding to slices 15, 25, and 35 (out of 50) for the MS pathology data set in the main body

FIGURE S19 Mean diffusivity images corresponding to slices 15, 25, and 35 (out of 50) for the MS pathology data set in the main body

FIGURE S20 Fractional anisotropy images corresponding to slices 15, 25, and 35 (out of 50) for the MS pathology data set in the main body

FIGURE S21 Mean kurtosis images corresponding to slices 15, 25, and 35 (out of 50) for the MS pathology data set in the main body

FIGURE S22 Zoomed pathology images from slice 35, showing MS lesions at b = 0 s/mm² and with MD, FA, and MK parameter maps

FIGURE S23 DWIs and parameter maps computed using the CCNN and MCNN models trained with only 1% of ImageNet data. In this case, the models were applied to data without partial Fourier acceleration. The resulting parameter maps are largely outside of physiological ranges

FIGURE S24 (top) Images of cervical spine data before (left) and after (right) MCNN deGibbsing. (bottom) Zoomed-in regions, highlighting deGibbsing effects in the box with the original image (left) and MCNN image (right)

APPENDIX A

PHASE SIMULATION

Inspired by results from functional approximation theory^46,47 and machine learning,⁴⁸ we approximate the phase as being a summation of Gaussian radial basis functions:

$$p_{\mathrm{sim}}(\mathbf{r})=\exp \left(i\sum _{s=1}^S\sum _{b=1}^{B_s}{a}_{b,s}{e}^{-\frac{1}{z_s}\Vert \mathbf{r}-{\mathbf{r}}_{0,b,s}|{|}_2^2}\right),$$ (A1)

where p_sim(r) is the phase map, r is a 2-length vector for spatial position, a_b,s is the amplitude of the (b,s)th basis function, r_0,b,s is the center of the (b, s)th basis function, and z_s governs the width of the basis functions in the sth subset. In functional approximation theory, formulations like (A1) are used to build a candidate for p_sim(r) given a set of points, (a_b,s, r_0,b,s), b ∈ [1, …, B_s] (z_s is usually chosen to be fixed). However, rather than estimate p_sim(r) from a measured cloud of points, our goal is to randomly generate an example from a synthetic cloud of points. For each training example, we randomly generate p_sim(r) according to the following model:

$$\begin{gathered} S\sim \text{Poisson}\left({\lambda }_S\right) \\ {B}_s\sim \text{Poisson}\left({\lambda }_B\right) \\ {z}_s\sim \left|\mathcal{N}\right|\left({\mu }_z,{\sigma }_z\right) \\ {a}_{b,s}\sim \mathcal{N}\left({\mu }_a,{\sigma }_a\right) \\ {r}_{0,b,s,j}\sim \mathcal{V}\left(r_{\min ,j},r_{\max ,j}\right), \end{gathered}$$

where $\mathcal{N}$ indicates a Gaussian distribution, $\left|\mathcal{N}\right|$ is a folded Gaussian distribution, and $\mathcal{V}$ indicates a uniform distribution. The parameters λ_S, λ_B, μ_z, σ_z, μ_a, and σ_a are set for training, and r_min,j and r_max,j are the minima and maxima for r in the jth imaging dimension. Contrary to practice in the approximation literature, we allow z_s to vary to avoid the degenerate training case where networks create filters to detect Gaussian functions of a fixed width.

When B_s and S are not too large, p_sim(r) will typically be smooth as in real application settings; however, sharp changes can also occur during training when basis function centers are near each other. As a further form of data augmentation, we include a 1% probability that no phase at all is simulated. Figure 1B,C shows an example of simulated phase compared to real phase from in vivo data. For our experiments, we used λ_S = 12, λ_B = 15, μ_z = 64 pixels² σ_z = 100 pixels², μ_a = 0°, and σ_a = 5°. We set r_min,j and r_max,j to restrict the center of the Gaussian basis function to the image support in the jth dimension.