Influence of Structural and Functional Brain Connectivity on Age-Related Differences in Fluid Cognition

Abstract

We used graph theoretical measures to investigate the hypothesis that structural brain connectivity constrains the influence of functional connectivity on the relation between age and fluid cognition. Across 143 healthy, community-dwelling adults 19–79 years of age, we estimated structural network properties from diffusion-weighted imaging (DWI) and functional network properties from resting-state functional magnetic resonance imaging (fMRI). We confirmed previous reports of age-related decline in the strength and efficiency of structural networks, as well as in the connectivity strength within and between structural network modules. Functional networks, in contrast, exhibited age-related decline only in system segregation, a measure of the distinctiveness among network modules. Aging was associated with decline in a composite measure of fluid cognition, particularly tests of executive function. Functional system segregation was a significant mediator of age-related decline in executive function. Structural network properties did not directly influence the age-related decline in functional system segregation. The raw correlational data underlying the graph theoretical measures indicated that structural connectivity exerts a limited constraint on age-related decline in functional connectivity.

1. Introduction

1.1. Age-related differences in brain connectivity and cognition

Fluid cognitive abilities, which depend on the rapid and flexible coordination of attention and memory, decline during healthy aging, relative to knowledge- and expertise-based (crystallized) abilities, which often exhibit age constancy (Craik and Bialystok, 2006; Kramer et al., 1994; Park et al., 2002; Salthouse, 1996). Previous neuroimaging studies with positron emission tomography (PET), structural magnetic resonance imaging (MRI), and functional MRI (fMRI) have demonstrated that aging is associated with alterations in brain structure and function, including a decrease in the integrity of white matter and decrease in the functional connectivity among cortical regions, which may contribute to the age-related decline in fluid cognition (Bennett and Madden, 2014; Fjell et al., 2016; Fjell and Walhovd, 2010; Grady, 2017; Hedden et al., 2016; Madden et al., 2017; Ruiz-Rizzo et al., 2019; Salat, 2011). Broadly, both structural connectivity (usually assessed from the integrity of the white matter pathways connecting cortical regions) and functional connectivity (usually assessed from the correlation of resting-state fMRI time series between cortical regions) tend to decrease with increasing age (Damoiseaux, 2017; Ferreira and Busatto, 2013; Sala-Llonch et al., 2015). The age-related decline in structural connectivity is consistent across studies. However, the functional connectivity between cortical regions may be indirect or rely on multiple white matter pathways (Damoiseaux and Greicius, 2009; Honey et al., 2009), and as a result, both increases and decreases in functional connectivity with age have been observed across selected cortical regions (Betzel et al., 2014; Biswal et al., 2010; Song et al., 2014; Tomasi and Volkow, 2012).

Studies of younger adults suggest that structural connectivity constrains functional connectivity, though these studies have focused primarily on the medial prefrontal and posterior cingulate regions comprising the default mode network (Greicius et al., 2009; Hermundstad et al., 2013; Honey et al., 2007; Zhu et al., 2014). Networks of structural and functional connectivity are not isomorphic, however, and tend to diverge in higher-order association cortical regions (Batista-García-Ramó and Fernández-Verdecia, 2018; Mišić et al., 2016; Vázquez-Rodríguez et al., 2019). Under the best of circumstances, structural connectivity accounts for 50% of the variance in functional connectivity(Suarez et al., 2020). In the first study to combine measures of structural and functional connectivity in the context of aging, Andrews-Hanna et al. (2007) reported age-related decline in functional connectivity strength of default mode cortical regions (e.g., posterior cingulate and medial prefrontal regions) and a dorsal attention system (e.g., intraparietal sulcus and frontal eye field). Andrews-Hanna and colleagues also found that the decline in functional connectivity was associated with declines in both white matter integrity and fluid cognition. Later studies have confirmed that structural and functional connectivity are statistical mediators of the relation between age and fluid cognition (Chen et al., 2009; Fjell et al., 2016; Hedden et al., 2016; Li et al., 2020; Madden et al., 2017).

The relation between age-related effects for structural and functional connectivity, however, is less clear. Andrews-Hanna et al. (2007) and Chen et al. (2009) both reported a positive relation between functional connectivity and regional white matter integrity (fractional anisotropy; FA) for older adults. Zimmerman et al. (2016) proposed that a specific pattern of structural-functional connectivity coupling predicted age more reliably than did either form of connectivity alone. Fjell et al. (2016) observed that structural connectivity was a better predictor of longitudinal decline in executive function than functional connectivity. In contrast, Fjell et al. (2017) found that functional connectivity within anatomically defined white matter tracts was not consistently higher than functional connectivity to regions outside of the tracts. Further, the cross-sectional age-related trajectories differed for structural and functional connectivity, and these measures changed in a largely independent manner across a 3.3 year longitudinal span, leading Fjell et al. (2017) to conclude that structural connectivity only weakly constrained the age-related differences in functional connectivity. Similarly, Tsang et al. (2017) found that cross-sectional age-related differences in structural and functional connectivity were unrelated to each other.

1.2. Graph theoretical measures of brain connectivity

As noted previously, structural connectivity is typically defined from some microstructural property of cerebral white matter pathways, such as FA or the number of white matter streamlines, derived from tractography. In contrast, functional connectivity is based on the correlation of fMRI time series, often measured during a resting state, obtained either from anatomically or functionally defined cortical regions of interest (ROIs), or from the whole brain in voxelwise analyses (e.g., independent component analysis; ICA). As a result, however, the variables comprising structural and functional connectivity data have qualitatively different measurement properties, which may contribute to the inconsistent findings that have been reported. Graph theory (Rubinov and Sporns, 2010; Rubinov and Sporns, 2011; Sporns and Betzel, 2016; Sporns et al., 2004; van den Heuvel and Sporns, 2013) provides a potentially useful conceptual and measurement framework in which to investigate age-related differences in both structural and functional connectivity. In graph theory, the brain is viewed as a network of nodes with structural or functional connections (edges) between them. Nodes are ROIs that can be defined either anatomically, as a set of cortical and subcortical gray matter regions (Desikan et al., 2006; Jao et al., 2013; Tzourio-Mazoyer et al., 2002), or functionally, as regions with consistent patterns of task-related or resting-state activity (Laird et al., 2011; Power et al., 2011; Wig et al., 2014; Yeo et al., 2011). The matrix of all possible connections between pairs of nodes represents the whole-brain network. If a network (either structural or functional) is not random, then it will comprise a number of communities, or modules, which are distinct sets of nodes that are highly interconnected.

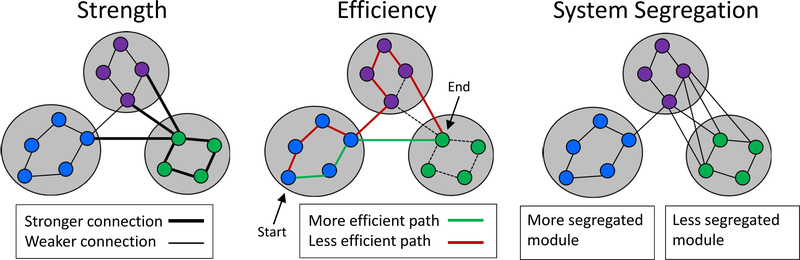
To date, MRI findings, derived primarily from younger adults, suggest that brain structure and function exhibit characteristically small-world properties, expressed as a limited number of modules that have high within-module connectivity, and fewer long-range connections across modules (Bassett and Bullmore, 2006; Bullmore and Sporns, 2009). These small-world properties, especially the presence of modules, are hypothesized to be an evolutionary adaptation that maximizes the efficiency of responding to task demands and resilience to focal damage (Achard and Bullmore, 2007; Crossley et al., 2013; Mišić and Sporns, 2016; Wig, 2017). Graph theoretical measures provide a fine-grained characterization of different properties of connectivity both within and between modules (Figure 1). In addition to the efficiency of information transmission (the number of intervening edges), the strength of connectivity can be defined for both structural data (e.g., the number of streamlines between nodes) and functional data (e.g., the strength of the correlation between nodes). Further, system segregation, defined as the relative preponderance of within-module connections to between-module connections, reflects the degree to which modules are distinct or differentiated from each other.

Figure 1.

Graph theoretical measures. Strength: the number of white matter streamlines, estimated from DWI, between nodes (anatomical regions of interest), for structural data, or the correlation of resting-state time series, between nodes, for functional data. Efficiency: the number of edges that must be traversed to connect two nodes, where fewer = better. System Segregation: the degree to which modules (sets of highly connected nodes) are distinct from each other, expressed as the ratio of within-module connections to between-module connections.

Previous MRI investigations applying graph theoretical measures to age-related differences in functional brain connectivity have been concerned primarily with resting-state connectivity. Age-related trends in functional network properties are not entirely consistent, but findings from several studies suggest that functional connectivity between modules is better preserved as a function of age than within-module connectivity (Damoiseaux, 2017; Sala-Llonch et al., 2015; Wig, 2017). As a result, functional modules become less distinct or separate with increasing age, expressed in graph theoretical terms as decreased modularity and system segregation. Chan et al. (2014), for example, have reported that system segregation in resting-state fMRI data declined with increasing age in healthy adults 20–89 years of age, reflecting a greater age-related decrease in the strength of within-module functional connectivity relative to between-module connectivity, particularly for modules in association cortex. This pattern of functional connectivity was more prominent for individuals over 50 years of age and was predictive of long-term memory function, independently of age. Chong et al. (2019) reported a longitudinal decline in system segregation, as well as a cross-sectional association between worse cognitive performance and lower module segregation and distinctiveness in older adults. Several other investigations have reported age-related decline in the distinctiveness of modules, based on measures of the strength and efficiency of within- and between-module connectivity (Bagarinao et al., 2019; Betzel et al., 2014; Cao et al., 2014; Geerligs et al., 2015; Grady et al., 2016; Song et al., 2014; Spreng et al., 2016). Overall, the graph theoretical investigations of resting-state functional connectivity support the concept of age-related neural dedifferentiation, the idea that aging is associated with a decline in the specialization or separation of functional neural modules (Geerligs et al., 2014; Goh, 2011; Park et al., 2004).

Graph theoretical investigations of age-related differences in brain structure more consistently report age-related decline in structural connectivity, with some variation in the degree to which strength and efficiency decline. The first application of graph theoretical measures to this issue (Gong et al., 2009) found that, in a sample of 95 healthy adults 19–85 years of age, the overall structural connectivity strength between cortical nodes declined with age, whereas the global efficiency of the connections (i.e., the shortest path between any two nodes in the whole network) was constant. Age-related differences were evident, however, in the efficiency of nodes within specific regions, such that the efficiency of nodes in occipital and parietal cortical regions decreased with age, whereas the efficiency of nodes in frontal and temporal regions increased. Zhao et al. (2015) reported a different pattern, in which both the global and local efficiency of network connections (both within-module and between-module) decreased with increasing adult age, particularly in bilateral prefrontal and temporal regions. Wu et al. (2012) found that structural global efficiency declined with increasing age to a greater extent than did local efficiency, and that fewer between-module connections were evident in the older adults’ data, yielding a more localized and segregated network.

1.3. Age-related differences in the interaction of structural and functional connectivity

A critical issue, which we address in this research, is the interactive influence of structural and functional connectivity on age-related differences in fluid cognition. Previous studies of these different forms of connectivity, in the context of aging (Andrews-Hanna et al., 2007; Chen et al., 2009; Fjell et al., 2016; Hedden et al., 2016; Madden et al., 2017), have most often treated structural and functional connectivity measures as parallel or separate variables and did not test their potential interactions. Applying graph theoretical methods, Betzel et al. (2014) observed that nodes with direct (efficient) structural connections exhibited relatively little age-related change in functional connectivity, whereas nodes with less efficient structural connections were more likely to exhibit an age-related increase in functional connectivity. This pattern suggests that the age-related decrease in functional system segregation reported in other studies (Chan et al., 2014; Chong et al., 2019) may be a result of decreased structural efficiency, with functional connections between structurally disconnected regions relying on indirect paths.

In this investigation, we obtained graph theoretical measures for both structural and resting-state functional connectivity, to determine the influence of these variables on age-related differences in fluid cognition. In a previously published analysis of this cross-sectional data (Madden et al., 2017), we established that measures of executive function exhibited age-related decline beyond that associated with perceptual speed and memory. Estimates of both structural and functional connectivity exhibited age-related decline, and functional connectivity within sensorimotor regions (visual, motor, and basal ganglia/thalamus) mediated the relation between age and executive function. However, as noted above, the earlier investigation did not test the potential influences between structural and functional connectivity, and the ICA methods used to define functional networks did not assess between-network connectivity.

We extend the earlier findings by using graph theoretical measures to characterize different aspects of network connectivity: strength, efficiency, and system segregation, for both structural and functional data, with three overarching hypotheses. First, in the functional connectivity data, we expected to confirm previous findings indicating that with increasing age, modules tend to become less distinct, as expressed in the age-related decline in the graph theoretical measure of functional system segregation (Chan et al., 2014; Chong et al., 2019; Wig, 2017). Second, based on prior findings of a positive relation between functional system segregation and memory performance, with age controlled statistically (Chan et al., 2014), we hypothesized that across a range of adult age (19–79 years), functional system segregation would have a mediating influence on the negative relation between age and fluid cognition. Finally, given the evidence that anatomy exerts some degree of constraint on functional connectivity (Greicius et al., 2009; Hermundstad et al., 2013; Honey et al., 2007; Zhu et al., 2014), and the previous findings indicating an association between age-related differences in structural and functional connectivity measures (Andrews-Hanna et al., 2007; Betzel et al., 2014; Chen et al., 2009; Fjell et al., 2016; Zimmermann et al., 2016), we hypothesized that structural connectivity would have a direct influence on functional connectivity in the context of neurocognitive aging.

2. Materials and methods

2.1. Participants

This research was conducted in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki) for experiments involving humans. The protocol was approved by the Duke University Institutional Review Board, and participants gave written informed consent at the start of the study. The participants were 153 community-dwelling individuals between 19 and 79 years of age. One hundred and forty-five of these individuals were included in the Madden et al. (2017) study. Eight participants had been excluded from the 2017 study due to missing data from another scan sequence (T2-weighted fluid-attenuated inversion recovery; FLAIR), which was not included in the present analyses, and these participants were added to the current data set. All participants were right-handed, had completed at least 12 years of education, did not report any major health issues, including atherosclerosis, neurological, and psychiatric disorders (Christensen et al., 1992).

The participants completed an initial screening session, which comprised the Freiburg Visual Acuity Test (FRACT; Bach, 1996), Dvorine color vision test (Dvorine, 1963), Beck Depression Inventory (BDI; Beck, 1978), Mini-Mental State Exam (MMSE; Folstein et al., 1975), vocabulary subtest of the Wechsler Adult Intelligence Scale-III (WAIS; Wechsler, 1997), and a practice version of the visual search task performed during the event-related functional imaging (reported separately). All participants had corrected visual acuity equal to or better than Snellen 20/40, scored 27 or higher on the MMSE, less than 11 on the BDI, higher than the 50^th percentile on the WAIS-III vocabulary subtest, and 12 or higher on the Dvorine color vision test. Data from nine individuals were excluded due to technical problems with their functional or structural imaging data, and one individual had an unusually high studentized residual score in the psychometric data. The final sample (Table 1) consisted of 143 participants (78 females) with 49 participants between the ages of 19 and 39 years (M = 25.14 years), 43 participants between the ages of 40 and 59 years (M = 51.40 years) and 51 participants between the ages of 60 and 79 years (M = 67.75 years).

Table 1.

Participant Characteristics

Variable	M	SD	Min	Max	r with age
Education (years)	16.80	2.05	12.0	20.0	0.42***
Color Vision	13.87	0.41	12.0	15.0	−0.23*
Visual acuity	−0.06	0.12	−0.23	0.34	0.33***
BDI	2.35	2.54	0.0	9.0	0.15
MMSE	29.09	0.97	27.0	30.0	−0.23*
Vocabulary	55.99	6.33	38.0	66.0	0.16

Note. n = 143. Color Vision = score on the Dvorine plates (Dvorine, 1963). Visual acuity is Log minimum angle of resolution (MAR). Log MAR of 0 corresponds to Snellen 20/20, with negative values corresponding to better resolution. Thus, the positive correlation for acuity represents age-related decline in this measure. BDI = Beck Depression Inventory (Beck, 1978); MMSE = Mini Mental State Exam (Folstein et al., 1975). Vocabulary is the raw score on the vocabulary subtest of the Wechsler Adult Intelligence Scale (Wechsler, 1997). Significance levels are Bonferroni-corrected for six comparisons.

^*p < 0.05 (corrected)

^**p < 0.01 (corrected)

^***p < 0.001 (corrected)

2.2. Cognitive measures

The cognitive outcome measures comprised nine tests of fluid cognition, which targeted three domains: elementary perceptual speed, executive function, and memory, with three indicator variables per domain. With the exception of two memory tests and one executive function test that were standardized psychometric tests, all of the tests were designed for computer administration within E-Prime (Psychology Software Tools, Sharpsburg, PA, USA), and responses were collected from response keys on the computer keyboard. The tests for perceptual speed included: a) simple reaction time (RT; pressing the space bar at the onset of a square); b) choice RT (pressing a left or right key at the appearance of a left- or right-facing arrow); and c) another version of choice RT drawn from the neutral trials of the Stroop task (pressing one of two keys to indicate the displayed color of a word). The tests for executive function included: a) a digit-symbol coding task (Salthouse, 1992); b) a verbal fluency task (Goodglass and Kaplan, 1972; Loonstra et al., 2001), using both letter and semantic category probes; and c) a version of Stroop interference (Stroop, 1935). The Stroop measure was RT to indicate the display color (red or blue) for the words red and blue, intermixed with the non-color (neutral) words art and game. The interference measure was the proportional increase in correct RT for the incompatible trials relative to the compatible trials. The tests for memory included: a) the WAIS Digit Span subtest (Wechsler, 1997); b) the delayed memory subtest from the California Verbal Learning Test (CVLT; Delis et al., 1987); and c) a visual working memory task similar to that of Saults and Cowan (2007). This latter task involved a comparison of two sequentially presented displays, each containing six colored squares. Duration for each display was 1050 ms, and a blank, inter-display interval was 1400 ms. The participant’s task was to make a yes/no keypress response as to whether one of the colored squares in the second display differed from the first display.

To define the cognitive outcome measures, we used a factor-analytic approach (Hedden et al., 2012; Hedden et al., 2016; Salthouse et al., 2015) to obtain domain-specific measures for perceptual speed, executive function, and memory. We obtained the first unrotated factor from a principal axis factor analysis of all nine cognitive tests, partialed for WAIS vocabulary and gender, and used the factor score (for each participant) from the first unrotated factor as a general summary measure of fluid cognition. We then used a similar approach to obtain the first unrotated factor for the three tests in each of the three domains of perceptual speed, executive function, and memory. Because all of the nine tests were intercorrelated, we obtained residual scores for each domain by partialing out the other six tests not associated with that domain, as well as gender and vocabulary. Madden et al. (2017) provide additional procedural details for the cognitive testing and construction of the factor scores.

2.3. MRI data acquisition

The MRI session was conducted approximately one month after the initial screening session. The functional and anatomical imaging data was collected on a 3 T GE MR750 whole-body 60 cm bore MRI scanner (GE Healthcare, Waukesha, WI, USA) equipped with 50 mT/m gradients and a 200 T/m/s slew rate. The scanner possessed an 8-channel head coil that was used for radio frequency reception. Participants wore earplugs to reduce scanner noise and foam pads were used to minimize head motion. Three-plane (straight axial/coronal/sagittal) localizer fast spin echo images were acquired at the start of the scan to define the volume for data collection. Global field homogeneity was ensured by the use of a semi-automated high-order shimming program. Two resting-state runs of T2*-weighted (functional) imaging sensitive to the blood oxygen-level-dependent (BOLD) signal, 4 or 5 runs of event-related T2*-weighted imaging (depending on the in-scanner task, not reported here), 1 run of T1-weighted anatomical images, 2 runs of diffusion-weighted imaging (DWI) and 1 run of T2-weighted FLAIR imaging were recorded.

Anatomical T1-weighted images included 166 straight axial slices that were attained using a 3D fast inverse-recovery-prepared spoiled gradient recalled (SPGR) sequence with repetition time (TR) = 8.13 ms, echo time (TE) = 3.18 ms, inversion recovery time (TI) = 450 ms, field of view (FOV) = 256 mm x 256 mm, flip angle = 12°, voxel size = 1 × 1 × 1 mm, 256 × 256 acquisition matrix, and a sensitivity encoding (SENSE) factor of 2, using the array spatial sensitivity encoding technique and extended dynamic range.

The DWI data of 68 contiguous slices was acquired along the AC-PC plane using dual-echo spin-echo parallel EPI pulse sequence; TR = 9000 ms, TE = 81.3 ms, FOV = 256 mm x 256 mm, flip angle = 90°, voxel size = 1 × 1 × 2 mm, acquisition matrix size = 128 × 128, and SENSE acceleration factor of 2. The DWI scan utilized 30 diffusion-encoding directions (b-value = 1000 s/mm²) with 1 non-diffusion-weighted b₀ (0 s/mm²).

For the resting-state scans, participants were instructed to remain awake with eyes open and to view a fixation cross throughout the run. T2*-weighted gradient-echo EPI functional images were 29 contiguous slices acquired at an axial oblique orientation, parallel to the plane including the anterior and posterior commissures (AC-PC plane) with TR = 1500 ms, TE = 27 ms, FOV = 240 mm x 240 mm, flip angle = 77°, voxel size = 3.75 × 3.75 × 4 mm, 64 × 64 acquisition matrix, and a SENSE factor of 1. Each of the 2 resting-state functional MRI (fMRI) runs comprised a time series of 162 brain volumes, collected over a period of 4.05 min. Four initial radio frequency excitations were performed to achieve steady state equilibrium and were subsequently discarded, resulting in 158 remaining brain volumes per run.

2.4. MRI preprocessing

Study-specific anatomical template

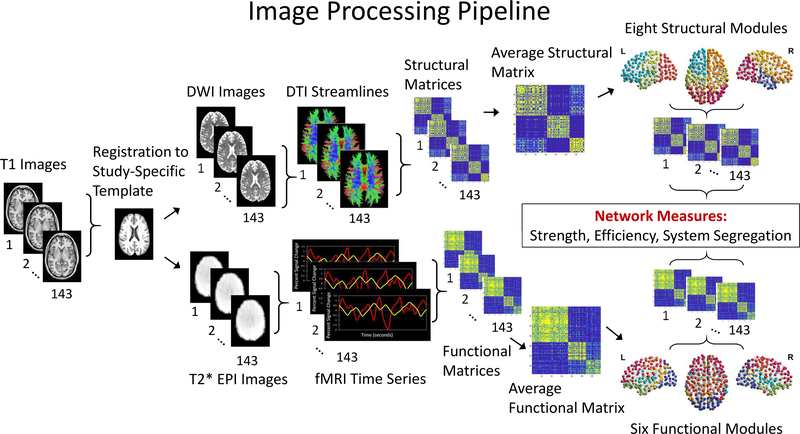
The image processing pipeline is illustrated in Figure 2. We created a study-specific anatomical template using the Advanced Normalization Tools (ANTs) script for multivariate template construction (https://github.com/ANTsX/ANTs/blob/master/Scripts/antsMultivariateTemplateConstruction.sh). First, we made an average T1 brain image from all 143 participants in the data set. Each individual T1 brain was then warped to this starting point average brain. The resultant individually warped T1 images were merged together to create a new averaged template, which became the starting point for the next iteration of warping individual T1 images. The iteration continued until the mean image converged, yielding the final study-specific template.

Figure 2.

Image processing pipeline.

Structural connectivity

To process the structural DWI data we used a custom shell script (https://github.com/ElectricDinoLab/Connectome/blob/master/connectome_maker.sh; Davis et al., 2019), which implements software packages in FSL (FMRIB Software Library) from the Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB; https://fsl.fmrib.ox.ac.uk/fsl/fslwiki; Jenkinson et al., 2012), and MRtrix3 (http://mrtrix.org). Two runs of DWI scans were collected for each participant, which were concatenated to generate one data set for the analysis. The concatenated data were first de-noised with MRtrix using the function dwidenoise, and the brain was extracted from the skull using BET (brain extraction tool) in FSL. The data were preprocessed using the MRtrix dwipreproc function. Head motion and eddy current distortion were corrected using the FSL eddy tool, and bias-field correction was completed with MRtrix function of dwibiascorrect. DWI intensity normalization was applied to the two DWI runs, which were averaged and prepared for tractography. Fiber orientation distribution (FOD) was calculated using dwi2fod with the option of constrained spherical deconvolution (CSD) followed by the generation of whole-brain, probabilistic tractography. MRtrix includes a simplified version of the spherical harmonic model to calculate the coefficient that is used in FOD to generate tracts. For CSD map generation, the maximum number of spherical harmonic terms was set to 8, and a single-fiber response kernel was estimated from white matter voxels with FA > 0.3.

In the tractography, Anatomically Constrained Tractography (ACT) was adopted to define the interface between white matter and grey matter where the streamlines were seeded, to improve the definition of the streamlines. The T1 image was registered to the diffusion image and segmented in FSL into five tissue types: cortical gray matter, subcortical gray matter, white matter, cerebrospinal fluid, and pathological tissue. Following segmentation, the ACT option was added to the tckgen function of MRtrix to anatomically constrain the extent of streamline propagation for the tractography. For each participant, ten million tracts were generated from an iterative procedure with random placement of seeds within the mask, with a step size of 0.2 mm. These tracts were then filtered using SIFT (spherical-deconvolution informed filtering of tractograms) in MRtrix, which identified the false positive tracts, from a cost-function based on the FOD (Yeh et al., 2016), yielding a final set of one million tracts per participant.

Regions of interest (ROIs) for both the structural and functional data sets were those defined by the subparcellated anatomical Harvard-Oxford Atlas (HOA; Jao et al., 2013; Monge et al., 2017) with 397 ROIs. This subparcellated atlas excludes the cerebellum, brain stem, cerebral white matter, and lateral ventricle regions. The regions were derived by sub-sampling the larger regions defined by the automated anatomical labeling (AAL) template image (Tzourio-Mazoyer et al., 2002) to yield a finer-grained parcellation with all regional parcels or nodes comprising an approximately equal number of voxels. This approach yielded a spatial scale of resolution larger than the individual voxel but also smaller than the regions within the AAL template, which can obscure some regionally specific effects (Zalesky et al., 2010). It is also possible to define nodes on the basis of functional connectivity (Wig et al., 2014; Yeo et al., 2011). We believed, however, that using nodes from known anatomy for both structural and functional data would be the least biased approach for defining modules for both types of data. As noted previously in this section, a study-specific template was created based on all 143 participants. The HOA regions were registered to the study-specific template using FLIRT (FMRIB’s linear image registration tool) in FSL and then mapped to the individual participant’s native space to extract the numbers of tracts for each participant. The weighted connectivity matrix of 397 × 397 ROIs was then computed, for each participant, based on the number of streamlines traversing between all pairs of ROIs. All 397 × 397 cells of the averaged matrix were used, and each ROI contained a connectivity value from at least 87% of the participants, although some matrix cells for individual participants were zero. The raw connectivity matrices (397×397×143) were then used for each participant as the basis for the graph theory analysis.

Resting-state functional connectivity

The resting-state fMRI data were preprocessed using an in-house pipeline (https://wiki.biac.duke.edu/biac:analysis:resting_pipeline#download_source) and FSL tools. Four brain volumes were removed from the start of each of the two resting state runs to ensure that the steady state equilibrium was attained. Each of the two runs was then corrected for the sampling offsets inherent in slice-wise EPI acquisition sequences using FSL slicetimer. The two runs were then demeaned and concatenated into a single data set comprising the 8.10 min period. Motion correction using MCFLIRT (motion correction using FMRIB’s linear image registration tool) was applied to the concatenated data set (Jenkinson et al., 2002). Twenty-four motion parameters that included the six realignment parameters, their temporal derivatives and squares were regressed from each voxel using linear regression (Friston et al., 1996). The brain was extracted from the skull with BET, and the data were first normalized into the study specific template and then the standard MNI152 T1 space using FLIRT and FNIRT (FMRIB’s nonlinear image registration tool). Next, signal from white matter and cerebrospinal fluid was regressed out on the basis of masks created with FAST (FMRIB’s Automated Segmentation Tool; Zhang et al., 2001). Global signal regression was not performed, because the global negative index (Chen et al., 2012) was greater than the critical value of 0.03 for each participant, indicating that regressing global signal would not be advantageous. Finally, temporal band-pass filtering limited the data to frequencies in the 0.001– 0.08 Hz range.

We performed additional motion scrubbing of volumes with either > 0.5 mm for framewise displacement (FD) or 0.5% for timecourse variance (DVARS; Power et al., 2012). Two brain volumes before and after the marked volumes were also excluded. From the total 45,188 volumes collected, 421 (0.93%) were excluded on the basis of these motion criteria. Motion-scrubbed volumes did not exceed 22% for any participant. In exploratory analyses, we examined the correlations between FD and the graph theoretical measures that we used as our imaging outcome variables, and none of these correlations was significant.

The resting-state fMRI time series for each participant consisted of 316 brain volumes (concatenated 8.10 min period). For each of the 397 HOA ROIs, for each participant, we first obtained the average time series for all the voxels in the ROI, across the 316 volumes, and then normalized (z-scored) the ROI time series. The normalized resting-state fMRI time series for each of the ROIs was then correlated with the corresponding value for each of the other remaining ROIs, yielding a 397 × 397 correlation matrix for each participant. The Pearson r correlation value in each matrix cell was transformed to Fisher-z.

Because there is ambiguity regarding the interpretation of negative correlations, negatively weighted edges and the diagonals were set to zero, as recommended by Rubinov and Sporns (2010). However, we also conducted an exploratory analysis to examine the nature of connectivity among these negative correlations. We constructed functional matrices with only the negative correlations and then set the diagonals and positive values to zero. We reversed the sign of the negative correlations, because the graph theoretical analyses require positive values. We derived both the network partitions and the modularity value (i.e., Q; the tendency of the network to segregate into partitions, as defined in the following section) for these negative functional matrices. The results indicated that our initial 397 ROIs (network nodes), were partitioned into 297 modules, with an average modularity value (Q) of essentially zero (0.0008). Because the negative correlations did not partition into a limited number of modules, these findings suggest that, in the present data set, the negative correlations were not a systematic source of variance in the functional connectivity data. All reported analyses are based on the positive correlations.

Functional matrices are typically more densely connected than structural matrices, reflecting the many indirect connections, with varying strength, in functional data. We conducted analyses on weighted matrices, rather than on thresholded binarized matrices, for both structural and functional data, to retain sensitivity to this variation in connection strength and to avoid introducing multiple statistical comparisons across different thresholds (Rubinov and Sporns, 2011).

2.5. Graph theoretical measures

In graph theory, a network consists of nodes and edges (connections between nodes), which can be segregated into non-overlapping modules or communities, characterized by stronger within-module and weaker between-module connections. Here, the network nodes were the 397 subparcellated HOA ROIs and the edges were the structural or functional connections between the nodes. We averaged connectivity matrices of all participants to obtain a single structural matrix and a single functional matrix. Module definition is an estimate of the community structure of the network and is influenced by many variables, including the resolution of the partitioning algorithm and the degree of interconnectedness between pairs of communities (Fortunato and Barthélemy, 2007; Traag et al., 2019). Many studies have used previously defined sets of modules, based on patterns of resting-state or task-related fMRI data (Power et al., 2011; Yeo et al., 2011). However, we defined modules in a data-driven manner, within the structural and functional domains, rather than using an independent definition of modular structure, so that the analyses would reflect the network community structure inherent in the data. To compute the optimal partitioning of the whole-brain data into modules, we applied the Louvain algorithm (Blondel et al., 2008) from the Brain Connectivity Toolbox (www.brain-connectivity-toolbox.net; Rubinov and Sporns, 2010) on the group-averaged structural and functional matrices.

For the structural data, using the default value (1.0) of the resolution parameter (gamma; y) of the Louvain algorithm yielded eight interpretable modules. For the functional data, however, using the default gamma of 1.0 yielded only four modules corresponding approximately to cortical lobes. Increasing the gamma to 1.15 yielded six modules that were more interpretable functionally and included anterior and posterior components of the default mode network. Increasing gamma further to 1.25 yielded seven functional modules, which were similar to the partitioning with gamma = 1.15 except that the posterior default mode region was divided into separate modules, which were less easily interpretable. We therefore maintained gamma at 1.15 for the functional data, which produced a modular structure corresponding most closely to previous literature and known anatomy.

Other than different resolution parameters, definition of the modules proceeded in a similar manner, in separate analyses, for the structural and functional data. We used the consensus clustering approach to obtain the optimal partitioning of modules (Lancichinetti and Fortunato, 2012). We ran the Louvain algorithm 150 times on the averaged matrix and calculated an agreement matrix from those 150 iterations, to obtain the proportion of times each pair of nodes were assigned to the same module. To remove any weak or spurious node agreements, we then thresholded the agreement matrices at 0.50, thus retaining values for only those pairs of nodes that were assigned to the same module at least 50% of the time. We then applied the optimal structural and functional modules, derived from the averaged data, to the connectivity data for each participant. The averaged connectivity matrices comprising the eight structural modules and six functional modules are described in more detail in Results (section 3.2.2.).

The term modularity refers to the degree to which all of the nodes in the network (in this case the brain) partition into modules, that is, groups of nodes with strong within-module connections and weaker between-module connections. For a network with c modules, modularity Q is defined by Equation 1:

$$Q=\frac{1}{2m}{\sum }_{i,j}\left[A_{ij}-\frac{k_i{k}_j}{2m}\right]\delta \left(c_i,c_j\right),$$ (1)

where A_ij represents the weight of the edge between nodes i and j, $k_i={\sum }_j{A}_{ij}$ is the sum of the weights of the edges attached to node i, c_i is the community to which node i is assigned, δ is the Kronecker delta function, and $m=\frac{1}{2}{\sum }_{ij}{A}_{ij}$ (Newman and Girvan, 2004).

In our primary analyses we imposed the group-averaged modular partition on the individual participants’ data, but we also examined individual differences in modular structure. When we estimated the structural modules at the individual participant level, the results yielded between eight and ten structural modules for 91.61% of the participants, and the correlation between the number of modules and age was not significant, r = 0.095, p = 0.261. The modularity value Q for the structural data (M = 0.682, SD = 0.011) did not vary significantly with age, r = 0.074, p = 0.382. For the functional data, 98.6% of the participants exhibited between three and six modules, and the number of modules did not vary significantly with age, r = −0.075, p = 0.372. However, Q (M = 0.174, SD = 0.039) decreased significantly with age in the functional data, r = −0.385, p < 0.001, indicating some age-related variation in modular structure.

We also measured the degree to which each person’s modular organization differed from that of the group-averaged data, using the partition_distance function from the Brain Connectivity Toolbox. This function estimates the variation of information (VI), which is a normalized information-theoretic measure of the distance between network organizations, where a VI of 0 represents perfect correspondence of partitions (Meilă, 2007). In the structural data, mean VI was 0.163 (SD = 0.032) and was not correlated with age, r = 0.026, p = 0.7606 (uncorrected). The mean VI for the functional data (M = 0.386; SD = 0.039) was correlated positively with age, r = 0.298, p < 0.0003 (uncorrected), indicating a greater disparity in the modular structure, with increasing age, relative to the average structure. Thus, although the functional data exhibited some age-related differences in modular structure, both the structural and functional data exhibited a constancy in the number of modules consistent with the group-averaged data.

Our analyses focus on four graph theoretical measures that reflect the properties of network information transmission: global efficiency, local efficiency, strength, and system segregation. As described in more detail in the immediately following paragraphs, these measures were calculated both at the whole-brain level and at the individual module level, for each participant, for the analyses of their relation to age and the cognitive outcome measures.

2.5.1. Efficiency

Considering information transmission as a path between two nodes, efficiency represents the number of intervening edges between the nodes, with more efficient paths being characterized by fewer intervening edges (Latora and Marchiori, 2001). Global efficiency is the measure of efficient information propagation across the whole network. It represents the average inverse shortest path length in the network, that is, the minimum number of edges to be traversed between each pair of nodes, averaged across all node pairs. It was calculated by Equation 2:

$$Globalefficiency=\frac{1}{n(n-1)}{\sum }_{i\ne j\in G}\frac{1}{l_{i,j}}$$ (2)

where, n is the number of nodes in the network, l is the shortest path length, and i and j are nodes in graph G. Local efficiency, in contrast, represents information propagation in the neighborhood of an individual node (i.e., nodes that are directly connected to the node). It was calculated by Equation 3:

$$Localefficiency=\frac{1}{n_i\left(n_i-1\right)}{\sum }_{j,k\in g}\frac{1}{l_{j,k}}$$ (3)

where, n_i is the number of nodes in the neighborhood of node i (excluding node i itself), l is the shortest path length, and j and k are nodes in subgraph g (consisting of neighborhood nodes of node i). At the whole-brain level, local efficiency was averaged across all nodes (i.e., the 397 ROIs), whereas at the module level, local efficiency was averaged across all the nodes within the module.

2.5.2. Strength

Strength refers to the strength of connections between two nodes, expressed as the number of streamlines in the case of the DWI data and the magnitude of the positive correlations in the case of the resting-state fMRI data. Three strength measures were obtained for each participant. First, average strength represents the strength of the connection of each node to every other node in the brain. At the whole-brain level, the estimate of strength was averaged across all nodes. At the module level, strength represents the averaged connection, for the nodes in the module, to all other nodes in the brain. Second, for each node, between-module strength represents the strength of a node’s connection to all other nodes outside its associated module. At the whole-brain level, the estimate was averaged across all nodes, whereas at the module level the estimate represents the averaged connections from the nodes within the module to all other nodes outside the module. Third, within-module strength represents the averaged strength of the connections among the nodes within each module. At the whole-brain level, this estimate was averaged across all nodes, whereas at the module level, within-module strength represents only the nodes within the module.

2.5.3. System segregation

System segregation represents the degree to which modules are separated from each other, expressed as the magnitude of the within-module strength relative to between-module strength (Chan et al., 2014; Wig, 2017). It was calculated by Equation 4:

$$Systemsegregation=\left({\overline{Z}}_w-{\overline{Z}}_b\right)/{\overline{Z}}_w$$ (4)

where, in the DWI data, ${\overline{Z}}_w$ is the mean number of streamlines between nodes within each module and ${\overline{Z}}_b$ is the mean number of streamlines between nodes of one module to nodes in all other modules. In the resting-state fMRI data, ${\overline{Z}}_w$ is the mean normalized correlation between nodes within each module and ${\overline{Z}}_b$ is the mean normalized correlation between nodes of one module to nodes in all other modules. For both modularity and system segregation, higher values indicate a more segregated network. At the whole-brain level, system segregation was averaged across all nodes, whereas at the module level, system segregation was defined on the basis of the nodes within the module.

2.6. Statistical analyses

Statistical analyses were conducted using SAS 9.4 (SAS Institute, Inc., Cary, NC, USA) within the general linear model. Mediation analyses were conducted to test models of the relation between age, the graph theoretical measures, and the cognitive outcome variables. The mediation analyses were conducted with the PROCESS macro for SAS (Hayes, 2013). We used the network-property measures that were available for analyses at both the whole-brain and individual module levels (efficiency, strength, and system segregation) as mediator variables. In each model, age was the predictor, the graph theoretical measures were the mediators, and the outcome variables were the cognitive measures (factor scores). In models with multiple mediators, the effects of individual mediators are covaried with respect to the other mediators. For each model, parameter estimates and 95% bootstrap confidence intervals were based on 10,000 bootstrap samples. Significance testing of parameter estimates for individual paths was conducted by t-test, but mediation (path interaction) effects were assessed by the confidence intervals, as these latter effects are typically not distributed normally (Hayes, 2013). Mediation effects were considered to be statistically significant when the associated 95% confidence interval did not include zero.

3. Results

3.1. Screening and cognitive measures

The screening measures in Table 1 indicate that increased age was associated with decreasing visual sensory function, as represented by declining visual acuity and color vision. A detectable decrease in MMSE with increasing age was also present, but this result is likely influenced by the limited variability associated with the inclusion criteria (MMSE = 27–30). No age-related decline in WAIS vocabulary was evident, and the years of education increased with age.

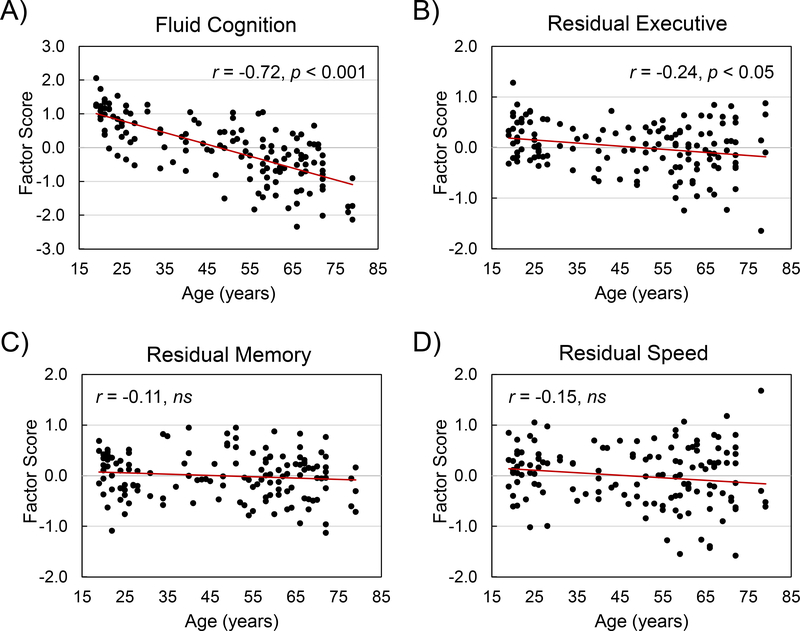
Overall fluid cognition, comprising the first factor score for the nine cognitive tests, partialed for gender and WAIS vocabulary, declined significantly with age, r = −0.718, p <0.0001 (Figure 3, Panel A). The factor scores for the three tests within each of the three individual cognitive domains, partialed for gender and WAIS vocabulary, also declined with age: executive function, r = −0.629, p < 0.0001, memory, r = −0.447, p < 0.0001, and speed r = −0.580, p < 0.0001. As noted previously in the Methods (section 2.2.), to control for the shared variance among the tests, we partialed the factor scores in each domain for the six tests not associated with that domain (Madden et al., 2017; Salthouse et al., 2015). The residual executive function score exhibited a significant decline with age (Figure 3, Panel B), whereas the residual scores for memory and speed did not exhibit an age-related decline, independently of the variance shared with tests outside their domain (Figure 3, Panels C and D).

Figure 3.

Cognitive measures as a function of age; n = 143. Fluid cognition is the factor score for all nine cognitive tests, partialed for gender and WAIS vocabulary (A). Factor scores for executive function (B), memory (C), and speed (D), are each based on three tests and then partialed for the six remaining tests, plus gender and WAIS vocabulary, Bonferroni corrected for four comparisons.

3.2. Graph theoretical measures

3.2.1. Whole-brain analysis

Correlation of whole-brain measures with age are presented in Table 2. Significance levels for the correlations are Bonferroni-corrected for six comparisons within the structural and functional domains. Five of the structural network-property measures related to efficiency and strength of connectivity declined with age, although structural system segregation was constant with age. In the functional measures, only system segregation declined with age.

Table 2.

Whole-Brain Graph Theoretical Measures

	M	SD	r with age
Structural Data
Global Efficiency	51.25262	5.84513	−0.30976**
Local Efficiency	9.35920	0.87052	−0.32981***
Strength	2341.00000	264.91236	−0.24684*
Between-Module Strength	8.47879	1.01790	−0.32609***
Within-Module Strength	59.67510	5.23890	−0.32179***
System Segregation	0.85780	0.01285	0.11109
Functional Data
Global Efficiency	0.31803	0.04720	0.17434
Local Efficiency	0.24162	0.09175	0.17274
Strength	63.54536	19.73774	0.16449
Between-Module Strength	0.27391	0.09351	0.20087
Within-Module Strength	0.44287	0.09511	0.09610
System Segregation	0.39044	0.06728	−0.37299***

Note. n = 143. Significance levels were Bonferroni-corrected for the six comparisons within each type of data.

^*p < 0.05 (corrected)

^**p < 0.01 (corrected)

^***p < 0.001 (corrected)

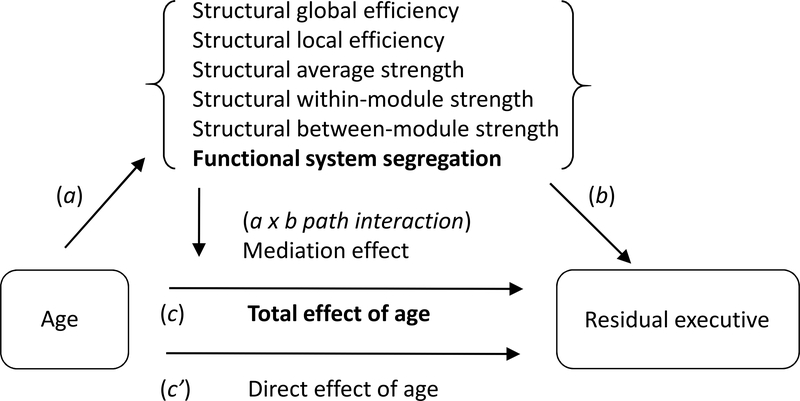
Because age-related decline was significant for overall fluid cognition and residual executive function (Figure 3), we constructed two separate mediation models for these variables (Table 3). In each model, age was the predictor, and the outcome variable was either overall fluid cognition (Model 1) or residual executive function (Model 2). The potential mediators were the network-property measures that varied significantly with age: structural global efficiency, structural local efficiency, structural average strength, structural within-module strength, and functional system segregation. These were parallel mediation models, in the sense that the mediators were assessed simultaneously, covaried for each other (Hayes, 2013). Within each of these models (Table 3), the a path (age ➔ mediator) was significant for all of the mediators, reflecting the basis for selecting these mediators. The b (mediator ➔ outcome) path was significant only for functional system segregation in Model 2. That is, among all the mediators, only the relation between functional system segregation and residual executive function was significant independently of age. The parameter estimate was positive, indicating that increasing functional system segregation was related to a higher level of executive function. The c path (total effect of age on the outcome measure) was significant for both models, with negative parameter estimates, because we selected the two outcome variables with age-related decline. Across the two models, the only mediation effect that was significant was associated with functional system segregation, which mediated the relation between age and residual executive function in Model 2 (Figure 4). The c ‘ path (direct effect of age) for residual executive function was not significant following mediation by functional system segregation.

Table 3.

Mediation of Age-Cognition by Functional System Segregation and Structural Graph Variables

	Effect	SE	t	p	Lower CI	Upper CI
Model 1: x = age; m = six whole-brain structural and functional graph theory measures that showed significant correlation with age; y = overall fluid cognition score
Age effect (a path)
Structural global efficiency	−0.0950	0.0251	−3.7778	0.0002	−0.1447	−0.0453
Structural local efficiency	−0.0151	0.0037	−4.0815	0.0001	−0.0224	−0.0078
Structural average strength	−3.4767	1.1646	−2.9852	0.0034	−5.7795	−1.1738
Structural within-module strength	−0.0886	0.0225	−3.9379	0.0001	−0.1331	−0.0441
Structural between-module strength	−0.0176	0.0044	−4.0400	0.0001	−0.0263	−0.0090
Functional system segregation	−0.0013	0.0003	−4.7420	0.0000	−0.0019	−0.0008
Mediator to outcome (b path)
Structural global efficiency	0.0282	0.0281	1.0034	0.3175	−0.0274	0.0838
Structural local efficiency	−0.1778	0.1670	−1.0649	0.2889	−0.5082	0.1525
Structural average strength	−0.0005	0.0007	−0.6793	0.4981	−0.0018	0.0009
Structural within-module strength	−0.0066	0.0298	−0.2226	0.8242	−0.0655	0.0523
Structural between-module strength	0.0471	0.1302	0.3621	0.7178	−0.2103	0.3046
Functional system segregation	0.0713	0.8840	0.0807	0.9358	−1.6773	1.8199
Total effect for age (c path)	−0.0351	0.0029	−12.1247	0.0000	−0.0408	−0.0294
Direct effect for age (c’ path)	−0.0363	0.0034	−10.6879	0.0000	−0.0430	−0.0296
Mediation effect (a x b path interaction)
Structural global efficiency	−0.0027	0.0028	—	—	−0.0088	0.0024
Structural local efficiency	0.0027	0.0027	—	—	−0.0023	0.0086
Structural average strength	0.0016	0.0024	—	—	−0.0028	0.0069
Structural within-module strength	0.0006	0.0026	—	—	−0.0047	0.0058
Structural between-module strength	−0.0008	0.0021	—	—	−0.0052	0.0036
Functional system segregation	−0.0001	0.0011	—	—	−0.0025	0.0020
Model 2: x = age; m = six whole-brain structural and functional graph theory measures that showed significant correlation with age; y = residual executive function score
Age effect (a path)
Structural global efficiency	−0.0950	0.0251	−3.7778	0.0002	−0.1447	−0.0453
Structural local efficiency	−0.0151	0.0037	−4.0815	0.0001	−0.0224	−0.0078
Structural average strength	−3.4767	1.1646	−2.9852	0.0034	−5.7795	−1.1738
Structural within-module strength	−0.0886	0.0225	−3.9379	0.0001	−0.1331	−0.0441
Structural between-module strength	−0.0176	0.0044	−4.0400	0.0001	−0.0263	−0.0090
Functional system segregation	−0.0013	0.0003	−4.7420	0.0000	−0.0019	−0.0008
Mediator to outcome (b path)
Structural global efficiency	0.0103	0.0201	0.5135	0.6084	−0.0295	0.0502
Structural local efficiency	−0.0247	0.1198	−0.2063	0.8369	−0.2617	0.2122
Structural average strength	−0.0006	0.0005	−1.3245	0.1876	−0.0016	0.0003
Structural within-module strength	0.0298	0.0214	1.3947	0.1654	−0.0125	0.0720
Structural between-module strength	−0.0045	0.0934	−0.0479	0.9619	−0.1891	0.1802
Functional system segregation	1.6494	0.6340	2.6014	0.0103	0.3952	2.9035
Total effect for age (c path)	−0.0062	0.0021	−2.9198	0.0041	−0.0104	−0.0020
Direct effect for age (c’ path)	−0.0030	0.0024	−1.2320	0.2201	−0.0078	0.0018
Mediation effect (a x b path interaction)
Structural global efficiency	−0.0010	0.0019	—	—	−0.0048	0.0028
Structural local efficiency	0.0004	0.0019	—	—	−0.0034	0.0041
Structural average strength	0.0022	0.0020	—	—	−0.0011	0.0067
Structural within-module strength	−0.0026	0.0022	—	—	−0.0075	0.0012
Structural between-module strength	0.0001	0.0019	—	—	−0.0034	0.0042
Functional system segregation	−0.0022	0.0010	—	—	−0.0045	−0.0004

Note. Due to three participants with missing psychometric data, n = 140. a, b, c, = paths in mediation model as illustrated in Figure 4, with x as predictor variable, y as outcome variable, and m as mediator; a = path from predictor to mediator; b = path from mediator to outcome, controlling for a path; c = total effect of predictor; c’ = direct effect of predictor, controlling for mediator; ab = interaction of a and b paths representing indirect influence of x as mediated by m; effect = regression coefficient; SE = standard error; Lower/Upper CI = lower/upper bounds of 95% confidence intervals, estimated from bootstrap sampling with 10,000 samples. Significant effects are presented in bold.

Figure 4.

Mediation model for residual executive function, with mediators in parallel. Significant mediators and effects are presented in bold.

To determine whether the structural network properties directly influenced functional system segregation, we constructed a model in which the structural measures of efficiency and strength were potential mediators of the relation between age and functional system segregation (Table 4). None of the structural measures, however, was a significant mediator, and none exhibited an age-independent relation to functional system segregation.

Table 4.

Mediation of Age-Functional System Segregation by Whole-Brain Structural Graph Variables

	Effect	SE	t	p	Lower CI	Upper CI
x = age; m = whole-brain structural graph variables; y = functional system segregation
Age effect (a path)
Structural global efficiency	−0.0962	0.0249	−3.8685	0.0002	−0.1453	−0.0470
Structural local efficiency	−0.0152	0.0037	−4.1483	0.0001	−0.0225	−0.0080
Structural average strength	−3.4730	1.1482	−3.0246	0.0030	−5.7430	−1.2030
Structural within-module strength	−0.0895	0.0222	−4.0357	0.0001	−0.1334	−0.0457
Structural between-module strength	−0.0176	0.0043	−4.0959	0.0001	−0.0261	−0.0091
Mediator to outcome (b path)
Structural global efficiency	0.0016	0.0027	0.5960	0.5522	−0.0037	0.0070
Structural local efficiency	0.0010	0.0160	0.0608	0.9516	−0.0307	0.0327
Structural average strength	−0.0000	0.0001	−0.5598	0.5765	−0.0002	0.0001
Structural within-module strength	−0.0003	0.0029	−0.1036	0.9176	−0.0060	0.0054
Structural between-module strength	−0.0085	0.0126	−0.6723	0.5025	−0.0333	0.0164
Total effect for age (c path)	−0.0013	0.0003	−4.7735	0.0000	−0.0019	−0.0008
Direct effect for age (c’ path)	−0.0015	0.0003	−4.7889	0.0000	−0.0021	−0.0009
Mediation effect (a x b path interaction)
Structural global efficiency	−0.0002	0.0003	—	—	−0.0007	0.0003
Structural local efficiency	−0.0000	0.0002	—	—	−0.0005	0.0004
Structural average strength	0.0001	0.0002	—	—	−0.0003	0.0006
Structural within-module strength	0.0000	0.0003	—	—	−0.0005	0.0005
Structural between-module strength	0.0001	0.0002	—	—	−0.0003	0.0007

Note. n = 143. a, b, c, = paths in mediation model as illustrated in Figure 4, with x (age) as the predictor variable, y (functional system segregation) as the outcome variable, and m (whole-brain structural graph variables) as mediators; a = path from predictor to mediator; b = path from mediator to outcome, controlling for a path; c = total effect of predictor; c’ = direct effect of predictor, controlling for mediator; ab = interaction of a and b paths representing indirect influence of x as mediated by m; effect = regression coefficient; SE = standard error; Lower/Upper CI = lower/upper bounds of 95% confidence intervals, estimated from bootstrap sampling with 10,000 samples. Significant effects are presented in bold.

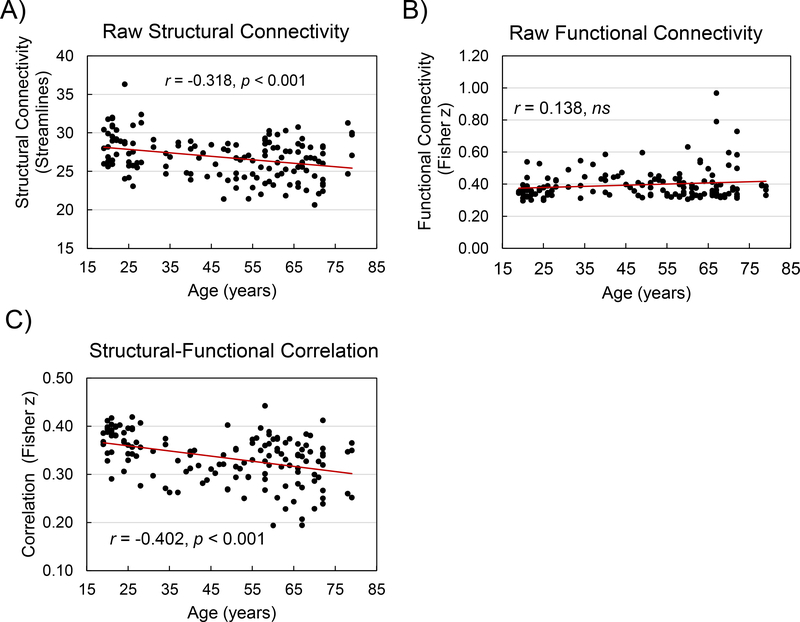
Although the direct influence of structural connectivity on functional connectivity was not significant in the context of the graph theoretical variables, we examined the relation between structural and functional connectivity in the raw matrix data underlying the graph theoretical analyses. We first restricted the data set to those cells in the structural connectivity matrix, for each participant, that contained a positive value, that is, pairs of nodes with a structural connection. We conducted four exploratory tests and Bonferroni-corrected the significance levels for these tests. The average number of streamlines per cell (i.e., node to node connection) in each person’s structural matrix declined significantly with age (Figure 5, Panel A), r = −0.318, p < 0.001 (corrected). The Fisher-z transformed correlation of the fMRI time series associated with these streamlines, however, did not exhibit age-related decline (Figure 5, Panel B). As an estimate of structural-functional connectivity, we obtained, for each participant, the Pearson r correlation between those structural connections (i.e., number of streamlines) and the functional connectivity in the corresponding cells of the functional connectivity matrix. The resulting correlations (Fisher-z transformed), were overall greater than zero, t(142) = 80.07, SE = 0.00418, p < 0.001 (corrected), and declined significantly with age (Figure 5, Panel C), r = −0.402, p < 0.001 (corrected).

Figure 5.

Connectivity in the raw data matrices, for those pairs of nodes with a positive number of white matter streamlines connecting them. Structural connectivity (A); functional connectivity (B), and the correlation between structural and functional connectivity as a function of age (C).

3.2.2. Individual modules

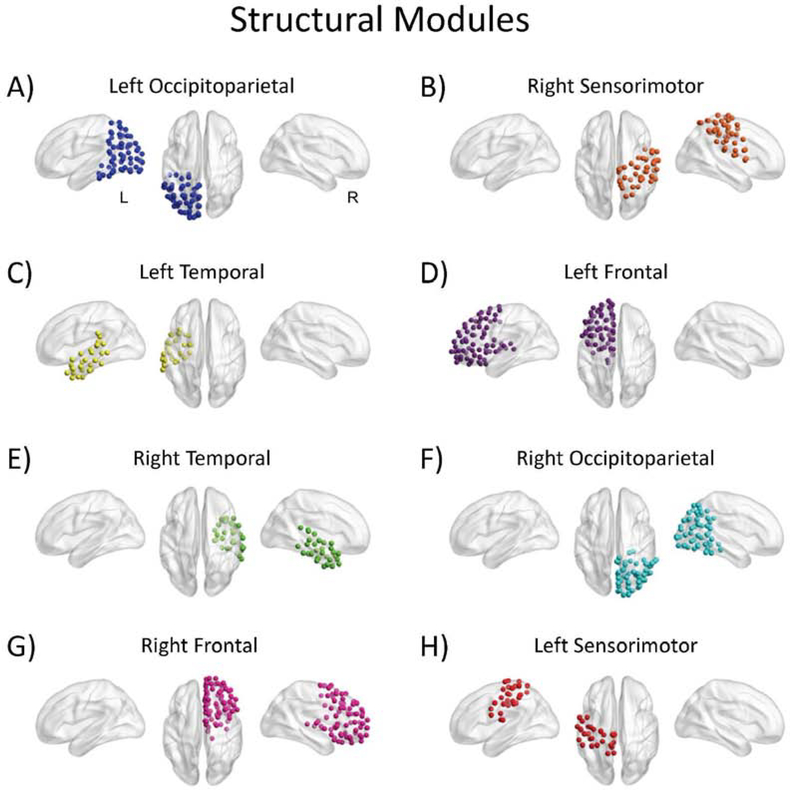
The group-averaged structural data yielded eight modules (Figure 6). These essentially reflected four modules with both left and right hemisphere versions: occipitoparietal regions (Figure 6, Panels A and F), sensorimotor regions (Figure 6, Panels B and H), temporal regions (Figure 6, Panels C and E), and frontal regions (Figure 6, Panels D and G).

Figure 6.

Modules estimated from the averaged structural connectivity matrix.

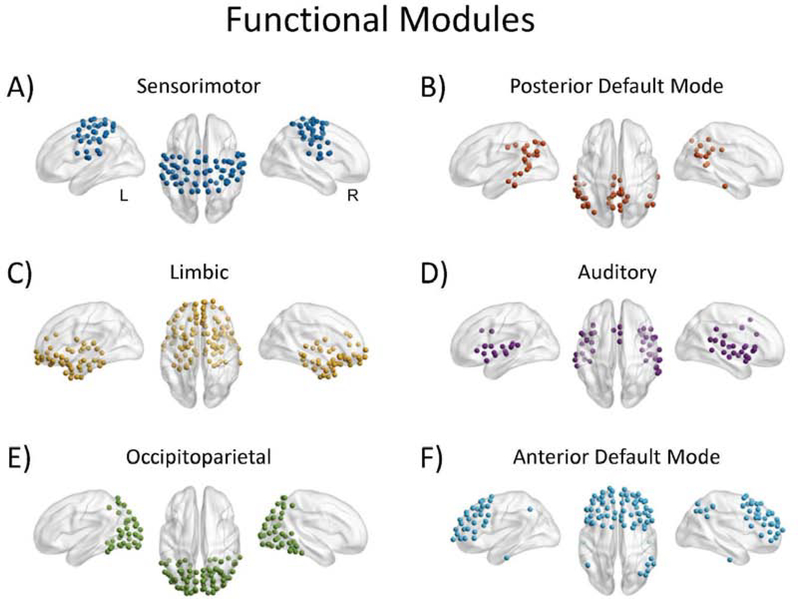
The group-averaged resting-state fMRI data yielded six functional modules (Figure 7). In contrast to the structural modules, which were all unilateral, the functional modules were all bilateral. These comprised sensorimotor regions (Figure 7, Panel A), anterior and posterior components of the default mode network (Figure 7, Panels B and F), limbic and orbitofrontal regions (Figure 7, Panel C), auditory (superior temporal) regions (Figure 7, Panel D), and occipitoparietal regions (Figure 7, Panel E).

Figure 7.

Modules estimated from the averaged functional connectivity matrix.

3.2.3. Age-related differences for individual modules

To investigate age-related differences for individual modules, we conducted a multiple regression model for each of the five network properties within both the structural and functional data for each module: local efficiency, average strength, between-module strength, within-module strength, and system segregation. (Because global efficiency refers to the whole-brain network, this measure was not analyzed at the level of the individual modules.) In each model, age was the outcome variable, and the individual modules (eight for the structural data, six for the functional data) were simultaneous predictor variables. Thus, a significant effect (beta value) for an individual module represented a contribution to the age-related effect above and beyond the other modules. Significance levels were Bonferroni-corrected for the five models in each domain.

These analyses indicated that significant age-related effects (from the combined effects of all modules) were present for local efficiency, average strength, between-module strength, within-module strength, and system segregation (Table 5). An age-related decline in structural connectivity (i.e., negative beta value) for the right frontal module contributed significantly to the overall age-related effects for average strength, within-module strength, and system segregation. In the structural data, the left occipitoparietal module also exhibited age-related decline in between-module strength. The right temporal module also exhibited a positive, though small, age-related effect for average strength (Table 5), which was also evident in the bivariate correlation between age and average strength, r = 0.159, p < 0.06 (uncorrected).

Table 5.

Age-Related Effects for Individual Structural Modules in Graph Theoretical Measures

	β	SE	t
Local Efficiency	F(8, 134) = 3.98*
Intercept	104.29229	18.92983	5.51***
Left Occipitoparietal	2.88457	2.39740	1.20
Right Sensorimotor	−1.83675	3.09747	−0.59
Left Temporal	−2.17130	1.41775	−1.53
Left Frontal	3.88666	3.42036	1.14
Right Temporal	−2.15465	1.44363	−1.49
Right Occipitoparietal	0.54483	1.92192	0.28
Right Frontal	−6.18217	3.19185	−1.94
Left Sensorimotor	−1.35082	3.32433	−0.41
Average Strength	F(8, 134) = 6.57 ***
Intercept	81.18864	13.48654	6.02***
Left Occipitoparietal	0.00190	0.00734	0.26
Right Sensorimotor	−0.00586	0.01185	−0.49
Left Temporal	−0.00004	0.00907	−0.00
Left Frontal	0.00534	0.01260	0.42
Right Temporal	0.02161	0.00811	2.67*
Right Occipitoparietal	−0.01011	0.00691	−1.46
Right Frontal	−0.03991	0.01255	−3.18**
Left Sensorimotor	0.00977	0.01066	0.92
Between-Module Strength	F(8, 134) = 5.01***
Intercept	84.18710	14.13182	5.96
Left Occipitoparietal	−10.41637	3.24369	−3.21**
Right Sensorimotor	1.40800	2.89122	0.49
Left Temporal	−1.12334	1.68364	−0.67
Left Frontal	−5.82625	4.08627	−1.43
Right Temporal	−2.34705	1.67931	−1.40
Right Occipitoparietal	7.41496	3.14906	2.35
Right Frontal	7.64155	3.95221	1.93
Left Sensorimotor	−0.22232	2.09323	−0.11
Within-Module Strength	F(8, 134) = 6.41***
Intercept	147.94979	18.03139	8.21***
Left Occipitoparietal	−0.35574	0.34412	−1.03
Right Sensorimotor	−0.37518	0.38439	−0.98
Left Temporal	0.16945	0.19609	0.86
Left Frontal	−0.30459	0.57252	−0.53
Right Temporal	0.11456	0.19559	0.59
Right Occipitoparietal	−0.27214	0.31227	−0.87
Right Frontal	−2.00110	0.61113	−3.27**
Left Sensorimotor	0.21976	0.25177	0.87
System Segregation	F(8, 134) = 7.52***
Intercept	35.72535	96.04730	0.37
Left Occipitoparietal	306.21984	100.15202	3.06*
Right Sensorimotor	−111.12542	69.84089	−1.59
Left Temporal	144.24193	106.03042	1.36
Left Frontal	142.51680	110.71806	1.29
Right Temporal	158.26074	92.95610	1.70
Right Occipitoparietal	−360.44381	143.11664	−2.52
Right Frontal	−397.03790	92.57621	−4.29***
Left Sensorimotor	114.35982	83.57336	1.37

Note. n = 143. In each model, the eight structural modules were simultaneous predictors of years of age. Significance levels were Bonferroni-corrected for the five models tested across the five graph theoretical measures.

^*p < 0.05 (corrected)

^**p < 0.01 (corrected)

^***p < 0.001 (corrected)

The only age-related effect in the regression models of the individual functional modules was associated with system segregation (Table 6), as in the whole-brain analyses (Table 2). The only unique contribution from an individual module was the age-related decline in system segregation for the occipitoparietal module.

Table 6.

Age-Related Effects for Individual Functional Modules in Graph Theoretical Measures

	β	SE	t
Local Efficiency	F(6, 136) = 1.80
Intercept	41.31116	5.146996	8.03***
Sensorimotor	56.07201	55.46622	1.01
Posterior Default Mode	44.73170	64.13577	0.70
Limbic	30.23440	60.34445	0.50
Auditory	−56.09747	59.58090	−0.94
Occipitoparietal	−117.48682	63.71440	−1.84
Anterior Default Mode	66.17992	51.26892	1.29
Average Strength	F(6, 136) = 1.67
Intercept	43.68244	6.90759	6.32***
Sensorimotor	0.10599	0.18766	0.56
Posterior Default Mode	0.06769	0.21881	0.31
Limbic	0.02701	0.20713	0.13
Auditory	−0.32386	0.19929	−1.63
Occipitoparietal	−0.08675	0.21428	−0.40
Anterior Default Mode	0.25262	0.14716	1.72
Between-Module Strength	F(6, 136) = 1.90
Intercept	43.22746	6.32220	6.84***
Sensorimotor	123.32941	71.23761	1.73
Posterior Default Mode	−34.07876	58.51800	−0.58
Limbic	33.01096	79.79670	0.41
Auditory	−68.39300	56.56471	−1.21
Occipitoparietal	−7.62831	71.276211	−0.11
Anterior Default Mode	−24.12699	66.81465	−0.36
Within-Module Strength	F(6, 136) = 2.39
Intercept	50.117151	9.61299	5.21***
Sensorimotor	12.563806	19.23348	0.65
Posterior Default Mode	9.630588	21.64333	0.44
Limbic	7.976398	21.98047	0.36
Auditory	−32.700663	21.31006	−1.53
Occipitoparietal	−42.584382	19.93200	−2.14
Anterior Default Mode	37.563381	15.59978	2.41
System Segregation	F(6, 136) = 7.15***
Intercept	82.352863	8.99377	9.16***
Sensorimotor	−18.320810	18.17476	−1.01
Posterior Default Mode	37.084187	17.61200	2.11
Limbic	−33.713374	18.21081	−1.85
Auditory	−30.072195	19.90084	−1.51
Occipitoparietal	−63.922704	15.18916	−4.21***
Anterior Default Mode	12.781443	21.30350	0.60

Note. n = 143. In each model, the six functional modules were simultaneous predictors of years of age. Significance levels were Bonferroni-corrected for the five models tested across the five graph theoretical measures.

^*p < 0.05 (corrected)

^**p < 0.01 (corrected)

^***p < 0.001 (corrected)

3.2.4. Alternative network partitions

The analyses reported above rely on one approach to defining structural and functional modules, in which the connectivity matrices for structural and functional data were each averaged across all participants, and the modules estimated from the averaged matrices were applied to individual participants’ data. We adopted this approach to identify a set of modules, within the structural and functional data, that would be comparable across participants and allow correlation with our cognitive outcome variables. We also explored two alternative methods of partitioning the networks, in which the structural modules were used to partition both the structural and functional data. In both of these approaches, we implemented consensus clustering, with 150 iterations of the Louvain algorithm, gamma = 1.0, and thresholding of the agreement matrices as described above (section 2.5., Graph theoretical measures). In the first approach, we used the averaged structural connectivity data to define the modules for both the structural and functional data, with the eight structural modules (Figure 6) applied to the functional data. In the second approach, we did not average the matrices, but instead used each participant’s module partition, from the structural data, for both the structural and functional data. That is, in this latter approach, we did not require that the individual modules be constant across participants.

The results of these two alternative approaches to partitioning the data, reported in Supplementary Material, yielded both similarities and differences to the findings reported in this Results section. When using the averaged structural modules to define the functional modules, the functional connectivity results were comparable to defining the modules from the functional data as reported in this Results section. With this alternative method of defining the functional modules, the age-related decline in system segregation remained the only age-related effect (Table S1). In a mediation analysis with functional system segregation and the structural whole-brain measures of strength and efficiency as mediators, functional system segregation was the only significant mediator of the age-related decline in residual executive function (Table S2), and no mediation was evident for overall fluid cognition. This is exactly the pattern reported in this Results section.

When, however, we allowed the modules to vary across participants and applied each participant’s structural modules to their functional data, a different pattern of age-related effects occurred. The structural and functional connectivity data for global efficiency, local efficiency, and average strength were identical across the different methods, by definition, because modular structure does not contribute to these whole-brain measures. The within-module and between-module strength values, however, do depend on modular structure, and in contrast to our primary analyses (Table 2), these latter values did not exhibit a significant age-related decline in structural connectivity when defined at the participant level (Table S3). In the functional data, system segregation continued to be the only variable exhibiting age-related decline (Table S3). When functional system segregation was included, along with structural global efficiency, local efficiency, and average strength, in a mediation model of the relation between age and residual executive function, none of the variables was significant as a mediator of either overall fluid cognition or residual executive function (Table S4).

4. Discussion

In the present analyses we used graph theoretical measures to characterize age-related differences in the strength and efficiency of structural brain connectivity (based on DWI) and functional brain connectivity (based on resting-state fMRI). Previous investigations have reported age-related decline in both structural and functional connectivity in relation to fluid cognition (Andrews-Hanna et al., 2007; Chen et al., 2009; Fjell et al., 2016; Hedden et al., 2016; Li et al., 2020; Madden et al., 2017). Structural and functional measures have typically been treated as separate variables, however, without considering that structural connectivity may constrain functional connectivity (Damoiseaux and Greicius, 2009; Greicius et al., 2009; Hermundstad et al., 2013; Honey et al., 2007; Honey et al., 2009; Zhu et al., 2014). Although some findings suggest that that age-related decline in functional connectivity is dependent on structural connectivity (Andrews-Hanna et al., 2007; Betzel et al., 2014; Fjell et al., 2016; Zimmermann et al., 2016), other investigations have suggested that structural connectivity only weakly constrains age-related differences in functional connectivity (Fjell et al., 2017; Tsang et al., 2017).

Graph theoretical measures have provided a common framework for characterizing the properties of structural and functional networks. Recent graph theoretical studies consistently observe age-related decline in structural connectivity (Gong et al., 2009; Wu et al., 2012; Zhao et al., 2015). Age-related differences in functional connectivity are more variable, but a decline in the segregation of functional modules (system segregation) has been a reliable pattern (Chan et al., 2014; Chong et al., 2019; Wig, 2017). However, no previous investigation has, to our knowledge, combined graph theoretical measures of structural and functional connectivity in the context of age-related differences in fluid cognition. Here, we investigated the relation between graph theoretical structural and functional brain network properties, in the context of age-related differences in fluid cognition. Our analyses were guided by three broad hypotheses: that the graph theoretical measure of functional system segregation would decrease with age, that functional system segregation would be a significant mediator of age-related decline in fluid cognition, and that structural connectivity would constrain the influence of functional connectivity on the age-cognition relation. We also investigated the potential contributions of individual modules comprising the structural and functional networks.

4.1. Age-related differences in brain connectivity and fluid cognition

We observed an age-related decline in functional system segregation (Table 2), which confirmed our first hypothesis, based on previous findings reported by Chan et al. (2014) and Chong et al. (2019). We extend these previous findings in two ways. First, the Chan et al. and Chong et al. studies did not include structural brain connectivity data. Our analyses, combining graph theoretical measures of structural and functional data, indicate that the age-related decline in system segregation (at the whole-brain level) is specific to functional connectivity and is not a feature of structural connectivity (Table 2). Second, analyses of the individual functional modules demonstrate a specific contribution from the occipitoparietal module to the age-related decline in system segregation (Table 6 and Figure 7). This pattern corresponds to the previous ICA analyses of resting-state functional connectivity of this data set (Madden et al., 2017), in which an ICA network that included visual sensory cortex exhibited the most pronounced age-related decline. Chan et al. proposed that the age-related decline in functional system segregation was more pronounced for modules comprising primarily association cortex, compared to those comprising primarily sensory cortex (Suarez et al., 2020). Here, the parietal nodes within the occipitoparietal module would be consistent with the Chan et al. results, whereas the occipital nodes (at least those within primary visual cortex) would not. The method for assigning nodes to modules differs across these studies, being data-driven here and defined by the results of an independent data set (Power et al., 2011) in the Chan et al. report, which may account for the different regional pattern.

Our second hypothesis was that functional system segregation would mediate the relation between age and fluid cognition. Previous analyses of this data set with ICA-based measures of connectivity (Madden et al., 2017), as well as other studies of brain connectivity not derived from graph theory (Chen et al., 2009; Fjell et al., 2016; Hedden et al., 2016; Li et al., 2020; Madden et al., 2017), have demonstrated that both structural and functional connectivity contribute as statistical mediators of the relation between age and cognitive performance. Investigations using graph theory have yielded some evidence that specific network properties, such as system segregation, contribute to age-related differences in cognition. Chan et al. (2014) and Chong et al. (2019), for example, both reported a positive relation between cognitive ability and graph theoretical measures of module distinctiveness, with age controlled statistically. Bagarinao et al. (2019) found that a graph theoretical measure of network integrity was a statistical mediator of the relation between age and global cognitive functioning. We extend these previous findings by showing that a specific, graph theoretical feature of resting-state functional modules, system segregation, has a mediating role in age-related cognitive decline. When the six graph theoretical measures that were age-sensitive (structural global efficiency, structural local efficiency, structural average strength, structural within-module strength, structural between-module strength, and functional system segregation) were included as potential mediators of the relation of age to the overall cognitive and residual executive function measures, only functional system segregation was a mediator in a model with residual executive function as the outcome measure (Figure 4; Table 3, Model 2). That is, the relation of age to residual executive function was indirect, operating through functional system segregation.

The path coefficient for the relation of functional system segregation to residual executive function, covaried for age (i.e., the b path in Table 3, Model 2), was positive, consistent with the previous findings indicating an underlying positive relation between the distinctiveness of functional modules and cognition (Bagarinao et al., 2019; Chan et al., 2014; Chong et al., 2019). The mediating effect of functional system segregation, however, was specific to residual executive function, even though the age-related effect size (r) for overall fluid cognition was much greater than the effect size for residual executive function (Figure 3). Thus, the mediating effect of system segregation is not driven by the age-related effect size of the cognitive outcome variable.

The pattern of age-related differences in the graph theoretical measures of structural connectivity were generally consistent with previous findings. We observed, consistent with earlier studies (Gong et al., 2009; Wu et al., 2012; Zhao et al., 2015), that the efficiency and strength of structural connectivity declined with age (Table 2). We also obtained specific regional effects of structural connectivity (Table 5), with prominent contributions from the right frontal module to age-related differences in average strength, within-module strength, and system segregation (Zhao et al., 2015). The left occipitoparietal module exhibited both a decline in between-module strength and an increase in system segregation. Interestingly, the overall model for age-related differences in structural system segregation was significant with the connectivity measures averaged per module (Table 5), whereas the initial analysis of the whole-brain measures of structural connectivity, averaging across all nodes, did not exhibit an age-related decline in system segregation (Table 2). These results appear to reflect an age-related decline in structural system segregation for the right frontal module, combined with an age-related increase for the left occipitoparietal module (Table 5), which may have cancelled each other in the whole-brain analysis.

The results provided limited support for our third hypothesis, that structural brain connectivity would constrain the pattern of functional connectivity. We based our prediction on previous findings (Andrews-Hanna et al., 2007; Betzel et al., 2014; Chen et al., 2009; Fjell et al., 2016; Zimmermann et al., 2016) suggesting that age-related differences in functional connectivity were dependent on structural connectivity, in line with data from younger adults (Damoiseaux and Greicius, 2009; Hermundstad et al., 2013; Honey et al., 2007; Honey et al., 2009). Having demonstrated a significant influence of functional system segregation in the relation between age and residual executive function (Figure 4; Table 3, Model 2), we asked whether aspects of structural connectivity influenced the relation of age to functional system segregation. The results, however, indicated that none of the graph theoretical measures of structural connectivity was a significant mediator of the age-related decline in functional system segregation (Table 4). But we also explored the raw structural and functional connectivity matrices, from which the graph theoretical measures were derived. In this exploratory analysis we restricted the matrices to those cells with a structural connection between nodes. At this raw matrix level, the relation between structural and functional connectivity declined with age (Figure 5, Panel C). This suggests that age-related decline in structural connectivity may contribute to decreased functional connectivity among regions, although a causal effect cannot be inferred from this correlation. Overall, our findings are in line with those of Fjell et al. (2017), who proposed that structural connectivity provided a measurable though relatively weak constraint on age-related differences in functional connectivity.

4.2. Limitations

Graph theory provides a theoretical and measurement context that can encompass structural and functional brain connectivity data, but alternative methods exist for defining nodes and comparing structural and functional modules. Different methods of defining nodes, partitioning modules, and many other stages within the analysis pipeline, will influence the results (Botvinik-Nezer et al., 2020; Gargouri et al., 2018; Sporns and Betzel, 2016; Zalesky et al., 2010). In our primary analyses, we defined a single modular structure, based on the participant-averaged structural and functional correlation matrices (Figure 2), but we allowed the module topology to differ between the structural and functional domains. We performed additional analyses with two alternative versions of this method of defining modules (Supplementary Material). In the first approach, the set of structural modules that we used in the primary analyses, defined from the participant-averaged correlation matrix, were applied to both the structural and functional data. In the second approach, the structural modules for each individual were applied to that individual’s structural and functional data.

As noted in Section 3.2.4. (Alternative network partitions), the results from the first approach were largely consistent with the results reported in the main text, in that the functional data yielded an age-related difference only for system segregation, and functional system segregation was the only significant mediator of the age-related decline in residual executive function. The second approach, however, with individually varying structural modules, did not yield the age-related decline in within- and between-module structural connectivity that we observed in the main analyses. With the individually varying structural modules, functional system segregation continued to exhibit age-related decline but did not mediate the relation between age and residual executive function. Thus, our findings for functional connectivity were consistent regardless of whether the functional data were based on structural or functional modules, when the modules were defined from the participant-averaged matrices. Participant-varying modules yielded different results.

Mediation analysis is a form of ordinary linear regression that is designed to identify the causal relations among variables (Hayes, 2013) in cross-sectional data. By defining the patterns of shared and unique variance across individuals we can interpret age-related differences, but these individual differences in cross-sectional data are not the same as change over time, which requires longitudinal analysis (Hofer and Sliwinski, 2001; Lindenberger et al., 2011). A limitation of longitudinal analysis is that scores are correlated across measurement occasions, and as a result the systematic variance in change over time may be small relative to the variance at each measurement occasion (Salthouse, 2011; Salthouse and Nesselroade, 2002). Converging information from cross-sectional and longitudinal studies would provide a more complete account of age-related effects.

4.3. Conclusion

From the application of graph theoretical analyses, these results demonstrate that structural and functional brain networks exhibit different patterns of age-related decline, that functional connectivity influences age-related differences in one form of fluid cognition (executive function), and that structural connectivity exerts a limited constraint on age-related decline in functional connectivity.

Age-related differences in structural connectivity were evident in the majority of the graph theoretical measures. Age-related decline was significant for whole-brain efficiency and strength of connectivity among all nodes, as well as in within- and between-module strength, though not in system segregation. Functional connectivity, in contrast, exhibited age-related decline only in system segregation, reflecting a decrease in the distinctiveness among modules with increasing age. Individual modules contributed prominently to the structural and functional age-related effects: right frontal and left occipitoparietal modules for age-related decline in structural connectivity, and a bilateral occipitoparietal module for age-related decline in functional system segregation. Mediation analyses demonstrated that functional system segregation had a specific influence on age-related decline in executive function, distinct from the fluid cognitive abilities shared by perceptual speed, executive function, and memory. The age-related differences in the graph theoretical measures of structural and functional connectivity were largely independent. In the underlying raw data matrices, however, the results suggested some degree of anatomical constraint on functional connectivity. For pairs of nodes with a structural connection, age-related decline in structural and functional connectivity were correlated. Overall, these findings suggest that specific aspects of structural and functional brain networks interact to define the pattern of age-related decline in fluid cognition.

Highlights.

• Graph theoretical measures characterize the topology of brain connectivity

• Age-related decline in strength and efficiency of structural brain connectivity

• Age-related decline in functional system segregation (module distinctiveness)

• Functional system segregation mediates age-related decline in executive function

• Structural connectivity exerts a limited constraint on functional connectivity