Different patterns of functional network re-organization across the variants of primary progressive aphasia: A graph theoretic analysis

Abstract

Primary progressive aphasia (PPA) is a neurodegenerative syndrome with three main variants (non-fluent, logopenic, semantic) that are identified primarily based on language deficit profiles and are associated with neurotopographically distinct atrophic patterns. We used a graph-theoretic analytic approach to examine changes in functional network properties measured with resting-state fMRI in all three PPA variants compared to age-matched healthy controls. All three variants showed a more segregated network organization than controls. To better understand the changes underlying the increased segregation, we examined the distribution of functional “hubs”. We found that while all variants lost hubs in the left superior frontal and parietal regions, new hubs were recruited in different areas across the variants. In particular, both logopenic and semantic variants recruited significant numbers of hubs in the right hemisphere. Importantly, these functional characteristics could not be fully explained by volume changes. These findings indicate that patterns of functional connectivity can serve as further evidence to distinguish the PPA variants, and provide a basis for longitudinal studies and for investigating treatment effects. This study also highlights the utility of graph-theoretic approaches in understanding the brain’s functional re-organization in response to neurodegenerative disease.

1. Introduction

Primary progressive aphasia (PPA) is a neurodegenerative syndrome that encompasses a wide variety of language deficits as well as neural degeneration patterns and histopathologies (Grossman, 2010; Gorno-Tempini et al., 2011). Three main variants of PPA, non-fluent (nfvPPA), logopenic (lvPPA), and semantic (svPPA), have been identified primarily based on specific behavioral features of their language impairment (Gorno-Tempini et al., 2011; Grossman, 2010; Mesulam et al., 2012). Traditionally, the different language deficit profiles observed in each variant have been associated with distinct cortical atrophy patterns based on structural neuroimaging and autopsy (e.g., Hodges et al., 1992; Grossman et al., 1996; Gorno-Tempini et al., 2004). Nonetheless, the correspondence between cortical atrophy and clinical syndromes is not straightforward and atrophy may be difficult to identify at early stages of the disease (Grossman, 2010; Mesulam et al., 2012). More recently, resting-state functional connectivity (RSFC), typically measured with functional MRI, has been shown to be a valuable tool for understanding the underlying neural mechanisms of PPA (e.g., Guo et al., 2013; Agosta et al., 2014; Whitwell et al., 2015; Mandelli et al., 2016; Ranasinghe et al., 2017; Battistella et al., 2019; Bonakdarpour et al., 2019).

One analytic approach to characterizing the properties of the highly complex, large-scale functional networks of RSFC is provided by graph theory (e.g., Bullmore and Sporns, 2009; Rubinov and Sporns, 2010). In clinical neuroscience, graph-theoretic approaches have been applied to understand how the brain’s structural and functional network organizations are affected in various diseases such as stroke (e.g., Gratton et al., 2012; Siegel et al., 2018; Tao and Rapp, 2019), Alzheimer’s disease (e.g., Stam et al., 2007; Brier et al., 2014), schizophrenia (e.g., Bassett et al., 2008), among others (see reviews by Fornito et al., 2015; Aerts et al., 2016). In primary progressive aphasia (PPA), graph-theoretic approaches have, to date, only been applied to study the RSFC of the non-fluent (Mandelli et al., 2018) and the semantic variants (Agosta et al., 2014). Both studies reported functional network changes even in brain areas without apparent atrophy, and thus suggested that functional changes may precede structural changes and may predict the disease progression trajectory¹. In the research we report on here, we build on this previous work using graph-theoretic analytic tools to examine whole-brain functional network organization in the three PPA variants. Specifically, we aimed to identify changes in the functional organization and how these changes are similar and different across the variants. The findings provide important foundations for a better understanding of the functional re-organization that occurs in response to the neural challenges in the different PPA variants.

Graph-theoretic approaches to the analysis of large-scale neural networks

The graph-theoretic approach considers the functional connectome as a graph (i.e., network) consisting of nodes and edges. Nodes correspond to brain regions and each edge represents the degree to which the activities of two nodes are correlated/synchronized (i.e., connectivity strength). The topological properties of the graph (i.e., network properties) as well as the connectivity properties of individual nodes can be quantified and characterized using graph-theoretic measures (see Rubinov and Sporns (2010) for a tutorial overview).

Generally speaking, most graph-theoretic measures can be considered to measure network integration or segregation: A network in which every node is connected to every other node will have high global integration (and thus low global segregation), conversely, in a network with high global segregation, nodes tend to form tight and separate clusters/modules. While the different graph-theoretic measures are related to each other to a certain degree, they can also reveal different specific aspects of a network’s topology. For instance, the measure characteristic path length is the average value of the shortest distance of all the node pairs in a network, thus a higher value indicates that on average one needs to a travel longer distance between point A to B in a given network, and therefore the network is considered more segregated and less integrated; Modularity (a.k.a. Newman’s Q) is a segregation measure which quantifies to what extent all the nodes in a network are grouped into non-overlapping modules, and thus a higher value indicates the network has high system segregation. The brain’s generally modular functional organization is well-suited for carrying out specialized and automatized cognitive operations (e.g., Dosenbach et al., 2007; Bertolero et al., 2015) and for containing the consequences of damage to relatively (functionally) local areas (e.g., Achard et al., 2006; He et al., 2007; Honey and Sporns, 2008. Also see a review on this topic by Wig, 2017).

In addition to providing a global characterization, network properties can also be measured for each node in a network, and notably nodes that are well-connected to other nodes and/or modules are referred to as “hubs”. Interestingly, it has been proposed that cortical “hubs” are particularly vulnerable to various brain diseases, which may be due to their high information processing workload and/or high metabolic demand (Buckner et al., 2009; Zhou et al., 2012; Crossley et al., 2014). More specifically, hub nodes which have connections across many different sub-networks (a.k.a. modules) are defined as “connector hubs” (e.g., Sporns, 2013; Wig, 2017). Connector hubs have been found to play a pivotal role in supporting global network organization, and although a modular network is robust to “random attack”, damage to connector hubs would have the most impact on the whole system (e.g., He et al., 2007; Honey and Sporns, 2008; Gratton et al., 2012). In sum, characterizing the manner in which the integration-segregation balance of functional networks is affected in neurological disease may deepen our understanding of the neural mechanisms of these diseases and provide a foundation for neuromodulatory approaches in rehabilitation.

Graph-theoretic approaches in studying PPA

In primary progressive aphasia (PPA), to our knowledge, there have been only two published studies applying graph-theoretic methods to study functional network organization, and each examined one variant, semantic (svPPA) and non-fluent (nfvPPA), respectively (Agosta et al., 2014; Mandelli et al., 2018). Both studies examined: (1) several graph-theoretic metrics that measure global network integration or segregation (across the whole brain or within specific functional networks), and, (2) changes in functional hub locations. Mandelli et al. (2018) found that, in comparison to healthy controls, in nfvPPA, the “speech production network” exhibited lower global integration as well as changes in the neurotopographic distribution of hubs, while in contrast, the default mode network (DMN), which was considered less affected in nfvPPAs, was largely unaffected. In addition, the authors argued that changes in hub distribution within the speech production network were mainly driven by changes in functional connectivity rather than volume loss. This claim was based on their finding that the differences in hub status relative to healthy controls (i.e., some brain regions “lost” their hub status while others became “new hubs”) were not explained by the gray matter volume loss in those regions. The authors interpreted this observation as supporting the network-specific hypothesis (e.g., Seeley et al., 2009) such that within the disease-targeted network, functional changes can be detected before discernable volume loss. Agosta et al. (2014) examined the whole-brain organization of svPPA and also found decreased global network integration compared to healthy controls. In terms of hub distribution, the svPPA cohort showed most “lost” hubs in the left inferior temporal and occipital lobe while “new hubs” were identified in the more dorsal areas, and the authors suggested that the shift in hub location might be related to structural damage, although the relationship between functional and structural changes was not explicitly examined in that study. In terms of the logopenic variant (lvPPA), to date no published study has reported a graph-theoretic evaluation of the network properties of RSFC.

The current investigation

In the work we report on here, we carried out two sets of graph-theoretic analyses to characterize the RSFC network properties of all three PPA variants with reference to a group of age-matched healthy controls (HC, N=17). First, following the Agosta et al. (2014) and Mandelli et al. (2018) studies, we evaluated a number of global network characteristics to determine if the increased network segregation they reported in the semantic (svPPA) and the non-fluent (nfvPPA) variant was: (a) replicated in new samples and (b) present in all the three variants. Those global graph-theoretic measures (e.g., characteristic path length, modularity) quantify global network properties with a single statistic but do not identify which regions within the network have been especially affected by the disease and whose connectivity may have undergone re-organization. Therefore, we carried out a second set of analyses that characterized nodal properties, quantifying the extent to which the connectivity profiles of specific nodes (brain regions) have been affected. We focused on the global “connector hubs” identified with the nodal graph-theoretic measure participation coefficient (or PC, Guimera and Amaral, 2005), a measure that quantifies the extent to which a node’s total connections are distributed across the different modules in a network. Connector hubs play a key role in determining global functional organization and, therefore, their disruption is likely to contribute importantly to changes in global functional network properties (e.g., He et al., 2007; Honey and Sporns, 2008; Gratton et al., 2012). Specifically, this analysis identified regions which, in comparison to healthy controls, had retained or lost their global connectivity and, additionally, we identified regions which had increased their global connectivity to become “new” hubs. Furthermore, for these regions, we examined the relationship between their functional and structural properties (gray matter volume) to evaluate the claim (e.g., Mandelli et al., 2018) that changes in hub status and functional connectivity may occur independently of volume changes, indicating that disruptions to functional networks may occur distally to atrophy epicenters.

2. Methods and Materials

2.1. Participants

Forty-two participants (18 females, mean age=67.02, SD=6.73) with PPA were recruited for a clinical trial (NCT02606422), and the current study examined data collected at the pre-treatment time-point. This cohort included 18 nfvPPA, 15 lvPPA, and 9 svPPA. All had a history of at least two years of progressive language deficits without other etiology (e.g., stroke, tumors, etc.) or primary memory deficits. Differential diagnosis was based on three types of evidence: neuropsychological and language testing, structural MRI, and clinical assessment, according to criteria in Gorno-Tempini et al. (2011). MRI data were also collected from a group of age-matched healthy controls (HC) with age >= 50 years old (N=17, 13 females, mean age=65.24, SD=8.18). Control participants were all right-handed and native speakers of English. The study was approved by the Johns Hopkins Hospital and Johns Hopkins University Institutional Review Board. All participants provided informed consent.

2.2. MRI data acquisition

All MRI data were collected using a Phillips 3T scanner at the F.M. Kirby Research Center for Functional Brain Imaging (Baltimore, MD, USA). The scanning protocol of each PPA participant included one session of resting-state and multiple structural scanning protocols, including a T1-weighted structural image included in this analysis. For 34 PPA participants, the resting-state fMRI (rs-fMRI) scan lasted 8.75 minutes (210 data-points), and for the other 8 the scan lasted 6.5 minutes (156 data-points). The acquisition parameters of the resting-state fMRI were as follows: TR = 2500ms, TE = 30ms, FOV = 240*141*240mm (ap, fh, rl), flip angle = 75°, voxel dimension = 3*3*3mm, data matrix = 80*80*47. The T1-weighted structural MRI acquisition parameters were as follows: TR = 8.1ms, TE = 3.7ms, FOV = 224*160*180mm (ap, fh, rl), flip angle = 8°, voxel dimension = 1*1*1mm, data matrix = 224*224*160.

For the healthy controls, 5 underwent the same scanning protocol as described just above for the PPA participants. The other 12 were scanned with a slightly different protocol as they were recruited for a different experiment: Two 7-minute runs of rs-fMRI (175 time-points) were carried out consecutively, the acquisition parameters were as follows: TR = 2400ms, TE = 20ms, FOV = 206*123*220mm (ap, fh, rl), flip angle = 90°, voxel dimension = 1.7*1.7*3mm, data matrix = 128*128*41. The T1-weighted structural MRI acquisition parameters were: TR = 6ms, TE = 2.9ms, FOV = 256*256*176mm (ap, fh, rl), flip angle = 9°, voxel dimension = 1*1*1mm, data matrix = 256*256*176. Note that despite some minor differences, both protocols used with the healthy controls included standard parameters for structural MRI and rs-fMRI acquisition. We also compared quantitatively both the functional connectivity (FC) strength and the graph-theoretic measure results (see Section 2.5 for the measures used in this study) of the two HC subgroups and found no difference between them (Supplementary Material 1), eliminating concerns about scanning protocol differences.

2.3. Neuroimaging data preprocessing

The MRI data preprocessing was carried out with MRICloud (mricloud.org), a publicly accessible cloud-based platform for automatic neuroimaging data analysis (Mori et al., 2016). MRICloud provides standardized data processing service with pre-tuned parameters, therefore here we only summarize the preprocessing procedure as provided by the developer. For details of the implementation we refer the readers to the published work by the development team (Faria et al., 2012; Mori et al., 2016). First, the T1 structural image of each individual (in native space) was parcellated into 283 anatomical structures (https://braingps.mricloud.org/t1prep, atlas version “Adult50_90yrs_283Labels_19atlases_M2_V9B”), from which 76 gray matter structures were identified to construct the functional connectome (Fig. 1a). The parcellation was conducted with a multi-atlas fusion label algorithm (MALF) and large deformation diffeomorphic metric mapping (LDDMM), an algorithm that minimizes mapping error due to atrophy or local shape deformation (Faria et al., 2012). Second, the resting-state fMRI images were preprocessed with MRICloud’s resting-state fMRI processing pipeline (https://braingps.mricloud.org/fmri), which included routines imported from SPM5. The preprocessing steps were: slice-timing correction, motion correction that realigned the images to the first volume, physiological nuisance removal with CompCor (Behzadi et al., 2007), outlier volume rejection with “ART” (https://www.nitrc.org/projects/artifact_detect). The functional images were then co-registered to the individual’s T1 scan with rigid-body transformation, and the averaged time-courses corresponding to the 76 gray matter regions-of-interest (ROIs, 38 in each hemisphere, Fig. 1a) were extracted, and then pairwise correlation values (Fisher’s z- transformed) were calculated to create a 76×76 symmetrical connectivity matrix for each participant. Note that tthe ROIs are also referred to as “nodes” in the following graph-theoretic analyses.

Figure 1. Regions-of-interest (ROI) parcellation and atrophy.

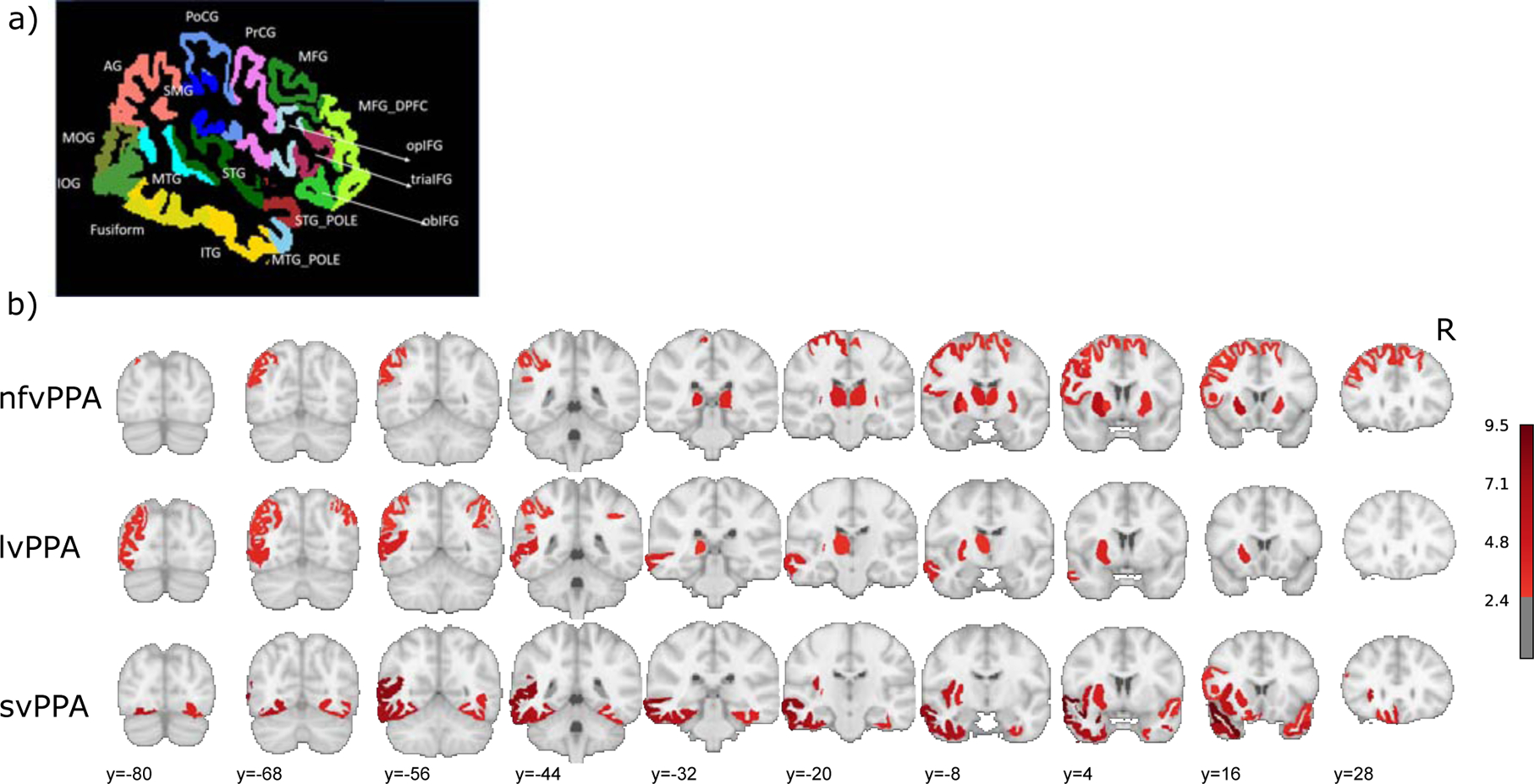
a) A lateral view of the atlas used for the parcellation (76 ROIs, the same 38 ROIs in each hemisphere. See section 2.3). ROIs that are visible on this view are labelled. b) Comparison of the grey matter volumes of the 76 ROIs between HC (N=17) and each variant (nfv N=18, lv N=15, sv N=9). The color scale indicates the t-value, thresholded by one-tailed p-values < 0.01 (uncorrected). Left hemisphere is on the left and the right is on the right.

2.4. Evaluating gray matter atrophy

To characterize the atrophy patterns of each variant, we compared the gray matter volume of each of the 76 ROIs resulting from the parcellation (described in Section 2.3) of each PPA variant to the age-matched healthy controls (HC). As the T1-parcellation was carried out in each individual participant’s native space, the volume values were normalized by each individual’s total intracerebral volume. Then, for each PPA variant, the normalized volumes of each region were compared to the HC group with two-sample t-tests.

2.5. Global graph-theoretic measures

We computed 8 global segregation/integration measures that have been previously reported in PPA (Agosta et al., 2014; Mandelli et al., 2018): global efficiency with and without infinite distance, assortativity, characteristic path length; mean clustering coefficient, small-worldness and two types of modularity. Global efficiency is the inverse of the average shortest distance, thus when there are graphs that are not fully connected (resulting in “infinite distance”), those values can be considered as having zero efficiency and can either be included in the average value or excluded from the analysis. Here we examined both types of global efficiency (including or excluding “infinite distance”). The two modularity measures differ according to whether or not it was calculated with an optimal modular organization identified individually for each participant or with a reference modular organization identified from the healthy control group (HC); thus, we refer to the individually and HC-based modularity measures as modularity(i) and modularity(hc), respectively. Specifically for modularity(i), the calculation of the modular organization for each individual is embedded in the computation of modularity implemented in Brain Connectivity Toolbox (see next paragraph). Briefly, the optimal modular organization for each individual was calculated by maximizing the number of within-module connections and minimizing the number of between-module connections. For computing modularity(hc), the HC reference modular organization was calculated with agglomerative hierarchical clustering algorithm with Ward’s criterion implemented in Matlab. This approach groups nodes with highly correlated time-series into clusters (or modules). Clustering was carried out with the mean correlation matrix of the HC group. Note that given the wide range of approaches available to quantifying network modularity, our goal in using these two kinds of modularity measure was to better capture the topological differences between the groups rather than to specifically compare them or to determine which is superior.

Additionally, because two of the global measures above, characteristic path length and clustering coefficient (CC), each consist of an aggregate of regional values, in addition to whole brain values, we also compared these values for each ROI to examine regional effects. Specifically, characteristic path length is the average of the shortest distance between each pair of nodes in the network, thus for each node we also calculated its average shortest distance to all the other nodes. Clustering coefficient (CC) is a nodal measure defined as the ratio of the number of observed triangles to the total number of possible triangles for a given node, and the global mean CC is simply the average across all the nodes. For these two nodal measures, the differences between HC and PPA for each node were compared with two-sample t-tests and corrected for the 76 ROIs with FDR correction.

All graph theoretic measures and analyses were carried out with the Brain Connectivity Toolbox (Rubinov and Sporns, 2011). Each individual participant’s connectivity matrix was first thresholded to preserve the strongest connections and then converted to an undirected binary graph (in which all connection strengths correspond to 1’s or 0’s). As there is no agreed-upon threshold, we applied a range of proportional threshold values (5%, 10%, 20%, 25%, 30%, 40%) to calculate the graph-theoretic measures, and then used the averaged values across the thresholds for all subsequent analyses. For each of the 8 graph-theoretic measures, the values of the HC group and each PPA variant group were compared with two-sample t-tests and corrected for multiple comparisons (Bonferroni). The three variants were compared with one-way-ANOVA.

2.6. Connector hubs: Identification and comparisons across variants

To examine which regions were especially affected by the disease and may have undergone re-organization, we focused on the global “connector hubs”. First, we identified the reference “connector hubs” in the healthy controls (HC) based on the graph-theoretic measure participation coefficient (PC) that quantifies the extent to which a node’s connections are distributed across all the modules (Guimera and Amaral, 2005) based on the HC reference modular organization defined in Section 2.5 (see Result Section 3.4.1, Supp Fig. 1). Specifically, for each HC participant, we calculated the PC values for all the 76 nodes and then the PC values were averaged across the HC participants to obtain a whole-brain PC template. Connector hubs were identified as nodes with PC values greater than one standard deviation above the mean across all the 76 nodes (see Supp Fig. 8a for the PC value distributions across all the nodes). For simplicity, we refer to the connector hubs as “hubs” for the remainder of the paper.

Second, we used precisely the same process to identify the hubs for each variant group (i.e., PC value > 1SD above the mean as calculated for each variant. See Supp Fig. 8a for the PC value distributions). Finally, to examine how the hub distribution of each PPA variant differed from the HC group, we identified “lost”, “retained” and “new” hubs for each variant by comparing the hubs identified for each PPA variant to the reference hubs identified for the HC group: Any node that was a hub in both the HC group and a PPA variant group was classified as a “retained” hub, any node that was identified as a hub for the HC group but not for the PPA variant group was classified as a “lost” hub, while any node identified as a hub in a PPA variant group but that was not a hub in the HC group, was classified as a “new” hub.

2.7. Evaluating hub properties

In order to better understand the basis for any changes in hub status of the nodes, we examined the relationship between PC values and gray matter volume for the retained, lost and new hubs identified in the previous step. First, we determined whether any of the three types of hubs exhibited abnormal connectivity levels in PPA compared to the HC group. This was necessary because, since the hubs were identified as the nodes with the highest PC values within each variant (PC > 1SD above the mean), changes in hub status could have been simply due to changes in their relative ranking within their variant rather than in terms of their absolute PC values. Given that we found (as will be reported in Section 3.4.1) that all three variants had the same lost and retained hubs, for these hubs we conducted comparisons of PC values between HC and all PPA (combining the variants, N=42). On the other hand, as the three variants recruited different new hubs (see result Section 3.4.1), the PC comparisons with the HC group for the new hubs were conducted for each variant separately. The comparisons were conducted with two-tailed independent t-tests followed by Bonferroni multiple comparisons correction for the three variants.

Second, to assesses whether the node status differences were driven by gray matter volume differences, for the three types of hubs we compared each PPA variant group’s gray matter volumes to those of the HC group as with the PC values above. The gray matter volume calculation was described in Section 2.4. Furthermore, we evaluated the relationships between PC and volume values for the different hub types with Pearson correlation; significance was assessed with Monte-Carlo permutation test (10K permutation).

3. Results

3.1. Demographics and behavioral assessment.

Age was comparable between the variant groups and healthy controls (HC) (t(57)=−0.87, p=0.39), and only marginally differed across the three PPA variants (f(2,39)=2.67, p=0.0822), driven by nfvPPA being older than lvPPA (nfv vs. lv: t(31)=2.08, p=0.0463; nfv vs. sv: t(25)=0.13, p=0.8995; lv vs. sv: t(22)=−1.52, p=0.1426). The three variants were also comparable in terms of time since disease onset (f(2,39)=0.55, p=0.58), the overall dementia severity rating (FTDL-CDR, Knopman et al. 2008. f(2,37)=0.08, p=0.9224, scores of two participants were missing) as well as the language severity rating (FTDL-CDR language component, f(2,38)=1.69, p=0.1972, the score of one participant was missing). The demographic characteristics of each variant are shown in Table 1. Each PPA participant was assessed with a comprehensive battery of cognitive tests reported in Table S1, showing that, as expected, the svPPA scores are significantly lower on semantic tasks while nfvPPA and lvPPA are more impaired in other tasks such as digit span forward.

Table 1.

Demographic characteristics of the healthy controls (HC) and the three PPA variants, the group mean and standard deviation values are shown.

	HC (N=17)	nfvPPA (N=18)	lvPPA (N=15)	svPPA (N=9)	f-value
Age	65 (8.18)	69 (5.37)	64 (8.12)	69 (5.25)	2.67~
Gender (N of female)	13	7	7	4	NA
Education (year)	16 (2.52)	16 (3.59)	16 (1.78)	16 (2.64)	0
Time since onset (year)	NA	3.58 (2.50)	3.97 (3.11)	4.78 (2.74)	0.55
Whole-brain gray matter volume (% out of the Intracranial volume)	76.78 (1.82)	73.72 (151)*****	74.24 (2.15)**	74.22 (2.56)**	0.34
FTDL-CDR (scale 0 – 15)	NA	5.71(4.27)	5.53(3.94)	6.25(4.08)	0.08
FTDL-CDR Language (scale 0 – 3)	NA	1.81(0.88)	1.33(0.86)	1.88(0.64)	1.69

Each PPA variant was compared to the HC goup with independent t-tests. The last column shows the results of one-way-ANOVA evalution of differences across the three variants.

^~:p<0.1;

^*:p<0.05;

^**:p<0.01;

^*****:p<1e–05.

3.2. Atrophy distribution across PPA variants.

For the 76 gray matter ROIs obtained from the segmentation algorithm, we compared the volumes (normalized by individual intracerebral volume) between HC and each variant group with independent t-tests. Fig. 1b. shows the ROIs that were significantly smaller for the variant group than the HC group (thresholded at uncorrected one-tailed p<0.01). As can be seen in Fig. 1b, the three variants presented very different patterns that are consistent with their prototypical atrophy patterns (e.g., Grossman, 2010; Gorno-Tempini e al., 2014). Specifically, for the nfvPPA group, 16 ROIs were smaller than HC, including: bilateral superior frontal and subcortical areas, left middle frontal, inferior frontal opercularis, precentral, and angular gyri. For the lvPPA group, 9 atrophic ROIs were found in the left parietal and occipital lobe, plus the right angular gyrus. For the svPPA group, 18 atrophic ROIs were found in the bilateral temporal lobes as well as left frontal areas. For all the variants, the majority of atrophic ROIs were in the left hemisphere (number of significant atrophic ROIs in the LH out of total: nfvPPA: 10 out of 16, lvPPA: 8 out of 9, svPPA: 11 out of 18).

3.3. Global graph-theoretic measures

The results for the 8 global graph-theoretic measures [global efficiency (exclude and include infinite distance), characteristic path length, assortativity, mean clustering coefficient, small-worldness, modularity(i) and modularity(hc)] are reported in Table 2. Three of those measures, characteristic path length, mean clustering coefficient, and modularity(i) exhibited significant differences between the PPA (all variants combined) and the HC groups after correction for multiple comparisons (p<0.05 after corrected for 8 comparisons. Fig. 2a). These results indicate that the overall network organization of the PPA group was more segregated and less integrated than it was for the HC group. This finding is in line with the previous reports that have examined the network organization with similar measures (Agosta et al., 2014; Mandelli et al., 2018). No significant differences were found across the variants (Table 2).

Table 2.

Results of the 8 global graph-theoretic measures measured in the healthy control (HC) and the PPA groups.

	HC (N=17)	PPA (all variants, N=42)	f-value	nfvPPA (N=18)	lvPPA (N=15)	svPPA (N=9)
Characteristic path length (L)	2.27(0.12)	2.38(0.12)*	0.53	2.41(0.13)	2.36(0.10)	2.38(0.15)
Global efficiency (exclude inf)	0.56(0.02)	0.55(0.01)	0.07	0.55(0.01)	0.55(0.01)	0.55(0.02)
Global efficiency (include inf)	0.47(0.03)	0.47(0.02)	0.48	0.47(0.03)	0.47(0.02)	0.46(0.02)
Assortativity	0.23(0.08)	0.25(0.07)	1.14	0.25(0.07)	0.23(0.06)	0.27(0.10)
Mean clustering coefficient (CC)	0.51(0.02)	0.54(0.03)**	1.76	0.55(0.02)	0.53(0.02)	0.54(0.03)
Small-worldness	1.64(0.34)	1.77(0.27)	0.51	1.85(0.31)	1.75(0.24)	1.75(0.37)
Modularity(i)	0.32(0.04)	0.36(0.05)*	0.17	0.36(0.05)	0.36(0.04)	0.35(0.05)
Modularity(hc)	0.23(0.04)	0.23(0.04)	0.47	0.24(0.04)	0.22(0.04)	0.24(0.05)

Group means and standard deviation values are shown. Values for PPA groups (all variants combined) were compared to HC values with independent t-tests, and significant comparisons are indicated in bold (corrected p<0.05). The three variants were compared with one-way-ANOVAs comparing the three variants.

^*:p<0.05,

^**:p<0.01, Bonferroni corrected.

Figure 2. Graph-theoretic measures for which PPA groups exhibited statistically significant differences from the healthy control (HC) group.

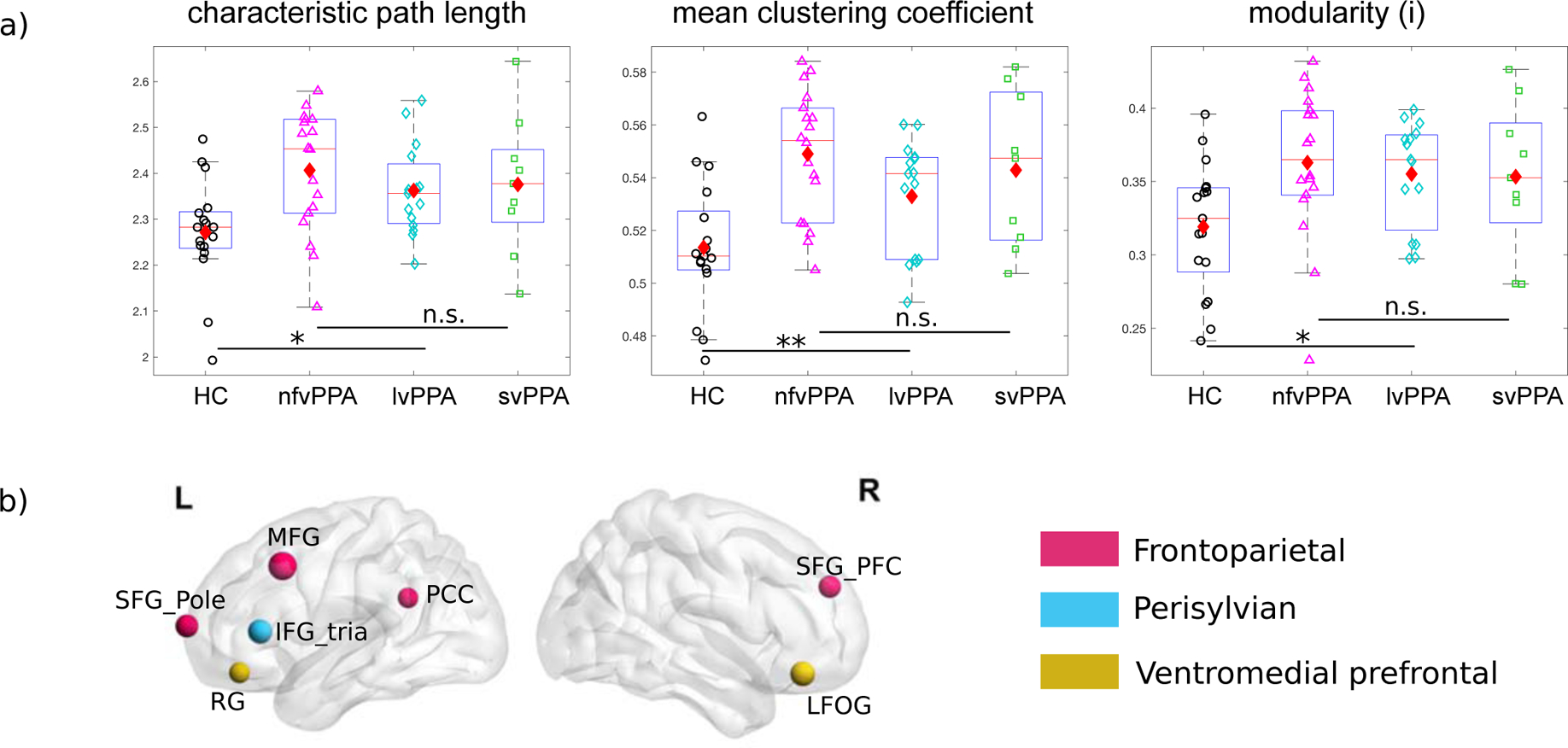
a) Left to right: characteristic path length, mean clustering coefficient, and modularity(i), all indicate that the PPA group had greater segregation (or lower integration) than the HC group. No difference was found among the three PPA variants. See Table 2 for results for all graph-theoretic measures evaluated. The boxplots show the lower to upper quartile of the data with a line indicating the median, the diamonds indicate the mean. *: p<0.05; **: p<0.01 Bonferroni corrected. b) ROIs that show higher nodal clustering coefficient in PPA than HC. The node sizes are proportional to the t-values and the colors indicate their module membership as in Supp Fig. 1. The nodes are found in three modules. Note that we color-code the module membership only to facilitate visual inspection and that module membership is not considered in this analysis. SFG_pole: superior frontal gyrus pole; SFG_PFC: superior frontal gyrus (prefrontal cortex), MFG: middle frontal gyrus, PCC: posterior cingulate cortex, IFG_tria: inferior frontal gyrus triangluaris, RG: rectus gyrus, LFOG: lateral frontal orbital gyrus.

In addition, we also examined the nodal differences between HC and PPA groups for the two measures, characteristic path length, clustering coefficient (CC), that can also be calculated for each node. As reported above, HC and PPA groups also differed in terms of these two measures on the global level. At the nodal level, we did not find any significant differences for characteristic path length; For clustering coefficient, 7 ROIs survived FDR correction (alpha=0.1), in which the PPA group had higher values than the HC group and these were mostly found in the frontal lobe (Fig. 2b). The results indicate that the elevated global mean clustering coefficient is driven primarily by increased segregation in frontal areas.

3.4. Evaluating connector hub properties

3.4.1. Connector hub distributions in healthy controls (HC) and PPA

We identified global connector hubs as nodes that have the most widespread connections across modules with respect to the reference modular network. This modular reference network (Supp. Fig. 1) consisted of 7 bilateral clusters (modules): 1) Temporal, 2) Ventromedial prefrontal, 3) Dorsal frontoparietal, 4) Perisylvian, 5) Subcortical, 6) Frontoparietal, 7) Occipital. On the basis of this reference modular structure, for each group (HC and the three variants) we identified hubs as nodes with average participation coefficient (PC) higher than one standard deviation above the mean across all the nodes for each group (see Supp. Fig. 8a for the PC value distributions across all the nodes), a commonly used criterion (e.g., Agosta et al., 2014; Mandelli et al., 2018).

For the HC group, 6 ROIs were identified as hubs: left superior frontal gyrus, left superior parietal gyrus and bilateral superior and middle temporal gyri (Fig. 3a. Also see Supplementary Material 4 for the reliability of the reference hubs identified with the HC). Those regions have been commonly identified in RSFC literature as making up part of the fronto-parietal network (FPN) and the default-mode network (DMN) (e.g., He et al., 2009; Warren et al., 2014; Power et al., 2013). However it is worth noting that resting-state networks and “hubs” have been identified in various ways and there is variability across studies, moreover it is not yet clear whether and if/how the functional organization shifts in older populations. We will return to this issue in the Discussion.

Figure 3. Connector hub distributions.

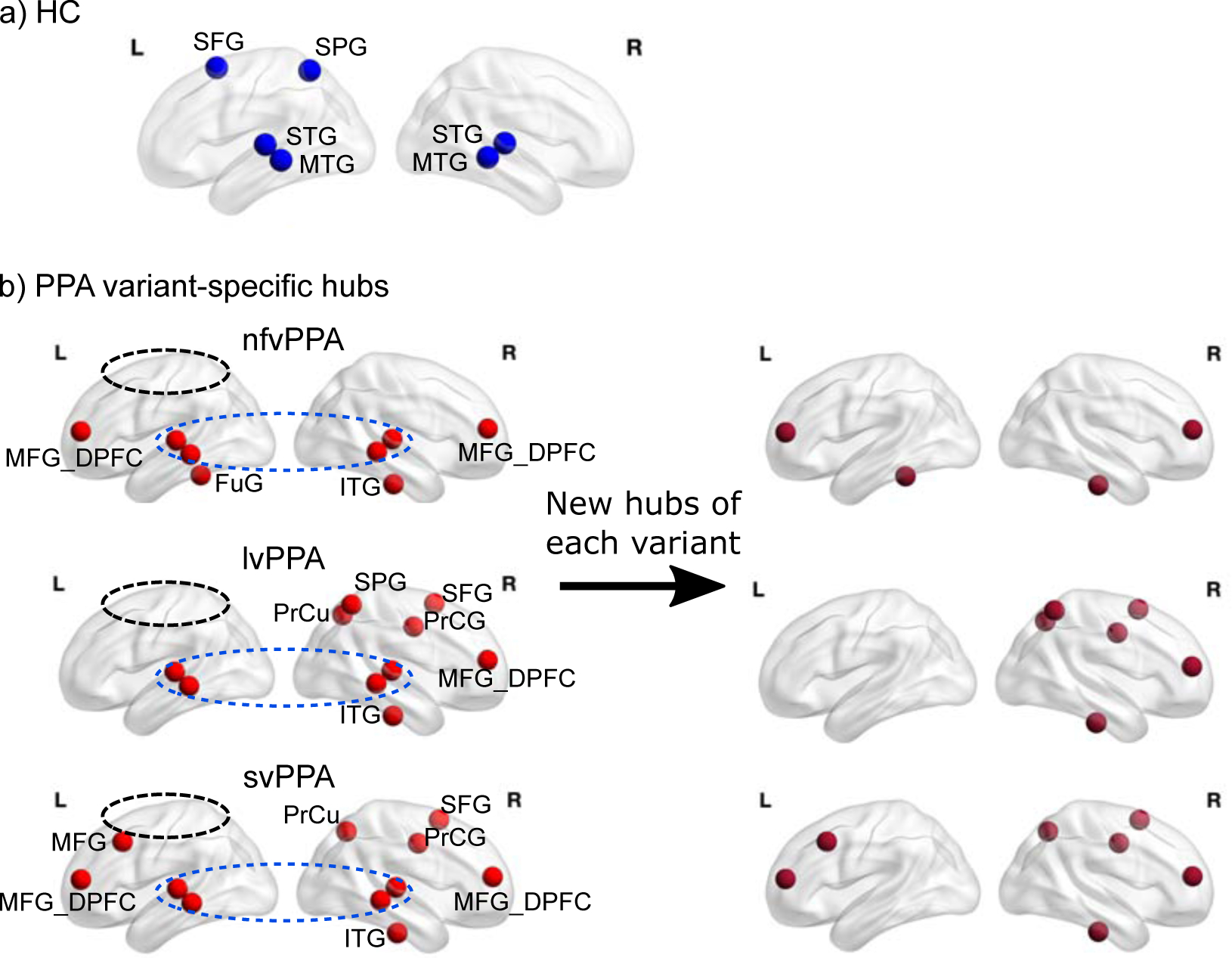
a) Connector hubs identified in the healthy control (HC) group which correspond to ROIs with the highest participation coefficient (PC) scores across the whole brain (>1SD above the mean). b) Connector hubs identified for each variant group, top to bottom: non-fluent (nfvPPA), logopenic (lvPPA), semantic (svPPA). Compared to the HC, all three variants “lost” the left SFG and the left SPG (circled) and the bilateral S/MTG are retained (circled). On the right panel the new hubs (present in PPA but not in the HC) for each variant are shown. SFG: superior frontal gyrus, SPG: superior parietal gyrus, S/MTG: superior/middle and temporal gyri, MFG: middle frontal gyrus, MFG_DPFC: middle frontal dorsal prefrontal cortex. ITG: inferior temporal gyrus, FuG: fusiform gyrus, PrCG: precentral gyrus, PrCu: precuneus.

Fig. 3b reports the hubs identified for each PPA variant. The left panel of the figure reveals clear differences in hub distributions across the variants. First, all variants had a larger number of hubs (8, 10 and 11, respectively) than the HC. Second, and most strikingly, both lvPPA and svPPA had strongly right lateralized hub distributions: This right lateralization of hubs was even more pronounced for the lvPPA group (2LH/8RH) than for the svPPA (4LH/11RH). For the nfvPPA group, the hubs were similarly distributed across the two hemispheres (4LH/4RH), concentrated in the temporal lobes. Third, the lvPPA group differed from the other two PPA groups in terms of the absence of any left frontal hubs.

3.4.2. Lost, retained, and new hubs.

A comparison of the hub distributions of the HC group with each of the PPA variants revealed which hubs were: 1) “lost” (i.e., nodes that were hubs for the HC, but in PPA were no longer highly connected across modules), 2) “retained” (i.e., nodes that were hubs in both the HC and PPA groups), and 3) “new” (i.e., nodes that became hubs although they had not been in the HC group). As shown in Fig. 3b, first, for all three variants, the lost hubs corresponded to the left superior frontal gyrus (SFG) and the superior parietal gyrus (SPG). These regions were part of the fronto-parietal network that has been associated with domain-general executive control processes (e.g., Cole et al., 2013), a topic we return to in the Discussion. Second, the three variants shared the same retained hub regions: bilateral STG and MTG. In other words, as in the HC group, across the PPA variants these nodes/regions continued to play a key role in cross-module communication/integration. With regard to new hubs, the three variants showed some similarities and differences (Fig. 3b, right column): (1) For all three variants the right prefrontal and right ventral temporal regions were recruited to serve as hubs; (2) both nfvPPA and svPPA recruited left prefrontal regions (more anterior and inferior to the lost left SFG hub) to serve as hubs, while there were no new left hemisphere hubs at all for the lvPPA group; 3) Both lvPPA and svPPA showed massive recruitment of right hemisphere regions to serve as hubs, with very similar distributions of these new hubs across the two variants, which were mostly found in the right dorsal frontal-parietal area.

3.4.3. Hub differences between PPA and HC: The relationship between PC and grey matter volume

First, because the hub status changes could have been simply due to the differences in the relative ranking within each variant, we evaluated if changes in hub status reflected actual differences in the participation coefficient (PC) values of those nodes compared to the HC group. The results (Fig. 4a) show that overall in PPA (collapsing across the three variants), the lost hubs (i.e., left SFG and SPG) had lower PC values in the PPA compared to the HC group (t(57)=2.25,p=0.028, with no difference across variants f(2,39)=1.67, p=0.20). The retained hubs (i.e., bilateral S/MTG) did not differ in PC from the HC group (t(57)=0.15, p=0.88) and likewise the variants did not differ from one another (f(2,39)=0.21, p=0.82). With regard to the new hubs, for each of the PPA variants these nodes had significantly higher (or numerically higher) PC values than they did in the HC group (nfv: t(33)=−1.79, p>0.1; lv: t(30)=−2.65, p<0.05; sv: t(24)=−2.66, p<0.05. P-values were Bonferroni corrected for 3 comparisons), indicating that those new hubs were not only the top ranking nodes within their respective PPA variant, but also exhibited higher than normal levels of global connectivity.

Figure 4. Global connectivitiy (PC) and gray matter volume of the lost, retained and new connector hubs.

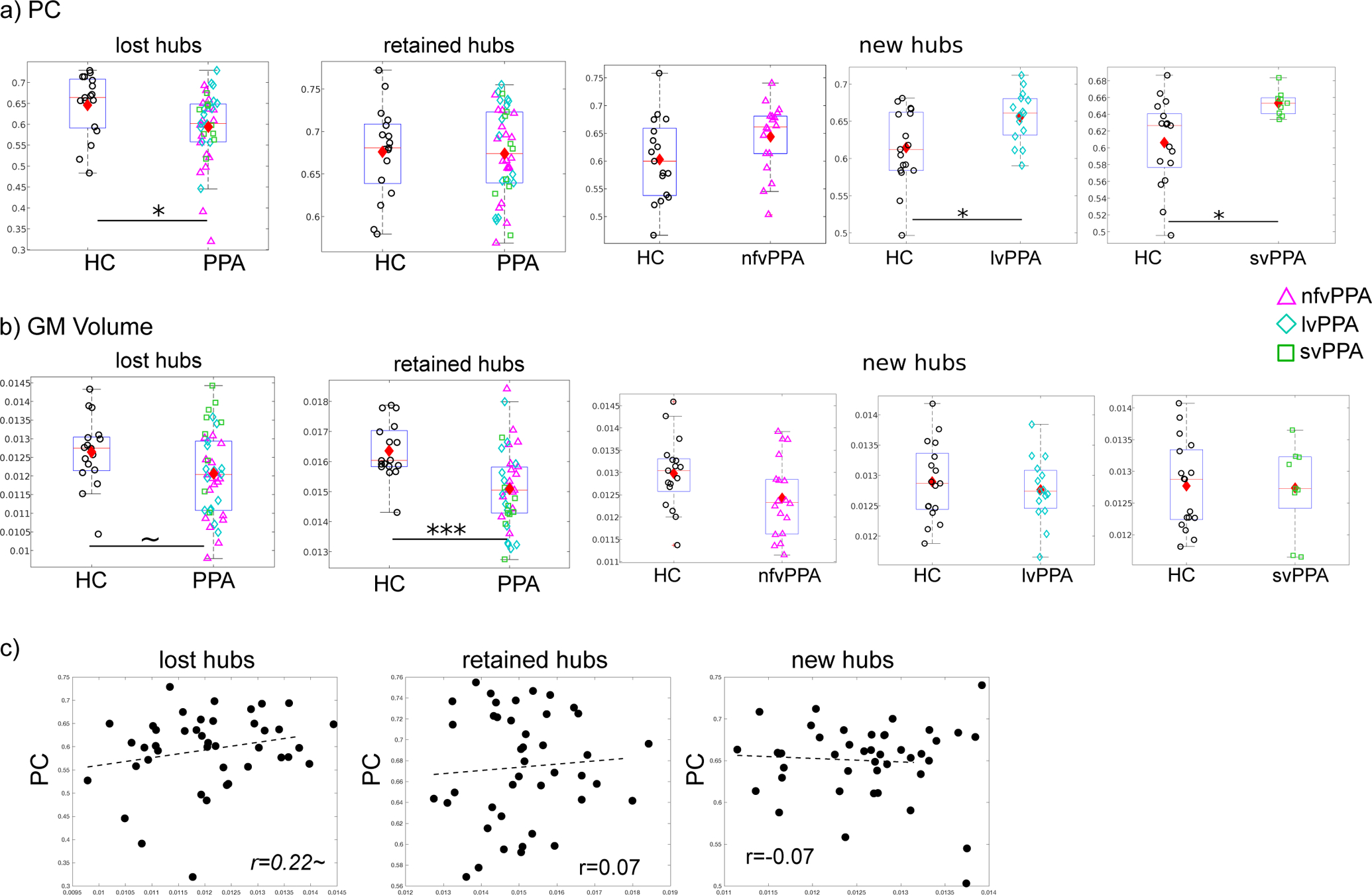
a) Comparison of PC values between healthy controls (HC) and PPA. For the two lost hubs shared by all variants (see Fig. 3), PPA had significantly lower average PC (p=0.028). For the four retained hubs that were also shared by all variants (see Fig. 3), PPA did not differ from the HC in terms of average PC (p=0.88). For the new hubs of each variant (see Fig. 3b), all variants showed higher (or numerically higher) PC values than HC (Top to bottom: nfv: p=0.25; lv:p=0.0384; sv: p=0.0408, Bonferroni corrected). b) Comparison of gray matter volume: Compared to the HC group, the PPA group showed marginally smaller volume (p=0.06) for the lost hubs and also significantly smaller volume for the retained hubs (p=0.0006). No significant differences between the groups was found for the new hubs. The boxplots show the lower to upper quartile of the data with a line indicating the median, the diamonds indicate the mean. c) Correlations between hub connectivity (PC, y-axis) and volume (x-axis) for the three types of hubs combining all PPA variants (N=42). ~: p<0.1, *: p<0.05, **: p<0.01, ***: p<0.001.

Comparisons of grey matter volumes between the PPA and HC groups for the three types of hubs (Fig. 4b) showed that the individuals in the PPA group (collapsing across variants) had only marginally lower volumes for the lost hubs (t(57)=1.89, p=0.0635) but significantly lower volume values for the retained hubs (t(57)=3.65, p=0.0006). For the new hubs of each variant, the PPA volumes did not differ from the HC (nfv: t(33)=1.97; lv: t(30)=0.62; sv: t(24)=0.11. All p-values > 0.1 after Bonferroni corrected for 3 comparisons).

The above comparisons did not reveal a clear correspondence between PC and volume differences. To examine this more closely, we directly correlated the PC values and volumes for the three types of hubs for the PPA participants. As seen in Fig. 4c, there was no relationship between PC and volume values for either the retained or the new hubs, with only a marginally positive correlation for the lost hubs (Lost: r=0.22, p=0.08; Retained: r=0.07, p=0.34; New: r=−0.07, p=0.66). In addition, results were very similar in either hemisphere alone (Retained: LH r=0.07; RH r=−0.04. New: LH r=−0.14; RH r=−0.04). Results were similarly not significant with each individual regions.

In sum, these results show that, consistent with their hub status changes, the lost hubs had lower than normal levels of global connectivity as compared to the HC, the retained hubs did not differ from the HC, while for the new hubs, global connectivity levels were generally higher than normal. Importantly, examination of the relationship between these PPA connectivity changes and grey matter volume changes did not reveal a strong correspondence between the two, except for a marginal correlation between the lost hubs’ connectivity and volume, a point we return to the in the Discussion.

3.5. Assessment of motion artifact

As motion can introduce significant artifact on FC (e.g., Power et al., 2012), we compared the amount of motion, measured by mean relative root mean square (RMS) of the 6 motion parameters, between the participant groups to determine if any of the reported differences between groups could be caused by motion. We found that there was no difference between the HC and the PPA groups (HC: 0.11+/−.05, PPA: 0.12+/−0.07, t(57)=−0.70, p=0.48). Furthermore, the three variants did not differ from each other (nfvPPA: 0.13+/−0.05; lvPPA: 0.11+/−0.06; svPPA: 0.14+/−0.11. F(2,39)=0.67, p=0.52), and none of the variants differed from the controls (HC vs. nfvPPA: t(33)=1.0, p=0.33, HC vs. lvPPA: t(30)=−0.12, p=0.91, HC vs. svPPA: t(24)=0.96, p=0.35).

4. Discussion

In this study, we investigated resting-state functional network properties in primary progressive aphasia (PPA) with graph-theoretic methods, an approach that evaluates the topological properties of functional network organization. We examined network characteristics in the three PPA variants: non-fluent, logopenic, and semantic (nfvPPA, lvPPA, svPPA), as compared to age-matched healthy controls (HC).

Our key findings were as follows: (1) Across a number of network measures, the three variants, compared to healthy controls, exhibited greater overall global segregation and, thus, lower global integration of the whole-brain network (Fig. 2); (2) All three variants showed functional loss of global connector hubs in the left superior frontal and superior parietal gyri (Fig. 3 and Fig. 4a); (3) The three variants displayed different variant-specific distributions of “new” hubs (i.e., regions that did not serve as connector hubs in the healthy controls but emerged as hubs in PPA. Fig. 3b and Fig. 4a); (4) Local volume loss did not explain the observed pattern of hub distribution changes (Fig. 4), supporting the previous claim (Mandelli et al., 2018) that at least some of the functional network disruptions in PPA are not directly attributable to volume loss and may, instead, result from disruptions to the brain’s functional organization. Overall, the current study highlights the utility of graph-theoretic approach for investigating and understanding the brain’s functional responses to the pathologies of the different PPA variants, providing a basis for future longitudinal studies, planning targeted neural interventions, and investigating treatment effects.

Graph-theoretic measures of brain-wide integration/segregation.

We computed a number of whole-brain global network integration and segregation measures that had been reported in the two previous graph-theoretic studies in PPA (Agosta et al., 2014; Mandelli et al., 2018. Table 2). We found that the three PPA variants significantly differed from the controls in several measures, all indicating increased levels of global segregation and thus, reduced global integration (Fig. 2). Specifically, characteristic path length is the average value of the shortest connection distance between all the pairs of nodes, with a higher value indicating, on average, more steps are required to travel from one node to another in the network; Clustering coefficient measures the fraction of a node’s neighbors that are also neighbors of each other (i.e., forming a triangle), such that a higher average value (averaged across all the nodes in the network) indicates that nodes in a network generally tend to form cliques; at last Modularity(i) measures the degree to which the nodes are grouped into non-overlapping modules based on each individual’s optimal modular structure. However, the PPA and HC groups did not differ on the other measures: global efficiency, assortativity, small-worldness, and modularity(hc). Global efficiency is the inverse of characteristic path length, and, hence, unsurprisingly we found that, similar to characteristic path length, there was a trend towards lower global efficiency (calculated without infinite distance) but it was not significant after correcting for multiple comparisons. Global efficiency calculated with infinite distance (i.e., zero efficiency) did not differ between HC and PPA groups. Assortativity is often used to quantify a hierarchical, “rich-club” organization of a network (i.e., nodes that have high connectivity tend to connect to each other and thus form a “rich club”). Small-worldness is a specific graph topological feature of a network that possesses both certain degree of segregation and integration, and the ratio between segregation and integration (i.e., small-worldness) of a healthy brain should be somewhat higher than 1. Lastly modularity(hc), in contrast to modularity(i), is modularity calculated relative to a reference modular organization, in the study derived from the HC group (Supp. Fig. 1). Although several of these measures are somewhat related, they can also capture different topological traits of a network and, thus, the current results indicate that the PPA groups and HC did not differ in terms of the specific aspects captured by these measures.

To summarize, despite some differences (discussed further below), overall our results confirm the conclusions drawn from the previous studies that examined these issues (Agosta et al., 2014; Mandelli et al., 2018) while also extending them to lvPPA. We found that individuals with PPA exhibited increased global segregation (i.e., decreased integration) in their functional network organization as revealed by several graph-theoretic measures. Because, for the first time, we evaluated the three variants with the same analytic procedures and found that they did not differ in any of those measures (Table 2), we are able to conclude that globally increased network segregation appears to be a shared feature of the PPA variants.

Lost, retained, and new connector hubs

Given that the PPA functional networks showed abnormally high levels of segregation and thus, were less globally integrated, we were motivated to examine the nodal global connectivity properties for the three PPA variants. We did so by comparing the three variants to the healthy control group in terms of the distribution of “connector hubs”, which are defined as the nodes with the highest global connectivity (i.e., participation coefficient, or PC, Guimera and Amaral, 2005) within each group (Fig. 3. Also see Supp. Fig. 8 for the PC values across all ROIs).

For the healthy controls (HC), connector hub regions were identified in the left superior frontal (SFG) and parietal gyri (SPG) as well as bilateral superior and middle temporal gyri (STG and MTG, Fig. 3a). These regions have been typically identified and associated with domain-general executive control processes in RSFC research (e.g., He et al., 2009; Cole et al., 2013; Power et al., 2013; Bertolero et al., 2015). Of course, however, research on domain-general networks remains an active field and the locations and exact definitions of the networks (e.g., default-mode network, dorsal attention network, frontal parietal control network) vary across studies. Moreover, age-related changes regarding these domain-general networks have been reported (e.g., Chan et al., 2014; Greeligs et al., 2015; Grady et al., 2016; Spreng et al., 2016). Therefore, how the changes observed here in PPA are related to aging in general and other neural degenerative disease is an important direction for future research.

A comparison of hub distributions across the three variants revealed a number of striking similarities (Fig. 3b). First, all three variants retained the STG and MTG hubs in both hemispheres. Second, for all three variants the right frontal and temporal regions were recruited as “new hubs. Third, all three variants “lost” the left hemisphere SFG and SPG hubs. The loss of the left hemisphere SFG and SPG hubs is particularly salient as it suggests significant disruption of domain-general, executive control networks, which may be related to other non-language deficits such as executive control and working memory that are often observed in PPA (e.g., Grossman, 2012). In terms of the new hubs, there were also a number of notable differences across variants in the neurotopography. While for nfvPPA hub changes were largely left-lateralized, lvPPA and svPPA were similar in their overall strong right-lateralization of new hubs, particularly in the right frontal-parietal regions. We discuss these specific patterns in more detail in the next section.

Why are hubs lost, gained and retained?

Possible explanations for the loss of hub connectivity are: (a) structural damage to the hub region itself (e.g., volume loss), (b) pathological changes at the cellular level in the hub region that precede detectable volume loss, and (c) structural damage elsewhere in the hub’s functional network that causes “downstream” functional disruption. The last account has been proposed in PPA and other neurodegenerative diseases (e.g., Seeley et al., 2009; Mandelli et al., 2016, 2018; Collins et al., 2017). For instance, in Mandelli et al. (2018), the authors argued that the changes of the hub distribution they observed in nfvPPA could not be accounted for by atrophy, instead, they attributed the changes to the network-wide functional alterations that stemmed from the nfvPPA’s atrophy epicenter left IFG. They reached this conclusion on the basis of the fact that they found no significant differences in gray matter volume for lost compared to new hubs.

There are several findings from this investigation that are also generally consistent with the third explanation. First, we found that despite very distinct patterns of atrophy (Fig. 1b), all three variants exhibited the same “lost hubs”, suggesting that volume loss is not likely to be the only basis for the loss of hub status. Second, we found that in a comparison to the HC, all types of hubs – whether they were lost, gained and retained had generally smaller volumes in PPA (significantly or numerically. Fig. 4b). Furthermore, a direct examination of the relationship between volume and global connectivity revealed no significant correlation between the two (Fig. 4c). This is a further indication that volume loss was not the major factor for explaining changes in hub status. However, it may be worth noting that for the lost hubs there was a marginally significant positive relationship in the expected direction (p=0.08, Fig. 4c) such that smaller volumes were to some degree associated with lower connectivity values. This may reflect the fact that volume loss may, not surprisingly, make some contribution to hub loss. After all, PPA is a neurodegenerative disease that involves volume loss and it would be surprising if this did not have any consequences vis-a-vis functional connectivity. What is interesting about our results, as well as the Mandelli et al. (2018) findings, is that volume loss does not seem to be the only explanation for these functional changes, raising a host of interesting questions regarding the manner in which functional networks are re-organized even in areas that may be distant from the structural damage.

In terms of the “retained hubs”, the three variants also had the same retained hubs (bilateral superior and middle temporal gyri) despite the fact that those regions suffered significant volume loss in all variants (Fig. 4b). However, as shown in Fig. 4, those regions retained the same level of global connectivity (PC) as was seen in the healthy controls, and no correlation was found between PC and atrophy, again demonstrating the dissociation between structural and functional changes in PPA. Although it is possible that more fine-grained spatial resolution (e.g., voxels) might reveal a different relationship between structural and functional changes, at the level of the anatomical ROIs, we found that volume loss cannot fully explain functional changes.

What might explain the emergence of new hubs? As we show in Fig. 4a, the new hubs did not simply correspond to the brain regions with the highest global connectivity (PC) within each variant group, but their PC values were even higher in the PPA groups than in the healthy controls. This indicates that re-organization in PPA involved global connectivity increases in different regions for all three variants. One might speculate that, at a general level, the fact that new hubs had higher than normal levels of global connectivity might reflect the brain’s response to offset the overall reduction in global integration that was reflected in the overall increased segregation values, discussed above.

With regard to the specific distribution of new hubs for each PPA variant, for the non-fluent variant (nfvPPA), Mandelli et al. (2018) also reported new hubs for nfvPPA in the anterior part of the frontal lobes bilaterally, similar to our results (Fig. 3b). Mandelli et al. attributed the recruitment of these new hubs to their adjacency to the posterior IFG, nfvPPA’s atrophy epicenter. Thus, the new hubs were within the yet relatively spared part of nfvPPA’s compromised functional network centered at the left posterior IFG (the speech production network), and hence might serve a compensatory role.

Regarding the logopenic variant (lvPPA), studies with conventional RSFC approaches have typically compared lvPPA to Alzheimer’s Diseases (AD) because of their often shared pathology. In the AD literature, it has been proposed that because the posterior parietal lobe is the most connected region in the brain, degeneration in this region may initially trigger a cascading increase in information processing demands in other brain areas, and that such high metabolic demands eventually result in widespread network failures at a later disease stage (Jones et al., 2016; Wiepert et al., 2017; also see Bakker et al., (2012) for similar proposal regarding the hyper-activation of the middle temporal lobe in AD). As both AD and lvPPA individuals typically suffer from damage in the posterior parietal lobe, the central area of functional hubs, the increase in hubs in the right hemisphere in lvPPA that we observed (Fig. 3b) may be a response to the left-lateralized parietal lobe atrophy.

In terms of the semantic variant (svPPA), in the graph-theoretic study by Agosta et al (2014), new hubs were also identified in the bilateral frontal areas which were largely structurally spared in svPPA, consistent with our current findings (Fig. 3b). Moreover, our observation that the svPPA group recruited almost the same hubs in the RH as the lvPPA group (Fig. 3b, right panel) suggests a shared mechanism of functional disruption and response to disruption in the two variants. SvPPA’s atrophy starts from the anterior temporal lobe and typically extends posteriorly and superiorly (e.g., Collins et al., 2017), and RSFC studies on svPPA have shown that besides the atrophy epicenter, functional abnormalities are often found in the posterior regions (Guo et al., 2013; Agosta et al., 2014; Ranasinghe et al., 2017; Battistella et al., 2019). Thus, one possible cause of the emergence of the new right hemisphere hubs in svPPA may be the functional disruptions in left posterior temporoparietal area that is also seen in lvPPA. It would be interesting to examine if this specific pattern of network changes is a general consequence of posterior temporoparietal damage even in different etiologies such as stroke or resection.

In sum, the results indicate that alterations in hub distribution cannot be fully explained by atrophy and, instead, may be driven by changes in functional connectivity that can have consequences beyond the sites of atrophy. In the future, it will be important to examine longitudinal data to track how hub distributions change in response to atrophy progression and their relationship with behavioral changes.

Comparison with the previous studies of PPA RSFC with complex network analysis

There are several differences in the findings between the current investigation and the two studies that also examined functional network properties with graph-theoretic methods in PPA (Agosta et al., 2014; Mandelli et al., 2018). First, as we indicated earlier, specific results regarding the general global graph-theoretic measures were not entirely consistent across the studies. Agosta et al. (2014) reported that, for the comparison of svPPA with healthy controls, they found lower global efficiency, mean clustering coefficient, and higher averaged path length and assortativity. Mandelli et al. (2018) reported lower global efficiency, assortativity, and higher mean clustering coefficient (and a trend for modularity). Here, we found PPA showed higher average path length, mean clustering coefficient, and modularity. Given the wealth of available graph-theoretic measures and the complex relationships among them, it is not yet known which are the more appropriate measures and, furthermore, findings are likely be affected by model construction and other specific properties of the dataset. Under these circumstances, it is especially important to examine multiple different measures and evaluate the convergent evidence. It is striking, that despite the differences, the overall results of all the three studies point to a less globally integrated, more segregated functional organization of PPA compared to healthy controls. Second, with respect to the “lost” and “new” hubs, we did not find precisely the same regions. For instance, Mandelli et al. (2018) also found that nfvPPA lost hubs in bilateral temporal lobe whereas we actually found new hubs for nfvPPA in this region. We suspect that those differences were also likely due to methodological differences discussed below.

It is worth noting several major methodological differences between Mandelli et al. (2018), Agosta et al (2014) and the current investigation. First, nodes were defined differently across the studies. Agosta et al. (2014) used the 90 AAL parcels (anatomical segments such as the STG, MTG) as “nodes”, whereas in Mandelli et al. (2018) “nodes” were 7mm cubes with 1mm gaps between them. Here we defined “nodes”, in a manner similar to Agosta et al., using large anatomical areas (Fig. 1a) (see Section 2.3). While large anatomical ROI-based nodes might be more suitable for analyzing imaging data with atrophy, they make it more difficult to detect effects at a more fine-grained scale. Clearly, future work should investigate similarities and differences in effects at different spatial scales. A second difference across the studies concerns the scope of the examined networks. Whereas the current study and Agosta et al. examined the whole brain, Mandelli et al. examined only the “speech production network” (and the default-mode network as a control). An examination of the entire brain is useful since we cannot predict where changes may take place. However, since it has been hypothesized that different neurodegenerative diseases may target specific networks (e.g., Seeley et al., 2009), analyses focusing on specific networks are also important. Third, here we defined hubs on the basis of the centrality measure participation coefficient (PC) while the other studies used degrees and betweenness centrality. Degrees simply counts how many other nodes a given node is directly connected with, whereas betweenness is a more global measure, defined as the fraction of all the shortest paths in the graph passing through a given node. In contrast, PC is calculated based on a given modular structure that quantifies the connectivity diversity of a given node: A node has a zero PC value if all its connections are within a single module, and its PC value approaches one if its connections are uniformly distributed across all the modules. It is not obvious, at this time, which of these or other centrality measures will prove to be most appropriate and they are likely to reflect different topological traits.

Limitation and future directions

First, the age-matched healthy control (HC) participants were scanned with two similar but not identical protocols, and the number of participants was relatively small (n=17). Although we verified that the resulting FC metrics did not differ between the two HC sub-cohorts (Supplementary Material 1), in the future, the use of larger data sets and/or validating the effects with other datasets should be considered. Second, in this study the preprocessing was carried out entirely with the publicly accessible cloud-based service MRICloud (mricloud.org) with pre-defined routines and parameters. Such a system provides excellent computational power and efficiency, therefore, although we do not consider it necessarily to be a limitation, we do acknowledge that the parcellation scheme (i.e., the definition of “nodes”) plays a critical role in determining the resulting connectivity pattern, and hence we can only draw conclusions on the basis of the current anatomical ROIs (Fig. 1a, see Section 2.3). As we have noted, future work should examine different parcellation schemes at different spatial scales. Third, we currently do not have a full understanding of the relationship between raw connectivity strength (often examined in traditional RSFC studies) and network topological properties (such as those examined here). In Supplementary Material 2 we report on various aspects of the relationship between the two and show that the topological differences between PPA groups and healthy controls reported in this study cannot be explained by raw FC strength. The relationship between the two types of measurements should be examined on a study by study basis, as an understanding of both will likely be needed to form a complete picture of the functional network organization in PPA. Fourth, we examined a number of global measures that aimed to replicate what had been reported previously as well as the nodal centrality measure participation coefficient. Nonetheless, given the wealth of available graph-theoretic measures (e.g., Rubinov and Sporns, 2011), the current findings are by no means comprehensive and specific effects could have been missed. Lastly, the relationship between the functional network changes and behavioral changes was not investigated in this work. Although the characterization of patterns of behavioral changes across PPA variants itself is a challenging topic, moving forward it will be important to examine the behavioral consequences of the functional network changes.

5. Conclusions

In this investigation we examined functional network organization measured by resting-state functional connectivity (RSFC) across the three variants of primary progressive aphasia (PPA) using a graph-theoretic analytic approach. We found that, in comparison to age-matched healthy controls (HC), the three PPA variants presented both shared and distinct patterns of changes to their functional network organization. Specifically, all three variants exhibited a more segregated, less integrated whole-brain functional organization. An examination of the neurotopography of the changes revealed that all three variants exhibited different distributions of network hubs. These differences could not be fully accounted for by volume loss and thus the findings support the view that at least some functional disruptions in PPA may not be directly caused by structural changes and are influenced by variant-specific functional network disruptions. In sum, the current study highlights the utility of graph-theoretic approach for understanding the brain’s functional network re-organization in response to the pathologies of the different PPA variants, and provides a basis for future longitudinal studies and investigating treatment effects.

Highlights.

• Graph-theoretic methods reveal altered functional network organization in PPA

• All PPA variants exhibited higher levels of whole-brain network segregation

• The different variants exhibited distinctive hub distributions compared to controls

• The functional network changes in PPA cannot be fully explained by atrophy