Estimation of the basic reproduction number (𝑅0) of the COVID-19 epidemic in Iran

Abstract

Background: Estimation of the basic reproduction number of an infectious disease is an important issue for controlling the infection. Here, we aimed to estimate the basic reproduction number (𝑅0) of COVID-19 in Iran.

Methods: To estimate 𝑅0 in Iran and Tehran, the capital, we used 3 different methods: exponential growth rate, maximum likelihood, and Bayesian time-dependent. Daily number of confirmed cases and serial intervals with a mean of 4.27 days and a standard deviation of 3.44 days with gamma distribution were used. Sensitivity analysis was performed to show the importance of generation time in estimating 𝑅0.

Results: The epidemic was in its exponential growth 11 days after the beginning of the epidemic (Feb 19, 2020) with doubling time of 1.74 (CI: 1.58-1.93) days in Iran and 1.83 (CI: 1.39-2.71) in Tehran. Nationwide, the value of 𝑅0 from February 19 to 29 using exponential growth method, maximum likelihood, and Bayesian time-dependent methods was 4.70 (95% CI: 4.23-5.23), 3.90 (95% CI: 3.47- 4.36), and 3.23 (95% CI: 2.94-3.51), respectively. In addition, in Tehran, 𝑅0 was 5.14 (95% CI: 4.15-6.37), 4.20 (95% CI: 3.38-5.14), and 3.94 (95% CI: 3.45-4.40) for exponential growth, maximum likelihood, and Bayesian time-dependent methods, respectively. Bayesian time dependent methods usually provide less biased estimates. The results of sensitivity analyses demonstrated that changes in the mean generation time affect estimates of 𝑅0.

Conclusion: The estimate of 𝑅0 for the COVID-19 ranged from 3.94 to 5.14 in Tehran and from 3.23 to 4.70 in nationwide using different methods, which were significantly larger than 1, indicating the potential of COVID-19 to cause an outbreak.

↑ What is “already known” in this topic:

COVID-19 is showing substantial transmissibility and causing outbreaks worldwide. The amount of basic reproduction number (𝑅0) has been estimated in a wide range in different studies. In most studies just 1 method and a specific serial interval has been used.

→ What this article adds:

We use 3 different methods, including exponential growth rate, maximum likelihood, and Bayesian time-dependent, and 2 sources of data, including reported and redistributed confirmed cases, to estimate 𝑅0 in Iran and in Tehran. We also demonstrated how 𝑅0 has varied in line with different mean generation times using sensitivity analysis. Our study showed that these differences are due to the effect of the selected serial interval distribution, duration of the study data, and method of estimation.

Introduction

The outbreak of the novel coronavirus disease (COVID-19) was first reported from Wuhan, China, on December 31, 2019 (1). Since then, the outbreak has dramatically worsened over a short period of time and has spread to other provinces and countries (2, 3). According to the world health organization, until March 25, 2020, the outbreak of COVID-19 was reported from 195 other countries worldwide (4). In the meanwhile, the number of confirmed cases was also increasing in Iran since the first cases were confirmed on February 19, 2020 (5). A daily reports of total and newly lab-confirmed cases, deaths, and recovered cases are provided by the Iran Ministry of Health in which they report cases from the previous day (5). As of March 25, 2020, a cumulative total of 27 017 COVID-19 cases, including 2206 new cases, 2077 deaths, and 9625 recovered cases were reported in Iran (6). Approximately 90% of laboratory confirmed patients have had mild to moderate disease, which includes non pneumonia and pneumonia cases, and 10% have had severe disease (6).

Early investigations of COVID-19 have provided evidence of human-to-human transmission (7-9). However, estimating the epidemiological characteristics of COVID-19 is critical to assess this ongoing outbreak with regards to transmissibility, prediction of the future trends of the epidemic, and the effectiveness of control strategies (10). The basic reproduction number (𝑅₀) is an important concept in infectious disease epidemiology and determines the transmissibility of a pathogen (11, 12). The 𝑅₀ denotes the expected number of secondary infectious cases produced by an index case in a completely susceptible population (12). If 𝑅₀ ˃ 1, the number of infected patients will be increased, and for 𝑅₀ ˂ 1, the transmission of infection will be reduced until it goes away. Estimating the 𝑅₀ is critical to predict the trend of an epidemic curve (13).

Liu et al examined 12 studies that estimated the 𝑅₀ of COVID-19 in China between January 1 and February 7, 2020. They found that 𝑅₀ ranged from 1.4 to 6.49 in China. Mean, median, and interquartile range (IQR) were estimated as 3.28, 2.79, and 1.16, respectively (14). In this study, we aimed to estimate the transmissibility of COVID-19 via the basic reproduction number, 𝑅₀, based on the limited data in the early phase of the outbreak in Tehran, the capital of Iran.

Methods

Weestimated 𝑅0 for the first 10-day period of epidemic and the first 23 days of epidemic interval using the exponential growth method, maximum likelihood, and Bayesian time-dependent method. The first period has been assumed as the duration of the natural spread of disease without interventions and the second as a changed epidemic curve because of interventions that have been done.

Data source

To estimate 𝑅0 in Iran and Tehran, we used daily number of confirmed cases of Iran and Tehran (acquired from the Ministry of Health and Medical Education of Iran). 𝑅0 estimation was also repeated with smoothed data by moving average, including the current day and one day before and after.

The daily data of cases with positive results of polymerase chain reaction (PCR) test of COVID-19 in Iran and Tehran provided by the Ministry of Health (MOH) may peak due to delays in responding on specific days. Thus, moving average smoothing with span 5 was used to address this issue. Results were reported for both official and smoothed data. Approval for the project was obtained from the School of Public Health & Neuroscience Research Center, Shahid Beheshti University of Medical Sciences, Tehran, Iran (IR.SBMU.RETECH.REC. 1398.875).

Inference about the serial interval

Since we did not have access to the full spectrum of distribution of the serial intervals, we assumed that the serial interval, at least at the beginning of the COVID-19 outbreak in Iran, was similar to what was observed in a study of 5405 confirmed cases with 139 chains of transmission in China (3). The estimated serial intervals in this study had a mean of 4.27 days and a standard deviation (SD) of 3.44 days. A range of serial intervals with a mean between 4.7 to 7.5 and a SD between 2.9 to 4.2 days have been also provided by other studies (15-18). In these studies, the overall sample size was between 28 to 425 confirmed cases. According to the sample size and method of estimation, we preferred the serial interval of the first study mentioned above but for the sensitivity analysis, we estimated the 𝑅0 based on other estimated serial intervals. We used a gamma distribution, with shape and scale parameters compatible with the mentioned mean and SD. All analyses were done using R version 3.6.3. Parameters were estimated using the exponential growth rate method, maximum likelihood estimation method, and Bayesian time-dependent method by the 𝑅0 package (19).

Exponential growth rate (EGR) method

The exponential growth method was introduced by walling and Lipstich (2) with the following formula:

$$R=\frac{1}{M(-r)}=\frac{1}{{\displaystyle {\int }_0^{\infty }{e}^{-rt}w(t)dt}}$$

in which M shows the moment-generation function (ie, Laplace transformation) of generation time function (w(t)) and r represents exponential growth rate that is determined by Poisson regression between number of new cases and time. The parameter r demonstrates the spreading rate of the disease (13).

Properties of the exponential growth rate method are as follow:

The aggregated and dispersion data have the least impact on estimation of basic reproduction number in the exponential growth method.

The exponential growth method as a simple method for estimating 𝑅0 may not be powerful for the early stage of the epidemic.

For estimating 𝑅0, we must consider a period in the epidemic curve on which growth is exponential.

There is no assumption about mixing population in this method (20, 21).

Maximum likelihood (ML) method

The maximum likelihood method was summarized by White and Pagano and assumes that N₀, N₁..., N_T represent the incident casesover time. In maximum likelihood method, a primary case generates the secondary cases according to a poisson distribution with mean R that is the maximum value of the log-likelihood function. The log-likelihood function is as follows:

$$\begin{array}{l}LL(R)={\displaystyle \sum _{t=1}^T\log (\frac{\exp (-{\mu }_t){\mu }_t^{N_t}}{N_t!})}\\ Where\\ {\mu }_t=R{\displaystyle \sum _{i=1}^t{N}_{t-i}{w}_i}\end{array}$$

The parameter w, generation time, is also estimated by maximizing log-likelihood function (3).

Properties of the maximum likelihood method are as follow:

• - There are some assumptions for the maximum likelihood method, such as no missing data, no imported cases, and uniformly-mixed population; the results will change by violation of any of the mentioned assumptions (22).

• - For the aggregated data, the reproduction number estimation in the longer periods will be increasingly underestimated (20, 21).

Bayesian time-dependent method

In this method, N(t+1) represents the number of new cases in time t+1, which have Poisson distribution approximately with mean N(t) e^w(R-1) and generation time function w (Generation time has exponential distribution.). The reproduction number is given by below formula:

$$P(R\left|N_0,\mathrm{...},N_{t+1}\right.)=\frac{P(N_{t+1}\left|R,N_0,\mathrm{...},N_t\right.)P(R\left|N_0,\mathrm{...},N_t\right.)}{P(N_0,\mathrm{...},N_t)}$$

In this formula,$P(R\left|N_0,\mathrm{...},N_{t+1}\right.)$ indicates posterior distribution for reproduction number. Also, a noninformative prior distribution (The posterior distribution of R for the previous day is used as prior for the next day.) is used to estimate R in this Bayesian approach (23).

Several methods of 𝑅0 estimation were compared in a simulation study and the results showed that the bias and MSE of Bayesian time dependent method were less than the maximum likelihood and exponential growth methods (20).

Limitations: Our model makes a number of assumptions. Our estimates of the basic reproduction number of this novel coronavirus are tied to the specific time period and data analyzed here, and this measure may change substantially over the course of this outbreak and as additional data are obtained.

Sensitivity analysis

Sensitivity analysis was performed to show the importance of generation time in estimating the reproduction number. Indeed, the reproduction number is sensitive to the generation time distribution function. In the sensitivity analysis, different estimates of 𝑅0 (95% CI) were computed by varying the mean serial interval between 4 and 8 and the mean standard deviation between 2 and 5 (21).

Results

The epidemic curve in Iran and also its capital city Tehran according to the moving average smoothed data of confirmed cases is presented in Figure 1. As it is depicted the epidemic was in its exponential growth at the 11 days of the beginning of the epidemic (19^th Feb) with doubling time of 1.74 (95% Confidence Intervals (Liu, #14): 1.58-1.93) days in Iran and 1.83 (95%CI: 1.39-2.71) in Tehran and then after beginning of interventions in the country the exponential growth rate of the epidemic decreases in the following 11 days.

Fig. 1.

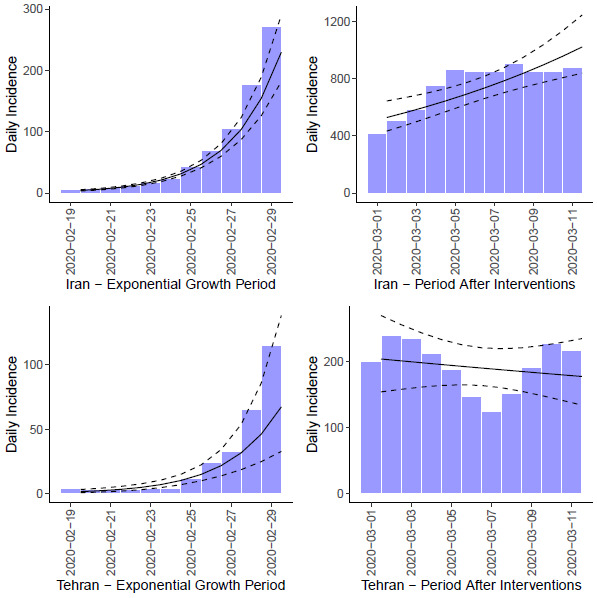
The epidemic curve of the COVID-19 in Iran (top) and Tehran (bottom) before the beginning of interventions (right) and after the beginning of interventions (left) according to the moving average smoothed data of confirmed cases.

Iran

In the whole country, the value of 𝑅0 from 19^th February to 29^th February was 4.70 (95%CI: 4.23-5.23) for daily reported confirmed cases by the MOH using exponential growth method. Also, we found that the estimated 𝑅0 in this setting by maximum likelihood was 3.90 (95%CI: 3.47-4.36) and 3.23 (95%CI: 2.94- 3.51) for Bayesian time-dependent methods (Fig. 2 A). The estimated 𝑅0_s (95%CI) for Iran (whole country) and Tehran are summarized in Table 1 and Figure 2 based on exponential growth, maximum likelihood, and Bayesian time-dependent methods.

Fig. 2.

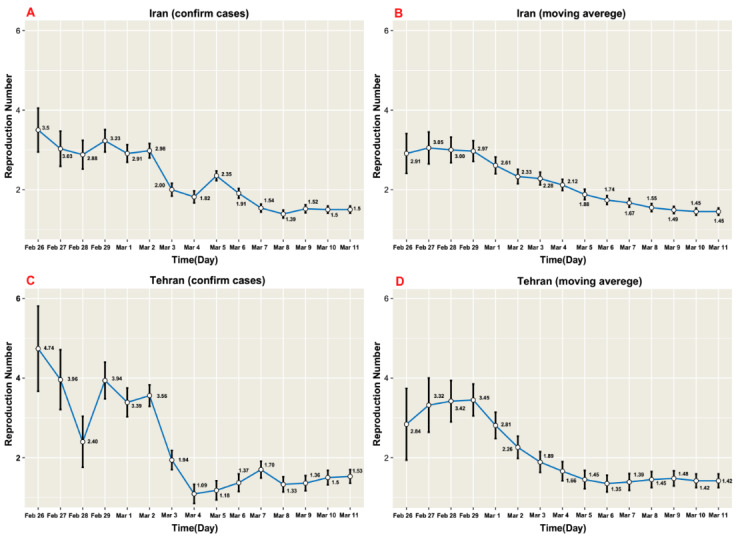
Estimation of the basic reproduction number by the Bayesian time-dependent method during the COVID-19 epidemic in Iran and Tehran up to 11^th March 2020.

Table 1. Estimation of basic reproduction number by exponential growth and maximum likelihood methods during the COVID-19 epidemic in Iran from 19^th February to 11^th March 2020 and Tehran from 21^st February to 11^th March 2020.

Location	Method	Period of estimation	𝑅 0 (95% CI)*	𝑅 0 (95% CI)**
Iran (whole country)	Exponential growth	19 Feb- 29 Feb	4.70 (4.23-5.23)	4.73 (4.30-5.21)
		19 Feb-11 Mar	1.91 (1.88-1.94)	1.87 (1.85-1.90)
	Maximum Likelihood	19 Feb- 29 Feb	3.90 (3.47-4.36)	3.93 (3.54-4.35)
		19 Feb-11 Mar	1.63 (1.59-1.68)	1.61 (1.56-1.65)
	Bayesian time-dependent	19 Feb- 29 Feb	3.23 (2.94- 3.51)	2.97 (2.71-3.23)
		19 Feb-11 Mar	1.50 (1.42- 1.59)	1.45 (1.37-1.54)
Tehran	Exponential growth	21 Feb-29 Feb	5.14 (4.15-6.37)	5.47 (4.65-6.46)
		21 Feb-11 Mar	1.67 (1.62-1.71)	1.68 (1.64-1.73)
	Maximum Likelihood	21 Feb-29 Feb	4.20 (3.38-5.14)	4.51 (3.79-5.32)
		21 Feb-11 Mar	1.55 (1.46-1.63)	1.51 (1.43-1.59)
	Bayesian time-dependent	21 Feb-29 Feb	3.94 (3.45-4.40)	3.45 (3.04-3.85)
		21 Feb-11 Mar	1.36-1.70)	1.42 (1.25-1.59)

* 𝑅0 was estimated using daily reported confirmed cases by the MOH

** 𝑅0 was estimated using moving average smoothing of the above mentioned data

In addition, the estimates of 𝑅0 from 19^th February to 11^th March for daily reported confirmed cases data by exponential and maximum likelihood methods were 1.91 (95% CI: 1.88- 1.94) and 1.63 (95% CI: 1.59-1.68), respectively. Moreover, the computed 𝑅0 for the mentioned data using Bayesian time-dependent method was 1.50 (95% CI: 1.42- 1.59) on the last day of the period (Fig. 2 A). The estimated 𝑅0 applying all methods were quite different compared to 𝑅0 from 19^th February to 29^thFebruary.

Moreover, the estimated 𝑅0 using moving average smoothing data for time period 19^th February-29^th February by exponential growth and maximum likelihood methods were 4.73 (95% CI: 4.30-5.21) and 3.93 (95% CI: 3.54-4.35), respectively. The computed 𝑅0 by the Bayesian time-dependent method was 2.97 (95% CI: 2.71-3.23) on the last day of period (Table 1).

We also fitted all mentioned methods to the moving average smoothing dataset of Iran throughout 19^th February -11^th March. The exponential growth method yielded an 𝑅0 of 1.87 (95%CI: 1.85-1.90) for Iran and by the maximum likelihood method, the value of 𝑅0 was 1.61 (95%CI: 1.56-1.65). The estimated 𝑅0 was1.45 (1.37-1.54) on the last day of period, applying the Bayesian time-dependent methods (Fig. 2 B).

Tehran

Using the daily reported confirmed cases of Tehran from February 21 to 29, the estimated 𝑅0_s were 5.14 (95% CI: 4.15-6.37) and 4.20 (95%CI: 3.38-5.14) for exponential growth and maximum likelihood methods. Also, the estimated 𝑅0 by the Bayesian time-dependent method was 3.94 (95% CI: 3.45, 4.40) on the last day (Table 1).

For daily reported confirmed cases data, the estimated 𝑅0_s from February 21 to March 11 were 1.67 (95%CI: 1.62-1.71) and 1.55 (95%CI: 1.46-1.63) applying exponential growth and maximum likelihood methods, respectively. According to the Bayesian time-dependent method, the computed 𝑅0s on the last day of period was 1.53 (95%CI 1.46, 1.63) (Fig. 2 C). Also, the estimated 𝑅0 of daily reported confirmed cases data for February 21 to 29 was different from that for February 21 to March 11 using all the 3 methods.

In addition, the 𝑅0 using moving average smoothing data of Tehran from February 21 to 29 using exponential growth method (5.47 (95%CI: 4.65-6.46)) was greater than that for maximum likelihood method (4.51 (95% CI: 3.79-5.32)). Bayesian time-dependent method provided a value of 3.45 (95%CI: 3.04 – 3.85) for the last day of the period (Table 1).

In the second time period, from February 21 to March 11, the computed 𝑅0_s for moving average smoothing data were 1.68 (95% CI: 1.64-1.73) and 1.51 (95%CI: 1.43-1.59) by exponential growth and maximum likelihood methods, respectively. Also, the Bayesian time-dependent method provided a value of 1.42 (95% CI: 1.25-1.59) for the last day of the period (Fig. 2 D).

Sensitivity analysis

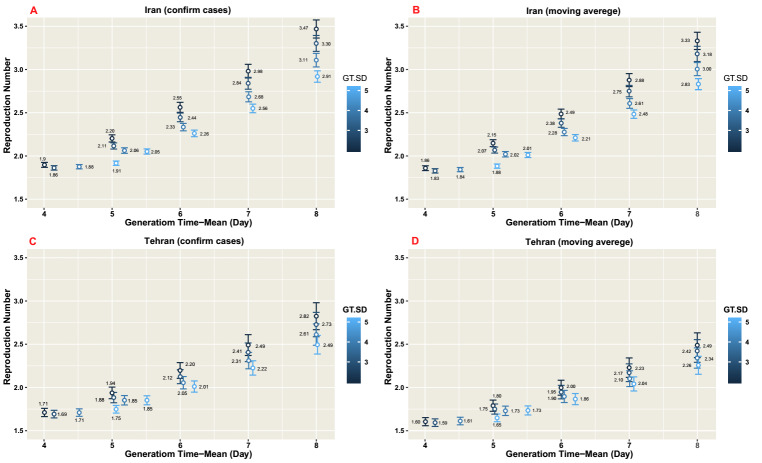
The results of sensitivity analysis using the daily reported confirmed cases data of Iran from February 19 to March 11, 2020 demonstrated that for a mean generation time of 4, 5, 6, 7, and 8 days with the same SD, 𝑅0 was 1.90, 2.20, 2.56, 2.98, and 3.45, respectively (Fig. 3 A).

Fig. 3.

Sensitivity analysis of basic reproduction number (𝑅0) with varying generation time distribution by exponential growth method in Iran and Tehran.

A: Daily reported confirmed cases by the MOH during the COVID-19 epidemic in Iran from 19^thFebruary to 11^th March 2020.

B: Moving average smoothing of data during the COVID-19 epidemic in Iran from 19^th February to 11^th March 2020.

C: Daily reported confirmed cases by the MOH during the COVID-19 epidemic in Tehran from 21^st February to 11^th March 2020.

D: Moving average smoothing of data during the COVID-19 epidemic in Tehran from 21^st February to 11^th March 2020

GT-SD: Generation time standard deviation

Using the same epidemic curve for moving average smoothing of data during the COVID-19 epidemic in Iran from February 19 to March 11, 2020, the reported 𝑅0s were 1.86, 2.15, 2.48, 2.88, and 3.33 for a mean generation time of 4, 5, 6, 7, and 8 days, respectively (Fig. 3 B), which were clearly close to 𝑅0s for the daily reported confirmed cases data of Iran. Overall, the estimates of 𝑅0 was sensitive to the mean of generation time distribution and increased with the mean generation time.

For Tehran, basic reproduction numbers were also computed using different mean generation times. Using daily reported confirmed cases data, the estimated 𝑅0 ranged between 1.71 and 2.82 when the mean generation time varied between 4 and 8 days (Fig. 3 C). The generation time varied for moving average smoothing data. Using the mentioned data, the computed 𝑅0_s were 1.60, 1.79, 1.99, 2.23, and 2.49 for the mean generation time of 4, 5, 6, 7, and 8 days, respectively, with the same SD (Fig. 3 D). The estimated 𝑅0_s using the daily reported confirmed cases data were a bit different from that for the moving average smoothing data. The results were less sensitive to the variation in the standard deviation.

Discussion

Reproduction number should be calculated for epidemic risk of disease, the effectiveness of interventions, and epidemic trends prediction.

For the first 10 days of the epidemic, 𝑅0 was about 4.7 and 3.9 in Iran and 5.5 and 4.5 in Tehran province based on the exponential growth rate method and the maximum likelihood model, respectively. 𝑅0_s estimation for the first 10 days for Tehran in all models was higher than the 𝑅0s estimation for the whole country. However, 𝑅0_s for Tehran for the 23-day period were much closer to those estimated for Iran. Considering that the first provinces involved in the COVID-19 epidemic in Iran were Tehran and Qom, in the first 10 days, the number of cases and the rate of transmission in Tehran province were higher than in Iran; thus, the 𝑅0 estimate was higher. Nevertheless, in the 23-day period, the gap diminished with the spread of the COVID-19 epidemic to other provinces of Iran.

Compared to other coronavirus epidemics (MERS and SARS) with 𝑅0_{, of} about 2 (14), the novel coronavirus epidemics have a higher risk of spread at the unit of time (24-27). This finding is consistent with higher 𝑅0 for the COVID-19 that was found in the present study.

In previous studies, based on China's epidemic data on COVID-19, 𝑅0 values have been reported with different values and a wide range (13, 18, 24, 27-29). The lowest value was 1.95 (1.4-2.5) for the WHO report (1), which is marginally lower than ours, and the highest was 6.47 (95% CI 5.71–7.23) (30). The study that reported a 𝑅0 number of 6.47 collected data during the Chinese New Year, a period of intensive social contacts (30). However, many of the existing 𝑅0 estimations range from 2 to 5 (24-27), which is in line with our results. In a review article of 12 studies, the average of 𝑅0 for the COVID-19 was estimated to be 3.28 (14); the results of the present study are slightly higher than the average of previous studies.

Moreover, the variability of the 𝑅0 is a methodological issue and there is no standard method for estimation (11, 31). The differences can be due to different calculation methods and different dynamics of transmission of the coronavirus in different populations and time zones (11, 32).

Comparison of 𝑅0_s over the investigation time

The duration of the study was effective. Studies using 10-day data have reported a higher 𝑅0 than studies using 2-week or 3-week data (26-28).

Results of this study showed that the estimated 𝑅0 for 23 days was less than the first 10 days. This difference reflects the delayed effect of all preventive interventions implemented in the epidemic duration. An alternative explanation for decreasing the trend of daily R is the increase in the slope of identification and reports of new cases as a result of missing the true first chain of infection and delayed recognition of the epidemic.

In this scenario, we have the same 𝑅0 in all the epidemic time zones under investigation, and the higher 𝑅0 number the in first days is reflecting underreporting in the first days and exponential increase in reporting in the following days. Perhaps, the difference among the estimates between these 2 time zones is the result of both scenarios.

The 𝑅0 estimate in the present study for the first 10 days was closer to the result of other studies using 10-day data. However, the 𝑅0 in the 3-week interval in our study was lower than the values reported with the same interval in China (27).

Given that the epidemic in Iran occurred a few weeks later than China, intervention seems to have started earlier in Iran, which is why the 𝑅0 value is less estimated in Iran in the 3 weeks’ interval data. Chinese researchers also reported that large-scale control interventions were initiated 3 weeks after the epidemic onset.

Sensitivity analysis of 𝑅0s based on different parameters of GT distribution

For estimation of 𝑅0, knowledge regarding the distribution of generation time is necessary. In the absence of local information about serial interval or generation time, we conducted the sensitivity analysis based on the previous means and standard deviations of GT for the COVID-19 worldwide.

According to the result of sensitivity analysis, the estimated 𝑅0 is sensitive to the selected distribution of generation time and larger means of generation time leads to the larger 𝑅0. However, based on an unpublished research in Iran, the selected distribution is compatible with the situation in Iran; thus, we should consider the effect of larger means of generation times on the reported 𝑅0. The high sensitivity of 𝑅0 to the GT variation must be taken into account in selection of GT from the result of studies about other strains of Corona viruses for the COVID-19 modeling in the absence of direct information of local GT.

Exponential growth, maximum likelihood, and Bayesian time-dependent methods were implemented for estimating the basic reproduction number as the key parameter of the epidemic. The exponential growth method has usually larger uncertainty, while maximum likelihood estimates are more consistent (20). In this study, cases were reported daily, and when the mean generation time was greater than the time scale of data, (greater than 1 in this study), all methods tend to be unbiased and performed appropriately. A simulation study performed by Obadia showed that the time-dependent method and ML have the closest value to the real 𝑅0 (21).

Application of 𝑅0 for epidemic monitoring and evaluation of interventions

The trend of 𝑅0 changes during the epidemic is a powerful tool for monitoring and forecasting the epidemic curve and the evaluation of epidemic control interventions. Reducing the 𝑅0 is pivotal for controlling the epidemic. Three components of 𝑅0 are contact rate, transmission probability, and duration of infectious period (33),which can be affected by a range of protective proceedings, such as community mitigation efforts–quarantine, health considerations enforcement, and isolation of the cases. By such interventions as increasing social distance (decreasing the contact rate), washing hands, and wearing masks (decreasing the transmission probability), and interventions that can diagnose COVID-19 earlier and isolate the patients and finally decreasing their contact with susceptible individuals, the value of 𝑅0 can be reduced. Moreover, hot weather may affect the transmission probability (29), which is an assumption which needs to be evaluated. Monitoring the trend of 𝑅0 after a notable decrease in the size of susceptible population (effective reproductionon number(Re)) and after implementing the control interventions (controlled reproduction number (Rc)) is more interpretable for evaluating the trend of this epidemic (3, 34).

Limitation

To estimate 𝑅0, we need data on daily counts of the disease, but our results are based on the reported confirmed cases of the disease, and these reported cases are much less than the real cases because not all cases are symptomatic to be referred for testing and not all symptomatic patients are being tested- due to laboratory limitations. There may also be some considerations in the announcement of real data. As long as there is a constant relation between the number of reported cases and the number of real cases, the estimated results are acceptable. The definition of symptomatic cases which were tested in Iran did not change during the course of the study, and hence we think that the ratio of confirmed cases to real cases has been constant and our data have caught the exponential growth of the real cases.

Given that the number of daily confirmed cases in the present study was based on the reported results of the PCR test, the trend of daily confirmed cases has been affected by the laboratory capacity for timely reporting during this epidemic. Therefore, in the absence of information on PCR sampling to result-reporting duration, we redistributed the number of daily reported confirmed cases using moving average with span 5 to smooth the curve and generate simulated daily confirmed cases. Therefore, smoothed data results are more reliable.

Conclusion

The estimate of R0 for the COVID-19 ranges from 3.94 to 5.14 in Tehran and from 3.23 to 4.70 in the whole country using different methods, and are significantly larger than 1, indicating the potential of COVID-19 to cause outbreak. Ffurthermore when the mean generation time is greater than the time scale of data, exponential growth, maximum likelihood, and Bayesian time-dependent methods tend to be unbiased and performed appropriately.

Acknowledgments

We appreciate the Research & Technology Chancellor in Shahid Beheshti University of Medical Sciences for financially supporting this study.

Conflict of Interests

The authors declare that they have no competing interests.

Cite this article as: Azimi SS, Koohi F, Aghaali M, Nikbakht R, Mahdavi M, Mokhayeri Y, Mohammadi R, Taherpour N, Nakhaeizadeh M, Khalili D, Sharifi H, Hashemi Nazari SS. Estimation of the basic reproduction number (𝑅0) of the COVID-19 epidemic in Iran. Med J Islam Repub Iran. 2020 (10 Aug);34:95. https://doi.org/10.34171/mjiri.34.95