Gastrointestinal arrhythmias are associated with statistically significant fluctuations in systemic information dimension

Abstract

Although cardiac arrhythmias have been studied extensively, little is known about arrhythmic phenomena in the gastrointestinal (GI) system. In this study, we demonstrate for the first time that the onset of GI arrhythmias is associated with statistically significant fluctuations in the information dimension of the associated systems. We induced gastric and intestinal arrhythmias in pigs using surgical stomach division and mesenteric artery ligation, respectively. Both conditions lead to a decreased supply of blood to the GI tract, which is associated in humans with various potentially lethal conditions including chronic mesenteric ischemia, whose mortality rate is over 60%. During our experiments, we recorded simultaneous magnetocardiographic, magnetogastrographic and magnetoenterographic signals and concluded that, when GI circulation is compromised, the information dimensionality of the system fluctuates significantly. In conclusion, dimensionality may be an important diagnostic factor for the characterization of arrhythmias in the context of GI pathophysiology.

Introduction

Chaos theory has been employed to differentiate between healthy and pathological states of the mammalian heart in various contexts, such as cardiac fibrillation, heart rate variability and chronic heart failure (Bonaduce et al 1999, Braun et al 1998, Garfinkel et al 1997, Mäkikallio et al 1999, Sugihara et al 1996). Nonlinear analysis techniques have also been useful for the study of various phenomena of the brain, including epilepsy, cerebral hemisphere synchronization, depression and schizophrenia (Babloyantz and Destexhe 1986, Quian Quiroga et al 2002, Stam 2005). Although recent literature describes the use of chaos analysis for the study of many other biological systems such as muscular structures, biliary ducts and renal calyces (Goldberger et al 2002), very little research has been conducted regarding the content and characteristics of chaos patterns in the gastrointestinal (GI) system (Hanson et al 1990). Two major phenomena of the GI tract—the electrical control and response activities (ECA and ERA, respectively)—are responsible for the measurable electric potentials and magnetic fields recorded via magnetogastrography and magnetoenterography. ECA originates in the gastric antrum due to the presence of the interstitial cells of Cajal, which impose periodic waves of cell membrane depolarization and repolarization that advance along the corpus of the stomach at a rate of 3–6 cycles per minute (cpm) in porcines and 2–4 cpm in man. Each wave consists of a potential upstroke followed by a plateau and then by a sustained depolarization phase. Gastric smooth muscle cells respond to this cycle by regulating L-type Ca2+ currents that are responsible for the contractile behavior of the stomach. Associated with this contractile behavior is gastric ERA, which is characterized by spiking potentials during the plateau phase of ECA (Irimia et al 2006). The electrical activity initiated in the stomach propagates along the entire length of the GI tract, although propagation frequencies depend upon position along the tract.

From the perspective of nonlinear dynamics, GI electrical activity can be modeled using a system of bidirectionally coupled relaxation oscillators where ERA interestingly represents a bifurcation solution to the set of partial differential equations governing the system (Sarna et al 1972). Previously, chaos in the GI system has been explored using the FitzHugh–Nagumo equations (Aliev et al 2000), albeit only within a simulational framework where Lorenz attractor characteristics were not explored. An attractor is the subspace of the total state space of a system to which the trajectory of the system converges after the initial transients have died out (Stam 2005). In this study, it is shown that, in the context of a porcine model, GI arrythmias are associated with statistically significant fluctuations in the information dimension of the associated nonlinear systems.

Experimental protocol

Two noninvasive magnetic recording techniques called magnetogastrography (MGG) and magnetoenterography (MENG) were used. Both have the demonstrated ability to differentiate between the healthy and pathological states of the stomach and bowel (Bradshaw et al 1997). As opposed to electrogastrography (EGG) and electroenterography (EENG), where the quality and strength of the recorded signals depend primarily upon the conductivity of tissues, both MGG and MENG are more strongly dependent on their permeability, which is approximately equal to that of free space (μ0). Because of this, EGG and EENG signals are much attenuated by the layers of fat and skin interposed between the GI tract and the recording electrodes, whereas MGG and MENG recordings have much higher signal-to-noise ratios (Mintchev and Bowes 1998). Because GI biomagnetic signals are of the order of 10–12 T, MGG and MENG recordings must be acquired using a superconducting quantum interference device (SQUID) biomagnetometer. A SQUID has a set of detection coils positioned at the bottom of an insulated dewar filled with liquid He at approximately 4.5 K. The coils are magnetically coupled to the SQUID coils, which convert magnetic flux incident on the detection coils to voltage signals that can be acquired digitally. In our experiments, each subject is positioned horizontally under the SQUID inside a magnetically shielded room; 20 healthy domestic pigs (sus domesticus) of approximately 20 kg each were used. Anesthesia consisted of Telazol, Ketamine and Xylazine, and each animal was also intubated and maintained on isoflurane anesthesia. Simultaneous MCG/MGG/MENG signals were acquired. In 10 of the 20 pigs used, the stomach was surgically divided and post-division data were acquired. In the other ten pigs, intestinal ischemia was surgically induced by ligating the mesenteric artery of each animal and post-ligation data were then recorded. Thus, exactly one abnormal condition of the gut—gastric electrical source uncoupling in the first case and mesenteric ischemia in the second case—was created. After 1 h of post-surgery recording time, euthanasia was induced using an intravenous injection of pentobarbital sodium.

Analysis

A common problem in nonlinear analysis is that there is usually not a one-to-one correspondence between the number of measured signals and the number of underlying sources. More often, the recorded signals are due to an unknown mixing of the true system variables (Stam 2005). In addition to our use of three-dimensional (3D) embedding (where simultaneous time series are converted to a series of vectors in a 3D space), we employed fast independent component analysis (fast ICA) to address this problem. Fast ICA is a data analysis technique that attempts to recover unobserved signals or ‘sources’ from observed mixtures, i.e. from the output of an array of sensors (Cardoso 1998). One of our previous studies (Irimia and Bradshaw 2005) demonstrated for the first time the use of ICA for noninvasive MGG signal processing. The fast ICA algorithm of Hyvarinen and Oja (1997) involves the minimization of the mutual information between the n scalar random variables that define the separated signals of interest. In Irimia and Bradshaw (2005) a detailed description of our approach to fast ICA is provided. According to Takens’ embedding theorem, if the embedding dimension of a group of time series is equal to at least twice the dimension of the systems attractor, then the equivalent attractor of the embedded system has the same dynamical properties as the true attractor (Stam 2005). Similar to Lorenz attractors are return maps, which are 2D phase space plots (Elbert et al 1994). A spatiotemporal return map (STRM) is a visualization technique that allows one to study the time evolution of a system’s return map. It consists of three dimensions (two spatial dimensions and time) and it is created by first finding the outline (perimeter) of a 2D return map for a time segment of data of appropriate length. This process is then repeated for the entire length of the data set, which results in the creation of m return map outlines, where m is the number of time segments into which the data set is divided. If y and z are the two spatial dimensions of the map, time can be plotted on the x dimension of a 3D plot and each 2D outline can be drawn on the yz plane at a constant value of x specified by the time span of the data segment from which the return map was generated. A 3D surface can then be drawn that connects the outlines of adjacent sections; this creates a 3D, spatiotemporal phase space return map, which demonstrates the evolution of the chaos content in the signal throughout time. In our approach, an active shape contour (commonly known as a ‘snake’ in the image processing literature) based on a gradient vector force (GVF) algorithm (Amini et al 1990) was employed to automatically determine the perimeter of each return map. Three common quantitative measures for studying nonlinear dynamics—capacity dimension, information dimension and correlation integral—were selected for our study. The capacity dimension of a system (also referred to as the Kolmogorov entropy or box-counting dimension) is a measure of the ‘spatial extent’ of an attractor. A 3D phase space attractor can be divided using a coarse-grained partition of boxes of edge length ε. If N(ε) is the minimum number of boxes required to cover the spatial extent of the attractor, the capacity dimension of the system can be defined as

$$C=\underset{\epsilon \to 0}{\text{lim}}\frac{\text{ln}N\left(\epsilon \right)}{\text{ln}(1/\epsilon )}$$

In a practical sense, the capacity dimension is a measure of how tightly packed the sheets of the attractor are. The second measure used is that of the information dimension δ. This generalization of the capacity dimension concept weighs each non-empty cube i by its probability p_i:

$$\delta =\underset{\epsilon \to 0}{\text{lim}}\frac{1}{\text{ln}\epsilon }\sum _{i=1}^N{p}_i\text{ln}(1/p_i)$$

This measure can be thought of as the number of information bits required to specify a certain point to a certain degree of accuracy specified by ε. Finally, we computed the correlation integral I(ε), which is defined as

$$I\left(\epsilon \right)=\underset{N\to \mathrm{\infty }}{\text{lim}}\frac{1}{N(N-1)}\sum _{i=1}^N\sum _{j=1}^N\mathrm{\Theta }(\epsilon -|{\mathbf{r}}_i-{\mathbf{r}}_j\left|\right)$$

where Θ(x) is the Heaviside function (−1 if x ≥ 0, 0 otherwise) and|r_i − r_i| is the distance between two points r_i and r_j.

Results and discussion

A sample cardiac STRM is presented in Figure 1. The color-coded arrows marked by ‘A’, ‘B’ and ‘C’ indicate the time points where the heart signals in the corresponding plots (A), (B) and (C) were acquired. At (A), heart activity is normal and the shape of the STRM remains approximately identical in the time interval between (A) and (B). A few minutes after (B), the euthanizing solution is administered and the resulting arrhythmic cardiac signal leads to large changes in the shape of the STRM. At (C), heart activity has ceased almost entirely and most of the recorded signal consists of environmental noise. In conclusion, our figure demonstrates that, for the example shown, the shape of the STRM is altered significantly when cardiac arrhythmia is present. Similar STRMs demonstrating the time evolution of gastric and intestinal signals are shown in Figure 2. An example of applying this technique to SQUID-acquired data from the stomach and intestine is shown in Figure 2, from which one can conclude that large fluctuations in 2D return map perimeter occur throughout time in the injured state. Before attempting to describe the chaotic content of our acquired signals using the quantitative measures already listed, we investigated their convergence behavior as a function of the parameter ε. It was thus found that, from among these three measures, the correlation integral I converged fastest as a function of ε. On the other hand, C and δ were found to best reflect the differences in nonlinear dynamics between the healthy and pathological states that we sought in our study. It was also found that a high degree of correlation existed between the values of C and δ (r = 0.996), whereas hardly any correlation existed between I and C (r = 0.024) or between I and δ (r = 0.021). Because of this behavior, δ is employed to present our results. The time evolution of this parameter in shown in figure 3. Because the purpose of the figure is to demonstrate the common behavior of δ for each animal with respect to time, δ values are shown after normalization, i.e. the normalized quantity $\tilde{\delta }\equiv \delta /〈{\delta }_{<}〉$ is plotted, where 〈δ_<〉 is the average value of δ before the onset of arrhythmia (〈∙〉 stands for the average). The average value of δ across all animals (〈δ〉) is also presented in Figure 3. It is important to mention that, due to logistic difficulties related to the implementation of the experimental protocol, each abnormal condition was induced at different times for every subject, such that the moment when pathology was established is different for each case. To present all subject data on one plot, time axes were therefore aligned so that the moment when pathology was induced was equal to the time point t = 0 min for all data sets. For this reason, each of the plotted functions appears to be of different length since data acquisition periods were different for each subject.

Figure 1.

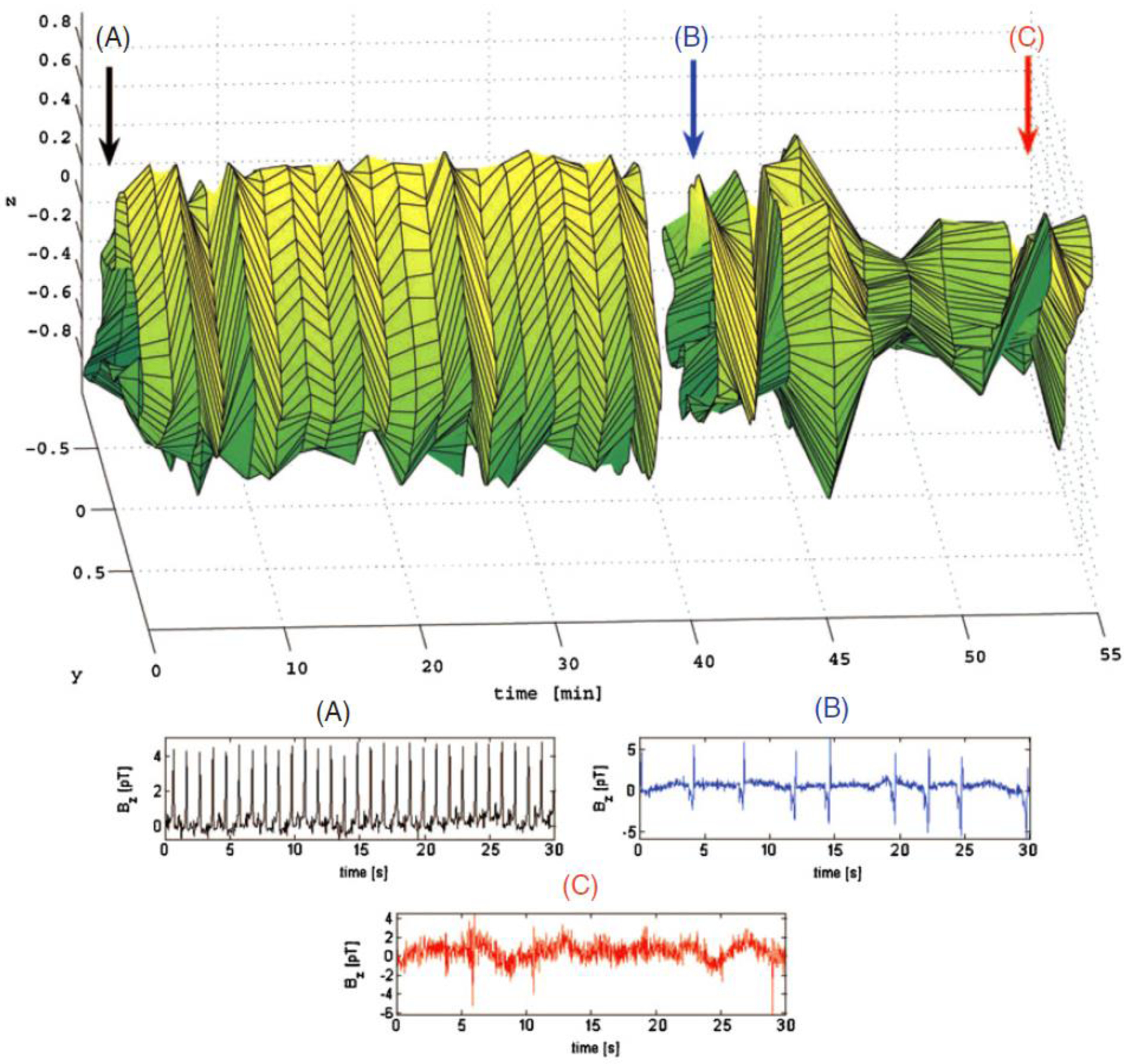
3D (x, y, t) STRM of cardiac activity evolution in an anesthetized domestic pig across a period of one hour of simultaneous MCG/MGG/MENG recordings. The point indicated by arrow (A) corresponds to the data plotted in (A), where cardiac activity is normal. Point (B) corresponds to several minutes after the administration of the euthanasic solution (data plot shown in (B)). At this point, a sharp variation in the chaos content of the system can be seen both from the STRM and from (B) due to cardiac arrhythmia. The amount of chaos varies highly over the ensuing 15 min. At (C), cardiac activity has ceased.

Figure 2.

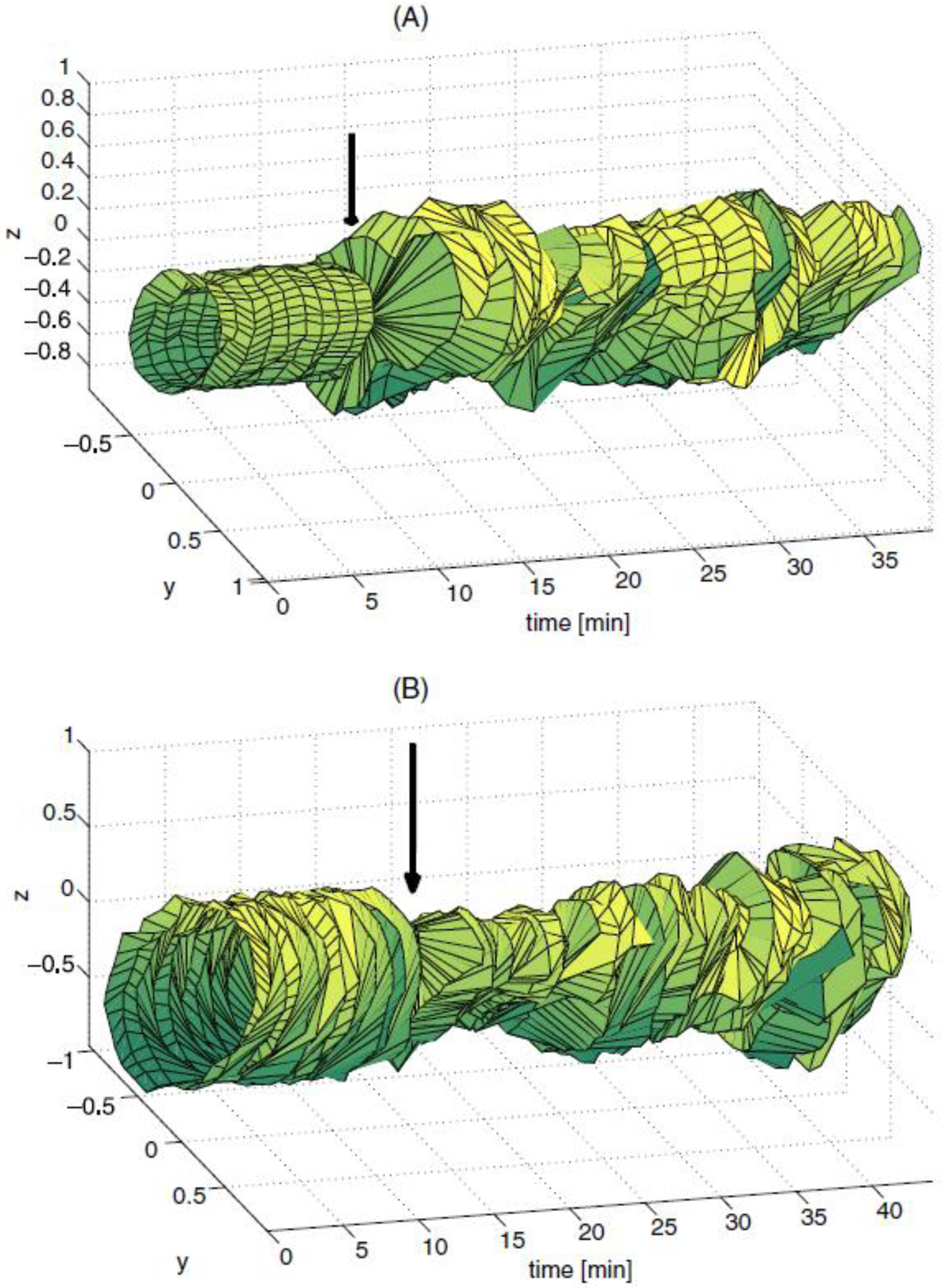
STRMs displaying the time evolution of gastric (A) and intestinal (B) electrical activities in two anesthetized domestic pigs. In the first pig (plot A), MGG normal data were first recorded. The stomach of the animal was then surgically divided and data were acquired again. The normal (baseline) STRM is displayed to the left of the vertical arrow, while the abnormal STRM is shown to the right of the arrow. In the second pig (B), MENG normal data were recorded from the bowel. Thereafter, intestinal ischemia was induced by ligating the mesenteric artery of the animal and data were acquired again. As in (A), the vertical arrow indicates the separation point in time between normal (left) and abnormal (right) STRMs. Whereas the STRM perimeter is relatively time-constant in the healthy state, it exhibits statistically significant variations in the injured state (B, D, p < 0.05).

Figure 3.

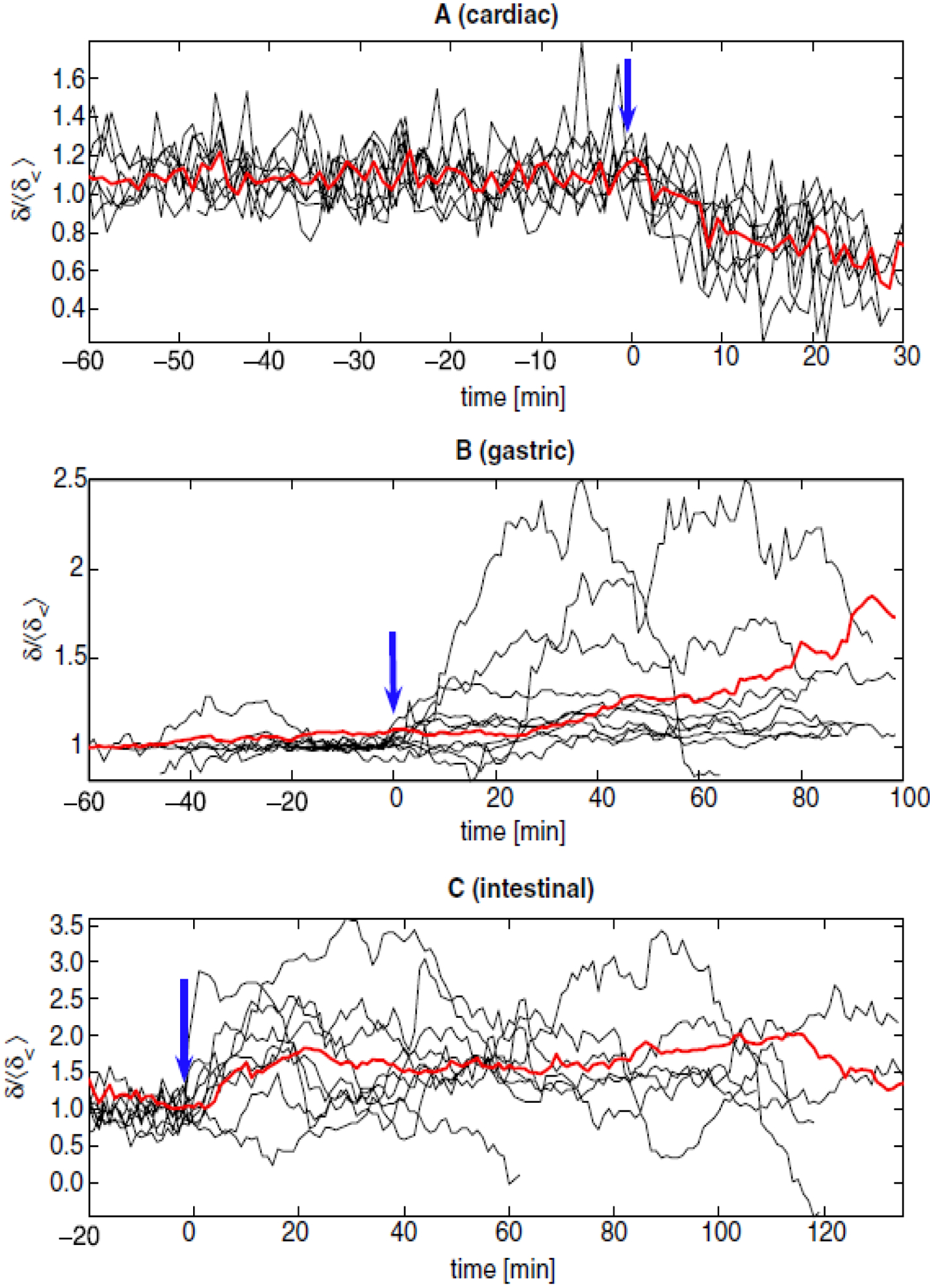
Temporal evolution of the normalized information dimension $\tilde{\delta }$ for all subjects (black) and 〈δ〉 (red). Changes from normal (t < 0 min) to pathological (t > 0 min) values of $\tilde{\delta }$ are indicated by blue arrows. These events are euthanasic injection (A), stomach division (B) and mesenteric artery ligation (C). Because experimental recording periods were not equal for each animal, plots are aligned so that the onset of pathology corresponded to the time t = 0 min. Nevertheless, recordings from the three organs were acquired simultaneously from each animal. Heart rate and $\tilde{\delta }$ values were found to be highly correlated (r = 0.917).

The essential observation to be made from the examination of figure 3 is the following. The information dimension of the cardiac, gastric and intestinal systems assumes a relatively constant value during the healthy state. Immediately after the onset of pathology, the value of δ begins to fluctuate dramatically such that differences between its pre- and post-operative values become significant. In the case of cardiac activity, as euthanasia is induced and heart activity decreases (see (A)), the information dimension decreases to values significantly lower than the ones in the healthy state (p < 0.05 for each subject). In the case of gastric and intestinal activity, information dimension fluctuates significantly in the pathological case. Statistically speaking, the variance of the information dimension in the arrhythmic state was found to differ significantly (p < 0.005 in all cases, as found using ANOVA) from the variance of δ in the healthy state.

Conclusion

We have presented evidence that, within the framework of a porcine model, GI arrhythmias are associated with statistically significant fluctuations in information dimensionality. This phenomenon was described using both visual (STRMs) and numerical (information dimension) measures. In the case of visual measures, distinguishable differences in STRM shape were made obvious between the healthy and pathological states. In the case of numerical measures, statistically significant differences in $\tilde{\delta }$ were shown to exist between the normal and arrhythmic state of each organ. It appears thus that the ECA-ERA complex—which is somewhat analogous to the PQRST complex of cardiac activity—is excellently suited for investigation via nonlinear analysis methods. Moreover, because the induced pathologies are similar to potentially lethal conditions in humans (such as chronic mesenteric ischemia, whose mortality rate is over 60%), chaotic system dimensionality may be an important diagnostic factor for the characterization of arrhythmias in the context of GI pathophysiology.