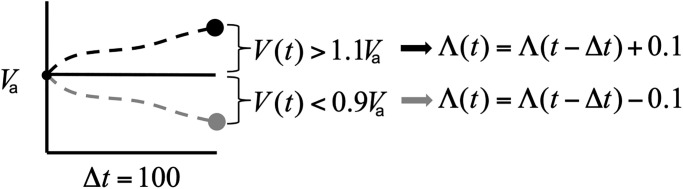Optimal control to reach eco-evolutionary stability in metastatic castrate-resistant prostate cancer

Abstract

In the absence of curative therapies, treatment of metastatic castrate-resistant prostate cancer (mCRPC) using currently available drugs can be improved by integrating evolutionary principles that govern proliferation of resistant subpopulations into current treatment protocols. Here we develop what is coined as an ‘evolutionary stable therapy’, within the context of the mathematical model that has been used to inform the first adaptive therapy clinical trial of mCRPC. The objective of this therapy is to maintain a stable polymorphic tumor heterogeneity of sensitive and resistant cells to therapy in order to prolong treatment efficacy and progression free survival. Optimal control analysis shows that an increasing dose titration protocol, a very common clinical dosing process, can achieve tumor stabilization for a wide range of potential initial tumor compositions and volumes. Furthermore, larger tumor volumes may counter intuitively be more likely to be stabilized if sensitive cells dominate the tumor composition at time of initial treatment, suggesting a delay of initial treatment could prove beneficial. While it remains uncertain if metastatic disease in humans has the properties that allow it to be truly stabilized, the benefits of a dose titration protocol warrant additional pre-clinical and clinical investigations.

1 Introduction

While overall survival of early stage prostate cancer is increasing due to early detection and improving therapy for local and regionally confined disease, the overall survival for metastatic prostate cancer patients remains bleak [1]. This is largely due to the ability of metastatic cancer populations to evolve resistance to all currently available therapies [2–7]. While the search for truly curative therapies continues, there is some evidence that patient outcomes can be improved using currently available therapies by integrating evolutionary principles that govern proliferation of resistant subpopulations into current treatment protocols [8–10]. Delaying or preventing the evolution of resistance, known as ‘evolutionary’ therapies, could prolong drug sensitivity and potentially allow for large increases in overall survival.

For instance, a type of evolutionary therapy known as adaptive therapy uses drug holidays timed specifically to each patients’ disease dynamics in an attempt to intentionally maintain a sufficient level of drug sensitive cells [8, 11–14]. Upon withdrawing therapy, these sensitive cells can compete with and suppress resistant cancer cells, thus prolonging drug efficacy. Continuous or maximum tolerated dose therapies quickly eliminate the entire sensitive population resulting in treatment failure as resistance cells can now grow unchecked. Adaptive therapy clinical trials are underway in multiple different cancers including trials in metastatic castrate-resistant prostate cancer (NCT02415621, NCT03511196), in melanoma—NCT03543969, and in thyroid—NCT03630120.

The design of these adaptive therapies is rooted heavily in the use of mathematical modeling, more specifically evolutionary game theory (EGT) [15–17], which helps us to model situations where multiple organisms interact and where interactions with individuals of different properties largely determine one’s chances of survival (fitness). Unlike in the classical game theory [18, 19], individuals are not expected to be overtly rational, and their ‘strategies’ are properties that they inherit from their predecessors. The EGT models build and test the fundamental understanding of the dynamical interactions underlying tumor population dynamics [20–25]. The development and study of mathematical models like these has suggested other possible evolutionary therapies beyond adaptive therapies, most notably the notion of long term stabilization [26]. One of the core properties of evolutionary systems that can be studied with EGT is the presence of an evolutionary stable strategy (ESS) [15–17], which corresponds to the stable equilibria of the tumor dynamics [27]. If such stable equilibria in tumors exist, reaching it using available therapies could provide a means for achieving long term stabilization of tumors and subsequent dramatic increase in progression-free survival [28, 29].

Previous theoretical work suggests that stable polymorphic equilibria could exist within tumor subpopulations [30, 31]. Interestingly, early preclinical in-vivo studies of adaptive therapy in OVCAR xenografts treated with carboplatin, and in MDA-MB-231/luc triple-negative and MCF7 estrogen receptor–positive (ER+) breast cancers treated with paclitaxel showed the ability to stabilize tumor volume, though the underlying subpopulations were not explicitly measured [32, 33]. In both of these studies, once initial tumor volume control using the maximum tolerable dose was achieved, it could be maintained with progressively smaller drug doses, suggestive of a stable equilibria. Furthermore, polymorphic stability in heterogeneous tumor cell populations has been shown to exist explicitly in breast cancer and neuroendocrine pancreatic cancer in-vitro [34, 35].

If these stable equilibria exist, the clinically relevant question is how can we use currently available drugs to arrive at these equilibria? The ‘evolutionary stable therapies’ attempt to maintain a stable polymorphic tumor composition of cells sensitive and resistant to therapy, in order to prolong treatment efficacy and progression free survival [36, 37]. Previous mathematical studies have developed examples of evolutionary stable therapies, by focusing only on stabilization of the frequency dynamics, while generally ignoring the density dynamics [38, 39]. Stabilization of only the underlying frequency dynamics is inadequate in the case of long term stabilization of a growing tumor where tumor cell density is paramount to patient health [40].

Here we develop an evolutionary stable therapy for the Zhang et al. mathematical model that was used to inform the adaptive therapy clinical trial in mCRPC [8]. First, stability analysis of the evolutionary game theoretic model of mCRPC allows for identification of basic properties of the model that are required for a stable equilibria to exist within constraints on density. Next, to identify an evolutionary stable therapy, we frame the problem of arriving at a stable equilibrium as an optimal control problem [41–46]. Interestingly, previous optimal control studies with the objective of lengthening patient overall survival identified stabilization techniques as optimal treatment strategies [47, 48]. The evolutionary stable therapy identified here with the explicit objective of reaching a stable equilibria is then translated into a clinically feasible strategy and performance is compared against simulated standard of care and adaptive therapy treatment protocols for >200, 000 virtual patients. The clinical and psychological implications of this new strategy are discussed.

2 Metastatic castrate-resistant prostate cancer growth model

We build upon the [8, 49], and [50] mathematical models that consider mCRPC as an evolutionary game between three cancer cell types:

• T⁺ cells requiring exogenous androgen;

• T^P cells expressing 17α-hydroxy/17,20-lyase (CYP17α) and producing testosterone; and

• T⁻ cells that are androgen-independent.

With abiraterone therapy, the patients are also on androgen deprivation therapy that suppresses the production of testosterone by the body. This suppression does not directly affect T^P or T⁻ cells, but it does mean that T⁺ can only exist in the presence of T^P cells because the T^P cells secrete testosterone as a public good that can support the T⁺ cells.

2.1 Lotka-Volterra model

The system of equations describes the interactions between T⁺, T^P, and T⁻ cell types, $i\in \mathcal{T}=$ {T⁺, T^P, T⁻}. The instantaneous rate of change in the population size of each cell type $i\in \mathcal{T}$, ${\dot{x}}_i\stackrel{\text{def}}{=}\frac{\mathrm{d}{x}_i}{\mathrm{d}t},$ is given by

$$\begin{array}{c}\hfill {\dot{x}}_i=r_i{x}_i(1-\frac{{\displaystyle \sum _{j\in \mathcal{T}}}{\alpha }_{ij}{x}_j}{K_i})\end{array}$$ (1)

where the parameters r_i, K_i, and α_ij correspond to the growth rates, carrying capacities, and competition coefficients, respectively.

2.2 Growth rates r_i

The growth rates of the three subpopulations in (1) were derived from the measured doubling times of representative cell lines. The LNCaP cell line (ATCC@CRL-1740) is representative of T⁺ cells with a measured doubling time of 60 hours. The H295R cell line (ATCC@CRL-2128) is representative of T^P cells with a doubling time of 48 hours. The PC-3 cell line (ATCC®CRL-1435) is representative of T⁻ cells with a doubling time of 25 hours. From these doubling times the growth rates of the T⁺, T^P, and T⁻ cells would be 0.27726, 0.34657, and 0.66542, (units of per day) respectively. These cell line derived growth rates are unlikely to be biologically feasible within a tumor environment with limited resources. We therefore scale these growth rates to r_T⁺ = 2.7726 ⋅ 10⁻³, r_T^P = 3.4657 ⋅ 10⁻³, and r_T⁻ = 6.6542 ⋅ 10⁻³ as in [8]. Note that the intrinsic growth rates do not influence the equilibrium frequency of the three cell types, only the rate at which the dynamics play out.

2.3 Carrying capacities K_i and the effect of abiraterone

In our model, the abiraterone dose Λ(t) ∈ [0, 1] equals 0 if no drug is given at time t, equals to 1 if the maximum tolerated dose is applied, and scales between (0, 1) at intermediate doses. The carrying capacity of T⁻ cells is independent of the abiraterone dose and we set it to K_T⁻(t) = 10000 for all t. The actual magnitude of K_T⁻ is arbitrary. What matters is how it scales relative to the carrying capacities of the other two cell types. The carrying capacities of T^P and T⁺ cells are affected by abiraterone dose. With no abiraterone given, the carrying capacity for T^P cells is 10000, the same as for T⁻. We assume that abiraterone directly affects the carrying capacity of T^P and reduces it linearly, to a minimum of 100 when abiraterone is administered at maximum tolerated dose, i.e. when Λ(t) = 1. Therefore, as in [50], we assume that K_T^P at time t is a linear function of the dose Λ(t) as follows:

$$\begin{array}{c}\hfill K_{T^P}(\Lambda (t\left)\right)=10000-9900\Lambda \left(t\right)\end{array}$$ (2)

Additionally, abiraterone affects the growth of T⁺ cells as the carrying capacity of the T⁺ cell population derives entirely from utilizing the endogenous testosterone produced by the T^P cells. We assume that the carrying capacity of T⁺ is a linear function of the density of T^P cells as defined by

$$\begin{array}{c}\hfill K_{T^{+}}(\Lambda (t\left)\right)=\mu (\Lambda (t\left)\right)·x_{T^P}\left(t\right)\end{array}$$ (3)

where

$$\begin{array}{c}\hfill \mu (\Lambda (t\left)\right)=1.5-\Lambda \left(t\right).\end{array}$$ (4)

In this way, the per cell contribution of T^P to K_T⁺ referred to here as the symbiosis coefficient μ(Λ(t)), has a maximum of 1.5 when no abiraterone is given and is lowered linearly to a minimum value of 0.5 as abiraterone dose increases to the maximum tolerated dose. When Λ(t) = 0 the carrying capacity of T⁺ cells could be as high as 15000 if the density of T^P cells was equal to K_T^P = 10000. Since the maximum carrying capacity of any one type of cell type is at least 10000, we must define the maximal tolerated tumor burden (viable total tumor population size) to be less than 10000. This ensures that a tumor burden that is untreated with abiraterone where Λ(t) = 0 for all t will result in patient death by any one cell type. We choose a relatively high maximal tolerated tumor burden of 9000 because we assume that clinically, patient death does not occur until the latest moment possible, only after the human body has exhausted all of its resources. This results in the following viability constraint:

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{T}}{x}_i\le 9000\end{array}$$ (5)

where $i\in \mathcal{T}=\{T^{+},T^P,T^{-}\}$.

2.4 Competition coefficients α_ijnd their impact on system stability

The behavior of the model, including stability, depends heavily on the 3 × 3 competition matrix that characterizes the evolutionary game between the three cancer cell types from the set $\mathcal{T}=${T⁺, T^P, T⁻}. Each competition coefficient represents the effect of an individual of type j on the growth rate of type i. The competition matrix used in [8] and analyzed here is

$$\begin{array}{c}\hfill A=\left({\alpha }_{ij}\right)=\left(\begin{array}{ccc}1& 0.7& 0.8\\ 0.4& 1& 0.6\\ 0.5& 0.9& 1\end{array}\right)\end{array}$$ (6)

Stability analysis is performed for different but constant values of Λ(⋅) ∈ [0, 1], as we are interested in situations where tumor burden can be maintained using a fixed amount of medication. A detailed explanation of the original development of this competition matrix and stability analysis is provided in detail in S1 in S1 File. The population densities $x_{T^{+}}^{*}$, $x_{T^P}^{*}$ and $x_{T^{-}}^{*},$ corresponding to stable equilibria for matrix (6) are shown in S2 in S1 File. While stable equilibria for (1) exist for this competition matrix, there are no stable equilibria that correspond to a total tumor volume less than the patient viability constraint (5), or even ${\sum }_{i\in \mathcal{T}}{x}_i\le 10000.$ The stable points are dominated by the resistant T⁻ cells, out-competing the T⁺ and T^P cells. While some stable points exist where T⁺ and T^P cells can contain the T⁻ cells, it requires so many T^P cells that the patient viability constraint must be broken.

From analysis in S3 in S1 File, the coefficients α₃₁ and α₃₂ describing the competition effect of T⁺ and T^P cells on T⁻ cells respectively, are the key parameters affecting containment of the T⁻ cells. Specifically, α₃₁ and/or α₃₂ must be greater than one. While the initial assumptions of the model required the competition coefficients to be within [0, 1], studies co-culturing sensitive and resistant cell lines show that competition coefficients between cancer cells may not be limited to this range. In-vitro and theoretical studies tend to suggest significant competition between cancer cells in non small cell lung cancer and breast cancer cell lines [28, 51, 52]. For example, results from a novel re-imagining of a Gause style experiment using two competing breast cancer cell lines, MCF7 and MB-MDA-231, with analysis using Lotka-Volterra models suggest that the competition coefficients between these cancer cell lines may be as high as 12.6 [34].

While the exact values of these competition coefficients in-vitro or in-vivo is currently unknown, here we consider a formulation of the model where we increase the competition effect of T^P cells on T⁻ cells, choosing a value of α₃₂ = 2. This value is chosen because 1) it is large enough to allow for stable equilibria within the patient viability constraint (5), and 2) is small enough to not eliminate T⁻ in the stable equilibria (which is the case for higher values of α₃₂, such as α₃₂ = 5, see S3 in S1 File). With α₃₂ = 2, the resistant T⁻ cells are still present in the tumor at stable equilibria, which would be expected clinically. The new matrix is shown below:

$$\begin{array}{c}\hfill A=\left({\alpha }_{ij}\right)=\left(\begin{array}{ccc}1& 0.7& 0.8\\ 0.4& 1& 0.6\\ 0.5& \mathbf{2}& 1\end{array}\right)\end{array}$$ (7)

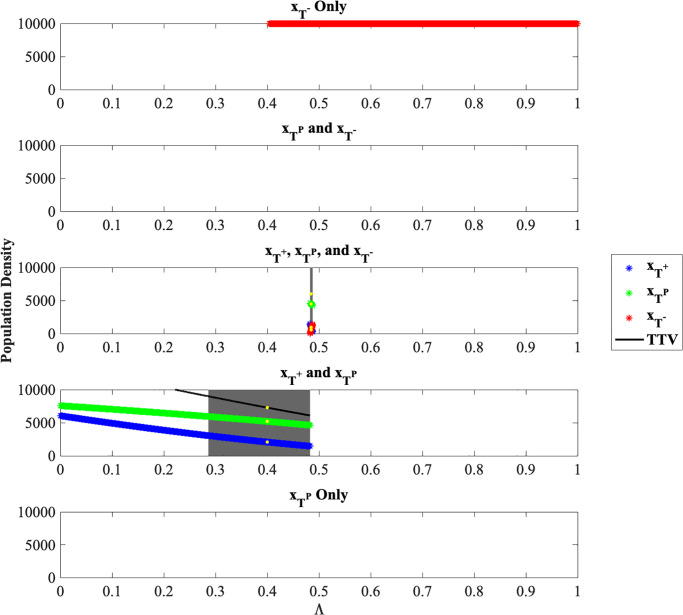
For the matrix A_ij = (a_ij) as defined in (7) the resulting stable equilibria are shown in Fig 1.

Fig 1. Population densities for stable equilibria.

Population densities $x_{T^{+}}^{*}$, $x_{T^P}^{*}$ and $x_{T^{-}}^{*},$ corresponding to stable equilibria for Λ ∈ [0, 1] and for α₃₂ = 2.0. The gray highlighted regions show the stable equilibria that are within the patient viability constraint (5). The yellow highlighted points represent two specific stable equilibria chosen for further analysis.

From Fig 1, for all values of Λ ≥ 0.4041, $(x_{T^{+}}^{*},x_{T^P}^{*},x_{T^{-}}^{*})=(0,0,10000)$ is a stable equilibrium. There are no stable equilibria for a polymorphic T^P and T⁻ tumor nor for the monomorphic T^P tumor. We can see that there is a bifurcation at about Λ = 0.4828: For any smaller Λ, a stable equilibrium contains a mix of T⁺ and T^P cells, while for Λ ∈ [0.4828, 0.4877), a stable equilibrium contains a mix of all three cell types. Regions of Λ where the total tumor burden of the stable equilibrium is within the patient viability constraint (5) are highlighted in gray.

3 Optimal control to arrive at stable equilibria

If the system is at a stable equilibrium with a constant dose of abiraterone, like those shown above, remaining at that dose will keep the system at that equilibrium indefinitely. However, the clinically relevant question is: Can we arrive at this equilibrium from any viable point x(t₀) = (x_T⁺, x_T^P, x_T⁻) corresponding to an incoming patient tumor composition, using only varying doses of abiraterone as the control? We frame the problem of arriving at an equilibrium point as an optimal control problem to identify the dosing schedule ${\Lambda }^{*}(·)\stackrel{\text{def}}{=}{\left[{\Lambda }^{*}\left(t\right)\right]}_{t\in [t_0,t_f]}$ that minimizes the average distance between the state of the system x(t) and the equilibrium point x* over time horizon between the initial time t₀ and the final time t_f:

$$\begin{array}{c}\hfill {\Lambda }^{*}(·)=\text{arg}\underset{\Lambda (·)}{min}{\int }_{t_0}^{t_f}\sqrt{{(x_{T^{+}}\left(t\right)-x_{T^{+}}^{*})}^2+{(x_{T^P}\left(t\right)-x_{T^P}^{*})}^2+{(x_{T^{-}}\left(t\right)-x_{T^{-}}^{*})}^2}\mathrm{d}t\end{array}$$ (8)

with respect to the system dynamics (1), growth rates r_T⁺ = 2.7726 ⋅ 10⁻³, r_T^P = 3.4657 ⋅ 10⁻³, r_T⁻ = 6.6542 ⋅ 10⁻³, carrying capacities for T^P and T⁺ given by Eqs (2) and (3), respectively, K_T⁻ = 10000, and with A = (α_ij) defined by (7).

The time horizon is set to 10000 as this is well beyond the lifespan of the typical patient presented with metastatic castrate-resistant prostate cancer (> 20 simulated years under the assigned growth rates). In this way, if the tumor volume remains below the patient viability constraint (5) over this time interval, the patient will most likely die from some other cause.

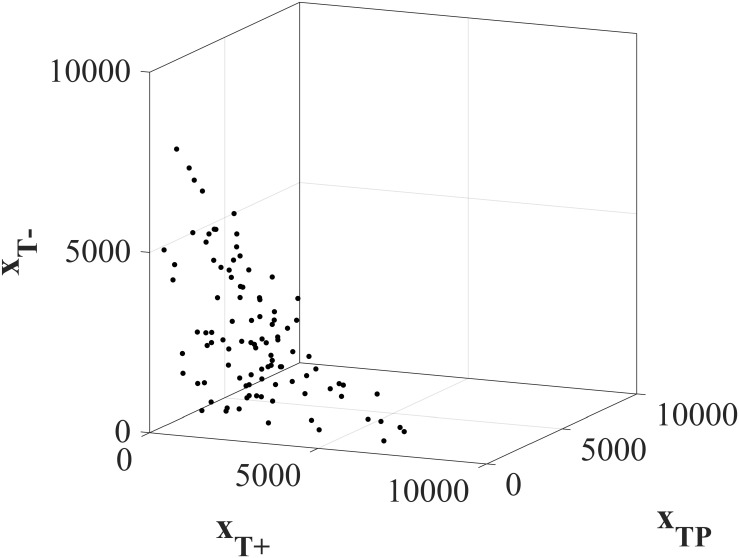
We vary the initial tumor compositions x(t₀) = (x_T⁺(t₀), x_T^P(t₀), x_T⁻(t₀)) to explore a wide range of possible initial conditions. 100 randomly selected tumors that satisfy the viability constraint (5) are explored in Fig 2.

Fig 2. Initial tumor compositions for Forwards Backwards Sweep analysis.

100 randomly selected initial tumor compositions used in the Forwards Backwards Sweep optimal control analysis. All initial total tumor volumes satisfy the patient viability constraint $\sum _{i\in \mathcal{T}}{x}_i\left(t_0\right)\le 9000$.

We know from Section 2.4 that two regions of stable equilibria in terms of Λ exist. For Λ ∈ [0, 0.4828), the two species T⁺ and T^P equilibrium is the stable equilibrium. We select (2082.76, 5206.90, 0.00), corresponding to Λ = 0.4, as x* in (8). For Λ ∈ [0.4828, 0.4877), the three-species equilibrium is a stable equilibrium. We select (863.45, 4436.73, 694.82), corresponding to Λ = 0.4848, as another possible x* in (8). These two points are shown with yellow highlights in Fig 1. While we chose these two equilibria to study specifically for (8), any equilibrium corresponding to Λ ∈ (0.2866, 0.4877) could be used as these equilibria fall within the patient viability constraint. Alternatively, we could adopt a reach-avoid formulation instead of selecting a specific x* in (8).

3.1 Forward Backwards Sweep method

Here we use the Forward Backward Sweep (FBS) numerical technique to find the dosing schedule Λ*(⋅) satisfying (8). The FBS method characterizes the optimal control problem using the Hamiltonian formulation. The Hamiltonian for this problem is given below as follows:

$$\begin{array}{cc}\hfill H\left(t\right)& =\sqrt{{(x_{T^{+}}\left(t\right)-x_{T^{+}}^{*})}^2+{(x_{T^P}\left(t\right)-x_{T^P}^{*})}^2+{(x_{T^{-}}\left(t\right)-x_{T^{-}}^{*})}^2}\\ & +{\mathit{\lambda }}_{T^{+}}\left(t\right)x_{T^{+}}\left(t\right)r_{T^{+}}(1-\frac{x_{T^{+}}\left(t\right)+{\alpha }_{12}{x}_{T^P}\left(t\right)+{\alpha }_{13}{x}_{T^{-}}\left(t\right)}{x_{T^P}\left(t\right)\left(K_{T^{+}}(\Lambda \left(t\right))\right)})\\ & +{\mathit{\lambda }}_{T^P}\left(t\right)x_{T^P}\left(t\right)r_{T^P}(1-\frac{{\alpha }_{21}{x}_{T^{+}}\left(t\right)+x_{T^P}\left(t\right)+{\alpha }_{23}{x}_{T^{-}}\left(t\right)}{K_{T^{+}}(\Lambda \left(t\right))})\\ & +{\mathit{\lambda }}_{T^{-}}\left(t\right)x_{T^{-}}\left(t\right)r_{T^{-}}(1-\frac{{\alpha }_{31}{x}_{T^{+}}\left(t\right)+{\alpha }_{32}{x}_{T^P}\left(t\right)+x_{T^{-}}\left(t\right)}{K_{T^{-}}})\end{array}$$ (9)

where λ_i’s are referred to as the costates or adjoint variables, given by ${\mathit{\lambda }}_i=-\frac{\partial H}{\partial x_i}$. The state equations given in (1) are subject to the initial conditions (x_T⁺(t₀), x_T^P(t₀), x_T⁻(t₀)) shown in Fig 2 and are solved forwards in time. The costate equation must satisfy a transversality condition λ_i(t_f) = 0 and are solved backwards in time, from the final time towards the beginning. A full explanation of FBS is given in [53] and in detail particularly for this system in S4 in S1 File. The solution provided by FBS approximates the treatment strategy Λ*(⋅) that minimizes the Hamiltonian (1), subject to initial conditions for state variables and final conditions for costates, which is equivalent to minimizing (8), subject to the system dynamics (1).

4 Optimizing abiraterone treatment to reach stable equilibrium

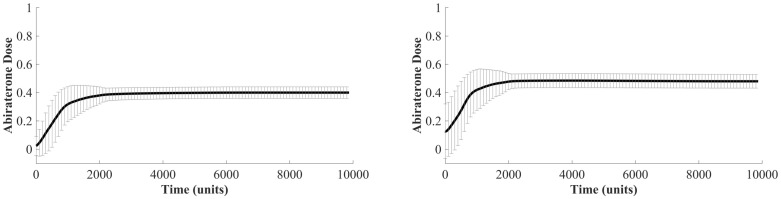
Adopting the Forward Backward Sweep method introduced in the previous section, we identified the optimized abiraterone treatment strategy for each of the 100 initial conditions (x_T⁺(t₀), x_T^P(t₀), x_T⁻(t₀)) shown in Fig 2. While the individual optimized treatment strategies of each of the 100 virtual patients are shown in the S5 in S1 File, Fig 3 shows the mean optimal treatment strategy where the objective is to reach the two-species equilibrium point (2082.76, 5206.90, 0.00), corresponding to Λ = 0.4 (left), and the three-species equilibrium (863.45, 4436.73, 694.82), corresponding to Λ = 0.4848 (right). To reach the two-species equilibrium point, the individual treatment strategies tend towards a Λ(t₀) = 0 while in some cases to reach the three-species equilibrium point a Λ(t₀)>0 is required. Interestingly, the average optimized treatment dose to arrive at either equilibrium point is a simple dose titration scheme that begins with a small abiraterone dose and increases slowly until the known equilibrium dose Λ = 0.4 and Λ = 0.4848, respectively, is reached.

Fig 3. Forwards Backwards Sweep optimized dosing schedules.

Forward Backwards Sweep results for optimal dosing schedule to arrive at two-species stability point (left panel) and three species stability point (right panel). The mean of all 100 paths is shown with symmetric one standard deviation error bars (dosage values <0 are not possible). Standard error of the mean is on the order of 10⁻³.

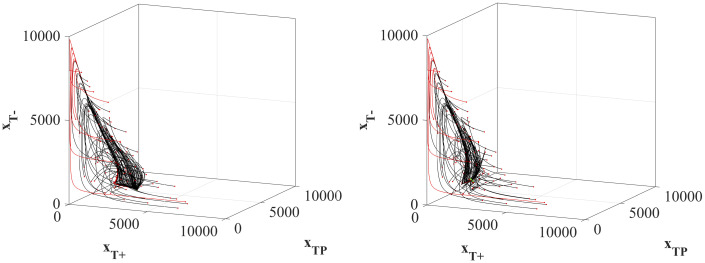
The state trajectory paths x(⋅) for each of the 100 initial tumors to the equilibrium with the optimized treatments are shown in Fig 4. It is important to note that while all 100 initial tumors can reach the stable equilibrium, a subset of the trajectories (13 initial tumors) result in patient death by violating the patient viability constraint (5). These trajectories are highlighted in red in both panels. The common characteristic of these initial tumors that cannot be stabilized without first causing patient death is that the initial value of x_T^P is ≤ 4.10% of the total tumor composition (S6 in S1 File). Because both equilibria require a significant amount of T^P cells, if there are very few of them to begin with, the only way to shift the composition of the tumor towards the equilibrium points is to allow for a very high tumor volume that, in this model, results in patient death. Increasing or decreasing the patient viability constraint will either rescue some of these lost patients or cause more of the patients to cross the constraint, respectively.

Fig 4. System state trajectories under optimal dose schedules.

State trajectories from each of the 100 initial tumor compositions to the two species equilibrium point (left panel) and the three-species equilibrium point (right panel). Paths highlighted in red breach the patient viability constraint before reaching the equilibrium point.

5 Clinical translation of dose titration

Can a dose titration of abiraterone be successfully implemented under clinical constraints to achieve the tumor stabilization or mCRPC? Dose titration is a very common clinical process of incrementally increasing the dose of a medication in order to find the most beneficial dosage and is commonly used to find the appropriate dose to manage other long-term illnesses such as diabetes and depressive disorders [54]. Generally, little information is available to the physician and dose changes are made based on benefits and side effects of the patient in real time. Similarly, in the case of titrating abiraterone, the physician will not know either the location or existence of an equilibrium nor the initial tumor composition. To address this lack of information, we analyze a variety of generalized dose titration schedules that do not require precise initial or final conditions, but instead rely on monitoring the total tumor volume (i.e. PSA measurement) in real time.

In all modeled titration protocols the total tumor volume $V\left(t\right)={\sum }_{i\in \mathcal{T}}{x}_i\left(t\right)$ is measured every 100 simulated time points (just over 3 months in real time). Since the equilibrium tumor volume V* corresponding to the equilibrium point x* that we want to reach will be unknown in the clinic, here we test two volumes V_a and V_b that can be measured clinically: 1. the incoming baseline tumor volume $V_a={\sum }_{i\in \mathcal{T}}{x}_i\left(t_0\right)$, and 2. a maximum tolerable tumor volume defined as a volume just smaller than the volume that causes a loss in quality of life (i.e. bone pain due to extensive metastases). In reality, this volume will vary greatly with age, demographics, general overall health, psychological comfort, and other patient-specific factors. Here, we choose a relatively large maximum tolerable tumor volume V_b = 7000 for all patients.

Here we allow ourselves to change the abiraterone dose in the increments of 0.1 (i.e. Λ(t) ∈ {0.1, …, 1}), where the dose change may occur at the time of volume measurement. If the current V(t) increases above 110% of the tumor volume we are attempting to maintain (V_a or V_b), the dose is increased by 0.1. If V(t) decreases below 90% of the tumor volume we are attempting to maintain, the dose is decreased by 0.1. If the tumor burden V(t) is within 0.9 and 1.1 of the target volume, the dose remains unchanged (Fig 5).

Fig 5. Dose adjustment schematic.

Schematic description of the dose adjustment rules based on the measured total tumor volume shown here, attempting to maintain a total tumor burden at V_a, though the same rules apply to V_b.

While the optimal control results suggest an initial dose Λ(t₀) = 0, here we run additional simulations to compare this optimized result to the protocols suggested in [32] and [33] in in-vivo stabilization studies where the initial dose is Λ(t₀) = 1 and the dose is titrated down. We compare all of the combinations of V_a, V_b, Λ(t₀) = 0 and Λ(t₀) = 1 to the clinical standard of care (maximum tolerated dose) where Λ(t) = 1 for all t ∈ [t₀, t_f] and the adaptive therapy protocol used in [8]. In this way, we model six clinically feasible protocols:

1. Maximum tolerated dose

2. Adaptive therapy cutting the initial volume by 50%.

3. Stabilization at initial tumor volume V_a, with Λ(t₀) = 1.

4. Stabilization at initial tumor volume V_a with Λ(t₀) = 0.

5. Stabilization at maximum tolerated tumor volume V_b with Λ(t₀) = 1.

6. Stabilization at maximum tolerated tumor volume V_b with Λ(t₀) = 0.

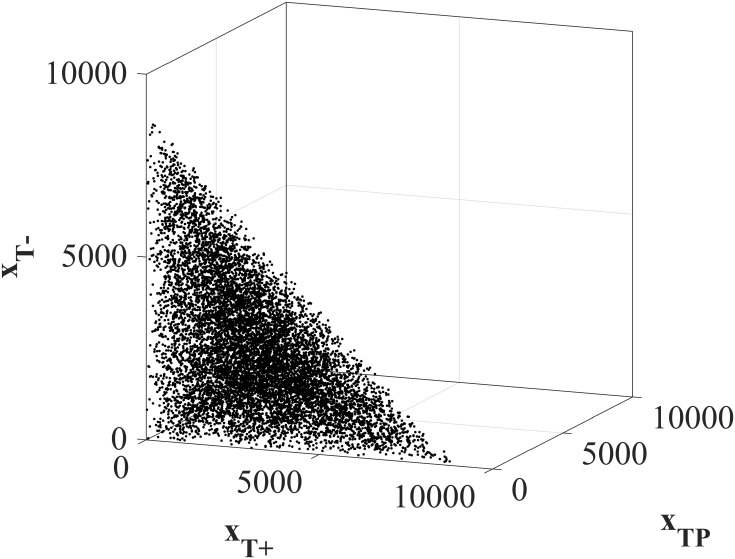
Since clinically the initial tumor composition will be unknown, we test 10, 000 initial tumor compositions (x_T⁺(t₀), x_T^P(t₀), x_T⁻(t₀)), as shown in Fig 6.

Fig 6. Initial tumor compositions for clinical feasible protocols.

10, 000 randomly selected initial tumor compositions used to analyze the clinically feasible protocols. All total tumor volumes satisfy the patient viability constraint ${\displaystyle \sum _{i\in \mathcal{T}}}{x}_i\left(t_0\right)\le 9000$.

6 Outcomes of clinically feasible protocols

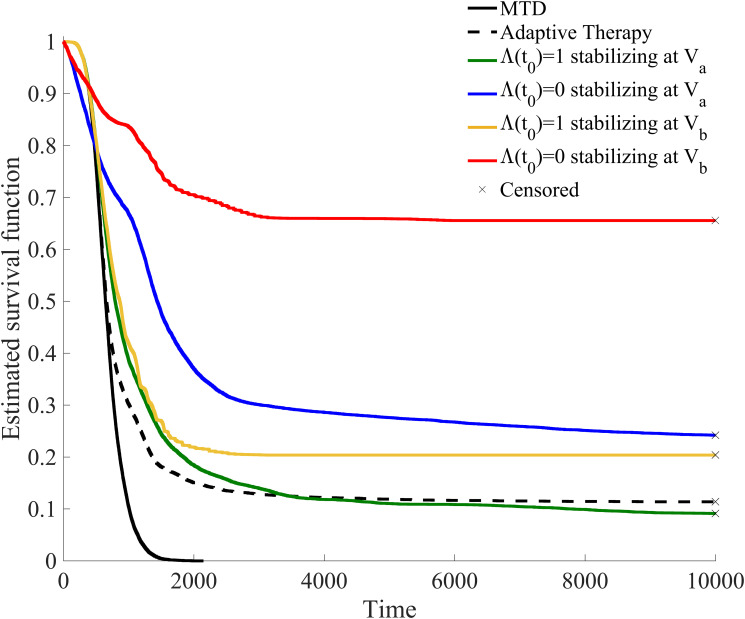
In Fig 7, a Kaplan-Meier survival analysis is provided for the total of 60, 000 simulated patients under the six treatment strategies.

Fig 7. Kaplan-Meier survival analysis for clinically feasible treatment strategies.

10, 000 patients were given each of the six clinically feasible treatment strategies. In this way this shows the outcome of 60, 000 simulated patients. Patients that had not yet breached the patient viability constraint by the end of the simulation are labeled as censored.

The percentage of these simulated patients that breached the patient viability constraint (5) and the mean and standard deviation of the time of this breach are summarized in Table 1. Each protocol is discussed in detail below, though three main takeaways are apparent:

Table 1. Survival statistics for clinically feasible treatment strategies.

Treatment	% Patients death	Mean (SD) time of death
MTD	100%	667.38(246.66)
Adaptive Therapy	88.61%	815.97(687.65)
Va, Λ(t0) = 1	90.78%	1112.62(1209.67)
Va, Λ(t0) = 0	75.80%	1412.53(1519.43)
Vb, Λ(t0) = 1	89.61%	817.07(429.51)
Vb, Λ(t0) = 0	34.45%	1108.09(918.98)

Percentage of simulated patients that breached the patient viability constraint before the end of simulation (t_f = 10000) and the average time of this breach.

1. MTD results in 100% of the patients violating the viability constraint at an average of 667.38 simulated time units or roughly corresponding to just over 21 months. This falls within the overall survival reported from patients with and without previous treatment with docetaxel (14.8 months and 53.3 months, respectively) [55, 56],

2. adaptive therapy can provide permanent control for only a small subset (11.39%) of initial tumor compositions, and

3. the most successful therapy in terms of patients surviving until the end of the simulation is titrating up from an initial dose of Λ(t₀) = 0 and allowing for a large tumor volume. This results in 65.55% of the 10, 000 initial tumor compositions simulated to not breach the patient viability constraint.

6.1 Maximum tolerated dose dynamics

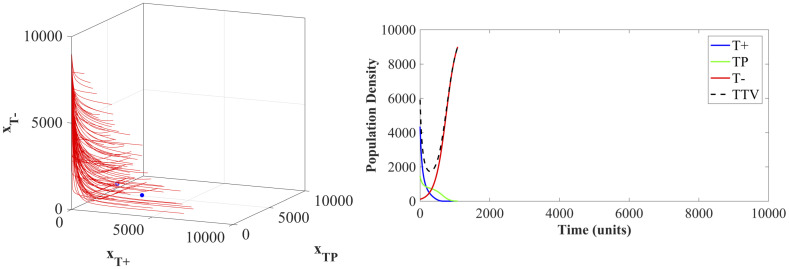
Using maximum tolerated dose (Λ(t) = 1 for all t ∈ [t₀, t_f]) eliminates the T⁺ and T^P cells and the tumor composition quickly becomes dominated by T⁻, as shown in Fig 8. All of the patients breach the viability constraint within a relatively short simulated time, with an average time of 667.38 time units.

Fig 8. Maximum tolerable dose state dynamics.

State trajectories for 100 initial tumor compositions (left panel), used for optimization of patients under the maximum tolerated dose protocol. All state trajectories end when the total tumor burden violates the patient viability constraint (5). The two blue dots show the location of the two equilibria (two- and three- species). The right panel shows the population densities of the three cell types in a representative case.

6.2 Adaptive therapy dynamics

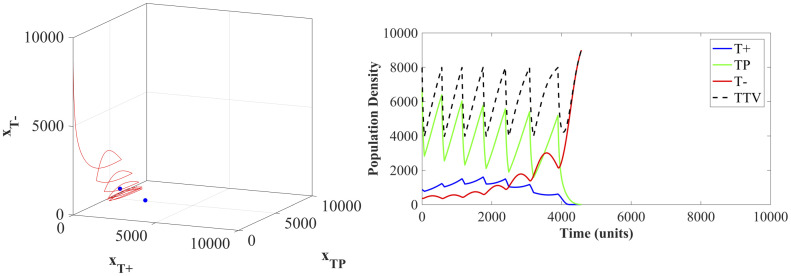
Adaptive therapy protocols result in an average time to breaching the viability constraint of 815.97 simulated time points. This increase in survival beyond the MTD standard of care is due to adaptive therapy delaying the competitive release of the T⁻ population. Unfortunately, the treatment windows where Λ(t) = 1 ratchet the population towards a tumor composed of all T⁻ cells and cause the state trajectories to miss the stable equilibria. An example of the ultimate failure of the adaptive therapy is shown in Fig 9.

Fig 9. Adaptive therapy state dynamics.

The state trajectory (left panel) and population densities (right panel) of an example patient under the adaptive therapy protocol. The two blue dots show the location of the two stable equilibria (two- and three- species).

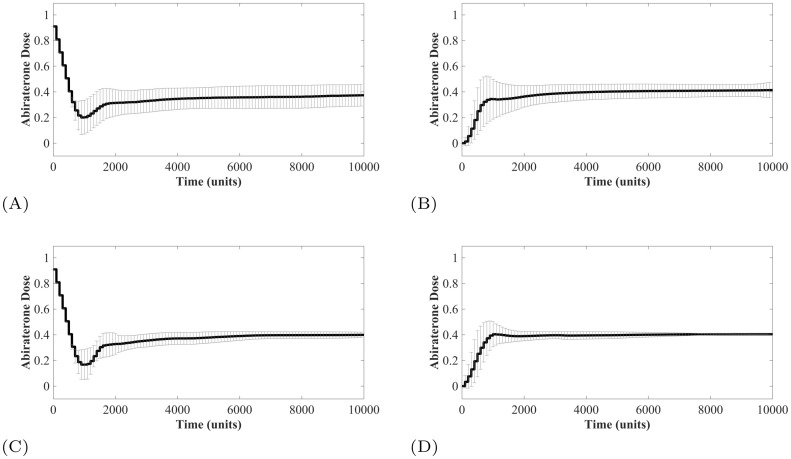
6.3 Dose titration dynamics

For the titration protocols, the mean successful treatment strategy of the surviving patients is shown in Fig 10. Of note, for the treatments with an initial dose Λ(t₀) = 0 (panel B and D), the titration protocol developed in real time directly mimics the protocol identified by the optimal protocol found by the optimal control analysis shown in (Fig 3). These results show that a simple set of titration rules with no prior knowledge of the initial tumor composition nor the existence or location of an equilibrium can be used to stabilize a population at an equilibrium point. Interestingly, all of these surviving simulated patients under the titration protocols end the simulation at the two-species equilibrium point where Λ = 0.4 with T⁺ = 2068.97 and T^P = 5172.41. Since intermediate values of Λ are not available in the chosen dosage scheme, the entire region Λ ∈ [0.4828, 0.4877) where a three-species equilibrium is located, is unreachable. While the population dynamics may pass by a three-species equilibrium point, stabilizing there is unlikely, due to the discrete values of Λ available. More gradual changes in dose will however allow to reach the three-species equilibrium.

Fig 10. Titration protocols resulting in patient survival.

Average titration protocols of patients that did not breach the patient viability constraint within the simulation time. The standard error of the mean (SEM) is on the order of 10⁻³ for all cases, therefore here the error bars show one standard deviation. (A) Λ(t₀) = 1 stabilizing at V_a. (B) Λ(t₀) = 0 stabilizing at V_a. (C) Λ(t₀) = 1 stabilizing at V_b. (D) Λ(t₀) = 0 stabilizing at V_b.

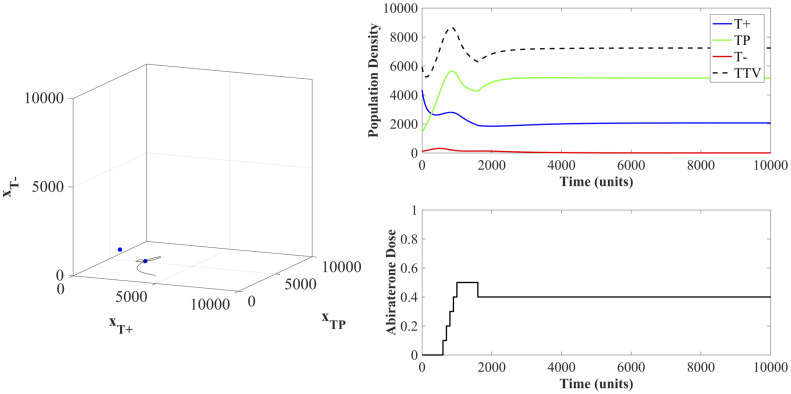
A specific example of dose titration with an initial dose of Λ(t₀) = 0 and attempting to stabilize at the previously defined maximum tolerated tumor volume of V_b = 7000 is shown in Fig 11. Interestingly, no drug was given for over 500 simulated time units. This is the time required for the tumor volume to exceed 7700 (110% of V_b = 7000) at which point the dose keeps increasing until the stabilizing dose of Λ = 0.4 in reached. The population dynamics show that while T⁻ cells are present in the initial tumor, allowing the T⁺ and T^P cells to remain and even increase in density prevents the competitive release of these T⁻ cells. In this example, the population of T⁺ and T^P cells can then be maintained at their equilibrium using a constant dose Λ = 0.4. An example of all six clinically feasible therapies on one simulated patient is available in S7 in S1 File.

Fig 11. State dynamics of patient undergoing titration protocol.

The dynamics here show an example patient under the initial dose of Λ(t₀) = 0 and attempting to stabilize at a tumor volume equal to V_b = 7000. The state trajectory in the left panel shows the population arriving at the two-species equilibrium. The population densities and abiraterone dose are shown in the right panel.

7 Effect of initial tumor composition on treatment outcome

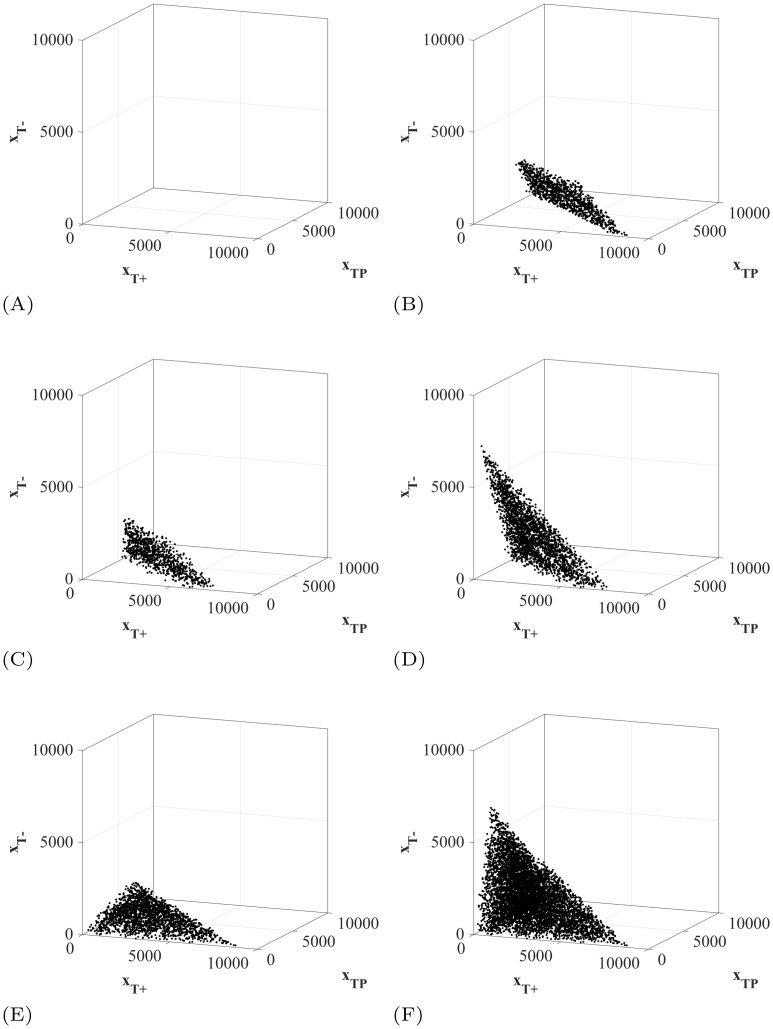
The initial tumor composition has a large effect on the outcomes of the treatment protocols. In Fig 12, we show the initial tumor compositions that survive until the end of the simulation time for each of the protocols studied. Firstly, no patients survive to the end of simulation under MTD (Fig 12A). More interestingly, the patients that survive using adaptive therapy all begin within a small region of initial tumor compositions (Fig 12B). Using adaptive therapy, the 11.39% of patients who survive have very large initial tumor volumes (>7774) and relatively small T⁻ populations (<33.6% of the initial tumor volume). This combination is required as even short doses at Λ = 1 allow the T⁻ opportunity to grow, as seen in Fig 9.

Fig 12. Initial tumor compositions of surviving patients.

The initial tumor compositions of the patients that did not breach the patient viability constraint within the simulation time for each of the six clinically feasible protocols. Their two dimensional projections are available in S9 in S1 File. (A) Maximum tolerable dose. (B) Adaptive therapy. (C) Λ(t₀) = 1 stabilizing at V_a. (D) Λ(t₀) = 0 stabilizing at V_a. (E) Λ(t₀) = 1 stabilizing at V_b. (F) Λ(t₀) = 0 stabilizing at V_b.

The patients that survive using the titration protocol attempting stabilization at initial tumor volume V_a with Λ(t₀) = 1 also have large initial tumor volumes (>5400) and small populations of T⁻ (Fig 12C). On the other hand, the titration protocol attempting stabilization at initial tumor volume where Λ(t₀) = 0 (Fig 12D) still requires a high tumor volume to survive, but can tolerate much higher initial densities of T⁻ cells. For both cases, the minimum tumor volume that could be stabilized was 5195. Again, an initial dose of Λ(t₀) = 0 allows patients with higher initial frequencies of T⁻ cells to survive as any doses at Λ = 1 allow the T⁻ opportunity to grow, as seen in Fig 9.

Furthermore, attempting stabilization at a maximum tolerated tumor volume allows patients with small initial tumor volumes to survive (Fig 12E and 12F). It is important to note that allowing these patients’ tumors to grow will not decrease their quality of life. So while it is psychologically difficult to intentionally let a small initial tumor burden grow, it could potentially provide clinical benefits. With an initial dose of Λ(t₀) = 1, the initial T⁻ population must still be small in order to avoid competitive release of the T⁻ population at early treatment stage, regardless of the tumor volume. By setting Λ(t₀) = 0, even patients with small initial tumor volumes and high initial frequencies of T⁻ cells can survive to the end of the simulation.

7.1 Tumor composition at time of death for clinically feasible protocols

It is important also to understand the composition of the tumor that caused the patient to cross the viability constraint to understand why the treatment failed. In Fig 13, the tumor composition at the time of crossing the patient viability constraint is presented for each treatment. For the treatment protocols giving high doses—MTD, adaptive therapy, and Λ(t₀) = 1 stabilizing at V_b—the vast majority of the patients died of tumors comprised completely of T⁻ cells. This makes sense as the high doses of abiraterone given throughout or early in treatment will eliminate the T⁺ and T^P cells, causing the competitive release of T⁻ and eventual treatment failure.

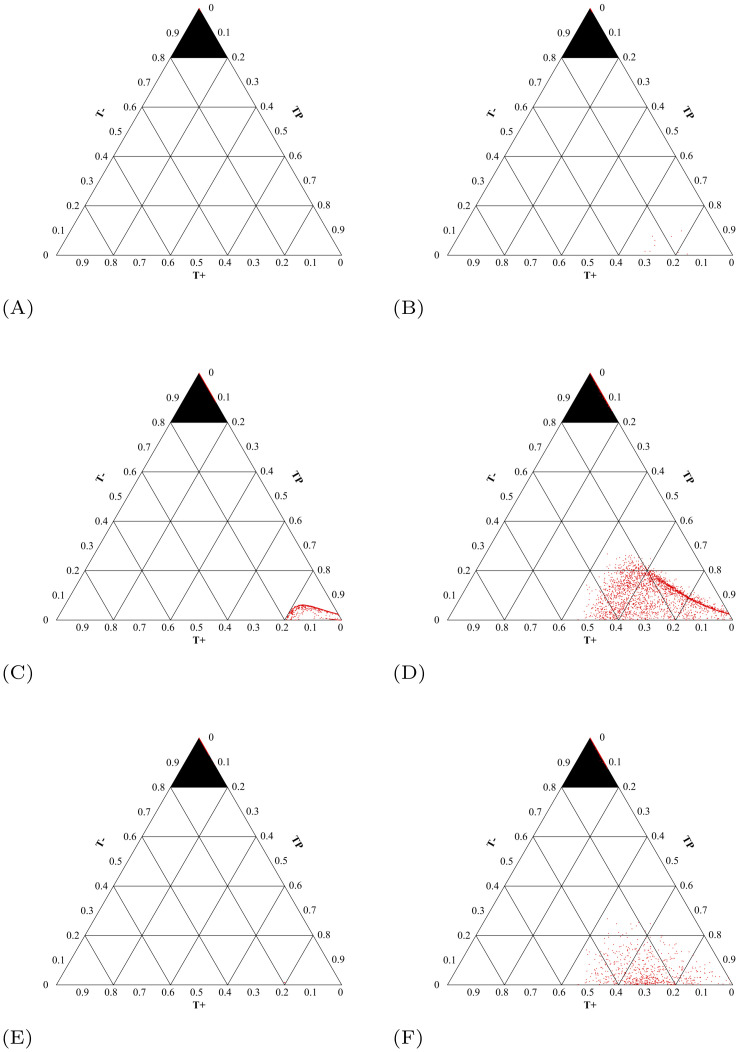
Fig 13. Tumor composition at time of viability constraint breach.

Ternary plots where each red dot indicates the tumor composition of T⁺, T^P, and T⁻ cells at the time a patient reached the viability constraint. (Figures made using [57].) The top highlighted triangle in each figure encompasses the tumor compositions with >80% T⁻ cells. Patients with tumor compositions located in this upper triangle suffered from competitive release of the T⁻ cells. Outside of this upper triangle, treatable cells were still present at the time of viability constraint breach. (A) 100% of patients are located in the top triangle: n = 10000. (B) Adaptive Therapy. 99.90% of patients are located in the top triangle: n = 8861. (C) Λ(t₀) = 1 stabilizing at V_a. 87.13% of patients are located in the top triangle: n = 9088. (D) Λ(t₀) = 0 stabilizing at V_a. 60.30% of patients are located in the top triangle: n = 7580. (E) Λ(t₀) = 1 stabilizing at V_b. 99.97% of patients are located in the top triangle: n = 7961. (F) Λ(t₀) = 0 stabilizing at V_b. 81.86% of patients are located in the top triangle: n = 3445.

For the patients undergoing the treatment protocol where Λ(t₀) = 1 stabilizing at V_a, the 12.87% that had a tumor comprised mostly of T⁺ and T^P at the time of treatment failure had large initial tumor volumes, and therefore large values of V_a that were >8000. In this way, while the initial dose of abiraterone was Λ = 1, the protocol titrates down very quickly in order to maintain the desired tumor volume. Unfortunately, this generally results in an under treatment of the tumor and the patient crossing the viability constraint with T⁺ and T^P cells remaining.

Additionally, the tumor compositions at the time of treatment failure of the patients receiving initial low doses of abiraterone—Λ(t₀) = 0 stabilizing at V_a and Λ(t₀) = 0 stabilizing at V_b—show that 39.7% and 18.14% of the patients who crossed the viability constraint, respectively, had high percentages of T⁺ and T^P cells remaining. Since these cells are treatable by abiraterone, these patients were indeed under treated by the treatment protocol.

These results show that there is an important balance between giving too much abiraterone causing competitive release of resistant cells, and not giving enough abiraterone causing treatment failure even with treatable cells remaining in the tumor.

8 Discussion

Here we developed and analyzed an ‘evolutionary stable therapy’ in mCRPC that can maintain a stable polymorphic tumor heterogeneity of sensitive and resistant cells to abiraterone, in order to prolong treatment efficacy and progression free survival. Surprisingly, in the majority of simulated patients, the optimal control analysis suggests a simple increasing dose titration protocol to achieve stabilization. While a single formulation of the competition matrix is presented here, three additional clinically relevant matrices were investigated resulting in the analysis of a total of seven possible stable points. The optimal control analysis consistently suggests a simple increasing dose titration protocol to achieve stabilization (see S5 in S1 File). Furthermore, the outcomes of the simulated clinically feasible protocols show that increasing dose titration protocols invariably increased progression free survival in the majority of patients (see S8 in S1 File). This suggests that if the properties of the underlying biology allow stabilization, regardless of the actual composition of the stable polymorphic tumor heterogeneity, an increasing dose titration protocol may, in general, provide an appropriate dosing strategy to achieve stabilization.

Dose titration is a very common protocol used with drugs like insulin, anti-depressants, and opioids, to find the optimal dose of a medication while minimizing the adverse side effects, physical or financial [58–60]. Most notably in oncology, a ‘ramp-up’ protocol for Venetoclax is used in patients with chronic lymphocytic leukemia in order to limit tumor lysis syndrome (physical toxicity) [61]. In patients with hepatocellular carcinoma a dose titration of sorafenib is used to significantly lower overall cost (financial toxicity) while maintaining equivalent survival [62]. Interestingly, some initial studies of dose titration protocols show benefit beyond toxicity management. For example, titration of axitinib resulted in a greater proportion of patients with metastatic renal cell carcinoma achieving an objective response and, incredibly, titration of regorafenib in patients with metastatic colorectal cancer actually increased median overall survival from 5.9 months (initiating treatment at standard dose) to 9.0 months [63, 64].

Interestingly, in the case of abiraterone titration, our analysis also showed that larger tumor volumes may counter intuitively be more likely to be stabilized if sensitive cells dominate the tumor composition at time of initial treatment, suggesting a delay of initial treatment could prove beneficial. This reiterates previous analysis of this model comparing intermittent abiraterone to optimized treatments concluding that delaying treatment for as long as possible, while increasing tumor volume, maintained a larger sensitive population and resulted in prolonged tumor control [50]. This result is also seen in other disciplines such as agricultural pest management, equine parasite management, and bacterial infection management where large sensitive populations can contain resistant populations [12, 65, 66].

If stabilization of the tumor is possible, the use of titration to reach an equilibrium of metastatic disease could have many benefits such as prolonging progression free survival and administering lower doses of drug leading to less cumulative drug over the length of the treatment. While the goal of treating any cancer is to allow the patient to live a normal life span, a titration protocol will also generally increase patient quality of life by limiting the toxicity related side effects of cancer drugs. Furthermore, delaying the absolute growth of disease within a patient could allow other physiological processes, such as vascular normalization and the immune system, that have little effect on large rapidly growing tumors to play a greater role in patient outcomes [33]. It is also possible that curative strategies using application of additional drugs or immune therapies could be more effective in a stabilized tumor environment [67–74].

With any novel treatment protocol, there are potential drawbacks. Analysis here showed that it is possible to either undertreat or overtreat patients using a titration protocol. If a patient is already experiencing quality of life issues because of high tumor burden, beginning at low doses in a titration protocol is not wise. For these patients, much like in the two mouse models where the initial exponential growth required immediate intervention, it may be necessary to use a more aggressive approach, like the decreasing dose titration protocol used in the in-vitro mouse models or adaptive therapy. Overtreatment, on the other hand, could be mitigated by more frequent PSA measurements in order to react more quickly to changes in tumor response and limit the competitive release of resistant cells during therapy [75]. In reality, it is likely that PSA alone will be insufficient to guide detailed evolutionary protocols such as the one discussed here [76]. Additional information particularly related to the underlying tumor composition such as DHT-PET imaging or AR-V7 expression from circulating tumor cells could greatly improve evolutionary management in mCRPC [77–80]. An ideal implementation would be to consider using drug pumps like those used in insulin management for continuous measurement and administration of cancer therapeutics [81].

The outcomes of this study are heavily dependent on the underlying mathematical model used and its parameterization [82]. As with any evolutionary game, the competition coefficients are of particular interest [83]. Once the clinical trial that was designed using the model studied here is completed, parameter optimization of the competition matrix using patient data from both the standard of care maximum tolerable dose cohort as well as the adaptive therapy cohort can be performed. While studies are now attempting to measure these intratumoral competitive properties in-vitro [34], more detailed experimental work will be required before understanding and attempting stabilization in-vivo [28].

Furthermore, this particular model studied here does not encompass the full complexity of metastatic disease within a patient. For example, phenotypic switching, which can be implicitly accounted for in population models like the one used here, is not modeled explicitly and could alter the dynamics of treatment outcomes [84–87]. Furthermore, this model assumes no new mutations resulting in novel phenotypes occur during treatment, which is likely not true. If a new resistant phenotype emerges, this will ultimately change the dynamics of the game and the stability properties [88]. It will require further in-vivo analysis to show that either new mutations cannot invade the tumor population or that these mutations occur late enough that the patient succumbs to another cause of death before treatment failure. As in other ecological systems, it is still unknown whether stability of both the ecological and evolutionary dynamics is feasible and robust, and will remain unknown in metastatic disease until further experiments along this line are performed [89, 90].

The effects of the spatial structure within a heterogeneous tumor population is not explicitly studied in this model, though have been shown to affect stabilization properties [91–94]. Interestingly, [49] added a spatial structure to the model used here and showed that the interaction neighborhood size and the effects of carrying capacity affect the stability properties. In this way, it would be of great interest to identify ‘evolutionary stable therapies’ in other models of prostate cancer that model treatments as death rates or reductions in growth rates, address the importance of cell turnover, and include spatial structure [95–103].

The clinical development of an evolutionary stable therapy described here could provide immediate and substantial benefits to both patient quantity and quality of life. A better understanding of the properties of disease that make evolutionary therapies superior to current standard of care and the psychological shift required are of great interest [67, 104]. While it remains uncertain if metastatic disease in humans has the properties that allow it to be truly stabilized, the benefits of a dose titration protocol warrant additional pre-clinical and clinical investigations.

Supporting information

S1 File

(ZIP)

Data Availability

All data and code files are available from GitHub (https://github.com/cunninghamjj/Optimal-Control-to-Reach-Eco-Evolutionary-Stability-in-mCRPC).

Funding Statement

This research was supported by the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 690817, the Dutch National Foundation (NWO) Visitor’s Travel Grant number 040.11.712, the James S. McDonnell Foundation grant, Cancer therapy: Perturbing a complex adaptive system, a V Foundation grant, NIH/National Cancer Institute (NCI) R01CA170595, Application of Evolutionary Principles to Maintain Cancer Control (PQ21), and NIH/NCI U54CA143970-05 [Physical Science Oncology Network (PSON)] Cancer as a complex adaptive system. This research benefited from the support of the FMJH ‘`Program Gaspard Monge for optimization and operation research and their interactions with data science" and from the support from EDF, Thales, Orange and Criteo.