Gaussian mixture model-based unsupervised nucleotide modification number detection using nanopore-sequencing readouts

Abstract

Motivation

Nucleotide modification status can be decoded from the Oxford Nanopore Technologies nanopore-sequencing ionic current signals. Although various algorithms have been developed for nanopore-sequencing-based modification analysis, more detailed characterizations, such as modification numbers, corresponding signal levels and proportions are still lacking.

Results

We present a framework for the unsupervised determination of the number of nucleotide modifications from nanopore-sequencing readouts. We demonstrate the approach can effectively recapitulate the number of modifications, the corresponding ionic current signal levels, as well as mixing proportions under both DNA and RNA contexts. We further show, by integrating information from multiple detected modification regions, that the modification status of DNA and RNA molecules can be inferred. This method forms a key step of de novo characterization of nucleotide modifications, shedding light on the interpretation of various biological questions.

Availability and implementation

Modified nanopolish: https://github.com/adbailey4/nanopolish/tree/cigar_output. All other codes used to reproduce the results: https://github.com/hd2326/ModificationNumber.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Modified nucleotides play critical roles in diverse biological processes (Li and Mason, 2014; Lyko, 2018). Oxford Nanopore Technologies (ONT) nanopore sequencing monitors ionic current signal shifts caused by various chemical structures of the nucleotides (Deamer et al., 2016), which opens up the possibility of routinely identifying DNA/RNA modifications (Korlach and Turner, 2012). Up to now, modification calling software has been shown to identify 6 mA (Liu et al., 2019; Ni et al., 2019; Rand et al., 2017), 5mC (Liu et al., 2019; Ni et al., 2019; Rand et al., 2017; Simpson et al., 2017), 5hmC (Rand et al., 2017) as well as the thymidine analogs EdU, FdU, BrdU, IdU (Mueller et al., 2019) in DNA and 6 mA (Workman et al., 2019), inosine (I) (Workman et al., 2019), 7-methylguanine (7mG) (Smith et al., 2019), pseudouridine (Q) (Smith et al., 2019) in RNA. All of these softwares require some models of the expected signals for given modifications. For instance, nanopolish (Loman et al., 2015; Simpson et al., 2017), signalAlign (Rand et al., 2017) and DNAscent (Mueller et al., 2019) perform modification calling based on a priori kmer models, which keep track of ionic current signals associated with all native and modified kmers. DeepMod (Liu et al., 2019) and DeepSignal (Ni et al., 2019) are deep learning-based modification detection algorithms, which identify modifications based on neural networks trained on control datasets. However, these algorithms can only analyze modifications appeared in labeled training data, thereby considered as supervised methodologies. Meanwhile, for unidentified modifications, potential sites can be inferred using unsupervised approaches, e.g. tombo (Stoiber et al., 2016) and nanocompore (Leger et al., 2019). However, these unsupervised modification analysis techniques do not include more detailed characterizations, such as modification numbers, corresponding signal levels and proportions. Understanding the number of modifications under specific sequence contexts can provide critical biological insights. For instance, during DNA demethylation, 5mC is sequentially converted into 5hmC, 5-flucytosine (5fC), 5-carboxylcytosine (5caC) and finally C. Therefore, the number and corresponding proportion of modifications would be indicator for DNA demethylation dynamics (Bhutani et al., 2011). Meanwhile, from a technological perspective, understanding the number of modifications is a crucial part of de novo modification characterization, which is considered as one of the most important topics in the nanopore-sequencing community.

2 Materials and methods

2.1 Data collection and preprocessing

Nanopore-sequencing datasets included here were composed of fast5 files, which contain raw ionic current readouts from the sequencer, together with fastq files, which contain sequences basecalled from corresponding fast5 records. The fast5 and fastq files are considered to be the ‘raw data’ to be collected and preprocessed. Specifically, in cases where fastq files were embedded in fast5 records, nanopolish extract (0.11.1) (Loman et al., 2015), followed by porechop demultiplexing (0.2.4), (Wick et al., 2017) was used to recover the fastq files. We used a Zymo native-synthesized oligo nanopore-sequencing dataset, which was provided by authors of the original study (Rand et al., 2017). We also used a thymidine analogs-containing primer extension and native yeast genomic DNA nanopore-sequencing datasets, which are available at GEO with accession number GSE121941 (Mueller et al., 2019). Specifically, for the thymidine analogs-containing primer extension dataset, EdU, FdU, BrdU and IdU were incorporated in the synthesized ‘head’ oligo (GAATTGGGCCCGCTCAGCAGACACAGAGCCTGAGCATCGCCGCGGAC, underscore denotes positions where thymidine analogs were incorporated). For a specific read, incorporated thymidine analog bases of the two positions are the same. And the portions of EdU, FdU, BrdU, IdU and T were the same. Then primer extension was performed, adding different extended ‘tail’ sequences to different modifications, such that these reads with different modifications can be separated by alignment. Our RNA control dataset is a NA12878 cell line mRNA dataset (UCSC Run1 of Oxford Nanopore Human Reference Datasets) is available at: https://github.com/nanopore-wgs-consortium/NA12878/tree/master/nanopore-human-transcriptome (Workman et al., 2019). The RNA modification dataset is an E.coli 16S rRNA knockdown experiment provided by authors of the original study (Smith et al., 2019). Three subdatasets were sequenced in this study, containing reads from native, pseudouridine-deficient (Psi516) and m7G-deficient (m7G) strains. For m7G strain, m7G at position 527 is substituted with G, while for Psi516 strain, Q at position 516 is substituted with U (Smith et al., 2019). For the m7G and Psi516 strains, mutations only affect m7G at position 527 and Q at position 516, respectively, and such mutation will cause 100% of the reads to be aberrantly modified.

2.2 Alignment, quality filtering and event table generation

For the Zymo native-synthesized oligo, thymidine analogs-containing primer extension, native yeast genomic DNA and NA12878 cell line mRNA nanopore-sequencing datasets, in total 38 685, 3 173 426, 121 266 and 1 291 028 reads were obtained. Such reads in fastq files were first indexed using nanopolish index (0.11.1) (Loman et al., 2015), to establish one-to-one correspondence between sequences and ionic current records. The indexed fastq files were then aligned using minimap2 (2.16-r922) (Li, 2018), followed by samtools view, sort and index (1.9) (Li et al., 2009), yielding sorted and indexed bam files. Specifically, without loss of generality, for yeast genomic DNA and NA12878 cell line mRNA datasets, only reads mapped to the first chromosome were used for downstream analysis. During the alignment, for ZYMO, primer extension, yeast genomic DNA and NA12878 cell line mRNA datasets, 35 280, 17 216, 117 970 and 1 269 076 reads were aligned, respectively. After alignment, reads with MAPQ score equal to 60 and without secondary and supplementary alignments were kept for downstream analysis. Specifically, for the thymidine analogs-containing primer extension dataset, only reads mapped to the forward strand, where thymidine analogs reside, were kept. After such data filtering, for ZYMO, primer extension, yeast genomic DNA and NA12878 cell line mRNA datasets, 30 241, 8450, 496 and 8640 reads were kept for downstream event level analysis, respectively. The event tables were generated using nanopolish eventalign, by taking fast5 files, bam files and indexed fastq files as described above. Event tables contain kmer sequences and statistics of corresponding ionic current signals, e.g. mean and standard deviation (SD) values. Here, we modified nanopolish eventalign so that it can also output per read event tables containing the position of each kmer from the fastq sequence. We used these event tables to retrieve corresponding CIGAR strings and Q-scores. Quality control results were shown in Supplementary Figures S1, S2, S6 and S9–S12. Specifically, filtered event tables for the 16S rRNA dataset were provided by authors of the original study, therefore the aforementioned procedures were not applied.

2.3 Optimal kmer length determination

We first explored the kmer length that affects the signal (effective length). So, in Figure 1,we analyzed both the native yeast genomic DNA and the NA12878 cell line mRNA datasets. Kmers with various lengths (4–8 for DNA, 3–7 for RNA) were generated based on the event tables (see previous section) and reference sequences. The event tables contain mapping positions of kmers, based on which sequences covering +2 to -2 positions (prolonged kmers) were retrieved from the references. These prolonged kmers were then trimmed centering around the original kmer. For instance, for native yeast genomic DNA read 001082a7-d27b-418c-85f6-a0297adb346b, the first signal event corresponded to ACGATT and mapped to position 11 571, based on which the prolonged kmer was determined as ATACGATTGC. This prolonged kmer was further trimmed into, e.g. {ATACGATT, TACGATTG, ACGATTGC} for length = 8, annotated by the corresponding trimming strategy as {8_2_0, 8_1_1, 8_0_2}. Since {ATACGATT, TACGATTG, ACGATTGC} were trimmed from the same signal event, they were corresponded to the same signal event level, in this case 71.89 pA. Following the same principle, we constructed other kmer trimming strategies including {4_2_0, 4_1_1, 4_0_2, 5_1_0, 5_0_1, 7_1_0, 7_0_1}. Such kmers, together with the above mentioned {8_2_0, 8_1_1, 8_0_2} and original kmer {6_0_0}, were all corresponded signal event level 71.89 pA. Then, for each trimming strategy, across all kmers included, we calculated the distribution of single event median absolute deviation (MAD). As described in the main text, such MAD distributions were used for determining optimal k for both DNA and RNA contexts.

Fig. 1.

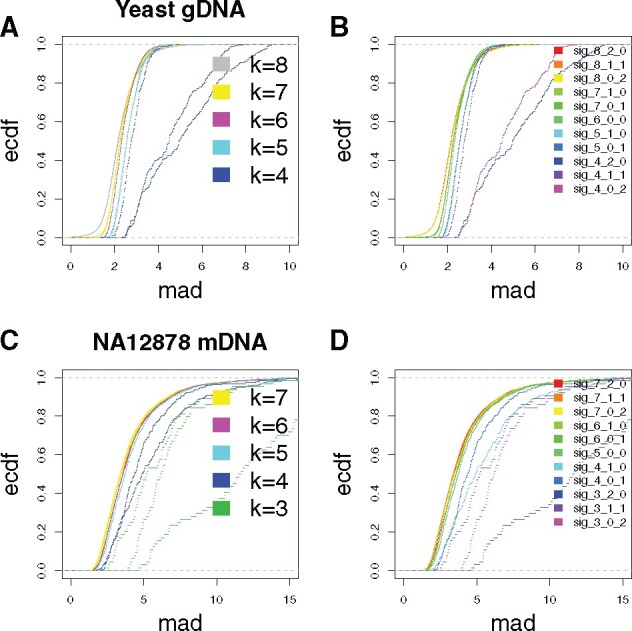
Optimal kmer length determination. For kmers with various lengths (4–8 for DNA, 3–7 for RNA, see Section 2 for kmer-constructing strategies), corresponding event signal MAD ecdf curve were shown. (A, B) Yeast genomic DNA and (C, D) NA12787 cell line mRNA datasets were analyzed as examples for DNA and RNA scenarios. The MAD distributions as opposed to kmer lengths and constructing strategies were shown in (A, C) and (B, D)

2.4 Assessing the contributions of kmer positions to the ionic current shifts

We then determined the effect of kmer positions on the signal, as shown in Supplementary Figures S4 and S5. We analyzed the same datasets from the previous section. Pairwise signal differences within kmer pth position quadruplet {N_p-1AN_k+1-p, N_p-1TN_k+1-p, N_p-1 GN_k+1-p, N_p-1CN_k+1-p} were analyzed to assess the contribution of position p, where k equals 6 (DNA) or 5 (RNA), integer p ranges from 1 to k, Ns range in {A, T, G, C} and are identical for the same position, the subscripts indicates the number of independently varying Ns. For instance, for DNA 6mer first position quadruplet {ATGCAT, TTGCAT, GTGCAT, CTGCAT}, six pairwise absolute value differences of kmer event signal medians (A–T, A–G, A–C, T–G, T–C, G–C) were calculated. Together with distance values generated from all other included DNA 6mer first position quadruplets, the contribution of first position can then be assessed. We then performed this analysis across all positions (1–6 for DNA, 1–5 for RNA) and used the distributions of absolute distance values as representations of kmer positional contributions. We further assessed the contribution of different nucleotides. For each nucleotide, e.g. A, at a given position p ({N_p-1AN_k+1-p}), we calculated the average pairwise distance of event signal medians from the corresponding three other nucleotides ({N_p-1TN_k+1-p, N_p-1GN_k+1-p, N_p-1 CN_k+1-p}). The distributions of positional average signal shift for each nucleotide were presented as quantification of nucleotide-specific contributions.

2.5 Skewness and kurtosis determination

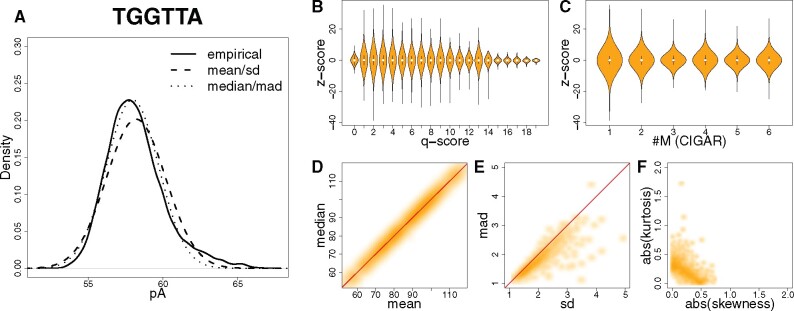
Skewness and kurtosis values were calculated using skewness() and kurtosis() functions in the CRAN R package {e1071}. As shown in Figure 2A–C, empirical signal distribution of kmers usually have long tails caused by outlier events, which will bias the determination of skewness and kurtosis. Therefore, for this specific analysis, we filtered out the following kmer event signal data points:

Fig. 2.

Nanopore-sequencing kmer signal events follow a normal distribution. (A) Signal event distribution for an example 6-mer TGGTTA from the Zymo dataset (Rand et al., 2017). Solid curve, empirical distribution; dashed curve, normal distribution fitted using mean and SD of signal event; dotted curve, normal distribution fitted using median and MAD of signal event. (B) Violin plot showing z-score distribution under different q-score categories. Z-scores were computed using median and MAD of signal events. (C) Violin plot showing z-score distribution under different CIGAR-string categories. Z-scores were computed using median and mad of signal events. #M denotes the number of matches in CIGAR strings. (D, E) Smoothscatter plots showing signal event mean–-median and SD–MAD relationship of kmers. Red dashed line, slope equals 1. (F) Smoothscatter plot showing signal event empirical distribution skewness–kurtosis relationship of kmers

1. s_i < median_s - 3 * MAD_s, or

2. s_i > median_s + 3 * MAD_s.

Subscript i denotes one specific signal event, and s denotes all corresponding events of a specific kmer.

2.6 Gaussian mixture model order determination

The order (number of components) of Gaussian mixture models were determined by the statistical test reported in Chen and Li (2009) and Chen et al. (2012), with the implementation of the emtest.norm() function in the CRAN R package {MixtureInf}. The statistical test was performed with the null hypothesis as order equals m0, against an alternative hypothesis where order equals 2m0. We search across various null hypotheses (m0 equals 1–9 and 1–4 for primer extension and rRNA datasets, respectively) for empirical kmer signal distributions, denoting the number of underlying Gaussian components of a certain empirical kmer signal distribution. To ensure correct inference, we used a more stringent filter to remove the following data points: as outliers, before performing the fitting, considering they might account for the ‘long tails’ of the empirical kmer signal distribution, further introducing additional Gaussian components as artifacts for determining number of modifications. Subscript i denotes one specific signal event, and s denotes all corresponding events of a specific kmer.

1. s_i < median_s - 2 * MAD_s, or

2. s_i > median_s + 2 * MAD_s.

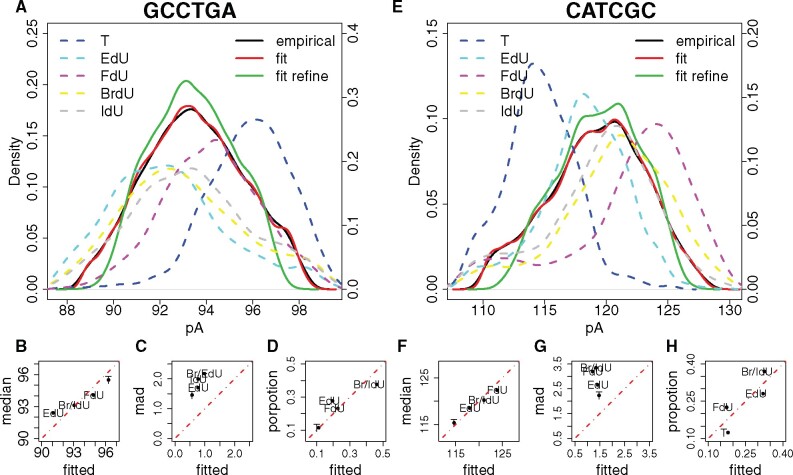
Elbow points on order-P-value curves were used to determine the number of components. P-values quantify significant levels of fitting performance gained by modeling with 2m0 as opposed to m0 components. Elbow points on the order-P-value curves denote marginal fitting performance gaining by including more components, therefore considered as optimal number of components. Following such principle, for both modified sites in the primer extension dataset, seven was considered as the optimal number of components. By filtering out components whose proportions were less than 10%, for both sites 4 components remained, corresponding to T-, FdU-, EdU- and BrdU-IdU-containing kmers. Removed Gaussian components usually account for noises. For instance, the first, second and seventh components of GCCTGA fitting were removed, and comparison between red (with all 7 components) and green (with remaining 4 components) curves in Figure 3A showed such filtering majorly affected the ‘tails’ of the signal distribution. Actually signal levels of the removed Gaussian components were 88.897, 89.692 and 97.499, which were in the range of the ‘tails’. For CATCGC (Fig. 3E), the signal levels of the three removed Gaussian components were 110.597, 111.911 and 126.550, which were also in the range of the ‘tails’. Specifically, BrdU- and IdU-containing kmers were considered as the same component due to close signal levels, which was further quantified by U-test (Supplementary Fig. S13A–F). For both modified sites in the rRNA dataset, two was considered as the optimal number of components, corresponding to the canonical and modified kmers (Supplementary Fig. S13G and H).

Fig. 3.

Unsupervised modification number detection. (A, E) Signal event distribution for the two modified kmers (GCCTGA and CATCGC) from the primer extension dataset (Mueller et al., 2019). Solid black curve, empirical distribution of all kmer signal events mapped to the specific position; solid red curve, fitted distribution with all Gaussian components of the mixture model; solid green curve, fitted distribution with Gaussian components that passed the mixing proportion threshold; dashed curves, empirical distribution of T (blue), EdU (cyan), FdU (purple), BrdU (yellow) and IdU (grey) kmer signal events. (B, C, D and F, G, H) Relationship between empirical and fitted kmer signal event medians values, kmer signal event MADs and mixing proportions, respectively. Red dashed line, slope equals 1

Reads were annotated based on their modification status in the original studies for both primer extension and rRNA datasets. Therefore, for every analyzed modification site, we took the original annotation of reads covering this specific site, and calculated the mixing proportions of modified kmers. We further calculated the median values (Equations 3 and 4) of these modified kmers. Such proportion and median values were further used as gold standard in evaluating the performance of Gaussian mixture model.

2.7 Clustering nanopore-sequencing reads

Only nanopore-sequencing reads covering all targeted positions (position 25–36 in the reference oligo sequence for primer extension dataset; position 511–515 and 522–526 in the reference transcript sequence for 16S rRNA dataset) were used for the analysis. Nanopore-sequencing positional kmer signal events were then represented in read-position matrices, where reads in rows, targeted positions in columns and corresponding signals as elements. Clustering analysis was performed based on such read-position matrices.

3 Results

3.1 Determining effective length for kmers

Shifts in ionic current (signal events) can be associated with nucleotide sequences (kmers) during their translocation through nanopores (Deamer et al., 2016). For multiple methods, characterizing such kmer–current relationships is essential to interpreting nanopore-sequencing readouts. We first demonstrate that for our purpose, an effective k for kmers (effective length for associating with the ionic current) equals six and five for DNA and RNA, respectively, consistent with the information provided by ONT. To determine an effective k for our datasets, we associated signal events to kmers of various lengths (4–8 for DNA and 3–7 for RNA). We chose a k that minimizes the variation in current observations between different instances of the kmer while maximizing the numbers of distinct observations of each kmer. Specifically, for every kmer, we used the event signal fluctuation (quantified by MAD) as the criterion for determining the optimal k (see Section 2). Here, we analyzed a native yeast genomic DNA dataset (Mueller et al., 2019) and one NA12878 cell line mRNA dataset (Workman et al., 2019) (see Section 2), as examples for DNA and RNA scenarios, respectively. Genomic and transcriptomic sequences were used to make sure abundant sequence contexts could be included. As shown in Figure 1, the MAD empirical cumulative distribution function (ecdf) curve started to dramatically shift rightward when k became smaller than six (DNA) or five (RNA). In contrast, marginal differences were observed among MAD distributions when k exceeded six (DNA) or five (RNA). Taken together, these indicate the effective sequence length for shifting ionic current during nanopore sequencing equals six and five for DNA and RNA. We also quantified pairwise Kolmogorov–Smirnov d-values between the ecdf curves of different kmer constructing strategies, as confirmation of the effective kmer lengths (Supplementary Fig. S3). We further assessed the contributions of kmer positions to the ionic current shifts by measuring the difference in signal among constructed sets of four kmers that are only different in one base at the examined position, e.g. {ATGCAT, TTGCAT, GTGCAT, CTGCAT} (see Section 2). Results suggested for DNA 6mers, the third position contributes the most, followed by the fourth position. The second and fifth positions have minor contributions and the first and sixth positions have least contributions. For RNA 5mers, the second position contributes the most, followed by the third and fourth positions, and the first and fifth positions have least contributions (see Supplementary Figs S4 and S5).

3.2 Empirical signal event distribution follows Gaussian

Gaussian has been widely used to model signal distribution. For instance, kmer models provided by ONT, as well as several widely acknowledged modification analysis algorithms (Loman et al., 2015; Mueller et al., 2019; Simpson et al., 2017; Stoiber et al., 2016), assume the kmer signal distribution follows Gaussian. Here, we further demonstrated, using quantitative measurements, that the empirical distribution of nanopore-sequencing kmer signal event means can generally be modeled by a normal distribution N (median, MAD). Specifically, we analyzed a Zymo-synthesized oligo dataset (Rand et al., 2017) (see Section 2), to make sure sequenced nucleotide molecules were well-controlled. Median and MAD are calculated from all signal events of the corresponding kmer (Fig. 2A). Compared to N (median, MAD), N (mean, SD) fittings tend to be ‘widened’ and ‘skewed’ compared to the empirical distributions (Fig. 2A). Such ‘widened’ and ‘skewed’ fittings can be explained by deviated means and increased SDs (Fig. 2D and E), which are caused by ‘long tails’ of kmer signal event empirical distributions. We argue such ‘long tails’ are outlier kmer signal events well modeled by accounting for low sequencing quality and compromised alignment, rather than being due to the nature of an underlying kmer signal event distribution. We used the z-score computed from the kmer signal event median and MAD as a measurement of the likelihood of being an outlier. As shown in Figure 2B, C and Supplementary Figure S7, the likelihood of being an outlier is correlated with sequencing quality (quantified by Q-score) and affected by alignment status (quantified by the number of matches in the CIGAR string), indicating that the ‘long tails’ are caused by outliers. Indeed most of the analyzed kmers can be well modeled by a normal distribution, suggested by absolute kurtosis and skewness (see Section 2): as shown in Figure 2F, for 90.4% of analyzed kmers, such values ranged in the interval [0, 0.5].

3.3 Gaussian mixture model-based modification number inference

Considering that the signal event distribution for a given kmer can be reasonably modeled as normal, we can use a Gaussian mixture model to determine the number of ‘isoforms’ for a specific kmer. If there’s no sequence variation, such as a single nucleotide variation, then we can consider such ‘isoforms’ as different base modifications. The number of modifications correspond to the order (number of components) of the Gaussian mixture model, determined by the statistical test reported in Chen and Li (2009) and Chen et al. (2012) (see Section 2). As a proof of concept, we analyzed a thymidine analog DNA primer extension dataset reported in Simpson et al. (2017). Thymidines in the sequence GAGCCTGAGCATCGCCG were substituted with EdU, FdU, BrdU or IdU, therefore we analyzed kmers GCCTGA and CATCGC (Fig. 3A–D and E–H). For both kmers, four components were detected (Supplementary Fig. S13A and D, see Section 2), corresponding to T-, FdU-, EdU- and BrdU-IdU-containing kmers. BrdU and IdU were considered as one component by the Gaussian mixture model, due to the similar kmer event signal levels (Fig. 3A and H, see Section 2). As negative controls, we analyzed those non-modified sites, and 23 out of 26 sites were modeled by a single Gaussian component (Supplementary Fig. S14). We further quantified the performance of a Gaussian mixture model in recapitulating signal event median and MAD values, as well as mixing proportion, for each kmer. As shown, median values were well recapitulated (Fig. 3B and F); mixing proportions were in general recapitulated (Fig. 3D and H); while inference on MAD values were unsatisfactory (Fig. 3C and G). Such biases were caused by the ‘long tails’ of the kmer signal event empirical distribution (Fig. 3A and H), as previously discussed in Figure 2. Although such unsatisfactory performance on MAD inference can be considered as a limitation of the method, we argue MAD values are not very informative for describing kmer signal events. As shown in Supplementary Figure S8 for kmer signal events >95% of the MAD values fall into the range of [1, 3], with no significant correlation with the corresponding median values. We speculate the variation of kmer signal events is largely caused by the noise associated with the nanopore-sequencing platform itself, rather than an inherent characteristic of individual kmer signal events.

We further applied the Gaussian mixture model approach in analyzing RNA modifications. Specifically, we analyzed the dataset reported in Smith et al. (2019), where E.coli 16S rRNAs from native, pseudouridine-deficient (Psi516) and m7G-deficient (m7G) strains were profiled. Compared to a native strain, in the Psi516 strain pseudouridine in UCCGUGCCA site is substituted with U, while in the m7G strain m7G in AGCCGCCGU site is substituted with G, therefore we analyzed kmers UGCCA and GCCGC. Following the same analytical pipeline as previously discussed for the DNA analysis (Supplementary Fig. S13G and H, see Section 2), we recapitulated the signal event median values, as well as the mixing proportions of the corresponding kmers (Supplementary Fig. S15).

To further explore the detection limit of our approach, we performed downsampling as well as remixing analysis. As a proof of concept, we focused on the RNA 5mer UGCCA and corresponding counterpart QGCCA (Q stands for pseudouridine), where we analyzed in Figure 3I. Specifically, we downsampled to 100, 1000 and 2000 observations, at various QGCCA fractions, including 0.01, 0.05, 0.1, 0.25 and 0.5. We performed such down-sampling as well as remixing 10 times. It is clearly shown in Supplementary Figure S16 that with as few as 100 observations, our approach can accurately recapitulate signal level and proportion of QGCCA component that accounts for 25% of total observations. If we have 2000 observations, such detection limits can further go down to only 1%. Taken together these suggested the high robustness and sensitivity of our approach.

3.4 Associating identified modifications

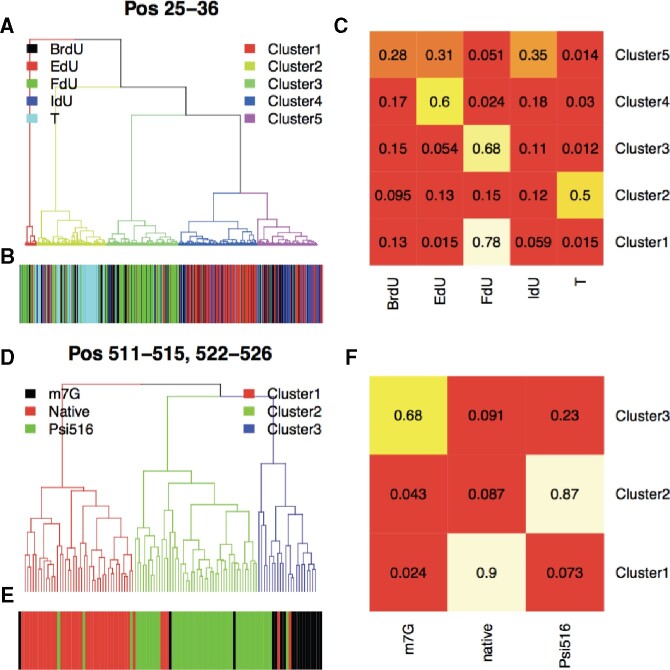
Now that we characterized the per sequence site modification pattern, the next question is how these modifications associate with each other. Therefore, we then performed sequencing read-level analysis to assess the association, e.g. the co-occurrence, mutual-exclusiveness or independence, of the detected modifications. Reads covering all the modified regions were represented in read-position signal matrices, based on which hierarchical clustering was performed (see Section 2). As shown in Figure 4A, for the primer extension dataset, four major clusters (Cluster2–5, account for ∼96% of total reads) were detected. We further quantified the composition of the four clusters, and as shown in Figure 4B and C, Cluster2–5 were majorly composed by T, FdU, EdU and Br/IdU reads, respectively. These results further suggested the expected co-occurrence of the T, FdU, EdU and Br/IdU (same modification at both T-sites), consistent with the experimental design. As shown in Figure 4D, for the 16S rRNA dataset, three major clusters (Cluster1–3) were detected, which were majorly composed of native, Psi516 and m7G reads, respectively. These results further suggested the mutual-exclusiveness of the U and G (in Psi516 strain pseudouridine is substituted with U, and in m7G strain m7G is substituted with G), again consistent with the experimental design.

Fig. 4.

Inferring association between modifications by read-level analysis. (A) Hierarchical clustering analysis on primer extension reads covering reference position 25–36 (see Section 2). Branches of dendrogram were color-coded according to the cluster assignments. (B) Corresponding read annotation, including T- (cyan), IdU- (blue), FdU- (green), EdU- (red) and BrdU-containing reads (black). (C) Read composition of each cluster. (D) Hierarchical clustering analysis on 16S rRNA reads covering reference position 511–515 and 522–526 (see Section 2). Branches of dendrogram were color-coded according to the cluster assignments. ≪ Please note that the part figures mentioned in second occurrence in Figure 4 have been changed from ‘B and C’ to ‘E and F’ respectively. Kindly check and confirm.≫(E) Corresponding read annotation, including Psi516 (green), Native (red) and m7G reads (black). (F) Read composition of each cluster

4 Discussion

Nanopore sequencing has the potential to detect every canonical and modified nucleotide accurately. Without improved de novo detection techniques, progress in modification detection will be dependent upon generating accurate labeled datasets for every modification. Currently, there are over 40 known DNA modifications (Sood et al., 2019) and over 150 known RNA modifications (Boccaletto et al., 2018). Also considering there might be modifications that have never been identified, generating labeled training datasets would be extremely challenging. Therefore, there is a pressing need for a de novo modification analysis pipeline. Such a pipeline can further be divided into three sequential steps, including de novo identification of modification sites, then de novo determination of modification numbers and finally de novo inference on the corresponding chemical structures. The first step has been successfully implemented by Tombo (Stoiber et al., 2016) and Nanocompore (Leger et al., 2019), and our study focuses on the second step, providing a novel algorithm for the community. Specifically, we first confirmed the effective length of kmers for shifting ionic current signals during their translocation through nanopores equals six and five for DNA and RNA, respectively. We then demonstrated the distributions of such kmer signals are mostly normal. A Gaussian mixture model can, therefore, be used for unsupervised modification number determination. Such a Gaussian mixture model-based approach can effectively recapitulate the number of modifications, the corresponding kmer signal event median values, as well as the mixing proportions, in both DNA and RNA contexts. By integrating information from multiple regions, we further assessed the association between the corresponding modifications, which will shed light on modification status of DNA/RNA molecules, allowing for insights into various biological questions. Now that we can accurately determine number, signal levels and proportions of modifications, the next question is what are the corresponding chemical structures for each determined modification component. Answering this question would complete the pipeline for de novo modification analysis, which should be one future direction to pursue.

One major limitation of the method, however, would be how to handle kmers with non-Gaussian signal distributions. For instance, as shown in Supplementary Figure S17, kmer TGATCC appeared in three different sequence contexts of the Zymo dataset (Rand et al., 2017), and in all cases a secondary peak was observed. Please note such secondary peaks were unlikely to be caused by quality issues, thus they cannot be removed by excluding low-quality reads. Such non-Gaussianity will introduce artifacts when analyzing modification numbers. We speculate the non-Gaussianity could be something related to the biophysical characteristics of the nanopores, which are largely unknown. Therefore, another future direction would be to find appropriate mixture models, for instance the extreme value mixture model as reported in the study by MacDonald et al. (2011), to model the modifications on non-Gaussian kmers.