Tutorial: Applying Machine Learning in Behavioral Research

Abstract

Machine-learning algorithms hold promise for revolutionizing how educators and clinicians make decisions. However, researchers in behavior analysis have been slow to adopt this methodology to further develop their understanding of human behavior and improve the application of the science to problems of applied significance. One potential explanation for the scarcity of research is that machine learning is not typically taught as part of training programs in behavior analysis. This tutorial aims to address this barrier by promoting increased research using machine learning in behavior analysis. We present how to apply the random forest, support vector machine, stochastic gradient descent, and k-nearest neighbors algorithms on a small dataset to better identify parents of children with autism who would benefit from a behavior analytic interactive web training. These step-by-step applications should allow researchers to implement machine-learning algorithms with novel research questions and datasets.

Machine learning is a subfield of artificial intelligence that specializes in using data to make predictions or support decision making (Raschka & Mirjalili, 2019). One specific use of machine learning is solving classification problems. A classification problem occurs when trying to predict a categorical outcome (Bishop, 2006). Examples in behavior analysis include what is the function of a behavior (attention, escape, nonsocial, or tangible), whether a behavior is occurring at a given moment, whether an independent variable is changing a behavior or whether a treatment is likely to be effective for a given individual. Supervised machine learning is well suited to provide solutions to these types of classification problems and support decision making.

In supervised machine learning, an algorithm (i.e., computerized instructions) trains a model using past observations to predict outcomes on new samples. In recent years, supervised machine-learning algorithms have been studied as useful aids to support decision making in multiple fields such as medicine, pharmacology, education, and health care (Coelho and Silveira, 2017; Miotto, Wang, Wang, Jiang, and Dudley, 2018). Some examples include identifying breast cancer (Rajaguru & Chakravarthy, 2019), diagnosing autism (Sadiq et al., 2019), predicting school dropout (Chung & Lee, 2019), and detecting unsafe workplace behavior (Ding et al., 2018).

In behavior analysis, both researchers and practitioners rely on data to make decisions on a regular basis. These decisions may involve determining whether an independent variable produced an effect on a behavior, selecting an assessment, identifying the function of behavior, or predicting whether an intervention will produce meaningful behavior changes in a specific individual. However, researchers and practitioners may make unreliable decisions, especially when using their professional judgment (Ninci, Vannest, Willson, & Zhang, 2015; Slocum et al., 2014). In consequence, relying on subjectivity for decision making may result in differences from one behavior analyst to another. One potential solution to this issue is to increase the use of machine learning in behavior analysis (Lanovaz, Giannakakos, & Destras, 2020).

Machine learning also has direct applications for the experimental analysis of behavior and translational research. For example, researchers could use machine learning to develop new models that aim to predict engagement in multiple competing responses (akin to the matching law) under varying experimental conditions. Furthermore, some algorithms may facilitate the identification of variables associated with certain behaviors that may be difficult to isolate experimentally (e.g., suicidal behavior, risky sexual behavior). Machine learning may even simulate responding to test hypotheses that may be difficult to assess with living organisms (see Burgos, 2003, 2007, for examples).

Despite the growing number of studies on the topic in the fields of health care and education, applications of machine learning in behavior analysis remain limited (Burgos, 2003, 2007; Lanovaz et al., 2020; Linstead et al., 2015, 2017). In experimental work, Burgos (2003, 2007) used machine learning to simulate latent inhibition, automaintenance, and autoshaping. The results indicated that it may be possible to simulate behavioral phenomena using artificial neural networks (i.e., a type of machine learning algorithm). In an applied example, Linstead et al. (2015, 2017) developed a machine-learning model to identify predictors of learning progress in children with autism spectrum disorder receiving behavior analytic services. Their results indicated that treatment intensity positively predicted children’s progress, but what is most interesting is that machine learning explained almost twice as much variance of this relationship than linear regression. Lanovaz et al. (2020) showed that machine-learning algorithms outperformed a structured visual aid to analyze simulated data from single-case AB graphs. Their study indicated that machine learning produced smaller Type I error rates and larger power than the dual-criteria method.

One potential explanation for the scarcity of research is that machine learning is not taught as part of training programs in behavior analysis. This lack of knowledge on machine learning and the absence of training for its application may result in researchers overlooking this tool to contribute to the development of the science. This tutorial aims to address this barrier by applying machine learning to a problem involving decision making in behavior analysis.

Machine Learning Procedures and Algorithms

One of the hallmarks of behavior analysis is the pervasive use of single-case designs, which require a small sample size. Given that machine learning is typically applied to large datasets (Raschka & Mirjalili, 2019), some researchers may believe that behavior analytic data are unsuitable for this type of analysis. As will be shown in the current tutorial, datasets with as few as 25 participants or 25 sessions may produce meaningful results using machine learning. With the growing use of consecutive case series designs in behavior analysis (e.g., Hagopian, 2020; Jessel, Metras, Hanley, Jessel, and Ingvarsson, 2020; Lomas Mevers, Muething, Call, Scheithauer, & Hewett, 2018; Rooker, Jessel, Kurtz, & Hagopian, 2013), several researchers and practitioners may already have sufficiently large datasets to apply such algorithms. Moreover, experimental researchers studying human and nonhuman organisms often use automated apparatus to monitor behavior, which provides sufficiently large datasets to potentially uncover novel relationships between variables. In the following sections, we present a step-by-step application of machine learning using data from a behavioral study published by Turgeon, Lanovaz, and Dufour (2020). As relevant, our article also includes instructions on how to apply the algorithms to other datasets. A repository containing our datasets and code is freely available on the Open Science Framework at https://osf.io/yhk2p/.

On Terms

Table 1 draws a parallel between behavioral terms and supervised machine learning. In supervised machine learning, an algorithm trains a model using samples, which is similar to using a specific teaching method when training a learner using exemplars. Thus, the algorithm, the model and the samples represent the teaching method, the learner, and the exemplars, respectively. Each algorithm has its own specific hyperparameters, which are functions or values provided to the algorithm that can be modified by the experimenter prior to training. These hyperparameters are equivalent to the teaching parameters for a teaching method (e.g., number of trials in discrete trial instruction, prompting procedure in direct instruction).

Table 1.

Parallels between Machine Learning and Behavior Analytic Terms

Machine Learning	Behavior Analysis
Algorithm	Teaching method
Model	Learner
Sample	Exemplar
Features	Discriminative stimuli
Class label	Correct response
Prediction	Learner’s response
Hyperparameter	Teaching parameter

In the application of machine learning in behavior analysis, a sample would typically involve the data from one participant or from one session. Supervised machine learning further divides samples into two components: features and class labels. The features involve the input data that are used by the algorithms. Features in machine learning are akin to discriminative stimuli in behavior analysis. The class labels represent the responses provided and predicted by the algorithm (i.e., the output variables). In sum, machine learning algorithms use features from samples to train models to predict class labels in a similar manner that teaching methods focus on using discriminative stimuli from exemplars to train learners to provide correct responses.

Our Dataset

To illustrate the application of machine learning, we used a previously published dataset involving behavior analytic procedures (Turgeon et al., 2020). Turgeon et al. assessed the effects of an interactive web training to teach parents behavior analytic procedures to reduce challenging behaviors in children with autism spectrum disorder. The results of the study showed that, on average, parents who completed the training reported larger reductions in child challenging behaviors than those who did not. However, eight children showed no improvement in challenging behaviors even though their parents had completed the training. As the behavior of individuals is central to research and practice in behavior analysis, one important question is “How can we predict which parent–child dyad are unlikely to benefit from the interactive web training?” Hence, a behavior analyst could recommend alternatives (e.g., in-person training) to families unlikely to benefit from web training.

Preparing the Data

Our dataset includes 26 samples, four features, and one class label. Table 2 presents the characteristics of our dataset. The samples involved 26 parents of children with autism spectrum disorder who completed the interactive web training. We provided four features to our machine learning algorithms: household income, most advanced degree of the parent, the child’s social functioning, and the baseline scores on parental use of behavioral interventions at home (prior to training). Parents initially rated their household income and most advanced degree on an ordinal scale. Because data were highly skewed and our sample was small, data for these features were dichotomized to create more balanced categories (i.e., categories with similar sample sizes).1 It should be noted that dichotomizing data entails many limitations when analyzing large datasets (e.g., loss of power, decreased effect size, and limited generalization of findings). You should avoid using this procedure with continuous and ordinal variables containing a large number of samples (see Dawson & Weiss, 2012; MacCallum, Zhang, Preacher, & Rucker, 2002; Irwin & McClelland, 2003; Sankey & Weissfeld, 1998). We chose the four features because three of them (i.e., most advanced degree, social functioning, and parental use of behavioral interventions) had the highest correlation with our class label values and the fourth feature (i.e., household income) had been previously shown to predict challenging behaviors (Leijten, Raaijmakers, de Castro, & Matthys, 2013; Shelleby & Shaw, 2014). Furthermore, our variables did not show multicollinearity.2 Our class label was whether the frequency of the child’s challenging behavior decreased from baseline to the 4-week posttest (i.e., 0 = no improvement, 1 = improvement) based on the Behavior Problem Inventory-01 (Rojahn, Matson, Lott, Esbensen, & Smalls, 2001). Table 3 contains our complete dataset, which is also available as a comma-separated values (.csv) file in the repository (see TurgeonetalData.csv).

Table 2.

Description of the Variables in the Dataset

Variable	Questionnaire	Type	Values
Feature 1
Household income		Binary	0 = Less than $90,000 1 = $90,000 or higher
Feature 2
Highest diploma		Binary	0 = College or lower 1 = University and higher
Feature 3
Social functioning	ABAS-II - Social domain	Continuous	z score
Feature 4
Parental use of behavioral interventions at baseline	Ad hoc questionnaire (see Turgeon et al., 2020)	Continuous	z score
Class Label
Improvement in the frequency of child challenging behaviors	BPI	Binary	0 = No improvement 1 = Improvement

Note. BPI: Behavior Problem Inventory (Rojahn et al., 2001); ABAS-II: Adaptive Behavior Assessment System (2^nd ed.) (Harrison & Oakland, 2011)

Table 3.

Complete Dataset with Feature and Class Label Values

Household Income	Most Advanced Degree	Social Functioning	Parental Use of Behavioral Interventions	Improvement in the Frequency of Child Challenging Behaviors
0.5*	0	70	17	1
0	0	75	14	1
1	1	70	18	1
0	1	68	15	0
0	0	55	18	1
0	0	68	15	0
0	0	58	12	0
1	1	77	18	1
0	1	87	16	0
0	0	90	17	1
0	0	55	15	1
0	0	68	18	1
1	1	70	18	1
1	0	87	18	1
1	1	71	19	1
1	1	75	14	1
0	0	58	17	1
0	1	95	16	0
0	1	89	18	1
1	0	70	14	1
1	1	93	15	0
1	1	66	15	1
1	1	61	15	0
0	1	80	17	1
1	1	114	13	0
0	1	87	17	1

*Missing value

We arranged the data of our dataset into five columns in our .csv file (i.e., four features and one class label). The first row of each column contains the name of the variable whereas subsequent rows contain the data from one sample. As such, the number of lines for each column equals the number of samples plus one. In our tutorial, we used 26 samples to train our machine learning models, which produced a total of 27 rows (including the header). You should save this file in your working directory (see below). If you want to organize your own data for analysis with machine learning, you may enter them in a spreadsheet in a .csv compatible program (e.g., Microsoft Excel, Google Sheets, Apple Numbers) and save your file as a .csv. Each row should include a single sample and each column a feature or class label (keep the class label in the rightmost column). To use the code in the current tutorial, your class label should remain a binary variable (see “Alternatives to Single Binary Classification,” below, for other options).

The Basics

Installing software and packages

To train our models, we used Python because it is free, offers many open access algorithms, functions the same across operating systems, and has a large network of community support (see Python tutorials in Appendix). The first step to training a machine-learning model is downloading a Python distribution. We strongly recommend that you download and install the Anaconda distribution of Python. This distribution facilitates package management and installation, and ensures that you have the same environment as ours to replicate the procedures presented in this tutorial. You may download and install Anaconda from https://www.anaconda.com. Once Anaconda has been installed, you should create a new virtual environment by opening Anaconda Prompt (in Windows) or Terminal (in macOS or Linux) and entering the following commands in a sequential order:conda create -n myenv python=3.7conda activate myenv

From now on, make sure you run “conda activate myenv” whenever you close and open Anaconda Prompt or Terminal.3 If not, your code may be unable to locate the packages to run the algorithms. Next, we must download and install three packages in this virtual environment: spyder, pandas, and scikit-learn. Spyder is an easy-to-use integrated development environment, pandas facilitates the loading of data in Python, and scikit-learn contains the machine-learning algorithms. To install the packages, run the following commands sequentially (i.e., one at a time) in myenv of Anaconda prompt (in Windows) or Terminal (in macOS or Linux):conda install spyderconda install pandasconda install scikit-learn

Whenever you receive a prompt, choose “y” to install the packages and their dependencies.

Initializing the integrated development environment

Once you have downloaded and installed the necessary programs and packages, open the spyder integrated development environment that you will use to write and run your code. To open spyder, run the following command in Anaconda Prompt or Terminal:spyder

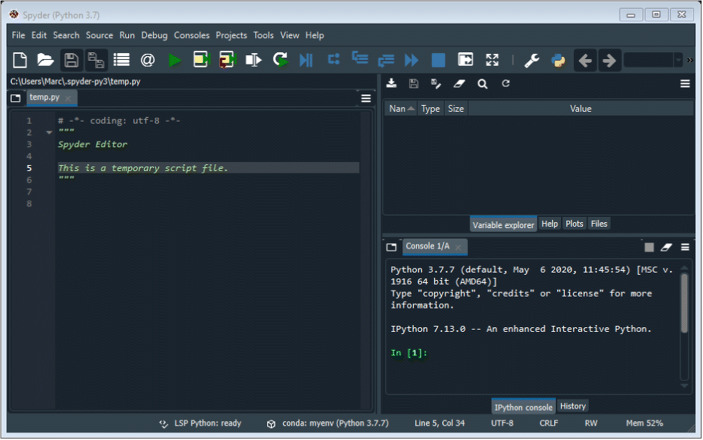
Figure 1 presents a screenshot of the integrated development environment. The integrated development environment is separated in three main work areas: the editor, the iPython console, and the variable explorer. You should write all your code in the editor (box on the left of your screen). To run a block of code from the editor, select the code by highlighting it with your cursor and press F9 (or click on “run selection” in the menu bar). When you run your code, any warnings, errors, or results that you print will appear in the iPython console (box on the lower right of your screen). If you assign a variable or load data, you can view it by clicking on the variable explorer tab of the upper right box.

Fig. 1.

Screenshot for the Spyder Integrated Development Environment

The first lines of code involve setting the working directory. That is, you need to instruct your environment where to find the path to access the folder in which you saved the TurgeonetalData.csv data file. To do so, write the following lines in your editor and run the selection4:1 import os2 os.chdir("PATH")

In the above command, you should replace PATH by your working directory5 where the .csv file is located. You should select these lines of code and press F9 to run the selection (or click on “run selection” in the menu bar above the editor).

Loading and preparing the data

Next, the lines of code below import the packages that include the functions that we need to load and organize the data:1 import numpy as np2 import pandas as pd

Once both packages have been imported, load the .csv data file into the environment with the following code:1 data = pd.read_csv("TurgeonetalData.csv")2 data_matrix = data.values

The first line loads our dataset and names it “data” whereas the second line transforms this data to a matrix, thus facilitating the manipulation of the data. When loading your own data, you should replace TurgeonetalData.csv by the filename of your own .csv file.

Prior to conducting machine learning, you must standardize the data of all nonnormally distributed continuous features. Nonstandardized data may render the machine-learning model unable to correctly use the features to predict the class labels (Raschka & Mirjalili, 2019). Therefore, we transformed the social functioning scores and the parental use of behavioral interventions scores to z scores. A z score is a standardized score that is obtained by subtracting the mean score from the raw score then dividing this value by the standard deviation. To transform the raw scores to z scores, we need to write and run the following instructions in the editor:1 from sklearn import preprocessing2 standard_scaler = preprocessing.StandardScaler()3 data_matrix[:,2:4] = standard_scaler.fit_transform(data_matrix[:,2:4])

The first and second lines of code import a function to rapidly transform the raw scores to z scores. The third line instructs the program to apply this standardization only to columns that include the social functioning and parental use of behavioral interventions scores.6 If you are using your own data, you should apply the standardization to all continuous variables that are not already standardized. The final step to preparing the data is separating the features from the class labels:1 x = data_matrix[:,0:4]2 y = data_matrix[:,4]

Matrix “x” now contains the four features whereas vector “y” contains the true class labels. When using your own data, you should replace number 4 in the code block by the number of features in your dataset.

Outcome Measures

The most common outcome measure for binary classifications is accuracy. Accuracy involves dividing the number of agreements between the true class label values and the predictions of the models by the total number of predictions (Lee, 2019). One drawback of accuracy is that it does not consider that some values may be correct as a result of chance, which may skew the results in favor of correct predictions. Kappa is a more stringent measure of performance than accuracy as it takes into consideration correct classifications due to chance (we refer the reader to McHugh [2012] for a demonstration on how to compute the Kappa statistic). The following lines import the functions to calculate these values for you:1 from sklearn.metrics import accuracy_score, cohen_kappa_score

For kappa, any value above .20 typically indicates that the model reliably predicts some of the class label values in the dataset, regardless of chance (McHugh, 2012). In contrast, benchmarks for accuracy do not exist as the measure is dependent on the distribution of the data.

Comparison Measures

Given that there is no fixed criterion to determine whether an accuracy value is adequate, we must compute comparison measures for accuracy. One potential measure represents the accuracy if predictions were randomly selected. The following lines of code use a Monte Carlo method to determine this accuracy value:1 np.random.seed(48151)2 y_random = []3 for i in range(100000):4 y_random_values = np.random.choice(data_matrix[:,4], 26, replace = False)5 y_random.append(accuracy_score(y, y_random_values))

The first line sets the random seed for numpy at 48151. Although not necessary in practice, we recommend that you implement this line of code so that your environment produces the same results as the ones reported in the tutorial. The next line (i.e., 2) creates an empty list in which the accuracy values are stored for each iteration. The third line is a loop instructing Python to repeat the procedures 100,000 times7 (Monte Carlo simulations). During each loop, the program first randomly permutates the values for the 26 samples, which produces a vector named random_values (line 4). The fifth line of code computes the accuracy score for these random_values and appends it to the list. Finally, to compute the accuracy of a random selection measure, we take the mean of these 100,000 iterations by running the following code:1 print(np.mean(y_random))

The print function displays the value in the iPython console. In our example, the iPython console should show that random selection produced an accuracy of .574 (i.e., it correctly guessed the class labels 57.4% of the time).

A second more stringent comparison measure involves reporting the class value with the highest probability response. That is, what is the best accuracy we could produce if we always guessed the same value? In our case, the most frequently observed class label value is improvement (n = 18), which would lead to an accuracy of .692 (18 divided by 26) if we simply predicted that all class label values were the same.

A third candidate for comparison is the logistic regression. Although sometimes categorized as a machine learning algorithm, logistic regression is a traditional statistical approach (i.e., a generalized linear model) that uses a linear boundary to separate data into classes (Stefanski, Carroll, & Ruppert, 1986). In a systematic review, Christodoulou et al. (2019) reported that machine learning does not systematically outperform logistic regression, which makes it a good comparison measure. It should be noted that the purpose of the tutorial is not to show that machine learning is always superior to the logistic regression, but how to apply machine learning in order to determine which provides the best predictions based on your data’s distribution. Presenting how to perform logistic regression using Python goes beyond the scope of this article. We have made the code accessible as a supplement document and invite the reader to consult Lee (2019) for more information on logistic regression and on how to apply this algorithm. The logistic regression yielded an accuracy of .731 and a kappa value of .428 when applied to our dataset.

Leave-One-Out Cross-Validation

Prior to training our machine learning models, we need to specify how to test them. One issue with machine learning is that using the same data to train and test a model may lead to overfitting. Overfitting carries the risk of fitting “the noise in the data by memorizing various peculiarities of the training data rather than finding a general predictive rule” (Dietterich, 1995, p. 327). In behavior analytic terms, the model would fail to generalize responding to novel, untrained exemplars. To address this issue, researchers use cross-validation methodology to assess their models. In cross-validation, the researcher removes part of the data during training. This removed data is then used to test for the generalization of the model. Therefore, researchers do not report the outcome for the training data, but rather for the test data, which were removed and not used during the development of the model.

For small datasets, researchers recommend the leave-one-out cross-validation methodology (Wong, 2015). The leave-one-out cross-validation methodology separates the dataset into two sets of data. The first set, the training set, contains the data of all samples except for one (hence the name leave-one-out). The machine learning model uses the features and true class labels of the training set to learn how to predict the class label values. The second dataset, the test set, contains the remaining sample (i.e., a single sample). The latter tests the model’s generalization to a novel, untrained sample. As such, the sample of the test set is not used during training. The leave-one-out cross-validation methodology is repeated N times (i.e., number of samples in the dataset) so that each sample is used as the test set once. In our tutorial, the leave-one-out cross-validation methodology was repeated 26 times as our dataset contained 26 samples. To import the leave-one-out cross-validation methodology, you should run the following code from the scikit-learn package:1 from sklearn.model_selection import LeaveOneOut2 loo = LeaveOneOut()

The first line imports the function whereas the second line defines the parameters of the function. In the example above, we kept the default parameters.

Some Algorithms

Many machine learning algorithms exist. In this tutorial, we selected four algorithms useful for classification problems with small datasets: random forest, support vector, stochastic gradient descent, and k-nearest neighbors classifiers. We targeted these four algorithms because they have been widely used and apply different underlying mathematical approaches (i.e., use the features differently to create a machine learning model; Lee, 2019; Raschka & Mirjalili, 2019).8 The purpose of the subsequent section is not to compare the machine-learning algorithms together, which would require a large number of datasets from other studies, but to show how to apply them.

Random forests

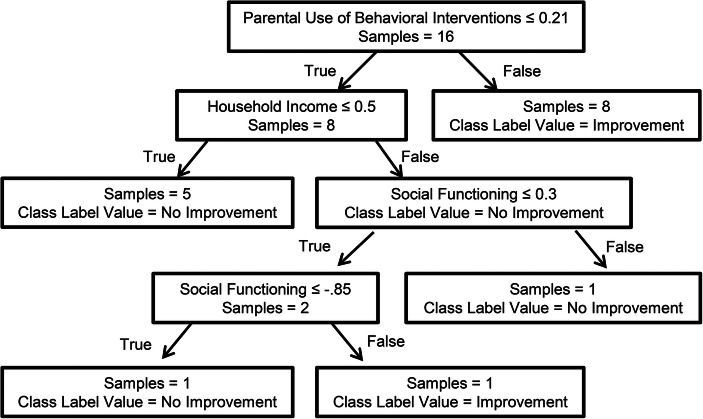
Random forests are machine-learning algorithms that use an ensemble of decision trees (called a forest) to predict an outcome (Breiman, 2001). These decision trees are a collection of nodes that describe conditions that can be true or false for a given dataset (see Figure 2). The algorithm follows different paths in the tree depending on whether the value of each condition in the tree is true or false. In brief, the algorithm creates individual decision trees by (1) randomly selecting a subset of the training set, (2) randomly selecting a subset of features at each split (i.e., node), and (3) keeping the feature that decreases entropy (or uncertainty of the decision) the most to create each decision node. The algorithm then repeats this process several times (100 by default with scikit-learn) to create a forest with many different trees. For classification problems, the predictions of all independent trees are aggregated and the most popular prediction is selected as the predicted class label. As an example, Figure 2 presents the first of the 100 trees in the random forest that we produced as part of the current tutorial. The algorithm used 16 samples to produce a tree with three features and four decision nodes. The model has 100 trees similar to the one depicted in Figure 2 that vote on the outcome. The most likely outcome becomes the prediction of the algorithm.

Fig. 2.

Visual Representation of the First Tree in the Random Forest

To apply the random forest algorithm, we must first import the random forest classifier function:1 from sklearn.ensemble import RandomForestClassifier2 rf = RandomForestClassifier(class_weight = 'balanced', random_state = 48151)

The second line of the code above provides the hyperparameters for the algorithm. The random_state variable is optional in practice, but it guarantees the production of a consistent output. Because there is a random component to the algorithm, setting the random_state will ensure that you obtain the same results as the ones presented in this tutorial every time you run the code in Python. Setting the class_weight as balanced ensures that both values of our class label carry the same weight, which is necessary because the number of samples with the class label value improvement (n = 18) was much larger than that of the no improvement (n = 8) class label value. Hence, balancing the weights of the class label values prevents the model from overclassifying predictions in the class label value with the largest number of samples.

Now, we need to run the code to train and test our models:1 rf_pred = []2 for train_index, test_index in loo.split(data_matrix):3 x_train, y_train, x_test, y_test = x[train_index, :], y[train_index], x[test_index, :], y[test_index]4 rf.fit(x_train, y_train)5 prediction = rf.predict(x_test)6 rf_pred.append(prediction)

The first line of code creates an empty list to store the prediction made by the random forest model after each iteration. The second line instructs Python to use the leave-one-out cross-validation methodology to train and test the random forest algorithm. The loop runs 26 iterations during which it trains and tests 26 models, which are each computed using a different sample as the test set. The code of the third line creates the training and test sets for the features (x) and the class labels (y) for each iteration. The next step (line 4) involves using the fit function to train the random forest machine learning model to solve your classification problem using the features (x_train) and class labels (y_train) of your training set. Finally, the fifth line predicts the class label of the test set using the test features (x_test) and the last line appends the results to the list.

Once Spyder has run the 26 iterations, we can write the following code to compute the accuracy and kappa scores:1 print(accuracy_score(rf_pred, y))2 print(cohen_kappa_score(rf_pred, y))

The rf_pred list contains the predictions whereas the y vector includes the true values. At this point, we remind the reader that these predictions were made on data not included in the set used to train the models (out-of-sample prediction) to prevent overfitting. In our example, the model trained using the random forest classifier produced an accuracy of .769. Put differently, using the models developed by the algorithms led to correctly predicting whether a child would benefit from their parent following the web training in 77% of the sample. The random forest algorithm outperforms all three comparison measures for this classification task (see left side of Table 4 for comparisons). In addition, the model produced a kappa value of .458, which represents a moderate agreement of the models with the actual observations (McHugh, 2012). The main advantage of random forests over the other proposed algorithms is that we can visualize the individual trees (see Figure 2), which may lead to the development of novel hypotheses on the contribution of each feature. For example, a researcher could print all the trees and examine how each feature influences categorization to develop hypotheses about the underlying decision-making process.

Table 4.

Comparison of Accuracy and Kappa Scores without and with Hyperparameter Tuning for Each Algorithm

Algorithm	No Tuning		Hyperparameter Tuning
	Accuracy	Kappa	Accuracy	Kappa
Random Selection	.574	.000
Highest Probability Response	.692	.000
Logistic Regression	.731	.428
Random Forest	.769	.458	.846	.639
Support Vector Classifier	.654	.264	.808	.532
Stochastic Gradient Descent	.692	.325	.731	.492
K-nearest Neighbors	.615	-.048	.808	.591

Support vector classifier

Support vector classifiers separate opposing class labels (i.e., in our example improvement and no improvement) using decision boundaries (called hyperplanes). In support vector classifiers, only extreme data points (i.e., those that are closest to the opposing class label) contribute to the development of the prediction model. Maximizing the margin (i.e., the space between the decision boundary and the nearest samples for each class) increases the model’s ability to correctly predict the class labels of untrained data (Bishop, 2006). Support vector classifier relies on linearity (i.e., a directly proportional relationship between the feature and the class label) to classify data into class labels. When the relation between the features and the class labels are nonlinear or use multiple features (i.e., more than two), a function is applied (called a kernel) to transform the data into a higher dimension (e.g., two-dimensions into three dimensions) so that data can be linearly separated with a hyperplane (Qian, Zhou, Yan, Li, & Han, 2015). Figure 3 presents an example of data that could not be separated linearly in a two-dimensional space, but that could be separated by a plane when a third dimension was added. The space (i.e., the area in the graph in relation to the plane or hyperplane) where a sample is located predicts the class label value.

Fig. 3.

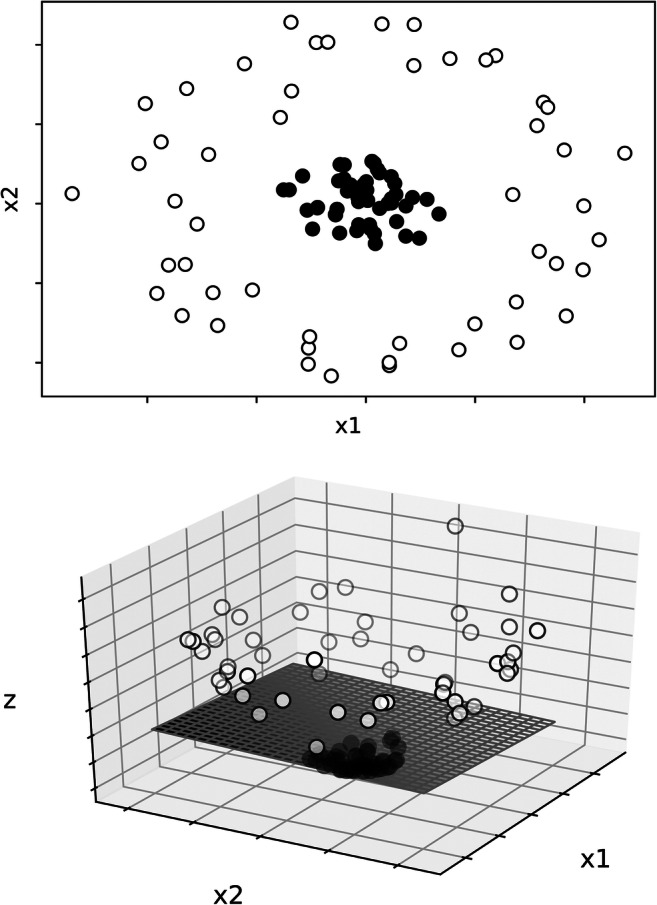
Example of a Dataset Separated by a Support Vector Classifier. Note. The upper panel shows a two-dimensional graph representing two features: x1 and x2. Closed points represent one category and opened points a different category. The lower panel depicts the addition of a higher dimension (z) and a linear plane that separates the two categories. Reprinted with permission from “Machine Learning to Analyze Single-Case Data: A Proof of Concept” by M. J. Lanovaz, A. R. Giannakakos, and O. Destras, 2020, Perspectives on Behavior Science (doi:1.1007/s40614-020-00244-0). CC BY 4.0

To apply the support vector classified algorithm, we start by importing the function from the scikit-learn package:1 from sklearn import svm2 svc = svm.SVC(class_weight = 'balanced')

We only specified one hyperparameter for this machine learning algorithm: the class weight. As per random forest, we balanced the class weights. The remaining code is identical to the one we have developed for the random forest algorithm, except that we replaced rf by svc:1 svc_pred = []2 for train_index, test_index in loo.split(data_matrix):3 x_train, y_train, x_test, y_test = x[train_index, :], y[train_index],x[test_index, :], y[test_index]4 svc.fit(x_train, y_train)5 prediction = svc.predict(x_test)6 svc_pred.append(prediction)7 print(accuracy_score(svc_pred, y))8 print(cohen_kappa_score(svc_pred, y))

The output should show an accuracy of .654 and a kappa of .264, which is marginally better than the random selection but not as accurate as the highest probability response and logistic regression comparison measures. When compared to other algorithms, the support vector classifier has the benefit of being deterministic, which makes the results easier to replicate. In other words, the algorithm does not contain a random component: it will thus always produce the same results given the same features. The kernel function also makes is suitable for nonlinear data.

Stochastic gradient descent

Stochastic gradient descent is an optimization algorithm designed to reduce the error produced by a function (Raschka & Mirjalili, 2019). As part of the tutorial, we focus on the logistic function as it is a common method to separate data into classes (Peng, Lee, & Ingersoll, 2002). The main difference with traditional logistic regression is that the response is optimized within an iterative process that produces a nonlinear transformation. During stochastic gradient descent, the features are multiplied by a matrix of weights and the algorithm calculates the prediction error using the logistic function. Based on this error, the algorithm applies a correction to adjust the weights decreasing the prediction error for each successive iteration, which are referred to as epochs. In other words, the process is akin to shaping in behavior analysis where the algorithm selects (reinforces) successively closer approximations (i.e., less error). That said, researchers must remain wary of running too many epochs as it may overfit the training data and fail to generalize to novel samples (faulty discriminative control). Compared to random forests that use multiple independent trees to make a prediction, stochastic gradient descent keeps a single model.

The first step to applying stochastic gradient descent is to import the function from scikit-learn and define the hyperparameters:1 from sklearn.linear_model import SGDClassifier2 sgd = SGDClassifier(class_weight = 'balanced', loss = "log", penalty="elasticnet", random_state = 48151)

In our example, we specified four hyperparameters: class weight, loss, penalty, and random state (see line 2). Given that the weight matrix is initialized using a random function, the random_state variable ensures that the results remain consistent. We balanced the class weights to prevent the model from always predicting the most probable response. The loss implements the logistic function. Finally, we added a penalty term to minimize overfitting. Elasticnet adds some variability when the algorithm updates the weights, which improves generalization to untrained samples. Once again, the code is the same as for the rf function except that we replace rf by sgd:1 sgd_pred = []2 for train_index, test_index in loo.split(data_matrix):3 x_train, y_train, x_test, y_test = x[train_index, :], y[train_index],x[test_index, :], y[test_index]4 sgd.fit(x_train, y_train)5 prediction = sgd.predict(x_test)6 sgd_pred.append(prediction)7 print(accuracy_score(sgd_pred, y))8 print(cohen_kappa_score(sgd_pred, y))

The iPython console shows that our stochastic gradient descent model produced an accuracy of .692 and a kappa of .325, outperforming the random selection comparison measure but not the highest probability response and the logistic regression. In the current study, we limited the application of the stochastic gradient descent to a logistic function. One of the advantages of the stochastic gradient descent is that its flexibility allows its application to other functions.

K-nearest neighbors

The k-nearest neighbors algorithm uses feature similarity between samples to predict a class label (Raschka & Mirjalili, 2019). In brief, the algorithm identifies samples that are most similar to a new sample (i.e., nearest neighbors). Using a predetermined number of nearest neighbors (i.e., k), the model makes a prediction based on the most popular class label. In the k-nearest neighbors algorithm, nearest neighbors are often identified by calculating the linear distance between two points. Selecting an appropriate k is essential because different numbers of nearest neighbors can result in different predictions (i.e., class labels).

As for the other algorithms, we must first import the k-nearest neighbors function and set its hyperparameters:1 from sklearn.neighbors import KNeighborsClassifier2 knn = KNeighborsClassifier()

In this example, the function uses the default hyperparameters, which involve the five closest neighbors (i.e., k = 5). Again, we then run the same code as for the random forest algorithm, replacing rf by knn:1 knn_pred = []2 for train_index, test_index in loo.split(data_matrix):3 x_train, y_train, x_test, y_test = x[train_index, :], y[train_index],x[test_index, :], y[test_index]4 knn.fit(x_train, y_train)5 prediction = knn.predict(x_test)6 knn_pred.append(prediction)7 print(accuracy_score(knn_pred, y))8 print(cohen_kappa_score(knn_pred, y))

The k-nearest neighbors algorithm produced the worst accuracy (i.e., .615) and kappa (i.e., -.048). This algorithm performed slightly better than the random selection comparison measure, but produced measures lower than those of the highest probability response and the logistic regression. Nonetheless, the k-nearest neighbors algorithm has the following advantages: it is deterministic, easy and fast to implement, and it can readily detect nonlinear patterns.

Hyperparameter Tuning

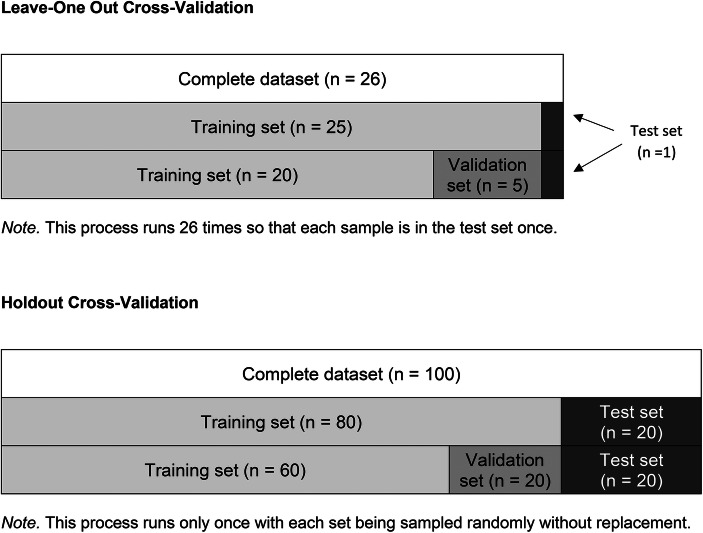
Three of the four machine-learning algorithms did not perform any better than the logistic regression. In all our applications, we generally used the default hyperparameters of the algorithms to train our models, which explains why the performance was not optimal. To improve accuracy, researchers should use a procedure referred to as “hyperparameter tuning” to set optimal values (Raschka & Mirjalili, 2019). In hyperparameter tuning, the experimenter (1) tests the accuracy (or error) of different combinations and values of hyperparameters, and (2) selects the one that produces the best outcome measure. This selection of the best outcome cannot rely on the test set because it may lead to overfitting and failures of the results to generalize to novel datasets. Therefore, we must create a new set, the validation set, on which to assess the outcome of hyperparameter tuning. The upper panel of Figure 4 shows how our code generated a validation set for the current dataset.

Fig. 4.

Visual Representations of Different Sets in the Leave-One-Out Cross-Validation and the Holdout Cross-Validation

In most cases, researchers are unaware of the best hyperparameter settings for each of their algorithms because these values vary across datasets. Therefore, we strongly recommend the use of hyperparameter tuning if no prior values are available for similar datasets in the research literature. These hyperparameters to tune vary across algorithms. Examples of hyperparameters are the number of trees in the random forest, the number of epochs (loops) in stochastic gradient descent, and the number of neighbors in the k-nearest neighbors algorithm. Given that the hyperparameters vary considerably across algorithms, we cannot provide a comprehensive list here. When unsure which hyperparameters to manipulate, we strongly recommend that researchers examine prior studies using the same algorithm. As an alternative, researchers may use grid search or random search procedures to conduct comprehensive tuning (see Appendix for a link on instructions on how to proceed).

Because the k-nearest neighbors algorithm performed worst in our prior analyses, we use it as an example to explain how to implement hyperparameter tuning. To facilitate hyperparameter tuning using leave-one-out cross-validation, we must program a function to conduct the tuning at each iteration. The first step is importing the joblib package, which allows us to save the best model:1 import joblib

Then, we must write a function that keeps the best model (i.e., the highest accuracy on the validation set) following each iteration of the leave-one-out cross-validation loop:1 def knn_train(x_train, y_train, x_valid, y_valid):2 k_values = np.arange(1, 11, 1)3 best_acc = 04 for k in k_values:5 knn = KNeighborsClassifier(k)6 knn.fit(x_train, y_train)7 prediction = knn.predict(x_valid)8 current_acc = accuracy_score(prediction, y_valid)9 if current_acc > best_acc:10 best_acc = current_acc11 filename = 'best_knn.sav'12 joblib.dump(knn, filename)13 best_knn = joblib.load('best_knn.sav')14 return best_knn

The first line informs Python that the subsequent indented lines define a function that takes our training data (x_train, y_train) and our validation data (x_valid, y_valid) as input. The second line provides the range of k values to test (1–10 neighbors) whereas the third line initializes the best accuracy value at 0. The code runs in a loop wherein each loop tests a different value of k (see line 4). Lines 5 and 6 train the model using the training set with k neighbors. The seventh and eight lines assess accuracy on the validation data. Line 9 contains a conditional formula that runs lines 10–12 only if the accuracy computed for this value of k on the validation set is higher than for any previous k value. The instructions involve three steps: replacing the best accuracy value by the current accuracy value (line 10), providing a name of the file where to save the model (line 11), and saving this model. The last two lines return the model (i.e., the model with the number of k neighbors) that produced the best accuracy on the validation set.

The next step is to run this function with each loop of the leave-one-out cross-validation to examine the effects of the model on the test set:1 from sklearn.model_selection import train_test_split2 best_knn_pred = []3 for train_index, test_index in loo.split(data_matrix):4 x_train, y_train, x_test, y_test = x[train_index, :], y[train_index],x[test_index, :], y[test_index]5 x_train, x_valid,y_train, y_valid = train_test_split(x_train, y_train, test_size = 0.20, random_state = 48151)6 best_knn = knn_train(x_train, y_train, x_valid, y_valid)7 prediction = best_knn.predict(x_test)8 best_knn_pred.append(prediction)9 print(accuracy_score(best_knn_pred, y))10print(cohen_kappa_score(best_knn_pred, y))

The reader should already be familiar with some of the code in the previous block because it is similar to the code used during training with the default hyperparameters. We will focus on the lines that differ. The first line imports a function that splits the training set into two subsets: the training set and the validation set (see line 5). The test_size parameter indicates that 20% of the data should be moved to the validation set and 80% should remain in the training set. Thus, the validation set contains 5 samples and the training set 20 samples. In line 6, we replace the knn.fit formula by our new function, which returns the tuned model that produces the best accuracy on the validation set. The output shows that the tuned model outperforms the model with the default hyperparameters. The accuracy on the test set increased from .615 to .808 whereas the kappa score increased from -.048 to .591.

In a similar manner, we could conduct hyperparameter tuning for the other machine-learning algorithms, but we leave it up to the reader to try it out on their own. The code is available in the ML_step-by-step.py file of the repository starting on line 162. Table 4 compares the results obtained by each algorithm without and with hyperparameter tuning so that the readers can compare their results. It is clear that conducting hyperparameter tuning leads to more accurate models. Except for the stochastic gradient descent, which produced similar results, all hypertuned models outperformed the simple logistic regression as well as the other comparison measures.

Practical Considerations

Selecting Features

The selection of features merits further discussion because careful selection may lead to better models and minimize overfitting (and the opposite is true for inadequate selection). First, researchers should avoid cherry-picking their features by selecting those that produce the most accurate model on the test set. This cherry-picking may lead to models that produce overfitting on novel, untrained exemplars. Instead, feature selection should involve a rigorous approach. In general, researchers categorize feature selection methods in three broad categories: filter, wrapper, and embedded (Cai, Luo, Wang, & Yang, 2018; Visalakshi & Radha, 2014). Filter methods typically involve keeping features with specific statistical properties (e.g., significant relationship with the outcome variable, correlation threshold). Wrapper methods consist of systematically searching different combinations of features to identify the one that produces the best outcome. Finally, embedded methods integrate feature selection within the machine learning algorithm by identifying or emphasizing features that produce the best predictions. Describing the advantages and disadvantages of these methods goes beyond the scope of this tutorial. We suggest that the reader consult Cai et al. (2018) and Visalakshi and Radha (2014) for a review of different feature selection methods.

In the tutorial, we selected three of our features because they had been shown to be correlated with the class label and displayed no multicollinearity, which is similar to a filter-based approach. As an alternative, our procedures could have involved hyperparameter tuning for feature selection (i.e., a wrapper method). In this alternative, the features included in the model would represent the hyperparameter. As indicated earlier, this approach is only viable if the selection of features relies on a validation set. We feel that it is important to repeat here that the selection of features should never rely on the results of the test set. Another consideration when selecting features is the measurement scale (e.g., nominal, ordinal, continuous). For the tutorial, we dichotomized two features. The dichotomization of the features was done to better balance the samples as the data were highly skewed. Although this procedure may lower chances of overfitting, the reader should bear in mind that decreasing the number of degrees of freedom may result in a loss of power.

Selecting an Algorithm

We reviewed four different types of algorithms as part of the current tutorial. One important question remains: When to select one algorithm over another? Unfortunately, the research literature does not provide a straightforward answer to this question and the results from this tutorial should not be used as performance indicators as we examined a single specific dataset. One solution is to compare the results across algorithms (as we have done with hyperparameter tuning) and to select the algorithm that produces the best outcome. The advantages of each algorithm may also guide the selection. The random forest and the k-nearest neighbors algorithms are easy to explain, intuitive, and allow an analysis of why the samples are categorized the way they are. In contrast, stochastic gradient descent models are like black boxes; even when accurate, we cannot clearly identify the underlying mechanisms that produced the outcomes. The k-nearest neighbors and support vector classifiers produce deterministic results, which renders them more stable than those that have a random component. Finally, the random forest may require little to no tuning to produce accurate predictions with small sets.

About Samples

Earlier in the tutorial, we suggested that the models could be trained with datasets with as few as 25 samples: a series of features and class labels for 25 exemplars on which you can make predictions. This rule-of-thumb is a lower limit. When everything else is kept equal, algorithms with more data will train more accurate models and reduce overfitting. The only dataset that we had at hand for the tutorial contained 26 samples, but we strongly recommend that you aim for more. Samples may take on many forms. For example, a sample may represent a participant and their responding to a treatment (as in our tutorial). In experimental research, a sample could involve the rate of lever presses by a rat within 1 min; each minute of the session would thus be a different sample. As an alternative, a sample could be a complete session if the models were designed to predict the percentage of behavior over longer periods of time. In this case, each session could count as a sample. Nevertheless, you would still want many different subjects (e.g., 10 subjects with 10 sessions) in order to measure and to validate the generalizability of the models within and across subjects.

Alternatives to Single Binary Classification

Our tutorial focused on one type of problem: binary classification. We can readily apply the same algorithms to multi label classification problems. Assume that we want to predict the function of a challenging behavior. The output would involve four class labels (columns), one per challenging behavior function. Each class label would remain binary: 1 = positive, 0 = negative.

Another type of problem that can be solved using machine learning is predicting specific values. For example, a researcher may aim to predict the percentage of behavior during a session based on some other variables. In this case, we recommend using a regressor rather than a classifier. It is fortunate that the packages that we have used for classification all have regressor equivalents: RandomForestClassifier becomes RandomForestRegressor, svm.SVC becomes svm.SVR, SGDClassifier become SGDRegressor, and KNeighborsClassifier becomes KNeighborsRegressor. The kappa and accuracy measures are not appropriate for regressors. Alternatives include the mean_squared_error and mean_absolute_error functions from the scikit-learn package.

Cross-Validation

In the tutorial, we reviewed only one type of cross-validation: the leave-one-out method. A second type of cross-validation is the holdout method, which divides datasets into a single training set and a single test set. The test set remains consistent across all analyses and is never used during training. Thus, we do not need to program a loop. To split the dataset, we run the following code:1 from sklearn.model_selection import train_test_split2 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.20, random_state = 48151)

The random_state parameter ensures that the results remain consistent across replications whereas the test_size parameter indicates the proportion of samples in the dataset that should be placed in the test set. Figure 4 (bottom panel) shows an example of holdout cross-validation with a hypothetical dataset containing 100 samples. In this case, a value of .20 produces a test set with 20 samples and a training set with 80 samples. Although generally applied when datasets are larger, Vabalas, Gowen, Poliakoff, and Casson (2019) found that a such approach to building and testing a machine learning model produced the least biased outcomes.

A third method relevant to behavioral researchers is the k-fold cross-validation method (Wong, 2015). The k-fold method is a hybrid between the leave-one-out and holdout methods. In the k-fold method, the k represents the number of times the cross-validation is repeated. For example, a k of 5 involves running the cross-validation five times. Each iteration, the algorithm uses four-fifths (80%) of the data for training and one-fifth (20%) of the data for testing. The data in testing differs across each iteration so that all samples are included in the test set exactly once. To implement k-fold cross-validation, we need to import the algorithm using:1 from sklearn.model_selection import KFold2 kf = KFold(k)

In the example above, k represents the number of folds, which should be an integer. Then, we replace the loo.split(data_matrix) loop by the following code:1 for train_index, test_index in kf.split(data_matrix):

The k-fold method is a strong alternative to the holdout method when the number of samples is limited as it rotates all the samples in the test set (see “Cross Validation” in Appendix).

Conclusion

As part of the current tutorial, we demonstrated how to apply four different machine learning algorithms to train models to predict whether specific parents of children with autism would benefit from an interactive web training. We developed this tutorial to raise awareness of the potential use of machine learning to support decision making in the field of behavior analysis. The purpose of our tutorial was to demonstrate how machine learning can aid researchers in analyzing small datasets and not to prove that machine learning always performs better than traditional statistics (which is not the case). Machine learning has the advantage of conducting nonlinear discrimination beyond the logistic regression and of analyzing small datasets that do not respect assumptions typically found in parametric tests. Thus, this article presents an approach, which behavioral researchers may add to their toolbox to address questions important to our understanding of human behavior.

In our tutorial, we showed that models developed with machine learning may predict which parents could benefit from an interactive web training. Until independent researchers replicate our procedures with more data and carefully examine its social validity, we do not recommend the adoption of these models in practice. If these models are further validated, they could lead to better decision-making. At present, behavior analysts rely on their professional judgment to decide whether a parent could benefit from a specific type of training. The machine-learning models may support behavior analysts in making more consistent and more accurate decisions. The litmus test for such an approach will be comparing the decisions of the models with the decisions taken by trained behavior analysts, which goes beyond the scope of a tutorial on how to apply these machine-learning algorithms.

The application of machine learning in behavior analysis is still in its infancy. If the rapid adoption of machine learning by other fields is any indication, we expect that behavior analysts will increasingly use this approach in their experimental work, applied research, and practice. Examples of uses wherein machine learning could support behavior analysts include the identification of novel variables that play a role in the development and maintenance of behavior, the prediction of intervention effects or rates of behavior within experimental settings, the measurement of behavior, the analysis of functional assessment data, and the inspection of single-case designs. The benefits may range from a better understanding of the causes behavior to practitioners making more reliable and accurate clinical and educational decisions. This tutorial may thus serve as a starting point for behavioral researchers looking for an introduction to machine learning and its applications.

Appendix

Free Online Resources

Learn More About Python

Learn Python—https://www.learnpython.org/

Google's Python Class—https://developers.google.com/edu/python

Python for Beginners—https://www.python.org/about/gettingstarted/

Learn More About Machine Learning

An Introduction to Machine Learning—https://www.digitalocean.com/community/tutorials/an-introduction-to-machine-learning

Google’s Introduction to Machine Learning—https://developers.google.com/machine-learning/crash-course/ml-intro

Introduction to Machine Learning for Beginners—https://towardsdatascience.com/introduction-to-machine-learning-for-beginners-eed6024fdb08

Learn More About Machine Learning in Python

Cross Validation in Python: Everything You Need to Know About—https://www.upgrad.com/blog/cross-validation-in-python/

An Implementation and Explanation of the Random Forest in Python—https://towardsdatascience.com/an-implementation-and-explanation-of-the-random-forest-in-python-77bf308a9b76

Implementing SVM and Kernel SVM with Python's Scikit-Learn—https://stackabuse.com/implementing-svm-and-kernel-svm-with-pythons-scikit-learn/

How To Implement Logistic Regression From Scratch in Python—https://machinelearningmastery.com/implement-logistic-regression-stochastic-gradient-descent-scratch-python/

Develop k-Nearest Neighbors in Python From Scratch—https://machinelearningmastery.com/tutorial-to-implement-k-nearest-neighbors-in-python-from-scratch/

Hyperparameter Tuning—https://towardsdatascience.com/hyperparameter-tuning-c5619e7e6624

Sci-Kit Learn: 3.2. Tuning the Hyper-Parameters of an Estimator—https://scikit-learn.org/stable/modules/grid_search.html

Compliance with Ethical Standards

Funding

This study was funded in part by a Graduate Scholarship from the Social Sciences and Humanities Research Council of Canada (SSHRC) to the first author and a salary award from the Fonds de recherche du Québec - Santé (#269462) to the second author.

Ethical Approval

All procedures performed in this study were in accordance with the ethical standards of the Canadian Tri-Council Policy Statement: Ethical Conduct for Research Involving Humans and with the 1964 Helsinki declaration and its later amendments.

Informed Consent

Parents provided informed consent for them and their child.

Conflict of Interest

The authors declare that they have no conflict of interest.

Availability of Code and Data

The code and data are freely available at https://osf.io/yhk2p/.