The Input-Output Relation of Primary Nociceptive Neurons is Determined by the Morphology of the Peripheral Nociceptive Terminals

Abstract

The output from the peripheral terminals of primary nociceptive neurons, which detect and encode the information regarding noxious stimuli, is crucial in determining pain sensation. The nociceptive terminal endings are morphologically complex structures assembled from multiple branches of different geometry, which converge in a variety of forms to create the terminal tree. The output of a single terminal is defined by the properties of the transducer channels producing the generation potentials and voltage-gated channels, translating the generation potentials into action potential (AP) firing. However, in the majority of cases, noxious stimuli activate multiple terminals; thus, the output of the nociceptive neuron is defined by the integration and computation of the inputs of the individual terminals. Here, we used a computational model of nociceptive terminal tree to study how the architecture of the terminal tree affects the input-output relation of the primary nociceptive neurons. We show that the input-output properties of the nociceptive neurons depend on the length, the axial resistance (Ra), and location of individual terminals. Moreover, we show that activation of multiple terminals by a capsaicin-like current allows summation of the responses from individual terminals, thus leading to increased nociceptive output. Stimulation of the terminals in simulated models of inflammatory or neuropathic hyperexcitability led to a change in the temporal pattern of AP firing, emphasizing the role of temporal code in conveying key information about changes in nociceptive output in pathologic conditions, leading to pain hypersensitivity.

SIGNIFICANCE STATEMENT Noxious stimuli are detected by terminal endings of primary nociceptive neurons, which are organized into morphologically complex terminal trees. The information from multiple terminals is integrated along the terminal tree, computing the neuronal output, which propagates toward the CNS, thus shaping the pain sensation. Here, we revealed that the structure of the nociceptive terminal tree determines the output of nociceptive neurons. We show that the integration of noxious information depends on the morphology of the terminal trees and how this integration and, consequently, the neuronal output change under pathologic conditions. Our findings help to predict how nociceptive neurons encode noxious stimuli and how this encoding changes in pathologic conditions, leading to pain.

Introduction

Peripheral terminals of nociceptive neurons are key structures in detecting, translating and transmitting noxious stimuli toward the CNS, thus setting the scene for the sensation of pain (Woolf and Ma, 2007; Basbaum et al., 2009; Dubin and Patapoutian, 2010; Gold and Gebhart, 2010; Binshtok, 2011). Single nociceptive terminals combine into complex terminals trees, which differ in number and form of their terminal branches. In some nociceptive terminal trees, the terminals do not branch after leaving a fiber and terminate at the target organ with a single terminal branch of different length (Zylka et al., 2005; Ivanusic et al., 2013; Alamri et al., 2015, 2018; Olson et al., 2017; Bouheraoua et al., 2019). Other nociceptive terminals do branch, creating a more complex termination (Ivanusic et al., 2013; Alamri et al., 2015, 2018; Olson et al., 2017). Thus, noxious stimuli activate morphologically complex excitable structures, which differ among primary nociceptive neurons. Importantly, morphology of terminal trees changes with age or under pathologic conditions (Cain et al., 2001; Chartier et al., 2018; Lakatos et al., 2020; Leibovich et al., 2020).

It has been shown that the morphology of dendrites and axons of central neurons (Manor et al., 1991; Mainen and Sejnowski, 1996; Williams and Stuart, 2003; Gidon and Segev, 2012; Jadi et al., 2012; Ferrante et al., 2013) and peripheral mechanosensitive neurons (Lesniak et al., 2014) shape their input-output properties. We, therefore, hypothesized that output of the nociceptive neuron might depend on the integration of outputs from the individual terminal branches and that this integration depends on the structure of the individual terminal and the morphology of the terminal tree.

Noxious stimuli are detected by activation of a specific repertoire of transducer channels expressed in the terminals. The biophysical properties and spatial distribution of functional transducer and voltage-gated channels expressed by nociceptive neurons are essential factors in defining the gain of the terminals, i.e., the number and pattern of action potential (AP) firing resulting from activation of the terminal by noxious stimuli (Dib-Hajj et al., 2010; Waxman and Zamponi, 2014; Goldstein et al., 2019). The current electrophysiological and imaging approaches allow studying how a single terminal encodes the information (Vasylyev and Waxman, 2012; Goldstein et al., 2019). Skin-nerve (Reeh, 1986) or teased fiber preparations (Tal and Devor, 1992) permit studying how the whole nociceptive terminal trees respond to stimulation. However, because of technical constraints, it is still unclear what is the contribution of a single terminal location and electrical properties to the output of the terminal tree and how different terminal tree architectures or a change in the specific architecture of the terminal tree relate to nociceptive function.

Here, we implemented a realistic computational model of the nociceptive terminal tree, which we build based on known terminal physiology in vitro (Vasylyev and Waxman, 2012; Goldstein et al., 2017) and in vivo (Barkai et al., 2017; Goldstein et al., 2019) to study structure-function relation of nociceptive terminals. We stimulated terminals of different terminal trees by a capsaicin-like stimulation and defined the output of the neurons by registering the resulting activity at the central terminal of the modeled nociceptive neuron. We show that the length and the axial resistance (Ra) of individual terminal branches affect the response of the whole terminal tree to a capsaicin-like current. Our model predicts that the activation of a longer terminal leads to a higher firing rate at the central terminals. Activation of the terminals with lower Ra leads to a decreased response. Our model also suggests that the activation of multiple terminals allows summation of responses of each individual terminal, thus facilitating the nociceptive response. Perturbations correlated with inflammatory and neuropathic conditions increase the gain of nociceptive input-output function and change the temporal pattern of the spike trains. Our results predict how noxious stimuli are integrated by nociceptive neurons and how structural changes of the nociceptive neurons in pathologic conditions can modify nociceptive responses.

Materials and Methods

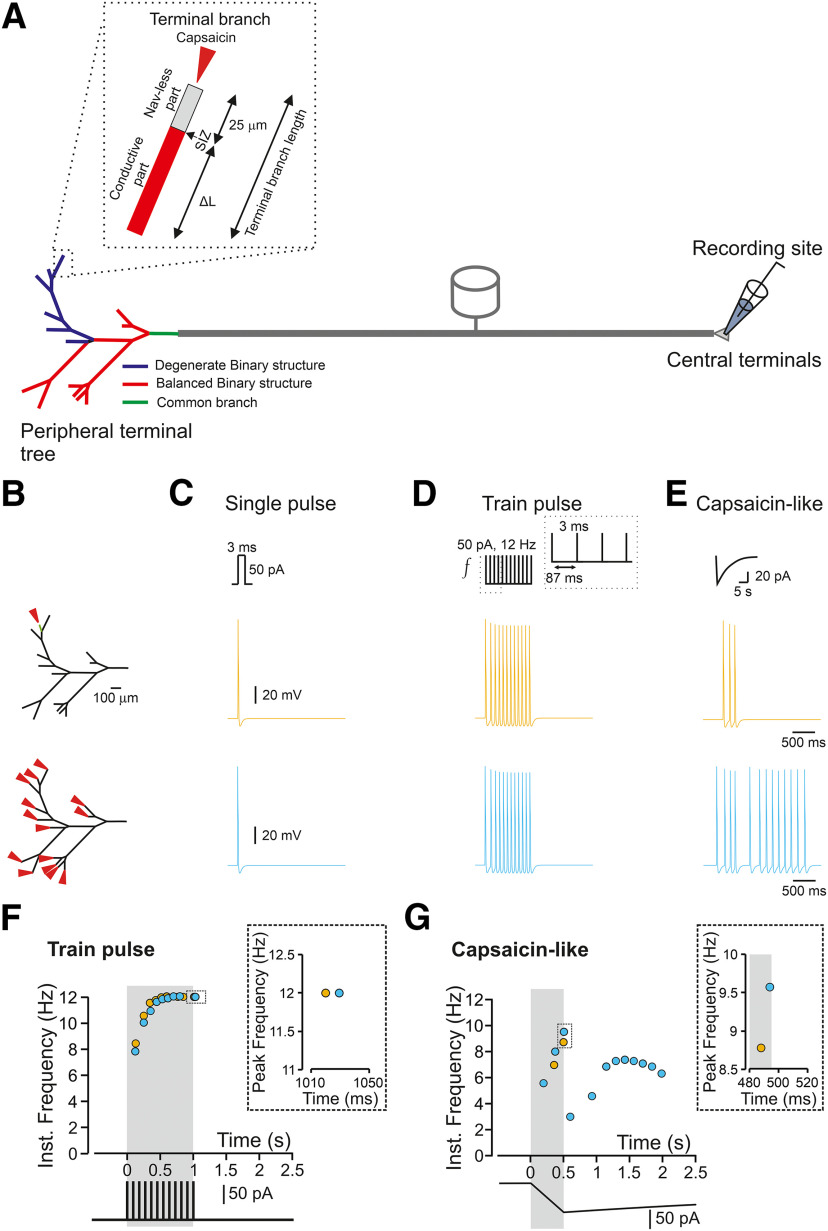
Simulations were performed using passive and active properties of the NEURON environment-based compartmental nociceptor model, which we previously developed (Barkai et al., 2017; Goldstein et al., 2019), with adaptations described below. Briefly, we developed a biophysically realistic multicompartment model of an unmyelinated axon, including the terminal tree (Barkai et al., 2017; Goldstein et al., 2019). The nociceptor morphology consisted of a 25-µm diameter soma-like compartment, connected to a stem axon expanding to peripheral and central axons which join at a T-junction bifurcation site (Fig. 1A).

Figure 1.

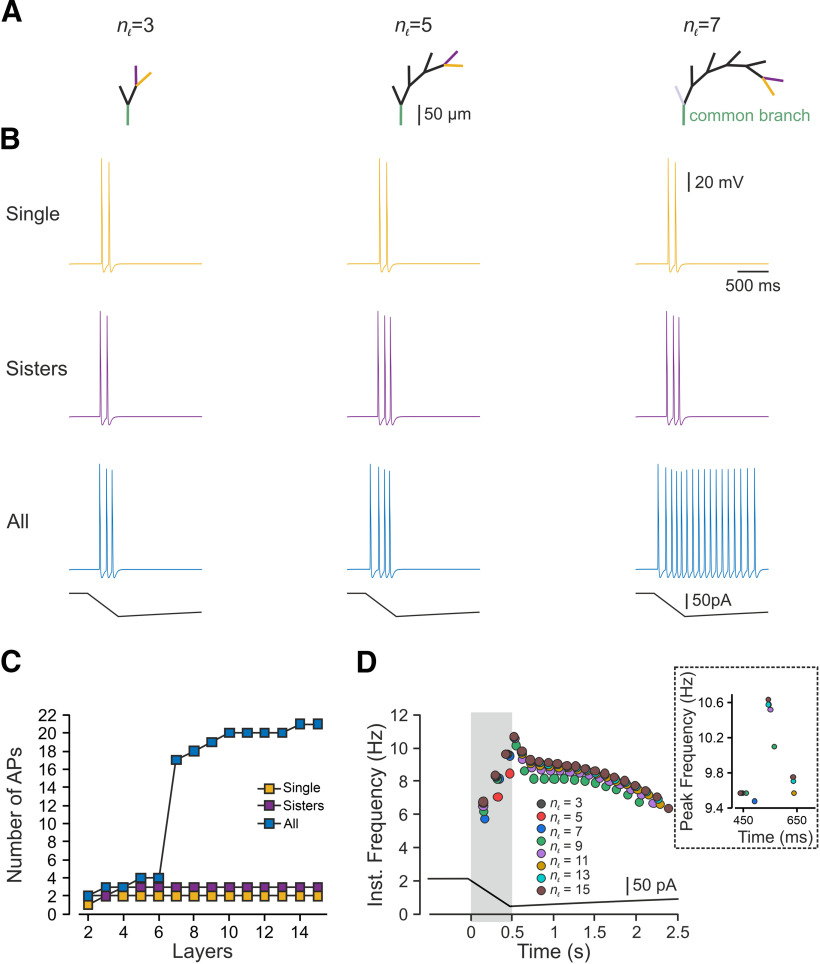
The response of a nociceptive neuron to a capsaicin-like current depends on the morphology of the nociceptive terminal tree. A, Scheme depicting the model of the primary nociceptive neuron. The peripheral terminal tree morphology is rendered from the structure of a terminal innervating glabrous skin of mice paw in vivo. The terminal tree consists of 14 terminal branches of different lengths. Inset, Functional organization of a terminal branch. The first 25 µm of each terminal branch does not express Navs (Nav-less, light gray). The Nav expression starts from the SIZ and continues for the rest of the fiber (conductive part, red). The terminal branch length is defined by the length of the conductive part, which differs among the terminals and the Nav-less part, which has a constant length of 25 µm. The complex terminal tree morphology consists of the simplified version of the balanced binary tree (red terminal branches), in which two branches converge into one node (convergence point) and a degenerate binary tree, in which one branch converges into the fiber (blue terminal branches). The terminal branches converge into the mother branches, which then converge into the common branch (green branch). The stimulations are applied to the terminal branch end (red arrow in the inset), and the recording electrode is placed at the central terminal. B, The locations of the stimulations. The stimulated terminal or all terminals are marked by the red arrows, and single stimulated terminals are color coded. C, D, Simulated voltage-clamp recordings from a central terminal following stimulation of a single terminal (yellow) and all terminals (light blue) by a single brief 3-ms square current of 50 pA (C) or train of brief 3-ms square current of 50 pA applied at 12 Hz (D). Note, no difference in firing between stimulating one or all terminals. E, Same as C, but the terminals are stimulated by simulated capsaicin-like current (see Materials and Methods). Note that in this case, the firing following stimulation of one terminal differs from the firing resulting from stimulation of all terminals. F, Instantaneous discharge frequencies following stimulation with a train of brief 3-ms square current of 50 pA applied at 12 Hz (lower inset) of a single terminal (yellow), and all terminals (light blue). Shadowed area outlines the time of the stimulation. Note, no difference in peak instantaneous frequency (upper inset). G, Same as in E but following stimulation with a capsaicin-like current (color coded as in E). Shadowed area outlines the 500 ms of a capsaicin-like current step. Note, an increase in peak instantaneous frequency when all the terminals are stimulated (upper inset, light blue).

Morphology

The morphology of the nociceptive neuron was based on our adaptation of Sundt et al.'s model of a nociceptive neuron (Sundt et al., 2015; Barkai et al., 2017). A cylindric soma (25 µm in diameter, 25 µm in length) was connected to a stem compartment (0.8 µm in diameter, 75 µm in length), which bifurcate to a T-junction, creating two branches, the first branch (0.8 µm in diameter, 100 µm in length) connected to a peripheral axon (0.8 µm in diameter, 5 mm in length) and the second branch (0.4 µm in diameter, 100 µm in length) connected to a central axon (0.4 µm, 5-mm length). All of the abovementioned compartments, apart from the soma, were subdivided into 100 segments each. The peripheral axon was then connected to a terminal tree structure, as described below.

Terminal tree structures

For the “realistic” type of the terminal tree, which was reconstructed according to one of our arbitrary experimental observations (Barkai et al., 2017), the distal axon ending tapered at its end and expanded into a terminal tree composed of 27 branches. For proper electrical propagation from the terminal tree to the peripheral axon, these two compartments were connected by a tapered cone-like axon with a linearly changing diameter over 100 µm of length.

The branches of the terminal tree were of variable lengths (50–300 μm) and of a diameter of 0.25 μm. These branches included 13 mother branches, which were connected from both ends to other branches and terminal branches, which were connected at the proximal end to a mother branch and had a free-nerve ending on the other end (Fig. 1A).

For binary tree models, balanced and degenerate binary tree structures were generated in and simulated in PyNeuron. All terminal tree branches, unless otherwise mentioned, were identical in length (50 µm). Binary tree structures were changed according to the number of their bifurcation stages (n_l), which controlled the total number of terminal branches (n_TB) according to n_TB = 2^n_l–1 (Jarvis et al., 2018).

The terminal branches of all types consisted of two sections separated by the spike initiation zone (SIZ; Goldstein et al., 2019): a 25-µm-long compartment which consisted of all the active conductances described in the “Active conductances” section, below but that did not contain voltage-gated sodium channel (Nav) conductances (Nav-less compartment) and a “conductive” compartment connecting between the Nav-less compartment and the mother branch (Fig. 1A). The conductive compartment possessed all the active conductances described in the “Active conductances” section, below. In some experiments, the length of either Nav-less or conductive compartments on all their properties was changed.

The 25-µm Nav-less compartment of the terminal branches was subdivided into 2.5-µm segments (10 segments). The conductive compartment was subdivided into 5-µm segments; thus, the number of segments changed according to the length of the compartment.

Passive membrane properties

The passive conductance equilibrium potential was set to −60 mV (Gudes et al., 2015). The simulated resting potential was −58 mV, in line with our experimental results (Barkai et al., 2017).

Membrane capacitance of 1 μF cm⁻² was set for all compartments. Passive membrane resistance of 10,000 Ω cm⁻² was set for all compartments apart from the terminal branch, which has a 4-fold somatic membrane resistance (Vasylyev and Waxman, 2012). Ra in all compartments, apart from the terminal branch, was 150 Ω cm. This is a generalized value representing the suggested Ra value for the mammalian cytoplasm (∼100 Ω cm; Jamieson et al., 2003); the Ra value for the cytosol of DRG neurons (123 Ω; Choi and Waxman, 2011) and a suggested Ra value for small-diameter fibers (200 Ω cm; Vasylyev and Waxman, 2012). The Ra of the terminal branch (Ra_TB) was set to 15-fold of Ra (Ra_TB = 2.25 MΩ cm; see Calculation of the terminal branch Ra_TB,, below). In some experiments, the value of Ra of the passive and conductive parts of the terminal branch was changed, and its effect on neuronal excitability was examined.

Calculation of the terminal branch Ra_TB

It has been demonstrated that the insertion of mitochondria into the dendrite increases Ra of the dendrite 15-fold (Bekkers, 2011). This experimental evidence is in line with our calculations for a terminal branch: we considered that the Ra of the terminal branch, Ra_TB, may be increased in a state in which the axoplasmic medium of the terminal branch is populated with intracellular organelles (i.e., mitochondria). The ratio between the axial terminal resistance with (${Ra}_{term+mit})$and without mitochondria $\left({Ra}_{term}\right)$ is inversely proportional to the axonal radial plane surface area:

$$\frac{{Ra}_{term+mit}}{{Ra}_{term}}\propto \frac{A_{term}}{A_{term}-n·A_{mit}},$$

where A represents the axonal radial plane surface, term+mit and term denote the terminal axon with or without intracellular mitochondria respectively, and $n$ is the number of mitochondria per length unit of the terminal branch, while the cylinder surface area is given by the following equation:

$$A_x=\pi r_x^2,$$

where x is a variable representing the terminal axons or mitochondrion, and $r_x$ is the radius of the specificied variable cylinder x.

In a condition in which there are no mitochondria within the terminal branch, $A_{term}\mathrm{i}\mathrm{s}$:

$$A_{term}=\pi r_{term}^2.$$

When mitochondria are present, the area is reduced by the number of mitochondria (n) aggregated within the branch compartment, depending on mitochondrion radius (r_mit), and therefore is:

$$A_{term}-n·A_{mit}=\pi r_{term}^2-n·\pi r_{mit}^2.$$

Thus, the ratio between the axial terminal branch resistance with (${Ra}_{term+mit})$ and without mitochondria $\left({Ra}_{term}\right)$ is:

$$\frac{{Ra}_{term+mit}}{{Ra}_{term}}\left(n\right)=\frac{A_{term}}{A_{term}-n·A_{mit}}=\frac{\pi r_{term}^2}{\pi r_{term}^2-n·\pi r_{mit}^2}=\frac{1}{1-n·{\left(\frac{r_{mit}}{r_{term}}\right)}^2}.$$

According to Heppelmann (Heppelmann et al., 1990) and Barrientos et al. (Barrientos et al., 2011), the mitochondrion radius in nociceptive terminals is $r_{mit}\sim 0.1\mathrm{\mu }\mathrm{m}$.

The terminal branch radius is set in our model to $r_{term}=0.25\mathrm{\mu }\mathrm{m}$ (see above, Terminal tree structures).

Finally, according to Heppelmann et al. (1994), we consider that either five or six mitochondria are situated within a length unit of a terminal axon (n = 5 or 6), assuming maximal mitochondria density in nociceptive terminal branches.

Thus,

$$\frac{R_{term+mit}}{R_{term}}\left(5\right)=5;\frac{R_{term+mit}}{R_{term}}\left(6\right)=25.$$

For a generalized approximation, we used the mean between the two cases (5 and 25):

$$\left(\frac{\overline{R_{term+mit}}}{R_{term}}\right)=15.$$

Active conductances

The model neuron of all tree structures includes the following Hodgkin–Huxley-type ion channels used in Barkai et al. (2017) and Goldstein et al. (2019):

Tetrodotoxin (TTX)-sensitive sodium current (I_NattxS), TTX-s sensitive persistent sodium current (I_NaP), Nav1.9 TTX-r sodium channels (I_Nav1.9), and Nav1.8 TTX-r sodium channels (I_Nav1.8). All channels parameters of the sodium currents were adapted from Herzog et al. (2001) and Baker (2005). Three types of potassium channels included: (1) the delayed rectifier channel (I_KDR) adapted from Herzog et al. (2001); (2) an A-type potassium channel (I_KA) adapted from Miyasho et al. (2001), whose activation and inactivation gates were shifted by 20 mV in the hyperpolarized direction to closely resemble kinetics of DRG neurons (Qu and Caterina, 2016); and (3) the Kv7/M channels which were adapted from Shah et al. (2008), and their activation curve parameters were tuned as in Barkai et al. (2017). The h-current (I_h) was also included and taken from Shah et al. (2008), the slope factor was tuned according to Komagiri and Kitamura (2003).

For simulating the excitable properties of a single-compartment neuron, we used the following fixed maximal conductance parameters:

$${\mathrm{g}}_{\text{Nav1.8}}=0.02S/c{m}^2,{\mathrm{g}}_{\text{Nav1.9}}=\mathrm{0.00,064}S/c{m}^2,{\mathrm{g}}_{\text{NaTTXS}}=0.0017S/c{m}^2,{\mathrm{g}}_{\text{NaP}}=\mathrm{0.00,005}S/c{m}^2,{\mathrm{g}}_{\text{KDR}}=\mathrm{0.00,083}S/c{m}^2,{\mathrm{g}}_{\text{KA}}=0.0015S/c{m}^2,{\mathrm{g}}_{\text{Kv7/M}}=\mathrm{0.00,034}S/c{m}^2,{\mathrm{g}}_{\text{H}}=\mathrm{0.00,033}S/c{m}^2\mathrm{.}$$

Calcium channels were adapted directly from Shah et al. (2008), and their conductance values were tuned according to the inward currents described previously (Blair and Bean, 2002). The T-type and L-type channels representing the low voltage-activated (LVA) and high voltage-activated (HVA) currents, respectively, were added with the following conductance values:

$${\mathrm{g}}_{\text{CaT}}=0.003S/c{m}^2,{\mathrm{g}}_{\text{CaT}}=0.001S/c{m}^2.$$

The reversal potentials for sodium (E_Na), potassium (E_K), and h-current (E_H) were set to +60, −85, and −20 mV, respectively. The passive reversal potential was set to −60 mV.

Apart from Nav conductances, which were unevenly distributed between Nav-less and conductive compartments, all other conductances were evenly distributed in all compartments.

The recordings were performed by positioning a NEURON “point-process” electrode at the terminal end of the central axon (Fig. 1A). In some experiments, the recording electrode was positioned at the Nav-less compartment, 2.5 µm before the SIZ or at the conductive compartment of the terminal branch, 2.5 µm after the SIZ.

Stimulation parameters

Simulations were performed, assuming a room temperature of 25°C. To avoid boundary condition problems, the stimulating electrode or capsaicin puff-like process were positioned at 10% of the terminal branch length taken from the terminal branch's tip.

For simulating an optogenetic stimulation, a short 3-ms square pulse of either 50 or 100 pA was applied into a single simplified voltage-clamp point-process at the distal end of the single or multiple terminal branches. In some experiments, these brief square pulses were applied at various frequencies.

A capsaicin-like stimulation was injected to single or multiple nerve-endings. To that end, a capsaicin-like current was introduced into a single simplified voltage-clamp point-process with fast exponential activation and slow exponential inactivation mimicking the experimental kinetics of puff-applied 1 μm capsaicin-induced current and sufficient to induce AP firing when applied onto the acutely dissociated dorsal root ganglion neuron (Nita et al., 2016). A similar current was used in Barkai et al. (2017) and Goldstein et al. (2019) to generate activity in the modeled nociceptive neuron when applied to the single 75-µm length terminal:

for t ≤ t_puff,

$$I_{Cap}=g_{Cap}\alpha \left(t-t_{onset}\right);$$

for t_puff < t,

$$I_{Cap}=g_{Cap}\alpha \left(t-t_{onset}\right)·\beta \left(t-(t_{onset}+t_{puff})\right),$$

$$\alpha \left(x_t\right)=1-e^{-\frac{x_t}{{\tau }_{\alpha }}},$$

$$\beta \left(x_t\right)=e^{-\frac{x_t}{{\tau }_{\beta }}},$$

where g_Cap is the maximal conductance, α(x_t) and β(x_t) are the activation and inactivation functions with ${\tau }_{\alpha }$ and ${\tau }_{\beta }$ as the activation and inactivation time constants, respectively. The values of the time constants were:

$${\tau }_{\alpha }=1\cdot {10}^6\mathrm{m}\mathrm{s},{\tau }_{\beta }=6500\mathrm{m}\mathrm{s},$$

t_onset and t_puff are the times at which the puff application simulation begins and the length of application, respectively.

To mimic the changes in membrane resistance following the opening of TRPV1 channels, the capsaicin-like current injection was accompanied by an opening of passive transducer channels (Goldstein et al., 2019). The conductance to this channel (${\overline{g}}_{Trans}$) was exponentially distributed and the exponential decay constant ($\gamma )$ was calculated to fit the diffusion of capsaicin and hence change in its concentration as a function of distance from the pipette tip as was previously calculated in Goldstein et al. (2017). In the experiments where the length of the terminal branches was changed, the distribution of the transducer conductances was adapted accordingly.

The final transducer distribution equation introduced into the model was:

$$g_{Trans}\left(x\right)={\overline{g}}_{Trans}·e^{-x/\gamma },$$

where x is the distance from the nerve ending, and the fixed parameters were:

$${\overline{g}}_{Trans}=0.0025S/c{m}^2,$$

$$\gamma =7.04\mu m.$$

Randomized onset timing

Onset time was generated with an addition of a normal distribution randomize value $N_R:$

$$T_{Rand}=T_{Onset}+{|N}_r\left(\mu ,{\sigma }_r\right)|,$$

where $\mu$ is the mean (and set to zero) and ${\sigma }_r$ is the SD. We modified the value of ${\sigma }_r$ to generate randomized onset timing. The randomized part of the equation was an absolute value since the onset of stimulation cannot occur before the stimulation time. Each generated stimulation was then applied to a single terminal.

“Inflammation” (SIZ shift) model

To simulate inflammatory hyperalgesia, we mimicked the distal shift of the SIZ (Goldstein et al., 2017) by shortening of the Nav-less compartment from its normal 25-µm lengths to 20 µm. The terminal's conducting compartment was elongated by the same length reduced from the passive compartment, leaving the total terminal length at a constant value. All the active and passive parameters were modified accordingly.

“Neuropathic pain” (noise) model

To simulate nerve injury-mediated hyperalgesia, an external noise conductance was incorporated into all terminal tree branches as previously described (Olivares et al., 2015; Barkai et al., 2017). The noise was injected into the whole terminal tree and was based on the Ornstein–Uhlenbeck process with a mean 0, and the current was taken from Olivares et al. (2015):

$$\frac{d{I}_{Noise}}{dt}=\frac{-I_{Noise}+\sigma N\left(t\right)}{{\tau }_{No\mathrm{i}se}},$$

where σ is the square root of the steady-state variance of the current amplitude; N is a normally distributed random variable with zero mean and variance = 1, and τ is the steady-state correlation time length of the current (was fixed to 1 ms).

Data analysis

To avoid artifacts resulting from the artificial instability of the NEURON simulation environment before reaching steady-state, we have allowed a long 500-ms initialization time before stimulation of the simulated neuron, and this time was discarded from the analysis.

Unless otherwise stated, the firing patterns were recorded from the central terminal compartment. Instantaneous spike frequencies were analyzed and plotted as previously described by Zimmermann et al. (2009).

All datasets generated during and/or analyzed during the current study are available in the main text or on request. The model files are uploaded to Model DB and are also available on request.

Results

Nociceptive terminal trees are complex structures composed of individual branches of different lengths and complexity (Treede et al., 1990; Zylka et al., 2005; Ivanusic et al., 2013; Alamri et al., 2015, 2018; Olson et al., 2017; Bouheraoua et al., 2019). The terminal branches, which ends at the target organ and detect the noxious stimuli consist of (1) the terminal, which is activated by noxious stimuli; (2) the passive part, an initial 20–30 µm of the terminal branch, in which the depolarization, resulting from the terminal activation, propagates without involving Navs; and (3) the conductive part where propagation is active as it involves Navs (Goldstein et al., 2019). The length of the terminal and the passive part of the terminal branch is similar among different terminals (Goldstein et al., 2019); thus, the length of the conductive part defines the overall length of the terminal branch. The terminal branches converging onto the fibers constructing the nociceptive terminal tree (Belmonte et al., 2004). To examine the effect of the morphology of the nociceptive terminal trees on their coding properties, we adapted a computational model of the nociceptive nerve fiber, which we previously described (Barkai et al., 2017; Goldstein et al., 2019). In this model, we first based the geometry of the terminal tree on the rendering of a nociceptive terminal tree visualized using in vivo two-photon microscopy (Barkai et al., 2017). The complex structure of the realistic modeled terminal tree can be simplified and represented as a combination of different “tree data structures”: a balanced binary tree, where each branching point, a node, bifurcates into two branches (Fig. 1A, red branches) and a degenerate binary tree, where each node gives rise only to one branch (Fig. 1A, blue branches). The nodes are branching points from an anatomic point of view. However, from a physiological point of view, these nodes in afferent neurons serve as merging or convergence points of voltage deflections from the converging terminal branches.

We adapted the physiological properties of the terminals from data obtained from recordings of capsaicin-mediated activity of corneal nociceptive terminals in vivo (Goldstein et al., 2019). Specifically, the contribution of Navs begins only 25 µm proximal to the terminal tip (Nav-less compartment; Fig. 1A, inset); thus, the SIZ is located 25 µm from the tip (Goldstein et al., 2019). Also, we increased the Ra of the terminal branches to reflect the presence of intracellular organelles, such as mitochondria (Heppelmann et al., 1994, 2001; Müller et al., 1996; Alamri et al., 2018). In these conditions, the AP conduction velocity along the terminal branch was 0.04 m/s, and the refractory period for a 3-ms, 50-pA stimulus was 49 ms. The refractory period in nociceptive c-fibers, obtained by stimulating the central process and recording from cell somata, was shown to vary between 4 and 45 ms (Gemes et al., 2013).

We first compared the nociceptive output following activation of a single terminal activation of all the terminals in the realistic terminal tree to examine how the structures of terminal trees affect the gain of the nociceptive neurons, i.e., the relation between the stimuli and the resulted AP firing (Kispersky et al., 2012). We activated the terminals with simulated rectangular or capsaicin-like currents (see Materials and Methods) and monitored the resulting activity by measuring the number of APs and their instantaneous frequency at the central terminal (see Materials and Methods; Fig. 1A). The stimulation was applied at the tip of a random terminal or all the terminals (Fig. 1B, red arrowhead; see Materials and Methods). First, we simulated the activation of a single terminal (Fig. 1B,C, green) with a length of 75 µm (25 µm of the Nav-less compartment + 50-µm conductive compartment; Fig. 1A, inset) using a brief (3 ms) suprathreshold (50 pA) rectangular current. We chose these parameters since the optogenetic stimulation of similar duration was sufficient to generate a single AP (Browne et al., 2017). Indeed, the stimulation of this terminal with a single short current pulse produced a single AP at the central terminal (Fig. 1C, upper panel, green). We next simulated the state in which the stimulus affects a wider area and simultaneously activates all terminals in the same receptive field (Treede et al., 1990). We asked whether stimulation of multiple terminals would amplify the resulting response of a nociceptive neuron. We simultaneously stimulated all terminals from the same fiber by a brief suprathreshold stimulus and showed that still only one AP was recorded at the central terminal (Fig. 1B,C, lower panel, light blue). These results are in line with recent findings showing that a 3-ms optogenetic stimulation of the terminal tree, which is not restricted to a single terminal branch, leads to the generation of one AP at the DRG soma (Browne et al., 2017).

Train of short single- AP-generating stimuli applied to a single terminal at 12 Hz produced a train of APs at the central terminals with identical frequency (Fig. 1D, upper panel, green). Moreover, the application of brief multiple stimuli to all terminals (Fig. 1D, lower panel, light blue) did not produce any increase in the number of APs fired. The simultaneous stimulation of all terminals also failed to produce a further increase in the firing frequency (Fig. 1F). The gradual increases of the instantaneous frequency toward the stimulation frequency (Fig. 1F) was not observed when recordings were performed from a single stimulated terminal before a conversion point but became apparent only when recordings were performed after the first conversion point and toward the central terminal (data not shown). Therefore, it is probably caused by the terminal tree's geometrical irregularity, such as successive arborizations, which may affect the velocities of APs (Manor et al., 1991). The increase in the stimulus amplitude to 100 pA also did not change the output of the terminals such that the modeled cell fired 12 APs for a 12-Hz stimulation (data not shown). These data suggest that activation of a single terminal by brief stimuli conveys the information similar to the information integrated from multiple terminals.

However, we previously showed that stimulation of a simulated single terminal by a prolonged continuous capsaicin-like current leads to firing of up to five APs (Goldstein et al., 2019). Recordings from C and Aδ fibers in skin-nerve preparation or teased fiber preparation showed that application of noxious stimuli to a receptive field, i.e., activation of multiple terminals, lead to a much higher AP firing (Levy et al., 2000; St Pierre et al., 2009; Zimmermann et al., 2009; Murthy et al., 2018; Vandewauw et al., 2018). These results, which describe the activation of the whole receptive field by a prolonged “natural” stimulus, suggesting that activation of multiple terminals by prolonged stimuli may lead to a summation of the responses and overall increase in AP number. To examine this statement, we stimulated either a single terminal or all the terminals by a simulated capsaicin-like current (Fig. 1E; see Materials and Methods) to mimic the natural activation of TRPV1 channels located at the terminals (Goldstein et al., 2019). The simulated capsaicin current (Fig. 1E) was modeled from a current evoked following a 500-ms puff application of 500 nm capsaicin, recorded from acutely dissociated nociceptive DRG neurons, held at −65 mV (Nita et al., 2016; Barkai et al., 2017; Goldstein et al., 2019). Stimulation of a single 75 µm terminal with a capsaicin-like current triggered three APs at the central terminal (Fig. 1E, upper panel, yellow). Importantly, stimulation of all terminal branches with the same capsaicin-like current substantially increased the AP firing (13 APs; Fig. 1E, lower panel, light blue), amplified the firing frequency (Fig. 1F), and shortened the first spike latency (191 ms when all terminals are stimulated vs 345 ms when only single terminal was stimulated).

These data predict that stimulation of multiple terminals by prolonged capsaicin-like current facilitates the response by increasing the firing and response frequency, differently from the activation by brief current pulses. This implies that longer activation of the terminal tree might increase the nociceptive response.

The activation of all terminals introduces a number of variables that may underlie the increased nociceptive output: (1) the increase in firing following stimulation of all terminals may result from the integration and summation of the responses from individual terminals at the convergence points; (2) since the structure of the tree is asymmetrical, the distance of the individual terminal from the common convergence point is different; thus the effect of the closest terminal may affect the overall nociceptive response; and (3) stimulation of all terminals activates terminals with different electrical properties, e.g., different length of the conductive part, which may contribute to the difference in the activation of a single terminal to that of multiple terminals. We, therefore, systematically studied the effect of these factors on nociceptive gain.

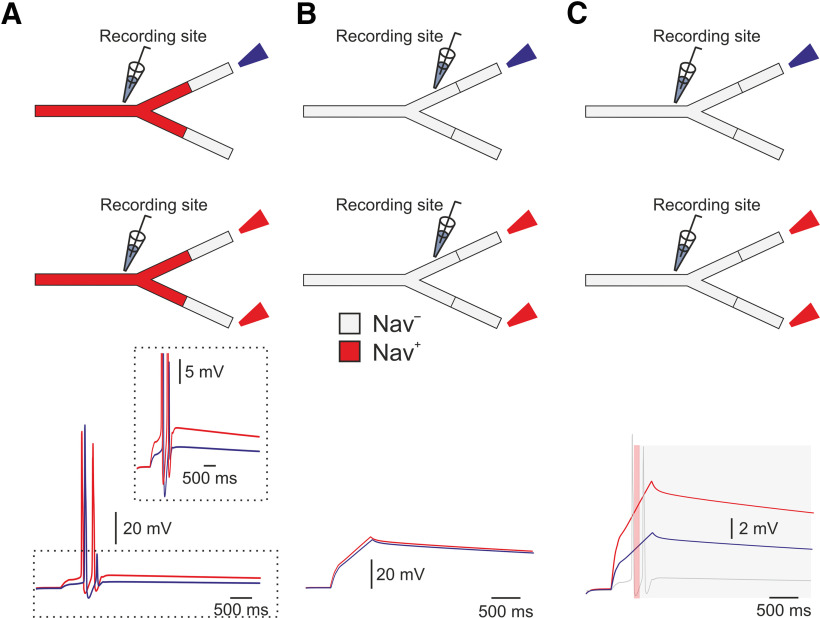
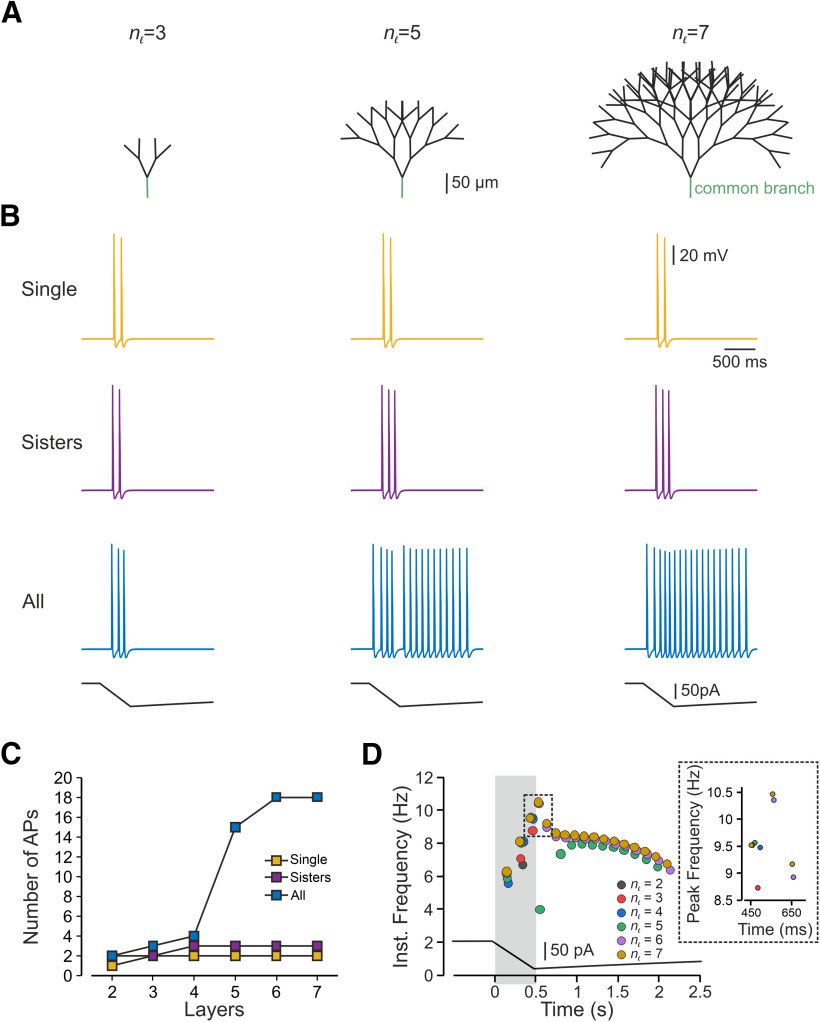
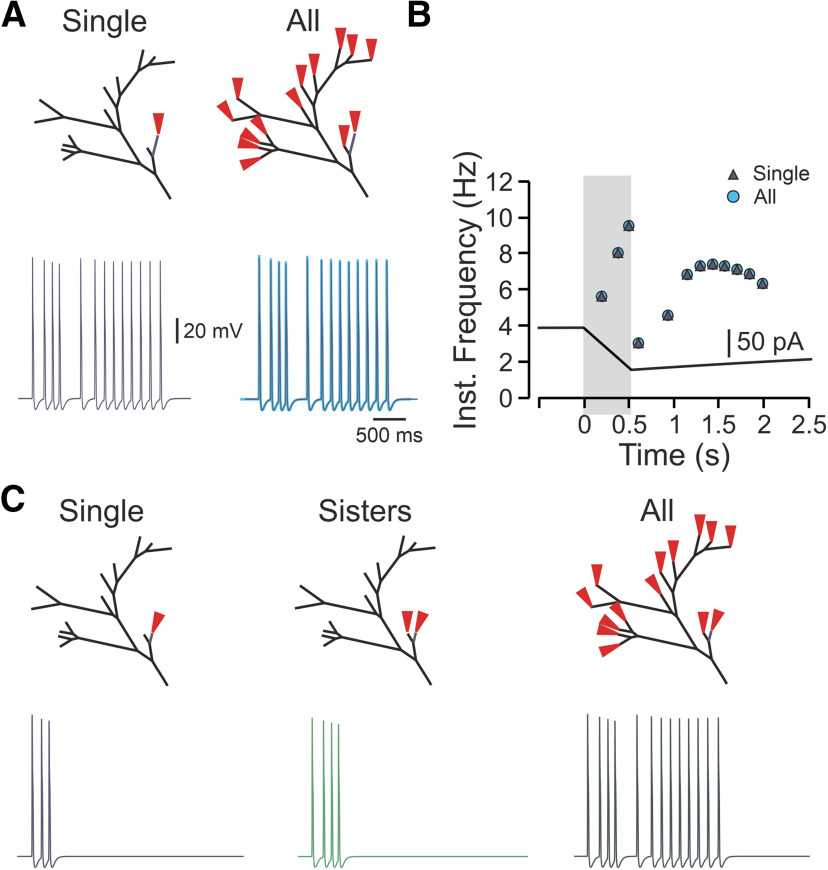
To prevent an effect of asymmetry in length and in the terminal location on nociceptive excitability and to examine only the effect of a number of activated terminals, we studied the impact of multiple stimulations on the symmetrical (balanced) binary trees (Fig. 1A, red branches) with similar terminal branch lengths. First, we applied a capsaicin-like current to either one or both terminal branches of a simple, symmetrical, balanced binary tree containing only one node and two symmetrical branches (Fig. 2A, upper panel). We measured the resulting changes in terminal voltage after the convergence point. Stimulation of a single terminal resulted in a single AP (Fig. 2A, bottom, blue trace). Simultaneous stimulation of both terminals by a capsaicin-like current generated two APs (Fig. 2A, bottom, red trace). This result is unexpected, as we assumed that at the convergence point, only one AP would propagate, resetting the other branches (Weidner et al., 2003; Gemes et al., 2013). We hypothesized that stimulation with a prolonged capsaicin-like current, differently from stimulation with a brief square-like current, might induce a long-lasting after-AP depolarization that persists after a refractory period of the first AP is over. In the case of a single stimulus, this after-AP depolarization may not be sufficient to generate additional AP. Simultaneous stimulation of both terminals might lead to the summation of an after-AP depolarization from two terminal branches, which, in this case, maybe suprathreshold and sufficient to generate a second AP. To examine this hypothesis and to examine whether, indeed, simultaneous stimulation facilitates after AP depolarization, we measured the voltage deflection resulting from a single stimulus or simultaneous stimulation of two terminals. To prevent the effect of Navs on the voltage deflection, we removed all Nav conductances from the simulation. Simultaneous stimulation of two terminals did not affect the voltage deflection measured at the SIZ of each of the branches (Fig. 2B) but substantially increased the voltage deflection after the convergence point (Fig. 2C). The summated voltage deflection persisted (Fig. 2C, gray shadowed area), succeeding the refractory period of the AP (49 ms; Fig. 2C, red shadowed area). These data suggest that an increase in the number of activated terminals facilitates nociceptive activation, by allowing the summation of the depolarizations from the converging terminal branches. To further validate this conclusion, we increased the complexity of the balanced binary tree type of the nociceptive terminal (Fig. 3). We systematically examined the activation of a single terminal branch, the simultaneous stimulation of two adjacent (sisters) terminal branches and all terminal branches at the terminal trees composed of a different number of terminal branches (n_TB) defined by the number of the “bifurcation stages” (n_l) according to n_TB = 2^nl–1 (Fig. 3A; see Materials and Methods; Jarvis et al., 2018). Activation of a single terminal branch by a capsaicin-like current in a n_l = 2 tree with two terminals, evoked one AP at the central terminal (Figs. 2, 3C) and two APs in more complex trees (Fig. 3B,C, yellow). As our model predicts (Fig. 2), activation of two (sister) terminals led to a moderate increase in firing at the central terminals (Fig. 3B,C, purple).

Figure 2.

Stimulation of multiple terminals allows summation of the voltage and facilitates nociceptive response. A, upper, Scheme depicting the experimental conditions: either one (blue) or both (red) 75-µm length terminal branches converging into the same convergence point in the symmetrical binary tree were stimulated by a capsaicin-like current. Lower, Resulted response recorded after the convergence point. Note that simultaneous activation of both terminals generated two APs (red trace), with higher after depolarization (inset). B, With all the Nav conductances annulled, activation of either one or two terminals with a capsaicin-like current produced similar depolarization measured before the bifurcation C, Activation of two terminals led to substantially higher depolarization (red) after the converging point than activation of only one terminal (blue). The AP firing following activation of two terminals, shown in A, is superimposed with the voltage traces to show that the depolarization evoked by the activation of two terminals remained high also at the time after the refractory period of the AP. The red shadowed area outlines the refractory period (49 ms), and the gray shadowed area outlines the time of the summated post-AP depolarization.

Figure 3.

In a symmetrical nociceptive terminal tree, an increased number of stimulated terminals facilitates nociceptive response. A, Scheme depicting the model of the symmetrical binary trees of different complexities determined by the number of bifurcation stages (n_l; see Materials and Methods), which defines the number of terminal branches. B, Responses detected at the central terminal following stimulation of either single terminal branch (yellow), pair of sister terminal branches converging into the same converging point (purple) and all terminals (blue) by a capsaicin-like current (depicted below the traces) applied to the representative n_l = 3, n_l = 5, and n_l = 7 trees. C, Number of APs plotted as a function of the number of bifurcation stages, following stimulation of a single terminal branch (yellow), pair of sister terminal branches converging into the same convergence point (purple) and all terminals (blue) by a capsaicin-like current. D, Instantaneous discharge frequencies following stimulation with a capsaicin-like current (shown below) applied to all terminals of the trees of different complexity (n_l). Inset, Peak instantaneous frequency (color coded as in D).

Activation of all terminals led to a substantial increase in the number of AP than activation of a single terminal in all examined trees (Fig. 3B, blue). Importantly, as the complexity increased, i.e., the number of the terminal branches increased, activation of all terminals led to a rise in AP firing at the central terminal (Fig. 3B,C, blue) with increased firing frequency (Fig. 3D). It is noteworthy that although the number of AP changes considerably between stimulations of terminal trees of different complexity, the instantaneous frequency and peak instantaneous frequency change a little (Fig. 3D). Together, the results from the symmetrical terminal tree analysis suggest that stimulation of more terminals (activation of a larger area or area with higher terminal density) leads to increased response. It also implies that an increase in terminal complexity might facilitate nociceptive gain.

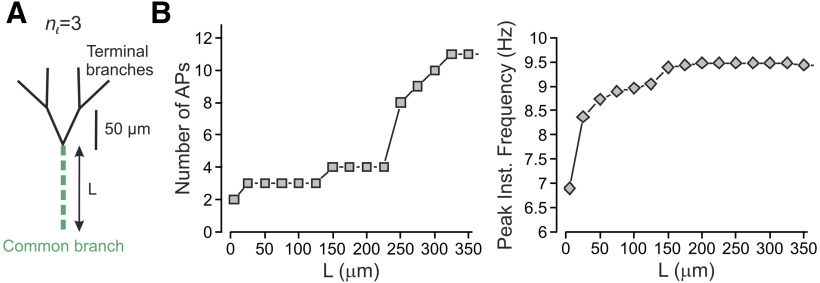
From a mechanistic point of view, the increase in gain in terminal trees with more bifurcation stages could be because of, as our model predicts, the depolarization summation at the convergence points (Fig. 2) or an increase in the length of Nav-expressing compartments of the terminal tree, which elongates as the tree complexity increases (Fig. 3). The elongation of Nav-expressing components was shown to increase neuronal excitability (Kuba et al., 2006). To distinguish between the effect of the activation of multiple branches and that of the length on nociceptive gain, we simultaneously stimulated all four terminals of n_l = 3 tree while changing the length of the common branch (Figs. 3A, green branch. 4A, green dashed line). In our model, the common branch is a part of the terminal tree. Accordingly, it possesses all the electrical properties of the mother branches and has a diameter of 0.25 µm. The common branch is connected to the thicker fiber (0.8 µm in diameter) by a tapered cone-like axon with a linearly changing diameter. Our data show that an increase in the length of the conductive components indeed leads to an increase in firing and frequency, at the central terminal (Fig. 4B), suggesting that the increase in overall length of Nav-expressing compartment of the terminal tree plays a role in the increased gain at the more complex terminals. However, the increase in length could account only for part of the increase in gain as stimulation of all terminals in a n_l =3 tree with a length equivalent to the length of a n_l = 7 tree (350 µm), although led to more firing than that of the shorter n_l = 3 tree, generated less firing than activation of all terminals in a n_l = 7 tree of the same length (11 vs 18 APs, Fig. 4B, left; see also Fig. 3C). Together, our data predict that activation of more terminals will lead to an increase in AP firing at the central terminal because of the summation of the depolarization at the convergence points, which in case of multiple terminal activations would “meet” higher Nav conductance, leading to more firing.

Figure 4.

Complex terminal trees affect nociceptive gain partially by virtue of the length of their conductive parts. A, Scheme of the experiment, the length of the common branch (green) was changed without changing the number of terminal branches. All terminals were simultaneously stimulated by a capsaicin-like current, and the resulted activity was measured at the central terminal. B, Number of APs recorded at the central terminal (left) and their peak instantaneous frequency (right) plotted as a function of the length of the common branch.

In addition to the balanced binary tree, the realistic terminal tree also consists of a part that can be simplified to a degenerate binary type of terminal (Fig. 1A, blue branches). In this type of binary tree, each node gives rise only to one terminal branch of a similar length (Fig. 5A). We examined the impact of the complexity of this type of terminal structure on its encoding properties. We used a degenerate tree with branches of a similar length (Fig. 5A), thus avoiding possible effects of the length of the terminal branch on the gain. Activation of all terminals in the degenerate tree led to a substantially higher number of APs than activation of a single terminal (Fig. 5A, yellow terminal), or sister terminals (Fig. 5A, yellow and purple terminals), in all examined trees (Fig. 5B). Also, in terminals with more bifurcation stages, the activation of all terminals led to increased AP firing at the central terminal (Fig. 5B, light blue), with increased firing frequency (Fig. 5B–D). These data suggest that in the degenerate terminal tree, activation of more terminals facilitates the response, similar to the balanced binary type of terminal tree. However, here, in addition to the number of convergence points, and the overall length of the Nav containing components, an additional level of complexity exists. In the balanced binary tree, the distances between each single terminal end to the beginning of the common branch are equal (Fig. 3A) such that the generated responses would arrive at the convergence points at the same time. In the degenerate binary tree, however, the distance between the different terminals to the common branch (Fig. 5A, green branch) are different (for example, the difference at a distance to a common branch between yellow and light blue terminals in Fig. 5A, n_l = 7 tree). This suggests that the signals from the simultaneously activated terminals would arrive at the common branch at different times and if one of the branches is situated closer to the common convergence point, the APs generated at this branch would reach the common convergence point before the APs generated by other terminals which are situated further away. The AP generated at the closest terminal branch would propagate both orthodromically and antidromically, on reaching the convergence point. In the latter case, it would render the rest of the terminal tree inactive, by inactivating Navs, and if the firing and following inactivation are long enough, it may prevent APs from other terminal branches to reach the central terminal. We stimulated the closest terminal to the common branching point of the realistic terminal tree with a capsaicin-like current to examine whether, indeed, the stimulation of the branch closest to the common convergence point would take over the activation of the whole terminal tree (Fig. 6A, deep navy-blue terminal). This terminal was of 175-µm length, and its activation led to the firing of 13 APs, which indeed reached the central terminal faster than other terminals (191 vs, for example, 345 ms from the terminal shown in Fig. 1A, bottom) and at the same time as when all the terminals were active (191 ms, both). Moreover, the activation of the closest terminal led to an identical pattern of firing to the firing evoked by stimulation of all terminals (Fig. 6A, right, B). These data suggest that the location of the terminal relative to the common convergence point is important in defining the effect of a terminal on nociceptive firing. We next examined how activation of other terminals contributes to nociceptive activity when the closest terminal does not produce dominant firing. The shortening of the closest terminal to 75 µm evoked three APs following activation by a capsaicin-like current (Fig. 6C, deep navy blue), and activation of sister terminals evoked four APs (Fig. 6C, green). In this case, activation of all terminals produced a firing of 13 APs (Fig. 6, dark green), leading to the facilitation of nociceptive response. The results of this experiment predict that the location of an individual terminal is important in defining the overall contribution of this terminal to the nociceptive response. The results showing that activation of terminals of different length (75 vs 175 µm) evoke different firing also suggest that apart from the location, the electrical properties of the individual terminals affect the nociceptive gain.

Figure 5.

In an asymmetrical degenerate nociceptive terminal tree, an increased number of stimulated terminals facilitates nociceptive response. A, Scheme depicting the model of the degenerate binary trees of different complexities determined by the number of bifurcation stages (n_l; see Materials and Methods), which defines the number of terminal branches. B, Responses detected at the central terminal following stimulation of either single terminal branch (yellow), pair of adjacent terminal branches (purple) and all terminals (blue) by a capsaicin-like current (depicted below the traces) applied to the representative n_l = 3, n_l = 5, and n_l = 7 trees. C, The number of APs plotted as a function of the number of bifurcation stages, following stimulation of a single terminal branch (yellow), pair of adjacent terminal branches (purple) and all terminals (blue) by a capsaicin-like current. D, Instantaneous discharge frequencies following stimulation with a capsaicin-like current (shown below) applied to all terminals of the trees of different complexity (n_l). Inset, Instantaneous peak frequency (color coded as in D).

Figure 6.

The location of a single terminal branch defines its contribution to the terminal response. A, upper panels, Schemes depicting the locations of the stimulation. Left lower panel, AP firing detected at the central terminal following stimulation of single 175 µm terminal branch located close to the terminal branch (navy blue terminal at the upper panel). Right lower panel, Superimposition of the traces obtained following stimulation of all terminal branches (light blue) and stimulation of a single 175-µm terminal branch shown in the left. Note that the firing is identical. B, Instantaneous frequencies plotted as a function of time, following stimulation by a capsaicin-like current of a single 175-µm terminal branch shown in A, left (navy blue triangle), or all terminal branches (light blue circle). Shadowed area outlines the 500 ms of a capsaicin-like current step. C, Same as A, but the terminal stimulated in A was shortened to 75 µm. The stimulation of this terminal branch resulted in the firing of three APs (lower left). The stimulation of this terminal branch, together with the similar adjacent terminal branch, led to the generation of four APs (lower middle) and was substantially lower than the firing resulted from stimulation of all the terminal branches (lower right).

We, therefore, examined the effects of the properties of individual terminals on the nociceptive gain. Nociceptive terminal trees are composed of terminal branches with different lengths and thicknesses (Zylka et al., 2005; Ivanusic et al., 2013; Alamri et al., 2015, 2018; Olson et al., 2017; Bouheraoua et al., 2019). Application of a simulated capsaicin-like current produced a variety of responses depending on the length of the individual stimulated terminals. Stimulation of the shortest single terminal (total length of 75 µm) triggered three APs at the central terminal (Fig. 7A). The same stimulation applied to a longer adjacent (distance-wise from the common branch), terminal produced a substantially higher firing at the central terminals (Fig. 7B), culminating at 13 APs following stimulation of the longest 175 µm terminal (Fig. 7C). The longest terminal was situated at the farthest distance from the common branch, suggesting that in addition to the location of the individual terminal, the length of the terminal branch is one of the factors defining the terminal gain.

Figure 7.

The length of the terminal branch affects the response to a capsaicin-like current. A–C, Simulated voltage-clamp recordings from a central terminal following stimulation of single terminal branches of different length [75 µm (yellow, A), 100 µm (green, B), and 175 µm (blue, C)], by a capsaicin-like current. Note that the firing depends on the lengths of the stimulated terminal branch.

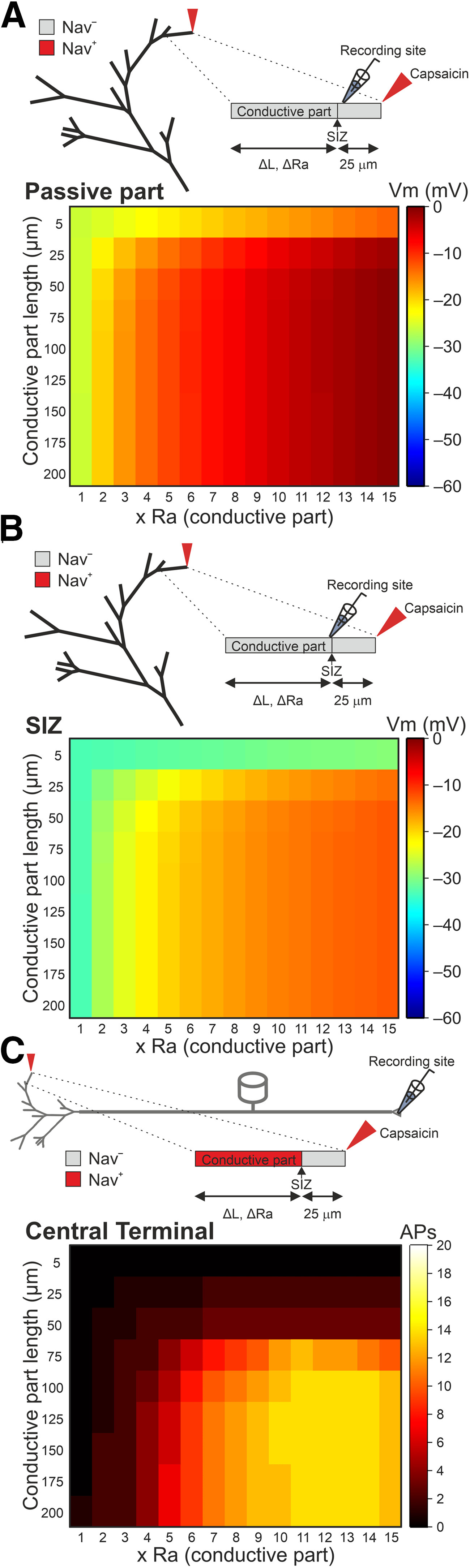
In our model, each terminal consists of two parts: a 25-µm, constant length distal “passive” part, which receives the stimulation, and does not contain Navs (Goldstein et al., 2019). The subsequent conductive part contains Navs, and it varies in length before it converges onto the fiber (Fig. 1A). In order to reflect the presence of intracellular organelles within the terminal branch (Müller et al., 1996; Bekkers, 2011; Alamri et al., 2018; Goldstein et al., 2019), we increased the Ra of the terminal branch (Ra_TB) 15 times that of the value of the fiber (Bekkers, 2011; Goldstein et al., 2019). In this respect, the passive part of the terminals, which receives the stimulus and is connected to the highly resistive conductive part, is somehow similar to a “head” of the dendritic spine connected to the spine neck (Nimchinsky et al., 2002). Accordingly, the voltage response of the passive part to a capsaicin-like current is dependent on its own resistive properties. The Ra of the passive part will determine its length constant and, therefore, will define how the capsaicin-like current-induced voltage deflection decays along the terminal. Indeed, when Ra of the passive part was equal to the fiber Ra, the voltage deflection (ΔVm, V – Vrest) measured at the SIZ, was ∼70 mV. When we increased the Ra of the passive part, the ΔVm decreased progressively, such that when Ra of the non-conductive part was 5-fold that of the fiber, ΔVm became 51 mV; for 10-fold, it became 38 mV; and at 15-fold that of the fiber, ΔVm became 29 mV. Additionally, the voltage response of the passive part may also depend on the Ra of the consecutive conductive part, such that, similarly to a spine head and neck, a high Ra component of the conductive part would lead to higher voltage deflection at the SIZ and hence a higher firing, by effectively decreasing the current sink (Segev and Rall, 1988). Consequently, we examined capsaicin-induced voltage deflection along the terminal branch, by stimulating the tip of the terminal by a capsaicin-like current and monitoring the resulting voltage deflection at the passive part, 2.5 µm before the SIZ (Fig. 8A) and at the SIZ, while changing the Ra of the conductive part (Fig. 8A,B). We removed all Nav conductances from the conductive part, to eliminate the effect of Nav activation and APs on the voltage deflection. To examine how voltage deflection at the SIZ affects the AP firing at the central terminal, we added back in the Nav conductances (Fig. 8C). When the Ra value of the conductive part was 15 times that of the fiber, stimulation of the terminal tip with a capsaicin-like current produced a voltage deflection of ∼60 mV, depolarizing the membrane potential (Vm) of the terminal end to 0 mV, which is equivalent to TRPV1's reversal potential (Fig. 8A). At the SIZ, the voltage deflection was smaller, probably because of the voltage decay resulting from the small space constant, reaching Vm_SIZ of –12 mV (Fig. 8B). This depolarization at the SIZ was sufficient to produce an excessive firing at the central terminal (13 APs; Fig. 8C). Reduction of the conductive part's Ra to that of the fiber's led to a smaller depolarization (ΔVm_Tip of 35 mV) at the terminal tip (Fig. 8A) and at the SIZ (ΔVm_SIZ of 25 mV; Fig. 8B). In these conditions no APs were evoked by stimulation with capsaicin-like current when Nav conductances were turned back on (Fig. 8C). These data predict that changes in Ra, solely in the conductive part, may strongly affect the terminal membrane depolarization and AP firing.

Figure 8.

The Ra of the terminal branch's conductive part determines the nociceptive gain. A, upper, Scheme of the stimulated terminal branch with the location of the recording pipette 2.5 µm before the SIZ. The Nav conductances at the conductive part were annulled to prevent the effect of the APs on the measurements of the terminal membrane potential. Lower, Heatmap representing the relation between the Ra of the conductive part (Ra), the conductive part length, and the depolarization of the terminal membrane recorded at the Nav-less part, 2.5 µm before the SIZ. The resulted membrane potential is color coded (shown on the right). Note that when the Ra of the conductive part is similar to the Ra of the proximal fiber (1 × Ra), the depolarization resulted from the application of a capsaicin-like current to the terminal tip is substantially lower than when Ra is higher. B, Same as A, but the recordings are performed at the SIZ. C, The relation between the Ra of the conductive part (Ra), the conductive part length, and the AP firing measured at the central terminal following stimulation of a single terminal. The Nav conductance of the conductive part is intact. The AP count is color coded (shown on the right).

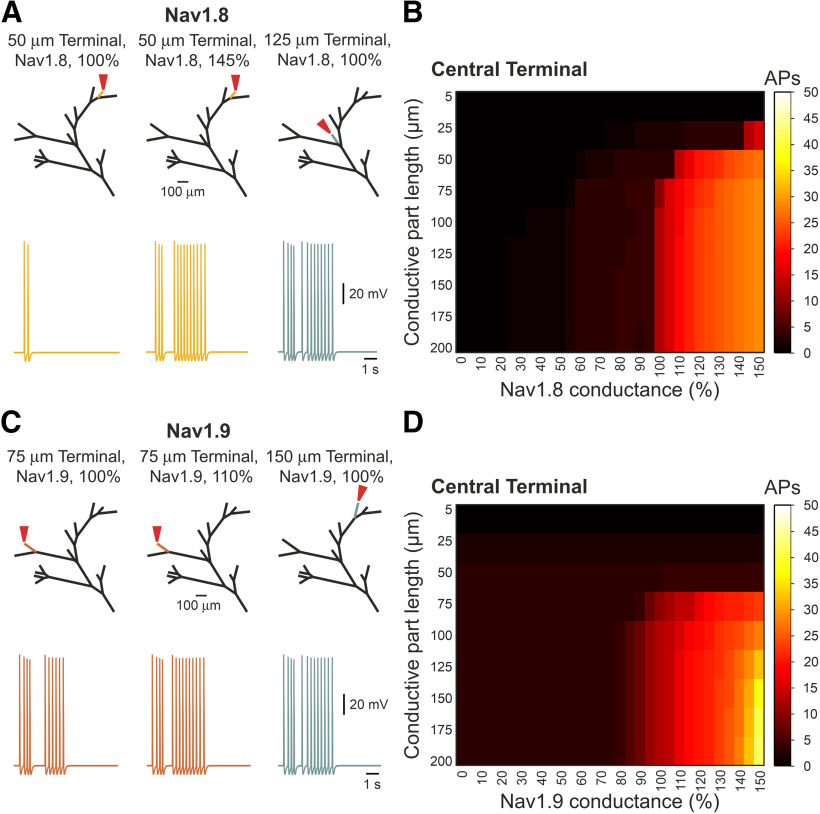
These results, however, do not explain the increase in firing when longer terminals are stimulated (Fig. 7) since all the terminals had a similar Ra. Indeed, the effect of length on the firing at the central terminals was independent of Ra values, and at any given Ra, the change in length of the conductive part affected the firing at the central terminal in a sigmoidal manner as the length increased (Fig. 8C). The shortening of the conductive terminal part below 25 µm prevented the generation of APs at all Ra values, whereas the elongation of the conductive part led to the increase in the firing at the central terminal, which peaked and plateaued when the conductive part was of 125 −150 µm (Fig. 8C). It has been shown that the length of the SIZ of central neurons defines neuronal excitability, by virtue of the amount of Nav conductance (Kuba et al., 2010). Our model suggests that an increase in the length of the Nav containing components enhances nociceptive gain (Fig. 4). Consequently, we examined whether the change in length of the terminals regulates the terminal gain through changes in Nav conductance. Nociceptive neurons express a variety of sodium channels. Among them, slow Nav1.8-mediated sodium current which defines the ability of a nociceptive neuron to fire repetitively (Blair and Bean, 2003). Persistent Nav1.9-mediated sodium current controls subthreshold excitability (Cummins et al., 1999; Herzog et al., 2001; Baker et al., 2003). Both Nav1.8 and Nav1.9 are expressed by nociceptive terminals (Persson et al., 2010). We stimulated a fixed-length terminal by a capsaicin-like current and mimicked the change of the terminal length by varying either Nav1.8 or Nav1.9 conductances. Increase in Nav1.8 conductance to 145% in short terminals of 50 µm (25-µm Nav-less compartment + 25-µm conductive, Nav-expressing, compartment), which generates two APs in control conditions, lead to the firing of 13 APs, which is comparable with the firing generated by a 125-µm-long terminal (Fig. 9A). In a 75-µm-long terminal (25-µm Nav-less compartment + 50-µm conductive, Nav-expressing, compartment), which fires three APs in normal conditions, the increase in Nav1.8 conductance to 110% was sufficient to generate 14 APs, which is comparable with the firing of a 125 µm terminal (Fig. 9A). Further increase in Nav1.8 conductance leads to higher firing, exceeding that of longer terminals with “normal” Nav1.8 conductance (Fig. 9B). Shortening of the terminal, by decreasing Nav1.8 conductance, reduces the firing in an abrupt manner, such that application of a capsaicin-like current to the terminal with 95% of Nav1.8 conductance leads to the generation of four instead of 13 APs and a decrease in Nav1.8 conductance below 55% prevented AP generation (Fig. 9B). Changing only Nav1.9 conductance resulted in a more gradual effect on AP firing (Fig. 9C,D), and in short terminals of 50 and 75 µm, the increase in Nav1.9 conductance to 150% was not sufficient to increase the terminal gain properties (Fig. 9D). In a longer terminal of 100 µm, an increase in Nav1.9 conductance by 10% increased the firing to levels comparable to the firing of longer terminals (Fig. 9C). Similar to Nav1.8 conductance, a further increase in Nav1.9 conductance in terminals longer than 100 µm produced substantially higher firing than the firing of the long terminals in normal conditions (Fig. 9D). The decrease in Nav1.9 conductance led to a gradual reduction of the firing, which was reduced but not annulled even when Nav1.9 conductance was zeroed (Fig. 9D). These data suggest that longer terminals are more excitable because of higher expression of Nav1.8 and Nav1.9 channels. The Nav1.8 conductance defines the repetitive firing, and Nav1.9 tunes it. The non-linearity between Nav1.8 and Nav1.9 conductances, the length, and the firing, could be explained by the effect of other conductances regulating the firing. Since we only manipulated Nav conductance and not the length of the conductive part, our manipulation left all other conductances intact; thus, an increase in Nav1.8 or Nav1.9 conductance was not counteracted by the increased potassium conductances, which normally restrain firing.

Figure 9.

The length of the conductive parts affects the nociceptive gain by defining the level of Nav1.8 and Nav1.9 conductances. A, left, A trace of the response to the stimulation (red arrow) of the 50 µm terminal branch (yellow) with the Nav1.8 conductance at the control level (100%). Stimulation of the same terminal branch but with increased Nav1.8 (145%) conductance led to higher firing (middle), which was compatible with the stimulation of longer (125 µm) terminal branch with the control (100%) Nav1.8 conductance (right). B, Heatmap representing the relation between the length of the conductive part, the relative level of Nav conductance, and the AP firing measured at the central terminal following stimulation of a single terminal. The AP count is color coded (shown on the right). Note that firing following the stimulation of the terminals with a 100% Nav1.8 conductance is increased when the Nav conductance is increased. Note also that the decrease in Nav1.8 conductance in the long terminal branches, which normally triggers a high number of APs, led to a dramatic reduction of firing. C, D, Same as A, B but showing the relation between Nav1.9 conductance, the conductive part length, and the AP firing at the central terminal.

Together, these data propose that the properties of the individual terminals and the complexity of the terminal tree affect the gain of nociceptive input-output function. The value of the generation potential is defined by the resistance of the terminal branch. The translation of the generation potential into AP firing depends on the length of Nav1.8-expressing and Nav1.9-expressing compartments and the integration of firing from multiple branches. All these factors contribute to the encoding properties of the nociceptive terminal.

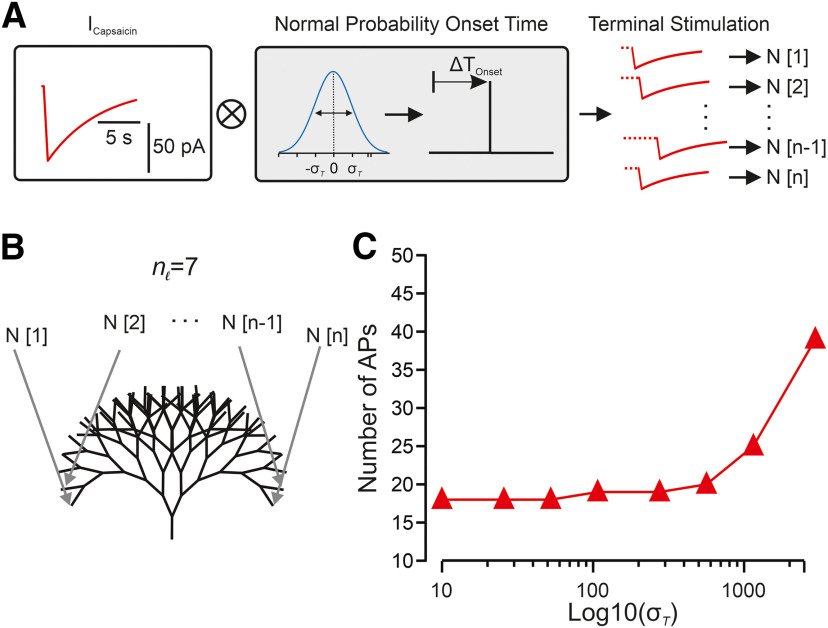
In all the experiments described above, we stimulated all the branches simultaneously. However, in physiological conditions, the stimulus (e.g., heat, cold, capsaicin) applied to a certain region area dissipates from the center of the stimulated areas into the surroundings. For example, in a case of nociceptive neurons with large receptive fields of back and leg (Mancini et al., 2014), the stimuli will first activate the terminals at the epicenter of the stimuli and only then at the surrounding areas as it dissipated there. But it is also true in a case of nociceptors with small receptive fields of palms and fingers (Mancini et al., 2014), as terminals vary in skin depth and distance from the stimulation point (Dezhdar et al., 2015; Alamri et al., 2018). Thus, each terminal receives the stimuli at different times, possibly leading to a temporal summation of the stimuli. At the dendrites, the differences in location and time of stimulation define the resulted output of the stimulated neuron (Magee, 2000; Magee and Johnston, 2005). Traditionally, the temporal proximity of a series of subthreshold synaptic events can, as a result of EPSP temporal integration, increase the output of the postsynaptic cell in terms of its firing probability and AP frequency. We, therefore, studied whether the temporal integration of noxious stimuli amplifies the nociceptor excitability. To simulate a stimulation of the receptive field with respect to time variance among terminals, we reformulated the capsaicin-like stimulations with the addition of a normally distributed probability of a randomized onset time variability (Fig. 10A). The simulations were then applied to all terminals of a complex n_l = 7 balanced binary type terminal tree (Fig. 10B). An increase in onset time probability from 10 to 2500 ms resulted in an exponential increase in total AP firing recorded at the central terminal over logarithmically increased onset time variance (Fig. 10C). Changes between 10 and 250 ms produced only a small increase in total AP firing over time (<20). However, the extension of onset time probability greatly increased the excitatory output (Fig. 10C) up to a 2-fold increase in longer onset times (Fig. 10C). These data indicate that the prolonged continuous capsaicin-like currents stimuli feature a temporal-summation characteristic such that the successive application of these stimuli leads to an increase in the response of nociceptive neurons. Our data also imply that the facilitation we observed in the degenerate binary tree (Fig. 5) could be because of the temporal integration of the responses from different terminals.

Figure 10.

Temporal summation by the nociceptive terminal tree. A, Scheme of normally distributed random time onset for a single of n terminal stimulations (N). After a capsaicin current is generated (red) its stimulation onset time is shifted to a normal distribution (blue) random onset time with a SD (σ); n stimulations are then each applied to a single terminal index with respect to its index (1..n). B, Scheme depicting the model of a seven bifurcation stage balanced binary tree. Each of the time-randomized stimulations (N[1..n]) is applied to a terminal nerve-ending (gray arrows). C, The number of APs generated as a function of the logarithmic scaling of normal distribution SD onset time of a capsaicin-like current in all terminals. The activity was measured at the central terminal.

While the simulations described above were performed in normal conditions, we next examined how nociceptive terminals integrate the increased responses to noxious stimuli in pathologic conditions. Many pathologic conditions lead to hyperalgesia, i.e., increased pain response to noxious stimuli (Sandkuhler, 2009). We previously demonstrated that inflammation leads to hyperalgesia by shifting the location of the SIZ of the nociceptive terminals closer to the terminal tip (Goldstein et al., 2019). Consequently, we shifted the location of the SIZ toward the terminal tip (Fig. 11A), to simulate the changes which occur during inflammatory hyperalgesia. Activation of all terminals with a capsaicin-like current under these conditions slightly increased the firing (15 instead of 13 APs; Fig. 11B) and the peak instantaneous frequency from 9.4 to 10.4 Hz (Fig. 11C). To simulate excitability changes in neuropathic pain, we conferred on nociceptive membrane subthreshold and suprathreshold perturbations of the membrane potential (Barkai et al., 2017). It has been demonstrated that nerve injury leads to an increase in the resting membrane potential voltage perturbations, which may initiate spontaneous ectopic activity (Amir et al., 1999; Liu et al., 2000; Rho and Prescott, 2012) and that this ectopic activity is correlated with neuropathic pain (Kleggetveit et al., 2012). Accordingly, we injected an Ornstein–Uhlenbeck-based current noise (Olivares et al., 2015), in which the amplitude of the injected current varies according to the normal distribution at each time step. We simulated subthreshold noise and suprathreshold spontaneous activity by varying the SD of the current amplitude's normal distribution (σ) between 0.006 and 0.007 µA/cm², respectively (Fig. 11A). In the higher σ of 0.007 µA/cm², the probability of reaching higher injected currents was higher; thus, it caused higher membrane fluctuation, which sometimes reached the threshold, and generated APs (Fig. 11A). In these conditions, activation of all terminals by a capsaicin-like current substantially increased firing (Fig. 11B) and the peak instantaneous frequency was slightly increased (9.9 Hz in subthreshold noise and 10.1 Hz in suprathreshold noise; Fig. 11C).

Figure 11.

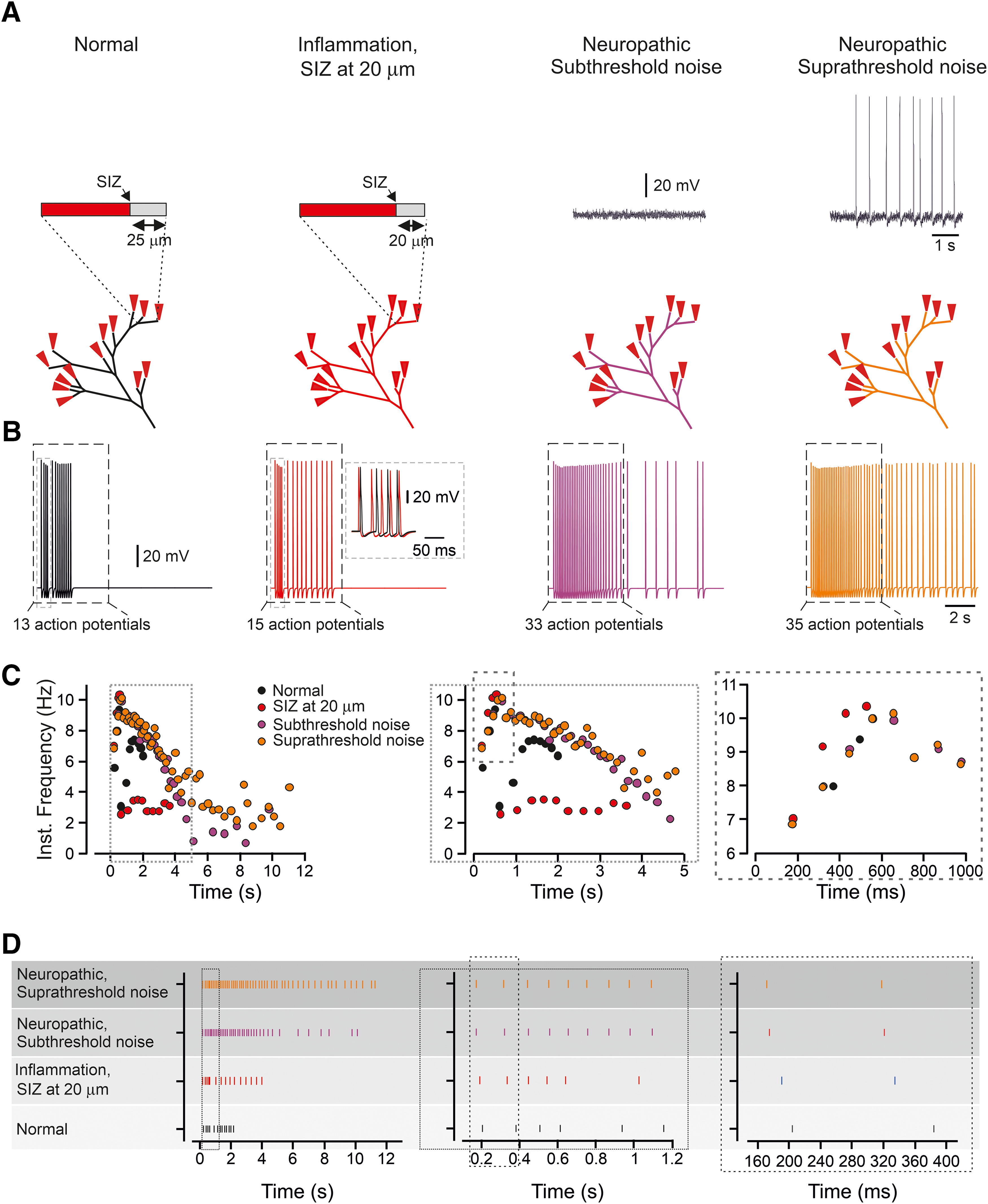
In modeled inflammatory and neuropathic conditions, the change in response is encoded by alteration in the temporal pattern of the spike trains. A, Scheme of the experiment: in normal condition, the SIZ is located 25 µm from the terminal end, and the terminal membrane potential is quiescent. The inflammatory hyperalgesia is modeled by shifting the SIZ 5 µm toward the terminal tip. The neuropathic hyperalgesia is modeled by injected to the model subthreshold or suprathreshold current noise (see Materials and Methods). Insets, Recording of the membrane voltage following the application of subthreshold and suprathreshold noise. B, Responses detected at the central terminals following activation of all terminal branches by a capsaicin-like current in normal conditions (black), in the conditions of inflammatory hyperalgesia (red), and in conditions of the neuropathic hyperalgesia with the injection of subthreshold noise (purple) and suprathreshold noise (orange). The AP count was performed for a first 5 s after a capsaicin-like current application (outlined by the dashed-line rectangle). Inset, Superimposition of the traces obtained in normal conditions and in the inflammatory hyperalgesia conditions at the time outlined by the gray dashed-line rectangle. Note the difference in the pattern of firing. C, Instantaneous discharge frequencies following stimulation with a capsaicin-like current (shown below) applied to all terminal branches in normal conditions (black), in the conditions of inflammatory hyperalgesia (red), and in the conditions of neuropathic hyperalgesia with the injection of subthreshold noise (purple) and suprathreshold noise (orange). Insets, Expanded x-axis. D, Spike raster plot showing the AP timing, following stimulation of all terminal branches with a capsaicin-like current, in normal conditions (black), in the conditions of the inflammatory hyperalgesia (red), and in the conditions of the neuropathic hyperalgesia with the injection of subthreshold noise (purple) and suprathreshold noise (orange). Insets, Expanded x-axis. The data describing the normal conditions are taken from Figure 1 and showed here for better comparison.

Our data demonstrate that activation of all terminals of the realistic terminal tree in normal conditions led to the generation of 13 APs, which fires at the central terminal with an instantaneous frequency peaked at 9.3 Hz (Figs. 1E, 11C). Activation of complex balanced or degenerate trees, although produced a higher firing (18 and 21 APs, respectively), the peak instantaneous frequency remained within a similar limit of 9–10 Hz (Figs. 3, 5). Similarly, in the simulated pathologic conditions, the peak instantaneous frequency was only slightly increased (Fig. 11C). This change in peak instantaneous frequency may be too narrow to encode and convey the changes in response to stimuli. We, therefore, hypothesized that in addition to the spike rate coding (Adrian and Zotterman, 1926), the nociceptive neurons might also use “temporal” coding to integrate and encode the information about different response properties via different timing patterns of spikes (Cho et al., 2016). Accordingly, we analyzed the spiking activity over time following a capsaicin-like current stimulation of all terminals in the realistic terminal tree in normal conditions, in inflammatory hyperalgesia conditions, in which the SIZ is shifted toward the terminals and in neuropathic pain conditions, in which subthreshold and suprathreshold current noises are injected (Fig. 11D). The simulation revealed that the peak discharge rate following the stimulation in different conditions was almost unchanged, while the patterns of the discharges evoked in different conditions were substantially different (Fig. 11D). These data propose that changes in temporal encoding of the spike trains from an individual nociceptive neuron may convey key information about changes in nociceptive output in pathologic conditions, thus defining abnormal nociceptive behavior after nerve injury or inflammation.

To summarize the effects of the different normal and abnormal morphology of nociceptive terminal tree on the nociceptive functions, we produced a simplified model of the realistic nociceptive terminal tree which contain “degenerative” and “symmetric” components steaming from the common branch, in which all terminal branches are of the same length (75 µm; Fig. 12A, black). Under these normal conditions, activation of this terminal tree by a capsaicin-like stimulus, i.e., simultaneous activation of all terminal branches by the capsaicin-like current generated 10 APs. We then simulated the morphologic changes in the terminal branches and the terminal tree and examined how these changes affect the terminal output. An increase in the number of terminal branches to 16, simulating hyperinnervation changes (Cain et al., 2001; Leibovich et al., 2020) led to an increase in firing (Fig. 12A, red). A decrease in the number of the terminal branches to seven, simulating a denervation state, substantially decreased the nociceptive gain (Fig. 12A, blue). Changes in the properties of individual terminal branches by shortening and decreasing Ra of the conductive part also substantially decreased nociceptive gain (Fig. 12A, green). An increase in the terminal branch length had an opposite effect on the nociceptive gain. Importantly, all the changes in the morphology of the nociceptive terminal tree affected also the pattern of firing (Fig. 12B,C, green), suggesting that in addition to changes in the number of APs, there is also a change in their timing for reaching the central terminal, which may be an important factor in nociceptive neuronal processing.

Figure 12.

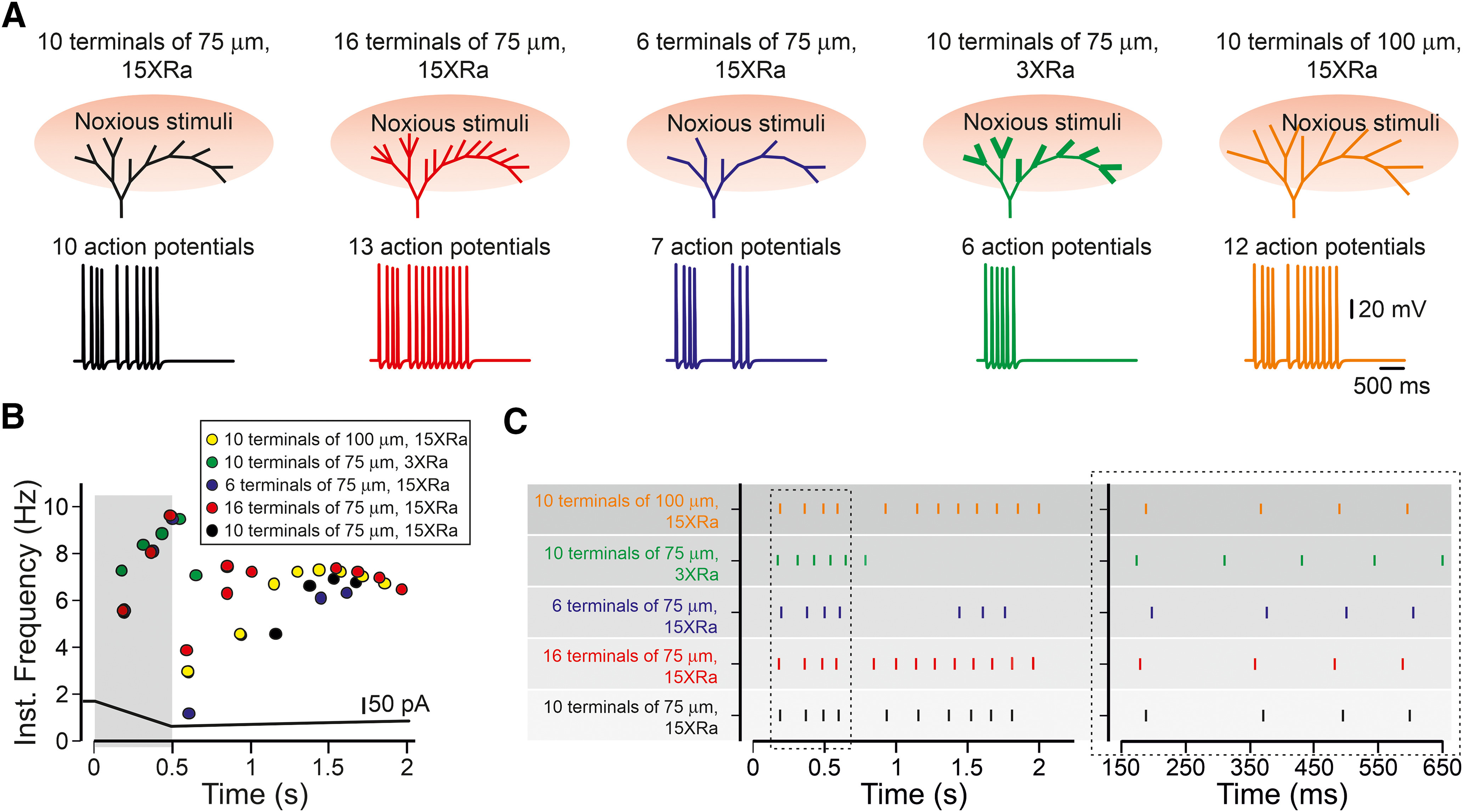
The effect of the morphology of the nociceptive terminal tree on the input-output properties of the primary nociceptive neuron. A figure summarizing the effect of the terminal structure on its function. Activation of all terminal branches in a simplified realistic terminal tree (all the terminal branches are of equal size of 75 µm, and they are evenly distributed along the degenerate and symmetrical parts of the complex terminal, black) by capsaicin-like stimulus led to the response whose gain (A, lower panels) and AP temporal pattern (B, C, showing the instantaneous frequency and spike raster plot, respectively) are dependent on the terminal morphologic characteristics, such as change in the number of terminal branches and the properties of the individual branch. The increase in the number of activated terminal branches (red) led to increased firing; the decrease in branching (blue) led to decreased firing. Terminal tree with short and thick (lower conductive part's Ra) terminal branches demonstrate lower gain (green), whereas a terminal tree with long terminals has a higher gain (orange). All the perturbations in terminal morphology change the timing pattern of firing (B, C).

Discussion

Nociceptive terminals innervate the tissue forming a variety of morphologically complex structures (Zylka et al., 2005; Ivanusic et al., 2013; Alamri et al., 2015, 2018; Olson et al., 2017; Bouheraoua et al., 2019). To examine the effect of the architecture of the whole terminal tree, together with morphologic and biophysical properties of its specific component on nociceptive input-output relation, we used a computational model. While building this in-silico nociceptive terminal tree, we used data from available experimental results acquired by us and others, but for some of the parameters, estimation and assumptions had to be made. We derived our conclusions by changing specific parameters through a range of values. We, however, make no claim that the model simulates all nociceptive neurons at all states. The purpose of the model was to generate plausible predictions for how the morphology of nociceptive terminal trees affects nociceptive signaling under the parameter constraints available in the literature.

The architecture of our model is based on the morphology of a representative nociceptive tree in vivo (Barkai et al., 2017), and it is composed of basic structural tree characteristics, which are universal for terminal tree architectures, such as symmetrical and degenerate tree structures. Therefore, our model, although does not represent in detail all types of terminal trees (Hoyes and Barber, 1976; Heppelmann et al., 1994, 2001; Müller et al., 1996; Zylka et al., 2005; Ivanusic et al., 2013; Alamri et al., 2015, 2018; Olson et al., 2017; Bouheraoua et al., 2019), could be adjusted to study structure-to-function relations in more specific terminal tree structures.

An important element of our model is the assumption that the terminal branch possesses a high Ra. We implemented the high (15×) axial resistivity of the terminal branches because of several reasons. First, EM evidence showing that intracellular organelles, such as mitochondria, are present at the terminal branches (Hoyes and Barber, 1976; Heppelmann et al., 1990, 1994; Müller et al., 1996). It has been suggested that the presence of mitochondria in terminals (Heppelmann et al., 1990) or dendrites (Bekkers, 2011) could increase Ra. Our theoretical calculations based on the terminal structure and mitochondria size (see Materials and Methods) show that the Ra of the terminal branch is 15× higher than the Ra of the terminal branch without intracellular organelles. Second, in line with our calculations, the presence of the mitochondria in a “pinched” dendrite increases its Ra 15-fold (Bekkers, 2011). The high Ra of the terminal branch explains, in part, our findings demonstrating that in corneal terminal branches in vivo an AP, initiated at the SIZ, does not propagate antidromically and does not reach the terminal tip (Goldstein et al., 2019). The high terminal Ra, producing a short space constant together with depolarization-mediated activation of outward conductances such as low threshold potassium channels such as Kv1, which were shown to regulate the conductive properties of the peripheral nociceptive fibers (Wang et al., 2016; Alvarez et al., 2019), could prevent antidromic AP propagation from the SIZ.

To simulate the activation of the terminal branch by noxious stimuli, we used capsaicin-like current-based stimuli instead of a TRPV1 channel model module. Although it is possible to build an ion-channel module for any given channel based on its biophysical properties (Hines and Carnevale, 1997), often, there is a need to investigate how a single current affects neural excitability without employing biophysical property detailing to simulate it. For example, point-process current-based stimulations similar to the one used here, are used to model the effects of various synaptic and dendritic properties on neuronal excitability, instead of using modules of synaptic or voltage-gated channels (Migliore et al., 1999; Magee and Cook, 2000). Here, we preferred to use current-based stimuli instead of using a complex multimodal model of TRPV1 channels since we use a capsaicin stimulation only as means of nociceptor activation. The usage of the point-process stimulation, instead of the complex model of TRPV1 channels, allows studying the effects of various types of noxious stimuli on nociceptive terminals in normal and pathologic conditions.

Our model predicts that the properties of an individual terminal have a prominent effect on nociception. The Ra determines the voltage response to the activating current and the resulting AP firing is defined by the length of the conductive part of the terminal. These features render the nociceptive terminal as a special unit combining properties of two structures known to affect the neuronal gain: a dendritic spine, which increases its synaptic gain by increasing spine-neck Ra (Segev and Rall, 1988; Beaulieu-Laroche and Harnett, 2018), and the AIS, a conductive compartment shown to elevate neural excitability with its elongation (Kuba et al., 2010). These two structures, although co-exist in a variety of neurons, they are functionally and topologically distant from each other, with spines defining the dendritic input function and the AIS attributed to axonal output function. Here, we show that the nociceptive terminal combines these two functional characteristics into one gain-defining compartment, the terminal branch. Interestingly, both spine-neck Ra and AIS length are considered key to neuronal plasticity (Magee, 2000; Grunditz et al., 2008; Sjöström et al., 2008; Grubb et al., 2011; Araya et al., 2014; Gulledge and Bravo, 2016; Yamada and Kuba, 2016). It is, therefore, reasonable to consider terminals as key regulatory sites for nociceptive plasticity. Thus, changes in the electrical properties of a terminal (Goldstein et al., 2019) could lead to changes in pain perception. For example, our data predict that the change in the density of intracellular organelles at the terminal branch can cause a local increase of the terminal Ra and thereby an increase in its excitatory characteristics, leading to increased pain. Changes in the electrical properties of a single terminal leading to an increase in its gain could serve as a possible explanation for the state in which a decrease in fiber density because of nerve degeneration leads to increased pain (Chiang et al., 2018).

It was recently demonstrated that neuropathic pain following nerve injury was associated with a decreased number of DRG neuronal somata innervating the hypersensitive area (Leibovich et al., 2020) and an increased number of axons innervating the area (Duraku et al., 2012). Together, these results suggest that each DRG neuron innervating the hypersensitive area increases the complexity of its terminal fibers. Our model predicts that the increase in terminal branching of individual DRG neurons following nerve injury (Leibovich et al., 2020) or inflammation or tumor formation (Cain et al., 2001) augments neuronal excitability and thus may contribute to the development of pain hypersensitivity in neuropathic conditions.

Our model also suggests how primary nociceptive neurons encode noxious stimuli and how this encoding may change under pathologic conditions. Neurons encode information using both spike rate coding (Adrian and Zotterman, 1926) and temporal coding (Panzeri et al., 2001; Johansson and Birznieks, 2004). Model simulation of hyperexcitable nociceptive states which mimics different pathologic conditions shows that nociceptive neuron' firing differs in the number of APs; however, the peak instantaneous frequency varies only slightly. These differences in spike rate may be too narrow to encode the differences in neuronal excitability. We show that in modeled pathologic conditions in which nociceptive neurons become hyperexcitable, the changes in their gain are encoded by the differences in the spike arrival time. The differences in spike patterns between capsaicin and GABA-evoked responses were recently correlated with the differences in the resulting pain sensation following either capsaicin or GABA stimulation (Cho et al., 2016). Thus, the difference in the timing pattern of spikes could convey important information regarding the gain of the input-output properties of the nociceptive neurons.

In summary, we introduced here a realistic model of the nociceptive terminal tree, which reveals that the structure of the terminal tree plays an important role in defining the function of nociceptive neurons. Our model predicts how activation of the nociceptive neurons with different terminal architecture would change the neuronal response. It also suggests that the changes in the tree architecture in pathologic conditions may be sufficient to modify the input-output relation of the primary nociceptive neurons, thus leading to pathologic pain. As in all models, although it does not reflect all neuronal morphologic and physiological properties, its simplicity allows examining how a change in a specific parameter affects the whole complex multiparameter system. It also could be used to test other hypotheses of the physiology and pathophysiology of nociception. For example, we used a capsaicin-like stimulus; however, our model could be adapted to predict how nociceptive neurons respond to other types of noxious stimuli and how these responses vary depending on changes in different ion conductances, electrical properties of the terminal, terminal architecture or under pathologic conditions. The knowledge collected from our model gives rise to predictions and speculations, which otherwise could not be achieved with the current experimental tools. Moreover, the results of this theoretical study open new avenues to follow and explore experimentally.