Tautomerism of Warfarin: Combined Chemoinformatics, Quantum Chemical, and NMR Investigation

Abstract

Warfarin, an important anticoagulant drug, can exist in solution in 40 distinct tautomeric forms through both prototropic tautomerism and ring–chain tautomerism. We have investigated all warfarin tautomers with computational and NMR approaches. Relative energies calculated at the B3LYP/6-311G+ +(d,p) level of theory indicate that the 4-hydroxycoumarin cyclic hemiketal tautomer is the most stable tautomer in aqueous solution, followed by the 4-hydroxycoumarin open-chain tautomer. This is in agreement with our NMR experiments where the spectral assignments indicate that warfarin exists mainly as a mixture of cyclic hemiketal diastereomers, with an open-chain tautomer as a minor component. We present a diagram of the interconversion of warfarin created taking into account the calculated equilibrium constants (pK_T) for all tautomeric reactions. These findings help with gaining further understanding of proton transfer and ring closure tautomerization processes. We also discuss the results in the context of chemoinformatics rules for handling tautomerism.

Graphical Abstract

INTRODUCTION

The identification and characterization of the tautomers of drug-like small molecules has important implications. This has been demonstrated by newly identified tautomers of well-known pharmaceuticals such as barbituric acid,¹ omeprazole,² ranitidine,³ sulfasalazine,⁴ irbesartan,⁵ and warfarin.⁶ Molecules capable of tautomerism behave like chameleons which have the ability to adapt their appearance to their environment. Solvent, pH, and temperature can all influence the tautomeric equilibrium.^7,8 In the solid state, the observed tautomeric form may differ from that which predominates in solution.⁹ Different tautomers will often have different physicochemical properties and different reactivities, which may change their metabolic profiles dramatically. Thus, it is very important to know which tautomeric form is present at each step of drug administration as well as during the drug development process.

Indeed, warfarin is an interesting example of the potential tautomeric complexity of drug molecules. Warfarin, 2-hydroxy-3-(3-oxo-1-phenylbutyl)chromen-4-one, is an anticoagulant drug commonly used to prevent thrombosis and thromboembolism. Warfarin decreases blood coagulation by inhibiting the active site of vitamin K dependent epoxide reductase (VKOR).¹⁰ In spite of the long-standing and widespread use of warfarin as a drug, its mechanism of action is still not completely clear. A possible contributing factor to the well-known difficulty in dose optimization that has been associated with warfarin’s bioavailability¹¹ could be the molecular-level complexity of warfarin. An important point that would contribute to an increased understanding of the function of warfarin as a drug is the identification of the exact molecular structure of the biologically active form of warfarin. For this, one needs to first understand and enumerate what tautomers warfarin may in principle adopt.

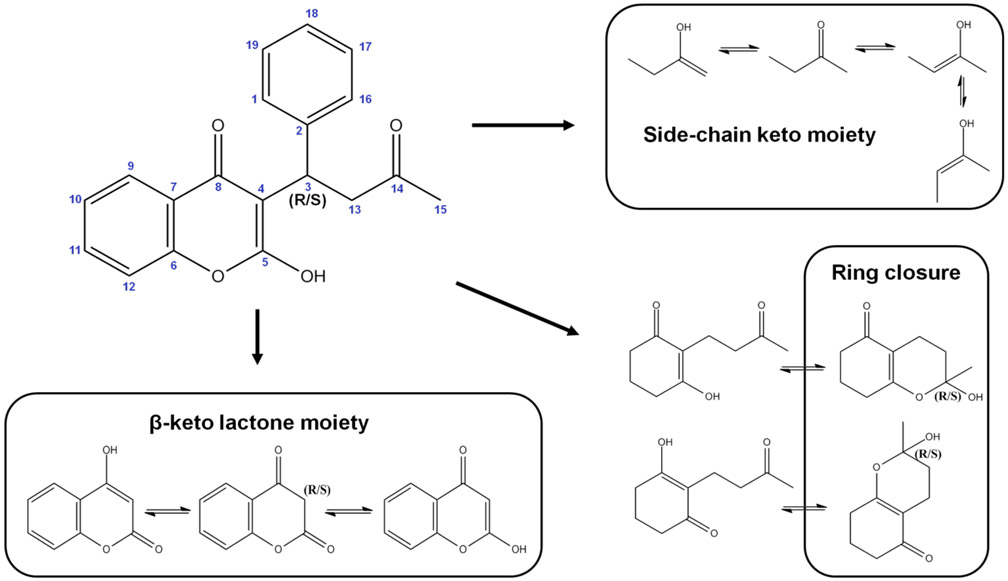
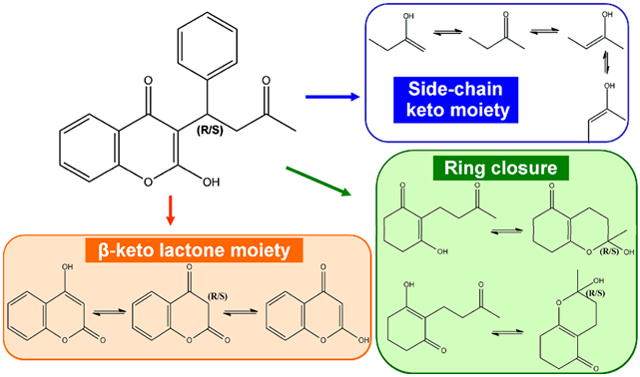
Warfarin can theoretically exist in 40 distinct tautomeric forms as shown in Figure 1. Warfarin exhibits prototropic tautomerism, the intramolecular movement of hydrogen from one atom to another, as well as ring–chain tautomerism where the movement of the proton is accompanied by ring opening or closing. All the open-chain forms of warfarin exhibit keto–enol tautomerism at both the β-keto lactone moiety and the side-chain keto moiety. Each of these moieties can exist in any of three tautomeric forms. However, since the β-keto lactone has a chiral center, there are actually two possible diastereomers, leading to four different possibilities. With the side-chain keto moiety, one enol form involving the terminal methyl has two possible isomers: E-configuration and Z-configuration. This creates four distinct forms for the tautomerization of the side-chain ketone. The combination of both moieties gives 16 distinct open-chain tautomers. The open-chain form can close to form either the 4-hydroxycoumarin cyclic hemiketal or the 2-hydroxychromone cyclic hemiketal. The ring closure creates a new center of asymmetry, so two possible diastereomers can form for each closure, for a total of four distinct ring tautomers. Taking into account both enantiomers of warfarin, the number of possible tautomers reaches a total of 40 as shown in Figure 1.

Figure 1.

Tautomerization of warfarin substructures, whose combination generates 40 distinct tautomeric forms of warfarin (see Figure 2).

However, warfarin is usually depicted in textbooks, review articles, and databases as the open-chain tautomer; why should this be? Is the bioactive form the most stable tautomer? Which form, the open-chain tautomer or the ring tautomer, is present in the solid state? Many questions regarding the tautomerism of warfarin are still unanswered, and the physical properties and chemical reactivity of warfarin can only be understood by accounting for the interconversion between different tautomeric forms.⁶

NMR studies have demonstrated that warfarin exists in a dynamic equilibrium between different isomeric forms. The distribution and types of isomers present were found to be dependent on solvent polarity and pH.¹² Warfarin in solution is shown to consist of three interconverting tautomeric structures, two of which are cyclic diastereomeric hemiketals, while the third and minor component is the open-chain intermediate form. Also, the cyclic hemiketal isomer was suggested to be the predominant structure in crystals and in nonpolar organic solvents.¹² However, the form of warfarin when bound to human serum albumin (HSA) is the deprotonated open side chain form.¹³ Other investigations suggested that the cyclic hemiketal form is responsible for the interaction with the enzyme cytochrome P450 (CYP2C9).¹⁴ Also, it has been shown that the enantiomer S-warfarin is two to five times more active than the R enantiomer.¹⁵

Several techniques and chemical methods have been applied to elucidate the tautomeric composition of warfarin. The kinetics of tautomeric equilibria and chemical derivatization are complex. Some computational studies using quantum chemical calculations have been done to elucidate the molecular properties of coumarinic anticoagulants¹⁶ along with the acid dissociation constants of warfarin.¹⁷ However, to our knowledge, a complete computational study of all warfarin isomers has not yet been reported. In this work, we present the results of quantum chemical calculations for all possible tautomers of warfarin. We also report results from structural investigations of warfarin by means of NMR spectroscopy. Finally, we also discuss the chemoinformatics implications of the chameleon-like nature of warfarin with its many possible tautomeric representations and its several “real” tautomers identified in experiments or determined to be energetically likely in biological contexts.

RESULTS AND DISCUSSION

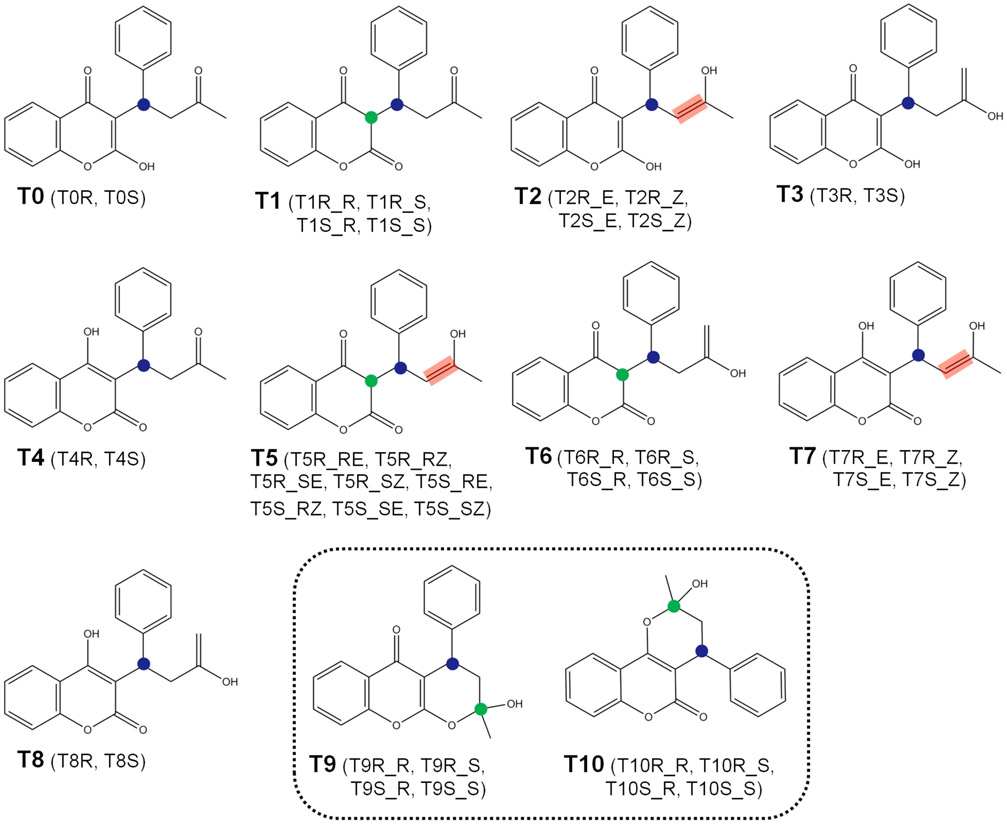
To make the referencing of warfarin tautomers in this paper easier, we developed a notation in the form Tij_k, where i indicates the numbering (0 to 10) as shown in Figure 2; j indicates the warfarin enantiomer (either R or S) determined by carbon atom 3; and k indicates the rest of the stereochemistry if applicable—R/S (stereocenter on carbon atom 4 or 14) and E/Z (stereobond between carbon atoms 13 and 14). For example, T10S_R is the closed form of (S)-warfarin with an (R)-chiral center on the ring closure moiety.

Figure 2.

Numbering for the tautomers of warfarin considered in the present work; in parentheses are listed all possible stereoisomers for each tautomer. Tautomers enclosed within the dashed line are closed-form. Circles represent the stereocenters of warfarin, the blue circle determines the warfarin enantiomer (either R or S), and the green one indicates the rest of the stereocenters; red rectangles represent the stereobonds of warfarin.

Chemoinformatics of Warfarin.

One of the fundamental tasks in chemoinformatics is the determination of the computer representation of a compound. Various types of chemical identifiers are typically used to uniquely identify compounds in a database.¹⁸ Therefore, tautomers represent a challenge for chemoinformatics tools because they are both different molecules with different connectivity and at the same time a molecule freely interconverting between different forms in solution. This stretches the conceptual limit of a unique chemical identifier. All 40 warfarin tautomers should be registered by the same identifier in order to be able to recognize they are the same compound; or at least it should be possible to automatically establish the connection between whatever tautomers of warfarin may have been submitted to one or several databases.

We calculated several identifiers for the warfarin tautomers (listed in Table S1 in the Supporting Information). These include the InChIKey identifier, a fixed-length hashed version of the InChI (International Chemical Identifier), SMILES (Simplified Molecular-Input-Line-Entry System) notation, and the NCI/CADD “FICuS” and “FICuu” identifiers developed in our group,¹⁹ based on the structure hash codes provided by the chemoinformatics toolkit CACTVS. The FICuu identifier, which is sensitive to neither tautomerism nor stereochemistry, was the same for all open-chain tautomers but different for the closed-form ones, which was to be expected because the set of ring–chain tautomer conversion rules we developed recently²⁰ is not yet currently implemented as a standard property in CACTVS. However, the InChIKey identifiers were different for each tautomer regardless of the type of tautomerism. While InChI includes the concept of mobile hydrogens along with an optional level of structural information called the “fixed H” layer intended to help with the handling of tautomerism, the current version does not recognize all forms of tautomerism. In particular, keto–enol and longer-range (1–5) transformations are not included in the standard InChI by default.²¹

Next we describe some examples of searching for “warfarin” by name in several types of databases. In the BindingDB [http://www.bindingdb.org], ChEMBL [https://www.ebi.ac.uk/chembl/], and PubChem [https://pubchem.ncbi.nlm.nih.gov/] databases, the T4R and T4S tautomers were the only ones found. However, when the search was done using SMILES notation for each tautomer, the T1?_?, T4R, T4S, T10R_?, and T10S_? tautomers were retrieved from these three databases (the use of “?” notation stands for nondefined stereochemistry) plus the T0?, T4R, and T4S tautomers from the database ChemSpider [http://www.chemspider.com/]. In the Protein Data Bank [http://www.rcsb.org/pdb/], the T4S and T4R tautomers were found complexed with HSA crystal structures. In the commercial Aldrich Market Select database [https://www.aldrichmarketselect.com/], we found the T4 tautomer as a sodium salt and the T1 tautomer without defined stereo-chemistry. Essentially, warfarin is represented as an open-chain tautomer in all databases, and the closed-form is not found linked to warfarin as a chemical name. It is clear that the curation of tautomers in chemical databases could be substantially improved, and warfarin provides a good example of issues that may be encountered.

Relative Stability.

Chemoinformatics approaches are rule-based, employing mathematical techniques such as statistical and combinatorial methods rather than being based on computationally more expensive physical first principles. In this sense, they do not usually try to recreate the chemistry of the molecule in its entirety. In order to study the geometry and the relative stability of all 40 tautomers we therefore applied quantum chemical methods, which recreate the electronic structure of the molecules.

(R)-Warfarin and (S)-warfarin are related to each other by a parity transformation (i.e., parity inversion transforms a chiral phenomenon into its mirror image). The relative stabilities of the optimized geometries of all (S)-warfarin tautomers in the gas phase and in water solution at DFT level of theory are listed in Table 1. In vacuum, the open-chain form T4S was the most stable, and the closed form T10S_R was the most stable in aqueous solution. However, the difference between both forms in both conditions was only on the order of 2 kcal/mol, and thus both forms should be detectable at room temperature. In both vacuum and in water, T3, T6, T2, T5, T8, and T7 were the least stable compounds; all of them were open-chain tautomers possessing the enol form of the side chain keto moiety. They are less likely to be observed experimentally because their relative energy is higher than 10 kcal/mol. T9, T1, and T0 had intermediate energy between 5 to 10 kcal/mol. Finally, T4 and T10 were the most stable tautomers. Among the E and Z stereoisomers in T2, T5, and T7, the Z form was always more stable than the E form. Regarding the second chiral center of warfarin, the differences were smaller between the diastereomeric tautomers, and there was not a global tendency for one or the other to be lower in energy. The inclusion of bulk solvent effects by the polarized continuum model of solvation (water) led to a slight decrease in the average free energies of about 2 kcal/mol. The solvent generally acts to stabilize all structures. The relative energies become smaller upon solvation due to the screening of charge differences.

Table 1.

Calculated Relative Stabilities^a (in kcal/mol) for the Tautomers of Warfarin in Gas and Aqueous Phase (PCM Solvation Model) at Different Computational Levels of Theory, with Population Percentages and Frontier Orbital Energy Differences Given

		Gas phase	Aqueous phase
Tautomer	Form	DFTb	DFTb	DFT-Dc	Boltzmann ratiod,e	HOMOe	LUMOe	AE
T0S	chain	7.17	6.07	7.2	0.003	−6.67	−1.81	4.86
T1S_R	chain	7.33	7.83	5.46	0	−7.09	−2.59	4.5
T1S_S	chain	7.03	7.48	5.29	0	−7.1	−2.6	4.5
T2S_E	chain	22.52	20.59	22.46	0	−6.55	−1.83	4.73
T2S_Z	chain	16.72	19.41	21.14	0	−6.64	−1.86	4.78
T3S	chain	24.87	23.29	23.93	0	−6.59	−1.85	4.74
T4S	chain	0	2.6	2.86	1.022	−6.7	−2.05	4.65
T5S_RE	chain	20.38	18.11	18.08	0	−6.52	−2.55	3.97
T5S_RZ	chain	20.15	16.54	17.21	0	−6.4	−2.49	3.9
T5S_SE	chain	19.96	18.27	18.12	0	−6.54	−2.52	4.02
T5S_SZ	chain	19.58	16.6	17.22	0	−6.37	−2.49	3.88
T6S_R	chain	21.7	19.29	18.73	0	−6.65	−2.54	4.11
T6S_S	chain	22.12	20.73	19.89	0	−6.63	−2.55	4.09
T7S_E	chain	15.03	12.96	14.7	0	−6.52	−1.96	4.56
T7S_Z	chain	10.14	11.87	13.46	0	−6.61	−2.01	4.6
T8S	chain	17.38	15.56	16.07	0	−6.61	−2.02	4.59
T9S_R	ring	9.42	8.07	8.35	0	−6.8	−1.85	4.95
T9S_S	ring	10	9.01	10.19	0	−6.73	−1.85	4.87
T10S_R	ring	1.59	0	0	82.817	−6.74	−1.97	4.76
T10S_S	ring	2.1	0.97	1.89	16.158	−6.71	−1.99	4.71

^aThe Gibbs free energy of the most stable tautomer is taken as the reference (0.0 kcal/mol); this is tautomer T4S for the gas phase and T10S_R for the aqueous phase.

^bDFT calculations performed using B3LYP/6-311++G(d,p).

^cDFT-D calculations performed using empirical dispersion method D3 added to the DFT computation as in [b].

^dCalculated according to the Boltzmann equation at T = 298.15 K.

^eCalculated based on DFT calculations in the aqueous phase.

Table 1 shows good agreement between the relative stabilities obtained using B3LYP levels of theory both with (“DFT-D”) and without (“DFT”) dispersion added. Similarly as we found here for warfarin, use of various levels of theory and basis sets in quantum-chemical calculations of the amide–iminol tautomerism of formamide had no significant effect (1 kcal/mol or less) on the relative energies of the tautomers.²² Again, T4S, T10S_R, and T10S_S were the most stable tautomers both in vacuum and in aqueous conditions. A slight trend toward higher numbers in the DFT-D calculations (only performed in aqueous environment) vs DFT can be observed. For 13 out of 20 tautomers, the DFT-D energy was higher, for 6 it was lower, with the differences being generally in the ±2 kcal/mol range (the reference molecule obviously has the same relative energy of 0 kcal/mol by definition). However, the overall picture of the tautomeric energies and their ranking remained the same. For this reason, only the results obtained with the B3LYP/6-311++G(d,p) method in solution will be used and referred to in the following analysis.

Since the HOMO–LUMO energy separation can aid in clarifying chemical reactivity and the kinetic stability of molecules, the HOMO–LUMO gap was calculated for all tautomers. Table 1 shows the HOMO, LUMO, and the interfrontier molecular orbital energy gap (AE) values for the species of concern. Tautomers T1S, T9S, and T10S are characterized by the highest HOMO energy values, while the T5S tautomers had the lowest HOMO energy values; this correlates with the fact that the tautomers with the highest HOMO values have the lowest energies and vice versa. T1S tautomers also had the highest LUMO energy values; T0S had the lowest LUMO energy value. As for the AE values, T9S tautomers possessed the largest energy gap, whereas T5S tautomers had the smallest one because they are energetically less stable, so they need less energy to move to an excited state.

The calculated Boltzmann ratio of warfarin tautomers showed that the distribution in solution would be 83% and 16% for the diastereomers of the 4-hydroxy coumarin cyclic hemiketal form (T10S_R and T10S_S), respectively, and only 1% of the open-chain tautomer form (T4). These results are quite different from the chemoinformatics results; i.e., the warfarin representations in the databases mentioned above do not correspond to the most stable tautomers identified in our quantum chemical computations.

Description of Optimized Structures.

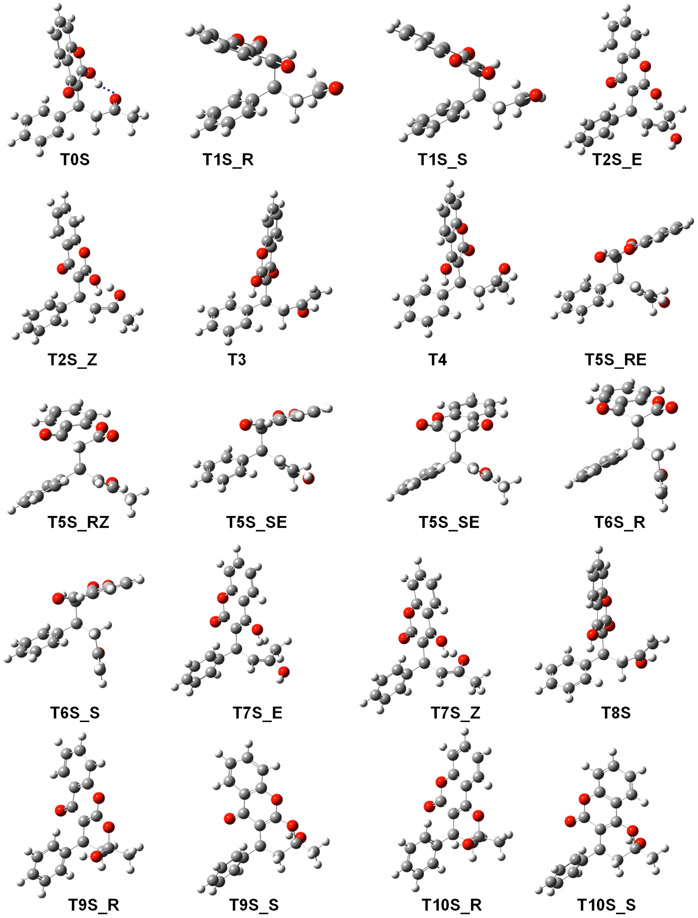
Figure 3 shows the geometry optimized structures of each warfarin tautomer (the Cartesian coordinates of these species are reported in the Supporting Information). T0S has a hydrogen bond (d = 1.7 Å) between the hydroxyl group of the chromenone ring and the keto group of the butanone moiety. In T1S_R and T1S_S, π-stacking interactions take place between the phenyl and chromenone aromatic groups. In T3S, T4S, and T10S_R, a polar hydrogen–π bond interaction occurs between the phenyl and the hydroxyl groups, with a distance from the hydrogen to the center of the aromatic ring of 2.8, 2.66, and 2.9 Å, respectively. In the T5S and T6S tautomers there occurs a polar–π interaction where the keto group is oriented toward the centroid of the phenyl group, with an average distance of 3.7 Å. The orientation of the chromenone group varies from one tautomer to the other. The conformations that appear on the figure are the most favorable ones out of the three low-energy structures that were selected from the conformational search.

Figure 3.

Geometry optimized structures of warfarin tautomers in solution (B3LYP/6-311**G(d,p)). The blue dashed line represents an intramolecular hydrogen bond.

Interconversion Diagram.

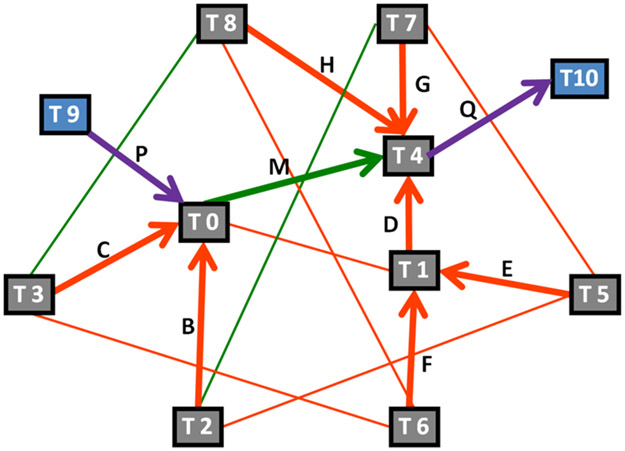
Taking into consideration the prototropic and ring–chain transformations that can occur in warfarin, we created a network diagram of its tautomeric interconversions (Figure 4). Since the transformations are stereochemistry-insensitive, only 11 tautomers (T0–T10) without defined stereochemistry are depicted in the diagram, which shows the reaction pathways between the possible tautomers of warfarin and describes how the 11 tautomeric forms of warfarin are connected to each other through tautomeric transformations. The size of this warfarin network is 11 vertices (i.e., tautomers) and 17 connections (i.e., transformations). The closed forms of warfarin, represented by blue boxes in the diagram, can only be obtained by the application of ring–chain rules for tautomeric transformation.

Figure 4.

Interconversion diagram of warfarin. Orange lines represent the 1.3 heteroatom H shift reaction, green lines are the 1.5 aro heteroatom H shift (1) reaction, and purple lines denote 6-exo-trig reactions. Blue squares represent closed-form tautomers, and gray squares are open-chain tautomers.

The warfarin network shows the connections between various tautomers by way of three different tautomeric rules. Two of them are prototropic rules: Rule 6, equivalent to the 1.3 heteroatom H shift; Rule 7, equivalent to the 1.5 aro heteroatom H shift (1);¹⁹ and one ring–chain rule called 6-exo-trig.²⁰ Prototropic rules handle hydrogen migration on aromatic hetero systems and aliphatic atoms. The difference between the two prototropic transformations is basically the distance of hydrogen migration, across three atoms for Rule 6 vs five atoms for Rule 7. The 6-exo-trig ring–chain rule encodes a ring closure through the nucleophilic attachment of the hydroxyl group from the coumarin moiety to the electrophilic carbon of the side-chain keto moiety forming a six-membered ring.

For example, starting from T6, one can reach T4 through T1 by applying the 1.3 heteroatom H shift rule twice. However, there is another pathway to get to T4 from T6 by going through T8 and also applying the 1.3 heteroatom H shift rule twice. The question then becomes which is the most energetically favorable path?

Determination of the Equilibrium Constants.

In order to determine the kinetic parameters of the transformations, in other words which reaction pathways are energetically favorable, we calculated their tautomeric equilibrium constants using the following formulas: K_T = exp(−ΔG/RT) and pK_T = −log K_T, where K_T is the equilibrium constant between the tautomers, the gas constant R is 1.987 × 10⁻³ kcal/mol, and the temperature T is 298.15 K. The quantity ΔG is the difference between the Gibbs free energy of the given tautomer with respect to the most stable one.

The calculated equilibrium constants pK_T are given in Table 2. Some pK_T values are positive and others are negative, the former implying that the equilibrium of the reaction is shifted toward reactants and vice versa. By considering the 17 pK_T values, we determined the most favorable equilibria corresponding to the most favorable thermodynamic direction for each tautomer. We represented these in Figure 4 by thick lines, with their directions marked with arrows. These ten equilibria correspond to the reactions B, C, D, E, F, G, H, M, P, and Q, respectively. Starting from any tautomer, the direction of the arrows indicates the shortest path toward the most stable tautomer T10. For example, from tautomer T3 three transformations are required to get to T10. First, T3 would tautomerize to T0 via a 1.3 heteroatom H shift, then a 1.5 aro heteroatom H shift would transform it into T4; and last, T4 would lead to T10 by a ring–chain interconversion rule.

Table 2.

Tautomeric Equilibrium Reactions of Warfarin

Reaction	Equilibrium	Rule	pKT
A	T0 ↔ T1	prototropic (Rule 6)	1.04
B	T0 ↔ T2	prototropic (Rule 6)	9.78
C	T0 ↔ T3	prototropic (Rule 6)	12.62
D	T1 ↔ T4	prototropic (Rule 6)	−3.58
E	T1 ↔ T5	prototropic (Rule 6)	6.64
F	T1 ↔ T6	prototropic (Rule 6)	8.65
G	T4 ↔ T7	prototropic (Rule 6)	6.80
H	T4 ↔ T8	prototropic (Rule 6)	9.50
I	T5 ↔ T2	prototropic (Rule 6)	2.10
J	T5 ↔ T7	prototropic (Rule 6)	−3.42
K	T6 ↔ T3	prototropic (Rule 6)	2.93
L	T6 ↔ T8	prototropic (Rule 6)	−2.73
M	T0 ↔ T4	prototropic (Rule 7)	−2.54
N	T2 ↔ T7	prototropic (Rule 7)	−5.52
O	T3 ↔ T8	prototropic (Rule 7)	−5.67
P	T0 ↔ T9	ring chain	1.47
Q	T4 ↔ T10	ring chain	−1.91

It would be very interesting to compare the energy barriers both for the prototropic transformations and for the ring–chain transformations. Their accurate calculation is however not trivial. In the Supporting Information, we provide the results of the determination of activation energies for the warfarin tautomers using the polarizable continuum model (PCM) without implicit water, being aware that the addition of a single water molecule to assist the proton transfers between tautomers may significantly decrease the barriers, as has been shown in several studies.^23-25

Interpretation of NMR Spectra.

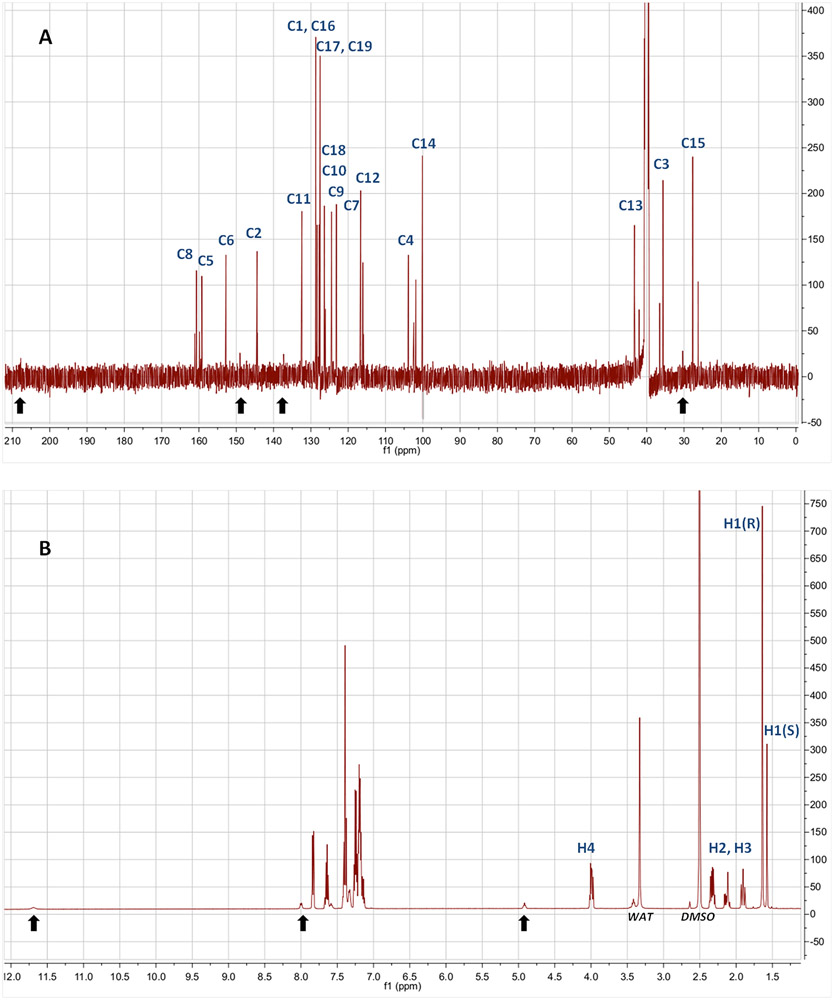
We conducted NMR experiments to analyze experimentally which tautomer or tautomers were present in a commercially acquired sample of warfarin. We compared this with our computational results. The ¹³C NMR spectrum (Figure 5A) shows a clear duplication of peaks with very similar chemical shifts, and the corresponding pairs of intensities have the same ratio (1:2.5) for all the peaks. This indicates that the warfarin sample contains at least two tautomers that are very similar to one another because their carbon chemical shifts are the same. The last signal, in the high-frequency range, appears at 161.12 ppm. There is no signal for the carbonyl carbon from the CH₂─CO─CH₃ fragment of the open form, which would be expected at 200 ppm. This confirms that the tautomers must be closed-form. Once we assigned the peaks (see Table 3), we determined that the duplication of the peaks results from the presence of the diastereomers of the 4-hydroxycoumarin cyclic hemiketal (i.e., T10S_S and T10S_R). There is additionally a set of peaks whose intensity is close to the baseline (lower than 30), indicated by black arrows on the spectrum, that consists of another warfarin tautomer as a minor component. One could suspect that the low intensity signal at 208 ppm is the carbonyl signal of an open-chain tautomer.

Figure 5.

¹³C NMR spectrum (A) and ¹H NMR spectrum (B) of warfarin. Arrows indicate peaks from the open-chain form of warfarin though the intensity is very low. See Figure 1 for numbering of the C atoms. H1(R) and H1(S) are connected to C15; H2 and H3 are connected to C13; and H4 is bonded to C3.

Table 3.

Experimental Chemical Shifts of Warfarin

	T10S_R		T10S_S		T4
atom	ppm	intensity	ppm	intensity	ppm	intensity
C15	27.7	238.6	26.2	101.5	30.4	28.4
C3	35.6	216.8	36.5	82.8	N/A	N/A
C13	43.3	162.8	42.0	64.6	N/A	N/A
C14	100.1	252.1	101.9	79.7	N/A	N/A
C4	103.9	108.8	102.4	64.9	N/A	N/A
C12	116.1	125.6	115.9	53.5	N/A	N/A
C7	116.6	209.3	116.7	77.7	N/A	N/A
C9	123.2	181	123.1	78.5	N/A	N/A
C10	124.5	179.3	124.5	75.2	N/A	N/A
C18	126.4	174.9	126.1	72.6	N/A	N/A
C17, C19	127.5	361.7	127.7	157.9	127.9	31
C1, C16	128.7	384.1	128.3	162	N/A	N/A
C11	132.4	176.5	132.5	72	N/A	N/A
C2	144.4	139.8	144.3	37.6	N/A	N/A
C6	152.8	148.4	152.8	47.4	N/A	N/A
C5	159.2	119.3	159.8	47	N/A	N/A
C8	160.7	105.1	161.1	42.4	N/A	N/A
H1 (C15)	1.64	740	1.57	301	2.29	23.4
H2 (C13)	1.90	63.1	1.88	30.2	2.37	10.1
H3 (C13)	2.34	62.7	2.16	25.8	2.64	10.9
H4 (C3)	4.00	51.8	4.02	20.3	4.92	9.6

For the interpretation of the ¹H NMR spectrum (Figure 5B), we focused on the nonaromatic hydrogens which are most useful for differentiating between tautomers. There are nine aromatic protons with chemical shifts between 7 and 8 ppm. Their assignment is complicated due to multiplicity and overlapping signals. Aside from the aromatic protons, there are four types of protons to be studied. The H1 type corresponds to a methyl group connected through C15; its chemical shift is three times more intense due to three hydrogens having the same signal, and it has no multiplicity. H2 and H3 are connected to C13, but they have different signals and coupling constants that lead to a doublet of doublets (dd) for each proton. H4, bonded to C3, also has a doublet of doublets but a higher chemical shift (around 4 ppm).

In the closed-form tautomers (T10S_R and T10S_S), a ketal ring is formed which can have several conformations. The preferred conformation (T10S_R) is a half-chair in which the phenyl and hydroxyl groups are oriented pseudoaxially and axially, respectively, with a favorable nonbonded contact (a polar hydrogen–π bond interaction) occurring between the two groups. In the T10S_S tautomer, the phenyl and hydroxyl positions are pseudoequatorial and axial, respectively, in the ketal ring, and the conformation is less stable. When comparing the computationally optimized dihedral angles within the ketal ring for both species, one sees that the hemiketal ring is flat except at the C3 position, where the direction of the tip of the half-chair conformation is opposite for each diastereomer. The torsion angles C4–C3–C13–C14 and C3–C13–C14–O for T10S_R are 48.92° and −53.28°, respectively, whereas for T10S_S they are −41.31° and 58.03°, respectively. Table 3 shows the assignment of the peaks. Three single signals were identified for H1, corresponding to the three tautomers T10S_R, T10S_S, and T4, respectively, yielding a ratio of 70:28:2. This ratio is completely in agreement with the Boltzmann distribution from our quantum chemical calculations in aqueous solution. The coumarin hemiketal ring tautomers maintain the same ratio as in the ¹³C NMR spectrum. The presence of the open-form tautomer, 4-hydroxy coumarin, is also confirmed by the presence of a small peak at 11.5 ppm, which corresponds to the OH group on the coumarin moiety. Though the computational studies were obtained by applying a water solvation model instead of DMSO solvation, we could expect a similar stability order of warfarin tautomers since both solvents are very polar with high dielectric constants.

CONCLUSION

We have conducted a theoretical study on the relative stabilities and the interconversion processes of warfarin tautomers. The computations at the B3LYP/6-311G++(d,p) level of theory showed that the closed-ring form T10 is the most stable tautomer in solution while the open-chain form T4 is preferred in vacuum, though the differences of energy were very small suggesting that these forms could interconvert. We have presented an intuitive and graphical network for the warfarin tautomers and their interconversion paths, which contains 17 tautomeric transformations. Since the network has 11 tautomers, there are ten paths that are the preferred ones (one for each tautomer) all finally leading toward the closed-ring form T10.

Our NMR analysis showed the presence of both closed-form and open-chain warfarin tautomers in DMSO solution. The ¹H and ¹³C NMR spectral assignments indicated that warfarin exists mainly as a mixture of the cyclic hemiketal diastereomers T10S_R and T10S_S (70% and 28%), along with a small portion of an open-chain form. These experimental ratios were in good agreement with the Boltzmann distributions calculated from the quantum-chemical energies.

A computational tool able to predict the most stable tautomer would be useful; however, the quantum calculations required are quite time-consuming. We can obviously not generalize from these results to predict that similar computations for other molecules would always find cyclic tautomers to be more stable; plus one must not forget that the solvent and other conditions influence the equilibrium, which one may or may not be able to take into account in the calculations. What one could in principle contemplate is to run this kind of high-level computational tautomerism analysis on a large number (hundreds or even thousands) of diverse molecules and use their results to build quantitative structure–tautomerism relationship models capable of predicting the most stable tautomers for any small molecule (in the model’s applicability domain), using appropriate molecular descriptors. We plan to explore these and other approaches in future studies of the tautomerism of small molecules.

COMPUTATIONAL METHODS

Tautomer Generation.

The chemoinformatics toolkit CACTVS²⁶ was utilized to enumerate all possible warfarin tautomers using both prototropic tautomerism rules and ring–chain tautomerism rules, which we developed recently.²⁰ All combinations of stereoisomers were generated by LigPrep.²⁷

Conformational Search.

To obtain structures for the global energy minimum for each tautomer, all structures were subjected to a conformational search using MacroModel.²⁸ The search method employed was a combination of random changes in torsion angles and/or molecular position from the MCMM (Monte Carlo Multiple Minimum) method, together with low-mode steps from the LMOD (Low-mode) method. The force field employed was OPLS_2005. The conformational search was performed twice, in vacuum and in aqueous solution using implicit solvent; the rest of the parameter values used were MacroModel’s default settings. The three lowest energy conformations of each tautomer in vacuum and in water were selected for further optimization at the density functional (DFT) level of theory.

Quantum Chemical Calculations.

The quantum chemical calculations were performed using the Gaussian 09 suite of programs.²⁹ Geometry optimizations for all tautomers were performed using the following levels of theory: DFT with the B3LYP functional, and DFT-D with the B3LYP functional using D3 dispersion correction, all in conjunction with the 6-311++G(d,p) basis set. Harmonic vibrational frequencies were computed at the same level of theory to verify the nature of each stationary point and also used to obtain the Gibbs free energy. Calculations were done in gas and aqueous phase. To estimate the effect of the solvent, in this case water, we employed the self-consistent reaction field theory (SCRF) polarizable continuum model (PCM), as implemented in Gaussian, at the B3LYP/6-311++G(d,p) level of theory. Population analysis of the warfarin tautomers was performed using the Boltzmann distribution formula:

$$ni=\frac{e^{-Ei-Eo∕kT}}{{\sum }_n{e}^{-En-Eo∕kT}}\times 100$$

where ni is the population (in %) of the ith tautomer, Ei is the Gibbs free energy of the ith tautomer, Eo is the energy of the most stable tautomer, k is the Boltzmann constant, and T is the temperature.

EXPERIMENTAL SECTION

NMR Measurements.

Warfarin was obtained from Aldrich Market Select (AMS; product IDs: CNC_ID: 183161455, Structure_ID: 27195049), a high-reliability catalog by Sigma-Aldrich (Milwaukee, Wisconsin, USA). The NMR spectra were obtained on a Bruker Avance III 500 MHz spectrometer, operating at 500 and 125 MHz for ¹H and ¹³C, respectively, equipped with a cryogenic triple resonance probe. NMR data were processed using MNova NMR software (Mestrelab, Escondido, CA). The chemical shifts are referenced to tetramethylsilane (TMS). The measurements in DMSO-d6 solution were carried out at ambient temperature (300 K).