Indices of non-ignorable selection bias for proportions estimated from non-probability samples

Summary.

Rising costs of survey data collection and declining response rates have caused researchers to turn to non-probability samples to make descriptive statements about populations. However, unlike probability samples, non-probability samples may produce severely biased descriptive estimates due to selection bias. The paper develops and evaluates a simple model-based index of the potential selection bias in estimates of population proportions due to non-ignorable selection mechanisms. The index depends on an inestimable parameter ranging from 0 to 1 that captures the amount of deviation from selection at random and is thus well suited to a sensitivity analysis. We describe modified maximum likelihood and Bayesian estimation approaches and provide new and easy-to-use R functions for their implementation. We use simulation studies to evaluate the ability of the proposed index to reflect selection bias in non-probability samples and show how the index outperforms a previously proposed index that relies on an underlying normality assumption. We demonstrate the use of the index in practice with real data from the National Survey of Family Growth.

1. Introduction

Probability sampling and corresponding design-based approaches to inference provide a mathematical basis for making unbiased inferential statements about specific features of finite populations. Arguably the most common descriptive quantity that is used by survey researchers to describe finite populations is a proportion, which quantifies the fraction of units in a target population that has some characteristic of interest. Given the selection probabilities for units in a probability sample and any additional information that is necessary to make population inferences (e.g. non-response adjustments, complex sample design features such as sampling stratum codes and replicate weights), a survey researcher can compute an unbiased estimate of a proportion, and an estimate of its sampling variance. The random selection of elements from a population of interest into a probability sample, where all population elements have a known non-zero probability of selection, ensures that the design-weighted units that are included in the sample mirror the population in expectation, i.e. the mechanism of selection into the sample is ignorable, following the theoretical framework for missing data mechanisms that was introduced by Rubin (1978).

The effectiveness of probability sampling for studies with these descriptive objectives has been declining in the modern survey research environment. Non-contact and non-response rates continue to increase in all modes of administration (face to face, telephone, etc.) (Brick and Williams, 2013), and the costs of collecting and maintaining probability samples are steadily rising (Presser and McCulloch, 2011). Consequently, there may be non-ignorable selection bias in survey estimates from probability samples, due to non-ignorable selection and non-response mechanisms.

Because of these issues and the increasing availability of other sources of data, survey researchers are turning to the ‘big data’ that are generated by inexpensive non-probability samples of population units (Wang et al., 2015; Shlomo and Goldstein, 2015; Miller et al., 2010; Bowen et al., 2007; Brooks-Pollock et al., 2011; Braithwaite et al., 2003; Eysenbach and Wyatt, 2002). These ‘infodemiology’ data might be scraped from social media platforms such as Twitter (e.g. Myslín et al. (2013), Nascimento et al. (2014), Reavley and Pilkington (2014), McCormick et al. (2017) and Nwosu et al. (2015)), or collected from other sources such as commercial databases, on-line searches (Shlomo and Goldstein, 2015; DiGrazia, 2015) and on-line surveys (e.g. Evans et al. (2007), Brooks-Pollock et al. (2011) and Heiervang and Goodman (2011)). Several researchers have used these sources of data to estimate the prevalence of health problems in larger populations (e.g. Zhang et al. (2013), Myslín et al. (2013), Evans et al. (2007) and Koh and Ross (2006)). However, these are ultimately non-probability samples, and inferential methods that assume ignorable sample selection may not be well justified (Pasek and Krosnick, 2011; Yeager et al., 2011). Therefore, sound measures are needed of the degree to which estimates of proportions from a non-probability sample are affected by non-ignorable selection bias.

The proportion of individuals in a finite target population that has some characteristic of interest is arguably the most commonly estimated descriptive parameter in survey research. This paper proposes measures of non-ignorable selection bias for estimates of population proportions computed from non-probability samples. Little et al. (2019) proposed and assessed indices of non-ignorable selection bias for means based on an underlying normal pattern-mixture model for the survey variables. Although these indices performed reasonably well for assessing selection bias in estimates of proportions, the indices had much better performance for means based on continuous variables, as would be expected given the underlying normal model. Andridge and Little (2019) have developed estimators of proportions based on a proxy pattern-mixture model for a binary outcome, in the context of non-ignorable survey non-response; we leverage these recent developments to develop improved indices of potential non-ignorable selection bias for estimates of population proportions computed from non-probability samples.

2. Background: non-ignorable sample selection

Rubin (1976) defined joint models for the data and the missingness mechanism, and sufficient conditions under which the missingness mechanism can be ignored, for likelihood and frequentist inference. This framework can also be applied to sample selection, with the indicator for response being replaced by the indicator for selection into the sample (Rubin, 1978; Little, 2003). We review the main ideas here.

Following Little et al. (2019), let Y = (y₁, … , y_N) be survey data for each unit i=1, … , N in the population, where y_i could be a vector. Let Z be a set of fully observed auxiliary or design variables, and let the sample inclusion indicators S = (S₁, … , S_N) take the values S_i = 1 if the unit i is included in the sample and S_i = 0 otherwise. We partition Y into (Y_inc, Y_exc), where Y_inc = {y_i} for units in the sample (i.e. with S_i = 1) and Y_exc = {y_i} for units not in the sample (S_i = 0).

Under a model-based (Bayesian) framework, we assume a model for the joint distribution of Y and S conditional on Z (Little, 2003). This joint distribution is factored as

$$f_{Y,S}(Y,S\mid Z,\theta ,\varphi )=f_Y(Y\mid Z,\theta )f_{S\mid Y}(S\mid Y,Z,\varphi ),$$ (1)

where the density for Y given Z is indexed by unknown parameters θ, and the density for S given Y and Z models the selection mechanism, and is indexed by unknown parameters ϕ. The full likelihood based on the observed data (Z and S for all units and Y for units selected into the sample only) is then given by

$$L\left(\theta ,\varphi \mid Y_{\text{inc}},S,Z\right)\propto f_{Y,S}\left(Y_{\text{inc}},S\mid Z,\theta ,\varphi \right)=\int f_Y(Y\mid Z,\theta )f_{S\mid Y}(S\mid Y,Z,\varphi )\text{d}{Y}_{\text{exc}}.$$ (2)

Letting p(θ, ϕ|Z) be a prior distribution for the parameters, the corresponding posterior distributions for θ, ϕ and Y_exc are

$$\begin{array}{c}p\left(\theta ,\varphi \mid Y_{\text{inc}},S,Z\right)\propto p(\theta ,\varphi \mid Z)L\left(\theta \mid Y_{\text{inc}},S,Z\right),\\ p\left(Y_{\text{exc}}\mid Y_{\text{inc}},S,Z\right)\propto \int p\left(Y_{\text{exc}}\mid Y_{\text{inc}},S,Z,\theta ,\varphi \right)p\left(\theta ,\varphi \mid Y_{\text{inc}},S,Z\right)\text{d}\theta \text{d}\varphi .\end{array}$$ (3)

Modelling the selection mechanism is challenging, and Rubin (1976) showed that it is unnecessary if the mechanism is ignorable. Two sufficient conditions for ignorability for Bayesian inference are selection at random (SAR) and Bayesian distinctness. SAR means that S and Y_exc are independent after conditioning Y_inc, Z and ϕ, i.e. f_S|Y (S|Y, Z, ϕ)=f_S|Y (S|Y_inc, Z, ϕ) for all Y_exc. Bayesian distinctness means that θ and ϕ have independent prior distributions, i.e. p(θ, ϕ|Z)=p(θ|Z)p(ϕ|Z). These conditions together imply that

$$\begin{array}{c}p\left(\theta \mid Y_{\text{inc }},Z\right)\propto p(\theta \mid Z)L\left(\theta \mid Y_{\text{inc }},Z\right),\\ p\left(Y_{\text{exc }}\mid Y_{\text{inc }},Z\right)\propto \int p\left(Y_{\text{exc }}\mid Y_{\text{inc }},Z,\theta \right)p\left(\theta \mid Y_{\text{inc }},Z\right)\text{d}\theta .\end{array}$$ (4)

Thus, when the ignorability assumption is correct, the model for the selection mechanism (the model for S) does not affect inferences about the parameters θ.

Probability sampling is a special form of SAR, where the selection mechanism is known and may depend on auxiliary variables Z but not on the survey outcomes Y. Thus, f_S|Y (S|Y, Z, ϕ) reduces to f_S|Y(S|Z). Probability sampling is stronger than SAR in three important respects. First, under complete response it is automatically valid, and not an assumption. Second, it implies that, conditional on Z, inclusion in the sample is independent of Y, and also any other unobserved variables that might be included in a model (e.g. latent variables). Third, it implies that S is independent of Y_inc, whereas SAR requires only the weaker assumption that S and Y_exc are independent after conditioning on Y_inc and Z. Although these properties make probability sampling highly desirable, it is not always attainable. Researchers making inferences based on a non-probability sample often implicitly assume SAR. However, although weaker than probability sampling, SAR may not be valid for non-probability samples. The indices of non-ignorable selection bias of Little et al. (2019) are designed to quantify the potential selection bias in estimated means of continuous survey variables. These indices use SAR as a starting point and quantify changes in estimates of the mean of Y if the SAR assumption does not hold (to varying degrees). Here we modify these indices to be specifically applicable to proportions.

3. Indices of non-ignorable selection bias for proportions

Let Y be a binary variable taking values 0 or 1, and assume that Y arises from an underlying normal latent variable U, with Y = 1 when U>0, and Y = 0 when U<0. Y is only available for cases that are selected in the non-probability sample. Let X be a proxy variable that is available for all units in the target population that has a reasonably strong correlation with the latent variable U. X may itself be a function of a vector of auxiliary variables Z, as in Andridge and Little (2018). In this case, Z must be available for all units in the non-probability sample, and either sufficient statistics (means, variances and covariances) or microdata for Z must be available for the non-selected units. As previously defined, let S be an indicator of being selected for the non-probability sample. Finally, let V be a set of other covariates that are independent of Y and X for selected units but that may be related to selection (i.e. associated with S).

We assume the following proxy pattern-mixture model (Andridge and Little, 2011, 2018) for U and X, conditional on V and S:

$$(U,X\mid V,S=j)~N_2\left\{\left(\begin{array}{c}{\beta }_{u0\cdot v}^{(j)}+{\beta }_{uv\cdot v}^{(j)}V\\ {\beta }_{x0\cdot v}^{(j)}+{\beta }_{xv\cdot v}^{(j)}V\end{array}\right),\left(\begin{array}{cc}{\sigma }_{uu\cdot v}^{(j)}& {\sigma }_{ux\cdot v}^{(j)}\\ {\sigma }_{ux\cdot v}^{(j)}& {\sigma }_{xx\cdot v}^{(j)}\end{array}\right)\right\}.$$ (5)

Here ${\beta }_{u0\cdot v}^{(j)}$ is the intercept, ${\beta }_{uv\cdot v}^{(j)}$ the coefficient of V and ${\sigma }_{uu\cdot v}^{(j)}$ the residual variance in the regression of U on V for pattern S=j. This model implies probit regressions of Y on X for the selected and non-selected cases.

The parameters in model (5) are not all identified. To identify them, we assume that selection into the sample is an unspecified function of V and a known linear combination of X and U:

$$\text{Pr}(S=1\mid U,X,V)=g\left\{(1-\varphi )X^{*}+\varphi U,V\right\}.$$ (6)

Here $X^{*}=X\surd \left({\sigma }_{uu}^{(1)}/{\sigma }_{xx}^{(1)}\right)$ is the proxy X rescaled to have the same variance as U in the population of selected cases, and ϕ is a sensitivity parameter, which we assume to be between 0 and 1 (inclusively). If we assume also that V is uncorrelated with X for non-selected cases (S=0) and that X is the best predictor of U for non-selected cases, then model (5) reduces to

$$\begin{array}{c}(U,X\mid V,S=j)~N_2\left\{\left({\mu }_u^{(j)},{\mu }_x^{(j)}\right),{\Sigma }^{(j)}\right\},\\ {\Sigma }^{(j)}=\left(\begin{array}{cc}{\sigma }_{uu}^{(j)}& {\rho }_{ux}^{(j)}\surd ({\sigma }_{uu}^{(j)}{\sigma }_{xx}^{(j)})\\ {\rho }_{ux}^{(j)}\surd ({\sigma }_{uu}^{(j)}{\sigma }_{xx}^{(j)})& {\sigma }_{xx}^{(j)}\end{array}\right).\end{array}$$ (7)

For the proof, see the on-line supplementary materials. Note that this model excludes the covariates V that are independent of Y and X but are related to selection (S). The inclusion of V in model (5) makes the assumed selection mechanism (6) more general, but our methods do not rely on the existence of such covariates.

Without loss of generality, we set $(U\mid S=1)={\sigma }_{uu}^{(1)}=1$. We note that ${\rho }_{ux}^{(j)}$, which is the correlation between latent U and X for selected (j=1) and non-selected (j=0) samples, is the biserial correlation of X and Y for pattern j (Tate, 1955). Of primary interest is the marginal mean of Y, which can be expressed as a function of the pattern-mixture model:

$${\mu }_y=\text{Pr}(Y=1)=\text{Pr}(U>0)=\pi \Phi \left({\mu }_u^{(1)}\right)+(1-\pi )\Phi \left({\mu }_u^{(0)}/\surd {\sigma }_{uu}^{(0)}\right),$$ (8)

where Φ(z) denotes the cumulative distribution function of the standard normal distribution, evaluated at z, and π is the proportion of selected cases in the population.

The parameters in the probit proxy pattern-mixture model (7) for the non-selected units (S =0), ${\mu }_u^{(0)}$, ${\sigma }_{uu}^{(0)}$ and ${\rho }_{ux}^{(0)}$, are just identified given the assumption about the selection mechanism in equation (6). Following Little et al. (2019), the parameter ϕ in the selection mechanism provides a measure of the degree of non-random selection after conditioning on X. If ϕ=0, the probability of being selected in the non-probability sample depends only on X and V, and thus selection is at random (SAR) since both are fully observed. In contrast, if ϕ=1, the probability of being selected in the non-probability sample depends on the value of the latent variable U (and thus the binary variable of interest, Y) and on V, and thus selection is not at random. As described in Andridge and Little (2011, 2018), the function g does not have to be specified for estimates based on this model to be valid.

Given these restrictions, Andridge and Little (2018) showed that the unidentified parameters ${\mu }_u^{(0)}$ and ${\sigma }_{uu}^{(0)}$ for a specific choice of ϕ are given by

$$\begin{array}{l}{\mu }_u^{(0)}={\mu }_u^{(1)}+\frac{\varphi +(1-\varphi ){\rho }_{ux}^{(1)}}{\varphi {\rho }_{ux}^{(1)}+(1-\varphi )}\frac{{\mu }_x^{(0)}-{\mu }_x^{(1)}}{\surd {\sigma }_{xx}^{(1)}},\hfill \\ {\sigma }_{uu}^{(0)}=1+{\left\{\frac{\varphi +(1-\varphi ){\rho }_{ux}^{(1)}}{\varphi {\rho }_{ux}^{(1)}+(1-\varphi )}\right\}}^2\frac{{\sigma }_{xx}^{(0)}-{\sigma }_{xx}^{(1)}}{{\sigma }_{xx}^{(1)}}.\hfill \end{array}$$ (9)

The difference of the proportion for selected cases from the overall proportion is therefore

$$\begin{array}{l}{\mu }_y^{(1)}-{\mu }_y={\mu }_y^{(1)}-\left\{\pi \Phi \left({\mu }_u^{(1)}\right)+(1-\pi )\Phi \left({\mu }_u^{(0)}/{\surd \sigma }_{uu}^{(0)}\right)\right\}\\ ={\mu }_y^{(1)}-\pi \Phi \left({\mu }_u^{(1)}\right)-(1-\pi )\times \Phi \left(\left\{{\mu }_u^{(1)}+\frac{\varphi +(1-\varphi ){\rho }_{ux}^{(1)}}{\varphi {\rho }_{ux}^{(1)}+(1-\varphi )}\frac{{\mu }_x^{(0)}-{\mu }_x^{(1)}}{\surd {\sigma }_{xx}^{(1)}}\right\}/\surd \left[1+{\left\{\frac{\varphi +(1-\varphi ){\rho }_{ux}^{(1)}}{\varphi {\rho }_{ux}^{(1)}+(1-\varphi )}\right\}}^2\frac{{\sigma }_{xx}^{(0)}-{\sigma }_{xx}^{(1)}}{{\sigma }_{xx}^{(1)}}\right]\right).\end{array}$$

For a given choice of ϕ, replacing the parameters by estimates (with the circumflex notation) yields a measure of the unadjusted selection bias for the proportion, MUBP(ϕ), for ${\widehat{\mu }}_y^{(1)}$:

$$\begin{array}{l}\text{MUBP}(\varphi )={\widehat{\mu }}_y^{(1)}-{\widehat{\mu }}_y\\ ={\widehat{\mu }}_y^{(1)}-\widehat{\pi }\Phi \left({\widehat{\mu }}_u^{(1)}\right)-(1-\widehat{\pi })\times \Phi \left(\left\{{\widehat{\mu }}_u^{(1)}+\frac{\varphi +(1-\varphi ){\widehat{\rho }}_{ux}^{(1)}}{\varphi {\widehat{\rho }}_{ux}^{(1)}+(1-\varphi )}\frac{{\widehat{\mu }}_x^{(0)}-{\widehat{\mu }}_x^{(1)}}{{\surd \sigma }_{xx}^{(1)}}\right\}/\surd \left[1+{\left\{\frac{\varphi +(1-\varphi ){\widehat{\rho }}_{ux}^{(1)}}{\varphi {\widehat{\rho }}_{ux}^{(1)}+(1-\varphi )}\right\}}^2\frac{{\widehat{\sigma }}_{xx}^{(0)}-{\widehat{\sigma }}_{xx}^{(1)}}{{\widehat{\sigma }}_{xx}^{(1)}}\right]\right).\end{array}$$ (10)

Calculation of the index (10) for a given choice of ϕ therefore requires estimates of π, which may be close to 0 for larger populations; the estimated biserial correlation of X and Y based on the selected non-probability sample, ${\widehat{\rho }}_{ux}^{(1)}$, and sufficient statistics for the proxy variable X for both the selected and the non-selected portions of the target population. We note that this last piece is a stronger requirement than the indices for continuous Y in Little et al. (2019), where only the mean of X was required and not its variance. Maximum likelihood (ML) estimates of these sufficient statistics for the selected cases can easily be computed by using the selected cases in the non-probability sample.

We estimate ${\rho }_{ux}^{(1)}$ by using the ‘two-step’ approach, which was originally proposed by Olsson et al. (1982), which outperformed ML when X is not normally distributed in simulations in Andridge and Little (2018). A desirable property of this approach is that, unlike ML, the estimated mean of the latent variable U in the selected sample is given by ${\widehat{\mu }}_u^{(1)}={\Phi }^{-1}\left({\widehat{\mu }}_y^{(1)}\right)$, i.e. the inverse probit function of the mean of Y in the selected sample. Parameters other than ${\rho }_{ux}^{(1)}$ are estimated by ML, so we call the resulting estimates ‘modified’ ML (MML).

Usually X is not directly available but instead computed as the linear predictor from a fitted probit model. In this case, steps should be taken to prevent optimistic estimation of ${\rho }_{ux}^{(1)}$ based on potential overfitting of the probit model to the data from the non-probability sample. In this case, we recommend computing ${\widehat{\rho }}_{ux}^{(1)}$ on the basis of multifold cross-validation. To do this, the probit model would be fitted to randomly selected subsamples of the non-probability sample, and the value of X for all observations calculated from each fitted model. Averaging the set of X-values across folds produces a single X-value for each observation; this cross-validated X should then be used to compute ${\widehat{\rho }}_{ux}^{(1)}$. The R functions that are provided in the on-line supplementary materials and available from https://github.com/bradytwest/IndicesOfNISB include a function (cv.glm) implementing this cross-validation step, the output of which can then be passed to another function that is used for two-step estimation of the biserial correlation.

Estimates of the sufficient statistics for X for the non-selected sample may be less readily available but, assuming a negligible sampling fraction, reasonable estimates based on the large number of non-selected cases in the target population could be computed from a population census or large survey that also collects measures of X. If X is the linear predictor from a probit regression of Y on Z in the non-probability sample, the mean of X could be computed by applying the same probit model coefficients estimated from the non-probability sample to overall population means on the auxiliary variables in the vector Z. In the presence of a non-negligible sampling fraction, and given an overall marginal population mean for X (denoted μ_x), the mean of X for non-selected cases could be approximated as ${\widehat{\mu }}_x^{(0)}=\left({\widehat{\mu }}_x-\pi {\widehat{\mu }}_x^{(1)}\right)/(1-\widehat{\pi })$. The variance of X for non-selected cases could be assumed to be the same as the population variance (in the absence of any additional information on changes in the element variance depending on selection).

When ϕ=0, selection into the non-probability sample is SAR, and the selection mechanism is ignorable. When ϕ=1, the non-ignorable selection mechanism depends entirely on U and V, but not on the proxy X. Following Little et al. (2019), we recommend computing the interval that is defined by [MUBP(0), MUBP(1)] to assess the range of potential selection bias values, depending on the choice of ϕ. As a compromise between the two extreme cases defining this interval, we recommend MUBP(0.5) as an ‘estimate’ of the bias, as this choice represents equal dependence of selection on the proxy X and the underlying latent value of the variable of interest U.

We also note that the MUBP-index is not always monotonic in ϕ over the [0,1] range. This property of the MUBP-index depends on the estimated values of ${\mu }_u^{(1)}$ and ${\rho }_{ux}^{(1)}$ (i.e. the mean of Y and the strength of the proxy in the selected sample) and how far apart the means and variances of the proxy variable X are for the selected and non-selected cases. Letting the standardized differences in the selected and non-selected means and variances of X be denoted $d_{\mu }=({\widehat{\mu }}_x^{(0)}-{\widehat{\mu }}_x^{(1)})/{\surd \sigma }_{xx}^{(1)}$ and $d_{\sigma }=\left({\widehat{\sigma }}_{xx}^{(0)}-{\widehat{\sigma }}_{xx}^{(1)}\right)/{\widehat{\sigma }}_{xx}^{(1)}$, then MUBP will be non-monotonic over the [0,1] interval if and only if

$${\widehat{\rho }}_{ux}^{(1)}<\frac{d_{\mu }}{d_{\sigma }{\widehat{\mu }}_u^{(1)}}<\frac{1}{{\widehat{\rho }}_{ux}^{(1)}}.$$

This condition will be satisfied when there are extreme differences between X in the selected and non-selected populations, there are large differences in the variance of X for selected and non-selected cases and/or weak correlation between U and X. If we assume that the proxy variances are equal for the selected and non-selected cases, as was suggested in the absence of information about the variance of X for the non-selected cases, then d_σ = 0, and MUBP is automatically monotone over the [0,1] interval.

At least a moderate biserial correlation between Y and X is important for any index to give an effective indication of selection bias. If this correlation is weak, [MUBP(0), MUBP(1)] will be very wide, sometimes even reaching the Manski (2016) bounds that are created by assuming that non-selected cases all have either Y = 0 or Y = 1.

We also consider a Bayesian approach to making inference about the MUBP-index, which enables us to account for uncertainty in the estimation of the coefficients of Z in the probit regression of Y on Z when forming the proxy variable X. We follow the Gibbs sampler approach that was outlined in section 4.2 of Andridge and Little (2018), which like the two-step estimates that were described earlier requires the availability of sufficient statistics for Z for the selected and non-selected cases. Since there is no information in the data about ϕ, one could follow two possible approaches. One option is to fix ϕ and to proceed with the Gibbs sampler (see below for details) for all other parameters, assuming non-informative prior distributions for the identified parameters. This approach accounts for uncertainty in the estimate of MUBP(0) and MUBP(1); one could form 95% credible intervals for both MUBP(0) and MUBP(1), enabling a description of the uncertainty in each ‘limit’ of the interval. An alternative approach is to draw values of ϕ from a prior distribution, e.g. uniform(0,1), and then proceed with the Gibbs sampler.

To initiate the Gibbs sampler, we first fit the probit regression model to the data on Y and Z from the cases that were selected for the non-probability sample, which yields starting values for the regression coefficients in this model. We then create the proxy variable X as a function of the coefficients. An iteration of the sampler (conditional on either a random draw of ϕ or a fixed choice of ϕ) then starts with draws of the latent variable U from a truncated normal distribution conditional on X (and thus also conditional on the probit model coefficients). We then select posterior draws of the regression coefficients in the probit model given the previous augmented values for U and recreate the proxy variable X given the current draws of the regression coefficients. This data augmentation approach in each iteration then enables posterior draws of the pattern-mixture model parameters that are defined in equations (7) and (9), following the explicit steps and constraints that were outlined in Andridge and Little (2011). We then generate the corresponding posterior draw of MUBP(ϕ) in equation (10) on the basis of the parameter draws. The Gibbs sampler then proceeds to the next iteration. Given a large number of draws of MUBP(ϕ) we can then generate 95% credible intervals for MUBP(ϕ).

4. Simulation study

We now describe a simulation study that was designed to illustrate the ability of MUBP(ϕ) to detect selection bias in estimated proportions based on simulated data and to show what can go wrong when applying the normal model of Little et al. (2019). All simulations and data analysis were performed by using the R statistical computing environment (R Core Team, 2018), and the code is available on request.

We generated populations of size 10000 containing a binary outcome variable Y and a single continuous auxiliary variable Z as follows. A single auxiliary variable z_i ~N(0, 1) was generated for all units. Then, for each of ρ_ux ={0.2, 0.5, 0.8}, a latent variable u_i was generated as [u_i|z_i]~N(α₀+α₁z_i, 1) with α₁=ρ_ux/√(1 − ρ_ux²). Then an observed binary variable y_i was created as y_i=1 if u_i>0 and y_i=0 otherwise. Note that, for this simulation, ρ_ux is the biserial correlation between Y and the proxy X=α₀ + α₁Z for the entire population: not for the selected sample. In this simulation Z was univariate, and thus ρ_ux≡corr(U, X)=corr(U, Z), but more generally Z could be a set of auxiliary variables and X the linear predictor from a probit regression of Y on Z for selected cases as described earlier. We set ${\alpha }_0={\Phi }^{-1}\left({\mu }_Y\right)\surd \left(1+{\alpha }_1^2\right)$ so that E(Y)=μ_Y. To assess how the indices performed for proportions of different magnitude, we simulated data by using μ_Y = {0.1, 0.3, 0.5}.

The sample selection indicator S_i was generated according to a logistic model,

$$\text{logit}\left\{\text{Pr}\left(s_i=1\mid z_i,u_i\right)\right\}={\beta }_0+{\beta }_Z{z}_i+{\beta }_U{u}_i,$$

and values of y_i were deleted for non-selected units, i.e. when s_i=0. We simulated a wide range of selection mechanisms, from selection dependent entirely on Z to dependent entirely on U, by varying the values of {β_Z, β_U}, as shown in Table 1, with the value of β₀ chosen to result in a 5% sampling fraction. The selection bias varied with β_Z and β_U, with larger values of β_Z or β_U leading to larger bias. We note that the resulting bias in the selected mean varied not only by selection mechanism but was also a function of ρ_ux and μ_Y. Once u_i had been used for data generation and sample selection, it was discarded.

Table 1.

Values of {β_Z, β_U} (log-odds ratios) that determine the selection mechanism for the simulation study

Selection mechanism	Values of {βZ,βU}
Z	{0.1,0}, {0.2,0}, {0.3,0}, {0.4,0}, {0.5,0}
3Z+U	{0.075,0.025}, {0.15,0.05}, {0.225,0.075}, {0.3,0.1}, {0.375,0.125}
Z+U	{0.05,0.05}, {0.1,0.1}, {0.15,0.15}, {0.2,0.2}, {0.25,0.25}
Z+3U	{0.025,0.075}, {0.05,0.15}, {0.075,0.225}, {0.1,0.3}, {0.125,0.375}
U	{0,0.1}, {0,0.2}, {0,0.3}, {0,0.4}, {0,0.5}

The process of generating {z_i, u_i, y_i, s_i} was repeated 1000 times for each combination of ρ_ux, μ_Y and {β_Z, β_U}. For each simulated data set, we calculated the indices MUBP(0), MUBP(0.5) and MUBP(1) as defined in equation (10), using a probit model of Y on Z (for selected cases) to estimate the proxy X (for all cases). We used the two-step estimator to obtain an estimate of the biserial correlation between the selected cases without cross-validation, since in this controlled simulation setting there was only one auxiliary variable Z. We also computed credible intervals by implementing the fully Bayesian approach for the MUBP, with draws of ϕ from a uniform(0,1) distribution, 20 burn-in draws of the Gibbs sampler and 1000 subsequent iterations. For comparison, we also calculated indices that were proposed by Little et al. (2019). Since the outcome is binary, we elected to calculate their measure of unadjusted bias, MUB(ϕ), instead of their standardized measure of unadjusted bias, SMUB(ϕ), so that it would be more directly comparable with MUBP(ϕ). We also calculated credible intervals for MUB(ϕ) by using a uniform prior for ϕ. For both MUBP- and MUB-indices, we used sufficient statistics for the auxiliary variable Z for the non-selected cases when calculating the indices though, with a 5% sampling fraction, results would probably not differ much if sufficient statistics for the entire population were used.

To assess the performance of the indices, we calculated the correlation of each index with the true estimated bias for each simulated data set, defined as the population mean of Y minus the mean of Y for the selected cases. We also assessed the ability of the ML- or MML-based intervals [MUB(0), MUB(1)] and [MUBP(0), MUBP(1)] to cover the true estimated bias, as well as the coverage of the Bayesian intervals for MUBP(ϕ) and MUB(ϕ).

The median estimated index values across replicates for MUBP(ϕ) and MUB(ϕ) for ϕ={0, 0.5, 1} are shown in Fig. 1, for the scenarios with E[Y]=0.3. For all selection mechanisms and correlations between the proxy and the outcome, both sets of indices ‘track’ with the estimated bias; as the estimated bias goes up, so does the index. When selection is a function of Z only, both MUBP(0) and MUB(0) produce unbiased estimates of bias for all proxy strengths (lines overlap on the plot). When selection is only a function of U, MUBP(1) is approximately unbiased and there is a substantial upward bias in MUB(1). More interesting, however, are the intermediate mechanisms, where selection is a function of both Z and U. In these cases, the intervals [MUBP(0), MUBP(1)] and [MUB(0), MUB(1)] cover the truth, with ϕ=0.5 coming closest to the truth most of the time. However, the interval widths are much wider for the normal model (MUB) than for the probit model (MUBP), even when the proxy variable is highly correlated with the outcome. Interestingly, the intervals based on the normal model are more exaggerated when selection depends more heavily on Z, the fully observed variable. Importantly, for weaker proxies (lower correlations), the normal model intervals have an implausible bound for ϕ=1, i.e. produce estimates of E[Y] that are outside the (0,1) interval, whereas the probit model intervals bound at the upper limit (i.e. E[Y]=1). In Fig. 1, the hitting of the upper bound can be seen by the curving of the full MUBP(1) line for selection based on Z and a weak proxy. Although the probit model produces plausible bounds in the presence of a weak proxy, these bounds may not be useful in practice as they may cover nearly the whole range from 0 to 1. Without auxiliary data that are moderately to strongly related to the binary Y-variables, we cannot estimate the bounds of potential selection bias with reasonable precision. In practice, we do not know the true selection mechanism, but using the probit model will give tighter intervals and produce index values that more closely reflect the bias, with both strong and weak proxies. Similar patterns are seen with E[Y]=0.1 and E[Y]=0.5 (on-line supplemental Figs 1 and 2).

Fig. 1.

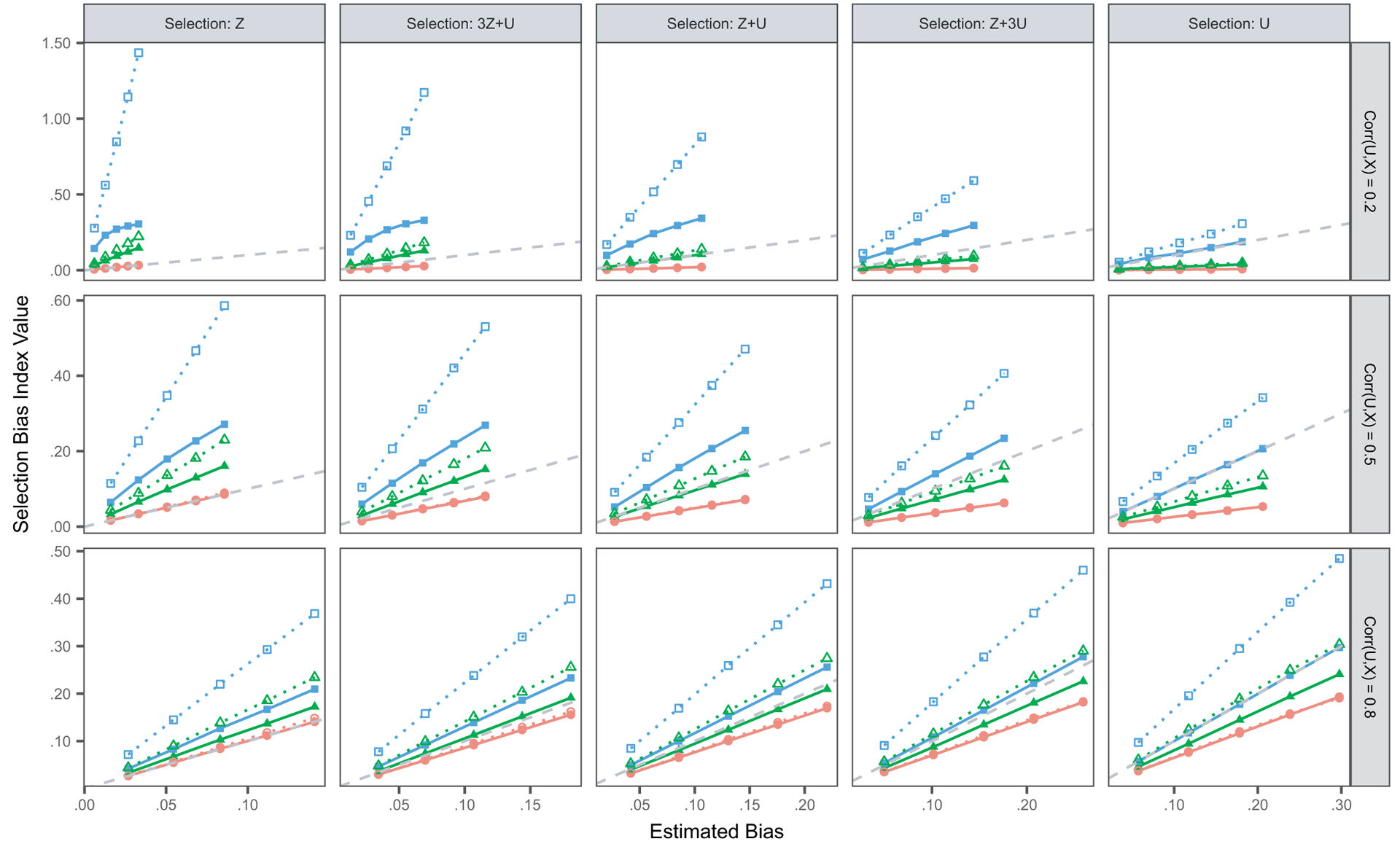
MUBP(ϕ) from the probit model and MUB(ϕ) from the normal model versus the true estimated bias, shown for combinations of the biserial correlation corr(U, X)=ρ_ux (rows) and the selection mechanism (columns), for E[Y]=0.3 (results are medians across 1000 simulated data sets for each scenario): ●, probit, MUBP(0); ▲, probit, MUBP(0.5); ■, probit, MUBP(1); ○, normal, MUBP(0); △, normal, MUBP(0.5); □, normal, MUBP(1); – – –, equality (index=estimated bias)

Not surprisingly, all indices have higher correlation with the true estimated bias for stronger proxies than for weaker proxies, as shown in Fig. 2. Generally, the patterns of correlations are similar across selection mechanisms, though there is more separation between the models (probit versus normal) for selection mechanisms that have larger dependence on Z. For rare outcomes (E[Y]=0.1), the MUBP(ϕ) index has a higher correlation with the estimated bias than the MUB(ϕ) index does across all selection mechanisms and proxy strengths. Strikingly, when E[Y]=0.1 and the proxy is weak, MUB(1) has essentially zero correlation with the truth, whereas MUBP(ϕ) has a noticeably higher correlation. This dramatic difference between the two models appears to be reduced when the mean of Y nears 0.5; some differences are still seen for E[Y]=0.3, but there are very few differences when E[Y]=0.5.

Fig. 2.

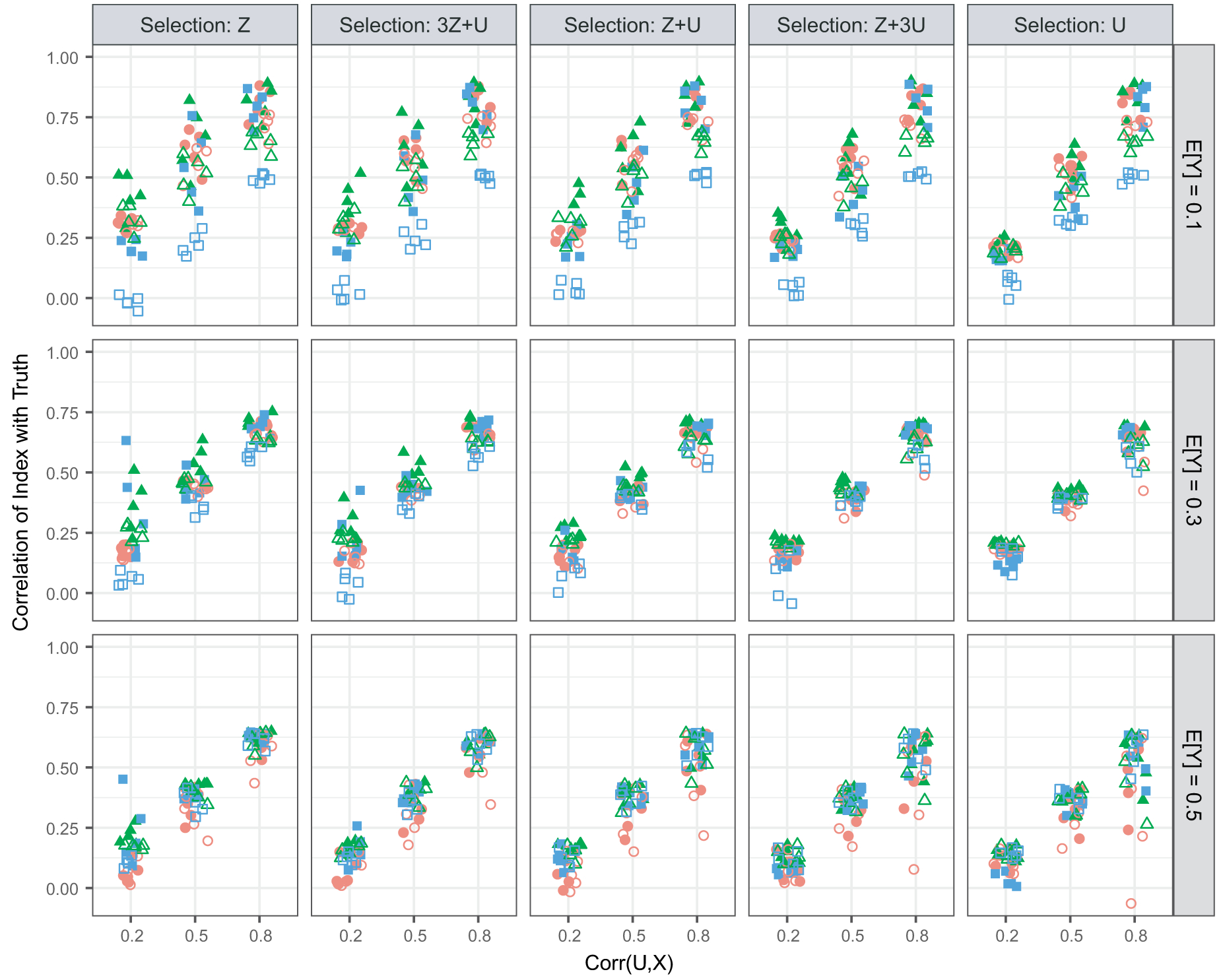
Correlation between MUBP(ϕ) and true estimated bias, and between MUB(ϕ) and true estimated bias, versus the biserial correlation corr(U, X)=ρ_ux, for combinations of selection mechanism (columns), μ_Y (rows) and ϕ (shape) (results from all estimated biases (all values of β_Z and β_U) are all plotted together; correlations are estimated from 1000 simulated data sets for each scenario): ●, probit, MUBP(0); ▲, probit, MUBP(0.5); ■, probit, MUBP(1); ○, normal, MUBP(0); △, normal, MUBP(0.5); □, normal, MUBP(1)

Fig. 3 shows coverage of intervals based on ML or MML and 95% Bayesian credible intervals for a subset of the selection models; results for all models are available in the on-line supplemental Fig. 3. Coverage of the Bayesian intervals is higher than that of the MML-based intervals for both models. The ML-based intervals tend to be wider and to have higher coverage for the normal model (MUB) than the MML-based intervals for the probit model (MUBP). At the two extremes of the selection models (based on Z; based on U), coverage is only around 50% for the probit model MML-based intervals regardless of proxy strength. This is not unexpected, since in these cases MUBP(0) and MUBP(1) are actually unbiased estimates. If the sampling distributions of MUBP(0) and MUBP(1) are roughly symmetric, we would expect the interval to cover the truth about only 50% of the time. The Bayesian credible intervals for MUBP(ϕ) show higher coverage at these extremes, with coverage at the nominal level (95%) for small estimated biases but decreasing as the bias increases.

Fig. 3.

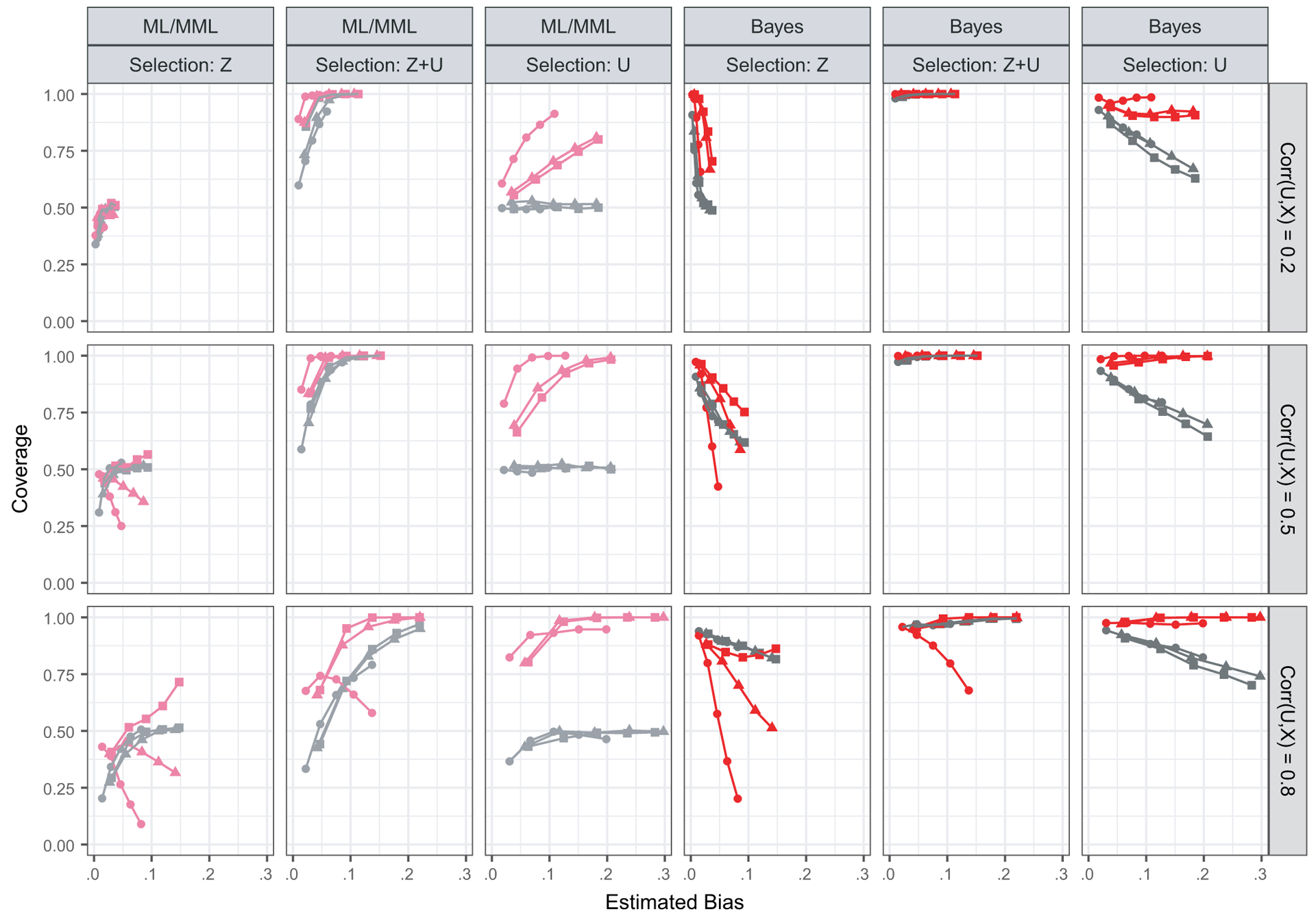
Coverage of [MUBP(0), MUBP(1)] and [SMUB(0), SMUB(1)] ML or MML intervals, and Bayesian credible intervals, shown as a function of the true estimated bias (x-axis), selection mechanism and estimation method (columns), proxy strength (rows) and E[Y] (shape) (coverages are estimated from 1000 simulated data sets): ●, normal–ML; ●, probit–MML; ■, normal–Bayes; ■, probit–Bayes; ●, E[Y]=0.1; ▲, E[Y]=0.3; ■, E[Y]=0.5

Coverage of both types of probit intervals does not depend on E[Y], but coverage for the normal model intervals does. For stronger proxies, coverage is lower for the normal model (both interval types) as E[Y] moves away from 0.5; more so for mechanisms that depend more on Z. Conversely, for weaker proxies and non-ignorable selection mechanisms, the coverage is higher for smaller E[Y], reflecting the fact that in these cases the intervals are very wide.

Overall, the MUBP-indices perform well across a variety of selection mechanisms. These probit model indices provide a more precise estimate of bias compared with the MUB-indices based on the normal model and do not return implausible estimates. As was suggested in Little et al. (2019) for the normal-based indices, at least a moderately strong predictor of Y is necessary for MUBP to be useful. In the simulation, scenarios with biserial correlations of 0.5 or 0.8 had stronger correlations between the estimated bias and the true bias than scenarios with a biserial correlation of 0.2. Note, however, that the biserial correlation is always greater than the Pearson correlation between X and binary Y, and how much larger it is depends on the mean of Y. In this simulation, the Pearson correlation ranged from 0.12 to 0.64, and a correlation between Y and X of 0.3 or greater appears to provide reasonable estimates of the selection bias.

5. Application

We now revisit an analysis of real survey data from the National Survey of Family Growth (NSFG) that was presented in Little et al. (2019). In this analysis, Little et al. (2019) used the publicly available NSFG sample as a hypothetical population and took the subsample of smartphone users as a hypothetical non-probability sample. They calculated their normal model-based selection bias indices, SMUB(ϕ), to evaluate potential selection bias in sample means for a variety of variables. Importantly, the SMUB(ϕ) index was applied to means estimated for a mixture of different types of survey variables, including binary variables. Of the 16 proportions that were analysed, the [SMUB(0), SMUB(1)] interval only ‘covered’ the actual bias in the smartphone proportions eight times. These results suggested that there was room for improvement in the performance of these indices for these binary variables. In the present application, we follow the same approach, and we seek to evaluate the improvement in coverage of actual bias based on the MUBP-measures that are proposed in the present study.

For each of the 16 binary variables in the NSFG data, we initially fitted probit regression models to the data from the smartphone sample, regressing the binary variable Y on the same covariates Z that were considered by Little et al. (2019). Values of the linear predictor X for the underlying variable U were then computed for both the selected cases and the non-selected cases, and the fivefold cross-validation approach that was described earlier was used for two-step estimation of the biserial correlation for each variable. We then computed the MUBP-indices that are defined in equation (10) and compared these with the known true difference between the proportion in the smartphone sample and that for the full ‘population’.

We also implemented the fully Bayesian inference approach for the MUBP-index that was described earlier, with draws of ϕ from a uniform (0,1) distribution, 20 burn-in draws of the Gibbs sampler and 2000 subsequent iterations. We then examined whether 95% credible intervals for the MUBP covered the true bias, expecting that coverage may improve (relative to the ML- or MML-based intervals) from exploitation of the uncertainty in the estimated parameters enabled by the presence of sufficient statistics for Z on the non-selected NSFG cases.

Table 2 compares the results of applying both the normal model of Little et al. (2019) and our probit model to the NSFG data. Though Little et al. (2019) reported standardized measures of bias (SMUB), Table 2 contains the non-standardized estimates (MUB) for direct comparison with the MUBP-index. Notably, the selection fractions for this hypothetical application were quite different from 0: for variables that were measured on males, the selection fraction was 0.788 (6942 smartphone users out of 8809 males) and, for variables that were measured on females, the selection fraction was 0.817 (8981 smartphone users out of 10991 females). Table 2 also includes the cross-validated ‘two-step’ estimates of the biserial correlations of the proxy variable X with the outcome Y among the selected cases.

Table 2.

True estimated bias for each of the 16 NSFG proportions, along with [MUB(0), MUB(1)] intervals based on the normal model, [MUBP(0), MUBP(1)] intervals based on the probit model and 95% credible intervals for MUBP based on the fully Bayesian approach^†

Binary NSFG variable (males or females)	Cross-validated biserial correlation (Y,X)	Population proportion	Smartphone proportion	True estimated bias (× 1000)	Results for normal model (MUB)		Results for probit model (MUBP)
					[MUB(0), Cover MUB(1)] TEB?		[MUBP(0), MUBP(l)] and Bayesian credible intervals for selected limits	MML interval cover TEB?	95% credible interval for MUBP	Bayesian interval cover TEB?
Never been married (males)	0.817	0.566	0.555	−11	[−8, −21]	Yes	[−10, −14]	Yes	[−7, −16]	Yes
Never been married (females)	0.726	0.468	0.466	−2	[−1,−4]	Yes	[−2, −5]	Yes	[i, −7]	Yes
Age = 30–44 years (males)	0.654	0.435	0.433	−2	[16,47]	No	[16, 39]	No	[14, 38]	No
							[(13,19), (31,46)]
Age = 30–44 years (females)	0.612	0.467	0.460	−8	[8,29]	No	[8, 24]	No	[7, 24]	No
							[(6,11), (17,31)]
Currently employed (males)	0.603	0.689	0.729	40	[16,58]	Yes	[16, 46]	Yes	[16, 45]	Yes
Children present in HU (males)	0.573	0.371	0.366	−5	[−2, −10]	Yes	[−2, −4]	Closet	[3, −10]	Yes
							[(−5,0), (−15,7)]
Currently employed (females)	0.482	0.626	0.657	31	[12,74]	Yes	[12, 50]	Yes	[11,47]	Yes
Children present in HU (females)	0.454	0.548	0.538	−10	[−10.5, −76]	No	[−10, −47]	Yes	[−10, −45]	Yes
‘Other’ race (females)	0.451	0.553	0.562	9	[11,85]	No	[11,54]	Close‡	[9, 51]	Yes
							[(9,13), (42,65)]
‘Other’ race (males)	0.410	0.590	0.596	6	[15, 135]	No	[14, 102]	No	[11,85]	No
							[(12,17), (78,129)]
Education: ‘some college’ (males)	0.368	0.299	0.322	23	[5,67]	Yes	[5, 17]	Close‡	[3, 21]	Close‡
							[(3,7), (5,29)]
Education: ‘some college’ (females)	0.340	0.328	0.342	14	[1,22]	Yes	[2, 16]	Yes	[0, 16]	Yes
Region =‘south’ (females)	0.274	0.438	0.445	7	[−3, −65]	No	[−3, −36]	No	[−2, −34]	No
							[(−5,−2), (−52,−20)]
Region =‘south’ (males)	0.253	0.418	0.431	13	[−1, −31]	No	[−1, −20]	No	[4, −26]	No
							[(−3,1), (−46,10)]
Income: $20000–59999 (males)	0.249	0.417	0.422	5	[−3, −72]	No	[−3, −123]	No	[−1, −120]	No
							[(−5,−1), (−130,−38)]
Income: $20000–59999 (females)	0.156	0.388	0.393	5	[0, 34]	Yes	[1, 72]	Yes	[−2, 72]	Yes

^†Values multiplied by 1000.

^‡Close, allowing for uncertainty in the input estimates (see the Bayesian credible intervals for selected limits).

As was seen in the simulation study, the MUBP-intervals are significantly narrower than the intervals for the same proportions based on the MUB-index, reflecting the sensitivity of the MUBP-index to the limited range and discrete nature of the binary survey variables. MUBP(ϕ) therefore provides a more precise sense of the potential selection bias that is associated with these estimates of the proportions than the normal-based estimates, and this result holds regardless of the biserial correlation. Importantly, MUBP(ϕ) tracks just as well with the true bias as MUB(ϕ) does; the correlations of MUBP(0.5) and MUB(0.5) with the true bias are 0.51 and 0.52 respectively. We therefore prefer the more precise MUBP-index to the MUB-index for binary Y-variables.

10 of the 16 estimated bias values are either directly covered or very nearly covered by the proposed [MUBP(0), MUBP(1)] interval, representing a slight increase in coverage relative to the normal model. Thus the gain in precision does not seem to diminish coverage properties relative to MUB. For example, considering the binary indicator of children being present in the household for males, we see that accounting for the uncertainty in the input estimates via the Bayesian approach for the fixed choices of 0 and 1 for ϕ would result in coverage of the estimated bias. The results are similar when applying the fully Bayesian approach with uniform draws for ϕ. Furthermore, as was noted by Little et al. (2019), a moderate biserial correlation (say, greater than 0.3) ensures that the interval proposed does a good job of covering the estimated bias; this was true for nine out of 12 proportions where the biserial correlation was 0.3 or larger in this illustration.

There are several cases where no approach to constructing an interval for MUBP covers the estimated bias, despite the fact that the biserial correlation between X and Y is relatively large (e.g. Age=30–44 years for males; biserial correlation 0.65). Since we had Y available for the entire NSFG ‘population’ in this example, we could fit a probit regression model to the selection indicator, regressing the indicator of owning a smartphone (‘selection’) on both X and Y to investigate further the ‘true’ selection mechanism. Surprisingly, we found that the estimated coefficient for X was positive whereas the estimated coefficient for Y was negative, and thus the probability of being selected into the NSFG smartphone ‘sample’ was a positive function of X and a negative function of Y. In our model, we assume in equation (6) that the selection mechanism is a function of (1−ϕ)X* + ϕU with ϕ restricted to be non-negative, and thus a selection mechanism that depends on X and Y in opposite directions will not be covered by the [MUBP(0), MUBP(1)] interval or the Bayesian intervals.

Little (1994), who defined the probability of non-selection underlying the proxy pattern-mixture in (equation 7) as Pr(S=0|U, X)=f(X+λU) with λ=ϕ/(1−ϕ), suggested that λ=−1 was a plausible value for this mechanism; in this case, selection would depend on the difference between X and U. Following our approach, λ=−1 would imply that ϕ=−∞.We subsequently computed MUBP(−∞) for the age 30–44 years indicator for males as an illustration and found that the resulting value was −0.024. Taken together with the MUBP(ϕ) values in Table 2,we find that the interval of [MUBP(−∞), MUBP(1)] for this proportion is [−0.024, 0.039]which does in fact cover the small estimated bias (−0.002). So, although this resulting interval is relatively wide, it does allow for the unusual but not implausible possibility that the probability of selection has a positive relationship with the proxy variable X and a negative relationship with U. Analysts can easily perform this computation (calculating MUBP(−∞)) by using the R functions at https://github.com/bradytwest/IndicesOfNISB to assess the implications of this plausible scenario for potential selection bias. We also note that this scenario is a problem only with strong proxy variables X that have a moderate-to-large biserial correlation with Y. With weak proxies, the interval proposed will basically cover the two extremes—the selection bias if all non-selected cases were 1s, and the selection bias if all non-selected cases were 0s.

6. Discussion

We have proposed simple model-based indices called MUBP that measure the potential selection bias in proportions estimated on the basis of non-probability samples, where the selection mechanism underlying the realized non-probability sample may be non-ignorable. These indices are easy to compute by using the R functions that are freely available from https://github.com/bradytwest/IndicesOfNISB. Via empirical simulation studies and an application to smartphone users in a real survey setting, we have demonstrated the ability of the MUBP-indices effectively to indicate potential selection bias for estimated proportions. Notably, the indices enable sensitivity analyses, allowing users to vary their assumptions about the amount of non-ignorability in the underlying selection mechanism.

The indices proposed also have a dual benefit in that the underlying methodology can be used to make inferences about the estimated proportions based on a non-probability sample. Making inference when following this approach requires means, variances and covariances for the auxiliary variables Z in the non-selected sample that are used to form the auxiliary proxy that is key to the effectiveness of this methodology. Although these sufficient statistics (and specifically the variances and covariances) may be difficult to obtain for non-selected cases in practice, one could at least assume that the variances and covariances are similar to those observed for the non-probability sample. In the absence of this information, and given that the auxiliary proxy X has a moderately strong (cross-validated) biserial correlation with the binary variable of interest Y, one could still use our methodology to identify those estimates that are at the highest risk of selection bias.

The MUBP-indices could also be used during on-going data collection to identify estimates that are becoming increasingly prone to selection bias as the data collection proceeds. In this sense, the indices could be used to inform adaptive survey designs that prioritize subgroups of cases which are predicted to have unique values on the binary variable of interest that may be underrepresented in the responding sample. We feel that future research could focus on this potential utility of the proposed indices to reduce selection bias in a realtime fashion.

The MUBP-index does have limitations, most notably that the proxy for Y must be moderately strong for the sensitivity analysis to produce intervals that are reasonable in width, and that uncertainty intervals do not cover the true bias with consistently high probability. However, even with weak proxies the MUBP-intervals are less conservative than the ‘worst-case’ bounds that are obtained by assuming that all non-selected cases have Y = 0 (lower bound) and Y = 1 (upper bound) (Manski, 2016). In the context of non-probability samples, the non-selected fraction is generally so large that such intervals would effectively range from 0 to 1. Another limitation of the MUBP-index is that, by reducing the auxiliary variables Z to the proxy X, we lose the ability to quantify the effect of specific Z-variables on the selection mechanism. The trade-off is simplicity, in the form of a single sensitivity parameter. Finally, as seen in the NSFG example, it is possible for the MUBP-intervals to ‘miss’ in the opposite direction of the true selection bias, in the unusual case when the selection mechanism depends on the outcome Y and the proxy X in opposite directions. The assumption underlying the MUBP-index is that the direction of the selection bias in X is the same as the direction of the selection bias in Y. Assumptions are unavoidable in assessing selection bias, and this assumption seems reasonable. To avoid making this assumption, analysts could calculate MUBP(−∞) as an alternative bound, but in practice this is likely to produce intervals that are too wide to be useful. The exception might be if using the MUBP-index to compare the potential bias across a set of variables; in this case the interval that contains MUBP(−∞) could be compared across Y-variables. We prefer the alternative of making the assumption that ϕ ∈ (0, 1) and acknowledging that this assumption may not hold (but that we have no way of validating this).

There are three key avenues for extending this work in the future. First, the pattern-mixture model here can be extended to estimated proportions for ordinal categorical variables (e.g. self-rated health) in a straightforward manner, as outlined in Andridge and Little (2018). In this case there would not be a single MUBP(ϕ) but a value of MUBP(ϕ) for each level of the outcome; future work could develop measures that combine these values into one (for each value of ϕ). Another important area of research is whether the MUBP(ϕ) index can be extended for multinomial categorical variables (e.g. political party preference). Finally, the development of measures of selection bias for other estimands besides the population proportion, e.g. for estimated regression coefficients in logistic regression models, is also necessary.