Development of a scanner-specific simulation framework for photon-counting computed tomography

Abstract

The aim of this study was to develop and validate a simulation platform that generates photon-counting CT images of voxelized phantoms with detailed modeling of manufacturer-specific components including the geometry and physics of the x-ray source, source filtrations, anti-scatter grids, and photon-counting detectors. The simulator generates projection images accounting for both primary and scattered photons using a computational phantom, scanner configuration, and imaging settings. Beam hardening artifacts are corrected using a spectrum and threshold dependent water correction algorithm. Physical and computational versions of a clinical phantom (ACR) were used for validation purposes. The physical phantom was imaged using a research prototype photon-counting CT (Siemens Healthcare) with standard (macro) mode, at four dose levels and with two energy thresholds. The computational phantom was imaged with the developed simulator with the same parameters and settings used in the actual acquisition. Images from both the real and simulated acquisitions were reconstructed using a reconstruction software (FreeCT). Primary image quality metrics such as noise magnitude, noise ratio, noise correlation coefficients, noise power spectrum, CT number, in-plane modulation transfer function, and slice sensitivity profiles were extracted from both real and simulated data and compared. The simulator was further evaluated for imaging contrast materials (bismuth, iodine, and gadolinium) at three concentration levels and six energy thresholds. Qualitatively, the simulated images showed similar appearance to the real ones. Quantitatively, the average relative error in image quality measurements were all less than 4% across all the measurements. The developed simulator will enable systematic optimization and evaluation of the emerging photon-counting computed tomography technology.

1. Introduction

Over the past several decades, computed tomography (CT) imaging has been extensively advanced to improve patient outcome by providing higher image quality at lower radiation risk. These developments include spiral imaging, multi-row detectors, higher rotation speed, dual-energy systems, and novel reconstruction algorithms.

A recent technological development in CT is the use of photon-counting detectors (PCD) [1–5], replacing conventional energy-integrating detectors (EID). PCDs are energy-sensitive detectors that directly convert an x-ray photon to electrical signal proportional to its energy [1]. Compared with EID-CT, recent studies on prototype PCD-CT systems have shown superior performance in terms of image noise, spatial resolution, contrast to noise ratio (CNR), artifacts, and material decomposition [6–15].

To bring the PCD-CT into clinical practice and to further enhance its performance, this technology still needs comprehensive assessments and application-based optimizations. These evaluations, ideally, need large scale application-based trials on actual patient images. However, such trials are challenging, considering the limited numbers of prototype PCD-CT scanners and the often-unknown ground-truth in the patient images. In addition, protocol optimization needs repetitive trials with multiple acquisitions at various imaging conditions. This is impractical in the context of patient trials due to radiation safety concerns and costs.

These challenges can be overcome by utilizing virtual clinical trials (VCTs), where an imaging experiment is performed using representative computational human and imaging models. VCTs are widely developed and utilized in x-ray-based imaging [16–24]. The utility of VCTs in PCD-CT is currently limited due to the lack of a standalone CT simulator that can generate PCD-CT images of computational phantoms with realistic considerations of a particular PCD-CT system.

We have recently developed and validated an EID-CT simulator, called DukeSim, that simulates vendor-specific EID-CT images [25]. Building upon our previous work, the purpose of this study was to extend DukeSim to simulate realistic PCD-CT images of voxelized computational phantoms while accounting for manufacturer-specific components including the geometry and physics of the x-ray source, filters, anti-scatter grids, and photon-counting detectors.

2. Materials and methods

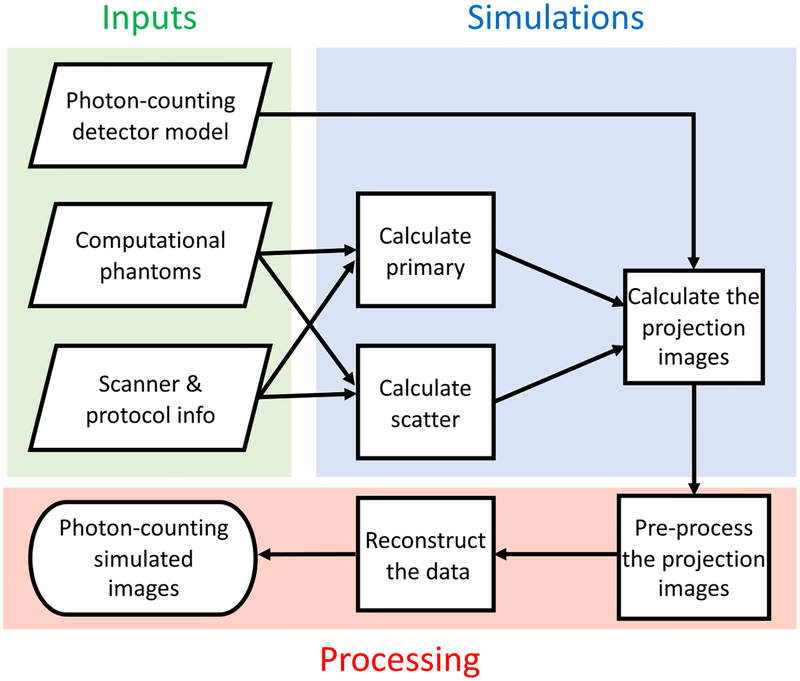
The framework for the DukeSim PCD-CT simulator is shown in figure 1. In summary, the procedure is divided into three parts: (1) inputs, (2) simulations, and (3) processing. The inputs include the computational phantoms, information regarding the scanner geometry and physics, and the PCD model. The simulations consist of calculating primary signal, scatter signal, and the final projection images. The last step performs the data pre-processing and reconstruction. The following sections further explain the details of these steps.

Figure 1.

The framework of the developed PCD-CT simulator.

2.1. Computational phantoms

The simulator works with voxelized phantoms with each structure set to a unique integer corresponding to material definitions in a material file. The density and elemental composition for each material are defined based on ICRU Report 46 [26]. A given phantom is read by the simulator and the poly-energetic linear attenuation coefficients of all the materials in the phantom are computed using tables generated from the xraylib package [27].

2.2. Scanner and protocol configurations

The scanner configuration can be setup with a user-defined focal spot size, tube photon flux spectrum (function of kV), tube current (mA), bowtie filter, beam collimation, focal spot wobbles (also known as flying focal spots), source to detector distance, source to isocenter distance, anti-scatter grids, detector size, number of detector rows and columns, detector energy thresholds, number of projections per rotation, scan range, rotation speed, and pitch. A parameter file is setup to specify these variables.

2.3. Photon-counting detector model

The simulator expects a detector response model of a prototype PCD [28–30] including the average, noise variance, and noise covariance (in case of multiple energy thresholds) signals of an incident photon hitting the detector. The implementation of the detector model in calculating the projection images is explained in the following sections.

2.4. Primary signal

Using a ray-tracing strategy, the simulator tracks the primary photons starting from the source towards each detector element. For each detector (i, j), at the projection angle α, the primary signal N_pr, is calculated using the Beer-Lambert law,

$$\begin{gathered} N_{pr}(E,i,j,\alpha )=\frac{1}{K}\sum _{k=1}^K{N}_0(E,i,j,\alpha ) \\ \times \text{\hspace{0.17em}exp}\left(-\sum _m\mu (E,m,k)l(i,j,\alpha ,m,k)\right) \end{gathered}$$ (1)

where N₀ is the number of photons at the source (post-bowtie filter), μ is the poly-energetic linear attenuation coefficient of material m (calculated using [28)), and l is the intersection length of the source-to-detector ray with the voxels of material m. To account for the finite sizes of the focal spot and detector elements, the ray-tracer calculates the intersection length K times, uniformly sampling the area of the focal spot and the detector elements. The effects of the bowtie filter (controlling N₀) are modeled by attenuating the source spectrum through a bowtie filter with known geometry and material.

Using the PCD response model for a set of n energy thresholds, the primary count at each detector is estimated with a multivariate Gaussian variable with a mean vector of

$$M{(pr)}_{1\times n}=\sum _E{N}_{pr}(E).R{\left(E,t_n\right)}_{1\times n},$$ (2)

and the covariance matrix of

$$K{(pr)}_{n\times n}=\left[\begin{array}{cccc}\ddots & \dots & \dots & ⋮\\ ⋮& \ddots & \dots & ⋮\\ ⋮& Cov{(pr)}_{v,w}& \ddots & ⋮\\ \dots & \dots & \dots & \ddots \end{array}\right],$$

$$Cov{(pr)}_{v,w}=\sum _E{N}_{pr}(E).Cov\left(E,t_v,t_w\right).$$ (3)

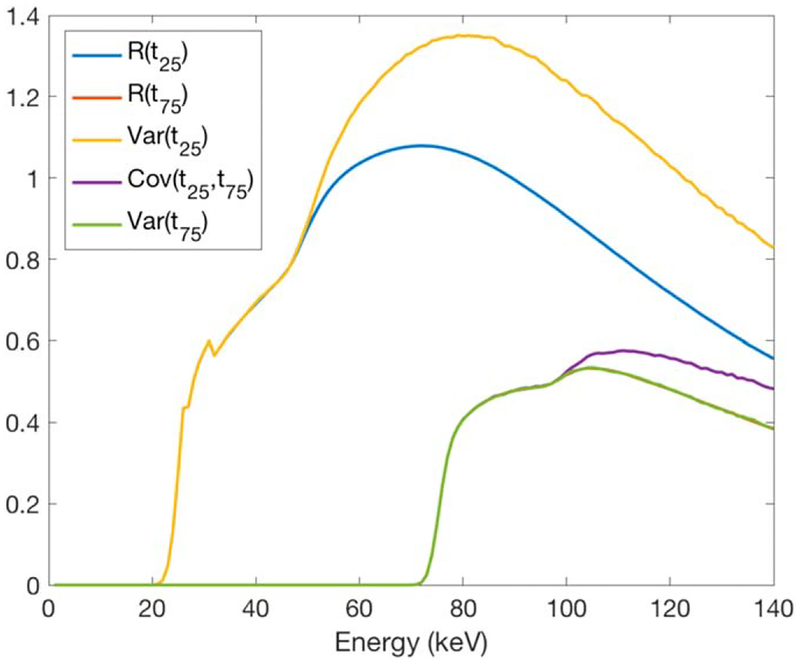
Here, R(E, t_n) is the probability of an incident photon at energy bin of E being detected at the energy threshold of t_n. Cov(E, t_v, t_w) is the covariance between the signals recorded at the energy thresholds of t_v and t_w for an incident photon at the energy bin E. The R(E, t) and Cov(E, t_v, t_w) used in this study were based on a MC simulation of a cadmium telluride (CdTe) detector with 5.86 g cm⁻³ density and 1.6 mm thickness. This MC simulation calculated the expected values and covariance matrix considering the x-ray effects (K escape and K reabsorption) and the electronic effects (charge sharing and electronic noise). Figure 2 shows an example of the model at the energy thresholds of 25 and 75 keV. More details on derivation of this detector model can be found in [28].

Figure 2.

The expectation, variance, and covariance values at energy thresholds of 25 and 75 keV, derived from a MC simulation [28].

2.5. Scatter signal

Since the ray-tracing module does not account for the scattered x-ray interactions, a MC tool based on the MCGPU framework [31] is used to estimate the scatter signal. The MC tool measures the scattered photons, N_sc(E, i, j, α), while rejecting the ones absorbed in the anti-scatter grids. The rejection is done using a rejection range distribution (provided by the manufacturer in this study and can also be measured empirically).

Similar to the primary signal, the scatter signal is estimated with a multivariate gaussian variable with the mean vector of

$$M{(sc)}_{1\times n}=\sum _E{N}_{sc}(E).R\left(E,t_n\right),$$ (4)

and the covariance matrix of

$$K{(sc)}_{n\times n}=\left[\begin{array}{cccc}\ddots & \dots & \dots & ⋮\\ ⋮& \ddots & \dots & ⋮\\ ⋮& Cov{(sc)}_{v,w}& \ddots & ⋮\\ \dots & \dots & \dots & \ddots \end{array}\right],$$

$$Cov{(sc)}_{v,w}=\sum _E{N}_{sc}(E).Cov\left(E,t_v,t_w\right),$$ (5)

where R(E, t) and Cov(E, t_v, t_w) are the same detector response values discussed in the previous section.

The MC output for the scatter simulation has fluctuation due to the finite number of simulated histories. This effect can be reduced by simulating a large number of histories, but that is computationally expensive. Therefore, those fluctuations are smoothed using an established smoothing scatter kernel [32]. Similar to how clinical scanners typically suppress the effects of scatter, the estimated scatter signals are corrected by measuring the scatter in a row outside the collimation and subtracting it from the other rows [33].

2.6. Projection images

To add noise to the detector signals, a correlated multivariate Gaussian random number generator is used with the mean vector of M(tot) = M(pr) + M(sc) and covariance matrix of K(tot) = K(pr) + K(sc).

Similar to clinical CT scans, the final simulated projection images for each energy threshold are computed as $S(t)=-\text{log}\left(\frac{N_t}{N_{0,t}}\right)$, where N_t is the noisy and detector signal at the energy threshold of t, and N₀ is the air scan in that threshold (detector unattenuated signal). For each energy bin (between two thresholds of t₁ and t₂), the projection images are calculated as $S_{bin}\left(t_1,t_2\right)=-\text{log}\left(\frac{N_{t1}-N_{t2}}{N_{0,t1}-N_{0,t2}}\right)$.

2.7. Beam hardening artifact correction

The simulator reduces the beam hardening effects, caused by the poly-energetic nature of the source spectrum, by applying a polynomial water correction [34]

$$S_{BHC}=\sum _{p=0}^{p=3}{b}_p(j,t,kV)S^p,$$ (6)

where the polynomial coefficients of b_p are calculated applying the fit of poly-energetic detector signals (of water with different diameters) to ideal mono-energetic ones. The coefficients are uniquely derived for different detector channels, energy thresholds (or energy bins), source spectrums, and bowtie filters.

2.8. Computational considerations

As discussed in [25], simulations of CT projection images are computationally expensive. The simulator loads a high-resolution voxelized phantom (sub-mm voxel size) and calculates projection signals for tens of thousands of detectors, thousands of projections per rotation, and multiple rotations, across hundreds of energy bins. This can be even more challenging in PCD simulations, where each detector can have multiple signals (multiple energy thresholds). To make the program computationally efficient, it was written in C++ and linked it to the NVIDIA CUDA libraries to calculate the independent measurements in parallel (e.g., the intersection path lengths for different detector elements and projection angles), using multiple graphical processing units (GPUs).

2.9. Validation

A validation study was done to evaluate the realism of the PCD-CT simulator by comparing the image quality of simulated PCD-CT data with real data acquired using an actual prototype scanner.

A physical CT ACR phantom was imaged with macro mode (0.5 mm detector size and 32 × 0.5 mm beam collimation) at four different dose levels (36, 72, 144, 216 mAs, corresponding to 4, 8, 16, and 24 mGy), 0.5 second of rotation time, body mode (with Siemens standard ‘body’ bowtie filter), a tube voltage of 140 kV, pitch of 1.0, and energy thresholds of 25 and 75 keV using a research prototype PCD-CT scanner (Siemens Healthcare, Germany) [35, 36] at the National Institutes of Health Clinical Center.

The simulator was setup to mimic the geometry and physics of the research prototype PCD-CT scanner (information was provided by the manufacturer), including spectrum, bowtie filter, focal spot size and positions, anti-scatter grids, and the detector model. A computational model of the ACR phantom was imaged using the developed PCD-CT simulator, with similar imaging conditions used in the actual scans. In the simulations, focal spot and detector elements were uniformly sub-sampled 4 times (total of 16) to approximate their finite sizes.

Both the real and simulated projection images were reconstructed with a weighted filtered back-projection algorithm using an open source reconstruction software, FreeCT [37] with the ‘Medium’ kernel. All the reconstructed images had 512 × 512 in-plane pixels, 215 mm reconstruction field of view, and 1.5 mm slice thickness.

The simulated and real images were compared with each other in terms of fundamental image quality metrics: noise magnitude, noise ratio (between energy thresholds), noise correlation coefficients (between energy thresholds), noise power spectrum (NPS), CT number, in-plane modulation transfer function (MTF), and slice sensitivity profile.

The noise measurements were done in the uniform sections of the phantom. The noise ensemble was sampled by placing squared regions of interests (ROIs, 25 mm in size) 50 mm away from the image center. All the noise measurements were done in 11 consecutive slices where the average image of those slices was subtracted to avoid deterministic signals in the noise calculations.

For each energy threshold and energy bin, the noise magnitude was calculated as the standard deviation, measured and averaged across all the ROIs. The noise ratio was calculated by dividing the 25 keV noise magnitude by the 75 keV noise magnitude. The correlation coefficient, CC, between the thresholds 25 and 75 keV, were measured as

$$C{C}_{25,75}=\frac{1}{Q}\sum _{q=0}^{1=Q}\frac{avg\left\{\left(RO{I}_{q,25}-avg\left(RO{I}_{q,25}\right)\right).\left(RO{I}_{q,75}-avg\left(RO{I}_{q,75}\right)\right)\right\}}{std\left\{RO{I}_{q,25}\right\}.std\left\{RO{I}_{q,75}\right\}},$$ (7)

where Q is the number of ROIs (8 in this study). The NPS was measured using the algorithm explained in [38] with the same ROIs as used for noise magnitude measurements.

The in-plane MTF was measured in the edges of the high-contrast inserts (Air and Bone) using the algorithm explained in [38]. The z-resolution was evaluated measuring slice sensitivity profiles of the two tungsten carbide beads (0.28 mm in diameter) available in the ACR phantom. For measuring these pro-files, both real and simulated projection images were reconstructed with a slice thickness of 0.5 mm and overlaps of 0.1 mm. ROIs were placed around the tungsten bead and the maximum value was measured in each slice. The profile was normalized to the range of [0, 1] and plotted as a function of ‘z’ position.

The simulator was further evaluated in terms of its utility in material quantification studies. A simulation was done by replicating a previous study [39] where multiple concentrations of bismuth (5, 10, 15 mg ml⁻¹), iodine (4, 8, 16 mg ml⁻¹), and gadolinium (4, 8, 16 mg ml⁻¹) were imaged at multiple energy thresholds with lower threshold of 20 keV and upper thresholds of 50, 60, 70, 80, 90 keV. The real images were acquired at 140 kV and ‘sharp’ mode (0.25 mm detector size for low-energy threshold and 0.5 mm detector size for high-energy threshold with 48 × 0.25 mm beam collimation), pitch of 1.0, using the prototype PCD-CT scanner (Siemens Healthcare, Germany), at the National Institutes of Health Clinical Center.

The simulation was setup to mimic the same scanner settings and contrast materials used in that study [39]. The linear attenuation coefficients were calculated using the xraylib package [27] and the elemental compositions for each material at each concentration levels. Both real and simulated images were reconstructed using the FreeCT [37] reconstruction software and the ‘Medium’ kernel. All the reconstructed images had 512 × 512 in-plane pixels, a 215 mm reconstruction field of view, and a 1.5 mm slice thickness. The CT values were recorded for all contrast vials in the real and simulated images and compared against each other.

3. Results

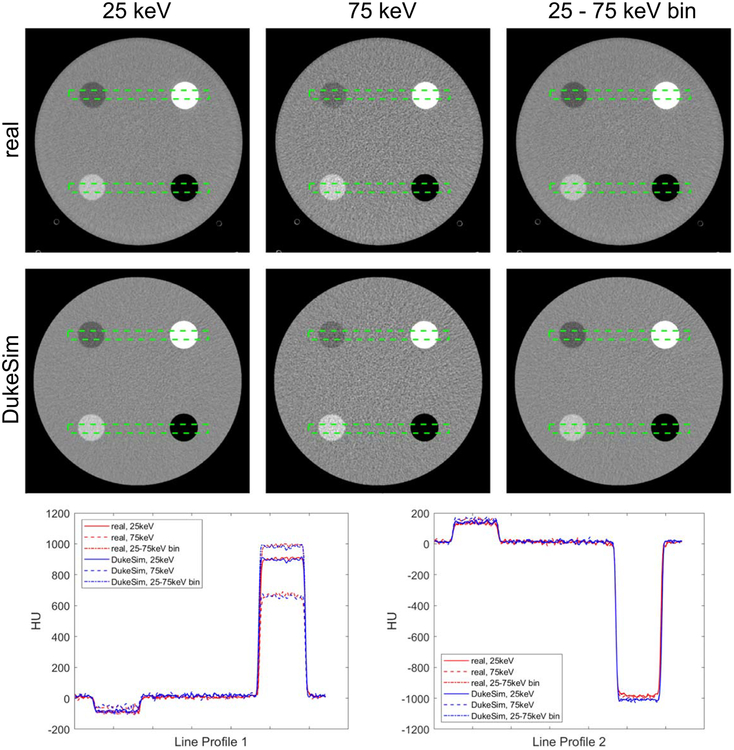
Figure 3 shows real and simulated PCD-CT images at 25 and 75 keV energy thresholds and the ‘25–75 keV’ energy bin. ‘Threshold’ images only reflect photons beyond an energy threshold, and ‘bin’ images reflect photons between two energy thresholds. With this definition, the ‘75 keV’ threshold images and the ‘75–140 keV’ bin images (140 is the tube voltage used in this study) are equivalent and thus, in this paper we referred to them as ‘75 keV’ threshold images terms.

Figure 3.

The real and simulated PCD images at 25 keV, 75 keV, and the bin between 25 and 75 keV. Two line profiles are shown comparing the intensity values. The images are shown with a window of 600 and level of 0 Hounsfield Units (HU), HU values were calculated setting the mass attenuation coefficient of water to be 0.0172 mm² g⁻¹.

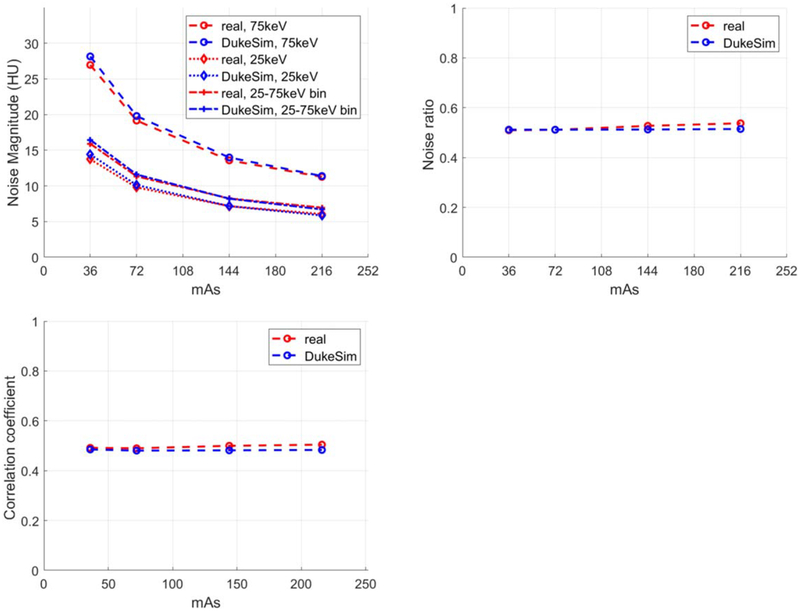
Qualitatively, the simulated and real images had similar appearances. In the lower threshold images, the images were less noisy because more photons are counted compared to the higher thresholds. The CT numbers extracted from both real and simulated cases are tabulated in table 1. Overall, the CT numbers in the simulated images are very close to real data with similar trends (changes in HU as a function of energy thresholds and bins). Minor discrepancies may be attributed to possible minor differences in the actual and simulated density values or minor unknown physical processes not explicitly modeled by the simulation. Figure 4 shows the noise magnitude, noise ratio, and noise correlation coefficient of the real and simulated images at the 4 dose levels. Results demonstrated that the simulated images had a noise magnitude similar to real images with 1.28 ± 3.6%, 3.03 ± 1.36%, and 0.44 ± 3.12% relative errors for 25 keV, 75 keV, and the ‘25–75 keV’ bin, respectively. For noise ratio, the error between real and simulations was −1.73 ± 2.26%. The correlation coefficient results demonstrate the existing correlation between the threshold images and the realistic modeling of this effect in the simulations with the relative error of −2.94 ± 2.13%. In the real data, a slight increase occurred in the noise ratio and correlation coefficient, suggesting slight non-linear effects (like dead-time losses) happening in the high dose regime.

Table 1.

CT numbers extracted from real and simulated images of ACR phantom averaged across 4 measurements (4 dose levels).

		Bone	Acrylic	Water	Polyethylene	Air
25 keV	Real	873.0 ± 2.4	121.3 ± 0.2	−2e-9 ± 1e-7	−96.3 ± 0.5	−972.1 ± 1.8
	DukeSim	865.9 ± 0.6	126.3 ± 0.3	−4e-8 ± 9e-8	−90.5 ± 0.0	−999.9 ± 0.1
75 keV	Real	642.6 ± 1.8	140.0 ± 1.5	−1e-8 ± 2e-7	−71.3 ± 1.8	−978.3 ± 2.1
	DukeSim	631.7 ± 0.8	145.1 ± 0.5	−6e-8 ± 4e-8	−62.7 ± 0.5	−1001 ± 0.7
25–75 keV	Real	956.8 ± 1.3	115.3 ± 0.2	2e-8 ± −1e-7	−104.6 ± 0.4	−971.3 ± 1.5
	DukeSim	947.3 ± 0.9	121.0 ± 0.3	1e-8 ± 1e-7	−98.6 ± 0.1	−999.9 ± 0.1

Figure 4.

Noise magnitude (top left), noise ratio of 25 keV over 75 keV (top right), and noise correlation coefficient (bottom) measured at multiple dose levels for both real and simulated images.

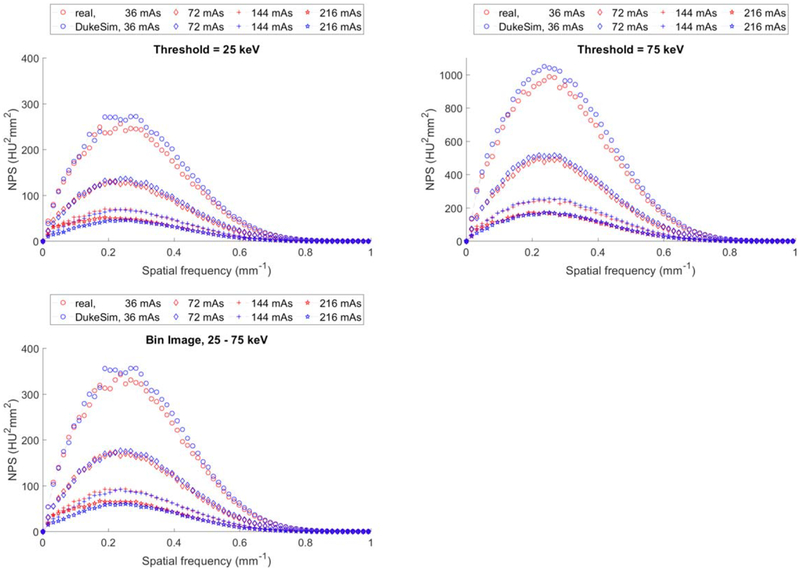
Figure 5 shows a comparison of the NPS curves for the real and simulated images. The simulations compare favorably to the real data, demonstrating that the noise texture in the simulations are similar to the noise texture in the real images. The relative errors for the average frequency of NPS curves were 4.08 ± 2.57%, 1.56 ± 1.09%, and 2.95 ± 2.01% for 25 keV, 75 keV, and the ‘25–75 keV’ bin, respectively.

Figure 5.

Noise power spectrum (NPS) measured in real (red) and simulated (blue) images at 25 keV (top-left), 75 keV (top-right), and 25–75 keV (bottom).

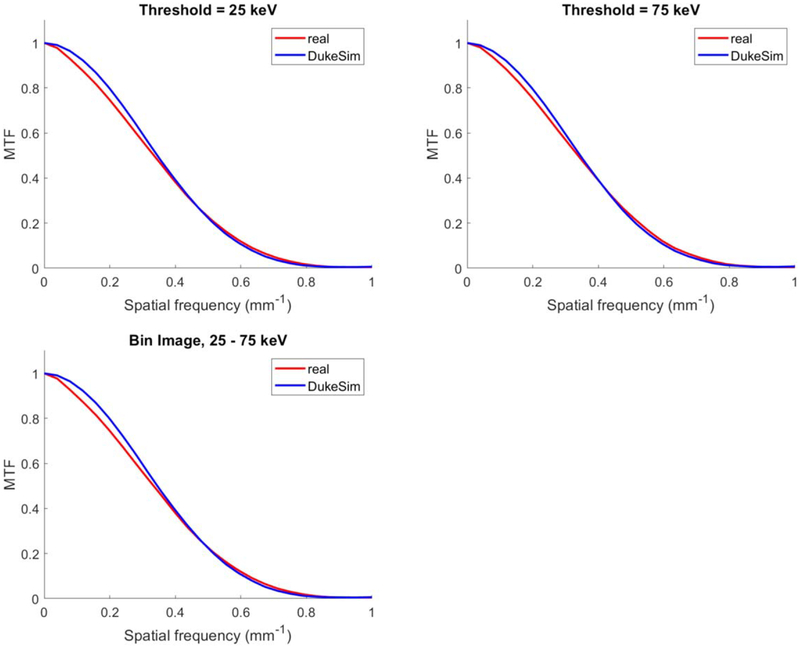
Figure 6 shows the in-plane MTF measurements for both real and simulated images. MTF curves show close agreements between the real and simulated images with relative errors in the half-value frequency listed in table 2.

Figure 6.

Modulation transfer function measured in the ‘Air’ insert in the real (red) and simulated (blue) images at 25 keV (top-left), 75 keV (top-right), and 25–75 keV (bottom).

Table 2.

Percent relative error between real and simulated images in terms of in-plane MTF half-value frequency.

	Air	Bone
25 keV	3.01 ± 2.00%	4.45 ± 0.44%
75 keV	1.90 ± 2.44%	3.35 ± 2.12%
25–75 keV	3.32 ± 1.87%	4.47 ± 0.32%

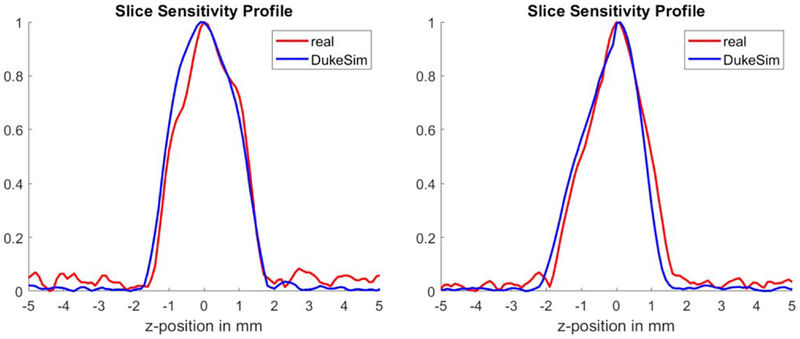
Figure 7 shows the slice sensitivity profiles for both real and simulated images, measured at the center and off-center of the phantom. The plots demonstrate that the real and simulated images have close z-resolution profiles with relative errors of 1.39% (at the center) and −0.73% (at the off-center) in terms of the full-width-at-half-maximum (FWHM). For both real and simulated cases, the FWHM was approximately 2 mm which is wider than typically expected for images with 0.5 mm slice thicknesses. This was due to the windmill artifact being present around the high contrast object (‘tungsten’) for both real and simulated images. More advanced reconstruction algorithms and more sampling in the z-direction (e.g., flying focal spots) would reduce the FHWM.

Figure 7.

Slice sensitivity profiles measured using the tungsten beads available in the center (left plot) and off-center (right plot) of the ACR phantom. Red plots are measured from the real data and blue plots are measured from simulations.

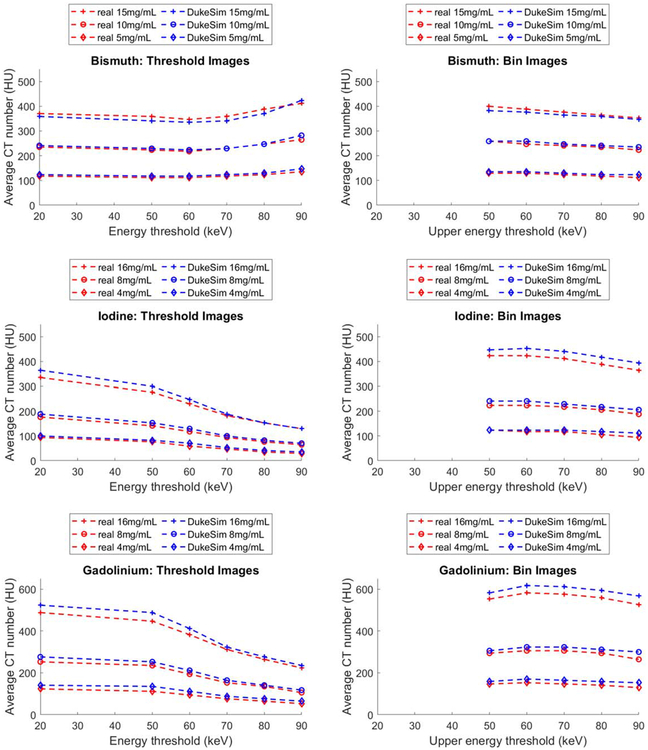
Figure 8 shows the average CT numbers for the three contrast agents at three concentration levels and six energy thresholds and corresponding energy bins for the real data and the simulations. The results demonstrate close agreement between HU values of the simulated and real images. Notably, the changes in CT numbers as a function of energy threshold and energy bin were similar for both real and simulated images. In the threshold images, for both real and simulated images, CT values decreased as a function of energy thresholds for iodine and gadolinium whereas they slightly increased for bismuth. In the energy bin images, for both real and simulated data, CT values decreased as a function of upper energy threshold (lower energy threshold was set to 20 keV), with the bismuth and gadolinium having a peak at energy bin of’20–60 keV’.

Figure 8.

Average CT numbers of Bismuth, Iodine, and Gadolinium contrast agents measured at 3 concentration levels and 6 energy thresholds in both real (red) and simulated (blue) images. For the bin images, the lower threshold was 20 keV. To convert the attenuation values to HU, the mass attenuation coefficient of water was assumed to be 0.0172 mm² g⁻¹.

The differences between the real and simulated images were 0.9 ± 10.2 HU (max = 17.6), 13.0 ± 9.3 HU (max = 29.4), and 20.8 ± 10.0 HU (max = 41.0) for bismuth, iodine, and gadolinium, respectively. These differences correspond to relative errors of 0.10 ± 0.84 %, 0.80 ± 0.57 %, and 1.89 ± 0.58% in the attenuation coefficient scale. Since the real and simulated results follow similar trends, these discrepancies could be due to potential minor differences between the concentrations of the real and simulated contrast agents or minor unknown physical processes not explicitly modeled by the simulation.

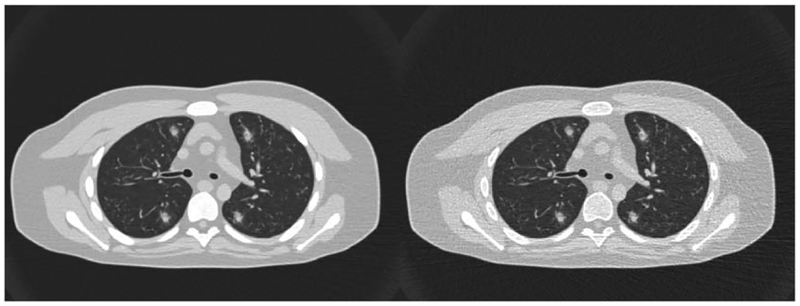
Figure 9 shows PCCT images of a computational human model (XCAT phantom) with simulated lesions inserted in the lungs, imaged with the developed PCCT simulator. This demonstrates the simulator capability in imaging human models with intra-organ heterogeneities and its utility for future virtual clinical trials.

Figure 9.

Photon-counting images an XCAT phantom with some inserted lesions, imaged with the developed simulator at images at 25 (left) and 75 (right) keV. Images are shown with a window/level of −400/1400 HU.

4. Discussion

The emerging and promising PCD-CT technology needs comprehensive evaluation and application-based optimizations to be widely used in the clinic. Realistic computer simulations can be utilized to speed up these assessments by performing relevant and large-scale experiments using representative human models and PCD-CT imaging models. In this work, we developed and validated a PCD-CT simulator that is able to image voxelized phantoms with manufacturer-specific considerations of the scanner geometry, physics of the x-ray source, filters, anti-scatter grids, and photon-counting detectors. We showed that our developed simulator can generate PCD-CT images with noise, image contrast, and resolution features similar to a research prototype scanner across multiple dose levels and energy thresholds.

To evaluate the performance of the simulator, one needs to perform one-to-one experiments using the real scanner and the simulator, and compare the results against one another. As such, the ‘object’ being imaged should be exactly the same in both real and simulated acquisitions, so any difference between the real and simulated results would be reflective of the performance of the simulator. Therefore, in the context of validating a simulator, clinical ‘patient’ images cannot be used as the exact ground truth of a given patient cannot be known. In this study, we thus deployed object of known ground truth as a basis to validate the accuracy of the simulator. Hinging on this first step, the simulator can be used to simulate imaging of computational phantoms with the confidence that the results would be reflective of images if such computational phantoms were physically imaged by the actual scanner.

Given a particular scanner configuration and detector model, the developed simulator is able to generate primary and scattered signals and model correlated noise for multiple energy thresholds. The developed simulator accounts for post-bowtie filter spectra, focal spot wobbles, finite sampling of the source and detector areas, detector response, and beam hardening correction. All of these features are developed in a modular way, so a user can adjust them based on a desired experiment. For example, if a new photon-counting detector is introduced, one can input the detector response model of that in the simulator and generate CT images for the particular detector. Or one can incorporate different bowtie filter models (e.g., with or without tin filters) depending on the study of interest.

Our simulator can be also used to optimize the imaging parameters and processing (such as spectrum, bowtie filter, focal spot wobbling, energy thresholds, detector sizes, beam hardening corrections, detector artifacts, reconstruction algorithm) in an application-specific manner.

The developed PCD-CT simulator is compatible with any given voxel phantom. This feature, not available in the surface-based simulators, would enable studying image quality using phantoms with sub millimeter voxel sizes (high-resolution) and intra-organ heterogeneities. Additionally, our simulation framework can be also used to validate the accuracy of the PCD response models against real data. For example, the detector response model used in this study, derived from (1), provided a realistic approximation of the detectors mean and variance (and covariance) in the range of 36 to 216 mAs dose levels.

This study had some limitations. The validations were done using a simplistic uniform phantom. While these validations are reflective of the accuracy of our simulator, they can be even stronger if they are done using physical heterogenous anthropomorphic phantoms (not currently available). Future work will pursue 3D printing of our recently developed anthropomorphic phantoms with the heterogenous intra-organs [40–42] for more extensive validations. The detector model used in this study did not account for pile-up effects which is a secondary effect for the phantom and conditions used in this study, as demonstrated in the validation results. Future work will be done to improve the accuracy of the detector model by incorporating pile-up effects.

The other limitation was that the validations were done using one PCD-CT mode and reconstructed with a manufacturer-generic reconstruction software. In a future study, using the modular nature of the simulator, we will model and validate our simulator against different PCD modes and scanners, and reconstruct them using manufacturer-specific reconstruction algorithms.

5. Conclusion

A realistic simulation platform for photon-counting CT paves the way towards evaluation and parameter optimizations of this promising technology. While not practical using expensive and ground truth-limited clinical trials, these studies can be explored using our developed photon-counting simulator, when combined with representative anthropomorphic phantoms.