Abstract
Hydrogel systems are an appealing class of therapeutic delivery vehicles, though it can be challenging to design hydrogels that maintain desired spatiotemporal presentation of therapeutic cargo. In this work, we propose a different approach in which computational tools are developed that creates a theoretical representation of the hydrogel polymer network to design hydrogels with predefined mesh properties critical for controlling therapeutic delivery. We postulated and confirmed that the computational model could incorporate properties of alginate polymers, including polymer content, monomer composition and polymer chain radius, to accurately predict cross-link density and mesh size for a wide range of alginate hydrogels. Additionally, the simulations provided a robust strategy to determine the mesh size distribution and identified properties to control the mesh size of alginate hydrogels. Furthermore, the model was validated for additional hydrogel systems and provided a high degree of correlation (R2 > 0.95) to the mesh sizes determined for both fibrin and polyethylene glycol (PEG) hydrogels. Finally, a full factorial and Box-Behnken design of experiments (DOE) approach utilized in combination with the computational model predicted that the mesh size of hydrogels could be varied from approximately 5 nm to 5 μm through controlling properties of the polymer network. Overall, this computational model of the hydrogel polymer network provides a rapid and accessible strategy to predict hydrogel mesh properties and ultimately design hydrogel systems with desired mesh properties for potential therapeutic applications.
Keywords: Hydrogels, Mesh Size, Computational Modeling, Cross-link Density, Mesh Size Distribution, Alginate, Fibrin, Polyethylene Glycol
Graphical Abstract
Introduction
Hydrogel systems have many promising clinical applications due to their ability to provide control over the presentation of therapeutic agents to the surrounding tissue environment. Hydrogels consist of cross-linked polymer chains that do not dissolve but can swell in water or aqueous solutions and can provide a wide range of controllable mechanical properties to exert their desired therapeutic mechanism1–3. One promising strategy to control therapeutic delivery involves designing hydrogels with predefined mesh sizes1, 3–5. The mesh size of a hydrogel could be defined as the distance between two adjacent cross-links and has a critical role in determining the diffusion of agents within the hydrogel network1, 6–8. Indeed, the mesh size is involved in determining the ability of therapeutic cargo to diffuse through the polymer system9–14 and the ability of encapsulated cells to interact with the surrounding environment for cell-based therapies15–17. The role mesh size has in providing controllable therapeutic delivery from hydrogel systems has prompted interest in designing hydrogels with desired mesh sizes.
Characterizing the mesh structure of a hydrogel system is one of the most critical parameters when designing hydrogels for drug delivery applications. Several approaches have been developed to characterize the mesh structure of hydrogel systems. Typical methods to determine the mesh size of hydrogels rely on swelling5, 18, rheology15, 19–24, small angle X-ray scattering25, cryoporometry26, dynamic light scattering27, low field nuclear magnetic resonance (NMR)26 and diffusion-based methods15, 28. However, many of these techniques require access to complex and expensive experimental setups and provide limited information on the distribution of mesh sizes within the hydrogel. Furthermore, applying these methods to develop hydrogel systems with the desired mesh structure can be challenging. An alternative strategy involves developing a computational model of the hydrogel that creates a theoretical representation of the actual cross-linked polymer structure to determine mesh properties. A computational strategy that incorporates specific properties of the polymer system could be advantageous by providing a rapid and accessible method to predict the hydrogel mesh structure and ultimately to help the design of hydrogels with controllable mesh properties.
Here, we propose developing a computational strategy that can mimic the polymer network of the hydrogel system to determine mesh properties. Alginate, a naturally occurring anionic polymer comprised of α-L-guluronic (G-block) and β-D-mannuronic (M-block) residues, was utilized as our hydrogel model system when developing and validating the computational model given it has extensive use for various therapeutic delivery applications15, 29–35. The computational model incorporated alginate polymer properties including polymer chain radius and monomer composition to determine hydrogel mesh properties. The model was then extended to predict the mesh properties of other popular hydrogel systems. Thus, applications of this computational model could provide an appealing strategy for predicting the mesh size distribution of various polymer systems to help the design of hydrogels for a variety of potential therapeutic applications.
We hypothesize that incorporating properties of the polymer system into our computational model will allow for accurate prediction of hydrogel mesh size and allow for the identification of properties most relevant to the mesh structure. In this work, we begin by designing the computational model of the hydrogel mesh structure and determining how the ratio of M/G-blocks and polymer content effects cross-link density and mesh size distribution. The mesh size of alginate hydrogels composed of polymers with various molecular weight, G-block content and polymer volume fractions were determined to validate the simulations. Then the design of experiments (DOE) was used to determine how the mesh size predicted from the model changes for hydrogels composed of both high G-block content (MVG) and low G-block content (MVM) polymers. Finally, the model was further validated for fibrin and PEG hydrogels and then extended to predict the mesh size of other hydrogels from the properties of the polymer system.
Materials and Methods
Computational Model of the Hydrogel Mesh structure
The hydrogel mesh structure was modeled as randomly oriented overlapping cylinders within a unit cell as previously described with modifications36–37. Briefly, polymers were approximated as unidirectional randomly oriented cylinders where one point on a face of the unit cell was randomly selected as the start of the cylinder and another randomly selected point on a different face of the unit cell was assigned as the end of the cylinder. The radii of the cylinders were set at 0.8 nm based on the estimated average radius of alginate polymers38–39 and the volume contribution of each simulated polymer was approximated as the volume of the cylinder. Simulated polymers were added to the unit cell until reaching a desired volume fraction. For alginate hydrogels, the cylinders were divided into segments of either M-blocks or G-blocks with varying lengths based on the desired M/G ratio and the Kuhn length of an alginate monomer (0.515 nm)40–41. Cross-links within the modeled alginate hydrogels were then determined from regions where two simulated polymers had four overlapping G-blocks (two from each polymer) based on the egg-box model for calcium alginate hydrogels42–45. Simulated hydrogels were assumed to have sufficient calcium to cross-link any four overlapping G-blocks and the number of cross-links within the unit cell was used to determine the cross-link density and the average distance between neighboring cross-links was calculated to determine mesh size. The cross-link density, mesh size and mesh size distribution were modeled for hydrogels over a wide range of polymer volume fractions and with alginate polymers containing varying G-block content. The normalized mesh distribution from the simulations was used to determine the probability of finding a mesh of size ξ (Equation 1):
| (1) |
Where S(ξ) is the generated best fit curve through the simulation data determined via nonlinear regression. For modeling the fibrin and PEG hydrogels, cylinders were set with a radius of 75 nm based on the estimated average radius of fibrin fibers46 or 0.51 nm based on the estimated radius of PEG47. For all simulations, the volume of the unit cell was large enough to ensure that mesh properties were calculated from at least 10,000 cross-links. All simulations were performed in Java using Eclipse and cross-link density, mesh size and mesh size distribution were calculated from multiple simulations (n =10) and the average values were reported.
Hydrogel Formulation
The alginate polymers used in this study were obtained from Novamatrix (FMC). The MVG alginate containing a higher G-block content (~70% G-block alginate as specified by the manufacturer) used in this study included a lower molecular weight (LMW) LF 10/60 and a higher molecular weight (HMW) LF 20/40. The MVM alginate used in this study contained a lower G-block content (~35% G-block alginate as specified by the manufacturer). The alginate polymers used in this study were treated with activated charcoal to further purify the material as previously described15, 34. Briefly, 1 g of alginate was dissolved in 100 ml of deionized (DI) water before being mixed with 0.5 g of activated charcoal (Sigma) for 30 minutes. The alginate solution was then sterile filtered (0.22 μm, Thermo Fischer Scientific) and lyophilized prior to starting hydrogel experiments. Hydrogels for the swelling, polymer volume fraction and storage modulus studies were prepared by dissolving alginate polymer powder in DI water overnight to minimize the contribution of salt when calculating polymer volume fraction. Hydrogels were prepared to create a final concentration of 1, 1.5, 2, 2.5 or 3% (w/v) polymer alginate solution and 0.42 mg of calcium sulfate (Sigma) per mg of alginate polymer. The alginate solution was then dispensed between two glass plates with 2-mm spacers height and allowed to gel for at least 25 minutes at room temperature before being cut with an 8-mm biopsy punch as previously described15, 23–24, 29. Hydrogels were then transferred to 24-well plates and swelled in 0.5 ml of DI water at 37°C for an additional hour prior to determining hydrogel properties. For the diffusion of FITC dextran studies, alginate polymer was dissolved in DI water supplemented with 10 mM HEPES (Sigma) to control the effect of pH on the fluorescence of FITC. Hydrogels were created with 2 or 3% (w/v) polymer content and were dispersed in 12-well plates to gel. Hydrogels then had a square region (~ 1 cm2) removed from the center of the hydrogel and were swelled in an additional 1 ml of 10 mM HEPES at 37°C for an hour. For the fibrin hydrogel studies, fibrinogen was dissolved in 0.9% NaCl (Sigma) and mixed with thrombin in 8-well plates (Lab-Tek) to create a final concentration of 2.5, 5, 7.5 or 10 mg/ml of fibrinogen and 1 unit of thrombin per mg of fibrin. Fibrin hydrogels were then incubated overnight at 37°C to ensure full gelation. For PEG hydrogels, PEG-diacrylate (PEGDA, 20K MW, Laysan Bio) was dissolved in HEPES-buffered saline (HBS, pH 7.4) to create a final concentration of 10, 15, 20 and 40% (w/v) containing 30 μg of 2,2-dimethoxy-2-phenyl-acetophenone (DMAP) in N-vinylpyrrolidone (NVP) per mg of PEGDA as previously described48. PEGDA solutions were dispensed into rubber molds with approximately 10 mm diameter and 1.5 mm height and exposed to UV light (UVL-56 UV Lamp, 365 nm) for half an hour to ensure full gelation. PEG hydrogels were transferred to 12 well plates, swelled in 1 ml of DI water for an hour at 37°C prior to determining swelling properties.
Polymer Molecular Weight and Characteristic Ratio
Briefly, alginate polymers were prepared at 0.01, 0.05, 0.1 and 0.15% (w/v) in various NaCl solutions and were transferred to an immersion cup with a cone plate in a rheometer (HR3, TA Instruments) to determine viscosity. The polymer solutions were strained over a range of 5–50 hertz and values of viscosity were obtained from the linear region. A Huggins plot (ηreduced/c vs c) was constructed to determine the intrinsic viscosity of alginate polymers and the average molecular weight and characteristic ratio (Cn) were calculated from empirically derived equations in previous work49 and reported.
Swelling, Polymer Volume Fraction and Rheological Characterization of Hydrogels
Alginate hydrogels were formulated from MVG or MVM alginate polymers as described above to obtain 1, 1.5, 2, 2.5 or 3% (w/v) final alginate polymer concentrations. Alginate hydrogels were then transferred to 24-well plates, each hydrogel was covered with 0.5 ml of DI water and incubated at 37°C for an hour. PEG hydrogels with 10, 15, 20 or 40% (w/v) final polymer concentrations were incubated at 37°C for an hour. Hydrogels were then removed (n = 5–6), and the hydrogels were weighed to obtain the wet weight (Ws). For swelling and polymer volume fraction studies, hydrogels were frozen overnight and lyophilized for at least 48 hours before weighing the hydrogels to obtain the dry weight of the polymer (WD). The following equation (Equation 2) determined the volumetric swelling ratio:
| (2) |
Where ρw is the density of water and ρP is the density of polymer as previously determined or specified by the manufacturer (Alginate: 1.6 g/ml16, 50, PEG 1.13 g/ml). Polymer volume fraction v2,3 is the volume the polymer occupies in the swelled hydrogel and was determined by taking the inverse of the volumetric swelling ratio. For fibrin hydrogels, the polymer volume fraction was determined from the ratio of fibrin concentration to the density of fibrin (0.4 g/ml)51. For rheological characterization, hydrogels were placed between parallel plates (axial force set at 0.01 N) in a rheometer. The hydrogels were strained from 0.001–5% at a frequency of 1 Hz and values of storage modulus (G’) were obtained from the linear viscoelastic region. At least a dozen points were used to obtain the average G’ value.
Mesh Size Calculations
Mesh size was estimated with two different approaches for alginate and PEG hydrogels. For PEG hydrogels, molecular weight between cross-links (MC) was determined via the Peppas-Merrill equation5, 18 (Equation 3):
| (3) |
Where Mn is the molecular weight of PEG (20,000), is the specific volume of the polymer (0.885 cm3/g for PEG), V1 is the molar volume of the solvent (18 cm3/g), X1 is the polymer-solvent interaction parameter (0.426 for PEG), v2,s is the polymer volume fraction in the swelled state and v2,r is the polymer volume fraction in the relaxed state.
Due to the anionic contributions of the alginate polymers, alginate hydrogel mesh size was determined from the swelling and rheometry data as previously described15, 20–21, 23–24. MC for alginate hydrogels was determined via the following equation19 (Equation 4):
| (4) |
Where CP is the polymer concentration, R is the gas constant and T is the measurement temperature. Mesh size (ξ) is then calculated as follows (Equation 5):
| (5) |
Where l is the Kuhn length of the repeating unit (Alginate: 5.15 Å, PEG: 1.46 Å), Mr is the molecular weight of the repeating unit (Alginate: 194 g/mol, PEG: 44.05 g/mol) and Cn is the determined characteristic ratio. Mesh sizes were obtained using this equation for alginate and PEG hydrogels and were plotted with the mesh size predicted from the computational simulations described above.
Diffusion Experiments to Determine Mesh Size
Diffusion of a fluorescent tracer through hydrogels were performed to further validate mesh size as previously described with modifications52. Alginate hydrogels in 12-well plates with a square cutout (~ 1 cm2) in the center of the gel were monitored with a fluorescent microscope (Axio Vert A.4, Zeiss) at 4X magnification. Approximately 100 microliters of a 100 μg/ml solution of FITC-dextran (20 kDa, Sigma) were carefully transferred to the cutout region and time-lapse imaging of the alginate hydrogel adjacent to the cutout region was performed using a 488-nm excitation filter every minute for the course of 30 minutes. Images were taken immediately after the addition of FITC-dextran to the cutout region and the normalized fluorescent intensity of five equally spaced regions of the alginate hydrogel were determined for each image over the course of 30 minutes. The effective isotropic diffusion coefficient (Deff) was determined from the data assuming that diffusion could be approximated as a one-dimensional, semi-infinite slab, and solving Fick’s second law (Equation 6):
| (6) |
Assuming the following initial and boundary conditions (Equations 7–9):
| (7) |
| (8) |
| (9) |
Solving Fick’s second law then yields the following solution as previously described52 (Equation 10):
| (10) |
Where t is time (seconds), x0 is the distance of the analyzed region to the edge of the reservoir and C0 is the intensity of FITC-dextran. The derivative of concentration with respect to time was approximated using a finite difference formula (Equation 11):
| (11) |
Cr is the intensity measured for any region at time tr. The diffusion coefficient was determined by plotting 1/t vs and applying linear regression to estimate the slope of the line (-x0/4Deff). Deff was determined for each region and the mesh size of the hydrogel was then determined via the following equation28 (Equation 12):
| (12) |
Where rs is the stokes radius of FITC-dextran in water (3.3 nm as specified by the manufacturer), yp is approximated as one when the mesh size is much greater than rs and ϕ is the polymer volume fraction. All images were analyzed with ImageJ (NIH) and the mesh size was calculated for each region and the average value per hydrogel (n = 4) was reported.
Design of Experiments (DOE)
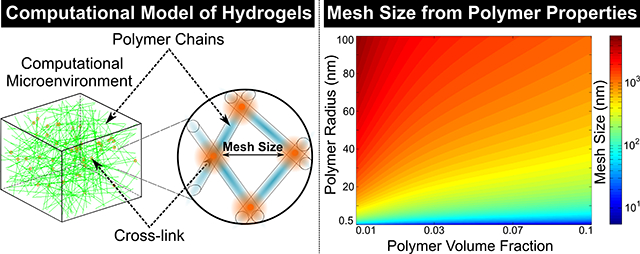
A Box-Behnken DOE experimental design was created with JMP software (SAS institute) to analyze how combining both MVM and MVG alginate polymers at different concentrations effect hydrogel mesh properties. Input parameters included ratio of MVG vs MVM polymer (0 to 1), G-block content of MVM alginate (30% to 50% G-block), G-block content of MVG alginate (60% to 100% G-block) and total polymer volume fraction (1% to 2%). Output parameters consisted of cross-link density and mesh size. The input variables were selected due to the effect G-block content of alginate polymers and polymer volume fraction has on modulating alginate hydrogel properties, including modulus, swelling and correspondingly mesh size53. The input variables were examined at high, medium and low conditions base on the Box-Behnken model to generate prediction maps of the input variables effect on hydrogel mesh properties. The significance of the input parameters was determined via the response surface predictions generated by the DOE software as previously described54. A full factorial approach was also utilized to determine how polymer radius and polymer volume fraction affect hydrogel mesh structure. Polymer chains with 0.5, 5, 10, 25, 50, 75 and 100 nm radii were modeled at 0.01, 0.025, 0.05, 0.075 and 0.1 polymer volume fraction to determine hydrogel mesh size. Heatmaps of the effect of inputs on hydrogel cross-link density and mesh size were plotted with MATLAB 2014a (Mathworks) and reported.
Confocal Reflection Microscopy
Confocal reflection microscopy was utilized to characterize the mesh size of fibrin hydrogels. Fibrin hydrogels were transferred to coverslips after gelation and were imaged with a Leica TCS SP8 STED 3x confocal microscope using the 615 nm laser line. Images were acquired for four regions of 2.5, 5, 7.5 and 10 mg/ml fibrinogen hydrogels and the average distance between adjacent cross-links was quantified with ImageJ (NIH) for at least 40 regions in each image to determine average mesh size. The average mesh size for each image was plotted with the mesh size predicted from the computational simulations described above.
Statistical Analysis
The coefficients of determination were calculated in order to determine the goodness of fit of the simulation model to the experimental data. DOE experiments were designed and analyzed using JMP 14.3 software (SAS institute) and significant interactions were asserted at P < 0.05. GraphPad Prism 8 software (GraphPad Software Inc.) was used to perform all regressions.
Results
Simulations Predict that Mesh Properties are Dependent on the G-Block Content of the Polymer and Polymer Volume Fraction.
A computational model of the alginate hydrogel was designed in order to predict various hydrogel mesh properties. The alginate hydrogel was modeled as overlapping randomly oriented cylinders and regions with overlapping G-blocks were designated as cross-links in order to determine cross-link density and mesh size (Fig. 1A). The computational model predicted that cross-link density increased exponentially for polymers with higher G-block content and higher polymer volume fractions, with cross-link density reaching approximately 188, 75, 38 and 12 μM for hydrogels composed of polymers with 100%, 70%, 50% and 30% G-block content respectively (Fig. 1B). Furthermore, the predicted mesh size from the computational model determined that hydrogel mesh size significantly decreases with higher polymer volume fractions and with polymers containing higher G-block content (Fig. 1C). The data from the simulations and nonlinear regressions were used to generate the mesh size equation based on polymer volume fraction and G-block content (Equation 13):
| (13) |
Fig 1. Design of a Computational Model that Mimics the Hydrogel Polymer Network and Enabled the Prediction of the Cross-link Density and Mesh Size of Various Alginate Hydrogels.
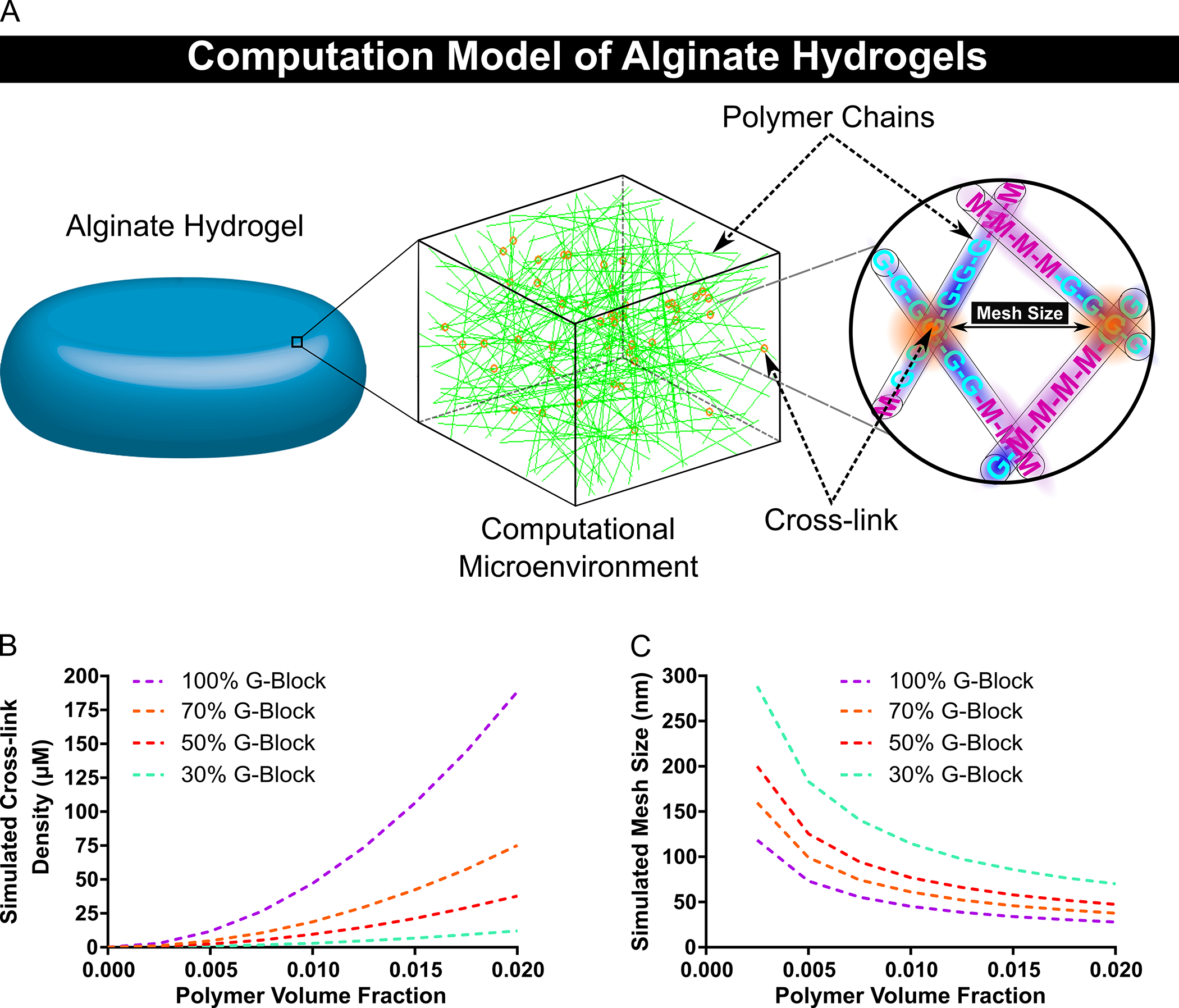
The cross-link density and mesh size of alginate hydrogels composed of various polymer volume fractions and percent G-block content were determined via computational simulations. A schematic of the computational model of the hydrogel is provided (A). The cross-link density of alginate hydrogels was predicted to exponentially increase for hydrogels with polymers containing higher G-block content (B). The model anticipated a wide range of alginate hydrogel mesh sizes based on polymer volume fraction and G-block content (C). In figure panel B and C, dashed lines represent mean. (B–C, n = 10).
Where and determine the magnitude of the decay phases which are dependent on the fraction of G-block () content of the polymers given by the following equations (Equations 14–15):
| (14) |
| (15) |
The Computational Model Predicted the Mesh Size of Alginate Hydrogels with Varying Properties
The computational model closely predicted the mesh size of alginate hydrogels over a range of polymer and hydrogel properties. Alginate hydrogels with varying mechanical properties were prepared from polymers with different molecular weight and G-block content (Table 1). Hydrogels with higher polymer and G-block content were found to have an increased storage modulus, with 3% (w/v) hydrogels having a storage modulus of approximately 11.8, 32.5 and 51.1 kPa for MVM, MVG LMW and MVG HMW hydrogels respectively (Fig. 2A). The swelling ratio was found to significantly increase with lower polymer content, with all hydrogels experiencing an approximately 3-fold greater swelling for 1% (w/v) hydrogels compared to 3% (w/v) hydrogels (Fig. 2B). As expected, the polymer volume fraction was found to increase for hydrogels with higher alginate percentages (Fig. 2C). The Mesh size of hydrogels was determined from the characteristic ratio of the polymer (Table 1), swelling ratio and storage modulus and was compared to the predictions from the computational simulations (Fig. 2D). The simulations provided a high degree of correlation to the mesh sizes determined for MVG LMW (R2 = ~0.91) and MVG HMW (R2 = ~0.96) alginate hydrogels for polymer volume fractions higher than 0.01. The computational simulations also predicted the mesh size of hydrogels composed of MVM polymer, with polymer volume fractions above 0.01 showing a close correlation to MVM (R2 = ~0.87) hydrogels (Fig. 2E).
Table 1.
G-block content, Intrinsic Viscosity, Average Molecular Weight (MW) and Characteristic Ratio of Alginates
| Alginate | G-block (%) | Intrinsic Viscosity (dL/g) | MW (kg/mol) | Characteristic Ratio (Cn) |
|---|---|---|---|---|
| MVG HMW | 70% | 3.94 | 238 | 22.96 |
| MVG LMW | 70% | 1.17 | 41 | 18.81 |
| MVM | 35% | 0.91 | 22 | 18.41 |
Fig 2. The Computational Model of the Hydrogel Polymer Network Provided a Strategy to Closely Estimate the Mesh Size of Alginate Hydrogels.
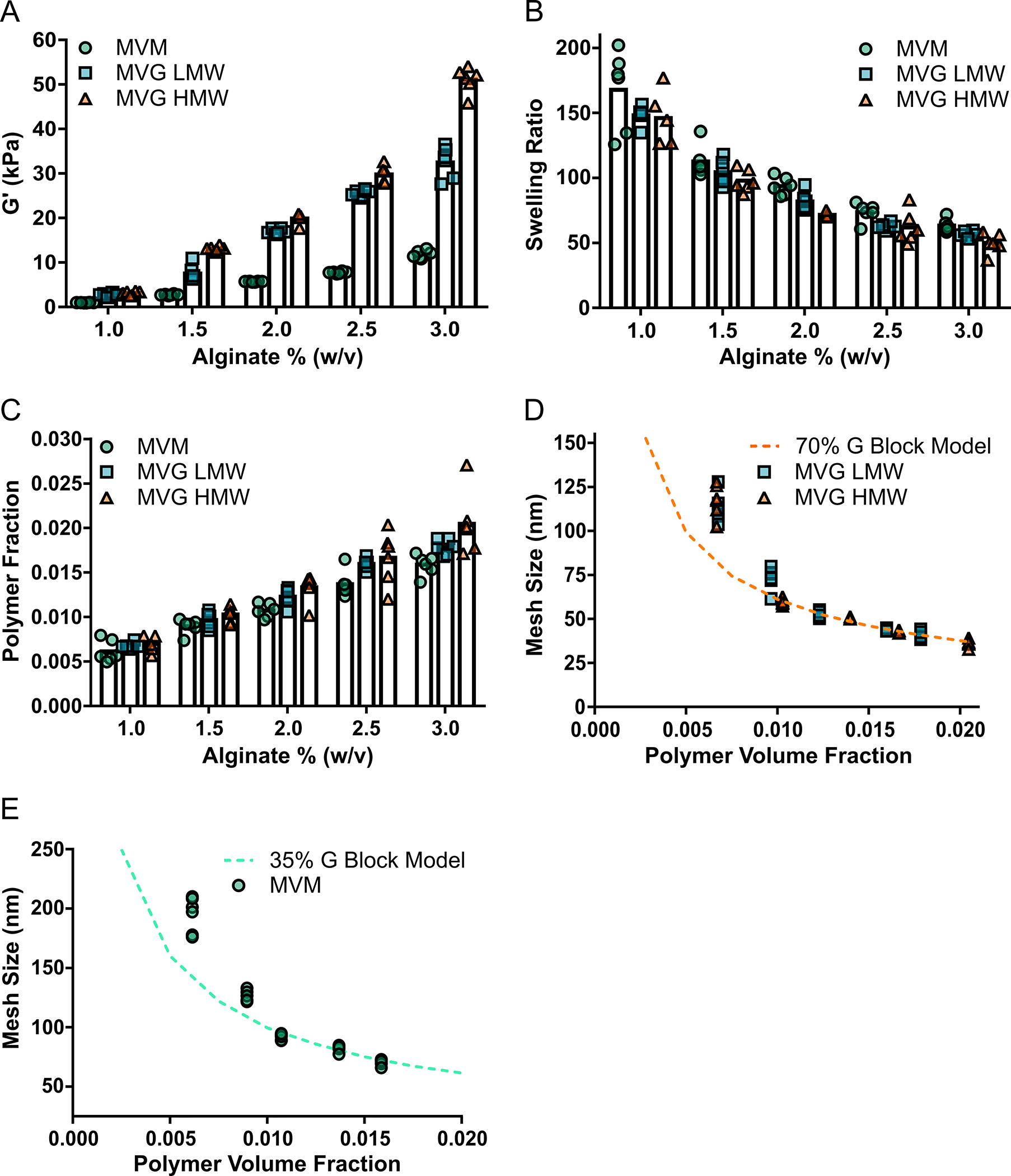
The computational model of the hydrogel mesh size provided a strong correlation to the mesh size of alginate hydrogels comprised of different mechanical and polymer properties. The storage modulus increased for hydrogels with greater alginate percent, G-block content and polymer molecular weight (A). Hydrogels with greater polymer content were determined to experience less swelling (B) and greater polymer volume fractions (C). The mesh size of MVG (high G-block content) alginate hydrogels were closely predicted by the computational model (D). The computational model provided a good estimation of the mesh size of the MVM (low G-block content) alginate hydrogels (E). In figure panel A, B and C, bar represents mean, scatter dot plots display individual measurements and error bars represent standard deviation. In figure panel D and E, scatter dot plots display individual measurements and dashed lines represent mean values determined from the simulations (A–E, n = 5–6).
Diffusion Based Methods for Determining the Mesh Size of Alginate Hydrogels Followed Model Predictions
The diffusion of FITC-Dextran within alginate hydrogels was observed to further validate the ability of the computational model to predict hydrogel mesh properties. FITC-dextran diffused from the reservoir into the surrounding hydrogel for 30 minutes (Fig. 3A). Alginate hydrogels were found to have slower diffusion of FITC-Dextran, and correspondingly smaller mesh sizes, with higher polymer volume fractions and for hydrogels comprised of polymers with higher G-block content. Hydrogels comprised of MVG polymers were determined to have diffusion derived mesh sizes close to the mesh size predicted from the computational model, with MVG HMW hydrogels showing a closer correlation to simulations than MVG LMW hydrogels (Fig. 3B). The simulations also provided a reasonable approximation of the diffusion derived mesh size of hydrogels comprised of MVM polymers (Fig. 3C).
Fig 3. A Diffusion-Based Strategy for Determining Alginate Hydrogel Mesh Size Further Validated the Computational Model’s Ability to Predict Hydrogel Mesh Properties.
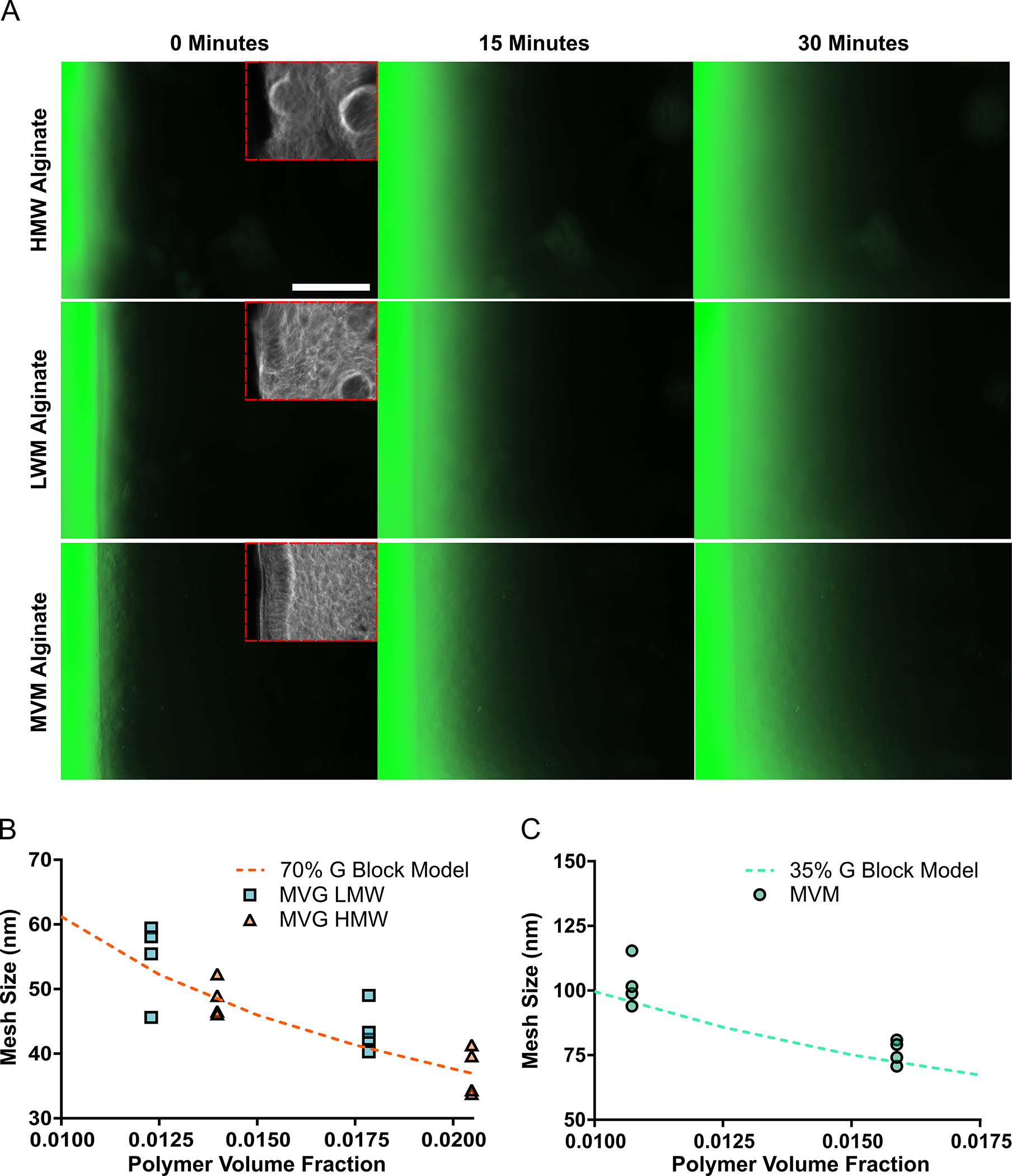
The mesh size of alginate hydrogels determined from the diffusion of FITC-dextran followed the mesh size predicted from the computational model. The diffusion of FITC-dextran from a reservoir into various alginate hydrogels was observed for 30 minutes. Scale bar represents 5 mm (A). The mesh size of MVG (high G-block content) hydrogels was determined from the effective diffusion coefficient of FITC-dextran within the polymer system and had similar mesh sizes predicted by the simulations (B). The computational model reasonably predicted the mesh size of MVM (low G-block content) hydrogels determined from the diffusion of FITC-dextran through the polymer system (C). In figure panel B and C, scatter dot plots display individual measurements and dashed lines represent mean values determined from the simulations (B–C, n = 4).
Simulations Provided Information on the Mesh Size Distribution of Alginate Hydrogels
The computational model provided a method to characterize the mesh size distribution of alginate hydrogels. The mesh size distribution was predicted for 1, 2 and 3% (w/v) alginate hydrogels composed of MVG HMW, MVG LMW or MVM alginate polymers (Fig. 4 A–C). In general, the simulations predicted that the mesh size distribution had a higher maximum frequency and lower standard deviation for hydrogels with higher alginate percent (w/v). Furthermore, hydrogels with less G-block content were observed to have a larger distribution of mesh sizes and a lagging region of mesh sizes extending to over 200 nm. The simulation data was used to determine P(ξ), which is the predicted percent of the total mesh structure with a specific mesh size. P(ξ) was also observed to have a greater amplitude, decreased standard deviation and smaller mean for hydrogels with more G-block content and alginate percent (w/v).
Fig 4. The Computational Model Provided a Method to Readily Characterize the Mesh Size Distribution of Various Alginate Hydrogels.
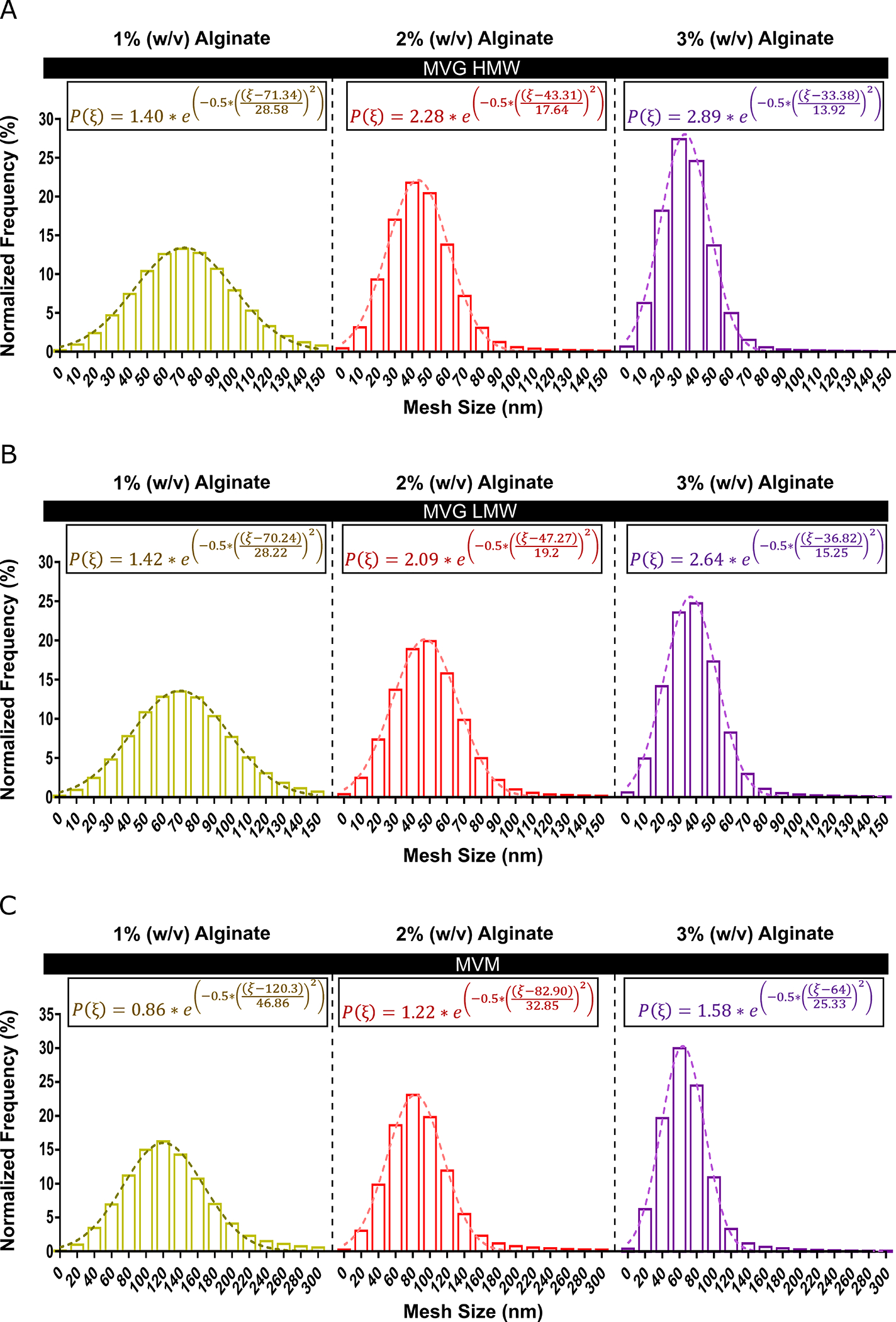
The computational model determined the mesh size distribution and the probability of finding a mesh size ξ for 1, 2 or 3% (w/v) MVM (low G-block content) or MVG (high G-block content) hydrogels. The mesh size distribution was found to experience greater amplitudes, lower means and decreased standard deviations for MVG hydrogels with greater polymer volume fractions (A–B). MVM hydrogels were predicted to have a lagging region of large mesh sizes extending over 300 nm (C). (A–C) Dashed lines were determined from nonlinear regression (A–C, n = 10).
Prediction of Alginate Hydrogel Mesh Properties by Experimental Design
A DOE approach could be used in conjunction with the computational model to predict further mesh properties of alginate hydrogels consisting of polymers with both high and low G-block content. The Box-Behnken DOE model generated 27 unique compositions of alginate hydrogels to model, and the computational simulations predicted the corresponding cross-link density, mesh size and mesh size distribution for each condition. The polymer volume fraction, the ratio of MVG to MVM polymer, the G-block content of MVG polymer and the G-block content of MVM polymers were determined to affect both hydrogel cross-link density and mesh size. The DOE software predicted that cross-link density could be varied from approximately 5 to 100 μM through varying the polymer volume fraction and G-block content of the MVG and MVM alginate polymers (Fig 5A). The mesh size was predicted to be inversely correlated to cross-link density, with simulated mesh sizes varying from approximately 30 to 90 nm through altering the input parameters (Fig 5B).
Fig 5. DOE Approach Predicted Hydrogel Design Properties to Control the Mesh Structure of Binary Alginate Hydrogels.
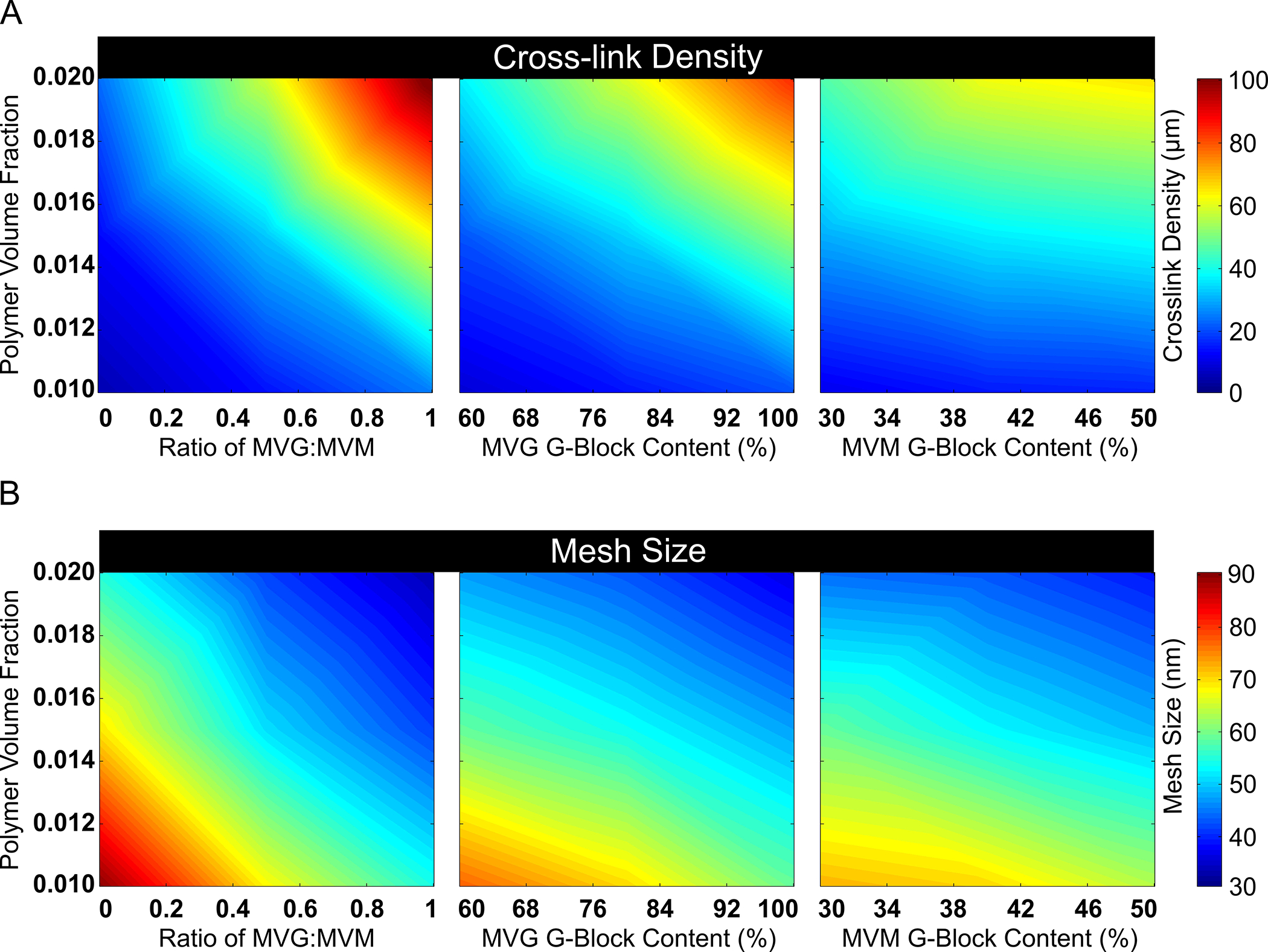
DOE was used to identify properties that could alter the cross-link density and mesh size of alginate hydrogels with MVM (low G-block content) and MVG (high G-block content) polymers. Response surface maps of hydrogel properties effect on cross-linking density are provided (A). Altering polymer volume fraction, the ratio of MVG to MVM polymers and G-block content of hydrogels predicted a large range of adjustable hydrogel mesh sizes (B). In figure panel A, the heat color map represents the range of cross-link density. In figure panel B, the heat color map represents the mesh size range (A–B, n = 10).
The Computational Model Predicts the Mesh Size of Fibrin and PEG Hydrogels
The computational model also provided a close prediction of mesh properties for other hydrogel systems. Hydrogels with 2.5, 5, 7.5 or 10 mg/ml of fibrinogen were imaged with confocal reflection microscopy to determine hydrogel mesh size (Fig 6A). The mesh size determined for the fibrin hydrogels were found to range from approximately 2.2 μm—5.6 μm and were very closely predicted (R2 > 0.99) by the computational model (Fig 6B). The mesh size of PEG hydrogels with varying polymer concentrations was also compared to the computational model, with the simulations providing a high degree of correlation (R2 = ~0.95) to PEG hydrogels (Fig. 6C).
Fig 6. The Computational Model Simulated the Mesh Structure of Other Hydrogel Systems.
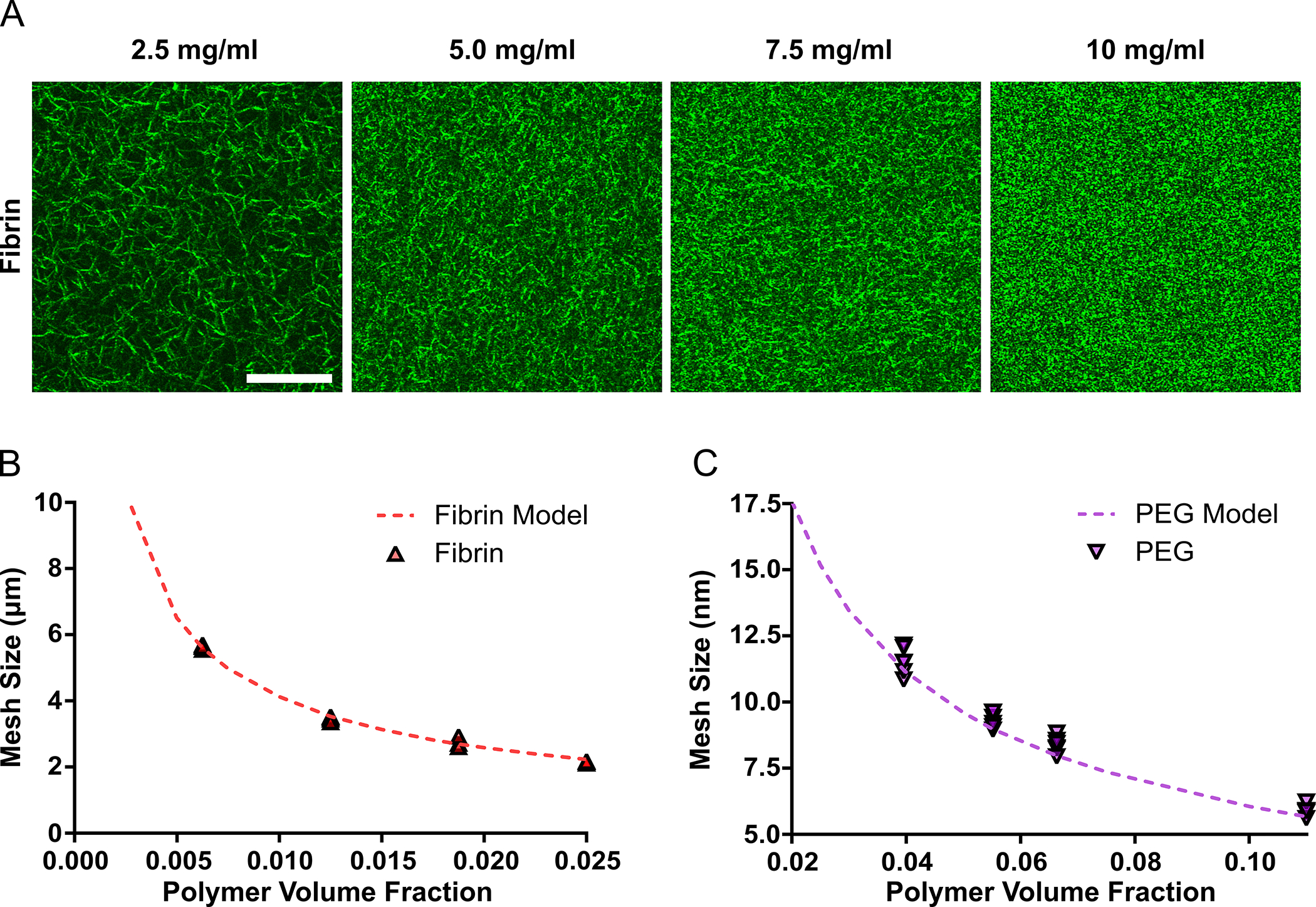
The computational-based strategy for determining hydrogel mesh size was further validated for fibrin and PEG hydrogels. Confocal reflection of the fibrin meshwork for 2.5, 5, 7.5 and 10 mg/ml hydrogels is provided. Scale bar represents 20 μm (A). The computational model provided a very close estimation of fibrin hydrogel mesh size determined from the confocal images (B). The mesh size of PEG hydrogels was accurately predicted by the simulations for varying PEG concentrations (C). In figure panel B and C, scatter dot plots display individual measurements and dashed lines represent mean values determined from the simulations (B–C, n = 4–6).
DOE Strategy to Design Hydrogels with Predefined Mesh Sizes Through Controlling Properties of the Polymer Network
A full factorial DOE approach was utilized to determine how the size of the polymer chains affects hydrogel mesh size. The full factorial model generated 35 unique compositions of hydrogels to model, and the computational simulations predicted the mesh size for each condition. The polymer volume fraction and the radius of polymer chains were determined to have a significant effect on the mesh size. The DOE results predicted that the mesh size was proportional to the polymer chain radius and could be varied from approximately 5 nm to 5.5 μm through varying the polymer chain radius and the polymer content (Fig 7). The data from the DOE were used to predict how mesh size depends on the polymer volume fraction and the polymer chain radius (RP) given by the following equation (Equation 16):
| (16) |
Fig 7. DOE Provided a Strategy to Predict the Mesh Size of Additional Hydrogel Systems.
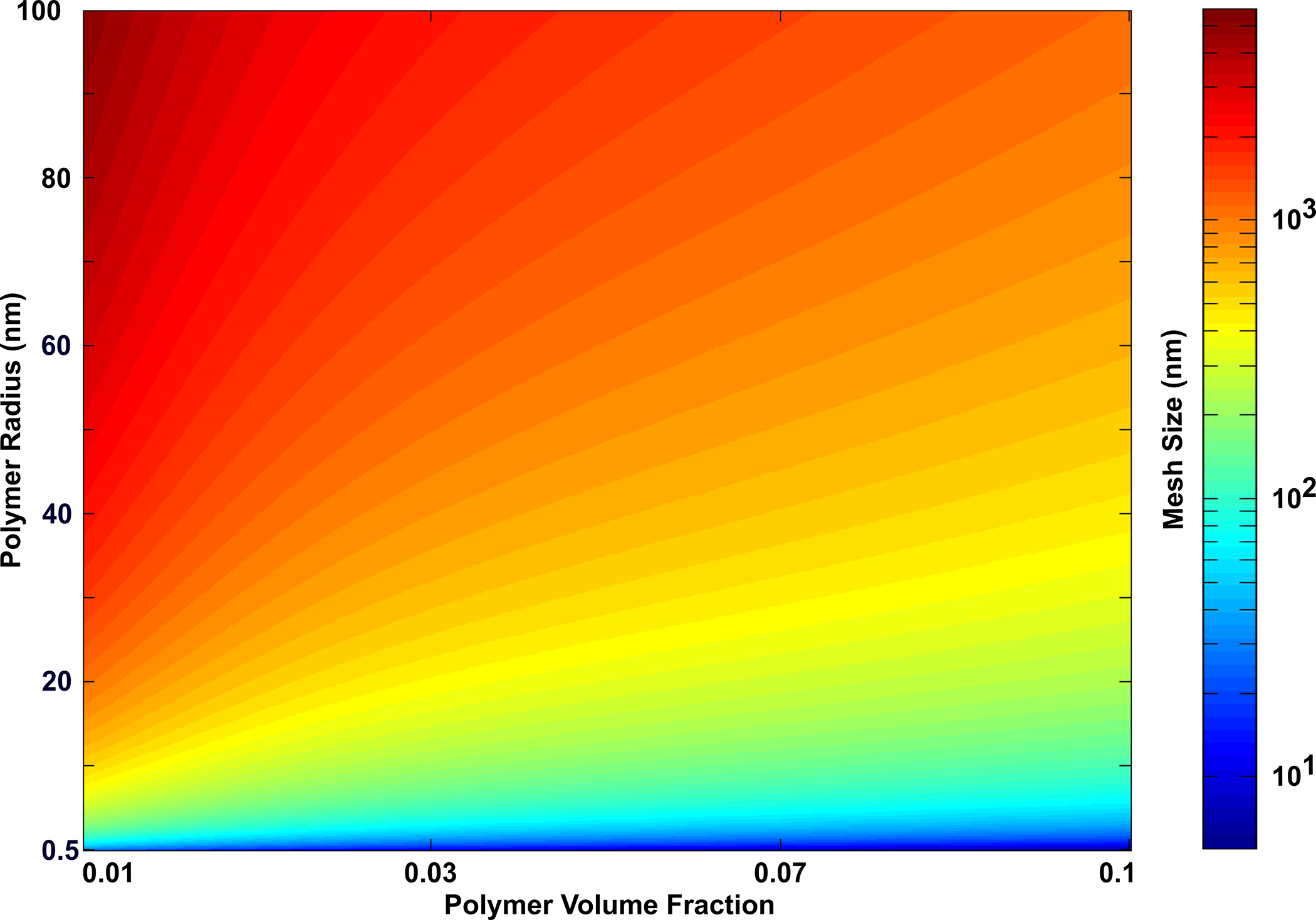
A full factorial DOE approach was utilized to predict the mesh size of hydrogels from the properties of the polymer system. The mesh size of hydrogels was predicted to increase with both polymer volume content and the polymer chain radius, with the polymer chain radius having the most effect on mesh size for the conditions tested. The heat color map represents the mesh size range (n = 10).
Discussion
This study investigates the utility of a novel computational model that mimics the hydrogel mesh structure and allows one to determine the hydrogel mesh properties critical for the design of hydrogels systems as therapeutic delivery vehicles. This work demonstrates that the computational model could accurately predict the mesh size of alginate hydrogels over a broad range of polymer and hydrogel properties. Additionally, the model provided information about the mesh size distribution of hydrogels and provided adjustable parameters to design alginate hydrogels with controllable mesh properties. Finally, the computational model also provided a close prediction of the mesh size for fibrin and PEG hydrogels and was further extended to predict the mesh properties of other hydrogel systems. To our knowledge, this is the first study of a computational model of the hydrogel polymer network to predict hydrogel mesh properties as a strategy to provide control over therapeutic delivery applications.
This work involved designing a computational model of the alginate hydrogel. In particular, the mesh size of hydrogels has an essential role in determining the diffusion of encapsulated therapeutic agents and regulating mass transport for cell-based therapies5–6, 18. In this study, we modeled the alginate polymers as a collection of rigid rods because the polymers in hydrogels experience tension following gelation due to various swelling forces acting on the polymer system59, with alginate hydrogels forming very rigid chains following calcium crosslinking55. Moreover, alginate polymers have previously been shown to be reasonably modeled as rigid rods, especially with polymers containing larger M block or G block regions56–58. Taken together, and while understanding some limitations, we still believe that modeling the crosslinked alginate polymers as rigid rods provides a computationally accessible strategy to approximate properties of the polymer system and derive hydrogel mesh properties. The model also determined cross-linking regions and correspondingly mesh size based on the egg-box model, where the α-l-guluronate (G) residues in the alginate polymer chain adopt a 21 helical conformation and the pair of G residues (“binding cavity”) surrounds the calcium ions60. Previous work has shown that cross-link density significantly increases for alginate hydrogels with more calcium16, 61–62 or more polymer content28. Similarly, this model predicted that the regions of overlapping G-blocks (i.e. cross-links) dramatically increased for hydrogels with higher polymer percentage and G-block content. Furthermore, the cross-link density predicted from the simulations for hydrogels with higher G-block content followed a similar trend to theory derived from Flory-Rehner16, 63–64. Finally, the model predicted that hydrogel mesh size increases for hydrogels comprised of lower G-block content and polymer volume fractions. Thus, this work provides a computational model that can incorporate properties of alginate hydrogels to provide a theoretical representation of the hydrogel mesh structure.
This study demonstrates that the model can accurately predict the mesh size of alginate hydrogels. Previous work has shown that alginate hydrogel properties can be modulated through controlling polymer properties, including molecular weight, polymer content and the ratio of M/G-blocks16, 21, 24, 28, 53, 65–66. Thus, in this work, hydrogels with varying polymer concentrations were prepared from polymers of various molecular weight and G-block content to validate the model. The mesh size of alginate hydrogels was determined from mechanical properties15, 20, 23–24 and from the diffusion of FITC-dextran through alginate hydrogels28, 52. Our results found that the mesh size determined from the simulations could accurately predict the mesh size of various alginate hydrogel compositions. Previous work has also shown that alginate hydrogels can display a wide range of mesh sizes from ~10 to 100 nm depending on the polymer and calcium cross-linking concentrations15–16, 20, 22, 26, 28, 65. The computational model was found to closely predict hydrogels with higher polymer content and also provided a good prediction of the mesh properties from other work using alginate hydrogels with greater calcium concentrations and higher polymer volume fractions67. However, the model underestimated the mesh size of hydrogels with lower polymer volume fractions. This is possibly the result of the simulations modeling the polymer structure as a collection of rigid cylinders, which is likely more valid for stiffer and more mechanically stable hydrogels composed of higher polymer volume fractions6. Overall, the computational model provided a robust prediction of the mesh size of alginate hydrogels for a wide range of hydrogel compositions and mechanical properties.
The computational model was then applied to predict the mesh size distribution of alginate hydrogels. Mesh size distribution has an important role in determining the probability of a solute encountering a sufficient opening within the hydrogel to allow for diffusion, the maximum size of therapeutic agents that can diffuse through the mesh structure and also has a role in modulating encapsulated cell and native tissue properties15–16, 68–70. Previous studies using NMR to characterize the mesh size distribution of alginate hydrogels composed of 2% (w/v) MVG polymers have shown a broad peak of mesh sizes near 30 nm and a lagging mesh region extending over 100 nm7, 71. The simulations determined a similar prevalence of mesh sizes between approximately 10 to 50 nm and a lagging region of mesh sizes exceeding 100 nm. The simulations also predicted mesh size distributions similar to other work with interpenetrating alginate hydrogels, with the model more closely following mesh size distributions predicted from cryoporometry26. This study found that the model could determine hydrogel mesh size distributions.
The results of this study predicted how varying properties of binary hydrogels effects hydrogel cross-link density and mesh size. Hydrogels consisting of both MVG and MVM polymers have been shown to exhibit different properties than hydrogels comprised of only MVG or MVM polymer, allowing for additional control over hydrogel mechanical properties72–73. In this study, a DOE design was utilized in conjunction with the computational model to predict how factors affected MVG and MVM binary hydrogel mesh properties. The ratio of MVG to MVM, polymer volume fraction and G-block content of the polymers were determined to have the most effect on both cross-link density and mesh size. In summary, the computational model determined important properties to control when designing alginate hydrogels with desired mesh properties.
This work also demonstrated that the computational model could be extended to predict the mesh properties of additional hydrogel systems. Fibrin and PEG hydrogels were used to further validate the model for hydrogels systems over a broad range of mesh properties. Fibrin is a naturally occurring polymer that aggregates into thick fibers and typically has hydrogels with mesh sizes in the micron range74–75. PEG is a synthetic polymer with a small polymer chain radius and forms nanoporous hydrogels47–48, 76. While the model does not account for structural defects and network non-ideality that can be present in PEGDA (or PEG-dimethacrylate) hydrogels77–78, the computational model accurately predicted the mesh size of both fibrin and PEG hydrogels. In this study, PEGDA hydrogels were prepared from polymers with high molecular weight and have a greater fully extended polymer length following gelation and swelling79 which could be reasonably represented by the unidirectional cylinders in the model. Furthermore, the higher PEG concentrations used in this work helped reduce the prevalence of network defects80, with certain defects including intra-chain cycles and dangling ends not contributing to the network-dependent properties of the hydrogel81. Interestingly, previous work has also modeled hydrogels made from Peg-b-PLA with end-capped acrylate functionalities as ideal networks to predict hydrogel properties including degradation82. Nevertheless, and while understanding some limitations, the model still provided a reasonable estimate of the mesh properties of other fibrin75, 83–84 and PEGDA47, 77, 85 hydrogels, especially for PEGDA hydrogels with higher polymer molecular weight and polymer volume fractions. The model was then extended to predict the mesh structure of other hydrogel systems from the polymer radius and content. Interestingly, the simulations determined that hydrogels with a larger polymer chain radius had significantly greater mesh sizes. Other work has also observed that hydrogels comprised of polymer chains with a small polymer radius (< 1 nm) commonly have mesh sizes in the tens of nanometer range85–86, while hydrogels comprised of polymers with a larger polymer fiber radius can have pore sizes into the micron range87–88. Taken together, the computational model can closely predict the mesh properties of multiple hydrogel systems and provides a robust strategy to predict the mesh size of hydrogels.
Conclusions
This study investigates the use of a computational model of the hydrogel mesh structure to predict important hydrogel properties conducive to therapeutic delivery. This work found that the model could incorporate various parameters of alginate hydrogels, including polymer fraction and G-block content, to predict cross-linking density, mesh size and mesh size distribution. The results from the simulations were found to closely correlate to the actual mesh size of alginate hydrogels, with higher polymer fractions providing a better correlation to mesh size. Furthermore, the simulations could predict the mesh size of hydrogels combining polymers with varying G-block content. Finally, the computational model was validated for fibrin and PEG hydrogel systems and was extended to predict the mesh properties of hydrogels from the polymer network. Future work will include applying additional modeling strategies and crosslinking paradigms into the simulations to further characterize specific hydrogel systems. Overall, this model provides a robust and accessible strategy to predict the mesh size of hydrogels and could have applications for designing hydrogels with controllable mesh properties for potential therapeutic delivery applications.
Acknowledgements
This work was supported by the American Heart Association grant #17IRG33420114 / Eduardo Silva / 2017 and grant # 19IPLOI34760654 / Eduardo Silva / 2019. K.T.C was supported by the NIH T32 predoctoral fellowship in basic and translational cardiovascular medicine at UC Davis (T32 HL086350). We want to express our gratitude to Dr. Alyssa Panitch for the use of equipment involved in acquiring this data.
References
- 1.Li JY; Mooney DJ, Designing hydrogels for controlled drug delivery. Nat Rev Mater 2016, 1 (12). DOI: ARTN 16071 10.1038/natrevmats.2016.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lee K; Silva EA; Mooney DJ, Growth factor delivery-based tissue engineering: general approaches and a review of recent developments. J R Soc Interface 2011, 8 (55), 153–170. DOI: 10.1098/rsif.2010.0223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hoare TR; Kohane DS, Hydrogels in drug delivery: Progress and challenges. Polymer 2008, 49 (8), 1993–2007. DOI: 10.1016/j.polymer.2008.01.027. [DOI] [Google Scholar]
- 4.Chai QY; Jiao Y; Yu XJ, Hydrogels for Biomedical Applications: Their Characteristics and the Mechanisms behind Them. Gels-Basel 2017, 3 (1). DOI: ARTN 6 10.3390/gels3010006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Peppas NA; Hilt JZ; Khademhosseini A; Langer R, Hydrogels in biology and medicine: From molecular principles to bionanotechnology. Advanced Materials 2006, 18 (11), 1345–1360. DOI: 10.1002/adma.200501612. [DOI] [Google Scholar]
- 6.Canal T; Peppas NA, Correlation between Mesh Size and Equilibrium Degree of Swelling of Polymeric Networks. J Biomed Mater Res 1989, 23 (10), 1183–1193. DOI: DOI 10.1002/jbm.820231007. [DOI] [PubMed] [Google Scholar]
- 7.Grassi M; Farra R; Fiorentino SM; Grassi G; Dapas B, Hydrogel Mesh Size Evaluation. Polysaccharide Hydrogels: Characterization and Biomedical Applications 2016, 139–165. [Google Scholar]
- 8.Rehmann MS; Skeens KM; Kharkar PM; Ford EM; Maverakis E; Lee KH; Kloxin AM, Tuning and Predicting Mesh Size and Protein Release from Step Growth Hydrogels. Biomacromolecules 2017, 18 (10), 3131–3142. DOI: 10.1021/acs.biomac.7b00781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Axpe E; Chan D; Offeddu GS; Chang Y; Merida D; Hernandez HL; Appel EA, A Multiscale Model for Solute Diffusion in Hydrogels. Macromolecules 2019. DOI: 10.1021/acs.macromol.9b00753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kim SW; Bae YH; Okano T, Hydrogels - Swelling, Drug Loading, and Release. Pharmaceut Res 1992, 9 (3), 283–290. DOI: Doi 10.1023/A:1015887213431. [DOI] [PubMed] [Google Scholar]
- 11.Liu L; Yao WD; Rao YF; Lu XY; Gao JQ, pH-Responsive carriers for oral drug delivery: challenges and opportunities of current platforms. Drug Delivery 2017, 24 (1), 569–581. DOI: 10.1080/10717544.2017.1279238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Miao TX; Wang JQ; Zeng Y; Liu G; Chen XY, Polysaccharide-Based Controlled Release Systems for Therapeutics Delivery and Tissue Engineering: From Bench to Bedside. Adv Sci 2018, 5 (4). DOI: ARTN 1700513 10.1002/advs.201700513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Peppas NA; Bures P; Leobandung W; Ichikawa H, Hydrogels in pharmaceutical formulations. European Journal of Pharmaceutics and Biopharmaceutics 2000, 50 (1), 27–46. DOI: Doi 10.1016/S0939-6411(00)00090-4. [DOI] [PubMed] [Google Scholar]
- 14.Sharpe LA; Daily AM; Horava SD; Peppas NA, Therapeutic applications of hydrogels in oral drug delivery. Expert Opin Drug Del 2014, 11 (6), 901–915. DOI: 10.1517/17425247.2014.902047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Campbell KT; Stilhano RS; Silva EA, Enzymatically degradable alginate hydrogel systems to deliver endothelial progenitor cells for potential revasculature applications. Biomaterials 2018. DOI: 10.1016/j.biomaterials.2018.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee BH; Li B; Guelcher SA, Gel microstructure regulates proliferation and differentiation of MC3T3-E1 cells encapsulated in alginate beads. Acta Biomater 2012, 8 (5), 1693–1702. DOI: 10.1016/j.actbio.2012.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Williams PA; Campbell KT; Silva EA, Biomaterials and Cells for Revascularization In Cell Therapy: Current Status and Future Directions, Emerich DF; Orive G, Eds. Springer International Publishing: Cham, 2017; pp 139–172. DOI: 10.1007/978-3-319-57153-9_8. [DOI] [Google Scholar]
- 18.Peppas NA; Merrill EW, Crosslinked Poly(vinyl-Alcohol) Hydrogels as Swollen Elastic Networks. J Appl Polym Sci 1977, 21 (7), 1763–1770. DOI: DOI 10.1002/app.1977.070210704. [DOI] [Google Scholar]
- 19.Lee KY; Rowley JA; Eiselt P; Moy EM; Bouhadir KH; Mooney DJ, Controlling mechanical and swelling properties of alginate hydrogels independently by cross-linker type and cross-linking density. Macromolecules 2000, 33 (11), 4291–4294. DOI: DOI 10.1021/ma9921347. [DOI] [Google Scholar]
- 20.Madrigal JL; Shams S; Stilhano RS; Silva EA, Characterizing the encapsulation and release of lentivectors and adeno-associated vectors from degradable alginate hydrogels. Biomater Sci-Uk 2019, 7 (2), 645–656. DOI: 10.1039/c8bm01218k. [DOI] [PubMed] [Google Scholar]
- 21.Madrigal JL; Sharma SN; Campbell KT; Stilhano RS; Gijsbers R; Silva EA, Microgels produced using microfluidic on-chip polymer blending for controlled released of VEGF encoding lentivectors. Acta Biomater 2018, 69, 265–276. DOI: 10.1016/j.actbio.2018.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Turco G; Donati I; Grassi M; Marchioli G; Lapasin R; Paoletti S, Mechanical Spectroscopy and Relaxometry on Alginate Hydrogels: A Comparative Analysis for Structural Characterization and Network Mesh Size Determination. Biomacromolecules 2011, 12 (4), 1272–1282. DOI: 10.1021/bm101556m. [DOI] [PubMed] [Google Scholar]
- 23.Williams PA; Campbell KT; Gharaviram H; Madrigal JL; Silva EA, Alginate-Chitosan Hydrogels Provide a Sustained Gradient of Sphingosine-1-Phosphate for Therapeutic Angiogenesis. Annals of Biomedical Engineering 2017, 45 (4), 1003–1014. DOI: 10.1007/s10439-016-1768-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Williams PA; Campbell KT; Silva EA, Alginate hydrogels of varied molecular weight distribution enable sustained release of sphingosine-1-phosphate and promote angiogenesis. J Biomed Mater Res A 2018, 106 (1), 138–146. DOI: 10.1002/jbm.a.36217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Amamoto Y; Kikuchi M; Masunaga H; Ogawa H; Sasaki S; Otsuka H; Takahara A, Mesh-size control and functionalization of reorganizable chemical gels by monomer insertion into their cross-linking points. Polym Chem-Uk 2011, 2 (4), 957–962. DOI: 10.1039/c0py00304b. [DOI] [Google Scholar]
- 26.Pescosolido L; Feruglio L; Farra R; Fiorentino S; Colombo I; Coviello T; Matricardi P; Hennink WE; Vermonden T; Grassi M, Mesh size distribution determination of interpenetrating polymer network hydrogels. Soft Matter 2012, 8 (29), 7708–7715. DOI: 10.1039/c2sm25677k. [DOI] [Google Scholar]
- 27.Sumitomo K; Mayumi K; Yokoyama H; Sakai Y; Minamikawa H; Masuda M; Shimizu T; Ito K; Yamaguchi Y, Dynamic light-scattering measurement of sieving polymer solutions for protein separation on SDS CE. Electrophoresis 2009, 30 (20), 3607–3612. DOI: 10.1002/elps.200900255. [DOI] [PubMed] [Google Scholar]
- 28.Grassi M; Sandolo C; Perin D; Coviello T; Lapasin R; Grassi G, Structural Characterization of Calcium Alginate Matrices by Means of Mechanical and Release Tests. Molecules 2009, 14 (8), 3003–3017. DOI: 10.3390/molecules14083003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Campbell KT; Hadley DJ; Kukis DL; Silva EA, Alginate hydrogels allow for bioactive and sustained release of VEGF-C and VEGF-D for lymphangiogenic therapeutic applications. Plos One 2017, 12 (7). DOI: ARTN e0181484 10.1371/journal.pone.0181484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen RR; Silva EA; Yuen WW; Mooney DJ, Spatio-temporal VEGF and PDGF delivery patterns blood vessel formation and maturation. Pharm Res 2007, 24 (2), 258–64. DOI: 10.1007/s11095-006-9173-4. [DOI] [PubMed] [Google Scholar]
- 31.Hadley DJ; Silva EA, Thaw-Induced Gelation of Alginate Hydrogels for Versatile Delivery of Therapeutics. Annals of Biomedical Engineering 2019, 47 (8), 1701–1710. DOI: 10.1007/s10439-019-02282-5. [DOI] [PubMed] [Google Scholar]
- 32.Hao X; Silva EA; Mansson-Broberg A; Grinnemo KH; Siddiqui AJ; Dellgren G; Wardell E; Brodin LA; Mooney DJ; Sylven C, Angiogenic effects of sequential release of VEGF-A165 and PDGF-BB with alginate hydrogels after myocardial infarction. Cardiovasc Res 2007, 75 (1), 178–85. DOI: 10.1016/j.cardiores.2007.03.028. [DOI] [PubMed] [Google Scholar]
- 33.Lee KY; Mooney DJ, Alginate: properties and biomedical applications. Prog Polym Sci 2012, 37 (1), 106–126. DOI: 10.1016/j.progpolymsci.2011.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Silva EA; Kim ES; Kong HJ; Mooney DJ, Material-based deployment enhances efficacy of endothelial progenitor cells. Proc Natl Acad Sci U S A 2008, 105 (38), 14347–52. DOI: 10.1073/pnas.0803873105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Silva EA; Mooney DJ, Spatiotemporal control of vascular endothelial growth factor delivery from injectable hydrogels enhances angiogenesis. J Thromb Haemost 2007, 5 (3), 590–8. DOI: 10.1111/j.1538-7836.2007.02386.x. [DOI] [PubMed] [Google Scholar]
- 36.Clague DS; Phillips RJ, Hindered diffusion of spherical macromolecules through dilute fibrous media. Phys Fluids 1996, 8, 1720–1731. DOI: 10.1063/1.868884. [DOI] [Google Scholar]
- 37.Clague DS; Phillips RJ, A numerical calculation of the hydraulic permeability of three-dimensional disordered fibrous media. Phys Fluids 1997, 9 (6), 1562–1572. DOI: Doi 10.1063/1.869278. [DOI] [Google Scholar]
- 38.Amsden B, Solute diffusion within hydrogels. Mechanisms and models. Macromolecules 1998, 31 (23), 8382–8395. DOI: DOI 10.1021/ma980765f. [DOI] [Google Scholar]
- 39.Phillips RJ, A hydrodynamic model for hindered diffusion of proteins and micelles in hydrogels. Biophysical Journal 2000, 79 (6), 3350–3353. DOI: Doi 10.1016/S0006-3495(00)76566-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Astbury WT, Structure of Alginic Acid. Nature 1945, 155 (3944), 667–668. DOI: DOI 10.1038/155667a0. [DOI] [Google Scholar]
- 41.Smidsrod O, Solution Properties of Alginate. Carbohyd Res 1970, 13 (3), 359-&. DOI: Doi 10.1016/S0008-6215(00)80593-5. [DOI] [Google Scholar]
- 42.Grant GT; Morris ER; Rees DA; Smith PJC; Thom D, Biological interactions between polysaccharides and divalent cations: The egg-box model. FEBS Letters 1973, 32 (1), 195–198. DOI: 10.1016/0014-5793(73)80770-7. [DOI] [Google Scholar]
- 43.Morris ER; Rees DA; Thom D; Boyd J, Chiroptical and stoichiometric evidence of a specific, primary dimerisation process in alginate gelation. Carbohyd Res 1978, 66 (1), 145–154. DOI: 10.1016/S0008-6215(00)83247-4. [DOI] [Google Scholar]
- 44.Plazinski W, Molecular basis of calcium binding by polyguluronate chains. Revising the egg-box model. J Comput Chem 2011, 32 (14), 2988–95. DOI: 10.1002/jcc.21880. [DOI] [PubMed] [Google Scholar]
- 45.Plazinski W; Drach M, Calcium-alpha-L-guluronate complexes: Ca2+ binding modes from DFT-MD simulations. J Phys Chem B 2013, 117 (40), 12105–12. DOI: 10.1021/jp405638k. [DOI] [PubMed] [Google Scholar]
- 46.Yeromonahos C; Polack B; Caton F, Nanostructure of the Fibrin Clot. Biophysical Journal 2010, 99 (7), 2018–2027. DOI: 10.1016/j.bpj.2010.04.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hagel V; Haraszti T; Boehm H, Diffusion and interaction in PEG-DA hydrogels. Biointerphases 2013, 8 DOI: Artn 36 10.1186/1559-4106-8-36. [DOI] [PubMed] [Google Scholar]
- 48.Hahn MS; Taite LJ; Moon JJ; Rowland MC; Ruffino KA; West JL, Photolithographic patterning of polyethylene glycol hydrogels. Biomaterials 2006, 27 (12), 2519–2524. DOI: 10.1016/j.biomaterials.2005.11.045. [DOI] [PubMed] [Google Scholar]
- 49.Chan AW; Neufeld RJ, Modeling the controllable pH-responsive swelling and pore size of networked alginate based biomaterials. Biomaterials 2009, 30 (30), 6119–6129. DOI: 10.1016/j.biomaterials.2009.07.034. [DOI] [PubMed] [Google Scholar]
- 50.Moya ML; Morley M; Khanna O; Opara EC; Brey EM, Stability of alginate microbead properties in vitro. J Mater Sci-Mater M 2012, 23 (4), 903–912. DOI: 10.1007/s10856-012-4575-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Papi M; Arcovito G; De Spirito M; Amiconi G; Bellelli A; Boumis G, Simultaneous static and dynamic light scattering approach to the characterization of the different fibrin gel structures occurring by changing chloride concentration. Appl Phys Lett 2005, 86 (18). DOI: Artn 183901 10.1063/1.1915526. [DOI] [Google Scholar]
- 52.Ghajar CM; Chen X; Harris JW; Suresh V; Hughes CCW; Jeon NL; Putnam AJ; George SC, The effect of matrix density on the regulation of 3-D capillary morphogenesis. Biophysical Journal 2008, 94 (5), 1930–1941. DOI: 10.1529/biophysj.107.120774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Drury JL; Dennis RG; Mooney DJ, The tensile properties of alginate hydrogels. Biomaterials 2004, 25 (16), 3187–3199. DOI: 10.1016/j.biomaterials.2003.10.002. [DOI] [PubMed] [Google Scholar]
- 54.Murphy KC; Whitehead J; Falahee PC; Zhou D; Simon SI; Leach JK, Multifactorial Experimental Design to Optimize the Anti-Inflammatory and Proangiogenic Potential of Mesenchymal Stem Cell Spheroids. Stem Cells 2017, 35 (6), 1493–1504. DOI: 10.1002/stem.2606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kong HJ; Kaigler D; Kim K; Mooney DJ, Controlling rigidity and degradation of alginate hydrogels via molecular weight distribution. Biomacromolecules 2004, 5 (5), 1720–1727. DOI: 10.1021/bm049879r. [DOI] [PubMed] [Google Scholar]
- 56.Aarstad O; Strand BL; Klepp-Andersen LM; Skjak-Braek G, Analysis of G-Block Distributions and Their Impact on Gel Properties of in Vitro Epimerized Mannuronan. Biomacromolecules 2013, 14 (10), 3409–3416. DOI: 10.1021/bm400658k. [DOI] [PubMed] [Google Scholar]
- 57.Harding S; Tombs MP; Adams GG; Paulsen BS; Inngjerdingen KT; Barsett H, An introduction to polysaccharide biotechnology, second edition. 2017; p 1–225. DOI: 10.1201/9781315372730. [DOI] [Google Scholar]
- 58.Hecht H; Srebnik S, Structural Characterization of Sodium Alginate and Calcium Alginate. Biomacromolecules 2016, 17 (6), 2160–2167. DOI: 10.1021/acs.biomac.6b00378. [DOI] [PubMed] [Google Scholar]
- 59.Carr DA; Peppas NA, Molecular Structure of Physiologically-Responsive Hydrogels Controls Diffusive Behavior. Macromol Biosci 2009, 9 (5), 497–505. DOI: 10.1002/mabi.200800235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sikorski P; Mo F; Skjak-Braek G; Stokke BT, Evidence for egg-box-compatible interactions in calcium-alginate gels from fiber X-ray diffraction. Biomacromolecules 2007, 8 (7), 2098–103. DOI: 10.1021/bm0701503. [DOI] [PubMed] [Google Scholar]
- 61.Jang J; Seol YJ; Kim HJ; Kundu J; Kim SW; Cho DW, Effects of alginate hydrogel cross-linking density on mechanical and biological behaviors for tissue engineering. J Mech Behav Biomed 2014, 37, 69–77. DOI: 10.1016/j.jmbbm.2014.05.004. [DOI] [PubMed] [Google Scholar]
- 62.Paradee N; Sirivat A; Niamlang S; Prissanaroon-Ouajai W, Effects of crosslinking ratio, model drugs, and electric field strength on electrically controlled release for alginate-based hydrogel. J Mater Sci-Mater M 2012, 23 (4), 999–1010. DOI: 10.1007/s10856-012-4571-0. [DOI] [PubMed] [Google Scholar]
- 63.Ruppender NS; Merkel AR; Martin TJ; Mundy GR; Sterling JA; Guelcher SA, Matrix rigidity induces osteolytic gene expression of metastatic breast cancer cells. PLoS One 2010, 5 (11), e15451 DOI: 10.1371/journal.pone.0015451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sperling LH, Introduction to Physical Polymer Science, 4th Edition Introduction to Physical Polymer Science, 4th Edition 2006, 1–845. [Google Scholar]
- 65.Kaklamani G; Cheneler D; Grover LM; Adams MJ; Bowen J, Mechanical properties of alginate hydrogels manufactured using external gelation. J Mech Behav Biomed 2014, 36, 135–142. DOI: 10.1016/j.jmbbm.2014.04.013. [DOI] [PubMed] [Google Scholar]
- 66.Maia FR; Fonseca KB; Rodrigues G; Granja PL; Barrias CC, Matrix-driven formation of mesenchymal stem cell-extracellular matrix microtissues on soft alginate hydrogels. Acta Biomater 2014, 10 (7), 3197–208. DOI: 10.1016/j.actbio.2014.02.049. [DOI] [PubMed] [Google Scholar]
- 67.Boontheekul T; Kong HJ; Mooney DJ, Controlling alginate gel degradation utilizing partial oxidation and bimodal molecular weight distribution. Biomaterials 2005, 26 (15), 2455–65. DOI: 10.1016/j.biomaterials.2004.06.044. [DOI] [PubMed] [Google Scholar]
- 68.Sutton S; Campbell NL; Cooper AI; Kirkland M; Frith WJ; Adams DJ, Controlled release from modified amino acid hydrogels governed by molecular size or network dynamics. Langmuir 2009, 25 (17), 10285–91. DOI: 10.1021/la9011058. [DOI] [PubMed] [Google Scholar]
- 69.Park H; Guo X; Temenoff JS; Tabata Y; Caplan AI; Kasper FK; Mikos AG, Effect of Swelling Ratio of Injectable Hydrogel Composites on Chondrogenic Differentiation of Encapsulated Rabbit Marrow Mesenchymal Stem Cells In Vitro. Biomacromolecules 2009, 10 (3), 541–546. DOI: 10.1021/bm801197m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Vining KH; Mooney DJ, Mechanical forces direct stem cell behaviour in development and regeneration. Nat Rev Mol Cell Bio 2017, 18 (12), 728–742. DOI: 10.1038/nrm.2017.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Abrami M; D’Agostino I; Milcovich G; Fiorentino S; Farra R; Asaro F; Lapasin R; Grassi G; Grassi M, Physical characterization of alginate-Pluronic F127 gel for endoluminal NABDs delivery. Soft Matter 2014, 10 (5), 729–37. DOI: 10.1039/c3sm51873f. [DOI] [PubMed] [Google Scholar]
- 72.Kong HJ; Alsberg E; Kaigler D; Lee KY; Mooney DJ, Controlling degradation of hydrogels via the size of cross-linked junctions. Advanced Materials 2004, 16 (21), 1917-+. DOI: 10.1002/adma.200400014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Kong HJ; Kim ES; Huang YC; Mooney DJ, Design of biodegradable hydrogel for the local and sustained delivery of angiogenic plasmid DNA. Pharmaceut Res 2008, 25 (5), 1230–1238. DOI: 10.1007/s11095-007-9526-7. [DOI] [PubMed] [Google Scholar]
- 74.Chernysh IN; Nagaswami C; Weisel JW, Visualization and identification of the structures formed during early stages of fibrin polymerization. Blood 2011, 117 (17), 4609–4614. DOI: 10.1182/blood-2010-07-297671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lang NR; Munster S; Metzner C; Krauss P; Schurmann S; Lange J; Aifantis KE; Friedrich O; Fabry B, Estimating the 3D Pore Size Distribution of Biopolymer Networks from Directionally Biased Data. Biophysical Journal 2013, 105 (9), 1967–1975. DOI: 10.1016/j.bpj.2013.09.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Lin CC; Anseth KS, PEG Hydrogels for the Controlled Release of Biomolecules in Regenerative Medicine. Pharmaceut Res 2009, 26 (3), 631–643. DOI: 10.1007/s11095-008-9801-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lin CC; Raza A; Shih H, PEG hydrogels formed by thiol-ene photo-click chemistry and their effect on the formation and recovery of insulin-secreting cell spheroids. Biomaterials 2011, 32 (36), 9685–9695. DOI: 10.1016/j.biomaterials.2011.08.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lin-Gibson S; Jones RL; Washburn NR; Horkay F, Structure-property relationships of photopolymerizable poly(ethylene glycol) dimethacrylate hydrogels. Macromolecules 2005, 38 (7), 2897–2902. DOI: 10.1021/ma0487002. [DOI] [Google Scholar]
- 79.Flory P, Principles of polymer chemistry. Oxford University Press: Ithaca, NY: 1953. [Google Scholar]
- 80.Metters A; Hubbell J, Network formation and degradation behavior of hydrogels formed by Michael-type addition reactions. Biomacromolecules 2005, 6 (1), 290–301. DOI: 10.1021/bm049607o. [DOI] [PubMed] [Google Scholar]
- 81.Beamish JA; Zhu JM; Kottke-Marchant K; Marchant RE, The effects of monoacrylated poly(ethylene glycol) on the properties of poly(ethylene glycol) diacrylate hydrogels used for tissue engineering. J Biomed Mater Res A 2010, 92a (2), 441–450. DOI: 10.1002/jbm.a.32353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Metters AT; Bowman CN; Anseth KS, A statistical kinetic model for the bulk degradation of PLA-b-PEG-b-PLA hydrogel networks. Journal of Physical Chemistry B 2000, 104 (30), 7043–7049. DOI: DOI 10.1021/jp000523t. [DOI] [Google Scholar]
- 83.Kotlarchyk MA; Shreim SG; Alvarez-Elizondo MB; Estrada LC; Singh R; Valdevit L; Kniazeva E; Gratton E; Putnam AJ; Botvinick EL, Concentration Independent Modulation of Local Micromechanics in a Fibrin Gel. Plos One 2011, 6 (5). DOI: ARTN e20201 10.1371/journal.pone.0020201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Piechocka IK; Bacabac RG; Potters M; MacKintosh FC; Koenderink GH, Structural Hierarchy Governs Fibrin Gel Mechanics. Biophysical Journal 2010, 98 (10), 2281–2289. DOI: 10.1016/j.bpj.2010.01.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Cruise GM; Scharp DS; Hubbell JA, Characterization of permeability and network structure of interfacially photopolymerized poly(ethylene glycol) diacrylate hydrogels. Biomaterials 1998, 19 (14), 1287–1294. DOI: Doi 10.1016/S0142-9612(98)00025-8. [DOI] [PubMed] [Google Scholar]
- 86.Stringer JL; Peppas NA, Diffusion of small molecular weight drugs in radiation-crosslinked poly(ethylene oxide) hydrogels. J Control Release 1996, 42 (2), 195–202. DOI: Doi 10.1016/0168-3659(96)01457-5. [DOI] [Google Scholar]
- 87.Laurens N; Koolwijk P; De Maat MPM, Fibrin structure and wound healing. Journal of Thrombosis and Haemostasis 2006, 4 (5), 932–939. DOI: DOI 10.1111/j.1538-7836.2006.01861.x. [DOI] [PubMed] [Google Scholar]
- 88.Yang YL; Leone LM; Kaufman LJ, Elastic Moduli of Collagen Gels Can Be Predicted from Two-Dimensional Confocal Microscopy. Biophysical Journal 2009, 97 (7), 2051–2060. DOI: 10.1016/j.bpj.2009.07.035. [DOI] [PMC free article] [PubMed] [Google Scholar]


