Abstract
To address the climate change caused by anthropogenic emissions of greenhouse gases into the atmosphere, it is essential to understand and quantitatively elucidate their cycling on the Earth’s surface. This paper first presents an overview of the global cycling of three greenhouse gases, carbon dioxide (CO2), methane (CH4), and nitrous oxide (N2O), followed by a description of their variations in the atmosphere. This paper then presents the recent global budgets of these greenhouse gases estimated using two different approaches, top-down and bottom-up. Discussions on our current knowledge regarding the global cycling of the three gases are also presented.
Keywords: greenhouse gas, carbon dioxide, methane, nitrous oxide, global cycling, climate change
1. Introduction
The Earth’s atmosphere has greatly changed since its birth 4.6 billion years ago. The present atmosphere consists mainly of nitrogen (N2; approximately 78.084% by volume of dry air), oxygen (O2; 20.947%), and argon (Ar; 0.934%). It also contains other constituents such as water vapor (H2O; variable), carbon dioxide (CO2; 0.04%), methane (CH4; 0.0002%), and nitrous oxide (N2O; 0.00003%). Because these constituents are almost transparent to solar radiation while strongly absorbing terrestrial radiation, they play an important role in producing the greenhouse effect, by which the global average surface temperature is raised by 33 ℃ to the observed value of about 15 ℃. Thus, owing to their role in producing the greenhouse effect, the aforementioned atmospheric constituents are called “greenhouse gases”.
It is known from the analyses of the air occluded in polar ice cores that the atmospheric burden of greenhouse gases fluctuated on timescales of glacial–interglacial cycles due to the changes in the Earth’s orbital parameters.1–3) It is also evident from polar ice core analyses and atmospheric observations4–9) that CO2, CH4, N2O, and other minor greenhouse gases, such as halocarbons and sulfur hexafluoride, have increased rapidly due to human activities. Such an increase would enhance the greenhouse effect and consequently change the state of climate globally. Global climate change (or “global warming”) is one of the most serious global environmental problems encountered today. The Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC)10) summarized our current scientific knowledge and showed that the global average surface temperature rose by about 0.85 ℃ from 1880 to 2012 and that its main cause is attributable to the increase in atmospheric greenhouse gases emitted by human activities.
Global warming is not just about the rise in surface temperature but also about the changes in the entire global climate system and poses a threat to the whole biosphere. To cope with this human-induced global climate change, it is important to predict future climate change based on our present knowledge of the global cycling of greenhouse gases. We can thereby estimate the future permissible emissions of greenhouse gases for the given climate stabilization targets to mitigate excessive radiative forcing by greenhouse gases. To achieve this objective, we need to understand in detail the spatiotemporal variations in atmospheric greenhouse gases and their related variables and quantitatively estimate the budgets of anthropogenic greenhouse gases based on this knowledge. Considerable efforts have been devoted to a better understanding of the global cycling of the gases not only by performing comprehensive observations using various platforms and tools but also by employing top-down and bottom-up approaches based on various types of models and data.
By analyzing the atmospheric CO2 data obtained using chemical measurement methods, G. S. Callendar claimed for the first time that atmospheric CO2 increased in the first half of the 20th century due to fossil fuel combustion, causing the surface temperature to rise.11) After his study, C. D. Keeling (Scripps Institution of Oceanography) began to systematically measure atmospheric CO2 at the South Pole in 1957 and Mauna Loa, Hawaii, in 1958 using a modern high-precision instrument called non-dispersive infrared analyzer.4,5) Similar systematic observations were also started by the scientists at Stockholm University, Sweden, the National Oceanic and Atmospheric Administration (NOAA), U.S.A., the Commonwealth Scientific and Industrial Research Organisation (CSIRO), Australia, Environment Canada (the current Environment and Climate Change Canada), Canada, and Tohoku University, Japan in the 1960s–1970s. Systematic observations were also initiated for CH4,12,13) N2O,14) and halocarbons8,15) around 1980. Currently, similar observations are being conducted at 100–150 places around the world, using in situ continuous measurement methods and sampling of air in flasks with subsequent laboratory analysis. In addition to these ground-based stations, aircraft, ships, balloons, and satellites are also used as part of the overall global network of observations.16–22)
Analysis of polar ice cores also began in the 1980s to reconstruct the past variations in atmospheric greenhouse gases.23) Quantitative studies on the global budgets of greenhouse gases were initially conducted for CO224–26) and then for CH4 and N2O.27–29) These studies have made considerable progress since the 2000s through the development of various types of models and the enrichment of related data.
This paper outlines our understanding of the global cycling of three greenhouse gases, namely, CO2, CH4 and N2O, and then describes their observed spatiotemporal variations in the atmosphere, along with some recent estimates of their global budgets. Further, this paper discusses the activities that must be performed to better understand the global cycling of these gases. A similar review has been extensively conducted five times by the IPCC since 1991, but this paper concisely summarizes our current knowledge on global cycling, including the results obtained after the Fifth Assessment Report was published in 2013.
2. Global cycling of carbon dioxide, methane, and nitrous oxide
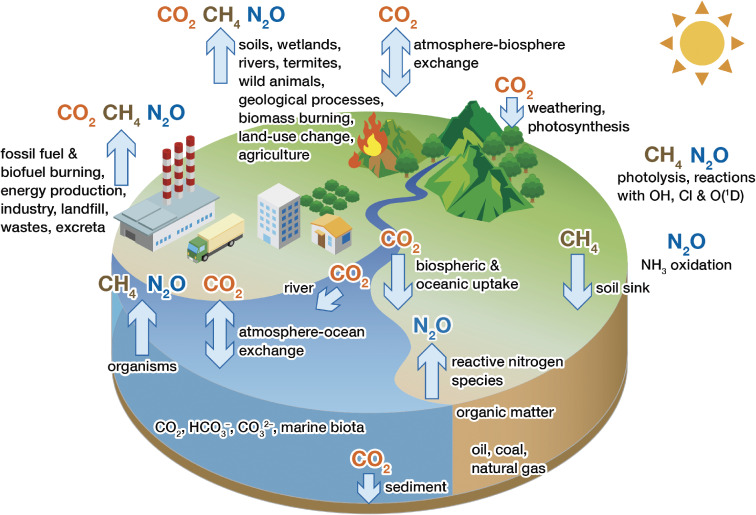
Figure 1 shows the conceptual illustration of the global cycling of CO2, CH4, and N2O. There are four major carbon reservoirs on the Earth’s surface, i.e., the atmosphere, terrestrial biosphere, ocean, and geological reservoir. Carbon is exchanged as CO2 between the atmosphere and terrestrial biosphere or ocean on timescales ranging from hourly to millennial, and carbon exchanges with geological reservoirs, such as limestone (CaCO3), occur on longer timescales. These exchanges among the four carbon reservoirs constitute an essential aspect of the carbon cycle. Carbon is stored as gaseous CO2 in the atmosphere, as organic matter in the terrestrial biosphere, and as dissolved inorganic carbon (DIC) (CO2, HCO3−, and CO32−, which are related by the chemical equilibria CO2 + H2O H+ + HCO3− 2H+ + CO32−) or dissolved organic carbon (DOC) in water. The carbon exchange with the terrestrial biosphere is mainly governed by photosynthesis and respiration, including the oxidation of organic matter in soil, (6CO2 + 6H2O C6H12O6 + 6O2), and the exchange with the ocean can be attributed to the difference between the partial pressures of CO2 in the surface ocean (pCO2,sea) and the atmosphere (pCO2,air) (ΔpCO2 = pCO2,sea − pCO2,air). There is also a small but persistent natural carbon flow, wherein organic carbon originating from the terrestrial biosphere and HCO3− produced by rock weathering on land are transported to the ocean by rivers and are then emitted into the atmosphere as CO2 or accumulate as sediments on the sea floor.30) These exchange processes are affected by climate change induced, for example, by the changes in the Earth’s orbital parameters (eccentricity, obliquity, and precession), the El Niño–Southern Oscillation (ENSO) events and volcanic eruptions. Thus, the atmospheric CO2 level fluctuated even in times when the influence of anthropogenic emissions was negligibly small.
Figure 1.
Conceptual illustration of the global cycling of CO2, CH4, and N2O.
The global carbon cycle has altered because of a large amount of CO2 emitted into the atmosphere by human activities, especially after the Industrial Revolution in the late 18th century.31) Its main sources are the combustion of fossil fuels such as coal, oil, and natural gas (CxHy + (x + y/4)O2 → xCO2 + (y/2)H2O), and man-made changes in land use such as deforestation and cultivation. A small amount of CO2 is also released into the atmosphere through cement production (CaCO3 → CaO + CO2). The global carbon cycle is also affected by the changes in the CO2 exchange between the atmosphere and terrestrial biosphere or ocean. Atmosphere–land CO2 fluxes have been changed by the CO2 fertilization effect caused by the increase in atmospheric CO2, forest regrowth and reforestation. Atmosphere–ocean CO2 fluxes due to the CO2 partial pressure difference have been enhanced by the increased atmospheric CO2, and ocean warming and ocean acidification have worked to decrease the fluxes. Both the atmosphere–ocean and atmosphere–land exchange processes would also have been affected by possible climate change over the past 100 years to some extent, and the magnitude of the exchange is likely to increase in the future. Some of anthropogenic CO2 emitted into the atmosphere is absorbed by the ocean and terrestrial biosphere, and the rest remains in the atmosphere. Therefore, we must achieve sufficient quantitative understanding of the processes that govern the partitioning of CO2 among these major carbon reservoirs under climate change (i.e., climate change–carbon cycle feedback effect) to predict the future atmospheric CO2 levels with a high degree of confidence.
CH4 emissions are classified into three categories, namely, biogenic, thermogenic, and biomass burning, based on their production processes.32,33) CH4 is emitted naturally into the atmosphere from wetlands, rivers, wild animals, termites, wildfires, geological processes, and oceans. CH4 is also released from anthropogenic sources such as consumption and production of fossil fuels, biomass and biofuel burning, ruminants, landfills, wastes, rice cultivation, and manure. On the other hand, CH4 is destroyed primarily via chemical reaction with OH in the troposphere and partly via reactions with OH, O(1D), and Cl in the stratosphere (CH4 + OH → CH3 + H2O, CH4 + O(1D) → OH + CH3, and CH4 + Cl → HCl + CH3). Thus, because OH is produced by O3 + hν (UV) → O2 + O(1D) and O(1D) + H2O → 2OH, the destruction of CH4 becomes the maximum in summer. There are two additional small CH4 sinks, i.e., methanotrophic bacteria in soils and reaction with Cl in the marine atmospheric boundary layer. The atmospheric CH4 level is determined by the balance of the source and sink strengths, and its variations are considerably affected by the changes in both these variables because the lifetime of CH4 in the atmosphere is relatively short, i.e., about 9 years.32,34)
N2O is a long-lived gas with an atmospheric lifetime of about 120 years,34–36) because this gas is very stable in the troposphere and destroyed only in the stratosphere through photolysis by ultraviolet light and chemical reactions with O(1D) (N2O + hν → N2 + O(1D), N2O + O(1D) → 2NO, and N2O + O(1D) → N2 + O2), and the contributions to the destruction are approximately 90%, 6%, and 4%, respectively.37) N2O is produced naturally via the microbial metabolic processes of nitrification under aerobic conditions (NH4+ → NH3 → NH2OH → NO2− → NO3−, NH2OH → N2O) and denitrification under anaerobic conditions (NO3− → NO2− → NO → N2O → N2) in the soil and ocean, and via the oxidation of NH3 in the atmosphere (NH3 + OH → NH2 + H2O, NH2 + NO2 → N2O + H2O).38,39) Anthropogenic N2O is produced by fossil fuel combustion, industrial processes (mainly nylon and nitric acid production), agricultural activities such as the usage of nitrogenous and organic fertilizers, biomass and biofuel burning, human excreta, and the deposition of reactive nitrogen species on the land and ocean.39) Due to the long life of N2O in the atmosphere, its atmospheric level on timescales ranging from a few decades to hundreds of years is more effectively affected by changes in emission rather than in destruction.
3. Variations in carbon dioxide, methane, and nitrous oxide in the atmosphere
As expected from the abovementioned source/sink processes, atmospheric CO2, CH4, and N2O are quite variable in time. They also exhibit spatial variability characterized by the presence of unevenly distributed sources and sinks on the Earth’s surface. In this section, the spatiotemporal variations in the three gases are concisely described.
3.1. Glacial–interglacial variations.
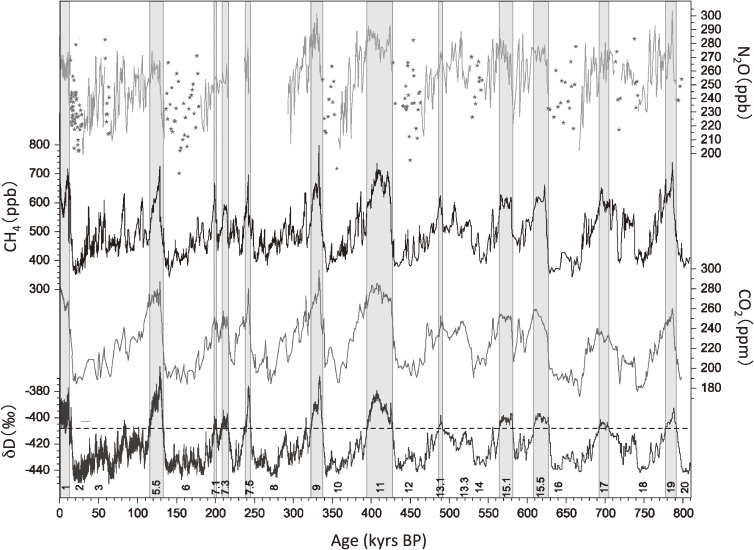
As mentioned above, atmospheric CO2, CH4, and N2O vary in response to the naturally occurring changes in the climate system. The most striking variation observed on the one-million-year timescale is the glacial–interglacial cycle that is spectrally consistent with the changes in the Earth’s orbital parameters, as shown in Fig. 2.3) The results shown in the figure were obtained by analyzing the air occluded in deep ice cores collected from Dome C and Vostok in Antarctica. The atmospheric abundance (in units of dry air mole fraction) fluctuates between 180 ppm during the glacial maximum and 280 ppm during the interglacial period for CO2 and between 350 and 700 ppb in the corresponding periods for CH4. The N2O data are considerably scattered during the glacial period, probably due to N2O produced in the Antarctic ice sheet by microbes transported from the continents. However, the mole fraction values appear to be lower in the glacial period than in the interglacial period.
Figure 2.
Variations of atmospheric CO2, CH4, and N2O and δDice obtained from the deep Antarctic ice cores (Schilt et al.3)). The stars plotted for N2O represent the data that could have been affected by N2O produced in the ice sheet. The numbers in the lowermost part of the figure indicate the marine isotope stage, and the vertically shaded bars denote the interglacial periods.
To interpret the low CO2 mole fractions during the glacial period, several hypotheses have been proposed. As can be understood from Fig. 1, we need to enhance the terrestrial biospheric and/or oceanic CO2 uptake to lower the atmospheric CO2 level. However, the enhancement of the terrestrial biospheric uptake would be a minor effect because the weather was cool and dry, solar radiation was reduced, and northern mid- and high-latitude continents with a large quantity of terrestrial biomass were covered by ice and snow in the glacial period. The isotope analyses of benthic foraminifera in the ocean floor sediments indicated that the carbon isotope ratio (δ13C), which will be defined in Section 3.2, was decreased by 0.03‰–0.04‰ in the glacial period, suggesting that there was an inflow of isotopically light biospheric carbon of 300–700 GtC from land.40) Therefore, the oceanic CO2 uptake is the remaining major mechanism by which atmospheric CO2 decreased during the glacial period. For this mechanism to work, the surface ocean CO2 partial pressure needs to be lower than the atmospheric CO2 partial pressure, and several potential processes have been proposed to achieve this. The surface ocean CO2 partial pressure can be reduced by (1) increasing the CO2 solubility of seawater because of decreasing temperature, (2) enhancing the marine biospheric activities by increased supply of nutrients, and/or (3) increasing the alkalinity of seawater because of changes in the ocean carbonate chemistry.41–44) It is also known that there is a good correlation between the atmospheric CO2 mole fraction and Antarctic air temperature. Based on this correlation, several studies have ascribed the cause to the Southern Ocean, i.e., the enhancement of marine biospheric activities by the increased supply of Fe from the continents under dry and windy weather conditions and the suppression of CO2 release due to the weakened upwelling of seawater by northward movement of the westerly wind zone or due to the expanded sea ice.45–47) Despite these previous studies, our knowledge of the paleocarbon cycle is still insufficient to conclude with certainty the process that played a more definitive role in reducing the glacial atmospheric CO2 mole fraction. However, it seems likely that all the processes identified above worked in combination to some extent to make an overall contribution.
To explain the low glacial atmospheric CH4 levels, both the decrease in emission and increase in sink should be considered. In the glacial period with cool and dry weather conditions and reduced solar radiation, the production of OH from H2O would have decreased, leading to a reduction in CH4 destruction. On the other hand, the emission of non-methane volatile organic compounds (NMVOCs), which react easily with OH, was considerably reduced due to the fact that northern mid- and high-latitude forests were covered by snow. In this regard, Levine et al.48) used a global atmospheric chemistry model to report that both the effects (decrease in OH production and NMVOC emissions) offset each other. Murray et al.49) also suggested that the tropospheric OH levels in the last glacial maximum and in the pre-industrial era were similar. Soil sinks are expected to be almost unchanged in these two periods, because boreal forests decreased while low-latitude deserts expanded in the last glacial maximum.50) Based on these results, the observed low glacial CH4 mole fractions can only be attributed to the reduction in CH4 emissions. The strongest natural CH4 source is wetlands. Based on the restoration of vegetation distributions and model analysis, it is suggested that global wetlands have halved in the last glacial maximum and that their CH4 emissions have decreased by 40% compared with the values in the pre-industrial Holocene.50,51)
It is not easy to exactly estimate the past lifetime of atmospheric N2O, but some model studies show that the lifetime varied within ±15% from the last glacial maximum to the present time, or that the lifetime is slightly longer during the glacial period than at the present time.34,52,53) If this is true, the low glacial N2O levels are primarily ascribed to the reduction in N2O emissions. From the analyses of Antarctic ice cores for N2O and its nitrogen and oxygen isotope ratios, it is reported that the N2O emission was reduced by 30%–40% around the time of the last glacial maximum compared to the pre-industrial Holocene values, with nearly equal contributions from soils and oceans.54,55)
3.2. Human-caused increase superimposed on natural variations.
3.2.1. Carbon dioxide.
Figure 3 shows the temporal variations of atmospheric CO2 at the South Pole and Mauna Loa.56) It also shows the long-term trends and growth rates derived using a digital filtering technique,57) El Niño periods, and volcanic eruptions. It is clearly seen that atmospheric CO2 increased over time, accompanied by a seasonal cycle and interannual variations with periods of a few or several years. The yearly mean CO2 mole fraction increased from 314–315 ppm in 1958 to 403–407 ppm in 2017, indicating a time-dependent growth rate from 1.0 ppm/yr during 1958–1960 to 2.6 ppm/yr during 2015–2017.
Figure 3.
Variations in the mole fraction (upper panel) and growth rate (lower panel) of atmospheric CO2 at Mauna Loa, Hawaii and the South Pole. The smooth lines in the upper panel show a long-term trend, and the shaded vertical bars in the lower panel represent El Niño occurrences.
The seasonal CO2 cycle can be mainly attributed to the seasonally dependent CO2 exchange between the atmosphere and terrestrial biosphere. Under the present condition, the δ13C of atmospheric CO2, which is expressed as
| [1] |
where the subscripts “sample” and “standard” represent the sample and international standard, respectively, is affected by −0.05‰/ppm due to the CO2 exchange between the atmosphere and terrestrial biosphere and by −0.003‰/ppm due to the exchange between the atmosphere and ocean. The observed seasonal cycles of atmospheric CO2 and its δ13C, especially in the northern hemisphere, yield about −0.05‰/ppm, suggesting the cause to be the atmosphere–terrestrial biosphere CO2 exchange.16,17) Therefore, the seasonal amplitude is larger at Mauna Loa than at the South Pole, reflecting the hemispheric difference in the terrestrial biomass, and the seasonal phases at the two stations are the opposite.
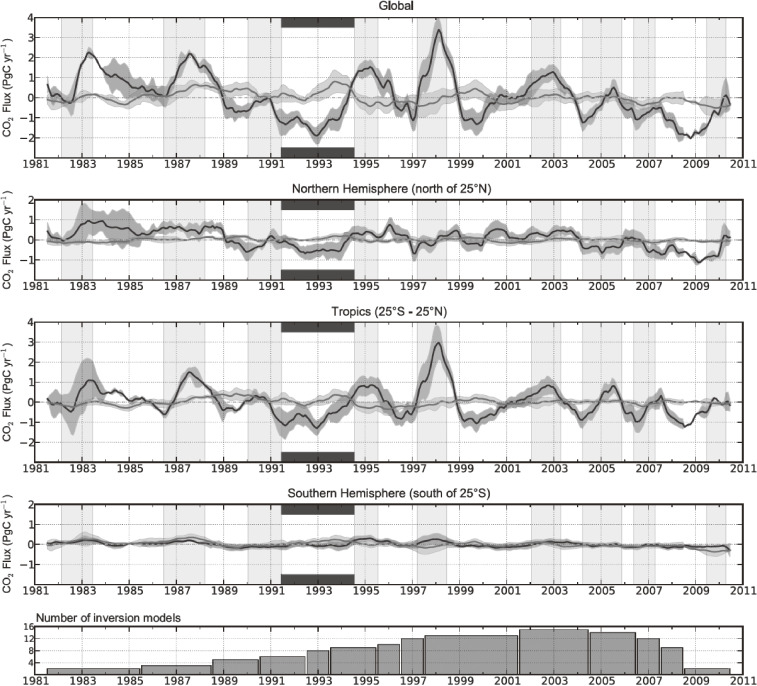
The interannual CO2 variations superimposed on the observed long-term upward trend correlate well with the El Niño events that generally result in high temperatures and dry conditions in many areas of the world, especially in the tropics. From the results of the Atmospheric Tracer Transport Model Intercomparison Project (TransCom) flux inversion calculations based on global atmospheric transport models constrained by the atmospheric CO2 observations,39) as shown in Fig. 4, the CO2 exchange between the atmosphere and terrestrial biosphere is considerably affected by the occurrence of an El Niño event. This implies that a large amount of terrestrial biospheric CO2 is emitted into the atmosphere through the enhanced respiration of plants, the accelerated decomposition of organic matter on/in soils, droughts, and forest fires. This idea is also supported by the δ13C observations.16,17)
Figure 4.
The atmosphere–ocean (gray lines) and atmosphere–terrestrial biosphere (black lines) fluxes of CO2 estimated by the TransCom flux inversion calculations for the global, northern (north of 25°N), tropical (25°N–25°S), and southern (south of 25°S) areas (Ciais et al.39)). The occurrences of El Niño are indicated by the lightly shaded vertical bars in each of the upper four panels, and the heavily shaded bars indicate the low-temperature period after the eruption of Mt. Pinatubo in 1991. The lowest panel shows the number of models used for atmospheric inversion.
The interannual variations in the atmosphere–terrestrial biosphere CO2 fluxes exhibited negative values during a few years after the eruption of Mt. Pinatubo, Philippines, in June 1991, although an El Niño event occurred at the same time. As a result of the volcanic eruption, large amounts of sulfate aerosols were produced in the stratosphere, reducing the amount of direct solar radiation reaching the surface and the surface temperature. This reduced the terrestrial biosphere respiration while enhancing photosynthesis by greater diffused radiation at the canopy level. On the other hand, it is evident from Fig. 4 that the CO2 fluxes between the atmosphere and ocean show smaller temporal variability than those between the atmosphere and terrestrial biosphere, although some inversion studies have shown an enhancement in oceanic sink during strong El Niño events, for example, in 1997–1998.58,59) As shown in Fig. 3, low growth rates are associated with the eruption of Mt. Agung, Indonesia, in March–May 1963, but an opposite situation could be observed after the eruption of Mt. El Chichón, Mexico, in March 1982 when the growth rate increased. The latter situation is likely due to the possibility that the El Niño effect overwhelmed the volcanic eruption effect.
Figure 3 indicates that the yearly mean CO2 mole fraction is always higher at Mauna Loa than at the South Pole and that the difference between the two stations has gradually expanded with time from 0.5 ppm at the beginning of the observation to 3.7 ppm during 2013–2017. The observed north–south difference implies that the CO2 sources (sinks) exist in the northern (southern) hemisphere and that their strength is enhanced over time. Considering the fact that atmospheric CO2 has increased rapidly since the late 1950s, the north–south difference can be attributed to the northern hemispheric sources, i.e., fossil fuel consumption. 95% of fossil fuels are currently consumed in the northern hemisphere.
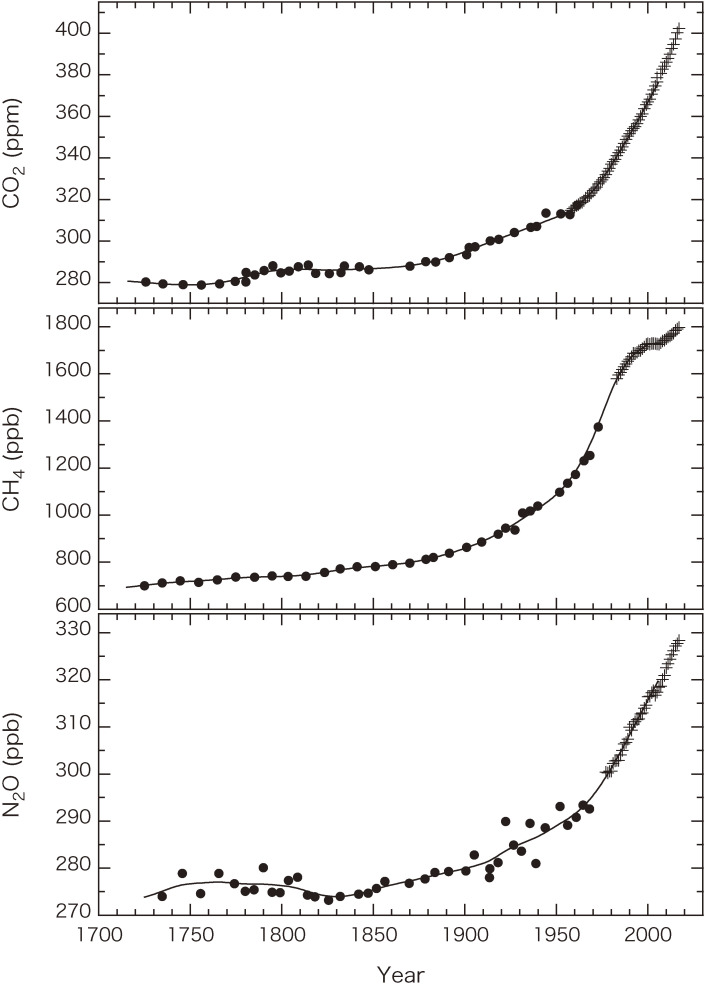
To understand the global carbon cycle, it is important to know the variations in atmospheric CO2 before the modern systematic observations were conducted. Therefore, considerable efforts have been devoted to reconstruct the past CO2 levels using various methods. Among these methods, the analysis of polar ice cores drilled at sites with high snow accumulation rates was the most promising. Figure 5 shows the variations of atmospheric CO2, CH4, and N2O over the past 300 years obtained from the analysis of an ice core collected at H15, Antarctica and the yearly mean values observed in the atmosphere at the South Pole or Cape Grim, Australia.6,8,56,60,61) The CO2 mole fraction remained almost constant at approximately 280 ppm in the mid-18th century, and it increased gradually until the mid-20th century and then quite rapidly thereafter toward the present level. The overall increase between the mid-18th century and present time amounted to more than 120 ppm, which is larger than the interglacial–glacial difference of about 100 ppm. Similar variations were also observed in other Antarctic ice cores.9) The air samples extracted from the ice cores were measured for obtaining the δ13C of CO2.9,62) Results show that δ13C decreased gradually from −6.4‰ at around 1750 to −7.0‰ at around 1950 and then rapidly to −7.8‰ at around 1980. The trend of δ13C is similar to that of CO2 but with an opposite sign. The observed good correlation between CO2 and δ13C suggests that the long-term CO2 increase over the last 250 years was mainly caused by emissions of isotopically light CO2 into the atmosphere via fossil fuel combustion (−27‰) and/or land-use change/deforestation (−25‰). The CO2 released from or taken up by the ocean (0‰–2‰) has very little influence on atmospheric δ13C because the kinetic isotope fractionation factors for the ocean-to-atmosphere and atmosphere-to-ocean CO2 exchange flows are different. Therefore, the δ13C values of CO2 added to and removed from the atmosphere are close to the atmospheric δ13C.16,17) The atmospheric δ13C value continued to decrease until its global average reached −8.5‰ in the mid-2010s.63)
Figure 5.
Variations of atmospheric CO2, CH4, and N2O reconstructed from the shallow Antarctic ice core, H15 (circles). The yearly means obtained from the systematic observations at the South Pole are also plotted for CO2 and CH4, and the values at Cape Grim, Australia, are plotted for N2O (crosses).
3.2.2. Methane.
As shown in Fig. 5, atmospheric CH4 was about 700 ppb in the early 1700s. Similar values have also been obtained using other Antarctic ice cores.9) On the other hand, the ice cores from Greenland indicate higher pre-industrial CH4 values by 30–50 ppb when compared with those from Antarctica due to natural CH4 emissions from boreal wetlands.9,64,65) It can be observed from Fig. 5 that the Antarctic CH4 mole fraction increases constantly from the pre-industrial levels to the present value of about 1790 ppb, with the increase being more than three times the interglacial–glacial difference of 350 ppb.
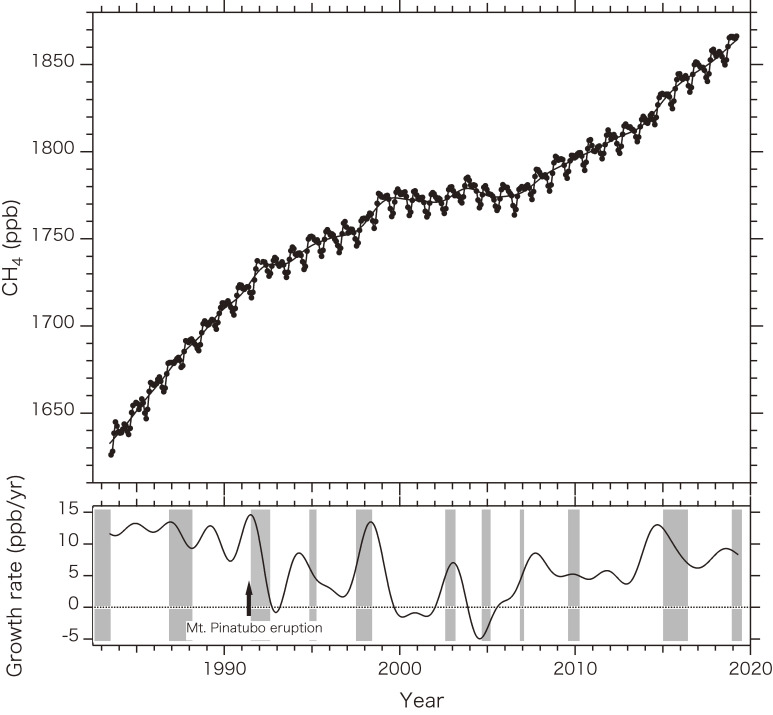
To examine the temporal variations in atmospheric CH4 in detail, the globally-averaged monthly mean values obtained by the NOAA/Earth System Research Laboratory (ESRL)/Global Monitoring Division (GMD)6) are plotted in Fig. 6 along with the best-fit curve, long-term trend, and growth rate. Similar to CO2, atmospheric CH4 shows a seasonal cycle, interannual variations, and a long-term increase. The seasonal CH4 cycle is a combined effect of the seasonally varying sources and sinks. Because the major sink of CH4 is the reaction with OH, its destruction is maximized during summer. The seasonality of CH4 emission is dependent on individual sources. For example, the CH4 emissions from wetlands and fossil fuel burning are enhanced in warm and cold seasons, respectively. However, because the seasonal CH4 minimum is observed in summer under baseline conditions, the sink effect takes precedence over the source effect. The observed interannual variations of atmospheric CH4 are caused by the ENSO events and volcanic eruptions. For example, a large amount of CH4 is released into the atmosphere through increased biomass burning under dry conditions during the El Niño event and increased tropical land precipitation during the La Niña event. High growth rates can be found even with respect to the globally averaged CH4 mole fractions shown in Fig. 6, especially during El Niño. The CH4 emissions from wetlands associated with the ENSO events and from the El Niño-related Indonesian fires were examined by various researchers, including Hodson et al.66) and Worden et al.67) Figure 6 indicates that the growth rate of CH4 is increased just after the eruption of Mt. Pinatubo in 1991 and decreased considerably thereafter. This can be attributed to attenuated ultraviolet actinic flux in the 290–310 nm wavelength range due to the absorption by SO2 injected into the stratosphere and perturbed ultraviolet flux by sulfate aerosols produced from SO2, and to decreased CH4 emissions from boreal wetlands due to low temperatures after the eruption.68)
Figure 6.
Globally averaged monthly means of the atmospheric CH4 mole fraction (circles in the upper panel) and the growth rate (solid line in the lower panel). El Niño periods are indicated by shaded vertical bars. The best-fit curve to the observed data and the long-term trend are shown by solid lines in the upper panel.
Figures 5 and 6 indicate that the atmospheric CH4 trend has behaved in an unexpected manner in the last few decades. It rose rapidly until 1991 and gradually from 1991 to 1999, leveled off in 1999–2006, and then increased again. By inspecting the CH4 data in the north and south polar regions, Dlugokencky et al.69) found that the average difference between the two regions was 140 ppb during 1984–1991, which is 3–5 times larger than the pre-industrial values probably due to human activities at northern mid- and high latitudes. It was also found that the difference decreased suddenly in 1992 and then gradually reduced with time until 2001. The decreasing interpolar difference and the decelerating CH4 growth in the 1990s would have resulted from a reduction in the fossil-fuel CH4 emissions associated with the collapse of the former Soviet Union and a reduction in leakage during natural gas and oil production and their transportation owing to subsequent facility improvements.6,69,70) Atmospheric CH4 began to increase in 2007 and the trend continued until 2018. Because the observed δ13C values of CH4 indicate a gradual decrease after 2007,71,72) the isotopically light biogenic CH4 sources would play an important role in the recent increase in the observed mole fraction.
To interpret the renewed increase of CH4 from 2007, scientists have analyzed the variations of CH4, δ13C, C2H6, or CH3CCl3 in the atmosphere. However, the cause is still under debate because there are large uncertainties not only in anthropogenic and natural sources but also in sinks.69,71,73–77) As mentioned above, the atmospheric CH4 burden is governed by the balance between emissions from various surface sources and destruction in the atmosphere, mainly by OH. However, it is impossible to derive a global OH concentration field from observations because its lifetime is very short, i.e., a few seconds, and its tropospheric concentration is very low (in the order of 106 molecules/cm3) and spatiotemporally variable.78) The calculation results obtained using the current atmospheric chemistry models are also diverse.79) The CH4 sources are unevenly distributed on the Earth’s surface, and their strengths are variable in time and space. Therefore, it is not easy to identify the process (or set of processes) that increased CH4 after 2007. By assuming OH to be invariant with time in case of global inverse modeling calculation constrained by the atmospheric CH4 observations, Patra et al.73) reported that the renewed CH4 increase from 2007 was caused by the biogenic emissions in tropical Asia and southern South America. Nisbet et al.71) suggested from their analyses of atmospheric CH4 and δ13C that the CH4 increase after 2007 can be attributed to the biogenic CH4 emissions particularly in the tropics, for example, through the expansion of tropical wetlands by positive rainfall anomalies or enhanced emissions from agricultural sources such as ruminants and rice paddies. They also reported that the changes in the removal rate by OH appear to be a small effect. Thompson et al.76) proposed from their simultaneous analyses of CH4, δ13C, and C2H6 that the biogenic and fossil-fuel CH4 emissions were responsible for the CH4 increase from 2007 and that the changes in the removal rate by OH do not appear to be a major factor. On the other hand, Rigby et al.74) and Turner et al.75) analyzed the observed trend of atmospheric CH3CCl3, the major sink of which is the reaction with tropospheric OH, using a box model inversion and reported that the global average OH concentration decreased from around 2003, resulting in the CH4 increase after 2007. Naus et al.77) identified biases in the two-box model approach based on the results of full three-dimensional transport model simulations and found that the tropospheric OH concentration increased gradually with time from 1994 to 2014 and that the CH4 emissions increased from 2007. Further advanced studies are required to obtain a more definitive conclusion on the recent unexpected but interesting CH4 trend.
3.2.3. Nitrous oxide.
Figure 5 shows that atmospheric N2O was approximately 275 ppb before the early 1800s and gradually increased from 1850 to 1960–1970 and then rapidly to about 328 ppb in 2017. The increase from the pre-industrial era to the present time is 53 ppb, indicating a 20% increase relative to the pre-industrial level. Similar variations were also reported from the analyses of other ice cores.9)
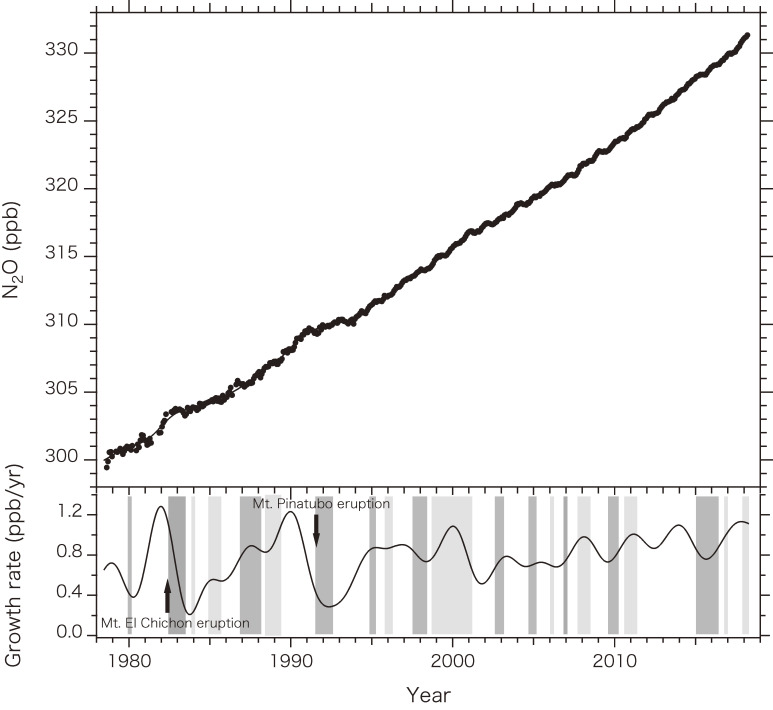
The global average monthly mole fractions of atmospheric N2O observed by the Advanced Global Atmospheric Gases Experiment (AGAGE) are shown in Fig. 78) along with the long-term trend and growth rate. Atmospheric N2O also shows a seasonal cycle, interannual variations and a long-term increase. Because N2O is very stable in the troposphere, the seasonal cycle and interannual variations would be closely related with the source activities and atmospheric transport. From the beginning of the atmospheric N2O observations, the seasonal N2O cycle has been difficult to detect, but a very small seasonality with a peak-to-peak amplitude of about 1 ppb was recently observed due to the improved measurement precision.8,20) The cause of the seasonal N2O cycle is not fully understood yet. However, because the timing of the appearance of the seasonal maximum and minimum seems to depend on the location of the observation, the seasonal N2O cycle is probably a result of the combination of some seasonally dependent processes such as, for example, troposphere–stratosphere air exchange, air transport in the troposphere, interhemispheric air mixing, N2O production by bacteria, and N2O exchange between the atmosphere and ocean. The N2O mole fraction is lower in the stratosphere and southern hemisphere when compared with those in the troposphere and southern hemisphere, respectively, and bacterial activities in soils and oceans are seasonally dependent.8,18,20,80)
Figure 7.
Global averages of the atmospheric N2O mole fraction (circles in the upper panel) and the growth rate (solid line in the lower panel). The solid line in the upper panel shows the long-term trend, and the dark and lightly shaded vertical bars in the lower panel represent the El Niño and La Niña periods, respectively.
As shown in Fig. 7, the growth rate of N2O is correlated with the occurrences of the El Niño and La Niña events, showing low values during the former and high values during the latter. It should be noted that the measurement precision is not the same throughout the period, but the good correlation can be interpreted as follows. Because the N2O emissions from the soil and ocean amount to 60% of the total emissions and the anthropogenic N2O emissions are considered to have very small year-to-year variations, such a correlation is likely to arise from the changes in N2O emissions from natural sources. It is known that the soil moisture, temperature, and precipitation are especially important for N2O production in soils. In general, the tropical and subtropical regions become hot and dry during El Niño and become cold and wet during La Niña. The oceanic N2O emissions are reduced by the suppressed upwelling in the eastern tropical Pacific during El Niño. Therefore, the N2O emissions from the soils and oceans at low latitudes would play an influential role with respect to the observed interannual variations of atmospheric N2O. This idea is also suggested by terrestrial biogeochemical modeling, atmospheric chemistry/transport modeling and shipboard observations in the Pacific Ocean.20,81,82) The low N2O growth rates observed after the eruptions of Mt. Pinatubo in 1991 and Mt. El Chichón in 1982 would be related to the decreased N2O emissions from soils due to low temperatures, in addition to the El Niño effect.
Atmospheric N2O increased from about 300 ppb in the late 1970s to the present value of 331 ppb, with an average growth rate of 0.78 ppb/yr. The average growth rates for 1979–1998 and 1999–2017 were 0.72 and 0.85 ppb/yr, respectively, implying that the N2O increase was enhanced more in the latter period than in the former period. Weiss14) reported, based on their measurements in 1976–1980, that the average N2O growth rate was about 0.5 ppb/yr, which is even lower than the value obtained during 1979–1998.
By analyzing the atmospheric N2O data collected systematically by the NOAA/ESRL/GMD, AGAGE and Tohoku University, it is found that the average mole fraction is the lowest at the South Pole, increases by about 1 ppb toward the equator, increases by an additional 1 ppb toward the northern mid-latitudes, and then declines by 0.5 ppb in the northern polar region. This latitudinal N2O distribution indicates the existence of N2O sources in regions extending from the tropics to northern mid-latitudes.
4. Global budgets of anthropogenic carbon dioxide, methane, and nitrous oxide
Our understanding of the global budgets of anthropogenic greenhouse gases is based on two approaches: “top-down” in which fluxes are inferred by analyzing the atmospheric observations using global atmospheric chemistry/transport models, and “bottom-up” in which inventories, extrapolation of local flux observations, and process models are used to estimate the fluxes. Both these approaches have advantages and disadvantages. Time-dependent global and/or regional fluxes can be derived using the top-down approach even from short records of atmospheric observations under the constraint that budgets are balanced. However, this approach is often afflicted by the coarse resolution of the data obtained from the observation network, the biases in measurement owing to the participation of various institutes and the usage of various observation methods, and our insufficient knowledge on atmospheric transport and sinks. On the other hand, in the bottom-up approach, we can estimate various fluxes associated with each of the source and sink processes. However, this approach is seriously affected by the uncertainties and potential biases in the usable statistical data, conversion factors for emissions and extrapolation to geographically large scales from a limited number of observations. Various budgets estimated by the bottom-up approach are not constrained for balance, for example, by atmospheric observations. Therefore, to accurately evaluate the global greenhouse gas budget, it is important to achieve a scientifically consistent merger of the results obtained using these multifaceted approaches.83)
In this section, the global budgets estimated for anthropogenic CO2, CH4, and N2O using the top-down and bottom-up approaches are presented and discussed.
4.1. Carbon dioxide.
The global budget for CO2 has been estimated using several methods. For example, Francey et al.84) and Goto et al.85) analyzed the atmospheric CO2 mole fraction and its δ13C. The δ13C values in the atmosphere, ocean and terrestrial biosphere are different, and the kinetic fractionation factors of CO2 flow from the atmosphere to the terrestrial biosphere or ocean and vice versa are also different. Based on these isotope properties, the global net terrestrial biospheric and oceanic carbon fluxes can be estimated by simultaneously solving a set of mass balance equations for atmospheric CO2 and 13CO2. The CO2 uptake inferred using the data obtained at Ny-Ålesund, Svalbard during 1996–2013 is presented in Fig. 8 along with the global fossil-fuel CO2 emissions.85) The average terrestrial biospheric and oceanic CO2 uptake values over 18 years were 1.3 and 2.6 GtC/yr, respectively, which are relatively consistent with the results obtained based on atmospheric O2 analyses that will be discussed below. It is also clearly shown in Fig. 8 that the terrestrial biosphere shows larger year-to-year variations in CO2 uptake when compared with the ocean uptake, which are correlated with the occurrences of the El Niño events. However, there was no considerable decrease in the terrestrial biospheric CO2 uptake during the 2009/2010 El Niño event, presumably due to the insufficient spatial representativeness of the CO2 and/or δ13C data used in the analysis. It is also obvious that the oceanic CO2 uptake increases with time, especially after 2000 when the fossil-fuel CO2 emissions were rapidly increasing. Because anthropogenic CO2 emitted into the atmosphere increases the CO2 partial pressure difference between the atmosphere and ocean, it is expected that the oceanic CO2 uptake has steadily increased. Previous studies reported that the oceanic CO2 uptake has been increasing for the past several decades,31) although the recent oceanic CO2 uptake shown in Fig. 8 appears to be slightly larger than their estimates.
Figure 8.
Terrestrial biospheric and oceanic uptake of anthropogenic CO2 estimated by the simultaneous analysis of atmospheric CO2 and δ13C (upper panel) and global fossil-fuel CO2 emissions (lower panel) for 1996–2013 (Goto et al.85)).
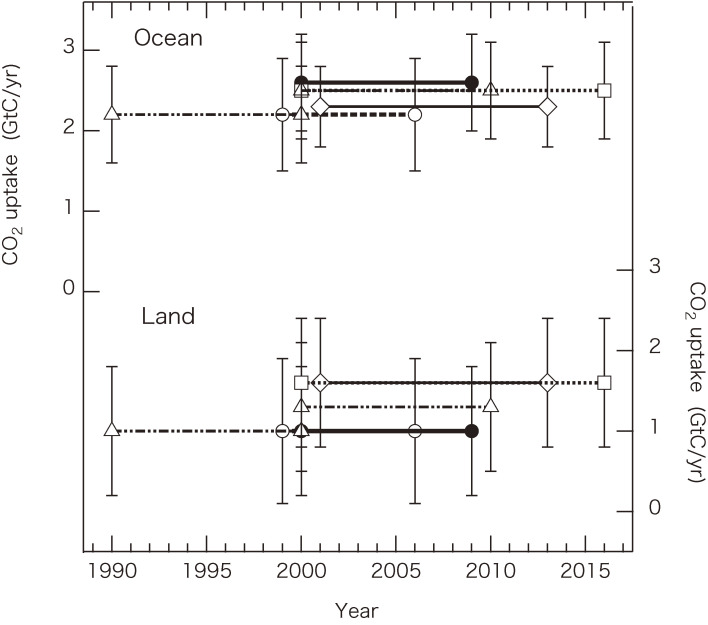
Keeling and Shertz86) proposed the mass balance analysis of atmospheric CO2 and O2 for estimating the global carbon budget. The atmospheric O2/N2 ratio is currently decreasing with time in contrast to the CO2 mole fraction, primarily due to fossil fuel consumption, and its trend is also related with the uptake or release of O2 by the terrestrial biosphere. The terrestrial biospheric and oceanic CO2 uptake values evaluated recently using this method are presented in Fig. 9.85,87–90) The CO2 uptake ranges between 1.0 and 1.6 GtC/yr for the terrestrial biosphere and between 2.2 and 2.6 GtC/yr for the ocean, with both showing a tendency to increase with time. This time-dependent increase is greater in case of the terrestrial biospheric uptake than in case of the oceanic uptake. Recently, Tohjima et al.88) analyzed their 19-year record of O2/N2 in the western Pacific and found that the 5-year average oceanic uptake monotonously increased with time in 2001–2014 and that the 5-year average terrestrial biospheric uptake showed a more complicated behavior, i.e., a rapid increase in 2001–2009 and a rapid decrease in the subsequent period. As indicated in Fig. 3, the growth rate of atmospheric CO2 exhibited almost no trend in the 2000s despite the continuously increasing fossil-fuel CO2 emissions (see Fig. 8) during the period. The observation of Tohjima et al.88) would lead to the possibility that anthropogenic CO2 emitted into the atmosphere during this period was more efficiently absorbed by the terrestrial biosphere, which is inconsistent with the result shown in Fig. 8. To resolve this contradiction, it is required to observe δ13C and O2/N2 over a wide geographical area and carefully assess the parameters used in the respective methods, e.g., the isotopic disequilibrium flux in the δ13C method and the oceanic O2 outgassing in the O2/N2 method.
Figure 9.
Terrestrial biospheric and oceanic uptake of anthropogenic CO2 estimated on the basis of atmospheric CO2 and O2. Open circles, solid circles, triangles, diamonds, and squares represent the respective results of Tohjima et al.,87) Ishidoya et al.,89) Keeling and Manning,90) Goto et al.,85) and Tohjima et al.88)
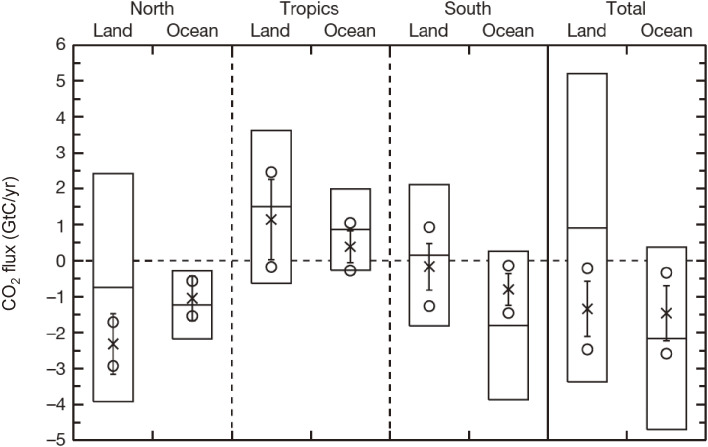
The estimations of the terrestrial biospheric and oceanic CO2 fluxes using the atmospheric Bayesian inversion technique have also been actively performed. In this approach, a priori fluxes (or a set of guessed flux values) are optimized using global atmospheric transport models and atmospheric CO2 observations, resulting in spatially distributed posterior flux values satisfying the uncertainties associated with a priori fluxes and observation data. The first extensive inversion project using three-dimensional atmospheric transport models was TransCom 3,91) in which 16 different models participated to infer the CO2 fluxes for 22 assigned regions of the world (11 for land and 11 for ocean) based on common CO2 observation data and a priori CO2 fluxes. Figure 10 shows the model average CO2 fluxes over 1992–1996 for ten abbreviated areas. As shown in this figure, the posterior CO2 fluxes are clearly different from the a priori fluxes, especially for the northern land and southern ocean regions, and the within-model uncertainties are smaller than the prescribed values, implying that the fluxes are well constrained by the atmospheric CO2 observations. However, the fluxes estimated for the tropical land and southern land areas exhibit large uncertainties due to a limited number of CO2 observations. The terrestrial biosphere serves as a source in the tropics and a sink in the northern area and is neutral in the southern area, and the ocean serves as a source in the tropics and a sink in the northern and southern areas.
Figure 10.
Average terrestrial biospheric and oceanic CO2 fluxes for global, northern, tropical, and southern areas over 1992–1996 derived from the TransCom 3 atmospheric inversions (Gurney et al.91)). The boxes represent the a priori fluxes (center) and their uncertainties (upper and lower bounds), the crosses and vertical bars indicate the average posterior fluxes and one-standard deviations of the results from 16 models, respectively, and the circles denote the average uncertainties of the posterior fluxes.
The TransCom 3 estimated the global oceanic CO2 uptake to be 1.3 (1.7–2.1), 0.8 (1.2–1.6), 1.4 (1.8–2.2), and 1.1 (1.5–1.9) GtC/yr for 1992–1996, 1980–1989, 1990–1999, and 1980–1999, respectively, and the corresponding terrestrial biospheric CO2 uptake to be 1.3 (0.9–0.5), 1.5 (1.1–0.7), 1.7 (1.3–0.9), and 1.6 (1.2–0.8) GtC/yr. Because the atmospheric inversion method infers only the net flux between the atmosphere and terrestrial biosphere or ocean at a specified time, it is necessary to correct for the riverine transport of carbon from land to oceans. The above numbers in parentheses represent the results corrected by assuming the pre-industrial steady-state fluxes to be 0.4–0.8 GtC/yr.30)
After the TransCom 3 exercise, atmospheric inversions were conducted more extensively not only by enriching the surface data but also by including aircraft or satellite observations, revealing spatiotemporal varying fluxes and changes in the global carbon cycle due to human activities.58,92–100) As mentioned above, TransCom 3 found a large tropical land CO2 source, but such a large source was later found to be in contradiction to the results obtained by Stephens et al.101) Smaller or almost zero emissions were suggested by the recent atmospheric CO2 inverse models with improved transport parameterization and a more advanced data assimilation framework.100) Although atmospheric inversion assumes anthropogenic CO2 emissions to be estimated with sufficient accuracy, their uncertainties have a non-negligible impact on the estimation of the terrestrial biospheric and oceanic fluxes.100,102)
More detailed global carbon budgets were examined by Le Quéré et al.31) for 1960–2017 as part of the Global Carbon Project (https://www.globalcarbonproject.org/). In their study, five components, i.e., the atmospheric CO2 growth rate (Gatm), CO2 emission from fossil fuel consumption/cement production (Eff), CO2 emission from land-use change (Eluc), oceanic CO2 sink (Socean), and terrestrial biospheric CO2 sink (Sland), were evaluated by primarily using the globally averaged surface CO2 data obtained by the NOAA/ESRL/GMD, energy consumption data combined with emission factors/cement production data, bookkeeping models, global ocean biogeochemistry models and dynamic global vegetation models, respectively. They also inspected Eluc and Socean using the global vegetation models and ΔpCO2 observations, respectively, and Socean and Sland using atmospheric inversions. It was found from their results that the CO2 fluxes derived using different methods for each component were close on average to each other, but the respective fluxes had large uncertainties. Their results are summarized in Table 1. Eff increases from 3.1 GtC/yr in 1960–1969 to 9.4 GtC/yr in 2008–2017, whereas Eluc is almost constant at 1.4 GtC/yr, indicating that the recent emissions of anthropogenic CO2 are mainly caused by fossil fuel combustion. The growth rate of atmospheric CO2 (Gatm) increases from 1.7 GtC/yr in 1960–1969 to 4.7 GtC/yr in 2008–2017. The terrestrial biospheric (Sland) and oceanic (Socean) sinks also intensify from 1.2 GtC/yr in 1960–1969 to 3.2 GtC/yr in 2008–2017 and from 1.0 to 2.4 GtC/yr in the corresponding periods, respectively. The global CO2 emissions must be equal to their partitions among the atmosphere, terrestrial biosphere, and ocean, but there is a small imbalance between Eff + Eluc and Gatm + Sland + Socean. Because the uncertainties of Gatm and Eff are small, the budget imbalance is primarily attributed to the model estimates of Eluc, Sland, and Socean.
Table 1.
Global budgets of anthropogenic CO2 estimated by Le Quéré et al.31) for six decadal periods from 1960 to 2017
| Mean (GtC/yr) | ||||||
|---|---|---|---|---|---|---|
| 1960–1969 | 1970–1979 | 1980–1989 | 1990–1999 | 2000–2009 | 2008–2017 | |
| Total emissions (Eff + Eluc) | ||||||
| Fossil CO2 emissions (Eff) | 3.1 ± 0.2 | 4.7 ± 0.2 | 5.4 ± 0.3 | 6.3 ± 0.3 | 7.8 ± 0.4 | 9.4 ± 0.5 |
| Land-use change emissions (Eluc) | 1.5 ± 0.7 | 1.2 ± 0.7 | 1.2 ± 0.7 | 1.4 ± 0.7 | 1.3 ± 0.7 | 1.5 ± 0.7 |
| Total emissions | 4.7 ± 0.7 | 5.8 ± 0.7 | 6.6 ± 0.8 | 7.6 ± 0.8 | 9.0 ± 0.8 | 10.8 ± 0.8 |
| Partitioning | ||||||
| Growth rate in atmospheric CO2 conc. (Gatm) | 1.7 ± 0.07 | 2.8 ± 0.07 | 3.4 ± 0.02 | 3.1 ± 0.02 | 4.0 ± 0.02 | 4.7 ± 0.02 |
| Ocean sink (Socean) | 1.0 ± 0.5 | 1.3 ± 0.5 | 1.7 ± 0.5 | 2.0 ± 0.5 | 2.1 ± 0.5 | 2.4 ± 0.5 |
| Terrestrial sink (Sland) | 1.2 ± 0.5 | 2.1 ± 0.4 | 1.8 ± 0.6 | 2.4 ± 0.5 | 2.7 ± 0.7 | 3.2 ± 0.7 |
| Budget imbalance | ||||||
| Bim = Eff + Eluc − (Gatm + Socean + Sland) | 0.6 | −0.3 | −0.3 | 0.2 | 0.2 | 0.5 |
The zonal mean CO2 fluxes deduced by Le Quéré et al.31) using the atmospheric inversions and process models show different temporal variations depending on the latitude zone. In the northern extratropics (north of 30°N), the atmosphere-to-land/ocean CO2 fluxes gradually increase with time, but the ensemble-mean total fluxes of the process models are lower than the estimates obtained using the inversions, mainly due to the difference in land flux between the two approaches. In the tropics (30°N–30°S), both the process models and inversions indicate that the carbon balance is almost neutral on average for land and ocean, with large year-to-year variability of land flux. In the southern extratropics (south of 30°S), the oceanic CO2 sink is gradually enhanced with time, while the land source and sink are almost balanced, and the oceanic uptake inferred from the atmospheric inversions is slightly higher than that obtained from the process models.
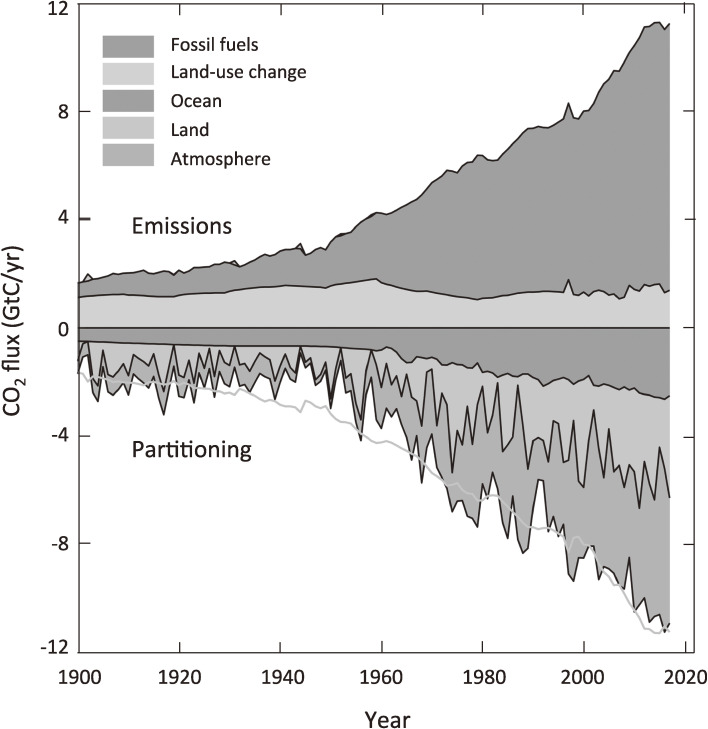
Le Quéré et al.31) reported the global anthropogenic carbon budget for 1750–2017. The five component values before 1960 were estimated using the energy consumption/cement production data for fossil-fuel CO2 emissions, the bookkeeping models for land-use change CO2 emissions, the ice core data for the growth rate of atmospheric CO2, the diagnostic ocean models for the oceanic CO2 uptake, and the global vegetation models for the terrestrial biospheric CO2 uptake. The results obtained are presented in Fig. 11. The fossil-fuel CO2 emissions increased gradually before and rapidly after the Second World War, and the terrestrial biospheric CO2 emissions gradually increased until around 1960 and then gradually decreased toward an almost constant value after 1980. The cumulative CO2 emissions for 1750–2017 are 430 ± 20 GtC for Eff and 235 ± 95 GtC for Eluc, showing a large uncertainty for Eluc. The anthropogenic CO2 is partitioned among the atmosphere (275 ± 5 GtC), terrestrial biosphere (215 ± 50 GtC), and ocean (165 ± 20 GtC), with large uncertainties for the terrestrial and oceanic CO2 uptake. Thus, the cumulative budget imbalance is 10 GtC. If the period is limited to 1850–2017, the budget imbalance increases to 25 GtC. This imbalance is probably due to the overestimation of Eluc and/or underestimation of the terrestrial and oceanic CO2 uptake from the mid-1920s to the mid-1960s because atmospheric CO2 shows no appreciable increase during this period.
Figure 11.
Global carbon budget based on two emissions of fossil fuels and land-use change and three sinks of oceanic uptake, terrestrial biospheric uptake, and atmospheric residue (from top to bottom in the figure) for 1900–2017 (Le Quéré et al.31)). The gray line in the lower panel represents the total emissions, the sign of which is reversed.
4.2. Methane.
By assuming the atmosphere to be one well-mixed box, the global mass balance of atmospheric CH4 can be expressed as
| [2] |
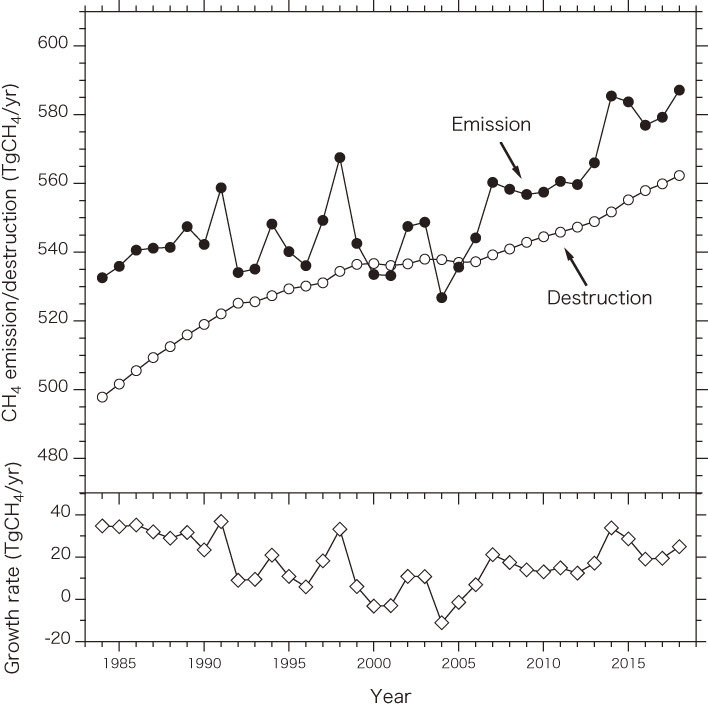
where mCH4 is the average molecular weight of CH4, nair is the number of moles of the atmosphere, CCH4 is the atmospheric CH4 mole fraction, SCH4 is the CH4 emission, and τCH4 is the lifetime of CH4 in the atmosphere. Figure 12 shows the global CH4 emission and destruction calculated for each year from 1984 to 2018 using the NOAA/ESRL/GMD global average CH4 data and the corresponding growth rate of atmospheric CH4 constrained by adopting an atmospheric CH4 lifetime of 9.1 years.34) As mentioned before, the CH4 growth rate gradually declined from around 1990 to the mid-2000s, which means that the global CH4 budget approached a steady state with no CH4 emission trend. The calculated CH4 emissions were almost constant at 542 TgCH4/yr for 1984–2005, and then increased with time until it became 587 TgCH4/yr in 2018. On the other hand, the CH4 destruction increased gradually from 498 TgCH4/yr in 1984 to 562 TgCH4/yr in 2018, and both the CH4 emission and destruction were 537 TgCH4/yr in 2000–2005 when the atmospheric CH4 increase stagnated.
Figure 12.
Global CH4 emission and destruction (upper panel) calculated for each year from 1984 to 2018 and the corresponding growth rate of atmospheric CH4 (lower panel).
Kirschke et al.32) evaluated the atmospheric CH4 lifetime to be 8–10 years by inspecting the results of earlier studies in terms of uncertainty and variability. If 8 and 10 years are employed as the lifetimes, the average CH4 emissions for 1984–2005 are 614 and 495 TgCH4/yr, respectively, with the difference between the two values being as much as 119 TgCH4/yr. This implies that an accurate determination of the CH4 lifetime, i.e., of the atmospheric OH concentration, is extremely crucial to understand the global CH4 budget.
The Global Carbon Project has published two papers to depict a current picture of the global CH4 budget based on the knowledge obtained using the bottom-up and top-down approaches.32,33) In this paper, we mainly discuss the results reported by Saunois et al.33) for 2003–2012 by citing Kirschke et al.32) when necessary. The average global CH4 budget obtained by Saunois et al.33) for 2003–2012 are presented in Table 2 along with that obtained by Kirschke et al.32) for 2000–2009. As can be understood from the maximum and minimum estimates in brackets, there is a considerable amount of uncertainty associated with the mean value reported for each sector. Based on the inventories for fossil fuels, agriculture, wastes, and biomass and biofuel burning, Saunois et al.33) estimated the mean anthropogenic CH4 emissions to be 352 TgCH4/yr for 2003–2012 and 338 TgCH4/yr for 2000–2009 (not shown in the table). The latter value is consistent with the value of 331 TgCH4/yr reported by Kirschke et al.32) for the same period using the same approach. The “agriculture and waste” sector constitutes the largest anthropogenic emission of CH4, followed by “fossil fuels”, with “biomass and biofuel burning” as the lowest contributor. On the other hand, natural CH4 emissions are clearly different between the two studies. Saunois et al.33) estimated the mean natural emissions to be 384 TgCH4/yr for 2003–2012 and 382 TgCH4/yr for 2000–2009, showing very little change in the emission between these two periods. However, their estimates are 10% larger than the value obtained by Kirschke et al.32) for 2000–2009. A large discrepancy between the two studies is found in case of “other natural sources”, resulting from “fresh waters” being grouped into “other land sources”, probably due to the use of different land surface models as well as the prescribed difference in the size of the wetland extent between the two studies. A large discrepancy is also found in “natural wetlands”. The CH4 emissions estimated by Saunois et al.33) for 2003–2012 and 2000–2009 are in good agreement with each other, but their estimates are 15% smaller than the value of Kirschke et al.32) for 2000–2009. With respect to the CH4 sinks, Saunois et al.33) adopted a climatological range, similar to Kirschke et al.32) for 2000–2009. As shown in the table, tropospheric Cl destroys only a small amount of CH4, but it is known that this element considerably affects the interpretation of the observed δ13C of atmospheric CH4 due to the large kinetic isotope effect in the reaction with CH4.103)
Table 2.
Global budgets of CH4 (TgCH4/yr) estimated by Saunois et al.33) for 2003–2012 and Kirschke et al.32) for 2000–2009 using the bottom-up and top-down approaches
| Saunois et al. (2016) Bottom-up | Saunois et al. (2016) Top-down | Kirschke et al. (2013) Bottom-up | Kirschke et al. (2013) Top-down | |
|---|---|---|---|---|
| Period of time | 2003–2012 | 2003–2012 | 2000–2009 | 2000–2009 |
| Natural sources | 384 [257–524] | 231 [194–296] | 347 [238–484] | 218 [179–273] |
| Natural wetlands | 185 [153–227] | 167 [127–202] | 217 [177–284] | 175 [142–208] |
| Other natural sources | 199 [104–297] | 64 [21–132] | 130 [45–232] | 43 [37–65] |
| Other land sources | 185 [99–272] | 112 [43–192] | ||
| Fresh waters | 122 [60–180] | 40 [8–73] | ||
| Geological (onshore) | 40 [30–56] | 36 [15–57] | ||
| Wild animals | 10 [5–15] | 15 [15–15] | ||
| Termites | 9 [3–15] | 11 [2–22] | ||
| Wildfires | 3 [1–5] | 3 [1–5] | ||
| Permafrost soils | 1 [0–1] | 1 [0–1] | ||
| Vegetation | ||||
| Ocean sources | 14 [5–25] | 18 [2–40] | ||
| Geological (offshore) | 12 [5–20] | |||
| Other (including hydrates) | 2 [0–5] | |||
| Anthropogenic sources | 352 [340–360] | 328 [259–370] | 331 [304–368] | 335 [273–409] |
| Agriculture and waste | 195 [178–206] | 188 [115–243] | 200 [187–224] | 209 [180–241] |
| Enteric fermentation & manure | 106 [97–111] | 101 [98–105] | ||
| Landfills & waste | 59 [52–63] | 63 [56–79] | ||
| Rice cultivation | 30 [24–36] | 36 [33–40] | ||
| Fossil fuels | 121 [114–133] | 105 [77–133] | 96 [85–105] | 96 [77–123] |
| Coal mining | 41 [26–50] | |||
| Gas, oil & industry | 79 [69–88] | |||
| Biomass & biofuel burning | 30 [27–35] | 34 [15–53] | 35 [32–39] | 30 [24–45] |
| Biomass burning | 18 [15–21] | |||
| Biofuel burning | 12 [10–14] | |||
| Sinks | ||||
| Total chemical loss | 515 | 604 [483–738] | 518 [510–538] | |
| Tropospheric OH | 528 [454–617] | |||
| Stratospheric loss | 51 [16–84] | |||
| Tropospheric Cl | 25 [13–37] | |||
| Soil uptake | 33 [28–38] | 28 [9–47] | 32 [26–42] | |
| Sum of sources | 736 [596–884] | 558 [540–568] | 678 [542–852] | 553 [526–569] |
| Sum of sinks | 548 | 632 [592–785] | 550 [514–560] | |
| Imbalance | 10 | 3 [−4–19] | ||
| Atmospheric growth | 10.0 [9.4–10.6] | 6 | ||
The top-down estimates by Saunois et al.33) for individual sources were obtained as ensemble averages of multi-atmospheric inversions, wherein the atmospheric lifetime of CH4 was reasonably assumed. The total global CH4 emission was 558 TgCH4/yr for 2003–2012 and 552 TgCH4/yr for 2000–2009. The latter value is very close to the value of 553 TgCH4/yr given by Kirschke et al.32) for the same period, indicating the effectiveness of the flux constraint based on atmospheric observations. However, these top-down estimates are considerably smaller than the high bottom-up value of 736 TgCH4/yr that can be primarily attributed to overestimation by the bottom-up method with no constraint based on atmospheric CH4 measurements. Among the total global CH4 emission for 2003–2012, 60% was allocated to anthropogenic sources, and the remaining 40% was allocated to natural sources. The atmospheric inversion results of 188, 105, and 34 TgCH4/yr for “agriculture and waste”, “fossil fuels”, and “biomass and biofuel burning”, respectively, are statistically consistent with the values obtained using the bottom-up approach. On the other hand, the CH4 emissions from natural sources are considerably different between the two approaches, and the top-down estimate of 231 TgCH4/yr is 60% of the bottom-up value of 384 TgCH4/yr, mainly due to a big discrepancy in the estimates for “other natural sources”. Similar agreement and disagreement between the two approaches are found in Kirschke et al.32)
Saunois et al.33) found that in 2003–2012, 64%, 32%, and 4% of the total global CH4 emissions originated from the tropics and southern latitudes (<30°N), the northern mid-latitudes (30°–60°N), and the northern high latitudes (>60°N), respectively. Majority of the emissions originated from Africa, South America, and South East Asia (73–86 TgCH4/yr), constituting about 44% of the total global emissions. These high-emission regions were then followed by China, central Eurasia and Japan, contiguous U.S.A., Russia, India, and Europe (28–58 TgCH4/yr). The remaining regions emit 7–20 TgCH4/yr of CH4. Saunois et al.33) reported that different CH4 budget estimates were obtained by replacing ground-based observations with satellite-based observations, especially in the tropical region in which surface observations were sparse. This attests to the fact that an extensive observational spatial coverage is crucial for obtaining realistic CH4 fluxes using the inversion approach.
4.3. Nitrous oxide.
To estimate the global N2O budget over the last 40 years, the one-box mass balance equation, i.e.,
| [3] |
is applied to the N2O data shown in Fig. 7. Here, the respective variables have almost the same meaning as the variables in Eq. [2]. The atmospheric lifetime is an essential factor for evaluating the N2O budget. Previous lifetime estimates range from 114 to 131 years, with an associated uncertainty of 10 to 30 years.34,36,39) Here, we employ 120 years as the N2O lifetime, which is widely used in other studies. The results obtained for 1979–2017 show that the atmospheric burden is 1513.7 TgN, the destruction is 12.6 TgN/yr, the atmospheric growth is 3.8 TgN/yr, and the emission is 16.4 TgN/yr. Based on the assumption that the atmospheric mole fraction and lifetime of N2O in the pre-industrial era were 270 ppb and 120 years, respectively, N2O emitted naturally from soils and oceans was calculated to be 10.8 TgN/yr, yielding an anthropogenic N2O emission of 5.6 TgN/yr for 1979–2017. With regard to the N2O lifetime, Prather et al.34) reported the current and pre-industrial (around 1750) values to be 131 and 142 years, respectively. If these lifetime values are used, the N2O destruction and emission for 1979–2017 decrease to 11.6 and 15.4 TgN/yr, respectively, and the natural N2O emission also decreases to 9.1 TgN/yr. Further, the anthropogenic N2O emission increases to 6.3 TgN/yr.
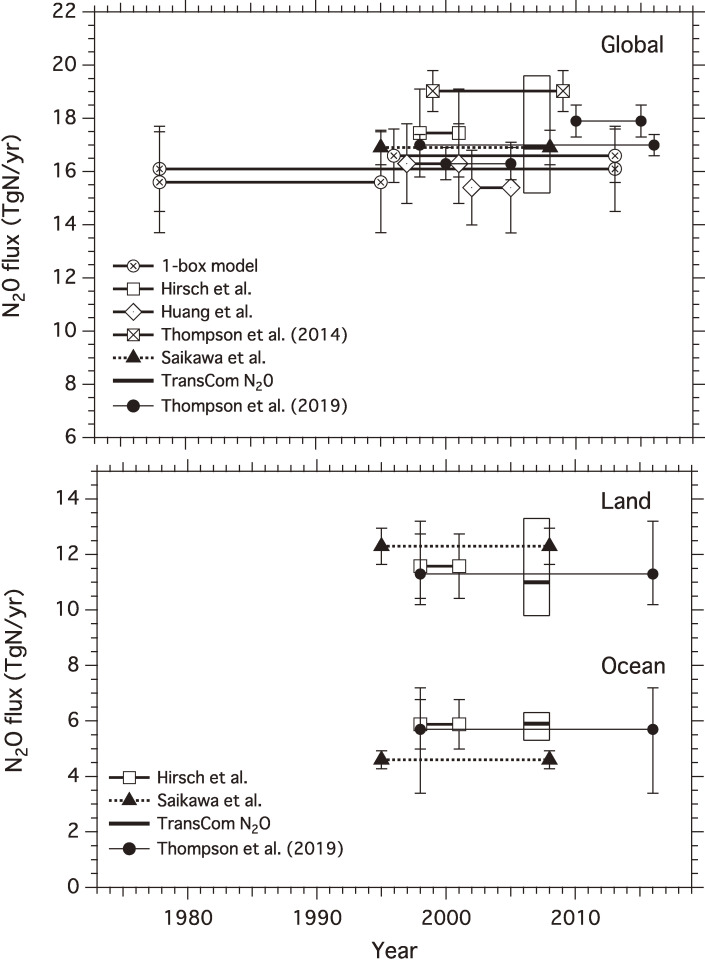
The atmospheric inversion technique was first applied by Hirsch et al.104) and then by Huang et al.,105) Saikawa et al.,106) and Thompson et al.82) In addition to these studies, TransCom N2O intercomparison107) and the analysis proposed by Thompson et al.108) were also conducted using different atmospheric inversion frameworks. The global, land, and ocean N2O fluxes obtained from these atmospheric inversions are shown in Fig. 13 along with the results of the aforementioned one-box model analysis with a lifetime of 120 years. The results obtained from different studies are generally consistent with each other within estimated uncertainties, except for the global N2O fluxes derived by Thompson et al.82) and by one of the participants in TransCom N2O, the values of which are appreciably higher than others. The results of Thompson et al.108) and the one-box model analysis indicate that global N2O emissions increased steadily with time. It is also shown in this figure that the N2O emissions from land are clearly higher than those from the ocean. The results of Hirsch et al.104) and Huang et al.105) allocated 2%, 28%, 50%, and 20% of the total global N2O emissions to 90°–30°S, 30°S–0°, 0°–30°N, and 30°–90°N, respectively, and 7%, 28%, 41%, and 23% were estimated for the corresponding latitude bands by the TransCom N2O intercomparison exercise. These values indicate that the northern tropics and subtropics are most important for N2O emissions, as suggested by the observed latitudinal distribution of atmospheric N2O. The results of the atmospheric inversions show high N2O emissions in East and South Asia, North, South, and Central America, and Africa on land and in the tropical (30°S–30°N) ocean.
Figure 13.
Global, land, and ocean N2O fluxes inferred from atmospheric inversions. The global flux obtained using the one-box mass balance analysis (cf. text) is also shown in the upper panel.
The global N2O budget was quantified using the bottom-up methods.39,109–111) For example, on the basis of the existing bottom-up estimates, Ciais et al.39) reported global N2O budgets for 2006 and the mid-1990s, as shown in Table 3. The 2006 budget indicates that agricultural activities are the strongest anthropogenic sources. The total N2O emissions from “rivers”, “estuaries”, “coastal zone”, and “atmospheric deposition on land and ocean” associated with anthropogenic reactive nitrogen species are also high (1.2 TgN/yr in total), followed by “fossil fuel combustion and industrial processes”, “biomass and biofuel burning”, and “human excreta”. The N2O emissions from agriculture increase from 3.7 TgN/yr in the mid-1990s to 4.1 TgN/yr in 2006, resulting in an increase of 6% with respect to the total global anthropogenic emissions. On the other hand, the natural N2O emissions from “soils under natural vegetation”, “oceans”, and “atmospheric chemistry” (mainly by NH3 oxidation) contribute 60%, 35%, and 5%, respectively, to the global total. The surface sink of N2O is also presented in the table, but its strength is negligibly small. The stratospheric N2O loss is usually inferred using atmospheric chemistry models,35) but a value of 14.3 TgN/yr for “stratospheric sink” in Table 3 was derived by adjusting the model-calculated sinks to become equal to the difference between the total emission and the observed growth rate. If we use this value for the stratospheric sink, then the lifetime of N2O is estimated to be 107 years because the atmospheric N2O burden was 1535 TgN in 2006. This lifetime is slightly shorter than the aforementioned lifetime of 114–131 years. It is likely that the natural and/or anthropogenic N2O emissions are overestimated. Table 3 shows that 6.5–6.9 TgN/yr of N2O has been recently emitted into the atmosphere due to human activities and that 11.0 TgN/yr of N2O has been emitted due to natural causes, with the total being 17.5–17.9 TgN/yr. These values are at the upper end of the results deduced from the abovementioned mass balance analyses and atmospheric inversions. The individual estimates are still rather scattered, and their uncertainties are considerably large. Further studies are required to more accurately infer the global N2O budget.
Table 3.
Global budgets of N2O (TgN/yr) estimated by Ciais et al.39) for 2006 and the mid-1990s
| 2006 | mid-1990s | |
|---|---|---|
| Anthropogenic sources | ||
| Fossil fuel combustion & industrial processes | 0.7 (0.2–1.8) | 0.7 (0.2–1.8) |
| Agriculture | 4.1 (1.7–4.8) | 3.7 (1.7–4.8) |
| Biomass & biofuel burning | 0.7 (0.2–1.0) | 0.7 (0.2–1.0) |
| Human excreta | 0.2 (0.1–0.3) | 0.2 (0.1–0.3) |
| Rivers, estuaries, coastal zones | 0.6 (0.1–2.9) | 0.6 (0.1–2.9) |
| Atmospheric deposition on land | 0.4 (0.3–0.9) | 0.4 (0.3–0.9) |
| Atmospheric deposition on ocean | 0.2 (0.1–0.4) | 0.2 (0.1–0.4) |
| Total anthropogenic sources | 6.9 (2.7–11.1) | 6.5 (2.7–11.1) |
| Natural sources | ||
| Soils under natural vegetation | 6.6 (3.3–9.0) | 6.6 (3.3–9.0) |
| Oceans | 3.8 (1.8–9.4) | 3.8 (1.8–9.4) |
| Atmospheric chemistry | 0.6 (0.3–1.2) | 0.6 (0.3–1.2) |
| Surface sink | −0.01 (0– −1.0) | −0.01 (0– −1.0) |
| Total natural sources | 11.0 (5.5–19.6) | 11.0 (5.4–19.6) |
| Total natural + anthropogenic sources | 17.9 (8.1–30.7) | 17.5 (8.1–30.7) |
| Stratospheric sink | 14.3 (4.3–27.2) | |
| Observed growth rate | 3.6 (3.5–3.8) | |
5. Concluding remarks
The observation of anthropogenic changes in atmospheric greenhouse gases serves as an indicator of the progress of human-induced climate change and is necessary for elucidating their global cycling. Such scientific knowledge forms the basis for formulating and implementing strategies to mitigate the radiatively forced climate change.
The present global network of greenhouse gas observations consists mainly of 100–150 ground-based sites. However, these sites are unevenly distributed in space, with a very limited number of observations in the tropics, such as Africa, South America, and continental interiors. To obtain a detailed picture of the variability of atmospheric greenhouse gases (mole fractions, isotope ratios, and other relevant elements) in space and time, it is important to not only fill in the geographically blank areas in the observation network with additional stations but also perform measurements using aircraft, balloons, and satellites. Because the satellite observations retrieve related variables from spectral radiance, careful validation of the results is indispensable for use along with direct and calibrated measurements. The data thus obtained will contribute to constraining the global budget estimations of anthropogenic greenhouse gases more robustly. They are also useful for developing and validating various types of models, including atmospheric chemistry/transport models, global ocean biogeochemistry models, and dynamic global vegetation models.
It is also important to know the temporal variations of atmospheric greenhouse gases before conducting modern systematic observations. The analysis of the air occluded in the polar ice cores was one of the most promising methods for this purpose. For example, deep Antarctic ice cores revealed that atmospheric CO2, CH4, and N2O fluctuated considerably over the last 800 kyrs, showing interglacial–glacial and interstadial–stadial cycles. The low mole fraction values observed in the glacial periods have been interpreted as an enhancement in the oceanic uptake of CO2 and a reduction in the emissions for CH4 and N2O, but their detailed processes and impact on global climate change are not yet fully understood. The high-resolution variations in atmospheric greenhouse gases over the past 2000 years have also been reconstructed from the air bubbles in polar ice cores drilled at locations with high snow accumulation rates, as well as from the firn air collected from the surface layer of the ice sheet. These data, which include isotope ratios, have been used to estimate the time-dependent emissions and sinks of greenhouse gases. However, to obtain more robust and quantitative knowledge on the global cycling of natural and anthropogenic greenhouse gases and their impact on climate, further detailed analyses using mole fraction and isotope data, climate proxies, and models are required.
Top-down and bottom-up approaches have been adopted to quantify the global budgets of anthropogenic greenhouse gases. In the top-down approach, emission balances the sum of sink and atmospheric growth, but the individual source and sink components are not quantified well. To employ this approach more effectively, it is necessary to reasonably estimate the lifetime of atmospheric greenhouse gases, collect atmospheric observation data from a close-configured station network, and develop well-validated atmospheric chemistry/transport models. For atmospheric inverse modeling, a priori fluxes and uncertainties must be realistically prescribed because posterior fluxes are sensitive to them. In the bottom-up approach, the fluxes of individual sources or sinks can be assessed independently, but their uncertainties are usually quite large, with the exception of fossil-fuel CO2 emissions, and large budget imbalances are often found in the results. Moreover, previous studies have often indicated that source and sink estimates obtained even in a similar way are different depending on individual studies. Thus, it is necessary that the respective approaches are improved and complement each other to achieve accurate budget assessments.
Further studies are needed to understand the response of global and regional source and sink fluxes to future climate change using global biogeochemical models coupled with climate models. To verify the results obtained from such studies, the naturally caused variations in the mole fraction, isotope ratios and other relevant components observed in the atmosphere or reconstructed from the polar ice cores and firn air would be helpful.
Acknowledgements
The author expresses his sincere thanks to Dr. R. F. Keeling (Scripps Institution of Oceanography), Dr. E. J. Dlugokencky (NOAA/ESRL/GMD), Dr. R. G. Prinn (Massachusetts Institute of Technology), and Dr. R. F. Weiss (Scripps Institution of Oceanography) for providing their updated mole fraction data for this paper, and to Ms. A. Okamoto and Dr. S. Nakaoka (National Institutes for Environmental Studies) for their help in preparing Fig. 1.
Profile
Takakiyo Nakazawa was born in 1947 in Shimane Prefecture. He is currently a professor emeritus at Tohoku University, where he has also served on the Faculty of Science/Graduate School of Science as an assistant professor, an associate professor, a professor and a visiting professor. He also served as a visiting researcher at the Scripps Institution of Oceanography, a visiting associate professor at the Institute of Space and Astronautical Science and the National Institute of Polar Research, a leader of the Greenhouse Gases Modeling Group at the Frontier Research Center for Global Change, and a visiting senior scientist of the Environmental Biogeochemical Cycles Research Program at the Japan Agency for Marine-Earth Science and Technology. His work has focused on elucidating the global cycling of greenhouse gases based on observations and modeling, after studying the light absorption properties of the atmospheric components. For these achievements, he was awarded the Award of the Meteorological Society of Japan, Yamazaki Award, Nissan Science Prize, Miyake Award, Shimadzu Award, Medal with Purple Ribbon, and Fujiwhara Award, and he was recognized as a Japan Geoscience Union Fellow.
References
- 1).Petit J.R., Jouzel J., Raynaud D., Barkov N.I., Barnola J.M., Basile I., et al. (1999) Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 399, 429–436. [Google Scholar]
- 2).Kawamura K., Parrenin F., Lisiecki L., Uemura R., Vimeux F., Severinghaus J.P., et al. (2007) Northern Hemisphere forcing of climatic cycles in Antarctica over the past 360,000 years. Nature 448, 912–916. [DOI] [PubMed] [Google Scholar]
- 3).Schilt A., Baumgartner M., Blunier T., Schwander J., Spahni R., Fischer H., et al. (2010) Glacial–interglacial and millennial-scale variations in the atmospheric nitrous oxide concentration during the last 800,000 years. Quat. Sci. Rev. 29, 182–192. [Google Scholar]
- 4).Keeling C.D., Adams J.A.J., Ekdahl C.A.J., Guenther P.R. (1976) Atmospheric carbon dioxide variations at the South Pole. Tellus 28, 552–564. [Google Scholar]
- 5).Keeling C.D., Bacastow R.B., Bainbridge A.E., Ekdahl C.A.J., Guenther P.R., Waterman L.S. (1976) Atmospheric carbon dioxide variations at Mauna Loa Observatory, Hawaii. Tellus 28, 538–551. [Google Scholar]
- 6).Dlugokencky E.J., Steele L.P., Lang P.M., Masarie K.A. (1994) The growth rate and distribution of atmospheric methane. J. Geophys. Res. 99, 17021–17043. [Google Scholar]
- 7).Machida T., Nakazawa T., Fujii Y., Aoki S., Watanabe O. (1995) Increase in the atmospheric nitrous oxide concentration during the last 250 years. Geophys. Res. Lett. 22, 2921–2924. [Google Scholar]
- 8).Prinn R.G., Weiss R.F., Arduini J., Arnold T., DeWitt H.L., Fraser P.J., et al. (2018) History of chemically and radiatively important atmospheric gases from the Advanced Global Atmospheric Gases Experiment (AGAGE). Earth Syst. Sci. Data 10, 985–1018. [Google Scholar]
- 9).Rubino M., Etheridge D.M., Thornton D.P., Howden R., Allison C.E., Francey R.J., et al. (2019) Revised records of CO2, CH4, N2O, and δ13C-CO2 from Law Dome, Antarctica. Earth Syst. Sci. Data 11, 473–492. [Google Scholar]
- 10).IPCC (2013) Summary for policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds. Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J. et al.). Cambridge University Press, Cambridge, United Kingdom and New York, U.S.A., pp. 3–29. [Google Scholar]
- 11).Callendar G.S. (1938) The artificial production of carbon dioxide and its influence on temperature. Q. J. R. Meteorol. Soc. 64, 223–237. [Google Scholar]
- 12).Fraser P.J., Khalil M.A.K., Rasmussen R.A., Crawford A.J. (1981) Trends of atmospheric methane in the Southern Hemisphere. Geophys. Res. Lett. 8, 1063–1066. [Google Scholar]
- 13).Blake D.R., Rowland F.S. (1986) World-wide increase in tropospheric methane, 1978–1983. J. Atmos. Chem. 4, 43–62. [DOI] [PubMed] [Google Scholar]
- 14).Weiss R.F. (1981) The temporal and spatial distribution of tropospheric nitrous oxide. J. Geophys. Res. 86, 7185–7195. [Google Scholar]
- 15).Elkins J.W., Thompson T.M., Swanson T.H., Butler J.H., Hall B.D., Cummings S.O., et al. (1993) Decrease in the growth rates of atmospheric chlorofluorocarbons 11 and 12. Nature 364, 780–783. [Google Scholar]
- 16).Nakazawa T., Morimoto S., Aoki S., Tanaka T. (1993) Time and space variations of the carbon isotopic ratio of tropospheric carbon dioxide over Japan. Tellus B 45, 258–274. [Google Scholar]
- 17).Nakazawa T., Morimoto S., Aoki S., Tanaka M. (1997) Temporal and spatial variations of the carbon isotopic ratio of atmospheric carbon dioxide in the western Pacific region. J. Geophys. Res. 102, 1271–1285. [Google Scholar]
- 18).Nakazawa T., Aoki S., Kawamura K., Saeki T., Sugawara S., Honda H., et al. (2002) Variations of stratospheric trace gases measured using a balloon-borne cryogenic sampler. Adv. Space Res. 30, 1349–1357. [Google Scholar]
- 19).Machida T., Matsueda H., Sawa Y., Nakagawa Y., Hirotani H., Kondo N., et al. (2008) Worldwide measurements of atmospheric CO2 and other trace gas species using commercial airlines. J. Atmos. Ocean. Technol. 25, 1744–1754. [Google Scholar]
- 20).Ishijima K., Nakazawa T., Aoki S. (2009) Variations of atmospheric nitrous oxide concentration in the northern and western Pacific. Tellus B 61, 408–415. [Google Scholar]
- 21).Yokota T., Yoshida Y., Eguchi N., Ota Y., Tanaka T., Watanabe H., et al. (2009) Global concentrations of CO2 and CH4 retrieved from GOSAT: First preliminary results. Sci. Online Lett. Atmos. 5, 160–163. [Google Scholar]
- 22).Eldering A., O’Dell C.W., Wennberg P.O., Crisp D., Gunson M.R., Viatte C., et al. (2017) The Orbiting Carbon Observatory-2: First 18 months of science data products. Atmos. Meas. Tech. 10, 549–563. [Google Scholar]
- 23).Neftel A., Oeschger H., Schwander J., Stauffer B., Zumbrunn R. (1982) Ice core sample measurements give atmospheric CO2 content during the past 40,000 yr. Nature 295, 220–223. [Google Scholar]
- 24).Revell R., Suess H.E. (1957) Carbon dioxide exchange between atmosphere and ocean and the question of an increase of atmospheric CO2 during the past decades. Tellus 9, 18–27. [Google Scholar]
- 25).Keeling, C.D., Piper, S.C. and Heimann, M. (1989) A three dimensional model of atmospheric CO2 transport based on observed winds: 4. Mean annual gradients and interannual variations. In Aspects of Climate Variability in the Pacific and the Western Americas (ed. Peterson, D.H.). American Geophysical Union, Washington, D.C., pp. 305–363. [Google Scholar]
- 26).Tans P.P., Conway T.J., Nakazawa T. (1989) Latitudinal distribution of the sources and sinks of atmospheric carbon dioxide from surface observations and an atmospheric transport model. J. Geophys. Res. 94, 5151–5172. [Google Scholar]
- 27).Ehhalt D.H. (1974) Atmospheric cycle of methane. Tellus 26, 58–70. [Google Scholar]
- 28).Fung I., John J., Lerner J., Matthews E., Prather M., Steele L.P., et al. (1991) Three-dimensional model synthesis of the global methane cycle. J. Geophys. Res. 96, 13033–13065. [Google Scholar]
- 29).Bouwman A.F., Taylor J.A. (1996) Testing high-resolution nitrous oxide emission estimates against observations using an atmospheric transport model. Global Biogeochem. Cycles 10, 307–318. [Google Scholar]
- 30).Resplandy L., Keeling R.F., Rodenbeck C., Stephens B.B., Khatiwala S., Rodgers K.B., et al. (2018) Revision of global carbon fluxes based on a reassessment of oceanic and riverine carbon transport. Nat. Geosci. 11, 504–509. [Google Scholar]
- 31).Le Quéré C., Andrew R.M., Friedlingstein P., Sitch S., Hauck J., Pongratz J., et al. (2018) Global carbon budget 2018. Earth Syst. Sci. Data 10, 1–54. [Google Scholar]
- 32).Kirschke S., Bousquet P., Ciais P., Saunois M., Canadell J.G., Dlugokencky E.J., et al. (2013) Three decades of global methane sources and sinks. Nat. Geosci. 6, 813–823. [Google Scholar]
- 33).Saunois M., Bousquet P., Poulter B., Peregon A., Ciais P., Canadell J.G., et al. (2016) The global methane budget 2000–2012. Earth Syst. Sci. Data 8, 697–751. [Google Scholar]
- 34).Prather M.J., Holmes C.D., Hsu J. (2012) Reactive greenhouse gas scenarios: Systematic exploration of uncertainties and the role of atmospheric chemistry. Geophys. Res. Lett. 39, L09803. [Google Scholar]
- 35).Minschwaner K., Salawitch R.J., McElroy M.B. (1993) Absorption of solar radiation by O2: Implications for O3 and lifetimes of N2O, CFCl3 and CF2Cl2. J. Geophys. Res. 98, 10543–10561. [Google Scholar]
- 36).Volk C.M., Elkins J.W., Fahey D.W., Dutton G.S., Gilligan J.M., Loewenstein M., et al. (1997) Evaluation of source gas lifetimes from stratospheric observations. J. Geophys. Res. 102, 25543–25564. [Google Scholar]
- 37).Kaiser J., Rockmann T., Brenninkmeijer C.A.M., Crutzen P.J. (2003) Wavelength dependence of isotope fractionation in N2O photolysis. Atmos. Chem. Phys. 3, 303–313. [Google Scholar]
- 38).Wrage N., Velthof G.L., van Beusichem M.L., Oenema O. (2001) Role of nitrifier denitrification in the production of nitrous oxide. Soil Biol. Biochem. 33, 1723–1732. [Google Scholar]
- 39).Ciais, P., Sabine, C., Bala, G., Bopp, L., Brovkin, V., Canadell, J. et al. (2013) Carbon and other biogeochemical cycles. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds. Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J. et al.). Cambridge University Press, Cambridge, United Kingdom and New York, NY, U.S.A., pp. 465–570. [Google Scholar]
- 40).Curry W.B., Duplessy J.C., Labeyrie L.D., Shackleton N.J. (1988) Changes in the distribution of δ13C of deep water ΣCO2 between the last glaciation and the Holocene. Paleoceanography 3, 317–341. [Google Scholar]
- 41).Broecker W.S. (1982) Ocean chemistry during glacial time. Geochim. Cosmochim. Acta 46, 1689–1705. [Google Scholar]
- 42).Sigman D.M., Boyle E.A. (2000) Glacial/interglacial variations in atmospheric carbon dioxide. Nature 407, 859–869. [DOI] [PubMed] [Google Scholar]
- 43).Kohfeld, K.E. and Ridgwell, A. (2009) Glacial-interglacial variability in atmospheric CO2 In Surface Ocean-Lower Atmosphere Processes (eds. Le Quéré, C. and Saltzman, E.S.). American Geophysical Union, Washington, D.C., pp. 251–286. [Google Scholar]
- 44).Sigman D.M., Hain H.P., Haug G.H. (2010) The polar ocean and glacial cycles in atmospheric CO2 concentration. Nature 466, 47–55. [DOI] [PubMed] [Google Scholar]
- 45).Martin J.H. (1990) Glacial-interglacial CO2 change: The iron hypothesis. Paleoceanography 5, 1–13. [Google Scholar]
- 46).Stephens B.B., Keeling R.F. (2000) The influence of Antarctic sea ice on glacial-interglacial CO2 variations. Nature 404, 171–174. [DOI] [PubMed] [Google Scholar]
- 47).Archer D.E., Martin P.A., Milovich J., Brovkin V., Plattner G.-K., Ashendel C. (2003) Model sensitivity in the effect of Antarctic sea ice and stratification on atmospheric pCO2. Paleoceanography 18, 1012. [Google Scholar]
- 48).Levine J.G., Wolff E.W., Jones A.E., Sime L.C., Valdes P.J., Archibald A.T., et al. (2011) Reconciling the changes in atmospheric methane sources and sinks between the Last Glacial Maximum and the pre-industrial era. Geophys. Res. Lett. 38, L23804. [Google Scholar]
- 49).Murray L.T., Mickley L.J., Kaplan J.O., Sofen E.D., Pfeiffer M., Alexander B. (2014) Factors controlling variability in the oxidative capacity of the troposphere since the Last Glacial Maximum. Atmos. Chem. Phys. 14, 3589–3622. [Google Scholar]
- 50).Chappellaz J.A., Fung I.Y., Thompson A.M. (1993) The atmospheric CH4 increase since the Last Glacial Maximum; (1) source estimates. Tellus B 45, 228–241. [Google Scholar]
- 51).Weber S.L., Drury A.J., Toonen W.H.J., van Weele M. (2010) Wetland methane emissions during the Last Glacial Maximum estimated from PMIP2 simulations: Climate, vegetation, and geographic controls. J. Geophys. Res. 115, D06111. [Google Scholar]
- 52).Crutzen P.J., Brühl C. (1993) A model study of atmospheric temperatures and the concentrations of ozone, hydroxyl, and some other photochemically active gases during the glacial, the pre-industrial Holocene and the present. Geophys. Res. Lett. 20, 1047–1050. [Google Scholar]
- 53).Martinerie P., Brasseur G.P., Granier C. (1995) The chemical composition of ancient atmospheres: A model study constrained by ice core data. J. Geophys. Res. 100, 14291–14304. [Google Scholar]
- 54).Sowers T., Alley R.B., Jubenville J. (2003) Ice core records of atmospheric N2O covering the last 106,000 years. Science 301, 945–948. [DOI] [PubMed] [Google Scholar]
- 55).Schilt A., Brook E.J., Bauska T.K., Baggenstos D., Fischer H., Joos F., et al. (2014) Isotopic constraints on marine and terrestrial N2O emissions during the last deglaciation. Nature 516, 234–237. [DOI] [PubMed] [Google Scholar]
- 56).Keeling, C.D., Piper, S.C., Bacastow, R.B., Wahlen, M., Whorf, T.P., Heimann, M. et al. (2005) Atmospheric CO2 and 13CO2 exchange with the terrestrial biosphere and oceans from 1978 to 2000: Observations and carbon cycle implications. In A History of Atmospheric CO2 and Its Effects on Plants, Animals, and Ecosystems (eds. Ehleringer, J.R., Cerling, T.E. and Dearing, M.D.). Springer Verlag, New York, pp. 83–113. [Google Scholar]
- 57).Nakazawa T., Ishizawa M., Higuchi K., Trivett N.B.A. (1997) Two curve fitting methods applied to CO2 flask data. Environmetrics 8, 197–218. [Google Scholar]
- 58).Patra P.K., Maksyutov S., Ishizawa M., Nakazawa T., Takahashi T., Ukita J. (2005) Interannual and decadal changes in the sea-air CO2 flux from atmospheric CO2 inverse modeling. Global Biogeochem. Cycles 19, GB4013. [Google Scholar]
- 59).Rödenbeck C., Bakker D.C.E., Metzl N., Olsen A., Sabine C., Cassar N., et al. (2014) Interannual sea-air CO2 flux variability from an observation-driven ocean mixed-layer scheme. Biogeosciences 11, 4599–4613. [Google Scholar]
- 60).Nakazawa, T., Machida, T., Tanaka, M., Fujii, Y., Aoki, S. and Watanabe, K. (1993) Atmospheric CO2 concentrations and carbon isotopic ratios for the last 250 years deduced from an Antarctic ice core, H15. In Proceedings of the 4th International Carbon Dioxide Conference. World Meteorological Organization, WMO/TD NO-361, Geneva, pp. 193–196. [Google Scholar]
- 61).Machida, T., Nakazawa, T., Tanaka, M., Fujii, Y., Aoki, S. and Watanabe, O. (1994) Atmospheric CH4 and N2O concentrations during the last 250 years deduced from H15 ice core, Antarctica. In Proceedings of the 5th International Symposium on Global Cycles of Atmospheric Greenhouse Gases, Sendai, pp. 113–116. [Google Scholar]
- 62).Francey R.J., Allison C.E., Etheridge D.M., Trudinger C.M., Enting I.G., Leuenberger M., et al. (1999) A 1000-year high precision record of δ13C in atmospheric CO2. Tellus B 51, 170–193. [Google Scholar]
- 63).Graven H., Allison C.E., Etheridge D.M., Hammer S., Keeling R.F., Levin I., et al. (2017) Compiled records of carbon isotopes in atmospheric CO2 for historical simulations in CMIP6. Geosci. Model Dev. 10, 4405–4417. [Google Scholar]
- 64).Nakazawa T., Machida T., Tanaka M., Fujii Y., Aoki S., Watanabe O. (1993) Differences of the atmospheric CH4 concentration between the Arctic and Antarctic regions in pre-industrial/pre-agricultural era. Geophys. Res. Lett. 20, 943–946. [Google Scholar]
- 65).Chappellaz J., Blunier T., Kints S., Daellenbach A., Barnola J.-M., Schwander J., et al. (1997) Changes in the atmospheric CH4 gradient between Greenland and Antarctica during the Holocene. J. Geophys. Res. 102, 15987–15997. [Google Scholar]
- 66).Hodson E.L., Poulter B., Zimmermann N.E., Prigent C., Kaplan J.O. (2011) The El Niño-Southern Oscillation and wetland methane interannual variability. Geophys. Res. Lett. 38, L08810. [Google Scholar]
- 67).Worden J., Jiang Z., Jones D.B.A., Alvarado M., Bowman K., Frankenberg C., et al. (2013) El Niño, the 2006 Indonesian peat fires, and the distribution of atmospheric methane. Geophys. Res. Lett. 40, 4938–4943. [Google Scholar]
- 68).Dlugokencky E.J., Masarie K.A., Lang P.M., Tans P.P. (1998) Continuing decline in the growth rate of the atmospheric methane burden. Nature 393, 447–450. [Google Scholar]
- 69).Dlugokencky E.J., Houweling S., Bruhwiler L., Masarie K.A., Steele L.P., Miller J.B., et al. (2003) Atmospheric methane levels off: Temporary pause or a new steady-state? Geophys. Res. Lett. 30, 1992. [Google Scholar]
- 70).Bousquet P., Ciais P., Miller J.B., Dlugokencky E.J., Hauglutaine D.A., Prigent C., et al. (2006) Contribution of anthropogenic and natural sources to atmospheric methane variability. Nature 443, 439–443. [DOI] [PubMed] [Google Scholar]
- 71).Nisbet E.G., Dlugokencky E.J., Manning M.R., Lowry D., Fisher R.E., France J.L., et al. (2016) Rising atmospheric methane: 2007–2014 growth and isotopic shift. Global Biogeochem. Cycles 30, 1356–1370. [Google Scholar]
- 72).Morimoto S., Fujita R., Aoki S., Goto D., Nakazawa T. (2017) Long-term variations of the mole fraction and carbon isotope ratio of atmospheric methane observed at Ny-Ålesund, Svalbard from 1996 to 2013. Tellus B 69, 1380497. [Google Scholar]
- 73).Patra P.K., Saeki T., Dlugokencky E.J., Ishijima K., Umezawa T., Ito A., et al. (2016) Regional methane emission estimation based on observed atmospheric concentrations (2002–2012). J. Meteorol. Soc. Jpn. 94, 91–113. [Google Scholar]
- 74).Rigby M., Montzka S.A., Prinn R.G., White J.W.C., Young D., O’Doherty S., et al. (2017) Role of atmospheric oxidation in recent methane growth. Proc. Natl. Acad. Sci. U.S.A. 114, 5373–5377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75).Turner A.J., Frankenberg C., Wennberg P.O., Jacob D.J. (2017) Ambiguity in the causes for decadal trends in atmospheric methane and hydroxyl. Proc. Natl. Acad. Sci. U.S.A. 114, 5367–5372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76).Thompson R.L., Nisbet E.G., Pisso I., Stohl A., Blake D., Dlugokencky E.J., et al. (2018) Variability in atmospheric methane from fossil fuel and microbial sources over the last three decades. Geophys. Res. Lett. 45, 11499–11508. [Google Scholar]
- 77).Naus S., Montzka S.A., Pandey S., Basu S., Dlugokencky E.J., Krol M. (2019) Constraints and biases in a tropospheric two-box model of OH. Atmos. Chem. Phys. 19, 407–424. [Google Scholar]
- 78).Lelieveld J., Dentener F.J., Peters W., Krol M.C. (2004) On the role of hydroxyl radicals in the self-cleansing capacity of the troposphere. Atmos. Chem. Phys. 4, 2337–2344. [Google Scholar]
- 79).Voulgarakis A., Naik V., Lamarque J.-F., Shindell D.T., Young P.J., Prather M.J., et al. (2013) Analysis of present day and future OH and methane lifetime in the ACCMIP simulations. Atmos. Chem. Phys. 13, 2563–2587. [Google Scholar]
- 80).Nevison C.D., Dlugokencky E., Dutton G., Elkins J.W., Fraser P., Hall B., et al. (2011) Exploring causes of interannual variability in the seasonal cycles of tropospheric nitrous oxide. Atmos. Chem. Phys. 11, 3713–3730. [Google Scholar]
- 81).Saikawa E., Schlosser C.A., Prinn R.G. (2013) Global modeling of soil nitrous oxide emissions from natural processes. Global Biogeochem. Cycles 27, 972–989. [Google Scholar]
- 82).Thompson R.L., Chevallier F., Crotwell A.M., Dutton G., Langenfelds R.L., Prinn R.G., et al. (2014) Nitrous oxide emissions 1999 to 2009 from a global atmospheric inversion. Atmos. Chem. Phys. 14, 1801–1817. [Google Scholar]
- 83).Kondo M., Patra P.K., Sitch S., Friedlingstein P., Poulter B., Chevallier F., et al. (2020) State of the science in reconciling top-down and bottom-up approaches for terrestrial CO2 budget. Glob. Change Biol. 26, 1068–1084. [DOI] [PubMed] [Google Scholar]
- 84).Francey R.J., Tans P.P., Allison C.E., Enting I.G., White J.W.C., Trolier M. (1995) Changes in oceanic and terrestrial carbon uptake since 1982. Nature 373, 326–330. [Google Scholar]
- 85).Goto D., Morimoto S., Ishidoya S., Aoki S., Nakazawa T. (2017) Terrestrial biospheric and oceanic CO2 uptake estimated from long-term measurements of atmospheric CO2 mole fraction, δ13C and δ(O2/N2) at Ny-Ålesund, Svalbard. J. Geophys. Res. Biogeosci. 122, 1192–1202. [Google Scholar]
- 86).Keeling R.F., Shertz S.R. (1992) Seasonal and interannual variations in atmospheric oxygen and implications for the global carbon cycle. Nature 358, 723–727. [Google Scholar]
- 87).Tohjima Y., Mukai H., Nojiri Y.U., Yamagishi H., Machida T. (2008) Atmospheric O2/N2 measurements at two Japanese sites: Estimation of global oceanic and land biotic carbon sinks and analysis of the variations in atmospheric potential oxygen (APO). Tellus B 60, 213–225. [Google Scholar]
- 88).Tohjima Y., Mukai H., Machida T., Hoshina Y., Nakaoka S. (2019) Global carbon budgets estimated from atmospheric O2/N2 and CO2 observations in the western Pacific region over a 15-year period. Atmos. Chem. Phys. 19, 9269–9285. [Google Scholar]
- 89).Ishidoya S., Aoki S., Goto D., Nakazawa T., Taguchi S., Patra P.K. (2012) Time and space variations of the O2/N2 ratio in the troposphere over Japan and estimation of global CO2 budget. Tellus B 64, 18964. [Google Scholar]
- 90).Keeling, R.F. and Manning, A.C. (2014) Studies of recent changes in atmospheric O2 content. In Treatise on Geochemistry (Second Edition) (eds. Holland, H.D. and Turekian, K.K.). Elsevier, Amsterdam, Vol. 5, pp. 385–404. [Google Scholar]
- 91).Gurney K.R., Law R.M., Denning A.S., Rayner P.J., Baker D., Bousquet P., et al. (2002) Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models. Nature 415, 626–630. [DOI] [PubMed] [Google Scholar]
- 92).Chevallier F., Fisher M., Peylin P., Serrar S., Bousquet P., Bréon F.-M., et al. (2005) Inferring CO2 sources and sinks from satellite observations. Method and application to TOVS data. J. Geophys. Res. 110, D24309. [Google Scholar]
- 93).Chevallier F., Ciais P., Conway T.J., Aalto T., Anderson B.E., Bousquet P., et al. (2010) CO2 surface fluxes at grid point scale estimated from a global 21 year reanalysis of atmospheric measurements. J. Geophys. Res. 115, D21307. [Google Scholar]
- 94).Patra P.K., Maksyutov S., Ishizawa M., Nakazawa T., Inoue G. (2005) Role of biomass burning and climate anomalies for land-atmosphere carbon fluxes based on inverse modeling of atmospheric CO2. Global Biogeochem. Cycles 19, GB3005. [Google Scholar]
- 95).Le Quéré C., Rödenbeck C., Buitenhuis E.T., Conway T.J., Langenfelds R., Gomez A., et al. (2007) Saturation of the Southern Ocean CO2 sink due to recent climate change. Science 316, 1735–1738. [DOI] [PubMed] [Google Scholar]
- 96).Peylin P., Law R.M., Gurney K.R., Chevallier F., Jacobson A.R., Maki T., et al. (2013) Global atmospheric carbon budget: Results from an ensemble of atmospheric CO2 inversions. Biogeosciences 10, 6699–6720. [Google Scholar]
- 97).Saeki T., Maksyutov S., Saito M., Valsala V., Oda T., Andres R.J., et al. (2013) Inverse modeling of CO2 fluxes using GOSAT data and multi-year ground-based observations. Sci. Online Lett. Atmos. 9, 45–50. [Google Scholar]
- 98).van der Laan-Luijkx I.T., van der Velde I.R., van der Veen E., Tsuruta A., Stanislawska K., Babenhauserheide A., et al. (2017) The CarbonTracker Data Assimilation Shell (CTDAS) v1.0: Implementation and global carbon balance 2001–2015. Geosci. Model Dev. 10, 2785–2800. [Google Scholar]
- 99).Palmer P.I., Feng L., Baker D., Chevallier F., Bösch H., Somkuti P. (2019) Net carbon emissions from African biosphere dominate pan-tropical atmospheric CO2 signal. Nat. Commun. 10, 3344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100).Gaubert B., Stephens B.B., Basu S., Chevallier F., Deng F., Kort E.A., et al. (2019) Global atmospheric CO2 inverse models converging on neutral tropical land exchange, but disagreeing on fossil fuel and atmospheric growth rate. Biogeosciences 16, 117–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101).Stephens B.B., Gurney K.R., Tans P.P., Sweeney C., Peters W., Bruhwiler L., et al. (2007) Weak northern and strong tropical land carbon uptake from vertical profiles of atmospheric CO2. Science 316, 1732–1735. [DOI] [PubMed] [Google Scholar]
- 102).Saeki T., Patra P.K. (2017) Implications of overestimated anthropogenic CO2 emissions on East Asian and global land CO2 flux inversion. Geosci. Lett. 4, 9. [Google Scholar]
- 103).Fujita R., Morimoto S., Maksyutov S., Kim H.-S., Arshinov M., Brailsford G., et al. (2020) Global and regional CH4 emissions for 1995–2013 derived from atmospheric CH4, δ13C-CH4, and δD-CH4, observations and a chemical transport model. J. Geophys. Res. 125, e2020JD032903. [Google Scholar]
- 104).Hirsch A.I., Michalak A.M., Bruhwiler L.M., Peters W., Dlugokencky E.D., Tans P.P. (2006) Inverse modeling estimates of the global nitrous oxide surface flux from 1998–2001. Global Biogeochem. Cycles 20, GB1008. [Google Scholar]
- 105).Huang J., Golombeck A., Prinn R., Weiss R., Fraser P., Simmonds P., et al. (2008) Estimation of regional emissions of nitrous oxide from 1997 to 2005 using multinetwork measurements, a chemical transport model, and an inverse method. J. Geophys. Res. 113, D17313. [Google Scholar]
- 106).Saikawa E., Prinn R.G., Dlugokencky E., Ishijima K., Dutton G.S., Hall B.D., et al. (2014) Global and regional emissions estimates for N2O. Atmos. Chem. Phys. 14, 4617–4641. [Google Scholar]
- 107).Thompson R.L., Ishijima K., Saikawa E., Corazza M., Karstens U., Patra P.K., et al. (2014) TransCom N2O model inter-comparison, Part II: Atmospheric inversion estimates of N2O emissions. Atmos. Chem. Phys. 14, 6177–6194. [Google Scholar]
- 108).Thompson R.L., Lassaletta L., Patra P.K., Wilson C., Wells K.C., Gressent A., et al. (2019) Acceleration of global N2O emissions seen from two decades of atmospheric inversion. Nat. Clim. Chang. 9, 993–998. [Google Scholar]
- 109).Sykila A., Kroeze C. (2011) The global nitrous oxide budget revisited. Greenh. Gas Meas. Manage. 1, 17–26. [Google Scholar]
- 110).Davidson E.A., Kanter D. (2014) Inventories and scenarios of nitrous oxide emissions. Environ. Res. Lett. 9, 105012. [Google Scholar]
- 111).Tian H., Yang J., Lu C., Xu R., Canadell J.G., Jackson R., et al. (2018) The global N2O Model Intercomparison Project (NMIP): Objectives, simulation protocol and expected products. Bull. Am. Meteorol. Soc. 99, 1231–1251. [Google Scholar]